Abstract
Nonlinear model predictive control has been established as a powerful methodology to provide feedback for dynamic processes over the last decades. In practice it is usually combined with parameter and state estimation techniques, which allows to cope with uncertainty on many levels. To reduce the uncertainty it has also been suggested to include optimal experimental design into the sequential process of estimation and control calculation. Most of the focus so far was on dual control approaches, i.e., on using the controls to simultaneously excite the system dynamics (learning) as well as minimizing a given objective (performing). We propose a new algorithm, which sequentially solves robust optimal control, optimal experimental design, state and parameter estimation problems. Thus, we decouple the control and the experimental design problems. This has the advantages that we can analyze the impact of measurement timing (sampling) independently, and is practically relevant for applications with either an ethical limitation on system excitation (e.g., chemotherapy treatment) or the need for fast feedback. The algorithm shows promising results with a reduction of parameter uncertainties for the Lotka-Volterra fishing benchmark example.
1. Introduction
We start by surveying recent progress of feedback via nonlinear optimal control under uncertainty, before we come to the main contribution of this paper, an investigation of the role of the measurement time grid. This can be seen as complementary and can be combined with almost all other aspects of efficient nonlinear model predictive control.
We are interested in controlling a dynamic process in an optimal way, under the assumption that model parameters are unknown. We assume that there are no systematic uncertainties, i.e., that the mathematical model represents the dynamics of the process sufficiently well and all measurement errors are normally distributed. One possible control task is controlling a dynamic system from an undesired cyclic steady state to a desired one in an optimal way. Such tasks arise in a large variety of applications in biology, chemistry, mechanics and medicine.
The dynamic system is described as a system of differential equations that involves a priori unknown model parameters. To cope with the uncertainty, optimization problems are solved on short time horizons, and new measurements are used to update the model parameters and thus the mathematical model as such. The feedback is calculated via model predictive control (MPC), an established method applicable for linear [1] as well as nonlinear models (NMPC) [2]. MPC is based on the assumption that new measurements arrive continuously, thus allowing an optimal feedback control that can be applied online. NMPC is in practice often combined with moving horizon estimation (MHE), or estimation on an expanding time horizon, which allow an update of state and parameter estimates based on new measurements [3].
NMPC and MHE are based on the calculation of optimal trajectories. As a fast feedback of the controller is important in many applications, clever approaches doing most of the necessary calculations before a new measurement arrives have been proposed in the literature. The most important numerical concepts comprise real-time iterations [4,5], multi-level iterations [6], parallel multi-level iterations [7], an exploitation of the KKT structures [8,9], adaptive control [10], automatic code export [11,12], and usage of parametric QPs [13,14]. For a benchmark problem, the continuously stirred tank reactor of [15], a speedup of approximately 150,000 has been achieved comparing the 60 seconds per iteration reported in 1997 [16] and the 400 microseconds per iteration reported in 2011 by [17]. This speedup is mainly due to the faster algorithms and only partially due to the hardware speedup. Surveys on efficient numerical approaches to NMPC and MHE can be found in, e.g., [7,18,19,20].
The state and parameter solutions of the maximum likelihood estimation problems are random variables, and are hence endowed with confidence regions. How the process is controlled and when and what is being measured have an important impact on the size of these confidence regions. Optimal experimental design (OED) is concerned with calculating controls and sampling decisions that minimize the size of the confidence regions of the state and parameter estimates. This special control problem is analyzed from a statistical and numerical point of view in several textbooks [21,22,23,24] and became a state of the art method in designing experiments in many fields of application. Also a lot of research has been done in sequential optimal experimental design (re-design of experiments) where iteratively optimal experimental designs are performed and parameters are estimated [25,26]. In the last decade, sequential OED has been extended by online OED in which the experiment is directly re-designed when a new measurement is taken [27,28,29,30,31].
Our algorithm is related in the spirit of dual control [32,33,34], as we want to learn model parameters at the same time as we are using them for NMPC. Note that for medical applications the situation is completely different than from industrial chemical engineering. In the latter mathematical modeling, experimental design, model calibration and analysis are typically performed beforehand with pilot plants, and the results are then transferred in a second stage such that NMPC can be applied over and over again to continuous or batch processes. For biological and medical applications a repetition is not possible, e.g., a chemotherapy treatment can only be performed once under identical conditions.
Recently, different economic objective functions have been proposed that incorporate the nested goals of excitation and exploration [35,36,37]. Also scenario trees [38,39] and set-based approaches [40] have been successfully applied.
In all mentioned publications the focus is on the control function, with an implicit assumption that measurements are available on a given sampling time grid. While this assumption is true for many applications in which sensors are routinely used, the situation is different in biological and medical applications, where measurements are often invasive and imply logistical, ethical, and financial overhead. In [41] we showed the large impact of optimal sampling on uncertainty reduction for patients suffering from acute myeloid leukemia. Uncertainty could be reduced by more than 50% by choosing the time points different from the standard daily routine, in an a posteriori analysis.
This motivates us to concentrate on the question of the optimal timing of measurements in a real-time algorithm. We propose a new feedback optimal control algorithm with sampling time points for the parameter and state estimation from the solution of an optimal experimental design problem. In our setting the control is assumed to be fixed for the experimental design problem, i.e., we do not excite the dynamics for the sake of information gain. Instead, we focus on determining the optimal measuring (sampling) times. The motivation considering the control as fixed for the experimental design problem is practically motivated by applications such as fishing or chemotherapy dosage in which there is an ethical, logistical, or financial reluctance to profit only indirectly from a system excitation. This decoupling may also be interesting for a different kind of applications for which fast feedback is necessary, as it results in a very efficient way to calculate the optimal sampling points.
Note that the question of optimal sampling of measurements is to a large extent independent from most of the aforementioned approaches to NMPC. Our approach is complementary in the sense that, e.g., the numerical structure exploitation, the treatment of systematic disturbances, the treatment of robustness, the formulation of dual control objective functions, the use of scenario trees or set-based approaches can all be combined with an adaptive measurement grid. This also applies to the nature of the underlying control task, where many extensions are possible, e.g., multi-stage processes, mixed path- and control constraints, complicated boundary conditions and so on. In the interest of a clear focus on our main results we choose a simple setting that allows to highlight the additional value of measurement grid adaptivity, and only show exemplarily the impact of one possible extension of our algorithm. We take the uncertainty with respect to model parameters into account on the level of optimal control and of the experimental design by calculating robust optimal controls and samplings, compare [42,43], and compare our new algorithm based on nominal solutions with the new algorithm with robust solutions.
Numerical results demonstrating the performance of the algorithm and underlying the theoretical finding are presented for the benchmark example called Lotka-Volterra fishing problem. This example is particularly suited for several reasons. First, it is prototypical for many biological, chemical, and medical processes as it captures the most basic dynamic behavior of oscillatory systems. Second, for fishing systems our basic assumption of a slow process with expensive measurements applies and processes related to sustainable fishing have been receiving increasing attention lately, e.g., [44,45]. Third, it has a prototypical objective for many medical applications, as we want to control from an undesired cyclic steady state to a desired steady state. Fourth, it is simple and small enough to visualize the impact of our approach in terms of uncertainty quantification and reduction. A transfer to larger and more complex processes is straightforward.
The paper is organized as follows: In Section 2 we give an overview over the different optimization subproblems that play a role. In Section 3 we present and discuss our novel feedback optimal control algorithm with sampling decisions from sequential optimal experimental designs, and we elaborate on the role of finite support designs. In Section 4 the theoretical findings are illustrated via numerical results for the mentioned Lotka-Volterra fishing example, followed by a discussion and conclusions.
2. On the Estimation, Control, and Design Problems
In this section, the mathematical formulation of the underlying dynamical system and of the three different types of optimization problems, i.e., parameter and state estimation, optimal control, and optimal experimental design are introduced. They are solved sequentially in our feedback optimal control algorithm with adaptive measurement grid that will be presented in Section 3. We explain the advantages of our decoupled dual control approach with respect to an efficient solution of the experimental design problem.
2.1. Nonlinear Dynamic Systems
We assume that dynamic processes can be described as an initial value problem (IVP), consisting of a system of nonlinear ordinary differential equations (ODEs) and initial values that may also depend on the model parameters p,
on a time interval with the differential state vector, a control function with a bounded set, and unknown model parameters . The function f is assumed to be Lipschitz, such that (1) has a unique solution on for all u and p. We calculate and its derivatives numerically by appropriate methods as described, e.g., in [46].
To formulate design problems and robust versions of control problems, we will need sensitivities . They can be calculated as the solution of the variational differential equations
with the solution of (1) and the partial derivatives written in short form. Note that here and in the following matrix equations are to be understood component-wise. Again, we assume unique solutions for (2).
2.2. State and Parameter Estimation Problems
The relation between the model (1) and the measured data for different measurement functions and time points for can be described by the nonlinear regression
The state depends as the solution trajectory of (1) implicitly on the model parameters p (possibly also via the initial values ). The measurements are described by the nonlinear model responses of the true, but unknown state trajectory plus some normally distributed measurement error with zero mean and variances . Note that the measurement, the model response, and the measurement error are vectors of dimension . Following a maximum-likelihood approach we estimate initial values and model parameters by solving the state and parameter estimation (SPE) problem in the form of a nonlinear weighted least squares problem
for given and fixed controls and weights . As the measurement times may be a priori unknown, we will in our analysis in Section 3.1 also look at the continuous analogue to (4). This is given by
By choosing the function space for such that we allow Borel measures on as solutions, we can define designs via and work with
There is a large variety of algorithms to solve (4), and of alternative formulations, compare [47] for a recent survey.
2.3. Optimal Control Problems
We consider an optimal control (OC) problem of the following form
with a Mayer term as an objective function. Note that we omit mixed path and control constraints and other possible and practically relevant extensions in the interest of a clearer presentation. The objective function comprises the main goal of the control task under uncertainty, such as minimizing the deviation from a target state or minimizing the number of cancer cells, and may of course also contain a Lagrange term by adding an additional state variable. Again, there is a large variety of algorithms to solve such control problems, comprehending dynamic programming, Pontryagin’s maximum principle, or direct methods, compare, e.g., [48,49].
2.4. Optimal Experimental Design Problems
We see the optimal experimental design (OED) problem as an optimal control problem with a particular structure, as suggested in [50]. The degrees of freedom in experimental design are the control functions u and the sampling decisions (or weights) w, which have been assumed to be fixed in Section 2.2. The control can be used to excite the system dynamics, and hence also the sensitivities. The sampling chooses time points or intervals with much information on the sensitivity of the model response with respect to the model parameters. We assume u to be fixed on the level of the experimental design problem for reasons to be discussed later, therefore we concentrate from now on on w as the only degree of freedom. The objective of experimental design is maximizing information gain. With the sensitivities (2), we can define the Fisher Information Matrix (FIM) as
for the discrete setting of (4) and as via the Borel measure
for the continuous measurement setting of (5).
Minimizing the uncertainty of state and parameter estimates, or maximizing information gain, can now be quantified via a scalar function of the FIM or its inverse, the variance-covariance matrix. A list of different objective functions (criteria), such as trace, determinant or maximum eigenvalue can be found, e.g., in [24]. To limit the amount of measurement, either an economic penalty in the objective as suggested in [50] can be used, or a normalization via constraints, e.g.,
for all ω and the discrete setting of (4) and as
for all ω and the continuous measurement setting of (5). Based on our assumptions and considerations, we define the OED problem with fixed u as
for the case of a discrete measurement grid and as
for the continuous measurement flow. Problems (11) and (12) can be solved numerically with the same methods as general optimal control problems, and with specialized ones that take the structure of the derivatives and sensitivities into account, [51]. Our assumption of a fixed u and the specific way w enters the right hand side allow an even more efficient approach, in which the expensive calculation of the states x and G is decoupled from the optimization over x and , see Algorithm 1.
| Algorithm 1 OED |
Input: Fixed p and u, initial values , possible measurement times
|
This decoupling is not the main motivation for our approach to optimize sequentially over u and w, but it should be exploited and might be an argument for time-critical processes.
Algorithm 1 operates with a (fine) time grid of possible time points that can be chosen to take a measurement. If one wants to leave the exact timings as degrees of freedom, one can apply a time transformation (switching time optimization), as suggested and discussed in the context of mixed-integer optimal control, e.g., in [52,53,54] with stage lengths . The variables become additional optimization variables, integration of x and G is performed on the interval and the dynamics ((1) and (2)) are scaled according to
Also continuity conditions at times need to be included, and a constraint like for fixed . The advantage of using ((13) and (14)) is the independence of an a priori grid. However, this comes at the price of not being able to decouple the calculation of x and G from w and F any more, of higher computational costs due to the extra variables, an increased nonconvexity of the dynamics, and possibly not practically realizable (e.g., irrational) measurement times . Therefore we prefer to use Algorithm 1 with a fine grid of possible measurement times.
3. A Feedback Optimal Control Algorithm With Optimal Measurement Times
We start by formulating the main algorithm, before we have a closer look at the role of optimal measurement times and one possible extension, the consideration of robustness.
As an alternative to a dual control approach which incorporates the system excitement, an optimizing control with respect to the control objective, and possibly also the choice of optimal measurement times into one single optimization problem, we propose a decoupled dual control approach. We formulate it for a shrinking horizon with respect to the control and experimental design tasks, and an expanding horizon with respect to state and parameter estimation, which can be easily adapted to a moving horizon setting if appropriate.
The algorithm iterates over time with a “current time” . It solves three subproblems that have been introduced in Section 2. The solution of the optimal control problem (6) provides a control which optimizes with respect to the main control objective. This control is applied until the next update at time . This time point is calculated by means of an optimal experimental design problem (11) as the first time point from a given fine grid of possible measurement points on which the calculated measurement weight is strictly positive. At this time a new measurement is performed, with a subsequent estimation of states and parameters. Based on the modified parameters, a new optimal control is calculated, based on the modified parameters and control, new measurement weights are calculated and so forth. Naturally, previous solutions can and should be used as initialization to speed up the calculations. Depending on the time scales of the process and the calculation times, there usually is a small time gap in which the old controls need to be applied. See, e.g., [17], for details on how to deal with this situation.
Figure 1 visualizes the start of one loop to the start of the next loop of Algorithm 2 applied to the Lotka-Volterra fishing example which is described and discussed in detail in Section 4. In Figure 1a an optimal control problem is solved with the initial values and on the interval . The initial values are obtained from a state and parameter estimation performed on the interval [0,15] with measurement time points derived from a optimal experimental design problem. The uncertainty tubes around the two trajectories are created by 100 simulations with parameter values randomly chosen from a normal distribution with the estimated parameters and corresponding uncertainties as mean and variance. Next, an optimal experimental design problem is solved for the optimal control strategy and the associated solution obtaining optimal measurement time points on the interval (see Figure 1b). From the optimal design the time point is chosen for which the corresponding entry is the first strictly positive one. In Figure 1c the optimal control is applied to the real system until time point at which a measurement is performed and the parameters and the initial states are re-estimated with the additional measurements. With the updated values we are back at the start of the algorithm’s loop and a new optimal control problem is solved with the updated values on the receding time horizon shown in Figure 1d. For the uncertainty tubes again 100 simulations with parameter values sampled from a normal distribution with updated values for the mean and the variance were used.
| Algorithm 2 FOCoed |
| Input: Initial guess , initial values , possible measurement times Initialize sampling counter , measurement grid counter and “current time” while stopping criterion not fulfilled do |
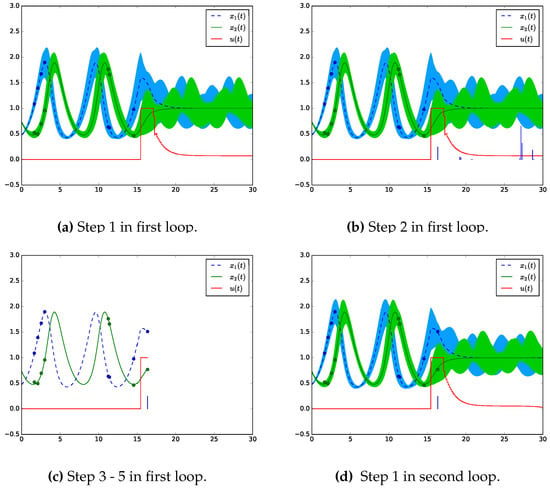
Figure 1.
Visualization of Algorithm 2 performing one loop applied to the Lotka-Volterra fishing example. In Figure 1a the first step, solving an optimal control problem, of Algorithm 2 is performed on the time interval with initial values from a parameter and state estimation on the interval [0,15] with measurements from an optimal experimental design problem. The uncertainty tubes are computed from 100 simulations with parameter samples from a normal distribution with the estimated parameters and uncertainties as mean and variance. In Figure 1b an optimal experimental design is computed on with the optimal control strategy. The strictly positive optimal sampling weights are visualized as vertical lines. Next, the optimal control strategy is performed until time point at which the first sampling weight is strictly positive and a measurement is taken. Afterwards a state and parameter estimation is performed (Figure 1c). The loop starts again with solving a OCP on [,30] with the estimated values. The new optimal control strategy is shown in Figure 1d with uncertainty tubes computed from 100 simulations with updated mean and variance.
The stopping criterion is formulated in a general way as it usually depends on the experimenter’s choice. Possible criteria are a minimum amount of uncertainty reduction, a fixed number of measurements, or an economic penalization term as proposed in [50].
3.1. Finite Support Designs
We look at the role of finite support for optimal experimental designs in more detail, as this will allow us to choose measurement points (and hence the sampling grid) in an optimal way. It is an interesting question how optimal solutions of the discrete OED problem (11) and of the continuous analogue (12) relate to one another. The answer is given by the following theorem, which states that to every optimal design there is a discrete design with finitely many measurement points resulting in the same Fisher information matrix. This is obviously a justification for our iterative approach in Algorithm 2, using a finite number of measurements. Theorem 1 presents a property of optimal designs for the Fisher information matrix.
Theorem 1.
Let . For any optimal design ξ of the OED problem (12) resulting in a nonsingular Fisher information matrix of the SPE problem (5) there exist a finite number N of measurement time points and positive real numbers with such that
with the bounds
is the number of parameters and is the dimension of the model response .
A proof can be found in [55,56]. It is based on the set of all matrices of the form (8) being a compact, convex set. The upper bound results from the Theorem of Carathéodory [21,24] and the solution of the dual problem which is located at the boundary of the convex set [57]. The lower bound is based on the assumption of having full rank , and every update having rank . Our setting is slightly more general, as we allow different measurement functions. However, the result carries over.
Corollary 1.
For any Theorem 1 applies with .
Proof.
The Minkowski sum of convex, compact sets is again a convex, compact set, and hence the argument for the representability due to the Theorem of Carathéodory and the upper bound are still valid. The maximum rank of the matrix update at time is . The lower bound on N is the quotient of the assumed full rank and this sum. ☐
This corollary directly implies that to every optimal solution of the continuous OED problem (12) there is an equivalent solution of the discrete OED problem (11).
We are further interested in (a posteriori) characterizing the optimal measurement times with corresponding . We make the following assumptions. Let an optimal solution of the optimization problem (12) with be given. Here is the Lagrange multiplier of the constraint (9). Let exist. We call
the global information gain matrix. Let be the objective function of the OED problem (12) (for other objectives similar expressions can be found in [50]).
Under the above assumptions in [50] it is shown that
The proof is based on an application of Pontryagin’s maximum principle, exploiting constant adjoint variables, and matrix calculus.
We want to join Theorem 1 with this insight, and look at the special case of . One particular case may arise when the lower bound on the number of support points in Theorem 1, i.e., is equal to one. For one single measurement it can happen that for one index, while otherwise the normalization constraint (9) ensures that all . For this particular case we define to be the maximum of (the Lagrange multiplier of the normalization constraint) and of the upper bound constraint . In most cases, however, .
Lemma 1.
Proof.
Corollary 1 states the existence and optimality of such a design. Assuming there exists with , it directly follows and with the normalization (9) that . The local impact on the optimal objective value is given by , the assumption of this value being strictly larger than both multipliers is hence a contradiction to optimization theory which states that the Lagrange multiplier of the active constraints give a local estimate for the change in the optimal objective function value. ☐
3.2. Robustification
As mentioned in the Introduction, there are many possible extensions to Algorithm 2. Highlighting its flexibility, we exemplarily look at a possible robustification of the optimal control and of the optimal experimental design problem.
The optimization problems (6) and (12) depend on given values of the model parameters and the computed control and measurement strategies are only optimal for the specific parameter values. If the true parameter values are known or the estimated parameter values are equal to the true values the optimal strategies can be applied to the real process without loss of optimality. However, in most cases the true parameter values are not exactly known. Then, the uncertainty of parameters in the spirit of confidence regions should be included into the optimization formulations to robustify the computed optimal control and measurement strategies. We apply a robustification approach suggested in [42,43,58]. The idea is to formulate a min-max optimization problem in which the maximal value of the objective function over the parameters’ confidence region is minimized. Applying Taylor expansion with respect to the parameters, a computationally feasible approximation based on first derivatives is used. It aims at preferring solutions with a “flat objective function”, i.e., which is not too sensitive with respect to the parameter value p.
Again, we assume that the parameters are normally distributed random variables with mean and variance . The confidence region of with confidence quantile γ is defined as the set
where the positive definite matrix induces the norm . Now, the OED objective function in (12) is augmented to
and similarly the robust OC objective function is defined as
No further modifications to Algorithm 2 are necessary. Note that the norms are evaluated pointwise, as Mayer term and the FIM in Problems (6) and (12) are evaluated at time . However, the analysis of Section 3.1 can not be applied in a straightforward way due to the derivative term in the objective function (20), as the weights may jump as changes locally. Intuition and numerical results hint into the direction that also for the robust case discrete designs are optimal, probably with the same bounds on the number of support points. But we only conjecture this and do not have a proof.
4. Numerical Examples
In this section we apply Algoritm 2 to the Lotka-Volterra fishing benchmark problem demonstrating the performance of the algorithm and separately analyze optimal finite support designs.
4.1. Lotka-Volterra Fishing Benchmark Problem
The Lotka-Volterra example is chosen as a well studied dynamic system representing the relation between two competing populations. The model can be modified analyzing disease spreading in an epidemiological context [59] or technological forecasting of stock markets [60] such that the model combines medical, biological and economical interests. The optimal control (OC) and optimal experimental design problem (OED) problem of the Lotka-Volterra fishing example are introduced and described in the following.
The goal of the OC problem is an optimal fishing strategy that brings the prey and predator populations into a steady state (22d), by penalizing deviations from the steady state over the whole time horizon . The optimal control problem of type (6) is
On the time grid with
The solution of problem (23) provides an optimal sampling design minimizing the uncertainties of the parameters and . The right upper entries of the Fisher information matrix (FIM) are considered as differential states in the optimization problem instead of all matrix entries due to symmetry properties of the FIM. Explicit values of the time horizon, the initial states, the parameters and the constants chosen for the numerical computations are given in the next subsection.
4.2. Software and Experimental Settings
Algorithm 2 is implemented as a prototype in the open-source software tool CasADi [61]. We used the version 3.1.0 together with Python 2.7.6. The finite dimensional nonlinear programs resulting from discretizing the optimal control problem (6) and optimal experimental design problem (11) are solved with IPOPT [62]. The parameter estimation problems are solved by a Gauss-Newton algorithm using IPOPT. The derivatives needed for the optimization problems and their robustifications are efficiently generated within CasADi using automatic differentiation [61]. In Subsection 4.3 the system of ODEs is solved using the in-house fixed-step explicit Runge-Kutta integrator and a single shooting method with a stepsize of . For the first state and parameter estimation problem on the time interval [0,15] the initial guess is . We assume that both states and can be measured and that no fishing is permitted on . The pseudo-measurements are derived from a simulation with the true parameters plus a measurement error according to Equation (3). For the OED problems only the uncertainty of the parameters is considered.
For the analysis of finite support designs in Subsection 4.4 the ODE system is solved with CVodes from the SUNDIALS suite [63] and a multiple shooting method with stepsize . The continuous version of the OED problem (23) is computed on the time grid [0,12] with . In both examples the discretization of the optimization variable coincides with the time grid of the ODE problem.
4.3. Three Versions of Algorithm FOCoed applied to the Lotka-Volterra fishing problem
We apply three versions of Algorithm 2 to the control problem (22a) to stress the relevance of optimal measurement time points and the influence of parameter uncertainty during optimization.
- with_OED. This is Algorithm 2, i.e., using measurement time points from non-robust OED.
- without_OED. The OED problem in Step 2 of Algorithm 2 is omitted, and an equidistant time grid is used for measurements.
- with_r_OED. The OC problem in Step 1 and the OED problem in Step 2 of Algorithm 2 are replaced with their robust counterparts as described in Section 3.2.
In the following the experimental setting is described independently of the chosen version of Algorithm 2. The experiment is performed on the time interval [0,30]. From 0 to 15 a first state and parameter estimation with seven measurements, initial guesses is performed. From time point , Algorithm 2 is performed with the estimated parameter values , the state values and the objective function of the optimization problem (11).
For a quantitative statement the three versions of Algorithm 2 are repeated 50 times with the normally distributed measurement error used for the generation of pseudo-measurements. The averaged estimated parameter values and the corresponding uncertainties after and are presented in Table 1 for the three different algorithm versions with_r_OED , with_OED and without_OED. The first column shows the objective function value of the optimal control problem (22) solved on with the true parameter values and the initial state values as the reference solution. The last row additionally presents the averaged objective function values of the three algorithm versions and the last three columns contain the relative uncertainty and objective function value improvements between the three algorithm versions.

Table 1.
Averaged estimated parameter values with their uncertainties and the objective function value () after 50 runs of the optimal control problem (22) solved with three versions of Algorithm 2 ( with_r_OED (A) , with_OED (B) , without_OED (C)). is the relative uncertainty and objective value improvement after and of column i compared to column j. Column OC contains the true parameter values with which the optimal control problem (22) is solved on and the resulting objective function value.
First of all, Table 1 indicates that the three versions of Algorithm 2 provide estimated parameters next to the true parameter values but the results qualitatively differ by means of the resulting parameter uncertainties and the optimal control objective function values. The use of measurement time points from optimal experimental designs (with_OED) compared to equidistant time points (without_OED) improves the parameter uncertainty by after and by after on average. The robustification of the OC and OED problems (with_r_OED) results in an improvement of the parameter uncertainties compared to version without_OED of after and of after on average and compared to the non-robust version with_OED of after and of after on average. The objective function of the optimal control problem is reduced by approximately , respectively , using version with_r_OED or version with_OED compared to version without_OED. The robustification of Algorithm 2 has a minor averaged improvement of .
Figure 2 shows exemplary the solution of the Lotka-Volterra fishing problem computed with the three versions with_r_OED, with_OED and without_OED of Algorithm 2.
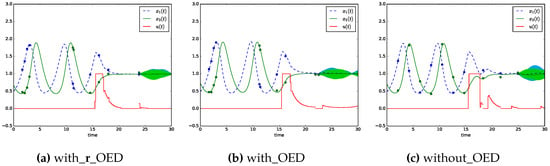
Figure 2.
Visualization of three versions (with_r_OED, with_OED and without_OED) of the feedback optimal control Algorithm 2 applied to the Lotka-Volterra fishing example. The algorithm is performed on the time interval [15,30]. On the time interval [0,15] seven measurements are taken for a state and parameter estimation. The estimated parameters with the corresponding uncertainties and initial states serve as input for the algorithm. In Figure 2a the robust version and in Figure 2b the non-robust version of Algorithm 2 is used with measurement time points from optimal experimental designs. Figure 2c presents the solution of algorithm 2 with measurements taken on an equidistant time grid. After the last measurement time point uncertainty tubes are computed by 100 simulations with parameter values sampled from a normal distribution with the estimated parameters as mean and variance in Figure 2a, and variance in Figure 2b and and in Figure 2c.
4.4. Analyzing Finite Support Designs of Optimal Experimental Design Problems
In this section we demonstrate the theoretical result of Lemma 1 on the Lotka-Volterra optimal experimental design problem.
The optimal solution and of the OED problem are plotted in Figure 3 together with the information gain matrices
and
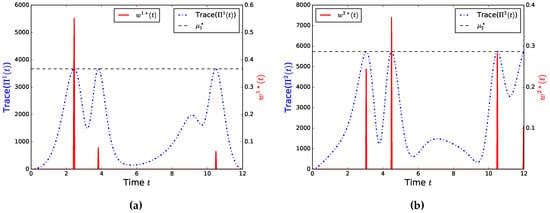
Figure 3.
Visual relation between the trace of the information gain matrices , the Lagrange multipliers and the optimized sampling decisions of the Lotka-Volterra optimal experimental design problem. (a) Information gain and sampling ; (b) Information gain and sampling .
The Lagrange multipliers are also shown as horizontal lines in Figure 3a,b. Both Figures visualize the result of Lemma 1 such that the touching of the information gains’ maxima is equivalent to a singular arc of the sampling decisions and .
4.5. Discussion
The measurement time points have a large impact on the uncertainty of the model parameters and consequently an impact on the optimal control solution, even if the optimizing control does not excite the system dynamics. The quantitative study of Subsection 4.3, which is summarized in Table 1, significantly shows that the optimal measurement time points taken from non-robust and robust optimal experimental designs lead to an averaged uncertainty improvement of , respectively , compared to equidistantly taken measurements. The qualitatively different measuring positions are visualized in Figure 2. The measurement time points of the optimal experimental designs are placed at the beginning and at the end of the time interval [0,15] in which a first state and parameter estimation is performed. During the optimal control phase starting from the non-robust and robust optimal experimental designs suggest measuring once, respectively twice, at the steep descent/ascent of the populations on the interval [15,20] where a larger information content is expected compared to the equidistant time points next to the trajectories’ steady state. The heterogeneity in the improvement of the parameters’ uncertainties results in the used objective function with which the averaged parameter uncertainty is minimized and not each uncertainty separately. This leads to slightly increased uncertainties of parameter after by the use of optimal experimental design. A different scalar function such as the determinant or the largest eigenvalue of the information matrix might prevent this problem but this analysis is not part of the work. Besides this minor increase, the estimated parameter values are closer to the true values using optimal experimental designs in comparison to equidistant measurement time points. The uncertainty tubes in Figure 2 give an indication that the reduced uncertainty of the parameters from Algorithm 2 has an indirect positive influence on the state uncertainty leading to tighter uncertainty tubes. The visual indication is strengthened by the last row of Table 1 presenting the optimal control objective function value of the reference solution and the averaged values resulting from the three different versions (with_r_OED, with_OED and without_OED) of Algorithm 2. The reduced parameter uncertainties obtained from non-robust and robust optimal experimental designs lead to a , respectively , objective function value compared to the version without_OED with measurements taken on equidistant time points.
Lemma 1 is visualized for the Lotka-Volterra optimal experimental design benchmark problem in Figure 3a,b. Whenever the Lagrange multiplier is equal to the value of the information gain matrix, the sampling decision variable is between 0 and 1.
5. Conclusions
The paper presents a novel algorithm for feedback optimal control with measurement time points for parameter estimations computed from optimal experimental design problems. It is based on a decoupled approach to dual control. The performance of the algorithm is shown by 50 runs of the Lotka-Volterra fishing benchmark example. The algorithm provides a averaged reduction of parameter uncertainties while applying an optimal control strategy when measurement time points are used from optimal experimental designs compared to heuristically chosen equidistant measurement time points for parameter estimations. A robustified version of the algorithm moreover reveals a averaged uncertainty reduction. Furthermore, a theoretical insight about the solution of the optimal experimental design problem is given. Therefore Pontryagin’s Maximum Principle is applied to the OED problem when the sum of optimization variables is constrained by one and a connection is drawn between the trace of the information gain matrix and the Lagrange multipliers for a discrete optimal design. The algorithmic and theoretical results are demonstrated on the Lotka-Volterra fishing benchmark problem.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 647573) and from the German BMBF under grant 05M2013 - GOSSIP, which is gratefully acknowledged.
Author Contributions
F.J. implemented the algorithm and did all numerical calculations and is the corresponding author of the article. T.T.-T.L. and S.S. contributed to the general idea, to the theoretical aspects, and to proof-reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| FIM | Fisher Information Matrix |
| MPC | Model Predictive Control |
| NLP | Nonlinear Program |
| ODE | Ordinary Differential Equation |
| OC | Optimal Control |
| OED | Optimal Experimental Design |
| SPE | State and Parameter Estimation |
References
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Henson, M. Nonlinear model predictive control: Current status and future directions. Comput. Chem. Eng. 1998, 23, 187–202. [Google Scholar] [CrossRef]
- Rawlings, J.; Mayne, D. Model Predictive Control: Theory and Design; Nob Hill Publishing, LLC.: Madison, WI, USA, 2009. [Google Scholar]
- Diehl, M.; Bock, H.; Schlöder, J. A real-time iteration scheme for nonlinear optimization in optimal feedback control. SIAM J. Control Optim. 2005, 43, 1714–1736. [Google Scholar] [CrossRef]
- Zavala, V.; Biegler, L. The advanced–step NMPC controller: Optimality, stability and robustness. Automatica 2009, 45, 86–93. [Google Scholar] [CrossRef]
- Frasch, J.; Wirsching, L.; Sager, S.; Bock, H. Mixed—Level Iteration Schemes for Nonlinear Model Predictive Control. In Proceedings of the IFAC Conference on Nonlinear Model Predictive Control, Noordwijkerhout, The Netherlands, 23–27 August 2012.
- Frasch, J. Parallel Algorithms for Optimization of Dynamic Systems in Real-Time. Ph.D. Thesis, Otto-von-Guericke University Magdeburg, Magdeburg, Germany, 2014. [Google Scholar]
- Steinbach, M. Fast Recursive SQP Methods for Large-Scale Optimal Control Problems. Ph.D. Thesis, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany, 1995. [Google Scholar]
- Frasch, J.V.; Sager, S.; Diehl, M. A parallel quadratic programming method for dynamic optimization problems. Math. Program. Comput. 2015, 7, 289–329. [Google Scholar] [CrossRef]
- Schlegel, M.; Marquardt, W. Detection and exploitation of the control switching structure in the solution of dynamic optimization problems. J. Process Control 2006, 16, 275–290. [Google Scholar] [CrossRef]
- Domahidi, A. Methods and Tools for Embedded Optimization and Control. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2013. [Google Scholar]
- Houska, B.; Ferreau, H.; Diehl, M. ACADO Toolkit—An Open Source Framework for Automatic Control and Dynamic Optimization. Optim. Control Appl. Methods 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Ferreau, H. qpOASES—An open-source implementation of the online active set strategy for fast model predictive control. In Proceedings of the Workshop on Nonlinear Model Based Control—Software and Applications, Loughborough, UK, 2007; pp. 29–30.
- Kirches, C.; Potschka, A.; Bock, H.; Sager, S. A Parametric Active Set Method for a Subclass of Quadratic Programs with Vanishing Constraints. Pac. J. Optim. 2013, 9, 275–299. [Google Scholar]
- Klatt, K.U.; Engell, S. Rührkesselreaktor mit Parallel- und Folgereaktion. In Nichtlineare Regelung—Methoden, Werkzeuge, Anwendungen; VDI-Berichte Nr. 1026; Engell, S., Ed.; VDI-Verlag: Düsseldorf, Germany, 1993; pp. 101–108. [Google Scholar]
- Chen, H. Stability and Robustness Considerations in Nonlinear Model Predictive Control; Fortschr.-Ber. VDI Reihe 8 Nr. 674; VDI Verlag: Düsseldorf, Germany, 1997. [Google Scholar]
- Houska, B.; Ferreau, H.; Diehl, M. An Auto-Generated Real-Time Iteration Algorithm for Nonlinear MPC in the Microsecond Range. Automatica 2011, 47, 2279–2285. [Google Scholar] [CrossRef]
- Diehl, M.; Ferreau, H.; Haverbeke, N. Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation. In Nonlinear Model Predictive Control; Magni, L., Raimondo, D., Allgöwer, F., Eds.; Springer Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2009; Volume 384, pp. 391–417. [Google Scholar]
- Zavala, V.M.; Biegler, L.T. Nonlinear Programming Strategies for State Estimation and Model Predictive Control. In Nonlinear Model Predictive Control; Springer: London, UK, 2009; pp. 419–432. [Google Scholar]
- Kirches, C.; Wirsching, L.; Sager, S.; Bock, H. Efficient numerics for nonlinear model predictive control. In Recent Advances in Optimization and its Applications in Engineering; Diehl, M., Glineur, F., Jarlebring, E., Michiels, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 339–359. [Google Scholar]
- Fedorov, V. Theory of Optimal Experiments; Academic Press: New York, NY, USA; London, UK, 1972. [Google Scholar]
- Atkinson, A.; Donev, A. Optimum Experimental Designs; Number 8 in Oxford Statistical Sciences Series; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Kitsos, C. Optimal Experimental Design for Non-Linear Models; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Pukelsheim, F. Optimal Design of Experiments; Classics in Applied Mathematics 50; Society for Industrial and Applied Mathematic (SIAM): Philadelphia, PA, USA, 2006. [Google Scholar]
- Körkel, S.; Bauer, I.; Bock, H.; Schlöder, J. A Sequential Approach for Nonlinear Optimum Experimental Design in DAE Systems. In Scientific Computing in Chemical Engineering II; Springer: Berlin/Heidelberg, Germany, 1999; pp. 338–345. [Google Scholar]
- Kreutz, C.; Timmer, J. Systems biology: Experimental design. FEBS J. 2009, 276, 923–942. [Google Scholar] [CrossRef] [PubMed]
- Stigter, J.; Vries, D.; Keesman, K. On adaptive optimal input design: A bioreactor case study. AIChE J. 2006, 52, 3290–3296. [Google Scholar] [CrossRef]
- Galvanin, F.; Barolo, M.; Bezzo, F. Online Model-Based Redesign of Experiments for Parameter Estimation in Dynamic Systems. Ind. Eng. Chem. Res. 2009, 48, 4415–4427. [Google Scholar] [CrossRef]
- Barz, T.; López Cárdenas, D.C.; Arellano-Garcia, H.; Wozny, G. Experimental evaluation of an approach to online redesign of experiments for parameter determination. AIChE J. 2013, 59, 1981–1995. [Google Scholar] [CrossRef]
- Qian, J.; Nadri, M.; Moroşan, P.D.; Dufour, P. Closed loop optimal experiment design for on-line parameter estimation. In Proceedings of the IEEE 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1813–1818.
- Lemoine-Nava, R.; Walter, S.F.; Körkel, S.; Engell, S. Online optimal experimental design: Reduction of the number of variables. In Proceedings of the 11th IFAC Symposium on Dynamics and Control of Process Systems, Trondheim, Norway, 6–8 June 2016.
- Feldbaum, A. Dual Control Theory. I. Avtom. Telemekhanika 1960, 21, 1240–1249. [Google Scholar]
- Wittenmark, B. Adaptive dual control methods: An overview. In Proceedings of the IFAC Symposium on Adaptive Systems in Control and Signal Processing, Budapest, Hungary, 14–16 June 1995; pp. 67–72.
- Filatov, N.M.; Unbehauen, H. Adapive Dual Control; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Recker, S.; Kerimoglu, N.; Harwardt, A.; Marquardt, W. On the integration of model identification and process optimization. Comput. Aided Chem. Eng. 2013, 32, 1012–1026. [Google Scholar]
- Bavdekar, V.A.; Mesbah, A. Stochastic model predictive control with integrated experiment design for nonlinear systems. In Proceedings of the 11th IFAC Symposium on Dynamics and Control of Process Systems, Including Biosystems, Trondheim, Norway, 6–8 June 2016.
- Telen, D.; Houska, B.; Vallerio, M.; Logist, F.; van Impe, J. A study of integrated experiment design for NMPC applied to the Droop model. Chem. Eng. Sci. 2017, 160, 370–383. [Google Scholar] [CrossRef]
- Lucia, S.; Andersson, J.; Brandt, H.; Diehl, M.; Engell, S. Handling uncertainty in economic nonlinear model predictive control: A comparative case study. J. Process Control 2014, 24, 1247–1259. [Google Scholar] [CrossRef]
- Lucia, S.; Paulen, R. Robust Nonlinear Model Predictive Control with Reduction of Uncertainty Via Robust Optimal Experiment Design. IFAC Proc. Vol. 2014, 47, 1904–1909. [Google Scholar] [CrossRef]
- Lucia, S.; Schliemann-Bullinger, M.; Findeisen, R.; Bullinger, E. A Set-Based Optimal Control Approach for Pharmacokinetic/Pharmacodynamic Drug Dosage Design. In Proceedings of the 11th IFAC Symposium on Dynamics and Control of Process Systems, Including Biosystems, Trondheim, Norway, 6–8 June 2016.
- Jost, F.; Rinke, K.; Fischer, T.; Schalk, E.; Sager, S. Optimum experimental design for patient specific mathematical leukopenia models. In Proceedings of the Foundations of Systems Biology in Engineering (FOSBE) Conference, Magdeburg, Germany, 9–12 October 2016.
- Ben-Tal, A.; Nemirovski, A. Robust Convex Optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.; Kostina, E. An approximation technique for robust nonlinear optimization. Math. Program. 2006, 107, 213–230. [Google Scholar] [CrossRef]
- Gjøsæter, H.; Bogstad, B.; Enberg, K.; Kovalev, Y.; Shamrai, E.A. (Eds.) Long term sustainable management of living marine resources in the Northern Seas. In Proceedings of the 17th Norwegian-Russian Symposium, Bergen, Norway, 16–17 March 2016.
- Jana, D.; Agrawal, R.; Upadhyay, R.K.; Samanta, G. Ecological dynamics of age selective harvesting of fish population: Maximum sustainable yield and its control strategy. Chaos Solitons Fractals 2016, 93, 111–122. [Google Scholar] [CrossRef]
- Gerdts, M. Optimal Control of Ordinary Differential Equations and Differential-Algebraic Equations; University of Bayreuth: Bayreuth, Germany, 2006. [Google Scholar]
- Kircheis, R. Structure Exploiting Parameter Estimation and Optimum Experimental Design Methods and Applications in Microbial Enhanced Oil Recovery. Ph.D. Thesis, University Heidelberg, Heidelberg, Germany, 2015. [Google Scholar]
- Biegler, L. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; Series on Optimization; Society for Industrial and Applied Mathematic (SIAM): Philadelphia, PA, USA, 2010. [Google Scholar]
- Betts, J. Practical Methods for Optimal Control Using Nonlinear Programming; Society for Industrial and Applied Mathematic (SIAM): Philadelphia, PA, USA, 2001. [Google Scholar]
- Sager, S. Sampling Decisions in Optimum Experimental Design in the Light of Pontryagin’s Maximum Principle. SIAM J. Control Optim. 2013, 51, 3181–3207. [Google Scholar] [CrossRef]
- Körkel, S. Numerische Methoden für Optimale Versuchsplanungsprobleme bei nichtlinearen DAE-Modellen. Ph.D. Thesis, Universität Heidelberg, Heidelberg, Germany, 2002. [Google Scholar]
- Gerdts, M. A variable time transformation method for mixed-integer optimal control problems. Optim. Control Appl. Methods 2006, 27, 169–182. [Google Scholar] [CrossRef]
- Sager, S.; Reinelt, G.; Bock, H. Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems. Math. Program. 2009, 118, 109–149. [Google Scholar] [CrossRef]
- Gerdts, M.; Sager, S. Mixed-Integer DAE Optimal Control Problems: Necessary conditions and bounds. In Control and Optimization with Differential-Algebraic Constraints; Biegler, L., Campbell, S., Mehrmann, V., Eds.; Society for Industrial and Applied Mathematic (SIAM): Philadelphia, PA, USA, 2012; pp. 189–212. [Google Scholar]
- Fedorov, V.; Malyutov, M. Optimal designs in regression problems. Math. Operationsforsch. Stat. 1972, 3, 281–308. [Google Scholar] [CrossRef]
- La, H.C.; Schlöder, J.P.; Bock, H.G. Structure of Optimal Samples in Continuous Nonlinear Experimental Design for Parameter Estimation. In Proceedings of the 6th International Conference on High Performance Scientific Computing, Hanoi, Vietnam, 16–20 March 2015.
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Körkel, S.; Kostina, E.; Bock, H.; Schlöder, J. Numerical Methods for Optimal Control Problems in Design of Robust Optimal Experiments for Nonlinear Dynamic Processes. Optim. Methods Softw. 2004, 19, 327–338. [Google Scholar] [CrossRef]
- Venturino, E. The influence of diseases on Lotka-Volterra systems. J. Math. 1994, 24, 1. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, D.J.; Oh, H.S. Technological forecasting at the Korean stock market: A dynamic competition analysis using Lotka-Volterra model. Technol. Forecast. Soc. Chang. 2005, 72, 1044–1057. [Google Scholar] [CrossRef]
- Andersson, J. A General-Purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, Arenberg Doctoral School, KU Leuven, Leuven, Belgium, 2013. [Google Scholar]
- Wächter, A.; Biegler, L. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Hindmarsh, A.; Brown, P.; Grant, K.; Lee, S.; Serban, R.; Shumaker, D.; Woodward, C. SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).