Abstract
The organic Rankine cycle (ORC) is a key technology for the recovery of low-grade waste heat, but its efficient and stable operation is challenged by complex kinetic coupling. This paper proposes a model partitioning strategy based on gap measurement to construct a high-fidelity ORC system model and combines the setting of observer decoupling and multi-model switching strategies to reduce the coupling impact and enhance adaptability. For control optimization, the reinforcement learning method of deep deterministic Policy Gradient (DDPG) is adopted to break through the limitations of the traditional discrete action space and achieve precise optimization in the continuous space. The proposed DDPG-MGPC (Hybrid Model Predictive Control) framework significantly enhances robustness and adaptability through the synergy of reinforcement learning and model prediction. Simulation shows that, compared with the existing hybrid reinforcement learning and MPC methods, DDPG-MGPC has better tracking performance and anti-interference ability under dynamic working conditions, providing a more efficient solution for the practical application of ORC.
1. Introduction
In the field of efficient energy utilization, the stepwise development of thermal energy resources has become a cutting-edge direction for technological breakthroughs [1]. Low-temperature thermal energy typically denotes thermodynamic resources with a relatively low energy quality, characterized by temperatures generally below 200 °C [2]. These resources are extensively found in waste energy and renewable energy sources, such as industrial process waste heat and solar thermal energy [3]. Against this backdrop, regenerative technologies represented by the organic Rankine cycle, through the stepwise utilization of energy [4], not only enable the in-depth development of waste heat resources but also systematically enhance the energy utilization efficiency of the entire industrial chain, which is of great significance for building a resource-conserving society [5].
In terms of model building, although ORC technology has significant advantages, its actual performance is restricted by multiple factors such as physical properties of the working medium, fluctuations of cold and heat sources, and component matching [6]. Xiao M et al., starting from mechanism analysis [7], regard the evaporator and condenser as one-dimensional heat transfer models, adopt the lumped parameter method for modeling, and regard the expansion process of the working medium as an isentropic process. Wei D proposed two methods for establishing dynamic models of organic Rankine cycles based on the moving boundary method and discretization technology, respectively [8]. In terms of response speed, the moving boundary model convergent faster and is more suitable for the related design of the controller. In order to improve the problems of model overfitting and underfitting, Ping X et al. proposed an efficient multi-layer adaptive modeling method for ORC systems from the perspectives of data selection, parameter association, and structural design [9], which improved the model generalization ability by 61.88%. Since the model structure determined by mechanism analysis cannot fully reflect the nonlinear coupling relationship in the actual working conditions, its adaptability to the unmodeled dynamics of the system is obviously limited. Therefore, this paper uses a mixed verification strategy: combining mechanism modeling with data-driven corrections through ridge regression to ensure the accuracy and physical interpretability of the ORC system model.
In industrial applications, the control of the organic Rankine cycle system is the core link to achieve efficient and stable operation. It is necessary to dynamically adjust system parameters to adapt to environmental conditions such as heat source fluctuations. The control objectives include the following: The ORC system belongs to a typical nonlinear, strongly coupled, and highly lagging multi-input multi-output system. The working conditions are complex, and it has significant hysteresis and parameter sensitivity. Under the rated conditions, making the evaporating pressure close to the saturation pressure of the heat source temperature change can improve thermal efficiency, usually by adjusting the working medium pump speed to achieve collaborative optimization, and the expansion machine can give attention to both security and expander power capability. The fluctuation of heat source temperature and mass flow rate, as well as the transition of the operating condition point of the system itself, will lead to changes in model parameters [10]. For model-based control systems, the variation of model parameters will greatly affect the control accuracy. It is necessary to reduce the influence of environmental disturbances on the control accuracy through feedforward compensation or feedback correction. For the evaporator temperature and expander output control of the ORC system, Chowdhury adopts the traditional PID controller and the self-adjusting PID controller based on fuzzy rules, respectively [11], which shows that the fuzzy self-adjusting PID controller is superior to the traditional PID controller in terms of control accuracy and anti-interference ability. Cabral I. M. points out that after similar simulations [12], those fuzzy methods can better adapt to system dynamic changes caused by predictable evaporation phenomena or external disturbances to obtain better control performance. Although PID control can get a better control effect locally, its limitations are that it is difficult to deal with the multivariable coupling and nonlinear system [13] and unable to realize overall control of the ORC system. According to the nonlinear characteristics of the ORC system, Reddy C. R. realizes the control of the superheat of the ORC system through the model predictive control algorithm [14], and the control accuracy is high. Aiming at the problem of complex computational complexity in MPC control, Shi Y proposed a dual-mode fast dynamic matrix control algorithm based on singular value decomposition and dynamic matrix control [15], which significantly improves the solution speed of model predictive control while ensuring control accuracy. Model predictive control can achieve the control of multi-input and multi-output systems, but it has limitations such as high computational complexity, reliance on model accuracy, insufficient real-time performance, and difficulty in constraint processing. In order to precisely control the superheat of ORC under transient heat sources, Xuan Wang et al. proposed two control methods based on deep reinforcement learning [16], indicating that the DRL agent can precisely perform control tasks under both trained and untrained transient heat sources; To address the failure of traditional control and the safety risks of DRL application caused by the variable working conditions of the ORC system, Lin R et al. proposed a DRL method based on Sim2Real transfer learning [17]. Similar simulations show that the agent training is accelerated and the generalization is improved, which can provide an efficient solution for industrial energy optimization.
Above all, the direct agent-based reinforcement learning control strategy is difficult to ensure the stability of the controller in [18], and the stable operation of the ORC system has brought certain risks. The improvement strategies based on fuzzy PID and adaptive PID are still within the traditional control framework of PID. Although they can achieve slightly better results under some working conditions, it is difficult to cover all working conditions. In multi-model predictive control, there is no specific processing for the system coupling relationship, while the ORC system needs to weaken the coupling of the target variable to improve the stability of the system operation. Furthermore, the selection of control parameters is as important as the design of the control strategy [19]. Therefore, it is necessary to combine the parameter optimization strategy to improve the performance indicators of the controller. Therefore, based on the model predictive controller, this paper selects to combine the decoupling strategy, the multi-model strategy, and the parameter optimization strategy based on reinforcement learning to achieve the precise control of the evaporation pressure and working medium temperature of the ORC system, thereby providing a practical and feasible solution for the control of the ORC system.
2. Mechanistic Model
The organic Rankine cycle system can be decomposed into four key energy conversion links [20], as shown in Figure 1 below: constant pressure heating of the working medium in the evaporator, adiabatic expansion of the working medium in the expander, constant pressure cooling in the condenser, and adiabatic pressurization in the working medium pump. By studying the mechanism model and control tasks of the ORC system [21], the evaporator and condenser are regarded as one-dimensional heat transfer models, and the total set parameter method is adopted for modeling. The expansion process of the working medium is regarded as an isentropic process [7]. The organic working medium is heated into high-temperature and high-pressure gas in the evaporator by the waste heat [22], and the gas expands in the expander. Convert thermal energy into mechanical energy [23] to drive the generator. The low-pressure exhaust gas condenses back into liquid in the condenser, is pressurized by the pump, and then returns to the evaporator to complete the cycle.
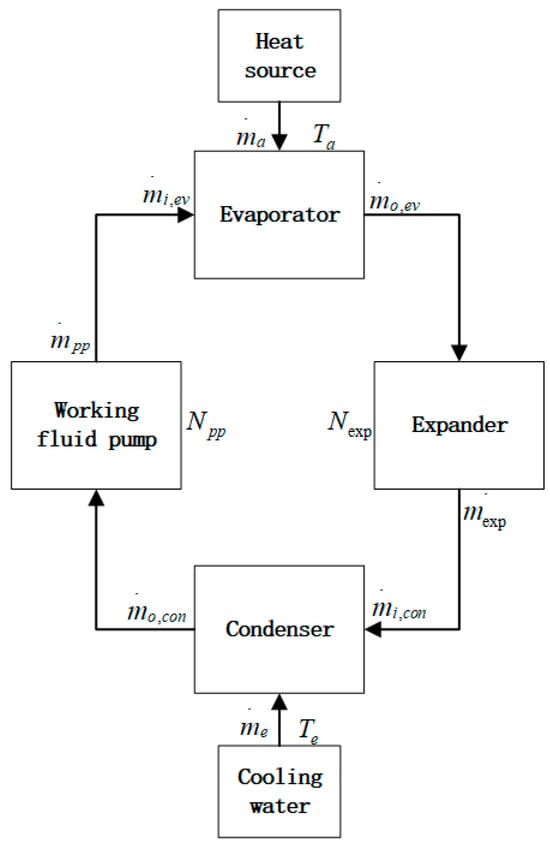
Figure 1.
The organic Rankine cycle system.
The state-space equations of the system are described as
where: , , , , is a self-set coefficient.
The specific parameters are shown in Table 1:

Table 1.
ORC System Parameter Table.
The ORC model of Equation (1) is a nonlinear model. To facilitate model verification through simulation data, in this paper, the linear sub model is obtained by the linearization method of Taylor expansion near the operating point, and then it is transformed into the transfer function matrix of a multi-input multi-output system. The discrete transfer function matrix based on time series is obtained through the discretization method of bilinear transformation. Finally, the least squares method is used for parameter fitting. The fitting results are compared with the directly calculated results to verify the accuracy of the ORC model designed in this paper.
Considering the linearization method of Taylor expansion, the ORC system equation near the operating point field can be transformed into a standard state space expression:
where: , ,
The transfer function of the system:
By using bilinear transformation to discretize the above equation, a discrete transfer function matrix can be obtained:
Suppose there are several data point fields, where the fields are input features and the fields are output values. The form of the linear regression model is
where: is the input feature matrix, is the parameter vectors, and is the error terms. The goal of the least squares method is to find the parameter vector and minimize the sum of squared errors:
The analytical solution of the least squares method:
where: is the transpositions of the input feature matrix, and is the inverse matrices of the matrix .
In this paper, the least squares method is used to fit the system parameters at the operating point, and the error between the data-driven system parameters and the actual operating data are statistically analyzed. The flue gas flow rate at the selected operating point is 0.85 kg/s, the flue gas temperature is 183 °C, the length of the two-phase zone is 40 m, the evaporation pressure is 1.5064 Mpa, the wall temperature of the evaporator tube is 390 K, the condensation pressure is 0.1084 Mpa, and the wall temperature of the condensation section is 283 K. The regularization coefficient is 0.85. The parameters of the system model can be obtained by fitting 100 sets of experimental data based on the least squares method, as shown in Table 2.

Table 2.
Model Parameter Table.
The parameters in Table 2 respectively correspond to the coefficients of the discrete transfer function of the evaporation pressure term. The coefficient of the evaporation pressure term is shown in the following Formula (9):
where: represent the evaporation pressure, represents the speed of the expander, and represents the speed of the working fluid pump.
Figure 2 and Figure 3 show the operation data of the ORC system and the fitting curves of the least squares method. The sum of the squares of the errors of the fitting results is shown in Table 2.
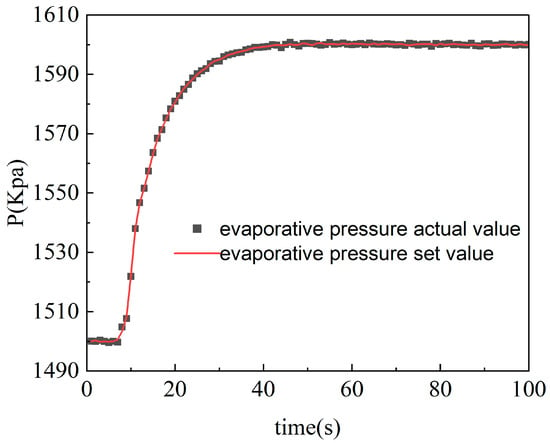
Figure 2.
Actual and fitted values of evaporative pressure.
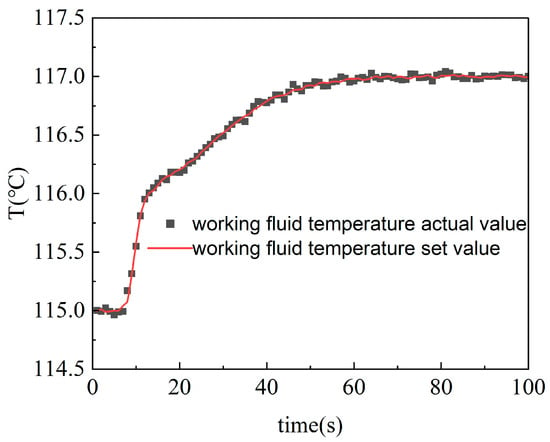
Figure 3.
Actual and fitted values of working fluid temperature.
In Table 3, err1 and err2 respectively correspond to the sum of squares of the fitting errors of the evaporation pressure and working medium temperature terms. The results show that the least squares method has a relatively high fitting accuracy, and the data errors are within the allowable range. Therefore, after determining the model order and system variables based on mechanism analysis in this paper, the method of fitting specific parameter values by the least squares method is feasible. This not only ensures that the error between the system model and the actual model is small but also saves the processing time of subsequent model linearization, providing convenience for the control design of the ORC system and working fluid temperature directly affect the energy transfer efficiency of the evaporator and the overall power generation efficiency. For the proposed two-input two-output control system, the inputs are the expander speed and the pump speed, while the outputs are the evaporation pressure and the working fluid temperature. Since the ORC (Organic Rankine Cycle) model is a typical thermodynamic model, its parameters tend to shift with changing operating conditions. Therefore, it is necessary to decompose the operating conditions of the ORC system and establish a multi-model strategy.

Table 3.
Parameter Error Table.
For multi-model theory, Zames and EI-Sakkary took the lead in introducing gap metric into this theoretical framework [24], and later studies confirmed that [25] compared with the traditional norm metric, gap metric can more accurately evaluate the generalized distance of two linear systems.
Definition: If there are two linear subsystems with the same inputs and outputs . It can be decomposed into mutual right and co-prime as . The clearance measure for the two systems can be calculated as follows:
where: , and represent the coprime decomposition of the two systems, respectively, is the open-loop gain of the system.
The gap metric has the following properties:
- (1)
- The gap metric between two systems can be used to measure the distance between two linear systems. Compared with traditional distance measures such as the H∞ norm and Euclidean distance, the gap metric focuses more on the directional differences in system dynamic characteristics. This method evaluates the stability compatibility of two systems under closed-loop control, meaning that if a controller can stabilize system P1, it can also stabilize system P2. This property makes it more suitable for addressing controller perturbations during model switching.
- (2)
- The higher the similarity between two linear systems, the closer their dynamic response characteristics and the smaller the gap metric. If the gap metric is zero, it indicates that the dynamic characteristics of the two linear subsystems are completely identical.
Using the gap metric, the distance between linear submodules can be determined. The next challenge is how to decompose a highly nonlinear system like the ORC, which operates across a wide range of conditions. Having too many linear submodules increases computational burden and severely affects the controller’s response speed, while too few models fail to fully represent the dynamic behavior of the nonlinear system, thus reducing model accuracy. Therefore, this paper proposes a method called Gap-M, which incorporates nonlinear model decomposition and determines the optimal number of submodules, as illustrated in the following Figure 4:
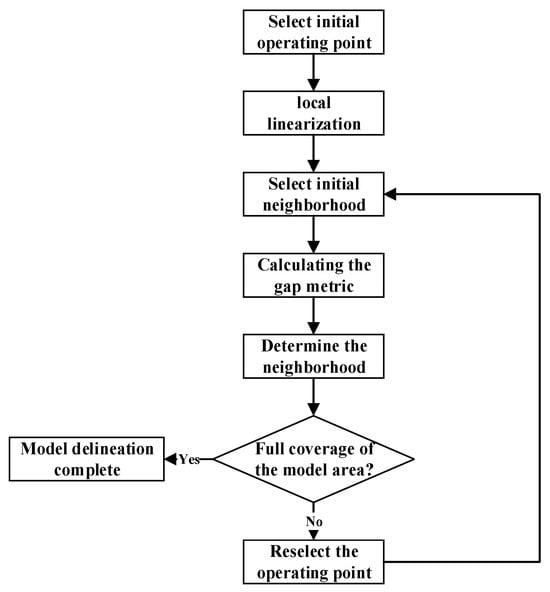
Figure 4.
Gap-M flowchart.
The specific implementation steps are as follows:
- (1)
- Select an initial equilibrium point of the system, linearize near the equilibrium point to obtain a local linear model, and select a large enough neighborhood range according to the variables used for the division of working conditions:
- (2)
- A model of a number of working points after linearization is calculated separately by taking a number of working condition points at a certain distance near the initial equilibrium point.
- (3)
- The gap measurement between several working points and the linear model of the initial equilibrium point is calculated separately.
- (4)
- Iterate through all clearance measures and retain all points less than the rated threshold, and the system range that can be characterized by the linear model of the working point can be obtained.
- (5)
- After obtaining the initial model, count the points with the largest gap between the working condition points and the initial equilibrium point in the working condition points that are not in the neighborhood, and repeat step (1) at this working condition point.
The flue gas temperature and mass flow directly affect the whole system model, which can be regarded as the basis for multi-model division, which can greatly reduce the amount of computation and characterize the physical state of the system.
It should be noted that the selection of the gap measurement threshold has a certain degree of subjectivity. If it is selected too small, it will result in an excessive number of sub-models in the entire system. If it is selected too large, it will cause an approximately imprecise effect. According to the relevant reference [26], the threshold selection range is 0.2 ≤ ≤ 0.4.
According to the Gap-M method, the system state is set as the initial equilibrium point when the flue gas temperature is 183 °C and the mass flow rate is 0.85 kg/s, the length of the two-phase zone is 40 m, the evaporation pressure is 1.5064 Mpa, the evaporator wall temperature is 390 K, the condensing pressure is 0.1084 Mpa, and the condensation section wall temperature is 283 K.
To estimate the neighborhood, first select a neighborhood that is large enough:
Approximately 336 linear models can be obtained by taking points every 1 °C for flue gas temperature and 0.02 kg/s for mass flow in the neighborhood and substituting these points into the Jacobian matrix to calculate the relevant parameters. Considering the complexity of the linearization process, the least squares method based on ridge regression was used for model parameter fitting. The calculated gap metrics for the model in the initial neighborhood and the initial equilibrium point model are shown in Figure 5 below:
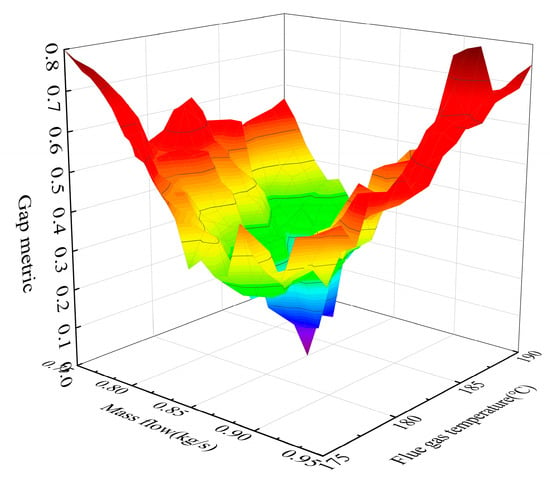
Figure 5.
Three-dimensional Gap Metric diagram.
According to the data analysis shown in Figure 5, the system clearance measurement shows a nonlinear growth trend with the deviation from the initial point of the operating conditions, and its distribution pattern is an irregular hourglass, which is in line with the relevant characteristics of the ORC system in operation. Projecting it onto a 2D plane, the result is shown in Figure 6 below:
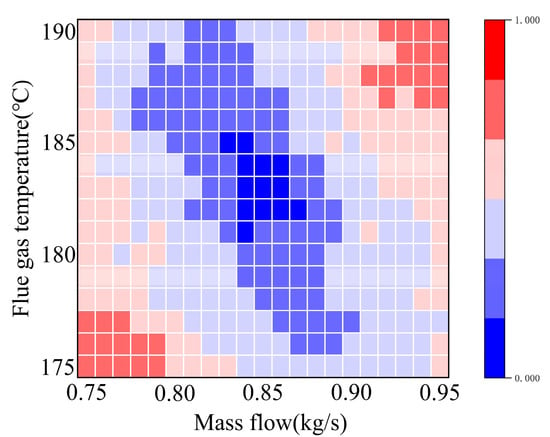
Figure 6.
Two-dimensional Gap Metric diagram.
Firstly, the threshold of the gap measurement is 0.3, so the area represented by the linear model with the gap measurement value less than 0.3 can be regarded as the range of working conditions that can be characterized by the initial model. Considering that the calculation of model parameters in local linearization is driven by industrial data, errors in data acquisition are inevitably introduced, so there is a certain ambiguity in the model boundary of the initial equilibrium point representation. In order to reduce the number of sub-models and keep them within the appropriate range, the threshold of the gap measurement in this paper is slightly adjusted to make the neighborhood covered as large as possible and improve the degree of boundary linearization. Therefore, the neighborhoods of the working point model corresponding to Figure 5 are adjusted to the M3 part of the figure below. According to the Gap-M multi-model selection strategy mentioned above, the equilibrium point farthest from the gap metric of the point is calculated, and the cycle repeats, and finally the model segmentation of the ORC system under each working condition can be obtained after calculation, as shown in the following Figure 7:
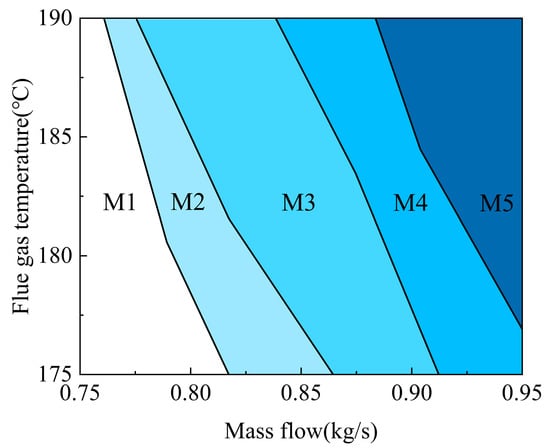
Figure 7.
Working condition division diagram.
Figure 7 shows five sets of linearization models, which cover the full operating conditions of the ORC system. Combined with the curvature of the change of working conditions, it can be found that the ORC system model is greatly affected by the flue gas mass flow, and the model parameters of the ORC system also change with the change of flue gas temperature and mass flow.
3. Generalized Model Predictive Control and Decoupling
Due to the strict constraints of the ORC system on the dynamic response performance of the controller [16], when the general model predictive control technology is based on the state space model of the system and solves it using quadratic programming, because it needs to handle high-dimensional intermediate variables [27], it is difficult to meet the real-time requirements during its online optimization. Generalized predictive control is a combination of classical control theory and the predictive control framework [28]. Based on inheriting the minimum variance control, it integrates the multi-step rolling optimization and feedback correction mechanism of model predictive control, solving the problems of multi-variable and strongly coupled system control in industry [29].
Starting from the CARIMA model, GPC uses the Diophantine equation to solve the relationship between the predicted output and input variables and then obtains the system control quantity. GPC control mainly includes the following three aspects:
- (1)
- System Description
In GPC, the system under stochastic disturbances is modeled using a Controlled Auto-Regressive Integrated Moving Average (CARIMA) framework:
where: is a first-order polynomial of degree , is a polynomial of degree , represents the disturbance term, is ,and is the delay operator. In this study, the controllable variables are the expander speed and fluid pump speed, while the target variables are the evaporation pressure and the superheat degree.
- (2)
- Optimal Output Prediction
The Diophantine equation is introduced to derive the optimal predicted output:
where: , .
Multiplying both sides of the CARIMA model by , we obtain
By solving the Diophantine equation, the optimal predicted output is derived as
In the above equation, the predicted value is composed of the known data at the current moment and the control inputs that need to be calculated for the future. Therefore, a second Diophantine equation is introduced to decompose it into past and future control inputs:
where: , .
The final optimal prediction is expressed as
- (3)
- Objective Function
An error weighting matrix is introduced to reflect the importance of the system output approaching the setpoint. Additionally, during the control process, excessive changes in control increments are often undesirable. For example, in the ORC system, excessive variations in control variables such as the fluid pump speed and the expander speed may pose safety risks to the system. Therefore, this factor needs to be considered in the objective function, which is defined as
where: , represents the softened reference trajectory, which helps reduce excessive control actions and ensures a smooth transition of the control system output to the setpoint. The smoothing factor significantly impacts the dynamic characteristics and robustness of the closed-loop system.
Minimizing the objective function , i.e., setting and , while satisfying the constraints, yields the optimal control law:
Coupling is widespread in ORC systems, where the relationships between variables in the waste heat power generation process are highly intricate. The fluctuation of one process variable often leads to changes in multiple variables, resulting in coupling [30]. Decoupling, therefore, is the process of eliminating such coupling relationships. Although Model Predictive Control can be used to handle multivariable systems [31] like ORC, similar simulations have shown that coupling effects in system responses after setpoint changes can impact control results [32]. This is unfavorable for ORC systems, which have high safety requirements.
This paper designs an ORC system based on a two-input, two-output control strategy, resulting in two control loops. When the setpoint of one control loop changes, the error weighting coefficient of the other loop increases, causing its output to closely follow its setpoint, thereby mitigating the effects of system coupling [33].
For example, if the setpoint sp1 of the evaporator pressure output y1 in the first loop increases, the weighting coefficient r2 of the second controller immediately increases. As sp1 decreases, r2 gradually returns to its initial value. This adjustment reduces the deviation of the second loop output y2 from its setpoint sp2 caused by changes in sp1, thus achieving partial decoupling. A similar response occurs when the setpoint sp2 of the second loop output y2 changes.
r2 is calculated by the following equation:
where: represents ’s initial value, and k2 is the amplification factor of the difference between the setpoint and actual output.
In an ORC system controlled by Generalized Predictive Control, disturbances in evaporation pressure occur when the superheat degree setpoint changes [34]. However, a GPC control system with a setpoint observer can effectively mitigate this issue. When the superheat degree setpoint changes, the control variable adjustments in the observer-based system are smoother, reducing disturbances to the evaporation pressure. Therefore, setpoint observer-based control decoupling can indeed weaken the interdependencies between variables in the ORC system to some extent.
4. Multi-Model Strategy Based on Gap Metric
Although the boundaries of each linear submodule are optimized based on the multi-model selection strategy based on the gap measurement, it is obviously not reasonable to switch or weight the model directly through flue gas temperature and mass flow. This paper mainly discusses the multi-model strategies for ORC systems. The ORC system is a high-order inertial system with a strong time delay, so the influence of flue gas temperature and mass flow on the system is not instantaneous, so it is necessary to use the error output of the actual system model and linear sub-model as the basis for model switching or weighting.
In this paper, the response characteristics of the ORC system based on the weighting and switching strategies [35] are tested, and the Gaussian membership function is selected as the switching function.
where: y1,y2 represents the system output, is the output of the i-th model, and denotes the membership degree of the i-th model. Calculate the membership of each model and select the optimal model based on the maximum value.
In the simulation, the flue gas temperature and mass flow rate are gradually increased at t = 20 s, and the system model will transition from working condition M3 to working condition M4, and at the same time, according to the control requirements of the ORC system, the evaporation pressure is set to rise from 1500 Kpa to 1650 Kpa, and the working fluid temperature rises from 115 °C to 121 °C, and the control parameters are as follows:
The response process of the ORC system is shown in the following Figure 8:
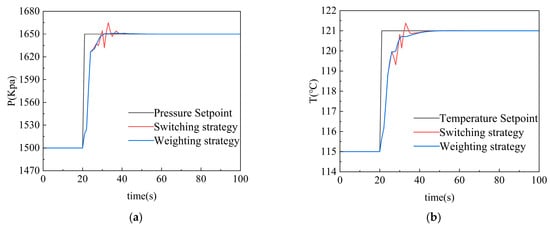
Figure 8.
ORC System Variable Operating Condition Response Diagram: (a) evaporative pressure response; (b) working substance temperature response.
The simulation results of variable working condition control of the ORC system show that the multi-model strategy based on switching can realize the working condition switching of the ORC system at 25 s time and ensure that the evaporation pressure and working fluid temperature finally converge to the target set range. However, the switching strategy has a relatively obvious switching oscillation phenomenon during model switching, and the jitter amplitude is large and the frequency is high, which directly affects the operation stability of the ORC system. In contrast, after the model weighting strategy is adopted, the dynamic response characteristics of the system are significantly improved, the smoothness of the transition curve is improved, and only the weak oscillations within the acceptable range are retained.
5. DDPG-Based Reinforcement Learning Strategy
Reinforcement Learning (RL) is a machine learning method with sequential decision optimization as its core. Through agents, the optimal mapping strategy from environmental states to actions can be learned [36]. The goal of reinforcement learning is to train the agent to learn a strategy during the interaction process to maximize the long-term cumulative reward. During this learning process, the agent continuously interacts with the established simulation platform, optimizes its own parameter structure, and thereby optimizes the control effect of the ORC system.
The ORC system is a multivariate system, and there are many control parameters involved in the system based on multi-model predictive control, and it is difficult to achieve global optimization by using only empirical methods for parameter selection, and it is easy to fall into the local optimal advantage. The ORC system established in this paper is divided into multi-model working conditions according to flue gas temperature and mass flow [37], and a single control parameter cannot meet the requirements of multi-model global regulation and control under the full range of working conditions. In the local operating area, even within a specific linearized model, the adjustment margin of the control parameters is still insufficient to maintain the global stability of the submodule. Therefore, this chapter uses a DDPG-based method to optimize the control parameters of the ORC system and proposes a strategy combining reinforcement learning and model prediction controller.
This paper uses the DDPG algorithm based on the Actor-Critic architecture. Its collaborative process can be briefly described as The Actor network generates and executes actions based on the state, the Critic network scores the value of these actions, and the target network provides reliable value references. Ultimately, the action generation capability of the Actor network and the value assessment accuracy of the Critic network are simultaneously optimized through error backpropagation. This architecture enables DDPG to handle both high-dimensional state Spaces and complex tasks that require fine motion adjustment. The specific process is as follows:
- (1)
- Deterministic actions are generated by the Actor network:
The noise types in Actor networks typically use OU noise or Gaussian noise to enhance exploration.
- (2)
- Experience replay:
Consistent with the processing in the DQN network, the transferred samples are stored in the experience pool to break the data correlation. Randomly sample N samples for batch training.
- (3)
- Update the Critic network:
Calculate the Q value of the target network:
Calculate and minimize the loss function of the Critic:
- (4)
- Update the Actor network: Maximize the Q value through gradient ascent:
Update the policy
- (5)
- Soft update of the target network, updating the target network in a small proportion:
The flowchart of the DDPG algorithm is shown in Figure 9:
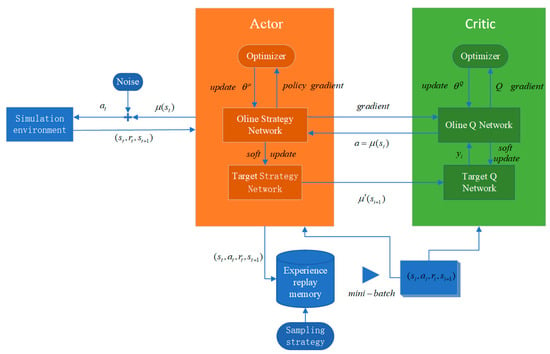
Figure 9.
DDPG flowchart.
The interaction between the agent, the controller, and the environment can be described as follows: When the set value of evaporation pressure and working fluid temperature changes, the agent selects a set of actions in the action space based on the state of the current ORC system, and its action is used as the control parameter of the controller. When the control parameters are transmitted to the GPC controller [38], the controller performs a control quantity adjustment according to the system error, and the change of the control quantity can adjust the output of the ORC system, and then the relevant feedback information is transmitted to the agent. According to the reward function, the agent optimizes the parameter selection of the controller before and after the controlled quantity reaches stability. Therefore, the agent can optimize the response curve of the system by outputting continuously changing control parameters in a control cycle so as to achieve the fast, accurate, and stable control requirements of the entire ORC system.
- (1)
- State space
Since state variables are sufficient to describe the future behavior of the system [39], the state variables in the ORC system are sent to the agent as observations, as described in Equation (1), which contains five state variables [40]: two-phase zone length, evaporation pressure, evaporation section wall temperature, condensation pressure, and condensation section wall temperature. Considering the characteristics of the ORC system and the sensor settings in practical applications, the evaporation pressure and the wall temperature of the evaporator are sent to the agent as the key state indicators, which can not only reduce the training cost but also conform to the data monitoring of the pressure and temperature sensors in the actual operation of the ORC. Secondly, the flue gas temperature and mass flow are sent to the agent as important environmental variables, which improves the performance of the agent to cope with the changes and disturbances caused by environmental changes. The control system is based on the two-input, two-output ORC model, so the instantaneous tracking error of the evaporation pressure and the temperature of the working fluid at the inlet of the expander are also regarded as observations, with a total of six observed variables.
- (2)
- Action space
In the design adopted in this paper, the action space of the agent is the relevant control parameter of the multi-model prediction controller mentioned above, which includes the softening factor and the control weight, and it can be determined that the softening factor is between 0.1 and 0.9 and the control weight is between 0.2 and 1.0 during the preliminary debugging, so the action space is a matrix with four rows and one column.
- (3)
- Reward function
The reward function [41] is used to evaluate the tracking performance of the control system’s setpoint. The agent strategy updates the rewards based on the different state-actions during the training process, thereby encouraging the expander action and the working fluid pump action to accurately track the evaporation pressure and working fluid temperature [42], while suppressing other undesirable actions. Therefore, it is very important to design an appropriate reward function to improve the training effect of agents and the control accuracy of the system.
The reward function used in this study is discrete, and the reward function corresponding to the temperature of the working fluid is shown in Equations (5)–(28). The first six items are used to evaluate the performance of the reference tracking, with smaller tracking errors corresponding to larger rewards. The penultimate item is used to avoid excessively frequent fluctuations in the actuator. If there is no penalty term, the agent may take on a “trick” behavior. In the control period before the evaporation pressure and working fluid temperature stabilize to the set value, frequent parameter changes will bring frequent jitter to the response curve of the system, resulting in the response curve not being smooth enough. Finally, if the reference setpoint is below or above the upper limit, the training will be stopped to save time, and a larger penalty value will be returned, as shown below for the reward and punishment function for the working fluid temperature.
The reward function for the evaporation pressure term looks like this:
In the ORC system control, it is desirable to prioritize the stability of the evaporation pressure, so the weight term of the evaporation pressure is increased in the reward function, and the total reward function is set to
The reward function comprehensively considers the characteristics and control requirements of the ORC system and provides comprehensive guidance for the training of agents so as to optimize the selection of control parameters of the ORC system so as to improve the control effect of the ORC system.
- (4)
- Network structure and related parameters
The network structure of Actors and Critics is shown in Figure 10:
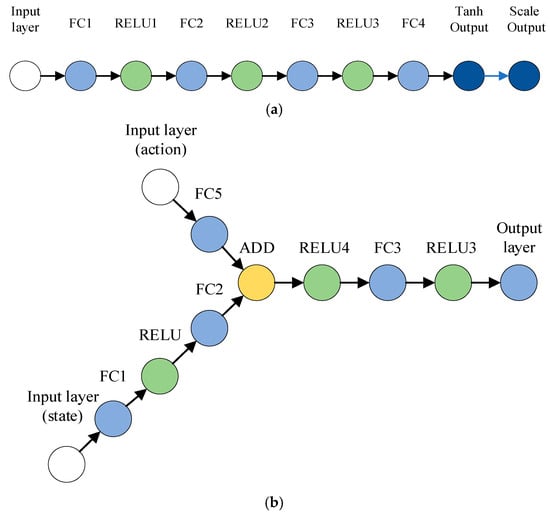
Figure 10.
Actor and Critic Network Structure: (a) Actor; (b) Critic.
Figure 10a shows that the actor network uses hierarchical feature extraction and dynamic adjustment mechanisms to achieve accurate mapping of the action space. The input layer directly receives the environmental observation signal, and the four fully connected layers each contain 200 nodes and cooperate with the Rectified Linear Unit (ReLU) activation function to gradually abstract the state characteristics and effectively capture the nonlinear relationship in the system dynamics. The output layer first constrains the original output of the network to the normalized interval through the Tanh function and then automatically calculates the linear transformation coefficient according to the preset action boundary so that the final action value is strictly adapted to the actual control range. This design avoids the defects of relying on manual calibration of the output scale in traditional methods and significantly improves the action adaptability of the algorithm.
Figure 10b shows that the Critic network constructs a shunt feature fusion framework to optimize the value function estimation. The state branch extracts the high-dimensional state representation through the double-layer fully connected network, and the action branch uses the single-layer network to realize the action vector encoding, and the two are interacted and fused through addition operation in the feature space. Compared with the traditional single-path structure, this shunt processing strategy reduces the connection parameters, reduces the complexity of the model, and enhances the explicit modeling ability of state-action association features, and the fusion features of the last layer of the ReLU network are mapped to Q value output after nonlinear activation.
- (5)
- Agent interaction and training:
The simulation platform is shown in Figure 11 below:
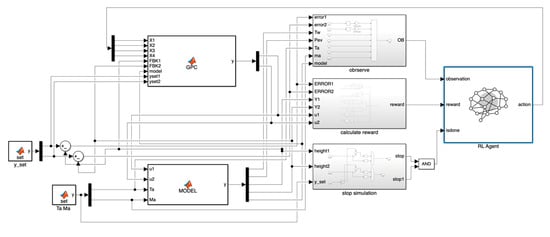
Figure 11.
ORC Simulation Platform.
The simulation platform includes a GPC controller with a set observer, an ORC system module, reinforcement learning-related components, and agents, in which a model weightier based on gap metrics is built into the ORC system module.
The Gaussian noise [43] enhances the exploration ability of the agent in the continuous action space in the environment, and on the basis of the deterministic action output of the strategy network, the Gaussian noise with an initial noise intensity of 0.4 and a linear attenuation coefficient of 0.0001 is superimposed to form the final execution action. This design has two advantages: on the one hand, it overcomes the problem of exploration direction deviation that may be caused by traditional correlated noise, which is especially suitable for multi-dimensional action scenarios such as ORC systems; on the other hand, this noise setting has been verified by similar simulations, which can ensure full exploration in the early stage of training and avoid the oscillation of value estimation caused by excessive noise in the later stage of strategy optimization [44].
When adjusting the training parameters, it was found that the discount factor had a significant impact on the training process. Some discount factors can make the training converge in a shorter period of time, but the cumulative reward is not ideal, while others may require a longer training time, but the cumulative reward is significantly larger. For the ORC-controlled agent, this paper tests the discount factor between 0.9 and 0.99 and finds that using the discount factor of 0.99 can produce the optimal value of the maximum cumulative reward.
The setting parameters and training parameters of the agent in similar simulations are shown in Table 4 below.

Table 4.
Agent Parameter Table.
Considering that the core starting point of this paper is to use the DDPG algorithm to optimize the control parameters of the generalized model prediction controller and set different evaporation pressure and working fluid temperature values in each training cycle and obtain the optimal set of control parameters through reinforcement learning. The variation range of the evaporation pressure is [0.14 Mpa, 0.25 Mpa], and the temperature of the working fluid is [110 °C, 140 °C]. In order to be consistent with the ORC control strategy, when the flue gas temperature fluctuates and the mass flow rate changes slightly, and the multi-model switcher shows that the system model remains unchanged, the evaporation pressure adjustment step is limited to ≤0.15 MPa and the working medium temperature step to ≤4 °C, maintaining the steady-state operation of the system.
When the flue gas temperature fluctuates or the mass flow rate changes significantly and the multi-model switcher shows that the model has changed, the evaporation pressure adjustment step is expanded to 0.3 MPa and the working medium temperature step to 8 °C, enhancing the dynamic response capability of the controller. The training results are shown in the following Figure 12:
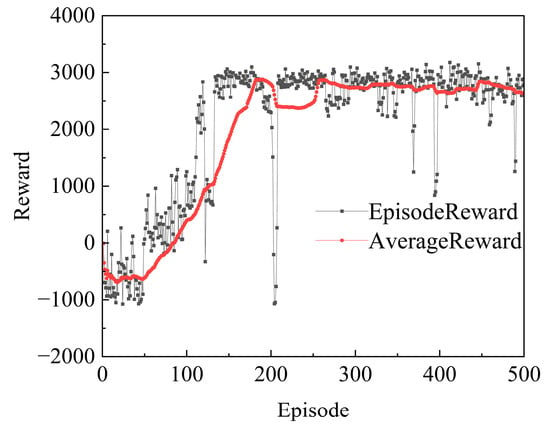
Figure 12.
Agent Training.
As can be seen from Figure 12, the reinforcement learning agent completes the convergence process within 150 training cycles, and its reward trajectory presents typical three-stage evolutionary characteristics: In the 0–50 cycle exploration stage, the system is in the early stage of strategy search, and the average reward value remains at the benchmark level; in the 50–150 cycle optimization stage, the non-linear growth of reward value is realized through strategy iteration, and the improvement is large. After 150 cycles, it enters the steady-state stage, and although it maintains a convergence trend, there are local fluctuations, indicating that the agent is still facing the challenge of environmental disturbance adaptability in the strategy fine-tuning period.
To evaluate the optimization performance of the deep deterministic policy gradient algorithm for agent parameters, the agent output was verified based on the typical working condition M3. The target value of the evaporation pressure was set to step from 1525 KPa to 1600 KPa, and the set value of the working medium temperature was increased from 112.25 °C to 114 °C. Similar simulation results are shown in Figure 13:
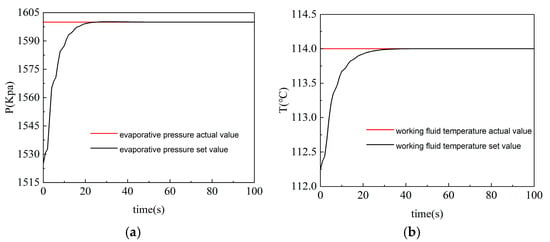
Figure 13.
Setpoint Tracking Test: (a) evaporative pressure response; (b) working fluid temperature response.
6. Simulation Results
When the evaporation pressure changes, the temperature of the working fluid will be disturbed to a certain extent, and this coupling relationship directly affects the dynamic performance of ORC, which is not conducive to the safe operation of the ORC system. Therefore, a control decoupling strategy based on set observers is proposed, which can be weakened by introducing error weights and adjusting the control weights in equal proportions. In order to test whether the optimization control parameters of the agent can improve the system coupling problem, two sets of similar simulations were set up under the same working conditions.
- (1)
- The evaporation pressure setpoint increased from 1500 Kpa to 1650 Kpa, and the working fluid temperature remained constant.
- (2)
- The temperature setting value of the working fluid is increased from 117.5 °C to 119.5 °C, and the evaporation pressure remains unchanged.
In order to test the decoupling performance of the DDPG-MGPC controller, the traditional PID controller is introduced as a comparison. The idea of PID control design is to control the evaporation pressure through the speed of the expander, and the temperature of the working substance is controlled by the speed of the working substance pump, and the parameters are optimized by the NCD toolbox of MATLAB_2024 software, which are as follows:
Among them, the parameters of the PID controller are set as shown in Table 5.

Table 5.
Parameter Settings of the PID Controller.
At the same time, in order to verify the effect of DDPG parameter optimization, a multi-model generalized prediction controller based on particle swarm optimization was introduced as a comparison. The control parameters obtained based on particle swarm optimization are as follows:
- (1)
- Single-variable regulation simulation
First, we conducted the first set of simulations, raising the evaporation pressure setting value from 1500 Kpa to 1650 Kpa while keeping the working fluid temperature constant. We expect that from the results, it can be observed that the evaporation pressure, after being regulated by the controller, increases from 1500 Kpa to 1650 Kpa. Meanwhile, the working medium temperature may undergo certain disturbances as the evaporation pressure rises, but ultimately the working medium temperature remains unchanged. The results of the first simulation are shown in Figure 14 below:
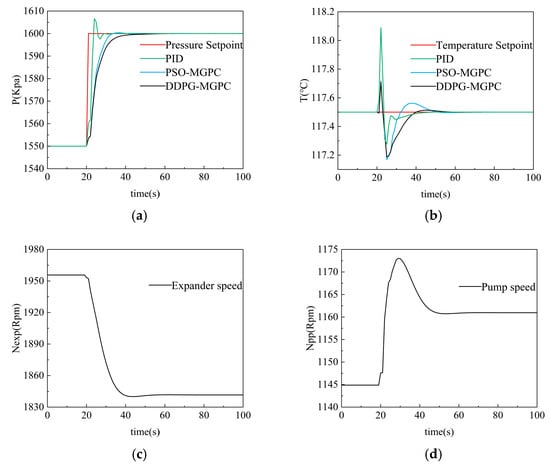
Figure 14.
ORC System Decoupling Strategy Validation 1: (a) evaporative pressure response; (b) working substance temperature response; (c) expander speed change; (d) pump speed change.
In the first set of similar simulations, the evaporation pressure setpoint was increased from 1500 Kpa to 1650 Kpa, and the working fluid temperature remained constant. The traditional PID controller shows extremely fast adjustment speed and short stability time in the process of evaporation pressure regulation, but its dynamic process has the problem of excessive overshoot, with a peak value of 1606.7 Kpa and a subsequent jitter with an amplitude of 2.5 Kpa, which exposes the limitations of classical control in a strongly coupled system. PSO-MGPC and DDPG-MGPC show similar fast-tracking characteristics in the early stage of dynamic response, but the convergence time of DDPG-MGPC to 1599 Kpa is 4 s longer than that of PSO-MGPC.
In the process of working fluid temperature adjustment, the initial response amplitude of the PID controller is the largest, with a peak value of 118.08 °C, and there are many jitters in the response process, and the time to return to steady state is the longest. The first return of PSO-MGPC to the setpoint was 12 s, but then there was an overshoot with a peak value of 117.56 °C. The ORC system under the control of DDPG-MGPC has the shortest temperature stability time and the smoothest response curve.
The performance comparison of the PID controller, PSO-MGPC controller, and DDPG-MGPC controller is shown in the following Table 6:

Table 6.
Comparison of working fluid temperature control effect.
Secondly, we conducted the second set of simulations, raising the working fluid temperature setting from 117.5 °C to 119.5 °C while keeping the evaporation pressure constant, in contrast to the first experiment. We estimate that the working medium temperature will rise from 117.5 °C to 119.5 °C after being regulated by three controllers at 20 s, while the working medium temperature will experience a sharp disturbance at 20 s and remain unchanged in the end. The results of second simulation are shown in Figure 15 below:
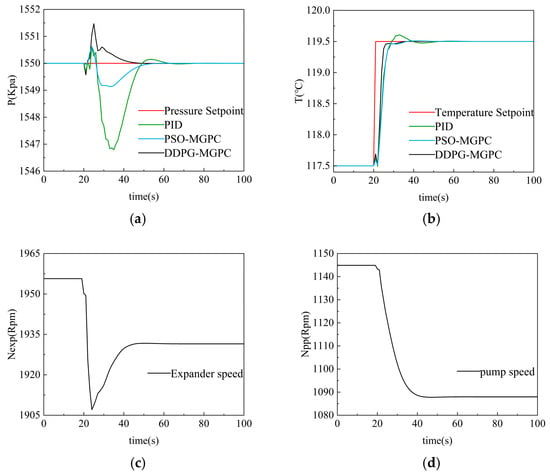
Figure 15.
ORC System Decoupling Strategy Validation 2: (a) evaporative pressure response; (b) working substance temperature response; (c) expander speed change; (d) pump speed change.
In the second group of similar simulations, the temperature setting value of the working fluid increased from 117.5 °C to 119.5 °C, and the evaporation pressure remains unchanged. The jitter frequency of the system under PID control was extremely high, with the lowest plunge to 1546.79 Kpa and the longest convergence time to 1550.01 Kpa. The ORC system based on DDPG-MGPC control has a jitter with a maximum amplitude of 1551.46 Kpa, and the return to steady state process is extremely fast. The PSO-optimized controller is softer and has a settling time between the DDPG-MGPC and the PID controller.
In the process of working fluid temperature regulation, the working fluid temperature of the system under PID control has a certain overshoot, and the peak value is 119.60 °C, which is the longest stability time. Among the two sets of curves based on PSO and DDPG, the ORC system based on DDPG-MGPC has the fastest response speed and the shortest stabilization time.
The performance comparison of PID controllers, PSO-MGPC, and DDPG-MGPC controllers is shown in Table 7:

Table 7.
Comparison of evaporative pressure control effects.
On the whole, although the traditional PID control can achieve the basic operation goal in the ORC system, because the PID is based on a model-free control strategy, it has certain limitations in dealing with MIMO systems, which is manifested in the problems of obvious jitter and excessive overshoot. The GPC controller combined with the decoupling observer has stronger decoupling performance than the PID algorithm, and the response process of the ORC system under the control of DDPG-MGPC is smoother, which greatly improves the response speed while suppressing the overshoot.
- (2)
- Multi-variable collaborative regulation simulation
In order to verify the control effect of DDPG-MGPC under variable working conditions, the flue gas flow rate and flue gas temperature are gradually increased at t = 20 s, and the system model will transition from working condition M3 to working condition M4. The evaporation pressure is increased from 1500 Kpa to 1650 Kpa, and the temperature of the working fluid is increased from 115 °C to 121 °C.
The simulation results are shown in Figure 16, which shows that the changes in flue gas temperature and mass flow rate of the heat source have a certain impact on the control effect of the system, resulting in a certain amount of jitter in the process of setting value tracking.

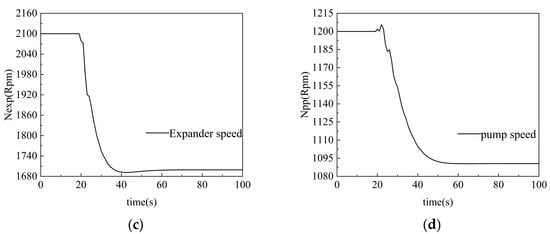
Figure 16.
ORC System Variable Operating Condition Response Diagram: (a) evaporative pressure response; (b) working substance temperature response; (c) expander speed change; (d) pump speed change.
Under the change of working conditions, the evaporation pressure of the ORC system under PID control increased sharply to 1675.38 Kpa, and the overshoot was 16.9%, and then it stabilized at 1650.0 Kpa after secondary oscillation. Both the PSO-MGPC and DDPG-MGPC controllers maintained good control performance under the multi-model weighting strategy, but the adjustment speed of the PSO-MGPC controller was slightly lower than that of the controller based on DDPG optimization, and the tracking speed of evaporation pressure lagged behind by about 2 s on average, and the stabilization time was also longer. The DDPG-MGPC controller exhibits similar dynamic characteristics to the PID strategy in the tracking of the working fluid temperature setpoint, with small jitter, but overall, within the acceptable range.
The performance comparison of PID, PSO-MGPC, and DDPG-MGPC controllers is shown in the following Table 8 and Table 9:

Table 8.
Comparison of evaporative pressure control effects (the evaporation pressure: 1500 Kpa; the temperature of the working fluid: 117.5 °C).

Table 9.
Comparison of working fluid temperature control effect (the evaporation pressure: 1500 Kpa; the temperature of the working fluid: 117.5 °C).
Overall, the ORC system optimized by the DDPG-MGPC controller shows significant advantages in variable operating conditions. The evaporation pressure under PID control shows obvious overshoot and jitter trends, while the adjustment speed of the PSO-MGPC controller is relatively slow, and the settling time and rise time are longer than those of the DDPG-MGPC controller.
However, there is still room for improvement in the current optimization scheme in terms of jitter suppression, which is manifested in the fact that although the jitter phenomenon generated by the system in the working condition change stage has been effectively attenuated, its fluctuation has not been completely eliminated. This shows that the multi-model coordination mechanism in the control strategy still has the potential to be optimized, and the subsequent research can improve the control continuity by constructing a finer model weight allocation function.
Overall, based on the generalized model predictive control, DDPG-MGPC, through the optimization of the controller structure and control parameters, achieves multiple improvements in overall suppression, steady-state accuracy, and robustness while ensuring the system response speed, providing an innovative solution for the efficient and precise control of the ORC system.
Since there will be certain interferences in the actual production, in order to test the robustness of the controller based on DDPG-MGPC against disturbances, the anti-disturbance ability test of the ORC system is added. Firstly, the environmental noise with a coefficient of 0.2 was added. Then, the flue gas temperature was increased from 180 °C to 181 °C, and the mass flow rate was increased from 0.80 kg/s to 0.81 kg/s. The static gains of the two circuits of the feedforward compensator were set at 0.08 and 0.02, respectively. It was observed whether the ORC system could still maintain around the set value. The similar simulation results are shown in the following Figure 17:
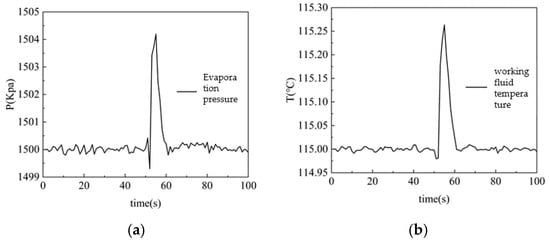
Figure 17.
ORC system robustness testing: (a) evaporative pressure change; (b) working fluid temperature change.
Similar simulation results show that the controller based on DDPG-MGPC architecture shows excellent interference suppression ability when facing the disturbance of gas temperature and mass flow rate. The evaporation pressure and working fluid temperature were always maintained within the set target interval, and the fluctuation amplitude was strictly constrained below the allowable engineering threshold. This proves that the controller can effectively offset the influence of external disturbance on the controlled quantity through the dynamic compensation mechanism and still maintain excellent tracking performance in complex operating environments. The performance is derived from the real-time adjustment of system control parameters by the DDPG strategy and the robustness and feedforward compensation effect of the generalized model predictive controller. Under the synergistic effect, it provides multiple guarantees for the safe and stable operation of the ORC system.
7. Conclusions
This paper conducts research on the modeling and control issues of the ORC system. The main contributions and innovation points are:
This paper designs a GAP-M multi-model strategy based on gap measurement. The working conditions are divided by flue gas temperature and mass flow rate, and the model segmentation is achieved through gap measurement and neighborhood estimation. In view of the strong coupling characteristics of the ORC system, a MIMO generalized predictive control framework is proposed. The coupling effect is reduced through dynamic observation and interference compensation, breaking through the limitations of traditional single-loop control. Based on the division of multiple models under working conditions and adopting the model weighting strategy, reinforcement learning is innovatively combined with multi-model predictive control. The DDPG network is utilized to autonomously optimize the controller parameters, avoiding the local optimum problem of traditional parameter tuning. The ultimate goal is to achieve real-time adjustment and global optimization of the control parameters of the ORC system. By comparing the simulation results with the traditional PID and PSO-MGPC strategies, the results show that the DDPG-MGPC control strategy proposed in this paper is significantly better than the existing methods in terms of dynamic response speed and steady-state accuracy, especially in complex working conditions. The research content of this paper provides a theoretical basis and technical path for the intelligent control of the ORC low-temperature waste heat power generation system.
Author Contributions
Conceptualization, J.L. and Z.G.; methodology, Z.G. and X.Z.; software, X.Z.; validation, Z.G., X.Z., and J.Z.; formal analysis, Z.G.; investigation, Z.G.; data curation, X.Z.; writing—original draft preparation, Z.G.; writing—review and editing, J.L. and X.Z.; visualization, Z.G. and X.Z.; supervision, J.L.; project administration, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was by the control research and development of the ORC low-temperature waste heat power generation system, led by Li Jing, a master’s supervisor from the Control Science and Engineering Team of the Engineering Technology Research Institute of University of Science and Technology Beijing, grant number 39320260.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Nomenclature | Subscript | ||
| q/Q | Heat (J) | a | Heat source |
| Mass flow rate (kg/s) | i | Inlet/inside | |
| h | Enthalpy value (J/kg) | o | Outlet |
| η | Efficiency | exp | Expander |
| ρ | Density | con | Condenser |
| A | Cross-sectional area (m2) | pp | Working medium pump |
| D | Cross-sectional diameter (m) | p | pump |
| P | Pressure (kPa) | amb | Ambient temperature |
| γ | Average gas content | rec | Heat recovery |
| L | Length (m)/Loss | l | Liquid |
| T | Temperature (K) | v | Gas |
| t | Time (s) | ev | Evaporator |
| V | Volume (m3) | w | wall |
| C | Specific heat capacity (J/(kg*K) | ||
| ff | Filling coefficient | ||
| N | Rotational speed (r) | ||
| v | Specific volume (m3/kg) |
References
- Guo, Z.; Wang, J.; Dong, F.; Xu, H. Multi-objective optimization of multi-energy complementary system based on cascade utilization of heat storage. Energy Convers. Manag. 2024, 299, 117864. [Google Scholar] [CrossRef]
- Damarseckin, S.; Kane, S.Y.J.; Atiz, A.; Karakilcik, M.; Sogukpinar, H.; Bozkurt, I.; Oyucu, S.; Aksoz, A. A comparative review of ORC and R-ORC technologies in terms of energy, exergy, and economic performance. Heliyon 2024, 10, e40575. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, D.; Gao, G.; Li, J.; Yang, Z.; Lin, R. Thermal performance study of a solar-coupled phase changes thermal energy storage system for ORC power generation. J. Energy Storage 2024, 78, 110126. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, G.; Li, L.; Yang, Q.; Tang, B.; Liu, Y. Expansion devices for organic Rankine cycle (ORC) using in low temperature heat recovery: A review. Energy Convers. Manag. 2019, 199, 111944. [Google Scholar] [CrossRef]
- Kumar, R.; Queyam, A.B.; Singla, M.K.; Louzazni, M.; Kumar, M.D. Optimizing Efficiency and Performance in a Rankine Cycle Power Plant Analysis. Energy Eng. 2025, 122, 1373–1386. [Google Scholar] [CrossRef]
- Wu, X.; Lin, L.; Xie, L.; Chen, J.; Shan, L. Fast robust optimization of ORC based on an artificial neural network for waste heat recovery. Energy 2024, 301, 131652. [Google Scholar] [CrossRef]
- Xiao, M.; Zhou, Y.; Miao, Z.; Yan, P.; Zhang, M.; Xu, J. Multi-condition operating characteristics and optimization of a small-scale ORC system. Energy 2024, 290, 130099. [Google Scholar] [CrossRef]
- Galindo, J.; Dolz, V.; Royo-Pascual, L.; Brizard, A. Dynamic Modeling of an Organic Rankine Cycle to recover Waste Heat for transportation vehicles. Energy Procedia 2017, 129, 192–199. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.; Zhang, H.; Xing, C.; Yang, H.; Wang, Y. An integrated online dynamic modeling scheme for organic Rankine cycle (ORC): Adaptive self-organizing mechanism and convergence evaluation. Appl. Therm. Eng. 2023, 234, 121256. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Y.; Xu, S. Temperature sensitivity characteristics of PEM fuel cell and output performance improvement based on optimal active temperature control. Int. J. Heat Mass Transf. 2023, 206, 123966. [Google Scholar] [CrossRef]
- Chowdhury, J.I.; Thornhill, D.; Soulatiantork, P.; Hu, Y.; Balta-Ozkan, N.; Varga, L.; Nguyen, B.K. Control of supercritical organic Rankine cycle based waste heat recovery system using conventional and fuzzy self-tuned PID controllers. Int. J. Control Autom. Syst. 2019, 17, 2969–2981. [Google Scholar] [CrossRef]
- Cabral, I.M.; Pereira, J.S.; Ribeiro, J.B. Performance evaluation of PID and Fuzzy Logic controllers for residential ORC-based cogeneration systems. Energy Convers. Manag. X 2024, 23, 100622. [Google Scholar] [CrossRef]
- Santos, M.; André, J.; Mendes, R.; Ribeiro, J.B. Optimization of ORC-Based Micro-CHP Systems: An Simulation and Control-Oriented Study. Processes 2025, 13, 1104. [Google Scholar] [CrossRef]
- Reddy, C.R.; Vinhaes, V.B.; Naber, J.D.; Robinett, R.D., III; Shahbakhti, M. Model predictive control of a dual fuel engine integrated with waste heat recovery used for electric power in buildings. Optim. Control Appl. Methods 2023, 44, 699–718. [Google Scholar] [CrossRef]
- Shi, Y.; Lin, R.; Wu, X.; Zhang, Z.; Sun, P.; Xie, L.; Su, H. Dual-mode fast DMC algorithm for the control of ORC based waste heat recovery system. Energy 2022, 244, 122664. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Jin, M.; Shu, G.; Tian, H.; Pan, J. Control of superheat of organic Rankine cycle under transient heat source based on deep reinforcement learning. Appl. Energy 2020, 278, 115637. [Google Scholar] [CrossRef]
- Lin, R.; Luo, Y.; Wu, X.; Chen, J.; Huang, B.; Su, H.; Xie, L. Surrogate empowered Sim2Real transfer of deep reinforcement learning for ORC superheat control. Appl. Energy 2024, 356, 122310. [Google Scholar] [CrossRef]
- Recht, B. A tour of reinforcement learning: The view from continuous control. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 253–279. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Stillman, B. The remarkable gymnastics of ORC. eLife 2022, 11, e76475. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhou, Y.; Wang, R.; Xu, J.; Fang, F. Modeling and constrained multivariable predictive control for ORC (Organic Rankine Cycle) based waste heat energy conversion systems. Energy 2014, 66, 128–138. [Google Scholar] [CrossRef]
- Zhang, J.; Li, K.; Xu, J. Recent developments of control strategies for organic Rankine cycle (ORC) systems. Trans. Inst. Meas. Control 2019, 41, 1528–1539. [Google Scholar] [CrossRef]
- Esposito, M.C.; Pompini, N.; Gambarotta, A.; Chandrasekaran, V.; Zhou, J.; Canova, M. Nonlinear model predictive control of an organic Rankine cycle for exhaust waste heat recovery in automotive engines. IFAC-Papers Online 2015, 48, 411–418. [Google Scholar] [CrossRef]
- Foias, C.; Georgiou, T.T.; Smith, M.C. Robust Stability of Feedback Systems: A Geometric Approach Using the Gap Metric. SIAM J. Control Optim. 2006, 31, 1518–1537. [Google Scholar] [CrossRef]
- Ahmadi, M.; Haeri, M. A systematic decomposition approach of nonlinear systems by combining gap metric and stability margin. Trans. Inst. Meas. Control 2021, 43, 2006–2017. [Google Scholar] [CrossRef]
- Du, J.; Song, C.; Li, P. Application of gap metric to model bank determination in multilinear model approach. J. Process Control 2009, 19, 231–240. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Gentil, G.; Batista, E.; Andrea, C. Development of a Generalized Predictive Control System for Polynomial Reference Tracking. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 2875–2879. [Google Scholar] [CrossRef]
- Abdenouri, N.; Zoukit, A.; Salhi, I.; Doubabi, S. Thermal management of an unloaded hybrid dryer by generalized predictive control. Dry. Technol. 2022, 40, 2836–2848. [Google Scholar]
- Horla, D. Simulation results on actuator/sensor failures in adaptive GPC position control. Actuators 2021, 10, 43. [Google Scholar] [CrossRef]
- Linnemann, A.; Maier, R. Decoupling by precompensation while maintaining sterilizability. IEEE Trans. Autom. Control 1993, 38, 629–632. [Google Scholar] [CrossRef]
- Djouadi, S.M. On robustness in the gap metric and coprime factor uncertainty for LTV systems. Syst. Control Lett. 2015, 80, 16–22. [Google Scholar] [CrossRef]
- Liang, W.; Amini, N.H. Model robustness for feedback stabilization of open quantum systems. Automatica 2024, 163, 111590. [Google Scholar] [CrossRef]
- Hespanha, J.; Liberzon, D.; Morse, A.S.; Anderson, B.D.O.; Brinsmead, T.S.; De Bruyne, F. Multiple model adaptive control. Part 2: Switching. Int. J. Robust Nonlinear Control 2001, 11, 479–496. [Google Scholar] [CrossRef]
- Narendra, K.S.; Balakrishnan, J. Adaptive control using multiple models. IEEE Trans. Autom. Control 1997, 42, 171–187. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Tang, Y. State tracking model reference adaptive control for switched nonlinear systems with linear uncertain parameters. J. Control Theory Appl. 2012, 10, 354–358. [Google Scholar] [CrossRef]
- Xie, J.; Li, S.; Yan, H.; Yang, D. Model reference adaptive control for switched linear systems using switched multiple models control strategy. J. Frankl. Inst. 2019, 356, 2645–2667. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Zhang, Z.; Zhang, D.; Qiu, R.C. Deep reinforcement learning for power system applications: An overview. CSEE J. Power Energy Syst. 2020, 6, 213–225. [Google Scholar]
- Qian, R.-R.; Feng, Y.; Jiang, M.; Liu, L. Design and Realization of Intelligent Aero-engine DDPG Controller. J. Phys. Conf. Ser. 2022, 2195, 012056. [Google Scholar] [CrossRef]
- Follansbee, P.S. Development and application of an internal state variable constitutive model for deformation of metals. J. Mater. Res. Technol. 2025, 36, 284–291. [Google Scholar] [CrossRef]
- Salam, Y.; Li, Y.; Herzog, J.; Yang, J. Human2bot: Learning zero-shot reward functions for robotic manipulation from human demonstrations. Auton. Robot. 2025, 49, 10. [Google Scholar] [CrossRef]
- Huang, C.; Wang, G.; Zhou, Z.; Zhang, R.; Lin, L. Reward-adaptive reinforcement learning: Dynamic policy gradient optimization for bipedal locomotion. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 7686–7695. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Duan, X.; Xiong, Z.; Yao, P. Tugboat scheduling method based on the NRPER-DDPG algorithm: An integrated DDPG algorithm with prioritized experience replay and noise reduction. Sustainability 2024, 16, 3379. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, J.; Wei, Z.; Wang, H.; Li, S. A UAV Pursuit-Evasion Strategy Based on DDPG and Imitation Learning. Int. J. Aerosp. Eng. 2022, 2022, 3139610. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).