Abstract
Accurate State of Charge (SOC) estimation is challenged by battery aging and complex internal dynamics. This work introduces a novel framework, Mamba-PG, that leverages the Mamba architecture to integrate internal gas pressure—a direct indicator of electrochemical state—for high-accuracy SOC estimation. The core innovation is a specialized pressure-aware gating mechanism designed to adaptively fuse the pressure signal with conventional electrical data. On a public dataset, our model achieved a state-of-the-art Mean Absolute Error (MAE) of 0.386%. Furthermore, we demonstrate that the gating mechanism learns a physically-plausible and interpretable strategy, dynamically adjusting the pressure signal’s influence based on its magnitude and the battery’s aging state. This study validates that the synergy of novel physical signals with efficient, interpretable architectures like Mamba presents a robust path toward next-generation Battery Management Systems.
1. Introduction
1.1. Background and Literature Review
With the widespread adoption of electric vehicles (EVs), renewable energy systems, and portable electronic devices, LIBs have emerged as a critical energy carrier. Their performance directly determines the efficiency and stability of the entire energy system. Among the key parameters for battery management, the SOC plays a pivotal role in evaluating the remaining capacity and lifespan of the battery. It serves as a core metric in Battery Management Systems (BMSs), supporting modules such as energy dispatch, fault diagnosis, and range prediction. Accurate SOC estimation is vital to ensuring system safety, preventing overcharging or overdischarging, extending battery life, and improving energy utilization efficiency.
However, SOC is an internal state variable that cannot be directly measured via sensors. Its estimation must rely on observable external signals, such as voltage, current, and temperature. This indirect estimation process faces numerous challenges, including the battery’s nonlinear dynamic behavior, aging effects, environmental disturbances, and long-term electrochemical parameter drift. Thus, achieving high-accuracy, robust, and real-time SOC estimation under complex application scenarios has become a key and difficult issue in the intelligent design of BMS.
SOC estimation methods are traditionally categorized into three types: direct measurement, model-based, and data-driven approaches. Direct methods, such as Coulomb counting and open-circuit voltage, are simple but prone to cumulative error and environmental interference, making them unsuitable for dynamic conditions [1]. Specifically, the reliance on precise initial SOC values and the sensitivity to current sensor drift make Coulomb counting unreliable over long driving cycles in EVs. Model-based methods rely on equivalent circuit models or electrochemical models, often coupled with Kalman filter algorithms [2]. While physically interpretable, these methods suffer from high modeling complexity and poor generalizability across varying operating conditions [3]. The core challenge lies in the fact that model parameters can drift significantly with battery aging and temperature, requiring frequent and complex re-parameterization to maintain accuracy.
In contrast, data-driven methods leverage machine learning to capture patterns in historical operational data, enabling strong nonlinear modeling capabilities without the need for physical models. Common approaches include support vector machines [4], artificial neural networks [5], and deep learning architectures. Among them, recurrent neural networks (e.g., Long Short-Term Memory (LSTM) [6,7] and GRU [8]) are particularly suited for time-series modeling and have shown promising results in SOC estimation. Their ability to process sequential information makes them inherently suitable for capturing the time-dependent dynamics of batteries. While LSTM and GRU improve sequence understanding over traditional artificial neural networks, they still struggle with long-term dependencies and computational efficiency [9]. This limitation can be particularly problematic when trying to model dependencies across entire charge–discharge cycles, which can span thousands of time steps.
To address these limitations, Transformer-based models have been introduced into SOC estimation tasks. Variants such as Informer [10] and BERT [11] utilize attention mechanisms to capture long-range dependencies effectively. However, the quadratic computational complexity of self-attention with respect to sequence length makes Transformers computationally intensive and hardware-demanding [12]. To further enhance predictive accuracy, hybrid architectures have also been explored. For instance, Liu et al. [13] proposed the MconvTCN-Informer model, which integrates multi-scale convolutional networks with the Informer architecture to effectively model both time-domain and frequency-domain features for SOC prediction. This creates a significant gap between their powerful offline modeling capabilities and the practical constraints of on-board deployment in resource-limited BMS hardware.
Addressing the efficiency challenge of Transformers, the Mamba architecture—a novel sequence modeling framework based on SSMs—has recently gained attention in battery health estimation tasks. Beyond direct battery state estimation, advanced deep learning models are also being deployed for operational strategies in energy markets. For example, Kırat et al. [14] developed an integrated system using the N-HiTS model for electricity price forecasting to optimize arbitrage strategies for second-life battery stations. Mamba achieves linear computational complexity and incorporates a selective memory mechanism that allows dynamic retention or suppression of information [15]. These advantages enable Mamba to maintain modeling accuracy while significantly reducing resource consumption. This efficiency is particularly critical for battery state estimation, as the ultimate goal is to deploy these models on resource-constrained Battery Management System (BMS) microcontrollers in electric vehicles and other edge device [16]. While Mamba has already demonstrated promising results in State of Health (SOH) [17] and Remaining Useful Life [18] estimation, its potential for the high-frequency task of SOC estimation remains unexplored.
In addition to conventional signals such as voltage, current, and temperature, recent studies have begun to explore gas-related signals generated during battery operation, including gas composition and pressure changes [19]. These signals provide a direct window into the battery’s internal electrochemical state, as key degradation and operational mechanisms are intrinsically linked to gas evolution. Specifically, processes such as the formation and decomposition of the Solid Electrolyte Interphase (SEI) layer, electrolyte oxidation at high states of charge, and even lithium plating during fast charging, are known to generate gases like , , and . The accumulation of these gases leads to measurable changes in the cell’s internal pressure. For example, in study [20], a built-in pressure sensor was used to map battery states to internal pressure variations, demonstrating the potential of this signal. Since these gas-generating reactions are highly dependent on the battery’s voltage and charge level, the internal pressure contains rich, nonlinear information directly correlated with SOC that is orthogonal to traditional electrical signals. However, despite the recognition of its potential, a systematic approach to effectively integrate this dynamic pressure signal into a high-precision SOC estimation framework is still lacking, see Table 1. Inspired by this strong physical evidence, we propose a novel approach to incorporate internal battery pressure data into the SOC estimation framework.

Table 1.
Taxonomy of recent SOC estimation methods.
1.2. Gaps and Contributions
Despite considerable progress in SOC estimation research, several gaps remain:
- Most existing SOC estimation methods rely on traditional signals (voltage, current, temperature), overlooking the potential of leveraging richer physical and chemical indicators such as internal gas pressure.
- There is a lack of specialized mechanisms to effectively extract and model the dynamics of gas pressure signals and their nonlinear relationship with SOC.
- Although the Mamba architecture has shown promise in SOH and RUL estimation, its application in SOC estimation has not yet been explored.
Based on these observations, this work makes the following contributions:
- We are the first to introduce internal gas pressure signals for SOC estimation, expanding the feature space beyond conventional measurements.
- We design a novel gating mechanism tailored for gas pressure signals, enhancing the model’s ability to capture and interpret their dynamic behavior.
- We pioneer the use of the Mamba architecture for SOC estimation, leveraging its linear complexity and selective memory mechanism to build a lightweight yet effective sequence model.
2. Methodology
This study proposes an enhanced SSM architecture based on the Mamba framework to improve battery SOC prediction. Specifically, we introduce a pressure-aware gating mechanism to integrate voltage, current, and internal gas pressure as multidimensional input features. The hidden state updates are performed using matrix exponential discretization, preserving the theoretical foundations and long-sequence modeling capabilities of the Mamba structure.
2.1. Input Embedding with Pressure-Aware Gating
A core innovation of this work is the introduction of a pressure-aware gating mechanism. The rationale is rooted in the fundamental electrochemical processes within LIBs, where the internal pressure provides a direct window into side reactions that are intrinsically linked to SOC. The rate of gas generation is not constant but is a complex, nonlinear function of the battery’s state. For instance, at high SOC, the elevated electrode potential accelerates electrolyte oxidation, leading to a significant increase in the generation rate of gases like and a corresponding sharp rise in pressure. This makes the pressure signal a highly sensitive indicator in this region. The informativeness of the pressure signal is therefore dynamic, and a simple static fusion would fail to capture its varying relevance. Our proposed pressure-aware gate is designed specifically to learn this dynamic, nonlinear relationship, allowing the model to adaptively weight the pressure input based on its physical relevance at each time step. This provides a strong physical basis for the model’s design and enhances its interpretability.
At each time step t, the raw sensor measurements are organized as:
where , , and denote the terminal voltage, current, and internal gas pressure, respectively.
We first project into a d-dimensional latent space via a linear mapping followed by a GELU activation:
where and are learnable parameters. To ensure that the third dimension of exclusively captures pressure information, we impose a structural constraint on the weight matrix . Specifically, the first two entries of its third row are fixed at zero, while all other entries (denoted by “*”) are freely learned:
where “*” denotes a freely learned entry. Consequently, and the first two entries of the third row are fixed at zero. Consequently,
guaranteeing that the third component of is a pure nonlinear embedding of the pressure signal.
Next, to dynamically modulate the impact of internal gas pressure, we define a scalar gating coefficient:
with , , and as the Sigmoid activation. This coefficient reweights only the pressure-related channel of the latent vector:
This selective modulation prevents both under- and overestimation of pressure influence, allowing its contribution to vary adaptively over time and operating conditions. Since the gating operation is differentiable and optimized jointly with all model parameters, the network can discover in a data-driven manner the true relevance of pressure for SOC prediction during training, as illustrated in Figure 1.
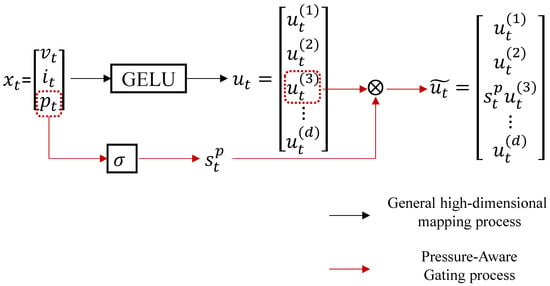
Figure 1.
Pressure gate mechanism.
2.2. State–Space Dynamics with Enhanced Mamba Formulation
The temporal modeling is built upon the Mamba architecture, a recent advancement in state–space sequence modeling that provides an efficient alternative to attention-based Transformers for long-range dependencies. Mamba approximates the sequence dynamics using a parameterized state–space model with a convolution kernel derived from a structured state equation, as illustrated in Figure 2.
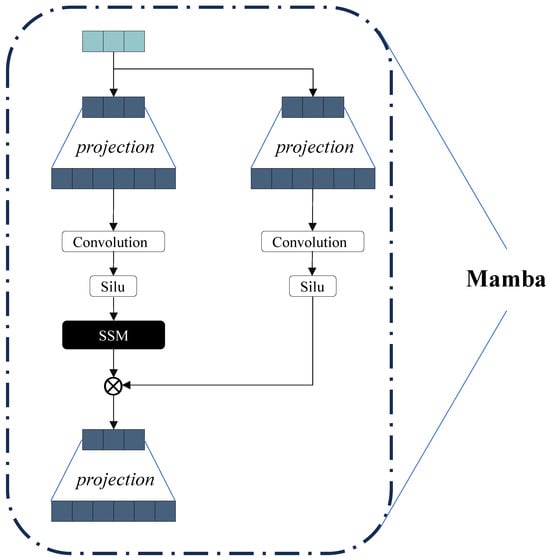
Figure 2.
Mamba block diagram.
The continuous-time formulation of the system is:
where is the system’s hidden state, and , , and are learned matrices governing the system dynamics.
To enable efficient implementation, Mamba leverages the linearity of the state–space equation to derive a convolutional form:
where the kernel encapsulates the system’s memory and response characteristics. This convolution can be discretized and efficiently implemented using fast Fourier transforms or linear recurrences.
To discretize the state dynamics, we use the matrix exponential method with fixed step size , giving:
where is the discrete-time transition matrix, and is the discrete-time input matrix. This allows the recurrent update of the hidden state:
where is a learnable output bias.
Notably, Mamba parameterizes the state matrix A in a structured diagonal plus low-rank format:
where is diagonal, and with , allowing fast computation of matrix exponentials via the Woodbury identity. This structure preserves long-range memory while maintaining low computational cost.
Overall, this formulation preserves the theoretical consistency of continuous-time dynamics, leverages the efficient convolutional structure of Mamba, and incorporates gated input modulation for adaptive sequence modeling in dynamic battery environments.
2.3. Loss Function and Optimization
The model is trained by minimizing a loss function composed of the mean squared error and an regularization term:
where is the ground truth SOC, is the regularization coefficient, and denotes all trainable parameters.
Optimization is performed using the Adam optimizer with hyperparameters . During training, a sliding window approach is adopted with sequence length L and batch size B. Learning rate scheduling strategies such as cosine annealing or step decay can be applied. Hyperparameters including d, N, , and are tuned via cross-validation.
3. Experiment
3.1. Dataset Description
The dataset used in this study [21] is derived from systematic experiments on commercial 21700-size lithium-ion cells produced by LG Chem (Seoul, South Korea), which use NMC 811 ternary materials as the positive electrode and graphite-SiOx composite materials as the negative electrode. The dataset focuses on the dynamic evolution of the gas pressure inside the cell, aiming to reveal the coupling relationship between internal gas generation and the SOC, temperature, and aging behavior of the cell. All experiments in the dataset were conducted under controlled isothermal conditions at 25 °C to isolate the effects of aging and SOC on the pressure signal. The experiment covers three stages: First, in the pretreatment stage, the initial internal gas pressure of the cell in the factory state is measured by a customized penetration test device to evaluate the gas accumulation under the formation cycle and initial SOC conditions to ensure that the test process has no significant impact on the cell structure and performance. Subsequently, in the instrumentation stage, high-precision micro pressure sensors are embedded in the cell to achieve in situ and real-time monitoring of the internal gas pressure, and performance verification experiments confirm that the impact of sensor integration on cell performance is negligible. In the subsequent aging test stage, the three cells undergo 100 standard charge and discharge cycles to track the irreversible accumulation effect of gas pressure with increasing cycle number. Taking battery W7 as an example, the voltage, current, and pressure data of the first 10 cycles are shown in Figure 3.
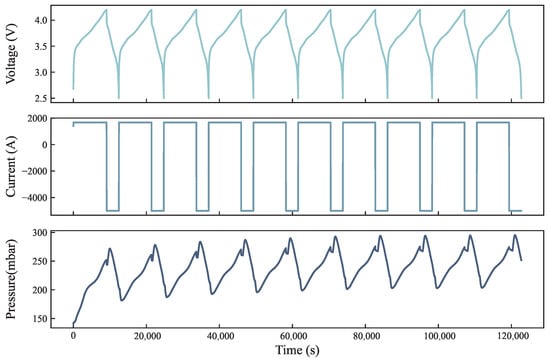
Figure 3.
Data set charging, discharging, and internal pressure data.
3.2. Experimental Setup
This section details the data preprocessing pipeline, the cross-validation strategy employed for robust model evaluation, and the specific implementation details of the training process.
3.2.1. Data Preprocessing and Feature Engineering
The input features selected for SOC estimation were the terminal voltage (), current (), and internal gas pressure () of the battery cells. The target variable was the . Both input features and the target SOC values were independently normalized to a range of . For each fold in the cross-validation, the normalization scalers were fitted exclusively on the raw data points corresponding to the training set of that particular fold and subsequently used to transform the training, validation, and test sets.
To prepare the data for the sequence models, time-series sequences were generated. A sequence length of 200 time steps and a sampling stride of 100 time steps were configured. This configuration results in each input sequence capturing 200 consecutive measurements of (), with subsequent sequences sampled by advancing the window 100 time steps, creating a 50% overlap between them. Critically, to maintain data integrity and contextual relevance, these sequences were generated independently for each battery cell’s complete operational data before any concatenation for training or validation set construction, thereby ensuring no sequence inadvertently spanned data from different cells or disjointed operational periods.
3.2.2. Cross-Validation Strategy
A 3-fold cell-wise cross-validation strategy was adopted to rigorously evaluate the generalization capability of the models on unseen battery cells. The dataset comprises three distinct cells. In each fold, data from two cells were allocated for training and validation, while data from the remaining cell were held out as the test set. This process was rotated three times, ensuring that each cell served as the test set once.
Within each fold, the sequences generated from the two designated training/validation cells were first combined and subsequently shuffled randomly. This combined and shuffled set of sequences was then partitioned into a training set (80%) and a validation set (20%). The validation set was utilized for model selection, primarily through an early stopping mechanism.
3.2.3. Implementation Details
All models were implemented using the PyTorch (version 2.1) framework in Python (version 3.10). Experiments were conducted on a high-performance computing platform equipped with NVIDIA A40 GPUs (NVIDIA Corporation, Santa Clara, CA, USA). The models were trained using the widely-used Adam optimizer with an initial learning rate of . The mean squared error was employed as the loss function, a standard choice for regression tasks. Training proceeded for a maximum of 30 epochs with a batch size of 256. To prevent overfitting, an early stopping criterion was applied: if the Mean Absolute Error (MAE) on the validation set did not show improvement for 10 consecutive epochs, the training for that specific model and fold was halted. The model parameters that yielded the best validation MAE were saved and used for final evaluation on the respective test set. Data loading was facilitated by the PyTorch DataLoader utility, configured with 2 worker processes to optimize data throughput.
3.3. Models and Evaluation Metrics
To comprehensively assess the efficacy of the proposed approach, a series of models were developed and evaluated. These include the primary proposed model, variants for ablation studies, and established RNN architectures serving as baselines. An overview of these models is presented in Table 2.

Table 2.
Overview of evaluated models for SOC estimation.
The primary proposed model, designated Mamba_PG, integrates the novel pressure-aware gating mechanism with a Mamba backbone. It utilizes terminal voltage (), current (), and internal gas pressure () as input features. The pressure-aware gate is designed to adaptively modulate the influence of the pressure signal before it is processed by the Mamba, which then captures the temporal dependencies within the sequence.
To dissect the contributions of the new feature and the proposed gating mechanism, two ablation models based on the Mamba architecture were implemented. The first, Mamba_VI, employs a Mamba backbone but is trained using only voltage and current inputs, thereby excluding the pressure signal and the associated gating mechanism. This model serves to quantify the collective benefit of incorporating pressure data through the proposed gating. The second ablation model, Mamba_VIP, also uses a Mamba backbone and all three input features (). However, it incorporates the pressure signal via a standard linear embedding layer common to all features, without the specialized pressure-aware gate. This allows for an assessment of the specific advantage conferred by the proposed adaptive gating mechanism over a simpler, non-adaptive fusion of the pressure signal.
Furthermore, a set of baseline models employing established RNN architectures, specifically LSTM and GRU networks, were evaluated. For each RNN type, two variants were considered: LSTM-VI and GRU-VI, which process only voltage and current inputs; and LSTM-VIP and GRU-VIP, which include voltage, current, and pressure inputs, with the pressure signal integrated through a standard embedding layer akin to the Mamba_VIP model. To provide a more challenging benchmark against modern architectures, we also include the Temporal Fusion Transformer (TFT), a powerful attention-based model designed for time-series forecasting. The TFT-VIP variant also uses voltage, current, and pressure inputs with a standard embedding, serving as a state-of-the-art baseline. These baselines provide a reference point against widely used sequence modeling techniques in the battery domain.
The performance of all models was quantified using three standard regression metrics: MAE, RMSE, and MAXE. These metrics were calculated on the true (unscaled) SOC values from the test set of each cross-validation fold. The final reported performance for each model is the average of these metrics, along with their standard deviations, computed across all three folds to ensure a robust and comprehensive evaluation. Their calculation formulas are as follows, where is the true SOC value at time step t, is the predicted value, and N is the total number of time steps in the test set:
3.4. Results and Discussion
This section presents the experimental results obtained from evaluating the proposed SOC estimation model and a range of ablation and baseline models. The performance is analyzed quantitatively using standard error metrics and qualitatively through the examination of SOC prediction trajectories. The discussion focuses on the overall accuracy achieved, the effectiveness of incorporating internal gas pressure via the proposed gating mechanism, and a comparison against established methodologies.
3.4.1. Overall Performance Comparison
The comprehensive performance of the proposed pressure-aware gated Mamba model (Mamba_PG) across the three-fold cell-wise cross-validation is summarized in Table 3. The reported metrics, MAE, RMSE, and MAXE, consistently demonstrate a high level of accuracy. On average, the model achieved an MAE of , an RMSE of , and an MAXE of . The low values across all three folds indicate robust performance and good generalization capability to unseen battery cells. Specifically, the MAE remained below (or 0.4% SOC error if SOC is scaled 0–1) for each fold, underscoring the model’s precision.

Table 3.
Experimental results with averages.
Qualitative validation of the model’s performance is provided in Figure 4, which illustrates the predicted SOC trajectories against the true SOC for representative cycles selected from each fold’s test set. Specifically, Figure 4a displays the results for the 2nd cycle from fold 1, Figure 4b for the 50th cycle from fold 2, and Figure 4c for the 90th cycle from fold 3. These cycles can be considered to represent varying states of battery usage or aging within the test data. Across these diverse examples, the predicted SOC closely tracks the ground truth during both charging and discharging phases. The model accurately captures the nonlinear dynamics of the SOC, including the sharp changes at the beginning and end of charge/discharge, as well as the more linear regions. This visual evidence corroborates the quantitative metrics, affirming the model’s capability to deliver precise and reliable SOC estimations under different operational conditions and for different cell instances. The consistent tracking across these cycles further suggests the model’s robustness.
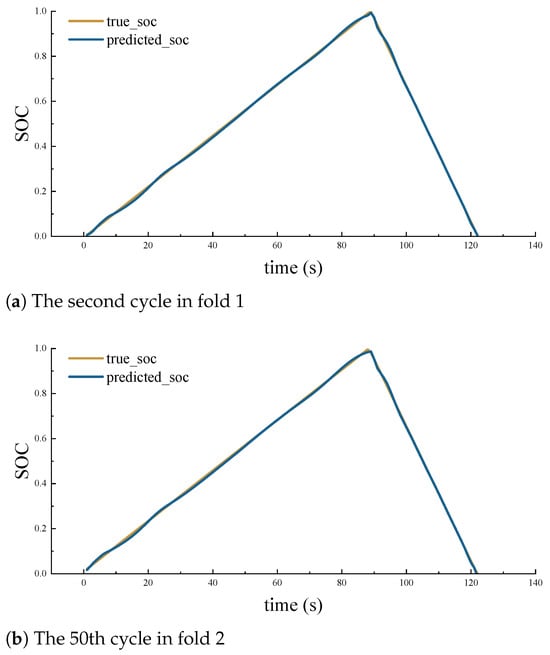
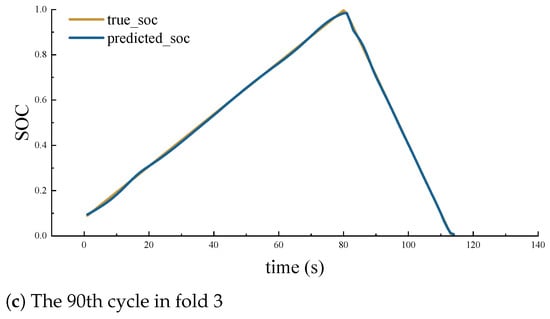
Figure 4.
Predicted–real SOC curves for different aging levels in each fold.
3.4.2. Ablation Study Results
To delineate the individual contributions of the internal gas pressure signal and the proposed pressure-aware gating mechanism, an ablation study was conducted. This study compares the performance of the main proposed model, Mamba_PG (which incorporates both innovations), against two variants: Mamba_VI (which excludes the pressure signal and gating, using only voltage and current) and Mamba_VIP (which includes the pressure signal alongside voltage and current, but processes it through a standard, non-gated embedding layer, referred to as naive fusion). The comparative results, in terms of mean MAE, RMSE, and MAXE across the three cross-validation folds, are presented in Figure 5.
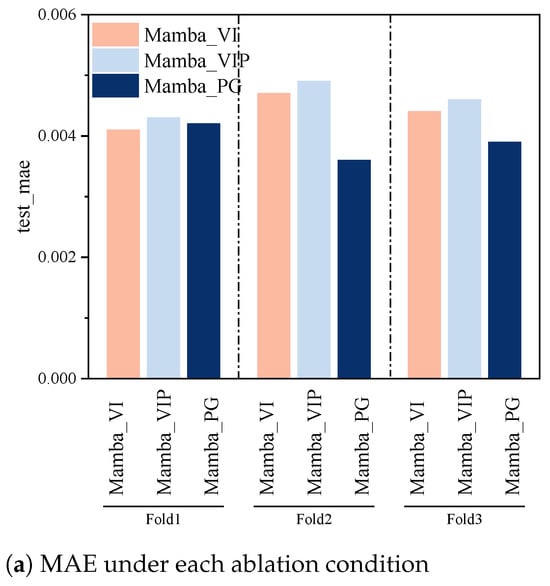
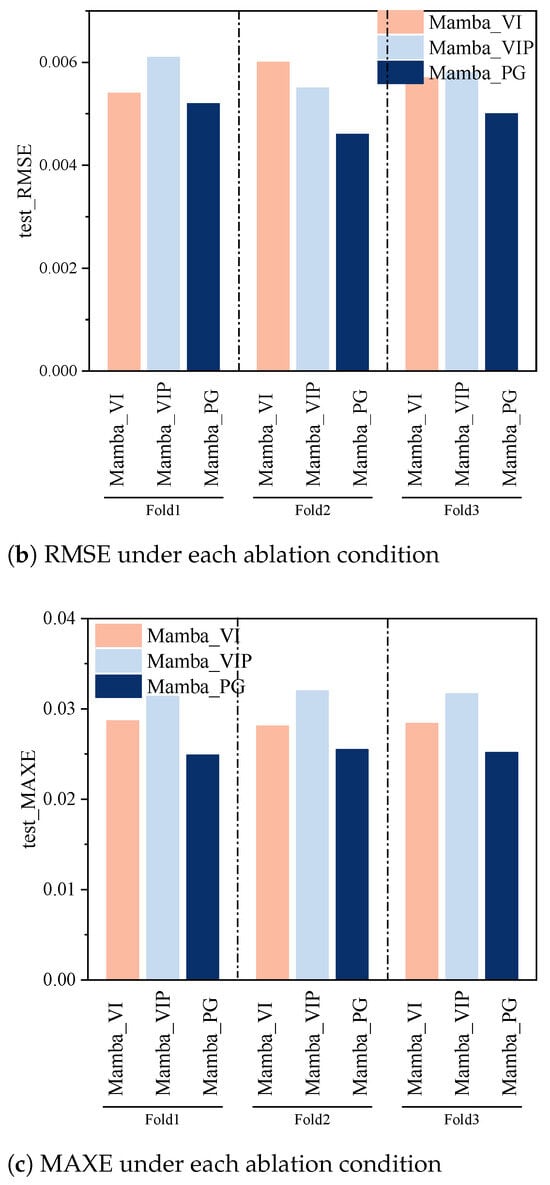
Figure 5.
Error metrics under various ablation conditions, comparing the proposed model (Mamba_PG) with variants lacking the pressure signal (Mamba_VI) or the specialized gate (Mamba_VIP).
As illustrated in Figure 5a, the Mamba_PG model consistently achieved the lowest MAE across all three folds, indicating its superior accuracy in SOC estimation. For instance, in fold 2, Mamba_PG yielded a significantly lower MAE compared to both Mamba_VI and Mamba_VIP. The Mamba_VIP model, which incorporates the pressure signal, albeit naively, generally outperformed the Mamba_VI model (which lacks pressure information), underscoring the inherent value of the internal gas pressure as an input feature. Similar trends are observable for the RMSE, as shown in Figure 5b. The Mamba_PG model again demonstrates the lowest RMSE values in all folds, suggesting not only higher accuracy but also a reduction in the magnitude of larger errors compared to the ablation variants. Figure 5c presents the MAXE for the ablation conditions. While maximum errors are inherently more susceptible to specific challenging instances in the test data, the Mamba_PG model generally maintains a competitive or lower MAXE.
3.4.3. Comparison with RNN Baselines
To further contextualize the performance of the proposed Mamba_PG model, its SOC estimation accuracy was benchmarked against several traditional RNN-based models. These included LSTM and GRU architectures, each implemented in two variants: one utilizing only voltage and current inputs (LSTM-VI, GRU-VI), and another incorporating voltage, current, and pressure inputs with a naive embedding strategy (LSTM-VIP, GRU-VIP). As an advanced attention-based benchmark, the TFT-VIP model was also included. Figure 6 visually summarizes the comparative performance in terms of MAE, RMSE, and MAXE, with specific average values provided by our experiments.
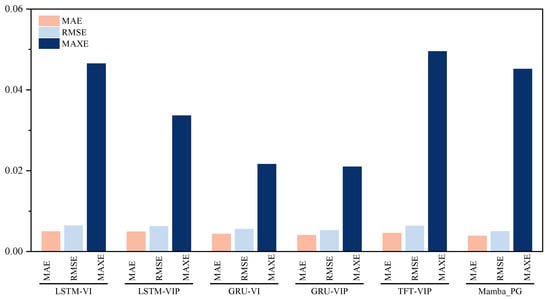
Figure 6.
Comparison with other baselines.
The results indicate that the proposed Mamba_PG model, with an average MAE of and RMSE of , generally surpasses the RNN-based counterparts. For instance, the GRU-VIP model, which was the best performing among the RNN baselines, achieved an MAE of and an RMSE of . The LSTM-VIP model recorded an MAE of and an RMSE of . The TFT-VIP model, in contrast, did not perform as well, exhibiting higher average errors than the GRU and Mamba models. This suggests that the architectural advantages of Mamba, combined with the specialized pressure-aware gating, yield a more accurate estimation compared to standard RNNs and even more complex Transformer models like TFT, especially when they are all enhanced with pressure data.
Analyzing the impact of the pressure signal on RNNs themselves, an improvement is observed when pressure is included. The LSTM-VIP model (MAE , RMSE ) performed slightly better than the LSTM-VI model (MAE , RMSE ). Similarly, the GRU-VIP model (MAE , RMSE ) showed a more noticeable improvement over the GRU-VI model (MAE , RMSE ). This confirms the utility of the internal gas pressure signal as an informative feature for SOC estimation, irrespective of the specific deep learning architecture.
However, the Mamba_PG model’s ability to more effectively process this pressure information is evident from its superior MAE and RMSE values. Interestingly, when considering the MAXE, the GRU-VIP () and GRU-VI () models exhibited slightly lower (better) maximum errors than the Mamba_PG model () in this particular set of experiments. The LSTM models showed higher MAXE values, with LSTM-VIP at and LSTM-VI being the highest at . Notably, the TFT-VIP model demonstrated the largest MAXE among all compared models, suggesting it was particularly prone to large errors on outlier data points. This suggests that while Mamba_PG offers better average precision, certain GRU configurations might be slightly more robust against extreme outliers in this dataset, a nuance warranting further investigation in varied conditions.
Overall, the comparison demonstrates that the proposed Mamba_PG model provides a compelling advancement over traditional RNN approaches for SOC estimation, particularly in terms of average error metrics. The benefits are attributed to both the incorporation of the novel pressure signal and the sophisticated mechanisms within the Mamba architecture, along with its dedicated gating for pressure, to process these complex temporal dependencies.
3.4.4. Analysis of the Pressure-Aware Gating Mechanism
To understand the learned behavior of the pressure-aware gate, we visualized its activation value () on representative early-, middle-, and late-life cycles (Cycle 5, 50, and 95) from the test set, as shown in Figure 7. The analysis reveals two key findings.
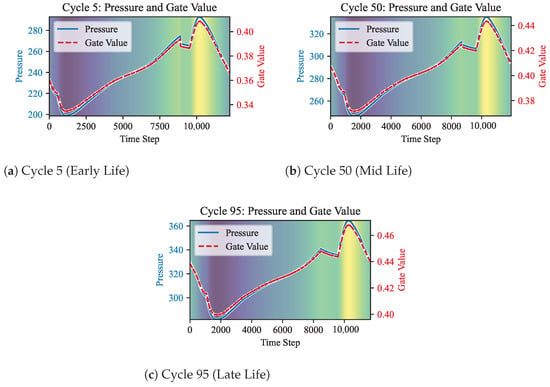
Figure 7.
Visualization of the pressure-aware gate activation value () versus the internal pressure signal across different stages of battery aging for the test cell GP7. Subplots (a–c) correspond to an early, middle, and late stage of life, respectively. The gate value (dashed line) closely tracks the pressure profile (solid line), demonstrating a learned, adaptive, and interpretable gating strategy.
First, the gate activation value directly and consistently tracks the profile of the internal pressure signal across all cycles. As pressure rises during charging, the gate value increases, and as pressure falls during discharging, the gate value decreases. Second, the mechanism adapts to battery aging. As the battery ages from Cycle 5 to Cycle 95, the baseline internal pressure increases due to gas accumulation. In response, the gate’s activation range also shifts upwards, from approximately 0.34–0.41 in Cycle 5 to 0.40–0.47 in Cycle 95.
These results demonstrate that the model has learned a clear and interpretable strategy: it applies a proportionally higher weight to the pressure signal as its magnitude increases, and this strategy adapts to the battery’s long-term aging. This validates the effectiveness of the proposed gating mechanism.
This adaptive behavior raises an important point regarding the long-term advantage of our proposed method. As the cell ages, gas-generating side reactions become more prominent, causing the pressure signal to become a stronger and more informative indicator of the battery’s internal state compared to early-life stages. The demonstrated ability of our pressure-aware gate to adapt to these long-term changes suggests that the model’s accuracy advantage relative to conventional models could potentially increase over the battery’s lifetime. By learning to rely more on a signal that becomes richer with degradation, the Mamba-PG model is well-positioned for robust performance throughout the entire operational life of the battery.
4. Conclusions
This paper introduced the Mamba-PG model, a novel framework for SOC estimation that successfully integrates internal gas pressure via a specialized pressure-aware gating mechanism. Our model achieved a state-of-the-art Mean Absolute Error of 0.386% and outperformed traditional RNN baselines. Crucially, ablation studies confirmed that both the pressure signal and our adaptive gate provided significant, distinct contributions to this high accuracy. Furthermore, the gating mechanism demonstrated an interpretable, physically-plausible strategy by adapting its focus on the pressure signal in response to both its magnitude and long-term battery aging. This research validates that fusing novel physical signals with efficient and explainable architectures is a promising direction for next-generation BMS.
We acknowledge that this study was conducted using data from a controlled temperature environment. Future work must therefore address the challenge of dynamic thermal conditions, which strongly influence both electrochemical reactions and internal gas pressure. Similarly, broader validation is needed across diverse battery chemistries, as the specific gas generation profiles of the NMC/Graphite-SiOx cells used here may differ from those of LFP or LTO cells. While our proposed architectural framework is designed to be broadly applicable, the model would require retraining on chemistry-specific datasets. Investigating real-time deployment feasibility also remains a key priority.
Author Contributions
Conceptualization, Q.W. and Y.H.; methodology, Q.W.; software, Q.W.; validation, Q.W., Y.H. and C.W.; writing—original draft preparation, Q.W.; writing—review and editing, Y.H.; supervision, C.W.; project administration, C.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Huzhou City, grant number 2024YZ10, and the General Scientific Research Project of the Department of Education of Zhejiang Province, grant number Y202455633.
Data Availability Statement
The data used in this study are publicly available and can be found in the work by Gulsoy et al. [21].
Acknowledgments
The authors would like to thank the original data providers for making their dataset publicly available for research purposes.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Demirci, O.; Taskin, S.; Schaltz, E.; Demirci, B.A. Review of battery state estimation methods for electric vehicles-Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.; Chen, Z.; Xiao, D. Anti-disturbance State-of-Charge Estimation for Lithium-ion Batteries Using Nonlinear Extended State Observers. IEEE Trans. Transp. Electrif. 2024, 11, 2918–2928. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.; Li, C.; Xiao, D. Robust State of Charge Estimation for Battery with Self-Adaptive Super Twisting Sliding Mode Observer. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Wang, S.; Wang, C.; Takyi-Aninakwa, P.; Jin, S.; Fernandez, C.; Huang, Q. An improved parameter identification and radial basis correction-differential support vector machine strategies for state-of-charge estimation of urban-transportation-electric-vehicle lithium-ion batteries. J. Energy Storage 2024, 80, 110222. [Google Scholar] [CrossRef]
- Ismail, M.; Dlyma, R.; Elrakaybi, A.; Ahmed, R.; Habibi, S. Battery state of charge estimation using an Artificial Neural Network. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Harbin, China, 7–10 August 2017; pp. 342–349. [Google Scholar]
- Xu, Q.; Ma, M.; Jiang, T.; Wu, H.; Wang, H. A trustworthy pipeline for data-driven estimation of lithium-ion battery electrochemical impedance spectroscopy using a Physics-Guided Neural Network. J. Energy Storage 2025, 123, 116454. [Google Scholar] [CrossRef]
- Wan, S.; Yang, H.; Lin, J.; Li, J.; Wang, Y.; Chen, X. Improved whale optimization algorithm towards precise state-of-charge estimation of lithium-ion batteries via optimizing LSTM. Energy 2024, 310, 133185. [Google Scholar] [CrossRef]
- Xu, Q.; Ma, M.; Jiang, T.; Hu, Q.; Wang, Z. A Data-Driven Surface Temperature Estimation Method for Lithium-ion Battery Based on GRU-RNN with Attention Mechanism. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 269–273. [Google Scholar]
- Shiri, F.M.; Perumal, T.; Mustapha, N.; Mohamed, R. A comprehensive overview and comparative analysis on deep learning models: CNN, RNN, LSTM, GRU. arXiv 2023, arXiv:2305.17473. [Google Scholar]
- Kuang, D.; Wang, Z.; Zhao, Y.; Li, L. Estimating the health status of lithium-ion batteries using deep learning method based on informer model. J. Power Sources 2025, 645, 237176. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Jena, P.; Padhy, N.P. TimeGAN-based Diversified Synthetic Data Generation Following BERT-based Model for EV Battery SOC Prediction: A State-of-the-Art Approach. IEEE Trans. Ind. Appl. 2025, 61, 4167–4185. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [PubMed]
- Liu, Z.; Tan, Z.; Wang, Y. A MconvTCN-Informer deep learning model for SOC prediction of lithium-ion batteries. J. Energy Storage 2025, 129, 117092. [Google Scholar] [CrossRef]
- Kırat, O.; Çiçek, A.; Yerlikaya, T. A New Artificial Intelligence-Based System for Optimal Electricity Arbitrage of a Second-Life Battery Station in Day-Ahead Markets. Appl. Sci. 2024, 14, 10032. [Google Scholar] [CrossRef]
- Hu, Z.; Daryakenari, N.A.; Shen, Q.; Kawaguchi, K.; Karniadakis, G.E. State-space models are accurate and efficient neural operators for dynamical systems. arXiv 2024, arXiv:2409.03231. [Google Scholar]
- Ma, M.; Xu, Q.; Chen, Q.; Jiang, T.; Wang, H. Interpretable and sensorless lithium-ion battery temperature estimation: A Temporal Fusion Transformer approach. J. Energy Storage 2025, 131, 117414. [Google Scholar] [CrossRef]
- Wang, H.K.; Gao, M.; Dai, X.; Cui, L. A multi-frequency feature extraction and sparse attention mechanism integrated Mamba model for lithium-ion battery state of health estimation. J. Energy Storage 2025, 123, 116643. [Google Scholar] [CrossRef]
- Liu, F.; Liu, S.; Chai, Y.; Zhu, Y. Enhanced Mamba model with multi-head attention mechanism and learnable scaling parameters for remaining useful life prediction. Sci. Rep. 2025, 15, 7178. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Li, W.; Singh, A.; Ren, D.; Hou, Z.; Ouyang, M. Effect of external pressure and internal stress on battery performance and lifespan. Energy Storage Mater. 2022, 52, 395–429. [Google Scholar] [CrossRef]
- Gulsoy, B.; Vincent, T.A.; Briggs, C.; Sansom, J.E.; Marco, J. In-situ measurement of internal gas pressure within cylindrical lithium-ion cells. J. Power Sources 2023, 570, 233064. [Google Scholar] [CrossRef]
- Gulsoy, B.; Vincent, T.; Briggs, C.; Kalathingal, A.; Niri, M.F.; Marco, J. Dataset of accumulated internal gas pressure and temperature during lithium-ion battery operation and ageing. Data Brief 2025, 59, 111420. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).