Abstract
Inertial confinement fusion (ICF) stands as one of the approaches to achieve controlled thermonuclear fusion, capable of supplying humans with abundant, economical, and safe energy. In this study, the high-order hybrid compact–WENO scheme is employed to simulate Rayleigh–Taylor instability (RTI) phenomena, one of the challenges hindering the realization of ICF, and to investigate the interaction of RTI phenomena in a multi-layer fluid system. To ensure a more reasonable comparison, the corresponding initial and boundary conditions for three-layer and four-layer fluids are derived based on the same Atwood number. Numerical results show that with the development of RTI phenomena, the interaction between interfaces can be gradually observed. The number of fluid layers exhibits an inhibitory effect on the development of RTI phenomena. When a pair of spike and bubble at two adjacent interfaces reach the same height, the evolution of the spike–bubble gap changes significantly.
1. Introduction
Inertial confinement fusion (ICF) is one of the ways to achieve controlled thermonuclear fusion. Compared with nuclear fission reactions, nuclear fusion reactions have the advantages of high energy conversion, abundant raw materials, and cleanliness. The ignition process of ICF can be summarized as follows [1]: the target containing deuterium-tritium (DT) fuel is ignited by a high-power energy source, causing the DT fuel to undergo the nuclear fusion reaction, and the reaction state is maintained by the energy released from the nuclear fusion reaction. Therefore, ICF may provide sufficient, economical, and safe energy for humanity. However, several difficulties prevent the achievement of ICF, one of which is Rayleigh–Taylor instability (RTI). RTI is a type of hydrodynamic instability and seriously affects the ignition process of ICF. The target used for ICF ignition consists of a spherical shell and internal DT fuel. The ICF shell is symmetrical in the ideal case but asymmetrical in practice. During the ignition process of ICF, small disturbances in the spherical shell increase sharply, and this instability is called RTI [2,3]. It typically occurs at the interface between two fluids of different densities when the low-density fluid accelerates the high-density fluid. The evolution of RTI can be divided into a linear stage and a nonlinear stage. For the linear stage of RTI, theoretical results consistent with experimental observations have been reported in [4]. Although some theories have been proposed for the nonlinear stage of RTI [4,5], a complete theory has not been established due to the strong nonlinearity of its governing equations. Thus, numerical simulation serves as a means to study the evolution of RTI.
In the last three decades, numerous numerical methods have been developed to study Rayleigh–Taylor instability (RTI). For example, Baker et al. [6] simulated RTI in two-dimensional inviscid incompressible fluids and analyzed the influence of medium thickness. Li et al. [7] employed a second-order TVD finite difference scheme with artificial compression to enhance the numerical resolution of RTI simulations. Tang et al. [8] combined the level set method with the Ghost method for RTI simulations. Ramaprabhu et al. [9] studied three-dimensional RTI under varying Atwood numbers. Wang et al. [10] proposed a lattice Boltzmann method for RTI simulations, focusing on the effects of viscosity and interfacial tension in two-phase flows. Sundaram et al. [11] performed groundbreaking 3D simulations using a non-overlapping parallel algorithm with 4.19 billion grid points, capturing ultrasonic wave-induced baroclinic instability across 200K temperature differentials. Joshi et al. [12] conducted highly resolved direct numerical simulations (DNS), identifying acoustic triggering as the fundamental mechanism for RTI and Kelvin–Helmholtz RTI while establishing new benchmark datasets through energy budget analysis.
The Weighted Essentially Non-Oscillatory (WENO) scheme [13,14] is a high-order shock-capturing method that achieves robust stability and high resolution near discontinuities while maintaining accuracy in smooth regions through an adaptive stencil weighting mechanism. Shi et al. [15] evaluated the numerical resolution and efficiency of high-order WENO schemes in simulating both the double Mach reflection (DMR) problem and RTI. They demonstrated that higher-order WENO schemes offer superior computational efficiency when resolving discontinuities and complex flow features. Han et al. [16] implemented finite-volume WENO schemes for high-density-ratio RTI, achieving accurate interface evolution even under extreme conditions. However, the WENO scheme has some disadvantages for certain classes of problems. For example, it is computationally expensive and more dissipative than linear schemes at a given order and resolution. Hybrid schemes provide a natural solution to mitigate the weaknesses of both high-order WENO and linear schemes, improving computational efficiency while maintaining accuracy. Various hybrid schemes have been developed over the last two decades, including: hybrid central-WENO schemes [17,18], hybrid compact–WENO schemes [19,20], characteristic-wise hybrid schemes [21], neural network-based hybrid detectors [22,23], well-balanced WENO schemes [24], and Hermite WENO schemes [25]. These approaches have been successfully applied to conservation laws, including compressible flows, shock-turbulence interactions, and shallow water equations.
The numerical simulation of RTI was mostly carried out for two layers of fluid with different densities. In fact, the RTI phenomenon in a multi-layer fluid may occur during the ignition process of ICF because the ICF shell has a multi-layer structure. So it is worth considering whether additional effects exist between different RTI phenomena at various interfaces. In this work, we employ the high order hybrid compact–WENO scheme with artificial neural network (ANN) edge detector [26], which will be detailed in Section 2 to simulate RTI phenomena in a multi-layer fluid and primarily study the interaction between the RTI phenomena. The corresponding initial and boundary conditions with three- and four-layer fluids are derived based on the same Atwood number to make the comparison more reasonable. We also investigate the numerical resolution, computational efficiency and the symmetrical property of the hybrid compact–WENO scheme by simulating classical RTI phenomenon in a two-layer fluid. Numerical results demonstrate that the interaction between interfaces can be observed gradually with the development of the RTI phenomena. The number of layers of fluid plays an inhibitory role in the development of RTI phenomena. When a couple of spike and bubble at two adjacent interfaces reach the same height, the evolution of spike–bubble gap changes significantly.
This paper is organized as follows. In Section 3, three cases of RTI are considered, and the initial boundary value conditions of three cases are designed for comparison. In Section 2, we briefly review the high order hybrid compact–WENO scheme with ANN edge detector. In Section 4, three cases of RTI are simulated and the results are discussed. The influence of the number of discontinuities for RTI is summarized in Section 5.
2. Hybrid Compact–WENO Scheme
In this section, we will provide a concise overview of the high-order hybrid compact–WENO finite difference scheme [19,26,27,28]. For details on the numerical schemes employed here, including the compact finite difference scheme, the WENO-Z finite difference scheme, the finite difference filtering, and the TVD Runge–Kutta scheme, the reader is directed to the sources mentioned above [19,26,27,28]. Furthermore, alternative approaches that use various shock detection algorithms can be considered for adaptive hybrid algorithms, including the entropy-based detector [17], Ducros shock sensor [27], wavelet-based indicator [7], neural network approach [2], pressure gradient method [14], and hybrid characteristic-wise scheme [11]. For further information, we recommend consulting the references and associated literature.
The hybrid scheme consists of five key steps. Initially, during the Runge–Kutta time step, a shock detection technique evaluates solution smoothness at designated grid points. Next, these points are labeled with a . Subsequently, a buffer zone is created around any detected non-smooth regions. The fourth step involves calculating the flux’s first derivative: non-smooth stencils employ the fifth-order WENO-Z scheme, whereas smooth regions use the sixth-order central compact scheme. Lastly, if required, the solution is stabilized in smooth stencils by applying an eighth-order finite difference filter at the end of the Runge–Kutta step [29].
In the subsequent discussion, we will employ the hybrid compact–WENO finite difference scheme with artificial neural network (ANN) discontinuous detector for numerical simulations.
Artificial Neural Network Discontinuous Detector
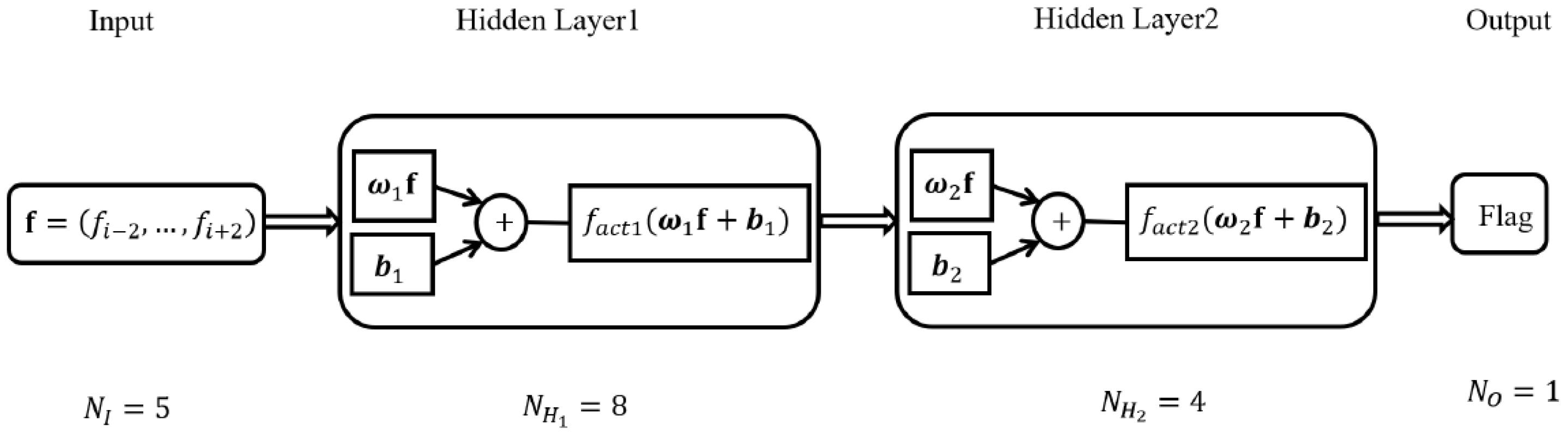
As a simple artificial neural network, a four-layer Back Propagation neural network is designed for the discontinuous detection algorithm. The topology of its network model consists of the input layer, hidden layers, and output layer, as illustrated in Figure 1.
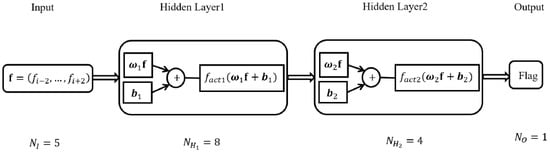
Figure 1.
The BP neural network for discontinuous detection.
The number of neurons in the input layer is set as . The input values are chosen to be the function values at five uniformly spaced points . To preprocess the input data, a linear normalization algorithm is utilized. This algorithm normalizes the function values of the input to the interval between and 1:
where is a normalized vector of .
There is only one neuron in the output layer, . The output value stands for the smoothness of . By rounding to get , we can use it to mark, via a , whether the function is discontinuous or smooth at the point as follows:
In this study, the BP neural network designed comprises two hidden layers, and . The number of neurons in each hidden layer is set as and respectively. For the hidden layers and , we select the ReLU (Rectified Linear Unit) activation function . This function serves to enhance the feature impact during the iterative process. In the output layer, the sigmoid function is used, which maps the output value to .
Based on the input and output values, and through the rational selection of functions and parameters, the function values within the training datasets are normalized to the range . The settings of the dataset are presented in Table 1. The domain selection for incorporated periodicity requirements and discontinuity locations to capture shock features. Key parameters were varied systematically: slope parameter for gradient strength, and jump magnitudes representing typical density/pressure jumps. These ranges, validated in [26], ensure optimal ANN performance for shock detection by distinguishing true discontinuities from smooth high-gradient regions.

Table 1.
Dataset setting: Functions with parameter values, definition domains D, the number of functions, and discontinuous labels .
3. Rayleigh–Taylor Instability
The two-dimensional RTI phenomenon satisfies the following hyperbolic conservation laws with source terms
where is density, is the velocity vector, E is the total energy, is the pressure, is the specific heat ratio of ideal gas and is the gravitational constant. All equations are non-dimensionalized using reference length , density , and characteristic velocity . Three initial boundary value problems corresponding to the RTI phenomena with two-, three- and four-layer fluids in the computational domain are derived, respectively, where the vertical dimension () captures the primary instability growth, while the reduced horizontal extent () provides sufficient scale separation with periodic boundary conditions.
3.1. Case 1: RTI in Two-Layer Fluid
The RTI phenomenon in two-layer fluid is the case with one interface. We can assume the initial conditions of Case 1 to be
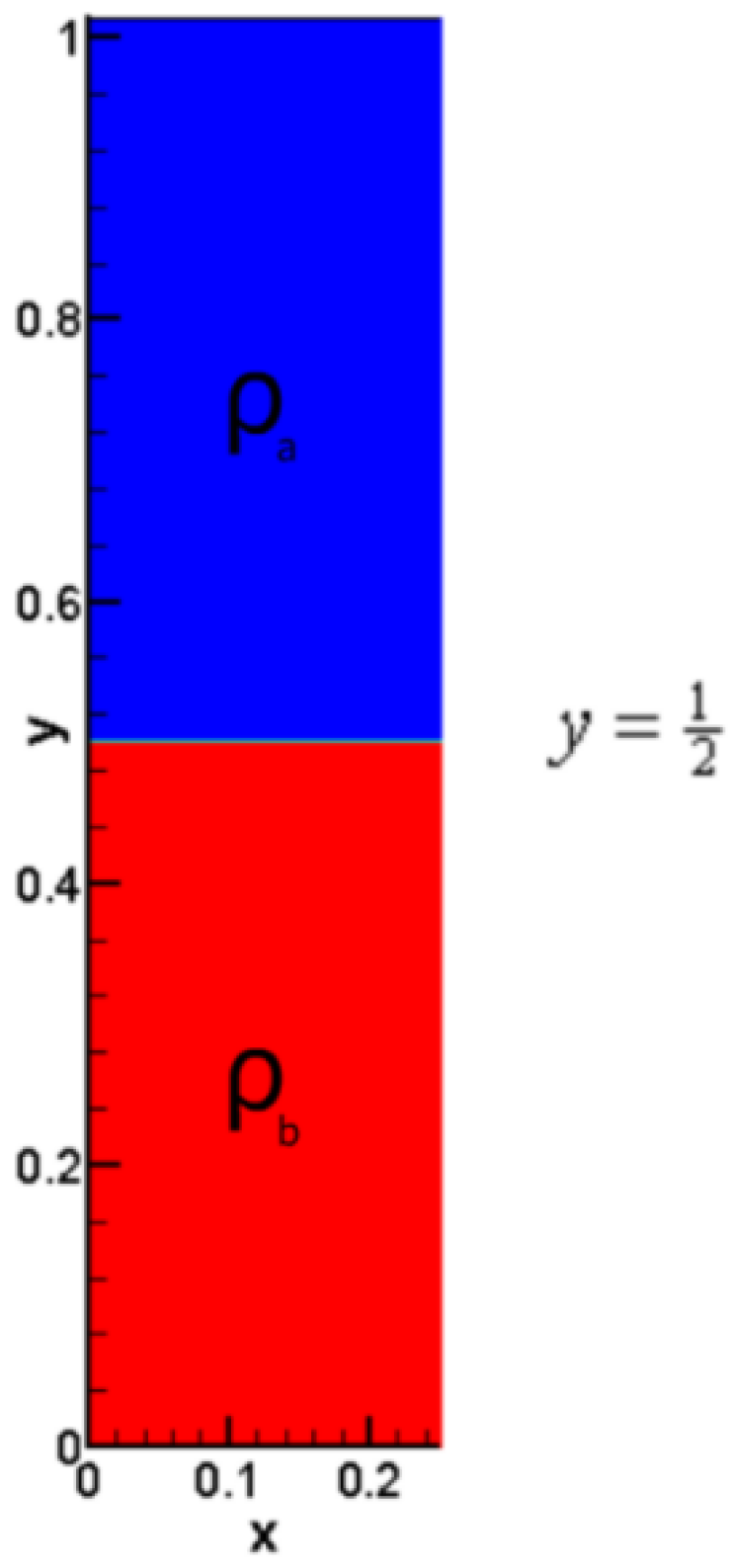
where is local sound speed, is the amplitude coefficient of perturbation. The initial conditions satisfy hydrostatic equation . The left and right boundary conditions are reflective boundary conditions, while the top and bottom boundary condition are and , respectively. As shown in Figure 2, two layers of fluid with different densities are separated by .
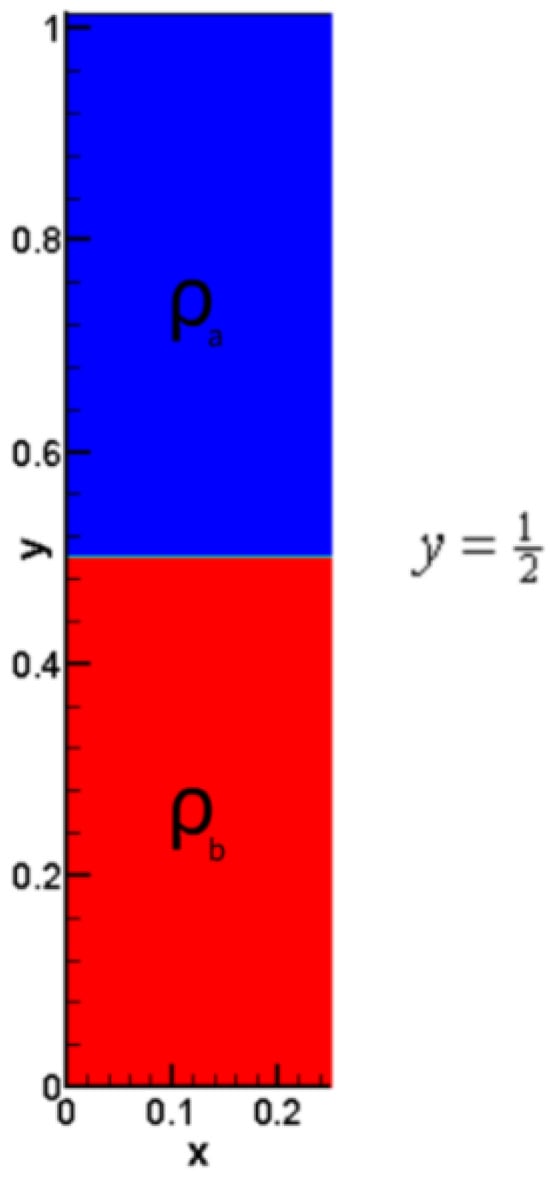
Figure 2.
The initial conditions of Case 1. The interface locates at . The densities of light and heavy fluids are and , respectively.
3.2. Case 2: RTI in Three-Layer Fluid
By adding a third layer of fluid between the two layers in Case 1, the Case 2 is designed to describe the RTI phenomenon of three-layer fluid interaction. For comparison, the initial boundary conditions outside the fluid layer added are the same as those in Case 1. Therefore, the positions of two interfaces between the three-layer fluid cannot be set randomly, but should be calculated as follows.
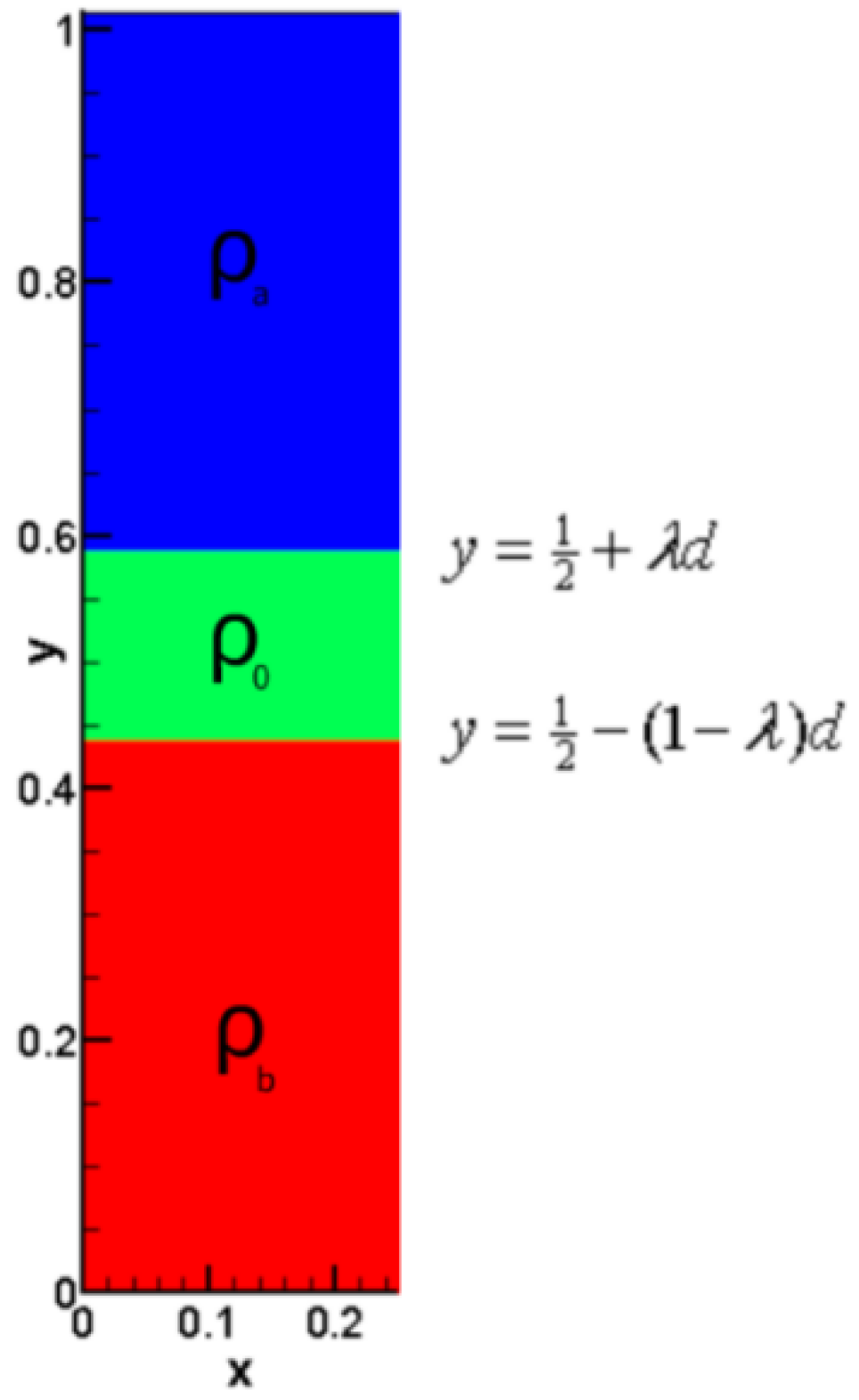
As shown in Figure 3, let the width and the density of the added layer be d and respectively. The top boundary of the added layer is and the bottom boundary is .
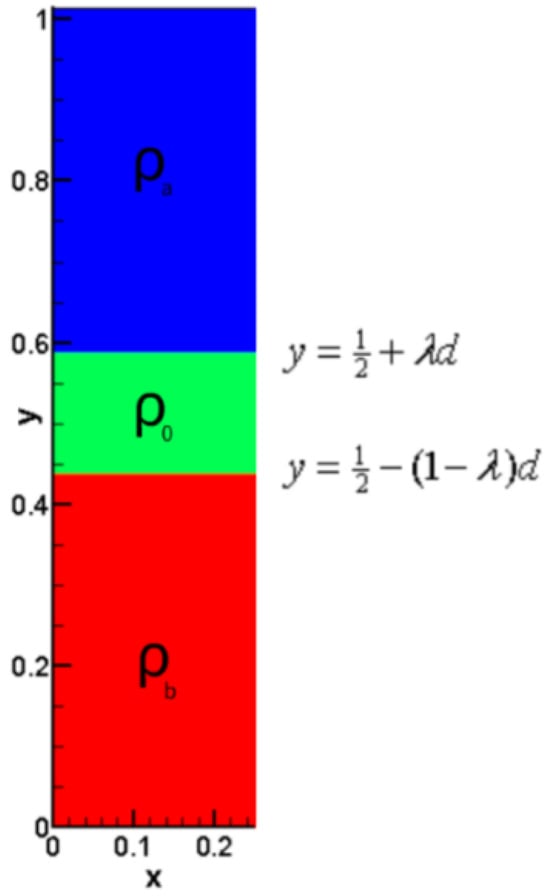
Figure 3.
The initial conditions of Case 2. The two discontinuities locate at and . Densities of different layers satisfy .
The initial conditions outsides are the same as Case 1. Thus the density of top layer and the density of bottom layer . The density of the added layer is computed by the Atwood number of the fluids. Atwood number plays an important role in the influence on the growth rate of RTI [3] and is defined as
where and are the densities of heavy and light layers of fluid, respectively. In order to observe the interaction between the two interfaces during the evolution in Case 2, the Atwood numbers of the two interfaces are equal to ensure that the evolutions of the two interfaces are consistent when they are independent. Thus, the densities of the three layers satisfy
Similarly to Case 1, the initial conditions of Case 2 have to satisfy the hydrostatic equation . Thus the pressure of added layer has the form that . It can be deduced that the initial conditions of Case 2 are
Combined with the continuity of pressure at two discontinuities, one can obtain , .
3.3. Case 3: RTI in Four-Layer Fluid
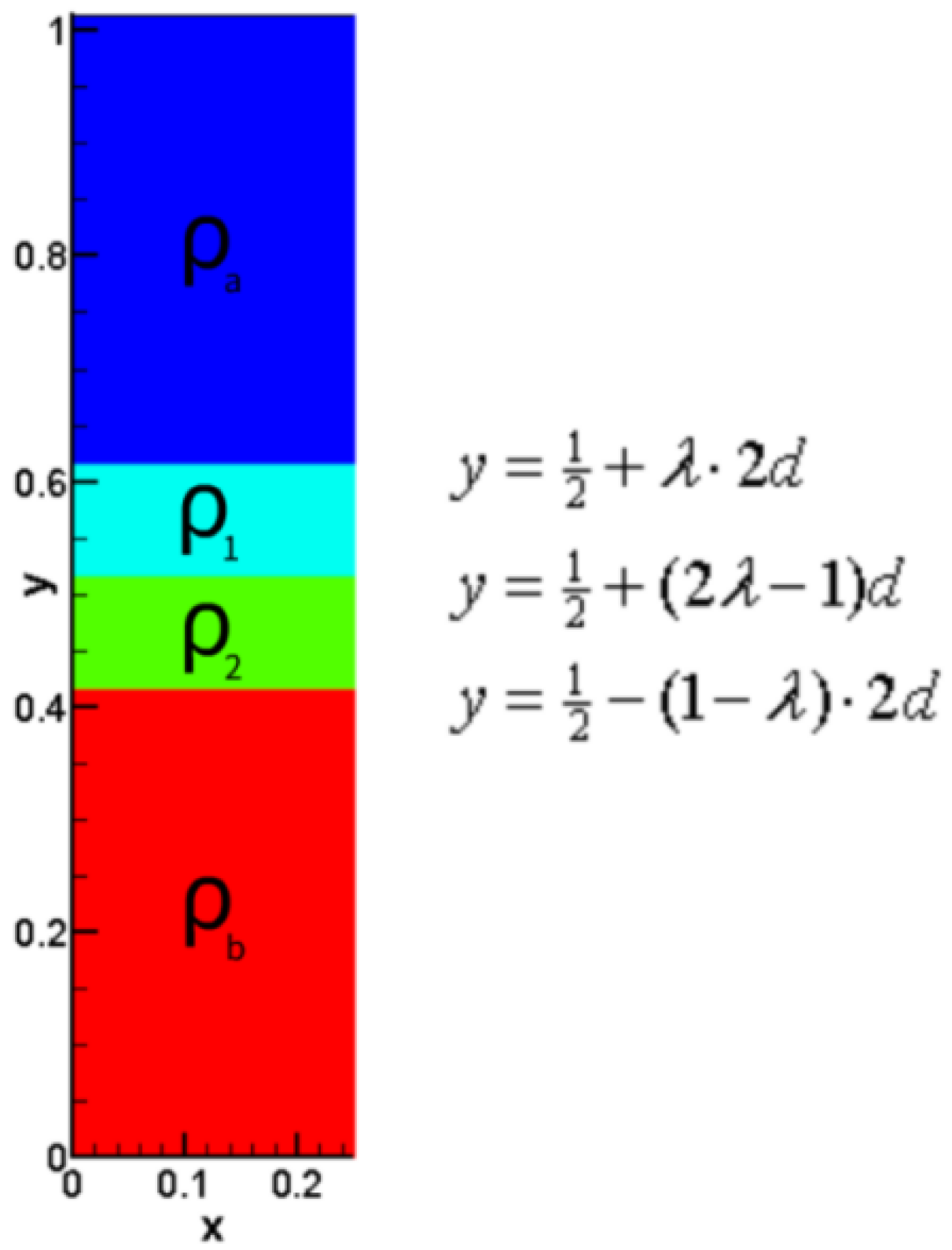
Case 3 can be constructed by adding two layers fluids between the two layers of Case 1. To eliminate the effect of width, the two added layers are set to have the identical width. Set the width of each layer as d, the density of the added light fluid as , the density of the added heavy fluid as . And let the top boundary of two added layers of fluid be , the bottom boundary be . Hence, the interface between the two added layers lies at as shown in Figure 4.
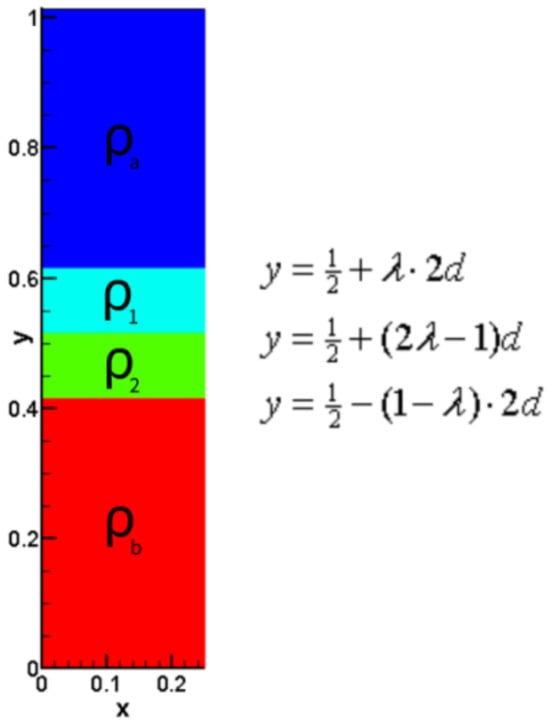
Figure 4.
The initial conditions of Case 3. The three interfaces locate at , and . Densities of different layers satisfy .
Let the Atwood numbers of three interfaces be equal to
According to the relationship between Case 1 and Case 3, it can be deduced that the density of light fluid and the density of heavy fluid , and the densities of added fluid , . The initial conditions of Case 3 are
According to the continuity of pressure, one can obtain , , .
4. Numerical Results
In this section, the high order hybrid compact–WENO scheme is used to simulate the three cases in Section 3. The grid resolution is and the final time is .
4.1. Results of Case 1
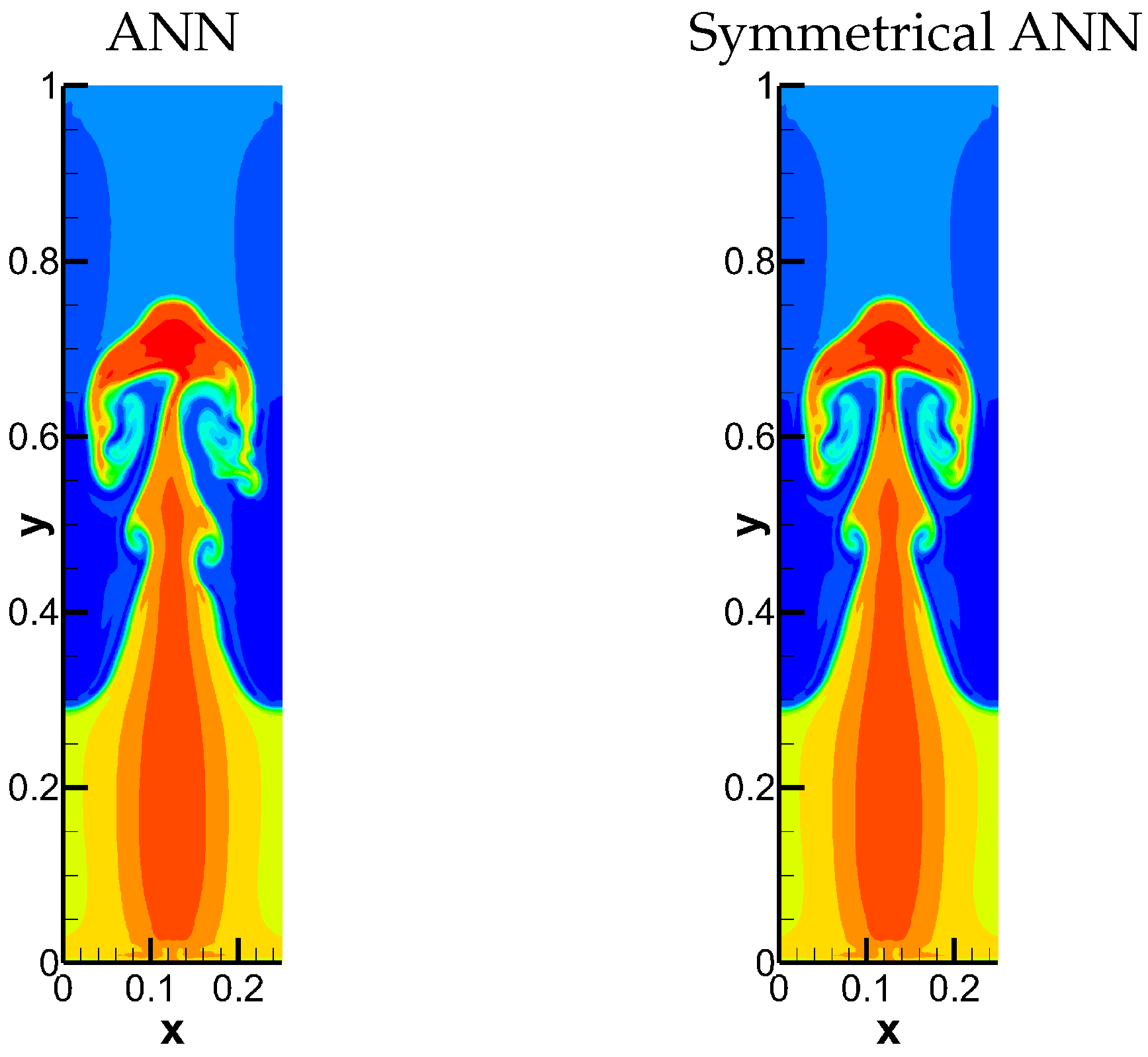
High order WENO scheme is one of popularly used numerical methods for simulating RTI and can generate reliable numerical results. However, it is too dissipation for resolving the fine scale structures, such as Kelvin–Helmholtz instability (KHI) [4] along the interface. Furthermore, when it comes to a specific order and resolution, the WENO scheme presents greater implementation complexity and demands more computational resources in comparison to linear finite difference schemes. Therefore, we conduct the numerical studies by high order hybrid scheme for simulating RTI phenomena and show the corresponding results in the left of Figure 5. One can easily find that the numerical result is asymmetrical at the top of structure of mushroom, which is inconsistent with the initial symmetrical setup. It is because the ANN shock detector does not maintain the symmetry. In order to overcome this shortcoming of ANN shock detector, we detect the shock locations starting from the symmetry axis to both sides, respectively. The correspondingly modified result with symmetrical ANN shock detector is shown in the right of Figure 5. It is obvious to find that the symmetry of RTI is maintained.
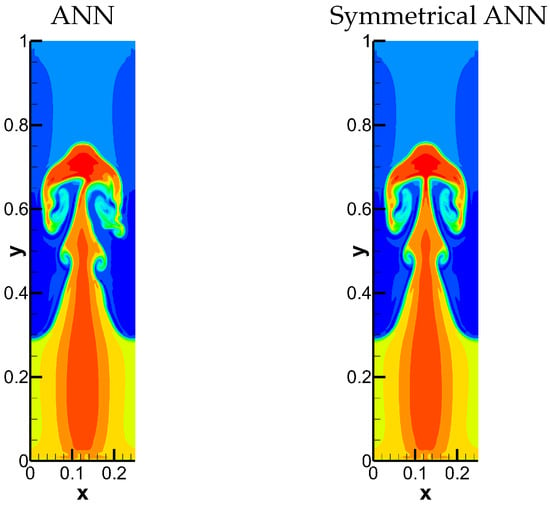
Figure 5.
The numerical results of Case 1 using (Left) ANN shock detector and (Right) symmetrical ANN shock detector.
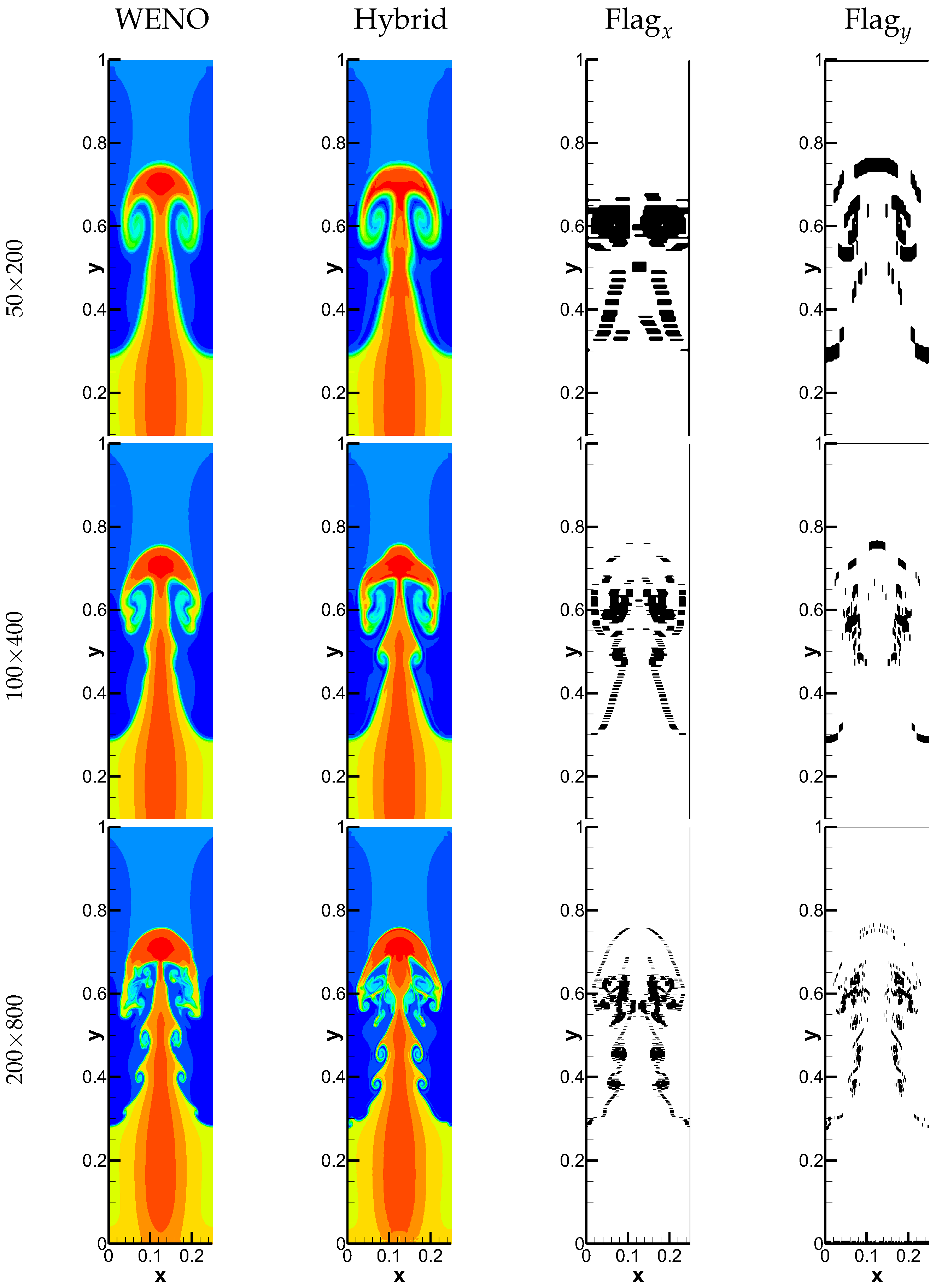
Figure 6 presents numerical results of the WENO and hybrid scheme with three different grid resolutions. More fine scale structures can be observed in the numerical results computed by the hybrid scheme with grid resolutions and which demonstrates higher numerical resolutions than the WENO scheme. The WENO and show that the modified ANN shock detector can capture the shock locations accurately and symmetrically.
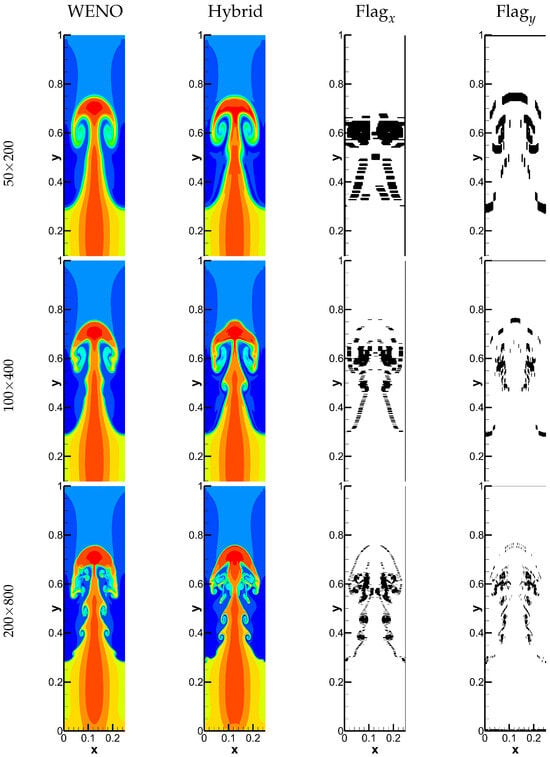
Figure 6.
The densities of Case 1 computed by the WENO scheme and hybrid scheme. The black areas in the Flag figure represents where the WENO scheme is used in the hybrid scheme.
Regarding computational efficiency, Table 2 showcases the CPU time during the simulation of Case 1 for both the WENO scheme and the hybrid scheme. As presented in the table, it is evident that the hybrid scheme outpaces the WENO scheme significantly. The speedup factor rises from to as the resolution goes up. Additionally, the proportion of the WENO scheme within the hybrid scheme drops as the grid resolutions increase, varying from 22% to 10%.

Table 2.
CPU time (in seconds) consumed by the two schemes of Case 1. The CPU times (in seconds), percentage of the WENO scheme, and speedup factors (SF) of the WENO and hybrid scheme.
4.2. Results of Case 2
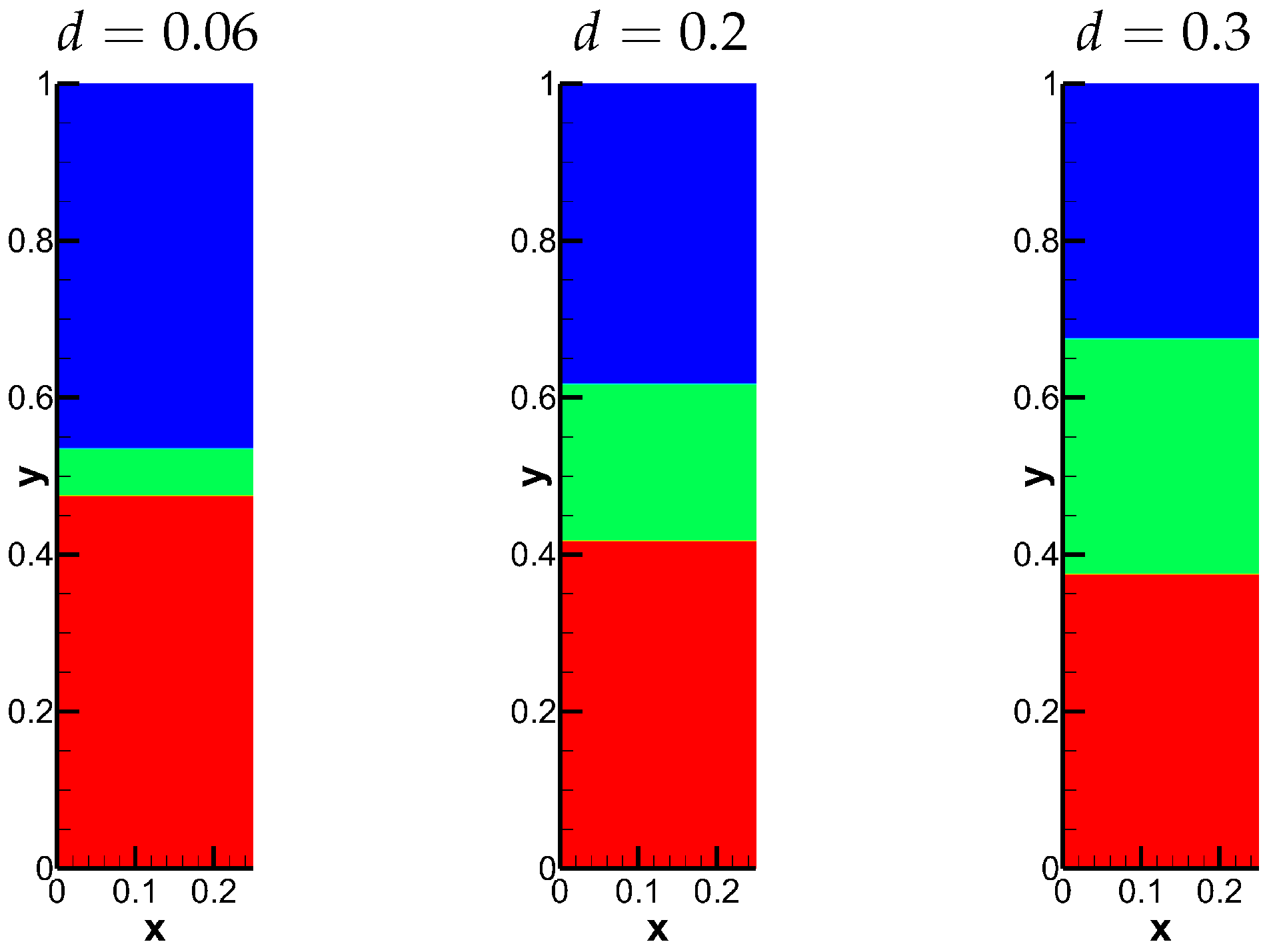
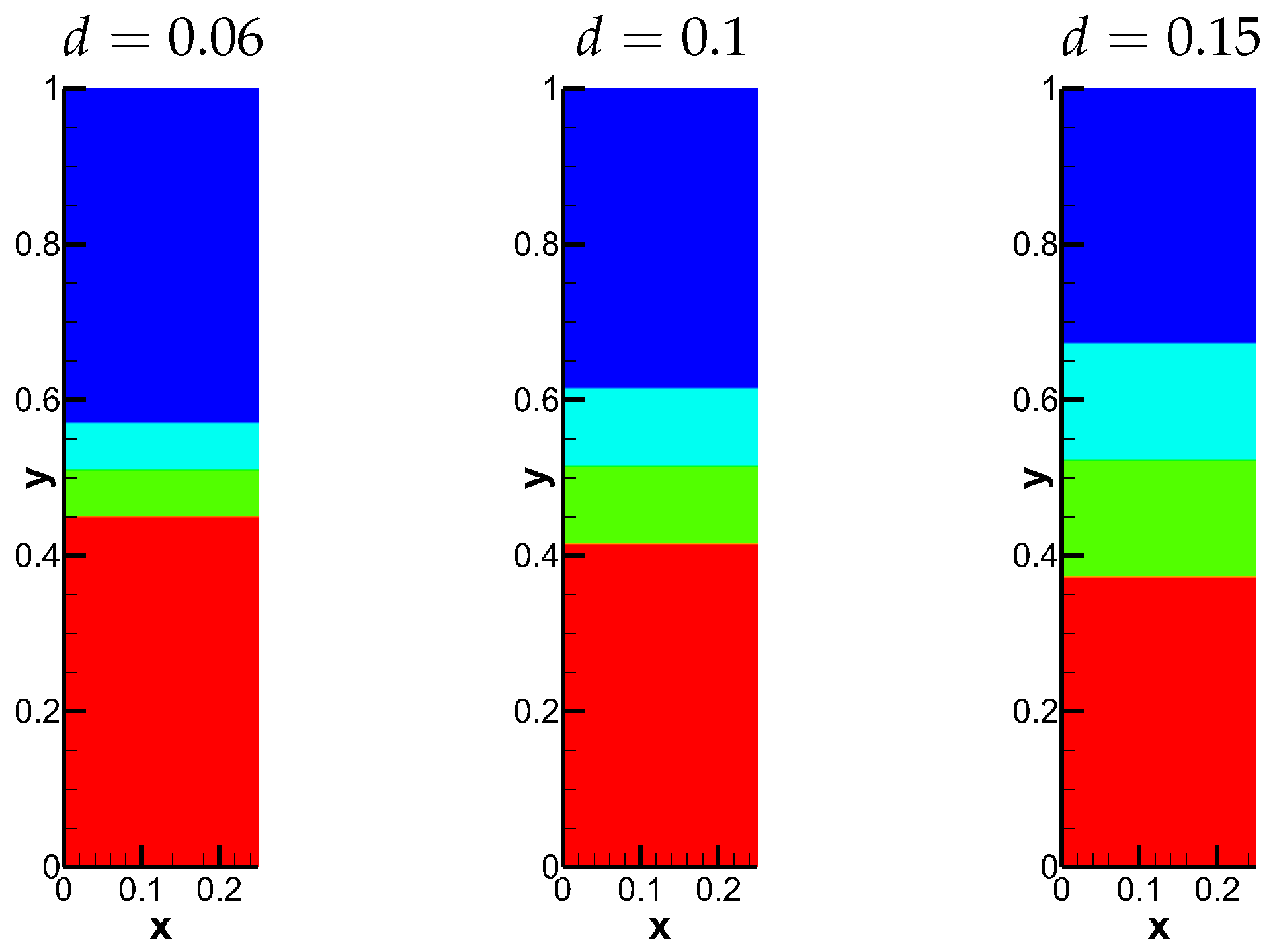
In Case 2, the coupling strength between interfacial Rayleigh–Taylor instabilities (RTI) is governed by the middle layer width d, exhibiting three distinct regimes: (1) for narrow widths, adjacent interfaces merge rapidly, reproducing single-interface (Case 1) behavior; (2) intermediate widths enable sustained multi-layer interactions with characteristic nonlinear coupling; and (3) wide spacings permit nearly independent interface evolution. In this work, we take for example and plot the initial conditions in Figure 7. The corresponding numerical results computed by the hybrid scheme are shown in Figure 8.
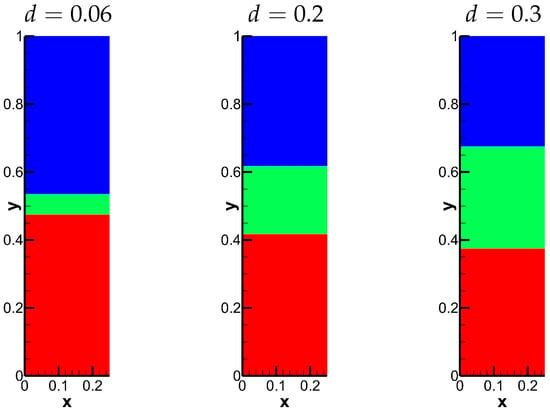
Figure 7.
The initial density of Case 2 with three different widths.
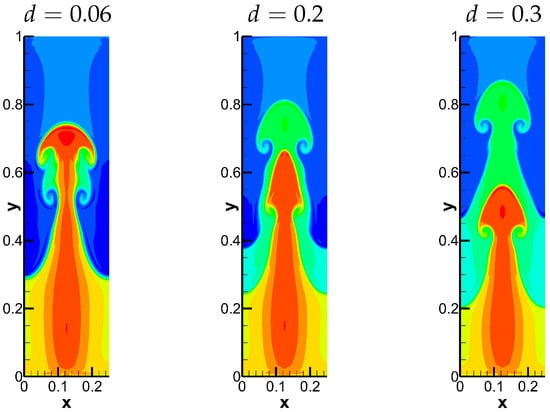
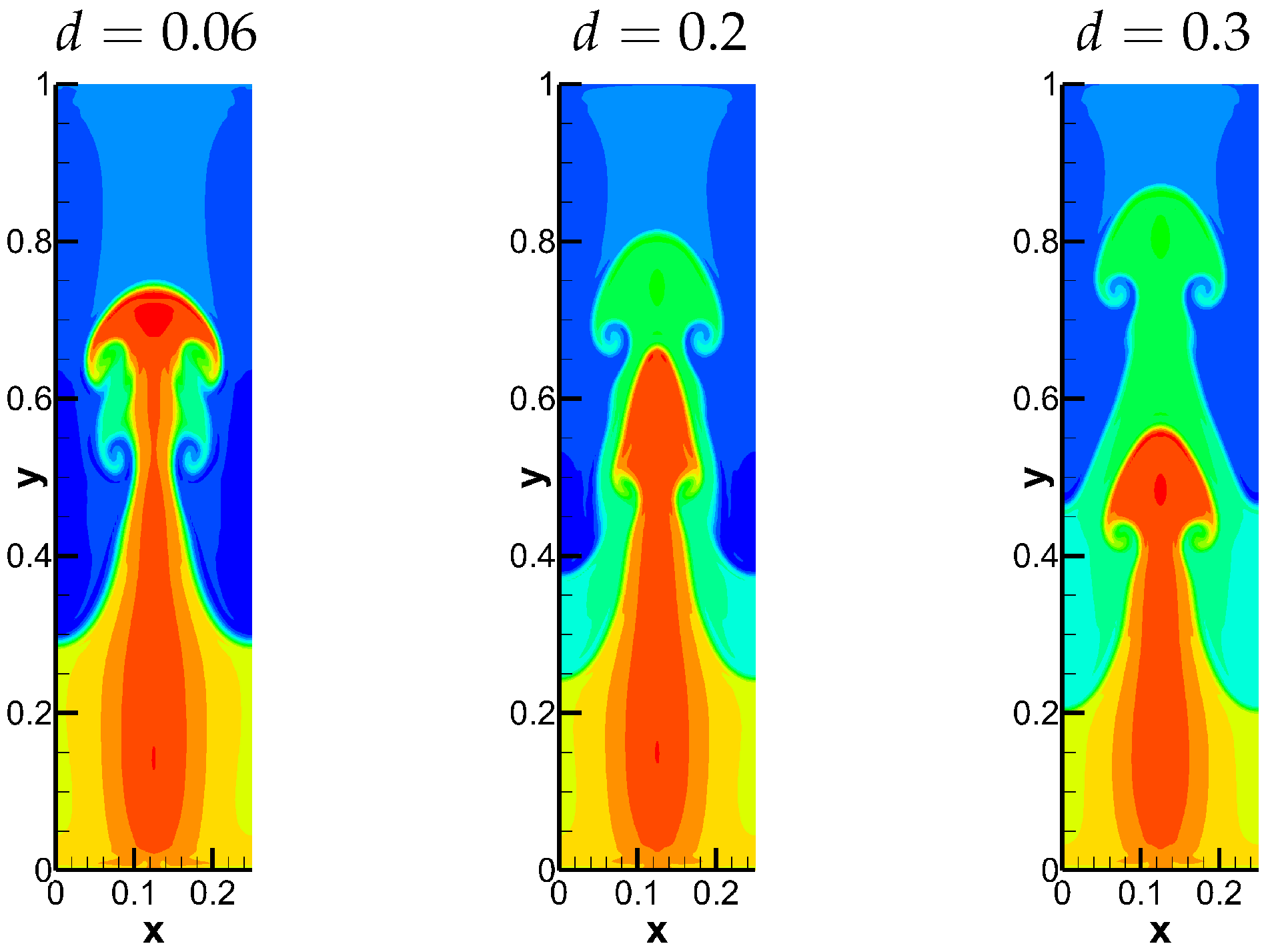
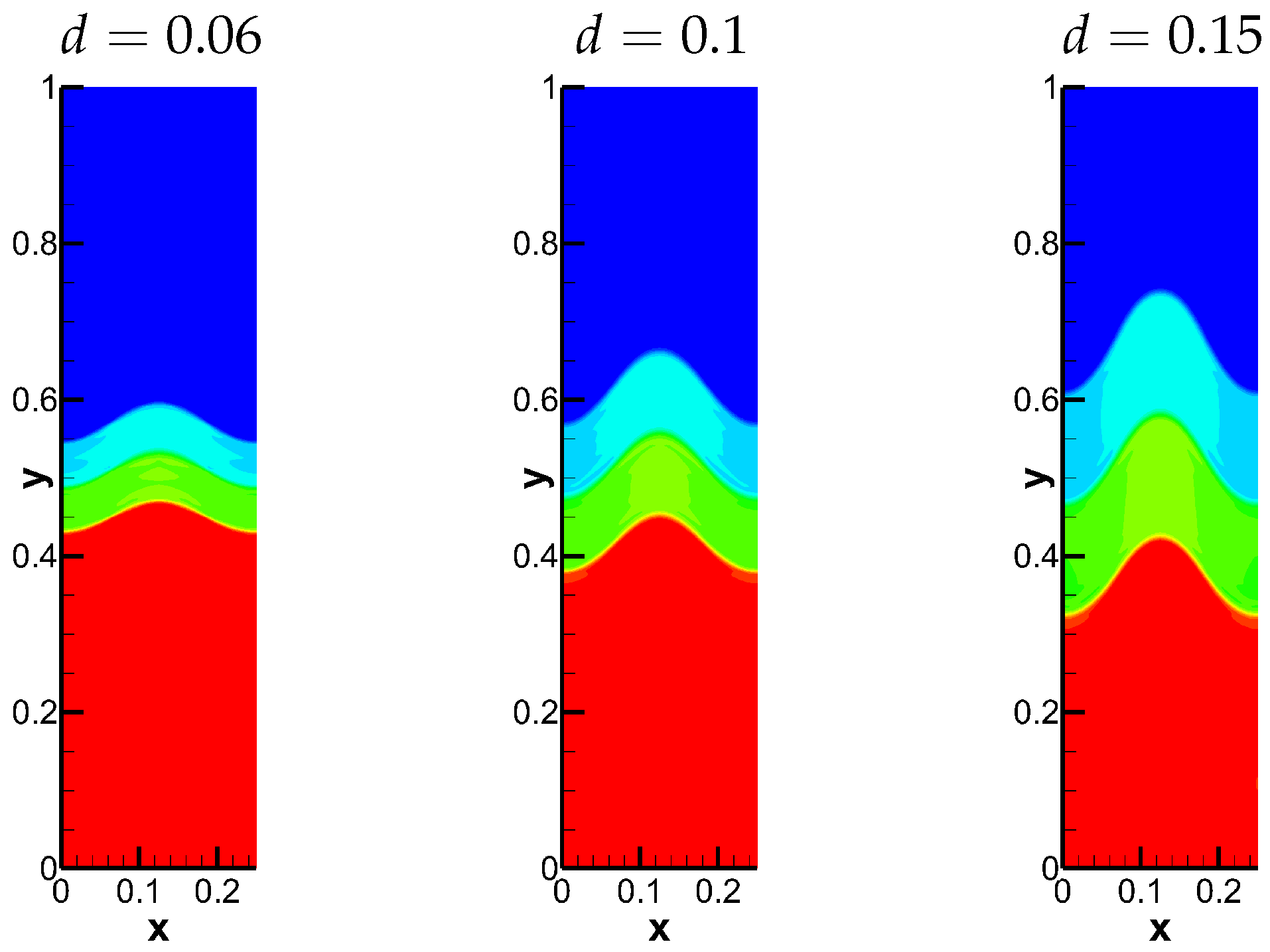
Figure 8.
The density of Case 2 with three different widths at the final time.
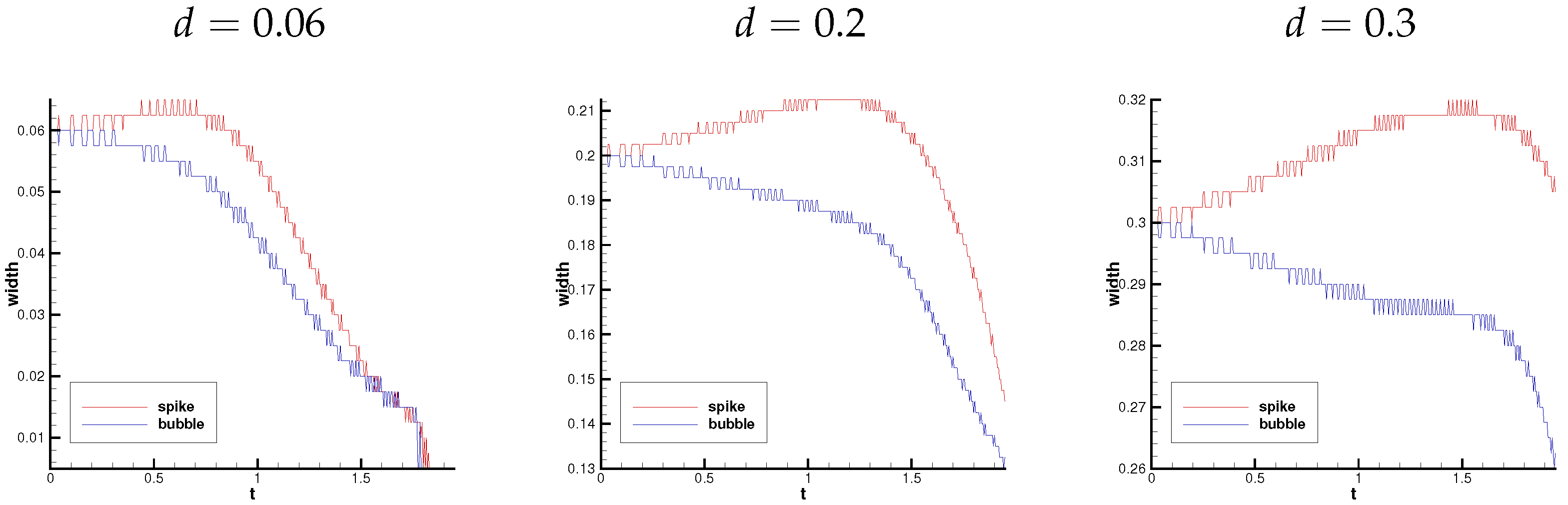
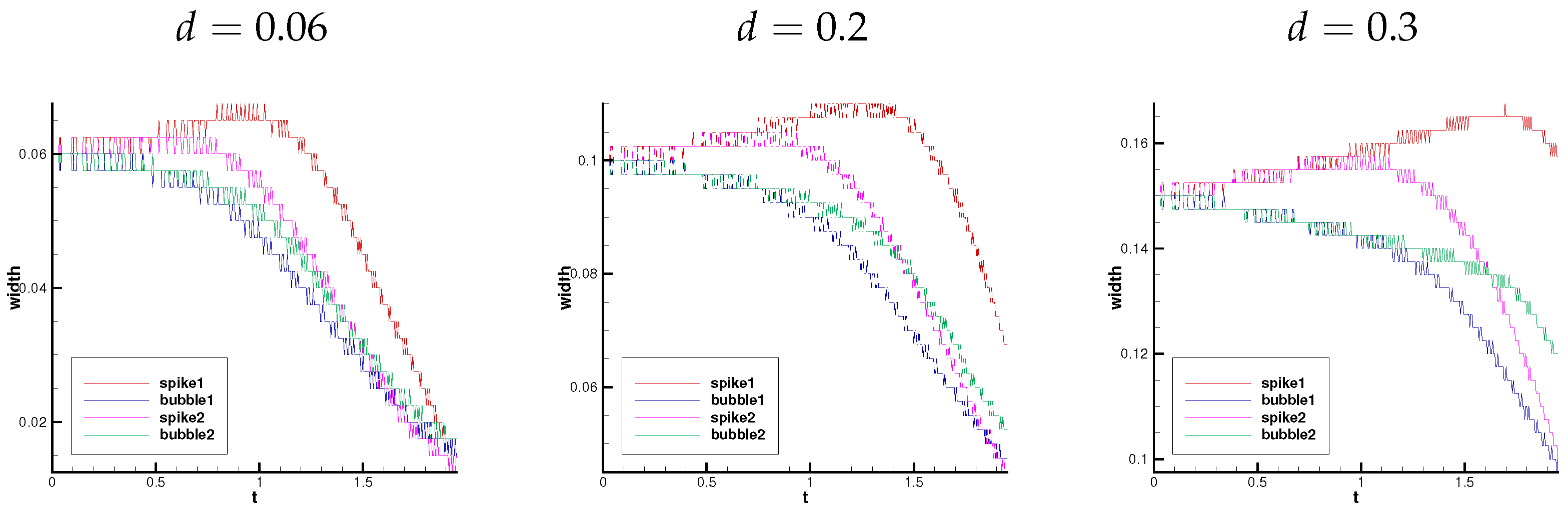
Spike and bubble are two important structures in the RTI phenomenon. Spike is the structure developed by a heavy fluid in a light fluid, while bubble is the structure developed by a light fluid in a heavy fluid. In order to clearly observe the development process of spike–bubble of two RTI phenomena, the temporal evolution of spike–bubble gap is drawn in Figure 9. From figure, one can find that the changing process of the gap widths between two interfaces can be divided into three stages roughly. In the first stage, the gap widths at the location of both spike and bubble remain the initial conditions for a short time. In the second stage, the gap width at the location of spike increases slowly, while the gap width at the location of bubble decreases slowly. In the third stage, the gap width at the location of spike begins to decrease rapidly, and the gap width at the location of bubble continues decreasing even faster. In the case of , the second and third stages are continuous, the gap width at the location of spike begins to decrease around and for and , respectively. When the initial gap width is larger , there is a stable period between the second stage and the third stage, during which the gap widths at the location of both spike and bubble remain unchanged. The gap widths at the location of both spike and bubble remain unchanged during . For initial gap width d is small and , the densities at the moment from the second stage to the third stage are shown in Figure 10. It can be observed that the height of the interfaces between two heavier layers at the location of spike is the same as that between two lighter layers at the location of bubble.
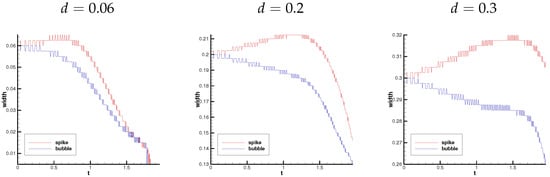
Figure 9.
The temporal evolution of the gap widths between two interfaces at the location of the spike and the bubble.
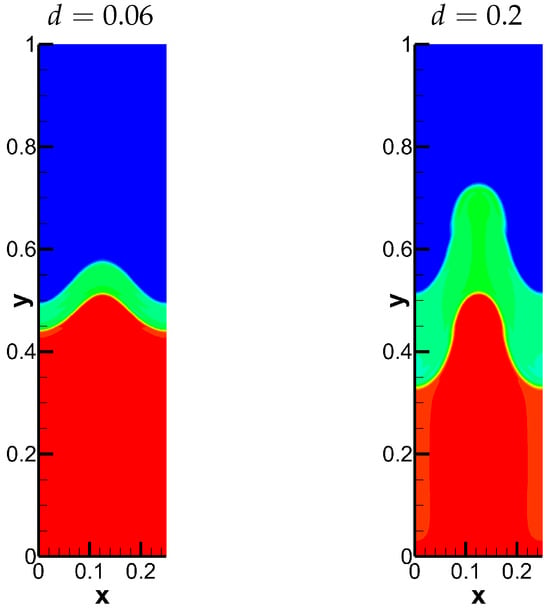
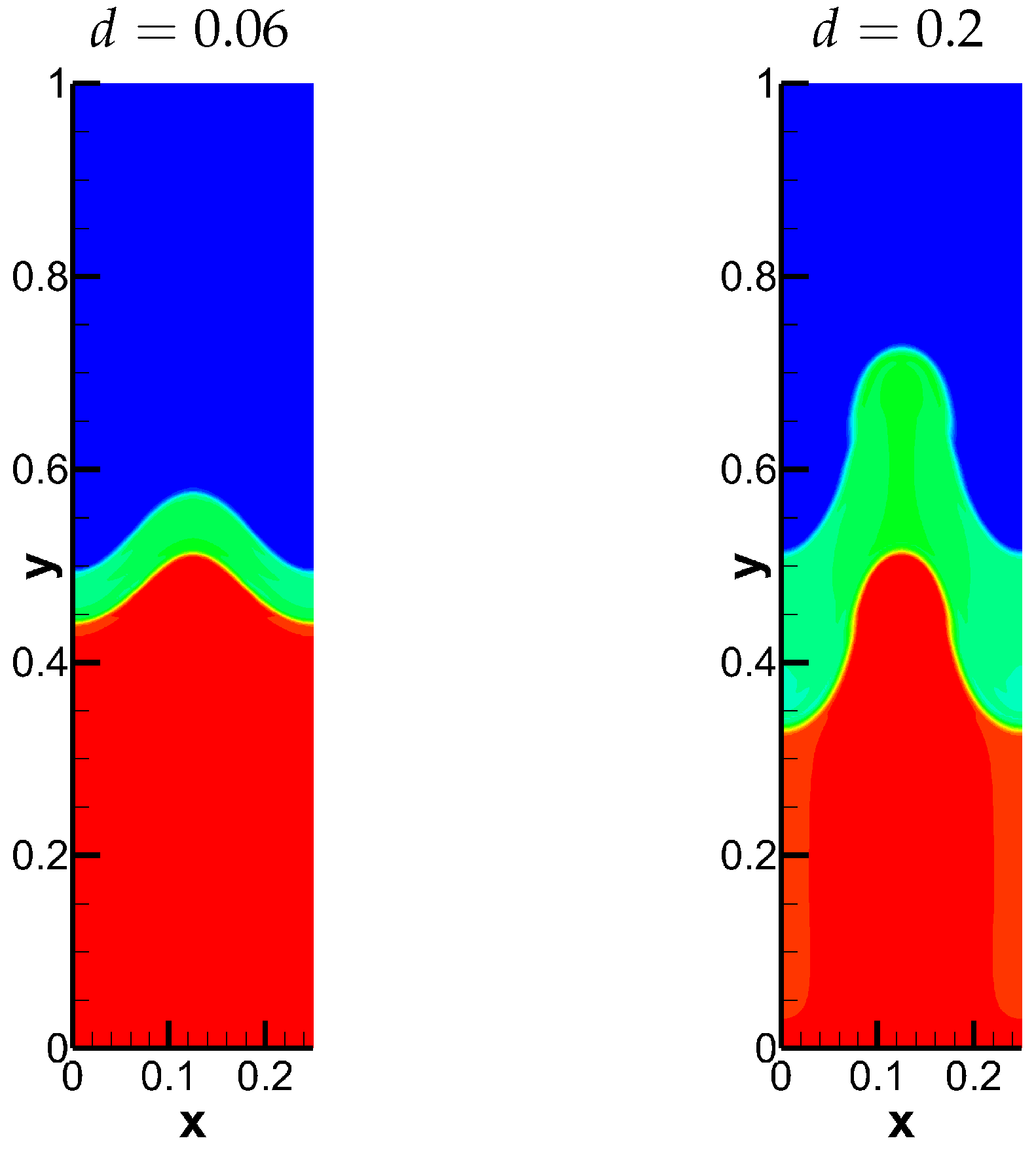
Figure 10.
The densities at the moment from the second stage to the third stage. The time is for and for , respectively.
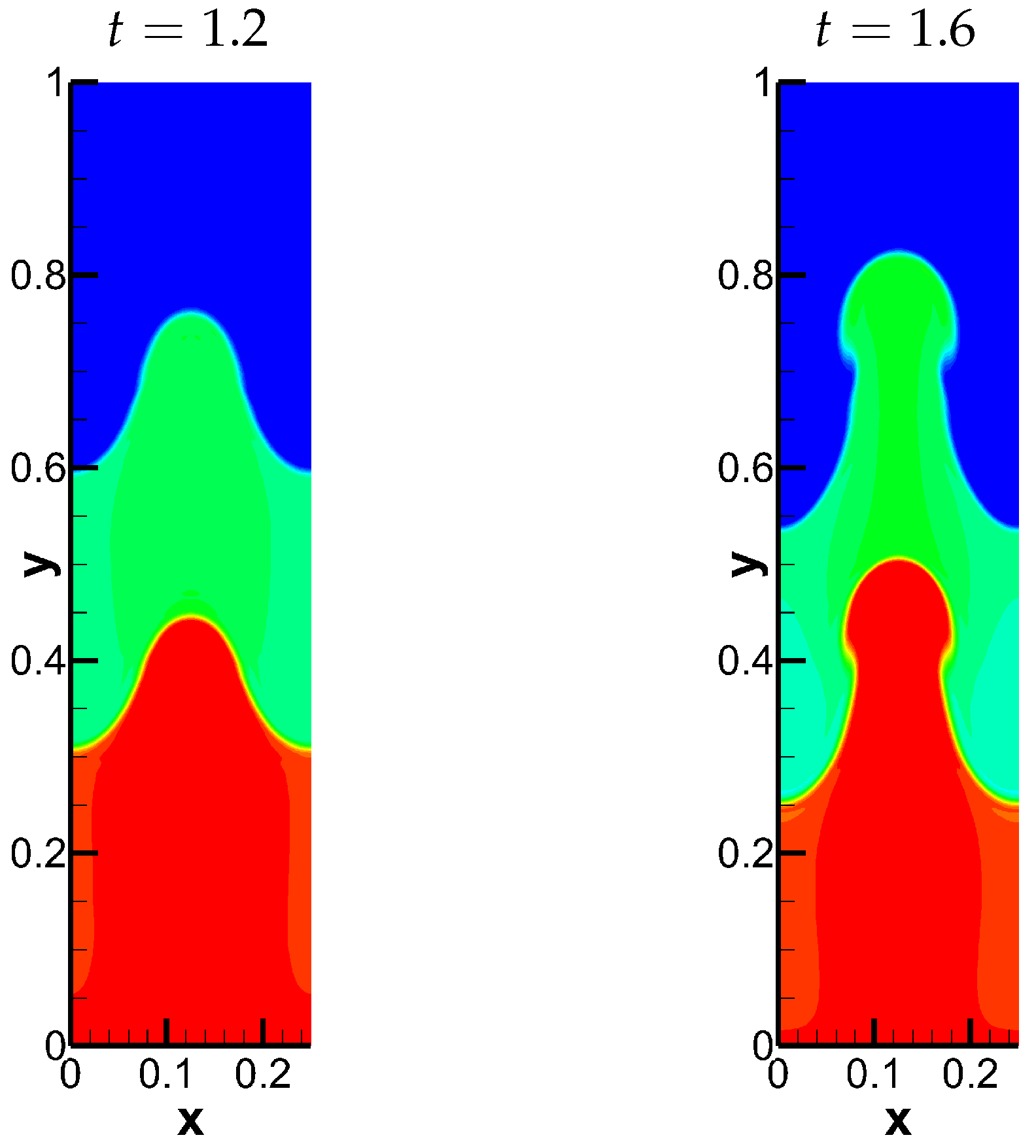
When d is relatively large, —the densities at the beginning time and the end time between the second stage and the third stage are shown in Figure 11. It can be observed that the relationship of spike and bubble is similar to that when d is small and . During the period between the second stage and the third stage, the gap widths remain unchanged. And at the end time, the height of the interfaces between two heavier layers at the location of spike is the same as that between two lighter layers at the location of bubble.
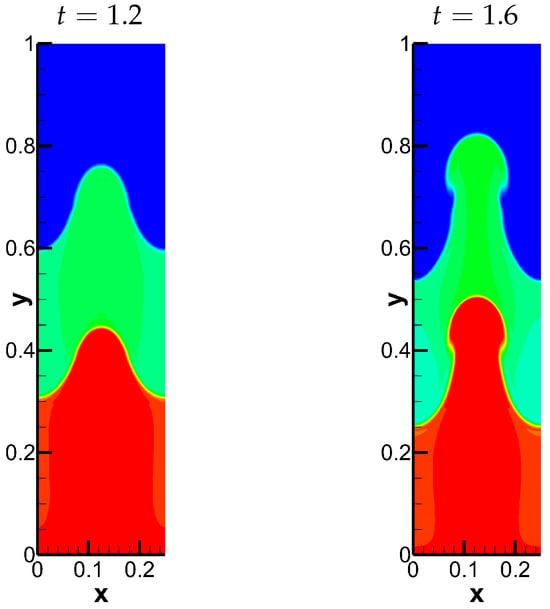
Figure 11.
The densities at the beginning time and the end time between the second stage and the third stage. The beginning time is and end time is for .
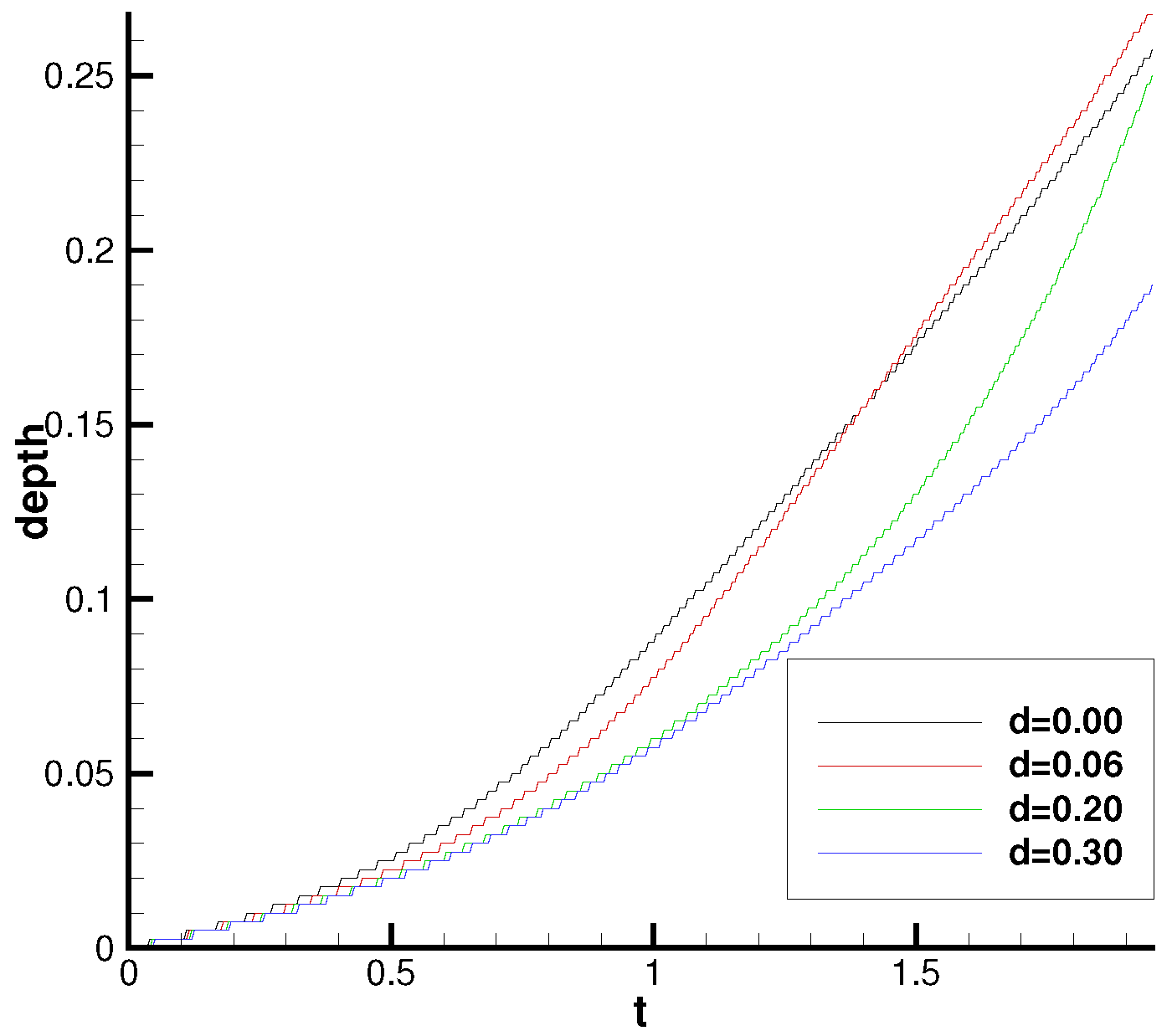
Another phenomenon can be observed in Figure 8, the penetration depth of the spike on the higher density side is related to the width of the middle layer. As shown in Figure 8, the evolution of spike is similar to Case 1 when the width of the middle layer d is small, while it penetrates shallower as d gets larger. The penetration depth–time image of the spike on the high density side is shown in Figure 12.
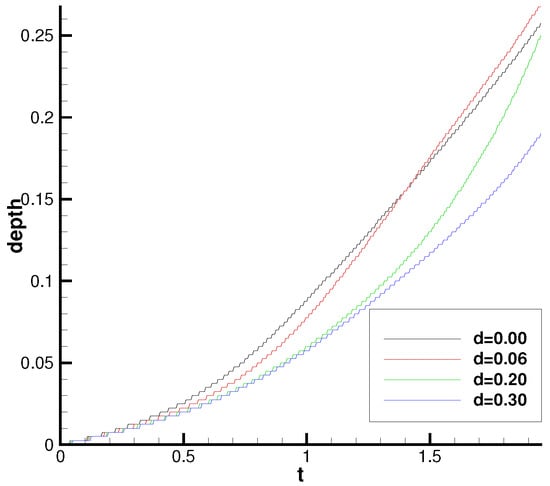
Figure 12.
The penetration depth-time image of the spike on the high density side. The line represents Case 1.
4.3. Results of Case 3
This case describes the RTI phenomenon with four layers of fluid. As mentioned in Section 3, we assume that two middle layers have the identical width d. We take as examples for numerical simulation and plot the corresponding initial density in Figure 13.
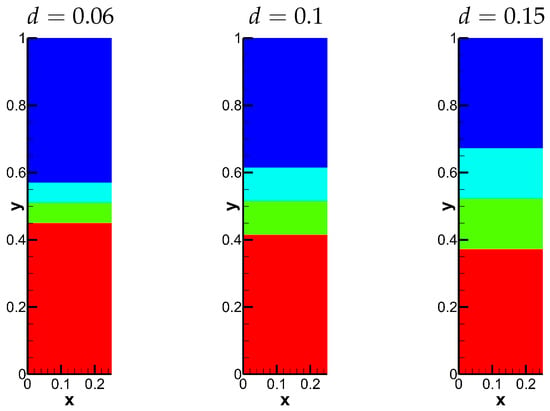
Figure 13.
The initial density of Case 3 with three different widths.
Similarly to the previous Section 4.2, the temporal evolution of spike–bubble gap is shown in Figure 14. One can find that the temporal evolution of spike–bubble width can be divided into two stages. In the first stage, the evolutions of two middle layers are almost the same, as for , for and for . At this stage, the gap width at the location of both spike and bubble are almost coincident, and the evolution law is similar to that of Case 2. Such an evolution law indicates that the interaction between the three interfaces is not obvious and the interaction between the two interfaces is dominant. In the second stage, the temporal evolutions of two middle layers are distinct. At the location of spike, the width of layer with lower density is gradually smaller than the width of layer with higher density. On the contrary, at the location of spike, the width of layer with lower density is gradually larger than the width of layer with higher density. The densities at the moment from the first stage to the second stage are shown in Figure 15, and the conclusion similar to Case 2 can also be obtained.
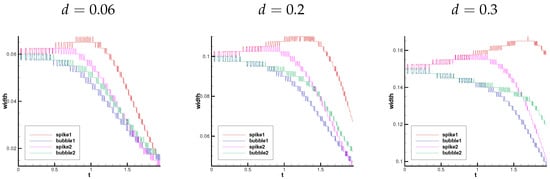
Figure 14.
The images of the gap widths between three discontinuities at the location of the spike and the bubble over time.
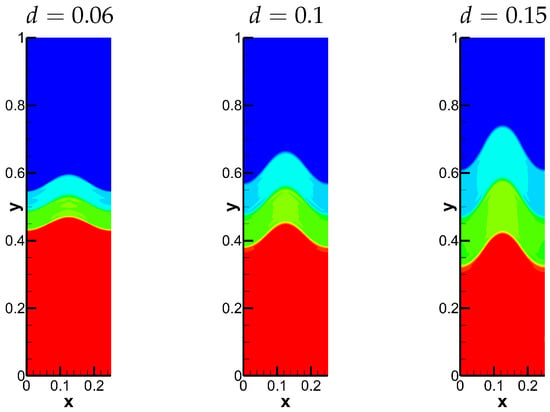
Figure 15.
The densities at the moment from the first stage to the second stage. The time is for , for and for , respectively.
4.4. Comparison Between Case 2 and Case 3
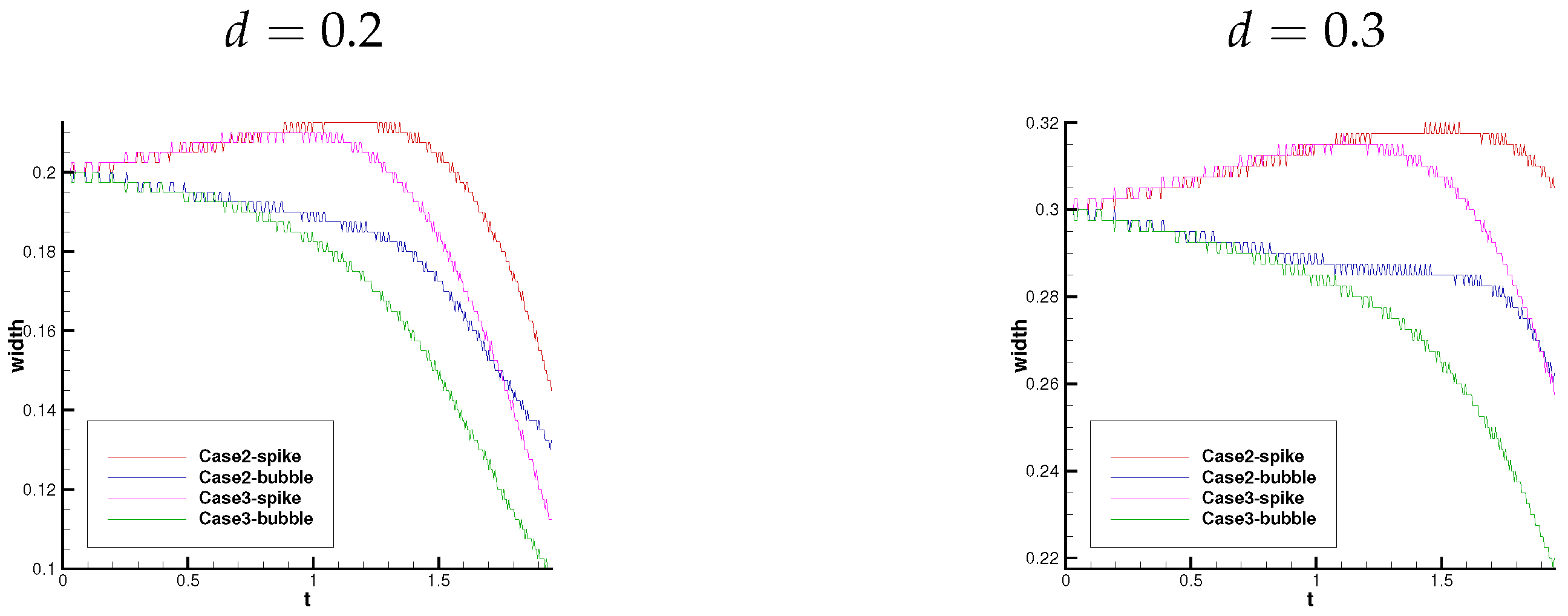
In order to study the effect of the number of interfaces on RTI phenomenon, the temporal evolutions of the width of the middle layer in Case 2 when is compared with those of the total width of the middle layer in Case 3 when are shown in Figure 16. At the first stage, the width of middle layer in Case 2 is basically consistent with the width of total middle layers in Case 3. At the second stage, the widths of total middle layers in Case 2 and Case 3 are not identical. In other words, the interaction of the three interfaces has not been developed at the first stage, then the interaction of three interfaces drives the widths of total middle layers in Case 3 less than that of middle layer in Case 2. The direct conclusion is that increasing the number of interfaces has an inhibitory effect on the spike–bubble development of RTI.
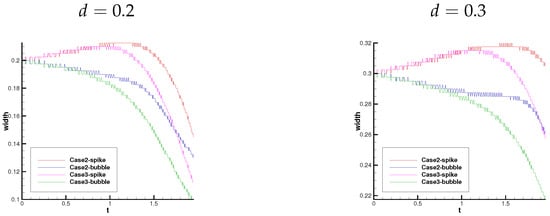
Figure 16.
The images of the gap widths between two discontinuities at the location of the spike and the bubble over time.
5. Discussion and Conclusions
5.1. Discussion
Our numerical experiments with the high-order hybrid compact–WENO scheme reveal three fundamental characteristics of multi-layer RTI dynamics that align precisely with the conclusions. First, we observe sequential staging behavior where interfacial interactions develop hierarchically. In three-layer systems, two-layer interactions initially dominate (e.g., Case 2 with ) before transitioning to three-layer coupling at , while four-layer systems exhibit analogous progression with distinct transitional timings (Figure 9 and Figure 14). This staging behavior confirms that RTI development follows deterministic layer-by-layer coupling mechanisms.
Second, quantitative analysis demonstrates clear layer-dependent suppression, where four-layer configurations exhibit slower spike growth rates compared to two-layer systems. The penetration depth measurements further validate this inhibition effect, showing a up to reduction when comparing versus cases. These findings directly support the conclusion that added fluid layers significantly mitigate RTI development.
The hybrid scheme’s 2.35 times speedup at resolution (Table 2) and reduced WENO usage (from to ) enable these precise measurements while maintaining solution accuracy through symmetrical shock detection. This computational efficiency was essential for capturing the detailed transition dynamics described in the conclusions, especially the subtle timing differences between various layer configurations.
5.2. Conclusions
This study employed a high-order hybrid compact–WENO scheme to simulate Rayleigh–Taylor instability (RTI) in multi-layer fluids (two-, three-, and four-layer systems). The results show that RTI evolves in stages, with interactions between layers increasing sequentially. For instance, in three-layer fluids, two-layer interactions occur first, followed by three-layer interactions, and similarly for four-layer fluids. Increasing the number of fluid layers inhibits RTI development, with more layers leading to greater mitigation of the phenomenon. When spikes and bubbles on adjacent interfaces reach the same height, the evolution of the spike–bubble gap changes significantly, marking a new stage in multi-layer fluid interaction. Initially, the widths between interfaces remain constant, indicating independent two-layer interactions. As RTI progresses, the middle layer width changes, signaling three-layer interactions. In four-layer systems, the evolution of fine-scale structures and spike–bubble formations is slower compared to fewer layers. The evolution law of middle layer widths changes when spikes and bubbles on adjacent interfaces align, indicating a shift in the interaction dynamics.
Author Contributions
Conceptualization, X.W.; methodology, X.W.; software, X.W. and X.C.; validation, X.W. and X.C.; writing—original draft preparation, X.W., C.F. and F.W.; project administration, X.W. and F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Shandong Provincial Natural Science Foundation of China (ZR2022QA002) and (ZR2022QA061)”.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jiang, S. Recent progress of inertial confinement fusion experiments in China. Ser. G Phys. Mech. Astron. 2009, 39, 1571–1583. [Google Scholar]
- Rayleigh, L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 1882, s1-14, 170–177. [Google Scholar] [CrossRef]
- Taylor, G. The formation of a blast wave by a very intense explosion. Math. Phys. Sci. 1950, 201, 159–174. [Google Scholar]
- Chandrasekhar, S.; Gillis, J. Hydrodynamic and hydromagnetic stability. Phys. Today 1962, 15, 58. [Google Scholar] [CrossRef]
- Ott, E. Nonlinear evolution of the Rayleigh-Taylor instability of a thin layer. Phys. Rev. Lett. 1972, 29, 1429–1432. [Google Scholar] [CrossRef]
- Baker, G.R.; Mccrory, R.L.; Verdon, C.P.; Orszag, S.A. Rayleigh-Taylor instability of fluid layers. J. Fluid Mech. 1987, 178, 161–175. [Google Scholar] [CrossRef]
- Li, X.L.; Glimm, J.; Jin, B.X. Numerical study for the three dimensional Rayleigh-Taylor instability through the TVD/AC scheme and parallel computation. J. Comput. Phys. 1996, 126, 343–355. [Google Scholar] [CrossRef][Green Version]
- Tang, W.J.; Zhang, J.L.; Li, X.L. The Ghost method for fluid interface instability in 3D. Chin. J. Comput. Phys. 2001, 02, 163–169. [Google Scholar]
- Ramaprabhu, P.; Dimonte, G.; Woodward, P. The late-time dynamics of the single-mode Rayleigh-Taylor instability. Phys. Fluids 2012, 24, 074107. [Google Scholar] [CrossRef]
- Wang, N.N.; Liu, H.H.; Zhang, C.H. Numerical simulation of Rayleigh-Taylor instability nased on lattice Boltzmann method. J. Eng. Thermophys. 2016, 37, 89–94. [Google Scholar]
- Sundaram, P.; Sengupta, A.; Sengupta, T. A non-overlapping high accuracy parallel subdomain closure for compact scheme: Onset of Rayleigh-Taylor instability by ultrasonic waves. J. Comput. Phys. 2022, 470, 111593. [Google Scholar] [CrossRef]
- Joshi, B.; Sengupta, A.; Ajanif, Y.; Lestandi, L. Spatio-temporal pulse propagation during highly-resolved onset of Rayleigh-Taylor and Kelvin-Helmholtz instabilities. arXiv 2025, arXiv:2505.07433. [Google Scholar]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Shu, C.-W. Essentially Non-Oscillatory and Weighted ENO Schemes for Hyperbolic Conservation Laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Quarteroni, A., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1697, pp. 325–432. [Google Scholar]
- Shi, J.; Zhang, Y.T.; Shu, C.-W. Resolution of high order WENO schemes for complicated flow structures. J. Comput. Phys. 2003, 186, 690–696. [Google Scholar] [CrossRef]
- Han, S.; Li, M.; Guo, B. The high order finite volume weighted essentially non-oscillatory schemes to solve the Rayleigh-Taylor Instability. In Proceedings of the AISS ’21: 3rd International Conference on Advanced Information Science and System, Sanya, China, 26–28 November 2021; Volume 60, pp. 1–5. [Google Scholar]
- Costa, B.; Don, W.S. High order hybrid central-WENO finite difference scheme for conservation laws. J. Comput. Appl. Math. 2007, 204, 209–218. [Google Scholar] [CrossRef]
- Pirozzoli, S. Conservative hybrid compact–WENO schemes for shock-turbulence interaction. J. Comput. Phys. 2002, 178, 81–117. [Google Scholar] [CrossRef]
- Don, W.S.; Gao, Z.; Li, P.; Wen, X. Hybrid compact–WENO finite difference scheme with conjugate Fourier shock detection algorithm for hyperbolic conservation laws. Siam J. Sci. Comput. 2016, 38, A691–A711. [Google Scholar] [CrossRef]
- Ren, Y.X.; Liu, M.; Zhang, H. A characteristic-wise hybrid compact–WENO scheme for solving hyperbolic conservation laws. J. Comput. Phys. 2003, 192, 365–386. [Google Scholar] [CrossRef]
- Gao, Z.; Don, W.S. Mapped hybrid central-WENO finite difference scheme for detonation waves simulations. J. Comput. Sci. 2012, 55, 351–371. [Google Scholar] [CrossRef]
- Guo, Q.L.; Sun, D.; Li, C.; Liu, P.X.; Zhang, H.X. A new discontinuity indicator for hybrid WENO schemes. J. Comput. Sci. 2017, 83, 28. [Google Scholar] [CrossRef]
- Wu, X.S.; Zhao, Y.X. A high-resolution hybrid scheme for hyperbolic conservation laws. Int. J. Numer. Methods Fluids 2015, 78, 162–187. [Google Scholar]
- Li, G.; Lu, C.; Qiu, J. Hybrid well-balanced WENO schemes with different indicators for shallow water equations. J. Comput. Sci. 2012, 51, 527–559. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Y.B.; Qiu, J.X. A hybrid Hermite WENO scheme for hyperbolic conservation laws. J. Comput. Phys. 2020, 405, 109175. [Google Scholar] [CrossRef]
- Wen, X.; Don, W.S.; Gao, Z.; Hesthaven, J.S. An edge detector based on artificial neural network with application to hybrid Compact–WENO finite difference scheme. J. Comput. Sci. 2020, 83, 49. [Google Scholar] [CrossRef]
- Gao, Z.; Wen, X.; Don, W.S. Enhanced robustness of the hybrid compact-WENO finite difference scheme for hyperbolic conservation laws with multi-resolution analysis and Tukey’s boxplot method. J. Comput. Sci. 2017, 73, 736–752. [Google Scholar] [CrossRef]
- Zhu, Q.Q.; Gao, Z.; Don, W.S.; Lv, X.Q. Well-balanced hybrid compact–WENO schemes for shallow water equations. Appl. Numer. Math. 2017, 112, 65–78. [Google Scholar] [CrossRef]
- Vasilyev, O.; Lund, T.; Moin, P. A general class of commutative filters for LES in complex geometries. J. Comput. Phys. 1998, 146, 82–104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).