Dynamic Response of Fracture Networks and the Evolution of Waterflood Fronts During Fracture-Flooding
Abstract
1. Introduction
2. Geomechanics-Flow Coupling Theoretical Model
2.1. Description of the Geological Model
2.2. Simulation of Fracture Network Propagation from a Fracture-Flooding Well
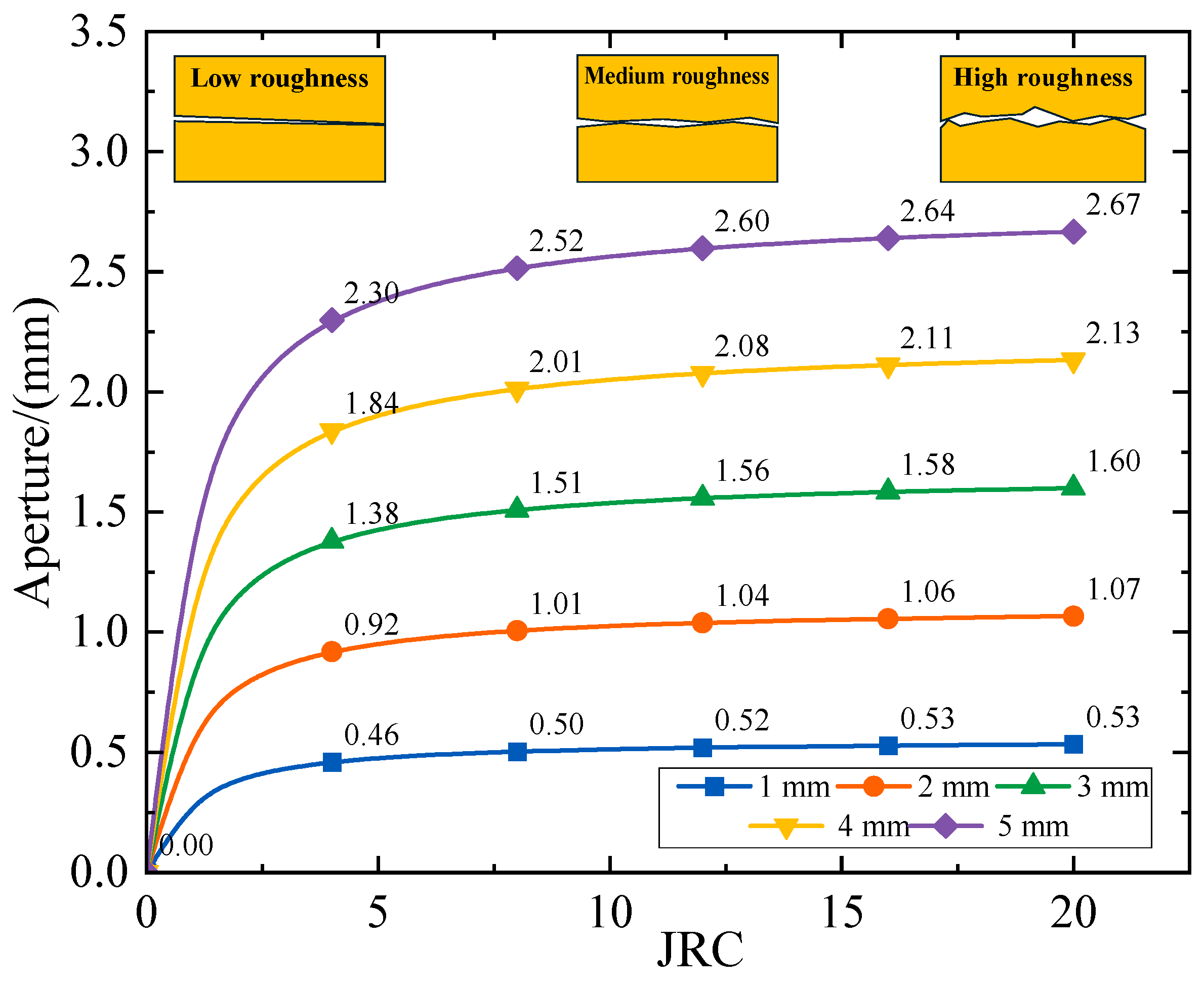
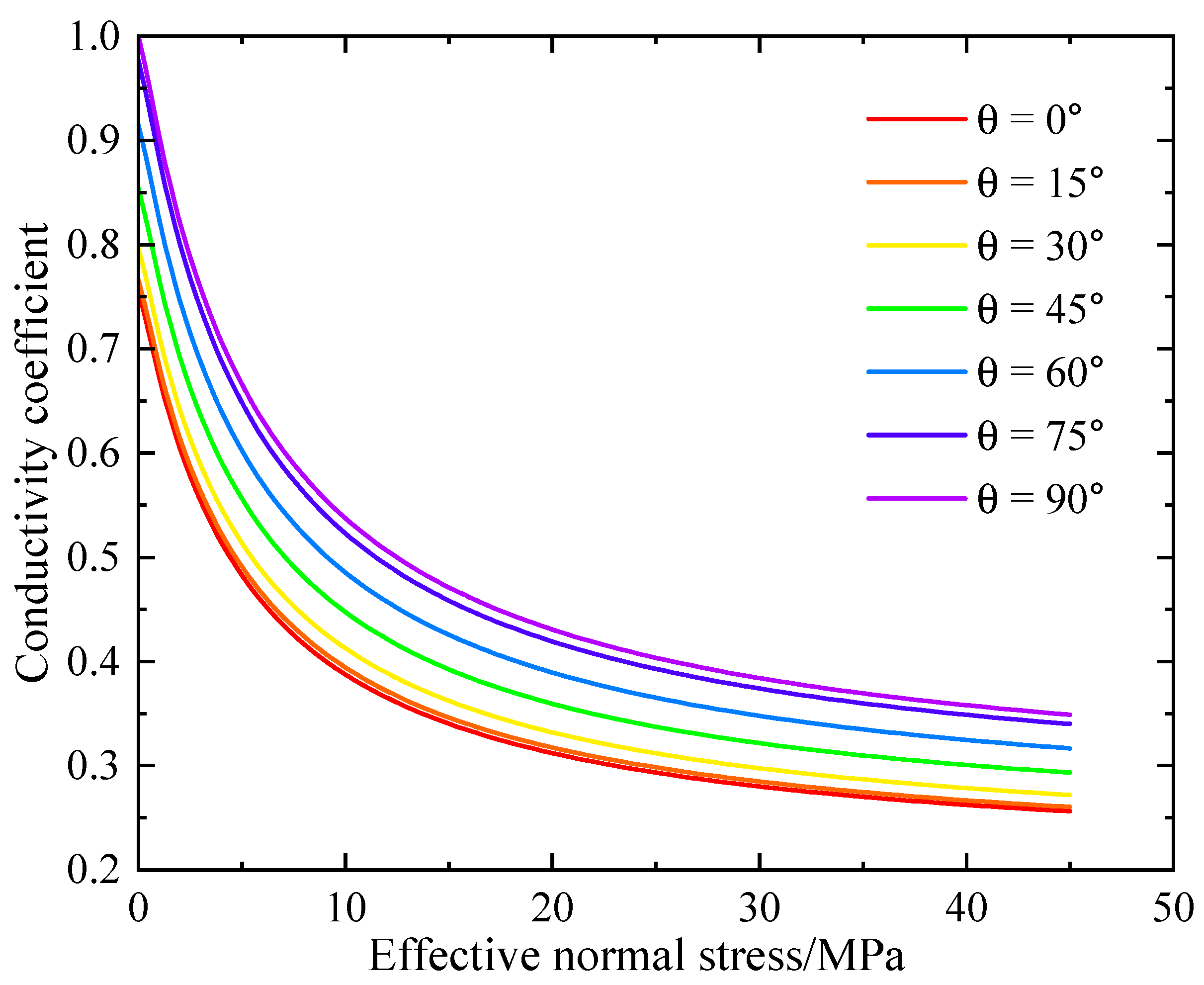
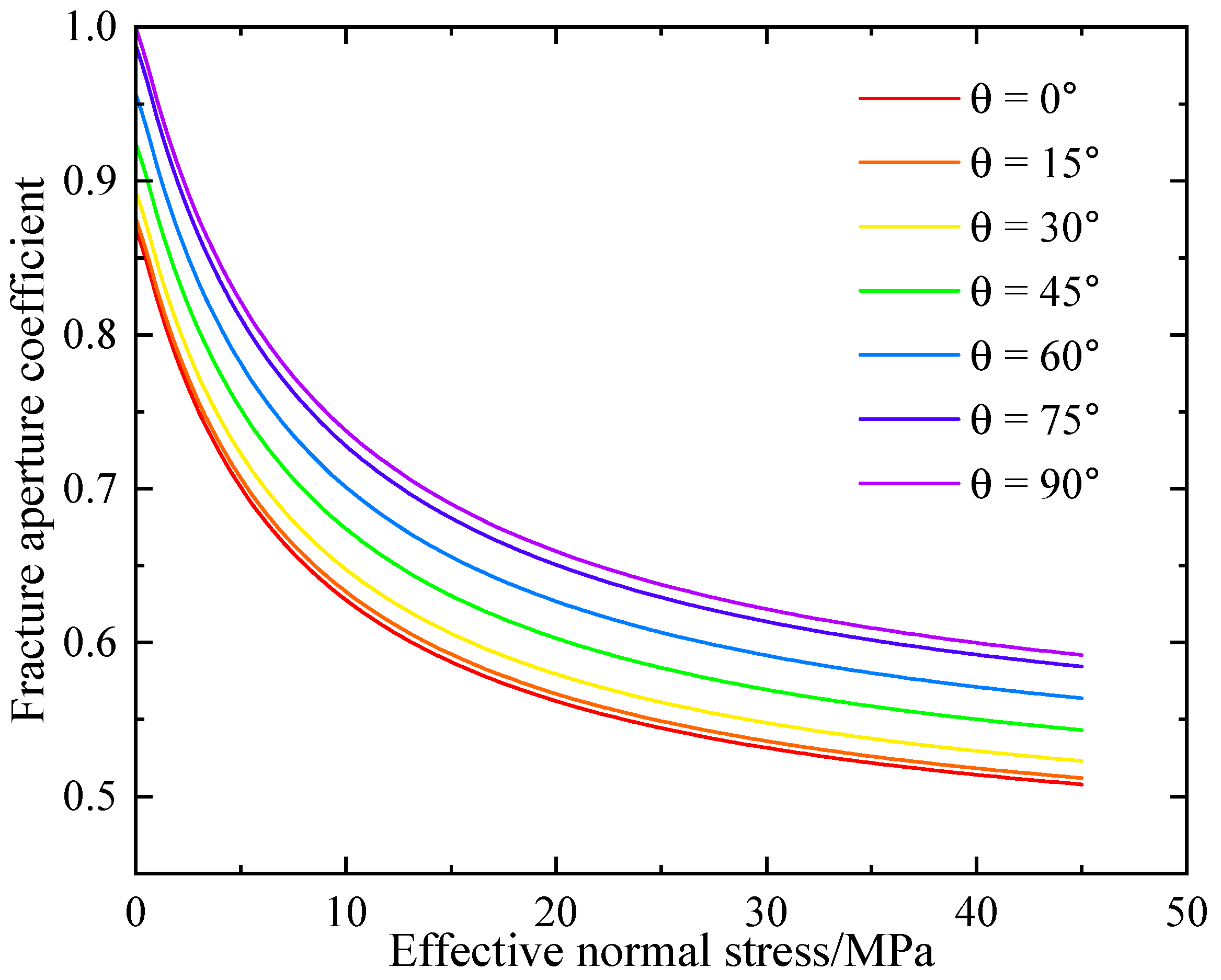
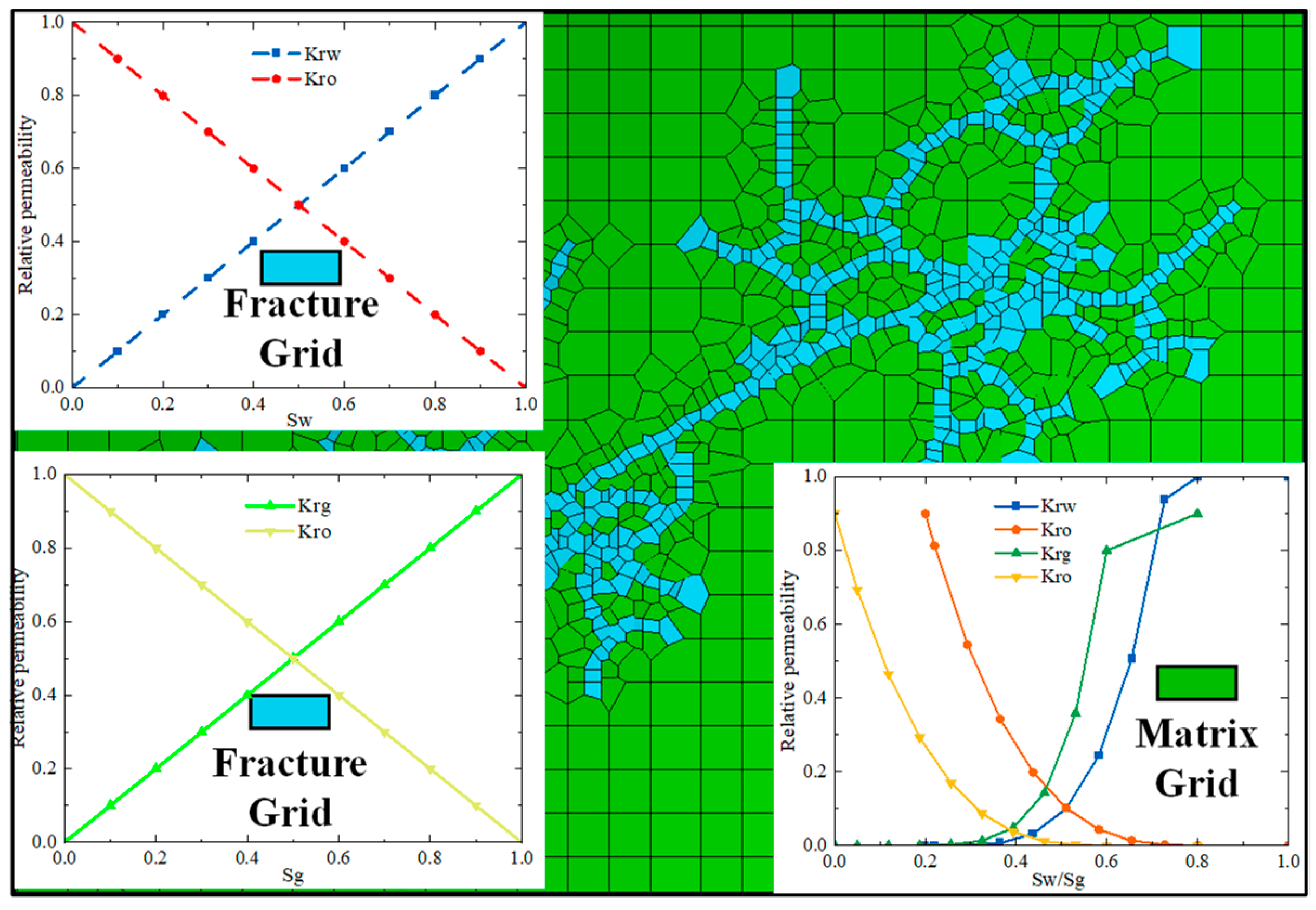
2.3. A Coupled Model of Fracture Nonlinear Deformation and Seepage Based on the Barton-Bandis Criterion
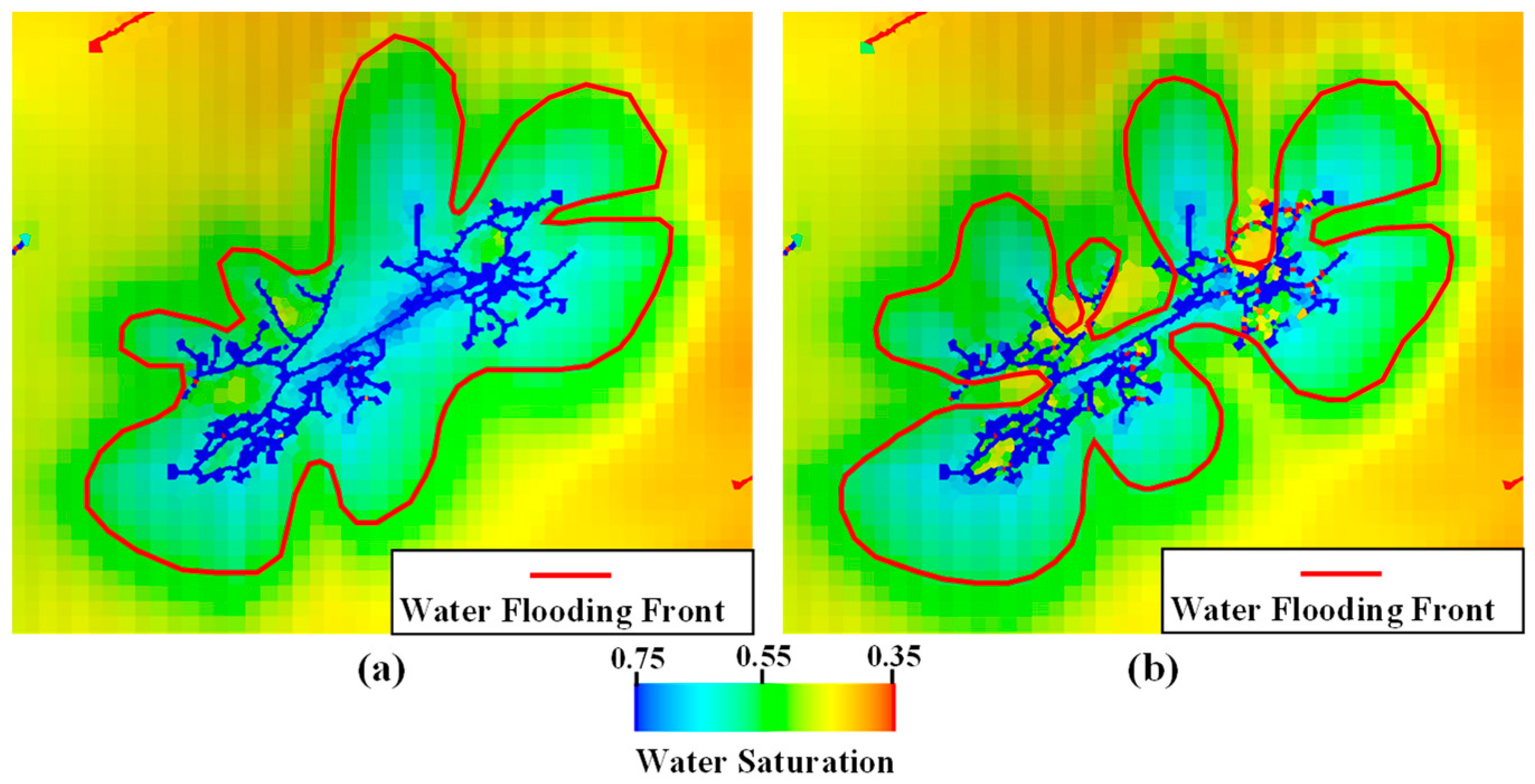
3. Analysis of Dynamic Responses of Fracture Networks and Evolution Patterns of Waterflood Fronts at the Field Scale
3.1. Model Overview Introduction
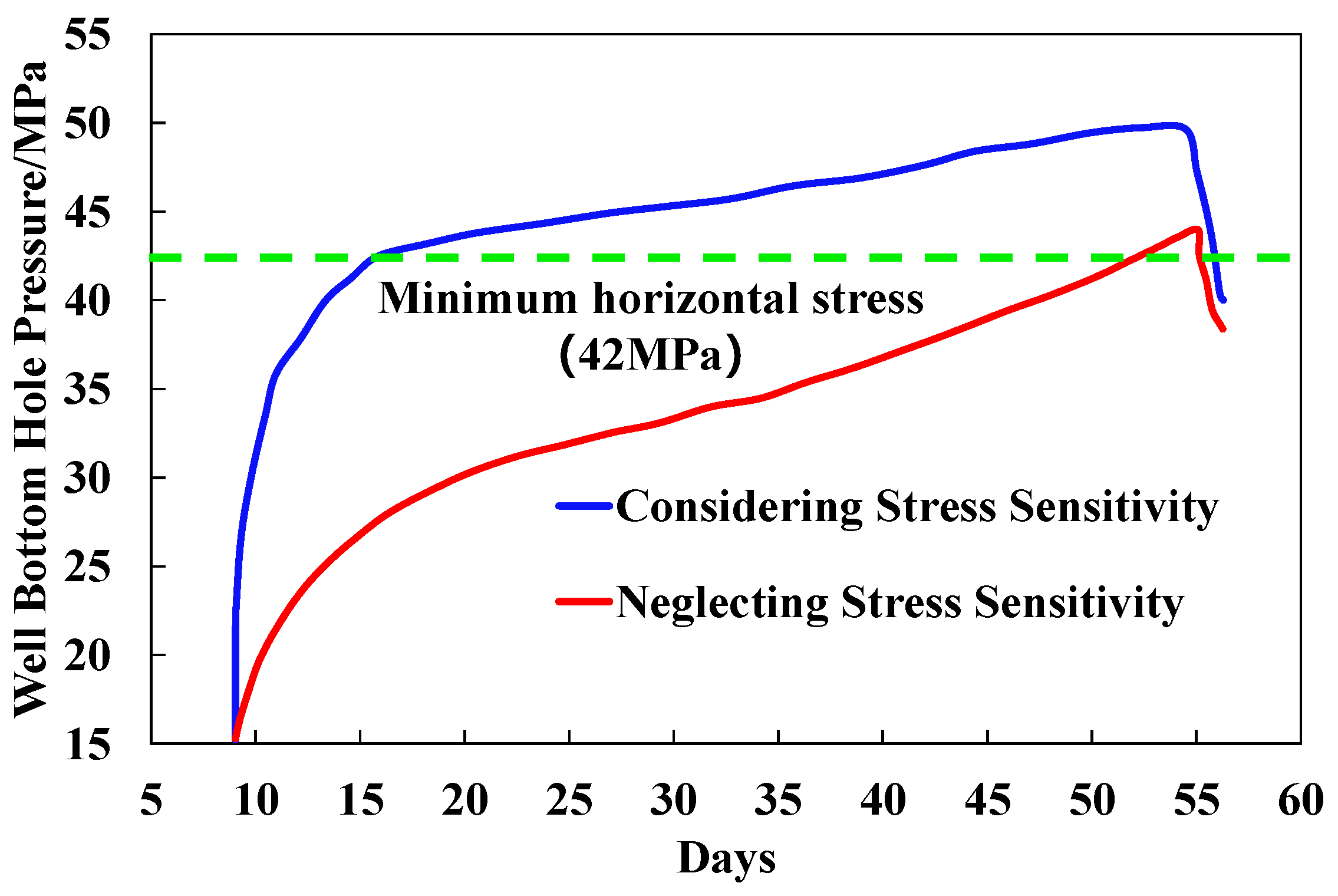
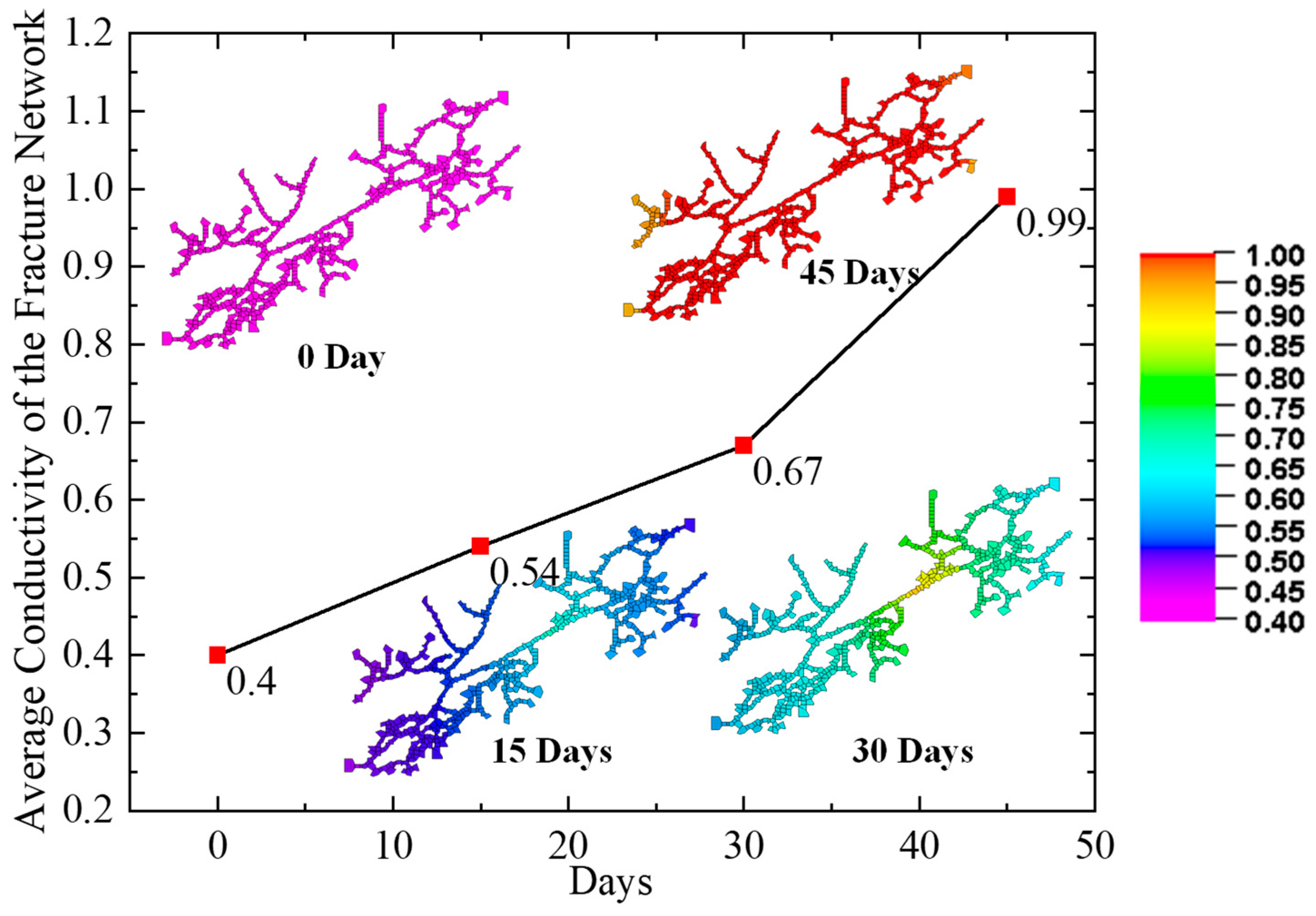
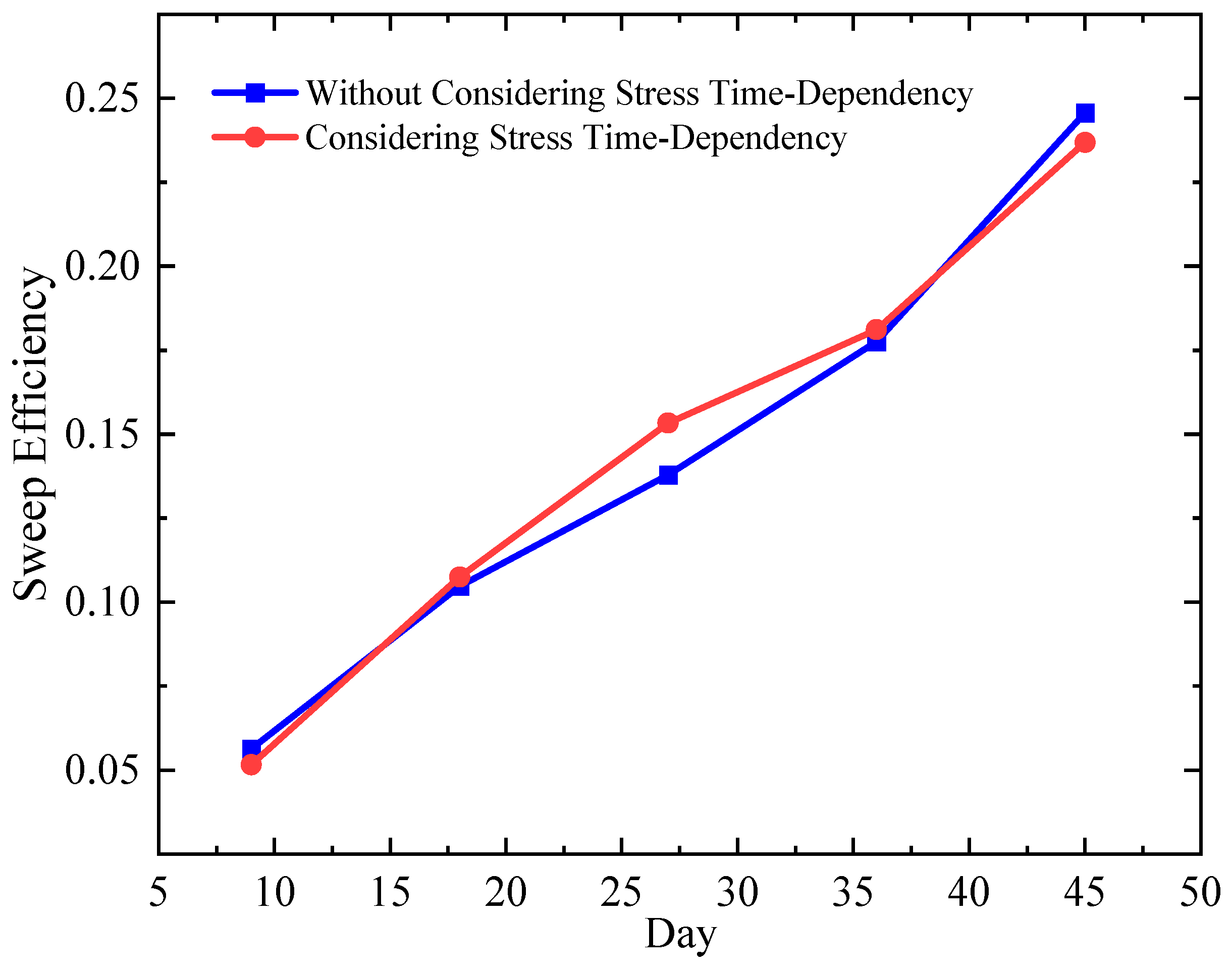
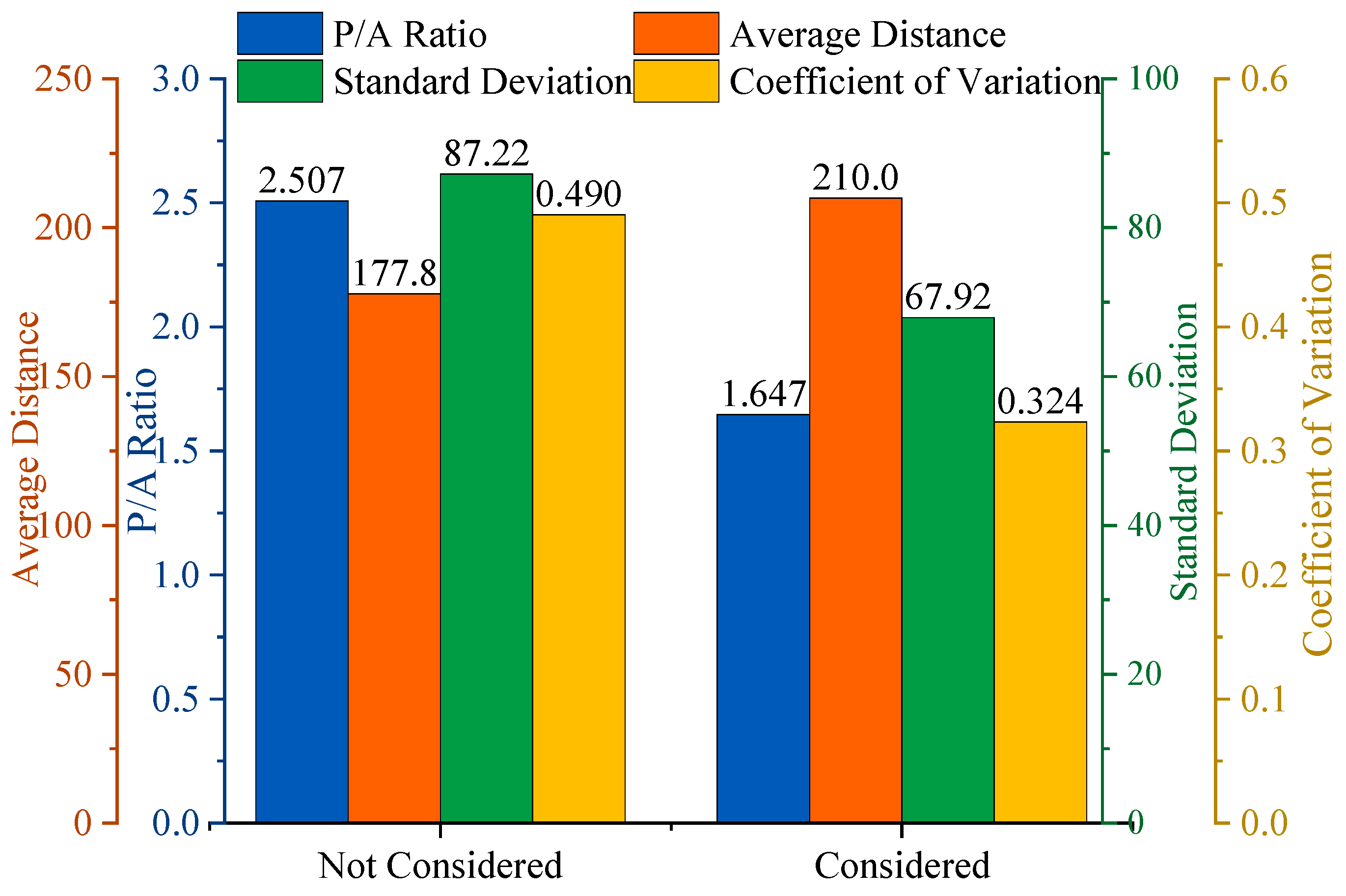
3.2. Spatiotemporal Evolution of Fracture Networks and Waterflood Fronts with Production Responses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hui, G.; Ren, Y.; Bi, J.; Wang, M.; Liu, C. Artificial intelligence applications and challenges in oil and gas exploration and development. Adv. Geo-Energy Res. 2025, 17, 179–183. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, Y.; Qi, M.; Dong, L.; Zhang, S.; Li, Y. Integrated detection of micro-pore structures and macro-mechanical responses for hydrate-bearing sediments. Adv. Geo-Energy Res. 2025, 17, 184–195. [Google Scholar] [CrossRef]
- Wei, Z.; Sheng, M.; Li, J.; Zhang, B.; Wang, B.; Li, G. Pressure diagnostics in hydraulic fracturing for unconventional completion optimization. Adv. Geo-Energy Res. 2025, 17, 196–211. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Ma, M.; Zhang, F.; Rui, Z.; Rezaeyan, A.; Ghanizadeh, A.; Hamdi, H.; Clarkson, C.R. Cyclic gas injection in low-permeability oil reservoirs: Progress in modeling and experiments. SPE J. 2024, 29, 6217–6250. [Google Scholar] [CrossRef]
- Xiliang, L.; Hao, C.; Yang, L.; Yangwen, Z.; Haiying, L.; Qingmin, Z.; Xianmin, Z.; Hongbo, Z. Oil production characteristics and CO2 storage mechanisms of CO2 flooding in ultra-low permeability sandstone oil reservoirs. Pet. Explor. Dev. 2025, 52, 196–207. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Su, Y.; Niu, H.; Hou, Z.; Hao, Y. Integrated study on CO2 enhanced oil recovery and geological storage in tight oil reservoirs. Geoenergy Sci. Eng. 2024, 241, 213143. [Google Scholar] [CrossRef]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and challenges in shale oil development: A critical review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Wei, B.; Qiao, R.; Hou, J.; Wu, Z.; Sun, J.; Zhang, Y.; Qiang, X.; Zhao, E. Multiphase production prediction of volume fracturing horizontal wells in tight oil reservoir during cyclic water injection. Phys. Fluids 2025, 37, 013304. [Google Scholar] [CrossRef]
- Chuan, C.; Huai, L.; Zhong, W. Analysis of pressures in water injection wells considering fracture influence induced by pressure-drive water injection. Pet. Reserv. Eval. Dev. 2023, 13, 686–694. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S.; Aleksandrov, A.N. Analysis of reservoir rock permeability changes due to solid precipitation during waterflooding using artificial neural network. J. Pet. Explor. Prod. Technol. 2025, 15, 17. [Google Scholar] [CrossRef]
- Wei, Z.; Su, Y.; Yong, W.; Liu, B.; Zhang, J.; Zhou, W.; Liu, Y. A Novel Quantitative Water Channeling Identification Method of Offshore Oil Reservoirs. Processes 2024, 12, 2363. [Google Scholar] [CrossRef]
- Du, D.; Liu, P.; Ren, L.; Li, Y.; Tang, Y.; Hao, F. A Volume Fracturing Percolation Model for Tight Reservoir Vertical Wells. Processes 2023, 11, 2575. [Google Scholar] [CrossRef]
- Zhao, M.; Guo, X.; Wu, Y.; Dai, C.; Gao, M.; Yan, R.; Cheng, Y.; Li, Y.; Song, X.; Wang, X. Development, performance evaluation and enhanced oil recovery regulations of a zwitterionic viscoelastic surfactant fracturing-flooding system. Colloids Surf. A Physicochem. Eng. Asp. 2021, 630, 127568. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, G.; Li, S.; Zhou, D.; Yu, C.; Sun, Q. Fracturing initiation and breakdown pressures in fracturing-flooding sandstone reservoirs. Rock Mech. Rock Eng. 2024, 1–18. [Google Scholar] [CrossRef]
- Moorman, E.D.; Xue, J.; Ibrahim, I.; Okeke, N.; Trabelsi, R.; Trabelsi, H.; Boukadi, F. Optimizing Intermittent Water Injection Cycles to Mitigate Asphaltene Formation: A Reservoir Simulation Approach. Processes 2025, 13, 2143. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, W.-D.; Su, Y.-L.; Chen, W.; Lei, Z.-D.; Li, L.; Hao, Y.-M. A semi-analytical model for coupled flow in stress-sensitive multi-scale shale reservoirs with fractal characteristics. Pet. Sci. 2024, 21, 327–342. [Google Scholar] [CrossRef]
- Zhang, J.; Standifird, W.; Roegiers, J.-C.; Zhang, Y. Stress-dependent fluid flow and permeability in fractured media: From lab experiments to engineering applications. Rock Mech. Rock Eng. 2007, 40, 3–21. [Google Scholar] [CrossRef]
- Wang, J.; Cui, C.; Wu, Z.; Qian, Y.; He, J. Optimization of Well Response Times in Fracturing-Flooding Using a Coupled Fluid-Solid Model for Heterogeneous Reservoirs. Geoenergy Sci. Eng. 2025, 254, 214022. [Google Scholar] [CrossRef]
- Cui, C.; Wang, J.; Qian, Y.; Li, J.; Lu, S. Fracturing–flooding for low-permeability oil reservoirs: A coupled model integrating DDM and black-oil model. Rock Mech. Rock Eng. 2025, 58, 4069–4089. [Google Scholar] [CrossRef]
- Xu, H.; Niu, B.; Huang, L.; Zhang, L.; Hao, Y.; Yue, Z. Study on the Influence Mechanisms of Reservoir Heterogeneity on Flow Capacity During Fracturing Flooding Development. Energies 2025, 18, 3279. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiang, S.; Lei, T.; Wang, J.; Zhang, Y. Optimization of key parameters of fracturing flooding development in offshore reservoirs with low permeability based on numerical modeling approach. J. Mar. Sci. Eng. 2025, 13, 282. [Google Scholar] [CrossRef]
- Wang, X.; Yu, W.; Xie, Y.; He, Y.; Xu, H.; Chu, X.; Li, C. Numerical simulation of the dynamic behavior of low permeability reservoirs under fracturing-flooding based on a dual-porous and dual-permeable media model. Energies 2024, 17, 6203. [Google Scholar] [CrossRef]
- Su, Y.; Jia, M.; Yao, Y.; Tong, G.; Xian, Y.; Wang, W. Investigation of fully coupled fracture propagation and oil–water two-phase flow mechanisms in fracturing flooding. Phys. Fluids 2025, 37, 056611. [Google Scholar] [CrossRef]
- Cordero, J.A.R.; Sanchez, E.C.M.; Roehl, D. Integrated discrete fracture and dual porosity-dual permeability models for fluid flow in deformable fractured media. J. Pet. Sci. Eng. 2019, 175, 644–653. [Google Scholar] [CrossRef]
- Rueda, J.; Mejia, C.; Noreña, N.; Roehl, D. A three-dimensional enhanced dual-porosity and dual-permeability approach for hydromechanical modeling of naturally fractured rocks. Int. J. Numer. Methods Eng. 2021, 122, 1663–1686. [Google Scholar] [CrossRef]
- Nie, R.-S.; Meng, Y.-F.; Jia, Y.-L.; Zhang, F.-X.; Yang, X.-T.; Niu, X.-N. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transp. Porous Media 2012, 92, 213–235. [Google Scholar] [CrossRef]
- Yang, S.; Lei, Y.; Chen, D.; Gao, L.; Wang, M.; Zheng, Q. Permeability model of coalbed methane reservoir with heterogeneous rough dual-porosity medium considering multiple gas flow mechanisms. Powder Technol. 2025, 464, 121174. [Google Scholar] [CrossRef]
- Xiong, D.; He, J. Evaluation of a complex fracture network in deep coalbed methane reservoir considering natural fracture tensile and shear failure. Phys. Fluids 2025, 37, 036601. [Google Scholar] [CrossRef]
- Li, N.; Zhu, S.; Li, Y.; Zhao, J.; Long, B.; Chen, F.; Wang, E.; Feng, W.; Hu, Y.; Wang, S. Fracturing-flooding technology for low permeability reservoirs: A review. Petroleum 2024, 10, 202–215. [Google Scholar] [CrossRef]
- Weng, M.-C.; Peng, C.-H.; Le, H.-K.; Shiu, W.-J.; Fang, C.-H. Discrete element analysis of hydraulic stimulation in a slate geothermal reservoir using the ubiquitous foliation model. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 37. [Google Scholar] [CrossRef]
- Lavoine, E.; Davy, P.; Darcel, C.; Munier, R. A discrete fracture network model with stress-driven nucleation: Impact on clustering, connectivity, and topology. Front. Phys. 2020, 8, 9. [Google Scholar] [CrossRef]
- Bahrainian, S.S.; Daneh Dezfuli, A.; Noghrehabadi, A. Unstructured grid generation in porous domains for flow simulations with discrete-fracture network model. Transp. Porous Media 2015, 109, 693–709. [Google Scholar] [CrossRef]
- Mehrdoost, Z. Multiscale finite volume method with adaptive unstructured grids for flow simulation in heterogeneous fractured porous media. Eng. Comput. 2022, 38, 4961–4977. [Google Scholar] [CrossRef]
- Li, X.; Zhu, B.; Xiao, W. A modified Barton-Bandis normal closure model for infilled rock joint. Environ. Earth Sci. 2025, 84, 403. [Google Scholar] [CrossRef]
- Bandis, S.; Lumsden, A.; Barton, N. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]

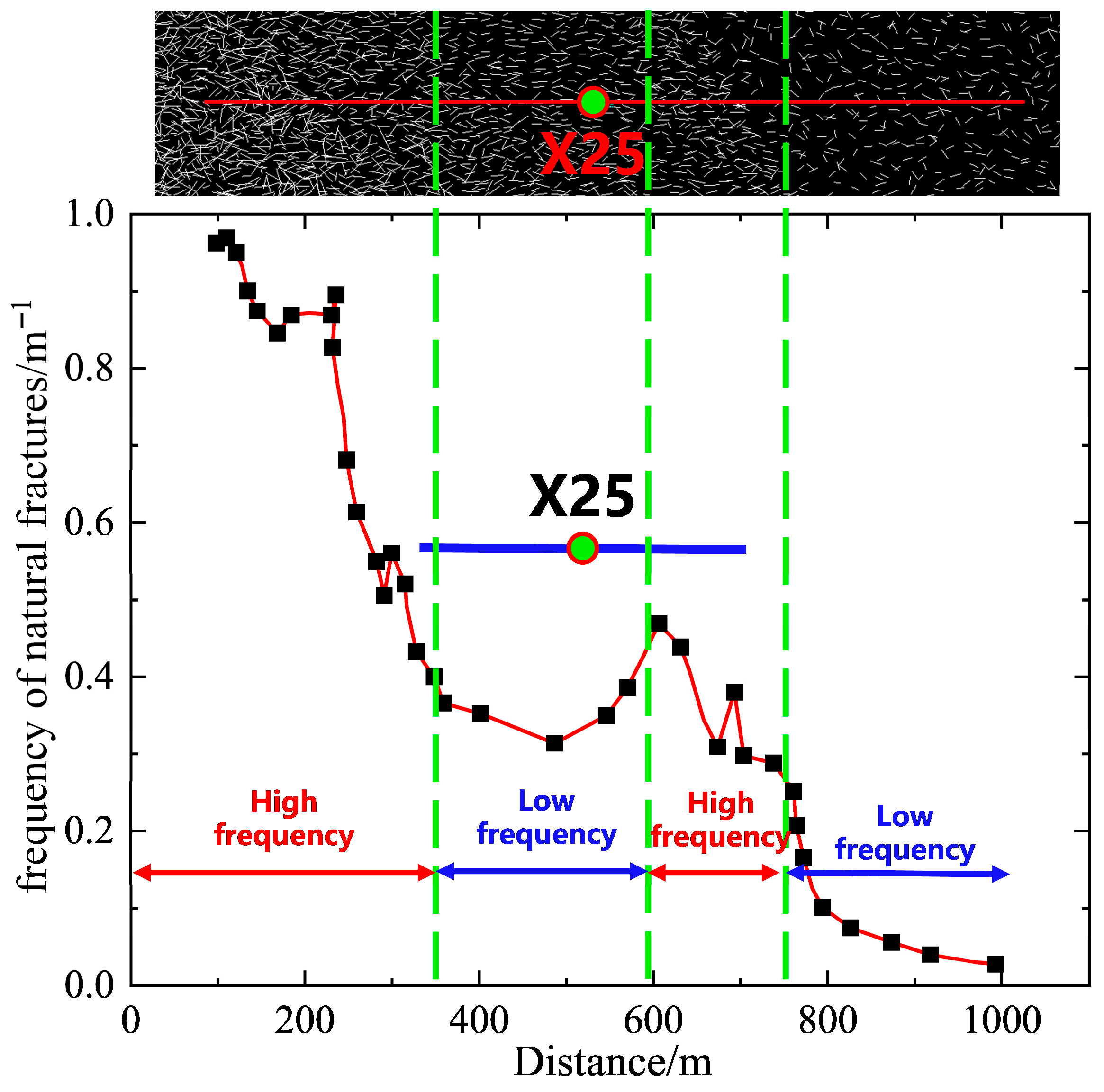
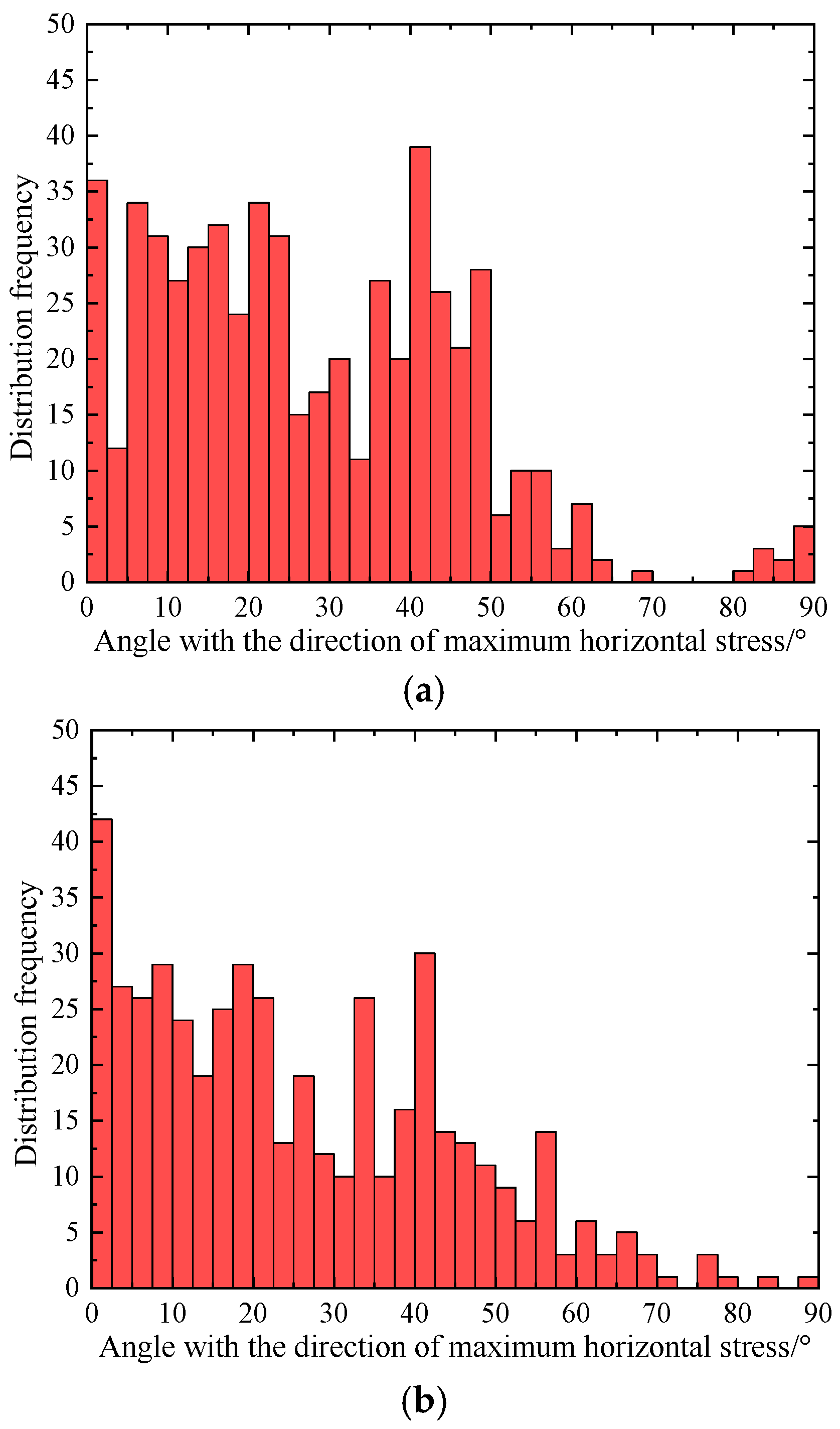


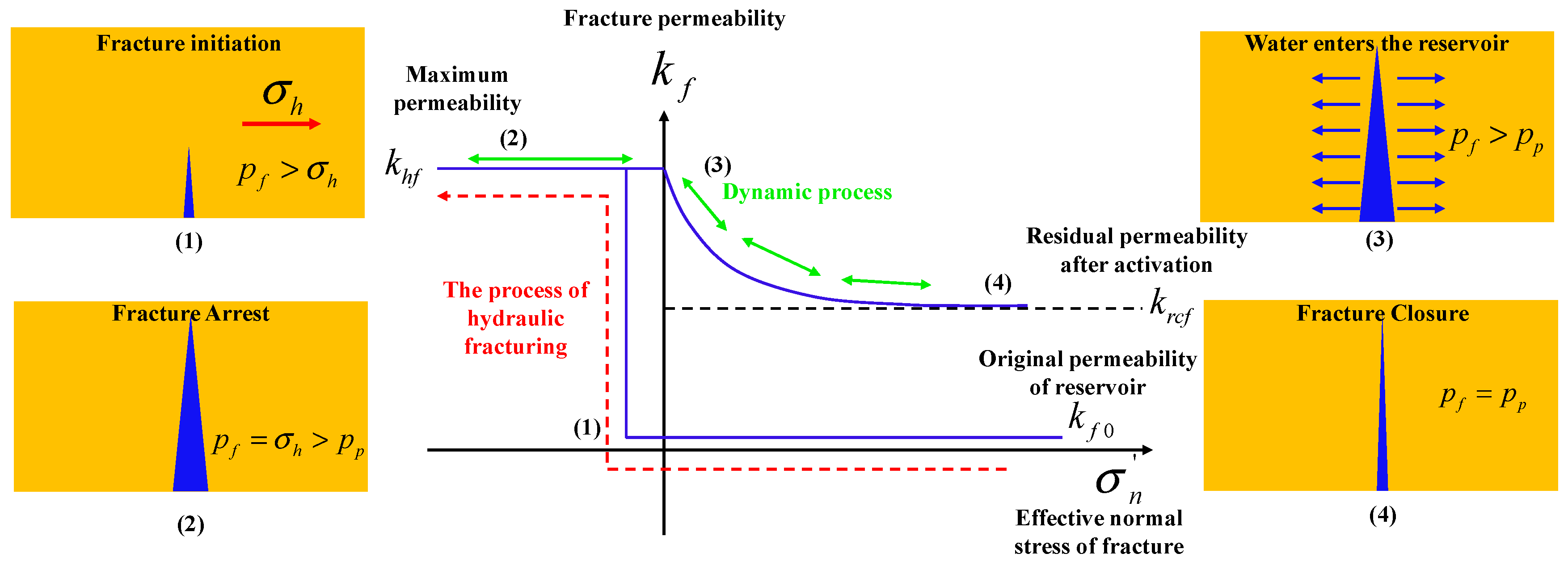
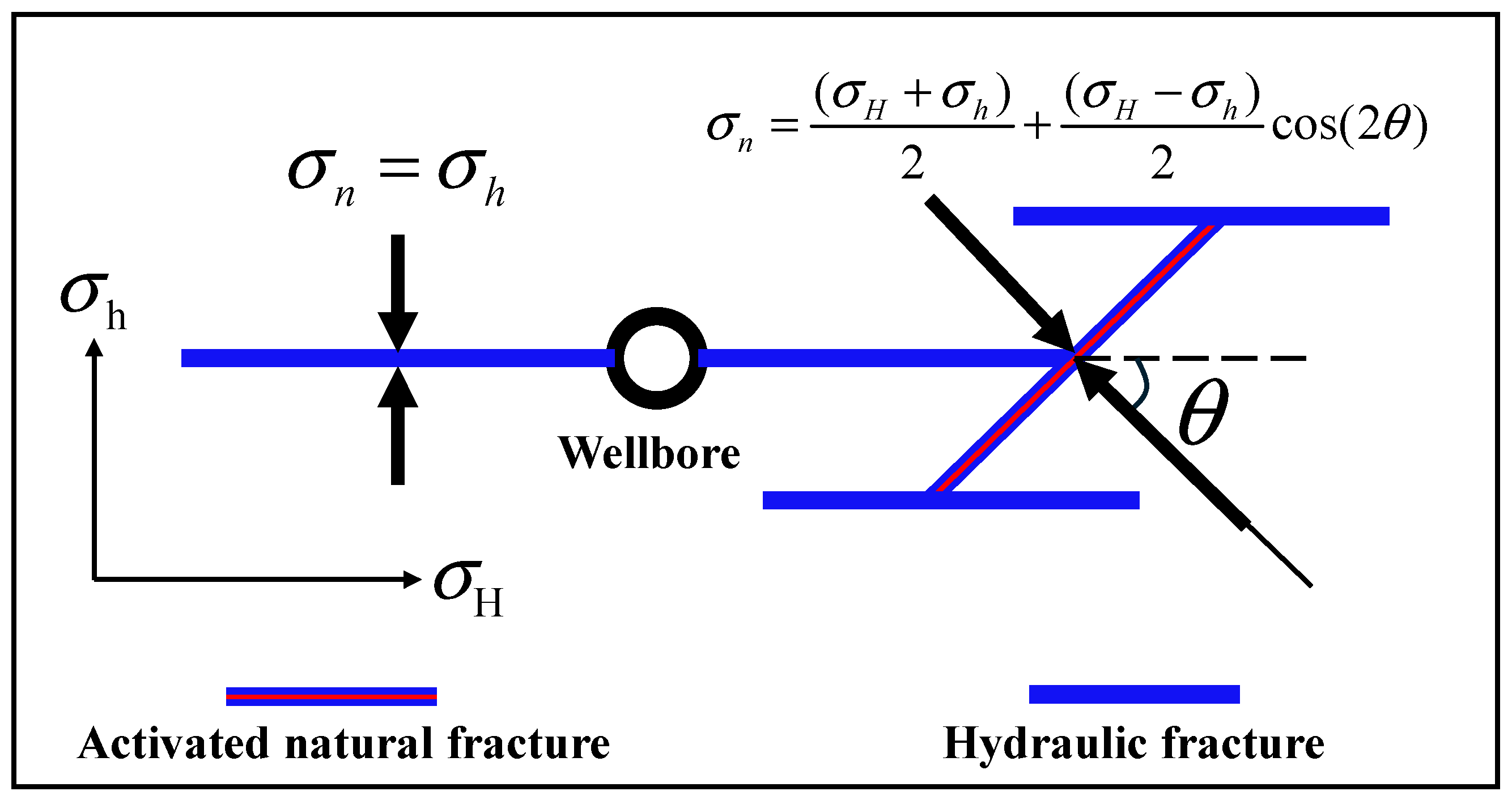




| Natural Fracture Properties | Value |
|---|---|
| Length range | 2–25 m |
| Average length | 12.36 m |
| Orientation range | 15°–105° |
| Average Orientation | 62.5° (northeast) |
| Average spacing | 8.35 m |
| Reservoir Physical Properties | Value |
|---|---|
| Range of porosity | 0.087–0.219 |
| Average porosity | 0.155 |
| Range of permeability | 0.544–1.472 mD |
| Average permeability | 1.01 mD |
| Range of water saturation | 0.267–0.598 |
| Average water saturation | 0.411 |
| Pressure | 29.36 MPa |
| Average maximum horizontal stress | 45 MPa |
| Average minimum horizontal stress | 42 MPa |
| Average overburden stress | 65 MPa |
| Other Parameters of the Fracture-Flooding Fracture Network | Value |
|---|---|
| Average fracture height | 9.90 m |
| Average fracture width | 3.52 mm |
| Total fracture surface area | 20,914.56 m2 |
| Parameter | Value | Well Name | Hydraulic Fracture Length |
|---|---|---|---|
| Minimum Bottom Hole Pressure (MBHP) | 15 MPa | X24 | 116.69 m |
| Duration of the First Depletion Production | 180 days | X26 | 167.49 m |
| Fracture-flooding Duration | 180 days | X27 | 207.22 m |
| Duration of the Second Depletion Production | 180 days | X28 | 186.88 m |
| Water Injection Rate During Fracturing Period | 0.6 m3/min | X29 | 227.55 m |
| Water Injection Rate During Conventional Waterflooding | 300 m3/d | X30 | 121.73 m |
| Water Injection Volume | 40,000 m3/d (Fracture-flooding) 20,000 m3/d (Water flooding) | X31 | 173.31 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, B.; Zhang, L.; Liu, Y.; Li, Y.; Zhang, Y.; Li, X.; Li, L. Dynamic Response of Fracture Networks and the Evolution of Waterflood Fronts During Fracture-Flooding. Processes 2025, 13, 3592. https://doi.org/10.3390/pr13113592
Zheng B, Zhang L, Liu Y, Li Y, Zhang Y, Li X, Li L. Dynamic Response of Fracture Networks and the Evolution of Waterflood Fronts During Fracture-Flooding. Processes. 2025; 13(11):3592. https://doi.org/10.3390/pr13113592
Chicago/Turabian StyleZheng, Bintao, Liaoyuan Zhang, Yunfan Liu, Yuan Li, Yuzhe Zhang, Xiaodan Li, and Lei Li. 2025. "Dynamic Response of Fracture Networks and the Evolution of Waterflood Fronts During Fracture-Flooding" Processes 13, no. 11: 3592. https://doi.org/10.3390/pr13113592
APA StyleZheng, B., Zhang, L., Liu, Y., Li, Y., Zhang, Y., Li, X., & Li, L. (2025). Dynamic Response of Fracture Networks and the Evolution of Waterflood Fronts During Fracture-Flooding. Processes, 13(11), 3592. https://doi.org/10.3390/pr13113592






