Air Quality Prediction Based on Spatio-Temporal Feature Fusion over Graphs

Abstract

Significant interest has been sparked in the monitoring and prediction of air quality due to the impact of air quality on human health. However, challenges arise from characterizing the complex spatial features and temporal features of monitored air quality data. In this paper, we develop an air quality forecasting model using spatio-temporal feature fusion over graphs. We use the location information of air quality monitoring stations to construct a directed graph adjacency matrix, which helps in extracting the spatial features of air quality data. A spatio-temporal feature extraction module is designed by explicitly involving the graph adjacency matrix to help characterize the coupled effects between spatial and temporal features of air quality data. Our proposed air quality prediction model was demonstrated using a real-world dataset collected over 35 air monitoring stations in Beijing. Numerical experiments demonstrate that our proposed model improves the air quality prediction over several existing models, e.g., 18.65 percent improvement in 24 h air quality prediction over the MAE metric and 15.91 percent improvement in 24 h prediction over the RMSE metric.

1. Introduction

Common air pollutants include various substances such as gases, dust, smoke, and odors that can cause health and environmental problems. One primary concern is particulate matter (PM), with PM_2.5 referring to fine particulate matter with a diameter of 2.5  μm or less. Cardiovascular disease, respiratory illnesses, and cancer can all be caused by exposure to fine particulate matter [1]. The monitoring of real-time air quality and the forecasting of the air quality index are attracting more and more attention. Pollution forecasts help decision-makers to implement pollution control measures in a timely manner, alert vulnerable populations, protect public health, and formulate sustainable policies to mitigate environmental damages. Many efforts have been made to predict air quality. These include physics-driven models, data-driven models, graph neural network-based models, and physics-informed neural network models.

1.1. Physics-Based Numerical Models

Air quality can be forecasted using physics-based methods that draw upon atmospheric science to establish governing equations for air dispersion [2]. For example, a three-dimensional real-time air quality forecasting model that couples meteorology and chemistry online, and includes their transitions, has been proposed. This model greatly helps us to understand the complex interplay of meteorology, emissions, and chemistry at scales ranging from global to urban [3]. However, physics-based numerical forecasting methods are time-consuming and labor-intensive because of the substantial computational resources they require. Data-driven air quality prediction methods are developed using their historical data [4]. For example, a model that uses an auto-regressive integrated moving average to forecast atmospheric environmental quality has been developed [4]. A hidden semi-Markov model-based prediction model is developed for high-PM_2.5-concentration-value forecasting [5]. These methods may strongly rely on the stationary assumption of the historical data.

1.2. Data-Driven Models

Air quality usually exhibits complex nonlinear temporal relationships. Hence, neural network-based methods are developed. For example, a hybrid deep learning framework has been proposed by combining a one-dimensional convolutional module and a bi-directional long short-term memory module [6]. A temporal denoising auto-encoder network and a hybrid PM_2.5 prediction framework are developed to rapidly extract complex features of air quality data [7]. An attention module is developed to capture the relationships between historical data and the temporal correlational data [8]. A category-based PM_2.5 prediction model [9] was designed using a category information-based representation module to produce a robust representation that is insensitive to local variation. A transformer-based model [10] was developed for PM_2.5 prediction by leveraging data embedding and different attention modules to characterize the temporal relationships between air quality data points. A hybrid model of a convolutional network and long short-term memory module was proposed for multiple-hour forecasting [11]. A three-dimensional convolutional unit with a gated recurrent unit has been developed, where a 3DCNN module captures the features of multi-dimensional data and the attention mechanism adjusts the influences of features to avoid the influence of random fluctuations [12]. A hybrid model of an empirical mode decomposition method with a transformer unit was proposed to improve the inference capability of air quality over a long period [13].

1.3. Graph Network-Based Models

Graph networks exhibit remarkable performance in air quality forecasting. A graph-based multi-level attention unit was designed to represent dynamic spatio-temporal dependencies between different monitoring data points, and a general fusion unit was proposed to incorporate features from different domains [14]. A spatio-temporal graph neural process (sTGNP) [15] was proposed to represent a spatio-temporal relationship based on stacking layers of graph convolutions, and a Bayesian graph aggregator was designed to address uncertainties in air quality data as well as the graph structure. A graph attention-based model [16] was proposed to cope with the accuracy of complex prediction problems utilizing both the spatial correlation (extracted with a graph attention unit) and the temporal periodicity (represented as multiple cycles in time series). A dynamic multiple-graph attention model [17] was developed for long-term spatio-temporal forecasting by integrating a graph attention unit and a spatial attention unit. A spatio-temporal model with a multi-attention unit [18] was proposed for long-term air quality prediction, where multiple graphs were designed to extract the relationships between air quality data points, and multiple attention modules were developed to extract different spatio-temporal correlations. A self-supervised hierarchical network [19] was proposed to predict air quality data, which uses historical data to represent the city-wide air quality distribution, and a hierarchical recurrent graph module was developed to represent the spatial hierarchy. A group-aware graph model [20] was developed that models latent relationships between different stations using a differentiable grouping module, and relationships between different groups are represented using a message-passing unit.

1.4. Physics-Informed Neural Network Models

The aforementioned methods do not take physical knowledge into account, which could result in limited generalization capabilities and interpretability. Therefore, the use of physics-guided deep learning methods in air quality forecasting has attracted increasing attention. Physics-informed neural networks [21] can incorporate deep neural networks alongside nonlinear partial differential equations to solve forward and inverse problems. This allows scientific predictions and discoveries to be made from incomplete data. A spatio-temporal field neural network (STFNN) [22] was proposed based on the combination of fields and graphs, which can implicitly represent the gradient of air quality data obtained from conventional direct estimation approaches. An Air-DualODE method [23] was proposed to integrate dual branches of ordinary neural differential equations for air quality prediction, where the first branch captures spatio-temporal relationships based on open system physical equations and the second branch is a data-driven module used to address the dependencies that are not involved in the first branch. AirRadar [24] uses local and global spatial graph learning modules to capture complex spatial dependencies. An adaptive weight structure allocates different weights to improve the generalization ability to diverse and previously unseen spatial relationships. A PM_2.5-GNN model [25] was proposed to explicitly incorporate the domain knowledge of PM_2.5 into graphs to represent the long-term relationships between air quality data. A transformer architecture called AirFormer [26] was proposed to collectively forecast air quality nationwide, using a bottom-up deterministic self-attention mechanism to capture the spatio-temporal relationships and a top-down stochastic module to model the uncertainty between monitoring data points. A physics guided network for air quality prediction (AirPhyNet) [27] was proposed that incorporates air particle movement, i.e., diffusion and advection, using well-established physics principles. Physics knowledge is integrated into a graph structure module, and latent relationships are exploited to model spatio-temporal relationships within the monitoring data.

In this paper, we aim to predict air quality based on physics-informed spatio-temporal features fusion over graphs. In the aforementioned methods, the graph adjacency matrix is often constructed as a symmetric matrix based on the attributes between different nodes. Different from integrating differential equation-based domain knowledge into the prediction model, we explicitly constructed a directed graph adjacency to model the relationships between different air quality monitoring stations, and thereafter developed a spatial feature module based on the pre-designed graph. The temporal relationships between air quality data points have been studied using the designed directed graph adjacency matrix, resulting in the coupled spatio-temporal features of the monitoring data. The spatial features and temporal features are fused with an output unit for air quality forecasting. The contributions of this study are summarized as follows:

A directed graph-based spatial feature module was designed to characterize and extract the spatial features of air quality data over different sensors, where the directed graph is constructed using the locations of the monitoring stations.

A temporal–spatial feature module was designed to further characterize the features of air quality data, where a temporal feature is coupled with the designed graph adjacency matrix and the spatial features of the monitoring data.

A multi-layer output module was designed to fuse the spatial features and temporal features to forecast the air quality data over sensors, which was validated to show superior performance over several existing methods on real-world datasets.

2. Materials and Methods

2.1. Data Used

In this study, we investigated a real-world air quality dataset [27] collected from Beijing. The monitoring data were collected over 35 stations, from 1 January 2017 to 30 May 2018. This dataset contains hourly air concentration data for major pollutants, e.g., PM_2.5, PM₁₀, O₃, NO₂, SO_2.5, and CO. All missing values were filled in using the monitoring station’s 24 h average measurement. Each air quality monitoring station has location information, i.e., its latitude and longitude. In this paper, we focus on PM_2.5 prediction using a short period of its historical data and the data of neighboring monitoring station.

2.2. Problem Formulation

Let $\mathit{x}={(x_0,x_1,\dots ,x_{N-1})}^T$ denote the air quality data with $x_n$ points collected over the n-th monitoring station. ${(·)}^T$ is the transpose of $(·)$, and $N=35$ is the number of stations. Let ${\mathit{x}}^k$ denote the air quality data at time point k. The air quality forecasting problem can be investigated using its historical data:

$${\mathit{X}}^{\left(k\right)}=[{\mathit{x}}^{k-1},{\mathit{x}}^{k-2},\dots ,{\mathit{x}}^{k-M}],$$

(1)

where M is the sequence length used for air quality forecasting. The location information of the monitoring stations is denoted by

$$\mathit{Y}=[{\mathit{y}}_1,{\mathit{y}}_2,\dots ,{\mathit{y}}_N],$$

(2)

where $y_i$ is the location of the i-th station. Then, the air quality prediction problem can be modeled by

$$min∥{\mathit{x}}^k-f\left({\mathit{X}}^{\left(k\right)}\right)∥.$$

(3)

That is, forecasting air quality at future times uses historical air quality data spanning a period of M. $f(·)$ is the air quality forecasting model under consideration.

2.3. Methods

This section studies the directed graph-based spatio-temporal air quality forecasting model. The framework of the air quality forecasting model is presented in Figure 1. Firstly, air quality data are fed into the temporal feature extraction module after pre-processing. The location information of monitoring stations is used to construct a graph adjacency matrix, which is then applied to the graph-based spatial feature extraction module as well as the graph-based spatial–temporal feature extraction module. Finally, the spatio-temporal features are fed into the output layer to forecast air quality at future times. The graph construction unit is presented in Section 2.3.1, the directed graph-based spatial feature unit is presented in Section 2.3.2, the spatio-temporal feature unit is investigated in Section 2.3.3, and the output layer is shown in Section 2.3.4.

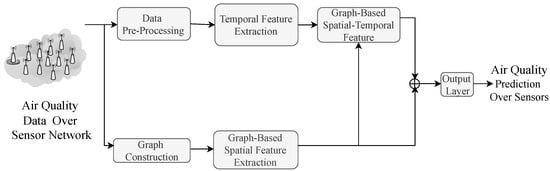
Figure 1. The framework of graph spatio-temporal fusion-based air quality prediction model.

2.3.1. Location-Based Directed Graph Design

We have the location information of the monitoring stations, i.e., ${\mathit{y}}_i$ and ${\mathit{y}}_j$; then, the distance of two stations can be calculated by

$$d_{i,j}=∥{\mathit{y}}_i-{\mathit{y}}_j∥$$

(4)

for $1\le i,j\le N$. Let $\tilde{\mathit{A}}$ denote an adjacency matrix of size N by N; then, its element ${\tilde{a}}_{i,j}$ can be calculated by [28]

$${\tilde{a}}_{i,j}=e^{-{\tilde{d}}_{i,j}^2}/\phantom{e^{-{\tilde{d}}_{i,j}^2}\sqrt{\sum _{k\in {\mathcal{N}}_i}{e}^{-{\tilde{d}}_{i,k}^2}\sum _{l\in {\mathcal{N}}_j}{e}^{-{\tilde{d}}_{j,l}^2}}}\sqrt{\sum _{k\in {\mathcal{N}}_i}{e}^{-{\tilde{d}}_{i,k}^2}\sum _{l\in {\mathcal{N}}_j}{e}^{-{\tilde{d}}_{j,l}^2}},$$

(5)

where ${\tilde{a}}_{i,j}$ is the $(i,j)$-th element of the adjacency matrix. ${\tilde{d}}_{i,j}$ can be calculated by

$${\tilde{d}}_{i,j}=d_{i,j}/\sigma ,$$

(6)

where $\sigma$ is a coefficient. ${\mathcal{N}}_i$ and ${\mathcal{N}}_j$ are the neighboring sets of the i-th and j-th stations, respectively.

We have introduced a self-loop to enhance the role of the historical data, that is,

$$\mathit{A}=\mathit{I}+\tilde{\mathit{A}},$$

(7)

where $\mathit{I}$ is the identity matrix of size N by N. The graph adjacency matrix constructed by (7) is a directed matrix because ${\mathcal{N}}_i$ and ${\mathcal{N}}_j$ are different.

2.3.2. Graph-Based Spatial Feature Module

In order to represent the spatial feature of the collected air quality data, let

$${\tilde{\mathit{x}}}_i^k={\mathit{A}}^i{\mathit{x}}^k$$

(8)

denote a vector of size $N\times 1$, where $i=0,1,\dots ,L$ is the order of spatial features. The i-th spatial feature is defined by

$${\mathit{s}}_i^k=[{\tilde{\mathit{x}}}_i^{k-1},{\tilde{\mathit{x}}}_i^{k-2},\dots ,{\tilde{\mathit{x}}}_i^{k-M}],$$

(9)

where ${\mathit{s}}_i^k$ is of size $N\times M$. A linear transform is applied to the spatial feature, i.e.,

$${\tilde{\mathit{s}}}_i^k={\mathit{s}}_i^k\mathit{H}.$$

(10)

Here, $\mathit{H}$ is a learnable matrix, which is of size $M\times R$.

2.3.3. Graph-Based Spatio-Temporal Feature Extraction Module

Let

$${\mathit{g}}^{k-1}={\tilde{\mathit{s}}}_0^{k-1}\oplus {\tilde{\mathit{s}}}_1^{k-1}\oplus \dots \oplus {\tilde{\mathit{s}}}_L^{k-1}\oplus {\mathit{x}}^{k-1},$$

(11)

$${\mathit{q}}^k=ReLU({\mathit{S}}_q{\mathit{g}}^{k-1}+{\mathit{U}}_q{\mathit{h}}^{k-1}+{\mathit{V}}_q{\mathit{x}}^{k-1}+{\mathit{d}}_q),$$

(12)

and

$${\mathit{p}}^k=ReLU({\mathit{S}}_p{\mathit{g}}^{k-1}+{\mathit{U}}_p{\mathit{h}}^{k-1}+{\mathit{V}}_p{\mathit{x}}^{k-1}+{\mathit{d}}_p),$$

(13)

where ${\mathit{S}}_q$, ${\mathit{S}}_p$, ${\mathit{U}}_q$, ${\mathit{U}}_p$, ${\mathit{V}}_q$, and ${\mathit{V}}_p$ are learnable matrices. $ReLU$ is the activation function. Let ${\mathit{d}}_q$ and ${\mathit{d}}_p$ denote two column vectors. Thereafter, the spatio-temporal feature can be represented by [29]

$${\mathit{h}}^k=(1-{\mathit{p}}^k)\odot {\mathit{h}}^{k-1}+{\mathit{p}}^k\odot {\tilde{\mathit{h}}}^k,$$

(14)

where

$${\tilde{\mathit{h}}}^k=tanh({\mathit{S}}_h{\mathit{g}}^{k-1}+{\mathit{U}}_h{\mathit{h}}^{k-1}+{\mathit{V}}_h{\mathit{x}}^{k-1}+{\mathit{d}}_h).$$

(15)

${\mathit{S}}_h$, ${\mathit{U}}_h$, and ${\mathit{V}}_h$ are learnable matrices.

In (11), the spatial feature ${\tilde{\mathit{s}}}_i^k$ is coupled with the air quality input ${\mathit{x}}^{k-1}$. The temporal feature of the air quality data can be recursively calculated using (14), which is also coupled with the spatial features obtained by (10).

2.3.4. Output Fusion Unit

Let ${\mathit{u}}_n^k$ denote the fused feature, i.e.,

$${\mathit{u}}_n^k={\mathit{h}}_n^{k-1}\oplus {\mathit{g}}^{k-1},$$

(16)

which incorporates the coupled spatio-temporal feature ${\mathit{h}}_n^{k-1}$ and the spatial feature of the air quality data ${\mathit{g}}^{k-1}$. A multi-layer unit is developed to forecast the air quality, i.e.,

$${\widehat{\mathit{x}}}^k=MLP\left({\widehat{\mathit{u}}}_n^k\right),$$

(17)

where

$${\widehat{\mathit{u}}}_n^k=ReLU\left(\mathit{C}{\mathit{u}}_n^k\right),$$

(18)

and $\mathit{C}$ is a linear transform applied to the coupled spatio-temporal features.

The spatial complexity of the proposed model is $O(MRL+N^{2}L)$, and the time complexity is also $O(MRL+N^{2}L)$.

3. Results and Discussions

3.1. Numerical Studies

In this section, we illustrate and validate the proposed air quality forecasting model based on a real-world dataset, for which data were collected over 35 air quality monitoring stations in Beijing, China. The period of data collection spanned from 1 January 2017 to 30 May 2018, collecting hourly data on PM_2.5. These data were divided following a 7:1:2 ratio, where 70 percent of data were used in training, 10 percent of the data were used for validation, and the remaining 20 percent were used for tests.

The graph adjacency matrix can be computed with Equation (7), where the latitudes and longitudes are used to calculate the distance between two monitoring stations. Each station chooses the closest five stations to build the adjacency matrix $\mathit{A}$. The directed graph is shown in Figure 2. The experimental parameter settings are presented in Table 1. Our model was developed using PyTorch 3.12 with an NVIDIA GeForce RTX 3090 GPU, and we used the Adam algorithm in the model training.

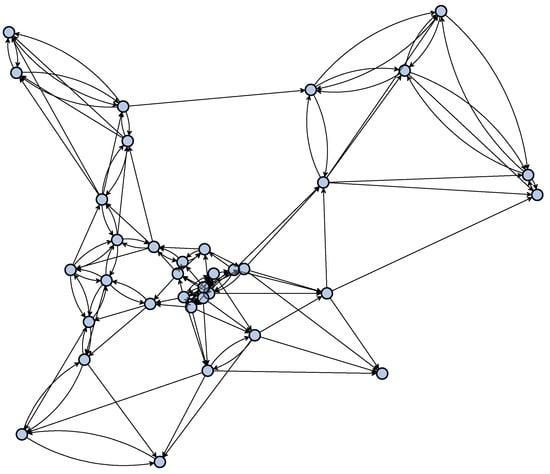
Figure 2. The graph constructed based on the locations of the air quality monitoring stations.

Table 1. Experimental settings.

Parameters	Value
Window Length M	24
Number of Monitoring Stations N	35
Spatial Feature Order L	2
Feature Length R	256
Learning Rate	4 $\times {10}^{-5}$
Number of Epochs	100
Weight Decay Parameters	0.005
Batch Size	32
$\sigma$	400

Baseline Model: We compared our proposed air quality forecasting model with the AirPhyNet model [27]. This model was designed for air quality prediction by integrating fundamental physics knowledge based on an ordinary differential equation into the forecasting model. AirPhyNet integrates physics knowledge based on graph structure to capture spatio-temporal relationships between data points using latent representation.

To align with the data settings of the baseline method, in this study, we set a time step of 3 h. We predicted the future 72 h of air quality data using the past 72 h of data. We used the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) to evaluate the hourly air quality prediction performance [30], i.e.,

$$MAE=1/N\sum _k∥{\widehat{\mathit{x}}}^k-{\mathit{x}}^k∥,$$

(19)

and

$$RMSE=\sqrt{1/N\sum _k{∥{\widehat{\mathit{x}}}^k-{\mathit{x}}^k∥}^2},$$

(20)

where ${\mathit{x}}^k$ is the true data collected over the monitoring stations. ${\widehat{\mathit{x}}}^k$ is the predicted data of our proposed model. We focus on the prediction of air quality data at an area monitored with a monitoring station. Table 2 and Table 3 present the prediction performance of the MAE and RMSE metrics over all 35 stations.

Table 2. Overall prediction performance comparison for the MAE metric.

	MAE 24 h	MAE 48 h	MAE 72 h
Model	(Standard Deviation)	(Standard Deviation)	(Standard Deviation)
AirPhyNet	29.11 (22.13)	36.69 (31.00)	42.23 (38.02)
Proposed Method	23.68 (18.25)	33.32 (28.60)	40.16 (35.08)

Table 3. Overall prediction performance comparison for the RMSE metric.

	RMSE 24 h	RMSE 48 h	RMSE 72 h
Model	(Standard Deviation)	(Standard Deviation)	(Standard Deviation)
AirPhyNet	42.16 (25.23)	48.66 (33.01)	53.07 (39.66)
Proposed Method	35.45 (20.68)	44.48 (30.47)	50.03 (36.49)

From Table 2, we can observe that the proposed spatio-temporal feature fusion over the graph model outperforms the other baseline models. The performance of 24 h prediction improved by 18.65 percent, and the performance improvement of 72 h prediction was 4.9 percent over the MAE metric. In Table 3, we can see that the proposed model has a 15.91 percent performance improvement in 24 h PM_2.5 prediction and 5.72 percent performance improvement in 72 h prediction over the RMSE metric. Our proposed model performs better in short-term forecasting than in long-term prediction. One possible reason is that the extracted spatial and coupled spatio-temporal features struggle to characterize changes in air quality effectively and accurately over time.

To obtain a straightforward illustration, the MAE metric was calculated over each air quality monitoring station, as shown in Figure 3. We can observe that the proposed spatio-temporal feature fusion over the graph-based air quality forecasting model can obviously improve the prediction performance in 24 h air quality prediction, and it has a small improvement in long-term air quality prediction, e.g., in the 72 h air quality forecasting. The improvement in air quality forecasting performance is primarily due to the location-informed directed graph adjacency matrix as well as the characterization and extraction of the coupled temporal–spatial features involved in the proposed air quality prediction model.

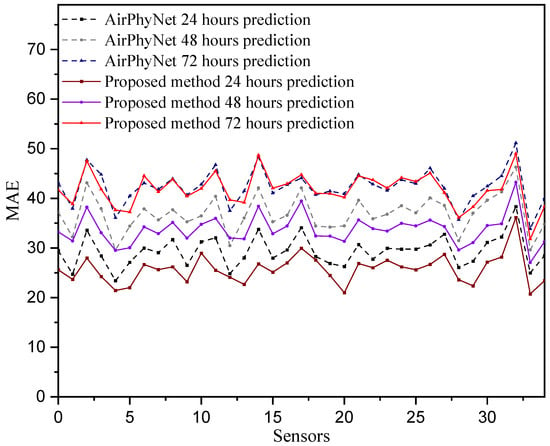
Figure 3. The average evaluation results of the MAE for all prediction performances across the entire test set at each monitoring station.

We show the comparisons of the true air quality data and the predicted data over all 35 sensors at the 24 h prediction performance in Figure 4. We can observe that the 24 h prediction of air quality of our proposed spatio-temporal feature fusion using graphs is very close to the true air quality value collected at the stations. The air quality prediction of AirPhyNet has large variations over several monitoring stations, leading to a worse performance in 24 h air quality prediction.

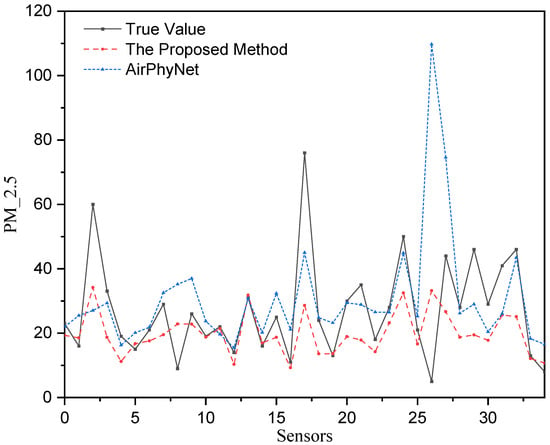
Figure 4. True air quality data vs. the predicted values over all 35 stations in 24 h prediction.

3.2. Discussions

The effects of different hyper-parameters on air quality prediction are studied. The prediction performance of the proposed model with different parameters L and R is presented in Table 4 and Table 5. As the order of spatial feature L increases from 0 to 2, more neighboring sensors are incorporated into the air quality prediction for the target sensor. Therefore, prediction performance improves as the order increases. If a sufficient number of neighboring nodes are participating, further increasing L will not improve air quality performance. A similar observation can be validated in Table 5 for the prediction performance with a different feature length R.

Table 4. Prediction performance with different L values in terms of the MAE metric.

L	MAE 24 h	MAE 48 h	MAE 72 h
0	25.34	34.01	40.64
1	24.81	33.91	40.97
2	23.68	33.32	40.16
3	25.22	33.93	40.52

Table 5. Prediction performance with different R values in terms of the MAE metric.

R	MAE 24 h	MAE 48 h	MAE 72 h
64	25.84	34.24	40.70
128	24.80	33.59	40.61
256	23.68	33.32	40.16
512	24.14	34.02	40.93

To further illustrate the effects of the proposed spatio-temporal feature fusion method using graphs, we present the ablation studies conducted on our proposed model in Table 6, specifically showing the results for our proposed model, the same model without spatial features in the output layer, the model same without spatial features coupled in the temporal module, and the same model without a temporal feature module. We can observe that the model with spatio-temporal feature fusion over graphs has the best prediction performance. If the spatial features or the temporal features are not considered in the proposed model, e.g., not included in the output layer or in the spatio-temporal feature extraction module, the prediction performance degrades.

Table 6. Ablation study on the MAE metric.

Model	MAE 24 h	MAE 48 h	MAE 72 h
Outlayer Without Spatial Feature	24.77	33.68	40.79
Temporal Feature Module without Spatial Feature	25.47	33.70	40.67
Model Without Temporal Feature	25.12	33.81	40.33
Proposed Method	23.68	33.32	40.16

4. Conclusions

We developed an air quality forecasting model based on spatio-temporal feature fusion over graphs in this study, including four major modules, i.e., the graph adjacency construction module, the spatial feature unit, the spatio-temporal feature unit, and the fusion output layer. The directed adjacency matrix is built using the location information of the air quality monitoring stations. This physical information greatly helps us represent the spatial relationships of the air quality data between monitoring stations and the neighboring stations. The spatial features and spatio-temporal features are extracted over graphs, which greatly improves the air quality forecasting. The proposed model has been illustrated and validated over a real-world dataset collected over 35 air quality monitoring stations. Numerical studies show that the proposed air quality forecasting model outperforms the baseline model. It achieved 18.65 percent and 15.91 percent performance improvements on the MAE and RMSE metrics, respectively. These indicate the broader practical implications of the proposed air quality prediction model for policymaking or early-warning systems. The focus of future studies could be on the long-term prediction using the temporal–spatial feature evolution over time. Future studies could focus on the scalability of the proposed model, on cases involving missing values, on performance improvement utilizing the relationship between PM_2.5 and other variables such as wind speed and humidity, sophisticated fusion mechanisms in the output layer, the impact of seasonal effects, and air quality prediction in unmonitored areas.