Structural Analysis of Octagonal Nanotubes via Double Edge-Resolving Partitions

Abstract

In materials science, the open nanotube derived from an octagonal grid is one of the most important and extensively researched compounds. Finding strategies for representing a variety of chemical compounds so that different compounds can have different representations is necessary for the investigation of chemical structures. In this work, the double edge-based resolving partition is discussed and the exchange property applied. Let $Q_1$ and $Q_2$ be two edge-resolving partition sets and $Q_1\ne Q_2$, such that $Q_1\cap Q_2\ne 0$. This shows that this structure has exchange property for edge partition. The exchange property in edge partitions is a novel work. It is introduced in this paper. The application of this work is to transform projects or objects to better places. The resolvability of these compounds is studied to gain an understanding of the chemical composition of the compounds. We perform this by using the terms vertex and edge-based distance and edge-resolving sets of graphs.

1. Introduction

Chemical graph theory serves as a powerful framework for analyzing chemical structures and mathematical characterization of various materials, including crystals, processes, clusters, molecules, and polymers. This method helps to describe the structural properties of these materials, and gives insight into emerging mathematical chemistry concepts [1] derived from octagonal nano-structures, which are great at materials science and are of interest. They find application in various fields like medicine, nanotechnology, etc. Understanding and characterizing these systems, and determining their peak-based metric dimensions, are important research aspects in this area [2,3,4]. For a detailed survey of mathematical chemistry associated with graph theory, you can refer to the work of Ahmed and Manzoor [5,6,7] Chemical graph theory simplifies and disconnects complex chemical systems, making them simpler to analyze and understand.

In graph theory, the concept of a solution structure plays an important role in distinguishing vertices based on their path. The vertices L of a graph G are considered as a set of solutions if any vertex in G can be uniquely identified based on its distance vector from the vertices in L [8,9,10]. This concept is important to characterize chemical structures and their smallest cardinality graph, known as the metric dimension [10,11,12]. Slater, in [13], first introduced the concept of finding a set one, and in 1976, Harari proposed a similar idea, calling it the metric dimension of a graph [14]. This idea originated in a monograph by Blumenthal who examined the use of metric spaces in a wider context in [15].

The concept of the metric dimension finds applications in various fields, and has been the subject of extensive research. Researchers have employed it in a wide range of applications, showcasing its versatility and importance. For instance, the metric dimension has been used to determine similarities between different medications [16]. Metamaterials refer to artificially designed materials and structures [17], which are crucial in the pharmaceutical industry. Other applications include solving combinatorial optimization problems [18], facilitating robot navigation [19], addressing pharmaceutical chemistry issues [20], optimizing computer networks [21], and canonically labeling graphs [22]. The utility of the metric dimension extends to solving location problems, aiding in the operation of sonar and coast guard Loran systems [13], facilitating image processing, and solving complex weighing problems [23]. Additionally, it has found applications in coding and decoding strategies for games like Mastermind [24]. For a more comprehensive understanding of the physical and chemical properties related to the metric dimension, further references [25,26] are available.

Throughout our consideration, the graph G is a simple, finite, plane, connected, and undirected graph. When two any minimal $RS$s for G are $R_1$ and $R_2$, let a vertex $v\in R_2$ and $u\in R_1$, such that $(R_1\setminus \left\{u\right\})\cup v$ is also a minimal resolving set. The exchange property in the graph is therefore said to be possessed by resolving sets (for more information, see [27]). Only finite, simple, and connected graphs are considered in this work. A graph’s exchange property also indicates its set resolution property. Nanotubes derived from octahedral networks are an exciting research area in nanotechnology. Unlike the extensively studied carbon nanotubes, which are based on a square carbon structure, these nanotubes are made of an octahedral structure The octahedral lattice structure gives these nanotubes unique properties, making them attractive for various applications, and as materials for planning.

The octagonal lattice consists of a recurring pattern of octagonal polygons, which gives rise to a different geometric structure compared to the hexagonal lattice. This octahedral structure can potentially change the electronic, mechanical, and thermal properties of carbon nanotubes. Larger portions of the octahedral have different curvatures and different possible ways in which the atoms interact with each other, affecting the overall nanotube stability and efficiency. The resources that can be used are electronic devices; the unique electronic properties of octahedral mesh-based nanotubes can be exploited in the design of new electronic devices, including transistors and sensors that require specific conductive semiconductor properties. Mechanical reinforcement: carbon nanotubes can be used as reinforcements in composite materials due to their unique mechanical properties, which can increase the strength and durability of materials. Heat conductivity: the thermal properties of these carbon nanotubes can provide advantages in terms of heat dissipation, making them suitable for use in temperature control systems [28,29] and more. The chemistry of carbon nanotubes is discussed by [30]. The use of carbon nanotubes in medicine is discussed by [31].

The partition dimensions have several applications in chemistry, and the partition dimension of different chemical systems has been studied in numerous articles. The partition dimension bounds of One Pentagonal Carbon Nanocone Structure [26] and carbon nanocone edge partitions were obtained in [32]. The partition dimension of a path graph is calculated in [33]. The partition resolvability of nanosheets and nanotubes derived from an octagonal grid is discussed in [34]. The utility of fault-tolerant partition resolvability in cycle-related graphs is determined in [35], and the partition dimension of generalized hexagonal cellular networks and its applications are mentioned in [36]. The metric dimensions of nanotubes of $V{C}_4{C}_7$ and H-Naphtalenic nano-tubes were studied in [10], resolving a hard and fast of silicate big name mentioned in [37]. The symmetric graphs metric dimensions were received by rooted product [38], and the metric size of crystal cubic carbon shape was determined in [39], The barycentric subdivision of the side metric dimension of Cayley graphs was carried out in [40]. Because of its applicability, the concept of the metric dimension is used to address a lot of challenging situations. Consult [41,42,43] for the resolvability parameters of different chemical systems.

In this paper, a few basic theorems are applied. The partition dimension 2, shown by $pd\left(p_n\right)=2$, is only for path graphs, as the author of [34] shows. For $n\ge 3$, it is further proven in [35] for cycle graph $pd\left(C_n\right)=3$.

Definition 1

([44]). Consider the basic undirected graph G, where the edges and vertices are denoted V(G) and E(G), respectively. The distance, often referred to as the geodesics, is between ${\xi }_1,{\xi }_2$$\in V\left(G\right)$. The distance in G that the shortest path takes to connect two vertices, ${\xi }_1-{\xi }_2$, is indicated by $\zeta ({\xi }_1,{\xi }_2)$.

Definition 2

([36]). The distance of a vertex to a set is defined as $d(v,R)=min\{d(v,v_1),d(v,v_2),d(v,v_3),\cdots d(v,v_h)\}$, where $v_1,v_2,v,v_3,\cdots vh$ are the elements of R.

In this article, we use $EPRS$ for the edge partition resolving set, $PD$ for the partition dimension, and $EP$ for the exchange property.

2. Double Edge Partition Resolving Sets for Nanotube

The structures that have double edge-resolving sets or more resolving sets also have $EXP$, which is very important for finding the best locations for projects.

Theorem 1.

Let $N{T}_{h,v}$ be an octagonal nanotube with $h,v\ge 1$; then, the double $EPRS$s of cardinality 4 exists.

Proof. 

Let us define two sets, $R_1$ and $R_2$, to prove the double $EPRS$ for nanotubes. Specifically, here, we aim to demonstrate that $R_1$ and $R_2$ are both $EPRS$s for nanotubes. Theorem 2 contains the proof of $R_1$, while Theorem 3 contains the proof of $R_2$. □

3. ${\mathit{R}}_{\mathbf{1}}$ Is an Edge Partition Resolving Set

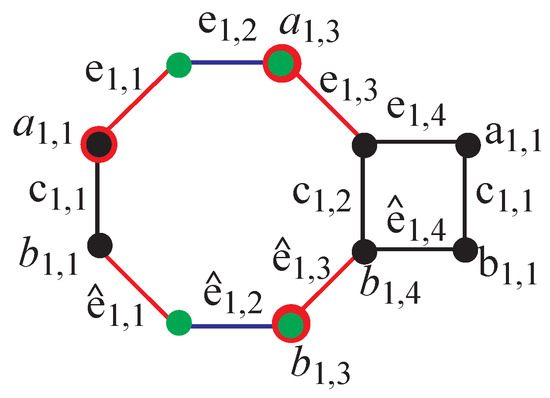
3.1. Construction of Figure 1 of $N{T}_{h,v}$ for $R_1$

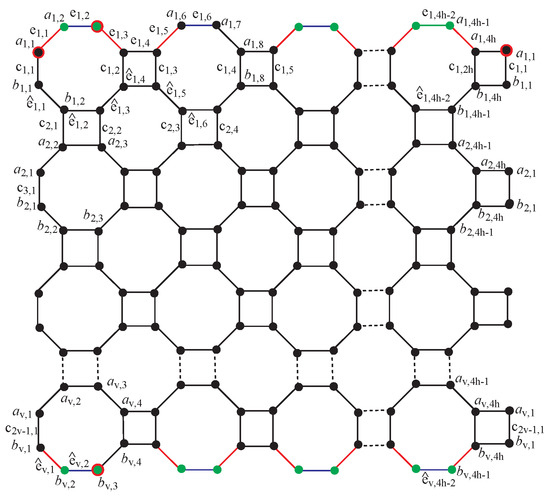
Figure 1. Generalize nanotube.

In Figure 1, edges with degrees of two and three endpoints are colored red. Any edges with degree 2 or degree 3 endpoints are colored blue, and all edges with degree 3 endpoints are colored black. The vertex color of a degree of two is green, and the vertex color with a degree of three is black. The vertex that constitutes the resolving set is colored double because of degree 3, and the point of resolution, $a_{1,1}$, is black and red, while $b_{V,3}$ and $a_{1,3}$ are red and green due to degree 2 and the point of $EPRS$.

Assume that h and v represent $C_8$’s horizontal and vertical numbers. There are 2h vertices of degree 2 and 8hv-2h vertices of degree 4. The $N{S}_{h,v}$ has a size of $\left|E\right(N{T}_{h,v}\left)\right|=12hv-2h$, and the order of $N{T}_{h,v}$ is $|V\left(N{T}_{h,v}\right)|=8\left(hv\right)$. In labeling, two parameters ($v,h$) and two indices ($j,i$) are utilized. I varies twice with v, and j changes four times with h.

The edges are labeled as $a_{i,j}{a}_{i,j+1}=e_{i,j}$, $b_{i,j},b_{i,j+1}={\widehat{e}}_{i,j}$, and $a_{i,j}{b}_{i,j}=c_{i,j}$ The nanotube vertices and edges sets are defined as follows:

$$\begin{array}{cc}\hfill V\left(NT\right)=& \{a_{i,j},b_{i,j};1\le i\le v,1\le j\le 4h\}\hfill \\ \hfill E\left(NT\right)=& \{a_{i,j}{a}_{i,j+1},b_{i,j}{b}_{ij+1};1\le i\le v,1\le j\le 4h\}\hfill \\ & \cup \{a_{i,j}{b}_{i,j};1\le i\le v,j=0,1\left(mod4\right)\}\hfill \\ & \cup \{a_{i,j}{b}_{i,j};1\le i\le v,j=2,3\left(mod4\right)\}\hfill \\ & \cup \{a_{i,1}{a}_{i,4h}{b}_{i,1}{b}_{i,4h};1\le i\le v,h\ge 1\}.\hfill \end{array}$$

Here is the proof that $R_1$ is an edge partition resolving set of cardinality 4 for nanotubes.

Theorem 2.

Let $N{T}_{h,v}$ be a nanotube for $h,v\ge 1$. Then, $R_1$ is the $EPRS$ of cardinality 4, and it is denoted by |R|$=4$.

Proof. 

To prove that $R_1$ is the $EPRS$ we define a partition set and then check the distances with edges of structure. Let $R_{1p_1}=\left\{a_{1,1}\right\},R_{1p_2}=\left\{a_{1,3}\right\},R_{1p_3}=\left\{b_{v,3}\right\}$ and $R_{1p_4}=\{\left(V\left(N{T}_{h,v}\right)\right)\setminus \{a_{1,1},a_{1,3},b_{v,3}\}\}$ be the subsets of the vertices of $N{T}_{h,v}$, such that $R_{1p_1}\cup R_{1p_2}\cup R_{1p_3}\cup R_{1p_4}=V\left(N{T}_{h,v}\right)$ and $R_{1p_1}\cap R_{1p_2}\cap R_{1p_3}\cap R_{1p_4}=\varphi$. The set $R=\{R_{1p_1},R_{1p_2},R_{1p_3},R_{1p_4}\}$ is known as $EPRS$ if it has unique representation with all the edges of $N{T}_{h,v}$. Here, wish to demonstrate that $R_1$ is a minimal $EPRS$ to demonstrate that $p{d}_e\left(N{T}_{h,v}\right)\le 4$. The distinct representations of each vertex and edge of $N{T}_{h,v}$ for $h,v=1$ are shown below. $R_1=\{R_{1p_1},R_{1p_2},R_{1p_3},R_{1p_4}\}$ be a $EPRS$. For this claim, follow the definition of $EPRS$. Let $R_1$ show a unique representation with edges.

The representation for $v=1=h$ is shown in Table 1.

Table 1. Edge coding for Figure 2.

$R_1=\{a_{1,1},R_{1p_2},b_{1,3}\}$
$Edges$	$e_{1,1}$	$e_{1,2}$	$e_{1,3}$	$c_{1,1}$
$r(.\mid R)$	(0,1,3,0)	(1,0,3,0)	(1,0,2,0)	(0,2,2,0)
$Edges$	${\widehat{e}}_{1,1}$	${\widehat{e}}_{1,2}$	${\widehat{e}}_{1,3}$	$c_{1,2}$
$r(.\mid R)$	(1,3,1,0)	(2,3,0,0)	(2,2,0,0)	(1,1,1,0)

3.1.1. Generalized Results

The octagonal nanotube generalized distance formulas for all edges demonstrate that the cardinality of the minimal $EPRS$ is 4, given that every distance is distinct. The generalized distance formulas are provided below, where $\zeta$ is considered as distance. Let $\zeta (e_{i,j},R_{1p_1})=w_1$, $\zeta (e_{i,j},R_{1p_2})=w_2$, $\zeta (e_{i,j},R_{1p_3})=w_3$, $\zeta (e_{i,j},R_{1p_4})=w_4$ and $r(e_{i,j}\mid R_1)=(w_1,w_2,w_3,w_4)$.

$$\begin{array}{c}\hfill w_1=\left\{\begin{array}{cc}i+j-2\hfill & \mathrm{if}i=1,1\le j\le 2h,\hfill \\ 4h+i-j-1\hfill & \mathrm{if}i=1\mathrm{and}2h+1\le j\le 4h,\hfill \\ 2i+j-3\hfill & \mathrm{if}2\le i\le v-1\mathrm{and}4i-6\le j\le 2h,\hfill \\ 4h+2i-j-4\hfill & \mathrm{if}2\le i\le v-2\mathrm{and}2h+1\le j\le 4h-4i+6,\hfill \\ 4h+2i-j-2+z+z_1\hfill & \mathrm{if}2\le i\le v-2\mathrm{and}4h-4i+7\le j\le 4h,\hfill \\ 4i+j-5-z_2-z_3\hfill & \mathrm{if}2\le i\le v-2\mathrm{and}1\le j\le 4i-7,\hfill \\ 4i+j-5-z_2-z_3\hfill & \mathrm{if}v-1\le i\le v\mathrm{and}1\le j\le 2h,\hfill \\ 3h+4i-j-4+z_4+z_5\hfill & \mathrm{if}v-1\le i\le v\mathrm{and}2h-1\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{4h-4i-j+11}{4}}⌋,\hfill & \mathrm{if}j\ge 4h-4i+6,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{4h-4i-j+12}{4}}⌋\hfill & \mathrm{if}j\ge 4h-4i+6,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j+3}{4}}⌋\hfill & \mathrm{if}1\le j\le 4i-7,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j+2}{4}}⌋\hfill & \mathrm{if}1\le j\le 4i-7,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+1}{4}}⌋\hfill & \mathrm{if}j\ge 2h,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h}{4}}⌋\hfill & \mathrm{if}j\ge 2h.\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_2=\left\{\begin{array}{cc}4i-j-2\hfill & \mathrm{if}1\le i\le v,j=1,2\hfill \\ 4i+j-7-z-z_1-2z_2\hfill & \mathrm{if}1\le i\le v,3\le j\le 2h+2,\hfill \\ 4h+2i-j+z_3+z_4\hfill & \mathrm{if}1\le i\le \lceil {\displaystyle \frac{v}{2}}\rceil 2h+3\le j\le 4h,\hfill \\ 4h+4i-j-8+z_5+z_6\hfill & \mathrm{if}\lceil {\displaystyle \frac{v}{2}}\rceil \le i\le v,2h+3\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-1}{4}}⌋\hfill & \mathrm{if}3\le j\le 4i-2\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2}{4}}⌋\hfill & \mathrm{if}3\le j\le 4i-2\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_2=\left\{\begin{array}{cc}2(i-1)\hfill & \mathrm{if}j\ge 4i-1\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j4h+4i-3}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j4h+4i-4}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+1}{4}}⌋\hfill & \mathrm{if}j\ge 2h+3\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_6=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h}{4}}⌋\hfill & \mathrm{if}j\ge 2h+3,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_3=\left\{\begin{array}{cc}4h-4i-j+4+z\hfill & \mathrm{if}1\le i\le v\mathrm{and}1\le j\le 4h,\hfill \\ 4h-4i+j-2-z_1-z_2\hfill & \mathrm{if}1\le i\le ⌊{\displaystyle \frac{v}{2}}+1⌋\mathrm{and}5\le j\le 2h+2,\hfill \\ j-2\hfill & \mathrm{if}i=v\mathrm{and}5\le j\le 2h+2,\hfill \\ j+2-z_3-z_4-2z_5\hfill & \mathrm{if}i=v-1\mathrm{and}5\le j\le 2h+2,\hfill \\ 7h-4i-j+5+z_6+z_7\hfill & \mathrm{if}1\le i\le v-1\mathrm{and}2h+3\le j\le 4h,\hfill \\ 6h-2i-j+3-z_8-z_9\hfill & \mathrm{if}2v-2\le i\le v-1\mathrm{and}2h+3\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j}{2}}⌋\hfill & \mathrm{if}1\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{c}⌊{\displaystyle \frac{j-3}{4}}⌋,\mathrm{if}5\le j\le 2h+2,\hfill \\ \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4}{4}}⌋\hfill & \mathrm{if}5\le j\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-3}{4}}⌋,\hfill & \mathrm{if}5\le j\le 8\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4}{4}}⌋\hfill & \mathrm{if}5\le j\le 8\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}2\hfill & \mathrm{if}j\ge 9\hfill \\ \\ 0\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_6=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+11}{4}}⌋\hfill & \mathrm{if}2h+3\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_7=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+10}{4}}⌋\hfill & \mathrm{if}2h+3\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_8=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+7}{4}}⌋\hfill & \mathrm{if}i=v-2\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_9=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+6}{4}}⌋\hfill & \mathrm{if}i=v-2\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let $\zeta ({\widehat{e}}_{i,j},R_{1p_1})=w_1^{\prime }$, $\zeta ({\widehat{e}}_{i,j},R_{1p_2})=w_2^{\prime },\zeta ({\widehat{e}}_{i,j},R_{1p_3})=w_3^{\prime },\zeta ({\widehat{e}}_{i,j},R_{1p_4})=w_4^{\prime }$

and $r({\widehat{e}}_{i,j}\mid R_1)=(w_1^{\prime },{w^{\prime }}_2,{w^{\prime }}_3,{w^{\prime }}_4)$.

$$\begin{array}{c}\hfill w_1^{\prime }=\left\{\begin{array}{cc}2i+j-2\hfill & \mathrm{if}1\le i\le 3\mathrm{and}4i-3\le j\le 2h,\hfill \\ 4h+2i-j-1\hfill & \mathrm{if}1\le i\le 3\mathrm{and}2h\le j\le 4h-4i+4,\hfill \\ 4i+j-4-z-z_1\hfill & \mathrm{if}2\le i\le v\mathrm{and}1\le j\le 4i-4\le 2h,\hfill \\ 3h+4i-j-3+z_2+z_3\hfill & \mathrm{if}4\le i\le v\mathrm{and}2h+1\le j\le 4h,\hfill \\ 4h+2i-j+z_4+z_5\hfill & \mathrm{if}2\le i\le 3\mathrm{and}4h-4i+5\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j+}{4}}⌋,\hfill & \mathrm{if}j\le 2h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j}{4}}⌋,\hfill & \mathrm{if}j\le 2h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+3}{4}}⌋,\hfill & \mathrm{if}j\ge 2h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+2}{4}}⌋,\hfill & \mathrm{if}j\ge 2h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{4h-4i-j+9}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{4h-4i-j+10}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h.\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_2^{\prime }=\left\{\begin{array}{cc}4i-j+z\hfill & \mathrm{if}1\le i\le v\mathrm{and}j=1,2,3,4,\hfill \\ 4i+j-6-z_1-z_2-2z_3\hfill & \mathrm{if}1\le j\le v\mathrm{and}5\le j\le 2h+2,\hfill \\ 4h+2i-j+1+z_4+z_5\hfill & \mathrm{if}1\le i\le \lceil {\displaystyle \frac{v}{2}}\rceil \mathrm{and}2h+3\le j\le 4h,\hfill \\ 4h+4i-j-5+z_6+z_7\hfill & \mathrm{if}\lceil {\displaystyle \frac{v}{2}}\rceil \le i\le v\mathrm{and}2h+3\le j\le 4h\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j}{2}}⌋\hfill & \mathrm{if}1\le j\le 4\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-3}{4}}⌋\hfill & \mathrm{if}5\le j\le 4i\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4}{4}}⌋\hfill & \mathrm{if}5\le j\le 4i\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}2(i-1)\hfill & \mathrm{if}4i+1\le j\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-1}{4}}⌋\hfill & \mathrm{if}4h-4i+4\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-2}{4}}⌋\hfill & \mathrm{if}4h-4i+4\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_6=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+1}{4}}⌋\hfill & \mathrm{if}j\ge 2h+3\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_7=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h}{4}}⌋\hfill & \mathrm{if}j\ge 2h+3\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_3^{\prime }=\left\{\begin{array}{cc}4h-4i-j+2\hfill & \mathrm{if}1\le i\le v\mathrm{and}j=1,2,\hfill \\ 4h-4i+j-3-z-z_1-2z_2\hfill & \mathrm{if}1\le i\le v\mathrm{and}3\le j\le 2h+2,\hfill \\ 7h-4i-j+2+z_3+z_4\hfill & \mathrm{if}1\le i\le v-2\mathrm{and}2h+3\le j\le 4h,\hfill \\ 7h-2i-j-4+z_5+z_6\hfill & \mathrm{if}i=v-3\mathrm{and}j=2h+3h\ge 6\hfill \\ 7h-2i-j+4+z_5+z_6\hfill & \mathrm{if}v-2\le i\le v-1\mathrm{and}2h+3\le j\le 4h\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-1}{4}}⌋\hfill & \mathrm{if}3\le j\le 2h+2,\hfill \\ \hfill & \mathrm{if}1\le i\lceil {\displaystyle \frac{v}{2}}\rceil \hfill \\ \lfloor {\displaystyle \frac{v}{2}}+1\rceil \le i\le v-1\hfill & \mathrm{if}j\le 3h-4i+8\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2}{4}}⌋\hfill & \mathrm{if}3\le j\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}2\left(v-i\right)\hfill & \mathrm{if}j\ge 3h-4i+9\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+1}{4}}⌋\hfill & \mathrm{if}2h+3\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h}{4}}⌋\hfill & \mathrm{if}2h+3\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4}{4}}⌋\hfill & \mathrm{if}i=v-1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_6=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+3}{4}}⌋\hfill & \mathrm{if}i=v-1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4^{\prime }=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let $\zeta (c_{i,j},R_{1p_1})=w_1^{\prime \prime }$, $\zeta (c_{i,j},R_{1p_2})=w_2^{\prime \prime },$$\zeta (c_{i,j},R_{1p_3})=w_3^{\prime \prime },$$\zeta (c_{i,j},R_{1p_4})=w_4^{\prime \prime }$ and $r(c_{i,j}\mid R_1)=(w_1^{\prime \prime },{w^{\prime \prime }}_2,{w^{\prime \prime }}_3,{w^{\prime \prime }}_4)$.

$$\begin{array}{c}\hfill w_1^{\prime \prime }=\left\{\begin{array}{cc}i+j-2\hfill & \mathrm{if}j-1\le i\le v-1\mathrm{and}1\le j\le h+1,\hfill \\ i+j-2\hfill & \mathrm{if}v-2\le i\le 2v-1\mathrm{and}1\le j\le h+1,\hfill \\ 2i+j-1+2z-z_1-z_2\hfill & \mathrm{if}2\le i\le v-1\mathrm{and}1\le j\le h+1,\hfill \\ 2i+j-1+2z+z_3\hfill & \mathrm{if}1\le i\le v-2\mathrm{and}h+2\le j\le 2h,\hfill \\ 2h+2i-j-2z_4-z_5\hfill & \mathrm{if}1\le i\le v-2\mathrm{and}h+2\le j\le 2h,\hfill \\ 2h+2i-j-1\hfill & \mathrm{if}v-2\le i\le 2v-1\mathrm{and}h+2\le j\le 2h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2}{2}}⌋\hfill & \mathrm{if}1\le j\le h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i-1}{2}}⌋\hfill & \mathrm{if}j=2E+1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋.\hfill & \mathrm{if}j=h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-h-2}{2}}⌋\hfill & \mathrm{if}j\ge h+2\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E+1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_2^{\prime \prime }=\left\{\begin{array}{cc}2i-j+1\hfill & \mathrm{if}1\le i\le v-1j=1,2\hfill \\ 2i+j-3\hfill & \mathrm{if}1\le i\le v-2\mathrm{and}3\le j\le i+2\hfill \\ 2i+j-3\hfill & \mathrm{if}v-2\le i\le 2v-1\mathrm{and}3\le j\le h+2\hfill \\ 2i+j-1+2z-2z_1\hfill & \mathrm{if}1\le i\le j-3\mathrm{and}4\le j\le h+2\hfill \\ 2h+2i-j+1\hfill & \mathrm{if}1\le i\le 3\mathrm{and}2h-i+1\le j\le 2h\hfill \\ 2h+2i-j+1\hfill & \mathrm{if}4\le i\le v-1,h+3\le j\le 2h\hfill \\ 4h+2i-j-2z_2\hfill & \mathrm{if}1\le i\le v-3,h+3\le j\le 2h\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-3}{3}}⌋\hfill & \mathrm{if}4\le j\le h+2\hfill \\ \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E\hfill \\ \\ ⌊{\displaystyle \frac{i+1}{2}}⌋\hfill & \mathrm{if}j=h+2,\hfill \\ ⌊{\displaystyle \frac{i+1}{2}}⌋\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E+1\hfill \\ \\ ⌊{\displaystyle \frac{i+1}{2}}⌋\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill w_3^{\prime \prime }=\left\{\begin{array}{cc}4h-2i-j+1\hfill & \mathrm{if}1\le i\le 2v-1j=1,2\hfill \\ 4h-2i+j-3\hfill & \mathrm{if}1\le i\le 2v-j+2,3\le j\le h+1,\hfill \\ 4h-2i+j-3\hfill & \mathrm{if}1\le i\le v+1j=h+2\hfill \\ 4h-2i+j+1+z-z_1\hfill & \mathrm{if}2v-j+3\le i\le 2v-1\mathrm{and}4\le j\le h+2\hfill \\ 4h-2i+j-1-2z_2+z_3\hfill & \mathrm{if}2v-4\le i\le 2v-1\mathrm{and}j=h+2\hfill \\ 6h-2i-j+1\hfill & \mathrm{if}1\le i\le 2v+j-12\mathrm{and}h+3\le j\le 2h\hfill \\ 6h-2i-j+3\hfill & \mathrm{if}j-1\le i\le v+j-4\le 2v-1\mathrm{and}h+3\le j\le 2h\hfill \\ 6h-2i-j+5\hfill & \mathrm{if}i=v,j=h+3\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4}{2}}⌋\hfill & \mathrm{if}4\le j\le h+2\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i-8}{2}}⌋,\hfill & \mathrm{if}j=2E\hfill \\ \\ ⌊{\displaystyle \frac{i-9}{2}}⌋\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i-9}{2}}⌋\hfill & \mathrm{if}2v-4\le i\le 2v-1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}2(i-1)\hfill & \mathrm{if}4i+1\le j\le 2h+2,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4^{\prime \prime }=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let ${\aleph }_1$ and ${\aleph }_2$ are two random edges on nanotube $N{T}_{h,v}$. Let $R=\{R_{1p_1},R_{1p_2},R_{1p_3},R_{1p_4}\}$.

• Case I: when ${\aleph }_1=e_{i,j}$ and ${\aleph }_2=e_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$, then three further cases arise.
• Case 1: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, because $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})+p$, where $p=j^{{ }^{\prime }}-j$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 2: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$, and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2})$, because $\zeta ({\aleph }_1,R_{1p_2})=\zeta ({\aleph }_2,R_{1p_2})+q$, where $q=2(i^{{ }^{\prime }}-i)$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, because $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})+(s+p)$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case II: when ${\aleph }_1={\widehat{e}}_{i,j}$ and ${\aleph }_2={\widehat{e}}_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$.
• Case 1: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, because $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})+p$, where $p=j^{{ }^{\prime }}-j$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 2: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$, and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2})$, because $\zeta ({\aleph }_1,R_{1p_2})=\zeta ({\aleph }_2,R_{1p_2})+q$, where $q=2(i^{{ }^{\prime }}-i)$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$ because $\zeta ({\aleph }_1,R_{1p_3})=\zeta ({\aleph }_2,R_{1p_3})+(s+p)$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case III: when ${\aleph }_1=e_{i,j}$ and ${\aleph }_2={\widehat{e}}_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$, then four further cases arise.
• Case 1: If $i=i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, because $\zeta ({\aleph }_1,R_{1p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{1p_1})+1$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 2: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$ because $\zeta ({\aleph }_1,R_{1p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{1p_1})+2$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$, and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2})$, because $\zeta ({\aleph }_1,R_{1p_2})$ is at least equal to $\zeta ({\aleph }_2,R_{1p_2})+3$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.
• Case 4: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, because $\zeta ({\aleph }_1,R_{1p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{1p_1})+2$, so $r({\aleph }_1\mid R_1)\ne r({\aleph }_2\mid R_1)$.

When $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$, the positions of ${\aleph }_1$ and ${\aleph }_2$, where $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})$, then $\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2})$, if at these positions $\zeta ({\aleph }_1,R_{1p_2})=\zeta ({\aleph }_2,R_{1p_2})$, then it is clearly $\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$.

Discuss all cases in which $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$, whatever $\zeta ({\aleph }_1,R_{1p_2})=\zeta ({\aleph }_2,R_{1p_2})$, $\zeta ({\aleph }_1,R_{1p_3})=\zeta ({\aleph }_2,R_{1p_3})$ if $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})$, then one of these is different: $\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1})$

or $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1})$,$\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$

or $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1}),$$\zeta ({\aleph }_1,R_{1p_2})=\zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$

or $\zeta ({\aleph }_1,R_{1p_1})\ne \zeta ({\aleph }_2,R_{1p_1}),$$\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_3})=\zeta ({\aleph }_2,R_{1p_3})$

or $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1}),$$\zeta ({\aleph }_1,R_{1p_2})\ne \zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$

or $\zeta ({\aleph }_1,R_{1p_1})=\zeta ({\aleph }_2,R_{1p_1}),$$\zeta ({\aleph }_1,R_{1p_2}=\zeta ({\aleph }_2,R_{1p_2}),$$\zeta ({\aleph }_1,R_{1p_3})\ne \zeta ({\aleph }_2,R_{1p_3})$.

There is no scenario when two representations are equivalent. Based on the representation discussed above, can see that every vertex provides a unique representation, satisfying the $EPRS$ condition and demonstrating that $|R_1|=4$.

3.1.2. Conversely

From the above discussion, have proved that the edge metric dimension of $N{T}_{h,v}$ is less than or equal to 4. Now, we want to prove that the $PD$ is not greater than 4, $\mathrm{if}di{m}_e(N{S}_{h,v}\ge 4\sim di{m}_e\left(N{S}_{h,v}\right)<4impliesdi{m}_e\left(N{S}_{h,v}\right)=2or3$.

The edge $PD$ is not 2 because is not a path graph. $PD$ is not three, so here, we cite an article in which the metric of this this structure is 3, so $PD$ is not possible [28]. If its metric dimension is 3, then its edge metric dimension is not less than 3, so its $PD$ is not 3. Hence, we prove that the $EPRS$ has cardinality 4. □

4. ${\mathit{R}}_{\mathbf{2}}$ Is Also an Edge Partition Resolving Set of Nanotube

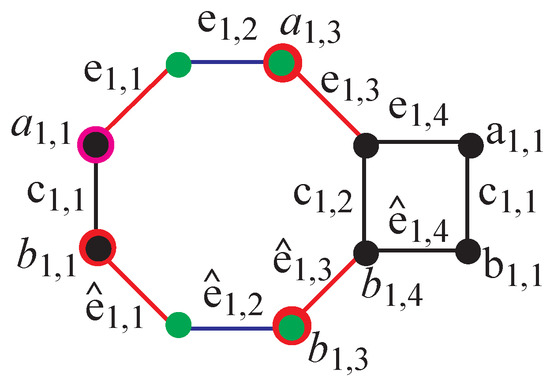
4.1. Construction Figure 3 of $N{T}_{h,v}$ for $R_2$

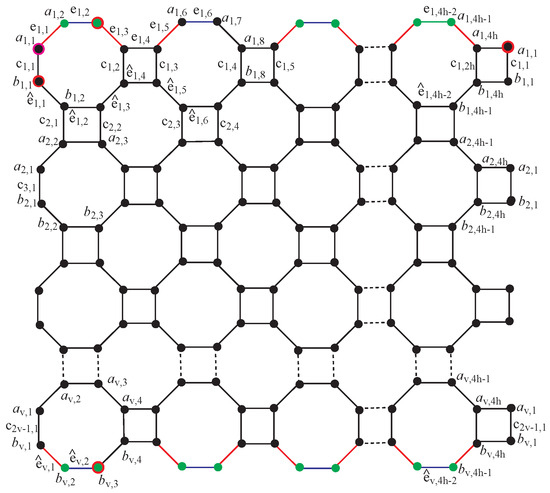
Figure 3. Generalized nanotube derived by octagonal grid.

In Figure 3, the edges of the second and third ends are red. $R_{b_{1,1}}$ is colored red and black because $EPRS$ is a three-point location; $a_{1,3},$$b_{v,3}$ are green and red because 2 is the degree $EPRS$ of the case. The pink color vertex is exchangeable.

Theorem 3.

Let $N{T}_{h,v}$ be a nanotube for $h,v\ge 1$. Then, $R_2$ is also edge partition resolving set of cardinality 4 for $N{T}_{h,v}$.

Proof. 

To prove that $R_2$ is also $EPRS$, we define a partition set. Let $R_{2p_1}=\left\{b_{1,1}\right\},R_{2p_2}=\left\{a_{1,3}\right\}$, $R_{2p_3}=\left\{b_{v,3}\right\}$ and $R_{2p_4}=\{\left(V\left(N{T}_{h,v}\right)\right)\setminus \{b_{1,1},a_{1,3},b_{v,3}\}\}$ be the subsets of the vertices of $N{T}_{h,v}$, such that $R_{2p_1}\cup R_{2p_2}\cup R_{2p_3}\cup R_{2p_4}=V\left(N{T}_{h,v}\right)$ and $R_{2p_1}\cap R_{2p_2}\cap R_{2p_3}\cap R_{2p_4}=\varphi$. The set $R=\{R_{2p_1},R_{2p_2},R_{2p_3},R_{2p_4}\}$ is known as $EPRS$ if it has unique representation with all the edges of $N{T}_{h,v}$. Now, we wish to demonstrate that $R_2$ is a minimal $EPRS$ to demonstrate that $p{d}_e\left(N{T}_{h,v}\right)\le 4$. The distinct representations of each vertex and edge of $N{T}_{h,v}$ for $h,v=1$ are shown below. $R_2=\{R_{2p_1},R_{2p_2},R_{2p_3},R_{2p_4}\}$ be a $EPRS$. For this claim, follow the definition of $EPRS$. Let $R_2$ show a unique representation with edges.

The representation for $v=1=h$ is shown in Table 2.

Table 2. Edge coding of Figure 4.

$R_2=\{R_{2p_1},R_{2p_2},R_{2p_3},R_{2p_4}\}$.
$Edges$	$e_{1,1}$	$e_{1,2}$	$e_{1,3}$	$c_{1,1}$
$r(.\mid R)$	(1,1,3,0)	(2,0,3,0)	(2,0,2,0)	(0,2,2,0)
$Edges$	${\widehat{e}}_{1,1}$	${\widehat{e}}_{1,2}$	${\widehat{e}}_{1,3}$	$c_{1,2}$
$r(.\mid R)$	(0,3,1,0)	(1,3,0,0)	(1,2,0,0)	(1,1,1,0)

4.1.1. Generalized Results

The octagonal nanotube generalized distance formulas for all edges demonstrate that the cardinality of the minimal $EPRS$ is 4, given that every distance is distinct. The generalized distance formulas are provided below, where $\zeta$ is considered as distance. Let $\zeta (e_{i,j},R_{2p_1})=w_1$, $\zeta (e_{i,j},R_{2p_2})=w_2,$$\zeta (e_{i,j},R_{2p_3})=w_3$, $\zeta (e_{i,j},R_{2p_4})=w_4$, and $r(e_{i,j}\mid R_1)=(w_1,w_2,w_3,w_4)$.

The generalized formulas of $w_2$ and $w_3$ are given in the proof of $R_1$, and the remaining are here.

$$\begin{array}{c}\hfill w_1=\left\{\begin{array}{cc}i+j-1\hfill & \mathrm{if}i=1\mathrm{and}1\le j\le 2h+1,\hfill \\ 4h+i-j+1\hfill & \mathrm{if}i=1\mathrm{and}2h+2\le j\le 4h,\hfill \\ 4i+j-7+z+z_1+z_2\hfill & \mathrm{if}2\le i\le v\mathrm{and}1\le j\le 4i-6,\hfill \\ 4h+2i-j+z_3+z_4\hfill & \mathrm{if}2\le i\le ⌊{\displaystyle \frac{v}{2}}⌋\mathrm{and}2h+2\le j\le 4h,\hfill \\ 4h+2i-j-2+z+z_1\hfill & \mathrm{if}⌊{\displaystyle \frac{v}{2}}+1⌋\le i\le v\mathrm{and}2h+2\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j+2}{4}}⌋\hfill & \mathrm{if}1\le j\le 4(i-1),\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2}{4}}⌋\hfill & \mathrm{if}1\le j\le 4(i-1),\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}2i-3\hfill & \mathrm{if}4(i-1)-1\le j\le 2h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-4}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-5}{4}}⌋\hfill & \mathrm{if}4h-4i+5\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let $\zeta ({\widehat{e}}_{i,j},R_{2p_1})=w_1^{\prime }$, $\zeta ({\widehat{e}}_{i,j},R_{2p_2})=w_2^{\prime },$$\zeta ({\widehat{e}}_{i,j},R_{2p_3})=w_3^{\prime },$$\zeta ({\widehat{e}}_{i,j},R_{2p_3})=w_4^{\prime }$ and $r({\widehat{e}}_{i,j}\mid R_1)=(w_1^{\prime },{w^{\prime }}_2,{w^{\prime }}_3,{w^{\prime }}_4)$.

The generalized formulas of ${w^{\prime }}_2$ and ${w^{\prime }}_3$ are give in the proof of $R_1$, and the remaining are here.

$$\begin{array}{c}\hfill w_1^{\prime }=\left\{\begin{array}{cc}4i+j-5-z-z_1-z_2\hfill & \mathrm{if}1\le i\le v\mathrm{and}1\le j\le 2h+1,\hfill \\ 4h+2i-j-1+z_3+z_4\hfill & \mathrm{if}1\le i\le ⌈{\displaystyle \frac{v}{2}}⌉\mathrm{and}2h+2\le j\le 4h,\hfill \\ 4h+4i-j-9+z_5+z_6\hfill & \mathrm{if}⌈{\displaystyle \frac{v}{2}}+1⌉\le i\le v\mathrm{and}2h+1\le j\le 4h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j+1}{4}}⌋\hfill & \mathrm{if}1\le j\le 4i-3,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j}{4}}⌋\hfill & \mathrm{if}1\le j\le 4i-3,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}2(i-1)\hfill & \mathrm{if}4i-3\le j\le 2h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-2}{4}}⌋\hfill & \mathrm{if}5h-4i\le jleq4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-4h+4i-1}{4}}⌋\hfill & \mathrm{if}5h-4i\le jleq4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h+1}{4}}⌋,\hfill & \mathrm{if}2h+1\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_6=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2h}{4}}⌋\hfill & \mathrm{if}2h+1\le j\le 4h,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4^{\prime }=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let $\zeta (c_{i,j},R_{2p_1})=w_1^{\prime \prime }$, $\zeta (c_{i,j},R_{2p_2})=w_2^{\prime \prime },\zeta (c_{i,j},R_{2p_3})=w_3^{\prime \prime },\zeta (c_{i,j},R_{2p_4})=w_4^{\prime \prime }$ and $r(c_{i,j}\mid R_1)=(w_1^{\prime \prime },{w^{\prime \prime }}_2,{w^{\prime \prime }}_3,{w^{\prime \prime }}_4)$.

The generalized formulas of ${w^{\prime \prime }}_2$ and ${w^{\prime \prime }}_3$ are give in the proof of $R_1$, and the remaining are here.

$$\begin{array}{c}\hfill w_1^{\prime \prime }=\left\{\begin{array}{cc}i+j-2\hfill & \mathrm{if}j-1\le i\le v-1,1\le j\le h+1,\hfill \\ i+j-2\hfill & \mathrm{if}v-2\le i\le 2v-1,1\le j\le h+1,\hfill \\ 2i+j-1+2z-z_1-z_2\hfill & \mathrm{if}2\le i\le v-1\mathrm{and}1\le j\le h+1,\hfill \\ 2i+j-1+2z+z_3\hfill & \mathrm{if}1\le i\le v-\mathrm{and}h+2\le j\le 2h,\hfill \\ 2h+2i-j-2z_4-z_5\hfill & \mathrm{if}1\le i\le v-2\mathrm{and}h+2\le j\le 2h,\hfill \\ 2h+2i-j-1\hfill & \mathrm{if}v-2\le i\le 2v-1,h+2\le j\le 2h,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill z=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-2}{2}}⌋\hfill & \mathrm{if}1\le j\le h\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_1=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_2=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i-1}{2}}⌋\hfill & \mathrm{if}j=2E+1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_3=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=h+1,\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill z_4=\left\{\begin{array}{cc}⌊{\displaystyle \frac{j-h-2}{2}}⌋\hfill & \mathrm{if}j\ge h+2\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.z_5=\left\{\begin{array}{cc}⌊{\displaystyle \frac{i}{2}}⌋\hfill & \mathrm{if}j=2E+1\hfill \\ \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill W_4^{\prime \prime }=\left\{\begin{array}{c}0\mathrm{for}\mathrm{all}.\hfill \end{array}\right.\end{array}$$

Let ${\aleph }_1$ and ${\aleph }_2$ are two arbitrary edges on nanotube. $N{T}_{h,v}$. Let $R_2=\{R_{2p_1},R_{2p_2},R_{2p_3},R_{2p_4}\}$

• Case I: when ${\aleph }_1=e_{i,j}$ and ${\aleph }_2=e_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$, then three further cases arise.
• Case 1: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$ because $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})+p$, where $p=j^{{ }^{\prime }}-j$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 2: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$ and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2})$, because $\zeta ({\aleph }_1,R_{2p_2})=\zeta ({\aleph }_2,R_{2p_2})+q$, where $q=2(i^{{ }^{\prime }}-i)$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$ then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$, because $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})+(s+p)$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case II: when ${\aleph }_1={\widehat{e}}_{i,j}$ and ${\aleph }_2={\widehat{e}}_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$.
• Case 1: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$, because $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})+p$, where $p=j^{{ }^{\prime }}-j$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 2: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$ and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2})$, because $\zeta ({\aleph }_1,R_{2p_2})=\zeta ({\aleph }_2,R_{2p_2})+q$, where $q=2(i^{{ }^{\prime }}-i)$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ({\aleph }_2,R_{2p_3})$, because $\zeta ({\aleph }_1,R_{2p_3})=\zeta ({\aleph }_2,R_{2p_3})+(s+p)$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case III: when ${\aleph }_1=e_{i,j}$ and ${\aleph }_2={\widehat{e}}_{i^{{ }^{\prime }},j^{{ }^{\prime }}}$, then four further cases arise.
• Case 1: if $i=i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$ because $\zeta ({\aleph }_1,R_{2p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{2p_1})+1$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 2: if $i=i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$, because $\zeta ({\aleph }_1,R_{2p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{2p_1})+2$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 3: if $i\ne i^{{ }^{\prime }}$, $j=j^{{ }^{\prime }}$ and without loss of generality, we can say that $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2})$, because $\zeta ({\aleph }_1,R_{2p_2})$ is at least equal to $\zeta ({\aleph }_2,R_{2p_2})+3$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.
• Case 4: if $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ and without loss of generality, we can say that $j<j^{{ }^{\prime }}$, $i<i^{{ }^{\prime }}$, then $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$, because $\zeta ({\aleph }_1,R_{2p_1})$ is at least equal to $\zeta ({\aleph }_2,R_{2p_1})+2$, so $r({\aleph }_1\mid R_2)\ne r({\aleph }_2\mid R_2)$.

When $i\ne i^{{ }^{\prime }}$, $j\ne j^{{ }^{\prime }}$ the positions of ${\aleph }_1$ and ${\aleph }_2$ where $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})$, then $\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2})$ if at these positions $\zeta ({\aleph }_1,R_{2p_2})=\zeta ({\aleph }_2,R_{2p_2})$, then it is clearly $\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ({\aleph }_2,R_{2p_3})$.

Discuss all cases in which $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1})$, whatever $\zeta ({\aleph }_1$, $R_{2p_2})=\zeta ({\aleph }_2$, $R_{2p_2})$, $\zeta ({\aleph }_1,R_{2p_3})=\zeta ({\aleph }_2,R_{2p_3})$ if $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})$, then one of these is different $\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1})$

or $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1}),$$\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ({\aleph }_2,R_{2p_3})$

or $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1}),$$\zeta ({\aleph }_1,R_{2p_2})=\zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ({\aleph }_2,R_{2p_3})$

or $\zeta ({\aleph }_1,R_{2p_1})\ne \zeta ({\aleph }_2,R_{2p_1}),$$\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_3})=\zeta ({\aleph }_2,R_{2p_3})$

or $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1}),$$\zeta ({\aleph }_1,R_{2p_2})\ne \zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ({\aleph }_2,R_{2p_3})$

or $\zeta ({\aleph }_1,R_{2p_1})=\zeta ({\aleph }_2,R_{2p_1}),$$\zeta ({\aleph }_1,R_{2p_2}=\zeta ({\aleph }_2,R_{2p_2}),$$\zeta ({\aleph }_1,R_{2p_3})\ne \zeta ,R_{2p_3})$.

There is no scenario where two representations are equal. As can be seen from the representational discussion above, every vertex provides a unique representation, which satisfies the requirement of $EPRS$, and which shows that $\left|R\right|=4$.

4.1.2. Contrary Case

From the above discussion, we proved that the edge metric dimension of $N{T}_{h,v}$ is less than or equal to 4. Now, we want to prove that the $PD$ is not greater than 4, $\mathrm{if}di{m}_e(N{S}_{h,v}\ge 4\sim di{m}_e\left(N{S}_{h,v}\right)<4impliesdi{m}_e\left(N{S}_{h,v}\right)=2or3$.

The edge $PD$ is not 2 because is not a path graph. The partition dimension is not 3 because its metric dimension is 3 (see [28]). If its metric dimension is 3, then its edge metric dimension is not less than 3, so its $PD$ is not 3. Hence, we prove that the $EPRS$ has cardinality 4. □

5. Exchange Property

A strong tool for material substitution while maintaining crucial characteristics like structural integrity, identification ability, and distance metrics is the exchange property in the mixed metric dimension framework for hexagonal nano-networks. This novel feature improves the fault tolerance, optimization, and design flexibility of nano-networks, which is a noteworthy development in the field. As we have seen, a subset of vertices W in a graph G is $RS$, such that any vertex in the graph G can be uniquely identified by its distance from the vertices of the subset W between them, which acts like a basis in the $RSs$ vector space because each vertex in the graph is related to vertices in these sets. It is known to be unique. Although the vector space of $RSs$ has many basis-like features, it may not always have the exchange feature from linear algebra. In this case, $EP$ is such that if S and $R_1$ are the minimum $RSs$ for G, then $r\in R_1$ and $s\in S$, such that ($S\setminus \left\{s\right\})\cup \{r\}$ is the minimum $RS$ for the G. The $RSs$ of graph G inside all have the same size when satisfying $EP$; this makes algorithmic methods for finding the metric dimension of G more practical. Therefore, to show that the $EP$ does not hold in a given graph, one only needs to show two minimal $RSs$ of different sizes. Note that the contrary is not true: the lack of the exchange condition does not entail the presence of minimal $RSs$ of different sizes. The following deductions about the $EP$ for $RSs$ were made in [27].

Theorem 4.

([27]). In trees for resolving sets, the $EP$ is valid.

Theorem 5.

([27]). Wheels $W_n$ and $n\ge 8$ for resolving sets do not have the $EP$.

The $EP$ for solving sets of necklace graphs $N{e}_n$ does not hold, as has recently been demonstrated.

Theorem 6.

([45]). The $EP$ is absent from the $RSs$ of the necklace graph $N{e}_n$ for $n\ge 4$.

Theorem 7.

([46]). For $n\ge 4$, the quasi-flower snarks do not satisfy the $EP$ for minimum $RSs$.

Theorem 8.

([47]). For $h,v\ge 1$, the $EP$ for minimal edge resolving sets holds in nanosheet derived from the octagonal grid.

Theorem 9.

The exchange properties with applications were discussed in [48].

Here, we prove that the $EP$ holds for $ERPSs$ of octagonal nanotube in the following theorem.

Theorem 10.

The $EP$ (exchange property) for $EPRS$ holds in the structure of an octagonal nanotube.

Now, we use the definition of $EP$ to support our claim. Let $u=R_{1p_1}$ and $u\in R_1,v=R_{2p_1}$ and $v\in R_2$, then $(R_1\setminus \left\{u\right\})\cup v$ is a minimal $EPRS$ as well. Suppose $(R_1\setminus \left\{u\right\})\cup v=Q$. Here, we need to demonstrate that Q is a minimal $EPRS$, as well for $N{T}_{h,v}$. Because $R_1=\{R_{1p_1},R_{1p_2},R_{1p_3},R_{1p_4}\}$ and $R_2=\{R_{2p_1},R_{2p_2},R_{2p_3},R_{2p_4}\}$, thus $(R_1\setminus \left\{u\right\})=\{R_{1p_2},R_{2p_3},R_{1p_4}\}\cup v=\{R_{2p_1},R_{1p_2},R_{1p_3,R_{1p_4}}\}=Q=R_2$, because $R_{1p_2}=R_{2p_2}$, $R_{1p_3}=R_{2p_3}$ and the representation of $R_{1p_4}{R}_{2p_4}$ is same. $R_2$ is the $EPRS$ proved in Theorem 3, which proved that $R_2$ is a minimal $EPRS$. Thus, we demonstrated the validity of the $EP$ in $N{T}_{h,v}$. $R_{2p_2},R_{2p_3}$ are common points in $R_1$ and $R_2$. So, $R_1$ and $R_2$ exchange u and v sets with each other.

6. Limitations and Future Work

The research presented in this article primarily offers a theoretical study of edge-partition resolving sets. The studies presented in this article broadly offer a theoretical observation of edge-partition resolving sets and their houses within systems derived from octagonal grids, including nanotubes. While the theoretical findings are promising, and advise capacity programs in various fields, they lack an experimental method to validate these principles in real-world settings. To show the applicability and practical use of these theoretical constructs, future work has to include experimental research that checks and affirms the effectiveness of edge-PRSs in real networks. By enforcing these ideas in actual-world situations, we can better recognize their realistic implications, discover potential barriers, and refine the theoretical fashions to higher in shape sensible applications. Experimental validation may even offer concrete evidence of the blessings and demanding situations related to edge-PRSs, thereby strengthening the overall impact and reliability of these studies.

7. Conclusions and Future Scope

In this work, two structures derived from the octagonal grid are discussed, focusing on nanotube configuration, specifically. With two partition resolving sets (PRSs) in nanotubes, each with a cardinality of four, it is confirmed that the $EXP$ holds for these structures, which enhances their application in community optimization, taking into account green placement modifications. The change in belongings is especially useful for addressing place problems, because it permits the moving of elements to more gold-standard positions based on resolvability parameters. The concept of $PD$ has numerous sensible programs throughout diverse fields. In telecommunications networks, partition size aids in fault diagnosis by efficiently finding and figuring out complex sections. It also allows for network optimization by way of enhancing routing and useful resource allocation, thereby enhancing normal network overall performance. In sensor networks, partition measurements permit green tracking and management by way of organizing sensor nodes into partitions. This enables higher data series, and minimizes redundant transmissions, which optimizes verbal exchange paths and increases the community’s operational lifetime. Smart grids also have advantages ranging from partition size through to progressed load management and fault isolation. By efficiently distributing masses, the partition dimension prevents overloads and complements grid balance. It additionally assists in speedy setting apart of faults, allowing faster repairs and lowering downtime. In urban visitor networks, the partition size optimizes traffic to go with the flow with the aid of improving visitors’ signal timings and course-making plans. This reduces congestion and complements normal traffic efficiency. Additionally, it aids in designing the most effective emergency response routes, ensuring the timely arrival of emergency services.