Effects of Aqueous Solubility and Geochemistry on CO₂ Storage in Offshore Basins

Abstract

The increasing global focus on carbon capture and storage (CCS) has highlighted the potential for offshore CO₂ sequestration, particularly following recent successes in onshore projects. This research investigates the qualitative analysis of carbon trapping efficiency in offshore basins, employing a GEM simulator to incorporate factors such as aqueous solubility and geochemistry. The findings reveal that anticlines represent ideal geological structures for carbon storage, effectively trapping a significant portion of injected CO₂. For effective mineralization, it is crucial to dissolve CO₂ into saline aquifers to generate H⁺, which facilitates the release of Ca²⁺ and Al³⁺ from anorthite. This process leads to the dissolution of anorthite and the precipitation of kaolinite, while calcite transitions from a dissolved state to a precipitated state over time. The analysis indicates that structural trapping provides the highest storage contribution during the injection phase, whereas residual gas trapping becomes dominant by the end of the simulation. Notably, it is observed that the storage contribution of structural trapping decreases from 28.39% to 19.05%, and the percentage increase in storage contributions of residual gas, solubility, ionic, and mineral trapping are 4.12%, 3.25%, 1.69%, and 0.28% for CO₂ plus water injection, thereby improving the long-term security of CO₂ storage in offshore basins. It is most beneficial to optimize the layout and design of the injection well to ensure a uniform distribution of carbon dioxide and to increase the injection rate.

1. Introduction

Using comprehensive data collections of global area coverage over both land and ocean surfaces, parts of Central and South America, Africa, Europe, northeastern North America, and central Asia experienced record warm temperatures in October 2023 (Figure 1). The global surface temperature in October 2023 was 1.34 °C (2.41 °F) above the 20th-century average of 14.0 °C (57.1 °F), making it the warmest October on record [1]. The past 10 years (2014–2023) have been the warmest years on record (Figure 2). Global warming is one of the main challenges for future decades, threatening the security of human life and the sustainable development of society, according to the Intergovernmental Panel on Climate Change (IPCC) Report [2,3]. The National Climate Assessment (NCA) offers a comprehensive overview of climate hazards and offers a valuable resource for researchers and policymakers in the United States [4]. The European Climate Risk Assessment report straightforwardly outlines information on managing climate risks and highlights priority measures within each area [5]. The storage of carbon dioxide in deep formations is being actively considered as an effective measure against global climate change, supporting the reduction in greenhouse gas emissions [6]. According to previous investigations, saline aquifers, coal seam, oil and gas reservoirs, igneous rocks, and organic-rich shales are predominantly candidates for geological CO₂ sequestration [7,8,9]. The global estimated carbon storage capacity for offshore basins is between 2000 Gt and 13,000 Gt [10,11,12,13].

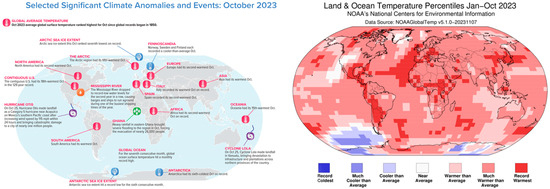
Figure 1. Selected significant climate anomalies and events (left) and land and ocean temperature percentiles (right).

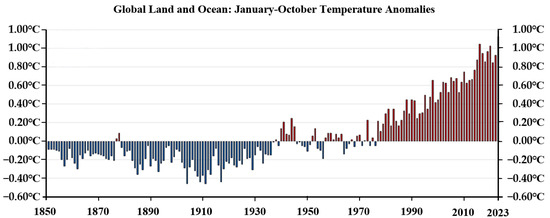
Figure 2. Temperature variation in the past 173 years (1850–2023) (Red bar indicates an increase in temperature, while blue bar indicates a decrease in temperature).

CO₂ trapping mechanisms are mainly structural or stratigraphic and involve residual gas, solubility, and mineral trapping [14,15,16,17,18]. Several researchers have investigated the trapping mechanisms to carry out multiphase flows, reactive transport, and chemical reactions during carbon storage. The influence of capillary pressure and caprock factors on the leaked CO₂ migration, distribution, and trapping has been quantitatively analyzed [19]. The efficiency of carbon mineralization and geochemical-induced changes resulting from mineralization trapping were analyzed for the siliciclastic aquifer [20]. Accounting for thermal effects, the phase conductivity and enthalpy have been derived, considering CO₂ dissolution in brines, and the field simulation results illustrate that the dissolution increases immediately when the convection dominates CO₂ migration [21]. Considering non-CO₂ species in density-driven convective mixing, such as N₂ and H₂S, it is concluded that CO₂ impurity would result in delayed onset and weakened convection [22]. Several studies have investigated the traditional four trapping mechanisms, providing valuable guidance for research in offshore basins.

There are many factors influencing CO₂ mobility and carbon storage capacity, such as rock and fluid properties, pressure, temperature, permeability, reservoir heterogeneity, and so on. The compressibility of the rock and of the fluid could influence the carbon storage capacity [23,24]. A quick assessment of the CO₂ storage capacity can be used to calculate the brine contributions in response to the estimated average pressure buildup in the field [25]. The effect of multi-scale heterogeneity on storage capacity, the design of injection wells, injection rate, CO₂ plume migration, and CO₂ potential leakage are investigated at the Rock Springs Uplift, Wyoming [26]. The relevance of representing relative permeability variations in the sealing formation is investigated, and the corresponding results illustrate that gradational changes at the base of the caprock could influence the pressure changes propagating vertically into the caprock from the saline aquifer [27].

Furthermore, many previous scholars have extensively investigated the measures required to maximize the carbon storage efficiency in a given reservoir. The selection of the optimal well location and extraction of native fluids from the storage reservoir can reduce the pressure build up, maximizing CO₂ storage [28]. The varying amplitude and frequency of injection were found to have no significant influence on pressure build up, but may influence the injectivity and storage capacity. Water displacing CO₂ in the post-injection period is considered an important procedure to improve injectivity and trapping efficiency [29,30]. However, there is very limited research regarding the qualitative analysis of carbon trapping efficiency in offshore basins.

Offshore basins generally hold vast reserves of oil and gas, and offshore exploration and production advances technology due to the demanding conditions of deep water and hash environments. Investing in offshore research and innovation facilitates the sustainable development of sustainable energy resources and contributes to mitigating climate change. There are some specific aspects of carbon trapping efficiency in offshore basins that have not been adequately studied. The impact of various geochemical reactions on CO₂ behavior and trapping mechanisms in offshore environments remains underexplored. Variations in sediment types and their influence on CO₂ solubility and trapping efficiency need more investigation, especially in heterogeneous formations. Therefore, it is necessary to advance the recognition of CO₂ injection in offshore basins by incorporating the following potential factors in the calculation: (1) reservoir heterogeneity, (2) aqueous solubility and geochemical reactions occurred in the gas/brine system, and (3) the storage contribution calculation of the structural, residual gas, solubility, ionic, and mineral trapping in carbon sequestration. CO₂ migration, the spatial distribution of dissolved species and minerals, and the storage contribution of each trapping mechanism are examined in the Wushi basin. Furthermore, the influence of water injection on the storage contribution of each mechanism is discussed.

2. Mathematical Formulations

The General Equation-of-State (EOS) Compositional Reservoir Simulator, GEM, is adopted for modeling aqueous solubility and geochemistry on CO₂ storage in offshore basins. The flowchart of the methodology implemented in CMG is displayed in Figure 3.

Figure 3. Flowchart of the methodology implemented in CMG.

2.1. Mass Transport Equations

Based on the mass balances of the gaseous phase in the geological system, the gaseous component transport equations are given as follows [31]:

$${\displaystyle \frac{\partial N_g^i}{\partial t}}=\nabla ·\left({\displaystyle \frac{{{\rho }_g\kappa k}_{rg}{M}_g^i}{{\mu }_g}}\left(\nabla p+\nabla p_{cwg}-{\rho }_{g}g\nabla \mathrm{z}\right)\right)+\nabla ·\left({\displaystyle \frac{{{\rho }_w\kappa k}_{rw}{M}_w^i}{{\mu }_w}}\left(\nabla p+\nabla p_{cwg}-{\rho }_{w}g\nabla \mathrm{z}\right)\right)+\nabla ·D_{ig}+{\gamma }_{ig,aq}+q$$

(1)

For the aqueous component, the mass transport equation is expressed by

$${\displaystyle \frac{\partial N_{aq}^i}{\partial t}}=\nabla ·\left({\displaystyle \frac{{{\rho }_w\kappa k}_{rw}{M}_{aq}^i}{{\mu }_g}}\left(\nabla p-{\rho }_{w}g\nabla \mathrm{z}\right)\right)+\nabla ·D_{iaq}+{\gamma }_{iaq,aq}+{\gamma }_{iaq,mn}+q$$

(2)

For the mineral, the mass transport equation follows

$${\displaystyle \frac{\partial N_m^i}{\partial t}}={\gamma }_{im,m}$$

(3)

where $N_g^i$ represents the number of moles of gas component $i$ per volume unit of the grid, $M_g^i$ and $M_w^i$ the mole fractions of gas component $i$ in the gas phase and aqueous phase, respectively, $D_{ig}$ the dispersion/diffusion of the gas component, $D_{iaq}$ the dispersion/diffusion of the aqueous component, $\nabla p_{cwg}$ the capillary pressure between the gas and water, ${\gamma }_{ig,aq}$ the reaction rate between the gaseous and aqueous components, ${\gamma }_{iaq,aq}$ the reaction rate between the aqueous and aqueous component, ${\gamma }_{iaq,mn}$ the reaction rate between the aqueous and mineral component, ${\gamma }_{im,m}$ the mineral reaction rate, ${\rho }_g$ the density of gas, ${\rho }_w$ the density of water, $k_{rg}$ the gas relative permeability, $k_{rw}$ the water relative permeability, $p$ the water pressure, and $z$ the depth.

2.2. CO₂ Solubility

The Peng–Robinson equation of state (PR-EOS) was adopted to calculate the gas fugacity of a component [32]. Henry’s law is adopted to model the solubility in the aqueous phase, and the fugacity formula is as follows:

$$f=x\ast H$$

(4)

where $f$ is the fugacity of the component, $x$ is the composition of the component in the aqueous phase, and $H$ is Henry’s law constant (atm$·$L/mol).

Henry’s law constant, at any pressure, $p$, is calculated as follows:

$$ln\left(H\right)=ln\left(H^{\mathrm{*}}\right)+v(p-p_{ref})/RT{a}^2+b^2=c^2$$

(5)

where $v$ is a set of real numbers for the partial molar volume of the components in water at an infinite dilution, $p_{ref}$ the reference pressures for the Henry’s law constants of the components (kPa), $H^{\ast }$ a set of real numbers for the reference of the Henry’s law constants of the components at the reference pressure (atm$·$L/mol), $R$ the universal gas constant (8.314 J$·$K⁻¹$·$mol⁻¹), and $T$ the temperature (°C).

2.3. Model for Relative Permeability

Gas relative permeability hysteresis is considered by adjusting the maximum residual gas saturation, and the maximum CO₂ residual saturation is 0.4. The relative permeability of CO₂ ($K_{rg}$) versus gas saturation ($S_g$) is shown in Figure 4.

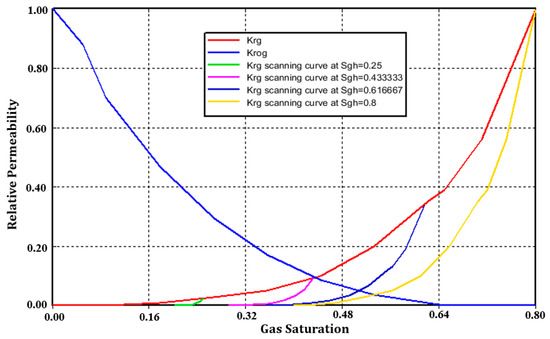
Figure 4. Gas relative permeability hysteresis ($K_{rg}$ is initially assumed to lie on the drainage curve; $S_{gh}$ is the value of $S_g$ when the shift to imbibition occurs).

2.4. Reaction Stoichiometry

The reactions between aqueous components in the aqueous phase have the following stoichiometry [31]:

$${\sum }_{i=1}^{naq}{v}_{ij}{A}_i=0,\mathrm{j}=1,\dots ,R_{aq}$$

(6)

where $R_{aq}$ is the number of reactions between the aqueous components, $n_{aq}$ is the number of components in the aqueous phase, $v_i$ is the stoichiometric coefficient of component $i$ in the aqueous phase, and $A_i$ is the chemical symbol for the i-th aqueous species.

The dissolution or precipitation of a mineral chemical reaction can be expressed as follows [31]:

$${\sum }_{i=1}^{n_{ct}}{v}_{ij}{A}_i=0,\mathrm{j}=1,\dots ,R_{mn}$$

(7)

where $R_{mn}$ is the number of reactions between the minerals and aqueous components and $n_{ct}$ is the total number of components.

2.5. Chemical Equilibrium Reactions

The reactions between the aqueous components in the aqueous phase are considered to be chemical equilibrium reactions.

Chemical equilibrium constants are adopted to compute the following chemical equilibrium reactions [33]:

$$Q_j-K_{eq,j}=0,j=1,\dots ,R_{aq}$$

(8)

$$Q_j={\prod }_{i=1}^{n_{aq}}{a}_i^{v_{ij}}$$

(9)

where $Q_j$ is the activity product of the aqueous reaction $j$, $a_i$ is the activity of component $i$, $v_{ij}$ is the stoichiometry coefficients, and $K_{eq,j}$ is the chemical equilibrium constant for the $j$-th aqueous reaction.

The activity $a_i$ is related to the molality as follows:

$$a_i={\gamma }_i{m}_i,i=1,\dots ,n_{aq}$$

(10)

where ${\gamma }_i$ is the activity coefficient.

The B-dot model is the preferred model to calculate the ionic activity coefficient:

$${\log \gamma }_i=-{\displaystyle \frac{A_{\gamma }{z}_i^2\sqrt{I}}{1+{\mathrm{å}}_i{B}_{\gamma }\sqrt{I}}}+\dot{B}I$$

(11)

where $A_{\gamma }$, $B_{\gamma }$, and $\dot{B}$ are temperature dependent parameters and ${å}_i$ is the ion size parameter.

$I$ is the ionic strength parameter, expressed by the following:

$$I={\displaystyle \frac{1}{2}}{\sum }_{j=1}^{n_{aq}}{m}_j{z}_j^2$$

(12)

where $m_j$ is the stoichiometric molality of the j-th ion, $z_j$ is the electric charge of the j-th ion.

2.6. Mineral Dissolution and Precipitation Reactions

The mineral dissolutions/precipitations of the solution are represented as rate-dependent reactions [33,34,35]:

$$r_j={\widehat{A}}_j{k}_j\left(1-{\displaystyle \frac{Q_j}{K_{eq,j}}}\right),\mathrm{j}=1,\dots ,R_{mn}$$

(13)

where $r_j$ is the rate of the mineral reaction, ${\widehat{A}}_j$ is the reactive surface area for j-th mineral, $k_j$ is the rate constant of the j-th mineral reaction, $K_{eq,j}$ is the chemical equilibrium constant for the j-th mineral reaction, and $Q_j$ is the activity product of the aqueous reaction $j$.

The rate of formation/consumption of the different aqueous species is calculated by the following:

$$r_{ij}=r_{ij}·r_j$$

(14)

The rate constant of the mineral reaction is reported at a reference temperature, $T_0$:

$$k_{\beta }=k_{0\beta }exp\left[-{\displaystyle \frac{E_{a\beta }}{R}}\left({\displaystyle \frac{1}{T}}-{\displaystyle \frac{1}{T_0}}\right)\right]$$

(15)

where $k_{0\beta }$ is the rate constant for reaction $\beta$ at $T_0$, $E_{a\beta }$ is the activation energy of the mineral reaction $\beta$.

The reactivate surface area of the j-th mineral reaction is obtained:

$${\widehat{A}}_j={\widehat{A}}_j^0·{\displaystyle \frac{N_j}{N_j^0}}$$

(16)

where ${\widehat{A}}_j^0$ is the reactive surface area at the initial time, $N_j$ is the mineral mole number per unit grid block volume at the current time, and $N_j^0$ is the mineral mole number per unit grid block volume at the initial time.

With mineral dissolution and precipitation, the Kozeny–Carman equation is used to calculate the absolute permeability:

$${\displaystyle \frac{k}{k_0}}={\left({\displaystyle \frac{\phi }{{\phi }_0}}\right)}^3·{\left({\displaystyle \frac{1-{\phi }_0}{1-\phi }}\right)}^2$$

(17)

where $k_0$ and ${\phi }_0$ are the initial permeability and porosity, respectively.

2.7. CO₂ Trapping Mechanisms

In order to establish a comparative analysis of storage contribution in CMG, the formulas below were adopted to calculate the storage contribution of each trapping:

$$Structural Trapping,\%={\displaystyle \frac{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}-\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d} \mathrm{S}\mathrm{g}<\mathrm{S}\mathrm{g}\mathrm{c}/\mathrm{H}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{s}}{Cumulative {CO}_2 injected }}\times 100\%$$

(18)

$$Residual Gas Trapping,\%={\displaystyle \frac{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d} \mathrm{S}\mathrm{g}<\mathrm{S}\mathrm{g}\mathrm{c}/\mathrm{H}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{s}}{Cumulative {CO}_2 injected }}\times 100\%$$

(19)

$$Solubility Trapping,\%={\displaystyle \frac{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{v}\mathrm{e}\mathrm{d} \mathrm{i}\mathrm{n} \mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{Cumulative {CO}_2 injected }}\times 100\%$$

(20)

$$Ionic Trapping,\%={\displaystyle \frac{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{i}\mathrm{n} \mathrm{A}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{o}\mathrm{u}\mathrm{s} \mathrm{I}\mathrm{o}\mathrm{n}\mathrm{s}}{Cumulative {CO}_2 injected }}\times 100\%$$

(21)

$$Mineral Trapping,\%={\displaystyle \frac{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{i}\mathrm{n} \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}{Cumulative {CO}_2 injected }}\times 100\%$$

(22)

3. Model Description

3.1. Geometric Model

The Wushi basin, located in the southern part of China, is one of the most favorable locations for oil and gas accumulation (Figure 5). The target CO₂ injection formation for this investigation is the Wei-2 formation. Based on the geological and petrophysical characteristics revealed by the borehole analyses, a Wei-2 sandstone formation, with a thickness of about 150 m, displays a strong lithological heterogeneity. The upper part of the Wei-2 sandstone formation comprises thick gray mudstone, maintaining caprock integrity. The Wei-2 formation is truncated by three faults, and the strike of the faults runs NE to SW (Figure 6). The permeability of the multilayered reservoir was calculated by the Sequential Gaussian Simulation method, using the SGSIM code (Figure 7).

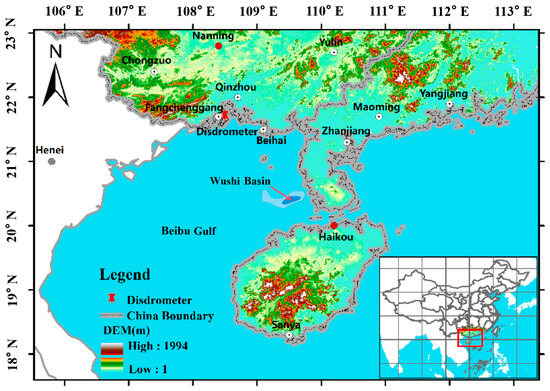
Figure 5. Location of the Wushi basin.

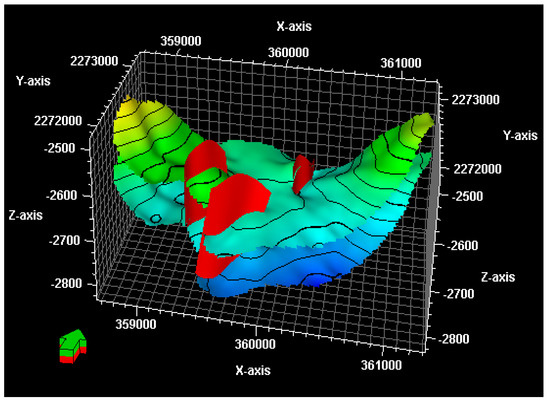
Figure 6. Three-dimensional model of the formation (light green layer) and fault (red planes) setting in the Wushi basin.

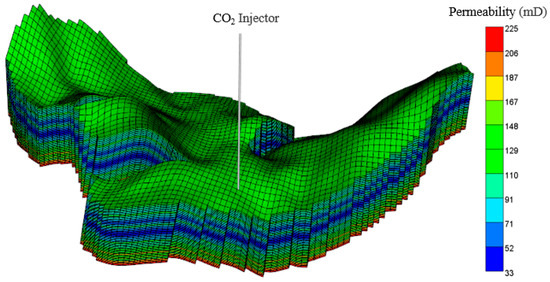
Figure 7. Three-dimensional model of CO₂ injection in the Wushi basin.

The static grid model parameters and reservoir parameters are given in Table 1.

Table 1. Summary of the parameters adopted for CO₂ injection.

Parameters	Symbol	Units	Values
Grid discretization	(nx, ny, nz)	[–]	(91, 41, 60)
Porosity	ϕ	[–]	0.18
Permeability	$k$	[mD]	33~255
Initial reservoir temperature	T	[°C]	50
Initial reservoir pressure	p	[MPa]	27
Nacl concentration	$m_l^S$	[mol/kg]	0.1
Diffusion coefficient	D	[m2·s−1]	2 × 10−5
Well radius	rw	[m]	0.1
Total injection mass	Minj	[t]	6.83 × 104
Simulation time	t	[years]	120

3.2. Geochemical System

There are three solubility reactions and three liquid–mineral reactions in the geochemistry system:

H₂O ⇔ H⁺ + OH⁻

(23)

$${\mathrm{CO}}_2 \left(\mathrm{aq}\right)+{\mathrm{H}}_2\mathrm{O} \iff {\mathrm{H}}^{+}+{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$$

(24)

$${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-} \iff {\mathrm{H}}^{+} + {\mathrm{C}\mathrm{O}}_3^{2-}$$

(25)

$$\mathrm{Calcite}+{\mathrm{H}}^{+} \iff {\mathrm{Ca}}^{2+}+{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$$

(26)

Anorthite + 8H⁺ ⇔ Ca²⁺ +2Al³⁺ + 2SiO₂ (aq) + 4H₂O

(27)

Kaolinite + 6H⁺ ⇔ 2Al³⁺ +2SiO₂ (aq) + 5H₂O

(28)

The composition of the formation’s initial water condition is described in Table 2. The chemical equilibrium constants for the three aqueous reactions are given in Table 3. The simulated cases with two different injection schemes for carbon storage are listed in Table 4. Parameters for mineral dissolution/precipitation calculation are given in Table 5.

Table 2. Initial concentrations of the aqueous species in the geochemical system.

Aqueous Species	Molality [mol/kg of Water]	Aqueous Species	Molality [mol/kg of Water]
H+	9.80415 × 10−8	SiO2	0.00301446
Ca2+	0.0124813	${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$	1 × 10−10
Na+	1.34529	OH−	1 × 10−10
Al3+	3.70625 × 10−5	${\mathrm{C}\mathrm{O}}_3^{2-}$	1 × 10−10

Table 3. Chemical equilibrium constants for aqueous reactions [36,37,38].

Aqueous Chemical Reactions	Log Keq
H2O ⇔ H+ +OH−	−13.2631
CO2 (aq) + H2O ⇔ H+ + ${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$	−6.3221
${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$ ⇔ H+ + ${\mathrm{C}\mathrm{O}}_3^{2-}$	−16.5563

Table 4. Two different injection schemes for carbon storage.

Case ID	Injection Scheme
Base Case	CO2 Injection (20 years)
Modified Case	CO2 Injection (20 years) + H2O Injection (10 years)

Table 5. Summary of the parameters adopted for GCS [36,37,38].

Aqueous Chemical Reactions	Log Keq	Reactive Surface Area [m2/m3]	Eaβ [J/mol]	Log kβ at 25 °C [mol/(m2s)]
Calcite + H+ ⇔ Ca2+ + ${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$	1.3560	88	41,870	−8.8
Anorthite + 8H+ ⇔ Ca2+ + 2Al3+ + 2SiO2 (aq) + 4H2O	23.0603	88	67,830	−12
Kaolinite + 6H+ ⇔ 2Al3+ + 2SiO2 (aq) + 5H2O	5.4706	17,600	62,760	−13

4. Simulation Results and Discussion

4.1. Base Case of Supercritical CO₂ Injection

The basic problem of interest is that CO₂ is injected at the bottom of the formation (Figure 8). CO₂ is injected at a fixed injection rate of 4500 m³/day under a standard surface gas rate with a maximum bottom-hole pressure of 44,500 kPa for the first 20 years. The initial well bottom-hole pressure was about 27.4 MPa, and the bottom-hole pressure rose to about 29.6 MPa after 20 years of continuous injection. The migration of supercritical CO₂ was carried out until 2150 (100 years). After the well shut-in, the well bottom-hole pressure decreased slowly. The bottom-hole pressure was about 29.4 kPa at the end of the simulation, higher than the initial value (Figure 9). The cumulative mass of the CO₂ injection was 6.83 × 10⁴ t.

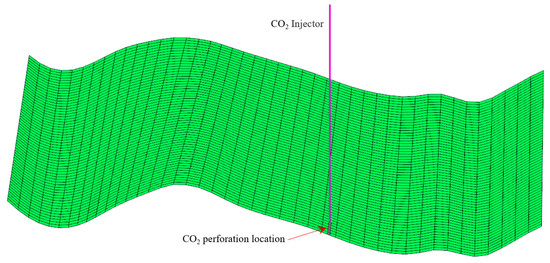
Figure 8. Sketch of the CO₂ perforation location.

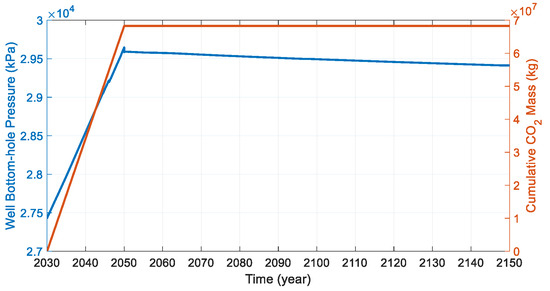
Figure 9. Injection profile of the supercritical CO₂ during the simulation (blue line is well bottom-hole pressure; orange line is cumulative CO₂ mass).

Figure 10 shows the spatial mobility and distribution of CO₂ saturation over time. Due to the density difference between the supercritical CO₂ and the aqueous phase, the low-viscosity CO₂ tends to migrate to the top of the geological formation. The highest concentration areas of CO₂ saturation are observed in the convex topography near the injection well. After the well shut-in, CO₂ continues to migrate to the anticline due to structural trapping (1 January 2060). After that, the CO₂ plume continues to move forward due to the accumulation of excess CO₂ in the anticline. At the end of the simulation period (1 January 2150), most of the CO₂ plume was still trapped at the top of the anticline in the Wei-2 formation.

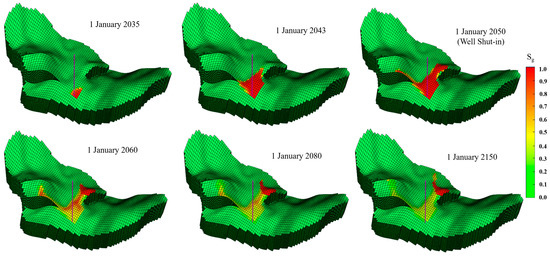
Figure 10. Spatial mobility and distribution of CO₂ saturation at various simulation times for CO₂ injection.

The CO₂ mole changes at various simulation times are plotted in Figure 11. At the beginning of the CO₂ injection, the supercritical CO₂ is injected and mixed with the initial water in the formation, forming a dissolved aqueous phase. The supercritical CO₂ continues to increase to a maximum value of 1.32 × 10⁹ moles in 2050. Due to the existence of initial water in the formation, the CO₂ aqueous ions and dissolved CO₂ measure 5.04 × 10⁸ and 0.575 × 10⁸ moles in 2030, respectively. At the end of the simulation, the CO₂ aqueous ions and dissolved CO₂ measure 6.8 × 10⁸ and 4.0 × 10⁸ moles in 2050. The dissolved-CO₂ curve shows an increasing trend during geological carbon storage. During the CO₂ injection period, the amount of CO₂ dissolved in the aqueous phase is more than that of trapped CO₂. There is a sharp increase in trapped CO₂ after the well shut-in, mainly due to CO₂ being trapped by the anticline.

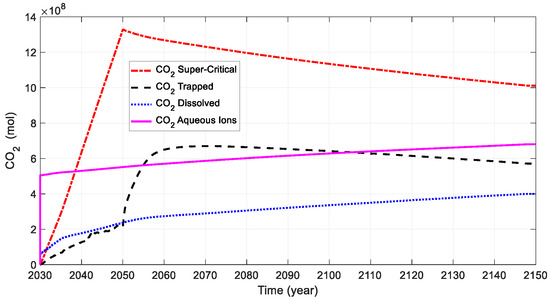
Figure 11. Evolution of CO₂ mole changes at various times for base case.

Figure 12 and Figure 13 show the mineral moles changes in anorthite, calcite, and kaolinite. Figure 14 shows the ion mole changes at the end of the simulation. It can be observed that the kaolinite is precipitated in the aqueous phase, while the anorthite is dissolved. Calcite is initially in the dissolved state, gradually converting to a precipitated state due to the continued geochemical reactions in the late storage period. The mole changes for anorthite, calcite, and kaolinite are −2.79 × 10⁷, 2.07 × 10⁷, and 7.85 × 10⁵ at the end of the simulation, respectively. As CO₂ is dissolved in the aqueous phase, there is a decrease in PH in the CO₂ migration areas (Figure 15). The porosity variation was insignificant at the end of the simulation (Figure 16). Anorthite, a calcium-rich mineral, is dissolved to provide Ca²⁺ and Al³⁺ in the aqueous phase due to the formation of carbonic acid. Ca²⁺ and Al³⁺ contribute to the precipitation of calcite and kaolinite with time. The mineral change in calcite is more than that of kaolinite precipitation. The precipitation of calcite consumed more Ca²⁺ compared with Al³⁺ consumed by kaolinite precipitation. The mole changes in Al³⁺ is more obvious than that in Ca²⁺ 100 years after the injection period.

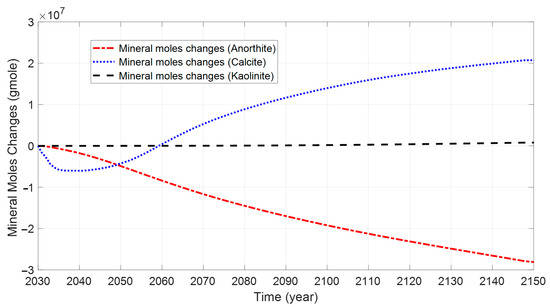
Figure 12. Evolution of mineral mole changes at various times for base case.

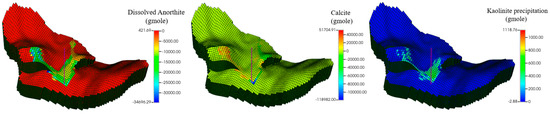
Figure 13. Spatial distribution of mineral changes 100 years after injection period.

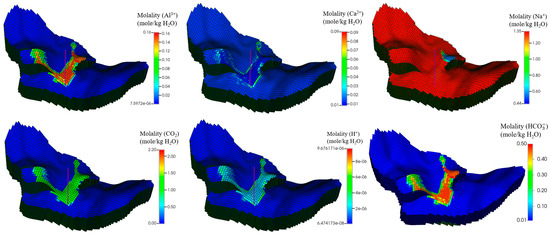
Figure 14. Spatial distribution of ion changes after simulation time of 100 years.

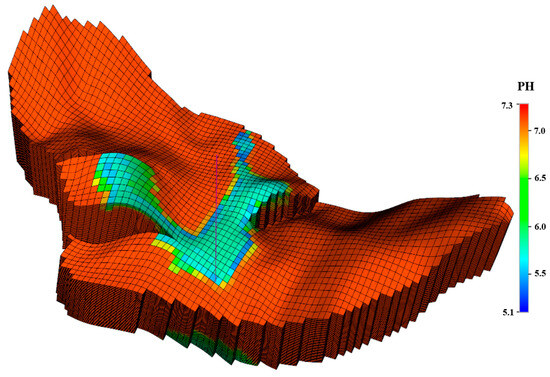
Figure 15. PH variation at the end of the simulation for CO₂ injection.

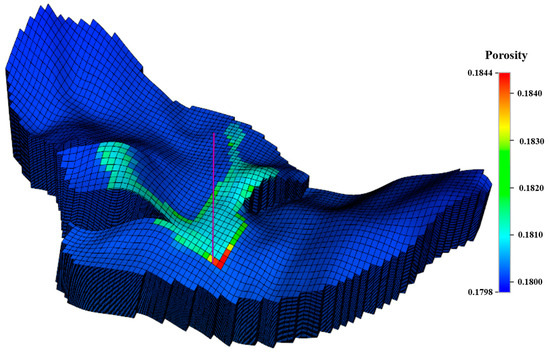
Figure 16. Porosity variation at the end of the simulation for the base case.

For the CO₂ injection, the CO₂ moles of different trapping mechanisms are illustrated in Figure 17. The trapping mechanisms of the structural, residual gas, solubility, ions, and minerals are considered in CO₂ storage amounts in the reservoir (Figure 18). During the CO₂ injection period, the storage contributions of structural and solubility trapping decrease with time, and the trapping contribution of residual gas is nearly fixed as a constant. When the injection well was shut down (1 January 2050), 72% of the primary 1.5512 × 10⁹ moles of injected CO₂ was trapped by structural trapping. The storage contributions of residual gas, solubility, ionic, and mineral trapping are 13.38%, 11.55%, 3.07%, and 0%, respectively. After the injection well was shut down, the contribution of structural trapping decreased from 72% to 28.39% with time. At the end of the simulation, 28.39%, 36.83%, 22.08%, 11.36%, and 1.34% of the injected CO₂ was stored by structural, residual gas, solubility, ionic, and mineral trapping, respectively.

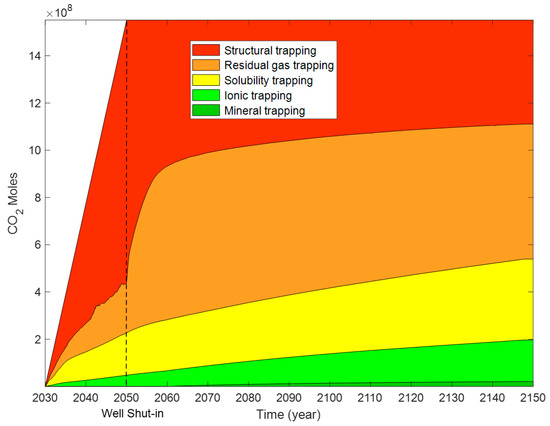
Figure 17. CO₂ moles of different trapping mechanisms.

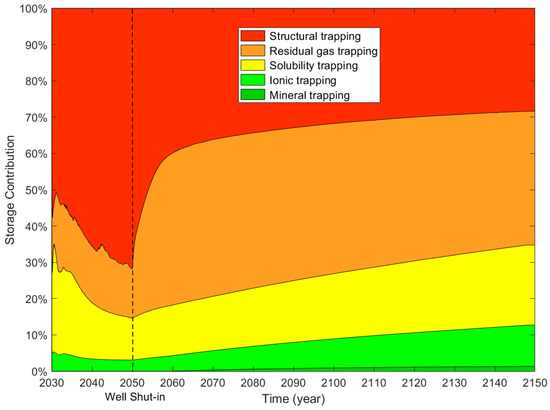
Figure 18. Storage contributions of different trapping mechanisms for base case.

4.2. Modified Case of Supercritical CO₂ + Water Injection

Improving carbon storage efficiency, the case is modified by adding a water injection to the CO₂ storage model. The water perforation location is above the CO₂ perforation location (Figure 19). Water is injected at a fixed injection rate of 25 m³/day under a standard surface water rate for the first 10 years, and supercritical CO₂ is injected for 20 years continuously.

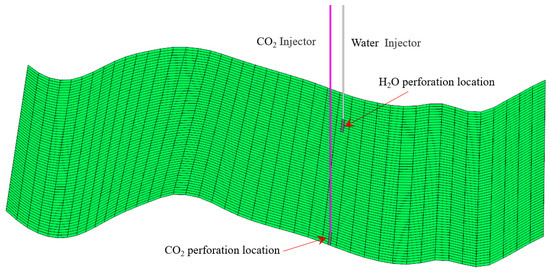
Figure 19. Sketch of the CO₂ and H₂O perforation locations.

Figure 20 shows the spatial distribution of CO₂ saturation after a simulation time of 100 years. It is observed that most of CO₂ plume was trapped on the top of the anticline in the Wei-2 formation, without migrating out of the anticline (2150-01-01).

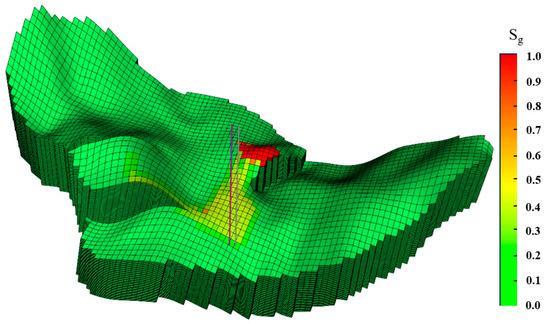
Figure 20. Spatial distribution of CO₂ saturation at various times (modified case).

Figure 21 illustrates the CO₂ mole changes at various simulation times for CO₂ and water injection. The CO₂ aqueous ions and dissolved CO₂ measure 7.06 × 10⁸ and 4.5 × 10⁸ moles in 2150, respectively.

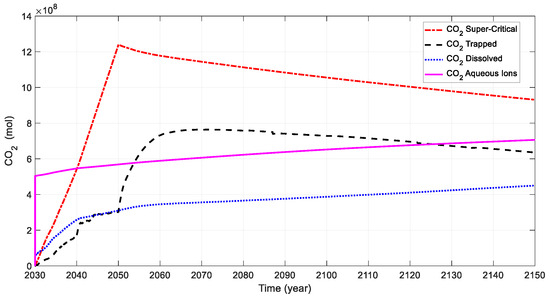
Figure 21. Evolution of CO₂ mole changes at various times for modified case.

Figure 22 displays the evolution of anorthite, calcite, and kaolinite mole changes at various simulation times for the CO₂ and water injections. The mole changes for anorthite, calcite, and kaolinite are −3.23 × 10⁷, 2.51 × 10⁷, and 9.3 × 10⁵ after well shut down after 100 years, respectively.

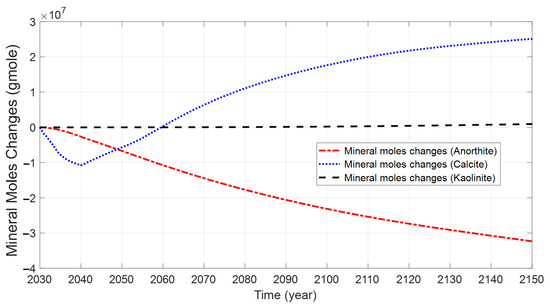
Figure 22. Evolution of mineral mole changes at various times for modified case.

For supercritical CO₂ plus water injection, the moles of different trapping mechanisms are illustrated in Figure 23, and the trapping contributions of different mechanisms are illustrated in Figure 24. During the CO₂ and water injection period, the storage contribution of structural trapping displays an initial decrease (10 years) and then shows an increasing trend (10 years) with time. When the injection well was shut down, 60.38% of the moles of injected CO₂ was trapped by structural trapping. The trapping contributions of residual gas, solubility, ionic, and mineral trapping are 19.16%, 16.28%, 4.18%, and 0%, respectively. One-hundred years after the injection well was shut down, the contribution of structural trapping decreased from 72% to 19.05% with time. At the end of the simulation (120 years), 19.05%, 40.95%, 25.33%, 13.05%, and 1.62% of the injected CO₂ was stored by structural, residual gas, solubility, ionic, and mineral trapping, respectively.

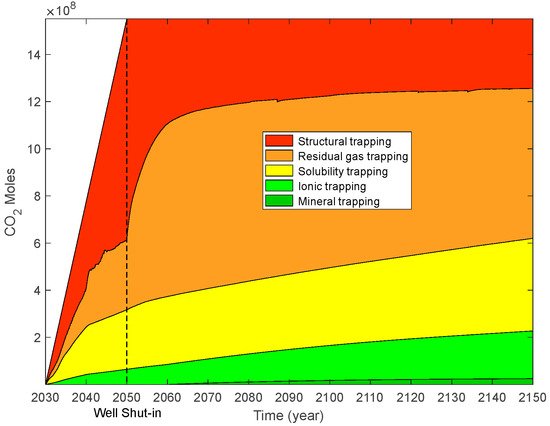
Figure 23. CO₂ moles of different trapping mechanisms for modified case.

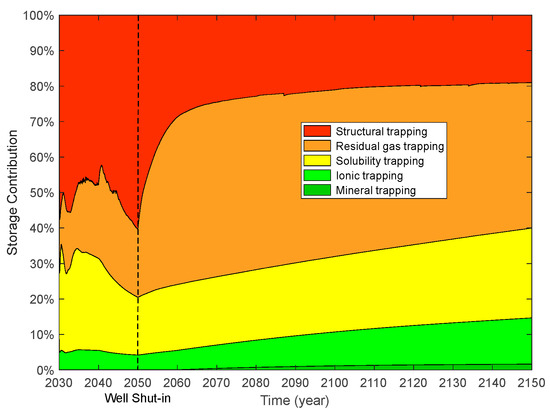
Figure 24. Storage contributions of different trapping mechanisms for modified case.

4.3. Comparisons of CO₂ Injection and CO₂ + Water Injection

Compared with CO₂ injection, the storage contribution of structural trapping decreases from 28.39% to 19.05% for CO₂ and water injection. It can be seen from Figure 25 that the storage contributions of residual gas, solubility, ionic, and mineral trapping increases at the end of the simulation for the modified case. The percentage increase in the storage contributions of residual gas, solubility, ionic, and mineral trapping due to water injection are 4.12%, 3.25%, 1.69%, and 0.28%. It is concluded that injecting water above the location of CO₂ injection is an effective method to improve the storage efficiency of residual gas, solubility, ionic, and mineral trapping, and provides an effective reference for CO₂ storage. Structural trapping was the maximum storage contribution when the well was shut down. At the end of the simulation, the residual gas trapping is the maximum storage contribution for CO₂ storage.

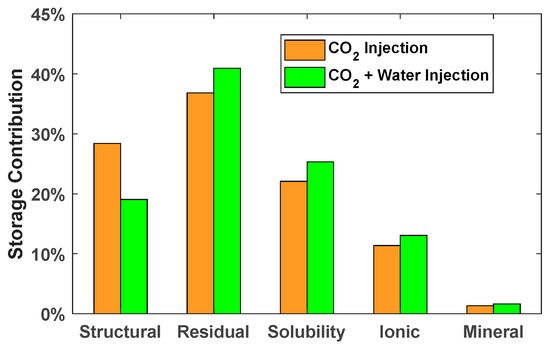
Figure 25. Storage contributions of CO₂ injection and CO₂ + water injection.

Water injection enhances storage efficiency mainly for the following reasons:

(1)

The injection of water can improve the mobility of carbon dioxide within the reservoir, promoting its uniform distribution and further enhancing storage effectiveness.

(2)

By creating a water layer through injection, a barrier can be formed to some extent, reducing the risk of carbon dioxide leaking to the surface or into other strata.

(3)

Additionally, water injection can increase the pressure in the underground reservoir, helping to drive carbon dioxide into deeper pore spaces, thereby improving the efficiency of CO₂ storage.

5. Conclusions

In this paper, the Sequential Gaussian Simulation is adopted to construct a multilayered offshore basin, and aqueous solubility and geochemistry are considered in CO₂ migration and the trapping process. The main conclusions are as follows:

(1)

An anticline is an ideal structural for geological carbon storage. The highest concentration areas of CO₂ saturation are observed in the convex topography near the injection well.

(2)

Mineral trapping does not contribute in any significant way to CO₂ storage capacity in a very short time scale, and the contribution of residual gas trapping is the greatest at the end of the simulation.

(3)

In order to sequestrate carbon by mineralization, it is necessary to dissolve CO₂ into a saline aquifer to form H⁺ for the generation of Ca²⁺ and Al³⁺ released by anorthite. Calcite and kaolinite are precipitated in the aqueous phase due to the continued geochemistry reactions after well shut-in.

(4)

The contribution of structural storage decreases from 28.39% to 19.05%, while the storage contributions from residual gas, solubility, ionic, and mineral trapping increase by 4.12%, 3.25%, 1.69%, and 0.28%, respectively, with CO₂ and water injection, thereby enhancing the long-term security of CO₂ storage in offshore basins.

(5)

Carbon dioxide migrates upward from the bottom, and choosing the appropriate CO₂ injection well design can effectively prevent carbon dioxide leakage. One can optimize the layout and design of the injection well to ensure a uniform distribution of carbon dioxide and to increase the injection rate.

(6)

A sensitivity analysis to assess the impact of variations in key parameters (e.g., injection rate, reservoir properties) on the simulation results will be carried out in future investigations.