An Efficient and Improved Coronavirus Herd Immunity Algorithm Using Knowledge-Driven Variable Neighborhood Search for Flexible Job-Shop Scheduling Problems

Abstract

By addressing the flexible job shop scheduling problem (FJSP), this paper proposes a new type of algorithm for the FJSP. We named it the hybrid coronavirus population immunity optimization algorithm. Based on the characteristics of the problem, firstly, this paper redefined the discretized two-stage individual encoding and decoding scheme. Secondly, in order to realize the multi-scale search of the solution space, a multi-population update mechanism is designed, and a collaborative learning method is proposed to ensure the diversity of the population. Then, an adaptive mutation operation is introduced to enrich the diversity of the population, relying on the adaptive adjustment of the mutation operator to balance global search and local search capabilities. In order to realize a directional and efficient neighborhood search, this algorithm proposed a knowledge-driven variable neighborhood search strategy. Finally, the algorithm’s performance comparison experiment is carried out. The minimum makespans on the MK06 medium-scale case and MK10 large-scale case are 58 and 201, respectively. The experimental results verify the effectiveness of the hybrid algorithm.

1. Introduction

The flexible job-shop scheduling problem (FJSP) is an extension of the classic job-shop scheduling problem, which is more suitable for the complex production environment faced by advanced modern manufacturing industries. The classic job-shop scheduling problem has been proven to be an NP-hard problem [1]. Based on the classic job-shop scheduling problem, the flexible job-shop scheduling problem relaxes the processing machine constraints of operations. At least one operation is allowed to be processed on two or more machines, and the time required for processing using different machines is different. The production environment represented by the flexible job-shop scheduling problem is more complex. It is necessary to consider the processing sequence of jobs and arrange the processing machines so that the operations can achieve the scheduling goal. Therefore, solving the problem is more difficult, but it can better simulate the current rapid development of the semiconductor manufacturing industry, automobile assembly industry, and other environments [2]. In recent years, this issue has received extensive attention from many researchers. The earliest research on this problem can be traced back to the middle of the last century [3]. Early research methods mainly used scheduling rules, branch and bound methods, etc. However, they were only applicable to small-scale problems. Thanks to the development of computer computing power, the swarm intelligence algorithm has become the current mainstream research method, such as genetic algorithm, gray wolf algorithm, particle swarm algorithm, etc.

The swarm intelligence algorithm can obtain an effective approximate solution to the FJSP within an acceptable time, so it has been extensively studied by many scholars. Zhang et al. [4] proposed a crossover operator that can avoid illegal solutions to optimize different performance indicators of the FJSP. Liu et al. [5] proposed an improved genetic algorithm with an active-schedule decoding mechanism to solve flexible job-shop scheduling problems. Sun et al. [6] proposed a variable neighborhood search strategy to improve the effective search efficiency of the genetic algorithm in order to optimize the makespan’s objective. Jiang [7] proposed a hybrid gray wolf algorithm combined with a variable neighborhood search and genetic operators to optimize the makespan objective of the FJSP. Ding et al. [8] proposed a hybrid algorithm combining the human learning optimization algorithm and particle swarm algorithm to solve the flexible job-shop scheduling problem. Zhang et al. [9] proposed an improved wolf pack algorithm to solve the multi-objective flexible job-shop scheduling problem. In view of the above literature for classical FJSPs, we summarize the contribution and related studies in this study. The results are shown in Table 1.

Table 1. Summary of related studies on classical FJSPs.

Author	Year	Method	Test Case	Potential Advantage
Zhang [4]	2009	Improved genetic algorithm	Muth and Thompson’s benchmarks	POX crossover operation can avoid illegal solutions.
Liu [5]	2009	Improved genetic algorithm	Kacem and Brandimarte’s benchmarks	Active scheduling schemes can use machine time effectively and rationally
Sun [6]	2023	Hybrid genetic algorithms	Brandimarte’s benchmarks	Machines with minimum processing time can be used as neighborhood knowledge.
Jiang [7]	2018	Hybrid gray wolf algorithm	Kacem and Brandimarte’s benchmarks	The gray wolf algorithm is applied to the FJSP.
Ding [8]	2020	Hybrid particle swarm algorithm	Brandimarte’s benchmarks	The hybrid particle swarm algorithm is applied to the FJSP.
Zhang [9]	2022	Improved wolf pack algorithm	Practical cases	The wolf pack algorithm is applied to the FJSP.

In addition, the actual production environment is complex and changeable, and many scholars have added conditional constraints on the basis of the FJSP to fit a variety of actual processing environments. Chen et al. [10] proposed an elitist genetic algorithm to solve the flexible job-shop scheduling problem with fuzzy processing time. Chen et al. [11] applied the improved particle swarm optimization algorithm to FJSP research by considering the transportation time. Zhang et al. [12] combined the particle swarm optimization algorithm with the simulated annealing algorithm to solve the flexible job-shop batch scheduling problem. Komakia et al. [13] used the improved gray wolf algorithm to solve the two-stage flow-shop scheduling problem with release time constraints.

Hybrid algorithms can reduce the limitations of a single algorithm and can effectively improve the performance of an algorithm. In many research fields, these hybrid algorithms have been extensively studied by many scholars. Coma et al. [14] combined genetic algorithms with gradient-based algorithms to optimize the active flow control problem over airfoils. Devarapalli et al. [15] combined the gray wolf algorithm and the sine cosine algorithm in order to effectively and quickly adjust the parameters of power system stabilizers. Knypinski [16] introduced the Hooke–Jeeves method in the cuckoo search algorithm to search for new cuckoo positions, greatly improving the optimization accuracy of a line-start permanent magnet synchronous motor. The nonlinear convergence factor is an effective method for improving the performance of algorithms. Knypinski [17] proposed a linear convergence factor for the gray wolf algorithm, which greatly improved the performance of the gray wolf algorithm in the line-start permanent magnet motor. Hegazy et al. [18] introduced the inertial weight strategy in the sarp group algorithm, which not only balanced global and local search capabilities but also improved the convergence of the algorithm.

The research on FJSP is still a focus of research in recent years. Aiming at this problem, the mainly used swarm intelligence algorithms can be divided into four types: genetic algorithm, gray wolf algorithm, particle swarm algorithm, and wolf pack algorithm. On the basis of the original algorithm, scholars have carried out detailed research on the gene update method and the neighborhood search’s structure. However, their populations often use a unified search scale to carry out searches within the solution space, and this cannot achieve refined searches. Additionally, they use a fixed mutation rate, which cannot balance the relationship between global and local searches, and there is a risk of falling into a local optimum. The existing neighborhood structure only comprises a random search, or the machine with the shortest processing time for the process is chosen, which lacks the use of existing knowledge. The solution space of the FJSP is large and complex, and the swarm intelligence algorithm is essentially an approximate solution algorithm. Effective methods for searching for a better solution within an effective time range still comprise a challenging task. Affected by randomness, there is currently no algorithm that can guarantee the optimal solution to this problem every time. To this end, this paper conducts research on the multi-scale solution space search. By summarizing the existing empirical knowledge, the knowledge-driven neighborhood structure search is realized.

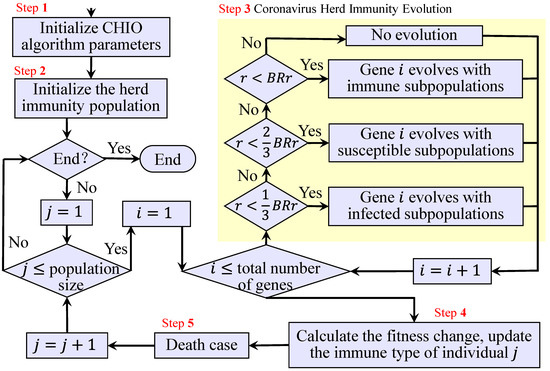
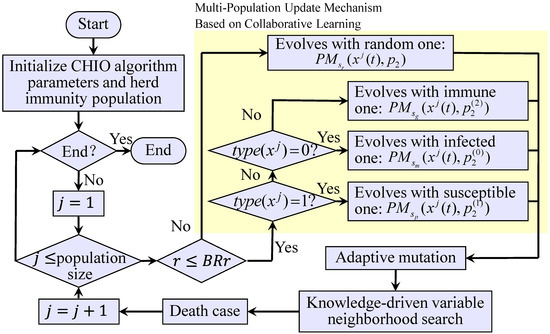
The coronavirus swarm immunity optimization (CHIO) algorithm is an emerging swarm intelligence optimization algorithm proposed by Al-Betar et al. [19] in 2020. Inspired by the novel coronavirus that is widespread around the world, the algorithm proposes an algorithm update theory that simulates the emergence of herd immunity. Although the algorithm appeared late, it has been verified on multiple functions and engineering optimization problems [19,20,21]. The CHIO algorithm proposed the concept of multi-population evolution for the first time. Although this point also exists in the gray wolf algorithm, the gray wolf algorithm mainly comprises the following concept: All individuals of other populations approach the head wolf population. The difference is that the CHIO algorithm performs an iterative update of genes both within the sub-population and between sub-populations, and the update mechanisms within different sub-populations are different, so it has a broader search capability. In addition, the CHIO algorithm adopts the “survival of the fittest” mechanism. If the individual has not been improved in the iteration process, the individual will be replaced by a randomly generated new individual when the maximum age is reached. This update mechanism is beneficial as individuals can escape the local optimal trap. The original CHIO algorithm uses floating-point numbers to encode individuals, so it needs to use a certain mapping method when it is applied to the FJSP. In addition, CHIO is a new algorithm, so there are few studies on the algorithm used in the field of job-shop scheduling. Only one research study [22] applies it to the solution of the replacement flow-shop scheduling problem. Compared with the replacement flow-shop scheduling problem, the FJSP needs to consider two sub-problems—operations arrangement and machine selection—at the same time, so the complexity of the problem is greater. For this reason, this paper attempts to extend the CHIO algorithm to solve the FJSP. In order to improve the global search and local search capabilities of the algorithm, on the basis of the traditional CHIO algorithm, a series of designs and improvements in line with the FJSP were constructed. In order to facilitate the description below, we named the improved algorithm for the FJSP the hybrid coronavirus swarm immunity optimization (HCHIO) algorithm. Combined with the characteristics of the FJSP, the discretized individual encoding and decoding schemes are redefined. FJSP is essentially a combinatorial optimization problem. During the solution process, all possible machine scheduling schemes need to be searched to find the optimal solution. However, in the worst case, the time complexity of this search process is exponential. Thus, the FJSP is an NP-hard problem. The solution space of this problem is large and complex. The difficulty related to producing a fast and efficient search scheme in such a large solution space is a meaningful problem that should be solved. Inspired by the way novel coronavirus spreads, a multi-population mechanism is established within the algorithm, and the discretized update actions of different scales are designed to achieve the efficient search of a solution space. An adaptive mutation operation is introduced to expand the diversity of the population while balancing the global search and local search capabilities of the algorithm.

In order to reduce the algorithm’s invalid neighborhood search, it is necessary to make full use of empirical knowledge. From a mathematical point of view, we can refer to empirical knowledge as the mathematical characteristics of the problem. Math-heuristic algorithms is a well-known method in the study of solving Np-hard problems and comprises using mathematical features. Burke and Brucker et al. [23] proposed a branch and bound algorithm for the cyclic job-shop problem by combining mathematical features and heuristic algorithms. However, there is a certain gap between the knowledge used in this article and the mathematical features in math-heuristic algorithms. The mathematical features in math-heuristic algorithms mostly comprise deep-level, complex linear or nonlinear properties, etc. The difference is that the knowledge used in this paper includes the following: the critical path of the directed acyclic graph and simple mathematical characteristics. The simpleness of the mathematical features used in this article is that the features only involve size comparisons and division operations. In our evolutionary algorithms, the purpose is to direct the neighborhood search, which originally may not involve a change in the scheduling target with respect to the neighborhood search, in such a manner that will inevitably lead to a change in the scheduling target. Thus, this neighborhood structure does not exhibit enough properties to be called a math heuristic. Thus, a variable neighborhood search strategy that is knowledge-driven is proposed to enhance the local search ability of the algorithm and improve the convergence efficiency of the algorithm.

The rest of this paper is organized as follows: Section 2 introduces the description of the FJSP. Section 3 shows the original CHIO algorithm. In Section 4, the proposed HCHIO algorithm is described in detail. The experimental results and analysis of the HCHIO algorithm are shown in Section 5. Section 6 states the conclusions and suggestions for future works.

2. Flexible Job-Shop Scheduling Problem Description and Formulation

The FJSP has been extensively studied by many scholars. In order to clearly describe our processing system of the FJSP and scheduling objective in this paper, this section will introduce the FJSP description and formulation.

2.1. Problem Description

The FJSP of this paper is almost identical to the framework of the flexible job shop in the book by Pinedo [24], but there are also minor differences. The detailed differences are introduced as follows: the flexible job-shop (${FJ}_c$) framework in Pinedo [24] first divides all machines into $c$ work centers. When a certain job passes through a certain work center more than once, it becomes a recirculation problem. The FJSP in this paper does not divide the work centers but provides optional processing machines for each operation, so there is no need to consider the recirculation problem. However, the FJSP is essentially derived from the flexible job-shop framework in the Scheduling.

The FJSP studied in this paper can simply be described as follows: In a factory processing workshop, we use $m$ machines $M=\left\{M_1, M_2, \cdots , M_m\right\}$ to process $n$ jobs $J=\left\{J_1, J_2, \cdots , J_n\right\}$. Each job $J_i$ to be processed contains a certain number of operations $O_i=\left\{O_{i1}, O_{i2}, \cdots , O_{i{n}_i}\right\}$, and the number of operations contained in different jobs can vary. Each operation of each job has a corresponding set of optional processing machines $M_{ij}$ where $M_{ij}\subseteq \mathrm{M}$, and the processing time of the operation on different machines can be different. Only when there is at least one or more operations with an optional machine set, $M_{ij}$, for which its cardinality is greater than or equal to 2 can it be called a flexibility problem; that is, there is process flexibility in the operations [25]. The FJSP requires a reasonable solution to the operation’s sequence and the machine selection of different operations in order to achieve the optimization goal. The FJSP studied in this paper has the following constraints:

(1)

The first operations of all jobs can be processed at the initial moment.

(2)

All machines are available at the initial moment.

(3)

The machine can only process one operation at a time.

(4)

The job can only be processed by one machine at the same time.

(5)

The process of each operation cannot be interrupted by others; that is, the machine cannot be preempted.

(6)

The processing of any job must be carried out in strict accordance with the preset sequence.

2.2. Problem Formulation

In order to clearly describe the flexible job-shop scheduling problem, the notations used for problem formulation are listed below.

(1)

Parameters

$m$: total number of machines.

$n$: total number of jobs.

$i$: index of jobs, $i\in \left\{1, 2, \dots , n\right\}$.

$g$: index of jobs, $g\in \left\{1, 2, \dots , n\right\}$.

$n_i$: the total number of operations included in job $i$.

$n_g$: the total number of operations included in job $g$.

$j$: index of operations included in job $i$, $j\in \left\{1, 2, \cdots , n_i\right\}$.

$h$: index of operations included in job $g$, $h\in \left\{1, 2, \cdots , n_g\right\}$.

$k$: index of machines, $k\in \left\{1, 2, \dots , m\right\}$.

$k^{\mathrm{’}}$: index of machines, $k^{’}\in \left\{1, 2, \dots , m\right\}$.

$O_{ij}$: the $j$th operation of job $i$.

$O_{gh}$: the $h$th operation of job $g$.

$M_{ij}$: the optional machine set of $O_{ij}$, $M_{ij}\subseteq \left\{1, 2, \dots , m\right\}$.

$M_{ijk}$: machine $k$ in the optional machine set of $O_{ij}$, $M_{ijk}\in M_{ij}$.

$T_{ijk}$: the processing time of $O_{ij}$ on machine $k$.

$T_{ghk}$: the processing time of $O_{gh}$ on machine $k$.

${JRt}_i$: the release time of the first operation of job $i$.

${ST}_{ijk}$: the start time of $O_{ij}$ on machine $k$.

${FT}_{ijk}$: the finish time of $O_{ij}$ on machine $k$.

${FT}_{ghk}$: the finish time of $O_{gh}$ on machine $k$.

(2)

Decision variables

The decision variables set in this paper are as follows:

$$x_{ijk}=\{\begin{array}{l}1,O_{ij}\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}k\\ 0,\mathrm{elsewise}\end{array}$$

$$y_{ijghk}=\{\begin{array}{l}1,O_{ij}\mathrm{is}\mathrm{processed}\mathrm{before}{O}_{gh}\mathrm{on}\mathrm{machine}k\\ -1,\mathrm{elsewise}\end{array}$$

$x_{ijk}$ determines which machine the operation $O_{ij}$ is assigned on, while $y_{ijghk}$ means the order of two different operations processed on the same machine.

(3)

FJSP formulation

In order to measure a scheduling scheme, makespan has been adopted by many scholars. Makespan is the maximum completion time of all the operations in a processing system, that is, the time required for the system to be completed. The FJSP studied in this paper uses the minimization of makespan as the scheduling objective—it can be expressed as Formula (1). Based on the above symbol definition, the FJSP formulation of this paper is as follows:

Objective:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} \mathrm{m}\mathrm{a}\mathrm{x}\left\{{FT}_{ijk}·x_{ijk}\right\}$$

(1)

Subject to:

$${JRt}_i=0$$

(2)

$${\sum }_{k=1}^m{x}_{ijk}=1$$

(3)

$$\left({FT}_{ijk}-{ST}_{ijk}-T_{ijk}\right){·x}_{ijk}=0$$

(4)

$${FT}_{ijk}\le {FT}_{i\left(j+1\right)k^{\mathrm{’}}}-T_{i\left(j+1\right)k^{\mathrm{’}}}$$

(5)

$${(FT}_{ghk}-T_{ghk}-{FT}_{ijk})·y_{ijghk}\ge 0$$

(6)

Equation (2) indicates that all jobs are ready at the initial moment. Equation (3) indicates that the operations can only be processed by one machine. Equation (4) indicates that the operations cannot be interrupted. Equation (5) indicates that the operations of one job can only be processed according to the preset sequential processing operation. Equation (6) indicates that the machine can only process one operation at a time.

3. Coronavirus Swarm Immunity Optimization Algorithm

The CHIO algorithm is a swarm intelligence optimization algorithm that is proposed based on the principle of herd immunity. Inspired by the transmission mode of the new coronavirus, the algorithm divides the population into three types—susceptible, infected and immune—based on the social distance and carries out gene exchanges within and between subpopulations. The “survival of the survivors” natural law is used to simulate the emergence of the new coronavirus herd immunity state.

The CHIO algorithm has three subpopulations and controls gene exchanges within or between subpopulations via the basic reproduction rate (BRr). A random number, r, is generated within the interval of $\left[0\right.,1)$, and an r in the different sub-intervals of BRr means that the current individual carried out gene exchange with the corresponding population within this interval. After gene exchange is carried out, the current individual’s type is updated according to the type of the current individual, the exchange population type, and the fitness value of all populations. The concept of maximum age (Max Age, MA) is established to control evolution’s upper limit and the replacement timing of individuals. The basic update formula of the algorithm is shown in Formula (7).

$$x_i^j(t+1)\leftarrow \{\begin{array}{c}{x}_i^j,r\ge BRr\\ x_i^j(t)+r\cdot (x_i^j(t)-x_i^f(t)),r<\frac{1}{3}BRr\\ x_i^j(t)+r\cdot (x_i^j(t)-x_i^s(t)),r<\frac{2}{3}BRr\\ x_i^j(t)+r\cdot (x_i^j(t)-x_i^m(t)),r<BRr\end{array}$$

(7)

In Formula (7), $x_i^j\left(t\right)$ represents the gene at position i of individual j in the population at the tth iteration; $x_i^f\left(t\right)$ represents the gene at position i of the individual selected from the infected subpopulation. Similarly, $x_i^s\left(t\right)$ and $x_i^m\left(t\right)$ represent individuals in susceptible and immune subpopulations, respectively. After the gene exchange, operations, such as updating the individual type and reaching the age of death, are required. The specific details are not stated here. For details, we refer the reader to Figure 1 and the related literature [14].

Figure 1. Flowchart of the CHIO algorithm.

4. Hybrid Coronavirus Swarm Immunity Optimization Algorithm

The previous section introduced the traditional CHIO algorithm. Based on the traditional CHIO algorithm and combined with the specific characteristics of FJSP, this paper makes some improvements to the CHIO algorithm, which we call the hybrid CHIO algorithm. In this section, we will introduce our improvement strategies and the specific implementation details of the hybrid CHIO algorithm.

4.1. Encoding Mechanism

The traditional CHIO algorithm searches the solution space in the continuous domain, while the FJSP is essentially a discrete combinatorial optimization problem, so the encoding and decoding mechanism of the CHIO algorithm needs to be redefined. In accordance with the characteristic that the FJSP can be divided into two sub-problems of operations with respect to ordering and machine selection, this paper adopts a two-stage coding mechanism [26]. This encoding mechanism solves the subproblems of FJSP simply and efficiently. More importantly, in the iterative process of the algorithm, only a certain strategy can be used to ensure that this encoding must be a feasible scheduling scheme. Let l ($l={\sum }_{i=1}^n{n}_i$) be the total number of operations; then, the individual code can be expressed as follows: $X=\left\{x\left(1\right),x\left(2\right),\cdots ,x\left(l\right),x\left(l+1\right),\cdots ,x\left(2l\right)\right\}$. The details are shown in Figure 2.

Figure 2. HCHIO algorithm encoding mechanism.

The number in the first segment of the code in Figure 2 corresponds to the serial number of the job to be processed, and the number of times a certain number repeats, which is counted from the left to the right side, represents the operation number of the job with the number. The number in the second code represents the machine selection result of the corresponding operation. For example, the number “1” that appears for the second time in the first code segment represents the second operation of job 1, and the number “1” in the corresponding position of the second segment code denotes that the operation is processed on machine 1.

4.2. Decoding Mechanism

Decoding refers to transforming encoded chromosomes into specific and feasible scheduling schemes. In view of the fact that FJSP is an NP-hard problem, the solution space is too large and complex, and the optimization goal studied in this paper is to minimize the makespan; thus, the greedy strategy-based plug-in active scheduling decoding method is used in the first segment of decoding [27]. The second code is the machine selection code, the gene at the corresponding position is the processing machine number of the operation, and the corresponding processing time can be obtained by accessing the optional machine table.

4.3. Genetic Evolution

The traditional CHIO algorithm update method is only suitable for floating-point gene updates, but this paper combines the characteristics of the FJSP and adopts discrete coding; thus, the gene update method of the CHIO algorithm needs to be redesigned. In this regard, this paper introduces the precedence operation crossover (POX) [28] and multi-point random crossover (MPX) operations, which are applied to the gene update of sequence coding and machine selection coding operations, respectively.

(1)

POX operation

The POX crossover operation is only applied to genes at which sequence codes are updated. The specific steps of the POX operation are as follows:

Step 1: According to the serial number of the job, the total job, n, is divided into two subsets, $s_1$ and $s_2$, and there are no elements that are the same in $s_1$ and $s_2$.

Step 2: The job number in collection $s_1$ in parent generation $p_1$ is copied to the same position in $c_1$, and the job number in collection $s_1$ in parent generation $p_2$ is copied to the same position in $c_2$.

Step 3: The job number in collection $s_2$ in parent generation $p_2$ is copied to the remaining positions of $c_1$ in the sequence, and the job number in collection $s_2$ in parent generation $p_1$ is copied to the remaining positions of $c_2$ in the sequence.

In this way, two individuals with different degrees of parental gene retention can be obtained. In order to clearly explain the POX operation process, the following figure is an example of the POX cross-operation process of two operational sequence codes containing four jobs, and the corresponding steps have been marked in Figure 3.

Figure 3. POX cross operation.

(2)

MPX Operation

The MPX crossover operation should only be applied to updated genes, which the code of the machine selects. The basic process of the MPX operation is as follows: First, a crossover vector consisting of only 0 or 1 is randomly generated; then, the machine selection results at the corresponding positions of two parent individuals $p_1$ and $p_2$ are exchanged according to the value in the crossover vector in order to obtain $c_1$ and $c_2$. Combined with the coding method in this paper, the machine selection code is first converted into the corresponding single-job machine selection code, and then, the MPX cross operation is performed. In order to clearly explain the MPX operation process, Figure 4 below shows the MPX cross process of two single-job machine selection codes.

Figure 4. MPX cross operation.

4.4. Multi-Population Update Mechanism Based on Collaborative Learning

The traditional CHIO algorithm divides the population into three types: susceptible, infected, and immune. According to the relationship between random number r and BRr, the evolution direction of the individual participating in the update is determined, and then the population of the individual is judged according to the evolution’s direction and the change in the fitness value. Although this method is conducive to ensuring the closeness of communication between populations, due to the large difference in the fitness values of different solutions for FJSP, the method will cause the population type to rapidly evolve into an immune type, fall into the local optimal solution, and lose its global search ability. In the iterative process of the algorithm, generating an illegal solution is an extreme waste of computing power. First, producing an illegal solution represents an invalid search. Second, illegal solutions need to be checked. Finally, the illegal solution needs to be corrected or replaced. Therefore, this paper combines the POX and MPX crossover operation based on a single-job machine selection code to redesign the multi-population update method of the CHIO algorithm in order to avoid illegal solutions.

This paper still divides the population into three types: susceptible, infected, and immune. When the random number is $r\le BRr$, the individuals participating in the update communicate within the population; when the random number is $r>BRr$, the individuals participating in the update communicate between the populations. Individual participation updates do not change the types. Inspired by the spreading power of novel coronavirus and considering the characteristics of POX and MPX operations, the HCHIO algorithm performs gene evolution at different magnitudes among different populations. The base size of set $s_1$ divided in the first step of the operation determines the extent of gene evolution. The new coronavirus spreads faster among susceptible populations, followed by infected and immune populations. To this end, this paper sets the bases of $s_1$ in susceptible, infected, and immune populations as $int(n/2)$, $int(n/3)$, and $\mathrm{i}\mathrm{n}\mathrm{t}\left(n/4\right)$, respectively, to simulate the difference in the transmission speed of the new coronavirus in order to achieve the multi-scale solution space search. The updated formula of the multi-population mechanism is shown in Formula (8).

$$x^j(t+1)\leftarrow \{\begin{array}{l}P{M}_{s_p}(x^j(t),p_2^{(1)}),r\le BRrtype(x^j(t))=1\\ P{M}_{s_m}(x^j(t),p_2^{(0)}),r\le BRrtype(x^j(t))=0\\ P{M}_{s_g}(x^j(t),p_2^{(2)}),r\le BRrtype(x^j(t))=2\\ P{M}_{s_r}(x^j(t),p_2),r>BRr\end{array}$$

(8)

In Formula (8), $type(x)$ is the function that obtains the population to which the current individual belongs, and the corresponding variables of susceptible, infected, and immune populations are 1, 0 and 2, respectively. $p_2^{(1)}$ indicates that the selection type is “1”; that is, the susceptible-type individual is used as the second parent; ${PM}_{s_p}(x^j(t),p_2^{(1)})$ indicates that the cross operation is performed on $x^j(t)$ and $p_2^{(1)}$ according to $s_p$. Among them, $n$ is the total number of jobs; $\left|s_p\right|=\frac{n}{2}$, $\left|s_m\right|=\frac{n}{3}$, $\left|s_g\right|=\frac{n}{4}$, $\left|s_r\right|$ is a random integer, which is in $\left[2,n-2\right]$; $p_2$ stands for any type of individual.

In the traditional CHIO algorithm, individual $j$ participating in the update performs genetic evolution on the individuals of other populations. However, there is a flaw here. This is a one-way type of genetic evolution; that is, this process of evolution only occurs on individual $j$. In this gene exchange, the population will not learn the dominant genes of individual $j$. This is contrary to the theory of evolution in nature, and learning should be mutual. Additionally, in the mainstream crossover operation [28,29], the greedy strategy is often used to replace the current individual from the two offspring individuals. Although this operation is beneficial to the convergence of the population, it reduces the diversity of the population and easily falls into a local optimum. To this end, this paper proposes a collaborative learning mechanism to enrich population diversity while ensuring convergence. In the second paragraph of Section 4.4, it has been demonstrated that the $p_1$ individual participating in the update retains some of the original genes and only learns part of the genes of the $p_2$ individual. Therefore, in the collaborative learning mechanism, the $p_1$ individual is only compared to $c_1$. This explains whether the $p_1$ individual learns genes better from the $p_2$ individual or not. In the same manner, $p_2$ is only compared to $c_2$, which explains whether the $p_2$ individual learns genes better from the $p_1$ individual or not. The specific details of the multi-population update mechanism based on collaborative learning are referred to in Algorithm 1.

Algorithm 1. Multi-population update mechanism based on collaborative learning

Input: population to be updated: $P\left(t\right)$, basic reproductive rate: BRr, population size: pop_size Output: updated population $P\left(t+1\right)$ 1: for j = 1: pop_size do 2:  $p_1\leftarrow x_j$ 3:  if $r\le BRr$ then 4:   if $x_j$ is susceptible individuals then 5:    select $x_k$ from the susceptible population, randomly select $s_1$ of size $\mathrm{i}\mathrm{n}\mathrm{t}(n/2)$ 6:   elif $x_j$ is infected individuals then 7:    select $x_k$ from the infected population, randomly select $s_1$ of size $\mathrm{i}\mathrm{n}\mathrm{t}(n/2)$ 8:   else 9:    select $x_k$ from the immune population, randomly select $s_1$ of size $\mathrm{i}\mathrm{n}\mathrm{t}(n/4)$ 10:   end if 11:  else 12:   select $x_k$ randomly, select $s_1$ randomly 13:  end if 14:  $p_2\leftarrow x_k$, according to $s_1$, perform POX and MPX operations on $p_1$ and $p_2$ to obtain $c_1$ and $c_2$ 15:  if $c_1$ is superior to $p_1$ then 16:   $x_j\leftarrow c_1$ 17:  end if 18:  if $c_2$ is superior to $p_2$ then 19:   $x_k\leftarrow c_2$ 20:  end if 21:  $\mathrm{j}\leftarrow \mathrm{j}+1$ 22: end for

4.5. Adaptive Mutation

Since its discovery, the new coronavirus has multiple branches around the world, which shows that the new coronavirus has a strong ability to mutate. In the later stage of the new crown pandemic, the virus’s ability to cause diseases becomes weaker, and this can be roughly summarized as a “weakening mutation ability”. The traditional CHIO algorithm only includes gene exchange between viruses, and it does not include the search method for mutations to generate new genes. This paper proposes an adaptive mutation operation to simulate the mutation evolution of the new coronavirus. The mutation operation is introduced to enrich population diversity and expand the search space. Operation coding and machine coding perform forward insertion mutations and machine random selection mutations, respectively. The specific steps of adaptive mutation operations are shown in Figure 5.

Figure 5. Adaptive mutation.

Forward insertion mutation: combined with the coding method in this article, in order to improve the effectiveness of the mutation, the forward insertion operation moves the current job number to the front of the first job number, which is different from the current job’s number.

Machine random mutation: Any machine from the optional machines of the current operation is randomly selected to replace the current machine.

On the basis of the mutation operation, nonlinear mutation factor $d$ is embedded to realize the adaptive adjustment of the mutation ability, and it balances the global search and local search capabilities of the algorithm. The updated formula of the nonlinear variation factor is shown in Formula (9):

$$d=d_{min}+\left(d_{max}-d_{min}\right)·[1-{(\frac{e^{\frac{t}{T}}-1}{e-1})}^{\beta }]$$

(9)

In Formula (9), $d, d_{max}$, and $d_{min}$ represent the mutation rate, the maximum value and the minimum value of the mutation rate, respectively. $t$ represents the current iteration number. $T$ is the maximum iteration number of the population, $\beta$ is a hyperparameter, and the recommended value is selected within the range of $\left[0.75,2\right]$.

4.6. Knowledge-Driven Variable Neighborhood Search

The neighborhood search strategy is based on the current solution, and it conducts a local fine search on the solution space near the current solution to find a better solution and fully exploit the potential of the current solution. The neighborhood search can effectively improve the quality of the solution, but there are many constraints in FJSP: The solution space is large and complex, and it is difficult to determine an effective and better neighborhood structure. Many scholars have designed neighborhood structures such as insertion, replacement, pseudo-random, and critical path [5,10,30,31] for this problem. However, these effects are not satisfactory. This paper proposes a knowledge-driven variable neighborhood search strategy for the directional and efficient search of process neighborhoods.

Knowledge 1: Knowledge 1 comprises the critical path. A feasible FJSP scheduling scheme can be represented by a disjunction graph [32]. The disjunctive graph is a directed acyclic graph, and the path corresponding to the maximum makespan is the key path of the disjunctive graph. Neighborhood search is used to optimize the neighborhood structure of the disjunctive graph. Although there are many neighborhood structures in current disjunction graphs, most are invalid neighborhoods. Only the neighborhood search for the critical path can change the scheduling objective, which is an effective search.

Knowledge 2: Knowledge 2 comprises the minimum processing time. The problem studied in this paper is the process flexibility of the operation, and the processing time of each operation on the optional machine is different. From qualitative analyses, it can be concluded that when all operations are processed on the machine corresponding to the shortest processing time, the maximum makespan is relatively smaller. Accordingly, the processing machine of the operations on the critical path can be replaced with the machine corresponding to the shortest processing time.

Knowledge 3: Machine utilization. From a global point of view, a high parallel state represents a more reasonable coordination of the machine system. That is to say that when the utilization rate of a certain machine is low, resources may be wasted. Accordingly, the operation on the critical path can be allocated to the machine with the lowest utilization rate; then, this operation can be reasonably arranged in combination with active scheduling decoding.

Using the knowledge of the current scheduling scheme, the knowledge-driven variable neighborhood search strategy can realize the directed neighborhood search. The specific implementation details of the search strategy are referred to in Algorithm 2.

Some variables are involved in Algorithm 2, and they need to be introduced in advance. N is an integer with a value that is the sum of operations contained in each job. C is a table; by visiting this table, we can obtain the set of optional machines for each operation and the corresponding processing time.

Algorithm 2. Knowledge-driven Variable Neighborhood Search

Input: current solution $x_j$, total number of operations N, optional machine table C, Output: new solution $x_j$ after knowledge-driven variable neighborhood search 1: Perform active scheduling decoding on $x_j$ to obtain a scheme and convert it into a disjunction graph, then get critical path table P and machine utilization table U 2: $temp\leftarrow x_j$ 3: for i = 1: N do 4:  if $temp\left(i\right)$ in P then 5:   if $rand\le 0.1$ then     Get the optional machines set S of $temp\left(i\right)$     Visit U and select the machine $LU$ with the lowest utilization rate from S     Visit C and select the machine $LP$ with the lowest processing time from S 6:    if $temp\left(i\right)$ is processed on $LP$ then 7:     $temp\left(i+N\right)$ $\leftarrow$ $LU$ 8:    elif $temp\left(i\right)$ is processed on $LU$ then 9:     $temp\left(i+N\right)$ $\leftarrow$ $LP$ 10:   else 11:     Randomly $temp(i+N)$ $\leftarrow LU$ or $LP$ 12:    end if 13:   end if 14:  end if 15:  $i\leftarrow i+1$ 16: end for 17: if $temp$ is superior to $x_j$ then 18:   $x_j\leftarrow temp$ 19: end if 20: return $x_j$

4.7. HCHIO Algorithm Framework

According to the characteristics of the FJSP, this paper redefines the population update mechanism on the basis of the traditional CHIO algorithm and proposes the concept of “cooperative learning” to ensure convergence and improve population diversity. The adaptive mutation operation is introduced to enrich the diversity of the population, expand the local search space of the current individual, and reasonably balance the global search and local search capabilities. A knowledge-driven variable neighborhood search strategy is proposed to fully tap the advantages of the current solution and realize effective neighborhood search. The basic steps of the algorithm are as follows:

Step 1: The algorithm parameters are set, the population is initialized randomly, and the population is divided into three sub-populations according to fitness.

Step 2: According to the relationship between random number r and BRr, the multi-population update operation is performed based on collaborative learning.

Step 3: According to a certain probability, the adaptive mutation operation on the individuals in the population is carried out one by one, and if the individual after the mutation is better than the original individual, the original individual is replaced.

Step 4: Empirical knowledge is calculated based on the scheduling scheme corresponding to the current individual, a knowledge-driven variable neighborhood search strategy is executed, and the best individual is selected and retained.

Step 5: the age of the individual is updated, the death operation is executed on the individual that reaches the maximum age, and a new individual is generated to replace the dead individual.

Step 6: Whether the number of population updates reaches the maximum value is determined. If it is not determined, step 2 follows; otherwise, step 7 follows.

Step 7: The algorithm ends.

The overall framework of the HCHIO algorithm is shown in Figure 6.

Figure 6. Framework of the HCHIO algorithm.

4.8. Algorithm Complexity Analysis

The HCHIO algorithm mainly includes three stages: the multi-population update mechanism based on collaborative learning, the adaptive mutation operation, and the knowledge-driven neighborhood search strategy. For a clear description, the following definitions are available: the code length of an individual is 2l, the population size is pop_size, and the number of iterations is epoch. One point that needs to be explained is that, according to the previous introduction, when the total number of operations is l, the code length is 2l; thus, the complexity of our algorithm is closely related to the specific case.

POX and MPX crossover operations are used in the multi-population update mechanism. Two parent individuals need to be selected for both operations. Both parents need to be traversed once, and the coding method comprises two-stage coding. Therefore, the complexity of the multi-population update mechanism is described in Formula (10):

$$\mathrm{O}\left(l\right)·2+\mathrm{O}\left(l\right)·2$$

(10)

The adaptive mutation operation performs mutation operations on genes at multiple sites. In order to ensure the effectiveness of the pre-insertion mutation in the operational segment, the forward insertion mutation operation needs to find a gene that is different from the gene waiting to mutate. The machine mutation comprises a random selection mutation; thus, the complexity degree of this stage in the worst case is calculated using Formula (11).

$$\mathrm{O}\left(l·l\right)+\mathrm{O}\left(l\right)$$

(11)

The complexity in the best case is Formula (12).

$$\mathrm{O}\left(l·1\right)+\mathrm{O}\left(l\right)$$

(12)

The variable neighborhood search strategy first needs to calculate the cumulative knowledge of the current scheduling scheme; then, it executes the neighborhood search operation based on empirical knowledge. The algorithm complexity is described in Formula (13):

$$\mathrm{O}\left(2l\right)+\mathrm{O}\left(l\right)$$

(13)

The above operations are performed on each individual in the population, and the complexity of the HCHIO algorithm is described in Formula (14):

$$\left(\mathrm{O}\left(l\right)·2+\mathrm{O}\left(l\right)·2+\mathrm{O}\left(l·l\right)+\mathrm{O}\left(l\right)+\mathrm{O}\left(2l\right)+\mathrm{O}\left(l\right)\right)·pop\_size·epoch=O\left(l^2\right)·pop\_size·epoch$$

(14)

5. Experimental Analysis

All experimental algorithms in this paper are programmed using Python language and run in the Windows 10 system and the Python version 3.8 environment. The computer hardware configuration is as follows: Intel Core i7-10700 CPU @2.9GHz and RAM 16GB. This paper chooses Brandimarte’s [33] benchmark and Hurink’s benchmark [34] to verify the performance of the HCHIO algorithm. Brandimarte’s benchmark is used the most in the papers we read, so we have chosen it as the main data set of this article. Brandimarte’s benchmark contains 10 cases named MK01-MK10, including various cases ranging from simple to complex; thus, it has been used by many scholars. The specific details of this benchmark are given in Table 2. Aiming at the problem of large differences in the makespan of different data sets, the relative percentage deviation (relative percentage deviation, RPD) index is introduced to uniformly measure the performance of the algorithm. The calculation formula of RPD is shown in Formula (15).

$$RPD=\frac{Get-Best}{Best}·100\mathrm{\%}$$

(15)

Table 2. Specific details of Brandimarte’s benchmark.

Test Cases	The Total Number of Jobs	The Total Number of Machines	The Total Number of Operations	Freedom
MK01	10	6	55	2
MK02	10	6	58	3.5
MK03	15	8	150	3
MK04	15	8	90	2
MK05	15	4	106	1.5
MK06	10	15	150	3
MK07	20	5	100	3
MK08	20	10	225	1.5
MK09	20	10	240	3
MK10	20	15	240	3

In Formula (15), Get is the solution obtained by the current algorithm, and Best is the optimal solution obtained by the algorithm in this paper.

5.1. Parameter Settings

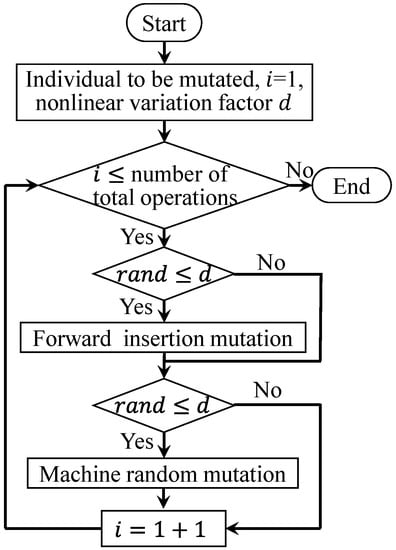
The main parameters in the HCHIO algorithm are epoch, pop_size, BRr, and MA. The variation ratio is set to 0.3 according to the research in the literature [7], and variation degrees $d_{max}$ and $d_{min}$ are set to 0.1 and 0.05, respectively. In order to analyze the influence of the main parameters on the performance of the algorithm, an orthogonal table was generated using Mintab software by creating a Taguchi design. According to the $L_9\left(3^4\right)$ orthogonal table, a four-factor three-level orthogonal experiment is carried out, and the parameter level settings are shown in Table 3.

Table 3. Parameter level.

Level	Parameter
	epoch	pop_size	BRr	MA
1	500	100	0.50	20
2	1000	200	0.65	30
3	1500	300	0.80	40

The MK06 data set (Best = 58) with a relatively moderate total number of jobs and machines is selected for orthogonal experiments. Each group runs independently 10 times in the MK06 environment, and the RPD index of the average makespan is calculated. The parameter settings of different experimental groups and the RPD index of the algorithm are shown in Table 4. According to the RPD values of each group of experiments in the orthogonal table, the response values and response graphs of different parameters relative to the algorithm’s performance can be obtained. The results are shown in Table 5 and Figure 7.

Table 4. Orthogonal tables and RPD values.

Number	Parameter				RPD
	epoch	pop_size	BRr	MA
1	1	1	1	1	0.068966
2	1	2	2	2	0.056897
3	1	3	3	3	0.072414
4	2	1	2	3	0.058621
5	2	2	3	1	0.048276
6	2	3	1	2	0.032759
7	3	1	3	2	0.058621
8	3	2	1	3	0.051724
9	3	3	2	1	0.029310

Table 5. Parameter response value.

Level	Parameter
	epoch	pop_size	BRr	MA
1	0.066092	0.062069	0.051149	0.048851
2	0.046552	0.052299	0.048276	0.049425
3	0.046552	0.044828	0.059770	0.06092
Range	0.019540	0.017201	0.011494	0.012069
Rank	1	2	4	3

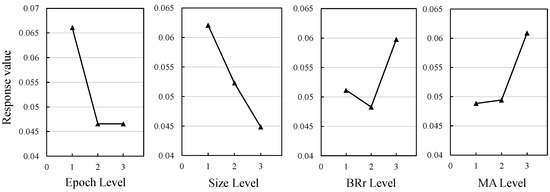
Figure 7. Parameter response plot.

From the analysis in Table 4, it is observed that epoch and pop_size have a greater impact on the algorithm, while BBr and MA have less impact. In Figure 7, the parameter levels corresponding to the smaller response value are better. In the Epoch Level diagram, the response values of levels 2 and 3 are smaller than level 1, indicating that a larger epoch is more conducive to optimization. However, the epoch response values of levels 2 and 3 are similar, indicating that at level 2, the performance of the algorithm has converged and stabilized. Similarly, in the size level response value diagram, it can be concluded that the larger the population size, the more conducive it is to finding the optimal solution. However, larger populations require more computing power. The optimal parameter level for BRr is level 2. For the MA parameters, the response values of level 2 and level 1 are not that different, indicating that the performance of the parameters of these two levels is similar to the MK06 data set.

Considering the characteristics of randomness in the swarm intelligence algorithm, the fact that the MK06 data set is a medium data set, and the running time of the algorithm, the parameters of the algorithm in this paper are uniformly set as follows: epoch = 1000, pop_size = 200, BRr = 0.65, and MA = 30. Given the fact that the size of the MK06 data set is 10 × 15 and the size of the MK10 data set is 20 × 15, combined with the analysis of the convergence curve during the experiment, epoch = 1500 of the MK10 data set is reset, and the other parameters are kept unchanged.

5.2. Verification of the Effectiveness of Innovations

This paper carries out a series of improvements relative to the traditional CHIO algorithm, and these improvements are in line with the characteristics of FJSP. The main innovations include the following: a multi-population update mechanism for collaborative learning, adaptive mutation, and a variable neighborhood search strategy that is knowledge-driven. In order to verify the effectiveness of innovation points, the following algorithm settings are now implemented. CHIO represents the traditional floating-point version of the CHIO algorithm. CHIOc abandons the floating-point number update method and incorporates the CHIO algorithm based on the multi-population update mechanism using collaborative learning. CHIOcm is a CHIOc algorithm with adaptive mutation operations. HCHIO (CHIOcmv) is an added CHIOcm algorithm based on the knowledge-driven variable neighborhood search strategy. The above algorithms are run 10 times (one by one) using Brandimarte’s cases, and the performance of the algorithm is evaluated using the four indicators of Opt, Avg, RPD, and Time. Opt represents the optimal solution obtained by the algorithm, Avg is the average makespan of running 10 times, RPD is the relative percentage deviation of Avg, and Time is the running time required for one iteration of the algorithm (unit: s).

As shown in Table 6, the bold font in the table is the optimal value of Opt and Avg. The traditional CHIO is updated in the floating-point number domain. This paper uses a discrete mapping scheme to convert the floating-point number into a shop-floor scheduling scheme, but the resulting RPD is large, which verifies that the solution space search in the floating-point number domain is unsuitable for the FJSP when using the CHIO algorithm. The main reason is that the floating-point number search method is inefficient, and retaining the characteristics of dominant genes is difficult. Compared with the CHIO algorithm, the RPD index of the CHIOc algorithm is greatly reduced, which fully demonstrates the rationality and effectiveness of the update method designed in this paper, and the update in the discrete domain is less time-consuming and more efficient than the floating-point number domain. After adding the adaptive mutation operation on the CHIOc algorithm to obtain the CHIOcm algorithm, although the RPD value did not decrease significantly, the mutation operation produced better solutions on MK04, 06, 07, and 10, which verified that the mutation operation can produce excellent genes and expand the search space of the current solution. The HCHIO (CHIOcmv) algorithm achieves the optimal mean value in all cases, which fully demonstrates the effectiveness of the neighborhood search knowledge used. As it is different from relying on the random method to introduce good genes, the neighborhood search method in this paper uses knowledge-driven methods to realize the directional search of the solution space in order to achieve the optimal value in all calculation examples. Figure 8 shows the convergence curves of the optimal solutions of all CHIO-based algorithms in each case of Brandimarte’s benchmark. It can be observed from the figure that HCHIO has a stronger searchability for the optimal solution and a faster convergence speed. The convergence details of all the above algorithms are shown in Figure 8.

Table 6. Verification of the effectiveness of innovation points.

Test Cases	CHIO				CHIOc				CHIOcm				HCHIO (CHIOcmv)
	Opt	Avg	RPD	Time	Opt	Avg	RPD	Time	Opt	Avg	RPD	Time	Opt	Avg	RPD	Time
MK01	45	47.9	19.8	0.42	40	40	0.0	0.26	40	40	0.0	0.34	40	40	0.0	0.47
MK02	42	43.3	66.5	0.43	26	26.8	3.1	0.28	26	26.5	1.9	0.34	26	26.2	0.8	0.52
MK03	282	293.5	43.9	1.07	204	204	0.0	0.85	204	204	0.0	1.17	204	204	0.0	1.61
MK04	82	83	38.3	0.65	62	63.4	5.7	0.44	61	62.7	4.5	0.58	60	62.5	4.2	0.86
MK05	196	201.7	16.6	0.77	173	173	0.0	0.76	173	173	0.0	0.95	173	173	0.0	1.40
MK06	127	134.9	132.6	1.10	62	63	8.6	0.90	60	62.9	8.4	1.11	58	60.3	4.0	1.63
MK07	215	219.1	57.6	0.74	140	141.2	1.6	0.62	139	140.9	1.4	0.77	139	140.1	0.8	1.21
MK08	596	601.3	15.0	1.63	523	523	0.0	1.60	523	523	0.0	2.09	523	523	0.0	2.99
MK09	478	484.5	57.8	1.76	307	307.7	0.2	1.64	307	307	0.0	1.98	307	307	0.0	3.18
MK10	395	405.9	101.9	1.78	217	219.9	9.4	1.59	204	206.7	2.8	1.99	201	205.3	2.1	2.97
Mean			55.0				2.9				1.9				1.2

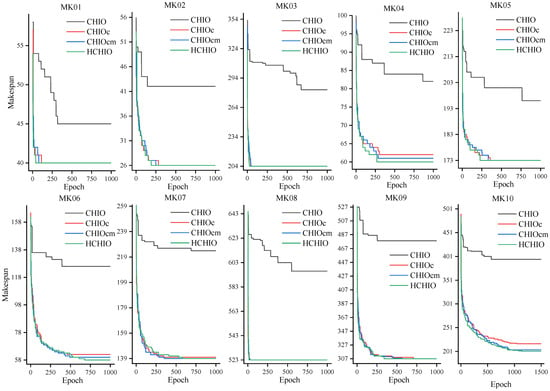
Figure 8. Convergence curves of the optimal solutions of all CHIO-based algorithms on Brandimarte’s benchmark.

5.3. Algorithm Performance Evaluation

In order to verify the effectiveness of the algorithm proposed in this paper, the algorithm proposed in this paper is compared with the hybrid gray wolf optimization algorithm (HGWO) proposed by Jiang [7], the improved particle swarm optimization algorithm (IPSO) proposed by Ding et al. [35], the mushroom picking framework (MPF) proposed by Jędrzejowicz et al. [36], and the hybrid genetic algorithm (HGA) proposed by Sun et al. [6]. The experimental results of these algorithms are all from the corresponding literature.

As shown in Table 7, the bold font in the table is the optimal value of Opt and Avg. Compared with other algorithms, the HCHIO algorithm obtained the optimal solution on all examples in the Opt index, which verified that the HCHIO algorithm can effectively learn the dominant genes during the update course and realize the directional and effective search of the current solution neighborhood. Among them, the optimal solution Gantt charts of MK06 and MK10 are shown in Figure 9 and Figure 10. In the Gantt chart, the blue number in the center below each operation is the processing time of the operation. In terms of the Avg index, the average value of the HCHIO algorithm in the nine cases is the best, which reflects the rationality of the HCHIO algorithm’s update mechanism designed in this paper, which can ensure the diversity of the population while maintaining convergence, and it does not easily fall into a local optimum. However, with respect to the MK04 data set, the HGA algorithm obtained a smaller average value. The reason may be that the adjacent excellent solutions of the MK04 example have a large difference, and this is unsuitable for the update mechanism in this paper. The RPD index shows that the HCHIO algorithm in this paper has the best comprehensive performance, which verifies the effectiveness of the algorithm proposed in this paper.

Table 7. Algorithm performance on Brandimarte’s benchmark.

Test Cases	Size	HGWO			IPSO			MPF			HGA			HCHIO
		Opt	Avg	RPD	Opt	Avg	RPD	Opt	Avg	RPD	Opt	Avg	RPD	Opt	Avg	RPD
MK01	10 × 6	40	41.6	4.0	40	42	5.0	41	41.9	4.8	40	40	0.0	40	40	0.0
MK02	10 × 6	29	30.3	16.5	29	32	23.1	28	28	7.7	26	26.6	2.3	26	26.2	0.8
MK03	15 × 8	204	204.1	0.0	204	204	0.0	204	204	0.0	204	204	0.0	204	204	0.0
MK04	15 × 8	65	67.4	12.3	66	70	16.7	67	67.4	12.3	60	61.4	2.3	60	62.5	4.2
MK05	15 × 4	175	178.2	3.0	175	181	4.6	176	176	1.7	173	173	0.0	173	173	0.0
MK06	10 × 15	79	79.9	37.8	77	84	44.8	69	69	19.0	61	63.5	9.5	58	60.3	4.0
MK07	20 × 5	149	156.4	12.5	145	151	8.6	143	147.9	6.4	140	140.3	0.9	139	140.1	0.8
MK08	20 × 10	523	523	0.0	523	523	0.0	523	523	0.0	523	523	0.0	523	523	0.0
MK09	20 × 10	325	342.3	11.5	347	347	13.0	333	338	10.1	307	309.1	0.7	307	307	0.0
MK10	20 × 15	253	262.7	30.7	256	256	27.4	237	242	20.4	214	216.9	7.9	201	205.3	2.1
Mean				12.8			14.3			8.2			2.4			1.2

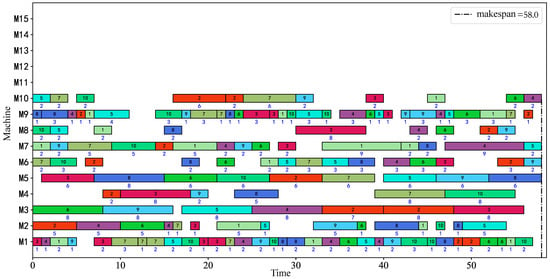
Figure 9. Gantt chart of MK06’s optimal solution (One color represents a job. The blue number below the rectangular block is the processing time).

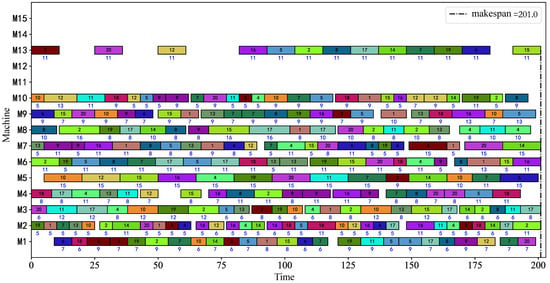
Figure 10. Gantt chart of MK10’s optimal solution (One color represents a job. The blue number below the rectangular block is the processing time).

Although Brandimarte’s benchmark already includes cases of various complexity, in order to fully verify the effectiveness of the algorithm in this paper, by searching other benchmarks of FJSP articles, we selected the Hurink benchmark to test the performance of the algorithm in this paper. The most complex category in this benchmark is Vdata. Thus, we chose the cases from Vdata_la1 to Vdata_la10 for experimentation. For this benchmark, the algorithm parameters of this paper are set as follows: epoch = 1500, pop_size = 200, BRr = 0.65, and MA = 30. The specific experimental results are shown in Table 8. The result of HCHIO is an average of 10 executions. The average results of the regular genetic algorithm (RGA), two-stage GA (2SGA), and deep reinforcement learning (DRL) in the table are all from the literature [32]. It can be observed in the table that the HCHIO algorithm outperforms the DRL and RGA algorithms in almost all aspects in terms of performance. Moreover, the HCHIO algorithm produces a state-of-the-art solution with respect to the current body of research on the la3-la5 cases. However, the performance in other cases is not as good as 2SGA. However, it is worth mentioning that the maximum number of iterations of the 2SGA algorithm is 3000, while the HCHIO algorithm only iterates 1500 times, which is only half of the 2SGA algorithm. The experimental results show that the gap between the HCHIO algorithm and the 2SGA algorithm is small, which fully demonstrates the effectiveness of our algorithm.

Table 8. Algorithm performance on Hurink’s benchmark.

Test Case	RGA	2SGA	DRL	HCHIO
Vdata_la1	577	572	610	576
Vdata_la2	535	532	555	534
Vdata_la3	485	481	532	481
Vdata_la4	510	506	530	504
Vdata_la5	468	463	507	463
Vdata_la6	804	801	820	805
Vdata_la7	756	751	757	754
Vdata_la8	768	766	782	769
Vdata_la9	858	854	879	858
Vdata_la10	808	806	862	808

6. Conclusions

This paper studies the FJSP and proposes an effective HCHIO algorithm based on the traditional CHIO algorithm. Combining the characteristics of the FJSP, this algorithm designs a discretized two-stage encoding and decoding scheme to solve the operation sequencing subproblem and the machine selection subproblem of the FJSP. Then, based on POX and MPX operations, the multi-population update mechanism is redesigned based on collaborative learning so that cross-individuals can collaboratively learn each other’s superior genes. This mechanism can simultaneously ensure the convergence of the algorithm and the diversity of the population. Inspired by the evolution of the new coronavirus, an adaptive mutation operation is proposed to realize dynamic gene mutations and increase the search space of the algorithm. In order to efficiently search for a better solution, this algorithm proposes a variable neighborhood search technology that is knowledge-driven, using the knowledge of critical paths, processing times, and machine utilization to realize the directional and effective search of the neighborhood solution space. Finally, the benchmark calculation example is tested and compared with other algorithms to verify the effectiveness of the algorithm proposed in this paper.

The next research plan Is as follows: (1) By combining the characteristics of the FJSP, we intend to dig deep into diversified mutation operations and search for dominant genes from different angles; (2) we continue to expand upon the empirical knowledge used in neighborhood search in order to achieve a more efficient neighborhood space search.