Abstract
The Renovation Wave for Europe initiative aspires to materialize the progressive greening of 85–95% of the continental older building stock as part of the European Green Deal objectives to reduce emissions and energy use. To realistically predict the energy performance even for a single apartment building is a difficult problem. This is because an apartment unit is inherently a customized construction which is subject to year-round occupant use. We use a standardized energy consumption response approach to accelerate the setting-up of the problem in pertinent energy engineering terms. Nationally instituted Energy Performance Certification databases provide validated energy consumption information by taking into account an apartment unit’s specific shell characteristics along with its installed electromechanical system configuration. Such a pre-engineered framework facilitates the effect evaluation of any proposed modifications on the energy performance of a building. Treating a vast building stock requires a mass-customization approach. Therefore, a lean-and-green, industrial-level problem-solving strategy is pursued. The TEE-KENAK Energy Certification database platform is used to parametrize a real standalone apartment. A supersaturated mini dataset was planned and collected to screen as many as 24 controlling factors, which included apartment shell layout details in association with the electromechanical systems arrangements. Main effects plots, best-subsets partial least squares, and entropic (Shannon) mutual information predictions—supplemented with optimal shrinkage estimations—formed the recommended profiler toolset. Four leading modifications were found to be statistically significant: (1) the thermal insulation of the roof, (2) the gas-sourced heating systems, (3) the automatic control category type ‘A’, and (4) the thermal insulation of the walls. The optimal profiling delivered an energy consumption projection of 110.4 kWh/m2 (energy status ‘B’) for the apartment—an almost 20% reduction in energy consumption while also achieving upgrading from the original ‘C’ energy status. The proposed approach may aid energy engineers to make general empirical screening predictions in an expedient manner by simultaneously considering the apartment unit’s structural configuration as well as its installed electromechanical systems arrangement.
1. Introduction
Improving the energy efficiency of the existing building stock has been given high priority in the European Green Deal [1]. On track to a climate neutral Europe by 2050, the ‘Renovation Wave for Europe’ initiative [2,3] calls for the progressive greening of 85–95% of the older building stock by reducing emissions and energy use. The imposing of such an emphasis on construction processes has transpired because 40% of the energy consumption and 36% of the energy-related greenhouse gas emissions in Europe are attributed to buildings [4,5,6]. Consequently, the ‘Renovation Wave for Europe’s aim is to campaign for action now in order to improve the energy consumption for a forecasted number of 35 million inefficient buildings by 2030; the initiative anticipates adherence to the target of reducing emissions by at least 55%. Meanwhile, the overall decarbonization of the heating and cooling processes are, of course, in direct alignment to the broader global sustainability goals as they are promulgated through the United Nations 17 Sustainable Development Goals (SDGs) [7]. Specifically, the impact of attaining several interlacing SDGs, such as Goal #7 (affordable and clean energy), Goal #11 (sustainable cities and communities), Goal #12 (responsible consumption and production), and Goal #13 (climate action), is envisaged through new-age, digitalized, and smarter home management, which is prognosticated to enhance the overall quality of life of the population.
Incentivizing green construction through effective government policies has shown promise through the concept of the Leadership in Energy and Environmental Design (LEED) certifications [8,9,10,11,12,13,14]. The Minimum Energy Performance (MEP) standards for existing buildings are formalized through the Energy Performance of Building Directive (EPBD). The Energy Performance Certificates (EPCs) are instituted on a national level; in essence, they encourage “progressive renovations over the lifetime of a building” through the establishment of the Building Renovation Passports (BRPs). The EPC is the rating output from a green-building certification system that assesses an apartment unit’s performance by employing a lifecycle method that considers specific design, construction, and operation details, while upholding the emphasis of quality on the environmental and sustainability perspectives [15].
To tackle the many barriers that hinder a realistic and optimized prediction of the year-round energy consumption of older-building apartment units, innovative solutions may be facilitated by the introduction of data-centric engineering know-how. Old-building stock renovation projects rely on suitable retrofitting modeling instruments that usually address the whole building as a problem [16,17,18,19,20,21,22,23,24]. From an energy engineer’s point of view, retrofitting is essentially a screening-and-optimization energy-performance exercise which is characterized by high complexity. To be pragmatic, the retrofitting optimization problem’s complexity should be simplified, as it is known to implicate contributions of uncertainty from the structural details of the examined apartment unit, its electromechanical systems configuration, the unit’s actual demands on annual local weather conditions, and indigenous occupant behavior tendencies [25,26,27,28,29,30,31,32,33]. A sophisticated multicriteria software tool is often necessitated in order to simulate and analyze improvement opportunities for various types of energy leaks, such as to prioritize the retrofitting tasks while paying heed to green considerations [34,35,36,37,38,39,40,41,42,43]. Of course, it is anticipated that the energy professional in charge of the retrofitting project should be skillful and knowledgeable in several areas of expertise, including designing and computing, to handle empirical modelling and complicated forecasts. Conducting optimization simulations for large buildings is becoming more common owing to simplification of the apartment unit problem, which allows for the relaxing of some technical assumptions. On the other hand, the energy-consumption optimization of micro- and small-scale systems is more perplexing to carry out than larger ones, because of constraints arising from unit-to-unit differentiation within a building, thus allowing the technical variability of these systems to be deemed substantial [44]. Moreover, an apartment renovation task is a more stringent problem to simulate because the energy efficiency optimization procedure may interrupt the current unit’s energy distribution practices. Nevertheless, the model calibration may be conducted on a standardized framework to be convincing and meaningful [45,46]. A major issue that arises from evaluating sustainable retrofits—key to successfully advancing the renovation process—is related to the optimal profiling of alternative retrofit scenarios [47,48,49,50,51]. The synchronous simplification of the complexity in the considered energy system is congruent to the extent of customization at the apartment unit level.
The novelty of this work rests on the notion that screening and optimizing the energy performance for an apartment unit may be facilitated after adopting the Lean Six Sigma initiative, a contemporary manufacturing philosophy which is applied to improving products, processes, and services by instituting a holistic and datacentric engineering strategy [52,53]. While the green Lean Six Sigma initiatives have been launched in the construction industry, instructive paradigms for the screening and optimization of energy performance studies are lacking [54,55]. The examined problem is an excellent paradigm of greening the energy consumption of a building by customizing the optimization solution at the point of interest, which is the apartment unit. The proposed tactic fosters a duality that merges lean thinking and quality improvement [56]. The lean and green aspects of a study are aligned to effectuate the sustainability aspect in a circular process [57,58,59,60,61,62,63,64]. The lean and green objectives are accomplished by: (1) screening and optimizing the reduction in an apartment unit’s energy consumption, and (2) introducing lean thinking into the problem-solving process itself. The benefits of the former objective are immediately evident: (1) lower overall energy demand, (2) lower gas emissions, and (3) lower bottom-line energy costs per apartment unit [65,66,67]. The latter objective may be viewed as more subtle because it regards the energy and resource commitment in order to research the problem. The lean thinking approach is applied in such a fashion as to greatly reduce the amount of work that is necessary to carry out this project. To be a practical and expedient project, it is necessary to save time and resources, thus shortening the data collection cycle. This effort appears innately time-consuming, because year-round data would be necessitated for a building energy-performance study to be rendered pertinent. Quite possibly, a simulation study would be valuable in understanding the mechanisms that regulate the energy distribution within an apartment [68,69,70,71,72,73,74,75,76]. The complete description of the inherent energy physics that govern the heat flow and the electricity distribution, across the installed electromechanical systems in a real apartment unit, would absorb a lot of resources and knowledge because the multifarious sources of uncertainties should also be accounted. Even so, it would be meaningful only for that specific single customized case. A more general method that relies on standardized data is greatly desirable to heed the practical aspect of the application; method agility and reliability are construed to be attractive features in product/process improvement studies.
To counter the perceived complexity surrounding the data collection part, the proposed methodology orients toward a strategy that draws valid data from a national Energy Performance Certification database [77,78]; it is a standardization output that has been established to track down the decarbonizing progress of existing building stocks. In this manner, the year-round energy parametrization of residential buildings is accomplished by considering the customized structural and electromechanical systems requirements, which are matched to their performances according to standardized specifications. Since the national Energy Performance Certification database holds an immense amount of customized and validated operational coefficients and parameters, any ensuing energy performance analysis is certainly amenable to any residential apartment unit. In Greece, an EU member state, this is transacted by the mandatory government-instituted Energy Certification program that permits, through a software platform, the TEE KENAK (1.31.1.19), the standardized parametrization of existing residential buildings [79,80]. The TEE KENAK software allows energy engineers to extract a vast amount of information in order to conduct energy studies which can lead to awarding an official certification of the energy consumption status to any residential apartment unit. It is on the TEE KENAK database that the energy consumption reduction will be carried out in this investigation.
An energy performance improvement study is a difficult task to undertake because there are, intrinsically, many controlling factors that should be considered. This is easily comprehended by merely interacting with the Energy Performance Certification software, which expects many building layout and operation parameters to be fed into the program [14]. Consequently, a design of experiments (DOE) plan [81,82] should involve a large number of controlling factors that are usually not convenient to program. Further, there is an enormous number of parameter setting combinations that should be organized which, in turn, is followed by the serial execution of the resulting factorial recipes on the Energy Performance Certification software. If this software is to be a realistically useful tool to an energy engineer, who regularly embarks on such renovation improvement studies, a more sophisticated data planning approach should be deployed. Industrial-level trial scheduling which allows for the implementation of an efficient DOE sampling scheme becomes imperative in such a situation [83,84]. Supersaturated factorial samplers, which are often used in large industrial studies, are very appealing because they allow for the disproportional screening of many controlling factors by extracting information from a modest number of data points which is much less than the number of screened factors [85,86,87,88,89,90].
Interestingly, it was suggested that it may be practical to pace the retrofitting process of older residential buildings by examining them on an apartment unit basis [91]. By taking advantage of the construction-design modularity and the comprehensive information on the electromechanical systems configuration, which are stored in the national building certification register platforms, EPC-generating software packages may be utilized to conveniently screen and optimize the energy-consumption performance of any residential apartment unit. Besides granting a green energy-efficiency rating to a residential structure, an EPC authentication is also accompanied with a MEP standard, which is a customized estimation for the particular apartment unit. Therefore, MEPs may be taken as consistent improvement yardsticks that could guide the apartment unit’s future renovation actions. MEPs summarize the yearly-weighted energy performance of a residential structure in a single estimation. A recently published case study on the retrofitting of an apartment unit in a residential building has demonstrated the usefulness on implementing EPC-created information to advance design of experiments (DOE) in order to screen a sizable number of exclusively electromechanical-system controlling factors [91]. The intention was to research a single apartment in a residential building, in which case each floor corresponded to a single apartment unit. The main objective was the minimization of the energy consumption of the single apartment unit which was situated at the highest floor. It became evident that it is a difficult task to successfully simulate an approximate distribution of the energy demands of an apartment unit under year-round realistic operating conditions. By considering the factual structural layouts and electromechanical systems operating information, simulations may be additionally hampered by the inherent high complexity of the problem which relies heavily on the interplay of the specifics of the installed electromechanical systems against the apartment unit’s real architectural details. To circumvent the exigent task of screening as many as 24 electromechanical controlling factors, Rousali and Besseris [91] developed an empirical tool that facilitated the estimation of the contributions of the screened strong factors from their regression analysis after pre-treating all of the factors according to their location and dispersion tendencies, using a modified Matrix Data Analysis Chart (MDAC) tool; the MDAC shortened the initial list of factors to a mere few that statistically outperformed the rest.
The challenge for this work is three-fold in terms of the newly introduced case study features: (1) attempt a screening study on a real single-family home, (2) introduce building shell components in the controlling factor list, (3) use tools that are directly accessible from mainstream statistical software packages, (4) extend the data analysis to implicate more advanced statistics. In comparison to the study by Rousali and Besseris [91], this proposal has several novelties. Firstly, it utilizes the latest version of the TEE KENAK software, since the previous publication was based on a software version which is now a decade old. This means that the updated version, which is utilized for this work, is commensurate to the current reality of using and operating a more modern apartment unit. Thus, there will be access to a more mature EPC platform in synergy with a more comprehensive and accurate database. Second, the study by Rousali and Besseris [91] ignored contributions from the unit’s shell properties. This weakness is remedied in this new attempt. Third, the overall type of building structure that will be studied here is significantly different from the apartment building studied in reference [91]. This means that a new and challenging case study is added in a very critical research area that now has commenced to investigate how to improve building’s energy performance—an objective that is highly prioritized by the EU. Finally, a new analysis methodology is suggested to alleviate the customized approach that was presented by Rousali and Besseris [91]. This means that only simple techniques are used which are immediately available to commercial and freeware statistical analysis software.
The developments of this paper are organized as follows. Next, the Materials and Methods section elucidates the technical description of the shell structural details and the installed electromechanical systems of the modeled apartment unit, along with the supersaturated data planning, collection, and analysis steps that also describe the computational support toolbox. The Results section provides the collected supersaturated dataset which was obtained by manipulating the apartment unit parameters on the TEE-KENAK platform. Subsequently, the factorial screening and optimization solutions are presented in a cooperative application of response graphs/tables and linear regression techniques. In the Discussion section, a peripheral analysis is appended to explore the validity of the predictions using partial least squares, analysis of variance, entropic representations, and hierarchical clustering treatments. Descriptive statistics, correlation analysis, and nonparametric comparisons complete the prediction validation of the proposed methodology. In the Conclusion section, the key findings are summarized and recommendations for further research are provided.
2. Materials and Methods
2.1. Technical Description of the Studied Building Apartment Unit
2.1.1. Basic Location and Energy Consumption Status Information for the Building Apartment Unit
The residential building that is modelled for this study is located in a suburban area in proximity to the city of Athens (Greece). The construction was erected in the year 2004. Regionally, the district is situated within Climate Zone “B” in Greece. For the particular apartment unit, the thermal space that will be examined has been projected to be a surface area of 174.90 m2. Based on the national cumulative statistics from the estimations on the issued Energy Performance Certificates, 83.82% of the residential buildings which have been constructed before the year 1980 (55% of the total available building stock) have been awarded an energy consumption status of ‘H’. Even for more contemporary buildings such as the one that will be analyzed in this work, the majority of the energy performance ratings have been categorized as either a ‘C’ or ‘D’ class. The particular apartment unit was certified to require a year-round primary energy consumption of 133.8 kWh/m2. This was compared against a (theoretical) reference-building energy demand of 129.2 kWh/m2. The ratio of the two energy consumption estimations (the former over the latter) provides a measure for the energy efficiency. Since the estimated energy efficiency corresponds to the standardized interval (1.00, 1.41), it was awarded a rating status of ‘C’. This study is meaningful because, to reach the desired transitory ‘yellow zone,’ the energy efficiency score should lie within the standardized interval (0.75, 1.00), which corresponds to an energy consumption grade of ‘B’. The top rating (class ‘A+’) is awarded for energy efficiency scores lower than 0.33. However, the ‘green’ status for a residential building is awarded upon certification after attaining at least a ‘B+’ rating, which corresponds to an energy efficiency standardized interval of (0.50, 0.75). Therefore, any recommended improvement interventions should lead, at least, to climbing up to the ‘yellow zone’ scale, before any apartment renovation gains become substantial enough to contribute to the ‘greener outlook’ of the building’s energy performance. Ostensibly, the respective intervention costs, the financial status of the apartment owners/occupants, and any potential government incentives may affect the pace of progress toward reaching an enhanced green building status.
2.1.2. Apartment Unit Structural Details
The complete layout for the apartment unit structure has been drawn in Figure 1 (AutoCAD, Autodesk, San Francisco, CA, USA). The building shell details have been tabulated in Table 1 [92]. They are required inputs for the software package TEE-KENAK (1.31.1.19) [79,80], which evaluates the energy consumption compared to a reference building, such that an energy performance certification can be issued. The case study is typical of a single-family (raised) residential unit with six rooms; two rooms (#1 and #2) are assessed as a single compartment. There are available windows in all of rooms; four out of five have exactly the same window surface area. Similarly, there are ventilation ductways for all rooms, with middling variations among them. For energy consumption estimates to be realistic, even moderate differentiations in the dimensions of the structural elements in the four sides of the construction (Figure 2) may become critical in rendering valid evaluations. The dimensional parameters (column, window, and brick wall surfaces) of all four apartment sides are also entered (Table 2) in the TEE-KENAK software package.
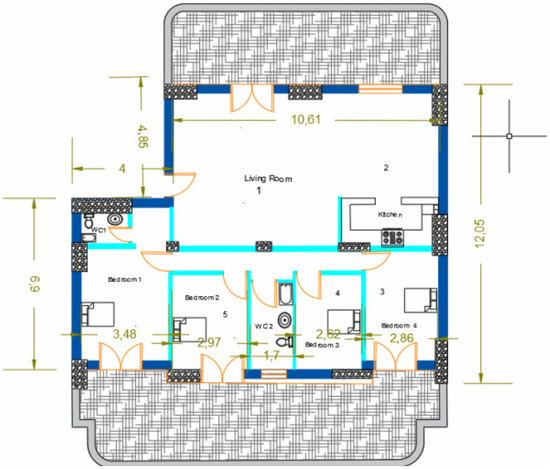
Figure 1.
Complete floor layout for the modeled apartment unit.

Table 1.
Apartment unit shell structural surfaces.
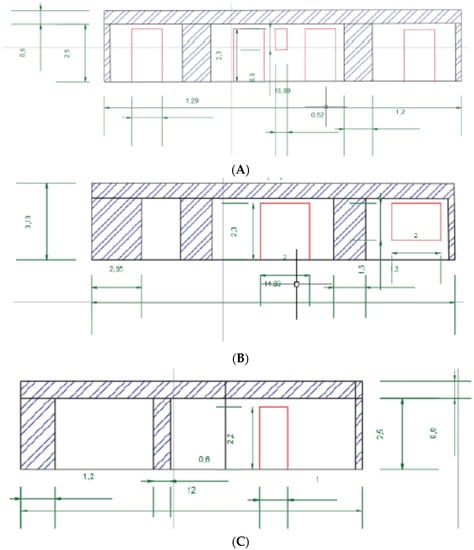
Figure 2.
Outer wall layout for each of the four sides: (A–D).

Table 2.
Apartment unit shell structural elements details.
In Table 3, shell elements are parametrized in terms of wall and window inputs, which are appropriately coded for orientation, surface area (F), and thermal permeability (k) properties. In Table 4, there is indicative information regarding the input unit block data, given the fact that the structure is raised such that the ground floor level can be used as a parking space as well as to support other auxiliary building facilities.

Table 3.
Apartment unit shell energy transfer data.

Table 4.
Apartment unit block data.
2.1.3. Electromechanical and Renewable Energy Systems
In Table 5, the basic characteristics of the electromechanical systems that were in operation during this study are listed. Natural gas was used as a heating source—the boiler power capacity was set at 25 kW. Refrigerant heat transfer was regulated by heat pumps with a total power capacity of 9 kW. Domestic hot water generation was attained by utilizing both solar and electricity resources. Renewable energy systems were solely based on solar panels that stored water in a building roof tank. The respective details for the renewable energy system characteristics are listed in Table 6.

Table 5.
Electromechanical systems data for the apartment unit.

Table 6.
Renewable energy systems data for the apartment unit.
2.1.4. The Energy Efficiency Certification Software Package TEE-KENAK
The TEE-KENAK (1.31.1.19) software was developed by the Energy Saving Team of the Institute for Environmental and Sustainable Development Research of the National Observatory of Athens in cooperation with the Technical Chamber of Greece [79,80]. This software applies appropriate algorithms for the valid calculation of the energy efficiency performance of buildings in Greece. It is based on a methodology that is outlined in the European-adopted energy performance standards (EN ISO 13790), as well as the relevant national standards for heating and cooling spaces, in conjunction with the Technical Guides of the Technical Chamber of Greece. According to the assessed output report from the TEE-KENAK software, a building apartment is officially certified to an energy efficiency class. The TEE-KENAK software requires entering basic factual information about the building characteristics. Formal input information includes the owner identification, the ownership status, the building address, and the year of issuance of the building permit. Technical details regarding the surfaces and volumes of the building (total surface area, heated surface area, cooled surface area, etc.) as well as information about the energy sources of the building are also keyed-in online. Opaque elements of the building are described by providing information on the orientation, the surface area, the coefficient of thermal permeability, and the pertinent shadowed area pattern. Dimensioning of the opaque surfaces with respect to the building foundations also involves lower and upper height details for each relevant structural element. Data for the transparent building surfaces additionally include glazing conditions, thermal break options, pane gap details, etc. The TEE-KENAK software package is compartmentalized to receive factual information with regards to the installed electromechanical systems in the apartment unit by considering energy demands for heating, cooling, and domestic hot water generation equipments, while also opting for renewable energy sources such as solar energy collection systems. The input data indicate the electromechanical system power demands/consumption, which are supplemented with their associated efficiency performance ratings. To estimate the solar collector contribution, specific details such as the usage rate, the effective surface area, and the optimal tilt and orientation angles are also submitted.
2.2. The Statistical Analysis Approach
The TEE-KENAK software platform permits a large number of relevant parameters to be synchronously investigated, whenever the scope of a study is to undertake energy-consumption reduction recommendations. This provision makes it impractical to test the energy consumption response by either a trial-and-error or a full factorial method. In fact, it was remarked [91] that succeeding in modeling the energy performance of an apartment unit is not adequate, if the modelling aspect is restricted solely to the installed electromechanical systems. It would not be convenient to carry out the resulting simulated estimations without resolving the drawback of voluminous (poly-factorial) combinatorial computations. Simulated predictions ought to be practical to allow for obtaining them on a per project basis and as part of an engineer’s daily routine if they are to be deemed helpful. It should be reiterated that this difficulty stemmed from the fact that, in attempting to simultaneously screen the tendencies of as many as 24 electromechanical controlling factors [91]—each factor minimally adjusted to two settings—the trial volume demand blew up (224 = 16,777,216 trials). The experimental tactic of resorting to supersaturated designs befits the condition to drastically compress the trial schedule. Therefore, the 14-run, 24-parameter supersaturated design of Williams [87], with its versatile parameter screening acceleration properties [89], which was implemented for the lean experimental data collection of Rousali and Besseris [91], is determined to be an attractive sampling planner for this work, as well. The adopted supersaturated design class is modified factorial half-fractions [88], which may also include the special case of half-split Plackett–Burman [93] design matrices. The 24 controlling factors which will be accommodated in the 14-run, 24-parameter supersaturated screening design have been tabulated in Table 7.

Table 7.
Controlling factors and their settings for influencing the energy consumption of the residential unit.
For the stepwise regression analysis procedure [94], the basic model is defined by the predictor matrix, X = {Xij}, of size n × m, where the number of the supersaturated design explanatory variables is m and the number of supersaturated design recipes is n. Then, the response matrix Y, of size n × r, where the number of responses is r = 1 for this work (energy consumption), and in conjunction with the prescribed condition for design supersaturation in m regressors, i.e., m > n + 1, is written as:
where βo and βj, with 1 ≤ j ≤ m, symbolize the coefficients of regression and is denoted as the error term for 1 ≤ i ≤ n, which is assumed to be an independent and identically distributed random normal variable. The stepwise regression method uses forward sequences of F-test applications, but the model selection technique alternatives will include assessments which consider: (1) the adjusted coefficient of determination (adj R2), (2) the Bayesian information criterion [95], and (3) the Mallow’s Cp metric [96] for best subsets regression.
To use the latent variable approach in the partial least squares (PLS) model [97,98], the number of the supersaturated design explanatory variables remains in the formalism m, the number of responses is r (r = 1), and the number of supersaturated design recipes is n. Then, the predictor matrix X, of size n × m, and the response matrix Y, of size n × r, are prescribed for m > n + 1:
X = CLXT+EX
Y = DLYT+EY
The projection matrices of X and Y are defined as C and D, respectively, and they are both of size n × p. The orthogonal loading matrices LX and LY correspond to the matrices X and Y, with dimensions m × p and r × p, respectively. The error terms, EX and EY, corresponding to the respective X and Y matrix models, are assumed to be independent and identically distributed random normal variables. The subsequent maximization of the covariance of the matrices C and D permits the decomposition of the matrices X and Y.
2.3. The Computational Aids
Descriptive statistics (median, interquartile range, skewness, and kurtosis) were computed per a factorial-setting basis using the ‘Frequencies’ selection from the IBM SPSS (v.29) software package. The ‘stepwise’ regression analysis was used to create a model summary with the statistically strong controlling factors using the probability of the F-distribution to sieve through the effects while adjusting the stepping method criteria for entry and removal at the α levels of 0.05 and 0.10, respectively. The model coefficients were supplemented with estimates of the coefficients of determination, collinearity diagnostics, Durbin–Watson residuals testing [99], and P-P plot residuals assessment.
To obtain the main effects plot for the 24-factor, 14-run supersaturated energy-consumption response dataset, the function ‘maineffectsplot()’ (MATLAB (R2022b) software package) was utilized after individually entering the poly-factorial combinations through the function ‘table2array()’ of the statistical freeware platform R [100].
The data analysis included the factorial coefficient predictions that were obtained from the partial least squares treatment (IBM SPSS v.29), which offer additional information such as the proportion of the explained variance by the investigated regressors, while testing the variable importance in the latent factorial projection. The selection cut of the strong predictors was also assessed using the Mallow’s Cp metric. Therefore, the best-subsetting factorial combinations of the supersaturated energy consumption dataset were determined using the linear regression outcomes from two R-packages (v.4.1), ‘leaps()’ (v.3.1) and ‘StepReg()’ (v.1.4.4).
The clustering analysis (IBM SPSS v.29) was implemented to refine the grouping tendency of the four summary estimators (median, interquartile range, skewness, and kurtosis) of the supersaturated dataset using an unsupervised classifier [101]. Correlation results (Spearman’s ρ coefficient [102]) among the four measures were pre-screened (IBM SPSS v.29). The goodness of clustering was obtained by estimating the gap statistic [103], using the function ‘clusGap()’ from the R-package ‘cluster()’ (v.2.1.2). Furthermore, to affirm the optimal cluster size, the auto-clustering method of the Schwarz’s Bayesian Criterion (BIC) was also employed (IBM SPSS v.29). The BIC change, the ratio of the BIC changes, and the ratio of the distance measures were computed. Hierarchical cluster sequence identifications were provided through a dendrogram. The statistical significance of the clustered groups of the four summary estimators was computed using the Mann–Whitney test [104] (IBM SPSS v.29).
The entropic screening of the predominant effects was carried out using the bin-discretization of the supersaturated energy-consumption dataset per a factorial setting basis. After partitioning in bins using the function ‘discretize2d()’ from the R-package ‘entropy()’ (v.1.3.1), the empirical (Shannon) mutual information [105] between same factor setting pairs was computed using the function ‘mi.empirical()’ from the R-package ‘entropy()’ (v.1.3.1). Supplementary information corrections, via the optimal shrinkage intensity estimations, were completed by implementing the function ‘entropy.shrink()’ from the R-package ‘entropy’ (v.1.3.1)).
2.4. The Methodological Outline
The methodology may be recapitulated in brief in the following steps:
- (1)
- Gather the required building apartment unit structural layout designs, along with the information for the installed electromechanical and renewable energy equipment information.
- (2)
- Determine which featured characteristics will be investigated for the selected apartment unit.
- (3)
- Determine the range values for the featured apartment unit characteristics and code them into controlling factor levels.
- (4)
- Select an appropriate supersaturated screening design to accommodate the large number of controlling factors from steps 2 and 3.
- (5)
- Execute the supersaturated plan runs by inputting each time trial recipe information (from step 4) into the TEE-KENAK software package.
- (6)
- Record the energy consumption (real and reference) estimates from each supersaturated trial run.
- (7)
- Prepare the response table and response graph for the energy consumption estimates.
- (8)
- Conduct stepwise regression analysis and evaluate the model summary results.
- (9)
- Determine the active controlling factors from step 8 and suggest a possible solution for the factorial settings.
- (10)
- Confirm the energy consumption performance improvement by inputting the optimal solution into the TEE-KENAK software package.
- (11)
- Assess and discuss the overall solution using other known methods such as PLS, entropic, and hierarchical clustering comparisons on key descriptive estimators of the energy consumption response.
3. Results
The results from executing the 14 poly-factorial recipes are tabulated in Table 8 in terms of the energy consumption response, along with its respective energy class. The energy consumption values ranged from 105.9 (trial #12) to 321.7 (trial #13) kWh/m2. Meanwhile, the corresponding energy classification ratings varied from status categories of ‘B’ (0.75–1.0 ratio to the reference building’s energy consumption) to ‘Z’ (2.27–2.73 times the reference building’s energy consumption). In Table 9, the energy demands and consumption details are indicatively tabulated for the first trial of the supersaturated trial-design schedule; they result from loading the software platform TEE KENAK 1.31.1.19 with the input from the prescribed recipe. From the ensuing response table (Table 10), it is observed that the factorial variability of the energy consumption performance declines from 102.8 (F4) to 2.11 (F16) kWh/m2. The two leading factors which contributed to the magnitude of the variability are: (1) the energy source for heating system’s power generation (F4), and (2) the thermal insulation of the roof (F20). This behavior becomes more transparent in the response graph (Figure 3 (MATLAB R2022b)), where the optimal settings are identified at the lower levels of both factors. Factor F4, adjusted at the ‘gas’ setting, reduces the energy consumption estimation down to as low as 171.07 kWh/m2 (an intra-factorial difference of 102.8 kWh/m2). Similarly, the ‘insulated roof’ option of factor F20 reduces the energy consumption to 179.87 kWh/m2 (an intra-factorial difference of 85.2 kWh/m2). From the response graph, it is apparent that factors such as F2, F3, F5, F17, F21, and F22 might also be statistically assessed for their contributing effects to the overall improved performance of the energy consumption response.

Table 8.
The response output for energy consumption (EC) in kWh/m2 and its energy classification status.

Table 9.
Energy demands and consumption results for the first simulation trial according to the supersaturated design schedule.

Table 10.
Response table for the factorial profiling of the energy consumption (EC) in kWh/m2.
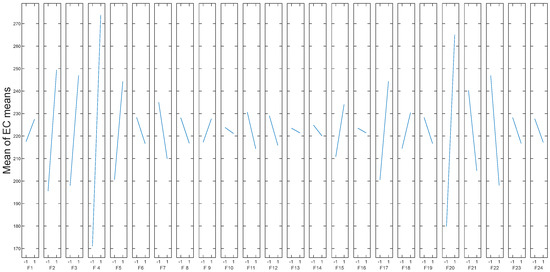
Figure 3.
Response graph (MATLAB R2022b) for the poly-factorial profiling of the energy consumption (EC) in kWh/m2.
A typical linear regression analysis for the supersaturated dataset is presented in Table 11 (IBM SPSS v.29). The ‘stepwise’ method was selected with entry and removal probabilities—to pace the stepping criteria—for the F-test values, at cutoff points of 0.05 and 0.10, respectively. The model summary indicates that four factors should be retained in the active factor group (F2, F4, F17, and F20); these adequately account for 96.2% of the total variation, according to the adjusted coefficient of determination (adj R2). Adding the last influence, F17, to the model corrected the prediction by only 0.041%; the factor F17 was found to be statistically significant at a level of 0.05. Overall, the four-factor prognostication is also statistically significant at a Bonferroni-corrected familywise error rate of 0.05. The two statistically stronger factors, F4 and F20, contributed 60% and 29% to the total variation, respectively. The Durbin–Watson statistic was estimated at a value of d = 3.17 (>dU = 2.296); it does not provide any hint that the successive error terms might be positively autocorrelated. Moreover, the alternative estimation, 4-d (= 0.833), is within the critical value interval (0.505, 2.296), as computed for the test parameters n = 14, k’ = 5, and α = 0.05. Hence, the test for the presence of a negative autocorrelation is inconclusive. The normal P–P plot (IBM SPSS v.29) of the regression-analysis standardized residuals (Figure 4) does not reveal any detectable abnormalities. The model coefficient and collinearity statistics (IBM SPSS v.29) are listed in Table 12. The unstandardized/standardized coefficients of the four active factors are statistically significant to at least an error rate of 0.01. Moreover, the variance inflation factor (VIF) has been estimated to a maximum value of 1.35. Thus, there seem to be no apparent multicollinearity tendencies across effects, with respect to the two leading factors (F4 and F20) in particular.

Table 11.
Stepwise-regression model summary (IBM SPSS v.29) for selecting statistically strong controlling factors.
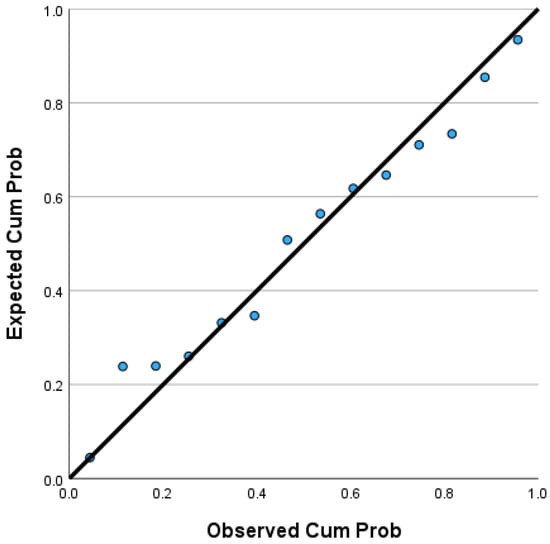
Figure 4.
Normal P–P plot of the regression standardized residuals for the dependent variable EC (IBM SPSS v0.29).

Table 12.
Stepwise-regression model summary coefficients and collinearity statistics (IBM SPSS v.29) for the statistically active controlling factors.
In Table 13, the optimal setting recommendations—in conjunction with the results of Figure 3—are summarized in terms of the four leading recommended modifications: (1) the thermal insulation of the roof, (2) the gas-sourced heating systems, (3) the automatic control category type ‘A’, and (4) the thermal insulation of the walls. The remaining 20 weaker factors may be adjusted by also considering practical/economic implications, or left at their original conditions. A complete final profiled-factor solution is shown in Table 13. At this point, it is worthwhile to assess the results by comparing the ‘before and after’ benefits that may be realized from this rudimentary study. The original (certifiable) energy consumption performance, as it was computed by the TEE KENAK 1.31.1.19 software program, was found to be 133.8 kWh/m2 (energy status ‘C’), and was to be contrasted against a reference building estimation of 129.2 kWh/m2. After completing the screening/optimization work, the recommended factorial settings from Table 13 were input to the TEE KENAK 1.31.1.19 software program to confirm any accruing energy savings. The improved solution delivered an energy consumption projection of 110.4 kWh/m2 (energy status ‘B’) for the apartment, which was to be contrasted against a reference building estimation of 125.9 kWh/m2. This is an almost 18% reduction in energy consumption, which may be considered satisfactory given the fact that only a subset of the total available variables in the TEE KENAK 1.31.1.19 software program was actually studied in this paradigm.

Table 13.
Optimal settings for several key controlling factors (Key Settings). Combination solution for all controlling factors (Full Settings).
4. Discussion
Supersaturated datasecorrelation coefficients and their respective ts require probing by a multitude of statistical techniques. The partial least squares (PLS) method is an alternative approach that might offer additional information about the validity of the factorial screening results, which were obtained in the preceding section. The proportion of the explained variance, using a maximum of five latent variables, is shown in Table 14 (IBM SPSS v.29). The output solution in Table 15 (IBM SPSS v.29) lists the factorial coefficients and their corresponding variable importance in the projection using the five latent factors. A practical roundup cut includes the candidate controlling factors F2, F3, F4, F5, F17, F20, and F22. In this profiling, only the solution factor members that were suggested in the Results section are considered.

Table 14.
The proportion of the explained variance for the supersaturated dataset using the PLS method.

Table 15.
The factorial coefficients and the variable importance (latent factors) in the projection for the supersaturated dataset using the PLS method.
Using the stepwise elimination option of PLS, the ANOVA treatment diagnostics (IBM SPSS v.29) reaffirm the high confidence to the previously recommended four-factor model (Table 16). To further study the possible inclusion of additional contributions, the Mallows’s Cp metric is utilized to reassess the linear regression results using the best subsets approach (R-packages ‘leaps()’ (v.3.1) and ‘StepReg()’ (v.1.4.4)). The suggested solution (F2, F4, F17, F22) achieves an adjusted R2 value of 96.2% and a corresponding Cp value of 28.1. Adding as many as five extra regressors (F5, F7, F11, F21, and F22) via the best subsetting approach increases the adjusted R2 to a value of 98.9% and, thus, substantially reduces the corresponding Cp value to 10.3. However, a 99% confidence interval estimation for the adjusted R2 in the original solution also includes the latter prediction. It is inferred that the small supersaturated dataset may not allow for discerning the need for additional predictors by relying only on the Cp criterion.

Table 16.
ANOVA results for the stepwise PLS treatment of the supersaturated dataset.
A convenient way to filter out the weak effects is to exploit the limiting dichotomous nature of the supersaturated dataset and the advantageously large number of the studied predictor variables. Consequently, essential information about the behavior of the energy consumption response may be synopsized by at least four statistical descriptive measures including the data location, dispersion, skewness, and flatness. The four respective statistical estimators, the median (M), the interquartile range (I), the skewness (S), and the kurtosis (K), re-organized the collected supersaturated dataset in terms of 48 individual factor levels. The summarized supersaturated EC dataset is listed in Table 17 (IBM SPSS v.29) in a data-reduced form and tabulated per each individual factor level. Before advancing the information generation process, the extent of potential correlations among the four summary estimators should be assessed. From Table 18, it can be observed that the two-variable correlation estimations, according to the Spearman’s ρ coefficient, returned three statistically significant outcomes (p < 0.001), in three out of the six possible pairings. The three detected estimator relationships were between: (1) the median and the skewness, (2) the interquartile range and the kurtosis, and (3) the skewness and the kurtosis. However, the magnitudes of the coefficients for the median–skewness and skewness–kurtosis pairs may not be considered strong. It is noteworthy that the resulting correlation between the median–kurtosis estimator pair does not show up as significant. For data processing purposes, it is assumed that there exists a mediocre correlation between the median–skewness and the skewness–kurtosis estimator relationships. Thus, both are retained in the succeeding data analysis steps. The interquartile range–kurtosis estimator pair may be rated close to strong, whereas the lower magnitude of its correlation coefficient does not also exclude a mediocre rating (|ρ| = 0.549). Therefore, the interquartile range is maintained in the analysis as well.

Table 17.
Summary statistics of the supersaturated dataset (median (M), interquartile range (I), skewness (S), kurtosis (K)) per factorial setting, and their hierarchical cluster identification.

Table 18.
Spearman’s ρ correlation coefficients and their respective 95% confidence intervals for median(M), interquartile range (I), skewness (S), and kurtosis (K) of the supersaturated dataset.
At this stage, an unsupervised screening approach is employed to cluster all individual factor levels by their grouping tendency to enter different memberships. To initiate the clustering process, the optimal cluster number is sought by computing the goodness of the clustering measure, the gap statistic (function ‘clusGap()’ in R-package ‘cluster()’ v.2.1.2); the ‘firstSEmax’ method is selected to evaluate the partitioning around the medoids (‘pam’) by generating 1000 simulated reference sets. From Figure 5, the optimal cluster number is found to be two. This outcome is also affirmed by the direct auto-clustering result (IBM SPSS v.29), which utilizes the Schwarz’s Bayesian Criterion (BIC) to locate the optimal change point of the measure (Table 19). From Figure 6, the cluster quality due to cohesion and separation is rated as ‘Fair’, according to the Silhouette measure evaluation (IBM SPSS v.29). Using hierarchical cluster analysis, the obtained identification cluster membership predictions are now tabulated in the right-hand side of Table 17.
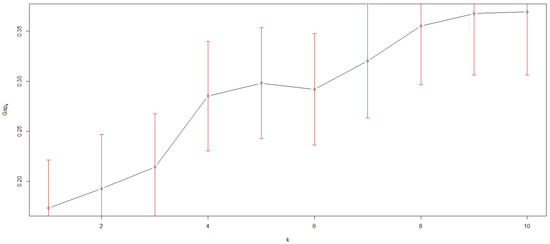
Figure 5.
Gap statistic performance for profiling optimal clustering size for the summarized supersaturated dataset of Table 17.

Table 19.
Auto-clustering of the summarized supersaturated datasets (Table 17) using the Schwarz’s Bayesian Criterion (BIC) (IBM SPSS v.29).
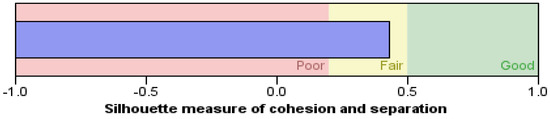
Figure 6.
Cluster quality rating using the silhouette measure of cohesion and separation (IBM SPSS v.29).
The rationale is that, as long as the two settings for the same controlling factor are found to belong to the same cluster, then the regressor cannot be further considered as a viable predictor of the total solution. In other words, an alternative method is attempted to reduce the initial regressor list of the supersaturated EC dataset. The hierarchical cluster distribution for the combined four statistical-estimator groupings is shown in Table 20 (IBM SPSS v.29). A total of 81.3% of the members are identified as belonging to cluster ‘1′; hence, there is a clear asymmetry in the factor-level distribution. Such asymmetry has been elicited owing to the cluster variability in the mean estimation for the interquartile range, and also for both skewness and kurtosis, based on their mean and their standard error for their respective mean estimations (Table 20). In Figure 7, the dendrogram for the hierarchical clustering solution (using median linkage) demonstrates the inherently complicated configuration display of all 48 factor-levelled EC-response datasets. To ensure that the dichotomizing of all four summarizing estimators is meaningful, in Figure 8, the distribution of the datapoints for the median, interquartile range, skewness, and kurtosis is contrasted with their clustered memberships. Further, the comparison application outcomes of the Mann–Whitney test aid in inferring that the cluster separations, for all four estimators, are statistically significant at least on the typical 0.05 level.

Table 20.
Hierarchical clustering and combined statistics for the four individual summarizing estimators (IBM SPSS v.29) from Table 17.
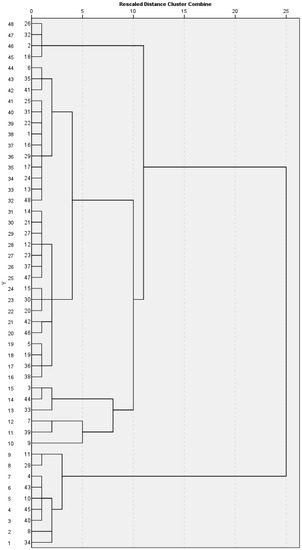
Figure 7.
Dendrogram using median linkage for the 48 factor levels resulting from the summarized four-estimator supersaturated dataset (IBM SPSS v.29).
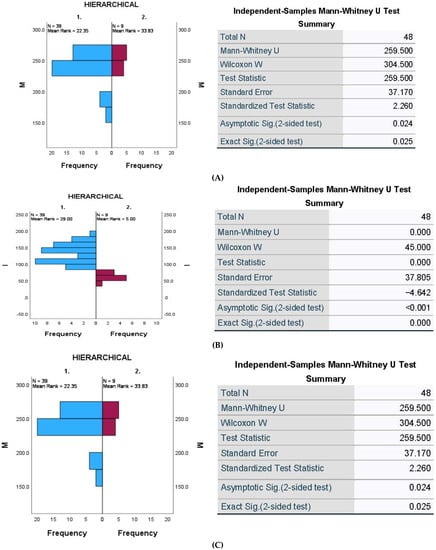

Figure 8.
Individually contrasting the clustered supersaturated datasets for their four summarizing estimators: (A) median (M), (B) interquartile range (I), (C) skewness (S), and (D) kurtosis (K).
Accordingly, returning to Table 17, the reduced list of the nominated controlling factors, in this instance, includes F2, F4, F5, F6, F14, F17, F20, F22, and F23. Repeating the stepwise selection process on this group of regressors, the resultant factorial profile appears identical to the regression solution which was obtained in the previous section, i.e., F2, F4, F17, and F20.
Finally, to examine the preponderance of the leading controlling factors from a non-parametric viewpoint, an entropic approach is implemented. A convenient way to achieve this is to evaluate, for all individual controlling factors, the joint distribution of their paired settings. Due to the small number of data points that needs to be accommodated by a larger factorial base, the continuous EC dataset was discretized each time to reflect the response data that corresponded to each factorial setting. To render a common bin number for all computations, the Freedman–Diaconis formula [106] was used, i.e., # of bins = rangeEC/h with h = 2·IQR/ (IQR = interquartile range, n = number of EC response entries). Inputting the values of rangeEC = 215.8 kWh/m2, IQR = 99.03 kWh/m2, and n = 14, the number of common bins was computed to be approximately three. Next, the synchronous two-setting discretization was conducted using the function ‘discretize2d()’ (R-package ‘entropy()’ (v.1.3.1)). Then, the empirical (Shannon) mutual information of the setting pairs was computed using the function ‘mi.empirical()’ (R-package ‘entropy’ (v.1.3.1)). The two controlling factors with the two lower mutual information estimations between settings, along with their lower-setting optimal shrinkage intensity estimations (function ‘entropy.shrink()’ from the R-package ‘entropy’ (v.1.3.1)), were found to be: (1) F20 (0.08 nats) with optimal shrinkage intensity lowered at 0.263 at the second level, and (2) F4 (0.202 nats) with optimal shrinkage intensity lowered at 0.263 at the second level.
5. Conclusions
The Renovation Wave for Europe is a great campaign under the European Green Deal which aims to effectuate the energy consumption and gas emission reduction of millions of older residential buildings in Europe. However, the energy performance improvement effort would be attained one apartment unit at a time. This complication might be remedied by adopting the mass customization philosophy that has been successfully espoused for several decades in industrial engineering. Consequently, a lean and green datacentric approach was attempted to carry out such a gradual improvement process, borrowing ideas and techniques from the Green Lean Six Sigma toolbox that is implemented to model and solve manufacturing problems. Therefore, the problem of examining the energy consumption reduction due to a candidate group of controlling factors was easily organized into a mini dataset with the aid of a supersaturated trial planner. The resulting empirical model is conveniently formulated, and the ensuing data analysis becomes manageable to expediently complete. The practicality of reaching a quick result is advantageous to an energy engineer. The proposed methodology demonstrated its responsiveness aspect toward attaining the goal of obtaining a solution quickly. The case study was a real-life standalone apartment unit that actually underwent a green certification process. By programming only 14 specific supersaturated recipe combinations for as many as 24 controlling factors, each factor was adjusted at two selected settings. The profiling relied on the variability potential that a factor carried to influence the energy consumption of the apartment unit. The novelty of this work is owed to the fact that it was the first time that shell properties and electromechanical system modifications were allowed to enter the empirical modelling effort. It is noted that it is a great advantage to prioritize the influence of the examined controlling factors on the standardized energy consumption ratings for two reasons. First, the generated dataset is trustworthy because it is based on derived estimations from a parametrized Energy Performance Certification database which is considered officially validated on a national level. Secondly, The Energy Performance Certification software platform (TEE-KENAK) generates actual and reference energy consumption ratings on the year-round performances of: (1) the original apartment unit and (2) on the apartment unit’s modifications.
An assortment of main effects plots, best-subsets partial least squares, and entropic (Shannon) mutual information predictions formed the profiler engine of the proposed methodology. The statistical filtering of the proposed apartment shell properties and its electromechanical system modifications identified four strong effects: (1) the thermal insulation of the roof, (2) the gas-sourced heating systems, (3) the automatic control category type ‘A’, and (4) the thermal insulation of the walls. The prediction for the optimal energy consumption corresponds to 110.4 kWh/m2 (energy status ‘B’) for the apartment. It accounts for an almost 20% reduction in energy consumption. Moreover, the ‘greener’ status rating has improved from the original ‘C’ status. Future work could involve forecasting the costs of apartment unit renovations and optimized predictions that combine economical and technical parameters, as well as occupant usage trends.
Author Contributions
Conceptualization, S.Z. and G.B.; methodology, S.Z. and G.B.; validation, S.Z. and G.B.; formal analysis, S.Z.; investigation, S.Z. and G.B.; resources, S.Z. and G.B.; writing—original draft preparation, G.B.; writing—review and editing, S.Z. and G.B.; supervision, G.B.; project administration, G.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data are available through Mr. Zarkadas’ thesis as submitted to the Kingston University depository per ref. [92].
Conflicts of Interest
The authors declare no conflict of interest.
References
- EC-COM(2019) 640 Final: The European Green Deal. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:b828d165-1c22-11ea-8c1f-01aa75ed71a1.0002.02/DOC_1&format=PDF (accessed on 30 March 2021).
- EC-COM(2020) 562 Final: Stepping Up Europe’s 2030 Climate Ambition. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52020DC0562&from=EN (accessed on 3 April 2021).
- EC-COM(2020) 662 Final: A Renovation Wave for Europe—Greening Our Buildings, Creating Jobs, Improving Lives. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2012:081:0018:0036:EN:PDF (accessed on 30 March 2021).
- IEA. Change in Final Energy Consumption by Sector, 2000–2018, and by Scenario to 2040; IEA: Paris, France, 2019. [Google Scholar]
- IEA. Tracking Buildings; IEA: Paris, France, 2019. [Google Scholar]
- IEA; IRENA; UNSD; WB; WHO. Tracking SDG 7: The Energy Progress Report; WB: Washington, DC, USA, 2019. [Google Scholar]
- United Nations Foundation. Sustainable Development Goals. 2023. Available online: https://unfoundation.org/what-we-do/issues/sustainable-development-goals/ (accessed on 30 January 2023).
- Bond, S.; Devine, A. Incentivizing green single-family construction: Identifying effective government policies and their features. J. Real Estate Financ. Econ. 2016, 52, 383–407. [Google Scholar] [CrossRef]
- Newsham, G.R.; Mancini, S.; Birt, B.J. Do LEED-Certified buildings save energy? Yes, but…. Energy Build. 2009, 41, 897–905. [Google Scholar] [CrossRef]
- Adekanye, O.G.; Davis, A.; Azevedo, I.L. Federal policy, local policy and green building certifications in the U.S. Energy Build. 2020, 209, 109700. [Google Scholar] [CrossRef]
- Porumb, V.A.; Maier, G.; Anghel, I. The impact of building location on green certification price premiums: Evidence from three European countries. J. Clean. Prod. 2020, 272, 122080. [Google Scholar] [CrossRef]
- Sanderford, A.R.; McCoy, A.P.; Keefe, M.J. Adoption of energy star certifications: Theory and evidence compared. Build. Res. Inf. 2018, 46, 207–219. [Google Scholar] [CrossRef]
- Kok, N.; McGraw, M.; Quigley, J.M. The diffusion of energy efficiency in building. Am. Econ. Rev. 2011, 101, 77–82. [Google Scholar] [CrossRef]
- Zhang, L.; Li, R. Impacts of Green Certification Programs on Energy Consumption and GHG Emissions in Buildings: A Spatial Regression Approach. Energy Build. 2022, 256, 111677. [Google Scholar] [CrossRef]
- Sołoducho-Pelc, L.; Sulich, A. Natural Environment Protection Strategies and Green Management Style: Literature Review. Sustainability 2022, 14, 10595. [Google Scholar] [CrossRef]
- He, Q.; Hossain, M.U.; Ng, S.T.; Skitmore, M.; Augenbroe, G. A cost-effective building retrofit decision-making model-Example of China’s temperate and mixed climate zones. J. Clean. Prod. 2021, 280, 124370. [Google Scholar] [CrossRef]
- Wilson, C.; Pettifor, H.; Chryssochoidis, G. Quantitative modelling of why and how homeowners decide to renovate energy efficiently. Appl. Energy 2018, 212, 1333–1344. [Google Scholar] [CrossRef]
- Jafari, A.; Valentin, V. An optimization framework for building energy retrofits decision-making. Build. Environ. 2017, 115, 118–129. [Google Scholar] [CrossRef]
- Chantrelle, F.P.; Lahmidi, H.; Keilholz, W.; El Mankibi, M.; Michel, P. Development of a multicriteria tool for optimizing the renovation of buildings. Appl. Energy 2011, 88, 1386–1394. [Google Scholar] [CrossRef]
- Jafari, A.; Valentin, V. Sustainable impact of building energy retrofit measures. J. Green Build. 2017, 12, 69–84. [Google Scholar] [CrossRef]
- Pardo-Bosch, F.; Cervera, C.; Ysa, T. Key aspects of building retrofitting: Strategizing sustainable cities. J. Environ. Manag. 2019, 248, 109247. [Google Scholar] [CrossRef]
- Ma, Z.; Cooper, P.; Daly, D.; Ledo, L. Existing building retrofits: Methodology and state-of-the-art. Energy Build. 2012, 55, 889–902. [Google Scholar] [CrossRef]
- Fan, Y.; Xia, X. Building retrofit optimization models using notch test data considering energy performance certificate compliance. Appl. Energy 2018, 228, 2140–2152. [Google Scholar] [CrossRef]
- Fan, Y.; Xia, X. Energy-efficiency building retrofit planning for green building compliance. Build. Environ. 2018, 136, 312–321. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stephan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Henggeler Antunes, C.; Dias, L. Multi-objective optimization for building retrofit strategies: A model and an application. Energy Build. 2012, 44, 81–87. [Google Scholar] [CrossRef]
- Castro, S.S.; Lopez, M.J.S.; Menendez, D.G.; Marigota, E.B. Decision matrix methodology for retrofitting techniques of existing buildings. J. Clean. Prod. 2019, 240, 118153. [Google Scholar] [CrossRef]
- Andrade-Cabrera, C.; O’Dwyer, C.; Finn, D.P. Integrated cost-optimal residential envelope retrofit decision-making and power systems optimisation using Ensemble models. Energy Build. 2020, 214, 109833. [Google Scholar] [CrossRef]
- Wu, R.; Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Multi-objective optimisation of energy systems and building envelope retrofit in a residential community. Appl. Energy 2017, 190, 634–649. [Google Scholar] [CrossRef]
- Schütz, T.; Schiffer, L.; Harb, H.; Fuchs, M.; Müller, D. Optimal design of energy conversion units and envelopes for residential building retrofits using a comprehensive MILP model. Appl. Energy 2017, 185, 1–15. [Google Scholar] [CrossRef]
- Costa, A.; Keane, M.M.; Torrens, J.I.; Corry, E. Building operation and energy performance: Monitoring, analysis and optimization toolkit. Appl. Energy 2013, 101, 310–316. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Waibela, C.; Evins, R.; Carmeliet, J. Co-simulation and optimization of building geometry and multi-energy systems: Interdependencies in energy supply, energy demand and solar potentials. Appl. Energy 2019, 242, 1661–1682. [Google Scholar] [CrossRef]
- Barber, K.A.; Krarti, M. A review of optimization based tools for design and control of building energy systems. Renew. Sustain. Energy Rev. 2022, 160, 112359. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimization methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2022, 160, 112359. [Google Scholar]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization from the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Balali, A.; Yunusa-Kaltungo, A.; Edwards, R. A systematic review of passive energy consumption optimization strategy selection for building through multiple criteria decision-making techniques. Renew. Sustain. Energy Rev. 2023, 171, 113013. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Kistelegdi, I.; Horvath, K.R.; Storcz, T.; Ercsey, Z. Building geometry as a variable in energy, comfort, and environmnetal design optimization-A review from the perspective of architects. Buildings 2022, 12, 69. [Google Scholar] [CrossRef]
- Hashempour, N.; Taherkhani, R.; Mahdikhani, M. Energy performance optimization of existing buildings: A literature review. Sustain. Cities Soc. 2020, 54, 101967. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, X.; Jin, X.; Zhou, X.; Si, B.; Shi, X. Towards adoption of building energy simulation and optimization for passive building design: A survey and a review. Energy Build. 2018, 158, 1306–1316. [Google Scholar] [CrossRef]
- Abbas, S.; Saleem, O.; Rizvi, M.A.; Kazmi, S.M.S.; Munir, M.J.; Ali, S. Investigating the Energy-Efficient Structures Using Building Energy Performance Simulations: A Case Study. Appl. Sci. 2022, 12, 9386. [Google Scholar] [CrossRef]
- Rong, A.; Su, Y. Polygeneration systems in buildings: A survey on optimization approaches. Energy Build. 2017, 151, 439–454. [Google Scholar] [CrossRef]
- Gassar, A.A.A.; Koo, C.; Kim, T.W.; Cha, S.H. Performance optimization studies on heating, cooling and lighting energy systems of buildings during the design stage: A review. Sustainability 2021, 13, 9815. [Google Scholar] [CrossRef]
- Azevedo, L.; Gomes, R.; Silva, C. Influence of model calibration and optimization techniques on the evaluation of thermal comfort and retrofit measures of a Lisbon household using building energy simulation. Adv. Build. Energy Res. 2021, 15, 630–661. [Google Scholar] [CrossRef]
- Bale, C.S.S.; Varga, L.; Foxon, T.J. Energy and complexity: New ways forward. Appl. Energy 2015, 138, 150–159. [Google Scholar] [CrossRef]
- Manson, S.M. Simplifying complexity: A review of complexity theory. Geoforum 2001, 32, 405–414. [Google Scholar] [CrossRef]
- Menassa, C.C. Evaluating sustainable retrofits in existing buildings under uncertainty. Energy Build. 2011, 43, 3576–3583. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Priesmann, J.; Nolting, L.; Praktiknjo, A. Are complex energy system models more accurate? An intra-model comparison of power system optimization models. Appl. Energy 2019, 255, 113783. [Google Scholar] [CrossRef]
- Pyzdek, T.; Keller, P. The Six Sigma Handbook; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- George, M.; Rowlands, D.; Price, M.; Maxey, J. The Lean Six Sigma Pocket Toolbook; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Hussain, K.; He, Z.; Ahmad, N.; Iqbal, M.; Nazneen, S. Mapping green, lean, Six Sigma enablers through the lens of a construction sector: An emerging economy’s perspective. J. Environ. Plan. Manag. 2023, 66, 779–812. [Google Scholar] [CrossRef]
- Hussain, K.; He, Z.; Ahmad, N.; Iqbal, M.; Saeed, M.Z. Establishing a Green, Lean and Six Sigma implementation model for sustainable construction industry: An analysis of driving forces through ISM-MICMAC approach. Environ. Sci. Pol. Res. 2023, 30, 30462–30492. [Google Scholar] [CrossRef]
- Womack, J.P.; Jones, D.T. Lean Thinking: Banish Waste and Create Wealth in Your Corporation, 2nd ed.; Revised and Updated; Free Press: New York, NY, USA, 2003. [Google Scholar]
- Dhingra, R.; Kress, R.; Upreti, G. Does lean mean green? J. Clean. Prod. 2014, 85, 1–7. [Google Scholar] [CrossRef]
- Johansson, G.; Sundin, E. Lean and green product development: Two sides of the same coin? J. Clean. Prod. 2014, 85, 104–121. [Google Scholar] [CrossRef]
- Garza-Reyes, J.A. Lean and green—A systematic review of the state of the art literature. J. Clean. Prod. 2015, 102, 18–29. [Google Scholar] [CrossRef]
- Fercoq, A.; Lamouri, S.; Carbone, V. Lean/Green integration focused on waste reduction techniques. J. Clean. Prod. 2016, 137, 567–578. [Google Scholar] [CrossRef]
- Rathi, R.; Kaswan, M.S.; Garza-Reyes, J.A.; Antony, J.; Cross, J. Green Lean Six Sigma for improving manufacturing sustainability: Framework development and validation. J. Clean. Prod. 2022, 345, 131130. [Google Scholar] [CrossRef]
- Jum’a, L.; Zimon, D.; Ikram, M.; Madzik, P. Towards a sustainability paradigm; the nexus between lean green practices, sustainability-oriented innovation and Triple Bottom Line. Int. J. Prod. Econ. 2022, 245, 108393. [Google Scholar] [CrossRef]
- Mishra, M.N. Identify critical success factors to implement integrated green and Lean Six Sigma. Int. J. Lean Six Sigma 2022, 13, 765–777. [Google Scholar] [CrossRef]
- Kalemkerian, F.; Santos, J.; Tanco, M.; Garza-Reyes, J.A.; Viles, E. Analysing the alignment between the Green Lean and Circular strategies: Towards a Circular Lean approach. J. Manuf. Technol. Manag. 2022, 33, 1059–1079. [Google Scholar] [CrossRef]
- Allouhi, A.; El Fouih, Y.; Kouskou, T.; Jamil, A.; Zeraouli, Y.; Mourad, Y. Energy consumption and efficiency in buildings: Current status and future trends. J. Clean. Prod. 2015, 109, 118–130. [Google Scholar] [CrossRef]
- Gabbar, H.A. Energy Conservation in Residential, Commercial, and Industrial Facilities, 1st ed.; Wiley-IEEE Press: Piscataway, NJ, USA, 2018. [Google Scholar]
- Harvey, L.D.D. Reducing energy use in the building sector: Measures, costs, and examples. Energy Effic. 2009, 2, 139–163. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H. Integrated energy performance optimization of a passively designed high-rise residential building in different climatic zones of China. Appl. Energy 2018, 215, 145–158. [Google Scholar] [CrossRef]
- Zhang, Y.; He, C.-Q.; Tang, B.-J.; Wei, Y.-M. China’s energy consumption in the building sector: A life cycle approach. Energy Build. 2015, 94, 240–251. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. A new comprehensive framework for the multi-objective optimization of building energy design: Harlequin. Appl. Energy 2019, 241, 331–361. [Google Scholar] [CrossRef]
- Sorrell, S. Reducing energy demand: A review of issues, challenges and approaches. Renew. Sustain. Energy Rev. 2015, 47, 74–82. [Google Scholar] [CrossRef]
- Yao, J. Energy optimization of building design for different housing units in apartment buildings. Appl. Energy 2012, 94, 330–337. [Google Scholar] [CrossRef]
- Merkel, E.; McKenna, R.; Fehrenbach, D.; Fichtner, W. A model-based assessment of climate and energy targets for the German residential heat system. J. Clean. Prod. 2017, 142, 3151–3173. [Google Scholar] [CrossRef]
- Benndorf, G.A.; Wystrcil, D.; Rehault, N. Energy performance optimization in buildings: A review on semantic interoperability, fault detection, and predictive control. Appl. Phys. Rev. 2018, 5, 041501. [Google Scholar] [CrossRef]
- Harish, V.S.K.V.; Kumar, A. Reduced order modeling and parameter identification of a building energy system model through an optimization routine. Appl. Energy 2016, 162, 1010–1023. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, J. Mathematical description for the measurement and verification of energy efficiency improvement. Appl. Energy 2013, 111, 247–256. [Google Scholar] [CrossRef]
- Dascalaki, E.; Droutsa, K.G.; Balaras, C.A.; Kontoyiannidis, S. Building typologies as a tool for assessing the energy performance of residential buildings—A case study for the Hellenic building stock. Energy Build. 2011, 43, 3400–3409. [Google Scholar] [CrossRef]
- Dascalaki, E.; Kontoyiannidis, S.; Balaras, C.A.; Droutsa, K.G. Energy certification of Hellenic buildings: First findings. Energy Build. 2013, 65, 429–437. [Google Scholar] [CrossRef]
- Technical Chamber of Greece TEE KENAK 1.31.1.19; Software Inspection & Certification Of Energy Buildings, Study of Energy Efficiency Boiler Inspection/Heating Installations and Facilities Air Conditioning-Manual. Technical Chamber of Greece: Athens, Greece, 2018.
- Technical Chamber of Greece TOTEE 20701-1/2017; Detailed National Specifications of Parameters for Calculating the Energy Efficiency of Buildings and the Issue of the Energy Performance Certificate. Technical Chamber of Greece: Athens, Greece, 2017.
- Fisher, R.A. The Design of Experiments; Macmillan: New York, NY, USA, 1971. [Google Scholar]
- Fisher, R.A. Statistical Methods, Experimental Design, and Scientific Inference; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Tanco, M.; Viles, E.; Ilzarbe, L.; Alvarez, M.J. Implementation of Design of Experiments projects in industry. Qual. Reliab. Eng. Int. 2009, 25, 478–505. [Google Scholar] [CrossRef]
- Ilzarbe, L.; Alvarez, M.J.; Viles, E.; Tanco, M. Practical applications of design of experiments in the field of engineering: A bibliographical review. Qual. Reliab. Eng. Int. 2008, 24, 417–428. [Google Scholar] [CrossRef]
- Satterthwaite, F. Random balance experimentation. Technometrics 1959, 1, 111–137. [Google Scholar] [CrossRef]
- Booth, K.H.V.; Cox, D.R. Some Systematic Supersaturated Designs. Technometrics 1962, 4, 489–495. [Google Scholar] [CrossRef]
- Williams, K.R. Designed Experiments. Rubber Age 1968, 100, 67–71. [Google Scholar]
- Lin, D.K.J. A New Class of Supersaturated Designs. Technometrics 1993, 35, 28–31. [Google Scholar] [CrossRef]
- Allen, T.T.; Bernshteyn, M. Supersaturated Designs That Maximize the Probability of Identifying Active Factors. Technometrics 2003, 45, 90–97. [Google Scholar] [CrossRef]
- Weese, M.L.; Smucker, B.J.; Edwards, D.J. Searching for powerful supersaturated designs. J. Qual. Technol. 2015, 47, 66–84. [Google Scholar] [CrossRef]
- Rousali, C.; Besseris, G. Lean Screening for Greener Energy Consumption in Retrofitting a Residential Apartment Unit. Appl. Sci. 2022, 12, 6631. [Google Scholar] [CrossRef]
- Zarkadas, S. Quality Optimization of Electromechanical Systems and Building Shell Insulation. Master’s Thesis, Advanced and Industrial Manufacturing Systems, Kingston University, London, UK, 2022. [Google Scholar]
- Plackett, R.L.; Burman, J.P. The design of optimum multifactorial experiments. Biometrika 1946, 33, 303–325. [Google Scholar] [CrossRef]
- Draper, N.; Smith, H. Applied Regression Analysis, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Schwarz, G.E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Mallows, C.L. Some comment on Cp. Technometrics 1973, 8, 661–675. [Google Scholar]
- Hair, J.F.; Sarstedt, M.; Hopkins, L.; Kuppelwieser, V.G. Partial least squares structural equation modeling (PLS_SEM). Eur. Bus. Rev. 2014, 26, 106–121. [Google Scholar] [CrossRef]
- Dijkstra, T.K.; Henseler, J. Consistent partial least squares path modeling. MIS Quart. 2015, 39, 297–316. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression. Biometrika 1950, 37, 409–428. [Google Scholar] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing, Version 4.2.2.; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 31 October 2022).
- Rousseuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Comp. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator L2 theory. Prob. Theory Rel. Fields 1981, 57, 453–476. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).