Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Fittings
Abstract
1. Introduction
2. Governing Equations and Theoretical Background
3. Numerical Set Up
4. Results
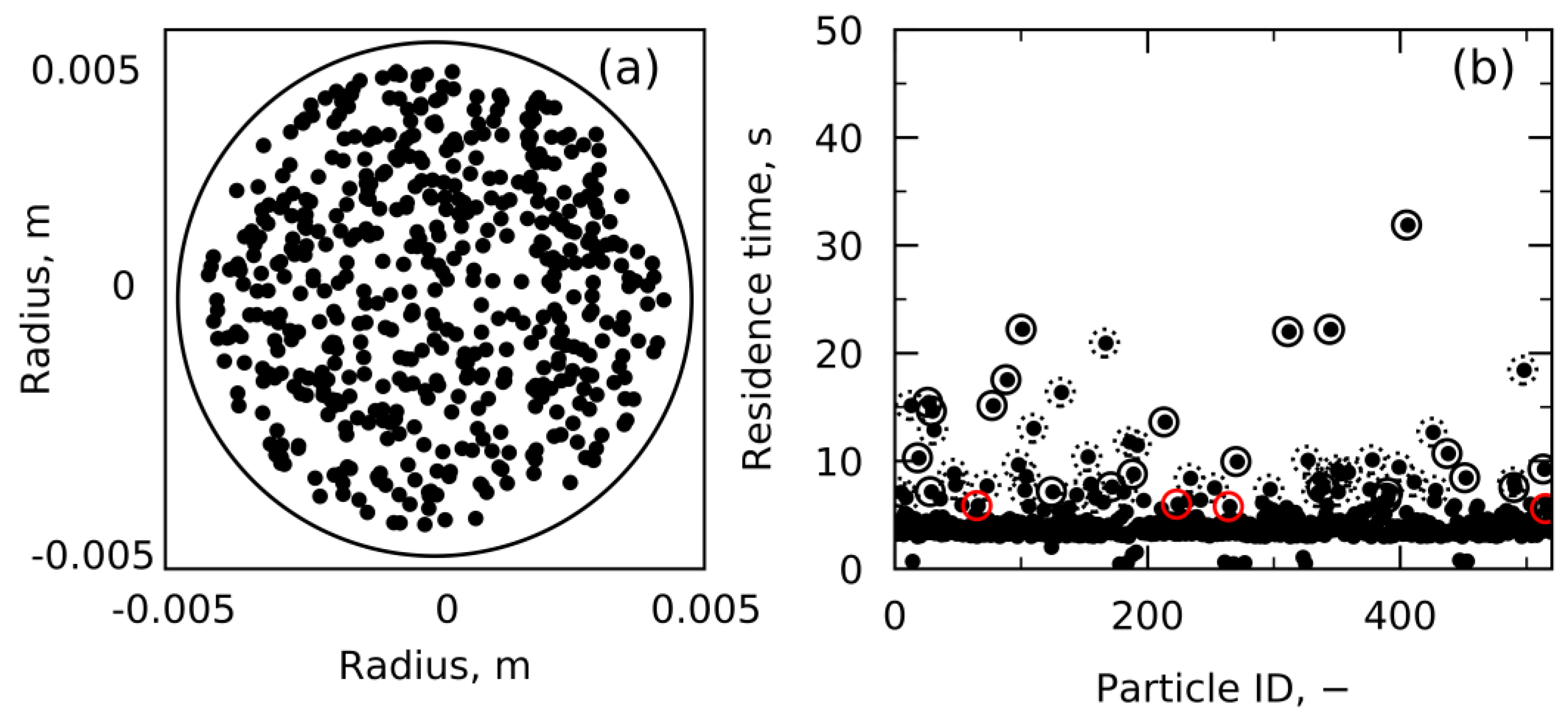
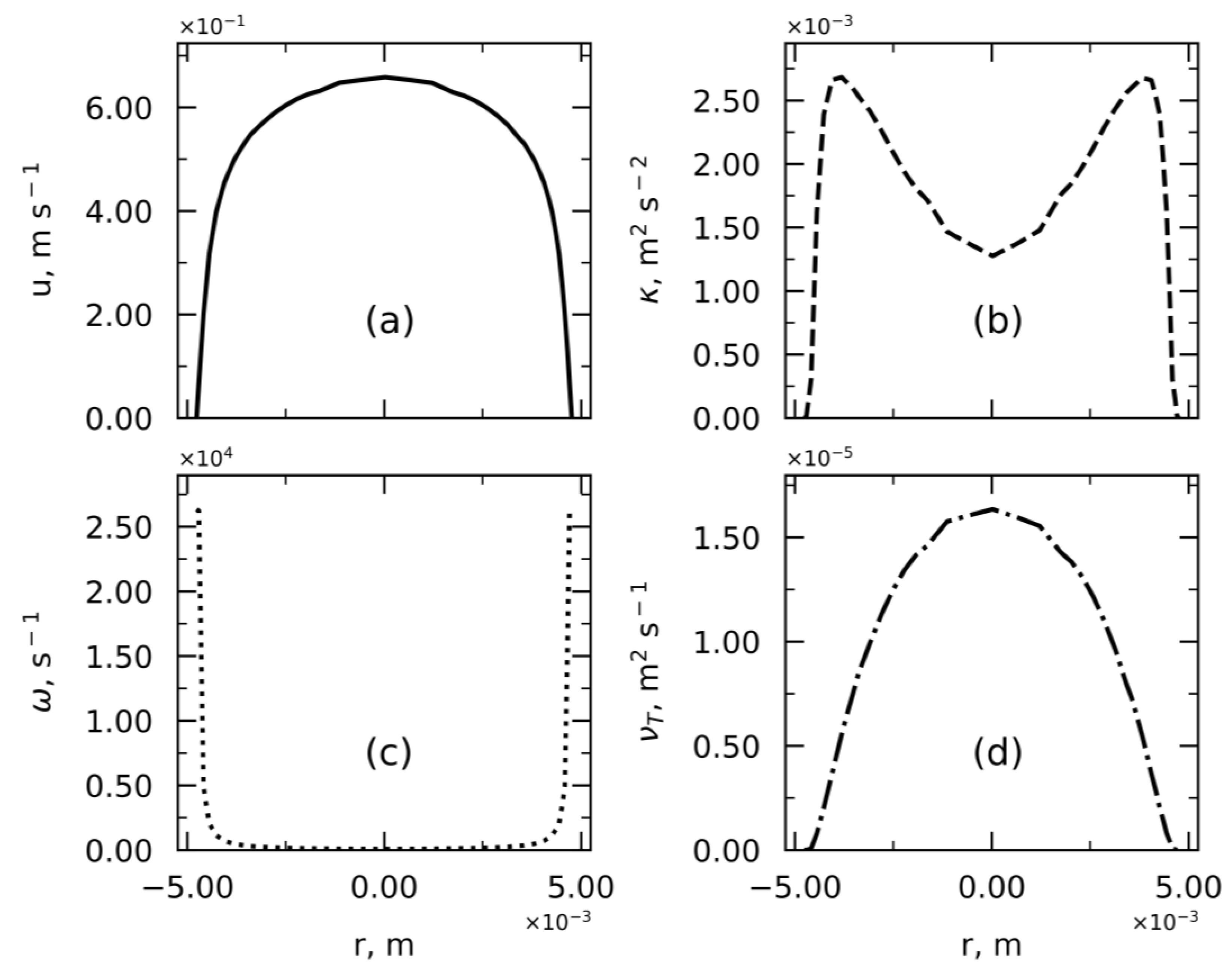
4.1. Velocity and Residence Time Study
4.2. First Case Study: Laminar Flow
4.2.1. Shear Stress Distribution
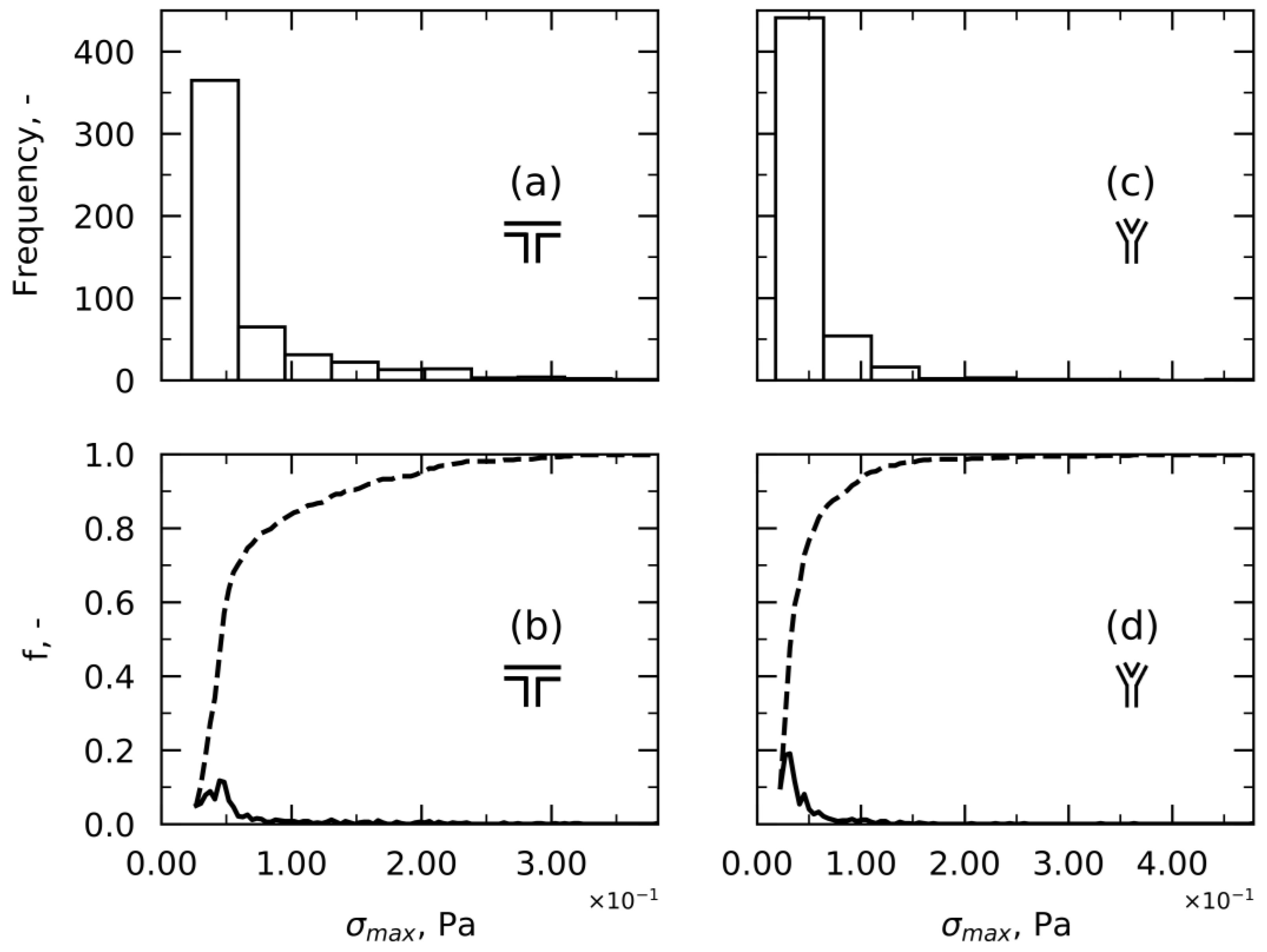
Approach 1—Maximum Shear Stress per Streamline
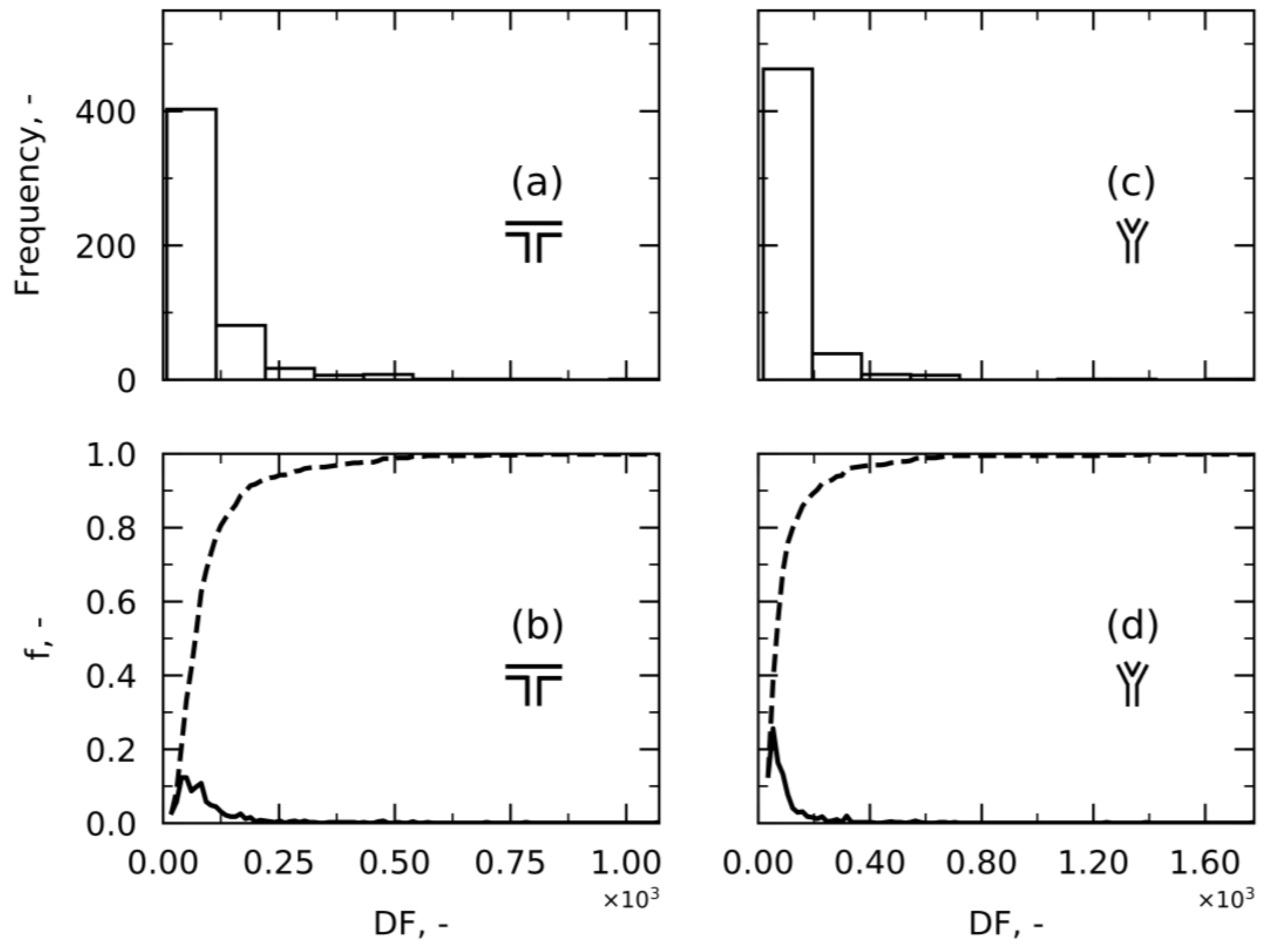
Approach 2—Damage Factor
Approach 3—Damage Fitting Factor
Approach 4—Damage Critical Factor
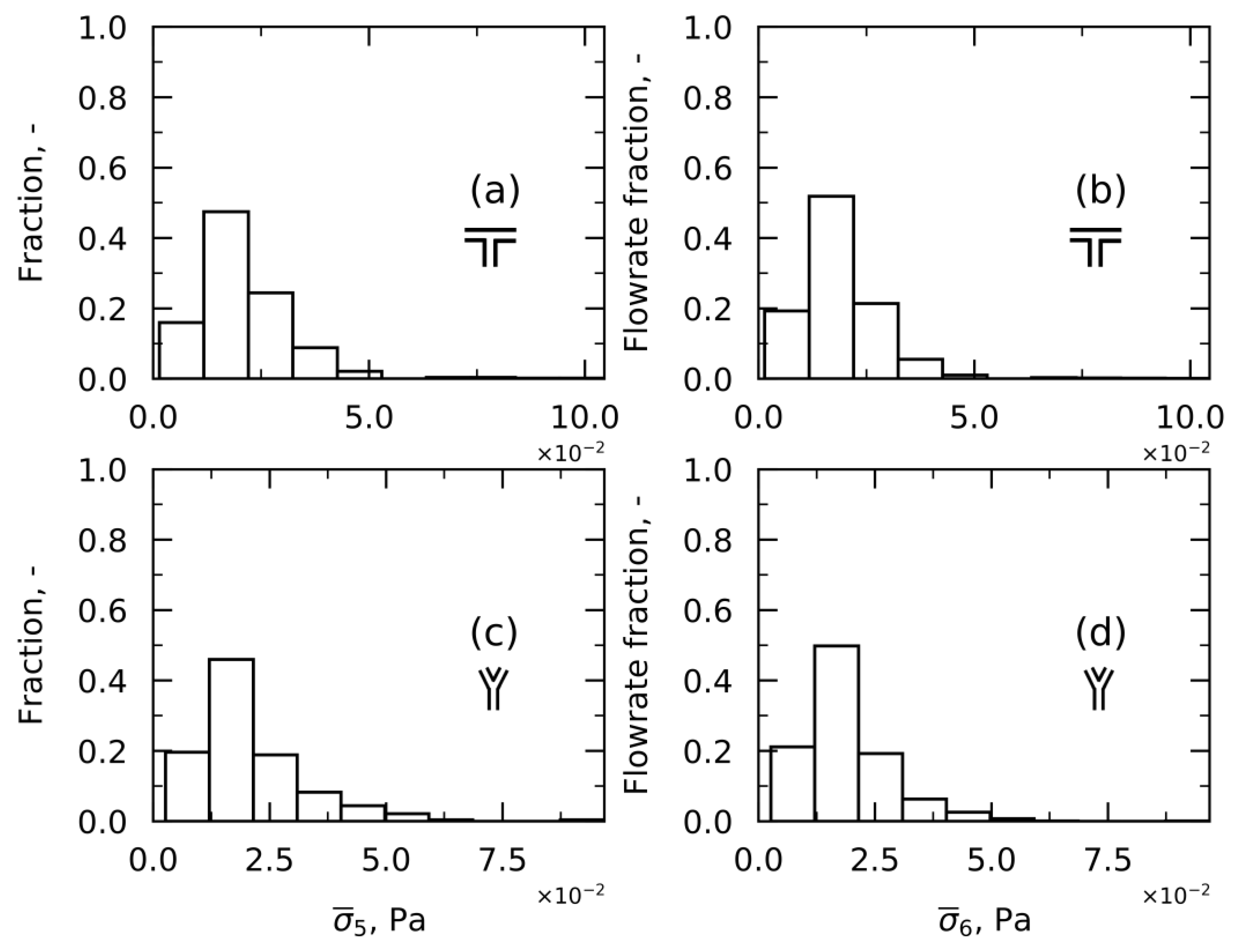
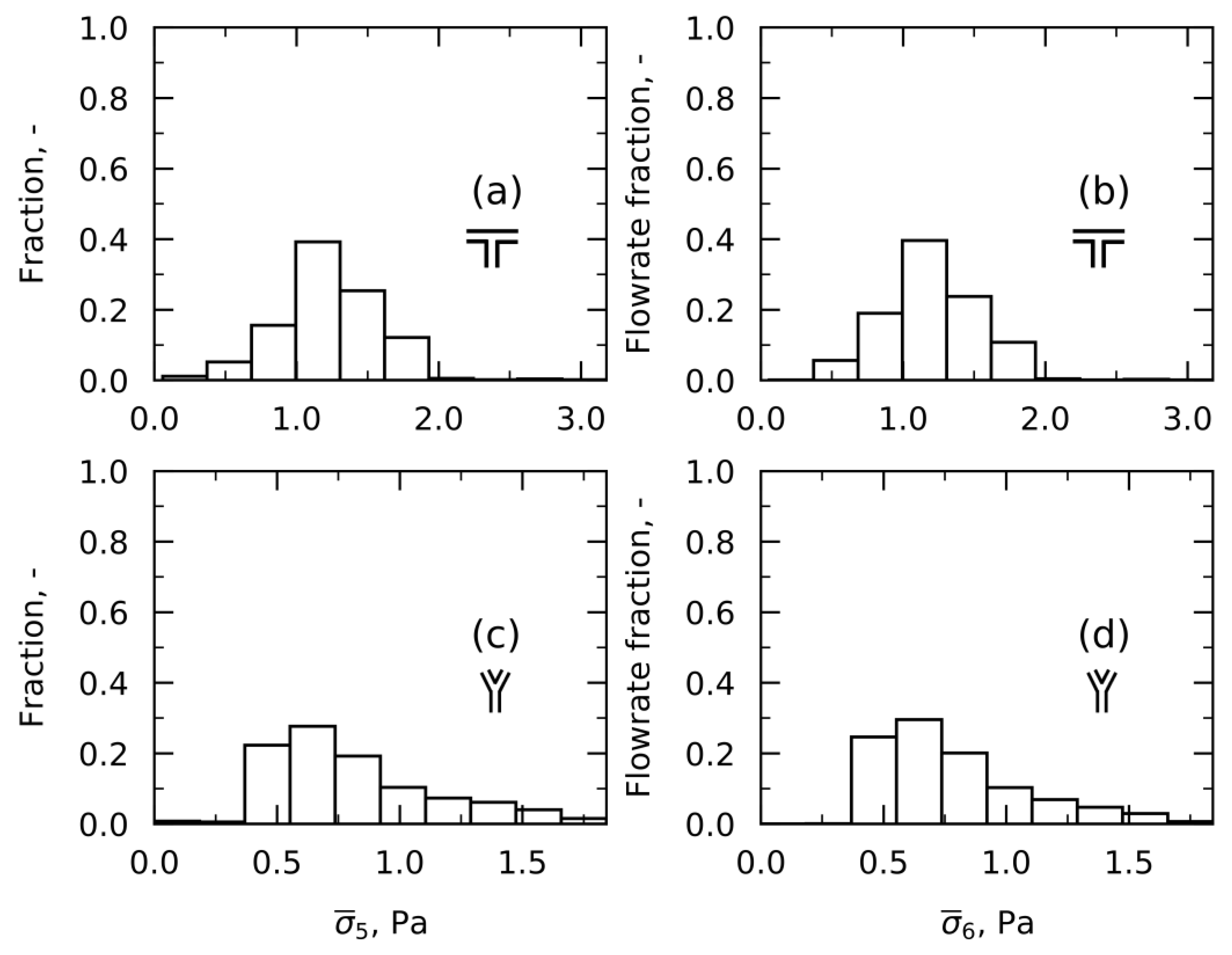
Approach 5—Time-Averaged Shear Stress
Approach 6—Time-Averaged Shear Stress weighted on Flowrates
4.3. Second Case Study: Turbulent Flow
Shear Stress Distribution
4.4. Comparison with Shear Stress in Straight Tubing
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| streamline area of influence, m2 | |
| skin friction factor, - | |
| coefficient of variation, - | |
| damage critical factor, - | |
| damage factor, - | |
| damage fitting factor, - | |
| turbulent kinetic energy, m2 s−2 | |
| number of streamlines, - | |
| factor, - | |
| fluid pressure, Pa | |
| volumetric flowrate, m3 s−1 | |
| distance from the center, m | |
| tubing radius, m | |
| Reynolds number, - | |
| Stokes number, - | |
| shear history, - | |
| time, s | |
| fluid velocity, m s−1 | |
| average fluid velocity, m s−1 | |
| friction velocity, m s−1 | |
| volumetric flowrate weight, m3 s−1 | |
| spatial coordinate, m | |
| absolute distance from the wall, m | |
| sub-layer scaled distance, - | |
| distance to the first cell center normal to the wall, m | |
| Greek letters | |
| turbulent model constant, - | |
| shear rate, s−1 | |
| difference, - | |
| turbulent dissipation rate, m2 s−3 | |
| turbulent kinetic energy, m2 s−2 | |
| dynamic fluid viscosity, kg m−1 s−1 | |
| kinematic viscosity, m2 s−1 | |
| turbulent kinematic viscosity, m2 s−1 | |
| fluid density, m3 kg−1 | |
| shear stress, Pa | |
| residence time, s | |
| filtered shear rate, s−1 | |
| fluid time scale, s | |
| particle response time, s | |
| specific turbulent dissipation rate, s−1 | |
| Subscripts | |
| fitting | |
| index | |
| index | |
| laminar | |
| maximum | |
| total | |
| tubing | |
| turbulent | |
| wall | |
| Abbreviations | |
| CDF | Cumulative Distribution Function |
| CFD | Computational Fluid Dynamics |
| GAMG | Geometric Agglomerated Algebraic Multigrid |
| Probability Distribution Function | |
| RANS | Reynolds Averaged Navier–Stokes |
| SST | Shear Stress Transport |
References
- Kovarcik, D.P. Critical Factors for Fill–Finish Manufacturing of Biologics. Bioprocess International. 17 May 2016. Available online: https://bioprocessintl.com/manufacturing/fill-finish/critical-factors-for-fill-finish-manufacturing-of-biologics/ (accessed on 10 March 2022).
- Martagan, T.; Akcay, A.; Koek, M.; Adan, I. Optimal production decisions in biopharmaceutical fill-and-finish operations. IISE Trans. 2020, 53, 149–163. [Google Scholar] [CrossRef]
- Das, T.K.; Sreedhara, A.; Colandene, J.D.; Chou, D.K.; Filipe, V.; Grapentin, C.; Searles, J.; Christian, T.R.; Narhi, L.O.; Jiskoot, W. Stress Factors in Protein Drug Product Manufacturing and Their Impact on Product Quality. J. Pharm. Sci. 2022, 111, 868–886. [Google Scholar] [CrossRef] [PubMed]
- Shire, S.J. Monoclonal Antibodies: Meeting the Challenges in Manufacturing, Formulation, Delivery and Stability of Final Drug Product; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Niazi, S. Pharmaceutical Manufacturing Formulations; Pharmaceutical Scientist, Inc.: Deerfield, IL, USA, 2009; Volume 6. [Google Scholar]
- Lapidus, L.J. Protein unfolding mechanisms and their effects on folding experiments. F1000Research 2017, 6, 1723. [Google Scholar] [CrossRef] [PubMed]
- Bekard, I.B.; Asimakis, P.; Bertolini, J.; Dunstan, D.E. The effects of shear flow on protein structure and function. Biopolymers 2011, 95, 733–745. [Google Scholar] [CrossRef] [PubMed]
- Charm, S.E.; Wong, B.L. Enzyme inactivation with shearing. Biotechnol. Bioeng. 1970, 12, 1103–1109. [Google Scholar] [CrossRef]
- Charm, S.E.; Wong, B.L. Shear degradation of fibrinogen in the circulation. Science 1970, 170, 466–468. [Google Scholar] [CrossRef]
- Thomas, C.R.; Dunnill, P. Action of shear on enzymes: Studies with catalase and urease. Biotechnol. Bioeng. 1979, 21, 2279–2302. [Google Scholar] [CrossRef]
- Jaspe, J.; Hagen, S.J. Do protein molecules unfold in a simple shear flow? Biophys. J. 2006, 91, 3415–3424. [Google Scholar] [CrossRef]
- Arsiccio, A.; McCarty, J.; Pisano, R.; Shea, J.E. Heightened Cold-Denaturation of Proteins at the Ice-Water Interface. J. Am. Chem. Soc. 2020, 142, 5722–5730. [Google Scholar] [CrossRef]
- Arsiccio, A.; McCarty, J.; Pisano, R.; Shea, J.E. Effect of Surfactants on Surface-Induced Denaturation of Proteins: Evidence of an Orientation-Dependent Mechanism. J. Phys. Chem. B 2018, 122, 11390–11399. [Google Scholar] [CrossRef]
- Arsiccio, A.; Pisano, R. The Ice-Water Interface and Protein Stability: A Review. J. Pharm. Sci. 2020, 109, 2116–2130. [Google Scholar] [CrossRef]
- Murphy, R.P.; Riedel, Z.W.; Nakatani, M.A.; Salipante, P.F.; Weston, J.S.; Hudson, S.D.; Weigandt, K.M. Capillary RheoSANS: Measuring the rheology and nanostructure of complex fluids at high shear rates. Soft Matter 2020, 16, 6285–6293. [Google Scholar] [CrossRef]
- Nesta, D.; Nanda, T.; He, J.; Haas, M.; Shpungin, S.; Rusanov, I.; Sweder, R.; Brisbane, C. Aggregation from Shear Stress and Surface Interaction: Molecule-specific or universal phenomenon? Bioprocess International. 17 April 2017. Available online: https://bioprocessintl.com/analytical/pre-formulation/aggregation-shear-stress-surface-interaction-molecule-specific-universal-phenomenon/ (accessed on 16 November 2021).
- Bee, J.S.; Stevenson, J.L.; Mehta, B.; Svitel, J.; Pollastrini, J.; Platz, R.; Freund, E.; Carpenter, J.F.; Randolph, T.W. Response of a concentrated monoclonal antibody formulation to high shear. Biotechnol. Bioeng. 2009, 103, 936–943. [Google Scholar] [CrossRef]
- Winter, K.G. An outline of the techniques available for the measurement of skin friction in turbulent boundary layers. Prog. Aerosp. Sci. 1979, 18, 1–57. [Google Scholar] [CrossRef]
- Pordal, H.S.; Matice, C.J.; Fry, T.J. The role of computational fluid dynamics in the pharmaceutical industry. Pharm. Technol. 2002, 26, 72–79. [Google Scholar]
- WHO. Annex 4 WHO Guidelines for Sampling of Pharmaceutical. WHO Guidel. Sampl. Pharm. Prod. Relat. Mater. 2005, 929, 61–93. Available online: https://apps.who.int/iris/bitstream/handle/10665/43157/WHO_TRS_929_eng.pdf (accessed on 15 December 2021).
- Moino, C.; Scutellà, B.; Bellini, M.; Bourlès, E.; Boccardo, G.; Pisano, R. Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Tubing. Processes 2023, 11, 833. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Kudela, H. Turbulent Flow and Turbulence Modeling. Notes 2011, 1–48. Available online: http://www.itcmp.pwr.wroc.pl/~znmp/dydaktyka/fundam_FM/Lecture_no3_Turbulent_flow_Modelling.pdf (accessed on 24 February 2022).
- Tu, J.; Yeoh, G.-H.; Liu, C. Computational Fluid Dynamics, 3rd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Byron Bird, R.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Guerrero, J. OpenFOAM Advanced Training. Turbulence Modeling in General CFD and OpenFOAM—Theory and Applications. 2022. Available online: http://www.wolfdynamics.com/tutorials.html?id=120 (accessed on 22 July 2022).
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, 2nd ed.; Pearson Education, Inc.: Harlow, UK, 2007. [Google Scholar]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware Inc.: Clifton Park, NY, USA, 2018; p. 274. Available online: https://www.mn.uio.no/astro/english/services/it/help/visualization/paraview/paraviewguide-5.6.0.pdf (accessed on 20 September 2022).
- Fischer, H.; Polikarpov, I.; Craievich, A.F. Average protein density is a molecular-weight-dependent function. Protein Sci. 2009, 13, 2825–2828. [Google Scholar] [CrossRef]
- Bachmann, M.F.; Jennings, G.T. Vaccine delivery: A matter of size, geometry, kinetics and molecular patterns. Nat. Rev. Immunol. 2010, 10, 787–796. [Google Scholar] [CrossRef]
- Moreland, K. The ParaView Tutorial; National Technology and Engineering Solutions of Sandia LLC: Mountain View, CA, USA, 2014. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley Publishing Company: Glenview, IL, USA, 1977. [Google Scholar]
- Duerkop, M.; Berger, E.; Dürauer, A.; Jungbauer, A. Influence of cavitation and high shear stress on HSA aggregation behavior. Eng. Life Sci. 2018, 18, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Kumar, G.; Banerjee, R.; Kr Singh, D.; Choubey, N.; Arnaw. Mathematics for Machine Learning. J. Math. Sci. Comput. Math. 2020, 1, 229–238. [Google Scholar] [CrossRef]
- Scott, D.W. Sturges’ rule. WIRES Comput. Stat. 2009, 1, 303–306. [Google Scholar] [CrossRef]
- Atkinson, K.E. An Introduction to Numerical Analysis, 2nd ed.; John Wildey & Sons: Toronto, ON, Canada, 1989. [Google Scholar]
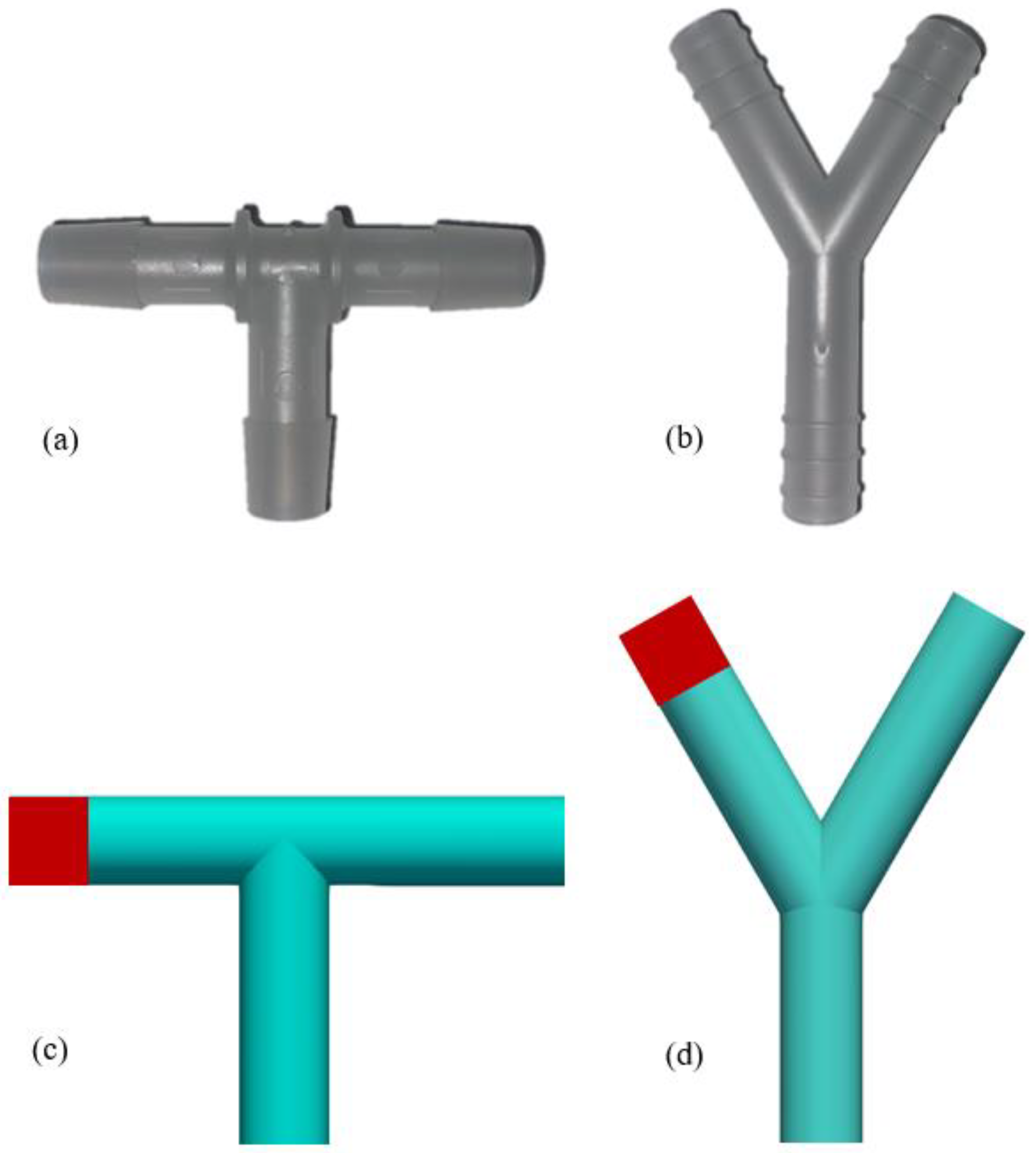
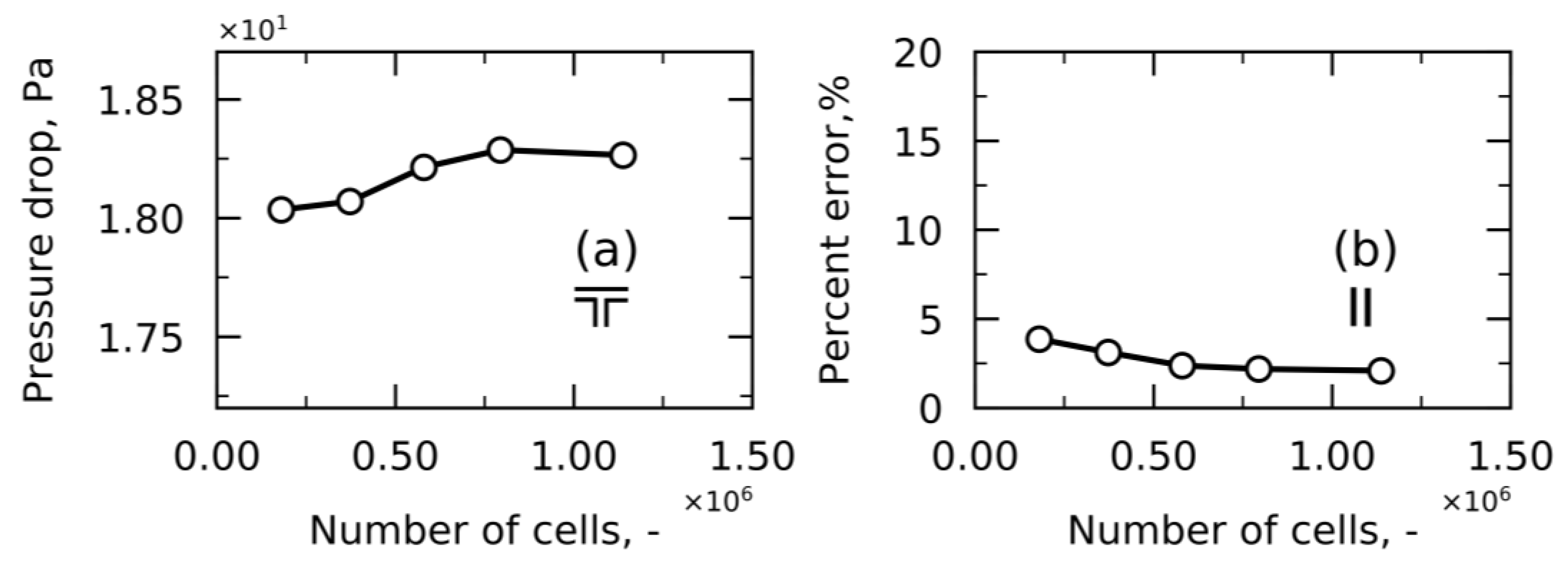
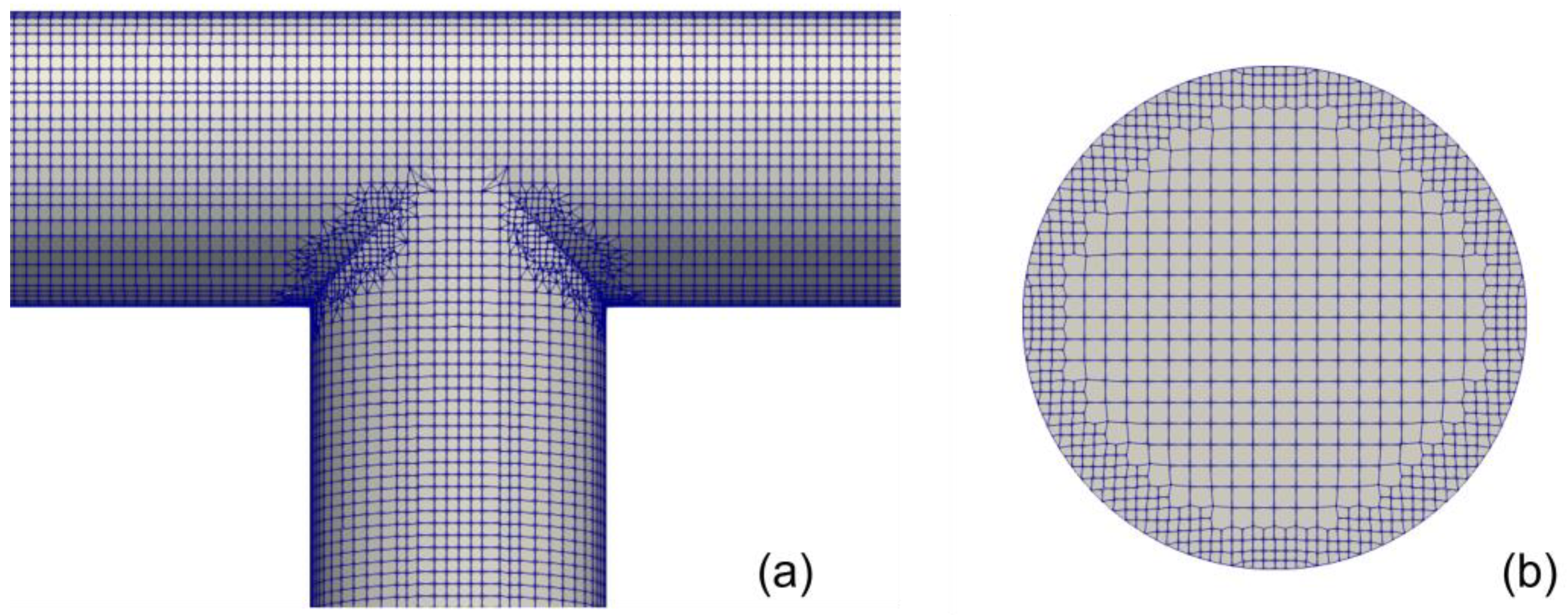
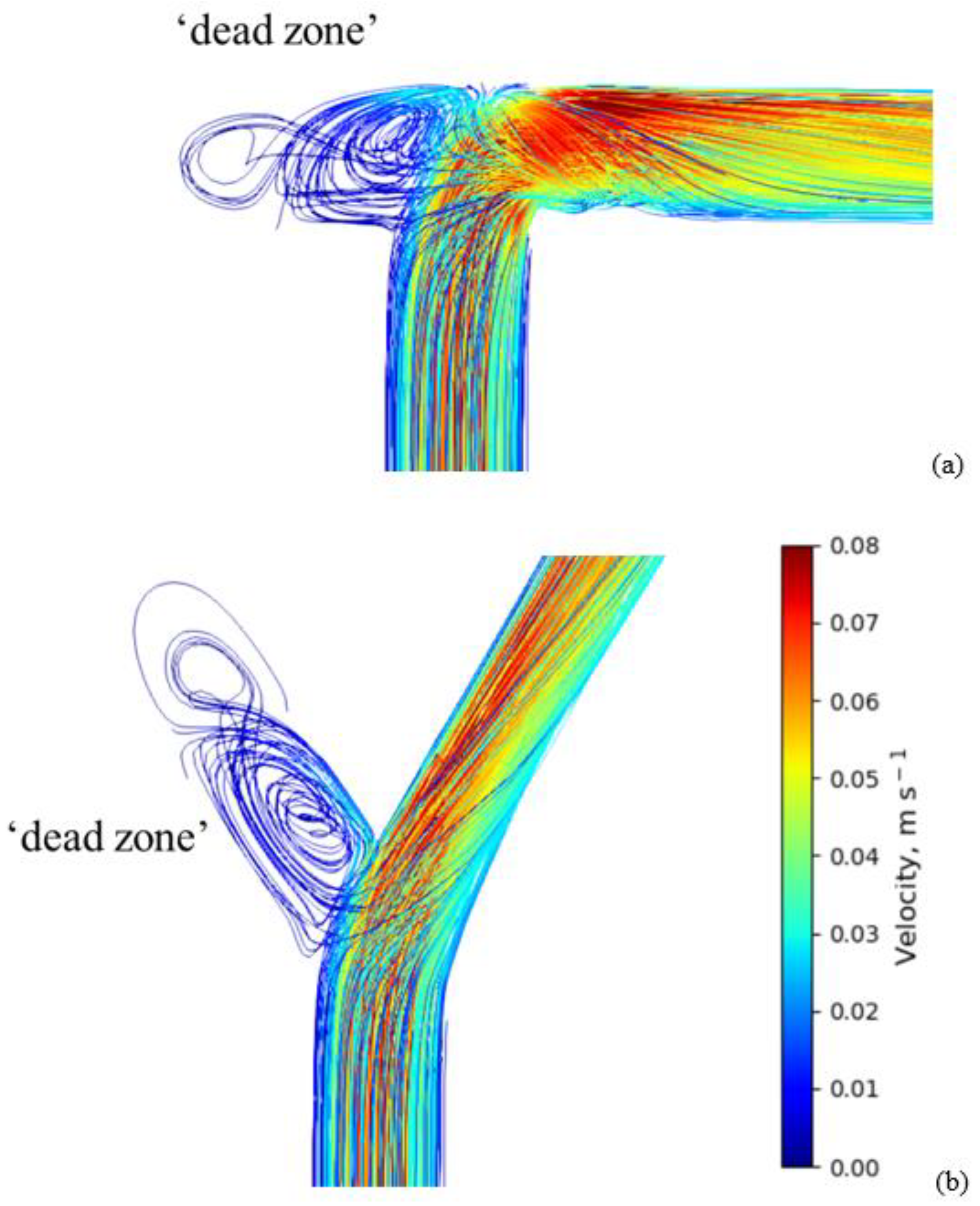

| Turbulence Property | Boundary Condition at the Wall | Estimation |
|---|---|---|
| fixedValue or kLowReWallFunction | ||
| omegaWallFunction | ||
| nutLowReWallFunction | ||
| Turbulence Property | Boundary Condition at the Inflow Patch | Estimation |
| fixedValue | ||
| fixedValue | ||
| calculated |
| Boundary Condition | ||
|---|---|---|
| Patch | ||
| inlet | zeroGradient | ) |
| outlet | uniformValue (0) | zeroGradient |
| wall | zeroGradient | noSlip |
| end | symmetry | symmetry |
| Case | ||||
|---|---|---|---|---|
| T- | ||||
| Y- |
| Case | Regime | |||||
|---|---|---|---|---|---|---|
| T- | Lam | |||||
| Y- | Lam | |||||
| T- | Turb | |||||
| Y- | Turb |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by GlaxoSmithKline Biologicals SA. Submitted for possible open access publication under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moino, C.; Scutellà, B.; Bellini, M.; Bourlès, E.; Boccardo, G.; Pisano, R. Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Fittings. Processes 2023, 11, 1797. https://doi.org/10.3390/pr11061797
Moino C, Scutellà B, Bellini M, Bourlès E, Boccardo G, Pisano R. Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Fittings. Processes. 2023; 11(6):1797. https://doi.org/10.3390/pr11061797
Chicago/Turabian StyleMoino, Camilla, Bernadette Scutellà, Marco Bellini, Erwan Bourlès, Gianluca Boccardo, and Roberto Pisano. 2023. "Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Fittings" Processes 11, no. 6: 1797. https://doi.org/10.3390/pr11061797
APA StyleMoino, C., Scutellà, B., Bellini, M., Bourlès, E., Boccardo, G., & Pisano, R. (2023). Analysis of the Shear Stresses in a Filling Line of Parenteral Products: The Role of Fittings. Processes, 11(6), 1797. https://doi.org/10.3390/pr11061797









