Optimal Control of Rural Water Supply Network Based on Intelligent Algorithm

Abstract

Optimizing Rural Water Supply Network (RWSN) is the basis for improving rural people’s lives and improving people’s health. Currently, the RWSN in China is relatively backward and can no longer meet the needs of the unified management of rural water resources. To optimize the RWSN, this study innovatively established a Multi-Objective Optimization Mathematical Model (MOMM) of RWSN, combining economic factors and reliability. This experiment first analyzes the characteristics of the RWSN system and then establishes a MOMM of a water supply network. NSGA-II algorithm and LM algorithm are introduced to handle the multi-objective model. The research results show that compared to Web decision tools, the RWSN based on the LM-NSGA-II algorithm can save 5.4% of the total annual cost of water supply pipelines. Therefore, the MOMM of the rural water supply pipeline based on the LM-NSGA-II algorithm has better economy and reliability. The experiment aims to provide certain reference values for the optimal control of RWSN through this study.

1. Introduction

With the continuous improvement of China’s economic level, the country attaches more attention to the development of rural areas. Rural water supply is an important means to improve the quality of life of rural residents and ensure the level of rural infrastructure. In the development of rural revitalization in recent years, the safety construction of rural drinking water has also become increasingly important [1]. However, the current configuration of RWSN in China is not perfect, and there are still many problems. For example, rural areas are prone to shortcomings such as limited budget funds for water supply projects and low construction standards. Therefore, it is necessary to select appropriate strategies to optimize and improve it. For the optimization and improvement of RWSN, it is not only required to consider the daily safe water use of residents but also needs to consider the economy of the network [2]. Thus, the design of RWSN needs to take into account the economy of the network project and the water supply’s reliability. This process usually involves the initial cost of water supply network construction and the operation cost in the long-term operation process. At present, many scholars have discussed the optimization of water supply networks. However, most of the proposed methods are single and limited, and their performance in practical applications needs to be further improved. In addition, the development of intelligent algorithms is in full swing, and they are widely used in various fields. In view of this, this research innovatively proposes an RWSN optimization control method based on the NSGA-II algorithm and introduces the LM algorithm to optimize its solution process. In addition, this study is the first to comprehensively consider the reliability and economy of water supply networks based on the construction of a multi-objective optimization mathematical model. The model is used in the experiment to balance the reliability and economy of RWSN [3,4]. The experiment aims to provide certain reference values for the optimal control of RWSN in China through this study [5].

2. Related Work

Many scholars have discussed rural water supply systems. Researcher Malima analyzed the current situation of water supply in rural areas and designed a hybrid method to evaluate the water supply in rural areas. Finally, the study suggested that local management structures should be established to intervene to increase the choice of water supply sources [6]. Hutchings and other scholars drew on the relevant views of political economics to analyze the rural water supply methods in the multi-village plan. The multi-village plan mainly referred to connecting hundreds of small villages and towns into a bulk water distribution network. The multi-village plan has strong complexity. Therefore, the experiment proposed that the community management water supply method in the multi-village plan needs to be updated to better adapt to the large scale involved in the multi-village plan [7]. Researcher Riswan conducted research on the current problem of the insufficient supply of water in rural areas. The experiment explored the feasibility of a community water supply scheme for managing rural water supply facilities. In addition, the experiment also discussed the effectiveness of the program in reducing water poverty in rural areas. The experimental results showed that relevant organizations needed to encourage and authorize community organizations to merge rural populations to alleviate the rural water supply crisis [8]. To reduce environmental pollution, the Hernández team focused on the water supply problem in rural communities. A pump station installed in a village settlement was designed. The pump station could meet the water demand of villagers and the settlement complex. The results demonstrated that the existing delivery capacity of the pumping station could meet the water demand of local villagers [9]. Cook and others proposed a new web-based decision-making tool from the rural water supply planning perspective. This tool could be used to simulate rural water supply scenarios. After analyzing the system in the experiment, it was applied to the water supply planning process in a rural area. The results indicated that the suggested tool could help relevant decision-makers provide useful information [10].

The NSGA-II algorithm is a multi-objective genetic algorithm. The NSGA-II algorithm has the feature of high speed and good convergence, so it can become the benchmark of MOOM performance. Xu and other researchers applied NSGA-II to the design of nuclear power plants. In the experiment, the reactor power controller was optimized by using the linear quadratic Gaussian method. After that, the experiment used NSGA-II to optimize the parameter factors in linear quadratic Gaussian. It was obvious that the proposed method has the advantages of fast response and high control accuracy [11]. Chai and other scholars established a multi-objective public transport network design model and its frequency setting. The model was implemented based on NSGA-II, which could solve multi-objective optimization issues with high complexity and strict constraints. The results concluded that the method had high global convergence and high applicability and could provide a reference value for policy formulation of urban transport networks [12]. Deng et al. applied NSGA-II to optimize the guide vane of the axial flow cyclone separator with multiple objectives to improve the separation performance of the guide vane. NSGA-II obtained the Pareto optimal solution in the experiment to help guide vane design. The experimental results were that the separation efficiency and pressure drop increase with the increase of the number of guide vanes as well as the winding angle. The proposed method effectively helped guide vanes to carry out reasonable design to a certain extent, thus achieving the performance required for separation [13]. Gu and other researchers constructed an RPS-NSGA-II algorithm. This method first proposed a strengthened dominance relationship based on reference points and then integrated it into the NSGA-II algorithm. The results illustrated that RPS-NSGA-II had performance advantages in 20 common benchmark problems involving up to 90 targets [14]. Ana’s team used NSGA-II to enhance the structure and building parameters. The experiment mainly used the NSGA-II algorithm and energy plus dynamic building energy simulation software to model the multi-objective optimization problem. The results indicated that the suggested model could achieve better solar gain [15,16].

To sum up, the improvement of rural water supply systems and the NSGA-II algorithm are widely used in their respective fields. However, the NSGA-II used for the optimal control of RWSN still has a large research space. Therefore, to optimize the RWSN, this experiment will establish a multi-objective optimization mathematical model combining economic factors for the first time. In addition, the experiment introduced the LM algorithm into the NSGA-II algorithm to optimize its solution process. Experiments validate the proposed model with examples.

3. Construction of Multi-Objective Optimization Model of RWSN Based on NSGA-II Algorithm

3.1. Research on Characteristics of RWSN System

The RWSN is different from the urban water supply network, and the RWSN needs to be stable and cost-effective. Optimization of the water supply network means that after optimization, the water supply network can meet people’s demand for water quantity and quality [17]. In addition, it can achieve the lowest construction and operation costs of the pipeline network. This study will establish a multi-objective pipeline network optimization model by determining the hydraulic characteristics, economic indicators and reliability indicators of RWSN [18,19]. To control the water source and the water pressure at each node, the hydraulic characteristics of the water pipe network need to be analyzed. It can ensure that the water pressure and water volume of users meet the daily use and are within the safe and controllable range. The expression for each node of the water pipe network is as follows.

$$A{q}_i{}_j+Q_j=0$$

(1)

In Equation (1), A represents the incidence matrix; $q_{ij}$ indicates the pipe section flow between node i and node j; $Q_j$ indicates the water demand of node j. In the annular water pipe network, its head loss closure is 0, and its energy balance equation can be expressed as follows.

$$L_{hk}=0$$

(2)

In Equation (2), L represents the loop matrix; $h_k$ is the head loss of the pipe section in ring k. When optimizing the pipe network, the pressure loss of the pipe section is usually not calculated, but only the loss of the head part. The expression of the pipe section pressure equation is shown below.

$$h_{ij}=H_i-H_j={Sq}_{ij}^n$$

(3)

In Equation (3), $h_{ij}$ represents the head loss of the pipe section; $H_i$ and $H_j$ respectively represents the water pressure elevation on both sides of the pipe section; S represents pipe section abrasion resistance; $q_{ij}$ refers to the pipe section flow between node i and node j; n is the coefficient. The adjustment between each node in the water supply network can be calculated by combining Equations (1)–(3).

3.2. Establishment of MOMM for Water Supply Network

The chapters above have mentioned that economic applicability is a factor that must be considered in the establishment of a rural water network. In this study, the economic indicators for the optimal design of the water supply network are composed of two aspects, namely, the energy cost required for the operation of the water supply network and the equipment wear cost. The expression is as follows.

$$W=M_1+M_2+C\times \frac{1}{t}$$

(4)

In Equation (4), W represents the water pipe network’s annual cost; $M_1$ represents the water supply network’s power cost; $M_2$ represents the depreciation and maintenance cost of pipeline equipment; C represents the one-time construction cost of the pipe network; t refers to the water supply network’s investment payback period. The power cost of the water supply is calculated according to the power cost of pumping [20,21], and its expression is as follows.

$$M_1=K{H}_{0}Q$$

(5)

In Equation (5), $K$ represents the economic index associated with the pumping cost; $H_0$ represents the net head of the water pump; $Q$ represents the pump or total flow $\left(L/S\right)$ input into the pipe network. The expression of the economic index $K$ associated with pumping cost is shown below.

$$K=\frac{0.01\times 24\times 365\times \beta \gamma }{\eta }$$

(6)

In Equation (6), $\beta$ is the water supply energy change parameter within the set time; $\gamma$ stands for electricity charge; $\eta$ represents the efficiency of the pumping station, and its value is usually 0.55~0.85 [22]. The expression of pipe network equipment depreciation and maintenance expense M2 is as follows.

$$M_2=\frac{P}{100}{\displaystyle \sum (a+bd\begin{array}{c}{}_a\\ {}^i\end{array})}{l}_i$$

(7)

In Equation (7), $\frac{P}{100}$ is the water supply network equipment’s depreciation and maintenance rate; $d_i$ is the pipe diameter of the water supply pipe $\left(mm\right)$; $l_i$ is the pipe length of the water supply pipe $\left(m\right)$; $a$, $b$ and $c$ are the basic parameters for the cost of a unit length pipeline, which are related to the economic development level of the project location. When there is a sufficient amount of actual pipeline cost data, the parameters $a$, $b$ and $c$ can be calculated using statistical methods; $C={\displaystyle \sum (a+bd\begin{array}{c}{}_a\\ {}^i\end{array})}{l}_i$ is the construction cost of the pipe network per unit length [23]. Substitute Equations (5)–(7) into Equation (4) to obtain the following expression of the water supply network’s annual cost.

$$W=(\frac{P}{100}+\frac{1}{t}){\displaystyle \sum (a+bd\begin{array}{c}{}_a\\ {}^i\end{array})l_i+K{H}_{0}Q}$$

(8)

When designing the water supply network, we should not only meet the needs of users, such as water quality, water pressure and water volume but also pay attention to creating the network to meet some constraints. The constraints mainly include boundary constraints and hydraulic constraints. The equations of hydraulic constraints are shown in Equations (1)–(3), while the boundary constraints include the constraints of node water pressure and pipeline diameter and flow velocity. The expression of the pipe network node water pressure limiting factor is as follows.

$$H_{j\min }\le H_j\le H_{j\max }$$

(9)

In Equation (9), $H_j$ denotes each node of the pipe network’s water pressure; $H_{j\min }$ represents the minimum water pressure; $H_{j\max }$ denotes the maximum water pressure at each node of the pipe network. The expression of pipeline diameter and flow velocity constraints is shown below.

$$V_j\le V_{j\max }$$

(10)

In Equation (10), $V_j$ represents each pipe section’s water flow rate in the water supply network; $V_{j\max }$ refers to the limited maximum flow velocity of each pipe section in the RWSN. When the water flow in the pipeline is too fast, it may cause the possibility of a pipe explosion. Therefore, in the process of water supply, the water flow speed must be strictly controlled to avoid the pipe network’s burst rate. The pipe network’s reliability can be described as reducing the pipe burst rate of the pipe network as much as possible under the basic premise of meeting the user’s water consumption. However, even after the pipe explosion accident, the water supply and demand can still be guaranteed to meet the user’s water demand. Figure 1 shows the relationship between investment cost and the reliability of the pipeline network [24].

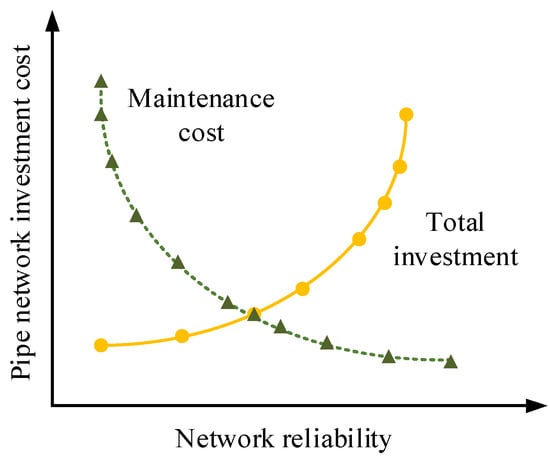
Figure 1. Relationship between investment cost and reliability of pipeline network.

As shown in Figure 1 above, the higher the total investment of the RWSN, the higher the reliability of the network, and the lower the maintenance costs required in the future. When the water supply network’s reliability is low, the total investment cost is lower, but the maintenance cost in the future is higher. Therefore, the water supply network’s reliability and the investment cost generally present a positive correlation. This study focuses on how to make the economy and reliability of the water supply network reach a reasonable balance. The node affluence head is used to represent the reliability of the pipe network [25]. The node excess head refers to the number of free heads in addition to the minimum head required for the specified node. Its quantity is inversely proportional to the reliability of the pipe network. When the node excess head is more, the water pressure is higher, and the reliability is lower. The expression of the node excess head is shown below [26].

$$I_{si}=H_i-H_{\min }, \mathrm{i}=1,2,\dots ,\mathrm{N}$$

(11)

The sum of node affluence head is shown below.

$$I_s={\displaystyle \sum _{i=1}^I{H}_i-H_{\min }}, \mathrm{i}=1,2,\dots ,\mathrm{N}$$

(12)

The weighted average affluence head expression of all nodes in the pipe network is as follows.

$$I_s=\frac{I_{s1}+I_{s2}+\cdots +I_{sN}}{I}$$

(13)

In this study, the weighted average of the node affluence head of the pipe network is used to express the pipe network’s reliability, and its expression is as follows.

$$I_s=\frac{{\displaystyle \sum _{i=1}^I{Q}_i(H_i-H_{\min })}}{{\displaystyle \sum _{i=1}^I{Q}_i}}$$

(14)

In Equation (14), $H_i$ represents the free head of $i$ at the corresponding node; $H_{\min }$ is the minimum free head required by the node; $Q_i$ is the water flow of the node. Based on the hydraulic characteristics, constraints and reliability analysis of the pipe network in the above chapters, the following multi-objective optimization model for the pipe network’s reliability and economy is established [27]. The model’s mathematical expression is shown.

$$\{\begin{array}{c}\min W=(\frac{P}{100}+\frac{1}{t}){\displaystyle \sum (a+bd\begin{array}{c}{}_a\\ {}^i\end{array})l_i+\frac{0.01\times 24\times 365\times \beta \gamma \rho g}{\eta }{H}_{0}Q}\\ \min I_s=\frac{{\displaystyle \sum _{i=1}^I{Q}_i(H_i-H_{\min })}}{{\displaystyle \sum _{i=1}^I{Q}_i}}\end{array}$$

(15)

4. Solution of MOMM of Water Supply Network Based on NSGA-II Algorithm

This experiment first constructs an NSGA-II model for the multi-objective problem of rural water supply networks. Later, in order to accelerate the speed of solving nonlinear equations during the solution process, the Lebenberg Marquardt (LM) iterative algorithm was introduced. The specific steps of the LM-NSGA-II algorithm constructed in this article are shown in Figure 2.

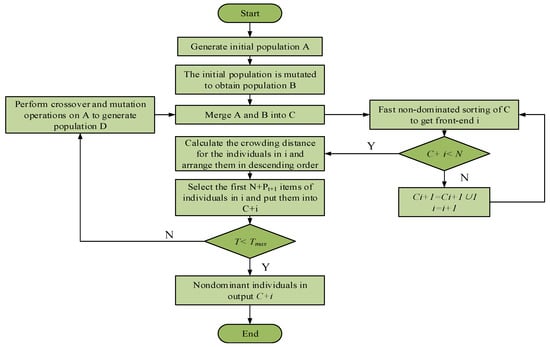
Figure 2. Specific process of NSGA-II algorithm.

The optimal solution-solving problem in multi-objective optimization is aimed at the set composed of all optimal solutions, that is, the non-inferior optimal solution set. Figure 3 shows the Pareto curve in front of the non-inferior solution under two objective functions.

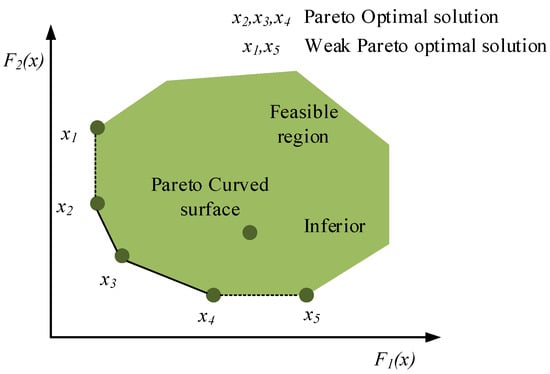
Figure 3. Leading edge surface.

At present, Non-dominated Sorting Genetic Algorithm-II (NSGA-II) has an excellent ability to handle multi-objective optimization issues. NSGA-II algorithm has high search speed and low complexity and is proper for solving multi-objective issues. Meanwhile, the algorithm can achieve fast convergence and ensure population diversity. Therefore, this study uses NSGA-II to handle the MOMM. First of all, the experiment is to encode and decode the pipe network. Use the integer of 1–9 to code the pipe diameter of each section, and match the code with the pipe diameter one by one. Then, the pump head is coded with a real number of 30–50. After completing the coding work, calculate the economic indicators such as water supply network material cost $C$ and operation electricity cost $E$ according to the equation in the above chapters. Then, calculate the water pressure adjustment of the pipe network to obtain the total surplus head $H$ at each node of the pipe network. Then, the node average affluence head is obtained by weighting, and the differentiability objective function is established.

Equations (1)–(3) are used to calculate the pipe network adjustment model in this study. In the process of solving, it is necessary to solve the nonlinear Equations. To quickly solve the nonlinear equations, the Lebenberg-Marquardt (LM) iterative algorithm is used in this study. LM algorithm has both the global specificity of the fastest descent method and the local characteristics of the Gauss–Newton method, which is an iterative technique. LM algorithm has an excellent performance in solving nonlinear equations. Assume that $n$ variables and m equations are set in the nonlinear equation system, which can be expressed as the following equation system.

$$\{\begin{array}{c}{f}_1(x_1,x_2,x_3)=0\\ f_2(x_1,x_2,x_3)=0\\ ⋮\\ f_m(x_1,x_2,x_3)=0\end{array}$$

(16)

Through the observation of Equation (16), it can be found that the solution process conforms to the number of all equation groups in the equation group. In addition, it can be further developed in the defined interval, as shown in the following equation.

$$\underset{(x_1,x_2,\dots ,x_n)\in D}{{\displaystyle \min }}F(x_1,x_2,\dots ,x_n)={\displaystyle \sum _{i=1}^m\left|f_i(x_1,x_2,\dots ,x_n)\right|}$$

(17)

Thus, the solution of the equation set is transformed into the solution of 9 $F(X*)=0$. That is, a set of numbers when solving the function $F(x_1,x_2,\dots ,x_n)=0$. In this study, the water supply pipe network’s pipe diameter and the head of each node are taken as independent variables, and the actual flow of each node and the water flow required by the node are controlled to the minimum.

LM is applied to solve the nonlinear equations composed of constraint conditions. In the calculation process, it is necessary to assume an initial value of pipe diameter. If the initial value setting is not ideal, the equations may be misunderstood, or it may be tough to find the best solution. Therefore, it is required to test the closure of the equations. When the equations are not closed, an infeasible solution can be given to the equations in the NSGA-II algorithm. After the argument is regenerated, skip this generation directly and solve it again. When the initial value meets the constraint conditions (1)–(3), the previously set pipe diameter will be further reduced, and the calculation and judgment will be performed again. If the pipe diameter can still meet the constraint conditions, reduce the pipe diameter again until the constraint conditions cannot be met. The NSGA-II algorithm improves the convergence speed of the whole model by quickly ranking the individuals of the population. The concepts of fast non-dominated sorting and crowding distance are applied in the NSGA-II algorithm, which can enhance the diversity of the population to a certain extent to avoid falling into local optimum. At present, the NSGA-II algorithm has become an excellent algorithm for solving multi-objective optimization issues [28].

5. Performance Verification of MOOM of RWSN Based on NSGA-II Algorithm

This study selected the water supply network of a town as the research object. The total water supply scale of the town’s water supply network is 20,000 m³. The water supply network system uses two water plants as water sources, and there are 36 nodes and 53 pipe sections in the network. The overall pipe network layout is shown in Figure 4 below.

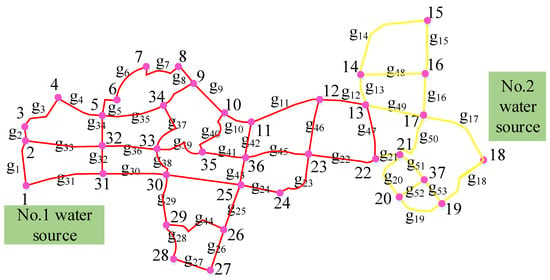
Figure 4. Schematic diagram of water supply network in a town.

Figure 4 above demonstrates a town’s water supply network, where two water sources are located at node 1 and node 18, respectively. The letter g in the figure represents the water supply node. The overall terrain of the town is relatively flat, with few rugged road sections. The maximum ground elevation difference between pipe network nodes is 10.8 m. The water supply of the No. 1 water source is 160 L/s, and its elevation is 2003.18 m. The No. 2 water supply is 81 L/s, and its elevation is 2004.36 m. Ductile iron pipes are used in the water supply network of the township. The length of each pipe section in the town’s water supply network is irregular and basically different. The price of nodular cast iron is set according to the average value of the local market price. NSGA-II’s initial population is 300; Make the number of iterations 20; The probability of variation is set to 0.04; The crossing probability is 0.5; The maximum genetic algebra is 200. Meanwhile, the reliability and economic factors are taken into consideration in the experiment, and a MOMM of the water supply network based on NSGA-II is established. The method described in the above chapters is used to solve it, and better results in each selection are retained.

Figure 5 shows the process of solving the multi-objective optimal solution of RWSN using the NSGA-II algorithm. From Figure 5a, the total cost in the life cycle of the RWSN decreases with the increase of iterations, which verifies the strong feasibility of NSGA-II for the optimization of RWSN. From Figure 5b, the average head margin of the pipe network also decreases with the increase of iterations. This situation shows that when the node excess head is less, the water pressure is lower, and the RWSN’s reliability is higher. Therefore, the result shows the whole process of the NSGA-II algorithm in solving the balance point between the economy and RWSN’s reliability. Meanwhile, the experimental results further verify the applicability of the NSGA-II algorithm for solving the optimal solution of RWSN. Then, without considering the accidents, such as pipe burst and pipe alignment, the Pareto optimal solution between the average head of the pipe network node and the annual cost can be obtained from the experiment, as shown in Figure 6 below.

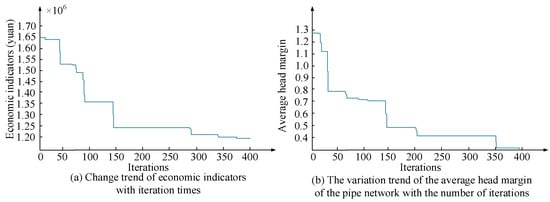
Figure 5. The process of solving the multi-objective optimal solution of RWSN using NSGA-II algorithm.

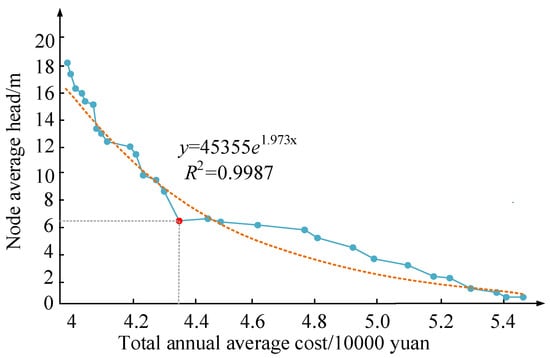
Figure 6. Multi-objective Pareto solution of RWSN based on NSGA-II algorithm.

The orange line in the figure represents the trend line of change, and the blue line represents the specific change between the average head of water supply network nodes and the annual cost of the network. From Figure 6, the average head of water supply network nodes is inversely proportional to the annual cost of the network. The node average head decreases with the increase in the annual cost. Therefore, both the reliability and economy of RWSN should be taken into consideration. As for the optimal solution selection, the annual cost of the water supply network should be as low as possible, and the reliability of the network should be as high as possible. By observing the above figure, we can choose the best point (4.38, 6.02). That is, the annual cost is CNY 438,000, and the average head of the pipe network node is 6.02 m. This point also ensures the economy and reliability of the pipe network.

Figure 7 illustrates the rural water supply pipeline optimization process combining the LM algorithm and NSGA-II algorithm. From Figure 7a,b when the iterations achieve about 210 generations, the RWSN’s economy is optimal; When the iterations achieve about 325 generations, the RWSN’s average head margin of the nodes is the best, that is, the RWSN’s reliability is the best at this time. From Figure 7c, the NSGA-II combined with LM takes less time at this time. Thus, the validity of the LM algorithm and the feasibility of NSGA-II for solving the optimization model of RWSN are verified. Subsequently, the experimental results shown in Table 1 can be obtained by calculating the hydraulic power of the water supply network through Equations (1)–(3) and (10)–(12).

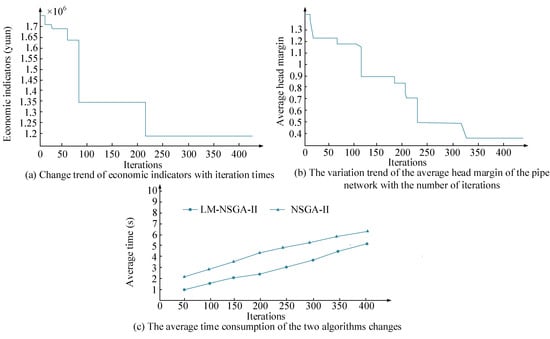
Figure 7. Optimization process of rural water supply pipeline based on LM-NSGA-II algorithm.

Table 1. Hydraulic calculation results of multi-objective water supply network.

Pipe Segment Number	g1	g2	g3	g4	g5	g6	g7	g8
Pipe length m	65	35	76	124	48	80	78	51
Pipe diameter mm	250	300	200	150	350	250	200	250
Flow L/s	24.13	26.74	35.21	23.35	32.31	27.84	13.65	11.05
head loss	1.701	1.251	0.854	1.741	0.103	0.325	0.337	0.436
Velocity m/s	1.34	0.67	0.76	1.32	0.58	0.32	0.33	0.47
Node excess head m	5.41	1.36	0.87	5.41	2.24	16.21	8.82	8.41
...	...	...	...	...	...	...	...	...
Pipe segment number	g49	g50	g51	g52	g53	/	/	/
Pipe length m	82	68	64	62	55	/	/	/
Pipe diameter mm	400	150	250	300	350	/	/	/
Flow L/s	4.33	2.01	0.98	3.11	10.72	/	/	/
head loss	0.053	0.031	0.011	0.054	0.032	/	/	/
Velocity m/s	0.04	0.15	0.41	0.14	0.23	/	/	/
Node excess head m	12.37	11.25	10.47	11.82	11.44	/	/	/

Table 1 above indicates the water calculation results. The table shows the length, pipe diameter, flow, head loss, flow rate and node excess head of each pipe section in the water supply network. Through the hydraulic check of the RWSN, the water pressure and flow rate of each node in the network meet the requirements. Therefore, based on the comprehensive consideration of economic factors and the reliability of the town, it can be concluded that the optimal node affluence head of the town’s water supply network is 6.02 m, and the annual operating cost is CNY 438,000. Comparing the results of the NSGA-II optimization model with the results based on existing traditional methods, we can obtain the results in Figure 8.

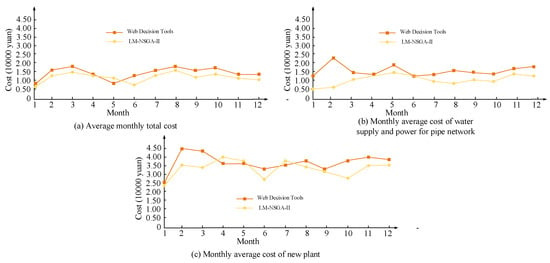
Figure 8. Comparison of optimization results between traditional methods and intelligent algorithms.

Figure 8 above shows the optimization results of the water supply network based on the Web decision-making tool in the literature [9] and the LM-NSGA-II algorithm [9]. This study will compare the solution results of water supply networks based on two methods. As shown in Figure 8, the optimal control results of water supply networks based on the LM-NSGA-II algorithm show that in terms of the cost of new water plants, the cost of the LM-NSGA-II algorithm is slightly higher than the cost of Web decision-making tools. In terms of the monthly average cost and the monthly average total cost of water supply power in the pipeline network, the cost of the LM-NSGA-II algorithm is lower than that of the Web decision-making tool. Overall, the LM-NSGA-II algorithm proposed in this study for optimizing water supply networks requires lower costs. The reliability research results of the water supply network are shown in Table 2.

Table 2. Reliability calculation results of water supply network.

Model	Hydraulic	Reliability	Entropy
Web Decision Tools	0.69	5.26	0.0541
LM-NSGA-II	0.78	5.99	0.0487

Table 2 above shows the reliability calculation results of the water supply network. From the above table, it can be seen that whether it is hydraulic reliability or entropy reliability, the reliability value of the water supply network based on the LM-NSGA-II algorithm is greater than the reliability value based on Web decision-making tools. In addition, the cost of unit reliability of water supply networks based on the LM-NSGA-II algorithm is less than that of Web decision tools. In summary, the LM-NSGA-II algorithm-based water supply network optimization method proposed in this study is not only economically applicable but also more reliable than a Web decision-making tool.

6. Conclusions

Improving the quality of life of rural residents has become an inevitable trend of rural development. To optimize the RWSN, the LM-NSGA-II algorithm is used in this study. In the experiment, the RWSN’s annual cost is used to express the RWSN’s economy, and the RWSN’s reliability is defined by the node average affluence head. After that, a MOMM was established and solved by the LM-NSGA-II algorithm. The proposed method is verified by an example. The results show that in the process of solving the optimal solution of RWSN using the NSGA-II algorithm, the economy and reliability of the network increase with the number of iterations. The results verify the applicability of the NSGA-II algorithm. The results of the NSGA-II combined with the LM algorithm show that the overall time of the model has decreased, which verifies the performance of the LM algorithm. The experimental analysis of the selected town shows that the optimal node affluence head of the town’s water supply network is 6.02m, and the annual operating cost is CNY 438,000. Finally, the experiment compares the results obtained by the LM-NSGA-II optimization model with the results obtained by the Web decision-making tool based on literature [9]. The results showed that the water supply network optimization method based on the LM-NSGA-II algorithm has higher economic applicability and reliability. The method proposed in this study shows good applicability. However, there are still some deficiencies in this study. For example, the situation is different in different towns across the country. Therefore, the universality of the study needs to be further enhanced.