A Calibration of the Contact Parameters of a Sesbania Seed Discrete Element Model Based on RSM

Abstract

In order to simulate and analyze the mechanized seeding process of sesbania seeds by using a discrete element method and improve the reliability of the discrete element simulation test, the contact parameters of sesbania seeds were calibrated in combination with the actual seed drop test and the simulated seed drop test. Through measurements, the intrinsic parameters of the sesbania seed were determined, and the discrete element simulation model of the sesbania seed was established. A measuring device that can simultaneously measure the resting angle and the stacking angle of the population was designed. The rest angle error and the stack angle error of the actual seed drop test and the simulated seed drop test were used as test indicators. The Plackett–Burman test screened out the contact parameters that had a significant effect on the test indicators. The response surface method (RSM) was used to carry out the three-factor quadratic rotation orthogonal combination test, and the mathematical regression model between the significant contact parameters and the test indexes was established. The optimal combination of contact parameters was determined using the multi-objective optimization method as follows: collision recovery coefficient between seeds of 0.463, static friction coefficient between seeds of 0.520, and rolling friction coefficient between seeds of 0.072. The discrete element model and calibration parameters of sesbania seeds were tested and verified using a fluted roller feed mechanism. The results showed that the average relative error between the measured value and the simulated value of the mass flow rate of the sesbania seeds was 2.74%, less than 5%, indicating that the discrete element simulation model of sesbania seeds and the calibration results of the contact parameters had high accuracy and reliability, which could be used for the discrete element simulation test of sesbania seeds.

1. Introduction

Sesbania is a one-year-old leguminous sesbania plant. It has the characteristics of strong nitrogen fixation ability, rich plant protein, and strong tolerance. As a high-quality green manure and forage grass, it is widely cultivated and becomes a pioneer plant for soil improvement in saline–alkali land [1,2]. In the field of agricultural mechanization, pneumatic seeders can realize the precision seeding of small particle-size seeds. At present, the pneumatic seeder is mainly for corn, soybean, wheat, and other economic crops [3]; however, there has been little research on the precision seeding of sesbania seeds. Vigorously promoting the process of the mechanized seeding of sesbania is of great significance for accelerating the development of agriculture and animal husbandry in China.

The discrete element method is a particulate material analysis method based on molecular dynamics characteristics [4]. In recent years, the discrete element method based on EDEM has been widely used, and it has gradually become the development trend used when studying the dynamics of agricultural particulate materials. It is mainly used in the interaction analysis between particulate materials and agricultural machinery equipment [5]. When the simulation analysis is carried out using EDEM discrete element software, the accuracy of the physical parameters of particulate materials is very important in maintaining the authenticity of the simulation results. The physical parameters of particulate materials are mainly divided into intrinsic parameters and contact parameters. The intrinsic parameters mainly refer to the inherent characteristic parameters of particulate materials, including Poisson’s ratio, density, shear modulus, and so on. Contact parameters mainly refer to the characteristic parameters between particulate materials and between particulate materials and agricultural machinery equipment, including collision recovery coefficient, static friction coefficient, dynamic friction coefficient, and so on [6]. Optimizing and calibrating the physical parameters of sesbania seed particle dispersion can effectively improve the consistency between EDEM discrete element simulation analysis results and real results, as well as provide an effective basis for the design and development of pneumatic seeder and greatly improve the working performance of seeding apparatus [7].

In recent years, scholars in different fields have conducted a lot of research on the calibration of seed particle parameters using the discrete element method [8,9,10]. In EDEM software, a single filling particle is spherical. Due to the irregularity of the seed particle shape, it is necessary to fill the 3D solid configuration of the seed with a template of multi-spherical particles; moreover, a different filling particle radius has a certain influence on the simulation results. Yan Jianwei et al. [11] used the method of multi-sphere-bonding polymerization and the EDEM automatic particle-filling module to establish a radish seed filling model. The influence of different filling particle radii on the rationality of the simulation results was studied and the optimal spherical filling particle radius was obtained. The purpose of the short simulation time and high precision was answered.

The resting angle and the stacking angle of granular particles are macroscopic parameters that reflect the discrete characteristics of particles and can characterize macroscopic characteristics such as friction performance and the flow performance of granular particles. Peng Fei et al. [12] independently developed a resting angle measuring device based on the injection cross-section method. The resting angle is directly measured using the cross-section profile curve of the particle accumulation body, which achieves the purpose of saving materials and offers a convenient basis from which to measure; based on MATLAB image processing technology, Li Zhanpeng et al. [13] extracted the boundary contour of the particulate material accumulation body and used the programming algorithm to fit the boundary contour line to obtain the stacking angle of the particulate material, which greatly reduced the angle error of the manual measurement; Ma Wenpeng et al. [14] proposed using either a single angle of resting or stacking angle as the test index; moreover, the parameter calibration results are only a set of solutions, which inevitably leads to a local optimal solution. Therefore, the practical significance of establishing a multi-index parameter optimization mathematical model is emphasized. On this basis, the main contact parameters of the discrete element model of alfalfa seeds were calibrated by taking the error between the measured values and the simulated measured values of the resting angle and the stacking angle of the particulate materials as the index.

Based on the Hertz–Mindlin (non-slip) contact model, Zhang Guozhong et al. [15] used the error between the measured value and the simulated value of the particle resting angle and the particle stacking angle as the response value and then determined the optimal discrete element parameter combination for the significant factors affecting the response value through the steepest ascent test; then, the reliability of the optimal parameter combination was verified using the hopper test. Ding Xinting et al. [16] used the Plackett–Burman design and the steepest ascent experiment to determine whether the static friction coefficient and rolling friction coefficient between rapeseed and steel plate have a significant effect on the stacking angle of the response value. The response surface method (RSM) and machine learning were used to optimize and compare the significant parameters. The results show that the BP artificial neural network based on a genetic algorithm (GA) has better prediction ability and stability. The results avoid the influence of local optimal solution in response surface analysis and can be used for discrete element model simulation. Some scholars have also performed a lot of research on the construction of particle models and the discrete element method (DEM). Qu Tongming et al. [17] trained a data-driven constitutive model using an RNN neural network based on triaxial test data and provided an alternative to the phenomenological model of granular materials currently used. Gao Wei et al. [18] proposed a three-dimensional isogeometric/multi-sphere discrete element coupling method that combines the advantages of strong particle shape expression, excellent robustness, and high accuracy in multi-sphere discrete element modeling and isogeometric analysis (IGA). They also used the discrete element method (DEM) to analyze the mixing performance of particles in a ribbon mixer with a double U-shaped vessel [19].

This paper takes sesbania seeds as the research object. A new type of seed-dropping device that can simultaneously measure the resting angle and stacking angle was designed. The discrete element model of sesbania seeds filled with multiple spherical particles was established by using EDEM software and the Hertz–Mindlin (non-slip) contact model. By importing the falling device model into EDEM software, and based on the actual physical experiment and simulation experiment, the error between the measured value and the simulated value of the resting angle and the stacking angle of the sesbania seeds was taken as the target, and the contact parameters that have a significant effect on the target value were selected using the Plackett–Burman design. RSM analysis was performed using a central composite design test, and a multiple regression mathematical model comprising significant parameters and target values was constructed. Multi-objective optimization was carried out using Design-Expert software (version 13) to obtain the optimal combination of contact parameters. The seeding test was then carried out. This paper aims to provide a theoretical basis for the establishment of the discrete element simulation model and parameter calibration of sesbania seed particles.

2. Simulation Parameter Calibration of Sesbania Discrete Element Model

The resting angle and the stacking angle are the angles between the free cone and the horizontal plane formed by the particulate material in the natural state. They can characterize the discrete properties of particulate materials, and the formation of natural resting angle and stacking angle is related to the physical properties of the particulate material itself and the contact material [20]. Therefore, they can be used as an important index for the calibration of discrete element model simulation parameters of particulate materials.

2.1. Actual Seed Drop Test

The resting angle and the stacking angle of sesbania seeds were measured simultaneously by using the self-developed measuring device for the seed drop test, as shown in Figure 1a. The device is mainly composed of two layers of seed boxes, and the baffle and the material of the device are made of transparent resin. The test material used was the Yan Jing No.1 sesbania seed. The test measurement method is as follows: firstly, insert the baffle into the side of the lower seed box; secondly, slowly fill the upper seed box with sesbania seeds until the seeds reach about 2/3 of the volume of the upper seed box, and try to ensure that the upper surface of the seed heap is horizontal; lastly, quickly pull the baffle upwards and the seeds in the upper seed box will flow into the lower seed box under the action of gravity; the remaining seeds form a stair-shaped seed pile in the upper seed box, and the seeds flowing into the lower seed box form another stair-shaped seed pile in the lower seed box. The acute angle between the horizontal plane and the slope of the stair-shaped seed pile in the upper seed box is the resting angle of the seed, which is recorded as θ; the angle between the horizontal plane and the slope of the stair-shaped seed pile in the lower seed box is the stacking angle of the seed and is recorded as φ.

Figure 1. Actual seed drop test: (a) geometric dimensions of the seed drop test device (unit: mm), (b) the beginning of the seed drop test, and (c) the result of the seed drop test.

In order to avoid the influence of human measurement error, the resting angle and stacking angle are measured using computer image processing technology. After the state of the seed pile is stable, use the camera to collect the image of the seed pile, and use the MATLAB software (version R2018a) to process the image of the resting angle and the stacking angle. Firstly, use the noise reduction processing tool to obtain the original image, as shown in Figure 2a. The left side is the image of the resting angle and the right side is the image of the stacking angle. Secondly, after the processing of the original images into grayscale and binary images, as shown in Figure 2b,c, extract the features of the edge pixel points of the seed pile; the connections of the edge pixel points comprise the boundary contour curve of the seed pile. Based on the least square method, fit the boundary contour curve of the seed pile to an optimal straight line. This optimal straight line is shown in Figure 2d, in which the line’s slope is the tangent value of the actual physical resting angle and the actual physical stacking angle of seeds.

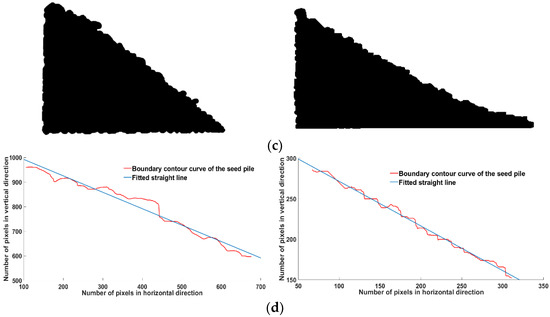
Figure 2. Seed heap image processing based on MATLAB software: (a) original image, (b) grayscale image, (c) binary image, and (d) line fitting image.

The resting angle and the stacking angle in the front and back directions of the upper and lower seed boxes were measured in each group of experiments, repeated 5 times, and the average value was calculated. Table 1 shows the measurement results: the average values of the resting angle and stacking angle in the test are 34.906° and 26.975°. The measurement method of the resting angle and stacking angle in the simulated seed drop test is the same as this method.

Table 1. Measurement results of repose angle and accumulation angle in actual seed drop test.

Test Serial Number	Resting Angle/°		Stacking Angle/°
	Front Direction	Back Direction	Front Direction	Back Direction
1	33.157	36.204	28.396	20.862
2	37.740	34.106	34.106	26.812
3	32.502	35.803	28.267	23.316
4	35.106	33.251	27.145	24.603
5	34.753	36.434	28.719	27.526
Mean value	34.906		26.975

2.2. Simulated Seed Drop Test

The basic physical parameters of sesbania seed measured using physical tests are shown in Table 2. Due to the irregular shape of sesbania seeds, it is necessary to establish the discrete element simulation model of sesbania seeds accurately; therefore, 500 seeds of Yan Jing No.1 sesbania seeds were selected randomly, the size of the three axes size was measured using a digital vernier caliper. Finally, the average length, width, and thickness of the seeds were obtained as follows: 4.07 mm, 2.52 mm, and 2.14 mm. Based on the actual measured seed triaxial size data, the sesbania seed particle that was similar to the average values of the length, width, and thickness was selected to establish the three-dimensional model. Based on the theory of reverse engineering, the contour shape of the seed surface is scanned using a 3D scanner and grating projection to obtain the point cloud image of the seed’s shape; then, SolidWorks software was used to export the point cloud data into a three-dimensional model of the seed contour, as shown in Figure 3.

Table 2. Basic physical parameters of sesbania seed.

Parameter	Value
Length/mm	4.07
Width/mm	2.52
Thickness/mm	2.14
Water content/%	10.81
Density/kg·m−3	1036.82
Thousand seed weight/kg	0.02
Moment of inertia/(kg/m2)	Jx	1.45 × 10−11
	Jy	1.57 × 10−11
	Jz	7.45 × 10−12

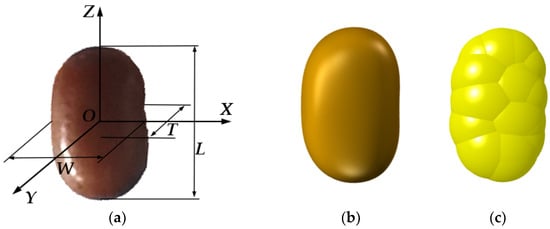
Figure 3. Establishment process of discrete element model of sesbania seed: (a) actual shape of the sesbania seed, (b) 3D model of sesbania seed, and (c) discrete element simulation model of sesbania seeds.

The sesbania seed model was imported using EDEM 2022 software. Due to the irregular shape of sesbania seeds, the method of multi-spherical particle filling was adopted. Therefore, the multi-sphere particle filling method and EDEM automatic particle filling module were used to establish a sesbania seed filling model. The smoothness was set to 4, the minimum spherical radius was 0.7 mm, and the grid elements in the X, Y, and Z directions were 45, 35, and 30 respectively. Figure 3c shows the seed discrete element multi-spherical filling model.

The actual size of the seed-dropping device was measured using SolidWorks 2022 to establish its 3D model. It was then saved in IGS format, and the model was imported and opened using EDEM 2022. After consulting the literature [21,22,23], Poisson’s ratio of transparent resin was set to 0.4, the density of the transparent resin was set to 1180 kg/m³, and the shear modulus of the transparent resin was set to 0.18 GPa.

Considering the relatively smooth surface and low water content of sesbania seeds, there is almost no bonding between the seeds [24]; therefore, the Hertz–Mindlin (no slip) contact model was selected as the contact model between the seeds and contact materials [25,26]. The generated number of seeds and the test process were the same as in the actual seed drop test. In the simulated seed drop test, the seed particles were dynamically generated into the seed box using the particle factory, and the total particle number of seeds was 5000. Meanwhile, the automatic particle filling module in the EDEM software used 22 discrete elements to fill a single seed particle, and the number of the discrete elements used in the simulated seed drop test was 1.1 × 10⁵. Figure 4 shows the process of the simulated seed drop test. After the simulation test was completed, the image of the resting angle and the image of the stacking angle were collected, using MATLAB software for image processing, and the simulated resting angle β and the simulated stacking angle γ were obtained. Then, the rest angle error and stack angle error between the actual seed drop test and simulated seed drop test were calculated, and the calculation formula is as follows:

$${\mathrm{Y}}_1=\frac{\beta -\theta }{\theta }\times 100\%$$

(1)

$${\mathrm{Y}}_2=\frac{\gamma -\phi }{\phi }\times 100\%$$

(2)

where the actual resting angle is θ; the actual stacking angle is φ; the rest angle error between the actual seed drop test and simulated seed drop test is Y₁, and the stack angle error between the actual seed drop test and simulated seed drop test is Y₂.

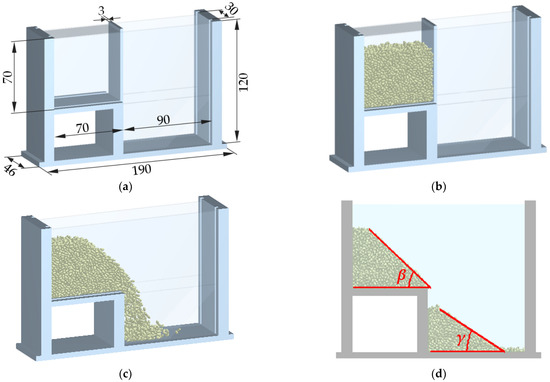
Figure 4. The process of the simulated seed drop test: (a) start state and geometric dimensions of the simulation model (unit: mm), (b) dynamic generation of sesbania seed particles, (c) pulling out of the baffle, and (d) the generated simulated resting angle and the simulated stacking angle.

2.3. Plackett–Burman Test

The Plackett–Burman test method is based on comparing the differences in the effects of two-level factors on the target response value and further screening out the parameters that have a significant effect on the target value [27]. Design-Expert software was used to design the Plackett–Burman test, taking the rest angle error Y1 and the stack angle error Y2 of the seed drop test as the response value and setting 11 factors; the parameters A~G are real simulation parameters, and the parameters H~K are virtual parameters. By consulting the relevant literature and a large number of pre-tests in the early stage, the value range of each influence parameter is selected. Each influence parameter is set to high and low levels according to their selection range, and the code values are 1 and −1, as shown in Table 3. Twelve groups of tests were set according to the coding value of the test, and each group repeated the simulated seed drop test five times and selected the average value of the angle before calculating the average of Y₁ and Y₂.

Table 3. The contact parameter values of the P-B test.

Contact Parameter	Meaning	Low Level (−1)	High Level (+1)
A	Collision recovery coefficient between seed and wall	0.1	0.9
B	Static friction coefficient between seed and wall	0.3	0.5
C	Rolling friction coefficient between seed and wall	0.05	0.45
D	Poisson’s ratio of seed	0.3	0.5
E	Collision recovery coefficient between seeds	0.17	0.73
F	Static friction coefficient between seeds	0.27	0.75
G	Rolling friction coefficient between seeds	0.01	0.13
H I J K	Virtual parameters

Table 4 shows the design scheme of the P-B test and the result of the simulated seed drop test. Design-Expert software was used to employ the analysis of variance (ANOVA) for the simulation test result and obtain the significance ranking of each parameter to the response value, as shown in Table 5.

Table 4. The design scheme of the P-B test and the result of the simulated test.

NO.	Level Value											Y1	Y2
	A	B	C	D	E	F	G	H	I	J	K
1	1	1	−1	1	−1	1	1	−1	−1	1	−1	22.133	32.211
2	−1	1	1	−1	1	1	1	−1	−1	−1	1	24.769	31.86
3	1	−1	1	1	1	−1	1	1	−1	−1	−1	23.933	26.919
4	−1	1	−1	1	1	1	−1	1	1	−1	−1	18.042	28.226
5	−1	−1	1	−1	−1	1	1	1	1	1	−1	24.115	29.134
6	−1	−1	−1	1	1	−1	1	−1	1	1	1	22.006	28.183
7	1	−1	−1	−1	1	1	−1	1	−1	1	1	21.149	25.561
8	1	1	−1	−1	−1	−1	1	1	1	−1	1	19.945	23.257
9	1	1	1	−1	1	−1	−1	−1	1	1	−1	12.692	20.881
10	−1	1	1	1	−1	−1	−1	1	−1	1	1	7.711	18.277
11	1	−1	1	1	−1	1	−1	−1	1	−1	1	13.462	22.711
12	−1	−1	−1	−1	−1	−1	−1	−1	−1	−1	−1	11.252	13.55

Table 5. Significance analysis of P-B test parameters.

Parameters	Y1				Y2
	Stdized Effct	Sum of Squares	%Contribution	Ranking	Stdized Effct	Sum of Squares	%Contribution	Ranking
A	0.90	2.45	0.67	7	0.39	0.44	0.13	6
B	−1.77	9.41	2.59	4	1.44	6.24	1.82	5
C	−1.31	5.13	1.41	5	−0.20	0.12	0.035	7
D	−1.11	3.67	1.01	6	2.05	12.57	3.67	4
E	4.00	47.89	13.19	3	3.75	42.15	12.32	3
F	4.36	56.90	15.67	2	6.44	124.40	36.35	2
G	8.77	230.50	63.47	1	7.06	149.52	43.70	1

Through the P-B test results, it can be concluded that the collision recovery coefficient between seeds E, the static friction coefficient between seeds F, and the rolling friction coefficient between seeds G have a significant effect on the rest angle error Y₁ and the stack angle error Y₂, and the effect of other parameters on the response value is not significant. Therefore, the significant parameters E, F, and G were optimized in the steepest ascent test. In this test, the C.V. were 7.28% and 5.18%, respectively, and they were all less than 10%. This shows that the test results are highly reliable. The adjusted R² were 0.9455 and 0.9459, respectively, and all were close to 1, showing that the regression model established in this test has better fitting superiority. Adeq Precision measures the signal-to-noise ratios, which were 16.633 and 17.449; their values were greater than four and are, thus, considered reasonable. Therefore, the data results of this test have high reliability.

2.4. Steepest Ascent Test

In order to optimize the contact parameters E, F, and G with significant influence and determine the high-level values, low-level values, and zero-level values of the three-factor quadratic rotation orthogonal combination test, based on the analysis results of the P-B test, the steepest ascent test was carried out. The parameters were set according to the insignificant effects on the middle values, that is, the collision recovery coefficient between seed and wall was 0.5, the static friction coefficient between seed and wall was 0.4, the rolling friction coefficient between seed and wall was 0.25, and Poisson’s ratio of seeds was 0.4. Because the standardized effect of the three significant parameters was positive in all, the parameter values were arranged from low to high. According to the steepest ascent test design, the simulated seed drop test was carried out using EDEM 2022 software. Each group of tests was conducted five times and the average value was selected; then, the rest angle error and the stack angle error were calculated. Table 6 shows the design scheme and results of the steepest ascent test.

Table 6. The design scheme and results of the steepest ascent test.

NO.	Collision Recovery Coefficient between Seeds E	Static Friction Coefficient between Seeds F	Rolling Friction Coefficient between Seeds G	Rest Angle Error Y1	Stack Angle Error Y2
1	0.17	0.27	0.01	19.86	21.93
2	0.31	0.39	0.04	11.68	8.94
3	0.45	0.51	0.07	3.12	2.79
4	0.59	0.63	0.1	9.90	8.65
5	0.73	0.75	0.13	29.37	24.94

The steepest ascent test results show that, with an increase in the collision recovery coefficient between seeds E, the static friction coefficient between seeds F, and the rolling friction coefficient between seeds G, both the rest angle error Y₁ and the stack angle error Y₂ showed a trend of decreasing first and then increasing. Among them, the rest angle error and the stack angle error in the third group of tests were the smallest. Therefore, it can be inferred that the optimal parameter range is around the level of the third set of tests; the second, third, and fourth groups of test levels were selected as the low, middle, and high levels of the three-factor quadratic rotation orthogonal combination test, and this established the RSM analysis and regression model. The optimization ranges of the collision recovery coefficient between seeds, the static friction coefficient between seeds, and the rolling friction coefficient between seeds were 0.31~0.59, 0.39~0.63, and 0.04~0.10, respectively.

2.5. Three-Factor Quadratic Rotation Orthogonal Combination Test

Taking the collision recovery coefficient between seeds E, the static friction coefficient between seeds F, and the rolling friction coefficient between seeds G as the test factors, according to the results of the steepest ascent test, the second, third, and fourth groups’ sets of tests are low level (−1), middle level (0), and high level (1), respectively, taking the rest angle error Y₁ and the stack angle error Y₂ as response value and carrying out a three-factor quadratic rotational orthogonal combination test.

The coded values of the test factors are shown in Table 7. Twenty-three test points were set for the test scheme, and the test scheme included 14 test analysis factors and 9 zero-point estimation errors. The test design scheme and results are shown in Table 8 (e, f, and g are the coded values of the test factors), repeating each experiment five times and taking the average value.

Table 7. The code values of the test factors.

Code Value	Collision Recovery Coefficient between Seeds E	Static Friction Coefficient between Seeds F	Rolling Friction Coefficient between Seeds G
−1.682	0.31	0.39	0.04
−1	0.37	0.44	0.05
0	0.45	0.51	0.07
1	0.53	0.58	0.09
1.682	0.59	0.63	0.10

Table 8. The test design scheme and results.

NO.	e	f	g	Response Value/%
				Y1	Y2
1	−1	−1	−1	17.257	21.619
2	1	−1	−1	20.040	19.560
3	−1	1	−1	16.856	17.255
4	1	1	−1	17.979	15.413
5	−1	−1	1	22.905	19.412
6	1	−1	1	15.214	16.686
7	−1	1	1	17.623	16.525
8	1	1	1	13.024	13.076
9	−1.682	0	0	21.652	18.496
10	1.682	0	0	18.376	8.920
11	0	−1.682	0	14.423	16.987
12	0	1.682	0	10.057	15.547
13	0	0	−1.682	23.478	19.387
14	0	0	1.682	16.913	12.648
15	0	0	0	0.758	2.814
16	0	0	0	2.513	1.167
17	0	0	0	0.268	2.628
18	0	0	0	1.325	2.156
19	0	0	0	1.516	3.926
20	0	0	0	1.264	0.854
21	0	0	0	2.518	0.941
22	0	0	0	3.524	2.874
23	0	0	0	0.656	4.165

3. Test Results and Analysis

3.1. Mathematical Regression Modeling and Significance Testing

3.1.1. Mathematical Regression Modeling and Significance Testing for Rest Angle Error

Design-Expert software was used to conduct multiple regression analysis for the test data and obtain the regression equation of the effect of each factor on the rest angle error:

$$\begin{array}{ll}{Y}_1& =434.02251-755.51025E-716.29295F-2012.16577G\\ & +30.13622EF-1363.36922EG-492.02847FG\\ & +914.83957E^2+705.33720F^2+20124.83960G^2\end{array}$$

(3)

The response surface analysis of the influencing factors was carried out using the central composite design (CCD), and the significance test results of the regression equation are shown in Table 9. In it, the p-value of the model is less than 0.0001, and the p-value of the Lack of Fit is 0.1416; therefore, the model is significant and the Lack of Fit is insignificant, which indicates that the regression model has a small percentage of non-normal errors. Therefore, the model can accurately express the relationship between response values and impact parameters. The R² and the adjusted R² are 0.9863 and 0.9767, suggesting that the regression equation possesses high reliability. Among them, the effects of F, EG, E², F², and G² on the repose angle error are highly significant (p < 0.01); the effects of E and G on the repose angle error are significant (p < 0.05).

Table 9. ANOVA for regression equations with CCD response surfaces.

ANOVA Object	Rest Angle Error				Stack Angle Error
	Sum of Squares	df	F-Value	p-Value	Sum of Squares	df	F-Value	p-Value
Model	1563.73	9	103.64	<0.0001 **	1215.33	9	48.43	<0.0001 **
E	14.13	1	8.43	0.0123 *	50.19	1	18.00	0.0010 **
F	21.86	1	13.04	0.0032 **	22.25	1	7.98	0.0143 *
G	15.20	1	9.07	0.0100 *	27.79	1	9.97	0.0076 **
EF	0.26	1	0.15	0.7021	0.032	1	0.011	0.9163
EG	32.79	1	19.56	0.0007 **	0.65	1	0.23	0.6382
FG	3.14	1	1.87	0.1945	0.51	1	0.18	0.6768
E2	638.59	1	380.92	<0.0001 **	290.55	1	104.21	<0.0001 **
F2	204.90	1	122.22	<0.0001 **	426.50	1	152.97	<0.0001 **
G2	651.58	1	388.67	<0.0001 **	412.10	1	147.81	<0.0001 **
Residual	21.79	13			36.25	13
Lack of fit	12.85	5	2.30	0.1416	24.26	5	3.24	0.0683
Pure Error	8.95	8			11.99	8
Cor Total	1585.52	22			1251.58	22

Note: * indicates significant effect (0.01 < p ≤ 0.05), ** indicates extremely significant effect (p ≤ 0.01).

3.1.2. Mathematical Regression Modeling and Significance Testing for Stack Angle Error

Design-Expert software was used to conduct a multiple regression analysis on the test data and obtain the regression equation of the effect of each factor on the accumulation angle error:

$$\begin{array}{ll}{Y}_2& =494.10418-559.57706E-1064.92559F-2335.38929G\\ & -10.64869EF-191.42391EG+197.79348FG\\ & +617.08715E^2+1017.63251F^2+16004.89795G^2\end{array}$$

(4)

The response surface analysis of the influencing factors was carried out using the central composite design (CCD), and the significance test results of the regression equation are shown in Table 9. The p-value of the model is less than 0.0001, and the p-value of the Lack of Fit is 0.0683; therefore, the model is significant and the Lack of Fit is insignificant. This indicates that the regression model has a small percentage of non-normal errors. Therefore, the model can accurately express the relationship between response values and impact parameters. The R² and the adjusted R² are 0.9710 and 0.9510, suggesting that the regression equation possesses high reliability. Among them, the effects of E, G, E², F², and G² on the accumulation angle error are highly significant (p < 0.01); the effects of F on the accumulation angle error are significant (p < 0.05).

3.2. The Influence of Interaction Term on Test Index

3.2.1. The Interaction Effect of Test Factors on Rest Angle Error

A response surface analysis of test data can reflect the interaction effect of the collision recovery coefficient between seeds, the static friction coefficient between seeds, and the rolling friction coefficient between seeds in relation to the rest angle error. The response surface is shown in Figure 5. As shown, the contour line of the response surface presents an ellipse with a large curvature, and this directly reflects that the interaction between factors has a significant effect on the response values. The rest angle error decreases first and then increases with an increase in the collision recovery coefficient between seeds, the static friction coefficient between seeds, and the rolling friction coefficient between seeds. When the collision recovery coefficient between seeds is 0.41~0.49, the static friction coefficient between seeds is 0.50~0.55, and the rolling friction coefficient between seeds is 0.067~0.078, the rest angle error is the smallest.

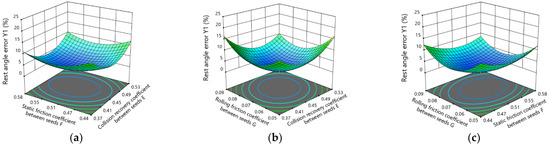
Figure 5. Effect of the interaction term of the test factors on the rest angle error: (a) influence of the interaction of collision recovery coefficient between seeds and static friction coefficient between seeds on rest angle error, (b) influence of the interaction of collision recovery coefficient between seeds and rolling friction coefficient between seeds on rest angle error, and (c) influence of the interaction of static friction coefficient between seeds and rolling friction coefficient between seeds on rest angle error.

3.2.2. The Interaction Effect of Test Factors on Stack Angle Error

The response surface reflecting the effect of the interaction between the test factors on the stack angle error is shown in Figure 6. As shown in Figure 5, the shape of the contour line is close to an ellipse; therefore, the interaction between the contact parameters is significant, and the stack angle error decreases first and then increases with an increase in the collision recovery coefficient between seeds, the static friction coefficient between seeds, and rolling friction coefficient between seeds. When the collision recovery coefficient between seeds is 0.41~0.49, the static friction coefficient between seeds is 0.50~0.55, and the rolling friction coefficient between seeds is 0.067~0.078, the stack angle error is the smallest.

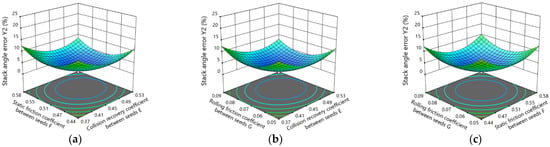
Figure 6. Effect of the interaction term of the test factors on the stack angle error: (a) influence of the interaction of collision recovery coefficient between seeds and static friction coefficient between seeds on stack angle error, (b) influence of the interaction of collision recovery coefficient between seeds and rolling friction coefficient between seeds on stack angle error, and (c) influence of the interaction of static friction coefficient between seeds and rolling friction coefficient between seeds on stack angle error.

3.3. Multi-Objective Optimization of Contact Parameters

To obtain the minimum rest angle error and minimum stack angle error as the objectives of test optimization, the collision recovery coefficient between seeds, the static friction coefficient between seeds, and the rolling friction coefficient between seeds, as independent parameters, were analyzed in relation to the response surface through Design-Expert software to optimize and solve the regression model. The objective function and constraints are as follows:

$$\{\begin{array}{l}\min \left(Y_1\left(E,F,G\right),Y_2\left(E,F,G\right)\right)\\ s.t.\{\begin{array}{l}0.41\le E\le 0.49\\ 0.50\le F\le 0.55\\ 0.067\le G\le 0.078\end{array}\end{array}$$

(5)

Considering the minimum rest angle error and minimum stack angle error, through our analysis, the optimal combination of contact parameters is obtained as follows: collision recovery coefficient between seeds is 0.463, static friction coefficient between seeds is 0.520, and rolling friction coefficient between seeds is 0.072. Under the optimal parameter combination, the rest angle error is 1.420%, and the stack angle error is 1.991%. After inputting the calibrated contact parameters into the EDEM software and conducting five simulated seed drop tests, the average value of the simulated resting angle is 35.382°, and the average value of the simulated stacking angle is 27.466°. The rest angle error is 1.364%, and the stack angle error is 1.821%. This shows that the calibration results of the optimal combination of the contact parameters are consistent with the actual results; therefore, the calibration results of the parameters can be applied to the subsequent EDEM simulation test.

4. Test Verification

In order to further verify the accuracy and reliability of the discrete element model of the sesbania seeds and calibrated contact parameters, experimental verification of the seeding test using a fluted roller feed mechanism was employed. The mass flow rate of the seeds at the seeding port was used as the test index to compare the measured and simulated values of the mass flow rate under the different rotating speeds of the sheave. The fluted roller feed mechanism is 3D printed, and the material used for 3D printing is resin, as shown in Figure 7. In this test, the seed of Yanjing No.1 sesbania was chosen as the test material. During the test, a certain amount of sesbania seeds were used to fill the seed box. The stepping motor was then started, which drives the sheave to rotate through the drive shaft, and the population is filled into the groove of the sheave under the action of gravity. After filling, protecting, and falling, the seeds fall to the collection plate below the seed outlet under the action of gravity, and the weight of the seeds is recorded in the collection tray every 1 min. Finally, the mass flow rate of the seed is calculated. This is repeated over five tests, and the average mass flow rate is calculated. The simulation model of the fluted roller feed mechanism is imported and the contact parameters are calibrated; then, the discrete element model of the sesbania seed is imported into the EDEM software, whereby simulated tests are carried out under the same conditions as the actual test. Finally, the mass flow rate of the seeding port is outputted.

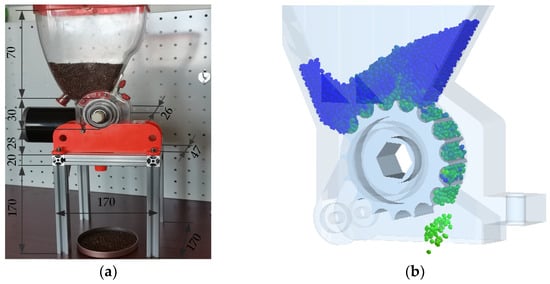
Figure 7. Verification test: (a) geometric dimensions and real physical test of the fluted roller feed mechanism, (b) simulation test.

Through an analysis, the measured and simulated values of the seed mass flow rate under the different rotating speeds of the sheave are shown in Figure 8. As shown in the figure, the trend of the measured and simulated values of the mass flow rate of the sesbania seeds is basically linear with the rotating speed of the sheave, and the average relative error is 2.74% (less than 5%); therefore, the discrete element simulation model of sesbania seeds and the calibration results of the contact parameters are in line with the actual situation. To sum up, they can be applied to discrete element simulation tests.

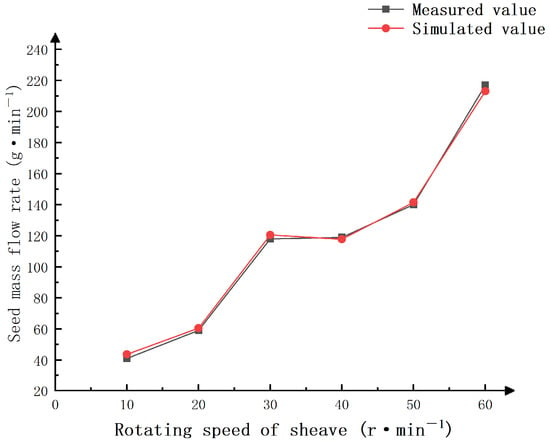
Figure 8. Result of the measured and simulated values of the seed mass flow rate under different rotating speeds of the sheave.

5. Conclusions

(1) We developed a new type of seed drop test device that can simultaneously measure the resting angle and the stacking angle and has the advantages of a simple and convenient operation. Taking sesbania seeds as the research object, through a seed dropping test, and based on the digital image processing technology of MATLAB software to fit the boundary contour curve of the seed pile to an optimal straight line, the actual resting angle and actual stacking angle of the seed pile were obtained as 34.906° and 26.975°;

(2) The three-axis size of the sesbania seeds was measured, and the selected seed particles that were similar to the average size of the three-axis were used in 3D scanning technology to obtain point cloud data on the seed surface; then, the point cloud data were exported to a three-dimensional model of the seed contour using SolidWorks software. Finally, a 3D model of a sesbania seed was imported into EDEM software. Based on the method of multi-spherical particle filling and the Hertz–Mindlin (no slip) contact model to establish a discrete element simulation model of the sesbania seed, we conducted a simulated seed drop test. Taking the rest angle error and stack angle error of the seed drop test as response values, the contact parameters with the most significant effect on the response values were screened using the Plackett–Burman test, including the collision recovery coefficient between seeds, static friction coefficient between seeds, and rolling friction coefficient between seeds; the optimal parameter range of these three contact parameters was further refined by the steepest ascent test. Taking these three contact parameters as test factors, and taking the rest angle error and stack angle error as response values, a three-factor quadratic rotation orthogonal combination test was carried out to establish a multiple mathematical regression model between test factors and response values. The ANOVA shows that the effects of the three contact parameters and their quadratic terms on the rest angle error and stack angle error are significant; using Design-Expert software to perform response surface analysis, the results showed that the interaction between each contact parameter has a significant effect on both the rest angle error and the stack angle error;

(3) Taking the minimum rest angle error and the minimum stack angle error as the optimization index, and taking the collision recovery coefficient between seeds, static friction coefficient between seeds, and rolling friction coefficient between seeds as the optimization object, we used Design-Expert software to optimize and solve the regression model, taking into account the minimum rest angle error and the minimum stack angle error. The optimal combination of contact parameters was obtained as follows: the collision recovery coefficient between seeds is 0.463; the static friction coefficient between seeds is 0.520; and the rolling friction coefficient between seeds is 0.072. At this time, the rest angle error is 1.420%, and the stack angle error is 1.991%;

(4) We conducted a seeding test through a fluted roller feed mechanism based on the discrete element simulation model of the sesbania seed and the calibrated contact parameter combination to conduct a simulated seeding test using EDEM software. The results of the validation test show that, under the condition of different speeds of the sheave, the average relative error between the measured value and the simulated value of the seed mass flow rate is 2.74%. Therefore, the discrete element model of sesbania seeds and the calibration results of the contact parameters established in this study are accurate and reliable and can be used for a discrete element simulation test.