A Novel MPPT Heating Control Strategy Applied to the Induction Heating System

Abstract

This study proposes an induction heating system with maximum power-point tracking (MPPT) control strategy. The system architecture adopts a 1.3 kW full-bridge series resonant circuit with a step-down transformer and adjusts the operating frequency by a microcontroller unit to improve the heating efficiency. Secondly, the proposed MPPT control strategy based on induction heating uses the relationship between the operating frequency and the system heating temperature to find the operating frequency corresponding to the maximum power point (MPP) quickly. Then, an additional hill-climbing algorithm adjusting the duty cycle is applied to reach the duty cycle corresponding to the MPP. Under the simulation and actual experimental measurement, the traditional control strategy has 76% and 68% at 500 and 750 degrees, respectively, and it takes 320 s for the system to reach 750 degrees. By contrast, the proposed MPPT control strategy achieves 96% efficiency when the system heating temperature is 500 and 750 degrees, and it only takes 120 s to reach the system heating temperature to 750 degrees. The contribution of this study is that the traditional full-bridge series resonant converter is implemented for the proposed induction heating system, where the proposed MPPT control strategy applied to the proposed induction heating system significantly has high efficiency, high stability, and high heating speed advantages, which can be accurately controlled.

1. Introduction

Traditional heating technology generates heat by burning coal, gas, biomass, etc. The process of burning causes problems, such as environmental pollution and low heating efficiency. Therefore, using the electric method for heating has been increasingly popular and well developed, including resistance heating [1], infrared heating [2], microwave heating [3,4], and induction heating [5,6,7,8], and other technologies. The comparison between these four heating methods is shown in Table 1. Induction heating has a simple mechanical structure, safety features without an open flame, and high heating efficiency within these heating technologies. Hence, the induction heating method is widely used in industrial applications (such as inductor applications [9,10]) and household applications (such as cooking appliances [11]). The induction heating method aims to improve power efficiency, longevity, and system controllability. In recent years, induction heating technology has been widely used in the metal industry, especially in metal heat treatment to increase metal wear resistance and toughness [12].

Table 1. Comparison among four heating methods.

Heating Method	Application	Characteristic
Resistance heating [1]	Low-temperature heating (electric kettles and pots)	Contact heating, simple heating method, low heating efficiency
Infrared heating [2]	Surface heating of various materials at the same time	Far and near-infrared has different heating effects for different materials
Microwave heating [3,4]	Heat rubber or food with more water content (microwave oven)	Rapid heating, suspicion of electromagnetic wave leakage, need to be isolated
Induction heating [5, 6, 7, 8]	Heating metal at high temperature (induction cooker)	Noncontact heating, using frequency to decide the heating depth, speed, and efficiency

To improve the efficiency of induction heating systems, the control strategies for induction heating systems are indispensable. Some control strategies have been applied to the induction heating systems: Yun and others introduced a new control strategy based on two different frequencies to improve induction heating efficiency [13]. Codecasa et al., discussed a high-speed heating control strategy. The control strategy is on the basis of nonlinear model order-reduction techniques, which can reduce the heating duration [14]. Aki et al. proposed a wireless constant temperature control strategy applied to the induction heating system. The proposed strategy can keep the induction heating system operating at a stable constant temperature depending on the superimposed voltage ratio and the heating distance relationship [15]. Villa et al., calculate the relationship between the equivalent load of the induction heating and the voltage phase with a deep-learning technique, to improve the system’s stability and accuracy [8].

The induction heating method has become more popular than other heating methods to protect the environment and improve heating efficiency. However, the heating effect (power change) is affected due to the heating load variation [16]. In order to design high-frequency resonant induction heaters, MOSFETs are usually used as power switches. If the system’s power is high, using IGBTs are required as power switches to withstand significant current stress [17]. The two most commonly used circuit structures in the induction heating system are the full-bridge resonant converter [18,19,20] and the half-bridge resonant converter [21,22]. Under the same conditions (the same input voltage and output power), the current stress on the power switches and maximum output voltage of the half-bridge resonant converter are twice those of the full-bridge. The switching loss generated by the power switches is also more significant than that of the full-bridge power switch. Thus, the full-bridge topology is more suitable for high-power occasions [18].

In conclusion, this study adopts a full-bridge series resonant converter as the main circuit structure of the induction heating system, where the power switches are IGBTs. Additionally, the equivalent model of the induction heating load is raised, and the load characteristics are analyzed. To effectively improve the heating efficiency and shorten the heating time, the feedback control method with optimal heating efficiency is proposed, which can change the system parameters according to the variation in load characteristics and maintain the safe operation of the system. This study proposes a maximum power-point tracking (MPPT) induction heating control strategy. The proposed strategy is compared with other control strategies, as shown in Table 2. Based on the comparison, the proposed control strategy has a lower complexity than the high-speed heating control, the wireless constant temperature control, or the deep-learning control. The proposed control strategy performs better than the two frequencies control. Additionally, the heating duration of the proposed control strategy is the least among these five control strategies.

Table 2. Comparison among five induction heating control strategies.

Control Method	Complexity	Performance	Heating Speed
Two frequencies control [13]	Low	Medium	Medium
High-speed heating control [14]	Medium	High	High
Wireless constant temperature control [15]	Medium	High	Medium
Deep-learning control [8]	High	High	Medium
Proposed	Low	High	High

The remaining work is structured as follows: First, the induction heating systems are described in Section 2. Section 3 includes the proposed MPPT control strategy. Experimental results are in Section 4. Finally, the concluding remarks showing the contribution of this study are offered in Section 5.

2. System Description of Induction Heating System

2.1. Principle of Induction Heating

Figure 1 shows a diagram illustrating the principle of induction heating. Induction heating is a technology that uses electromagnetic induction to heat metals. According to Faraday’s law of electromagnetic induction, as shown in Figure 1, when current i passes through the heating coil, a magnetic field φ will be generated around it, and the eddy current produces the effect of Joule heating, which increases the temperature of the workpiece [23]. According to Joule’s law, the heat generated by the eddy current is determined as follows:

$$Q=I^{2}Rt$$

(1)

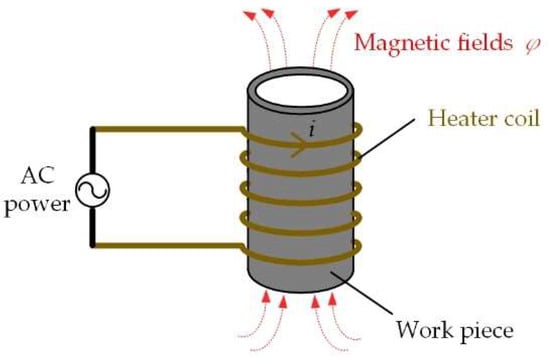
Figure 1. Diagram showing the principle of induction heating.

Through Formula (1), if the heating effect needs to be enhanced, the current passing through the heater coil should be increased.

Figure 2 shows a schematic diagram of a barrel helical heating coil. The heating coils in the induction heating equipment are all designed in the shape of the processed object. In general, if there is no special requirement, a pure copper tube with a small resistivity is usually processed into an inductor of the hollow core, which is wound in a round barrel helical coil (Figure 2). Its inductance depends on the characteristic of the coil (turns, shape, size, etc.). The value can be estimated by Formula (2), where L is the inductance of the heating coil (H), N is the turns of the coil, D is the average diameter of the coil (cm), H is the coil length (cm), and a is the coil wall thickness (cm).

$$L=\frac{D^2{N}^2}{50\left(D+2H+\frac{1.3aH}{D}\right)}$$

(2)

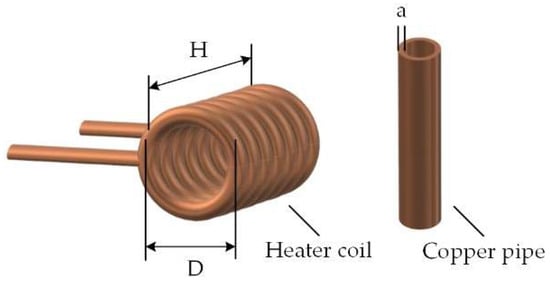
Figure 2. Schematic diagram of a round barrel helical heating coil.

Figure 3 shows a schematic diagram of the Curie temperature. The Curie temperature can be represented by the symbol T_c, whose definition is shown in Figure 3. The Curie temperature is the intersection of the two-point line (80% μ_max and 20% μ_max points) extending to the temperature axis [24]. If the temperature of the workpiece reaches T_c, the ferromagnetism of the workpiece changes into paramagnetism, which means the magnetism disappears.

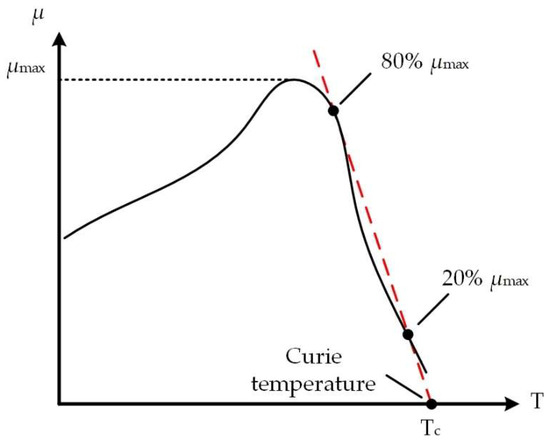
Figure 3. Schematic diagram of the Curie temperature.

There are two ways to generate heat energy during the process of electromagnetic induction heating of the ferromagnetic workpiece. One of them is generated by an eddy current, and the other (hysteresis thermal energy) is caused by hysteresis losses. Hysteresis losses are produced by repeated magnetization and demagnetization of the processed object during electromagnetic induction [25].

The load of the induction heating system includes the heating coil and the processing workpiece, as shown in Figure 4a, which can be equivalent to an inductive load, as shown in Figure 4b, which consists of a resistance R_eq and the inductance L_eq [26,27].

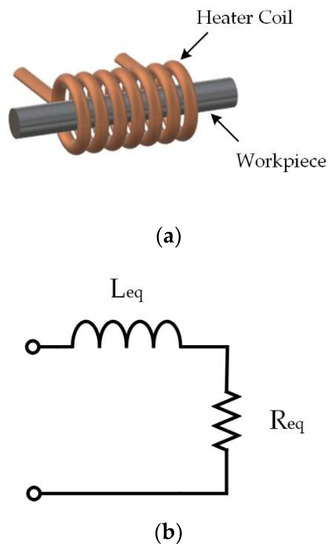
Figure 4. The heater coil and workpiece: (a) schematic diagram, (b) equivalent circuit model.

The physical variation of the processing workpieces affects their equivalent resistance and inductance during the heating process. It causes the circuit parameters to change in the induction heating system.

The equivalent inductance of the workpiece increases with the increase in temperature while heating [28]. When the temperature of the heating workpiece exceeds the Curie temperature T_c, the ferromagnetism of the workpiece disappears and converts into paramagnetism. The phenomenon causes the variation trend of the equivalent resistance and inductance value with temperature variation, as shown in Figure 5. Figure 5a is a schematic diagram of the variation trend of equivalent resistance with temperature. Figure 5b is a schematic diagram of the variation trend of equivalent inductance with temperature. In conclusion, it is necessary to note the influence of temperature on the parameters of the induction load while designing the induction heating system.

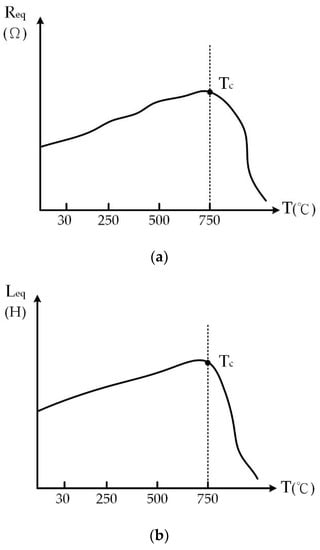
Figure 5. Schematic diagram of the trend: (a) variation in equivalent resistance with temperature, (b) variation in equivalent inductance with temperature.

2.2. Design Consideration of the Components

Figure 6 shows the circuit architecture diagram of the LC series resonant converter proposed in this study, where Figure 6a,b is based on the half-bridge converter and the full-bridge converter, respectively. This study focuses on the full-bridge LC series resonant converter because the full-bridge topology is more suitable for high-power occasions [29]. In addition, the induction load of the heating system, which is the heating coil and the workpiece, can be equivalent to an inductance L_eq and a resistance R_eq. The commonly known equivalent model for the transformer includes a magnetizing inductance L_m and a leakage inductance L_k. Since the L_m of the step-down transformer is much larger than the leakage inductance L_k and the equivalent inductance L_eq of the heating coil, L_m does not participate in the resonance. To simplify the proposed structure, this study ignores the effects of L_m and combines the external inductance L_r1 and the leakage inductance L_k into L_r, which considers their effects simultaneously.

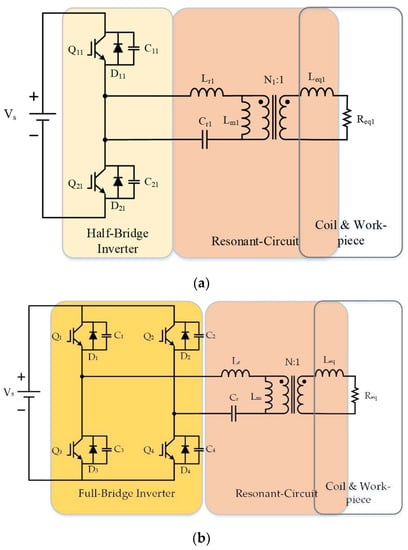
Figure 6. Architecture diagram of the LC series resonant converter: (a) half-bridge, (b) full-bridge.

Table 3 presents the specification of the full-bridge LC series resonant converter, where the rated power is 1.3 kW, the input voltage V_s is 250 V_DC, the system operating frequency range f_s is from 44 to 50 kHz, and the maximum heating temperature is 750 °C.

Table 3. Specification of the full-bridge LC series resonant converter.

Parameter	Value
Rated power	1.3 kW
Input voltage Vs	250 VDC
System operating frequency range fs	44 to 50 kHz
Maximum heating temperature	750 °C

This study analyzes the proposed full-bridge LC series resonant converter under the steady-state condition. The fundamental waveforms and the operation modes can be obtained in Figure 7 and Figure 8, respectively. The operation modes are divided into six intervals, which describe the timing relationship between the IGBTs’ control signal v_GE1(v_GE4), v_GE2(v_GE3); the voltage across the IGBTs v_CE1(v_CE4), v_CE2(v_CE3); the current of the resonant inductor i_L; the voltage across the heating coil v_o; and the turn-on current of the IGBTs i_CE1. Since the first three operation modes (t₀–t₃) and the last three operation modes (t₃–t₆) are symmetrical, the following only displays the operation and the equivalent models of the first three operation modes (t₀–t₃).

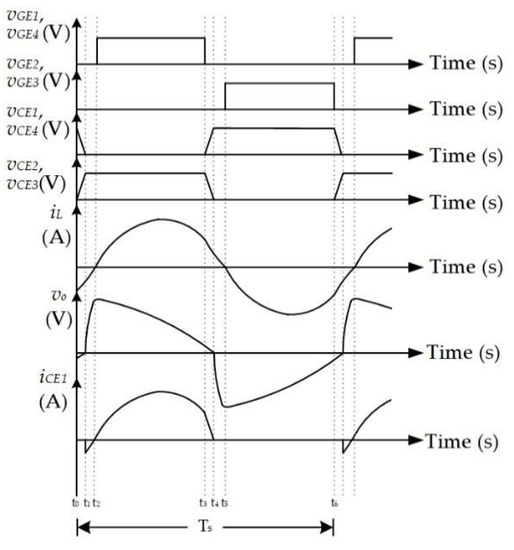
Figure 7. Fundamental waveforms of the full-bridge LC series resonant converter.

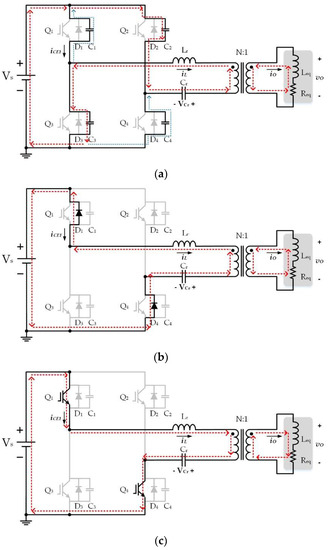
Figure 8. Operation modes of the full-bridge LC series resonant converter: (a) Interval I (t₀−t₁), (b) Interval II (t₁−t₂), and (c) Interval III (t₂−t₃).

Figure 8 shows the first three operation modes of the full-bridge LC series resonant converter. In Interval I (t₀−t₁), as shown in Figure 8a, the IGBTs Q₁, Q₂, Q₃, and Q₄ are off. Meanwhile, the current of the resonant inductor i_L maintains the current flow due to the characteristic of the inductor. The parasitic capacitances of the IGBTs C₁ and C₄ discharge the energy to the parasitic capacitances of the IGBTs C₂ and C₃ through i_L. When C₂ and C₃ are wholly charged, this interval ends. In Interval II (t₁−t₂), as shown in Figure 8b, the IGBTs Q₁, Q₂, Q₃, and Q₄ are off, and D₁, D₂ are on. Meanwhile, the processes of C₁, C₂, C₃, and C₄ are over; v_CE1 and v_CE4 are clamped at zero potential and remain until the next interval. This interval ends when Q₁ and Q₄ turn on. For Interval III (t₂−t₃), as shown in Figure 8c, Q₁, Q₄ turn on, Q₂, Q₃ stay off, and D₁, D₂ turn off at time t = t₂. Since v_CE1 and v_CE4 are clamped at zero potential in Interval II, Q₁, Q₄ achieve the ZVS operation. Meanwhile, charge L_r and C_r through i_Lr pass through Q₁, Q₄. The flow of i_Lr reverses during this interval. This interval ends when Q₁ and Q₂ turn off.

2.3. Transfer Function Analysis of Full-Bridge LC Series Resonant Converter

The parameters of the heating coil and the workpiece to be heated should be taken into consideration in the transfer function analysis. As shown in Figure 9, the equivalent model considers the transformer, the heating coil, and the processing workpiece, including the transformer magnetizing inductance L_m, the leakage inductance L_k, and the L_eq and R_eq of the heating coil and the processed object. After the parameters on the secondary side are equivalent to the primary side, the equivalent model is modified, as shown in Figure 10.

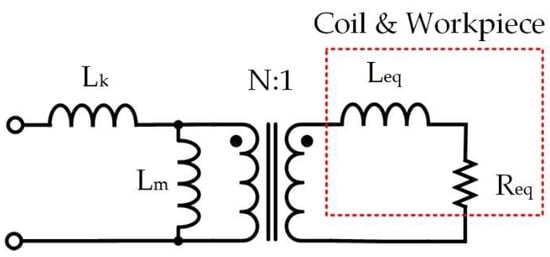
Figure 9. Equivalent simplified model of a heating coil and workpiece combined with a transformer.

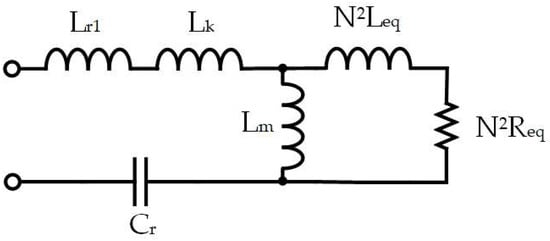
Figure 10. Modified equivalent model of a heating coil and workpiece combined with a transformer.

The value of L_m in the proposed architecture is about 1.3 mH, which is much larger than the heating coil equivalent inductance L_eq (1.25 μH), by about 1000 times. Therefore, L_m does not participate in the resonance. Thus, the equivalent model can be further modified into an RLC series resonant circuit, as shown in Figure 11, by simplifying L_r1, L_k, N²L_eq into L_r, and N²R_eq into R_o. The formulas of L_r and R_o are shown as follows:

$${\mathrm{L}}_{\mathrm{r}}={\mathrm{L}}_{\mathrm{r}1}+{\mathrm{L}}_{\mathrm{k}}+{\mathrm{N}}^2{\mathrm{L}}_{\mathrm{eq}}$$

(3)

$${\mathrm{R}}_{\mathrm{o}}={\mathrm{N}}^2{\mathrm{R}}_{\mathrm{eq}}$$

(4)

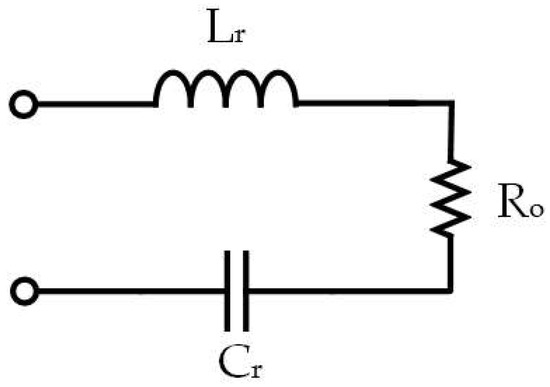
Figure 11. RLC series resonant circuit.

This study investigates the characteristics of the aforementioned RLC series resonant circuit. The first harmonic approximation (FHA) is used to draw the input equivalent circuit of the RLC series resonant circuit, as shown in Figure 12, where the proposed equivalent circuit transfers to the model under the frequency domain.

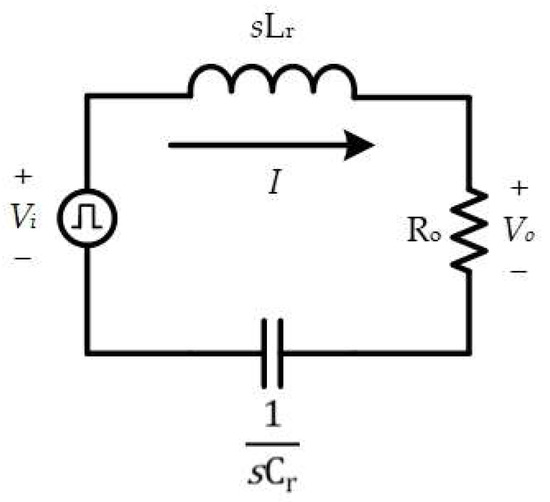
Figure 12. RLC series resonant equivalent circuit under the frequency domain.

The mathematical model of the RLC resonant converter is analyzed as follows:

First, ω, ω_r, and Q are regarded as operating frequency, resonant frequency, and quality factor, respectively, as shown in Formulas (5) and (6).

$${\omega }_r=\frac{1}{\sqrt{{\mathrm{L}}_{\mathrm{r}}{\mathrm{C}}_{\mathrm{r}}}}$$

(5)

$$\mathrm{Q}=\frac{{\omega }_r{\mathrm{L}}_{\mathrm{r}}}{{\mathrm{R}}_{\mathrm{o}}}=\frac{1}{{\omega }_r{\mathrm{C}}_{\mathrm{r}}{\mathrm{R}}_{\mathrm{o}}}$$

(6)

According to Figure 12, Formula (7) can be obtained by using the Kirchhoff voltage law (KVL).

$$V_i=V_{L_r}+V_{C_r}+V_o=I\left({\mathrm{R}}_{\mathrm{o}}+s{\mathrm{L}}_{\mathrm{r}}+\frac{1}{s{\mathrm{C}}_{\mathrm{r}}}\right)$$

(7)

Substituting s = jω into Formula (7) gives Formula (8).

$$V_i=V_{L_r}+V_{C_r}+V_o=I\left({\mathrm{R}}_{\mathrm{o}}+j\omega {\mathrm{L}}_{\mathrm{r}}+\frac{1}{j\omega {\mathrm{C}}_{\mathrm{r}}}\right)$$

(8)

According to the voltage divider rule, the formula of the voltage across R_o can be obtained as follows:

$$V_o=V_i\cdot \frac{{\mathrm{R}}_{\mathrm{o}}}{{\mathrm{R}}_{\mathrm{o}}+j\omega {\mathrm{L}}_{\mathrm{r}}+\frac{1}{j\omega {\mathrm{C}}_{\mathrm{r}}}}$$

(9)

The transfer function of V_o to V_i can be obtained by rearranging Formula (9), as shown in Formula (10).

$$\frac{V_o}{V_i}=\frac{{\mathrm{R}}_{\mathrm{o}}}{{\mathrm{R}}_{\mathrm{o}}+j\omega {\mathrm{L}}_{\mathrm{r}}+\frac{1}{j\omega {\mathrm{C}}_{\mathrm{r}}}}$$

(10)

Substituting Formulas (5) and (6) into Formula (10), Formula (11) can be derived.

$$\frac{V_o}{V_i}=\frac{1}{1+jQ(\frac{\omega }{{\omega }_r}-\frac{{\omega }_r}{\omega })}$$

(11)

The norm of $\frac{V_o}{V_i}$ (voltage gain) is displayed in Formula (12).

$$\left|\frac{V_o}{V_i}\right|=\frac{1}{\sqrt{1+Q^2{(\frac{\omega }{{\omega }_r}-\frac{{\omega }_r}{\omega })}^2}}$$

(12)

When the operating frequency is equal to the resonant frequency ($\omega ={\omega }_r$), the voltage gain will be 1, as shown in Formula (13).

$$\left|\frac{V_o}{V_i}\right|=\frac{1}{\sqrt{1+Q^2{(\frac{\omega }{{\omega }_r}-\frac{{\omega }_r}{\omega })}^2}}=1$$

(13)

Meanwhile, current $I=\frac{V_i}{R_o}$. The voltage across inductor V_Lr and capacitor V_Cr are given in Formulas (14) and (15).

$$V_{L_r}=I\cdot j{\omega }_r{\mathrm{L}}_{\mathrm{r}}=j\frac{V_i}{{\mathrm{R}}_{\mathrm{o}}}\cdot \sqrt{\frac{{\mathrm{L}}_{\mathrm{r}}}{{\mathrm{C}}_{\mathrm{r}}}}=j\cdot Q\cdot V_i$$

(14)

$$V_{C_r}=I\cdot \frac{1}{j{\omega }_r{\mathrm{C}}_{\mathrm{r}}}=-j\frac{V_i}{{\mathrm{R}}_{\mathrm{o}}}\cdot \sqrt{\frac{{\mathrm{L}}_{\mathrm{r}}}{{\mathrm{C}}_{\mathrm{r}}}}=-j\cdot Q\cdot V_i$$

(15)

When the operating frequency is equal to the resonant frequency, the impedance effects of the inductor L_r and the capacitor C_r cancel each other out. Thereby, all of the input energy transfers to resistor R_o, which means the system reaches the maximum voltage gain and input current. In the LCR series resonant circuit, it can be seen that the partial voltage of components can be changed by adjusting the operating frequency to achieve the control of the voltage V_o [30].

The transfer function of voltage gain can be plotted as voltage gain curves, as shown in Figure 13. It can be observed that the voltage gain is at its maximum (=1) when $f_s=f_r$. Meanwhile, the current is at its maximum, and its phase with voltage is 0. Under this circumstance, the power utilization is the highest. When the operating frequency f_s is greater than the resonant frequency f_r, the system operates in the ZVS region; when the operating frequency f_s is less than the resonant frequency f_r, the converter will operate in the ZCS region.

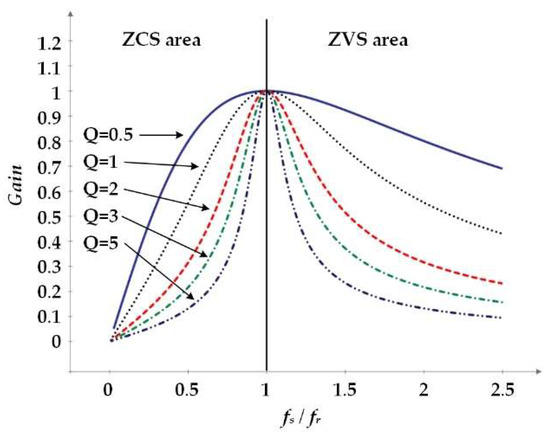
Figure 13. Transfer function curves of RLC series resonant converters under different quality factors.

3. Proposed Maximum Power-Point Tracking Heating Technology

3.1. Heating Control Technology

During induction heating, as the temperature changes, the load characteristics of the processed workpiece also changes, which affects the circuit parameters of the induction heating system, such as the resonance frequency f_r. Suppose the operating frequency f_s is not adjusted accordingly. In that case, the system is unable to reach the maximum power output, the heating efficiency decreases, and even the power switch loses its ZVS operation, resulting in the problem of significant voltage, current stress, and switching loss. To solve these problems, this study proposes a feedback control base on optimized heating efficiency. The following proves how the system maintains a higher efficiency output through theoretical and mathematical derivation of the resonant circuit.

The voltage across R_o, as shown in Figure 12, is expressed in Formula (16).

$$\begin{gathered} V_o=V_i\cdot \frac{{\mathrm{R}}_{\mathrm{o}}}{{\mathrm{R}}_{\mathrm{o}}+j\omega \mathrm{L}+\frac{1}{j\omega \mathrm{C}}} \\ \left|V_o\right|=V_i\cdot \frac{{\mathrm{R}}_{\mathrm{o}}}{\sqrt{{\mathrm{R}}_{\mathrm{o}}^2+{(X_L-X_C)}^2}} \end{gathered}$$

(16)

The loop current is calculated as shown in Formula (17).

$$\begin{gathered} I=\frac{V_i}{{\mathrm{R}}_{\mathrm{o}}+j\omega \mathrm{L}+\frac{1}{j\omega \mathrm{C}}} \\ \left|I\right|=\frac{V_i}{\sqrt{{\mathrm{R}}_{\mathrm{o}}^2+{(X_L-X_C)}^2}} \end{gathered}$$

(17)

Then, the phase of the input voltage and current is given in Formula (18).

$$\theta ={\tan }^{-1}\left[\frac{\left(X_L-X_C\right)}{{\mathrm{R}}_{\mathrm{o}}}\right]$$

(18)

Finally, the power on the resistor R_o is expressed in Formula (19):

$$P_o=V_o\times I\times \cos \theta$$

(19)

In an ideal case, when the resonant circuit operates at the resonance point ($f_s=f_r$, $X_L=X_c$), the voltage across the resistor R_o at the resonance point can be obtained in Formula (20) through Formulas (16)–(18).

$$\left|V_o\right|=V_i\cdot \frac{{\mathrm{R}}_{\mathrm{o}}}{\sqrt{{\mathrm{R}}_{\mathrm{o}}^2+0^2}}=V_i$$

(20)

The loop current is calculated as shown in Formula (21).

$$\left|I\right|=\frac{V_i}{\sqrt{{\mathrm{R}}_{\mathrm{o}}^2+0^2}}=\frac{V_i}{{\mathrm{R}}_{\mathrm{o}}^{}}$$

(21)

Then, the phase of the input voltage and current are calculated as shown in Formula (22).

$$\theta ={\tan }^{-1}\left(\frac{0}{{\mathrm{R}}_{\mathrm{o}}^{}}\right)=0$$

(22)

Substituting Formulas (20)–(22) into Formula (19), the power on the resistor R_o can be obtained as shown in Equation (23).

$$P_o=V_o\times I\times \cos (0)=V_i\times I\times 1$$

(23)

From above, the induction heating system can change the phase between the voltage and current by adjusting the operating frequency, which changes the output power. When $f_s=f_r$, the power factor is 1 because the voltage and current have the same phase, and then the induction heating system achieves the maximum power point (MPP).

To determine the influence of the load characteristic variation on the system parameters during the heating process, this study draws the curve of the output power p_o corresponding to the operating frequency f_s, considering the load characteristic variation. The resonant frequency f_r is expressed in Formula (24). As shown in Figure 14, when the induction heating system is heating the load with the fixed input voltage, the equivalent inductance L_eq and equivalent resistance R_eq increase with higher temperature. When the temperature rises, the equivalent inductance L_eq increases, which causes the resonant frequency to decrease, and the resonant point gradually shifts to the left (low-frequency direction). Meanwhile, the equivalent resistance R_eq increases the same as the equivalent L_eq. This decreases the loop current, resulting in a drop in the output power. Summarizing, the frequency−power curve drawn according to the change of load characteristics gradually shifts to the left (lower resonant frequency) and down (lower output power) as the heating temperature increases.

$$f_r=\frac{1}{2\pi \sqrt{{\mathrm{L}}_{\mathrm{eq}}{\mathrm{C}}_{\mathrm{eq}}}}$$

(24)

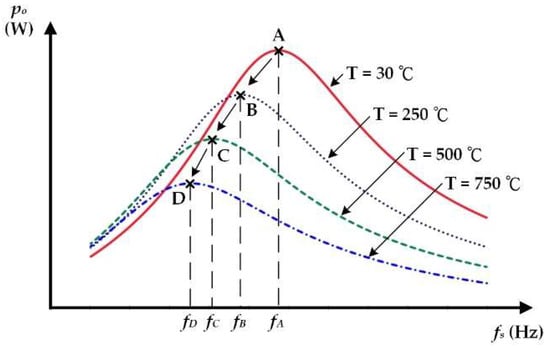
Figure 14. Frequency−power curve trend of the proposed system with temperature change.

From these curves, the output power and the resonant frequency f_r of the induction heating system both decrease (A→B→C→D) when the temperature rises during the heating process.

3.2. Proposed MPPT Control Strategy

This study proposes a maximum power-point tracking control strategy to help the proposed induction heating system achieve the optimal operating frequency and duty cycle. The details follow:

Figure 15 shows the relationship between the heating power and the operating frequency of the proposed induction heating system. The corresponding formula is obtained by using Microsoft Excel’s curve fitting function, as expressed in Formula (25). Through Formula (25), the best operating frequency can be obtained in time.

$$f_s=a\cdot p_o^2+b\cdot p_o+c$$

(25)

where a = −0.3044, b = 1054.7, and c = −413788.

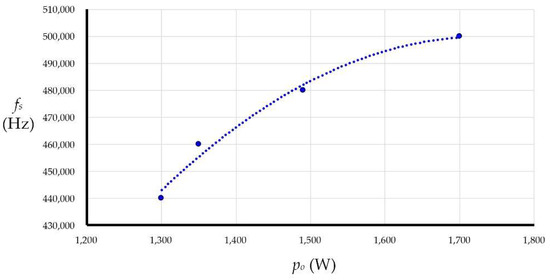
Figure 15. Relationship between the heating power and the operating frequency of the proposed induction heating system.

Although the system operation has the best operating frequency, this study also improves the system flexibility. The improvement of the system flexibility is realized by an adjustable duty cycle to stabilize the system’s output power and heating performance. Figure 16 is the schematic diagram of the hill-climbing algorithm, where the red dot is the MPP of p_o, and A₁, A₂ are the operating points close to the MPP. If the current operating point is A₁, which falls on the left half plane (LHP), the hill-climbing algorithm [31] adjusts the duty cycle close to the MPP by comparing the two powers (previous and current). On the contrary, if the current operating point is A₂, which falls on the right half plane (RHP), the duty cycle is adjusted (similar to A₁) close to the MPP.

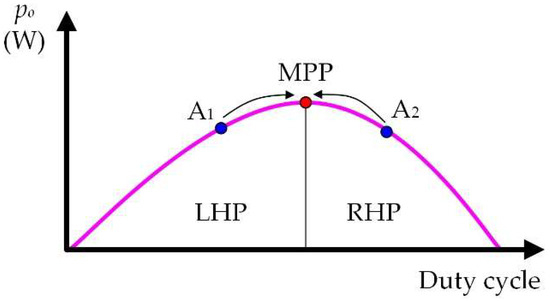
Figure 16. Schematic diagram of the hill-climbing algorithm.

Figure 17 shows the flow chart of the proposed MPPT heating strategy. First, the output voltage v_o and output current i_o are measured to calculate the output power p_o (n−1) and p_o (n). Second, according to Formula (25), the optimal operating frequency of the induction heating system can be obtained. Finally, the hill-climbing algorithm estimates the optimal duty cycle of the induction heating system by comparing p_o (n−1) and p_o (n). Therefore, the proposed MPPT heating strategy can precisely control the heating system to achieve higher efficiency and stability.

Figure 17. Flow chart of the proposed MPPT heating strategy.

4. Experiment Results

In this study, the proposed induction heating system is implemented and shown in Figure 18, where the proposed is mainly composed of a full-bridge LC series resonant converter, a microcontroller unit (MCU) (brand: Microchip, model: TMS320F28035), and an auxiliary power supply circuit. The system’s output power can be adjusted by adjusting the operating frequency of the power switches. The operating frequency ranges from 44 to 50 kHz, and the maximum input power of this system is 1.3 kW.

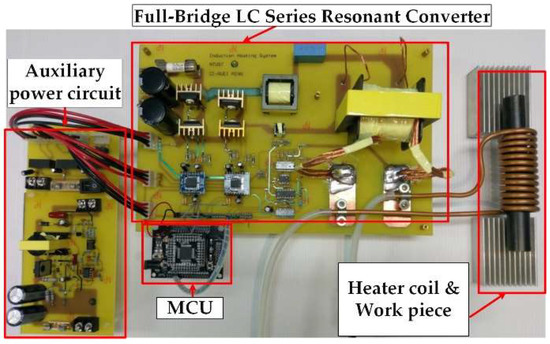
Figure 18. A prototype of the proposed induction heating system.

Table 4 shows the specification of the proposed induction heating system, where the input voltage is 250 V_DC; the resonant inductor L_r = 150 μH; the resonant capacitor C_eq = 33 nF; the equivalent inductance of heating coil L_eq is 1.25 μH; the equivalent resistance of heating coil R_eq is 0.5 Ω, the turn ratio of the transformer N₁:N₂ = 10:1; the heating coil has a 2.5 cm inner diameter and 13 turns; and the workpiece is a 2 cm diameter and 15 cm long cylindrical low-carbon iron.

Table 4. Specification of the induction heating system.

Parameter	Value
Input voltage	250 VDC
Resonant inductor	150 μH
Resonant capacitor	33 nF
Equivalent inductance of heating coil Leq (temperature of 750 °C and frequency of 44 kHz)	1.25 μH
Equivalent resistance of heating coil Req (temperature of 750 °C and frequency of 44 kHz)	0.5 Ω
Turn ratio (transformer)	N1:N2 = 10:1
Heating coil	Inner diameter 2.5 cm, 13 turns
Workpiece	Cylindrical low-carbon iron (2 cm diameter, 15 cm long)

4.1. Simulation Experiment Results

In this study, the simulation results are tested under the conditions that the workpiece’s temperature is 500 and 750 °C. Figure 19 and Figure 20 show the simulation result of the proposed induction heating system, which operates with the traditional control strategy (fixed operating frequency) and the proposed MPPT heating control strategy, respectively.

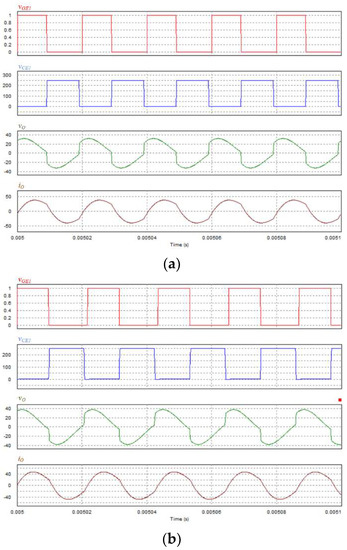
Figure 19. Simulation waveforms v_GE1 (duty cycle), the voltage across the power switch voltage v_CE1, the output voltage v_o, and the output current i_o under the condition that the workpiece is 500 °C: (a) traditional control strategy, (b) proposed MPPT heating control strategy.

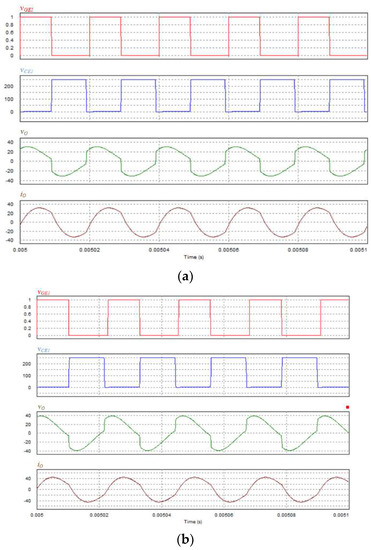
Figure 20. Simulation waveforms v_GE1 (duty cycle), the voltage across the power switch voltage v_CE1, the output voltage v_o, and the output current i_o under the condition that the workpiece is 750 °C: (a) traditional control strategy, (b) proposed MPPT heating control strategy.

Figure 19a shows the control signal of the traditional control strategy, where the workpiece’s temperature is 500 °C, the operating frequency is 45 kHz, v_GE1 (duty cycle) is 0.45, the peak value of the power switch voltage v_CE1 is 250 V, the peak value of the output voltage v_o is 30 V_AC, and the peak value of the output current i_o is 40 A_AC. The proposed MPPT heating control strategy (Formula (25) and hill-climbing algorithm) is shown in Figure 19b, where the operating frequency is 46 kHz, v_GE1 (duty cycle) is 0.43, and the peak value of the power switch cross-voltage v_CE1 is 250 V, the peak output voltage v_o is 39.5 V_AC, and the peak output current i_o is 43 A_AC.

Figure 20a shows the control signal of the traditional control strategy, where the workpiece’s temperature is 750 °C, the operating frequency is 45 kHz, v_GE1 (duty cycle) is 0.45, the peak value of the power switch voltage v_CE1 is 250 V, the peak value of the output voltage v_o is 32 V_AC, and the peak value of the output current i_o is 35 A_AC. The proposed MPPT heating control strategy (Formula (25) and hill-climbing algorithm) is shown in Figure 20b, where the operating frequency is 44 kHz, v_GE1 (duty cycle) is 0.44, and the peak value of the power switch cross-voltage v_CE1 is 250 V, the peak output voltage v_o is 40 V_AC, and the peak output current i_o is 42 A_AC.

From the simulation results in Figure 19 and Figure 20, it can be observed that no matter which heating method is used, when the workpiece temperature increases, the output voltage and the output current decrease. Using the proposed MPPT heating control strategy can improve power loss more than the traditional control strategy, proving the high heating performance of the proposed MPPT heating control strategy.

4.2. Hardware Experiment Results

In this study, the hardware experiment is tested with the workpiece’s temperature at 500 and 750 °C. Figure 21 and Figure 22 show results of the experiments for the proposed induction heating system, which operates with the traditional control strategy (fixed operating frequency) and the proposed MPPT heating control strategy, respectively.

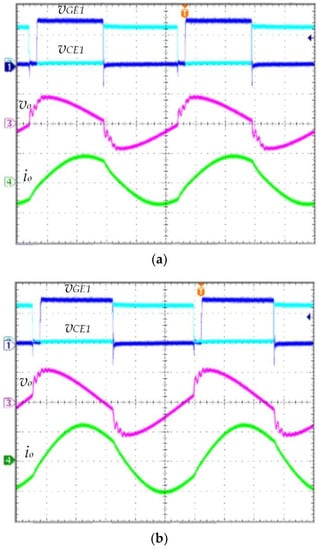
Figure 21. Hardware experimental waveforms v_GE1 (duty cycle), the voltage across the power switch voltage v_CE1, the output voltage v_o, and the output current i_o under the condition that the workpiece is 500 °C: (a) traditional control strategy, (b) proposed MPPT heating control strategy. (v_GE1: 10 V/div; v_CE1: 200 V/div; v_o: 40 V/div; i_o: 40 A/div; and Hor: 4 μs/div).

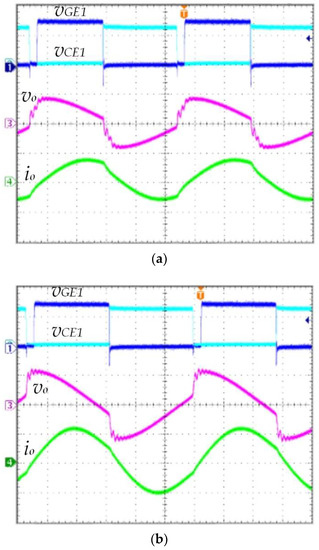
Figure 22. Hardware experimental waveforms v_GE1 (duty cycle), the voltage across the power switch voltage v_CE1, the output voltage v_o, and the output current i_o under the condition that the workpiece is 750 °C: (a) traditional control strategy, (b) proposed MPPT heating control strategy. (v_GE1: 10 V/div; v_CE1: 200 V/div; v_o: 40 V/div; i_o: 40 A/div; and Hor: 4 μs/div).

Figure 21a shows the control signal of the traditional control strategy, where the workpiece’s temperature is 500 °C, the operating frequency is 45 kHz, v_GE1 (duty cycle) is 0.45, the peak value of the power switch voltage v_CE1 is 250 V, the peak value of the output voltage v_o is 35 V_AC, and the peak value of the output current i_o is 40 A_AC. The proposed MPPT heating control strategy (Formula (25) and hill-climbing algorithm) is shown in Figure 21b, where the operating frequency is 46 kHz, v_GE1 (duty cycle) is 0.43, the peak value of the power switch cross-voltage v_CE1 is 250 V, the peak output voltage v_o is 41 V_AC, and the peak output current i_o is 43 A_AC. The hardware experiment results (Figure 21) are similar to the simulation results (Figure 19).

Figure 22a shows the control signal of the traditional control strategy, where the workpiece’s temperature is 750 °C, the operating frequency is 45 kHz, v_GE1 (duty cycle) is 0.45, the peak value of the power switch voltage v_CE1 is 250 V, the peak value of the output voltage v_o is 35 V_AC, and the peak value of the output current i_o is 35 A_AC. The proposed MPPT heating control strategy (Formula (25) and hill-climbing algorithm) is shown in Figure 22b, where the operating frequency is 44 kHz, v_GE1 (duty cycle) is 0.43, the peak value of the power switch cross-voltage v_CE1 is 250 V, the peak output voltage v_o is 42 V_AC, and the peak output current i_o is 42 A_AC. The hardware experiment results (Figure 22) are similar to the simulation results (Figure 20).

From the measured waveform results (Figure 21 and Figure 22), it can be observed that the output current decreases as the temperature increases (R_eq increases). In the proposed MPPT heating control strategy, the operating frequency f_s follows the variation in the resonant frequency f_r so that the system can operate near the resonant point. Therefore, compared with the traditional heating control strategy (fixed frequency operation), the proposed system has a larger output voltage and current, increasing the output power and optimizing the heating efficiency.

Figure 23 shows that the proposed induction heating system heats the workpiece (a 2 cm diameter and 15 cm long cylindrical low-carbon iron) to 753.3 °C, measured by the infrared thermal imager.

Figure 23. Actual photo of the induction heating system heating the workpiece to 753.3 degrees Celsius, measured by the infrared thermal imager.

Figure 24 shows the heating duration of the proposed induction heating system, where the traditional heating control strategy (the blue dotted line) takes 320 s to reach 750 °C, and the proposed MPPT heating control strategy (the solid orange line) reaches 750 °C in 120 s.

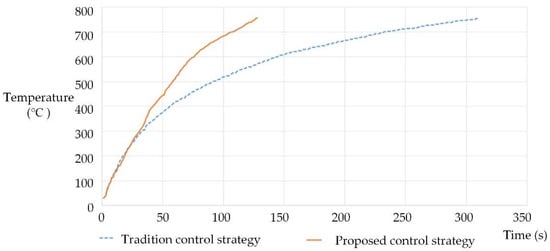
Figure 24. Comparison of the traditional control strategy and proposed MPPT heating control strategy for the heating duration of the proposed induction heating system.

Table 5 shows the comparison between the simulation results and the experiment results of the proposed and the traditional control strategies. During heating, the proposed control strategy adjusts the operating frequency and the duty cycle with the heating temperature rising, while the traditional control strategy keeps the operating frequency and the duty cycle fixed. The peak value of v_o and i_o are higher than the traditional one. Therefore, the proposed control strategy performs better than the traditional one in heating speed (Figure 24).

Table 5. Comparison between the simulation results and the experiment results of the proposed and the traditional control strategies.

Heating Temperature	Measurement	Simulation		Experiment
		Traditional	Proposed	Traditional	Proposed
500 °C	frequency	45 kHz	46 kHz	45 kHz	46 kHz
	duty cycle	0.45	0.43	0.45	0.43
	peak value of vo	30 VAC	39.5 VAC	35 VAC	41 VAC
	peak value of io	40 AAC	43 AAC	40 AAC	43 AAC
750 °C	frequency	45 kHz	44 kHz	45 kHz	44 kHz
	duty cycle	0.45	0.44	0.45	0.44
	peak value of vo	32 VAC	40 VAC	35 VAC	42 VAC
	peak value of io	35 AAC	42 AAC	35 AAC	42 AAC

This study verifies the feasibility of the proposed induction heating system and the performance of the proposed MPPT heating control strategy, which is better than the traditional heating control strategy (fixed-frequency operation). In addition, Table 6 shows the comparison between the traditional heating control strategy and the proposed MPPT heating control strategy. When the workpiece reaches 500 and 750 °C, the efficiencies of the traditional heating control strategy are 76% and 67%, respectively. By contrast, the efficiencies of the proposed MPPT control strategy are both 96%. Therefore, the proposed MPPT heating control strategy is far better than the traditional one.

Table 6. Performance comparison between the traditional heating control strategy and the proposed MPPT heating control strategy.

Control Method	Heating Temperature
	500 °C	750 °C
Traditional (Efficiency)	76%	68%
Proposed (Efficiency)	96%	96%

5. Conclusions

This study realized a 1.3 kW induction heating system based on a full-bridge LC series resonant converter. An MPPT heating control strategy was proposed to improve the heating performance, which uses the relationship between the resonant frequency and the workpiece’s heating temperature to find the optimal operating frequency. To further improve the induction heating system, this study also utilized the hill-climbing algorithm to calculate the duty cycle that reaches the MPP for heating. The proposed heating control strategy considered the operating frequency and duty cycle to improve the problems of the traditional heating control strategy. The proposed heating induction system had high efficiency, stability, and accurate control. Under the simulation and hardware experiment measurement, the traditional heating control strategy had 76% and 68% efficiencies, respectively, when the workpiece reached 500 and 750 °C. By contrast, the proposed heating control strategy had 96% efficiency when the system heating temperature was 500 and 750 °C. Furthermore, the traditional heating control strategy took 320 s to reach 750 °C, and the proposed MPPT heating control strategy reached 750 °C in 120 s. This study’s contribution is that the proposed control strategy dramatically improves the traditional full-bridge LC series resonant induction heating system, reducing power loss and heating time.

Future work on the induction heating system can simulate and measure different types of workpieces and analyze the influence of the workpiece material and heating coil type on heating speed. Further, methods to reduce the power loss and reduce the size of the circuit are also research directions to consider.