The Influence of Effective Prandtl Number Model on the Micropolar Squeezing Flow of Nanofluids between Parallel Disks

Abstract

A mathematical model of micropolar squeezing flow of nanofluids between parallel planes is taken into consideration under the influence of the effective Prandtl number using ethyl glycol $\left(C_2{H}_6{O}_2\right)$ and water $\left(H_{2}O\right)$ as base fluids along with nanoparticles of gamma alumina $\left(\gamma A{l}_2{O}_3\right)$. The governing nonlinear PDEs are changed into a system of ODEs via suitable transformations. The RKF (Range–Kutta–Fehlberg) technique is used to solve the system of nonlinear equations deriving from the governing equation. The velocity, temperature, and concentration profiles are depicted graphically for emerging parameters such as Hartmann number $M,$ micronation parameter $K,$ squeeze number $R$, Brownian motion parameter $N_b$, and thermophoresis parameter $N_t$. However, physical parameters such as skin friction coefficient, Nusselt number, and Sherwood number are portrayed in tabulated form. The inclusion of the effective Prandtl number model indicated that the effect of the micropolar parameter $K$ on angular velocity h(ξ) in both suction and injection cases is opposite for both nanofluids. It is observed that the increase in angular velocity is rapid for $\gamma {Al}_2{O}_3-C_2{H}_6{O}_2$ throughout the study.

1. Introduction

Recent technological advancements have renewed interest in non-Newtonian fluid flows. These fluids play an important role in many situations. Engineers, mathematicians, modelers, physicists, and computer scientists have been interested in the flows of these fluids in recent years due to their applications in industry and technology. In addition to the Navier–Stokes equations, the governing equations of non-Newtonian fluids are of a higher order and highly nonlinear, which are presented in [1,2,3]. Non-Newtonian fluid flows have been the subject of even more research. Micropolar fluids differ from non-Newtonian fluids in that they exhibit microscopic characteristics such as micro-rotational and rotational inertia. The theory of micropolar fluids was initially suggested by [4]. Micropolar fluids are essential for the movement of colloidal suspensions, liquid crystals, additive-containing fluids, suspension solutions, animal blood, and other fluids. Ariman T [5] discusses the application of micro-continuum fluid mechanics. Ezzat [6] and Helmy [7] presented some uses of the magnetohydrodynamic (MHD) boundary layer flow. Raees [8] and Jena [9] incorporate the applications of the Free Convection Flow of a Micropolar Fluid from a Vertical Flat Plate. The application of stagnation point flow of micropolar fluid flow was investigated by Guram [10] and Nazar [11]. Similarly, Ahmadi [12] and Takhar [13] have investigated the flow of micropolar fluids in various configurations to accomplish such applications. Recently, Ramesh et al. [14] have investigated the time-dependent Casson-micropolar nanofluid squeezing flow with suction/blowing and slip effects. By contrast, Kumbinarasaiah et al. [15] used the Hermite wavelet approach to solve coupled nonlinear differential equations occurring in a rotating micropolar nanofluid flow system. Later on, Shamshuddin et al. [16] demonstrated the influences of different aspects of micropolar nanofluids such as a chemically reactive Casson fluid treated to a rotatory system with electrical and Hall currents between parallel plates. Hussain et al. [17] investigated multiple slip effects in a biothermal MHD convection flow of a micropolar nanofluid between two parallel discs, while Sastry et al. [18] incorporated the application to cardiovascular problems of unsteady 3D micropolar nanofluid flow through a squeezing channel.

Squeezing flows are also common in hydrodynamic machines, polymer processing, compression and injection molding models, lubrication processes, and polymer processing procedures, among other things. The time-dependent squeezed flow is frequently addressed in industrial situations to characterize fluid movement along a prescribed length of contracting area. A preliminary sluggish liquid may be placed between a pair of rectangular parallel discs and planes to show the associated mathematical models upon such planes of coordinates, and this flow can be set up. Usha [19] found an exact solution to a similar problem in a couple of elliptic plates using a multifold time-dependent series. The time-dependent viscous squeezing flow between two parallel plates with a constant temperature was investigated by [20]. Grimm [21] looked at the squeezing flows of Newtonian liquid plates.

Furthermore, in the last two decades engineers have turned their attention to a new form of fluid known as “nanofluid.” Nanofluids are fluids that include nanometer-sized particles in a suspension, also known as nanoparticles. Nanomaterials are important because of their high thermal and mechanical properties. The properties of the nanoliquids created by each nanomaterial are considerably altered by these materials. Among nanomaterials, there is a substance known as aluminum alloys, in which aluminum plays a significant role. Aluminum alloys are divided into two categories: heat-treatable and non-heat-treatable. Some of the most commonly used nanofluids are water $\left(H{}_{2}O\right)$, ethyl glycol $\left(C_2{H}_6{O}_2\right),$ and oil. Choi [22] was the first to demonstrate that putting these nanoparticles into a base fluid enhanced its thermal conductivity. Buongiorno [23] proposed a mathematical model to emphasize the significant impacts of the Brownian motion and thermophoretic diffusion of nanoparticles.

Soundings into the flow dynamics of $Al{}_{2}O{}_3$ nanofluids have revealed their importance in cooling operations by Popa [24], T.M.O. Sow [25], and H. Beiki [26]. To cool an engine, Moghaieb [27] employed an $Al{}_{2}O{}_3-H{}_{2}O$ nanofluid. Ganesh [28] and Rashidi [29] demonstrated that similarity solutions improved the flow properties of $Al{}_{2}O{}_3$ nanofluids over stretchy surfaces. They used experimentally-based thermophysical properties in their studies to ensure the physical pertinence of gamma alumina nanoparticles.

A careful review of the literature finds that no one has studied the effects of an experimentally based Prandtl number model on the squeezing flow of micropolar fluids flow of $\gamma Al{}_{2}O{}_3-H{}_{2}O$ (gamma alumina and water) and $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ (gamma alumina and ethyl glycol) across parallel plates, to the author’s knowledge. In light of this, we investigate the impact of an effective Prandtl number model on the squeezing flow of nanoparticle micropolar fluid between parallel planes. As a result, the squeezing flow of $\gamma Al{}_{2}O{}_3-H{}_{2}O$ (gamma alumina and water) and $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ (gamma alumina and ethyl glycol) between two parallel planes is explored in this study under the impact of the effective Prandtl number. The analytical solutions generated are being utilized to investigate the influence of various factors on the squeezing flow between two parallel planes.

2. Mathematical Analysis

Consider the two-dimensional axisymmetric flow of incompressible nanofluid between two parallel planes with vertical magnetic fields proportional to $B_o{\left(1-at\right)}^{-1/2}$. As for low Reynold numbers, the magnetic field is neglected. It contains nanoparticles such as aluminum oxide $\left(Al{}_{2}O{}_3\right)$ and gamma aluminium oxide $\left(\gamma Al{}_{2}O{}_3\right)$ in base fluids such as water $\left(H{}_{2}O\right)$ and ethylene glycol $\left(C_2{H}_6{O}_2\right)$. The lower plane is at Z = 0, and the upper plane is separated by $Z=h\left(t\right)=H{\left(1-at\right)}^{1/2}.$ As shown in the Figure 1, the upper plane moves toward or away from the lower plane at a velocity of $\frac{aH}{2{\left(1-at\right)}^{1/2}}$.

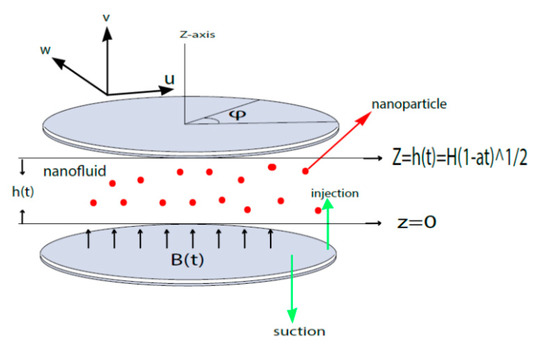
Figure 1. Geometry of the problem.

The following are the governing equations for two-dimensional axisymmetric and unsteady fluid flow, as well as heat transfer in viscous fluids:

$$\frac{\partial ŭ}{\partial r}+\frac{ŭ}{r^2}+\frac{\partial ŵ}{\partial z}=0$$

(1)

$$\frac{\partial ŭ}{\partial t}+ u\frac{\partial ŭ}{\partial r} + ŵ\frac{\partial ŭ}{\partial z}=\frac{-1}{{\rho }_{nf}}\frac{\partial P}{\partial r}+\frac{-1}{{\rho }_{nf}}\left({\mu }_{nf}+k^{*}\right)\left[\frac{{\partial }^2ŭ}{\partial t^2}+\frac{1}{r}\frac{\partial ŭ}{\partial r}-\frac{ŭ}{r^2}+\frac{{\partial }^2ŭ}{\partial z^2}\right]-\frac{k^{*}}{{\rho }_{nf}}\frac{\partial N}{\partial z}-\frac{{\sigma }_{nf}}{{\rho }_{nf}}{B}^2\left(t\right)ŭ$$

(2)

$$\frac{\partial ŵ}{\partial t}+ŭ\frac{\partial ŵ}{\partial r} + ŵ\frac{\partial ŵ}{\partial z}=\frac{-1}{{\rho }_{nf}}\frac{\partial P}{\partial z}+\frac{-1}{{\rho }_{nf}}\left({\mu }_{nf}+k^{*}\right)\left[\frac{{\partial }^2ŵ}{\partial t^2}+\frac{1}{r}\frac{\partial ŵ}{\partial r}+\frac{{\partial }^2ŵ}{\partial z^2}\right]-\frac{k^{*}}{{\rho }_{nf}}\left[\frac{\partial N}{\partial r}+\frac{N}{r}\right]$$

(3)

$$\frac{\partial \mathrm{Ň}}{\partial t}+ ŭ\frac{\partial \mathrm{Ň}}{\partial r} + ŵ\frac{\partial \mathrm{Ň}}{\partial z}=\frac{\gamma }{{\rho }_{nf}}\frac{1}{j}\left[\frac{{\partial }^2\mathrm{Ň}}{\partial r^2}+\frac{1}{r}\frac{\partial \mathrm{Ň}}{\partial r}+\frac{{\partial }^2\mathrm{Ň}}{\partial z^2}-\frac{\mathrm{Ň}}{r^2}\right]-\frac{k^{*}}{{\rho }_{nf}}\frac{1}{j}[2N+\frac{\partial ŵ}{\partial r}-\frac{\partial ŭ}{\partial z}]$$

(4)

$$\frac{\partial \mathrm{Ť}}{\partial t}+ ŭ\frac{\partial \mathrm{Ť}}{\partial r} + ŵ\frac{\partial \mathrm{Ť}}{\partial z}={\alpha }_{nf}\left[\frac{{\partial }^2\mathrm{Ť}}{\partial r^2}+\frac{1}{r}\frac{\partial \mathrm{Ť}}{\partial r}+\frac{{\partial }^2\mathrm{Ť}}{\partial z^2}\right]+\tau \left[D_b\left(\frac{\partial C}{\partial r}\frac{\partial \mathrm{Ť}}{\partial r}+\frac{\partial C}{\partial z}\frac{\partial \mathrm{Ť}}{\partial z}\right)+\frac{D_t}{T_m}{\left(\frac{\partial \mathrm{Ť}}{\partial r}\right)}^2+{\left(\frac{\partial \mathrm{Ť}}{\partial z}\right)}^2\right]$$

(5)

$$\frac{\partial \mathrm{Č}}{\partial t}+ ŭ\frac{\partial \mathrm{Č}}{\partial r} + ŵ\frac{\partial \mathrm{Č}}{\partial z}=D_b\left[\frac{{\partial }^2\mathrm{Č}}{\partial r^2}+\frac{1}{r}\frac{\partial \mathrm{Č}}{\partial r}+\frac{{\partial }^2\mathrm{Č}}{\partial z^2}\right]+\frac{D_t}{T_m}\left[\frac{{\partial }^2\mathrm{Ť}}{\partial r^2}+\frac{1}{r}\frac{\partial \mathrm{Ť}}{\partial r}+\frac{{\partial }^2\mathrm{Ť}}{\partial z^2}\right]$$

(6)

Subject to auxiliary conditions [30]

$$[ŭ=0, ŵ=\frac{dh}{dt}, \mathrm{Ň}=-n\frac{\partial ŭ}{\partial z}, \mathrm{Ť}={\mathrm{Ť}}_h, \mathrm{Č}={\mathrm{Č}}_h]{ }_{z=h\left(t\right)}$$

(7)

$${[ŭ=0, ŵ=-{ŵ}_{°}, \mathrm{Ň}=-n\frac{\partial ŭ}{\partial z}, \mathrm{Ť}={\mathrm{Ť}}_w, D_b\frac{\partial \mathrm{Č}}{\partial z}+\frac{D_t}{T_m}\frac{\partial \mathrm{Ť}}{\partial z}=0]}_{z=0}$$

(8)

The velocity components in the $r$ and $z$ directions are represented by $ŭ$ and $ŵ$, respectively, while the azimuthal component of micro-rotation is represented by $\mathrm{Ň}$. The concentration of nanoparticles in the fluid is denoted by $\mathrm{Č}$. ${\mathrm{Č}}_w$ and ${\mathrm{Č}}_h$ represent nanoparticle concentrations, while ${\mathrm{Ť}}_w$ and ${\mathrm{Ť}}_h$ represent constant temperature at the lower and upper planes, respectively. ${\rho }_{nf}$ is the effective density, ${\alpha }_{nf}$ is efficient thermal diffusion, ${\mu }_{nf}$ is dynamic viscosity of nanofluids, ${\kappa }^{*}$is vortex viscosity, $\nu$ is kinematic viscosity, $p$ indicates pressure, and $C_p$represents specific heat capacitance. Furthermore, $D$ is the mass diffusion coefficient, $D_b$ is the Brownian motion coefficient, and $D_t$ is the thermophoretic diffusion coefficient. $\mathrm{Ť}$ is temperature, and $T_m$is the mean fluid temperature. Furthermore, $\tau$ represents a non-dimensional parameter, which is the ratio of the nanoparticle’s effective heat capacity to the fluid’s heat capacity. ${ŵ}_o$ is assumed to be constant and represents wall injection and suction velocity. $n$ is assumed to be constant and $\gamma =\left({\mathsf{\mu }}_{nf}+\frac{{\mathrm{k}}_{nf}}{2}\right)j$, where $\mathrm{j}=\frac{v\left(1-\mathrm{at}\right)}{a}$ represents the refrence length. ${\mathsf{\sigma }}_{nf}$ is the effective electrical conductivity of nano liquids. Moreover, the effective density ${\mathsf{\rho }}_{nf}$ and dynamic viscosity ${\mathsf{\mu }}_{nf}$ of the nanofluid [24] are as follows:

$${\rho }_{nf}=\left(1-\varphi \right)+\varphi {\rho }_s,$$

(9)

$$\frac{{\mu }_{nf}}{{\mu }_f}=123\varphi ²+7.3\varphi +1 (\gamma Al{}_{2}O{}_3-H{}_{2}O)$$

(10)

$$\frac{{\mu }_{nf}}{{\mu }_f}=306\varphi ²+0.9\varphi +1 (\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2)$$

(11)

Nanofluid’s effective Prandtl number [30,31] is demarcated as

$$\frac{P{r}_{nf}}{P{r}_f}=82.1\phi ²+3.9\phi +1 (\gamma Al{}_{2}O{}_3-H{}_{2}O)$$

(12)

$$\frac{P{r}_{nf}}{P{r}_f}=254.3\varphi ²+3\varphi +1 (\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2)$$

(13)

Nanofluid’s effective electrical conductivity is given as

$$\frac{{\sigma }_{nf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }\right]$$

(14)

The thermophysical characreristics of nanoparticles are painted in Table 1 [31].

Table 1. Thermal and physical properties of base fluids and nanoparticles.

Models	${\mathit{C}}_{\mathit{p}} \left(\mathrm{k}{\mathrm{g}}^{-1} {\mathrm{K}}^{-1}\right)$	$\mathit{\rho } \left(\mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}\right)$	$\mathit{k} \left(\mathrm{W} {\mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$	$\mathit{\sigma }$	$\mathit{P}\mathit{r}$
$\mathit{C}{}_{\mathbf{2}}{\mathit{H}}_{\mathbf{6}}\mathit{O}{}_{\mathbf{2}}$	2382	1116.6	0.249	5.5 × 10−6	204
$\mathit{H}{}_{\mathbf{2}}\mathit{O}$	4179	997.10	0.613	0.0005	6.96
$\mathit{\gamma }\mathit{A}\mathit{l}{}_{\mathbf{2}}\mathit{O}{}_{\mathbf{3}}$	765	3970	40	3.5 × 107	-----

Under the following similarity transformation [32] to reduce the constitutive Equations (2)–(6) as:

$$\begin{array}{c}ŭ=\frac{ar}{2\left(1-at\right)}{f}^{\prime }\left(\mathsf{\xi }\right), ŵ=\frac{-aH}{\sqrt{\left(1-at\right)}}f\left(\mathsf{\xi }\right), \mathrm{Ň}=\frac{ar}{2H{\left(1-at\right)}^{\frac{3}{2}}}h\left(\mathsf{\xi }\right), \\ \xi =\frac{Z}{H\sqrt{\left(1-at\right)}}, \theta \left(\xi \right)=\frac{\mathrm{Ť}-{\mathrm{Ť}}_h}{{\mathrm{Ť}}_w-{\mathrm{Ť}}_h}, \beta \left(\xi \right)=\frac{\mathrm{Č}-{\mathrm{Č}}_h}{{\mathrm{Č}}_w-{\mathrm{Č}}_h}, \\ B\left(t\right)=B_o{\left(1-at\right)}^{-1/2}\end{array}$$

(15)

2.1. Model of $\gamma Al{}_{2}O{}_3-H{}_{2}O$

Using similarity transformations (15), we get transform equations for $\gamma Al{}_{2}O{}_3-H{}_{2}O.$

$$\left(A_2+K\right)f^{⁗}\left(\xi \right)-A_1\left(\frac{R}{2}\right)\left[3f^{″}\left(\xi \right)+\xi f^{‴}\left(\xi \right)-2f\left(\xi \right)f^{‴}\left(\xi \right)\right]-K{h}^{″}\left(\xi \right)-A_4{M}^{2}R{f}^{″}\left(\xi \right)=0,$$

(16)

$$\left(A_2+\left(\frac{K}{2}\right)\right)h^{″}\left(\xi \right)-KR\left(2h\left(\xi \right)-f^{″}\left(\xi \right)\right)-A_1\left(\frac{R}{2}\right)\left[3h\left(\xi \right)+\xi h^{\prime }\left(\xi \right)+f^{\prime }\left(\xi \right)h\left(\xi \right)-2h^{\prime }\left(\xi \right)f\left(\xi \right)\right]=0,$$

(17)

$$\left(\frac{A_2}{A_1}\right){\theta }^{″}\left(\xi \right)+P{r}_f{A}_4\frac{R}{2}\left(2f\left(\xi \right){\theta }^{\prime }\left(\xi \right)-\xi {\theta }^{\prime }\left(\xi \right)\right)+P{r}_f{A}_4{N}_b{\theta }^{\prime }\left(\xi \right){\beta }^{\prime }\left(\xi \right)+P{r}_f{A}_4{N}_t{\left({\theta }^{\prime }\left(\xi \right)\right)}^2=0,$$

(18)

$${\beta }^{″}\left(\xi \right)+\left(\frac{R}{2}\right)Le\left[2{\beta }^{\prime }\left(\xi \right)f\left(\xi \right)-\xi {\beta }^{\prime }\left(\xi \right)\right]+\frac{N_t}{N_b}{\theta }^{″}\left(\xi \right)=0$$

(19)

where,

$$\begin{array}{c}{A}_1=\frac{{\rho }_{nf}}{{\rho }_f}=\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}, \\ A{}_2=\frac{{\mu }_{nf}}{{\mu }_f}=123\varphi ²+7.3\varphi +1, \\ A_3=\frac{{\sigma }_{nf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }\right], \\ P{r}_{f}A{}_4=P{r}_{nf}=82.1\phi ²+3.9\phi +1.\end{array}$$

2.2. Model of $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$

Using similarity transformations (15), we get transform equations for $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$

$$\left(B_2+K\right)f^{⁗}\left(\xi \right)-B_1\left(\frac{R}{2}\right)\left[3f^{″}\left(\xi \right)+\xi f^{‴}\left(\xi \right)-2f\left(\xi \right)f^{‴}\left(\xi \right)\right]-K{h}^{″}\left(\xi \right)-B_4{M}^{2}R{f}^{″}\left(\xi \right)=0$$

(20)

$$\left(B_2+\left(\frac{K}{2}\right)\right)h^{″}\left(\xi \right)-KR\left(2h\left(\xi \right)-f^{″}\left(\xi \right)\right)-B_1\left(\frac{R}{2}\right)\left[3h\left(\xi \right)+\xi h^{\prime }\left(\xi \right)+f^{\prime }\left(\xi \right)h\left(\xi \right)-2h^{\prime }\left(\xi \right)f\left(\xi \right)\right]=0$$

(21)

$$\left(\frac{B_2}{B_1}\right){\theta }^{″}\left(\xi \right)+P{r}_f{B}_4\frac{R}{2}\left(2f\left(\xi \right){\theta }^{\prime }\left(\xi \right)-\xi {\theta }^{\prime }\left(\xi \right)\right)+P{r}_f{B}_4{N}_b{\theta }^{\prime }\left(\xi \right){\beta }^{\prime }\left(\xi \right)+P{r}_f{B}_4{N}_t{\left({\theta }^{\prime }\left(\xi \right)\right)}^2=0$$

(22)

$${\beta }^{″}\left(\xi \right)+\left(\frac{R}{2}\right)Le\left[2{\beta }^{\prime }\left(\xi \right)f\left(\xi \right)-\xi {\beta }^{\prime }\left(\xi \right)\right]+\frac{N_t}{N_b}{\theta }^{″}\left(\xi \right)=0$$

(23)

where,

$$\begin{array}{c}{B}_1=\frac{{\rho }_{nf}}{{\rho }_f}=\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}, \\ B{}_2=\frac{{\mu }_{nf}}{{\mu }_f}=306\varphi ²+0.9\varphi +1, \\ B_3=\frac{{\sigma }_{nf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }\right], \\ P{r}_{f}B{}_4=P{r}_{nf}=254.3\varphi ²+3\varphi +1.\end{array}$$

The non-dimensionalized boundary conditions are

$$\begin{array}{c}{f}^{\prime }\left(1\right)=0,f\left(1\right)=\left(1/2\right), h\left(1\right)=-n{f}^{″}\left(1\right), \\ f^{\prime }\left(0\right)=0,f\left(0\right)=S,h\left(0\right)=-n{f}^{″}\left(0\right), \\ \theta \left(1\right)=0, \beta \left(1\right)=0, \\ \theta \left(0\right)=1, N_b{\beta }^{\prime }\left(0\right)+N_t{\theta }^{\prime }\left(0\right)=0\end{array}$$

The following non-dimensionized parameters are used in the flow model.

$$\begin{array}{c}K=\frac{{\kappa }^{*}}{{\mu }_{nf}}, M^2=\frac{{\sigma }_f{B}_o^2}{a{\rho }_f}, R=\frac{a{H}^2}{{\nu }_f}, Le=\frac{{\nu }_f}{D_b}, P{r}_f=\frac{\mu C_p}{k}=\frac{v_f}{{\alpha }_f}\\ N_t=\frac{D_t{\left(\rho C_p\right)}_f\left(T_w-T_h\right)}{T_m}, N_b=\frac{D_t{\left(\rho C_p\right)}_f\left(C_w-C_h\right)}{T_m{\nu }_f}, S=\frac{w_o\sqrt{1-at}}{aH}\end{array}$$

where $K$ is Micropolar parameter, $M$ is Magnetic parameter (Hartmann number), $R$ is Squeezed Reynolds number, $Le$ is Lewis number, $N_t$ is Thermophoresis parameter, $N_b$ is Brownian motion parameter$P{r}_f$ is Prandtl number, and $S$ is suction or injuction parameter.

The skin friction coefficient $C_{fr}$, local nusselt number $N_u$, and sherwood number $S_h$ at both upper and lower disks are demarcated [30] as

$$C_{fr}=\frac{{({\tau }_{rz})}_{r=0}}{\frac{1}{2}{\rho }_{nf}{\left(\frac{-ar}{\left(1-at\right)}\right)}^2} , N_u=\frac{H{q}_w}{k\left({\mathrm{Ť}}_w-{\mathrm{Ť}}_h\right)} , S_h=\frac{H{j}_w}{D_b\left({\mathrm{Č}}_w-{\mathrm{Č}}_h\right)}.$$

where,

$${\tau }_{rz}=\left({\mu }_{nf}+k^{*}\right)\left[\frac{\partial u}{\partial r}+\frac{\partial w}{\partial r}\right] , q_w=-k\left(\frac{\partial T}{\partial z}\right), j_w=-D_b\left(\frac{\partial C}{\partial z}\right)$$

The transformed form of $C_{fr}$, $Nu, Sh$ for the model $\gamma Al{}_{2}O{}_3-H{}_{2}O$ is

$$\begin{array}{cc}{C}_{1fr}=\frac{1}{R_r{A}_1}\left(A_2+K\right)f^{″}\left(1\right),& C_{0fr}=\frac{1}{R_r{A}_1}\left(A_2+K\right)f^{″}\left(0\right),\\ Nu{}_1{\left(1-at\right)}^{1/2}=-{\theta }^{\prime }\left(1\right),& Nu{}_0{\left(1-at\right)}^{1/2}=-{\theta }^{\prime }\left(0\right),\\ Sh{}_0{\left(1-at\right)}^{1/2}=-{\beta }^{\prime }\left(1\right),& Sh{}_0 {\left(1-at\right)}^{1/2}=- \beta { }^{\prime }\left(0\right),\end{array}$$

and for the model $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ is

$$\begin{array}{cc}{C}_{1fr}=\frac{1}{R_r{B}_1}\left(B_2+K\right)f^{″}\left(1\right),& C_{0fr}=\frac{1}{R_r{B}_1}\left(B_2+K\right)f^{″}\left(0\right),\\ Nu{}_1{\left(1-at\right)}^{1/2}=-{\theta }^{\prime }\left(1\right),& Nu{}_0{\left(1-at\right)}^{1/2}=-{\theta }^{\prime }\left(0\right),\\ Sh{}_1{\left(1-at\right)}^{1/2}=-{\beta }^{\prime }\left(1\right),& Sh{}_0 {\left(1-at\right)}^{1/2}=-{\beta }^{\prime }\left(0\right).\end{array}$$

where $R_r=\frac{arH}{v_f{\left(1-at\right)}^{1/2}}$ is local squeezed Reynolds number.

3. Method of Solutions

The numerical procedure known as the Runge–Kutta–Fehlberg method (or RKF method) is used to solve mathematical equations with the computational error being demarcated as $1\times {10}^{-7}$. In the discipline of numerical analysis, the RKF method is a method for solving numerical solutions to ODEs.

• The coupled system of equations is first converted into a collection of initial value problems, which are then solved by the shooting method.
• Secondly, the Runge–Kutta–Fehlberg Method, is employed to collect the outcomes. All of the imitations and graphically recognized analyses are brought out using the software Mathematica.

With the aid of Equation (15), we engrave Equations (16)–(19) as follows:

$$f^{⁗}\left(\mathsf{\xi }\right)=\frac{A_{1}R}{2\left(A_2+K\right)}\left[3f^{″}\left(\mathsf{\xi }\right)+\xi f^{‴}\left(\mathsf{\xi }\right)-2f\left(\mathsf{\xi }\right)f^{‴}\left(\mathsf{\xi }\right)\right]+\frac{K}{\left(A_2+K\right)}{h}^{″}\left(\mathsf{\xi }\right)+\frac{A_4{M}^{2}R}{\left(A_2+K\right)}{f}^{″}\left(\mathsf{\xi }\right),$$

$$h^{″}\left(\mathsf{\xi }\right)=\frac{KR}{\left(A_2+\frac{K}{2}\right)}\left(2h\left(\mathsf{\xi }\right)-f^{″}\left(\mathsf{\xi }\right)\right)+\frac{A_{1}R}{2\left(A_2+\frac{K}{2}\right)}\left[3h\left(\mathsf{\xi }\right)+\xi {h^{\prime }}^{\left(\mathsf{\xi }\right)}+f^{\prime }\left(\mathsf{\xi }\right)h\left(\mathsf{\xi }\right)-2h^{\prime }\left(\mathsf{\xi }\right)f\left(\mathsf{\xi }\right)\right],$$

$${\theta }^{″}\left(\xi \right)=-\frac{A_4{A}_{1}R}{2A_2}P{r}_f\left(2f\left(\xi \right){\theta }^{\prime }\left(\xi \right)-\xi {\theta }^{\prime }\left(\xi \right)\right)-\frac{A_1{A}_4{N}_b}{A_2}P{r}_f{\theta }^{\prime }\left(\xi \right){\beta }^{\prime }\left(\xi \right)-\frac{A_4{A}_1{N}_t}{A_2}P{r}_f{\left({\theta }^{\prime }\left(\xi \right)\right)}^2,$$

$${\beta }^{″}\left(\xi \right)=-\frac{R}{2}Le\left[2{\beta }^{\prime }\left(\xi \right)f\left(\xi \right)-\xi {\beta }^{\prime }\left(\xi \right)\right]-\frac{N_t}{N_b}{\theta }^{″}\left(\xi \right).$$

Let us take

$$\begin{array}{c}{x}_1=f, x_2=f^{\prime }, x_3=f^{″}, x_4=f^{‴}, x_5=h, x_6=h^{\prime }, x_7=\theta ,\\ x_8={\theta }^{\prime }, x_9=\beta , x_{10}={\beta }^{\prime }. \end{array}$$

By using the above substitution, we get

$$\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\\ x_3^{\prime }\\ x_4^{\prime }\\ x_5^{\prime }\\ x_{\begin{array}{c}6\\ \end{array}}^{\prime }\\ x_7^{\prime }\\ x_8^{\prime }\\ x_9^{\prime }\\ x_{10}^{\prime }\end{array}\right]= \left[\begin{array}{c}{x}_2\\ x_3\\ x_4\\ \frac{A_{1}R}{2\left(A_2+K\right)}\left[3x_3+\xi x_4-2x^{1x_4}\right]+\frac{K}{\left(A_2+K\right)}{x}_6^{\prime }+\frac{A_4{M}^{2}R}{\left(A_2+K\right)}{x}_3\\ \frac{KR}{\left(A_2+\frac{K}{2}\right)}\left(2x_5-x_3\right)+\frac{A_{1}R}{2\left(A_2+\frac{K}{2}\right)}\left[3x_5+\xi x_6+x_2{x}_5-2x_6{x}^1\right]\\ -\frac{A_4{A}_{1}R}{2A_2}P{r}_f\left(2x_1{x}_8-\xi x_8\right)-\frac{A_1{A}_4{N}_b}{A_2}P{r}_f{x}_8{x}_{10}-\frac{A_4{A}_1{N}_t}{A_2}P{r}_f{\left(x_8\right)}^2\\ -\frac{R}{2}Le\left[2x_{10}{x}^1-\xi x_{10}\right]-\frac{N_t}{N_b}{x}_8^{\prime }\end{array}\right]$$

The relevant boundary conditions are

$$\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\\ x_9\\ x_{10}\end{array}\right]=\left[\begin{array}{c}0\\ 1/2\\ S\\ 0\\ -n{f}^{″}\left(0\right) \\ -n{f}^{″}\left(1\right) \\ 1\\ 0\\ 0\\ 0\end{array}\right]$$

This is the approach that was developed for $\gamma Al{}_{2}O{}_3-H{}_{2}O$. Similarly, we obtain this approach for $\gamma {\mathrm{Al}}_2{O}_3-C_2{H}_6{O}_2.$

4. Graphical Results

We analyze how changing values of emerging parameters affect flow pattern behavior and variations in radial velocity $f^{\prime }\left(\xi \right),$ rotational velocity$h\left(\xi \right)$, temperature field $\theta \left(\xi \right),$ and concentration profile $\beta \left(\xi \right).$ It should be noted that $S>0$indicates suction flow, whereas $S<0$ indicates injection or blowing.

4.1. Radial Velocity

The effects of many evolving parameters on radial velocity, such as the micropolar parameter $K$, squeezed Reynolds number $R$, and Hartmann number $M$, are depicted in Figure 2, Figure 3 and Figure 4.

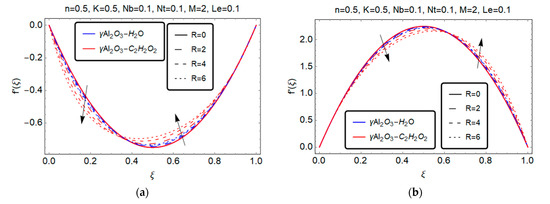
Figure 2. Effect of squeezed number $R$ on $f^{\prime }\left(\xi \right)$. (a) S > 0; (b) S < 0.

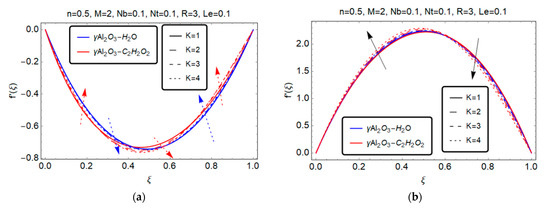
Figure 3. Effect of micropolar parameter $K$ on $f^{\prime }\left(\xi \right)$. (a) S > 0; (b) S < 0.

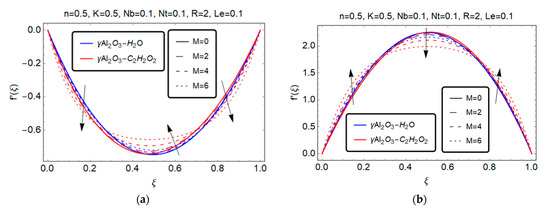
Figure 4. Effect of Hartmann number M on $f^{\prime }\left(\xi \right)$. (a) S > 0; (b) S < 0.

For $S>0$ (suction), the magnitude of radial velocity $f^{\prime }\left(\xi \right)$ elevates rapidly as the squeeze number $R$ increases in the range of $0 \le \xi \le 0.4$. Furthermore, the flow behavior of nanofluid water $\left(H{}_{2}O\right)$ and ethyl glycol$\left(C_2{H}_6{O}_2\right)$ fluctuates in the 0.4 < ξ ≤ 1 region, showing that $f^{\prime }\left(\xi \right)$ increases as Reynold number $R$ goes up, as shown in Figure 2a. For $S<0$, radial velocity decelerates upon a rising value of $R$ in the range $0\le \xi \le 0.6$, then starts accelerating as illustrated in Figure 2b. Physically, when the surfaces move closer together, the fluid is forced out of the channel, slowing the velocity in the boundary area. Contrarily, when the surfaces move faster, the fluid is squeezed into the channel, increasing the velocity of the boundary area.

Figure 3 depicts the effect of the micropolar parameter $K$ on the radial velocity $f^{\prime }\left(\xi \right).$ For $S>0$ (suction), the radial velocity $f^{\prime }\left(\xi \right)$ decreases with the increase in the micropolar parameter $K$, but the variation in the flow behavior of the nanofluids, water, and ethyl glycol with the suspended gamma alumina particles occurs around 0.7, after which $f^{\prime }\left(\xi \right)$increases with the increase in the micropolar parameter $K$, as shown in Figure 3a. In the case of injection, an opposite behavior is observed.

Figure 4 depicts the behavior of Hartmann number $M$ on the radial velocity. In the suction case, radial velocity $f^{\prime }\left(\xi \right)$ decreases at the wall region for both models $\left(\gamma {\mathrm{Al}}_2{O}_3-C_2{H}_6{O}_2\right)$and $\left(\gamma Al{}_{2}O{}_3-H{}_{2}O\right)$, as Hartmann number $M$ increases. Physically, the Lorentz force, which slows fluid motion at the boundary layer when the plates come together, causes the velocity distribution to drop as the magnetic parameter increases. Furthermore, when $S<0$ and two plates are very close to each other, the scenario causes an unfavorable pressure gradient, which is exacerbated by the retarding Lorentz force. When such forces act over a long period of time, a point of separation may arise, resulting in backflow. Furthermore, as the plates separate (i.e., S > 0), the magnetic parameter rises and the velocity distribution falls. S > 0 has a somewhat different cause than $\left(S<0\right)$. When two plates separate, a vacant space is created, and the fluid in that region moves at a high velocity, ensuring that mass flow conservation is maintained. As a result, a faster flow is observed.

4.2. Angular Velocity

Figure 5 and Figure 6 are painted to investigate the influence of physical parameters on angular velocity for both models $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ and $\gamma Al{}_{2}O{}_3-H{}_{2}O.$

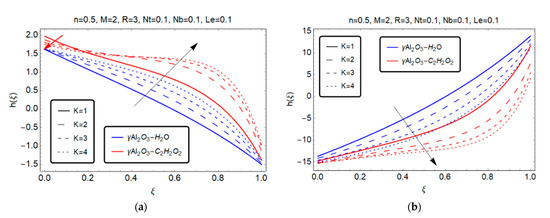
Figure 5. Effect of micropolar parameter $K$ on $h\left(\xi \right)$. (a) S > 0; (b) S < 0.

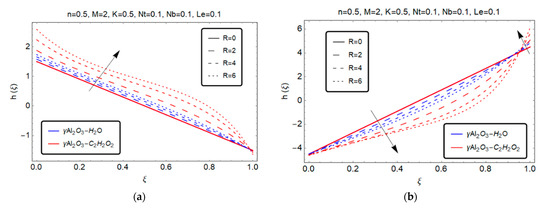
Figure 6. Effect of squeezed Reynold number $R$ on $h\left(\xi \right)$. (a) S > 0; (b) S < 0.

Figure 5a shows that when the micropolar parameter $K$ is increased in the suction condition, the angular velocity $h\left(\xi \right)$ initially falls at the area of $0\le \xi \le 2$for the $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$model, then increases with increasing values of $K$. For the model $\gamma Al{}_{2}O{}_3-H{}_{2}O$, the angular velocity initially increases with the increment of values of $K$ for $S>0$. For $S<0$, the angular velocities $h\left(\xi \right)$ of both models decrease as the micropolar prameter $K$ increases, as shown in Figure 5b. But the behavior of the graph 5b shows that the angular velocity is increased in the region of $0.65\le \xi \le 1$, more rapidly for the model $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$.

Figure 6a pointed out that, for $S>0,$the angular velocities $h\left(\xi \right)$of both models $\gamma Al{}_{2}O{}_3-H{}_{2}O$ and $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ increased as the squeeze number $R$ increased. By contrast, in the case of injection, the opposite phenomenon occurs at the region $0\le \xi \le 0.9$ with rising values of $R$, after which the angular velocities $h\left(\xi \right)$ increase with increasing squeezed number $R$.

4.3. Temperature Field

Figure 7 and Figure 8 depict the effect of important flow factors on the temperature distribution, including the thermophoresis parameter $N_t$and the squeezed number R.

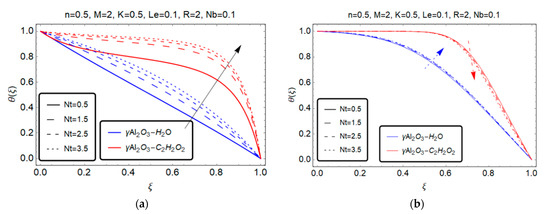
Figure 7. Effect of thermophoresis parameter $N_t$ on $\theta \left(\xi \right)$. (a) S > 0; (b) S < 0.

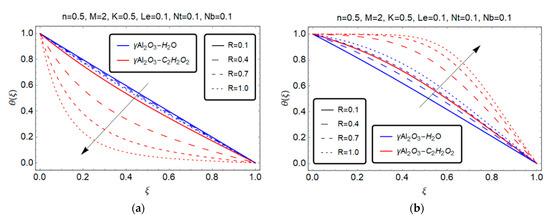
Figure 8. Effect of squeezed Reynold number R on $\theta \left(\xi \right)$. (a) S > 0; (b) S < 0.

For $S>0$, the temperature distribution $\theta \left(\xi \right)$ rises with increasing values of the thermophoresis parameter $N_t$ for both models $\gamma Al{}_{2}O{}_3-H{}_{2}O$ and $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ as shown in Figure 7a. By contrast, in the case of injection, the temperature distribution $\theta \left(\xi \right)$ slowly increases with increasing values of $N_t$only for the $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ model, but for the $\gamma Al{}_{2}O{}_3-H{}_{2}O$ model, the temperature distribution remains unchanged until it approaches the neighborhood of 0.5, after which it slowly decreases until it approaches 1.

Figure 8a depicts the temperature distribution $\theta \left(\xi \right)$ of the $\gamma Al{}_{2}O{}_3-H{}_{2}O$model gradually increasing with rising values $R$, and temperature distribution $\theta \left(\xi \right)$ of the $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ model rapidly increasing in comparison to the $\gamma Al{}_{2}O{}_3-H{}_{2}O$ for $S>0$. By contrast, in the case of blowing the opposite effect is observed for both models. Physically, the temperature in the flow increases as $S<0$ increases the kinetic energy of fluid particles due to the bigger channel volume. The lower channel volume, on the other hand, reduces the kinetic energy of fluid particles, slowing down the temperature field.

4.4. Concentration Profile

The influence of several physical parameters, $Le,R,N_b,N_t$, on the concentration profile is incorporated in Figure 9, Figure 10, Figure 11 and Figure 12.

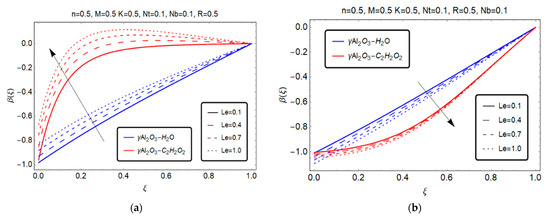
Figure 9. Effect of Lewis number $Le$ on $\beta \left(\xi \right)$. (a) S > 0; (b) S < 0.

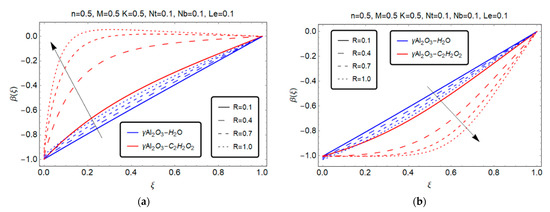
Figure 10. Effect of Reynold number R on $\beta \left(\xi \right)$ on $\beta \left(\xi \right)$. (a) S > 0; (b) S < 0.

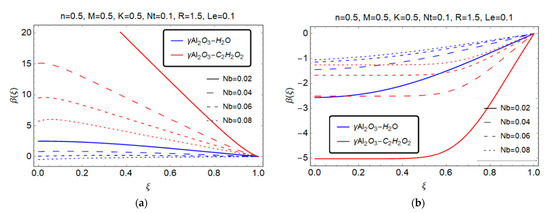
Figure 11. Effect of Brownian motion $N_b$ on $\beta \left(\xi \right)$. (a) S > 0; (b) S < 0.

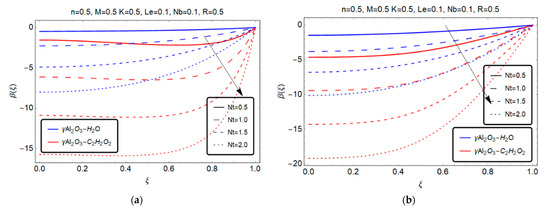
Figure 12. Effect of Thermophoresis parameter $N_t$ on $\beta \left(\xi \right)$. (a) S > 0; (b) S < 0.

Figure 9a and Figure 10a indicate that for both models $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ and $\gamma Al{}_{2}O{}_3-H{}_{2}O$ in suction ($S>0$), the variation of the concentration profile $\beta \left(\xi \right)$ rises immediately with the increase in the Lewis number $Le$ and the squeezed number $R$. By contrast, Figure 9b and Figure 10b show the opposite phenomenon for both models in the case of injection ($S<0$).

Figure 11a and Figure 12a demonstrate the impact of Brownian motion parameter $N_b$ and thermophoresis parameter $N_t$ on concentration profile $\beta \left(\xi \right)$. They demonstrate that for both models, $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ and $\gamma Al{}_{2}O{}_3-H{}_{2}O$, $\beta \left(\xi \right)$ is inversely proportional to Brownian motion $N_b$ and thermophoresis parameter $N_t$. Figure 11b demonstrates that $\beta \left(\xi \right)$ is directly proportional to Brownian motion $N_b$, whereas Figure 12b demonstrates that $\beta \left(\xi \right)$ is directly proportional to $N_t$for both models $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ and $\gamma Al{}_{2}O{}_3-H{}_{2}O$ in the case of injection ($S_0<0$), respectively.

5. Numerical Results

To validate our present study, the impact of different emerging parameters such as Hartmann number $M$, microrotation parameter $K,$ and local squeezed Reynold number $R_r$ on shear stresses, rate of heat transfer, and mass transfer are portrayed in tabulated form.

Table 2 and Table 3 illustrate how different emerging parameters of the model $\gamma Al{}_{2}O{}_3-H{}_{2}O$ affect the skin friction coefficient in upper and lower planes with strong $\left(n=0\right)$ and weak $\left(n=0.5\right)$. interactions. When $S>0$, increasing Hartmann number M in the upper plane causes the skin friction coefficient to rise, but increasing Hartmann number M in the top plane causes the skin friction coefficient to fall. However, for both strong and weak connections, opposing behaviors are observed at the lower and higher planes for $S<0$. As the local compressed Reynolds number R_r increases, the skin friction coefficient in the upper and lower planes decreases, resulting in both weak and strong interactions for $S>0$ and $S<0$. The influence of the micropolar parameter K on the skin friction coefficient in both the upper and lower planes is equivalent to the Hartmann number M. As a result, for both strong and weak contacts, the skin friction coefficient at the top plane increases with increasing values of $M$ and $K$ for S > 0, but the opposite phenomenon occurs for rising values of $M$ and $K$ for $S<0$. Similarly, Table 4 and Table 5 report on gamma alumina with ethyl glycol $\left(\gamma A{l}_2{O}_3-C_2{H}_6{O}_2\right),$which we have observed for gamma alumina with water$\left(\gamma Al{}_{2}O{}_3-H{}_{2}O\right).$

Table 2. Skin friction coefficient for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with strong interaction $n=0$.

M	${\mathit{R}}_{\mathit{r}}$	K	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{b}}$	Le	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$
						$S<0$		$\mathit{S}>\mathbf{0}$
0	1	0.1	0.1	0.1	0.1	−45.1832	43.7022	14.6922	−15.1944
2						−47.0076	45.5841	15.3251	−15.8074
3						−49.2057	47.8431	16.0844	−16.5456
4						−52.1434	50.8501	17.0943	−17.5317
1	1					−45.6450	44.1793	14.8527	−15.3496
	2					−23.4159	21.9825	7.45172	−7.94571
	3					−15.9965	14.5936	4.98694	−5.47814
	4					−12.2800	10.9059	3.75607	−4.24461
	1	1.0				−48.4571	46.9880	15.7893	−16.2863
		1.5				−51.2647	49.7912	16.7243	−17.2211
		2.0				−54.0685	52.5890	17.6581	−18.1540
		2.5				−56.8692	55.3817	18.5908	−19.0853

Table 3. Skin friction coefficient for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with weak interaction $n=0.5$.

M	${\mathit{R}}_{\mathit{r}}$	K	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{b}}$	Le	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$
						$S<0$		$S>0$
0	1	0.1	0.1	0.1	0.1	−45.1259	43.7491	14.6863	−15.1923
2						−46.9502	45.6308	15.3191	−15.8052
3						−49.1482	47.8896	16.0782	−16.5434
4						−52.0857	50.8963	17.0881	−17.5293
1	1					−45.5877	44.2262	14.8468	−15.3475
	2					−23.3601	22.0249	7.44590	−7.94341
	3					−15.9422	14.6321	4.98121	−5.47564
	4					−12.2270	10.9408	3.75044	−4.24193
	1	1.0				−48.2876	47.1301	15.7579	−16.3017
		1.5				−50.9318	50.0707	16.6493	−17.2712
		2.0				−53.5242	53.0429	17.5223	−18.2536
		2.5				−56.0689	56.0424	18.3782	−19.2472

Table 4. Skin friction coefficient for $\left(\gamma A{l}_2{O}_3-C_2{H}_6{O}_2\right),$ at lower and upper plane with strong interaction $n=0$.

M	${\mathit{R}}_{\mathit{r}}$	K	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{b}}$	Le	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$
						$S<0$		$S>0$
0	1	0.1	0.1	0.1	0.1	−82.366	80.8770	27.0855	−27.5867
2						−83.396	81.9250	27.4365	−27.9314
3						−86.421	85.0008	28.4666	−28.9442
4						−91.266	89.9166	30.1123	−30.5659
1	1					−97.679	96.4075	32.2845	−32.7117
	2					−41.561	40.0819	13.4851	−13.9875
	3					−27.958	26.4895	8.95236	−9.45590
	4					−21.156	19.6978	6.68652	−7.19122
	1	1.0				−85.339	83.8491	28.0764	−28.5775
		1.5				−88.309	86.8176	29.0662	−29.5671
		2.0				−91.276	89.7827	30.0550	−30.5555
		2.5				−94.241	92.7444	31.0430	−31.5428

Table 5. Skin friction coefficient for $\left(\gamma A{l}_2{O}_3-C_2{H}_6{O}_2\right),$ at lower and upper plane with weak interaction $n=0.5$.

M	${\mathit{R}}_{\mathit{r}}$	K	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{b}}$	Le	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(1\right)$	$\frac{\left(\mathit{A}{}_2+\mathit{K}\right)}{\mathit{R}\mathit{A}{}_1}{\mathit{f}}^{″}\left(0\right)$
						$S<0$		$S>0$
0	1	0.1	0.1	0.1	0.1	−82.3327	80.9058	27.0818	−27.5859
2						−83.3621	81.9538	27.4328	−27.9306
3						−86.3872	85.0294	28.4628	−28.9434
4						−91.2322	89.9451	30.1085	−30.5650
1	1					−97.6452	96.4359	32.2805	−32.7107
	2					−41.5276	40.1092	13.4815	−13.9866
	3					−27.9255	26.5154	8.94874	−9.45498
	4					−21.1241	19.7223	6.68293	−7.19024
	1	1.0				−85.2370	83.9390	28.0570	−28.5878
		1.5				−88.1049	86.9985	29.0196	−29.5997
		2.0				−90.9377	90.0822	29.9701	−30.6206
		2.5				−93.7370	93.1882	30.9090	−31.6498

The influence of the local Nusselt number $N{u}_r$ on the model of Gamma Alumina with Water $\left(\gamma Al{}_{2}O{}_3-H{}_{2}O\right)$ under the influence of physical parameters with strong and weak contacts at the upper and lower disks is explored in Table 6 and Table 7. For rising values of local squeezed Reynold number, in the presence of strong and weak contacts, the rate of heat transfer increases at the upper disc but decreases at the lower disc for both suction and injection. When the Brownian motion parameter is present, the rate of heat transfer decreases as the Brownian motion $N_b$ at the upper disc grows for both strong and weak contacts at a lower disc. However, for both $S>0$ and $S<0$, the local Nusselt number $N{u}_r$ is proportional to the thermophoresis parameter $N_t$ in the upper disc. In both circumstances of suction and injection, the inverse proportionality is observed at the lower discs. Similarly, in Table 8 and Table 9, the same phenomenon occurred for $\left(\gamma A{l}_2{O}_3-C_2{H}_6{O}_2\right)$.

Table 6. Local Nusselt number for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with strong interaction $n=0$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	1.48384	0.221317	0.701408	1.80446
1.0						1.84085	0.0403327	0.450991	2.97432
1.5						2.09948	0.0066876	0.265785	4.47949
2.0						2.29856	0.0010552	0.144852	6.22556
1.0	0.04					1.85575	0.0396013	0.934255	1.88609
	0.06					1.85225	0.0397719	0.832706	2.05523
	0.08					1.84729	0.0400145	0.676884	2.36365
	0.10	0.10				1.84085	0.0403327	0.450991	2.97432
		0.15				1.85109	0.0397001	0.934701	1.88795
		0.20				1.85811	0.0392336	1.230040	1.49615
		0.25				1.86379	0.0388371	1.448710	1.27278

Table 7. Local Nusselt number for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with weak interaction $n=0.5$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	1.48366	0.221367	1.23587	0.478392
1.0						1.84025	0.040373	1.43581	0.213998
1.5						2.09832	0.006703	1.59833	0.091349
2.0						2.29675	0.001059	1.72926	0.037776
1.0	0.04					1.85517	0.0396406	0.934255	1.88609
	0.06					1.85166	0.0398116	0.832706	2.05523
	0.08					1.8467	0.0400546	0.676884	2.36365
	0.10	0.10				1.81700	0.041681	0.450991	2.97432
		0.15				1.85051	0.039739	0.934701	1.88795
		0.20				1.85754	0.039272	1.23004	1.49615
		0.25				1.86323	0.038874	1.44871	1.27278

Table 8. Local Nusselt number for $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ at lower and upper plane with strong interaction $n=0$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	1.61644	0.07899360	0.240449	4.76968
1.0						1.92813	0.00454138	0.027828	10.7220
1.5						2.10042	0.00023705	0.002258	16.8806
2.0						2.20862	0.00001188	0.000158	22.9631
1.0	0.04					1.93302	0.00451046	2.072230	2.84345
	0.06					1.93186	0.00451776	1.622490	3.44193
	0.08					1.93023	0.00452806	0.853611	4.93379
	0.10	0.15				1.92812	0.00452196	2.072280	2.85230
		0.20				1.92711	0.00450889	3.156690	1.82724
		0.25				1.92570	0.00449839	3.804380	1.39570

Table 9. Local Nusselt number for $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ at lower and upper plane with weak interaction $n=0.5$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$	$-{\mathit{\theta }}^{\prime }\left(1\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	1.61636	0.07900400	0.240449	4.76968
1.0						1.92785	0.00454404	0.027828	10.7220
1.5						2.09989	0.00023737	0.002258	16.8806
2.0						2.20780	0.00001191	0.000158	22.9631
1.0	0.04					1.84122	0.00472995	1.769690	2.94372
	0.06					1.83969	0.00473938	1.407540	3.51668
	0.08					1.83753	0.00475268	0.796204	4.89733
	0.10	0.15				1.92785	0.00452458	2.072280	2.85230
		0.20				1.92684	0.00451149	3.156690	1.82724
		0.25				1.92543	0.00450098	3.804380	1.39570

Table 10 and Table 11 indicate the effect of critical flow parameters on the local Sherwood number $S{h}_r$ at the upper and lower discs for the model $Al{}_{2}O{}_3-H{}_{2}O$ in the presence of weak and strong interactions. For $S>0$, the rate of mass transfer at the upper plane rises as $R_r$ increases, whereas for both weak and strong contacts, the rate of mass transfer at the bottom plane decreases. However, the opposite behavior is expected for $S<0$. The mass transfer rate is increased when there is an increase in Brownian motion parameter $N_b$only at the upper plane, while at the lower plane the rate of mass transfer decreases for $S<0$. Also, it decreases at both planes for $S>0$. Similarly, when increases occur in the thermophoresis parameter$N_t$, decreasing mass transfer occurs at the upper plane at both suction and injection, while the opposite behavior occurs at the lower plane at both suction and injection for both weak and strong interaction, respectively. However, for $S>0$, the local Sherwood number $S{h}_r$ is directly proportional to the Lewis number Le, but for $S<0$, it is inversely proportional.

Table 10. Local Sherwood number for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with strong interaction $n=0$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-\mathit{\beta }\prime \left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	−1.50067	−0.221317	−0.68695	−1.80446
1.0						−1.86495	−0.040332	−0.41822	−2.97432
1.5						−2.12752	−0.006687	−0.21164	−4.47949
2.0						−2.32936	−0.001055	−0.06762	−6.22556
1.0	0.04					−4.61182	−0.015840	1.59704	−0.75443
	0.06					−3.08245	−0.023863	0.79820	−1.23314
	0.08					−2.32023	−0.032011	0.22908	−1.89092
	0.10	0.15				−2.77784	−0.026466	0.17420	−1.25863
		0.20				−3.70217	−0.019616	−0.22011	−0.74807
		0.25				−4.63333	−0.015534	−0.95475	−0.50911
		0.10	0.4			−1.91284	−0.040951	−0.34587	−2.93256
			0.7			−1.96588	−0.041638	−0.28195	−2.89362
			1.0			−2.02491	−0.042406	−0.22545	−2.85727

Table 11. Local Sherwood number for $\gamma Al{}_{2}O{}_3-H{}_{2}O$ at lower and upper plane with weak interaction $n=0.5$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	−1.5005	−0.221367	−1.24594	−0.47839
1.0						−1.86434	−0.040373	−1.45211	−0.21399
1.5						−2.12634	−0.006703	−1.61848	−0.09134
2.0						−2.32752	−0.001059	−1.75191	−0.03777
1.0	0.04					−4.61025	−0.015856	1.59704	−0.75443
	0.06					−3.08141	−0.023887	0.79820	−1.23314
	0.08					−2.31946	−0.032043	0.22908	−1.89092
	0.10	0.15				−2.77691	−0.026493	0.17420	−1.25863
		0.20				−3.70094	−0.019636	−0.22011	−0.74807
		0.25				−4.63182	−0.015549	−0.95475	−0.50911
		0.10	0.4			−1.91222	−0.040992	−0.34587	−2.93256
			0.7			−1.96523	−0.041680	−0.28195	−2.89362
			1.0			−2.02425	−0.042449	−0.22545	−2.85727

Table 12 and Table 13 indicate the effect of critical flow parameters on the local Sherwood number $S{h}_r$at the upper and lower planes for the model ${\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$at both strong and weak contacts. For both strong and weak contacts, this model is the same as the above model for $S<0$ in both upper and lower planes. By contrast, for $S>0$ only the squeezed Reynolds number and Brownian motion parameters differ from the above model, indicating that as $R_r$ increases in the upper plane, it decreases in the lower plane. When $N_b$ increases, the Sherwood number also increases in the upper plane while it decreases in the lower plane.

Table 12. Local Sherwood number for $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ at lower and upper plane with strong interaction $n=0$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	−1.62287	−0.07899360	−0.221793	−4.76968
1.0						−1.93618	−0.00454138	0.015677	−10.7220
1.5						−2.10922	−0.00023705	0.065547	−16.8806
2.0						−2.21788	−0.00001188	0.090940	−22.9631
1.0	0.04					−4.84292	−0.00180418	0.709440	−1.13738
	0.06					−3.22822	−0.00271066	0.924862	−2.06516
	0.08					−2.42076	−0.00362245	1.140900	−3.94703
	0.10	0.15				−2.90039	−0.00301465	−0.750449	−1.90154
		0.20				−3.86339	−0.00225444	−3.597290	−0.91362
		0.25				−4.82470	−0.00179935	−6.605030	−0.55828
		0.10	0.4			−1.93123	−0.00461210	0.126931	−10.5036
			0.7			−1.92640	−0.00468721	0.221523	−10.2906
			1.0			−1.92173	−0.00476716	0.301313	−10.0838

Table 13. Local Sherwood number for $\gamma {\mathit{Al}}_2{O}_3-C_2{H}_6{O}_2$ at lower and upper plane with weak interaction $n=0.5$.

${\mathit{R}}_{\mathit{r}}$	${\mathit{N}}_{\mathit{b}}$	${\mathit{N}}_{\mathit{t}}$	Le	M	K	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$	$-{\mathit{\beta }}^{\prime }\left(1\right)$	$-{\mathit{\beta }}^{\prime }\left(0\right)$
						$S<0$		$S>0$
0.5	0.1	0.1	0.1	1.0	0.5	−1.62278	−0.0790040	−0.221793	−4.76960
1.0						−1.93590	−0.0045440	0.015677	−10.7220
1.5						−2.10868	−0.0002373	0.065547	−16.8806
2.0						−2.21705	−0.0000119	0.090940	−22.9631
1.0	0.04					−4.80642	−0.0018919	0.989687	−1.17749
	0.06					−3.20384	−0.0028436	1.004340	−2.11001
	0.08					−2.40241	−0.0038021	1.085500	−3.91786
	0.10	0.15				−2.89998	−0.0030163	−0.750449	−1.90154
		0.20				−3.86284	−0.0022557	−3.597290	−0.91362
		0.25				−4.82402	−0.0018003	−6.605030	−0.55828
		0.10	0.4			−1.93095	−0.0046147	0.126931	−10.5036
			0.7			−1.92613	−0.0046899	0.221523	−10.2906
			1.0			−1.92145	−0.0047699	0.301313	−10.0838