Stochastic Stabilization for Discrete-Time System with Input Delay and Multiplicative Noise in Control Variable

Abstract

The stabilization problems for time-delay stochastic systems with multiplicative noise in the control variable are investigated in this paper. The innovative contributions are described as follows. Since the past work on stabilization is based on some delay-dependent algebraic Riccati equation (DARE), how to numerically calculate the stabilizing solution remains an unsolved and open problem. On the one hand, an iterative algorithm for computing the unique stabilizing solution of DARE is proposed, while the convergence property is also proved. On the other hand, the concepts of critical stabilization and essential destabilization are proposed as a supplement to stochastic stabilization in terms of spectrum technique. Moreover, the Lyapunov-based necessary and sufficient conditions are developed.

1. Introduction

It is becoming increasingly clear that areas such as network control, finance, power systems, robotics, and a large range of practical engineering systems can be described as stochastic models [1,2,3,4,5]. In the actual system, due to the limited capacity between different parts of the actual system, the uncertainty of the external environment changes, etc., time delay is a common phenomenon in system modeling. For the actual system in engineering, time delay will cause some negative impacts that cannot be ignored, such as the instability of the system and the decline in system performance. In recent years, stochastic systems with time delay have been extensively studied, especially for the issues such as LQ optimal control, stochastic stabilization, observability, mixed $H_2/H_{\infty }$ control and $H_2$ control. One of the crucial problems is the stabilization problem, which is a scheme for obtaining closed-loop stability control.

Over the past few decades, the research on stochastic systems with input delay has attracted widespread attention; see [1,2,6,7]. The vast majority of stability studies use the method of the generalized Lyapunov equation (GLE) [8,9,10]. This approach can provide easy-to-verify stability standards, but there is nothing that can be done to deal with some important issues. Recently, in an input-delay-free stochastic system, refs. [11,12,13], a random spectral analysis method has been adopted to study the stability problem for some linear time-invariant (LTI) models. Notice that the role of spectral analysis is irreplaceable by the Lyapunov functional approach. Based on the spectrum theory, the concepts of asymptotic mean square stabilization, critical stabilization, and essential destabilization are defined, which are effective and meticulous. However, we find that there are very few stabilization results for stochastic dynamics with input delay. And due to the interference of input delay factors, the delay-dependent Lyapunov operator and operator spectrum is much more complex than the generalized Lyapunov operator and its operator spectrum. How to utilize the available information to determine the necessary and sufficient conditions for critical stabilization and essential destabilization is very difficult. As far as we know, there are no relevant research results on time-delay stochastic systems. On the other hand, since the past work on stabilization is based on the DARE, the analysis for the nonlinear DARE is challenging. How to use the convergence algorithm to numerically calculate the unique stabilizing solution of DARE deserves in-depth study. This has greatly stimulated the motivation and confidence in our scientific research of this paper.

The objective of this paper is to obtain the necessary conditions for asymptotic mean square stabilization, while at the same time we define critical stabilization and essential destabilization as a supplement to the asymptotic mean square stabilization. We propose an iterative algorithm for computing the stabilizing solution and give the proof of convergence of the algorithm. In addition, we provide a set of necessary and sufficient conditions to confirm critical stabilization and essential destabilization.

To be specific, our research layout and methodology are described as follows. Section 2 formulates the systems under consideration and also presents preliminary results which will express our results more precisely. The main results are given in Section 3, Section 4 and Section 5 in terms of methods such as convergence algorithm, recursion, delay-dependent Lyapunov equation (DLE), resizing algorithm, etc. Section 6 provides two examples to show the effectiveness of our theoretic results.

Notations: $ker(A)$ means its kernel space and let I be the identity matrix with appropriate dimension. $A\otimes B$ represents the Kronecker product of the matrices A and B. ${\delta }_{ks}$ is a Kronecker function. Let $S^n$ be the space of all n-dimensional symmetric matrices. $D[0,1]=\{z|z\in C,|z-0|\le 1\}$. $e_k$ means a sequence of real random variables defined on the complete probability space $(\Omega ,\mathcal{F},\mathcal{P},{\mathcal{F}}_t)$ with ${\mathcal{F}}_t=\sigma \{e_s,s=0,\dots ,t\}$. Define ${\widehat{x}}_{t|s}=E[x_t|{\mathcal{F}}_s]$ to be the conditional expectation $x_t$ w.r.t. the filter ${\mathcal{F}}_s$.

2. Problem Formulation and Preliminaries

Consider the following discrete time stochastic dynamics

$$x_{k+1}=A{x}_k+B{v}_{k-d}+e_{k}C{v}_{k-d},$$

(1)

where $e_k$ is assumed to be a scalar random white noise satisfying $E(e_k)=0$ and $E(e_k{e}_s)={\sigma }^2{\delta }_{ks}$, $d>0$ is a positive number representing time delay in control input. To condense the formula, let us define $[A,B,C|d]$ representing the system (1). Note that the mean square stabilization problem of stochastic system has been fully studied in [14,15,16,17] and the study in [18,19,20,21,22,23,24,25] also extended the theoretical results to a more general level.

Remark 1.

For a stochastic system with input delay and multiplicative noise in the control variable, it is worth mentioning that this stochastic dynamic model has a wide application in engineering practice. Specifically, consider an NCS operating over a reliable communication channel, in which the control signal is assumed to suffer both packet loss and network-induced delay from the controller to the actuator. As shown in [17], the overall NCS can be modelled by

$$x_{k+1}=A{x}_k+{\eta }_{k}B{v}_{k-d}$$

(2)

where the packet loss process of ${\gamma }_k$ follows the Bernoulli distribution with $\mathcal{P}({\eta }_k=0)=s\in [0,1]$. When we denote $e_k={\eta }_k-(1-s)$, system (2) is equivalent to

$$x_{k+1}=A{x}_k+(1-s)B{v}_{k-d}+e_{k}B{v}_{k-d}$$

(3)

which is a special case of system $[A,B,C|d]$.

Facilitated by stochastic control techniques, the objective is to find the necessary conditions for the asymptotic mean square stabilization. More importantly, explore the equivalent conditions for the critical stabilization and essential destabilization of the system (1) under consideration. To express our results more precisely, we need to introduce the following definitions and lemmas. Different from the previous work, one significant contribution is that our control law is designed as the feedback of an extended state that contains the recently available state information and part values from previous control inputs.

Here we recall some basic definitions and lemmas related to stabilization in the mean square sense, which are necessary for the exposition in this paper. For additional details and other basics, we refer the reader to [14,26,27,28].

Definition 1.

System $[A,B,C|d]$ is asymptotically mean square stabilizable, if there exists a control input with $v_{k-d}=K{\widehat{x}}_{k|k-d-1}$, $k\ge d$, such that

$$x_{k+1}=A{x}_k+[B+e_{k}C]K{\widehat{x}}_{k|k-d-1}$$

(4)

is asymptotically mean square stable.

In order to make the description and research more convenient, we define the following operators. For system $[A,B,C|d]$, let ${\mathcal{F}}_K^{[A,B,C|d]}$ be a linear operator from $S^n$ to $S^n$ defined as follows

$${\mathcal{F}}_K^{[A,B,C|d]}(M)=(A+BK)M{(A+BK)}^{\prime }+{\sigma }^2{A}^{d}CKM{K}^{\prime }{C}^{\prime }{(A^{\prime })}^d.$$

(5)

The adjoint operator ${\mathcal{F}}_K^{*}$ of ${\mathcal{F}}_K^{[A,B,C|d]}$ from $S^n$ to $S^n$ is given as

$${\mathcal{F}}_K^{*}(M)={(A+BK)}^{\prime }M(A+BK)+{\sigma }^2{K}^{\prime }{C}^{\prime }{(A^{\prime })}^{d}M{A}^{d}CK.$$

(6)

The spectral set of $\mathcal{F}$ is represented by

$$\begin{array}{cc}\hfill & \rho ({{\mathcal{F}}_K}^{[A,B,C|d]})=\{\lambda ,{{\mathcal{F}}_K}^{[A,B,C|d]}(M)=\lambda M,M\in S^n,M\ne 0\}.\hfill \end{array}$$

(7)

Moreover, for system $[A,B,C|d]$, the nonlinear Riccati operators ${\mathcal{R}}^{[A,B,C|d]}$ from $S^n$ to $S^n$ is defined as

$${\mathcal{R}}^{[A,B,C|d]}(M)=A^{\prime }MA-L^{\prime }{U}^{-1}L+Q,$$

(8)

where $Q\ge 0$, $R>0$ and

$$\begin{array}{cc}\hfill L=& B^{\prime }MA,\hfill \\ \hfill U=& B^{\prime }MB+R+{\sigma }^2{C}^{\prime }QC+{\sigma }^2\sum _{k=0}^{d-1}{C}^{\prime }{(A^{\prime })}^{k+1}Q{A}^{k+1}C+{\sigma }^2{C}^{\prime }{(A^{\prime })}^d(M-Q)A^{d}C.\hfill \end{array}$$

(9)

Lemma 1.

([29]). The equivalent conditions for the mean square stabilization of system $[A,B,C|d]$ are given as follows.

(a) 

System $[A,B,C|d]$ is stabilizable in the mean square sense, if and only if there admit K and $P>0$ satisfying the following equation

$$P=Q+(A+BK)P{(A+BK)}^{\prime }+{\sigma }^2{A}^{d}CKP{K}^{\prime }{C}^{\prime }{(A^{\prime })}^d,\forall Q>0.$$

(10)

(b) 

System $[A,B,C|d]$ is stabilizable in the mean square sense, if and only if there exists a constant matrix K such that $|\rho ({\mathcal{F}}_K^{[A,B,C|d]})|<1$.

(c) 

The mean square stabilization of system $[A,B,C|d]$ is equivalent to that of the following delay free system

$$z_{k+1}=A{z}_k+B{u}_k+e_k{A}^{d}C{u}_k.$$

(d) 

The mean square stabilizable of system $[A,B,C|d]$ is equivalent to the following DARE

$$P=A^{\prime }PA-L^{\prime }{U}^{-1}L+Q,\forall R>0,Q>0.$$

(11)

admits a unique stabilizing solution $P_s>0$, where L and U satisfy (9).

By Lemma 1, the stabilization of $[A,B,C|d]$ is equivalent to the existence and uniqueness of stabilizing solution to DARE. It is remarkable that in contrast to the standard algebraic Riccati equation (ARE) or modified ARE, how to calculate this stabilizing solution to the DARE remains an open problem. Until now, to the best of our knowledge, there have been no firm results to these related problems.

3. The Necessary Condition of Asymptotic Mean Square Stabilization

In this section, we propose an algorithm for numerically solving the unique stabilizing solution of DARE, which is based on the asymptotic properties of the stabilizing solution. To begin with, for system $[A,B,C|d]$, let ${\mathcal{G}}_K^{[A,B,C|d]}$ be a linear operator from $S^n$ to $S^n$, and it is defined as

$$\begin{array}{cc}\hfill {\mathcal{G}}_K^{[A,B,C|d]}(M)=& {(A+BK)}^{\prime }M(A+BK)+K^{\prime }RK+Q+\sum _{k=0}^{d-1}{\sigma }^2{K}^{\prime }{C}^{\prime }{(A^{\prime })}^{k+1}Q{A}^{k+1}CK\hfill \\ \hfill & +{\sigma }^2{K}^{\prime }{C}^{\prime }{(A^{\prime })}^d(M-Q)A^{d}CK+{\sigma }^2{K}^{\prime }{C}^{\prime }QCK,\hfill \end{array}$$

where $Q>0$, $R>0$. Then the linear operator ${\mathcal{G}}_K^{[A,B,C|d]}$ can be defined in terms of (6) as

$${\mathcal{G}}_K^{[A,B,C|d]}(M)={\mathcal{F}}_K^{*}(M)+\widehat{Q}>{\mathcal{F}}_K^{*}(M),$$

(12)

where

$$\begin{array}{cc}\hfill \widehat{Q}=& K^{\prime }RK+Q+\sum _{k=0}^{d-1}{\sigma }^2{K}^{\prime }{C}^{\prime }{(A^{\prime })}^{k+1}Q{A}^{k+1}CK-{\sigma }^2{K}^{\prime }{C}^{\prime }{(A^{\prime })}^{d}Q{A}^{d}CK\hfill \\ \hfill & +{\sigma }^2{K}^{\prime }{C}^{\prime }QCK>0.\hfill \end{array}$$

When the gain is defined by $K_M=-U^{-1}L$, (8) can be written as

$$\begin{array}{cc}\hfill {\mathcal{R}}^{[A,B,C|d]}(M)=& A^{\prime }MA-L^{\prime }{U}^{-1}L+Q\hfill \\ \hfill =& {(A+B{K}_M)}^{\prime }M(A+B{K}_M)+\sum _{k=0}^{d-1}{\sigma }^2{K}_M^{{}^{\prime }}{C}^{\prime }{(A^{\prime })}^{k+1}Q{A}^{k+1}C{K}_M\hfill \\ \hfill & +{\sigma }^2{K}_M^{{}^{\prime }}{C}^{\prime }{(A^{\prime })}^d(M-Q)A^{d}C{K}_M+{\sigma }^2{K}_M^{{}^{\prime }}{C}^{\prime }QC{K}_M+K_M^{{}^{\prime }}R{K}_M+Q\hfill \\ \hfill =& {\mathcal{G}}_{K_M}^{[A,B,C|d]}(M).\hfill \end{array}$$

(13)

By utilizing the definitions of the delay-dependent algebraic Riccati operator ${\mathcal{R}}^{[A,B,C|d]}$ and the linear operator ${\mathcal{G}}_K^{[A,B,C|d]}$, we have the following lemmas. Since the proof is similar to that of Lemmas 3 and 4 in [30], the details are omitted here.

Lemma 2.

Suppose $d>0$, then one has the following statements.

(a) 

For any $M\ge 0$,

$${\mathcal{R}}^{[A,B,C|d]}(M)=\underset{K}{min}{\mathcal{G}}_K^{[A,B,C|d]}(M).$$

(14)

(b) 

If $M_2\ge M_1\ge 0$, then,

$${\mathcal{R}}^{[A,B,C|d]}(M_2)\ge {\mathcal{R}}^{[A,B,C|d]}(M_1).$$

(c) 

For system $[A,B,C|d]$, define $X_{k+1}={\mathcal{R}}^{[A,B,C|d]}(X_k)$ and $Y_{k+1}={\mathcal{R}}^{[A,B,C|d]}(Y_k)$, then, for any $k\ge 0$,

$$X_0\ge Y_0\ge 0\Rightarrow X_k\ge Y_k\ge 0.$$

Lemma 3.

Suppose there exists K and $\overline{M}>0$, such that $\overline{M}>{\mathcal{F}}_K^{*}(\overline{M})$. For any $M\ge 0$, there is a limit satisfying ${\displaystyle \underset{k\to \infty }{lim}}{\underbrace{{\mathcal{F}}_K^{*}({\mathcal{F}}_K^{*}(\cdots {\mathcal{F}}_K^{*}}}_k(M)))=0$.

Below, by exploiting Lemmas 2 and 3, the stabilizing solution of DARE can be obtained immediately.

Theorem 1.

For $P_k$ ($k\ge 0$) that satisfies $P_{k+1}={\mathcal{R}}^{[A,B,C|d]}(P_k)$, where the initial value $P_0\ge 0$ is arbitrary, it is bounded and converges to the unique stabilizing solution $P_s>0$ of DARE (11), if the stochastic system $[A,B,C|d]$ is mean square stabilizable, where $Q>0$ and $R>0$.

Proof. 

Suppose system $[A,B,C|d]$ is stabilizable in the mean square sense where $Q>0$, $R>0$. It follows from $(d)$ of Lemma 1 that there admits a unique stabilizing solution $P_s>0$ for DARE, which implies that $P_s={\mathcal{R}}^{[A,B,C|d]}(P_s)$ holds.

Define the gain $K_{P_s}=-U_s^{-1}{L}_s$. By (12) and (13), one has

$$P_s={\mathcal{R}}^{[A,B,C|d]}(P_s)={\mathcal{G}}_{K_{P_s}}^{[A,B,C|d]}(P_s)={\mathcal{F}}_{K_{P_s}}^{*}(P_s)+{\widehat{Q}}_s>{\mathcal{F}}_{K_{P_s}}^{*}(P_s),$$

(15)

where

$$\begin{array}{cc}\hfill {\widehat{Q}}_s=& {K_{P_s}}^{\prime }R{K}_{P_s}+Q+\sum _{k=0}^{d-1}{\sigma }^2{K}_{P_s}^{{}^{\prime }}{C}^{\prime }{(A^{\prime })}^{k+1}Q{A}^{k+1}C{K}_{P_s}-{\sigma }^2{K}_{P_s}^{{}^{\prime }}{C}^{\prime }{(A^{\prime })}^{d}Q{A}^{d}C{K}_{P_s}\hfill \\ \hfill & +{\sigma }^2{K}_{P_s}^{{}^{\prime }}{C}^{\prime }QC{K}_{P_s}\ge 0.\hfill \end{array}$$

Lemma 3 means that there exists $K_{P_s}$ and $P_s>0$, such that $P_s>{\mathcal{F}}_{K_{P_s}}^{*}(P_s)$. In this case, we have

$$\mu P_s>{\mathcal{F}}_{K_{P_s}}^{*}(P_s),$$

where $0<\mu <1$, which implies that

$$\underset{k+1}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(P_s)))<\mu \underset{k}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(P_s)))<\cdots <{\mu }^{k+1}{P}_s.$$

(16)

For any $P_0\ge 0$, according to (12)–(14), one has

$$\begin{array}{c}\hfill P_{k+1}={\mathcal{R}}^{[A,B,C|d]}(P_k)={\mathcal{G}}_{K_{P_k}}^{[A,B,C|d]}(P_k)=\underset{K}{min}{\mathcal{G}}_K^{[A,B,C|d]}(P_k)\\ \hfill \le {\mathcal{G}}_{K_{P_s}}^{[A,B,C|d]}(P_k)={\mathcal{F}}_{K_{P_s}}^{*}(P_k)+{\widehat{Q}}_s.\end{array}$$

(17)

Similarly, we have

$$\begin{array}{cc}\hfill P_k\le {\mathcal{F}}_{K_{P_s}}^{*}& (P_{k-1})+{\widehat{Q}}_s,\hfill \\ \hfill P_{k-1}\le {\mathcal{F}}_{K_{P_s}}^{*}& (P_{k-2})+{\widehat{Q}}_s,\hfill \\ \hfill & ⋮\hfill \\ \hfill P_1\le {\mathcal{F}}_{K_{P_s}}^{*}& (P_0)+{\widehat{Q}}_s.\hfill \end{array}$$

(18)

Via (18), the inequality (17) leads to

$$\begin{array}{cc}\hfill P_{k+1}\le {\mathcal{F}}_{K_{P_s}}^{*}(P_k)+{\widehat{Q}}_s\le & {\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(P_{k-1})+{\widehat{Q}}_s)+{\widehat{Q}}_s\hfill \\ \hfill =& {\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(P_{k-1}))+{\mathcal{F}}_{K_{P_s}}^{*}({\widehat{Q}}_s)+{\widehat{Q}}_s\hfill \\ \hfill \le & \cdots \hfill \\ \hfill \le & \underset{k+1}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(P_0)))+\underset{k}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}({\widehat{Q}}_s)))\hfill \\ \hfill +& \underset{k-1}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}({\widehat{Q}}_s)))+\cdots +{\mathcal{F}}_{K_{P_s}}^{*}({\widehat{Q}}_s)+{\widehat{Q}}_s.\hfill \end{array}$$

(19)

For $P_0\ge 0$, one has $P_0\le {\delta }_0{P}_s$ where ${\delta }_0$ is a normal number. Similarly, for ${\widehat{Q}}_s\ge 0$, one has ${\widehat{Q}}_s\le {\delta }_{Q_s}{P}_s$ where ${\delta }_{Q_s}$ is a normal number. Therefore, we have

$$\underset{k+1}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(P_0)))\le {\delta }_0\underset{k+1}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(P_s)))<{\mu }^{k+1}{\delta }_0{P}_s.$$

(20)

Similarly, for $1\le i\le k$, it follows that

$$\underset{i}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}({\widehat{Q}}_s)))<{\mu }^i{\delta }_{Q_s}{P}_s.$$

(21)

According to the method of inequality scaling and (19)–(21), it can be seen that $\left\{P_k\right\}$ is bounded.

To give the stabilizing solution of (11), set $X_0$ and $Y_0$ to be 0 and $P_0+P_s$, respectively. Then one has $X_0\le P_0\le Y_0$.

Suppose $X_0=0$, by (b) in Lemma 2, it is known that

$$X_1=Q\ge X_0=0,$$

which implies that

$$X_k\ge X_{k-1}\ge \cdots \ge X_1\ge X_0.$$

Note it has been proved that $\left\{X_k\right\}$ is bounded. Then the sequence $\left\{X_k\right\}$ must have a limit, i.e.,

$$\underset{k\to \infty }{lim}{X}_k={\mathcal{R}}^{[A,B,C|d]}(\underset{k\to \infty }{lim}{X}_{k-1})=\overline{X},$$

where $\overline{X}$ is the limit of sequence $\left\{X_k\right\}$. As as result, the above equivalent can be rewritten as

$$\overline{X}={\mathcal{R}}^{[A,B,C|d]}(\overline{X}),$$

and the unique stabilizing solution $P_s>0$ of (11) is equal to its positive definite solution in [30]. Thus, $\overline{X}=P_s$.

Suppose $Y_0=P_0+P_s$, by (b) and (c) in Lemma 2, it is known that

$$Y_1={\mathcal{R}}^{[A,B,C|d]}(P_0+P_s)\ge P_s,$$

which implies that $Y_k-P_s\ge 0(k\ge 0)$. So, together with (17) and Lemma 3, we have

$$\begin{array}{cc}\hfill & Y_k-P_s\le {\mathcal{F}}_{K_{P_s}}^{*}(Y_{k-1}-P_s)\le \underset{k}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(Y_0-P_s))),\hfill \\ \hfill & \underset{k\to \infty }{lim}\underset{k}{\underbrace{{\mathcal{F}}_{K_{P_s}}^{*}({\mathcal{F}}_{K_{P_s}}^{*}(\cdots {\mathcal{F}}_{K_{P_s}}^{*}}}(Y_0-P_s)))=0.\hfill \end{array}$$

That is, ${\displaystyle \underset{k\to \infty }{lim}}{Y}_k=P_s$ is established.

By item (b) in Lemma 2, one has $X_k\le P_k\le Y_k$, and it is known from the Squeeze Theorem

$$\underset{k\to \infty }{lim}{P}_k=P_s,$$

which ends this proof. □

4. Critical Stabilization

Next, we introduce another concept of stochastic stabilization which will be called critical stabilization and use DLE to give necessary and sufficient conditions for judgment.

Definition 2.

System $[A,B,C|d]$ is said to be critically stabilizable, if there is a feedback control $v_{k-d}=K{\widehat{x}}_{k|k-d-1}$, $k\ge d$ such that $|\rho ({\mathcal{F}}_K^{[A,B,C|d]})|\subset D[0,1]$.

Now, we will use the resize method to prove the following theorem to judge critical stabilization. For the sake of discussion, we introduce the following stochastic dynamics notated as $[A,B,C|d,\alpha ]$

$$x_{k+1}=(\frac{A}{\sqrt{\alpha }})x_k+(\frac{B}{\sqrt{\alpha }})v_{k-d}+e_k(\frac{C}{\sqrt{\alpha }})v_{k-d}.$$

(22)

Correspondingly, for system $[A,B,C|d,\alpha ]$, define ${{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]}$ be a linear operator from $S^n$ to $S^n$ satisfying

$${{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]}(M)=(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)M{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }+{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}KM{K}^{\prime }\frac{C^{\prime }}{\sqrt{\alpha }}{(\frac{A^{\prime }}{\sqrt{\alpha }})}^d.$$

(23)

The spectral set of $\mathcal{F}$ is represented by

$$\rho ({{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]})=\{{\lambda }_{\alpha },{{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]}(M)={\lambda }_{\alpha }M,M\in S^n,M\ne 0\}.$$

(24)

Theorem 2.

The following statements are equivalent.

(i) 

System $[A,B,C|d]$ is critical stabilization.

(ii) 

There exists matrix K, $K\in S^n$, such that for any $\alpha >1$ and $Q>0$, the following DLE

$$P=Q+(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)P{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }+{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}KP{\left[{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K\right]}^{\prime },$$

(25)

admits a unique positive solution $P\in S^n$, $P>0$.

(iii) 

There exists matrix K, $K\in S^n$, such that for any $\alpha >1$, the following inequality

$$P-(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)P{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }-{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}KP{\left[{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K\right]}^{\prime }>0,$$

(26)

admits a positive solution $P\in S^n$, $P>0$.

(iv) 

There exists matrices K, $K\in S^n$, such that for any $\alpha >1$ and $Q>0$, the following inequality

$$P=Q+{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }P(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)+{\sigma }^2{K}^{\prime }\frac{C^{\prime }}{\sqrt{\alpha }}{(\frac{A^{\prime }}{\sqrt{\alpha }})}^{d}P{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K,$$

(27)

admits a unique solution $P\in S^n$, $P>0$.

Proof. 

Interestingly, (ii)⇔(iii), what we have to do is to prove (i)⇔(ii), (iii)⇔(iv). First, we give a simple proof to show (i)⇔(ii).

Sufficiency: From the conditions, it can be seen that (25) has a unique solution $P\in S^n$, $P>0$ which is equivalent to the asymptotically mean square stabilization of the following system

$$z_{k+1}^{\alpha }=\frac{A}{\sqrt{\alpha }}{z}_k+\frac{B}{\sqrt{\alpha }}{u}_k+e_k{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}{u}_k.$$

(28)

From Theorem 2 in [29], it can be seen that the system (28) is asymptotically mean square stabilizable, which is equivalent to that system $[A,B,C|d,\alpha ]$ is stabilizable. By applying (b) in Lemma 1, it is easy to know that $|\rho ({\mathcal{F}}_K^{[A,B,C|d,\alpha ]})|<1$. Then, let $\alpha \to 1$, with the continuity of spectrum, it follows that $|\rho ({\mathcal{F}}_K^{[A,B,C|d]})|\le 1$, which completes the proof of Sufficiency part.

Necessity: Using the Kronecker product theory and the definition of the spectrum yields the following formula

$$\lambda \overrightarrow{X}=[(A+BK)\otimes (A+BK)+{\sigma }^2{A}^{d}CK\otimes {(A)}^{d}CK]\overrightarrow{X}.$$

Compared with

$${\lambda }_{\alpha }\overrightarrow{X}=[{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K\otimes {(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K+(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)\otimes (\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)]\overrightarrow{X},$$

(29)

where $\overrightarrow{X}$ is a column monomial matrix by all elements of X, one obtains that the relationship between $\lambda$ and ${\lambda }_{\alpha }$ can be inferred as $\lambda \ge {\lambda }_{\alpha }$, which means that $|{\lambda }_{\alpha }|<1$. Combining with (a) and (b) in Lemma 1, the necessity of the proof is proved.

Next, we prove that (iii) and (iv) are equivalent. From Theorem 1 in [31], it is easy to find that (iii) and (iv) are equivalent when system $[A,B,C|d,\alpha ]$ is stabilizable. □

It is worth noting that the condition of critical stabilization is weaker than that of asymptotic mean square stabilization. According to the distribution of the spectrum of the operator on the complex plane, in the next section, we will propose the concept and related properties of the essential destabilization.

5. Essential Destabilization

In this section, we focus on an interesting concept of stochastic stabilization which will be called essential destabilization with the spectrum technique. More importantly, the Lyapunov-type necessary and sufficient conditions will be proposed.

We start this section by defining essential destabilization. The following definition and lemmas are necessary to establish our main theoretical results.

Definition 3.

System $[A,B,C|d]$ is called to be essentially destabilizable, if for any feedback $v_{k-d}=K{\widehat{x}}_{k|k-d-1}$, the closed-loop dynamic system $x_{k+1}=A{x}_k+[B+e_{k}C]K{\widehat{x}}_{k|k-d-1}$ is essentially unstable, i.e., there exists ${\lambda }_i\in \rho ({{\mathcal{F}}_K}^{[A,B,C|d]})$ satisfying $|{\lambda }_i|>1$.

For any $X_n={(x_{ij})}_{n\times n}\in S^n$, define two column vectors $\overrightarrow{X_n}$ and $\widetilde{X_n}$, where $\overrightarrow{X_n}$ is with all elements of $X_n$ and $\widetilde{X_n}$ formed by different elements of $X_n$. $\mathbb{T}(n^2,\frac{n(n+1)}{2})$ denotes the transform matrix from $\widetilde{X_n}$ to $\overrightarrow{X_n}$.

As stated in [21], $\mathbb{T}(n^2,\frac{n(n+1)}{2})$ has the following properties

• Matrix $\mathbb{T}(n^2,\frac{n(n+1)}{2})$ has column full rank.
• Matrix ${\mathbb{T}}^{\prime }(n^2,\frac{n(n+1)}{2})\mathbb{T}(n^2,\frac{n(n+1)}{2})$ is invertible.

Besides, let us define

$$\begin{array}{cc}\hfill \Im (\mathbb{T}(n^2,\frac{n(n+1)}{2}),A,B,C|d)& ={\left[{\mathbb{T}}^{\prime }(n^2,\frac{n(n+1)}{2})\mathbb{T}(n^2,\frac{n(n+1)}{2})\right]}^{-1}{\mathbb{T}}^{\prime }(n^2,\frac{n(n+1)}{2})\hfill \\ \hfill & \times [(A+BK)\otimes (A+BK)+A^{d}CK\otimes A^{d}CK)]\mathbb{T}(n^2,\frac{n(n+1)}{2}).\hfill \end{array}$$

Lemma 4.

([31]).

$$\rho ({\mathcal{F}}_K^{[A,B,C|d]})=\rho (\Im (\mathbb{T}(n^2,\frac{n(n+1)}{2}),A,B,C|d)).$$

Lemma 5.

Assume that ${\lambda }_i\ne 1$ holds for any ${\lambda }_i\in \rho ({\mathcal{F}}_K^{[A,B,C|d]})$. Then for any given symmetric matrix $Q\in S^n$, the following delay-dependent equation

$$(A+BK)P{(A+BK)}^{\prime }+{\sigma }^2(A^{d}CK)P{(A^{d}CK)}^{\prime }-P=Q,$$

(30)

has a unique solution $P\in S^n$.

Proof. 

First, Let us define the following Jordan canonical form of $\Im (\mathbb{T}(n^2,\frac{n(n+1)}{2}),A,B,C|d)$

$$J=\left[\begin{array}{cccc}{J}_1& & & \\ & J_2& & \\ & & \ddots & \\ & & & J_s\end{array}\right]$$

with Jordan blocks

$$J_i={\left[\begin{array}{cccc}{\lambda }_i& 1& & \\ & \ddots & \ddots & \\ & & \ddots & 1\\ & & & {\lambda }_i\end{array}\right]}_{k_i\times k_i}$$

where ${\displaystyle \sum _{i=1}^s}{k}_i=\frac{n(n+1)}{2}$. Then, take the basis $\mathfrak{B}=\{v_1^1\cdots v_{k_1}^1,v_1^2\cdots v_{k_2}^2,\cdots ,v_1^s\cdots v_{k_s}^s\}$ of $C^{\frac{n(n+1)}{2}}$ and define $V=[v_1^1\cdots v_{k_1}^1,v_1^2\cdots v_{k_2}^2,\cdots ,v_1^s\cdots v_{k_s}^s]$, where $v_1^1\cdots v_{k_1}^1$, $v_1^2\cdots v_{k_2}^2$, ⋯, $v_1^s\cdots v_{k_s}^s$ are linear and independent eigenvectors to ${\lambda }_i$, $i=1,2,\cdots s$. It follows that

$$V^{-1}\Im (\mathbb{T}(n^2,\frac{n(n+1)}{2}),A,B,C|d)V=J,$$

or equivalently

$$\Im (\mathbb{T}(n^2,\frac{n(n+1)}{2}),A,B,C|d)V=VJ.$$

(31)

Then it follows that $X_1^1\cdots X_{k_1}^1$, $X_1^2\cdots X_{k_2}^2$, ⋯, $X_1^s\cdots X_{k_s}^s$ consititute a complete basis $\mathfrak{B}$ of $S^n$. Moreover, it follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{{\mathcal{F}}_K}^{[A,B,C|d]}(X_1^i)={\lambda }_i{X}_1^i,i=1,2,\cdots ,s\hfill \\ {{\mathcal{F}}_K}^{[A,B,C|d]}(X_{ij}^i)={\lambda }_i{X}_j^i+X_{ji-1}^i,j_i=2,3,\cdots ,k_i\hfill \end{array}\right.\end{array}$$

(32)

Now, we begin to show that the symmetric solution of (30) exists and is unique. Since $\mathfrak{B}$ is a basis of $S^n$, each matrix Q in $S^n$ can be uniquely expressed as

$$\begin{array}{c}\hfill Q=[c_1,c_2,c_3\cdots c_{n(n+1)/\phantom{n(n+1)2}2}]\left[\begin{array}{c}{x}_1^1\hfill \\ ⋮\hfill \\ x_{k_1}^1\hfill \\ ⋮\hfill \\ x_{k_s}^s\hfill \end{array}\right]\end{array}$$

(33)

Without losing generality, it is assumed that P follows the following structure

$$\begin{array}{c}\hfill P=[b_1^1,\cdots ,b_{k_1}^1,b_1^2,\cdots ,b_{k_2}^2,\cdots ,b_1^s\cdots b_{k_s}^s]\left[\begin{array}{c}{x}_1^1\hfill \\ ⋮\hfill \\ x_{k_1}^1\hfill \\ ⋮\hfill \\ x_{k_s}^s\hfill \end{array}\right]=\sum _{i=1}^s\sum _{ji=1}^{k_i}{b}_{ji}^i{x}_{ji}^i.\end{array}$$

(34)

Due to the fact that (31) is linear w.r.t. P, when we take (33) and (34) into (30), we obtain that

$$\begin{array}{c}{\displaystyle \sum _{i=1}^s}{\displaystyle \sum _{ji=1}^{k_i}}{b}_{ji}^i{{\mathcal{F}}_K}^{[A,B,C|d]}(x_{ji}^i)-{\displaystyle \sum _{i=1}^s}{\displaystyle \sum _{ji=1}^{k_i}}{b}_{ji}^i{x}_{ji}^i=[c_1,c_2,c_3\cdots c_{n(n+1)/2}\hfill \end{array}]\left[\begin{array}{c}{x}_1^1\hfill \\ ⋮\hfill \\ x_{k_1}^1\hfill \\ ⋮\hfill \\ x_{k_s}^s\hfill \end{array}\right]$$

that is

$$\begin{array}{cc}\hfill & [b_1^1,\cdots ,b_{k_1}^1,b_1^2,\cdots ,b_{k_2}^2,\cdots ,b_1^s\cdots b_{k_s}^s]J^{\prime }-[b_1^1,\cdots ,b_{k_1}^1,b_1^2,\cdots ,b_{k_2}^2,\cdots ,b_1^s\cdots b_{k_s}^s]\hfill \\ \hfill =& [c_1,c_2,\cdots c_{n(n+1)/\phantom{n(n+1)2}2}],\hfill \end{array}$$

or equivalently

$$\begin{array}{c}\hfill P{J}^{\prime }-PI=Q.\end{array}$$

(35)

By this condition, it is known that ${\lambda }_i\ne 1$. Note that $J^{\prime }-I$ is invertible, then P exists and is unique. □

Theorem 3.

System $[A,B,C|d]$ is essentially destabilizable, if and only if for any K and $W>0$, there exists a constant $\alpha >1$, such that the following DLE

$$V+W=(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)V{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }+{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}KV{K}^{\prime }\frac{C^{\prime }}{\sqrt{\alpha }}{(\frac{A^{\prime }}{\sqrt{\alpha }})}^d,$$

(36)

admits a unique symmetric matrix V with at least one positive eigenvalue.

Proof. 

First, let’s generalize a further relationship between $\lambda$ and ${\lambda }_{\alpha }$. Utilizing Kronecker matrix theorem, (7) can be rewritten as

$$[(A+BK)\otimes (A+BK)+{\sigma }^2{A}^{d}CK\otimes A^{d}CK]\overrightarrow{X}=\lambda \overrightarrow{X}.$$

Compared with

$$\begin{array}{c}\hfill [(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)\otimes (\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)+{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K\otimes {(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K]\overrightarrow{X}={\lambda }_{\alpha }\overrightarrow{X},\end{array}$$

(37)

one obtains the following relationship

$$\frac{{\lambda }_i}{{\alpha }^{d+1}}<{\lambda }_{\alpha ,i}<\frac{{\lambda }_i}{\alpha }<{\lambda }_i,$$

(38)

where the ${\lambda }_i\in \rho ({\mathcal{F}}_k^{[A,B,C|d]})$, ${\lambda }_{\alpha ,i}\in \rho ({{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]})$, and $\overrightarrow{X}$ is a column monomical matrix constructed by all elements of X.

Sufficiency: We assume that the system $[A,B,C|d]$ is stabilizable. Then $|\rho ({{\mathcal{F}}_K}^{[A,B,C|d,\alpha ]})|$$<1$ can be derived from item (b) in Lemma 1 and the former statements.

Compared with condition, we have

$$-(V+W)=(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)(-V){(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }+{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K(-V)K^{\prime }\frac{C^{\prime }}{\sqrt{\alpha }}{(\frac{A^{\prime }}{\sqrt{\alpha }})}^d.$$

We can conclude that the matrix $-V$ is positive definite, that is, V is a negative definite matrix, which contradicts the problem condition. Therefore, $[A,B,C|d,\alpha ]$ is not asymptotically mean square stabilizable.

From the former result, we can find a ${\lambda }_{\alpha ,i}\in \{{\lambda }_{\alpha },|{\lambda }_{\alpha }|\ge 1\}$. Denote ${\lambda }_{\alpha ,i}^{*}$ to be the maximum spectrum in ${\lambda }_{\alpha }$. With the condition $\alpha >1$ and the the relationship between ${\lambda }_{\alpha }$ and $\lambda$, there exists a $|\lambda |>1$, which implies that the system is essentially destabilizable.

Necessity: Set $\beta =min\{|{\lambda }_j|,{\lambda }_j\in \rho ({\mathcal{F}}_K^{[A,B,C|d]}),|{\lambda }_j|>1\}$. Clearly, we have $\beta >1$, since the possible value of ${\lambda }_j$ is finitely many, there exists a ${\alpha }^{d+1}\in (1,\beta )$ such that $\alpha \in (1,\beta )$, for any ${\lambda }_i\in \rho ({\mathcal{F}}_K^{[A,B,C|d]})$.

According to such $\alpha$, conbined with (38), for any ${\lambda }_j\in \rho ({\mathcal{F}}_K^{[A,B,C|d]}),|{\lambda }_j|>1$, we have ${\lambda }_{\alpha ,j}>1$. Moreover, for any ${\lambda }_i\in \rho ({\mathcal{F}}_K^{[A,B,C|d]}),|{\lambda }_i|\le 1$, it is easy to get ${\lambda }_{\alpha ,i}\ne 1$. It follows from Lemma 5 that for any given $W>0$, (36) has a unique solution $V^{\prime }=V$, which implies that V is not a negative definite matrix by item (a) in Lemma 1.

To show the existence of positive eigenvalues of V, we have the following discussions.

(i)

When $ker(V)=0$, V is a column full rank matrix. Since V is not a negative definite matrix, V must have a positive eigenvalue.

(ii)

When $ker(V)\ne 0$, for any non-zero $x_0\in ker(V)$, pre-multiplying $x_0^{\prime }$ and post-multiplying $x_0$ on both sides of (36), we have

$$\begin{array}{cc}\hfill & x_0^{\prime }(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)V{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }{x}_0+x_0^{\prime }{\sigma }^2({(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K)V{({(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}K)}^{\prime }{x}_0\hfill \\ \hfill & =x_0^{\prime }W{x}_0.\hfill \end{array}$$

Together with the positive definiteness of W, since V is not a negative definite matrix, We have that V must not be a zero matrix. That is, V has a positive eigenvalue. □

6. Simulation

In this section, we will verify the validity of the developed theoretic results, including Theorem 1 and Theorem 3, through two illustrative examples.

Example 1.

Consider system $[A,B,C|d]$, with $d=1$, ${\sigma }^2=1$, $Q=I$, $R=I$ and A, B and C respectively meet the values as shown in Table 1.

Table 1. Three sets of values of real system parameters in stochastic system $[A,B,C|d]$.

	A	B	C
1	$\left[\begin{array}{ccccc}\frac{1}{3}& 0& ;& 0& -\frac{1}{5}\end{array}\right]$	$\left[\begin{array}{ccccc}1& \frac{1}{5}& ;& 0& -\frac{1}{3}\end{array}\right]$	$\left[\begin{array}{ccccc}-\frac{1}{5}& \frac{1}{3}& ;& 0& \frac{1}{5}\end{array}\right]$
2	$\left[\begin{array}{ccccc}1& -\frac{1}{5}& ;& 1& -\frac{1}{7}\end{array}\right]$	$\left[\begin{array}{ccccc}1& \frac{1}{4}& ;& 2& \frac{1}{4}\end{array}\right]$	$\left[\begin{array}{ccccc}\frac{1}{3}& \frac{1}{5}& ;& 0& 2\end{array}\right]$
3	$\left[\begin{array}{ccccc}1& -\frac{1}{4}& ;& 1& \frac{1}{7}\end{array}\right]$	$\left[\begin{array}{ccccc}2& -\frac{1}{3}& ;& 1& \frac{1}{2}\end{array}\right]$	$\left[\begin{array}{ccccc}1& -\frac{1}{2}& ;& \frac{1}{3}& \frac{1}{4}\end{array}\right]$

First, we need to verify the mean square stabilization for each system in Table 1. Similar to Theorem 2 in [29], we have that system $[A,B,C|d]$ is stabilizable if and only if there exist matrices H and $Z>0$ satisfying

$$\left[\begin{array}{ccc}-Z& *& *\\ AZ+BH& -Z& *\\ {\sigma }^2{A}^{d}CH& 0& -Z\end{array}\right]<0,$$

(39)

where * represents the corresponding transpose part. By using the LMI toolbox in MATLAB, we can obtain the corresponding values of H, $Z>0$ for three different stochastic systems as shown in Table 1, which illustrates that each system is stabilizable.

It is remarkable that for DARE with $Q>0$ and $R>0$, Theorem 1 defines a numerically iterative algorithm for obtaining the unique stabilizing solution, i.e., for any initial value $P_0\ge 0$, the matrix sequence satisfying $P_{k+1}={\mathcal{R}}^{[A,B,C|d]}(P_k)$ can converge to the unique solution. In Table 2, the value of $P_0$ is assumed to be positive semi-definite. Then, for any state dimension case, we can choose any positive semi-definite $P_0\ge 0$ as an initial value. Perform iterative calculation $P_{k+1}={\mathcal{R}}^{[A,B,C|d]}(P_k)$ until $P_{k_0+1}=P_{k_0}$. In this case, we have $P_{k_0+1}=P_{k_0}=P_s$. Besides, to illustrate the effectiveness of the developed algorithm, we provide the iteration N in Table 3. Based on the simulations, the convergence rate is fast.

Table 2. Three sets of simulation results of LMI toolbox.

	H	Z	${\mathit{P}}_0$
1	$\left[\begin{array}{cc}-174.5693& 52.8967\\ -11.6459& -276.5355\end{array}\right]$	$\left[\begin{array}{cc}532.7641& 0.3806\\ 0.3806& 531.4675\end{array}\right]$	$\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]$
2	$\left[\begin{array}{cc}-44.0803& 6.0853\\ -150.2109& 29.4270\end{array}\right]$	$\left[\begin{array}{cc}109.7799& 1.6274\\ 1.6274& 115.1478\end{array}\right]$	$\left[\begin{array}{cc}4& 6\\ 6& 9\end{array}\right]$
3	$\left[\begin{array}{cc}-69.6452& 1.8577\\ -113.4397& -18.3662\end{array}\right]$	$\left[\begin{array}{cc}117.1685& 2.5141\\ 2.5141& 117.3061\end{array}\right]$	$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$

Table 3. Results of three sets of simulation series.

	${lim}_{\mathit{x}\to \mathit{\infty }}{\mathit{P}}_{\mathit{k}}$	N
1	$\left[\begin{array}{cc}1.0304& 0.9834\\ 0.9834& 1.0120\end{array}\right]$ > 0	11
2	$\left[\begin{array}{cc}1.6470& 0.8792\\ 0.8792& 1.0231\end{array}\right]$ > 0	27
3	$\left[\begin{array}{cc}2.6428& 0.8405\\ 0.8405& 1.0700\end{array}\right]$ > 0	19

By introducing the obtained ${\displaystyle \underset{k\to \infty }{lim}}{P}_k$ into Equation (11), we can verify that the limit is the stabilizing solution of DARE.

Example 2.

For system $[A,B,C|d]$, we take the following matrix coefficients into account

$$A=\left[\begin{array}{cc}-1& 5\\ 1& 3\end{array}\right],B=\left[\begin{array}{cc}-1& 0\\ 2& 0.7\end{array}\right],C=\left[\begin{array}{cc}-1& 2\\ 1& -1\end{array}\right],d=1.$$

In this case, one obtains that the control law follows

$$v_{k-1}=K{\widehat{x}}_{k|k-2}=K(A{x}_{k-1}+B{u}_{k-2}).$$

To begin with, we first check the given system is not stabilizable in the mean square sense by utilizing inequality (39). Then, to study the essential destabilization, we choose different feedback gain $K_i$ as shown in Table 4. It follows from Theorem 3, the following inequality holds for each $K_i$, which can be solved by LMI in Matlab with

$$\begin{array}{c}\hfill V-(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)V{(\frac{A}{\sqrt{\alpha }}+\frac{B}{\sqrt{\alpha }}K)}^{\prime }-{\sigma }^2{(\frac{A}{\sqrt{\alpha }})}^d\frac{C}{\sqrt{\alpha }}KV{K}^{\prime }\frac{C^{\prime }}{\sqrt{\alpha }}{(\frac{A^{\prime }}{\sqrt{\alpha }})}^d>0.\end{array}$$

Table 4. Results of three kinds of feedback design for the system.

	K	${10}^{-8} \mathit{W}$	${10}^{-6} \mathit{V}$	${10}^{-5} {\mathit{\lambda }}_{\mathit{V}}$
1	$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$	$\left[\begin{array}{cc}0.3936& 0.0582\\ 0.0582& 1.8208\end{array}\right]$	$\left[\begin{array}{cc}6.5492& 6.8033\\ 6.8033& 6.8989\end{array}\right]$	$\left[\begin{array}{cc}-0.8200& 135.00\end{array}\right]$
2	$\left[\begin{array}{cc}5& 0\\ 0& 5\end{array}\right]$	$\left[\begin{array}{cc}0.6375& -0.2810\\ -0.2810& 1.8007\end{array}\right]$	$\left[\begin{array}{cc}0.5420& 0.48857\\ 0.48857& 0.476510\end{array}\right]$	$\left[\begin{array}{cc}0.0398& 9.8566\end{array}\right]$
3	$\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]$	$\left[\begin{array}{cc}0.6467& 0.5164\\ 0.5164& 2.5623\end{array}\right]$	$\left[\begin{array}{cc}6.0390& 22.4000\\ 22.4000& 31.8010\end{array}\right]$	$\left[\begin{array}{cc}-692.0000& 447.5900\end{array}\right]$

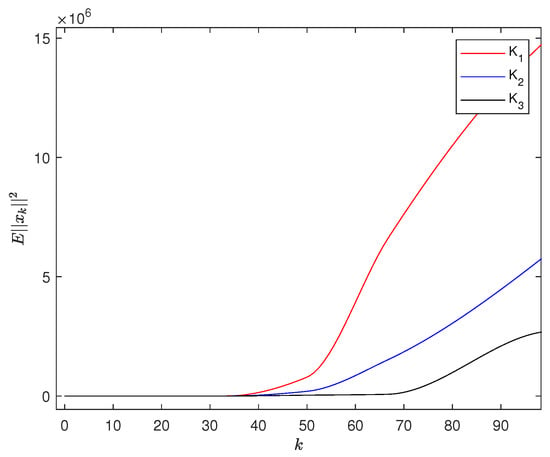
For the given matrix M, there exist $\alpha =2$ and a unique symmetric matrix, such that (36) holds. Utilizing the conventional calculation method, one obtains that V has at least one positive eigenvalue. Figure 1 shows the essential destabilization of the considered system.

Figure 1. Simulation of ${\displaystyle \underset{k\to \infty }{lim}}E||x_k|{|}^2$ with $K_1$.

7. Conclusions

We study the stochastic stabilization problems with the co-existence of input delay and multiplicative noise in the control variable. First, as the necessary condition of asymptotic mean square stabilization, we derive an iterative algorithm to solve the DARE. Then, the concepts of critical stabilization and essential destabilization are defined by operator spectrum theory. Utilizing DLE, the necessary and sufficient conditions are developed for dynamic models under consideration. However, how to utilize the spectrum theory and Lyapunov technology to study the stochastic stabilization for a more general time-delay stochastic system with multiplicative noises remains an open question, which defines a meaningful research direction. On the other hand, applying online Reinforcement Learning (RL) technology to solve DARE with partial system information is another promising research direction.