Abstract
Heat transfer is a crucial aspect of thermochemical conversion of pulverized fuels. Over-predicting the heat transfer during heat-up leads to under-estimation of the ignition time, while under-predicting the heat loss during the char conversion leads to an over-estimation of the burnout rates. This effect is relevant for dense particle jets injected from dense-phase pneumatic conveying. Heat fluxes characteristic of such dense jets can significantly differ from single particles, although a single, representative particle commonly models them in Euler–Lagrange models. Particle-resolved direct numerical simulations revealed that common representative particles approaches fail to reproduce the dense-jet characteristics. They also confirm that dense clusters behave similar to larger, porous particles, while the single particle characteristic prevails for sparse clusters. Hydrodynamics causes this effect for convective heat transfer since dense clusters deflect the inflowing fluid and shield the center. Reduced view factors cause reduced radiative heat fluxes for dense clusters. Furthermore, convection is less sensitive to cluster shape than radiative heat transfer. New heat transfer models were derived from particle resolved simulations of particle clusters. Heat transfer increases at higher void fractions and vice versa, which is contrary to most existing models. Although derived from regular particle clusters, the new convective heat transfer models reasonably handle random clusters. Contrary, the developed correction for the radiative heat flux over-predicts shading effects for random clusters because of the used cluster shape. In unresolved Euler–Lagrange models, the new heat transfer models can significantly improve dense particle jets’ heat-up or thermochemical conversion modeling.
1. Introduction
Computational investigation of industrial processes or virtual prototyping has become popular in research and development, while lab-scale equipment can be simulated in high detail, current computational resources prohibit the fully resolved investigation of larger or industrial-scale facilities. Among others, pulverized coal furnaces [1,2] and blast furnaces [3,4] are examples of industrial processes subject to numerical investigation for optimization. The common feature of these processes is that pulverized particles are injected into the furnace and that the initial thermochemical conversion of the particles starts in the introduced jets. The initial solid-to-gas mass ratio can exceed 100, since particles are injected by dense-phase pneumatic conveying [5,6,7,8]. The ratio of the coal jet and cross-flow momentum determines the jet breakup process. Puttinger et al. [9] showed that dense jets can penetrate the furnace before the particle jet disperses. Heat-up and thermochemical conversion experience group combustion effects under such conditions, which need to be accounted for when simulating industrial systems.
Eulerian–Lagrange (EL) approaches are commonly used to model the pulverized particles’ motion, heat-up, and thermochemical conversion. EL models use an Eulerian carrier phase (gas phase) and track the Lagrangian particles (pulverized fuel) on the carrier phase’s velocity field.
Particles are lumped into computational parcels to decrease the numerical effort. This parcel approach implies simplifications to the conservation equations of parcels since poly-disperse particle mixtures are cut down to single representative particles [10,11]. The convective and radiative heat flux towards such computational parcels might be over-predicted if parcels are interpreted as physical particle clusters in turbulent flow because the modeling approach disregards flow shielding and radiation shading of the particles in the central cluster regions [12,13,14]. These effects might be captured by suitable representative particles or appropriate heat transfer correlations. An external surface area correction might be a suitable approach to capture the void fraction effects for radiative heat transfer.
Inter-particle effects in parcels or between parcels are also disregarded for simplicity in common Euler–Lagrange models. Haugen [12], Liberman et al. [13], Forgber and Radl [15] showed that these effects are essential to correctly predict the heat transfer within clouds of pulverized particles. Furthermore, thermochemical conversion is also affected by clustering effects. Depletion of the gaseous educts in clusters reduces conversion rates compared to single particles [16,17,18,19]. Temperatures also significantly influence conversion rates due to their non-linear correlation described by the Arrhenius law [20,21]. Therefore, over-predicting temperatures results in an over-prediction of the thermochemical conversion rates and can give misleading results for process optimization. The aim is to derive heat transfer models suitable for Lagrangian parcels. The correct heat exchange between carrier phase and particle (including radiation) is a prerequisite for modeling thermochemical particle conversion in particle jets.
Various particle resolved direct numerical simulation (DNS) studies on the heat transfer between fluids and solids have already been published in the literature [22,23,24,25,26,27,28,29,30,31]. These studies are used to either improve heat transfer prediction of continuous phase models [28,30], e.g., two-fluid models (TFM), or derive functional heat transfer expressions for unresolved modeling from resolved data [24,25,26,27,29]. Municchi and Radl [25], Singhal et al. [26], Singhal et al. [27] used the Discrete Element Method (DEM) to produce realistic packings of various void fraction and different particle shapes to derive heat transfer correlations for unresolved EL modeling, while [24,29] used random particle arrays to derive heat transfer correlations. Besides computational studies, experimental measurements of heat transfer in packed beds have also been used to derive heat transfer closures [32,33] for gas-solid flows.
A typical property of the proposed heat transfer models is that they were developed for gas-solid flows in fluidized bed, fixed bed, or moving bed reactors. Under these conditions, relative velocities and particle Reynolds numbers can reach high values, whereas the relative velocities for pulverized particle clusters are around the slip velocity. In addition, the resolved simulations focus on convective heat transfer and disregard radiative heat transfer. Both aspects contradict the underlying physics of the heat-up of pulverized particle jets [34,35,36,37], because (i) dense and dispersed jet regions exist, (ii) computational parcels can be seen as particle agglomerates, (iii) which move with the fluid, and (iv) radiative heat transfer is critical at combustion temperatures. Furthermore, the geometrical configuration and the resulting cluster flow patterns might significantly differ from the resolved heat transfer simulations of densely packed particle beds.
In order to obtain suitable heat transfer models for unresolved particle clusters, the heat-up of a synthetic particle cluster is investigated using particle resolved direct numerical simulations (DNS) (Section 3) and compare the results with common single particle approximations, e.g., size, mass, surface area, or surface area and mass equivalent particles (Section 4). A systematic approach is then used to derive convective heat transfer correlations and a correction for the radiative heat transfer from a set of resolved steady-state synthetic particle cluster simulations (Section 5). A short introduction of the heat transfer equations employed for unresolved EL modeling is given in Section 2, before the synthetic cluster and reference sphere simulations are presented.
2. Heat Transfer Modeling in Lagrangian Parcels
Lagrangian approaches for pulverized particles typically assume isothermal particles and lump them into computational parcels [10,11]. These parcels can be interpreted as particle clusters and are described by a single reference particle. The Sauter diameter () is often used as the representative particle diameter, while temperature, composition, and other properties are assumed to be identical for all particles in the cluster. The Sauter diameter is defined as the diameter of a particle with the same volume to surface area ratio as the poly-dispersed particles of Lagrangian parcels:
where , , , and are the representative particle diameter, the number of particles in the cluster, and the volume and surface area of the i-th particle of the Lagrangian parcel, respectively.
Representative conservation equations are solved for each parcel based on this average single particle. Disregarding chemical heat sources and assuming gray radiation, the energy conservation equation of a particle is given by [11]:
where , , t, , , , , , , , , and G are the parcel mass, the specific parcel internal energy, the time, the integral convective and radiative heat flux, the convective heat transfer coefficient, the projected particle surface, the bulk and particle temperature, the particle emission coefficient, the Stefan-Boltzmann constant, and the incident radiation, respectively. The particle surface and projected area are based on the particle diameter ():
Multiple correlations have been proposed in the literature to calculate the heat transfer coefficient between fluid and single particles [38,39]. The correlation proposed by Whitaker [40] for the heat transfer coefficient is commonly used in Euler–Lagrange simulations:
with , , and being the fluid thermal conductivity, the Prandtl number, and the particle Reynolds number, respectively, where the last is defined as:
where and are the relative velocity magnitude between fluid and particle and the kinematic viscosity of the fluid, respectively.
The presence of the particles also affects radiation. The contribution of a parcel to radiation can be expressed by the following source term [41,42]:
Assuming that the emissivity and absorptivity are equal, the particle emissivity coefficient is approximated by [43]:
These equations disregard any particle-particle interaction or other effects related to the swarm behavior of particles. The same holds for the Lagrangian equation of motion and species conservation equations. This state-of-the-art EL modeling approach will be used to validate the newly developed heat transfer models in Section 6.
3. Synthetic Particle Cluster
Synthetic particle clusters are used to reference the heat transfer in particle clusters. Although particles agglomerate to randomly shaped clusters in turbulent flows [14,44,45], a regular shaped cluster is used in the reference case. The cluster shape and size were chosen in lieu of experimentally derived ones, while the individual particle size is based on typical particle sizes in pulverized fuel combustion. The reference particle cluster consists of 44 spherical particles, each with a diameter of 60 m, and is of rhomboid shape with the particle centers equally spaced. Figure 1 illustrates the particle array, while Figure 2 shows a cross-section of one of the cluster’s main axes.
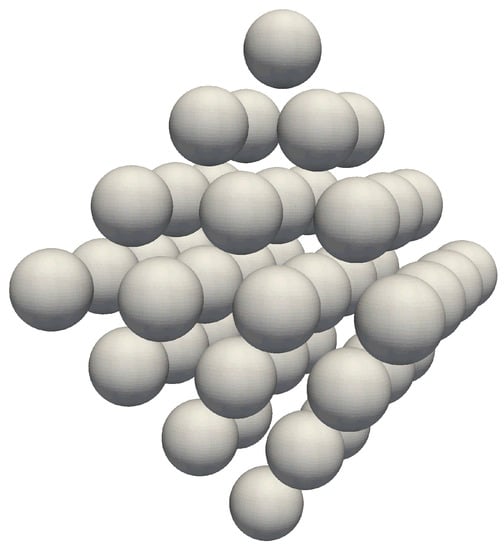
Figure 1.
Synthetic rhomboid-shaped particle cluster with a void fraction () of 0.741 (120 distance between particle centers).
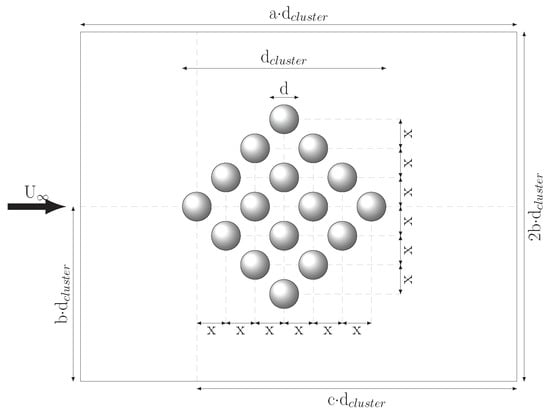
Figure 2.
Horizontal cross-section of the synthetic particle cluster. 2 × x is the distance between the particle centers, which is varied to obtain clusters with different void fraction. Cuts through all Cartesian axis planes look identical. The scaling factors of the simulation domain are a = 12, b = 3.75, c = 10.
We vary the distance between the particle centers to evaluate the influence of void fraction on the heat transfer. In addition, fluid velocities are varied to evaluate the effect of the relative velocity or particle Reynolds number. Table 1 summarizes the variations of the cluster reference cases.

Table 1.
Reference cases for the particle cluster heat-up.
The cluster void fractions were calculated based on the rhomboid region spanned by the six corner spheres’ centers as follows:
The constant 17.8251 was graphically determined and represents the number of spheres inside the rhomboid region.
We used the chtMultiRegionFoam solver of the open-source CFD toolbox OpenFOAM® v7 [46] for the simulations of the heat-up of the particle clusters. chtMultiRegionFoam couples fluid and solid regions explicitly in space and time. This approach is referred to as loose coupling in the literature [47] and requires suitable time stepping and mesh resolution [48]. The boundary conditions of the fluid are representative for the pulverized particle jet entering the raceway zone of blast furnaces [21,49]. Temperatures were kept constant at 2500 K, outlet pressure was set to 5 bar(a), while the inlet velocity was varied according to Table 1. The initial particle clusters temperature is 400 K.
The velocities defined in Table 1 denote relative velocities since the particle cluster is stationary in the simulations, while a constant gas-phase stream is introduced via the inlet.
All simulations were fully resolved (DNS) in space and time. Therefore, no turbulence model was necessary for the simulations. The estimated Kolmogorov length scale for the different cases is between 13 and 291 m, while the Kolmogorov time scale varies between 1.5 × 10−6 and 7.5 × 10−4 s for the investigated cases. The overall mean cell size of the fluid grid is between 20 and 30 m, with significant refinement near the particles. The time step is of order 10−7 to 10−8 seconds for the 0.5 and 13 m/s relative velocities. Therefore, the chosen mesh resolution and time step sizes suit DNS. The grid independence of the cluster simulations is discussed in Appendix A.1. Thermal radiation is modeled by the finite volume discrete ordinates model (fvDOM) [41] with 16 discrete rays (two azimuthal angles in /2 on X-Y plane and two polar angles in between the Z and X-Y plane). Gas-phase radiation contribution is approximated by grey mean absorption [50]. According to Narayanaswamy and Chen [51], Song et al. [52], near-field effects between the solid particles can be disregarded for the investigated cases. The OpenFOAM® fvDOM implementation has been validated in the literature [53,54,55], while the flow and convective heat transfer is validated using single sphere simulations, which are given in Appendix A.1.
The imposed boundary conditions mimic an undisturbed flow field surrounding the particles. A fixed value is set at the inlet patch and a zero gradient at the outlet patch, while a slip condition is applied at the domain walls. Static pressure boundary conditions are set to zero gradient except for the outlet patch, where a fixed value one is used. Temperature boundary conditions are zero gradient for all patches except for the inlet patch, which is set to fixed value. The gas-solid interface is modeled as a wall. No slip and zero gradient boundary conditions are applied for velocity and pressure. A coupled boundary condition is for temperature used. This boundary condition couples the heat transfer between both regions using diffusive, convective, and radiative heat fluxes. All patches are treated as gray bodies having an emissivity of unity to simplify the evaluation of the heat fluxes. Table 2 summarizes the boundary conditions.

Table 2.
Summary of boundary conditions.
The thermophysical properties of the GRI3.0 mechanism [56] are applied for the gas phase species. Table 3 summarizes the gas phase composition and thermophysical properties of the solid particles, which are assumed to be constant for simplicity.

Table 3.
Gas-phase composition and thermophysical properties and solid thermophysical properties used in the simulations.
Figure 3 and Figure 4 show the mean cluster temperatures versus the residence time for the cases presented in Table 1. The red and blue curves correspond to cases with and without radiative heat transfer coupling at the particle surface, while both cases consider convective heat transfer at the particle surface. The shadings indicate the temperature range spanned by the synthetic clusters’ minimum and maximum mean particle temperature. Comparing the mean cluster temperature and the particle temperature variations shows that intra-cluster temperature differences increase with higher relative velocities and reduce with residence time.
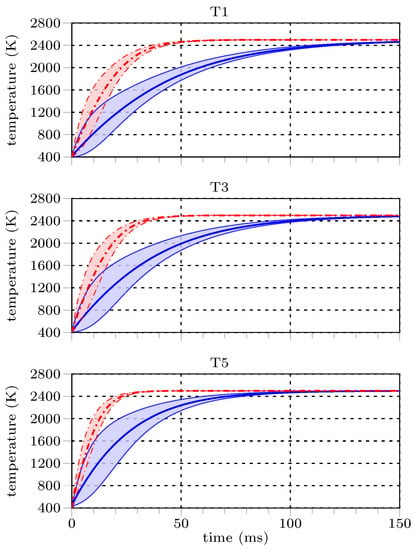
Figure 3.
Comparison of mean cluster temperature (solid) and range of individual particle temperatures (shaded area) during the heat-up at 0.5 m/s relative velocity ( = 0.29), as defined in Table 1. red ( ): convective and radiative region coupling; blue (
): convective and radiative region coupling; blue ( ): convective region coupling.
): convective region coupling.
 ): convective and radiative region coupling; blue (
): convective and radiative region coupling; blue ( ): convective region coupling.
): convective region coupling.
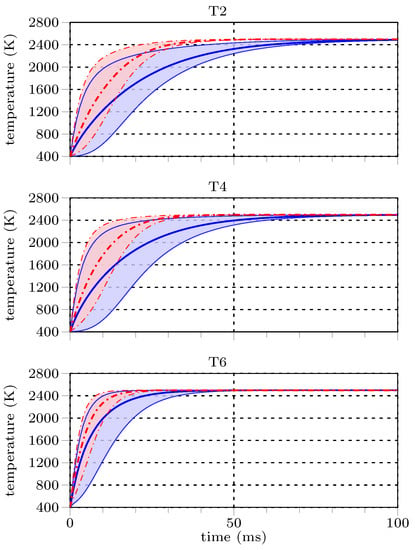
Figure 4.
Comparison of mean cluster temperature (solid) and range of individual particle temperatures (shaded area) during the heat-up at 13 m/s relative velocity ( = 7.50), as defined in Table 1. red ( ): convective and radiative region coupling; blue (
): convective and radiative region coupling; blue ( ): convective region coupling.
): convective region coupling.
 ): convective and radiative region coupling; blue (
): convective and radiative region coupling; blue ( ): convective region coupling.
): convective region coupling.
In general, heat-up times, e.g., the time until the mean cluster temperature reaches 99% of the bulk gas phase temperature, correlate with the relative velocity and the cluster void fraction. Higher void fraction and higher velocity reduce the heat-up time. Increasing the void fraction exposes a more significant portion of the projected surface area to the surroundings and allows higher radiative heat fluxes. Moreover, temperature variations within the cluster tend to decrease with void fraction.
Far-field radiative heat transfer significantly reduces the heat-up times and intra-cluster temperature variations (compare blue ( ) and red (
) and red ( ) graphs in Figure 3 and Figure 4). The additional radiative heat flux causes faster heat-up, while the flow independent radiative heat flux can explain the decreasing temperature variations. These results are in line with the findings of Haugen [12], Forgber and Radl [15].
) graphs in Figure 3 and Figure 4). The additional radiative heat flux causes faster heat-up, while the flow independent radiative heat flux can explain the decreasing temperature variations. These results are in line with the findings of Haugen [12], Forgber and Radl [15].
 ) and red (
) and red ( ) graphs in Figure 3 and Figure 4). The additional radiative heat flux causes faster heat-up, while the flow independent radiative heat flux can explain the decreasing temperature variations. These results are in line with the findings of Haugen [12], Forgber and Radl [15].
) graphs in Figure 3 and Figure 4). The additional radiative heat flux causes faster heat-up, while the flow independent radiative heat flux can explain the decreasing temperature variations. These results are in line with the findings of Haugen [12], Forgber and Radl [15].In the subsequent section, the capabilities of commonly used representative particle approaches are evaluated to reproduce the cluster heat-up characteristics.
4. Single Sphere Reference Cases
We define four representative particle diameters to evaluate suitable representative diameters for the modeling of heat transfer between fluid and particle clusters in Euler–Lagrange simulations:
- size equivalent case (SE)
- mass equivalent case (ME),
- surface area equivalent case (AE), and
- surface area and mass equivalent case (AME).
The case setup for these simulations is the same as for the cluster simulations (see Table 2), except for the particle cluster being replaced by a single sphere varying in size for the different approaches.
Figure 5 shows the generic geometry of the single sphere reference case. Both regions were scaled according to the sphere size to ensure similar geometric constraints for all single sphere cases. The grid independence of the single sphere mesh is discussed in Appendix A.2.
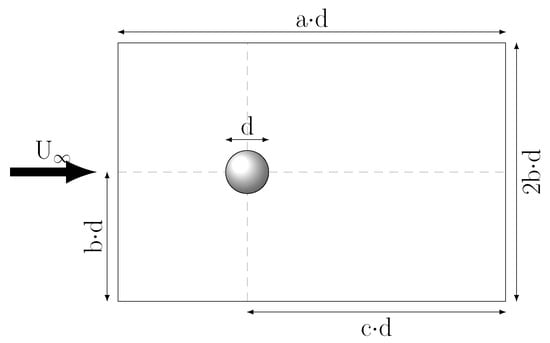
Figure 5.
Horizontal cross-section of the size equivalent sphere cases. Cuts through all Cartesian axis planes look identical. The scaling factors of the simulation domain are a = 23, b = 8, c = 14.5.
Size Equivalent Sphere (SE)
The synthetic cluster used in Section 3 consists of 44 equally sized spherical particles. Thus, the size equivalent particle is similar to the size of the particles in the cluster (60 ). The mean diameter or the Sauter diameter could be used for poly-dispersed clusters. For the current cluster configuration, the Sauter diameter is equal to the size of the individual particle.
Mass Equivalent Sphere (ME)
The mass equivalent sphere approach uses a spherical particle with the same mass as the particle cluster, resulting in a larger particle size than that of the individual cluster particles. Assuming homogeneous density, the mass equivalent particle has a diameter of 211.8 , which is almost four times the size of the individual particles.
Surface Area Equivalent Sphere (AE)
The surface area equivalent approach defines the reference particle as a particle with the same surface area as the cluster. Consequently, the reference particle is significantly larger than the particles in the cluster. Assuming homogeneous density, the surface area equivalent particle has a diameter of 397.8 , which is more than six times the original particle size.
Surface and Mass Equivalent Sphere (AME)
The surface area and mass equivalent case defines the representative particle as a particle having the same surface area and mass as the cluster. The particle size is equivalent to the AE cases, but the particle density is reduced to 165.8 kg/m3 to ensure mass equivalence.
Table 4 summarizes the simulated reference particle cases and the corresponding particle size, Reynolds number, and particle mass.

Table 4.
Summary of single sphere reference cases.
Figure 6 compares the mean temperature profiles of the different representative spheres and the synthetic clusters. The hatched area indicates the temperature profiles spanned by the corresponding dense and dispersed clusters. Comparing the reference particle and cluster temperature profiles reveals that the AME cases reproduce the cluster heat-up better than the remaining reference particle cases. The SE cases over-predict the heat-up, while the ME and AE cases under-predict it. In other words, the representative particle approaches fail to predict particle temperatures and integral heat flux towards particle clusters.
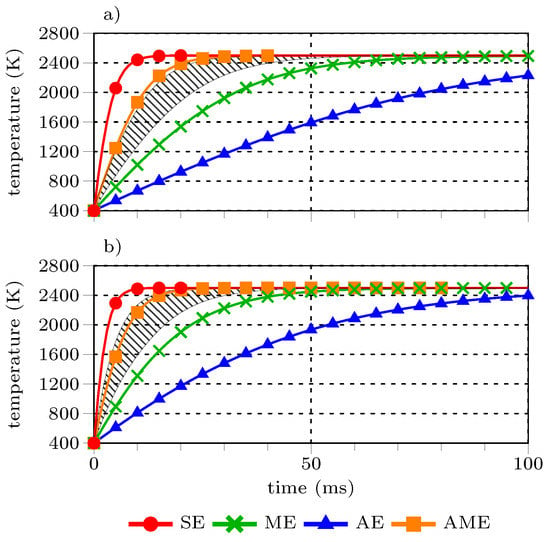
Figure 6.
Comparison of cluster and equivalent sphere temperature profiles (a) 0.5 m/s (b) 13 m/s relative velocity. Hatched areas represent cluster temperature profiles. SA, ME, AE, and AME are the size, mass, surface area, and surface area and mass equivalent case, respectively.
A comprehensive expression for the heat transfer between fluid and particle clusters needs to account for particle size, cluster void fraction, and relative velocity or particle Reynolds number. In the next section, a heat transfer model for the convective heat transfer and a correction function for the projected surface area participating in radiation is derived.
5. Cluster Heat Transfer Models
A simulative approach is used to obtain the integral heat fluxes between the fluid or the surroundings and the synthetic particle cluster because such data is not accessible via experiments. Subsequently, the integral heat flux is referred to as heat flux for simplicity. Table 5 summarizes the cluster void fractions and relative velocities used to derive the heat transfer model. The used physical parameter range comprises Reynolds numbers between 0.3 and 14.4 and cluster void fractions between 0.477 and 0.999 (or or solid loading ratios between 1 and 1737). The same computational grid and settings as in Section 3 are used, except that fixed particle surface temperatures (2450 K) and a steady-state simulation approach are used. These simplifications enable a simpler evaluation of the integral heat fluxes. The steady-state simulations were stopped after the drag force and heat transfer rates converged to a steady value.

Table 5.
Summary of particle cluster variations.
The total heat flux is split into convective and radiative heat flux for the model fitting procedure to derive a correction for the projected surface area participating in radiation and convective heat transfer models. Figure 7 and Figure 8 compare the steady-state heat fluxes for the cases given in Table 5 versus the cluster void fraction and particle Reynolds number. One can see that the radiative heat flux solely depends on the cluster void fraction, while the convective one is a function of void fraction and Reynolds number. These results confirm that the shading effects of the outer particles reduce the radiative heat transfer towards particle clusters. The convective heat transfer depends on the peculiarity of the bulk flow penetration towards the inner particles of the cluster, which is characterized by the gas-cluster relative velocity, cluster void fraction, and the fluid temperatures inside the cluster.
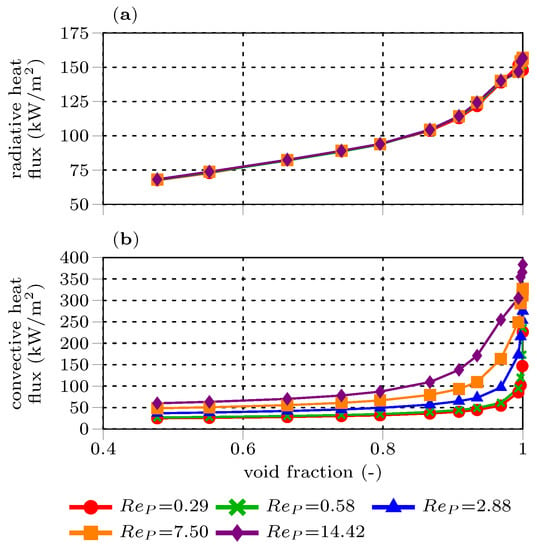
Figure 7.
Comparison of specific radiative (a) and convective (b) integral heat flux towards the particle cluster versus the cluster void fraction for different particle Reynolds numbers ().
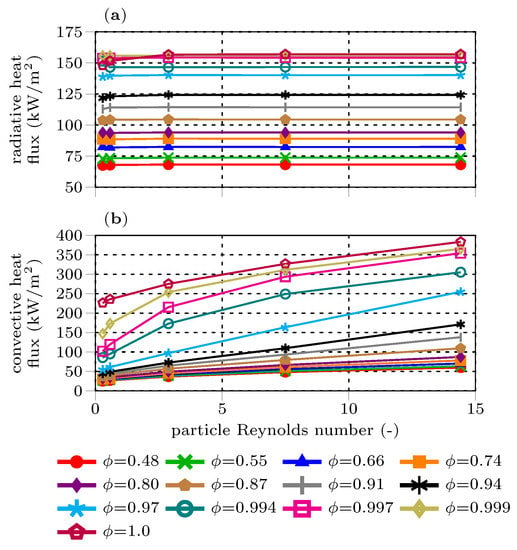
Figure 8.
Comparison of specific radiative (a) and convective (b) integral heat flux towards the particle cluster versus the particle Reynolds number for different void fractions ().
Two different model types are developed based on these observations: (i) a correction for the projected cluster surface area participating in the radiative heat transfer and (ii) a convective heat transfer model taking into account the cluster void fraction and relative velocity. The radiative heat transfer correction reduces the heat flux toward the particle cluster but lacks a back coupling on radiation. In addition, such a model cannot be derived from the conducted particle-resolved simulations. One approach to account for these effects could be the expression for a void fraction dependent cluster emissivity coefficient [43]:
where is the mean beam length, which must be determined from the particle cluster properties. However, deriving a radiation attenuation model is out of the scope of this work.
A common approach to developing convective heat transfer models is based on the fundamental connection between drag and convective heat transfer [57,58]. Determining Nusselt number correlations based on this observation is referred to as the Lévêque approach. Given that the drag coefficients need to be calculated in Lagrangian simulations in any case, two correlations for the convective heat transfer are derived: (i) one based on multiple linear regression (MLR) [59,60] and (ii) one based on the Lévêque approach. The developed heat transfer correlations can be employed in Euler–Lagrange simulations using the SE approach to account for particle clustering in heat transfer.
5.1. Projected Surface Area Correction
The radiative heat flux correlates with the cluster void fraction and can be approximated by:
where , , and are the specific radiative cluster heat flux, the external, illuminated cluster surface area, and a correction function based on the cluster void fraction, respectively. The correction function is the ratio of to which is equivalent to the ratio of the heat flux towards the cluster () and heat flux towards a single particle ():
is calculated using the single sphere diameter equal to the Sauter diameter for this case.
The correction function (Equation (12)) is bounded for to unity and approaches an asymptotic value for . Assuming that the cluster is of perfect spherical shape for , the asymptotic value is given by , which is equal to 0.283 for the synthetic cluster with 44 particles. Taking into account these bounds and the shape given in Figure 7a, the correction function should be of exponential form. The correction function and its coefficient of determination () are given as:
Figure 9a compares the correlation given by Equation (13) and the values determined from the simulations. The correction expression complies with the lower and upper bounds. The asymptotic correction value is approximately double the theoretical one because of the higher surface area caused by the cluster geometry. In general, the correction function depends on the void fraction, the cluster shape, the number of particles, and the particle shape. Therefore, the correlation might not apply to other cluster and particle shapes. Figure 9b shows residuals of Equation (13) compared to the simulated data. The residuals are defined as:
where and are the values obtained predicted by the correlation and the values extracted from the simulations. Deviations of up to 5% appear for the projected surface are correction and the correlation over-predicts the simulation data at low and high void fractions. At the same time, it under-predicts them around = 0.7.
5.2. Convective Heat Transfer Model
The specific convective heat flux evaluation towards the particle cluster confirmed that the relative velocity or and the cluster void fraction () affect the convective heat transfer. A Nusselt correlation is determined using a multiple linear regression approach [59,60] and the Lévêque approach [57,58].
5.2.1. Multiple Linear Regression Approach (MLR)
The Nusselt number () is determined from the simulated heat fluxes and the cluster parameters using the general definition of the heat transfer coefficient:
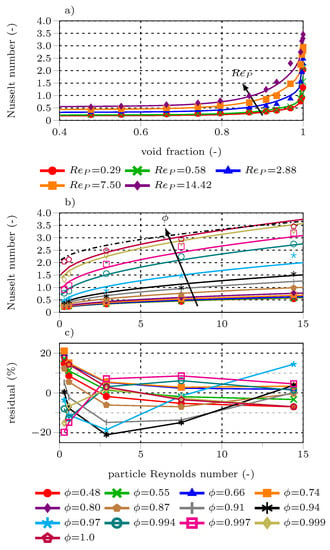
with being the thermal conductivity of the fluid; the bulk gas phase properties are given in Table 3. Based on the convective heat flux dependence on the void fraction () and , the functional expression for should include a void fraction dependent offset to account for the stagnant case, while additional exponential or power-law terms are required for the and relationship. Additional cross-correlation functions might also be required to ensure a proper fit, given that the regression function depends on two independent variables [59,60]. Equation (16) gives the best fit, functional expression. The cross-correlation functions for void fraction and are of potential and exponential form, respectively. The correlation and the coefficient of determination are given by:
The particle Reynolds number and the Nusselt number are based on the bulk fluid properties and the representative particle diameter (Equation (6)). Figure 10a,b compare the Nusselt correlation and the simulation-based Nusselt numbers. The expression shows asymptotic behavior for , which is reasonable and increases exponentially for . The upper boundary for = 1 should be the single sphere Nusselt number. According to Whitaker [40], the Nusselt number of a single sphere in a stagnant fluid equals two. This limit is not ensured by the current expression for → 0 and → 1. A drawback of the expression is its boundlessness for →∞.
5.2.2. Lévêque Approach (GLE)
An alternative way to calculate the convective heat transfer coefficient is to use pressure drop and heat transfer analogy. This analogy is described by the generalized Lévêque Equation (GLE) [58]:
where , L, and are the hydraulic diameter, the length in flow direction, the drag coefficient due to fluid friction, and the Prandtl number. The latter is defined as:
where is the drag coefficient, is the share of the drag coefficient due to fluid friction, sums the surface forces due to fluid friction, is the stagnation pressure, and A is the reference area.
In this study, the single particle diameter is the reference diameter ( = ) and the total cluster cross-section is the reference area (A = 44/4). According to Martin [61], the ratio of the hydraulic diameter to the length L in the GLE for packed beds can be calculated as a function of the void fraction according to . The hydraulic diameter for packed beds can be defined as . For a single sphere, is equal to unity, and the hydraulic diameter is equal to the particle diameter = . The simulated clusters in this work range from void fractions comparable to packed beds ( = 0.477) to a single sphere ( 1). The ratio used in this study was calculated from Equation (17) and is given by Equation (19) as a function of and . The comparison of simulated and fitted and the relative deviations are shown in Figure 11. The relative error is <40% in most cases. The deviation of the simulated values from the just mentioned extreme cases (packed bed and single sphere) could be interpreted as the influence of on effective cross-sectional area A of the clusters. Because of the singularity of the first term on the right-hand side of Equation (19) for , the correlation fails to predict for the single sphere cases (ST61–ST65).
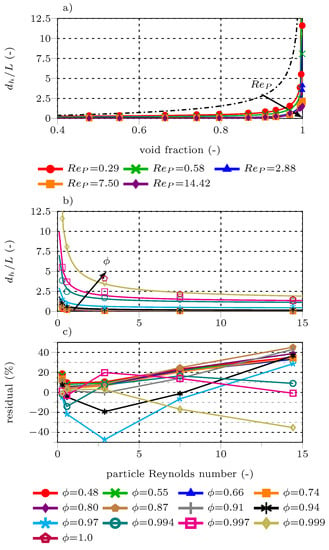
The cluster simulations showed that assuming a constant value of = 2/3 is a reasonable assumption in all simulated cases. The maximum relative deviation from = 2/3 is 21% for case ST5. The value of = 2/3 is enforced by Stokes law ( 1) for spheres [61].
Drag Coefficient
The drag coefficient for the different particle clusters is calculated from Equation (18). The correlation for and the coefficient of determination are given by Equation (20). Figure 12 shows the drag coefficient as a function of the particle Reynolds number and the cluster void fraction . The relative error is shown in Figure 12c. The highest relative error (32.6%) appears for case ST25, while deviations are <30% in all other cases.
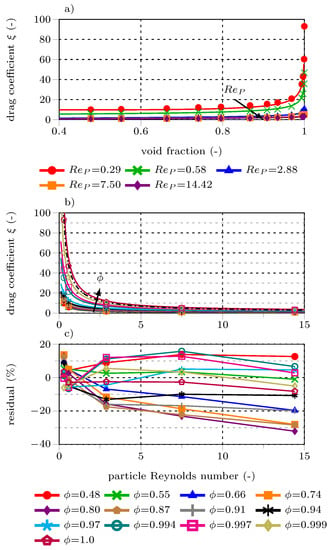
Figure 12.
Comparison of drag coefficient correlation given by Equation (20) ( ) with simulation data (●) and the drag coefficient according to Brauer [62] (
) with simulation data (●) and the drag coefficient according to Brauer [62] ( ) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (20) compared to CFD-simulated data is presented in (c).
) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (20) compared to CFD-simulated data is presented in (c).
 ) with simulation data (●) and the drag coefficient according to Brauer [62] (
) with simulation data (●) and the drag coefficient according to Brauer [62] ( ) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (20) compared to CFD-simulated data is presented in (c).
) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (20) compared to CFD-simulated data is presented in (c).
Nusselt Number
Figure 13 compares the Nusselt correlation based on the GLE approach and the simulation-based Nusselt numbers to calculated from Equation (5). Using Equation (17) combined with Equations (19) and (20), and assuming = 2/3, the deviation of from is , except for case ST43 and ST60. Here the relative errors are 30.1% and 28%, respectively, (Figure 13c). Equation (17) fails to fulfill the single sphere case because of the singularity for of the first term on the right-hand side of Equation (19).
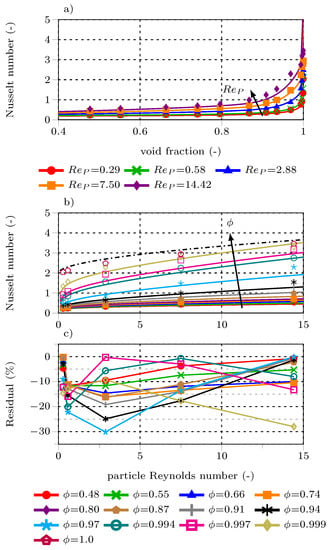
Figure 13.
Comparison of Nusselt number calculated using Equations (17) and (20), = 2/3 and Equation (19) ( ) with values determined from simulations (●) and Equation (5) (
) with values determined from simulations (●) and Equation (5) ( ) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (17) compared to CFD-simulated data is presented in (c).
) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (17) compared to CFD-simulated data is presented in (c).
 ) with values determined from simulations (●) and Equation (5) (
) with values determined from simulations (●) and Equation (5) ( ) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (17) compared to CFD-simulated data is presented in (c).
) versus the cluster void fraction (a) and particle Reynolds number (b). The relative errors of Equation (17) compared to CFD-simulated data is presented in (c).
5.3. Comparison with Random Cluster Simulations
As particles in turbulent flows tend to agglomerate to randomly shaped clusters [14,44,45], the above derived correlations are compared with simulation results of random particle clusters (random in particle size and in particle position). Four different random particle clusters (R1-R4) with a void fraction of = 0.935, consisting of 44 particles with a particle size distribution (PSD) according to the Weibull distribution [63,64], were created. The probability density function of the Weibull distribution is given in Equation (22), where x is the distributed parameter. The particle diameters were determined for a shape parameter of k = 1.14 and a scale parameter of = 120 m. Simulations were carried out for conditions described in Section 5. The results were evaluated for the actual cluster cross-section area, the surface area, and the mean particle diameter. Here the mean particle diameter was determined for each individual cluster (● in Figure 14) and from the first moment of the PSD: (○ in Figure 14).
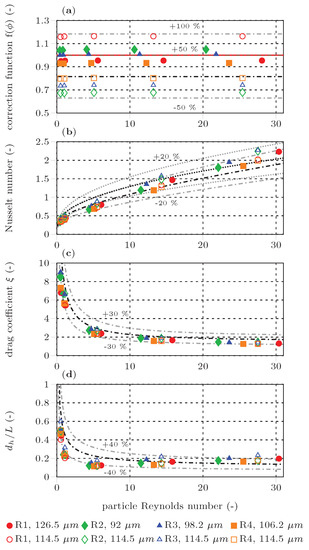
Figure 14.
Comparison of (a) the projected surface area correction calculated using Equation (13) ( ) (b) the Nusselt number calculated using Equation (16) (
) (b) the Nusselt number calculated using Equation (16) ( ) and Equation (17) (
) and Equation (17) ( ), (c) the drag coefficient according to Equation (20) (
), (c) the drag coefficient according to Equation (20) ( ), and (d) calculated using Equation (19) (
), and (d) calculated using Equation (19) ( ) with values determined from simulations (●) versus the cluster particle Reynolds number.
) with values determined from simulations (●) versus the cluster particle Reynolds number.
 ) (b) the Nusselt number calculated using Equation (16) (
) (b) the Nusselt number calculated using Equation (16) ( ) and Equation (17) (
) and Equation (17) ( ), (c) the drag coefficient according to Equation (20) (
), (c) the drag coefficient according to Equation (20) ( ), and (d) calculated using Equation (19) (
), and (d) calculated using Equation (19) ( ) with values determined from simulations (●) versus the cluster particle Reynolds number.
) with values determined from simulations (●) versus the cluster particle Reynolds number.
Figure 14a compares the projected area correction function (Equation (13)) with the projected surface area extracted from the R1-R4 cases. The reference radiative heat flux (single particle) is approximated for the random clusters by:
The simulations deviate from the correlation by up to ±50% for the cluster mean particle diameter, while the statistical mean diameter deviate up to ±100%. The statistical mean diameter falsifies the comparison because of a wrong reference heat flux. The higher values of the mean diameter cases clearly indicate a bias of the regular synthetic cluster arrangement, which maximizes the shading effects. Furthermore, the correction values reveal an additional dependence on the particle size, which was disregarded in this work.
Per definition, the surface area correction function is unity for a single particle or a void fraction of unity. The determined values above unity are most likely caused by the reference radiative heat flux approximation.
A comparison of the simulated and calculated Nusselt number, drag coefficient, and ratio is presented in Figure 14b–d, respectively. A good agreement of correlations and simulations is found. When using the individual mean particle diameter for calculations, most results are within the bounds of the respective correlation. Deviations are higher when using the statistical mean particle diameter. The results suggest that the derived correlations can also be used for random particle clusters if the void fraction and the mean particle diameter are known.
5.4. Comparison of Nusselt Correlations from Literature
Various Nusselt number correlations for dense gas-solid flows have been proposed in the literature. Gnielinski [32] corrected the Nusselt number by a linear function of the void fraction to correctly predict the heat transfer in packed beds:
In a review of heat transfer in packed beds, Achenbach [33] suggested an alternative correlation for the heat transfer:
The new correlation predicts significantly lower heat transfer rates than the Gnielinski [32] correlation at low .
A well know correlation for heat transfer in packed beds was derived by Gunn [65]:
Among others, Deen et al. [66] and Sun et al. [24] have proposed modified versions of the Gunn correlation based on DNS simulation data.
Sun et al. [24] also proposed a scaling function for the Nusselt number to provide consistent heat transfer rates for unresolved EL simulations:
Thiam et al. [29] proved that this scaling function can relate bulk fluid temperatuers and mean fluid temperatures in the packing and improve the heat transfer in gas-solid flows.
Municchi and Radl [25] proposed a Nusselt number correlation for poly-dispersed packings from resolved CFD-DEM simulations based on the GLE approach. The correlation for the mono-dispersed case is given by:
Figure 15 compares the Nusselt number correlations from the literature with the ones derived in this work versus (a) and (b). The correlations from the literature give the same trends: the heat transfer decreases at higher void fractions but increases at higher relative velocity or . The correlation of Achenbach [33] is an exception to this trend and gives increasing heat transfer rates at high void fractions. In general, the correlation of Municchi and Radl [25] gives the highest heat transfer rates at < 0.7, while the correlation by Achenbach [33] gives the lowest rates in this region.
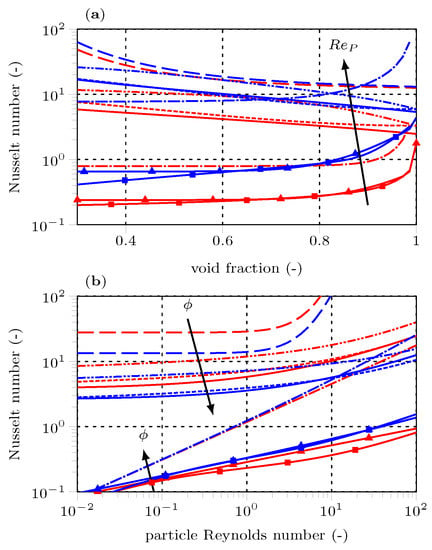
Figure 15.
Comparison of various Nusselt number correlations from the literature (Achenbach [33] ( ), Gnielinski [32] (
), Gnielinski [32] ( ), Gunn [65] (
), Gunn [65] ( ), Sun et al. [24] (
), Sun et al. [24] ( ), Municchi and Radl [25] (
), Municchi and Radl [25] ( )) with the multiple linear regression (MLE) of Equation 16 (
)) with the multiple linear regression (MLE) of Equation 16 ( ) and the Lévêque (GLE) of Equations (17)–(19) (
) and the Lévêque (GLE) of Equations (17)–(19) ( ) correlations versus void fraction (a) and particle Reynolds number (b). Red: (a) lower ReP, (b) lower void fraction; Blue: (a) higher ReP, (b) higher void fraction.
) correlations versus void fraction (a) and particle Reynolds number (b). Red: (a) lower ReP, (b) lower void fraction; Blue: (a) higher ReP, (b) higher void fraction.
 ), Gnielinski [32] (
), Gnielinski [32] ( ), Gunn [65] (
), Gunn [65] ( ), Sun et al. [24] (
), Sun et al. [24] ( ), Municchi and Radl [25] (
), Municchi and Radl [25] ( )) with the multiple linear regression (MLE) of Equation 16 (
)) with the multiple linear regression (MLE) of Equation 16 ( ) and the Lévêque (GLE) of Equations (17)–(19) (
) and the Lévêque (GLE) of Equations (17)–(19) ( ) correlations versus void fraction (a) and particle Reynolds number (b). Red: (a) lower ReP, (b) lower void fraction; Blue: (a) higher ReP, (b) higher void fraction.
) correlations versus void fraction (a) and particle Reynolds number (b). Red: (a) lower ReP, (b) lower void fraction; Blue: (a) higher ReP, (b) higher void fraction.
The correlations proposed in this work show similar trends concerning void fraction as the Achenbach [33] correlation but are in line with the other correlations from the literature for dependency. Furthermore, the new models tend to predict significantly lower heat transfer rates than the well-established models. This behavior is clearly a consequence of the conceptual differences in the heat transfer characteristics in fixed beds or dense gas-solid flows compared to small particles in dispersed clusters. Considering a particle cluster in turbulent flow, the heat flux towards the central particles is lower if the particles are closely packed because the particles at the cluster surface shield and shadow them. Besides reduced radiative heat flux, the fluid flow field around particles is different for dense agglomerates than dispersed clusters. These differences reduce the fluid flow rates and, consequently, the heat flux towards the cluster center.
Achenbach [33] took heat transfer measurements for > 500 and mass transfer measurements for the low region to fit the heat transfer correlation. The different characteristics of their results might be caused by the measurement setup, which is based on single representative spheres inside a random packing from which mean or average heat transfer rates were extrapolated. This can be interpreted similarly to our synthetic cluster simulations and explains the heat flux increase at increasing void fraction. In contrast, the other heat transfer models give decreasing fluxes at higher void fractions.
6. Euler–Lagrangian Validation Simulations
The developed heat transfer models are verified by simulating cases T1–T6 from Table 1 with the unresolved EL approach. The radiation correction and convective heat transfer models are tested independently to ensure both works as expected. First, the radiative heat transfer is neglected to evaluate the convective heat transfer models. In a second step, radiation is added to evaluate the radiative heat transfer prediction.
The Lagrangian case setup consists of a square channel segment with the Lagrangian parcel consisting of 44 particles of 60 in the center. Apart from the box size, all settings are identical to those used in the transient cluster simulations (see Section 3). The transient heat-up is also simulated using the SE and AME representative particle approaches employing the Whitaker [40] heat transfer model for comparison.
6.1. Convective Heat Transfer Model Validation
Figure 16 compares the mean cluster temperature profiles of the resolved and Lagrangian cluster simulations neglecting radiation. The newly developed convective heat transfer models (Equations (16)–(19)) under-estimate the heat transfer towards the cluster at lower cluster void fraction, e.g., cases T1 and T3 (Figure 16a), while the temperature profiles are similar for the resolved and unresolved T5 case. The MLR correlation gives slightly lower temperatures than the resolved and GLE simulations. The reference temperature profiles (black) indicate a significant over-estimation of the integral heat flux towards the particle cluster. Temperatures are within ±100 K for both cluster heat transfer models for the higher relative velocity (Figure 16b). Furthermore, the deviation of the reference cases to the resolved cases is notably lower for the higher relative velocity than the lower one. These results can be explained by the residuals of the correlations, which are generally higher for low and high .
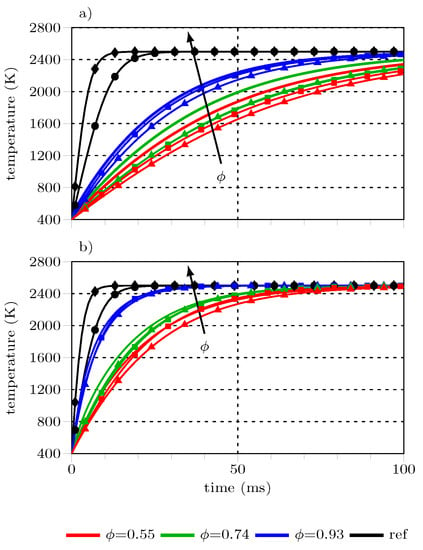
Figure 16.
Comparison of resolved cluster mean temperatures ( ) and Lagrangian parcel temperatures using the multiple linear regression (MLR) (
) and Lagrangian parcel temperatures using the multiple linear regression (MLR) ( ) and the Lévêque (GLE) (
) and the Lévêque (GLE) ( ) Nusselt correlation for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent (
) Nusselt correlation for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent ( ) and surface and mass equivalent (
) and surface and mass equivalent ( ) reference cases use the Whitaker heat transfer model.
) reference cases use the Whitaker heat transfer model.
 ) and Lagrangian parcel temperatures using the multiple linear regression (MLR) (
) and Lagrangian parcel temperatures using the multiple linear regression (MLR) ( ) and the Lévêque (GLE) (
) and the Lévêque (GLE) ( ) Nusselt correlation for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent (
) Nusselt correlation for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent ( ) and surface and mass equivalent (
) and surface and mass equivalent ( ) reference cases use the Whitaker heat transfer model.
) reference cases use the Whitaker heat transfer model.
Differences of up to 100 K exist between the MLR and the GLE Nusselt correlation for the cases T1, T2, T5, and T6. The the GLE Nussel correlation simulations tend to give better results for the mean cluster temperatures. However, both convective heat transfer correlations significantly improve the predicted heat-up characteristics compared to the SE and AME reference cases using the Whitaker heat transfer model.
6.2. Projected Surface Area Correction Validation
Figure 17 compares the resolved and unresolved temperature profiles of T1–T6, including radiative heat transfer. The correction for the projected surface area (Equation (13)) is combined with the convective heat transfer correlations of the previous section. In general, the EL simulations preserve the trends observed for the pure convective heat transfer presented in Section 6.1. The mean temperatures are well predicted by the proposed convective heat transfer models combined with the surface area correction for all cases.
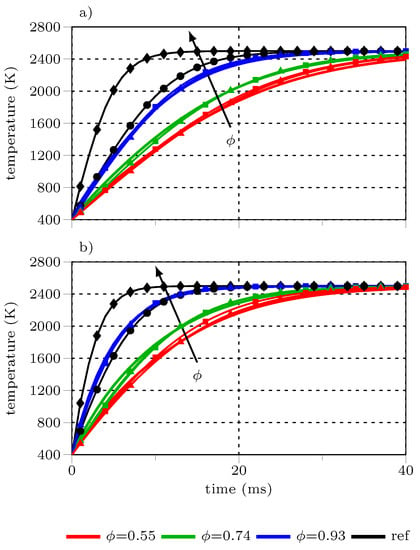
Figure 17.
Comparison of resolved cluster mean temperatures ( ) and Lagrangian parcel temperatures using the radiative heat transfer correction and the Nusselt correlation (
) and Lagrangian parcel temperatures using the radiative heat transfer correction and the Nusselt correlation ( ) and the Lévêque approach (
) and the Lévêque approach ( ) for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent (
) for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent ( ) and surface and mass equivalent (
) and surface and mass equivalent ( ) reference cases use the Whitaker heat transfer model.
) reference cases use the Whitaker heat transfer model.
 ) and Lagrangian parcel temperatures using the radiative heat transfer correction and the Nusselt correlation (
) and Lagrangian parcel temperatures using the radiative heat transfer correction and the Nusselt correlation ( ) and the Lévêque approach (
) and the Lévêque approach ( ) for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent (
) for relative velocities of 0.5 m/s (a) and 13 m/s (b). Size equivalent ( ) and surface and mass equivalent (
) and surface and mass equivalent ( ) reference cases use the Whitaker heat transfer model.
) reference cases use the Whitaker heat transfer model.
The unresolved reference cases provide better approximated the mean cluster temperature when radiation is considered. The AME case reasonably predicts the cluster heat-up of dispersed clusters (T5 and T6). Nevertheless, the heat-up characteristic is significantly improved by the proposed heat transfer correlations compared to the single sphere reference cases, especially at low cluster void fraction.
7. Summary and Conclusions
The heat transfer between a synthetic particle cluster and the surrounding fluid has been studied in this work using particle-resolved CFD simulations. This setup is critical when modeling heat transfer between fines, e.g., dust or pulverized fuels, injected into furnaces. The results demonstrate that the integral heat flux between the particle cluster and surroundings is highly dependent on the cluster void fraction.
Reduction of external surface area and reduced flow penetration through the cluster are responsible for the correlation between void fraction and integral heat flux. The simulation results clearly show that dense clusters behave like larger, porous particles, while sparse ones approach single particle characteristics. These effects must be considered in EL simulations to improve heat transfer predictions and related processes like thermochemical conversion. Radiative heat transfer proved to correlate with the illuminated surface area, which was used to determine a functional expression to correct the integral radiative heat flux towards a cluster for the representative particle (Equation (13)). Two convective heat transfer correlations, one based on a multiple linear regression (MLR) (Equation (16)) the other based on the Lévêque approach (GLE) (Equations (17)–(19)), were determined from the resolved particle simulations. The models were derived for Reynolds numbers between 0.3 and 14.4 and cluster void fractions between 0.477 and 0.999 ( or solid loading ratios between 1 and 1737).
The derived heat transfer models and projected surface area correlation were crosschecked on four random clusters consisting of 44 particles of non-uniform size and having a void fraction of 0.935. The surface area correction function shows a clear bias of the chosen synthetic cluster, which maximizes the shading compared to randomly structured clusters. Results of the synthetic particle clusters can be interpreted as the lower heat flux limit for radiation since radiation is more biased by geometrical constraints and the employed cluster maximizes the shading effects. The convective heat transfer models are capable of predicting the heat transfer reasonably for the random clusters. These results indicate that the new convective heat transfer correlations are independent of cluster shape and particle locations and valid for < 30 and < 1. In addition, applying the newly developed heat transfer correlations in EL simulations gave reasonable results compared to resolved cluster simulations.
It was shown that simulations using common representative particles fail to predict the correct heat-up characteristics of clustered particles. The surface area and mass equivalent (AME) approach can reproduce the cluster temperatures only for high void fractions. The investigated size equivalent (SE) particle approach over-predicts the heating rates, while the surface equivalent (AE) and mass equivalent (ME) approaches under-predict them.
Additional investigations should focus on a step-wise increase of complexity. The next step should investigate the influence of the particle cluster properties, e.g., particle number and locations and cluster shape, on the heat transfer. These investigations may include truly random particle clusters and varying particle size distributions. Subsequently, the interaction between multiple clusters should be evaluated, eventually considering a realistic cluster system.
A drawback of the models is the utilization of the cluster void fraction. Developing a model for the cluster void fraction is not within the scope of this work but one approach can be to determine suitable correlations from experimental measurements in particle image velocimetry (PIV) or particle tracking velocimetry (PTV), which determine particle densities [67,68]. Alternative approaches might use resolved simulations to determine correlations for the cluster void fraction [69].
Author Contributions
Conceptualization, M.B. and M.P.; methodology, M.B. and M.P.; software, M.B. and M.P.; validation, M.B. and M.P.; formal analysis, M.B., M.P. and M.H.; investigation, M.B. and M.P.; resources, M.H.; data curation, M.B. and M.P.; writing—original draft preparation, M.B. and M.P.; writing—review and editing, M.B., M.P. and M.H.; visualization, M.B. and M.P.; supervision, M.H.; project administration, M.B. and M.H.; funding acquisition, M.B. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Austrian program for competence centers contracted under the FFG (Austrian Research Promotion Agency) grant no. 844607 and 869295.
Data Availability Statement
The data will be published in MDPI data—data-1573033—which is still under review.
Acknowledgments
The authors gratefully acknowledge the funding support of K1-MET GmbH, metallurgical competence center. The research program of the competence center K1-MET is supported by COMET (Competence Center for Excellent Technologies), the Austrian program for competence centers. COMET is funded by the Federal Ministry for Transport, Innovation and Technology, the Federal Ministry for Science, Research and Economy, the provinces of Upper Austria, Tyrol, and Styria, and the Styrian Business Promotion Agency. The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC). The authors acknowledge the TU Wien University Library for financial support through its Open Access Funding Programme.
Conflicts of Interest
The authors declare no conflict of interest.
Symbols
The following abbreviations are used in this manuscript:
Latin Symbols
| symbol | unit | description |
| A | [m2] | area |
| cp | [Jkg−1K−1] | specific heat capacity |
| d | [m] | diameter |
| d32 | [m] | Sauter diameter |
| e | [Jkg−1] | specific internal energy |
| Ff | [N] | drag force |
| f (φ) | [-] | radiation correction function |
| G | [Wm−2] | incident radiation |
| hconv | [Wm−2K−1] | convective heat transfer coefficient |
| I | [Wm−2] | radiative intensity |
| k | [-] | shape parameter of the Weibull distribution |
| L | [m] | length scale |
| m | [kg] | mass |
| Np | [-] | number of particles |
| Nu | [-] | Nusselt number |
| Pr | [-] | Prandtl number |
| Q | [W] | integral heat flux |
| R | [-] | coefficient of determination |
| ReP | [-] | particle Reynolds number |
| t | [s] | time |
| U | [ms−1] | velocity |
| x | [-] | distribution parameter |
| xf | [-] | frictional drag force share |
Greek Symbols
| symbol | unit | description |
| ε | [-] | emissivity |
| κ | [Wm−1K−1] | thermal conductivity |
| λ | [-] | scale parameter of the Weibull distribution |
| µ | [Pas] | dynamic viscosity |
| ν | [m2s−1] | kinematic viscosity |
| φ | [-] | void fraction |
| ρ | [kgm−3] | density |
| σ | [Wm−2K−4] | Stefan-Boltzmann constant |
| ξ | [-] | drag coefficient |
| ξf | [-] | drag coefficient due to fluid friction |
Subscripts
| symbol | description |
| C | cluster |
| conv | convective |
| GLE | Generalized Lévêque equation |
| h | hydraulic |
| ∞ | bulk fluid |
| MLR | multiple linear regression |
| P | particle |
| R | projected/illuminated |
| rad | radiative |
| rel | relative |
| S | surface |
Appendix A. Grid Independence Study
The influence of the simulation domain size on drag and heat transfer has been extensively studied in the literature [39,70,71,72,73,74]. These findings are used as initial guesses for the subsequent evaluation of the domain size effects on the drag and heat transfer of the synthetic cluster and reference sphere cases.
Appendix A.1. Synthetic Cluster
The required simulation domain size for the synthetic particle cluster simulations was determined by comparing the overall drag coefficient for different domain sizes. The domain size was varied according to Table A1. The variables a, b, and c of the domain size correspond to the box dimensions of Figure 1. All simulations were carried out using the synthetic cluster with X = 100 m ( = 0.552). First, the influence of the domain height was investigated (cases 1 to 4). Based on the results, case 3 was then used to investigate the influence of the domain length on the drag coefficient (cases 5 and 6). The simulation domain size according to case 6 was used in all synthetic cluster simulations. The variables a, b, and c of the domain size correspond to the dimensions of Figure 2.

Table A1.
Domain size study of synthetic cluster cases.
Table A1.
Domain size study of synthetic cluster cases.
| Scaling Factors | = 2.058 | |||||
|---|---|---|---|---|---|---|
| id | a | b | c | (-) | Error (% of 4) | Error (% of 6) |
| 1 | 2.66 | 1.25 | 1.83 | 1.649 | 10.49 | 24.48 |
| 2 | 2.66 | 2.5 | 1.83 | 1.503 | 0.66 | 13.41 |
| 3 | 2.66 | 3.75 | 1.83 | 1.492 | 0.03 | 12.63 |
| 4 | 2.66 | 5 | 1.83 | 1.492 | - | 12.66 |
| 5 | 7 | 3.75 | 5.33 | 1.358 | - | 2.47 |
| 6 | 12 | 3.75 | 10 | 1.325 | - | - |
The cell size dependence of the simulations was investigated by varying the cell size by ±20% and evaluating the steady-state drag coefficient and Nusselt numbers. The base mesh consists of roughly 4 mio. cells. The results of the grid independence study are given in Table A2 and show that the chosen grid is reasonably well refined.

Table A2.
Cell size study of synthetic cluster cases.
Table A2.
Cell size study of synthetic cluster cases.
| Cell Size | (-) | Deviation (%) | (-) | Deviation (%) |
|---|---|---|---|---|
| −50% | 2.2341 | −0.62 | 0.3283 | −0.43 |
| −20% | 2.2257 | −0.25 | 0.3288 | −0.58 |
| base | 2.2202 | - | 0.3269 | - |
| +20% | 2.2122 | 0.36 | 0.3250 | 0.58 |
| +50% | 2.2059 | 0.65 | 0.3242 | 0.83 |
Appendix A.2. Representative Particle
To determine a sufficient domain size, simulations with five different domain sizes at different Reynolds numbers according to Table A3 have been carried out. The variables a, b, and c of the domain size correspond to the dimensions of Figure 5. The simulated drag coefficient was compared to the drag coefficient calculated as = 27/ and = 16.7/ for Re = 2.058 and Re = 51.469, respectively, [75]. The simulated drag coefficient is within 5% of the theoretical value for all cases. Based on the results presented in Table A3, case 3 was selected for the single spheres reference simulation cases, considering computational resources and accuracy.

Table A3.
Domain size study of reference particle cases.
Table A3.
Domain size study of reference particle cases.
| Scaling Factors | = 2.058 | = 51.469 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| id | a | b | c | (-) | Error (% of 5) | (-) | (-) | Error (% of 5) | (-) |
| 1 | 15 | 4 | 11 | 15.353 | 6.65 | 15.153 | 1.579 | 2.38 | 1.569 |
| 2 | 19 | 6 | 13 | 14.765 | 2.57 | 1.556 | 0.88 | ||
| 3 | 23 | 8 | 15 | 14.586 | 1.33 | 1.549 | 0.42 | ||
| 4 | 27 | 10 | 17 | 14.474 | 0.55 | 1.546 | 0.21 | ||
| 5 | 37 | 15 | 22 | 14.394 | - | 1.542 | - | ||
The cell size dependence of the simulations was investigated by varying the cell size of the mesh. Steady-state drag coefficient and Nusselt numbers are compared with literature values to assess the suitability of the mesh. The Whitaker Nusselt correlation (Equation (5)) is used for the heat transfer comparison. The base mesh consists of 60,000 cells. The investigated mesh variations and the results of the grid independence study are given in Table A4. The difference between the simulated drag coefficient and the theoretical one is below 3% for any case. The deviations between simulated Nusselt number and the Whitaker correlation are below 8%.

Table A4.
Cell size study of reference particle cases for = 51.469.
Table A4.
Cell size study of reference particle cases for = 51.469.
| Cell Size | (-) | Deviation (%) | (-) | Error (%) | (-) | Deviation (%) | (-) | Error (%) | |
|---|---|---|---|---|---|---|---|---|---|
| −50% | 1.530 | 1.21 | 1.567 | 2.51 | 5.687 | −1.1 | 5.279 | −7.72 | |
| −20% | 1.545 | 0.24 | 1.567 | 1.55 | 5.639 | −0.25 | 5.279 | −6.82 | |
| base | 1.548 | - | 1.567 | 1.31 | 5.625 | - | 5.279 | −6.55 | |
| +20% | 1.550 | −0.11 | 1.567 | 1.21 | 5.618 | 0.12 | 5.279 | −6.45 | |
| +100% | 1.553 | −0.28 | 1.567 | 1.04 | 5.612 | 0.23 | 5.279 | −6.30 |
References
- Prokhorov, D.A.; Piralishvili, S.A. Numerical simulation of pulverized coal combustion and comparison with in-furnace measurements. AIP Conf. Proc. 2020, 2211, 040008. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, P.; Shen, Z. Simulation of Turbulent Combustion in a Large Pulverized Coal Boiler Based on Turbulent Radiation Interaction and the Modified Soot Model. ACS Omega 2020, 5, 23822–23835. [Google Scholar] [CrossRef] [PubMed]
- Kuang, S.; Li, Z.; Yu, A. Review on Modeling and Simulation of Blast Furnace. Steel Res. Int. 2018, 89, 1700071. [Google Scholar] [CrossRef]
- Abhale, P.B.; Viswanathan, N.N.; Saxén, H. Numerical modelling of blast furnace—Evolution and recent trends. Miner. Process. Extr. Metall. 2020, 129, 166–183. [Google Scholar] [CrossRef]
- Konrad, K. Dense-phase pneumatic conveying: A review. Powder Technol. 1986, 49, 1–35. [Google Scholar] [CrossRef]
- Cai, L.; Liu, S.; Pan, X.; Guiling, X.; Xiaoping, C.; Changsui, Z. Influence of carbonaceous powders on flow characteristics of dense-phase pneumatic conveying at high pressure. Exp. Therm. Fluid Sci. 2014, 58, 121–130. [Google Scholar] [CrossRef]
- Liang, C.; Xu, P.; Xu, G.; Chen, X.; Zhao, C.; Duan, L. Comparison on Flow Characteristics of Dense-phase Pneumatic Conveying of Biomass Powder and Pulverized coal at High Pressure. Energy Source Part A Recover. Util. Environ. Eff. 2015, 37, 583–589. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, H.; Guo, X.; Gong, X. Application of CPFD method in the simulation of vertical dense phase pneumatic conveying of pulverized coal. Powder Technol. 2019, 357, 343–351. [Google Scholar] [CrossRef]
- Puttinger, S.; Holzinger, G.; Pirker, S. Investigation of highly laden particle jet dispersion by the use of a high-speed camera and parameter-independent image analysis. Powder Technol. 2013, 234, 46–57. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Zhou, G.; Xie, J.; Zhang, H. CFD simulation of dense particulate reaction system: Approaches, recent advances and applications. Chem. Eng. Sci. 2016, 140, 16–43. [Google Scholar] [CrossRef]
- Zhou, L. Theory and Modeling of Dispersed Multiphase Turbulent Reacting Flows; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Haugen, N.E.L.; Mitchell, R.E. Modeling radiation in particle clouds: On the importance of inter-particle radiation for pulverized solid fuel combustion. Heat Mass Transf. 2015, 51, 991–999. [Google Scholar] [CrossRef]
- Liberman, M.A.; Kleeorin, N.; Rogachevskii, I.; Haugen, N.E.L. Multipoint radiation induced ignition of dust explosions: Turbulent clustering of particles and increased transparency. Combust. Theory Model. 2018, 22, 1084–1102. [Google Scholar] [CrossRef]
- Banko, A.J.; Villafañe, L.; Kim, J.H.; Esmaily, M.; Eaton, J.K. Stochastic modeling of direct radiation transmission in particle-laden turbulent flow. J. Quant. Spectrosc. Radiat. Transf. 2019, 226, 1–18. [Google Scholar] [CrossRef]
- Forgber, T.; Radl, S. A novel approach to calculate radiative thermal exchange in coupled particle simulations. Powder Technol. 2018, 323, 24–44. [Google Scholar] [CrossRef]
- Bermúdez, A.; Ferrín, J.; Liñán, A.; Saavedra, L. Numerical simulation of group combustion of pulverized coal. Combust. Flame 2011, 158, 1852–1865. [Google Scholar] [CrossRef]
- Haugen, N.E.L.; Krüger, J.; Mitra, D.; Løvås, T. The effect of turbulence on mass transfer rates of small inertial particles with surface reactions. J. Fluid Mech. 2018, 836, 932–951. [Google Scholar] [CrossRef]
- Krüger, J.; Haugen, N.E.L.; Løvås, T. Correlation effects between turbulence and the conversion rate of pulverized char particles. Combust. Flame 2017, 185, 160–172. [Google Scholar] [CrossRef]
- Krüger, J.; Haugen, N.E.; Mitra, D.; Løvås, T. The effect of turbulent clustering on particle reactivity. Proc. Combust. Inst. 2017, 36, 2333–2340. [Google Scholar] [CrossRef]
- Skinner, F.D.; Smoot, L.D. Heterogeneous Reactions of Char and Carbon. In Pulverized-Coal Combustion and Gasification: Theory and Applications for Continuous Flow Processes; Smoot, L.D., Pratt, D.T., Eds.; Springer: Boston, MA, USA, 1979; Chapter 9; pp. 149–167. [Google Scholar] [CrossRef]
- Bösenhofer, M.; Wartha, E.M.; Jordan, C.; Feilmayr, C.; Stocker, H.; Hauzenberger, F.; Rieger, J.; Tjaden, S.; Walk, A.; Harasek, M. Suitability of pulverised coal testing facilities for blast furnace applications. Ironmak. Steelmak. 2020, 47, 574–585. [Google Scholar] [CrossRef]
- Tavassoli, H.; Kriebitzsch, S.; van der Hoef, M.; Peters, E.; Kuipers, J. Direct numerical simulation of particulate flow with heat transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Tenneti, S.; Sun, B.; Garg, R.; Subramaniam, S. Role of fluid heating in dense gas-solid flow as revealed by particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2013, 58, 471–479. [Google Scholar] [CrossRef]
- Sun, B.; Tenneti, S.; Subramaniam, S. Modeling average gas-solid heat transfer using particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2015, 86, 898–913. [Google Scholar] [CrossRef]
- Municchi, F.; Radl, S. Consistent closures for Euler–Lagrange models of bi-disperse gas-particle suspensions derived from particle-resolved direct numerical simulations. Int. J. Heat Mass Transf. 2017, 111, 171–190. [Google Scholar] [CrossRef]
- Singhal, A.; Cloete, S.; Radl, S.; Quinta-Ferreira, R.; Amini, S. Heat transfer to a gas from densely packed beds of monodisperse spherical particles. Chem. Eng. J. 2017, 314, 27–37. [Google Scholar] [CrossRef]
- Singhal, A.; Cloete, S.; Radl, S.; Quinta-Ferreira, R.; Amini, S. Heat transfer to a gas from densely packed beds of cylindrical particles. Chem. Eng. Sci. 2017, 172, 1–12. [Google Scholar] [CrossRef]
- Esteghamatian, A.; Hammouti, A.; Lance, M.; Wachs, A. Particle resolved simulations of liquid/solid and gas/solid fluidized beds. Phys. Fluids 2017, 29, 033302. [Google Scholar] [CrossRef]
- Thiam, E.I.; Masi, E.; Climent, E.; Simonin, O.; Vincent, S. Particle-resolved numerical simulations of the gas–solid heat transfer in arrays of random motionless particles. Acta Mech. 2019, 230, 541–567. [Google Scholar] [CrossRef]
- Lei, H.; Zhu, L.T.; Luo, Z.H. Study of filtered interphase heat transfer using highly resolved CFD–DEM simulations. AICHE J. 2020, e17121. [Google Scholar] [CrossRef]
- Rauchenzauner, S.; Schneiderbauer, S. A dynamic Spatially Averaged Two-Fluid Model for heat transport in moderately dense gas-particle flows. Phys. Fluids 2020, 32, 063307. [Google Scholar] [CrossRef]
- Gnielinski, V. Wärme- und Stoffübertragung in Festbetten. Chem. Ing. Tech. 1980, 52, 228–236. [Google Scholar] [CrossRef]
- Achenbach, E. Heat and flow characteristics of packed beds. Exp. Therm. Fluid Sci. 1995, 10, 17–27. [Google Scholar] [CrossRef]
- Crowe, C.T.; Smoot, L.D. Multicomponent Conservation Equations. In Pulverized-Coal Combustion and Gasification: Theory and Applications for Continuous Flow Processes; Smoot, L.D., Pratt, D.T., Eds.; Springer: Boston, MA, USA, 1979; Chapter 2; pp. 15–54. [Google Scholar] [CrossRef]
- Naruse, I.; Inada, T. Advanced Pulverized Coal Injection Technology and Blast Furnace Operation; Characteristics of Pulverized Coal Combustion; Elsevier Science Ltd.: Oxford, UK, 2000; pp. 15–35. [Google Scholar]
- Cai, J.; Handa, M.; Modest, M.F. Eulerian–Eulerian multi-fluid methods for pulverized coal flames with nongray radiation. Combust. Flame 2015, 162, 1550–1565. [Google Scholar] [CrossRef]
- Wu, B.; Roy, S.P.; Zhao, X.; Modest, M.F. Effect of multiphase radiation on coal combustion in a pulverized coal jet flame. J. Quant. Spectrosc. Radiat. Transf. 2017, 197, 154–165. [Google Scholar] [CrossRef]
- Will, J.; Kruyt, N.; Venner, C. An experimental study of forced convective heat transfer from smooth, solid spheres. Int. J. Heat Mass Transf. 2017, 109, 1059–1067. [Google Scholar] [CrossRef]
- Ellendt, N.; Lumanglas, A.; Moqadam, S.I.; Mädler, L. A model for the drag and heat transfer of spheres in the laminar regime at high temperature differences. Int. J. Therm. Sci. 2018, 133, 98–105. [Google Scholar] [CrossRef]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer, 3rd ed.; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Modest, M.F.; Haworth, D.C. Radiative Heat Transfer in Turbulent Combustion Systems; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Trivic, D.N.; Djordjevic, B.; Grbavcic, Z.B. Influence of particles size and concentration in particles cloud radiation by Mie theory. In Proceedings of the International Thermal Science Seminar Bled, Bled, Slovenia, 11–14 June 2000; Begellhouse: Danbury, CT, USA, 2000. [Google Scholar] [CrossRef]
- Squires, K.D.; Eaton, J.K. Preferential concentration of particles by turbulence. Phys. Fluids A Fluid Dyn. 1991, 3, 1169–1178. [Google Scholar] [CrossRef]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Ferrer, P.M.; Causon, D.; Qian, L.; Mingham, C.; Ma, Z. A multi-region coupling scheme for compressible and incompressible flow solvers for two-phase flow in a numerical wave tank. Comput. Fluids 2016, 125, 116–129. [Google Scholar] [CrossRef]
- Kiss, M.; Bösenhofer, M.; Schatzl, M.; Harasek, M. Region Coupling Algorithms in OpenFoam. In Proceedings of the 16th Minisymposium Verfahrenstechnik and 7th Partikelforum, Vienna, Austria, 21–22 September 2020; TU Wien: Vienna, Austria, 2020; p. DiV2–(01). [Google Scholar] [CrossRef]
- Babich, A.; Senk, D.; Born, S. Interaction between Co-injected Substances with Pulverized Coal into the Blast Furnace. ISIJ Int. 2014, 54, 2704–2712. [Google Scholar] [CrossRef]
- Grosshandler, W.L. RADCAL: A Narrow-Band Model for Radiation–Calculations in a Combustion Environment; Technical Note 1402; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 1993.
- Narayanaswamy, A.; Chen, G. Thermal near-field radiative transfer between two spheres. Phys. Rev. B 2008, 77, 075125. [Google Scholar] [CrossRef]
- Song, B.; Fiorino, A.; Meyhofer, E.; Reddy, P. Near-field radiative thermal transport: From theory to experiment. AIP Adv. 2015, 5, 053503. [Google Scholar] [CrossRef]
- Krishnendu, G.S.; Jayakumar, J.S. CFD Analysis of Combined Thermal Radiation and Conjugate Heat Transfer in a 3D FFS. In Materials, Design, and Manufacturing for Sustainable Environment; Mohan, S., Shankar, S., Rajeshkumar, G., Eds.; Springer: Singapore, 2021; pp. 835–850. [Google Scholar]
- Sinn, C.; Kranz, F.; Wentrup, J.; Thöming, J.; Wehinger, G.D.; Pesch, G.R. CFD Simulations of Radiative Heat Transport in Open-Cell Foam Catalytic Reactors. Catalysts 2020, 10, 716. [Google Scholar] [CrossRef]
- Verderio Junior, S.A.; Scalon, V.L.; Avallone, E.; Mioralli, P. Numerical validation of viewFactor and FVDOM radiation models of OpenFOAM® and application in the study of food furnaces. Ingeniare-Rev. Chil. Ing. 2018, 26, 546–556. [Google Scholar] [CrossRef][Green Version]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C., Jr.; et al. GRI-Mech 3.0. 2018. Available online: http://combustion.berkeley.edu/gri-mech/ (accessed on 12 December 2021).
- Duan, Z.; He, B.; Duan, Y. Sphere Drag and Heat Transfer. Sci. Rep. 2015, 5, 12304. [Google Scholar] [CrossRef]
- Martin, H. A theoretical approach to predict the performance of chevron-type plate heat exchangers. Chem. Eng. Process. Process. Intensif. 1996, 35, 301–310. [Google Scholar] [CrossRef]
- Freedman, D. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, NY, USA, 2009. [Google Scholar]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar] [CrossRef]
- Martin, H. The generalized Lévêque equation and its use to predict heat or mass transfer from fluid friction. In Proceedings of the 20th National Heat Transfer Conference, Maratea, Italy, 27–29 June 2002; pp. 21–29. [Google Scholar]
- Brauer, H. Impuls-, Stoff- und Wärmetransport durch die Grenzfläche kugelförmiger Partikeln. Chem. Ing. Tech. 1973, 45, 1099–1103. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of Strength of Materials; Ingeniörs Vetenskaps Akademiens Handlingar, Royal Swedish Institute for Engineering Research: Stockholm, Sweden, 1939; No. 151; pp. 5–45. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw-Hill Series in Electrical and Computer Engineering; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Gunn, D. Transfer of heat or mass to particles in fixed and fluidised beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Deen, N.G.; Peters, E.; Padding, J.T.; Kuipers, J. Review of direct numerical simulation of fluid–particle mass, momentum and heat transfer in dense gas-solid flows. Chem. Eng. Sci. 2014, 116, 710–724. [Google Scholar] [CrossRef]
- Monchaux, R.; Bourgoin, M.; Cartellier, A. Preferential concentration of heavy particles: A Voronoï analysis. Phys. Fluids 2010, 22, 103304. [Google Scholar] [CrossRef]
- Petersen, A.J.; Baker, L.; Coletti, F. Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 2019, 864, 925–970. [Google Scholar] [CrossRef]
- Falkinhoff, F.; Obligado, M.; Bourgoin, M.; Mininni, P.D. Preferential Concentration of Free-Falling Heavy Particles in Turbulence. Phys. Rev. Lett. 2020, 125, 064504. [Google Scholar] [CrossRef] [PubMed]
- Constant, E.; Favier, J.; Meldi, M.; Meliga, P.; Serre, E. An immersed boundary method in OpenFOAM Verification and validation. Comput. Fluids 2017, 157, 55–72. [Google Scholar] [CrossRef]
- Farazi, S.; Sadr, M.; Kang, S.; Schiemann, M.; Vorobiev, N.; Scherer, V.; Pitsch, H. Resolved simulations of single char particle combustion in a laminar flow field. Fuel 2017, 201, 15–28. [Google Scholar] [CrossRef]
- Jayawickrama, T.R.; Haugen, N.E.L.; Babler, M.U.; Chishty, M.; Umeki, K. The effect of Stefan flow on the drag coefficient of spherical particles in a gas flow. Int. J. Multiph. Flow 2019, 117, 130–137. [Google Scholar] [CrossRef]
- Richter, A.; Nikrityuk, P.A. Drag forces and heat transfer coefficients for spherical, cuboidal and ellipsoidal particles in cross flow at sub-critical Reynolds numbers. Int. J. Heat Mass Transf. 2012, 55, 1343–1354. [Google Scholar] [CrossRef]
- Safronov, D.; Kestel, M.; Nikrityuk, P.; Meyer, B. Particle resolved simulations of carbon oxidation in a laminar flow. Can. J. Chem. Eng. 2014, 92, 1669–1686. [Google Scholar] [CrossRef]
- Schubert, H. Handbuch der Mechanischen Verfahrenstechnik, 1st ed.; Wiley-VCH: Zürich, Switzerland, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).