Dynamic Performance Assessment of PMSG and DFIG-Based WECS with the Support of Manta Ray Foraging Optimizer Considering MPPT, Pitch Control, and FRT Capability Issues

Abstract

Wind generators have attracted a lot of attention in the realm of renewable energy systems, but they are vulnerable to harsh environmental conditions and grid faults. The influence of the manta ray foraging optimizer (MRFO) on the dynamic performance of the two commonly used variable speed wind generators (VSWGs), called the permanent magnet synchronous generator (PMSG) and doubly-fed induction generator (DFIG), is investigated in this research article. The PMSG and DFIG were exposed to identical wind speed changes depending on their wind turbine characteristics, as well as a dangerous three-phase fault, to evaluate the durability of MRFO-based wind side controllers. To protect VSWGs from hazardous gusts and obtain the optimum power from incoming wind speeds, we utilized a pitch angle controller and optimal torque controller, respectively, in our study. During faults, the commonly utilized industrial approach (crowbar system) was exclusively employed to aid the studied VSWGs in achieving fault ride-through (FRT) capability and control of the DC link voltage. Furthermore, an MRFO-based PI controller was used to develop a crowbar system. The modeling of PMSG, DFIG, and MRFO was performed using the MATLAB/Simulink toolbox. We compared performances of PMSG and DFIG in reference tracking and resilience against changes in system parameters under regular and irregular circumstances. The effectiveness and reliability of the optimized controllers in mitigating the adverse impacts of faults and wind gusts were demonstrated by the simulation results. Without considering the exterior circuit of VSWGs or modifying the original architecture, MRFO-PI controllers in the presence of a crowbar system may help cost-effectively alleviate FRT concerns for both studied VSWGs.

1. Introduction

The International Energy Agency (IEA) report released in 2020 to address electrical power systems (EPSs) security concerns states that, until 2040, the average yearly contribution of renewable energy sources (RESs) will reach 45% of all generations. The security of EPSs is jeopardized by the changeable nature of RESs [1]. EPS security procurement is now much more essential in light of recent pandemics, such as COVID-19 [2]. To make EPSs resilient to grid faults and the fluctuating power output of RESs, security considerations must be incorporated into their operation [3]. One of the RESs that has been rapidly expanding as a source of power in recent years is wind energy (WE), which is used to contribute to the demand side of the electricity supply chain. This RES is used to address issues such as global CO₂ emissions, inadequate load demands, and fossil fuel shortages [4]. Global installed WE capacity will continue to increase due to the decreased costs and high reliability of these systems [5]. WE generation from on- and off-shore wind turbines (WTs) has gained pace, and is currently the cheapest kind of energy in many major markets, signaling that WE is a viable option [5,6]. During electricity transition, the most critical challenges are cost, efficiency, supply security/timing, and wind integration [7,8,9].

WGs in WE markets these days are based on fixed or variable speed concepts in the market [9]. In the past, WGs were based on fixed concepts due to their features such as simplicity and low cost; however, the main drawback was its need for reactive power (Q) to assist voltage support. The latest standard for installed WE is variable-speed wind generators (VSWGs). VSWGs efficiently capture energy and have good voltage control [9,10]. Widely used VSWGs include the doubly-fed induction wind generator (DFIWG) and permanent magnet synchronous wind generator (PMSWG), with a back-to-back (BTB) power converter strategy [8,11,12]. The DFIWG contains a gearbox, and only 20–30% of its BTB converter rating is needed for its working speed range of 0.7–1.3 pu; however, the PMSWG has a high initial cost due to its use of full-rated BTB power converters [13]. Due to features such as gearless design, minimal maintenance, decreased losses, strong controllability, realized MPPT, new grid code requirements, and high efficiency, the PMSWG is recommended [14].

Utilizing the greatest amount of WE possible is crucial given the growing uptake of WE in the power grid. To do this, the WE system must monitor the maximum power point. There is a respectable range of publication reports on maximum power point tracking (MPPT) algorithms for WE systems. However, selecting the precise MPPT algorithm for a given situation requires considerable expertise because each method has its own advantages and disadvantages. In [15], various MPPT algorithms that could be used to extract the most power were discussed. These techniques were categorized based on whether they use a direct or indirect power controller to monitor power. The benefits, drawbacks, and a thorough comparison of the various MPPT algorithms were also described in terms of their complexity, required wind speed, prior training, speed responses, etc., as well as their capacity to obtain maximum energy production. The presented study in [16] used a control method called Kalman MPPT for the extraction of maximum power from grid-connected wind systems under speed variations; moreover, the pitch angle control (PAC) effect was negligible. To achieve faster convergence and less oscillation when used with variable power sources, the golden section search (GSS), perturb and observe (P&O), and incremental conductance (INC) approaches for MPPT were combined in [17]. The results demonstrate the viability and efficacy of the suggested MPPT technique, but harmonic and fault analyses were not conducted. The work in [18] used a real-time fuzzy-based MPPT controller to provide the extremely efficient operation and step-up power conversion of a standalone PV system under low voltage penetration. Grid-connected PV using FLC has major limitations that are not demonstrated. In order to gain quick and maximum PV power with no oscillation tracking, Ref. [19] offered an adaptive neuro-fuzzy inference system–particle swarm optimization (ANFIS–PSO)-based hybrid MPPT method. However, the suggested ANFIS–PSO continues to introduce greater power oscillations over a longer length of time.

In the DFIWG, the BTB power converter lies between the rotor and the grid side. The DFIWG may run at various speeds depending on the incoming wind speeds, allowing for improved WE harvesting [20]. Due to the PAC and dynamic slip management methods of the DFIWG, rebuilding the terminal voltage after a grid disruption is considerably simpler [21]. Furthermore, with the DFIWG, controlling active power (P) and Q using decoupling principles is significantly easier. When the power converters of the DFIWG are exposed to lower voltages, they fall into standby mode [22]. However, during grid faults over threshold voltages, the DFIWG quickly synchronizes with the electricity grid [22]. In comparison with the DFIWG, the PMSWG provides more flexibility [23,24]. As a result, while employing the PMSWG, P and Q regulation is more successful.

Under fault conditions, WTs may be disconnected from the grid, necessitating the use of new grid codes to improve fault ride-through (FRT) capabilities. FRT has two requirements: WTs must remain connected to the grid even if the voltage is above or below the rated value, and Q injections must occur under abnormal situations such as faults [25,26]. DFIWG stator terminals are directly connected to the grid and their rotor terminals are connected to the grid via a BTB converter. Its smaller size converter leads to reduced power losses and is cost-efficient, although Q supply capability is small due to its size. FACTS devices are equipped with the DFIWG to increase Q supply. Grid faults lead to oscillations in rotor speed and electromagnetic torque, which is transferred to the grid voltage. The rotor side converter (RSC) is deactivated with only a conventional crowbar, and this leads to a reduction of injected Q [27,28]. The PMSWG is directly connected to the power grid through a full-scale BTB converter. This converter decouples the PMSWG from the grid, making it less sensitive to grid faults compared with the DFIWG. It is capable of injecting the rated Q to fully meet grid code requirements for voltage support [29].

For improving the transient stability of the DFIWG and PMSWG, different FRT control strategies have been presented in the literature, such as fault current limiters (FCLs), a crowbar switch, DC chopper circuitry, a parallel capacitor, energy storage systems, FACTS, and sliding mode controls (SMC) [30,31,32,33,34,35,36,37]. Different studies evaluated the DFIWG utilizing various control techniques [38], with a focus on the usage of MPPT and PAC using different algorithms [39], whereas peak current limiting and MPPT were used by [40,41], respectively. For augmentation of the FRT capability of the DFIWG, a series of FCL was combined with a metal oxide varistor [42]. The use of a multistep bridge-type FCL for the PMSWG was reported by [43] to increase its FRT performance. The FRT capability of a wind farm (WF) constituting of DFIWGs was improved using a neuro-fuzzy-logic-controlled (FLC) parallel-resonance-type FCL scheme by [44], whereas complete power systems utilizing an FLC capacitive-bridge-type FCL scheme were examined by [45]. An SMC based on the bridge-type FCL was employed in [46] for the FRT-improved DFIWG performance, whereas another way of employing a dynamic multi-cell FCL was reported to enhance the FRT performance of the WF, based on DFIWG control [47]. FRT capability enhancement methods for WGs are summarized in the literature [30].

By providing a comparative analysis between the proposed work for the PMSWG and DFIWG with recently published methods based on FLC, model predictive controller (MPC), SMC, and optimization concepts, we demonstrate the role of MRFO. Table 1 presents and summarizes a comparison of the results between the proposed and previously published techniques in the PMSWG. Furthermore, this comparison is performed for the DFIWG in Table 2.

Table 1. Comparison of the proposed work with previously published works on PMSWG.

Refs.	Publisher	Year	Developed Controllers		Contribution of Study			Remarks
			MSC	GSC	MPPT	PAC	FRT
[13]	Elsevier	2017	✓	✗	✓	✗	✓	Three different control systems (PI, ISMC, and FCS-MPC) were provided, and their effectiveness was evaluated. Outcome: FCS-MPC was the fastest controller, whereas ISMC had the best performance.
[23]	Springer	2020	✓	✗	✓	✗	✓	A PSO, WOA, and GWO-based PI controller was given. GWO performed more smoothly and quickly than the other approaches that were being compared.
[48]	IEEE	2018	✓	✓	✗	✗	✓	The system was improved by figuring out the PI controller optimum gain values using the GWO, GA, and simplex methods. The GWO method was reported to have the best convergence to the minimal value, as well as the finest reaction to faults.
[49]	MDPI	2021	✗	✓	✗	✗	✓	The variable switching frequency issue in the traditional FCS-MPC was fixed by a unique MMPC, which also resulted in decreased THD in stator current and shorter simulation times. A coordinated LVRT was used under faults, and the MMPC operated smoothly and with a quick dynamic response.
[50]	MDPI	2022	✓	✓	✓	✗	✗	Adjusted the machine and GSC to follow the MPPT-established standard for wind speed and to address the chattering issue brought on by the traditional SMC. It was superior to five modern controllers under wind variations.
[51]	Springer	2022	✓	✗	✓	✓	✗	OTC along with an FLC was implemented to decrease installation costs and improve the system’s overall efficiency. FLC was superior to PI under two wind profiles.
[52]	Taylor & Francis	2022	✓	✗	✓	✗	✓	Optimized PI controller with WHO was presented. WHO was superior to the Ziglar–Nicolas method in terms of fast transient response and smooth operation.
[53]	SAGE	2021	✗	✓	✗	✗	✓	In addition to backing choppers, FLC was employed to enhance system performance in the event of three-phase faults. In terms of quick transient reaction and lag-free operation, FLC outperformed PI.
Current study			✓	✗	✓	✓	✓	With the MRFO-PI control of MSC and BC, the three issues are realized. This is the first study that considers the three issues. The optimized controller has a fast response and smooth operation

Table 2. Comparison of the proposed work with previously published works on DFIWG.

Refs.	Publisher	Year	Developed Controllers		Contribution of Study			Remarks
			RSC	GSC	MPPT	PAC	FRT
[54]	IEEE	2018	✓	✗	✗	✗	✓	Applied feed-forward current control that reduced the transient current in the rotor circuit when a fault quickly occurred.
[55]	IET-Wiely	2018	✗	✓	✗	✗	✓	The overcurrents in the stator and rotor were decreased, and Q was quickly injected during voltage dips, using a combined vector and direct power controller.
[56]	IEEE	2021	✓	✓	✓	✗	✓	In order to mitigate (malfunctioning of sensors and parameter fluctuations) and assure acceptable performance during faults or wind speed conditions, a modified adaptive control architecture was added to the existing conventional vector control and was effective.
[47]	Hindawi	2020	✗	✗	✗	✗	✓	To improve system performance, a nonlinear SMC-based FCL was linked at the POCC. The results showed that SMC performs well with nonlinear dynamics and unanticipated voltage dip levels.
[46]	MDPI	2020	✗	✗	✗	✗	✓	The dynamic adaptive multi-cell FCL topology was coupled at the POCC, which significantly improved system performance and offered an adaptable voltage dip compensation mechanism depending on the level of voltage. Comparison assessment with the single-cell FCL verified the suggested scheme’s efficacy.
[57]	Elsevier	2021	✓	✓	✓	✓	✗	Performance comparisons between the FLC, H infinity (H∞), and PI controllers were conducted, and H∞ was shown to be the best. Mixed controllers, calledthe FL-H∞, and PI- andPID-filter derivative (Fd)-H∞ gave better performance and resulted in decreasing harmonics.
[58]	MDPI	2022	✓	✗	✓	✓	✗	The precision of the three controllers (SM, PI, and advanced backstepping (AB)), which provided the lowest tracking error, was studied and assessed. The ABC’s benefits included target monitoring, current waveform compatibility, quick response times, and robustness.
[59]	MDPI	2022	✓	✗	✓	✓	✗	The MPC system was utilized to maximize the amount of wind energy extracted, even when the wind speed was erratic or the WT was uncertain, and it was more efficient than the PI type.
Current study			✓	✗	✓	✓	✓	With the MRFO-PI control of RSC and crowbar, the three issues were realized. This is the first study that considers the three vital issues. The optimized controller had a fast response and smooth operation.

To resolve thought-provoking engineering challenges in geometry, a wide variety of algorithms motivated by societal, cosmological, and animal behavior have been suggested. The manta ray foraging optimizer (MRFO) technique is applied to optimal controller design (PI) to enhance the dynamic performance of the PMSWG and DFIWG under regular and irregular conditions. As PMSWGs and DFIWGs are widely used and account for the biggest proportion of WE markets, we were interested in investigating their impact on power systems. In light of the earlier discussion, this comparative study presents the effects of wind gusts and grid faults on the dynamic performance of the PMSWG and DFIWG, considering FRT capability, MPPT operation, and PAC issues. Previous research investigations did not include the application of the MRFO technique for the operation of optimum controllers based on the PMSWG and DFIWG. Furthermore, gathering the three issues for the two investigated renewable generators has not appeared in any single research article. As a result, our research aims to fill the gap in the literature. The DFIWG and PMSWG are discussed in terms of their properties, modeling, and control systems. The PMSWG and DFIWG that were tested had the same capacity and were subject to identical wind gusts and severe faults. Furthermore, both VSWTs operated at their rated speed under the assumed fault state (85% voltage dip), depending on their MPPT characteristics. The main benefit of this control technique is its high effectiveness, small overshoot, quick dynamic response, and successful handling of three critical issues in dominant VSWGs.

This paper is prepared as follows: The introduction, relevant literature, and purpose are described in Section 1 of this work, which is divided into six parts. Modeling, development, and the failure ratio of VSWGs and basic concepts of the investigated WE systems are presented in Section 2. In Section 3, the application of the MRFO method is discussed in detail. In Section 4, control of the crowbar system with MRFO-PI is studied for solving FRT issues in the investigated VSWGs. A discussion of simulated results is described in Section 5. Finally, concluding remarks are found in Section 6.

2. Modeling of the Studied WE Systems

Kinetic energy is converted into mechanical energy with a WT. The modeling of WT is discussed in detail [30,34].

$${\mathrm{P}}_{\mathrm{M}}=0.5C_{\mathrm{p}}\left(\mathsf{\lambda }.\mathsf{\beta }\right){ \mathsf{\rho }\mathrm{A}\mathsf{\nu }}_W{}^3$$

(1)

$$C_{\mathrm{p}} \left(\mathsf{\lambda }.\mathsf{\beta }\right)=0.5176\left(\frac{116}{\mathsf{\lambda }\mathrm{i}}-0.4\mathsf{\beta }-5\right){\exp }^{-\frac{21}{\mathsf{\lambda }\mathrm{i}}}+0.0068\mathsf{\lambda }$$

(2)

$$\frac{1}{\mathsf{\lambda }\mathrm{i}}=\frac{1}{\mathsf{\lambda }+0.08\mathsf{\beta }}-\frac{0.035}{{\mathsf{\beta }}^3+1}$$

(3)

$$\mathsf{\lambda }=\frac{{\mathsf{\omega }}_{\mathrm{r}} \mathrm{R}}{{\mathrm{V}}_W}$$

(4)

From Equation (4), we can obtain the value of ${\mathsf{\omega }}_{\mathrm{r}}$ at optimal $\mathsf{\lambda }$ and operated ${\mathrm{V}}_W$:

$${\mathrm{T}}_{\mathrm{m}}=\frac{{\mathrm{P}}_{\mathrm{M}}}{{\mathsf{\omega }}_{\mathrm{r}}}$$

(5)

$${\mathrm{T}}_{\mathrm{m}}={\mathrm{J}}_{\mathrm{eq}}\frac{{\mathrm{d}\mathsf{\omega }}_{\mathrm{r}}}{\mathrm{dt}}+{\mathrm{B}}_{\mathrm{eq}}{\mathsf{\omega }}_{\mathrm{r}}+{\mathrm{T}}_{\mathrm{e}}$$

(6)

where the variables ${\mathrm{T}}_{\mathrm{m}}$, ${\mathrm{J}}_{\mathrm{eq}}$, ${\mathrm{B}}_{\mathrm{eq}},$ and ${\mathrm{T}}_{\mathrm{e}}$ are the turbine torque, total equivalent inertia of turbine, generator, damping coefficient, and electromagnetic torque of the generator, respectively.

Modeling of WT was performed according to Equations (1)–(6), as shown in Figure 1. The WE power capture is maximized at different wind speeds; the VSWG has the capability to do this for a wide speed range. PAC, one of the software solutions, assists in FRT by keeping the generator operating at rated wind speeds. When a WT is exposed to wind gusts, PAC increases to reduce Cp by controlling the yaw mechanism, and therefore, output power decreases where PA equals zero at normal wind speeds are shown in Figure 2. A variety of MPPT control strategies have been developed, thence MPPT with optimal torque control (OTC) is proposed to be applied due to its merits, such as its power smoothing capability. Figure 3 shows the OTC-MPPT algorithm of WECS.

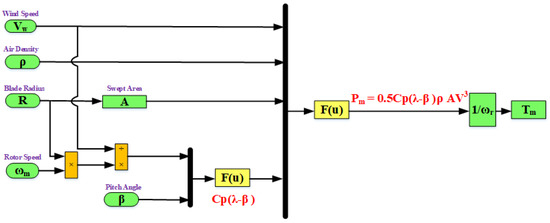
Figure 1. Modeling of a WT.

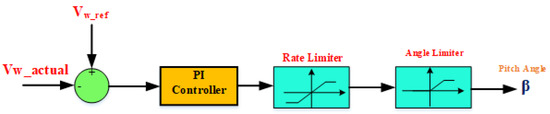
Figure 2. PAC system.

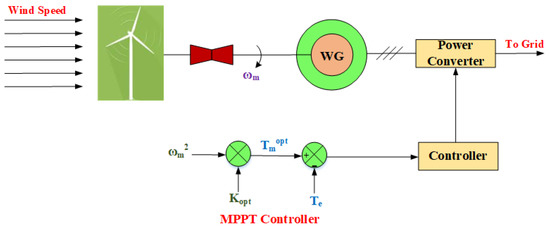
Figure 3. OTC method for MPPT operation.

2.1. Modeling of the PMSWG

The PMSWG model was run using a d-q equivalent electrical circuit. A full description of the proposed PMSWG with its control system is shown in Figure 4. The parameter definitions are found in [60]. Dynamic equations of the mathematical model are as follows [13,52]:

$${\mathrm{V}}_{\mathrm{ds}}={\mathrm{R}}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{d}}+{{\mathsf{\lambda }}^{.}}_{\mathrm{d}}-{\mathsf{\omega }}_{\mathrm{e}}{\mathsf{\psi }}_{\mathrm{q}}$$

(7)

$${\mathrm{V}}_{\mathrm{qs}}={\mathrm{R}}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{q}}+{{\mathsf{\lambda }}^{.}}_{\mathrm{q}}-{\mathsf{\omega }}_{\mathrm{e}}{\mathsf{\psi }}_{\mathrm{d}}$$

(8)

$${\mathsf{\psi }}_{\mathrm{d}}={ \mathrm{L}}_{\mathrm{d}}{\mathrm{I}}_{\mathrm{d}}+{\mathsf{\psi }}_{\mathrm{pm}}$$

(9)

$${\mathsf{\psi }}_{\mathrm{q}}={ \mathrm{L}}_{\mathrm{q}}{\mathrm{I}}_{\mathrm{q}}$$

(10)

$${\mathsf{\lambda }}_{\mathrm{d}}={ \mathrm{L}}_{\mathrm{d}}{\mathrm{I}}_{\mathrm{d}}+{ \mathsf{\psi }}_{\mathrm{pm}}$$

(11)

$${\mathrm{T}}_{\mathrm{e}}=\frac{3}{2}{ \mathrm{n}}_{\mathrm{p}}\left({\mathsf{\psi }}_{\mathrm{pm}}{\mathrm{I}}_{\mathrm{q}}\right)$$

(12)

$$\mathrm{C}\frac{{\mathrm{dV}}_{\mathrm{dc} }}{\mathrm{dt}}=\frac{{\mathrm{P}}_{\mathrm{MSC} }}{{\mathrm{V}}_{\mathrm{dc} }}-\frac{{\mathrm{P}}_{\mathrm{GSC} }}{{\mathrm{V}}_{\mathrm{dc} }}$$

(13)

$${\mathrm{V}}_{\mathrm{gd}}{}^{*}={ \mathrm{V}}_{\mathrm{id}}-{\mathrm{R}}_{\mathrm{g}}{ \mathrm{I}}_{\mathrm{gd}}-{ \mathrm{L}}_{\mathrm{g}} \frac{\mathrm{d}}{\mathrm{dt}}{ \mathrm{I}}_{\mathrm{gd}}-{\mathrm{L}}_{\mathrm{g}}{\mathsf{\omega }}_{\mathrm{e}}{ \mathrm{I}}_{\mathrm{gq}}$$

(14)

$${\mathrm{V}}_{\mathrm{gq}}{}^{*}={ \mathrm{V}}_{\mathrm{iq}}-{\mathrm{R}}_{\mathrm{g}}{ \mathrm{I}}_{\mathrm{gq}}-{ \mathrm{L}}_{\mathrm{g}} \frac{\mathrm{d}}{\mathrm{dt}}{ \mathrm{I}}_{\mathrm{gq}}-{\mathrm{L}}_{\mathrm{g}}{\mathsf{\omega }}_{\mathrm{e}}{ \mathrm{I}}_{\mathrm{gq}}$$

(15)

$${\mathrm{P}}_{\mathrm{g}}=\frac{3}{2}{\mathrm{V}}_{\mathrm{gd} }{\mathrm{I}}_{\mathrm{gd}}$$

(16)

$${\mathrm{Q}}_{\mathrm{g}}=\frac{3}{2}{\mathrm{V}}_{\mathrm{gd} }{\mathrm{I}}_{\mathrm{gq}}$$

(17)

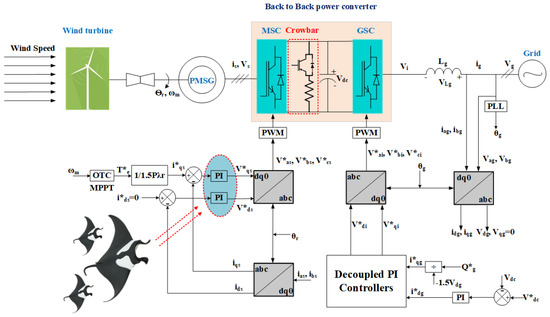
Figure 4. PMSWG with its proposed control system.

Equations (16) and (17) indicate that ${\mathrm{P}}_{\mathrm{g}}$ and ${\mathrm{Q}}_{\mathrm{g}}$ are controlled by controlling ${\mathrm{I}}_{\mathrm{gd}}$ and ${\mathrm{I}}_{\mathrm{gq}}$ currents, respectively. To transfer all of the ${\mathrm{P}}_{\mathrm{g}}$ generated from the wind turbine, DC-bus voltage must be constant, according to Equation (13). ${\mathrm{P}}_{\mathrm{GSC} }$ and ${\mathrm{P}}_{\mathrm{MSC} }$ are the active power to the grid and from the WG, respectively.

2.2. Modeling of the DFIWG

The DFIWG is represented through a fifth-order model [30,61]. This model consists of four electrical differential equations (two equations for both the stator and rotor voltages). The electrical equations, expressed in the direct-quadrature (dq) reference frame rotating at synchronous speed $\left({\mathsf{\omega }}_{\mathrm{S}}\right)$, are given by Equations (18)–(26). The DFIWG with its proposed control configuration is depicted in Figure 5.

$$V_{ds}=R_S I_{ds}-\frac{d{\psi }_{ds}}{dt}-{\omega }_S {\psi }_{qs}$$

(18)

$$V_{qs}=R_S I_{qs}+\frac{d{\psi }_{qs}}{dt}+{\omega }_S {\psi }_{ds}$$

(19)

$$V_{dr}=R_r I_{dr}+\frac{d{\psi }_{dr}}{dt}-\left({\omega }_S-{\omega }_r\right){\psi }_{qr}$$

(20)

$$V_{qr}=R_r I_{qr}+\frac{d{\psi }_{qr}}{dt}+\left({\omega }_S-{\omega }_r\right) {\psi }_{dr}$$

(21)

$${\psi }_{ds}=L_s I_{ds}+L_m I_{dr}$$

(22)

$${\psi }_{qs}=L_s I_{qs}+L_m I_{qs}$$

(23)

$${\psi }_{dr}=L_r I_{dr}+L_m I_{dr}$$

(24)

$${\psi }_{qr}=L_r I_{qr}+L_m I_{qs}$$

(25)

$$T_e=\frac{3}{2} P \left({\psi }_{ds} I_{qs}-{\psi }_{qs} I_{ds}\right)$$

(26)

where V denotes voltage, $\psi$ represents magnetic flux, R denotes resistance, I denotes current, L denotes inductance, the index m denotes magnetization, ${\mathrm{T}}_{\mathrm{e}}$ is the electromagnetic torque of the generator, P is number of pole pairs, and indexes s and r refer to stator and rotor, respectively.

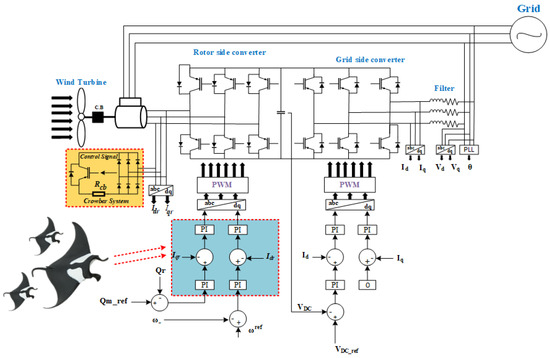
Figure 5. DFIWG with its proposed control system.

2.3. Development and Failure Ratio of Wind-Driven Power Generators

The failure ratio in WG components is shown in Figure 6 [62,63,64]. PAC systems and power converters represent a high ratio of failure for these components, and this is due to the mechanical stress that happens due to the nature of wind speed and faults, where faults lead to an increase in the speed of WG. Thus, protection topologies have great importance, and aid in decreasing the failure ratio [60,65,66]. Manufacturers and technologies for the top five WTs are shown in Table 3. From this table, it can be deduced that the PMSWG and DFIWG are produced by dominant manufacturing companies. With the fastest growth rate in WE between 2009–2018, full-scale power converter WGs, such as the PMSWG, have become dominant in the WE market. Table 4 indicates the top ten biggest turbines [8,9].

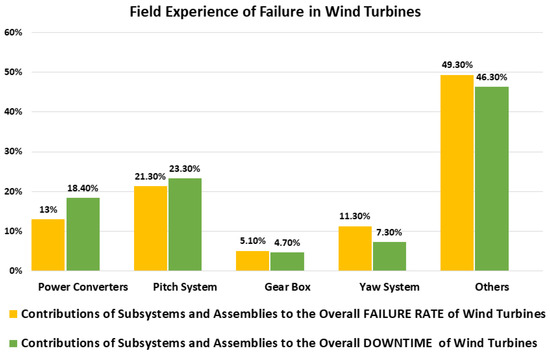
Figure 6. Failure in WE system components.

Table 3. Top 5 WT manufacturers and technologies.

Manufacturer	Concept	Rotor Diameter (m)	Power Range (MW)
Vestas (Denmark)	DFIG	90–120	2.0–2.2
	PMSG	105–162	3.4–9.5
Siemens Gamesa (Spain)	SCIG	154–167	6.0–8.0
	DFIG	120–142	3.5–4.3
	PMSG	114–145	2.1–4.5
Gold wind (China)	PMSG	-	2.0–6.0
GE (USA)	DFIG	116–158	2.0–5.0
	PMSG	150	6.0
Enercon (Germany)	WRSG	82–138	2.0–4.2

Table 4. Top 10 biggest WTs.

Manufacturer	Power Rating (MW)	Rotor Diameter (m)	Drive Train	IEC Class
MHI Vestas	9.5	164	Medium-speed geared	S
Siemens Gamesa	8	167	Direct drive	S (IB)
Gold wind	6.7	154	PM direct drive	I
Senvion	6.15	152	High-speed geared	S
GE	6	150	Direct drive	IB
Ming Yang	6	140	Medium-speed geared	IIB
Doosan	5.5	140	High-speed geared	I
Hitachi	5.2	126–136	Medium-speed geared	S
Nbjj	5	151	High-speed geared	IIB
Adwen	5	135	Low-speed geared	IA

3. MRFO Algorithm

(a) 

MRFO mathematical model

A novel meta-heuristic technique called MRFO is motivated by the smart and strategic behavior of manta rays (MRs) when they are looking for prey. It has already been demonstrated that using this approach to solve engineering challenges yields remarkably positive outcomes. Chain foraging, cyclone foraging, and somersault foraging are the three processes that the MRFO mimics in the MR eating technique, as depicted in Figure 7 [67,68,69].

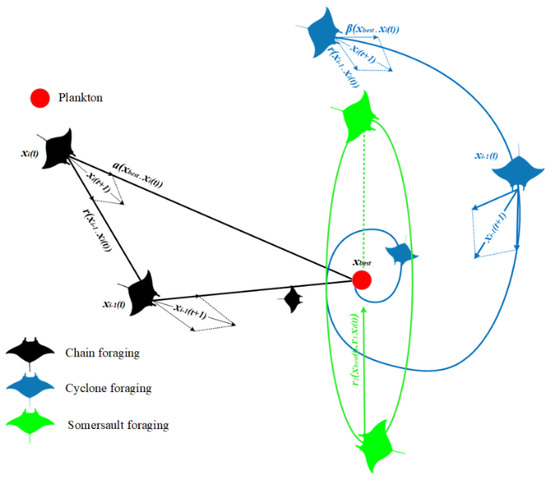
Figure 7. MRFO strategy.

Step 1: chain foraging

MRs move in a foraging chain by swimming together to an area with more plankton. The other MRs track the first as it goes toward the meal, each moving in the same direction as the first. At every time point, an MR adjusts its place with the best option that is open to both it and the one in front of it. Equation (27) provides the mathematical formulation of this circumstance [68,69].

$$X_i{}^d\left(t+1\right)=\left\{\begin{array}{c}{X}_i{}^d\left(t\right)+(X_{best}{}^d\left(t\right)-X_i{}^d\left(t\right)) \left(r+\alpha \right) if i=1\\ X_i{}^d\left(t\right)+r\left(X_{i-1}{}^d\left(t\right)-X_i{}^d\left(t\right)\right)+\alpha (X_{best}{}^d\left(t\right)-X_i{}^d\left(t\right)) else\end{array}\right\}$$

(27)

where $X_i{}^d\left(t\right)$ and $X_{best}{}^d\left(t\right)$ are the place of the ith individual and the finest solution, respectively, in the t iteration. The random vector (r) ranges from [0–1]. The weighting coefficient (α) is presented in Equation (28).

$$\alpha =2r{\left|\log \left(r\right)\right|}^{0.5}$$

(28)

Step 2: cyclone foraging

Each MR in the second step tracks the one next to it while also pursuing the meal by spinning its body around. The scenario’s model is provided in Equation (29) [67].

$$\begin{array}{c}{X}_i\left(t+1\right)=X_{best}+r\left(X_{i-1}\left(t\right)-X_i\left(t\right)\right)+e^{bw}\cos \left(2\pi \omega \right)\left(X_{best}-X_i\left(t\right)\right)\\ Y_i\left(t+1\right)=Y_{best}+r\left(Y_{i-1}\left(t\right)-Y_i\left(t\right)\right)+e^{bw}\sin \left(2\pi \omega \right)\left(Y_{best}-Y_i\left(t\right)\right)\end{array}$$

(29)

where $\omega$ is a random number ranging from [0,1]. If the motions made by MRs are enlarged in the d space, its model can be written as in Equation (30).

$$X_i{}^d\left(t+1\right)=\left\{\begin{array}{c}(X_{best}{}^d\left(t\right)+(X_{best}{}^d\left(t\right)-X_i{}^d\left(t\right)) \left(r+\beta \right) if i=1\\ (X_{best}{}^d\left(t\right)+r\left(X_{i-1}{}^d\left(t\right)-X_i{}^d\left(t\right)\right)+\beta (X_{best}{}^d\left(t\right)-X_i{}^d\left(t\right)) else\end{array}\right\}$$

(30)

where β denotes the weighting factor, as seen in Equation (31).

$$\beta =2e^{\frac{r_1\left(T-t+1\right)}{T} sin\left(2\pi r_1\right)}$$

(31)

In this case, T stands for the total number of iterations, and r₁ is a random number between [0, 1]. At this point, the MRs leave the area and assume new places, aiding in the search method. Consequently, a thorough global investigation is carried out. The following is the plot’s mathematical formula [67,69].

$$X_{rand}{}^d=L{b}^d+r\left(U{b}^d-L{b}^d\right)$$

(32)

$$\begin{array}{l}{X}_i{}^d\left(t+1\right)\\ =\left\{\begin{array}{c}(X_{rand}{}^d\left(t\right)+(X_{rand}{}^d\left(t\right)-X_i{}^d\left(t\right)) \left(r+\beta \right) if i=1\\ (X_{rand}{}^d\left(t\right)+r\left(X_{i-1}{}^d\left(t\right)-X_i{}^d\left(t\right)\right)+\beta (X_{rand}{}^d\left(t\right)-X_i{}^d\left(t\right)) else\end{array}\right\}\end{array}$$

(33)

where $X_{rand}{}^d$ is an arbitrary number in the search planetary. The $L{b}^d$ and $U{b}^d$ are the upper and lower limits of the d^th dimension, respectively.

Step 3: somersault foraging

The third step is where the meal is noticed as the key element. Each MR now usually swims back and forth to the center, changing positions. As a result, each MR’s location is constantly changed to be at the ideal location. This group’s model is described in Equation (34).

$$X_i{}^d\left(t+1\right)=X_i{}^d\left(t\right)+S\left(r_2 X_{best}{}^d\left(t\right)-r_3{X}_i{}^d\left(t\right)\right)$$

(34)

where S refers to the MR somersault factor value, and r₂ and r₃ are two randomly selected values between [0, 1]. Each MR can therefore go to any position between their current location and the search space. As a result, the change in individuals’ present positions becomes increasingly smaller as they eventually get closer to the ideal answer. The actions taken are shown in Figure 8.

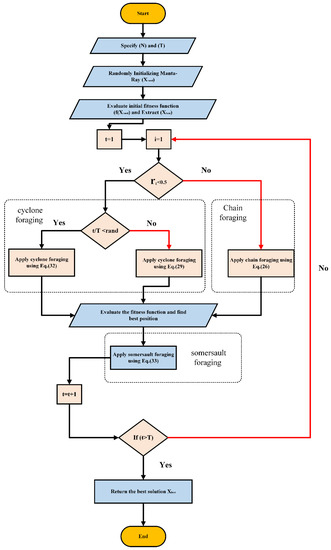
Figure 8. MRFO flowchart.

(b) 

Application of MRFO

MRFO is applied on the machine side controllers of the PMSWG and DFIWG to fine-tune the PI controllers’ gains. This tuning is performed to improve the dynamic performance of the investigated systems during normal and abnormal conditions. The optimization of the systems under study (taking control cost (CC) into account) can be formally represented in Equation (35). Table 5 and Table 6 list the findings of controller gain calculations based on the MRFO approach. Furthermore, the other controller system gains used in grid-side controllers are presented in these tables. The objective function for CC that is employed is written as follows: Minimize F(x)

$$\begin{gathered} =\underset{0}{\overset{T}{{\displaystyle \int }}}{W}_1\left|P-P^{*}\right|+W_2\left|{\omega }_m-{\omega }^{*}{}_m\right|+W_3\left|Q_s-Q^{*}{}_s\right|+W_4\left|V_{dc}-V^{*}{}_{dc}\right| \\ +W_5\left|C_P-C^{*}{}_P\right| \end{gathered}$$

(35)

where W₁, W₂, W₃, W₄, and W₅ are constants used for the estimation of the CS function, which is 4 × 10⁵ here. T denotes the average time and 100 and 6 are the number of iterations and agents, respectively.

Table 5. Data of converter controller for PMSWG.

Technique	Optimized MSC Controller Gains		GSC Controller Gains
	Gain	Value	Gain	Value
MRFO	Kp1	2.8971	Kp3	0.83
	Ki1	199.7842	Ki3	5
	Kp2	2.8971	Kp4	8
	Ki2	199.7842	Ki4	400
	-	-	Kp5	0.83
	-	-	Ki5	5

Table 6. Converter controller data for DFIWG.

Technique	Optimized RSC Controller Gains						GSC Gains
	Voltage Regulator		Torque Regulator		Voltage Regulators		Voltage Regulator		Torque Regulator		Voltage Regulators
MRFO	Kp = 7.9712	Ki = 0.0319	Kp = 2.7839	Ki = 0.0937	Kp = 0.2981	Ki = 97.278	Kp = 3	Ki = 0.02	Kp = 8	Ki = 500	Kp = 1.2	Ki = 5

4. Crowbar Control System for Improving FRT Capability

Faults on the grid have an adverse effect on the dynamic performance of WGs. These faults lead to generator speed-ups, oscillations in electromagnetic torque, overcurrents, overvoltages at the DC link, and reduction of the output P from the VSWG [25,30]. Power electronic converters are exposed to damage due to current limitations of the converters, and these converters are the highest cost of the system; thus, hardware and software solutions have been implemented by researchers to protect the VSWGs from all mentioned bad results. Reliability/security of supply, efficiency, cost, volume, protection, control of P and Q power electronics-enabling technology, and ride-through operation are the important issues for the converters used in WECS [70].

A braking chopper/crowbar is chosen as a hardware solution to successfully protect the DC capacitor from overvoltages by dissipating the surplus energy during abnormal conditions. It has been inserted with the PMSWG to enhance its dynamic performance during grid faults, as seen in Figure 4. It is only inserted during voltage sag [31]. An active crowbar is used to protect the RSC of the DFIWG and improve its dynamic behavior during grid faults, as depicted in Figure 5. Utilizing a crowbar allows the DFIWG to ride through the fault and continue the power supply, even during grid faults. The optimized values of K_p and K_i are 0.06993 for the PMSWG. The optimized values of K_p and K_i are 0.05417 for the DFIWG. The monitored and referenced values are the controller’s inputs, and the controller’s output determines how to operate the system while taking into account the sawtooth signal. The proposed control strategy of the crowbar for both investigated VSWGs is depicted in Figure 9. Hence, a comparison between different hardware protection apparatuses used for FRT enhancement based on cost is shown in Table 7 [29]. A comparison of FRT strategies of different crowbar protection circuits is shown in Table 8 [27].

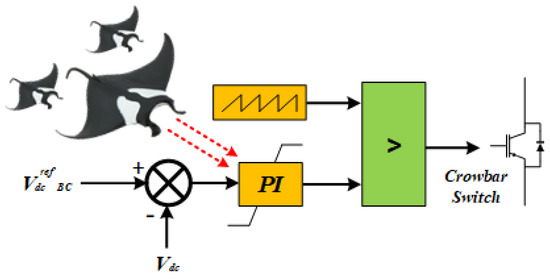
Figure 9. Control of crowbar system based on MRFO.

Table 7. Comparison of different hardware systems used for FRT enhancement based on cost.

Hardware Protection Device	Price (US$)
Classical DVR	67,229.99
Low-cost DVR	36,778.79
STATCOM	200,000.00
Conventional crowbar	5.00–75.00
Active crowbar	85.00

Table 8. Comparison of FRT strategies of different protection circuits for DFIWG.

Protection Scheme	Rotor Current Limit (pu)	Status of RSC	${\mathit{V}}_{\mathit{D}\mathit{C}}$ Limit (pu)	Remarks
Crowbar circuit with resistances only	<2.4	Blocked	<1.25	Useful for symmetrical faults only
Crowbar with DVR	<2.0	Partly maintained	<1.25	Useful for all fault types
Crowbar with chopper	<2.4	Blocked	<1.25	Useful for all fault types
Crowbar with R–L	<2.4	Partly maintained	<1.25	Useful for all fault types
ACB_P	<2.0	Partly maintained	<1.08	Useful for all fault types

5. Simulation Results and Discussion

Simulation for the investigated WGs is carried out by using MATLAB/Simulink to verify the aforementioned analysis and the effectiveness of proposed schemes which are PAC and OTC. Models’ solutions are tested on a detailed model and in MW class-based WECS. The point of common coupling (POCC) is a significant point in which a bolted fault occurs to evaluate FRT capability. To validate the simulation models, the crowbar parameters are listed in Table 9 [29] and the PMSWG and DFIWG data are listed in Table 10 [13,27]. Furthermore, the impact of the inertia of the dynamic systems is deliberated on in the Appendix A.

Table 9. Crowbar resistance parameters.

Resistance	1.5 Ω
Rated power	12 kW
Maximum temperature	150 °C
Thermal time constant	4 min
Weight	30 kg
Dimensions	(750.330.150) mm

Table 10. Simulated WG data.

PMSWG Parameters	Value	DFIWG Parameters	Value
Rated power	1.5 MW	Rated power	1.5 MW
Rated stator voltage	575 V	Rated stator voltage	575 V
Rated frequency	60 Hz	Rated frequency	60 Hz
DC-link voltage	1150 V	DC-link voltage	1150 V
Pole pairs	40	Pole pairs	3
Generator inductance in the d frame	0.7 pu	Stator resistance	0.023 pu
Generator inductance in the q frame	0.7 pu	Rotor leakage inductance	0.16 pu
Generator stator resistance	0.01 pu	Mutual inductance	2.9 pu
A flux of the permanent magnets	0.9 pu	Stator leakage inductance	0.18 pu
Line inductance	0.3 pu	Rotor resistance	0.016 pu
Line resistance	0.003 pu	Inertia constant	0.685 pu

5.1. Impact of Wind Speed Variation under Regular Grid Conditions

The studied system is illustrated in Figure 4, where the wind speed profile is applied to two worst case scenarios. In the former, a lower wind speed is applied to verify the system in extracting MPPT, and in the other case, the system is exposed to wind gusts to verify the effectiveness of PAC, as depicted in Figure 10a. If the PA equals zero, this signifies MPPT realization; if it is bigger than zero, this means the WG does not operate at MPPT to prevent the WT from wind gusts that may cause a failure in the system components. Figure 10b,c show both $\lambda$ and $C_{\mathrm{p}},$ where they quickly track the wind speed profile and achieve optimal values, respectively. $C_{\mathrm{p}} \mathrm{is}$ affected by the step change in wind speed that is due to changes in $\lambda$ and the earliest operator change, according to Equation (4). Figure 10d depicts the PAC response where the PA increases to reach 2.974⁰. Figure 10e,f display the changes in both ${\mathrm{T}}_{\mathrm{e}}$ and ${\omega }_r$ as a result of wind speed changes, respectively. Figure 10g depicts the injected P and Q to the grid as a result of wind speed changes. The Q is kept at zero because the system operates at unity power factor (UPF). Equations (1), (13), (14), and (15) give a strong explanation for ${\mathrm{T}}_{\mathrm{e}}$, ${\omega }_r$, and the P and Q responses, respectively. Figure 10h depicts that the $V_{DC}$ is constant, indicating that all generated power is transferred into the grid. Oscillations that occur in the simulated parameters are very small and indicate the success of PAC and OTC in the presence of MRFO-PI controllers.

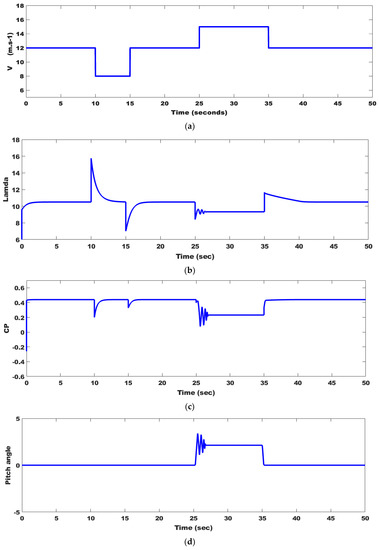
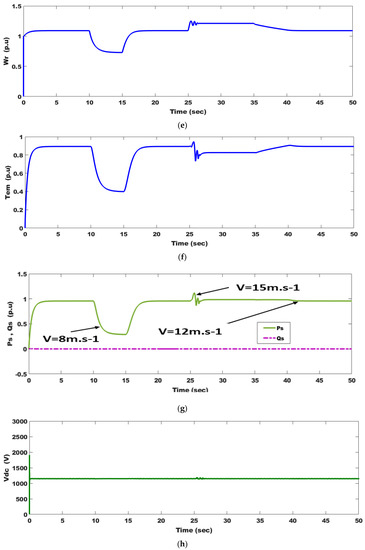
Figure 10. PMSWG system parameter responses as a result of wind speed changes: (a) wind speed profile; (b) tip speed ratio; (c) power coefficient; (d) pitch angle; (e) angular speed; (f) electromagnetic torque; (g) injected active and reactive power to the grid; and (h) DC-link capacitor voltage.

5.2. Realization of FRT under 85% Voltage Dip

Transient response enhancement during and after clearing the fault becomes a crucial requirement for new grid codes. The fault is assumed to occur at 3 s and cleared at 3.15 s in the grid voltage, as seen in Figure 11a, and wind speed is constant at 12 m·s⁻¹. During the fault period, both P and ${\mathrm{T}}_{\mathrm{e}}$ decrease, as seen in Figure 11c,f, respectively, but an increase occurs in I, Q, $V_{DC}$, and ${\omega }_r,$ as seen in Figure 11b,d,e,g, respectively, because of this voltage dip. The braking chopper gets rid of surplus power by dissipating it in the form of thermal power to keep $V_{DC}$ in the whole rated range. The proposed technique is successful in this issue where the overshoot of P, oscillations in ${\omega }_r$, and all parameters are damped. Injection of Q after clearing the fault and the PMSWG maintaining grid connection shows FRT capability realization.

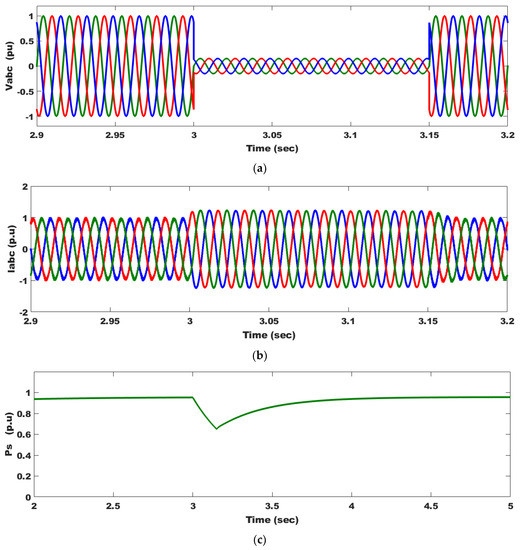
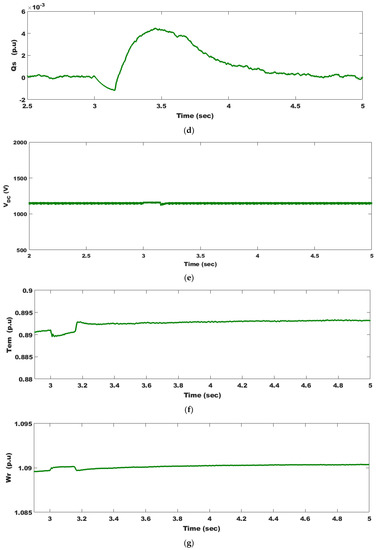
Figure 11. PMSG system parameter responses as a result of an 85% voltage dip: (a) system voltage; (b) system currents; (c) injected active power to the grid; (d) injected reactive power to the grid; (e) DC-link voltage; (f) electromagnetic torque; and (g) angular speed.

5.3. Impact of Wind Speed Variation under Regular Grid Conditions

The investigated wind system is shown in Figure 5. Figure 12a shows the variations in the studied wind speed profile. Both $\lambda$ and $C_{\mathrm{p}}$ are depicted in Figure 12b,c, respectively, and they quickly track the wind speed profile and achieve their desired values. In response to a step change in wind speed, $C_{\mathrm{p}}$ is impacted by $\lambda$. Figure 12d depicts the PAC response where the PA increases to reach 9.874⁰. The PAC successfully prevents the DFIWG from overwinding speeds by increasing PA from when PA is larger than zero. The parameters $\mathsf{\lambda }$ and $C_{\mathrm{p}}$ decrease to reduce output power until this gust disappears to keep the WT working. Figure 12e,f display the changes in both ${\mathrm{T}}_{\mathrm{e}}$ and ${\omega }_r$ as a result of wind speed changes, respectively. P and Q are shown in Figure 12g as a function of changing wind speeds. Due to the UPF operation, Q is maintained at zero. The unchanging $V_{DC}$ in Figure 12h implies that all produced electricity is transmitted to the power grid. Very minor oscillations in the simulated parameters show the effectiveness of PAC and OTC in the presence of MRFO-PI controllers. The findings of the simulation indicate that the DFIWG has more variability than the PMSWG.

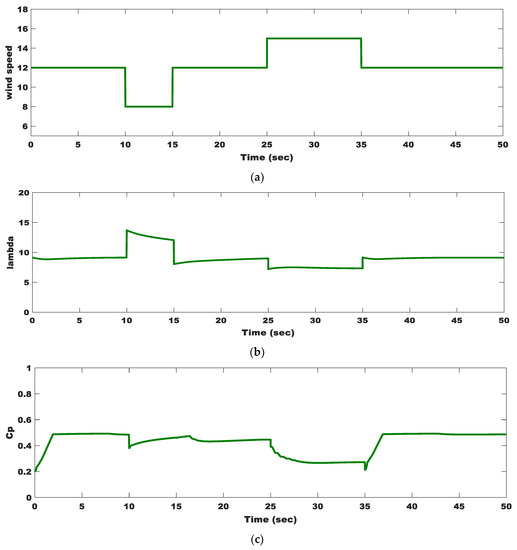
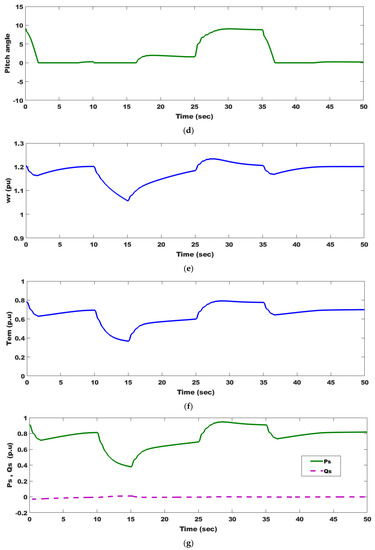
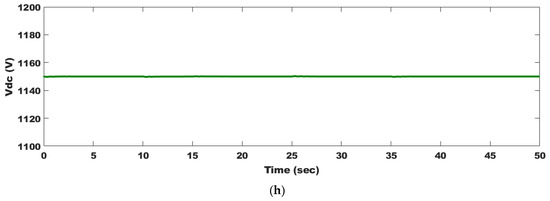
Figure 12. DFIWG system parameter responses as a result of wind speed changes: (a) wind speed profile; (b) tip speed ratio; (c) power coefficient; (d) pitch angle; (e) angular speed; (f) electromagnetic torque; (g) delivered active and reactive powers to the grid; and (h) DC-link voltage.

5.4. Realization of FRT at 85% Voltage Dip

The performance of the DFIWG with a proposed active crowbar and optimized controllers under an 85% voltage dip on the grid, as seen in Figure 13a, is evaluated in this section. The duration of the fault period is assumed to be 150 ms, according to the worst case in new grid codes, to test the efficacy of the proposed schemes. During the fault, both P and ${\mathrm{T}}_{\mathrm{e}}$ decrease, as seen in Figure 13c,f, but an increase occurs in I, Q, $V_{DC}$, and ${\mathsf{\omega }}_{\mathrm{r}},$ as seen in Figure 13b,d,e,g, respectively, because of the drop in the grid voltage. In order to keep $V_{DC}$ within the specified range, the braking chopper dissipates excess power as thermal energy, as seen in Figure 13e. The suggested method works well in this case, where all parameters, including oscillations in ${\omega }_r$ and overshoot of P, are damped. When Q is injected after a fault has been repaired and the DFIWG is still tied to the grid, FRT capability is achieved. The observed simulated results show that the DFIWG continues to operate appropriately, even in the face of serious failures. All the studied systems’ parameter fluctuations for the cases under study are summarized and listed in Table 11.

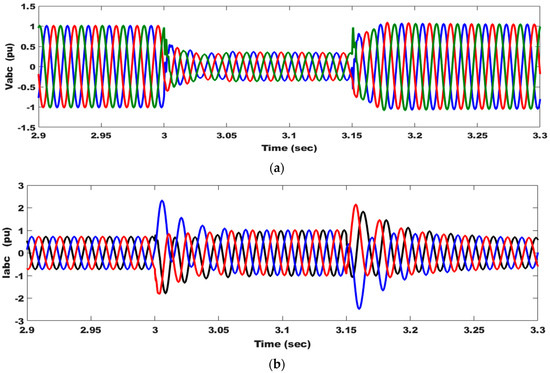
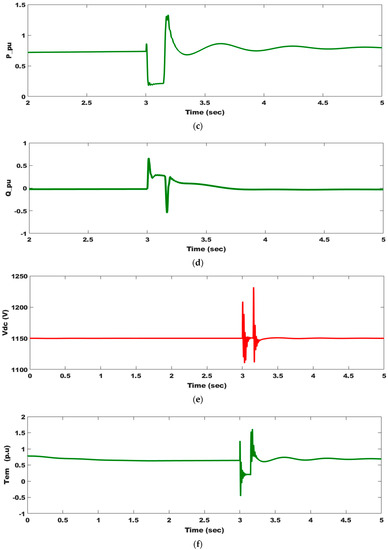
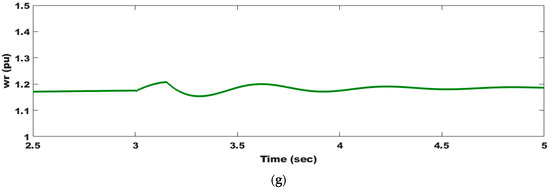
Figure 13. DFIWG system parameter responses as a result of 85% voltage dip: (a) system voltage; (b) system current; (c) supplied active power to the grid; (d) supplied reactive power to the grid; (e) DC-link voltage; (f) electromagnetic torque; and (g) angular speed.

Table 11. All investigated systems’ parameter changes for the scenarios under study.

Studied Cases	Parameters
	DFIWG	PMSWG
Wind speed scenario	$C_p$ change (0.2 $\to$ 0.48) $V_{DC}$ ripple (±14 V) $\mathsf{\lambda }$ change (8.7 $\to$ 12.9) P change (0.3 $\to$ 0.97) $T_e$ change (0.3 $\to$ 0.8) ${\omega }_r$ change (1.03 $\to$ 1.24)	$C_p$ change (0.18 $\to$ 0.44) $V_{DC}$ ripple (±9 V) $\mathsf{\lambda }$ change (7 $\to$ 16) P change (0.27 $\to$ 1.03) $T_e$ change (0.28 $\to$ 0.93) ${\omega }_r$ change (0.72 $\to$ 1.19)
Voltage dip scenario	Overvoltage at $V_{DC}$ 1.0783 pu P change ≈ (0.17 $\to$ 1.28) $T_e$ change ≈ (−0.53 $\to$ 1.63) ${\omega }_r$ change ≈ (1.15 $\to$ 1.22) Q change ≈ (−0.54 $\to$ 0.61) I change (−2.27 $\to$ 2.27)	Overvoltage at $V_{DC}$ 1.0584 pu P change ≈ (0.64 $\to$ 0.965) $T_e$ change ≈ (0.889 $\to$ 0.894) ${\omega }_r$ change ≈ (1.087 $\to$ 1.095) Q change ≈ (−0.001 $\to$ 0.005) I change (−1.2$\to$ 1.2)

6. Conclusions

We investigated the dynamic performances of the DFIWG and PMSWG with MRFO support during wind speed fluctuations (8–15 $\uparrow \downarrow$) and an 85% grid voltage decrease while taking advantage of MPPT, PAC, and FRT capability. MRFO-based wind side controllers and a chopper controller was designed and implemented for the optimum performance of both the PMSWG and DFIWG. The DFIWG’s performance during regular grid and transient operation was significantly enhanced and the $V_{DC}$ was maintained below the permitted limits when using optimized controllers. Simulated results of the DFIWG’s system parameters showed that the system successfully operated at MPPT and PAC regions and realized an enhanced FRT capability. When the PMSWG operated with optimized controllers, its performance during normal grid and transient operation was greatly improved and the $V_{DC}$ was kept below its allowable limits. Simulated results of the PMSWG’s system parameters showed that the system successfully operated at MPPT and PAC regions and realized an enhanced FRT capability. With the proposed control schemes, the obtained results indicate that:

• Both WGs are able to function in the PAC zone, have FRT capabilities, and have optimized controllers, all of which have a significant impact on how well they perform in the instances under study.
• The FRT issues may be made easier with an appropriate choice of controller gains based on the WT design. Compared with the majority of current FRT methods for WTs, this may be a more affordable method without taking external circuitry into account.
• Blocking of converters for the DFIWG was eliminated with the proposed technique, which is the main problem for DFIWGs.
• The change in the parameters of the studied wind systems was evident due to the violent change in wind speed and three-phase fault. The change was smaller in the PMSWG in the case of wind speed because it contained more poles; the change was smaller in the case of the fault due to the direct connection of the DFIWG to the network. Table 11 summarizes all the events and changes in parameters.
• The simulation results showed that the PMSWG was able to track the reference wind speed faster than the DFIWG, where the settling time for C_P was found to be 0.784 s with the PMSWG compared with 1.248 s with the DFIWG.
• The results showed that, with the prosed schemes, the $V_{DC}$ was below limits (1.02 under regular conditions and below 1.1 pu under faults).
• A small oscillation in the PMSWG, compared with the DFIWG, reveals that it has more power-smoothing capability.
• The simulation results showed the superiority of the PMSWG over the DFIWG, especially in the event of large disturbances due to the latter’s direct connection to the grid.