Dread Disease and Cause-Specific Mortality: Exploring New Forms of Insured Loans

Abstract

The relevance of critical illness coverage and life insurance in cause-specific mortality conditions is increasing in many industrialized countries. Specific conditions on the illness and on death event, providing cheapest premiums for the insureds and lower obligations for the insurers, constitute interesting products in an insurance market looking to offer appealing products. On the other hand, the systematic improvement in longevity gives rise to a market with agents getting increasingly older, and the insurer pays attention to this trend. There are financial contracts joined with insurance coverage, and this particularly happens in the case of the so-called insured loan. Insured loans are financial contracts often proposed together with a term life insurance in order to cover the lender and the heirs against the borrower’s death event within the loan duration. This paper explores new insurance products that, linked to an insured loan, are founded on specific illness hypotheses and/or cause-specific mortality. The aim is to value how much the insurance costs lighten with respect to the traditional term insurance. The authors project cause-specific mortality rates and specific diagnosis rates, in this last case overcoming the discontinuities in the data. The new contractual schemes are priced. Numerical applications also show, with several graphs, the rates projection procedure and plenty of tables report the premiums in the new proposed contractual forms. The complete amortization schedule closes the work.

1. Introduction

In many industrialized countries, the progressive ageing process of the population determines a significant incidence of diseases, which strongly increase with age. Today’s individuals are expected to live longer than previous generations, but some of these extra years of life may not necessarily be healthy. There are two outlooks of ageing and morbidity that contradict each other. The Morbidity Compression Hypothesis predicts that health problems will occur at higher ages, given a rectangularization of the health profiles (Schoder and Zweifel 2011). On the contrary, the Morbidity Expansion Hypothesis predicts the gradual medicalization of society as the longevity improves (Gruenberg 1977; Olshanksy et al. 1991; Doblhammer and Kytir 2001). The debate on the topic is ongoing. In either case, the morbidity phenomenon calls for deep consideration, particularly from the insurance perspective.

The financial impact of diseases due to costs for healthcare, rehabilitation, as well as temporary and permanent assistance has led to a variety of supplementary insurance for health in current health systems. Various classes of products have been developed by the insurance industry to specifically fulfil the needs of an ageing population facing health risks, and this insurance market sector is growing in many countries. While the insurance market moves towards an increasing segmentation, in order to get the competitive advantages deriving from a deep knowledge of the consumer, the general guidelines indicate to pay attention to the consumer’s protection and to the improvement of the quality of life. Policies like Critical Illness match these two aspects. In this sense, it is interesting to also consider coverage in case of specific cause of death, also in light of the increasing availability of data concerning these events.

Our focus is centered on the impact this subject has on financial contracts such as loans, in which a relevant role is held by the exposition to long-term biometric risks such as mortality and morbidity of the borrower. Both critical illness and disability insurance can reveal themselves as usefully inserted in the contractual structure of the insured loans; an example for all can be found in the Government of Canada (2017) webpage, in which Critical Illness Insurance and Disability Insurance are considered within credit or loans.

Generally, the loan contract, in its standard form, can concern the guarantee of the repayment provided by an insurance company in case of the borrower’s death during the loan duration due to any cause. The insured loan is protected against default in the sense that if default occurs, the insurance company will pay the lender what is owed. In this work, we propose more detailed coverage within the loan contract, lowering the pricing structure.

The European supervisory authorities’ attention is focused on topics connected to the socio-demographic dynamics, particularly when setting guidelines in designing insurance coverage at adult and old ages.

Already in 2013, the Basel Committee on Banking Supervision addressed Mortgage insurance issues, especially with regards to market structure and policy implementation (see Basel Committee on Banking Supervision 2013, p. 1), following the global financial crisis’ impact. It drew attention—among other things—to the need for a regulatory system able to ensure flexibility in the loan-to-value dimension (known in banking practices as LTV), coupled with effective and harmonious risk management, obtainable via targeted standards.

In the Basel Committee on Banking Supervision (2013), the Joint Forum essentially discussed about various risk elements, which, because of their impact on such contracts, can easily trigger “stress in the worst tail events”. It was from this perspective that the document proposed a series of recommendations for policymakers and supervisors.

Within the context of insured loans, the European Standardized Information Sheet (ESIS) grants borrowers information warranties, which ought to characterize their engagement with lenders. It must be pointed out, however, that several questions inherent to insurance policies, contractual transparency, or the interest of the various counterparts remain open. Addressing them is even more urgent if one is to tackle the connection with discrete mortality causes or diseases occurring during the contract’s duration.

In February 2017, the European Insurance and Occupational Authority (EIOPA) took upon itself the duty of addressing, among other things, financing constraints, “in view of removing barriers to investments in […] loans” (see EIOPA 2017). The results of these initiatives will be made available in 2018.

The potential increasing achievement of new products connected to the lengthening of human life, and in particular to its consequences in terms of critical illness and disability covers, is triggering a new push in the scientific research. Many are contributing to improving the insurer’s costs valuations in this field. Baione and Levantesi (2014) met the lack of data in critical illness presenting a parametric model for pricing health insurance, and Fellingham et al. (2015) proposed moving from parametric to non-parametric techniques for the cost estimation in healthcare, highlighting their higher flexibility. Hambel et al. (2017) deepened the reasons, inducing only a restrained appealing of long-term life insurance, pinpointing that the core of the question is the high costs of a policy revision in the event of a health shock. Pitacco (2016) pointed out that the analysis of the sensitiveness of the premium structure to the biometric bases is a useful tool in designing new long-term care policies. The growing flurry of topics referring to health and illness—specifically oriented towards pricing questions—seems to leave out the interesting flexibility of covers referred to the human health, in particular developing their practical potentiality inside popular financial contracts.

In this paper, we will focus on new products tailored to the specific profile of the insured in the terms discussed above, with the aim of protecting lenders and borrowers in the event a borrower ever stopped making payments for serious specific diseases or for specific mortality. The paper focuses on the insured loan product design when the borrower is a private person.

The aim of the paper is the pricing of the proposed products. The results will be considered within the insured loan amortization schedule, stressing the amount of the reduction in prices with respect to the standard insured loan contracts. The content of the paper can be also a useful tool for practitioners in the insured loan contract structuring process.

Note that the pricing procedure must be carefully handled. The structural breaks in the cause-specific mortality time series indicate the difficulty in predicting cause-specific mortality rates, as widely explained in Haberman and Villegas (2014). To perform this phase, the mortality rates must be adjusted and projected.

The paper is organized as follows. Section 2 introduces the mathematical structure of the main characteristics of the standard insured loan contract. Financial and actuarial details are analyzed. In Section 3 we design new insured loan contracts, “specialized” according to specific death cause or specific illness. Within this Section, the products are introduced and formally described. In Section 4, the procedure for fitting and projecting the cause-specific death rates is illustrated with figures, and the new products are priced. The results are illustrated in several tables and discussed in Section 4.2. Section 5 is an outlook on some new perspectives for going forward in the development of the research. In the Appendix A, we provide some results collected in tables and graphs concerning the empirical application.

2. Standard Insured Loan Contract

In the standard amortization method, the borrower refunds the lender, paying instalments at periodic intervals. Usually the amortization schedule spreads over a time interval large enough to consider the operation affected by the insolvency risk due to all the events related to the duration of the human life, whatever the age at issue of the borrower is. For these reasons, it is efficient to insert an insurance policy into the contract for covering the risk that the debtor dies before having completely extinguished the debt. Broadly speaking, if the borrower dies before the contract expiry, the insurer pays to the lender the outstanding loan balance evaluated at that time. The loan becomes an insured loan, and the insolvency risk due to the debtor’s eventual death is cut down.

In Coppola et al. (2009), a wide financial analysis of the insured loan is developed: formulas for single and periodic premiums, benefits, and reserves are provided within the cash flow analysis. In that paper, the authors deepen the risk analysis aspects, dwelling in particular on the Model Risk and the Mortality Risk (the first due to the randomness in the choice of the mortality rate set and the second due to the random deviations of deaths from the expected values), considering a pooling technique rather unfeasible in the specific matter at hand.

Following Coppola et al. (2009), supposing the borrower/insured’s debt is one monetary unit, we can write:

$${{\displaystyle \sum }}_{k=0}^{n-1}{P}_k{A}_{\overline{x:k}|}^1=1,$$

(1)

where $P_k$ is the instalments paid by the insured at the beginning of each year and $A_{\overline{x:k}|}^1$ (Bowers et al. 1997) is the actuarial present value of a k-year pure endowment of 1 monetary unit paid in case of life by an insured aged $x$, given by the following expression:

$$A_{\overline{x:k}|}^1=v\left(0,k\right){}_k{p}_x.$$

(2)

In Formula (2), ${}_k{p}_x$ is the survival probability of an insured aged $x$ at inception to be alive at time $k$, and $v\left(o,k\right)$ is the value in t = 0 of 1 at time k. The annual anticipated payments $P_k$ include the principal repaid $C_k$, the interest paid $I_k$ on the outstanding balance $D_{k-1}$ valued at time $k-1$, the actuarial premium covering the outstanding loan balance at the beginning of each year, if the death occurs before the expiration date. That circumstance implies a temporal misalignment between the premium payments and the debt repayments.

The following subsection is concerned with the financial structure of $P_k$, observing that the actuarial premium and the loan instalment can be paid together to one counterparty (i.e., a bank) or separately to the lender and to an Insurance Company. These two circumstances will not have any consequence on the financial cash flows we are going to describe. The financial description will be developed in a deterministic environment, even if the stochastic approach for depicting the evolution in time of the interest rate curve could be easily implemented within a numerical application.

Insured Loan: Installment and Actuarial Premium Analysis

Let us consider that the borrower (aged $x$) will repay 1 monetary unit to the lender in $n$ years by means of $n$ constant instalments paid at the end of each year, at a given fixed annual rate of interest $i$ or a variable one $i_h$. For simplicity, we will present the payment components in the fixed rate hypotheses. The constant annual payment amount $R_h=R$ ($h=1,2,\dots ,n$) and the outstanding loan balance $D_h$ valued at the end of year $h$ are, respectively:

$$R_h=R=\frac{1}{a_{\overline{n|}}}{D}_h=\frac{a_{\overline{n-h|}}}{a_{\overline{n|}}},$$

(3)

with $a_{\overline{n|}}$, as usual, being the present value of a periodic (annual) constant unitary income at the end of each period for $n$ periods, at a fixed periodic interest rate. By means of the insurance component, if the borrower dies during the contract duration, the insurer will repay to the lender the obligations still due by the borrower at that time. We will assume that this payment will be done at the end of the year in which the eventual death occurs. If the death event happens at time $t$, $h-1<t\le h$, what is due to the lender consists of the outstanding balance at time $h-1$ plus the annual interest on this sum. The value $B_h$ of the benefit payable at time $h$ if the insured-borrower aged x at issue dies during the h-th year and the probability of this event are, respectively (cf. Coppola et al. 2009):

$${\mathrm{B}}_{\mathrm{h}}=\frac{1}{a_{\overline{n|}}}{\ddot{a}}_{\overline{n-h+1|}}{}_{\mathrm{h}-1/1}{\mathrm{q}}_{\mathrm{x}},$$

(4)

where ${\ddot{a}}_{\overline{n-h+1|}}$ refers to the anticipated case.

The constant actuarial premium which the borrower/insured pays at the beginning of the first m years ($0<m\le n,0\le h<m-1)$ if alive, is given by:

$${}_{/\mathrm{m}}{\mathrm{P}}_{\mathrm{x},\mathrm{h}}={}_{/\mathrm{m}}{\mathrm{P}}_{\mathrm{x}}=\frac{1}{a_{\overline{n|}}}{}_{/\mathrm{m}}{\mathsf{\pi }}_{\mathrm{x}},$$

(5)

in which:

$${}_{/\mathrm{m}}{\mathsf{\pi }}_{\mathrm{x}}=\frac{1}{{\ddot{a}}_{\overline{x,m|}}}{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{n}-1}{}_{j/}{a}_{\overline{n-j|}}{}_{\mathrm{j}/1}{\mathrm{q}}_{\mathrm{x}}.$$

If $k_x$ is the curtate future lifetime of the insured aged $x$ at issue, in the case of anticipated constant annual payments, the flow $X_h$ at the beginning of year $h$ is given by the following scheme:

$$X_h=\{\begin{array}{ccc}-{}_{/m}{P}_{x,h}& k_x\ge h& 0\le h\le m-1\\ 0& k_x\ge h& h\ge m\\ \frac{1}{a_{\overline{n|}}}{\ddot{a}}_{\overline{n-h+1|}}& h-1\le k_x<h& 1\le h\le n\end{array},$$

(6)

with $h=0,1,\dots ,n;P_n=0.$

3. Cause of Death and Diagnosis Event: Impact on Loan Repayment

The cost of funding health care for the elderly is continuously growing due to the increasing life expectancy. The topic is studied here within the insured loan financial structure.

There are two basic points which we will develop:

(1)

if a critical illness is diagnosed, the affected individual could be unable to completely or partially perform the engagements in his working activity, and in the specific case of the onset during the loan duration, this could involve the inability to fulfil the obligation as expected. In the basic critical illness insurance (cf. Haberman and Pitacco 1998), the insurer pays a lump sum upon the occurrence or diagnosis of the pre-specified dread diseases. Typically, the contractual options within the critical illness general scheme are the Stand Alone and the Accelerated. The first covers the insured just in case of diagnosis of illnesses, while the second guarantees payments in case of illness and in case of death.

(2)

within the traditional insured loan contract (setting the coverage in case of the borrower’s death), we will study the case of a death-specific cause. In the basic n-year term insurance, insertable in the loan amortization process, the insurer pays the benefit if the insurer dies within the n (or h ≤ n) years of the loan duration, with no specifications about the death cause. In the following, the n-year term insurance will be studied with regard to a specific death cause.

Both cases appear tailor-made contractual forms providing lower costs for the insured and the insurer. Our idea is to propose an insured loan form in which the insurance coverage involves critical illness diagnosis and/or cause-specific death.

This paper focuses on insured loans in which such cause-specific insurance products are included, in order to explore new scenarios tending to personalize the loan contractual forms.

The aim of the analysis will be the pricing of the actuarial insurance coverage we propose and next the drawing up of the amortization schedule in which the annual instalment includes both the actuarial premium and the financial repayment process.

3.1. New Proposals for Insured Loans

In what follows, we pose the borrowed capital equal to 1 at time 0 while the amount the insurer will pay under the specified contractual conditions is the amount still owed; that is, the residual debt valued at the time of the benefit payment in case of the borrower’s death. Note that all of the contracts in the following are designed considering the main aim of the operation, which is the resolution of the debt in case of the borrower’s insolvency. This implies contracts built according to the amortization schedule, and consequently the analysis needs a discrete approach.

In what follows, we will present and briefly describe the three new contractual forms we introduce. According to the notation in Haberman and Pitacco (1998), in what follows we will indicate by $p_x^{aa}$ the probability that a person aged $x$ is healthy at age $x+1$, and by

$${}_h{p}_x^{\underset{\_}{aa}}=p_x^{aa}{p}_{x+1}^{aa}\dots p_{x+h-1}^{aa}$$

the probability of being healthy at least until age $x+h$.

Death-Specific Insured Loan—SpeIL

The idea is to design a product in which the loan is saved in case of the borrower’s death for a specific cause. The death cause is precisely defined in the contract (e.g., ischemic heart disease, stroke, lower respiratory infections, and chronic obstructive lung disease). If $q_{x+h}^{\left(c\right)}$ is the probability that an individual aged $x+h$ dies within one year because of a specific cause, we can write that

$${}_{h/1}{q}_x^{\left(c\right)}={}_h{p}_x^{\underset{\_}{aa}}{q}_{x+h}^{\left(c\right)}$$

is the probability that an individual aged $x$ at issue dies between ages $x+h$ and $x+h+1$ due to a specific cause.

The value of the insurer’s obligations $A_{SpeIL}$ valued at time 0 is given by:

$$A_{SpeIL}={{\displaystyle \sum }}_{h=0}^{n-1}\frac{{\ddot{a}}_{\overline{n-h|}}}{a_{\overline{n|}}}v\left(0,h+1\right){}_{h/1}{q}_x^{\left(c\right)},$$

(7)

in which $v\left(0,h+1\right)$ is the discount factor for valuing in t = 0 one monetary unit in h + 1. The equation involving the insured’s obligations is:

$$A_{SpeIL}={{\displaystyle \sum }}_{h=0}^{n-1}{P}_{h}v\left(0,h\right){}_h{p}_x,,$$

(8)

where $P_h$ is the premium the insured pays at the beginning of year $h$.

Standard Critical Illness Loan (Stand Alone)—SCILsa

Here the insurance protection inserted in the loan concerns the coverage of the risk of suffering a particular specified disease.

The equation concerning the insurer obligations follows:

$$A_{SCILsa}={{\displaystyle \sum }}_{h=0}^{n-1}\frac{{\ddot{a}}_{\overline{n-h|}}}{a_{\overline{n|}}}v\left(0,h+1\right){}_{h/1}{w}_x^{\left(d\right)},$$

(9)

in which, if $w_{x+h}^{\left(d\right)}$ is the probability that the insured aged $x+h$ checks a specified diagnosis $d$ during the year $h,h+1$, we can write that

$${}_{h/1}{w}_x^{\left(d\right)}={}_h{p}_x^{\underset{\_}{aa}}{w}_{x+h}^{\left(d\right)}$$

is the probability that a person aged $x$ at the issue time is healthy at age $x+h$ and checks the diagnosis $d$ between the ages $x+h,x+h+1$ (cf. Haberman and Pitacco 1998).

The insured’s obligations are given by the equation:

$$A_{SCILsa}={{\displaystyle \sum }}_{h=0}^{n-1}{P}_{h}v\left(0,h\right){}_h{p}_x^{\underset{\_}{aa}}.$$

(10)

Standard Critical Illness Loan (Accelerated)—SCILa

In this case, the insurer will pay the amount if the insured suffers a specified disease or dies from any cause of death. The premium flow provides an accelerated benefit, covering the policyholder both in case of a specified critical illness and in case of death from any cause. The following equation holds:

$$A_{SCILa}={{\displaystyle \sum }}_{h=0}^{n-1}\frac{{\ddot{a}}_{\overline{n-h|}}}{a_{\overline{n|}}}v\left(0,h+1\right)\left({}_{h/1}{\tilde{q}}_x\right),$$

(11)

in which:

$${}_{h/1}{\tilde{q}}_x={}_h{p}_x^{\underset{\_}{aa}}\left(q_{x+h}^{\left(c\right)}+w_{x+h}^{\left(d\right)}\right).$$

Concerning the insured’s obligations, we can write:

$$A_{SCILa}={{\displaystyle \sum }}_{h=0}^{n-1}{P}_{h}v\left(0,h\right){}_h{p}_x^{\underset{\_}{aa}}.$$

(12)

4. Numerical Applications

4.1. Data Source

The empirical analysis we perform in this section aims to develop the amortization schedules for loans covered in case of death and/or critical illness of the borrower, as clarified in Section 3.1. We will determine the global instalment periodically due by the debtor/insured, inclusive of both the payment amount for repaying the loan and the actuarial premium for the insurance coverage. We will assume different loan durations (10–20 years) and that the debtor/insured was a 40 and 60 year-old person in 2014. The study will be done referring to different cohorts (males, females, smokers, non-smokers) in order to point out how the different basic characteristics impact the contract pricing. The valuations referring to the two cohorts of smokers and non-smokers can provide useful information towards the aim of loading strategies. Due to the availability of the data, we will refer to the U.K. population and will consider the major causes of death according to the diagnosis rates ranging from 1950 to 2009. The diagnosis rates for a Stand Alone cover and for a Full Accelerated cover can be downloaded from the Continuous Mortality Investigation Bureau (CMI WP 14 2005; CMI WP 18 2005; CMI WP 50 2011; CMI WP 58 2011), and concern in particular cancer and circulatory system diseases (Brett and du Toit 2007). Data concerning mortality disaggregated for causes of death are available at the Mortality Database administered by the World Health Organization (WHO 2009). The aggregated data (all causes) can be obtained from the Human Mortality Database (Wilmoth et al. n.d.), containing relevant demographic information such as the number of deaths for many countries over the last 50 years for five-year age groups; data concerning death for any cause and/or diagnosis (accelerated from) are available in the CMI Working Paper 14. The aggregated death (and survival) probabilities were obtained by means of a Poisson Lee–Carter model (Renshaw and Haberman 2003).

4.2. Actuarial Premiums

We will consider the specific death cause and/or illness cause “cancer and circulatory system illness”, taken from International Classification of Diseases (ICD). To develop the actuarial analysis, we need to determine the adjusted mortality indexes for each cohort and specified illness and project them along the loan duration. The procedure we will perform is quite complex, and consists of three basic steps concerning, respectively, the survival probabilities, the diagnosis probabilities, and the cause-specific death probabilities. In the following, we synthetically present the procedures for each point.

The Survival Probabilities

We chose to describe the annual mortality rates by means of the Poisson log-bilinear Lee–Carter Model (Renshaw and Haberman 2003) and project the mortality indexes of the model by an ARIMA process. According to Alho (2000), the basic Lee–Carter model, as in (Lee and Carter 1992), is not well suited to the construction of projected lifetables. Moreover, Alho observes that, due to the smaller absolute number of deaths at older ages, the logarithm of the observed force of mortality is much more variable at older ages than at younger ones. Considering also that the number of deaths is a counting random variable, according to Brillinger (1986), the Poisson assumption appears to be plausible. In order to circumvent the problems associated with the Ordinary Least Square (PLS) method, we can write (cf. Brouhns et al. 2002):

$$D_{x,t}~Poisson\left(E_{x,t}\left(m_{x,t}\right)\right)\mathrm{with}{m}_{x,t}=exp\left({\alpha }_x+{\beta }_x{k}_t\right)$$

(13)

where the parameters are subject to the constraints ${\displaystyle \sum }_t{k}_t=0,{\displaystyle \sum }_x{\beta }_x=1$, as in the Lee–Carter basic model (Lee and Carter 1992). The force of mortality is thus assumed to have the log-bilinear form: $ln\left(m_{x,t}\right)={\alpha }_x+{\beta }_x{k}_t$. The meaning of the parameters ${\mathsf{\alpha }}_{\mathrm{x}},{\mathsf{\beta }}_{\mathrm{x}}$, and ${\mathrm{k}}_{\mathrm{t}}$ is essentially the same as in the classical Lee–Carter model (Lee and Carter 1992).

Considering that the main drawback of the OLS estimation via Singular Value Decomposition (SVD) is that the errors are assumed to be homoscedastic, here we estimate ${\mathsf{\alpha }}_{\mathrm{x}},{\mathsf{\beta }}_{\mathrm{x}}$, and ${\mathrm{k}}_{\mathrm{t}}$ maximizing the log-likelihood:

$$L\left(\alpha ,\beta ,k\right)={{\displaystyle \sum }}_{x,t}\left[D_{x,t}\left({\alpha }_x+{\beta }_x{k}_t\right)-E_{x,t}exp({\alpha }_x+{\beta }_x{k}_t)\right]+constant.$$

(14)

The Diagnosis Probabilities

The diagnosis rates represent the principal end product of a program of work carried out by the CMI 2011 Critical Illness Committee to develop tables of critical illness diagnosis rates based on recent UK insured lives experience, together with sufficient supporting information to enable appropriate practical use by actuaries involved in this business (CMI, Working Paper 58). The diagnosis rates, divided by age, sex, smokers, and non-smokers for durations of 5 years, are available for “cancer and circulatory system illness” in CMI publications, 2005. Here such probabilities are just used for pricing the standard critical illness covers.

The Cause-Specific Death Probabilities

As mentioned above, the death cause we consider is “cancer and circulatory system illness”. Once the cohort under consideration is specified, we first provide the calculation of the annual mortality rates, attainable as the ratio between the number of deaths and the number of survivors at the beginning of each year (cf. WHO 2009). After the model parameters estimation, we will project the mortality indexes by an ARIMA process following Haberman and Villegas (2014) and Villegas (2015). It is crucial to observe that the ICD changed three times between 1950 and 2009, from ICD 7–8, ICD 8–9 and ICD 9–10; this is due to the changes in science and technology and to the refining of the classification itself. This circumstance implies that data are not directly comparable each other when referring to these three different periods. As the authors show, it is possible to smooth mortality rates across the various classifications. Following this paper, in order to mitigate the discontinuities in the mortality time series (referred to the cause “cancer and circulatory system illness”), we assume that the number of deaths D_xt of individuals aged x at time t are independent Poisson responses following the form:

$$D_{xt}~Poisson\left(e_{xt}{\mu }_{xt}\right).$$

Let:

$$S=\left\{s_1,s_2,\dots ,s_j\right\}$$

be the times at which coding changes occur. In order to account for the coding changes, we assume as in Haberman and Villegas (2014) and Villegas (2015) that the force of mortality is given by:

$$log{\mu }_{xt}=a_x+b_x{k}_t+{{\displaystyle \sum }}_{i=1}^k{\delta }_x^{\left(i\right)}{f}^i\left(t\right),$$

(15)

where:

• ${\mu }_{xt}$ is the age-specific death rate for age $x$ and year $t$
• ${\mathrm{a}}_{\mathrm{x}}$ is the average age-specific mortality
• $k_t$ is the mortality index in year $t$, capturing the underlying mortality trend
• $b_x$ is the deviation in mortality due to changes in the $k_t$ index

$f^i\left(t\right),i=1,2,\dots ,j$ is an indicator function valued at time $t$, taking the value $0$ if no new classification occurs in $t$ and value $1$ otherwise. The index $i$ means the numbers of ICD coming true in the considered period. In this application, $j=3$.

${\delta }_x^{\left(i\right)}$ measures the magnitude of coding changes at age $x$ and captures the discontinuities in the mortality trend induced by the changes in the coding system. It is necessary to verify if $f^{\left(i\right)}\left(t\right)$ = 1; only in this case are the ${\delta }_x^{\left(i\right)}$ values meaningful for the fitting data procedure.

4.3. Empirical Evidence and Illustrations

The Probabilities

This section is focused on the parameter estimations of the models described above, performed on the basis of the data in Section 4.1. For sake of clarity, we will explain the procedure according to the scheme in Section 4.2.

The Survival Probabilities

The trend of parameters $a_x,b_x$, and $k_t$ of model (15) obtained as outputs of the procedure in Section 4.2 are illustrated in Figure 1 in the male case. Moving clockwise, the first subplot on the left shows the trend of parameter $a_x$, the second on the right the trend of $b_x$ as a function of $x$, and the third on the bottom the adjusted $k_t$ as a function of $t$.

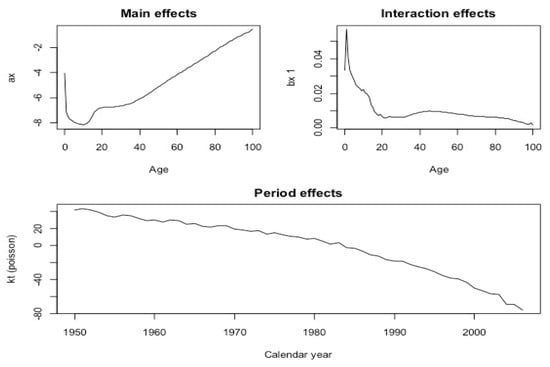
Figure 1. Model parameters, U.K. male.

The Diagnosis Probabilities

As we already said, in the case of cancer and circulatory system illnesses, the probabilities for pricing both the critical illness covers (Accelerated and Stand Alone) are available. In particular, in the case of the Standard Critical Illness Loan (Accelerated), we have to consider that a high proportion of deaths from cancer, and a possibly smaller proportion of deaths from circulatory system illness, must be removed from the “all causes” death rates to avoid double-counting of claims. The probabilities reported in the above Haberman and Villegas (2014) consider this circumstance.

The Cause-Specific Death Probabilities

The parameters $a_x,b_x,k_t$, and ${\delta }_x^{\left(i\right)}$ of model (20) are illustrated in Figure 2: their estimated values and the forecasted $p_x$ values for males and females are reported in the Appendix A (Table A1 and Table A2). Moving clockwise in Figure 2, the first subplot shows the trend of the sum of the two parameters $a_x$ and ${\delta }_x^{\left(i\right)}$. The second subplot shows the trend of the parameter $b_x$ as function of $x$, and the third reports the adjusted $k_t$ trend as a function of $t$. The three vertical red segments point out the reclassification times: as is evident, no more jumps are present in the graph.

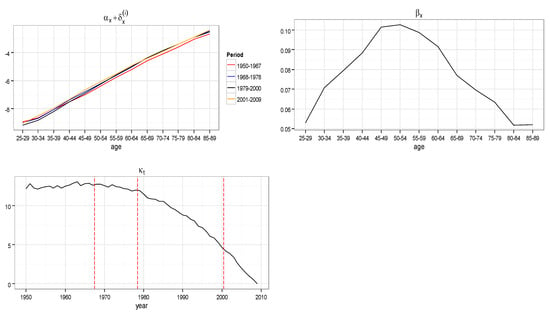
Figure 2. Model parameters, Cancer and Circulatory System Illness, UK Male population. On the axes of ordinates the parameter values.

In Figure 2, we show in an orderly way the model parameters and the adjusted mortality rates for males and females in the UK population and cancer and circulatory system illness case. Moving clockwise, in Figure 2 the first subplot shows the trend of the sum of the two parameters $a_x$ and ${\delta }_x^{\left(i\right)}$. Being $a_x$ constant with respect to $t$ over the whole observed period, the four curves refer to the four different values of ${\delta }_x^{\left(i\right)}$ obtained in the four intervals: 1950–1967, 1968–1978, 1979–2000, and 2001–2009. These intervals have been pointed in the ICD years (1968, 1979, 2001). The second subplot shows the trend of the parameter $b$ as a function of $x$, and the third reports the adjusted $k_t$ trend as a function of $t$. The three vertical red segments point out the reclassification times: as evident, no more jumps are present in the graph. The four subplots in Figure 3 show the adjusted mortality index trends, and in particular show how the discontinuities have been mitigated. As an example, they refer to four different age intervals (40–44, 50–54, 60–64, 70–74): the red dots are the adjusted values of $k_t$, the black dots are the observed data, and the continuous line represents the fitted data. The plots in Figure 4 and Figure 5 show the same quantities in the case of the female population.

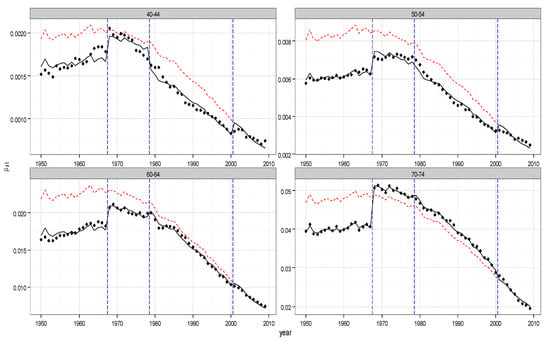
Figure 3. Adjusted mortality index, Cancer and Circulatory System Illness, UK Male population, age groups 40–45, 50–54, 60–64, 70–74.

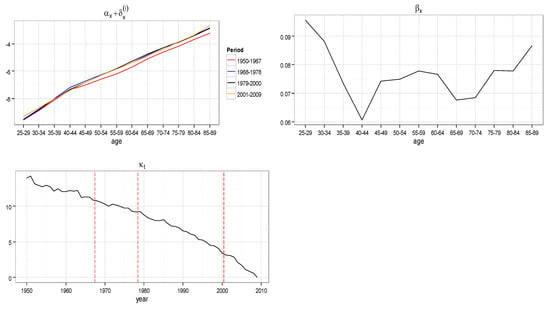
Figure 4. Model parameters, Cancer and Circulatory System Illness, UK Female population. On the axes of ordinates the parameter values.

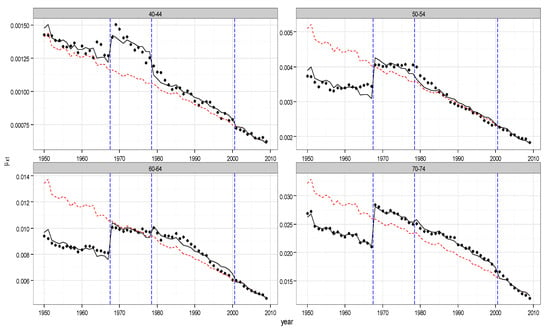
Figure 5. Adjusted mortality index- Cancer and Circulatory System, UK Female population, age groups 40–44, 50–54, 60–64, 70–74.

The Insurance Contracts: Pricing

In this section, we develop the amortization schedules for loans covered in case of death or/and critical illness of the borrower as clarified in Section 3.1.

The following groups of Tables report the constant premiums payable in all the contractual forms considered in Section 3.1, in the case of UK female and male populations. We fixed the loan annual interest rate $i=0.07$ and the technical actuarial valuation rate $r=0.02$. The contracts were issued in 2014. In particular, in the Table group 1, Table 1b refers to SpeIL and the premium is determined by Formulas (7) and (8). This case is compared with the standard form SIL (Standard Insured Loan), providing the coverage in case of death for any cause, whose premium values are in Table 1a (see Formula (5)). As expected, premiums fell when only a specific cause of death—even if so relevant—was considered. Table 2a,b concern the forms indicated as SCILsa and SCILa for female non-smokers; in Table 3a,b, there are the same results in the female smokers case. The premiums were calculated by Formulas (9)–(12). It is self-evident how cheap the coverage is in the Specific Insured Loan case and how it increases if the population refers to smokers. We observe in which measure the highest premium is that one referred to SCILa, offering the widest coverage: in this case the insurer will pay what is owed from the amortization schedule in case of death (for any cause) and in case of the specific illness diagnosis. Moreover, the results highlight that the diagnosis rates for female non-smokers aged 40–70 are higher than the corresponding one for the female smokers. Consequently, in the case of SCILsa, female non-smokers will pay more than the female smokers. This evidence works only in the Stand Alone cases. In the Accelerated coverage, this effect is compensated by the expected behavior of the death probabilities, and is not visible. Table 4, Table 5 and Table 6 contain the same values referring to the male population. A comparison between the two groups points out the general lower premiums for the females. In spite of this, it is interesting to highlight that in the considered age interval, the female non-smokers have diagnosis rates slightly higher than the male non-smokers. This circumstance turns into higher premiums for serious illness coverage in the case of female non-smokers.

Table 1. Actuarial periodic premium—female. Issue time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Insured Loan—SIL
10	90.19	749.04
20	175.95	1320.07
b. Specific Insured Loan—SpeIL
10	62.65	532.64
20	120.72	981.14

Table 2. Actuarial periodic premium—female non-smokers. Issue time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Critical Illness Loan (Stand Alone)—SCILsa
10	262.38	831.53
20	422.28	1198.74
b. Standard Critical Illness Loan (Accelerated)—SCILa
10	285.62	925.37
20	456.98	1424.16

Table 3. Actuarial periodic premium—female smokers. Issue time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Critical Illness Loan (Stand Alone)—SCILsa
10	213.79	805
20	273.18	925.80
b. Standard Critical Illness Loan (Accelerated)—SCILa
10	352.21	1304.30
20	580.70	2034.17

Table 4. Actuarial periodic premium—male. Issue time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Insured Loan—SIL
10	108.23	1251.55
20	231.06	2106.08
b. Specific Insured Loan—SpeIL
10	64.87	746.67
20	129.59	1440.78

Table 5. Actuarial periodic premium—male non-smokers. Issue time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Critical Illness Loan (Stand Alone)—SCILsa
10	218.68	1339.71
20	429.84	2049.66
b. Standard Critical Illness Loan (Accelerated)—SCILa
10	260.27	1515.15
20	498.18	2373.22

Table 6. Actuarial Periodic Premium—Male smokers. Issue Time 2014, r = 2%, i = 7%, C = 200,000.

Age at Entry/Duration	40	60
a. Standard Critical Illness Loan (Stand Alone)—SCILsa
10	440.72	2378
20	834.17	3590.64
b. Standard Critical Illness Loan (Accelerated)—SCILa
10	547.70	2975
20	1035.35	4686.70

5. Amortization Schedule

The global obligations of the borrower/insured arise from the amortization schedule for their financial obligations, and from the premiums calculated in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 of the preceding section for their insurance coverage. They will pay the sum between the constant financial installment and the specific premium referred to the chosen insurance contract. In Table 7, we report the amortization schemes of a loan issued in 2014 at a fixed rate of 7%, initial debt of C = 200,000, and with duration 10 years (Table 7a) and 20 years (Table 7b).

Table 7. Amortization schedules.

Maturity	Financial Instalment	Payment Due in Case of Insolvency
a. Amortization Schedule. Issue Time 2014, r = 7%, C = 200,000, n = 10
1	28,475.5	214,000
2	28,475.5	198,511.2
3	28,475.5	181,938.2
4	28,475.5	164,205.1
5	28,475.5	145,230.7
6	28,475.5	124,928
7	28,475.5	103,204.2
8	28,475.5	79,959.72
9	28,475.5	55,088.1
10	28,475.5	28,475.5
Maturity	Financial Instalment	Payment Due in Case of Insolvency	Maturity	Financial Instalment	Payment Due in Case of Insolvency
b. Periodic Amortization Schedule. Issue Time 2014, r = 7%, C = 200,000, n = 20
1	18,878.59	214,000	11	18,878.59	141,877
2	18,878.59	208,779.9	12	18,878.59	131,608.3
3	18,878.59	203,194.4	13	18,878.59	120,620.8
4	18,878.59	197,218	14	18,878.59	108,864.1
5	18,878.59	190,823.1	15	18,878.59	96,284.51
6	18,878.59	183,980.7	16	18,878.59	82,824.33
7	18,878.59	176,659.2	17	18,878.59	68,421.95
8	18,878.59	168,825.3	18	18,878.59	53,011.41
9	18,878.59	160,443	19	18,878.59	36,961.41
10	18,878.59	151,473.9	20	18,878.59	18,878.59

We report in particular the constant instalment due by the borrower in case of insolvency throughout the loan duration (column 2) and the payment due by the insurer in case of the borrower’s insolvency, if this event happens during the year preceding the date of valuation (column 3). As an example, in the case of SCILsa, female non-smokers, the global annual obligation, calculated including the actuarial obligations, is shown in Table 8a. It is possible to appreciate the contribution of the illness diagnosis coverage inclusion in the global amount to pay if compared with results in Table 8b, referred to the traditional SIL contractual form.

Table 8. Global annual obligation.

Age at Entry/Duration	40	60
a. Global annual obligation. Insured Loan and Stand Alone—SCILsa Female non-smokers, C = 200,000, i = 7%, r = 2%
10	28,738.88	29,307.03
20	19,300.87	20,077.33
b. Global annual obligation. Standard Insured Loan—SIL Female non-smokers, C = 200,000, i = 7%, r = 2%
10	28,565.69	29,224.54
20	19,054.54	20,198.66
c. Global annual obligation. Specific Insured Loan—SpeIL Female non-smokers, C = 200,000, i = 7%, r = 2%
10	28,538.15	29,008.14
20	18,999.31	19,859.73
d. Global annual obligation. Insured Loan and Accelerated—SCILa Female non-smokers, C = 200,000, i = 7%, r = 2%
10	28,761.12	29,400.87
20	19,335.57	20,302.75

Table 8c,d show the global obligations in the same general conditions and in the SpeIL and SCILa cases, for which a cause-specific death and a dread disease are considered.

6. Future Developments

This paper focused on the conjoint consideration of the financial product loan to private persons and the insurance coverage in case of specific causes of death and illness.

On the one hand, the loan is very much diffused and is quite often affected by very long duration; this circumstance involves a strong insolvency risk due to critical illnesses or death of the borrower. On the other hand, we can observe the general tendency in specializing insurance contracts particularly in the more advanced countries; this happens in order to offer more efficient and cheaper products from both counterparties’ points of view. Moreover, we can add that these kinds of contracts are increasingly computable in light of the increasing extent of specific data. So, the idea was to explore new insurance coverage within the standard financial loan. Toward this aim, it was necessary to project the survival probabilities and cause-specific mortality rates. In this paper, the relevant question of the discontinuities in the mortality rates due to the reclassification of the data (ICD) was fronted using a recent model able to mitigate the jumps in the data themselves. It has been possible to infer the projected data, to price the proposed contractual forms, and to build the final borrower/insured payment scheme.

Future research in this topic can be developed following two different lines. The first one is connected with the increasing interest in the specialization of the insurance contracts. We will propose new forms covering insolvency not due to death or illness but to other relevant circumstances such as the layoff of the borrower. The second will investigate the question of the eventual existence of dependence among all causes of death, in order to better understand the mortality phenomenon and their interactions. This topic is presently a subject of debate in actuarial literature, and could be fronted by means of cointegration procedures (see Arnold and Sherris 2013).

7. Conclusions

The increasing trend of human life expectancy is generally known as longevity. One of the components of longevity is the expansion phenomenon, which is the random advancement of the ultimate lifetime towards increasingly higher ages. Today’s individuals are expected to live longer than previous generations, but some of these extra years of life may not necessarily be healthy. As one of the consequences of this scenario, the interest in a prudential cover in case of specific illness and/or in case of death for specific or generically for all causes is growing in the insurance market. This is proved by an intense reinforcement of the offer of this kind of product and by a strong expression of interest by the European Institution involved in the insurance contracts linked to human life. The scientific literature is active in many of the main aspects of such contracts, such as the lack of data, their sensitivity to biometric assumptions, or broadly speaking, to pricing problems.

In addition, we want to point out that a challenging characteristic of these products is their flexibility and adaptability to be inserted inside other contractual structures. In particular, our interest is focused on the insured loan contract in which some covers are linked to critical illness and/or specific cause death. Some very recent proposals show the actual interest of the insurance market in this sense.

The aim of this paper is to structure a new kind of insured loan contract that, meeting the increase in the individual health information and the general tendency for insurance products to be increasingly tailor-made, can generate lowering prices. We propose three new insured loan contracts containing specified insurance covers, indicated with the acronyms: SpeIL, SCILsa, SCILa. In them, the letters SC stand for Standard Critical Illness, IL stand for Loan, sa for stand alone, a for accelerated, Spe for Death Specific.

In the application, we consider the specific death cause and/or illness cause “cancer and circulatory system illness”, taken from the International Classification of Diseases (ICD). The procedure for performing the practical implementation of data provides for the arrangements of the survival probabilities, the diagnosis probabilities, and the cause-specific death probabilities. In particular, the discontinuities problem was fronted following Haberman and Villegas (2014) and Villegas (2015). Downstream of such accommodations, we performed the contract pricing in all three proposed cases, and then we inserted them in the amortization scheme of the insured loan, chosen as an example. Several tables and graphics illustrate the empirical case we study.