Abstract
This paper presents a novel risk-based approach for an optimal asset allocation problem with default risk, where a money market account, an ordinary share and a defaultable security are investment opportunities in a general non-Markovian economy incorporating random market parameters. The objective of an investor is to select an optimal mix of these securities such that a risk metric of an investment portfolio is minimized. By adopting a sub-additive convex risk measure, which takes into account interest rate risk, as a measure for risk, the investment problem is discussed mathematically in a form of a two-player, zero-sum, stochastic differential game between the investor and the market. A backward stochastic differential equation approach is used to provide a flexible and theoretically sound way to solve the game problem. Closed-form expressions for the optimal strategies of the investor and the market are obtained when the penalty function is a quadratic function and when the risk measure is a sub-additive coherent risk measure. An important case of the general non-Markovian model, namely the self-exciting threshold diffusion model with time delay, is considered. Numerical examples based on simulations for the self-exciting threshold diffusion model with and without time delay are provided to illustrate how the proposed model can be applied in this important case. The proposed model can be implemented using Excel spreadsheets.
1. Introduction
Risk measurement and management are crucially important issues in the modern finance and insurance industries. Some recent major financial crises, such as the Asian financial crisis and the Global Financial Crisis (GFC) may be partly attributed to inappropriate risk management practices. Since the GFC, the credit risk, in particular the default risk, has regained increasing attention around the globe. Some “too big to fails”, such as Lehman Brothers, encountered financial difficulties which may be attributed to default events. The debt crises of Dubai and European countries may present real-world evidence that not only corporations may default. It may not be unreasonable to say that the traditional perception that some financial instruments traded in markets are perfectly risk-free may be an illusion. Even U.S. treasury debts may be downgraded regardless of its triple-A status for more than 70 years by major rating agencies1. In that sense, every investor should be cautious about default risk when making investment decisions. Indeed, due to the highly leveraged nature of derivative securities and structured products with default risk, trading these products could be a highly risky business. Appropriate practices in risk measurement and management of these defaultable products may protect both institutional and individual investors against massive exposure to these risky products. As many traded derivative securities have sophisticated structures, advanced quantitative tools may be needed to understand and evaluate the risk inherent from trading these securities.
Some quantitative risk measures have been proposed in the literature. Value at Risk (VaR) is popular among market practitioners. Regulators recommend the use of VaR for regulatory capital determination while risk managers adopt VaR for allocating capital and imposing risk limits to different trading desks. For more details about VaR, see, for example, Jorion (2001), J.P. Morgan’s Risk Metrics—Technical Document, Duffie and Pan (1997) and El-Jahel et al. (1999), among others. It is known in the literature that VaR is not sub-additive and penalizes diversification of risk. This does not appear to be consistent with financial intuition. Partly motivated by this observation, Artzner et al. (1999) proposed an axiomatic approach to risk measures and the notion of coherent risk measures. The introduction of coherent risk measures provides a remedy to overcome some defects of VaR. However, it was argued in Frittelli and Rosazza Gianin (2002) and Föllmer and Schied (2002) that, in practice, the risk of a trading position might increase nonlinearly with the size of the position. This is attributed to the lack of liquidity for a large trading position. To incorporate the nonlinear dependence of the risk of a trading position on the additional liquidity risk, Frittelli and Rosazza Gianin (2002) and Föllmer and Schied (2002) extended the class of coherent risk measures to that of convex risk measures. They replaced the sub-additive and positive homogeneous properties of coherent risk measures by a convexity property. In Frittelli and Rosazza Gianin (2002) and Föllmer and Schied (2002), convex risk measures quantify today’s risk of financial positions whose value will be realized at a future date T. In this sense, these convex risk measures are considered in a static setting.
Based on backward stochastic differential equations (BSDE) and the g-expectation, Frittelli and Rosazza Gianin (2004) and Rosazza Gianin (2006) extended a static convex risk measure to a dynamic one which evaluates the risk of a financial position at various intermediate times between today and the final date. Delbaen et al. (2008, 2010) represented, through BSDEs driven by Brownian motions, the penalty term of a time-consistent dynamic convex risk measure in an integral form. An integral representation of the penalty term for a time-consistent dynamic convex risk measure was extended to the case with jumps by Tang and Wei (2012). Elliott and Siu (2011a) applied a BSDE approach to study a risk-based, optimal investment problem of an insurer, where the risk faced by the insurer was described by a convex risk measure and the problem was formulated as a zero-sum stochastic differential game. Some other papers which concern risk-based asset allocation and possibly related problems include, for example, Øksendal and Sulem (2009), Elliott and Siu (2010a, 2010b, 2011b), Siu (2012), Zhang et al. (2012, 2013), Meng and Siu (2014) and Siu and Shen (2017), among others. Some of the literature used a BSDE approach to study the optimal control problems arising from risk-based asset allocation while some of them adopted the dynamic programming approach based on Hamilton-Jacobi-Bellman (HJB) equations.
Although the monotonicity and the convexity axioms may have been generally accepted, the cash additivity axiom (the translation invariance axiom) on convex risk measures may look controversial. In particular, El Karoui and Ravanelli (2009) pointed out that the cash additivity axiom fails to hold when the interest rate is stochastic or when the risky position is defaultable. In fact, convex risk measures (cash additive risk measures) are unable to account for the ambiguous discount factor. By replacing the cash additivity axiom with a cash sub-additivity axiom, El Karoui and Ravanelli (2009) proposed cash sub-additive risk measures, which can be used to quantify risks when a stochastic interest rate and defaultable contingent claims are present.
Default risk, or credit risk, has been widely studied in the literature. Merton (1974) pioneered the structural approach to model default risk, where the firm value is assumed to be observable and default occurs when a firm’s asset is not sufficient to cover its liability. Although a considerable effort has been made on extending Merton’s structural model (1974) in different directions, the observable firm value assumption is questioned from the practical perspective. Another approach to price default risk is a reduced-form intensity-based approach, which assumes that the default is triggered exogenously. Under this approach together with the assumption of the recovery in market values, the classical term structure machinery can be applied to model default risk. Previous works on the intensity-based approach, to name a few, include Madan and Unal (1998), Duffie and Singleton (1999), Collin-Dufresne et al. (2004), Jarrow et al. (2005), and etc. For a survey of both approaches, interested readers may refer to Bielecki and Rutkowski (2002)’s monograph on credit risk. Recently, there has been a growing interest in optimal investment problems with default risk. Hou (2003) and Jin and Hou (2003) considered an optimal investment problem of a portfolio with diversifiable default risk under the Vasicek-type models for both the short rate and the credit spread. Korn and Kraft (2003) discussed a continuous-time portfolio optimization problem with a defaultable bond and several stocks where the Merton structural firm value model was used to model default risk. For more general results, one may refer to the thesis by Kraft (2004). Bielecki and Jang (2006) studied a portfolio optimization problem with undiversifiable default risk in a deterministic short rate and credit spread modelling framework. Kraft and Steffensen (2008) investigated an optimal portfolio decision making problem in the presence of corporate bonds, where default risk was modeled by a reduced-form intensity-based model. Bo et al. (2010, 2013) considered optimal investment-consumption problems with defaultable bonds in an infinite-horizon modelling set up. Lim and Quenez (2011) studied the indifference pricing of a defaultable contingent claim via an exponential utility maximization problem. Capponi and Figueroa-Lopez (2014) investigated a portfolio optimization problem with defaultable securities in a Markovian regime-switching modelling environment. Some recent works along this direction include Jiao et al. (2013), Bo and Capponi (2016), and Zhao et al. (2016), among others.
In this paper, an optimal asset allocation problem of an investor in the presence of a defaultable security is discussed in a general non-Markovian economy. Specifically, a continuous-time financial market with three primitive assets, namely a money market account, an ordinary share and a defaultable security, is considered. The price process of the ordinary share is modelled by a non-Markovian geometric Brownian motion with random parameters. The intensity-based, reduced-form approach is adopted to model the default risk of the defaultable security. A general situation where model parameters such as interest rate, default intensity, appreciation rate and volatility are non-Markovian random processes is considered. A risk-based asset allocation problem for an investor, whose goal is to select an optimal portfolio with a view to minimizing the risk described by a sub-additive risk measure of his/her terminal wealth is described. The sub-additive risk measure is adopted here to take into account the effect of interest rate risk or stochastic discount factor. The investment problem is formulated as a two-person, zero-sum, stochastic differential game. In this game problem, the investor and the market act antagonistically to each other so as to achieve an equilibrium state in the sense of the Nash equilibrium in the game theory. We employ the BSDE approach as in, for example, Elliott and Siu (2011a) and Øksendal and Sulem (2011, 2014) to discuss the game problem. The advantage of using the BSDE approach is that it provides a solid theoretical basis to study the investment problem in a non-Markovian modelling framework. Closed-form solutions to the asset allocation problem are obtained when the penalty function is a quadratic function and when the risk measure is a sub-additive coherent risk measure. An important case of the non-Markovian general model, namely the self-exciting threshold diffusion model with time delay, is considered. This model can be thought of as a continuous-time version of one of the oldest and important classes of parametric nonlinear time series models, namely the self-exciting threshold autoregressive models, pioneered by Tong (1977, 1978, 1983). Numerical examples based on simulations for the self-exciting threshold diffusion model with and without time delay are provided to illustrate how the model may be applied. The proposed model can be implemented quite easily using Excel spreadsheets.
The rest of the paper is structured as follows. In Section 2, the model dynamics of the money market account, the ordinary share and the defaultable security are presented. A brief review on some key concepts of dynamic sub-additive convex risk measures is provided and the asset allocation problem is formulated as the two-person, zero-sum, stochastic differential game problem in Section 3. In Section 4, some results of backward stochastic differential equations are first discussed and then applied to solve the game problem. Closed-form solutions to the game problem are derived in some particular cases in Section 5. In Section 6, the self-exciting threshold diffusion model with time delay is first described. Then the simulation procedures and numerical results are presented and discussed. The final section gives concluding remarks.
2. The Model Dynamics
We consider a simplified continuous-time financial market with three primitive assets, namely, a money market account B, an ordinary share and a defaultable security . The market is assumed to be arbitrage-free, frictionless and continuously open in a finite time horizon , where . To describe uncertainty, we consider a complete probability space , which is assumed to be rich enough to carry all stochastic processes. Here is the reference probability measure, from which a family of equivalent probability measures can be generated.
Let and be two -standard Brownian motions, where is a right-continuous, -complete natural filtration generated by and . For each , write . Suppose that and are correlated with the variance-covariance matrix given by
where the correlation process satisfies , .
Let be a random variable on the probability space such that
Here represents the default time of the defaultable security. As it is well known in the intensity-based credit risk model, (see, for example, Lando (2009), chp. 5), we define a default indicator process by setting , for each . Let be a right-continuous, -complete natural filtration generated by the indicator process N, where , for each . Let be the minimal -field containing both and , for each . Denote . Note that is an -stopping time but not necessarily a -stopping time. In fact, is the minimal enlargement of such that is an -stopping time, (see, for example, Elliott et al. (2000) for some discussions on certain filtrations in intensity-based models).
As in Kusuoka (1999), we make the following assumptions:
- (A1)
- There exists a -adapted (intensity) process such thatis an -martingale.
- (A2)
- Every -local martingale is an -local martingale.
It is worth mentioning that Condition (A2) is usually called the H-hypothesis, and under this condition and are also two -Brownian motions.
Let . We next define the following, (path), spaces:
- (1)
- is the set of -progressively measurable, -valued processes on the product space ;
- (2)
- is the set of -measurable, -valued, essentially bounded random variables;
- (3)
- is the set of -measurable, -valued random variables such that
- (4)
- is the set of -adapted, -valued, essentially bounded, càdlàg processes;
- (5)
- is the set of -adapted, -valued, càdlàg processes such that
- (6)
- is the set of -predictable, -valued processes such that
- (7)
- is the set of -predictable, -valued processes such that
Let be the instantaneous, continuously-compounded, risk-free rate of interest at time t, where for each . Then the price process of the money market account evolves over time as
Let and denote the appreciation rate and the volatility of the ordinary share at time t, respectively. The price process of the ordinary share is governed by the following geometric Brownian motion (GBM) with random parameters:
Let and denote the appreciation rate and the volatility of the defaultable security at time t, respectively, and the proportion of downward jumps in the price of the defaultable security at time t when a default of the firm issuing the security occurs. Adopting the intensity-based approach, we assume that the dynamics of the defaultable security is governed by the following stochastic differential equation:
We assume that , , , , and , for each , are -predictable, uniformly bounded processes on , and further require that , for each . This assumption allows that the model dynamics (1)–(3) have random coefficients. Furthermore, the dynamics of the ordinary share and the defaultable security are not necessarily Markovian. That is, for each , the appreciation rates and , the volatilities and , the proportion of downward jumps could be functionals of the price processes and . One of the key motivations of applying the BSDE approach is to deal with non-Markovian controlled state processes with random coefficients.
Let be a portfolio process, where and represent the proportions of the wealth invested in the ordinary share and the defaultable security at time t, respectively. Then, the proportion that the investor allocates to the money market account is at time t. Let be the wealth process of the investor with the portfolio process . Then the evolution of the wealth process over time under the reference measure is governed by:
where
We say a portfolio process is admissible if it satisfies the following standard conditions:
- (1)
- is -predictable;
- (2)
- , for a.a. , where is a compact subset of ;
- (c)
- , for a.a. .
3. Risk-Based Asset Allocation Problem
In this section, we introduce sequentially the concepts of convex risk measures (cash additive measures) and cash sub-additive convex risk measures. Furthermore, we present an integral representation for the penalty term when the risk measure is time-consistent. Then we specify a family of real-world probability measures equivalent to the reference probability measure by a version of Girsanov’s theorem. Finally, we state the risk-minimization problem.
The concept of convex risk measures was introduced independently by Frittelli and Rosazza Gianin (2002) and Föllmer and Schied (2002). It generalizes the notion of coherent risk measures proposed by Artzner et al. (1999). Before we discuss the concept of cash sub-additive convex risk measures, we review the definition of a convex risk measure (a cash additive risk measure).
Let be the space of -measurable random variables. The space consists of random variables describing risky financial positions whose values will be realized at the terminal time T. Then a convex risk measure is defined as follows:
Definition 1.
A convex risk measure is a functional such that it satisfies the following three axiomatic properties:
- (1)
- Cash additivity (or cash invariance) : if and , then .
- (2)
- Monotonicity : for any , if , for all , then .
- (3)
- Convexity : for any and , then .
The convexity axiom reflects the situation that the risk of a trading portfolio might increase in a nonlinear fashion with the size of the portfolio that is attributed to the liquidity risk of a large portfolio, (see Frittelli and Rosazza Gianin (2002) and Föllmer and Schied (2002) for original discussions on the motivation of developing convex risk measures). With the cash additivity and the normalization assumption that , can be interpreted as the minimum amount of capital which is required to make the financial position described by X acceptable.
Although it seems that the monotonicity and the convexity axioms may have been quite well-accepted, the cash additivity axiom is rather controversial. El Karoui and Ravanelli (2009) pointed out that while regulators and financial institutions determine reserves or capitals today to cover losses due to future risky positions, the cash additivity axiom requires that the risky positions and the reserved capital are expressed in terms of the same numéraire. Implicitly, the risky positions should be discounted before calculating the convex risk measure, with the assumption that the discounting procedure does not involve any additional risks. However, if the interest rate is stochastic or the future risky position is defaultable, the cash additivity axiom may be questioned. That is, a convex risk measure (a cash additive risk measure) is unable to account for an ambiguous discount factor. By replacing the cash additivity axiom with the cash sub-additivity axiom, El Karoui and Ravanelli (2009) introduced a cash sub-additive convex risk measure, which can be used to model stochastic interest rate and defaultable contingent claims.
Definition 2.
A sub-additive convex risk measure is a functional such that it satisfies the following three axiomatic properties:
- (1)
- Cash sub-additivity : if and , then .
- (2)
- Monotonicity : for any , if , for all , then .
- (3)
- Convexity : for any and , then .
In fact, El Karoui and Ravanelli (2009) introduced a sub-additive risk measure by setting , where is a (stochastic) discount factor. The cash sub-additivity axiom allows that the functional is expressed in terms of the current numéraire but directly defined on the future risky position expressed in terms of the future numéraire. In other words, using a sub-additive convex risk measure, reserves or capitals may be determined in advance to make the financial position acceptable without recourse to the discounting procedure.
The following theorem is due to El Karoui and Ravanelli (2009). It provides a representation for a sub-additive risk measure. One may refer to El Karoui and Ravanelli (2009) for the proof.
Theorem 1.
Let be a family of sub-probability measures on . Define a function such that , . Then if a sub-additive risk measure satisfies the assumption of continuity from below, there exists a family and a function η such that
In the sequel, a family of sub-probability measures associated with the reference measure will be defined by using a version of Girsanov’s transformation. Firstly, we introduce processes , , and the discount rate process , which parameterize the family of sub-probability measures. Suppose that the process satisfies the following conditions:
- (1)
- is -predictable;
- (2)
- , for a.a. , where is a compact subset of ;
- (3)
- for some constant C, for a.a. ;
- (4)
- , for a.a. ;
We denote the space of all these processes by . A process is said to be an admissible strategy.
First, we define a real-valued, -adapted, process on by putting
Applying Itô’s differentiation rule to ,
For each , we define a probability measure equivalent to as:
Then, a sub-probability measure is defined by
The sub-probability measures may be related to state price densities in the asset pricing literature.
Therefore, the family of sub-probability measures, i.e., , can be generated as:
Denote by , and . Then, for each , a controlled state process satisfies
Recall that associated with any , the wealth equation admits a unique solution , i.e., the SDE (10) has a unique solution , for any . Similarly, associated with any , the SDE (9) has a unique solution , for any . To simplify our notation, we suppress the subscripts and and write, for each , , , and for , , and , respectively.
We now specify a penalty function , which admits an integral representation. Note that for each , and , where and are compact metric spaces in and , respectively. Let be a bounded, measurable convex function. To simplify the notation, we denote unless otherwise stated. We consider a penalty function of the following form:
Here is an expectation under . As shown in El Karoui and Ravanelli (2009), if F is finite and independent of , then is the penalty function representing a sub-additive risk measure . In fact, a sub-additive risk measure has an integral representation which is similar to that of a convex risk measure (see, for example, Delbaen et al. (2010) and Tang and Wei (2012)).
We now specify a cash sub-additive risk measure for the terminal wealth of the investor as:
The objective of the investor is to minimize the risk measure by selecting an optimal portfolio process . Consequently, the optimization problem of the investor can be described as the following min-max problem:
Denote the initial value of the controlled processes as . Recalling the form of the penalty function and using a version of Bayes’ rule,
Write, for each ,
Then
Therefore, the problem can be considered as a two-person, zero-sum, stochastic differential game between the investor and the market, (see, for example, (Øksendal and Sulem) (2011, 2014)). Here the investor selects an admissible strategy so as to minimize the risk measure of the wealth process at the terminal time T. On the other hand, the market responds antagonistically to the investor’s action by selecting a combination of the stochastic discount factor and the real-world probability measure, respectively, indexed by and , corresponding to the worst-case scenario where the risk is maximized. To solve the game problem, one must determine the optimal strategies and of the investor and the market, respectively. In reality, the global financial market does not normally respond to a single investor unless he/she is a large institutional trader, or a representative trader from a theoretical perspective. However, the interpretation for a market in the game problem here is a “fictitious” player who would tend to select the worst-case market scenario to induce a conversative outcome for the robust optimal asset allocation problem of the investor. The stochastic differential game approach is similar to the idea of worst-case portfolio optimization in Korn and Steffensen (2007). However, in Korn and Steffensen (2007), the market selects large financial shocks, or crashes, instead of worst-case probability scenarios.
It is anticipated that financial institutions pursuing a prudent investment approach may find the risk-based allocation approach relevant. Pension and endowment funds may perhaps serve as two examples of such institutions. The risk-based asset allocation approach may be different from some traditional investment methodologies such as those based on utility maximization and mean-variance optimization since the former does not treat maximizing investment returns as one of the main objectives while the latter does. In a sense, the risk-based asset allocation approach would tend to produce a conservative result. Having said that, there are some empirical evidence, (see, for example, Lee (2011) and the relevant references therein), that risk-based portfolios, which are seemingly return-insensitive, quite surprisingly outperform market capitalization-weighted portfolios and mean-variance efficient portfolios.
4. The BSDE Approach to the Game Problem
In this section, we first discuss the solvability of Backward Stochastic Differential Equations (BSDEs) driven by the Brownian motion and the martingale M, which will be used to solve the game problem described in the previous section. We then present a result which gives the solution of the game problem as a solution of a BSDE. Finally, we solve the game problem.
First of all, we introduce a BSDE with random default time.
Definition 3.
Let ξ be a real-valued, -measurable terminal condition and be a -measurable driver function, where , and are the -predictable σ-field on , the Borel σ-fields of ℜ and , respectively. Then a solution of the BSDE associated with the terminal value ξ and the driver g is a triplet of processes satisfying
Alternatively, in a differential form,
The following existence and uniqueness theorem is due to Peng and Xu (2010) (see also some possibly related results presented in Shen and Elliott (2011) for BSDEs driven by single jump processes). So we state the result here without giving the proof.
Theorem 2.
Suppose that and the following two conditions hold:
- (i)
- ;
- (ii)
- the Lipschitz condition: for each , there exists a constant such that
Then the BSDE (11) has a unique solution.
The following theorem is similar to Proposition 2.2 in El Karoui et al. (1997). It provides a link between the solution of a BSDE and the solution of the game problem. Since El Karoui et al. (1997) only considered the BSDE driven by Brownian motions, we extend the theorem to the BSDE with random default time by giving a sketch of the proof. Although similar results for different versions of BSDEs with jumps have been considered in literature (see, e.g., Delong (2013)), we relegate the proof to the appendix to make the paper self-contained. Note that the driver of the linear BSDE (13) does not satisfy the Lipschitz condition in the sense of Theorem 2 due to the fact that the coefficient of in the driver is linear in rather than . Therefore, instead of relying on Theorem 2, we discuss the solvability of (13) by using the martingale representation theorem directly.
Theorem 3.
Let , , and be -predictable, uniformly bounded processes taking values in ℜ, ℜ, and ℜ, respectively. Suppose that . Then, the following linear BSDE:
has a unique solution . Furthermore, Y has the following expectation representation:
where the double-indexed process is the adjoint process satisfying the following forward linear SDE:
and satisfies the following semi-group property:
Proof.
See the Appendix. ☐
The following theorem is a comparison theorem for BSDEs, which is slightly different from Theorem 3.3 in Peng and Xu (2010). Theorem 3 is an essential ingredient for the proof of the following theorem, which is very similar to that of Theorem 3.3 in Peng and Xu (2010). So we omit the proof here.
Theorem 4.
Suppose that , and and are two drivers satisfying Conditions (i)-(ii) in Theorem 2. Let and be the unique solutions of BSDEs corresponding to and , respectively. If
- (a)
- , a.e., a.s.,
- (b)
- , a.e., a.s., and
- (c)
- for each and , where , the following inequality holds:
then
Recalling the processes , and defined in Equations (6), (9) and (10), we apply Itô’s differentiation rule to calculate
Using the isometry formula for jump processes, we have
For each ,
Denote for each ,
Write, for each ,
Then
Write, for each ,
Thus, the stochastic differential game discussed in Section 4 is equivalent to the following stochastic differential game:
We now define the Hamiltonian of the game problem as follows:
The Hamiltonian H is said to satisfy Isaacs’ condition if
It is well known that H satisfies Isaacs’ condition if and only if there exist two measurable functions and such that
To make Isaac’s condition hold, we require that the Hamiltonian H is convex in and concave in . In other words, it is required that the function is concave in and convex in . Interested readers may refer to Friedman (1975) and Elliott (1976) for the detail of the relation between Isaacs’ condition and stochastic differential games. From now on, we assume that Issacs’ condition holds for the Hamiltonian H.
The following lemma verifies the solvability of the BSDE with the Hamiltonian given by the driver.
Lemma 1.
For any , the following BSDE
has a unique solution .
Proof.
Note that the admissible strategy and the function F are bounded. Moreover, we know that , for any . Observing
we can conclude that the Hamiltonian is square integrable, i.e., . By Theorem 2 or Theorem 3, we obtain that for any , the BSDE has a unique solution . ☐
The following theorem relates the solution of the game problem to the solution of a BSDE with random default time. Interested readers may find the proof in De Scheemaekere (2008) and Elliott and Siu (2011a). Although the BSDE considered in this paper is different from those in De Scheemaekere (2008) and Elliott and Siu (2011a) due to the presence of random default time, the proof is almost the same via using Theorems 2–4 and Lemma 1.
Theorem 5.
Suppose that Isaacs’ condition and the two conditions in Theorem 2 hold. Then there is a unique solution of the BSDE associated with the driver , :
Furthermore, the pair of strategies is a saddle point of the zero-sum stochastic differential game, and
The BSDE approach was also adopted in Elliott and Siu (2011a) to discuss the optimal investment problem. Our paper differentiates with Elliott and Siu (2011a) in three aspects. Firstly, we consider the asset allocation problem for a general investor while Elliott and Siu (2011a) discussed an optimal investment problem for an insurer. Secondly, the BSDE in our paper is driven by both a Brownian motion and a single jump process while that in Elliott and Siu (2011a) is only driven by a Brownian motion. Thirdly, due to presence of the stochastic discount factor, we use the sub-additive convex risk measure as a proxy of risk while Elliott and Siu (2011a) applied the convex risk measure. Due to the first and third differences between the current paper and Elliott and Siu (2011a) as mentioned, it does not seem that our results simply reduce to those in Elliott and Siu (2011a) even if the single jump process is absent.
5. Particular Cases
In this section, we discuss the problem for two parametric forms of the penalty function F. In both cases, we obtain the optimal strategies for the investor and the market. In the first case, we consider the quadratic penalty function, motivated by the entropic penalty function considered in, for example, Delbaean et al. (2008). More specifically, we assume that F is a quadratic function of . In the second case, we consider a zero penalty function, which was proposed by Jarrow (2002) for put option premiums. This case may also be related to coherent measures of risk.
5.1. Quadratic Penalty Function
Suppose that the penalty function has the following quadratic form:
Note that, for each , , -a.s.. Thus, F is convex in and .
Observing Equation (15), we see that the Hamiltonian is given by:
The first-order condition for maximizing the Hamiltonian with respect to gives the following equation:
By the definition of the admissible strategy set , we know that is bounded. If we further assume that , then . So the optimal discount rate is attained at .
The first-order condition for maximizing the Hamiltonian with respect to gives the following three equations:
The first-order condition for minimizing the Hamiltonian with respect to gives the following two equations:
Then the optimal strategy of the market is given by:
- Pre-default case:
- Post-default case:
The optimal strategy of the investor is given by:
- Pre-default case:
- Post-default case:
For simplicity, we assume that the compact sets and are sufficiently large and the coefficients satisfy proper conditions (e.g., boundedness and strict positivity) so that the obtained optimal strategies satisfy the boundedness conditions in the definitions of the admissible spaces, i.e., and .
Prior to default, the default risk has impacts on the optimal proportions invested in both the ordinary share and the defaultable security, if we assume that there is non-zero correlation, i.e., , for each , between the dynamics of the ordinary and defaultable shares. After default, the price of the defaultable security jumps to zero2, and hence the investor is unwilling to invest into the defaultable security. In this case, the investor allocates his/her wealth between the ordinary share and the money market account according to the Sharpe ratios. Simple calculations lead to the following closed-form expression for the difference of the optimal proportions invested in the ordinary share before and after default:
Consequently, under the assumption that , we have the following observations:
- The investor should decrease (resp. increase) his investment in the ordinary share after default, i.e., (resp. ), if the Sharpe ratios of the ordinary share and the defaultable security satisfy the following condition:
- The investor should maintain his investment in the ordinary share after default, i.e., , if the Sharpe ratios of the ordinary share and the defaultable security satisfy the following condition:
If the ordinary share and the defaultable security are issued by two affiliated entities, it may not be unreasonable to assume that their dynamics are correlated. If this is the case, for the sake of diversification, the investor allocates his/her money in the ordinary share and the defaultable security issued by two independent corporations, then it is not unreasonable to assume that , i.e., , for each . Thus, it is clear that the default risk can only affect the optimal proportion of the defaultable security and the optimal proportion of wealth invested in the ordinary share remains unchanged before and after default.
Jarrow et al. (2005) showed that if there are a countably infinite number of identical corporations whose default times are independent of each other, the martingale part M can be diversified away. Now we assume that the default risk is diversifiable. In this case, the optimal strategy of the investor is simplified as:
if , . That is, the investor allocates his/her money in the ordinary share and the defaultable security according to their respective Sharpe ratios. The optimal market prices of risk are:
Thus, the associated probability measure is a risk-neutral measure in this case.
5.2. Sub-Additive Coherent Risk Measure
Suppose that the penalty function is
Then the sub-additive risk measure becomes a sub-additive coherent risk measure. Jarrow (2002) discussed a similar risk measure, namely, the put premium risk measure. The put premium is the insurance cost that makes a firm’s net value remains solvent. Jarrow (2002) argued that adding alpha dollars to the firm will reduce the put premium by less than alpha dollars. This is exactly the idea of the put premium risk measure discussed in Jarrow (2002). Compared with coherent risk measure in Artzner et al. (1999), the put premium risk measure weakens the translation invariance axiom to a translation monotonicity axiom.
If we further assume that , the Hamiltonian becomes:
The first-order condition for maximizing/minimizing with respect to and gives:
and
So the Hamiltonian can be simplified as:
If we assume that , the optimal discount rate is . Therefore, the maximum value of the Hamiltonian becomes:
It follows from Theorem 5 that , for each . In other words, the sub-additive risk measure vanishes in the zero-sum game. This result is accordance with intuition thanks to the following facts:
- (1)
- The default risk is assumed to be zero (the martingale part M has been diversified away);
- (2)
- The diffusion risk is offset by holding opposite positions in and ;
- (3)
- The discount risk is hedged by investing the outstanding proportion of wealth into the money market account.
6. Numerical Examples on the Self-Exciting Threshold Diffusion
In this section, the continuous-time self-exciting threshold diffusion model with time delay is first presented. We intend to illustrate that the BDSE approach for the risk-based optimal asset allocation is flexible enough to incorporate this important case motivated by one of the oldest and important classes of parametric nonlinear time series model pioneered by Tong (1977, 1978, 1983). Then the simulation procedures of the model are presented and the numerical results based on simulations for the models with and without time delay are presented and discussed.
6.1. Self-Exciting Threshold Diffusion Model
A distinctive feature of the self-exciting threshold diffusion model is that regime switches are introduced without introducing an additional state process. Whereas, for a Markovian regime-switching process, an additional state process usually described by a finite-state Markov chain is required to model regime switches. Regime switches in the self-exciting threshold diffusion model are introduced by the threshold principle, where a set of threshold parameters is introduced to partition the state space of a past value of the process. The threshold parameters may act as tipping points for transitions of different regimes of the dynamics and may entail different interpretations in diverse fields. See, for example, Siu (2016) for related discussions as well as discussions on the distinction between the self-exciting threshold regime switching processes and the Markovian regime-switching processes. The continuous-time self-exciting threshold diffusion model have been applied in the literature for asset allocation and option valuation. See, for example, (Meng et al. 2013; Su and Chan 2016; Siu 2016; Chi et al. 2017). However, it seems that many of these applications do not consider the situation where there is a time delay in the price dynamics. Essentially speaking, the threshold models with time delay are non-Markovian, while those without time delay are Markovian models. In the sequel, the continuous-time self-exciting threshold diffusion models with time delay for the asset price dynamics are presented. It is obvious that the continuous-time self-exciting threshold diffusion models without time delay are obtained by setting the time delay parameter in the models with time delay equal to zero.
We assume that the price process of the risky share is governed by the following self-exciting threshold diffusion model with time delay:
Here R is the threshold parameter dividing the state space of the price of the risky share ; is the indicator function of an event E; d is the time delay parameter and ; when , the self-exciting threshold diffusion model with time delay in Equation (16) reduces to the one without time delay; and are the expected rates of return from the risky share in a good economic state and a bad one, respectively; and are the volatilities of the risky share in a good economic state and a bad one, respectively. Regime switches or transitions in economic states are introduced by the threshold parameter R. In particular, if , the economy at time t is said to be in a good state; otherwise, it is in a bad one.
Furthermore, it is supposed that the price process of the defaultable security is governed by another self-exciting threshold diffusion model with time delay:
Here a common threshold parameter R and a common time delay parameter d are used for convenience. In general, one may consider a different threshold parameter dividing the state space of the price of the defaultable security and a different time delay parameter; and are the expected rates of return from the defaultable security in a good economic state and a bad one, respectively; and are the volatilities of the defaultable security in a good economic state and a bad one, respectively. and are the proportions of down draws in the price of the defaultable security when a default of the firm issuing the security occurs in a good economic state and a bad one, respectively. It is assumed that , and hence, they are interpreted as proportions. If , the economy at time t is said to be in a good state; otherwise, it is in a bad one.
Note that
where is another standard Brownian motion which is independent of the Brownian motion .
Suppose, first, that the correlation coefficient is given by:
Then the price process of the defaultable security in Equation (17) can be expressed as:
In other words, the price process of the defaultable security is governed by:
For the specification of the bond price dynamics, there are at least two possibilities to incorporate the self-exciting threshold regime-switching effect. The following two cases are considered:
Case I: The price process of the bond B is governed by:
Here and are the constant continuously compounded interest rates of the bond in a good economic state and a bad one, respectively.
Case II: The price process of the bond B is governed by:
The difference between this case and Case I is that the price of the defaultable security at time is used to specify which regime of the bond price process is in force just right after time t.
To describe the switching behavior of the process of instantaneous correlation coefficients between the two correlated Brownian motions and , we consider two cases again.
Case I: The process of instantaneous correlation coefficients is governed by:
where and are the correlation coefficients in a good economic state and a bad one, respectively.
Case II: The process of instantaneous correlation coefficients is governed by:
6.2. Simulation Procedures and Numerical Results
In the numerical experiment, we suppose that the price of the share at time t will be used to determine which regime of the bond price process is in force just right after time t when computing the optimal investment in the share . We also assume that the price of the defaultable security at time t will be used to specify which regime of the bond price process is in force just right after time t when computing the optimal investment in the defaultable security . The same principle applies to determine which regime of the process of instantaneous correlation coefficients is in force at a particular time. However, when we simulate the price process of the share , the price of the defaultable security at time t is used to determine which regime the process of instantaneous correlation coefficients is in force at time t.
To perform the simulations of the price processes, we first discretize them using the standard Euler forward discretization scheme. For each , let be the logarithmic return from the security i. Applying Itô’s lemma to and gives:
and
We divide the finite time horizon into N sub-intervals of equal length . For simplicity, we assume that for some non-negative integer . Of course, when , the model has no time delay. Then using the standard Euler forward discretization scheme, the discretized price process of the logarithmic return process of the share is given by:
where is a sequence of independent and identically distributed standard normal random variables, and to simplify the notation, we write for , for and for . Note that is the (cumulative) logarithmic return from time 0 to time . In other words, is the one-period logarithmic return from time to time .
The simulated default time, say , is given by the greatest integral part of the multiple of an exponential random variable with rate parameter , denoted by , and the time duration , where is the constant default intensity of the default indicator process N. That is, if is a simulated random variable from , then
Then
where .
Consequently,
Then using the standard Euler forward discretization scheme, the discretized price process of the logarithmic return from the defaultable security is given by:
where is a sequence of independent and identically distributed standard normal random variables such that and are stochastically independent.
In the sequel, the numerical results based on simulations are presented and discussed. The results are computed using Excel spreadsheets. For illustration, the following configuration of model parameters are used in the computations of the numerical results:
A simulated path for the return process from each of the ordinary share and the defaultable security is depicted in Figure 1 as follows:
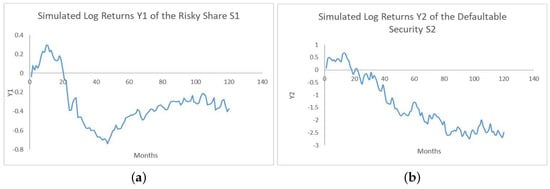
Figure 1.
Simulated log returns and for the risky share and the defaultable security. Panel (a) for the ordinary share and Panel (b) for the defaultable security.
A simulated path for the price process from each of the ordinary share and the defaultable security is depicted in Figure 2 as follows:
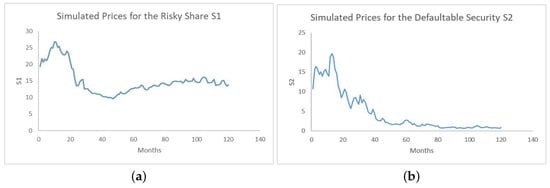
Figure 2.
Simulated prices for the risky share and the defaultable security . Panel (a) for the ordinary share and Panel (b) for the defaultable security.
Based on the simulated price or return paths for the ordinary share and the defaultable security depicted in Figure 2 or Figure 1 as above, the optimal portfolio strategies from the model with time delay and without time delay are depicted in Figure 3 and in Figure 4 as follows:
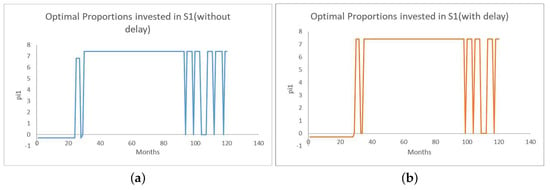
Figure 3.
Simulated optimal proportions invested in for the cases without and with delay. Panels (a) and (b) for the optimal proportions invested in the ordinary share with and without time delay.
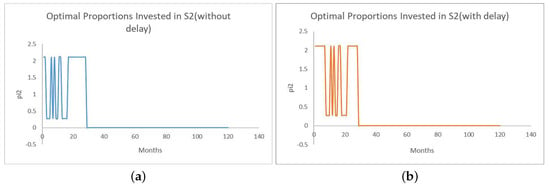
Figure 4.
Simulated optimal proportions invested in for the cases without and with delay. Panel (a) and (b) for the optimal proportions invested in the defaultable security with and without time delay.
It can be seen that when there is time delay, the optimal proportions are almost delayed versions of optimal proportions in the case without delay. Although time delay is present in the threshold models (16) and (17), it has no impact on the default time of the defaultable security. Therefore, once a default occurs, the optimal proportions invested in drops to zero simultaneously in the cases with and without delay. Of course, for each time that the simulations are done, the simulated paths for the returns and the prices of the two securities could be very different even with the same set of model parameters. The simulation results could vary significantly. Moreover, the optimal portfolio strategies computed from different simulated price or return paths could be very different as well. Nevertheless, the optimal proportion strategies with and without time delay are computed using the same simulated price or return paths. This may hopefully provide a simple simulation-based example for illustrating some potential differences between the optimal portfolio strategies with and without time delay.
A potentially interesting feature of the simulations is the rapid pulsing behavior of optimal investment strategies. Due to the absence of transaction costs, there is no cost for the investor to adjust invested proportions of the ordinary share and the defaultable security. This may probably lead to the rapid pulsing behavior as depicted in Figure 3 and Figure 4. It may be interesting to extend our results to more realistic situations where transaction costs are present and the order book model is adopted to describe the investment behavior of larger investors.
7. Conclusions
We applied a BSDE approach to discuss the optimal asset allocation problem with default risk. The investor aimed to minimize the risk of terminal wealth, which was described by a sub-additive convex risk measure. We studied the asset allocation problem from a game theoretic perspective and formulated the problem as a two-person, zero-sum, stochastic differential game. Closed-form solutions of the optimal strategies adopted by the investor and the market were derived in the particular cases where the penalty function is quadratic or zero. For the former case, the investor allocates his/her wealth into the ordinary and defaultable shares in accordance with the Sharpe ratios if the default risk is diversifiable and the dynamics of the ordinary share and the defaultable security are uncorrelated. For the latter case, if the default risk has been diversified away in the market, i.e., the default risk is idiosyncratic, the investor can offset all the risks in the portfolio by allocating appropriate proportions of his/her wealth among the money market account, the ordinary share and the defaultable security. Two parametric models for price processes based on self-exciting threshold regime-switching processes were considered. Numerical examples based on simulations were provided to illustrate the implementation of the models.
Acknowledgments
Yang Shen would like to thank the Natural Sciences and Engineering Research Council of Canada; Tak Kuen Siu would like to thank the Australian Research Council.
Author Contributions
Yang Shen and Tak Kuen Siu both contributed the development and writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix: Proof of Theorem 3
Proof.
Let us first prove the existence and uniqueness of a solution to the linear BSDE (13). We consider an -adapted, real-valued process satisfying
A probability measure equivalent to is constructed as:
Under ,
is a two-dimensional Brownian motion with the same variance-covariance matrix as under , and
is an -martingale, that is, under the intensity of is . Then, the -dynamics of the BSDE (13) is given by
Denote by
Since , and are bounded, is a square-integrable, -martingale. By the martingale representation theorem, there exists a unique pair of processes such that
Denote by
Applying Itô’s differentiation rule to , we can verify that under the triplet satisfies the linear BSDE (A3). Therefore, under the triplet is the unique solution of the linear BSDE (13). Moreover, from the relation (A6), we obtain
Here the second equality is guaranteed by Bayes’ rule. We can further deduce by the product rule that
Combining (A7) and (A8) leads to the expectation representation (14) for . ☐
References
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bielecki, Tomasz R., and Inwon Jang. 2006. Portfolio optimization with a defaultable security. Asia-Pacific Financial Markets 13: 113–27. [Google Scholar] [CrossRef]
- Bielecki, Tomasz R., and Marek Rutkowski. 2002. Credit Risk: Modeling, Valuation and Hedging. Berlin: Springer. [Google Scholar]
- Bo, Lijun, Yongjin Wang, and Xuewei Yang. 2010. An optimal portfolio problem in a defaultable market. Advances in Applied Probability 42: 689–705. [Google Scholar] [CrossRef]
- Bo, Lijun, Yongjin Wang, and Xuewei Yang. 2013. Stochastic portfolio optimization with default risk. Journal of Mathematical Analysis and Applications 397: 467–80. [Google Scholar] [CrossRef]
- Bo, Lijun, and Agostino Capponi. 2016. Optimal investment in credit derivatives portfolio under contagion risk. Mathematical Finance 26: 785–834. [Google Scholar] [CrossRef]
- Capponi, Agostino, and José E. Figueroa-Lopez. 2014. Dynamic portfolio optimization with a defaultable security and regime-switching. Mathematical Finance 24: 207–49. [Google Scholar] [CrossRef]
- Chi, Zeyu, Fangyuan Dong, and Hoi Ying Wong. 2017. Option pricing with threshold mean reversion. Journal of Futures Markets 37: 107–31. [Google Scholar] [CrossRef]
- Collin-Dufresne, Pierre, Robert Goldstein, and Julien Hugonnier. 2004. A general formula for valuing defaultable securities. Econometrica 72: 1377–407. [Google Scholar] [CrossRef]
- Delbaen, Freddy, Shige Peng, and Emanuela Rosazza Gianin. 2008. Representation of the penalty term of a dynamic convex risk measure. Paper presented at Princeton Conference, Torino, Italy. [Google Scholar]
- Delbaen, Freddy, Shige Peng, and Emanuela Rosazza Gianin. 2010. Representation of the penalty term of dynamic concave utilities. Finance and Stochastics 14: 449–72. [Google Scholar] [CrossRef]
- Delong, ukasz. 2013. Backward Stochastic Differential Equations with Jumps and Their Actuarial and Financial Applications. London: Springer. [Google Scholar]
- De Scheemaekere, Xavier. 2008. Risk Indifference Pricing and Backward Stochastic Differential Equations. CEB Working Paper No. 08/027. Brussels, Belgium: Solvay Business School. [Google Scholar]
- Duffie, Darrell, and Jun Pan. 1997. An overview of Value at Risk. Journal of Derivatives 4: 7–49. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling term structure of defaultable bonds. The Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Duffie, Darrell, and David Lando. 2001. Term structures of credit spreads with incomplete accounting information. Econometrica 69: 633–64. [Google Scholar] [CrossRef]
- El-Jahel, Lina, William Perraudin, and Peter Sellin. 1999. Value at risk for derivatives. Journal of Derivatives 6: 7–26. [Google Scholar] [CrossRef]
- El Karoui, Nicole, Shige Peng, and Marie Claire Quenez. 1997. Backward stochastic differential equations in finance. Mathematical Finance 7: 1–71. [Google Scholar] [CrossRef]
- El Karoui, Nicole, and Claudia Ravanelli. 2009. Cash subadditive risk measure and interest rate ambiguity. Mathematical Finance 19: 561–90. [Google Scholar] [CrossRef]
- Elliott, Robert J. 1976. The existence of value in stochastic differential games. SIAM Journal on Control and Optimization 14: 85–94. [Google Scholar] [CrossRef]
- Elliott, Robert J., Monique Jeanblanc, and Marc Yor. 2000. On models of default risk. Mathematical Finance 10: 179–95. [Google Scholar]
- Elliott, Robert J., and Tak Kuen Siu. 2010a. On risk minimizing portfolios under a Markovian regime-switching Black-Scholes economy. Annals of Operations Research 176: 271–91. [Google Scholar] [CrossRef]
- Elliott, Robert J., and Tak Kuen Siu. 2010b. Risk-based indifference pricing under a stochastic volatility model. Communications on Stochastic Analysis 4: 51–73. [Google Scholar]
- Elliott, Robert J., and Tak Kuen Siu. 2011a. A BSDE approach to a risk-based optimal investment of an insurer. Automatica 47: 253–61. [Google Scholar] [CrossRef]
- Elliott, Robert J., and Tak Kuen Siu. 2011b. A risk-based approach for pricing American options under a generalized Markov regime-switching model. Quantitative Finance 11: 1633–46. [Google Scholar] [CrossRef]
- Föllmer, Hans, and Alexander Schied. 2002. Convex measures of risk and trading constraints. Finance and Stochastics 6: 429–47. [Google Scholar] [CrossRef]
- Friedman, Avner. 1975. Stochastic Differential Equations and Applications. Mineola: Dover Publications. [Google Scholar]
- Frittelli, Marco, and Emanuela Rosazza Gianin. 2002. Putting order in risk measures. Journal of Banking and Finance 26: 1473–86. [Google Scholar] [CrossRef]
- Frittelli, Marco, and Emanuela Rosazza Gianin. 2004. Dynamic convex risk measures. In Risk Measures for the 21st Century. Edited by Giorgio Szegö. New York: Wiley, pp. 227–48. [Google Scholar]
- Hou, Yuanfeng. 2003. Integrating Market Risk and Credit Risk: A Dynamic Asset Allocation Perspective. Working Paper. New Haven, CT, USA: Yale University. [Google Scholar]
- Jarrow, Robert A. 2002. Put option premiums and coherent risk measures. Mathematical Finance 12: 135–42. [Google Scholar] [CrossRef]
- Jarrow, Robert A., David Lando, and Fan Yu. 2005. Default risk and diversification: Theory and empirical implications. Mathematical Finance 15: 1–26. [Google Scholar] [CrossRef]
- Jiao, Ying, Idris Kharroubi, and Huyen Pham. 2013. Optimal investment under multiple defaults risk: A BSDE decomposition approach. The Annals of Applied Probability 23: 455–91. [Google Scholar] [CrossRef]
- Jin, Xiangrong, and Yuanfeng Hou. 2003. Optimal Investment With Default Risk. FAME Research Paper No. 46. Available online: https://ssrn.com/abstract=372020orhttp://dx.doi.org/10.2139/ssrn.372020 (accessed on 14 December 2017).
- Jorion, Philippe. 2001. Value At Risk: The New Benchmark for Managing Financial Risk, 2nd ed. McGraw-Hill: New York. [Google Scholar]
- Korn, Ralf, and Holger Kraft. 2003. Optimal portfolios with defaultable securities—A firm value approach. International Journal of Theoretical and Applied Finance 6: 793–819. [Google Scholar] [CrossRef]
- Korn, Ralf, and Mogens Steffensen. 2007. On worst-case portfolio optimization. SIAM Journal on Control and Optimization 46: 2013–30. [Google Scholar] [CrossRef]
- Kraft, Holger. 2004. Optimal portfolios with stochastic interest rates and defaultable assets. In Lecture Notes in Economics and Mathematical Systems. Heidelberg: Springer. [Google Scholar]
- Kraft, Holger, and Mogens Steffensen. 2008. How to invest optimally in corporate bonds. Journal of Economic Dynamics and Control 32: 348–85. [Google Scholar] [CrossRef]
- Kusuoka, Shigeo. 1999. A remark on default risk models. Advances in Mathematical Economics 1: 69–82. [Google Scholar]
- Lando, David. 2009. Credit Risk Modeling: Theory And Applications. Princeton: Princeton University Press. [Google Scholar]
- Lee, Wai. 2011. Risk-based asset allocation: A new answer to an old question? The Journal of Portfolio Management 37: 11–28. [Google Scholar] [CrossRef]
- Lim, Thomas, and Marie Claire Quenez. 2011. Exponential utility maximization in an incomplete market with defaults. Electronic Journal of Probability 16: 1434–64. [Google Scholar] [CrossRef]
- Madan, Dilip B., and Haluk Unal. 1998. Pricing the risks of default. Review of Derivatives Research 2: 121–60. [Google Scholar] [CrossRef]
- Meng, Hui, Fei Lung Yuen, Tak Kuen Siu, and Hailiang Yang. 2013. Optimal portfolio in a continuous-time self-exciting threshold model. Journal of Industrial and Management Optimization 9: 487–504. [Google Scholar] [CrossRef][Green Version]
- Meng, Hui, and Tak Kuen Siu. 2014. Risk-based asset allocation under Markov-modulated pure jump processes. Stochastic Analysis and Applications 32: 191–206. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Øksendal, Bernt, and Agnes Sulem. 2009. Risk indifference pricing in jump diffusion markets. Mathematical Finance 19: 619–37. [Google Scholar] [CrossRef]
- Øksendal, Bernt, and Agnes Sulem. 2011. Portfolio optimization under model uncertainty and BSDE games. Quantitative Finance 11: 1665–74. [Google Scholar] [CrossRef]
- Øksendal, Bernt, and Agnes Sulem. 2014. Forward-backward stochastic differential games and stochastic control under model uncertainty. Journal of Optimization Theory and Applications 161: 22–55. [Google Scholar] [CrossRef]
- Peng, Shige, and Xiaoming Xu. 2010. BSDEs with random default time and related zero-sum stochastic differential games. Comptes Rendus de l’Académie des Sciences-Series I 348: 193–98. [Google Scholar] [CrossRef]
- Rosazza Gianin, Emanuela. 2006. Risk measures via g-expectations. Insurance: Mathematics and Economics 39: 19–34. [Google Scholar] [CrossRef]
- Shen, Leo, and Robert J. Elliott. 2011. Backward stochastic differential equations for a single jump process. Stochastic Analysis and Applications 29: 654–73. [Google Scholar] [CrossRef]
- Siu, Tak Kuen. 2012. A BSDE approach to risk-based asset allocation of pension funds with regime switching. Annals of Operations Research 201: 449–73. [Google Scholar] [CrossRef]
- Siu, Tak Kuen. 2016. A self-exciting threshold jump-diffusion model for option valuation. Insurance: Mathematics and Economics 69: 168–93. [Google Scholar] [CrossRef]
- Siu, Tak Kuen, and Yang Shen. 2017. Risk-minimizing pricing and Esscher transform in a general non-Markovian regime-switching jump-diffusion model. Discrete and Continuous Dynamical Systems-Series B 22: 2595–626. [Google Scholar]
- Su, Fei, and Kung-Sik Chan. 2016. Option pricing with threshold diffusion processes. North American Actuarial Journal 20: 133–41. [Google Scholar] [CrossRef]
- Tang, Shanjian, and Wenning Wei. 2012. Representation of dynamic time-consistent convex risk measures with jumps. Risk and Decision Analysis 3: 167–90. [Google Scholar]
- Tong, Howell. 1977. Discussion of a paper by A.J. Lawrance and N.T. Kottegoda. Journal of Royal Statistical Society: Series A 140: 34–35. [Google Scholar]
- Tong, Howell. 1978. On a threshold model. In Pattern Recognition and Signal Processing. NATO ASI Series E: Applied Science 29; Edited by C. H. Chen. Alphen aan den Rijn: Sijthoff and Noordhoff, pp. 575–86. [Google Scholar]
- Tong, Howell. 1983. Threshold Models in Non-Linear Time Series Analysis. New York: Springer. [Google Scholar]
- Zhang, Xin, Robert J. Elliott, and Tak Kuen Siu. 2012. A Risk-Based Investment-Reinsurance Problem Under a Markov Regime-Switching Jump-Diffusion Model. Unpublished Manuscript. [Google Scholar]
- Zhang, Xin, Robert J. Elliott, and Tak Kuen Siu. 2013. Risk-Based Optimal Investment-Reinsurance Problem of An Insurer: A BSDE Approach. Unpublished Manuscript. [Google Scholar]
- Zhao, Hui, Yang Shen, and Yan Zeng. 2016. Time-consistent investment-reinsurance strategy for mean-variance insurers with a defaultable security. Journal of Mathematical Analysis and Applications 437: 1036–57. [Google Scholar] [CrossRef]
| 1 | |
| 2 | One reviewer points out that in practice, defaultable bonds could have non-zero recoverable value and that along the line of thought of the Duffie-Lando model (see Duffie and Lando 2001), there could be different opinions on whether an equity may be valued zero if default is not certain. While we reckon that these could be practically relevant issues, we posit that the abstraction that the price of the defaultable security is zero after default may not be unreasonable from the theoretical perspective. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).