Abstract
Swarm intelligence has appeared as an active field for solving numerous machine-learning tasks. In this paper, we address the problem of clustering data with missing values, where the patterns are described by mixed (or hybrid) features. We introduce a generic modification to three swarm intelligence algorithms (Artificial Bee Colony, Firefly Algorithm, and Novel Bat Algorithm). We experimentally obtain the adequate values of the parameters for these three modified algorithms, with the purpose of applying them in the clustering task. We also provide an unbiased comparison among several metaheuristics based clustering algorithms, concluding that the clusters obtained by our proposals are highly representative of the “natural structure” of data.
1. Introduction
Clustering has become crucial in several areas of scientific research, and it has also a significant impact in the theoretical development and applied research in several scientific disciplines [1,2,3]. Despite the very large number of methods to perform clustering, the use of swarm intelligence algorithms has become increasingly relevant in order to perform this task [3,4,5,6]. However, given the ample diversity of fields, topics, and problems studied, a particular phenomenon may very well be described by both numerical and categorical variables (mixed or hybrid data). Additionally, the appearance of missing values has become increasingly common in data measurement and sampling processes (missing data). There are several actors that can cause the missing values. Among them, the most important ones can be mentioned: the impossibility to perform some measurements, the loss of already taken samples, or even the non-existence of information about the data being described.
Data described by hybrid or mixed features (or simply mixed data) represent a challenge to most automatic learning algorithms. This is due to the generally accepted assumption of data are described by features of the same kind. Consequently, most pattern recognition algorithms are designed to tackle problems whose attributes are all the same kind. Thus, some methods assume the existence of a metric space (e.g., k-Means algorithm [7]), while other clustering algorithms require the instances to be described only by categorical features (e.g., Partitioning Around Medoids PAM [8]).
Unlike mixed data, missing or incomplete data do not depend on the features describing the phenomenon of interest, but rather appear due to the lack of the value for a particular attribute, on a specific instance. A particular value of a specific object may be unknown for numerous causes. Among the most frequent are: the inability to measure the desired variable; lack of knowledge regarding the phenomenon of interest [9] (commonly occurring in social sciences, where the data represents people under study); and the loss of a previously acquired value [10] (e.g., due to data sampling or storing equipment failure, contamination, or data loss during transmission).
It is commonly agreed upon by the scientific community of pattern recognition that the presence of missing values in a particular dataset implies an additional challenge for automatic learning algorithms. This is due to the prevailing trend of designing such methods to handle whole datasets: that is, with no missing information.
On the other hand, most of the proposed algorithms for clustering operate only over numerical data [2,3,5,6,11,12,13,14]. This unfortunate situation causes that several applications, which are relevant for human activities and whose data are described not only by numeric attributes, cannot be solved effectively.
Considering the previously described scenario, the methods and algorithm for clustering over mixed and incomplete data, are an evident minority in scientific literature [15]. The above considerations show the need of carried out thoughtful and systematic scientific research for the creation, design, implementation and application of methods and algorithms to perform intelligent clustering over mixed and incomplete data. The proposal of this paper clearly aligns along with the presented need.
In this paper, we use swarm intelligence algorithms, which are applied to clustering mixed and incomplete data in a unified and satisfactory approach. In addition, we perform a large amount of thoughtful and systematics numerical experiments. It is well-known among specialized swarm intelligence researchers that those algorithms are overly sensitive to parameter configuration; however, despite this being a highly relevant issue, to date we cannot find systematic studies analyzing the sensibility to parameter configuration for clustering trough swarm intelligence algorithms. We also address this issue in this paper.
The obtained results allow us to determine experimentally the adequate parameter configuration to obtain clusters of high quality over mixed and incomplete data. The above is done in such a way that the comparative studies performed allow us to state that, beyond doubt, the results obtained in this research are superiors to others reported in the literature.
The rest of the paper is organized as follows: Section 2 reviews some previous works for mixed and incomplete data clustering. Section 3 explains the proposed generic framework for swarm intelligence algorithms for clustering of mixed and incomplete data. Section 4 explores some case of study, and Section 5 addresses the experimental outline, the obtained results, and discusses them. The article ends with the conclusions and future works.
2. Background
Handling patterns described by mixed data or those who include missing values represents an additional challenge to tackle for automatic learning algorithms. The problem of mixed data (also known as hybrid data) can be defined as follows:
Let
be a dataset (i.e., set of objects, instances, or samples) in a universe U, where each object is described by a set of features or attributes ; each feature has associated a definition domain , which in turn may be of Boolean, k-valued, integer, real, or another kind [16].
Usually, the lack of information is denoted with the symbol “?” in many datasets available in public repositories, such as the UCI Machine Learning Repository [17] or the KEEL Project Repository [18,19]. Following this criterion, the value “?” is included in the domain of definition of the dataset feature; thus, the description of an incomplete object has the value “?” in place of the missing value. On the other hand, it is entirely possible that hybrid features, while also presenting missing values for some patterns describe a dataset. In this instance, the challenge faced by classification algorithms is even greater, since they need to handle both problems.
The solutions developed to manage such situations can be grouped mainly in two general strategies: they may work either by modifying the dataset before presenting it to the classification method; or by giving a particular algorithm the mechanisms to work with hybrid data, missing values, or both. The current section is dedicated to discussing some of the most well-known alternatives for solutions to one or both problems.
2.1. Data Level Solution for Clustering Mixed and Incomplete Data
Many automatic learning algorithms are designed to work only with numerical data, or only with categorical data, or only with complete data (i.e., no missing values). Thus, data-level solutions to these problems by means of pre-processing techniques [20] are primarily focused on one (or several, depending on the situation) of the following tasks: coding categorical data into a numerical representation, discretizing numerical data into a categorical representation, or solving missing values by eliminating or completing the corresponding patterns.
Despite the numerous advances in this regard, every data-level solution has an unavoidable impact on the dataset, since they will inevitably transform the data and even alter the intrinsic semantic relationships associated to the original representation of such data. This, in turn, has given rise to a spreading opinion among researchers and practitioners, in the sense that a more adequate solution to the problems of mixed data and missing values rests in developing automatic learning algorithms able to internally handle both aspects.
2.2. Algorithm Level Solution for Clustering Mixed and Incomplete Data
In this approach, the responsibility of handling mixed and incomplete data representations falls on the learning algorithm, considering that said method must include mechanisms aimed at such kinds of data. A recent review of clustering algorithms for mixed data can be found in [15].
Most of the algorithms for clustering mixed data rely on dissimilarity functions able to deal with such kind of data [21]. This approach backs to 1997, when Huang proposed the k-Prototype algorithm [22]. k-Prototype is an extension of the k-Means algorithm [23]. The extension is based on the definition of a dissimilarity function to compare the mixed instances, and in a new strategy to compute the cluster centroids.
All such mixed dissimilarity-based algorithms, as k-Prototype, do not consider the attribute dependences. This is due to these algorithms analyze the numerical and categorical features separately, and some of them separately construct the clusters centroids. Finally, the use of arbitrarily dissimilarity function may be inadequate for some domains.
Another strategy for mixed data clustering is to separately analyze the features, by projecting the instances. That is, the mixed dataset is divided into several subsets according to the different types of attributes, and each subset is clustered using according to some algorithms, and then, the results are combined as a new categorical dataset and then are clustered [24]. This idea has an obvious impact on the dataset, since they will transform the data twice and even alter the intrinsic semantic relationships associated with the original representation of such data.
A combination of the above alternatives is also presented in the literature. Some algorithms do divide the data, and also use mixed dissimilarity functions. By doing this, the disadvantages of both strategies are conserved. An example is the HyDaP algorithm [25]. It has two steps. The first one involves identifying the data structure formed by continuous variables and recognizing the relevant features for clustering. Then, the second step involves using a dissimilarity measure for mixed data to obtain clustering results.
In our opinion, a better solution can be found by applying bio-inspired algorithms. To the best of our knowledge, the AGKA algorithm by Roy and Sharma [4] is the first algorithm using bio-inspired strategies for dealing with the clustering of mixed data. It uses a genetic algorithm to obtain the clusters.
The representation used is a string having as length the instance count, where the i-th element of the string contains the cluster index to which the i-th instance is assigned. To obtain the cluster centers, the AGKA algorithm uses the centroid representation strategy and the dissimilarity function proposed in [21].
Despite the advantage of considering an evolutionary approach to clustering, the use of a pre-defined dissimilarity function is a drawback of the AGKA algorithm. In addition, the centroid description used may be inadequate to obtain few clusters, due to the characteristics of the cluster centroid description. On the other hand, the representation used by the AGKA algorithm makes difficult for the application of traditional operators to evolve the individuals. In addition, having thousands of instances implies having individuals described by string of thousands of lengths, which makes AGKA inadequate to handle medium and big size data.
To solve these drawbacks, we propose a generic framework for dealing with mixed and incomplete data clustering, in a more suitable way.
3. Generic Framework for Bio-Inspired Clustering of Mixed and Incomplete Data
Swarm intelligence is directly related to the intelligent behavior of collections of individuals or agents (birds, ants, fish, bats, bees, etc.) that move in an apparently unorganized way. In this context, this branch of scientific research aims to develop processes and algorithms that model and simulate the actions that these individuals perform to search for food [3,4].
There is an impressive range of possibilities for scientists to choose the types of agents that exhibit cooperative and self-organizing behavior. In addition to insects, birds and fish, it is also possible to consider the growth of bacteria or even swarms of robots that make up cellular robotic systems [5].
Typically, the individuals in the swarm are simple entities, but active and with their own movements. These individual movements, when incorporated into the swarm, allow generating a cooperative movement that results in collective search strategies, which significantly improve random searches. This is precisely called swarm intelligence, whose rules are so simple that it is a cause for wonder to realize how efficiently searches are performed [6,11].
In the following, we will supply a generic framework for mixed data clustering using bio-inspired algorithms. We propose a unified representation of the solutions, and a strategy to update the clustering solutions in the optimization process. Our approach is quite generic, and we believe that our proposal can be easily applied to several bio-inspired algorithms. It should be noted that we only focus on iterative improvement metaheuristics, not constructive ones. Constructive algorithms obtain the desired solution by parts. That is, there is no solution to the problem until the algorithm finishes. On the other hand, improvement heuristics start with an entire solution or set of solutions (usually random), and then refine them in the iterative process. This characteristic allows the user to have at least one solution to the problem at every iteration of the algorithm.
Our rationale is that using a unified strategy to model the clustering problem as an optimization problem, will lead to good clustering results, despite the swarm intelligence algorithm used. We bet on selecting a suitable representation, a useful updating strategy and an adequate optimization function. Our hypothesis is that if we manage to model mixed and incomplete data clustering as an optimization problem, we can obtain competitive results, and we will be able to obtain a clustering that fits the natural structure of data.
3.1. Representation
The representation of candidate solutions is one of the key aspects in metaheuristic algorithms. In fact, the representation used defines the operators applicable to the candidate solutions. For example, in real-valued representations, it is possible to consider a new solution by increasing the value of the current one with an epsilon value. In binary representation, the only modification allowed is the bit changing. In order-related representations, a solution is changed or updated by swapping some of its elements (ex. 2-opt operators [26]).
For clustering numerical data, the usual representation has been a matrix of size , where is the number of clusters and is the number of feature values [27]. However, as we are dealing with mixed values, with some absences on information, we adopted a simpler approach: we consider a candidate solution as an array of cluster centers.
Instead of creating an artificial center of a cluster , with , which is a clear disadvantage of previous proposals, we used the notion of prototype, in which the cluster center is defined as the instance who minimizes the dissimilarity with respect to the rest of instances in the cluster. It is not worthy to mention that we can use any dissimilarity function in the algorithms. By doing this, we also solve the drawback of using predefined functions. In Figure 1, it is shown an example of computing the center of a cluster, using the Euclidean distance.
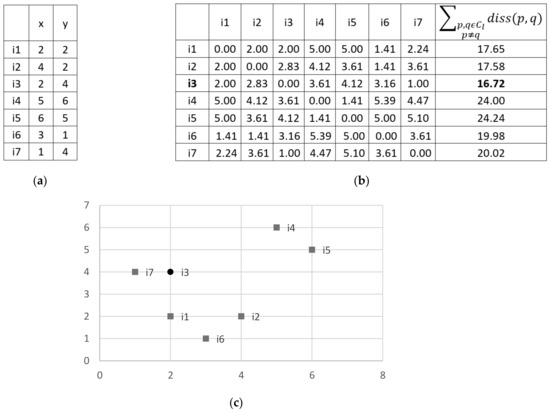
Figure 1.
Example of computation of a cluster center with 2D instances. (a) Instances in the cluster (b), Total dissimilarity among instances (using in this case the Euclidean distance) and (c) Instances in 2D; the cluster center (instance having minimum overall dissimilarity) is highlighted by a circle.
Formally, let be the dissimilarity among instances and , belonging to a cluster . The cluster center is selected as following:
If the minimum dissimilarity value is obtained with more than one instance, we can select as cluster center any of the instances that minimize the dissimilarity.
Thus, the proposed representation is an array, formed by the selected center of each cluster . Each individual is represented as . Considering this representation, an individual will have its current location (array of cluster centers) as well as other algorithm-dependent parameters. The swarm will know the set of instances to be clustered, and the optimization functions associated to the clustering problem.
From an implementation perspective, we can easily simplify this representation, by using the indexes of the selected cluster center instead of the information of the cluster center itself. Figure 2 shows the implementation of the proposed representation of a candidate solution, using the indices instead of the feature values of the cluster centers.
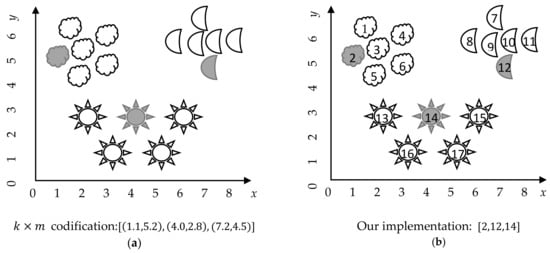
Figure 2.
Dataset composed by 17 instances, described by features (x and y), forming clusters. The cluster centers are highlighted in gray. (a) The traditional representation; (b) Our proposed implementation. Note that our implementation has a constant size , despite the number of features in the dataset.
This representation is simple, suitable, and easy to update, fulfilling the desirable characteristics for candidate solution representation in optimization problems. We consider that this proposal simplifies the optimization process, and is computationally effective, due to it consumes lower storage memory (just ) than the usual matrix representation. It is important to note than some problems have a large number of instances (i.e., m parameter), on the order of thousands and even hundreds of thousands, which makes the traditional representation computationally impractical. Our proposed representation contributes to computational efficiency, by diminishing the storage cost of the solution from to just .
3.2. Updating Strategy
All iterative improvement metaheuristic algorithms have in common that they update the current solution (or solutions) during the iterative cycle. The updating of the solutions usually takes into consideration the current solution, another solution in the population, the best solution in the population, and perhaps some randomly generated number (most programming languages include the capability of generating random number, usually by following a Uniform distribution. Unless specified otherwise, all random numbers referred in this paper follow a uniform distribution.). In this paper, we propose a unified updating strategy for dealing with the mixed clustering problem. Our proposal consists of changing a cluster center in the current solution. We generate a random number, representing the cluster whose center will be changed. Then, we selected from this cluster a random instance to replace the cluster center (Figure 3).
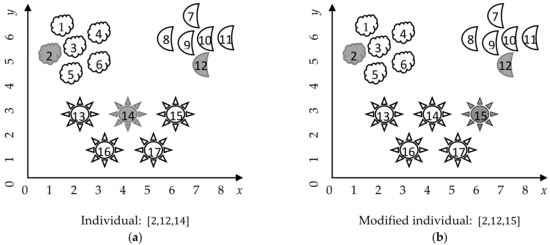
Figure 3.
Modification strategy for updating individuals. (a) The instances in 2D, with cluster centers highlighted in gray, and the corresponding individual, (b) the same instances in 2D, with the updated centers after the modification of the individual.
This strategy, although very simple, has two main advantages. It maintains a balance between exploration (by considering each instance in a cluster to be the new center) and exploitation (by considering only the instances already in the cluster to be center); and it directly handles the presence of attribute dependence, by selecting existent instances instead of independently modifying the features values of the centers.
Considering this updating strategy, it is possible to integrate it in the iterative improvement metaheuristic algorithms, while preserving the major characteristics of each of the original algorithms. In addition, this strategy is computationally simple due to it consisting only of updating the cluster centers.
In our implementation, we only need to generate a random number in the interval, which is very fast. In addition, because we only have a solution of size instead of a matrix, our procedure is inexpensive. The pseudocode of the proposed updating procedure is detailed in Algorithm 1. This simple procedure will be used in the three analyzed swarm intelligence algorithms.
| Algorithm 1. Pseudo code of the Updating procedure in the proposed framework to clustering mixed data. |
| Updating procedure |
| Inputs: : individual; : dataset of instances |
| Output: : modified individual |
Steps:
|
3.3. Fitness Functions and Dissimilarities
It has been assumed so far that there is a dissimilarity measure to compute the dissimilarity between instances in the clustering process. For experimental purposes, in this research, we used the Heterogeneous Euclidean Overlap Metric HEOM dissimilarity [28] to compare instances in such way. The HEOM dissimilarity was introduced by Wilson and Martínez [28] as an attempt to compare objects having mixed numerical and categorical descriptions. Let there be two instances and , and the HEOM dissimilarity is defined as:
By using the HEOM dissimilarity, we are able to directly compare mixed and incomplete instances, and to carried out the clustering process and to evaluate the resulting clustering, with the selected optimization functions. In addition, due to its simplicity and low computational cost, the HEOM dissimilarity is a feasible choice as an optimization function in evolutionary algorithms.
In addition, we have also assumed that there is a fitness or optimization function to guide the search process of the metaheuristic algorithms. In this research, we explore the use of three different optimization functions to guide the search process. The selected functions are validity indexes that have been widely used to determine the clustering quality [29]. Two of them correspond to maximization functions, that is, the greater the value, the better the clustering and the later corresponds to a minimization function.
The silhouette is the average, for all clusters, of the silhouette width of the instances belonging to that cluster [29]. Let be an instance of the cluster. Its silhouette width is defined as where is the average dissimilarity among and the other instances in its cluster, calculated as and is the minimum of the average dissimilarities among and the instances belonging to every other clusters, and it is defined as . The silhouette index of a set of clusters is defined by:
For an instance , its silhouette width is in the [−1, 1] interval. The greater the silhouette, the more compact and separated are the clusters.
The Dunn’s index for clustering considers the ratio between the minimum distance between two clusters, and the size of the bigger cluster. The same as the silhouette index, greater values correspond to better clustering [29].
The Davies–Bouldin index is a well-known unsupervised cluster validity index [30]. It considers the dispersion of instances in a cluster and the dissimilarity of clusters . The Davies–Bouldin index measures the average similarity between each cluster and its most similar cluster. The lower the values of the Davies–Bouldin index, the more compact and separated are the clusters. Formally, Davies–Bouldin index is defined as:
where is usually defined as .
There are defined several inter-cluster dissimilarities, as well as measures of cluster size. In this research, we used the centroid dissimilarity, as the inter-cluster measure, and the centroid measure for the cluster size.
4. Case Study
As a case study, to solve the clustering of mixed and incomplete data, we analyze three bio-inspired algorithms: the Artificial Bee Colony (ABC) algorithm [31], the Firefly Algorithm (FA) [32], and the Novel Bat Algorithm (NBA) [33], a recent development of the Bat Algorithm (BA) [34]. We selected these metaheuristic algorithms for four main reasons:
- All of them are metaheuristic algorithms, with a recent successful application to several optimization problems [35,36,37].
- They mimic different social behaviors, resulting in different approaches to explore the solution space.
- They have different approaches to exploit the best solutions, while avoiding trapping in local optima.
- ABC, FA, and BA algorithms have been successfully applied to clustering numerical data [5,11,12].
There are other bio-inspired algorithms fulfilling the above-mentioned reasons, such as Whale Optimization Algorithm [17], Dragonfly Algorithm [19], and others. However, we selected just three algorithms as a case of study, because the very large number of experiments needed to be performed for assessing their capabilities for clustering mixed and incomplete data. We suppose that the framework introduced in Section 3 is applicable to other bio-inspired algorithms as well.
In the later, we explain the selected metaheuristic algorithms, and we analyzed the common elements among them.
The Artificial Bee Colony (ABC) algorithm was introduced in 2007 [31], and it mimics the foraging of honey bees. The algorithm considers three kinds of bees: employed, onlooker, and scout bees. The solutions of the optimization problem are called food sources and have a position in the n-dimensional search space. Each food source has a nectar amount, corresponding to the desired fitness function of the optimization problem.
The ABC algorithm (Algorithm 2) start by sending the scout bees into the search space to randomly generate the initial food sources. Once obtained, the employed bees are assigned to the food sources. Then, each employed bee searches for a nearby food source in which the bee is employed. This searching for a new food source can be viewed as an updating mechanism, in which intervene the current solution, a randomly selected solution, and random numbers. If the new food source is better than the previous one, the employed bee discards the previous, and considers the new solution as its employed solution.
| Algorithm 2. Pseudo code of the ABC algorithm. |
| ABC optimization algorithm |
| Inputs: fitness function of D dimensions; : number of iterations; : population size; limit of food sources |
| Output: best solution |
Steps:
|
Based on the nectar amount of the food sources retained in the previous step, the ABC algorithm probabilistically determines which solutions the onlooker bees will visit. The onlooker bees visit those solutions and then fly around them to search for near food sources. Then, the algorithm considers a greedy selection process (same as the one carried out by the employed bees). After that, the scout bees search for exhausted food sources (not improved in iterations) and replace them by randomly generated new food sources. At the end of the pre-defined iterations, the ABC returns the best food source found.
The FA (Algorithm 3) was introduced in 2009 [32]. It mimics the coordinated flashing of fireflies. Although the real purpose of the bioluminescent behavior of fireflies is a current research topic for biologists, it is believed that it is related to finding mates, protecting against predators, and attracting potential preys. The FA algorithm consider some simplified rules about the behavior of fireflies: all are unisex, the attractive of a firefly is proportional to its brightness (the less attractive fireflies will move toward the most attractive fireflies) and the brightness of the fireflies is associated to a certain fitness function.
The attractiveness of fireflies is proportional to the intensity of the flashing seen by adjacent fireflies. The movement of a firefly being attracted by a firefly is determined by where the second term of the expression is due to the attractive , and the third term is a vector of random variables from a Gaussian distribution [32]. Best firefly moves randomly, that is, .
| Algorithm 3. Pseudo code of the FA algorithm. |
| FA optimization algorithm |
| Inputs: fitness function of D dimensions; : number of iterations; : population size; |
| Output: best solution |
Steps:
|
In 2009, Lukasik y Zak [38] experimentally obtained the optimum values for the parameters of the FA algorithm. They conclude that the best values of the parameters are , and the population number varying among 15 and 50 fireflies. These conclusions allow us to simplify the movement of a firefly, as follows: , with and .
Thus, the movement of the firefly becomes . That is, the movement of a firefly being attracted by a firefly is determined by just a modification (or update) of the position of the firefly.
The Novel Bat Algorithm (NBA) was proposed in 2015 [33] as an extension of the Bat Algorithm [34]. The NBA incorporates the compensation of the Doppler Effect in echoes by the bats. In addition, in NBA, the bats can forage in different habitats [33]. NBA uses a probability-based approach to determine the habitat selection of the bats. The bats use either a quantum-based approach, or a mechanical approach for habitat selection. In the quantum approach, the bats consider their positions, the position of the best bat and the mean position of the swarm to obtain new solutions. On the contrary, in the mechanical approach, the bats compensate the Doppler Effect and use the information in the updating process. Finally, the bats perform a local search based on the position of the best bat. The parameters of the NBA algorithm are updated with each iteration. Algorithm 4 shows the main steps of the NBA algorithm.
Although different, the analyzed algorithms have two things in common: They start by randomly generating the solutions, and then they modify the current solutions by considering a single solution (as in FA) or a combination of the current solution with another solution (as in ABC and NBA).
In either case, a random variation is introduced. Thus, the analyzed bio-inspired algorithms can be considered to operate in three stages: initialization, updating and returning. The updating stage, although different in every algorithm, includes a mechanism to modify or to update the current solutions. We used this common behavior to provide a unified representation of the solutions, and a strategy to update the clustering solutions in the optimization process.
We consider that the proposed framework for solution representation and updating is applicable to several other bio-inspired algorithms.
In the following, we explain the proposed integration into the three analyzed swarm intelligence algorithms. We introduce three clustering algorithms: The clustering based on Artificial Bee Colony (CABC), the clustering based on Firefly Algorithm (CFA), and the clustering based on Novel Bat Algorithm (CNBA). For the CABC algorithm, the pseudo code of the clustering approach is given in Algorithm 5. Note that the ABC original idea is preserved but contextualized to the mixed data clustering problem. On the other hand, for the CFA algorithm, we include the updating strategy as shown in Algorithm 6, to obtain the desired clustering.
Finally, for the CNBA algorithm, which has a more complex structure, we include the updating strategy as in Algorithm 7. In each case, we considered the elements that intervene in the updating of a certain solution, and integrate then in the proposed modification strategy, by considering the best solutions so far, the current solution, and a random process. Our approach, although quite simple, is very effective in modelling the mixed data clustering as optimization problem. In addition, we consider that this approach is useful, and can be effortless applied to other swarm intelligence algorithms.
| Algorithm 4. Pseudo code of the NBA algorithm. |
| NBA optimization algorithm |
| Inputs: f: fitness function of D dimensions; : number of iterations; : population size; : probability for habitat selection; : pulse emission rate of the i-th bat, w: inertia weight; Dopp: the compensation rates for Doppler effect in echoes; h: contraction–expansion coefficient; G: the frequency of updating the loudness and pulse emission rate; : parameters in basic Bat Algorithm |
| Output: best solution |
Steps:
|
| Algorithm 5. Pseudo code of the CABC algorithm to clustering mixed data. |
| CABC mixed clustering algorithm |
| Inputs: : dataset of instances; : cluster number; : number of iterations; : population size; limit of food sources |
| Output: : clustering of instances |
Steps:
|
| Algorithm 6. Pseudo code of the CFA algorithm to clustering mixed data. |
| CFA mixed clustering algorithm |
| Inputs: : dataset of instances; : cluster number; : number of iterations; : population size |
| Output: : clustering of instances |
Steps:
|
| Algorithm 7. Pseudo code of the CNBA algorithm to clustering mixed data. |
| CNBA mixed clustering algorithm |
| Inputs: : dataset of instances; : cluster number; : number of iterations; : population size; : probability for habitat selection; : pulse emission rate of the i-th bat |
| Output: : clustering of instances |
Steps:
|
5. Results and Discussion
In this section we explain the experiments made, as well as the used datasets, performance measures and statistical analysis, to determine the performance of the proposed clustering framework for mixed and incomplete data, by using Swarm Intelligence.
5.1. Datasets and Cluster Definition
To compare the proposed algorithm for clustering mixed and incomplete data, we used 15 mixed and/or incomplete datasets from the University of California at Irvine (UCI) repository of Machine Learning [17]. Table 1 gives the description of the considered datasets.

Table 1.
Description of the datasets used in the numerical experiments.
All the selected datasets have labelled instances; thus, it is possible to compare the results obtained by the clustering algorithms with respect to the labels of the data. Although in several studies the cluster number is greater than the number of classes (ex. having clusters, and only two or three classes [21]), we want to explore the use of bioinspired algorithms for finding the natural structure of data.
We are considering in the experiments that the natural structure of data is represented by the class labels. Thus, in our experiments, the instances of the same class should belong to the same cluster. We are not dealing with the issue of possible mislabeled or noisy instances. That is the reason why, in our experiments, the number of clusters to obtain was set as the number of classes in the corresponding dataset (column “Classes” of Table 1). Thus, our cluster number is in the set.
5.2. Performance Metrics and Statistical Tests
For comparing the results obtained by the algorithms, we used the cluster error measure [29]. Cluster error is one of the most used validity indexes. It matches the clusters obtained by the clustering algorithm with the clusters in the ground truth clustering.
Then, it counts the instances whose cluster assignment differs. The cluster error measure is the opposite of the purity measure, who counts the instances having equal cluster assignment in and . The lower the cluster error, the better the clustering. Let be the ground truth clustering, the obtained clustering and the number of instances in cluster . Let be the total number of instances, the number of instances in the cluster , not belonging to the cluster . The cluster error is given by:
We also use the adjusted Rand Iindex (ARI) [39] as the cluster performance measure. ARI is based on the computation of a contingency table between the real and obtained data partitions. Let us have instances, and two partitions, and . The partition has clusters, and the partition has clusters. We first compute a contingency table as in Figure 4, where the cells with represent the number of instances in both and clusters.

Figure 4.
Contingency table for the computation of the adjusted Rand index.
Then, we set three auxiliary variables x, y and z, to compute the ARI as , , and , and the ARI is computed as follows:
For the statistical comparison of results, we used the Wilcoxon signed-rank test to compare pair of algorithms. This is a non-parametric test for comparing paired differences among related samples. This test has been recommended by Demsar [40] for comparing pairs of algorithms over multiple datasets.
We use the Wilcoxon signed-rank test to determine the existence of significant differences in the clustering obtained by the different algorithms. We used the IBM SPSS Statistics 20 for computing this test [41].
We also used the Friedman test for related samples [25,35], followed by the Holm’s post-hoc test [36], to compare multiple samples over multiple datasets. Both tests are recommended in [15]. We used the KEEL software [24] for computing both tests. Our samples are related, due to the clustering algorithms are applied over the same datasets.
For all statistical tests, we set the null hypothesis as no differences, and the alternative hypothesis considering differences in performance. We use a significance level of 0.05, for a 95% level of confidence.
5.3. Experimental Design
For all experiments, we evaluated ten independent executions of the algorithms and averaged the results. We reported in the Supplementary Data Files the average and standard deviation obtained by the algorithms in all experiments according to cluster error and adjusted Rand index (ARI), as well as the results of the application of the statistical tests for cluster error. In this section, we will report the results of the Friedman and Holm tests for ARI measure, and the numerical results for both measures at Section 5.3.3.
5.3.1. Parameter configuration
First, to tune the main parameters of the metaheuristic algorithms, we carried out two experiments. The Experiment #1 was to determine the adequate iteration number of the algorithms, considering a small population (only 10 individuals). We evaluated the proposed algorithms considering 50, 100, 500, and 1000 iterations. We used the Davies–Bouldin index as the fitness function. We report in Table 2 and Table 3 the results of the Friedman test ranking and Holm’s post-hoc tests, respectively.

Table 2.
Ranking of Friedman test comparing the results of the proposed algorithms with different iteration number, according to ARI measure.

Table 3.
Results of the Holm test comparing the best performed iteration number of each algorithm with respect other iteration number, according to ARI measure.
The Friedman test rejected the null hypothesis for algorithms CABC and CNBA, therefore, we applied the Holm test (Table 3). Holm’s procedure rejects those hypotheses that have an unadjusted p-value lower or equal than 0:025, for both algorithms.
For CABC, Holm’s test does not reject the null hypothesis while comparing the results of using 100 iterations with the results of using 50 and 500 iterations. However, the test rejects the null hypothesis with respect using 1000 iterations. Considering the results of ARI, for using 100 and 1000 iterations (Supplementary Table S4), we can conclude that using 1000 iterations is worse than using 100. In our opinion, this is due to the CABC algorithm is overtrained.
For CNBA, the Holm’s test does not reject the null hypothesis while comparing the results of using 50 iterations with the results of using 500 and 1000 iterations. However, the test rejects the null hypothesis with respect using 100 iterations. Considering the results of ARI, for using 50 and 100 iterations (Supplementary Table S6), we can conclude that using 50 iterations is better than using 100. This result can be due to CNBA algorithm can lose good solutions and replace them by worse solutions (as does NBA), showing this good initial (50 iterations) and final (500 and 1000 iterations) behavior, with a gap of suboptimal performance at 100 iterations.
Due to the above results, we conclude than 50 iterations were sufficient to obtain high quality clusters.
Experiment #2 was to determine the adequate population size for the proposed algorithms. In this experiment, we evaluated populations of 10, 20, 30, and 40 individuals. Again, we used the the Davies–Bouldin index as fitness function. We want to test the influence of the population size in the performance of the algorithms, due to swarm intelligence algorithms are sensible to changes in population size [6]. Therefore, establishing an adequate population number for clustering will help the user to select good parameters for the proposed algorithms. In Table 4 we report the results of the statistical tests made to assess the existence or not of significant differences in performance of the three proposed algorithms, while using different population sizes.

Table 4.
Ranking of Friedman test comparing the results of the proposed algorithms with different population size, according to the ARI measure.
As shown, the Friedman test did not reject the null hypothesis for any of the compared algorithms, and no significant differences were found regarding the use of different population sizes. As shown, increasing the population number did not improve the results of the clustering process. The above results show the capabilities of our proposal, which obtained good clustering with only ten individuals and 50 iterations. These numbers are quite low and allows applying the algorithms over large datasets. In addition, we can conclude that those parameter values are good enough to obtain high-quality clusters.
5.3.2. Influence of the Fitness Function in the Clustering Results
The choice of an adequate fitness function is crucial for metaheuristic algorithms, due to the fitness values guide the optimization processes. We tested the influence of the fitness function in the results obtained by the proposed algorithms for clustering mixed and incomplete data. We compared the results using the Davies–Bouldin index, the Dunn´s index and the Silhouette index as fitness functions.
In this experiment, we again evaluated the clustering results considering cluster error and adjusted Rand index. In the Supplementary Data, we show the results of the algorithms considering these functions.
For the cluster error measure, the Friedman tests obtained p-values of 0.361799, 0.627089, and 0.165299 for CABC, CFA and CNBA, respectively. The tests did not find significant differences in the performance of the proposed algorithms, while using different fitness functions. The tests support the hypothesis of similar performance disregarding the validity index used by our modification of the bio-inspired algorithms for mixed and incomplete data clustering. These results confirm that the proposed algorithms are robust and do not heavily depend on the optimization function used by the optimization procedure, while using cluster error measure.
For the adjusted Rand index measure, the Friedman tests (Table 5) also support the hypothesis of equal performance disregarding the fitness function used, for both CFA and CNBA algorithms. However, for the CABC algorithm, the test rejects the null hypothesis and we applied the Holm’s test (Table 6).

Table 5.
Ranking of Friedman test comparing the results of the proposed algorithms with different fitness functions, according to ARI measure.

Table 6.
Results of the Holm test comparing the best performed fitness function of each algorithm with respect other fitness functions, according to the ARI measure.
The Holm’s procedure rejects those hypotheses that have an unadjusted p-value lower or equal than 0:05. That is, the test rejects the null hypothesis of equal performance while using Davies–Bouldin as fitness function, with respect using Dunn’s index. Considering the results of the CABC using both functions (Supplementary Table S18), the use of Dunn’s index is better than using Davies–Bouldin as the fitness function, with respect to the adjusted Rand index measure.
5.3.3. Comparison with Respect to Other Clustering Algorithms
At this point, we compare the proposed algorithm for clustering mixed and incomplete data with respect to previously reported algorithms. We used the algorithms k-Prototypes [22], AGKA [4] and AD2011 [21] in the comparisons. All of them deal with mixed data. The k-Prototypes algorithm has a specific dissimilarity function, which separates the computation of numeric and categorical feature dissimilarities, as well as missing feature values. The AGKA uses a dissimilarity function proposed by Ahmad and Dey in 2007 [42]. Such dissimilarity considers separately numeric and categorical features, and accounts for categorical feature value dissimilarities, in a personalized way. The same authors (Ahmad and Dey) refined their 2007 algorithm, and the result is the AD2011 algorithm.
For handling missing values directly, we modified the k-Prototypes algorithm in the following:
- (a)
- We did not consider missing values in mean nor in mode computations.
- (b)
- For numerical missing values, we replace the missing value by the mean value in the dissimilarity computation.
- (c)
- For categorical missing values, we consider them to be different to every other (non-missing) value, for the dissimilarity computation, and equal to other missing values.
For the AD2011 and AGKA algorithms, which use the same dissimilarity function and the same procedure for computing cluster centers, we modify the algorithms to make them able to deal with missing values, in the following:
- (a)
- We did not consider numerical missing values for the discretization procedure.
- (b)
- For numerical missing values, we replace the missing value by the mean value in the dissimilarity computation.
- (c)
- For categorical attributes, we consider the value “missing” as another admissible value in the procedures for finding significance and for computing cluster centers.
As performance measures, we considered cluster error and adjusted Rand index. The proposed algorithms used the Dunn’s index as fitness function, as well as ten individuals and 50 iterations. Table 7 show the obtained results for cluster error, and the best results are highlighted in Supplementary Data Files.

Table 7.
Performance results according to cluster error of CABC, CFA and CNBA with respect to other algorithms.
As shown in Table 7, the proposed algorithm for clustering mixed and incomplete data clearly outperformed previously reported algorithms, but for datasets postoperative and vowel. Table 8 show the obtained results for adjusted Rand index.

Table 8.
Performance results according to adjusted Rand index of CABC, CFA and CNBA with respect to other algorithms.
To establish if the differences in performance were significant or not, we again applied non-parametric statistical tests. The results for the Friedman tests are shown in Table 9, while the ones for Holm’s tests are shown in Table 10.

Table 9.
Ranking of Friedman test comparing the results of algorithms, according to cluster error and ARI measures.

Table 10.
Results of the Holm test comparing the best performed algorithm with respect others, according to the cluster error and ARI measures.
As shown, Friedman tests reject the null hypothesis for both the cluster error and ARI measures, evidencing the existence of significant differences in the performance of the algorithms. For the cluster error measure, Holm’s procedure rejects those hypotheses that have an unadjusted p-value lower or equal than 0.025, and for ARI, the ones with an unadjusted p-value lower or equal than 0.016667. Therefore, and analyzing the results of Table 7 and Table 8, we can conclude that the proposed CABC algorithm is significantly better than k-Prototypes, AGKA and AD2011 for the cluster error, and better than AGKA and AD2011 for ARI measure.
These numerical experiments allow us to conclude that the proposed strategy for clustering mixed and incomplete data using metaheuristic algorithms is highly competitive and leads to better results than other clustering algorithms.
As result of our research, we propose a representation of the clusters, which selects as cluster centers instances of the dataset. This is the first contribution to handle mixed and incomplete data. We did not create artificial instances by averaging numerical feature values and using the mode for categorical features; instead, we consider feature dependencies by selecting existing instances of the dataset. Second, we update the cluster centers by an updating procedure which changes the cluster center by another existing instance, instead of creating and artificial instance to be the center. In addition, we make our proposal able to be used with any dissimilarity function (HEOM is just an example used for the experiments), which allows the user to cluster the data with any function of their choice. This is a fundamental difference of previous proposals, which use fixed dissimilarity functions.
6. Conclusions
We have used several swarm intelligence algorithms to solve mixed and incomplete data clustering. Our proposal is emerging as a valuable contribution to the field, because most of the proposed algorithms for clustering operate only over numerical data, and therefore these algorithms are not capable of solving problems that are relevant for human activities and whose data are described not only by numeric attributes, but by mixed and incomplete data. Our proposal becomes a response to a problematic situation related to the fact that the methods and algorithm for clustering over mixed and incomplete data, are an evident minority in scientific literature, in addition to being ineffective.
In order to achieve an effective proposal that solves these types of problems, we have introduced a generic modification to three swarm intelligence algorithms (Artificial Bee Colony, Firefly Algorithm, and Novel Bat Algorithm). We also provide an unbiased comparison among several metaheuristics based clustering algorithms, concluding that the clusters obtained by our proposals are highly representative of the “natural structure” of data.
Our proposal significantly outperformed the k-Prototypes, AGKA and AD2011 clustering algorithms according to cluster error, and AGKA and AD2011 according to the adjusted Rand index. The numerical experiment allows us to conclude that the proposed strategy for clustering mixed and incomplete data using metaheuristic algorithms is highly competitive and leads to better results than other clustering algorithms. In addition, the experiments showed that the proposed algorithms are robust and do not heavily depend on the optimization function used. However, for CABC, we find that using Dunn’s index as fitness function led to better results according to the adjusted Rand index.
In addition, after a thoughtful analysis and a very large number of experiments, the statistical tests shown several useful results about the adequate parameter configuration for some metaheuristic algorithms applied to clustering mixed and incomplete data. Thus, according to the Wilcoxon test, we cannot reject the hypothesis of equality of performance between 10 individuals and greater number of individuals (20, 40, and 50); in addition, the test cannot reject the hypothesis of equality of performance between using 50 iterations and great number of iterations (100, 500, and 1000), in clustering mixed and incomplete data.
Supplementary Materials
The following Supplementary are available online at https://www.mdpi.com/article/10.3390/math9070786/s1, Table S1: Cluster error results of the CABC algorithm, with different iteration number; Table S2: Cluster error results of the CFA algorithm, with different iteration number, Table S3: Cluster error results of the CNBA algorithm, with different iteration number, Table S4: Cluster error results of the CABC algorithm, with different population sizes, Table S5: Cluster error results of the CFA algorithm, with different population sizes, Table S6: Cluster error results of the CNBA algorithm, with different population sizes, Table S7: Cluster error results of the CABC algorithm, with different fitness functions, Table S8: Cluster error results of the CFA algorithm, with different fitness functions; Table S9: Cluster error results of the CNBA algorithm, with different fitness functions.
Author Contributions
Conceptualization: Y.V.-R. and C.Y.-M.; methodology: Y.V.-R.; software: E.B.-C.; validation: E.B.-C. and Y.V.-R.; formal analysis: C.Y.-M.; investigation: O.C.-N.; writing—original draft preparation: Y.V.-R.; writing—review and editing: C.Y.-M.; visualization: Y.V.-R.; supervision: O.C.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All used datasets are publicly available at the Machine Learning repository of the University of California at Irvine (https://archive.ics.uci.edu/mL/datasets.php). accessed on 31 January 2021.
Acknowledgments
The authors would like to thank the Instituto Politécnico Nacional (Secretaría Académica, Comisión de Operación y Fomento de Actividades Académicas, Secretaría de Investigación y Posgrado, Centro de Investigación en Computación, and Centro de Innovación y Desarrollo Tecnológico en Cómputo), the Consejo Nacional de Ciencia y Tecnología, and Sistema Nacional de Investigadores for their economic support to develop this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grabowski, J.; Smoliński, A. The Application of Hierarchical Clustering to Analyzing Ashes from the Combustion of Wood Pellets Mixed with Waste Materials. Environ. Pollut. 2021, 276, 116766. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, K.; Balezentis, T.; Streimikiene, D.; Zhang, C. Extreme point bias compensation: A similarity method of functional clustering and its application to the stock market. Expert Syst. Appl. 2021, 164, 113949. [Google Scholar] [CrossRef]
- Yiping, W.; Buqing, S.; Jianjun, W.; Qing, W.; Haowu, L.; Zhanxiang, L.; Ningning, Z.; Qingchao, C. An improved multi-view collaborative fuzzy C-means clustering algorithm and its application in overseas oil and gas exploration. J. Pet. Sci. Eng. 2021, 197, 108093. [Google Scholar] [CrossRef]
- Roy, D.K.; Sharma, L.K. Genetic k-Means clustering algorithm for mixed numeric and categorical datasets. Int. J. Artif. Intell. Appl. 2010, 1, 23–28. [Google Scholar]
- Karaboga, D.; Ozturk, C. A novel clustering approach: Artificial Bee Colony (ABC) algorithm. Appl. Soft Comput. 2011, 11, 652–657. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S.; Paprzycki, M. Population size influence on the genetic and ant algorithms performance in case of cultivation process modeling. In Recent Advances in Computational Optimization; Springer: Berlin/Heidelberg, Germany, 2015; pp. 107–120. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data-An Introduction to Cluster Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Acock, A.C. Working with missing values. J. Marriage Fam. 2005, 67, 1012–1028. [Google Scholar] [CrossRef]
- Graham, J.W. Missing data theory. In Missing Data. Analysis and Design; Graham, J.W., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–46. [Google Scholar]
- Senthilnath, J.; Omkar, S.; Mani, V. Clustering using firefly algorithm: Performance study. Swarm Evol. Comput. 2011, 1, 164–171. [Google Scholar] [CrossRef]
- Komarasamy, G.; Wahi, A. An optimized K-means clustering technique using bat algorithm. Eur. J. Sci. Res. 2012, 84, 26–273. [Google Scholar]
- Wang, J.; Cao, J.; Li, B.; Lee, S.; Sherratt, R.S. Bio-inspired ant colony optimization based clustering algorithm with mobile sinks for applications in consumer home automation networks. IEEE Trans. Consum. Electron. 2015, 61, 438–444. [Google Scholar] [CrossRef]
- Serapiao, A.B.S.; Correa, G.S.; Goncalves, F.B.; Carvalho, V.O. Combining K-Means and K-Harmonic with Fish School Search Algorithm for data clustering task on graphics processing units. Appl. Soft Comput. 2016, 41, 290–304. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Ruiz-Shulcloper, J. Pattern recognition with mixed and incomplete data. Pattern Recognit. Image Anal. 2008, 18, 563–576. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Alcalá, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. J. Mult. Valued Log. Soft Comput. 2010, 17, 11. [Google Scholar]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ahmad, A.; Dey, L. A k-means type clustering algorithm for subspace clustering of mixed numeric and categorical datasets. Pattern Recognit. Lett. 2011, 32, 1062–1069. [Google Scholar] [CrossRef]
- Huang, Z. Clustering large data sets with mixed numeric and categorical values. In Proceedings of the 1st Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Singapore, 23–24 February 1997; pp. 21–34. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Triguero, I.; González, S.; Moyano, J.M.; García, S.; Alcalá-Fdez, J.; Luengo, J.; Fernández, A.; del Jesús, M.J.; Sánchez, L.; Herrera, F. KEEL 3.0: An open source software for multi-stage analysis in data mining. Int. J. Comput. Intell. Syst. 2017, 10, 1238–1249. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Osaba, E.; Yang, X.-S.; Diaz, F.; Lopez-Garcia, P.; Carballedo, R. An improved discrete bat algorithm for symmetric and asymmetric Traveling Salesman Problems. Eng. Appl. Artif. Intell. 2016, 48, 59–71. [Google Scholar] [CrossRef]
- José-Garía, A.; Gómez-Flores, W. Automatic clustering using nature-inspired metaheuristics: A survey. Appl. Soft Comput. 2016, 41, 192–213. [Google Scholar] [CrossRef]
- Wilson, D.R.; Martinez, T.R. Improved heterogeneous distance functions. J. Artif. Intell. Res. 1997, 6, 1–34. [Google Scholar] [CrossRef]
- Rendón, E.; Abundez, I.; Arizmendi, A.; Quiroz, E.M. Internal versus external cluster validation indexes. Int. J. Comput. Commun. 2011, 5, 27–34. [Google Scholar]
- Maulik, U.; Bandyopadhyay, S. Performance evaluation of some clustering algorithms and validity indices. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1650–1654. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Meng, X.-B.; Gao, X.; Liu, Y.; Zhang, H. A novel bat algorithm with habitat selection and Doppler effect in echoes for optimization. Expert Syst. Appl. 2015, 42, 6350–6364. [Google Scholar] [CrossRef]
- Yang, X.-S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Chen, G.; Qian, J.; Zhang, Z.; Sun, Z. Applications of novel hybrid bat algorithm with constrained Pareto fuzzy dominant rule on multi-objective optimal power flow problems. IEEE Access 2019, 7, 52060–52084. [Google Scholar] [CrossRef]
- Lukasik, S.; Zak, S. Firefly algorithm for continuous constrained optimization tasks. In Computational Collective Intelligence. Semantic Web, Social Networks and Multiagent Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 97–106. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Verma, J.P. Data Analysis in Management with SPSS software; Springer Science & Business Media: Delhi, India, 2013. [Google Scholar]
- Ahmad, A.; Dey, L. A k-mean clustering algorithm for mixed numeric and categorical data. Data Knowl. Eng. 2007, 63, 503–527. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).