Can Artificial Neural Networks Predict the Survival Capacity of Mutual Funds? Evidence from Spain

Abstract

Recently, the total net assets of mutual funds have increased considerably and turned them into one of the main investment instruments. Despite this increment, every year a considerable number of funds disappear. The main purpose of this paper is to determine if the neural networks can be a valid instrument to detect the survival capacity of a fund, using the traditional variables linked to the literature of disappearance funds: age, size, performance and volatility. This paper also incorporates annualized variation in return and the Sharpe ratio as variables. The data used is a sample of Spanish mutual funds during 2018 and 2019. The results show that the network correctly classifies funds into surviving and non-surviving with a total error of 13%. Moreover, it shows that not all variables are significant to determine the survival capacity of a fund. The results indicate that surviving and non-surviving funds differ in variables related to performance and its variation, volatility and the Sharpe ratio. However, age and size are not significant variables. As a conclusion, the neural network correctly predicts the 87% of survival capacity of mutual funds. Therefore, this methodology can be used to classify this financial instrument according to its survival or disappearance.

1. Introduction

In recent years, the total net assets of Spanish mutual funds have experienced a significant increase and became one of the main investment instruments used by investors. By the end of 2019, Spanish mutual funds had reached €276,866 millions of total net assets, outstripping the historical maximum reached in 2006. Furthermore, on analyzing the evolution of the risk profile of Spanish investors, it can be observed that they have channeled their investments towards more dynamic positions with a greater amount of equities component in their profiles. Among the reasons for this behavior, the most outstanding is the negative evolution of interest rates, which has forced participants to look for an extra return on their investments. The other main reason is structural and consists in the increasing financial culture among the average Spanish savers.

Despite this increment in the assets of mutual funds, every year a considerable number of funds disappear. In particular, there was a total of 273 disappearances between 2018 and 2019. Therefore, the main purpose of this paper is to determine if the neural networks can be a valid instrument to detect the survival capacity of mutual funds, as an alternative technique to existing ones. It will also allow us to contrast which variables are significant in the survival of the funds. If the error produced by the network is small, it can be analyzed which factors describe the disappearance of mutual funds and thus provide additional information about the risk of this product for both investors and managers.

In [1], a systematic review of the literature is carried out, finding that certain variables affect the survival capacity of mutual funds.

The two most analyzed variables in the literature are the size of the fund and the return of the fund. Numerous studies have stated that the most profitable funds and those with a greater asset volume have a greater probability of survival [2,3,4,5,6,7].

There is a lack of agreement as to over how many years prior to disappearance the return of a fund must be analyzed. To this effect, refs. [8,9,10] analyze the minimum period with negative returns before the fund disappears. While [8] finds that a fund with negative returns for three consecutive years is more likely to disappear, ref. [9] observes that funds that present bad results are more likely to continue behaving this way and do not survive if they exhibit negative returns for up to five years before their disappearance. Consequently, 1- and 3-year returns, and annualized variations in returns 1, 2 and 3 years before the disappearance, have been included in the present analysis.

Other studies also analyze what happens with investment flows prior to disappearance. In [3] mutual fund mergers and liquidations are analyzed, finding that smaller funds with lower inflows are more likely to disappear to the market. This finding is in line with [2,11,12].

Recently, refs. [6,13] analyze the characteristics of the target and acquiring funds. The study in [6] is one of the few that analyzes the Sharpe ratio as a determinant of mortality, concluding that target portfolios have lower Sharpe ratios in the pre-merger period than their acquiring portfolios. On the other hand, ref. [13] shows that the likelihood of disappearance is not significantly related to past performance because the worsening performance is a temporary phenomenon. Moreover, this author exposes that the risk measured as volatility is not significantly related to the probability of disappearance. Consequently, this study incorporates the traditional variables reported in the literature—age, size, investment flows, return, and risk—while also adding others considered as suitable to complement the study: annualized variation in return and the Sharpe ratio.

The use of an artificial neural network is proposed in this paper to analyze the incidence of these variables in the survival capacity of mutual funds. The applied network is the Self Organizing Maps (SOM) introduced by T. Kohonen.

This kind of artificial neural network has been applied in numerous studies in the field of finance, marketing and management, among others [14]. Regarding the application of this methodology to mutual funds, ref. [15] used SOM to evaluate the official classification of Spanish mutual funds by the CNMV (Spanish National Securities Market Commission) and Inverco (Spanish Association of Investment and Pension Funds), aiming to improve this classification with nonlinear techniques. Ref. [16] used SOM to determine if the characteristics which define the non-surviving funds are different according to their investment objectives. Recently, ref. [7] tested the suitability of SOM to predict the survival of mutual funds. Other authors have focused on forecasting the net asset value of mutual funds [17] and mutual fund performance [18,19], using other types of artificial neural networks such as back-propagation neural networks.

This paper aims to contribute towards the financial literature on mutual funds from three points of view. Firstly, using SOM to define the survival capacity of mutual funds as a complementary method to econometric models. Secondly, analyzing in a different market to the US, since this is the focus of most previous studies [1] and, thirdly, using other variables to those traditionally used. This paper is a totally complementary study to the previous ones because [16] used SOM to cluster mutual funds that disappear during 2013–2015 and analyzed if the variables, which define the survival capacity, take similar values for all of them or were different depending on the funds’ investment objectives. On the other hand, ref. [7] used the Cox model to define the survival model of Spanish mutual funds.

The paper is structured as follows. Section 2 describes the methodology applied, the Self-Organizing Maps, Section 3 explains the evolution of the Spanish industry and how the data are processed, Section 4 shows the empirical results and the final section presents the discussion of the paper.

2. Self Organizing Maps

SOM are a particular kind of artificial neural network. As part of them, this tool, developed by Teuvo Kohonen [20], is inspired by human neural functioning. SOM are based on the human brain’s ability to store similar information in a nearby area. For this reason, SOM are unsupervised neural networks, that is, they do not use external information for their learning algorithm, but rather use the similarity between the input information to create a features map where the input patterns are located according to the similarity between all their characteristics. SOM are formed by two layers with input and output neurons completely connected. A weight is associated with each connection or synapsis. In addition, to accomplish the training process, the output neurons (which form a bidimensional map) are connected among them and with themselves (lateral and auto-recurrent connections, respectively).

The implementation of this methodology has been carried out using the Toolbox for Matlab developed by the Laboratory of Computer and Information Science at the Helsinki University of Technology. Briefly, we can explain how SOM work in the following steps:

• Each pattern from the input information is represented by a vector, in which each component collects the value of a variable that defines the pattern. In this paper, the patterns are mutual funds, and the components that form the vectors are the variables that influence their survival capacity. Thus, an input pattern is represented as $X^p=\left(x_1^p,x_2^p,\dots ,x_i^p,\dots ,x_n^p\right),$ where p refers to the pattern and i to the variable, having a total of n variables that will coincide with the number of input neurons in the SOM. To homogenize the data, all the variables are normalized, so the variance of all of them is equal to one.
• As SOM use a competitive learning process, neurons in the output layer compete to become the winning neuron or the Best Matching Unit (BMU). For a pattern p, its BMU is the output neuron that accomplishes ${\mathit{min}}_k·\{\parallel X^p-W_{ki}\parallel \}$, where $\parallel \hspace{1em}\parallel$ symbolizes a measure of distance, $W_{ki}$ is the vector of weights formed by the weights that connect each input neuron i with an output neuron k, and k* refers to the BMU. When using the Euclidean distance, the criterion for determining the BMU for a pattern p is ${min}_{k\ast }\left(\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(x_i^p-w_{ki}\right)}^2}\right)$. Initially, we consider all the weights as random values.
• Once the BMU for a pattern has been determined, the weights associated with this neuron, as well as its neighbor neurons, are modified. The objective of this process is that patterns with similar characteristics also have the same BMU or another located close to it. The way to define the neighborhood area is by using a function that decreases as the distance between the output neurons increases. The function used in this case is the Gaussian function, $h_{k\ast k}\left(t\right)=e^{-\frac{\parallel r_{k\ast }-r_k\parallel }{2{\sigma }_t^2}}$, where $\parallel r_{k\ast }-r_k\parallel$ indicates the distance between an output neuron and the BMU, and σ is the neighborhood radius that decreases when the number of iterations increases. The new weights, then, are calculated as follows: $w_{ki}\left(t+1\right)=w_{ki}\left(t\right)+\alpha \left(t\right)·h_{k\ast k}\left(t\right)·\left[x_i^p-w_{ki}\left(t\right)\right]$, where $\alpha \left(t\right)$ is the learning rate. This rate, for convergence reasons, must decrease, using in our case $\alpha \left(t\right)={\alpha }_0/\left(1+100t/T\right)$, where ${\alpha }_0$ is the initial learning rate (by default, 0.5) and T is the total number of iterations.
• All the patterns are introduced into the network until obtaining the location of all patterns on the map (their position is determined by the corresponding BMU). In this way, the n-dimensional patterns are placed on a bidimensional map, with the most similar patterns being close and those that are different being further away.

It is important to note that SOM allows us to analyze non-linear relationships between variables without previously defining a specific relationship between them.

SOM can be applied to solve different problems; however, in the vast majority of studies, they are used for interpreting data, identifying objects, clustering and even reducing the dimension of the problem [21,22].

In this article, SOM is applied to cluster funds according to the variables analyzed in the financial literature on the survival capacity of mutual funds.

3. Data

3.1. Context of Spanish Mutual Funds Industry

Our study is placed in the context of the Spanish mutual fund industry. This section highlights some key features of this industry, and the data and variables used in this analysis are presented.

Figure 1 shows the total number of non-surviving funds each year and the annual mortality rate. This rate relates the number of disappeared funds in a period with the total number of live funds in the previous period.

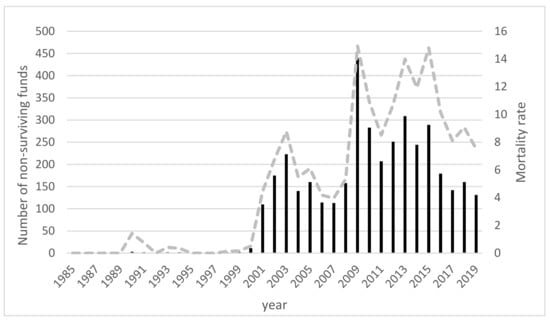
Figure 1. Evolution of the number of non-surviving funds in the Spanish market, 1985–2019.

Figure 1 clearly shows two time periods with high fund mortality, 2001–2003 and, even more obviously, 2008–2015. The first period coincides with the bursting of the technological bubble, causing huge losses among mutual fund holders, especially if they were particularly linked with the technological sector.

The second period coincides with the financial crisis which began in 2007, with a significant increase in the number of funds disappearing in 2009, reaching a total of 440 funds and a mortality rate of approximately 15%, representing the worst year ever for these funds in the Spanish market. There was also high mortality in the period 2013–2015, with a total of 309 (14% of the mortality rate) and 289 (14.8%) funds disappearing in the years 2013 and 2015, respectively. Notably, many fund disappearances in this period came about because of the major financial restructuring that occurred in Spain in this period, causing a process of mergers forced by the absorption or acquisition of fund companies.

As of 2016, the number of disappearances reduced, although more than 100 were still reported per year.

This study focuses on the years 2018 and 2019 because it is a period without external effects (for example, the financial restructuring that took place in Spain in the previous years) that may condition the results. Furthermore, this period is not directly affected by any of the financial crises that occurred in the early years of this century.

3.2. Sample

The data have been obtained from the Morningstar Direct database, which contains information on mutual funds around the world. In the database, there are a total of 1778 Spanish surviving funds at the end of 2019 and 291 corresponds to non-surviving funds during the last two years (2018 and 2019).

The funds that disappeared in the years covered in this study, 2018 and 2019, and the variables included in the analysis, were extracted from this database. Notably, only those funds for which data were available for up to 4 years prior to their disappearance, or those alive as of 2019, were used, because the analysis of certain variables, three-year annualized return and three-year standard deviation, limits the sample. Moreover, it is worth mentioning that the sample excludes all the guarantee funds in the Spanish market. These funds, by definition, have inception and obsolete dates a priori, so their inclusion could distort the results.

Once the funds that do not fulfill these characteristics have been removed, a sample of 142 non-surviving funds is obtained and 142 surviving funds are randomly added from the total available sample that met the requirements. It is important to point out that surviving funds and non-surviving funds have the same weight in the sample because the aim of our study is to understand which variables have a greater impact on survival capacity.

The variables were selected considering the theoretical framework of survival capacity of mutual funds. Table 1 details the variables selected for the analysis and their description and Table 2 presents the descriptive statistics of the sample divided into surviving and non-surviving funds.

Table 1. List and definition of variables.

Variable	Definition
Age	Number of years since the creation of the fund until its disappearance or, if it is alive, between its creation and 2019
Size	Natural logarithm of the total net assets (TNA) on 31 December 2019 or on the date of disappearance
VarSize1y	Variation in total net assets, expressed in percentage, in the year prior to its disappearance or the change between 31 December 2018 and 31 December 2019 if the fund is still alive. It is calculated using the formula: $flow{s}_t=\frac{TN{A}_t-TN{A}_{t-1}·\left(1+R_t\right)}{TN{A}_{t-1}}·100$, where $TN{A}_t$ and $TN{A}_{t-1}$ are the total net assets in year t and t − 1, respectively, and $R_t$ is the fund return in year t.
VarSize2y	Variation in total net assets, expressed in percentage, two years prior to its disappearance or the change between 31 December 2017 and 31 December 2019 if the fund is still alive
1-Year Return	Annual return obtained by the fund in 2019 or in the year of its disappearance
VarReturn1y	Annual variation, in relative terms, of return 1 year prior to its disappearance or if the fund is still alive the annual variation between 2018 and 2019
VarReturn2y	Annual variation, in relative terms, of return 2 years prior to its disappearance or the change between 2017 and 2018 if the fund is still alive
VarReturn3y	Annual variation, in relative terms, of return 3 years prior to its disappearance or the change between 2016 and 2017 if the fund is still alive
3-Year Annualized Return	Three-year annualized return obtained by the fund in 2019 or in the three years prior to its disappearance
1-Year Standard Deviation	Annual standard deviation calculated from monthly returns in 2019 or in the year of its disappearance
3-Year Standard Deviation	Standard deviation in the three previous years calculated from monthly returns in 2019 or in the year of its disappearance
Sharpe Ratio	The Sharpe ratio of the fund in the year prior to its disappearance or in 2019 if the fund is still alive. It is calculated using the formula: $SR=\frac{R_t-R_{fr}}{{\sigma }_t}$, where $R_t$ is the fund return in year $t, R_{fr}$ is the risk-free rate in year t (Spain 3-year Bond), and ${\sigma }_t$ is the volatility of the fund in year t.

Table 2. Descriptive statistics.

		Non-Surviving Funds				Surviving Funds
Code	Variable	Mean	Std dev	Min	Max	Mean	Std dev	Min	Max
Var1	Age	12.55	7.74	5.00	28.00	15.97	7.59	4.00	32.00
Var2	Size	16.65	1.70	6.35	21.78	17.57	1.58	14.23	23.10
Var3	VarSize1y	−0.19	0.35	−0.83	1.80	−0.10	0.49	−0.93	2.88
Var4	VarSize2y	−0.13	1.22	−0.91	11.61	0.22	1.14	−0.96	6.86
Var5	1-Year Return	−1.81	5.40	−19.30	31.27	11.13	7.94	0.43	32.40
Var6	VarReturn1y	−3.67	7.17	−65.29	5.98	3.21	3.56	0.58	26.73
Var7	VarReturn2y	−0.15	2.93	−10.33	12.99	−2.59	1.16	−6.57	0.61
Var8	VarReturn3y	−0.12	5.04	−15.28	41.69	1.89	3.22	−3.56	15.12
Var9	3-Year Annualized Return	−0.10	2.14	−5.99	10.62	2.62	2.97	−2.83	16.00
Var10	1-Year Standard Dev.	2.89	3.90	0.01	21.39	6.94	4.59	0.36	18.11
Var11	3-Year Standard Dev.	3.48	3.98	0.04	18.65	6.67	4.11	0.51	15.16
Var12	Sharpe Ratio	−8.75	18.03	−51.01	4.63	1.60	0.74	−0.06	4.13

Table 3 presents the correlation matrix. A high correlation between the variables related to performance (variables 5 and 9) and fund risk (variables 10 and 11) is found. In order not to overrepresent these variables in the network, one-year return (variable 5) and one-year standard deviation (variable 10) are excluded from the analysis, maintaining the three-year annualized return (variable 5) and the three-year deviation (variable 11).

Table 3. Correlation matrix.

	Var1	Var2	Var3	Var4	Var5	Var6	Var7	Var8	Var9	Var10	Var11	Var12
Var1	1
Var2	0.089	1
Var3	0.088	0.190	1
Var4	−0.021	0.256	0.552	1
Var5	0.120	0.243	0.033	0.102	1
Var6	0.194	0.294	0.183	0.155	0.535	1
Var7	−0.064	−0.173	−0.073	−0.037	−0.397	−0.178	1
Var8	0.022	−0.017	−0.042	0.015	0.158	0.003	−0.216	1
Var9	0.078	0.196	0.064	0.120	0.814	0.485	−0.160	0.216	1
Var10	0.208	−0.101	−0.039	0.005	0.492	0.155	−0.055	0.208	0.403	1
Var11	0.209	−0.095	−0.007	0.007	0.543	0.225	−0.050	0.179	0.455	0.940	1
Var12	0.127	0.057	0.100	0.026	0.249	0.183	−0.041	0.135	0.209	0.330	0.343	1

All variables are normalized. This process is necessary because the input variables are measured on different scales.

4. Results

When the network is implemented, it generates an output map of dimension 12 × 7 (12 rows × 7 columns). The dimension of the map depends on the number of units in it. When no number of units is specified, the default value assigned by the Toolbox is 5 times the square root of the number of patterns. Since we work with 284 mutual funds, the map will have 5 ∗ sqrt (284) = 84.26 units, which is rounded to 84 units. The number of rows and columns are then determined by calculating the two biggest eigenvalues of the input vectors. The ratio between side lengths is established to be the closest possible to 84, the value that in our case coincides with the product of 12 × 7.

Since the aim of this paper is to determine if the neural networks can be a valid instrument to detect the survival capacity of mutual funds in the Spanish market, it is established to force the output into two groups.

Figure 2 shows this map, where the corresponding patterns (funds) have been numbered and “YES” or “NO” indicate whether the fund disappeared or not at the end of 2019. If the fund disappears, the year of disappearance is also detailed (“18” or “19”).

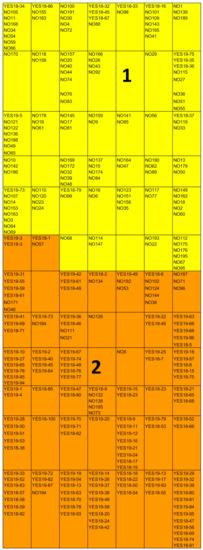
Figure 2. Self Organizing Maps (SOM) for Spanish mutual funds.

Group 1, located at the bottom, is formed by 133 funds of which 119 are surviving funds and 14 are non-surviving funds. Group 2, located at the top, contains 151 funds, specifically 23 surviving funds and 128 non-surviving funds.

Table 4 shows the accuracy percentage of the model, the error percentages of each type, and the total percentage error. As can be seen, the SOM correctly predicts 86.97% of the survival capacity of mutual funds in the Spanish market. Therefore, neural networks can be used to classify this financial instrument. If the variables analyzed in this work for a fund are included, this methodology makes it possible to predict with high accuracy the possibility that the fund will disappear or not.

Table 4. Error and accuracy percentages.

	Error		Accuracy		Total
	Number of Funds	%	Number of Funds	%	Number of Funds
Type I	14	10.53%	119	89.47%	133
Type II	23	15.23%	128	84.77%	151
Total	37	13.03%	247	86.97%	284

Once the methodology is validated, the second step is to analyze which variables define the survival capacity of mutual funds. To carry out this analysis, it is necessary to interpret the map of features (Figure 3). The map of features shows the value taken for each variable in the corresponding cell of the SOM (Figure 2). This value is represented by a color scale, where the highest values correspond to the red color, while the minimum values of each variable are represented in blue (Figure 3). The best expected value for some variables (volatility, for example) is represented by a low value (blue color), whereas for other variables (return, Sharpe ratio) a high level (red color) is desirable.

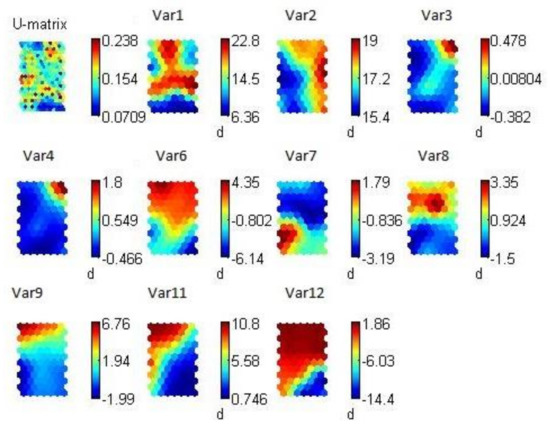
Figure 3. Map of features (The scale of values next to each map shows the rank of values which are taken by the representative patterns of all the mutual funds located in one cell).

Figure 3 shows that variables 6–9 and 12 present a location of high and low values similar to the SOM groups. This distribution is not observed in variables 1–5 and 11. For example, for group 1 of SOM (surviving funds), variable 1 (age) includes the full scale of values (from blue to red), so this group includes young and old funds, while the variable 6 (VarReturn1y) clearly shows that there are only high values of this variable in the group 1 (surviving funds) and there are medium and low values for group 2 (non-surviving funds).

Table 5 summarizes each group’s characteristics with their corresponding mean and standard deviation of each variable.

Table 5. Mean and standard deviation of variables in each group.

	Var1		Var2		Var3		Var4		Var6
Group	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev
1	15	7	17.60	1.60	−0.06	0.53	0.33	1.30	2.86	3.14
2	13	8	16.67	1.67	−0.21	0.30	−0.21	1.02	−2.95	7.61
	Var7		Var8		Var9		Var11		Var12
Group	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev	Mean	Std Dev
1	−2.58	1.58	2.35	4.19	3.13	3.08	7.52	3.91	1.58	0.83
2	−0.30	2.73	−0.40	4.06	−0.39	1.38	2.92	3.48	−8.11	17.66

5. Discussion

The map of SOM (Figure 2) and features (Figure 3), and Table 5 allow us to observe the similarities between the funds included in each group.

If each variable is analyzed separately, it can affirm that age (variable 1) and size (variable 2) do not determine the survival capacity of Spanish mutual funds during 2018 and 2019. This result is different from findings by [3,4,5,6,7,13,23], among others.

Regarding the variation of size (variables 3 and 4), they do not define the survival of funds, however, group 2 shows investment outflows as average in 1 (mean: −0.21) and 2 (mean: −0.21) years prior to the study in comparison to group 1 which presents investment inflows (mean: 0.33). This finding is in line with [2,3,7,11,12,16].

On the other hand, it can be observed that the annualized variation of return (variables 6, 7 and 8), three-year return (variable 9) and the Sharpe ratio (variable 12) define the mortality of Spanish funds because they are clearly different in each group. The average performance is clearly higher in surviving than in non-surviving funds over the long term, in line with other studies [2,4,7,12].

The Sharpe ratio, which is considered as a variable different from traditional, is higher as average in surviving funds (mean: 1.58) in comparison to non-surviving funds (mean: −8.11).

In conclusion, group 1, which includes the surviving funds, is characterized by high performance in three years, high volatility, and a high value of the Sharpe ratio, while group 2 (non-surviving funds) shows the following characteristics: low performance, low volatility and, moreover, funds of this group show investment outflows.