On an Intuitionistic Fuzzy Form of the Goguen’s Implication

Abstract

In the present paper we construct a new intuitionistic fuzzy implication, giving intuitionistic fuzzy form to Goguen’s implication. Some of its basic properties are studied and illustrated with examples. Geometrical interpretations of the different forms of the new implication are given. Other forms of the Goguen’s implication are discussed.

1. Introduction

Joseph Amadee Goguen (28 June 1941–3 July 2006) is the first PhD student of Lotfi Zadeh, working in the area of fuzzy sets. Its name is related to the following fuzzy implication (see, e.g., [1]):

$$a\to b=\left\{\begin{array}{cc}1,\hfill & \mathrm{i}\mathrm{f}a\le b,\hfill \\ {\displaystyle \frac{b}{a}},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

In the present paper, for the first time, an intuitionistic fuzzy form of the Goguen’s implication will be introduced.

Some years after the introduction of the concept of intuitionistic fuzziness, intuitionistic fuzzy logics (propositional, predicate, modal and temporal) were developed (see [2]). In the frames of the propositional intuitionistic fuzzy logic now there have been defined more than 190 different intuitionistic fuzzy implications. Except for the authors, intuitionistic fuzzy implications have been researched in details also by L. Atanassova, who in [3,4,5,6] introduced 11 implications (${\to }_{139},\dots ,{\to }_{149}$), and by P. Dworniczak [7,8,9] (who generalized these to implications ${\to }_{150},\dots ,{\to }_{152}$). In [10,11], L. Atanassova modified Dworniczak’s implications to ${\to }_{154},\dots ,{\to }_{165}$.

The aim of this whole direction of research over the intuitionistic fuzziness is to define a large set of possible implications and determined among them such a subset of implications that have the most suitable form and properties allowing for real use in different decision making applications.

In some definitions we shall use functions $\mathrm{s}\mathrm{g}$ and $\overline{\mathrm{s}\mathrm{g}}$:

$$\mathrm{s}\mathrm{g}\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}x>0\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}x\le 0\hfill \end{array},\right.\overline{\mathrm{s}\mathrm{g}}\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{i}\mathrm{f}x>0\hfill \\ 1\hfill & \mathrm{i}\mathrm{f}x\le 0\hfill \end{array}.\right.$$

Let everywhere intuitionistic fuzzy truth values of variables x and y be: $x=⟨a,b⟩,y=⟨c,d⟩.$

The geometrical interpretation of an element $x\in E$ with degrees ${\mu }_A\left(x\right)$ and ${\nu }_A\left(x\right)$ are shown on Figure 1 (see [2]).

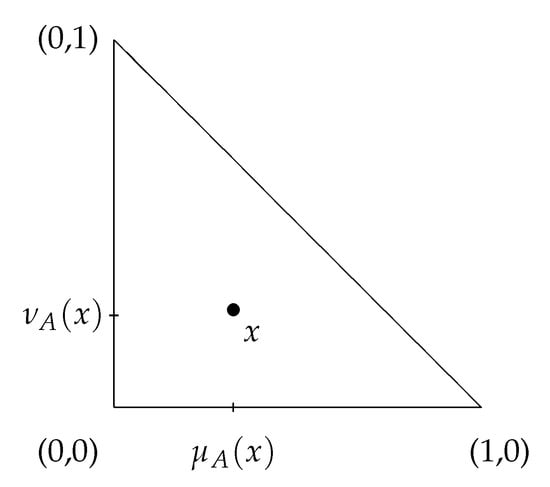
Figure 1. The geometrical interpretations of elements $x\in E$.

In [12], these pairs are called Intuitionistic Fuzzy Pairs (IFPs). The IFP $⟨a,b⟩$ is:

• A tautology if and only if (iff) $a=1$ and $b=0$;
• An intuitionistic fuzzy tautology (IFT) iff $a\le c\&b\ge d.$

For the two IFPs x and y, let $x\le y\mathrm{iff}a\le c\mathrm{and}b\ge d.$

2. Main Results

Let us suppose everywhere below that for each $p>0$,

$$\mathrm{s}\mathrm{g}\left(0\right)\frac{p}{0}=0.$$

Let us define for the IFPs x and y:

$$⟨a,b⟩\to ⟨c,d⟩=⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}⟩$$

First, we shall show that the definition of the new implication is correct.

Let $a,b,c,d\in [0,1]$ such that $a+b\le 1$ and $c+d\le 1$. Then, obviously:

$$\begin{array}{cc}\hfill 0& \le \overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\hfill \\ \hfill 0& \le \mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}.\hfill \end{array}$$

On the other hand, let

$$\begin{array}{cc}\hfill X& \equiv \overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\hfill \\ \hfill Y& \equiv \mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}.\hfill \end{array}$$

If $a\le c$, then

$$\begin{array}{cc}\hfill X& =1+0=1,\hfill \\ \hfill Y& =0\hfill \end{array}$$

and if $a>c$, then

$$\begin{array}{cc}\hfill X& =0+\frac{c}{1-b}\le \frac{c}{a}<1,\hfill \\ \hfill Y& =\frac{a-c}{1-b}\le \frac{a-c}{a}<1.\hfill \end{array}$$

Finally, let

$$X\equiv \overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}+\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}.$$

If $a>c$, then $b<1$, $\mathrm{s}\mathrm{g}(a-c)=1$ and $\overline{\mathrm{s}\mathrm{g}}(a-c)=0$, i.e.,

$$X=0+\frac{c}{1-b}+\frac{a-c}{1-b}=\frac{a}{1-b}\le 1.$$

If $a\le c$, then, $\mathrm{s}\mathrm{g}(a-c)=0$ and $\overline{\mathrm{s}\mathrm{g}}(a-c)=1$, i.e.,

$$X=1+0+0=1.$$

Therefore, the definition of the new implication is correct.

Now, we see that

$$⟨a,b⟩\to ⟨c,d⟩=\left\{\begin{array}{cc}⟨1,0⟩,\hfill & \mathrm{i}\mathrm{f}a\le c\hfill \\ ⟨{\displaystyle \frac{c}{1-b}},{\displaystyle \frac{a-c}{1-b}}⟩,\hfill & \mathrm{i}\mathrm{f}a>c\hfill \end{array}\right.$$

When we have fuzzy but not intuitionistic fuzzy variables, i.e., $b=1-a,d=1-c$, then

$$\begin{array}{cc}\hfill ⟨a,1-a⟩\to ⟨c,1-c⟩& =⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{a},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{a}⟩\hfill \\ \hfill & =\left\{\begin{array}{cc}⟨1,0⟩,\hfill & \mathrm{i}\mathrm{f}a\le c\hfill \\ ⟨{\displaystyle \frac{c}{a}},1-{\displaystyle \frac{c}{a}}⟩,\hfill & \mathrm{i}\mathrm{f}a>c\hfill \end{array}\right.\hfill \end{array}$$

Therefore, we obtain the standard Goguen’s implication.

In Figure 2, Figure 3, Figure 4 and Figure 5, we illustrate the proposed here intuitionistic fuzzy Goguen’s implication for the four basic possible scenarios for the mutual placement of the elements x and y, with particular numerical values.

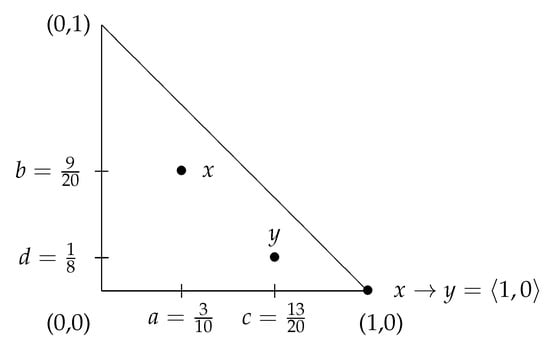
Figure 2. The geometrical interpretations of elements x, y and $x\to y$: first scenario.

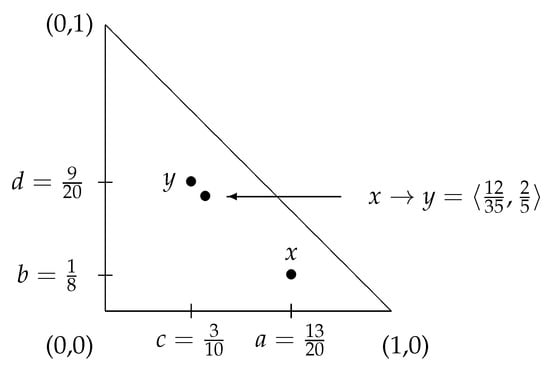
Figure 3. The geometrical interpretations of elements x, y and $x\to y$: second scenario.

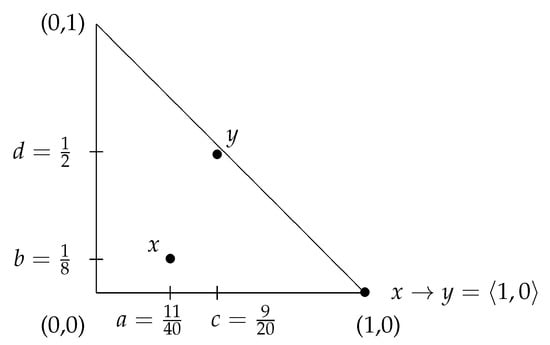
Figure 4. The geometrical interpretations of elements x, y and $x\to y$: third scenario.

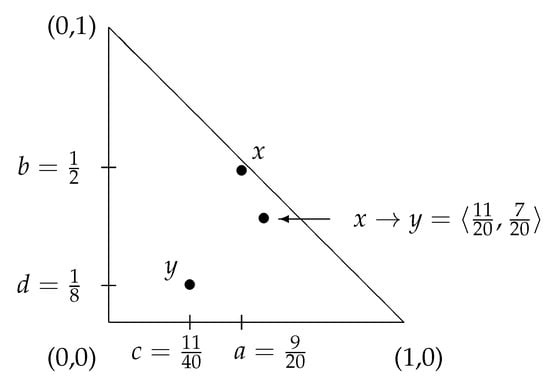
Figure 5. The geometrical interpretations of elements x, y and $x\to y$: fourth scenario.

The new implication generates the following negation.

$$\begin{array}{cc}\hfill \neg ⟨a,b⟩& =⟨a,b⟩\to ⟨0,1⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}\left(a\right)+\mathrm{s}\mathrm{g}\left(a\right)\frac{0}{1-b},\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}\left(a\right),\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}⟩\hfill \\ \hfill & =\left\{\begin{array}{cc}⟨1,0⟩,\hfill & \mathrm{i}\mathrm{f}a=0\hfill \\ ⟨0,{\displaystyle \frac{a}{1-b}}⟩,\hfill & \mathrm{i}\mathrm{f}a>0\hfill \end{array}\right.\hfill \end{array}$$

Now, we check directly the following equalities:

$$\begin{array}{cc}\hfill ⟨0,1⟩\to ⟨0,1⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨0,1⟩\to ⟨0,0⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨0,1⟩\to ⟨1,0⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨0,0⟩\to ⟨0,1⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨0,0⟩\to ⟨0,0⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨0,0⟩\to ⟨1,0⟩& =⟨1,0⟩,\hfill \\ \hfill ⟨1,0⟩\to ⟨0,1⟩& =⟨0,1⟩,\hfill \\ \hfill ⟨1,0⟩\to ⟨0,0⟩& =⟨0,1⟩,\hfill \\ \hfill ⟨1,0⟩\to ⟨1,0⟩& =⟨1,0⟩.\hfill \end{array}$$

Theorem 1.

The new implication

(a)

satisfies $x\to x$ as a tautology;

(b)

satisfies $x\to \neg \neg x$ as a tautology;

(c)

does not satisfy $\neg \neg x\to x$ even as an IFT.

Proof. 

First, we see that for each real number p:

$$\begin{array}{cc}\hfill \overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(p\right)\right)& =\left\{\begin{array}{cc}0,\hfill & \mathrm{i}\mathrm{f}p\le 0\hfill \\ 1,\hfill & \mathrm{i}\mathrm{f}p>0\hfill \end{array}\right.=\mathrm{s}\mathrm{g}\left(p\right),\hfill \\ \hfill \overline{\mathrm{s}\mathrm{g}}\left(\mathrm{s}\mathrm{g}\left(p\right)\right)& =\left\{\begin{array}{cc}1,\hfill & \mathrm{i}\mathrm{f}p\le 0\hfill \\ 0,\hfill & \mathrm{i}\mathrm{f}p>0\hfill \end{array}\right.=\overline{\mathrm{s}\mathrm{g}}\left(p\right),\hfill \\ \hfill \mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}\left(p\right)\right)& =\left\{\begin{array}{cc}1,\hfill & \mathrm{i}\mathrm{f}p\le 0\hfill \\ 0,\hfill & \mathrm{i}\mathrm{f}p>0\hfill \end{array}\right.=\overline{\mathrm{s}\mathrm{g}}\left(p\right),\hfill \\ \hfill \mathrm{s}\mathrm{g}\left(\mathrm{s}\mathrm{g}\right(p\left)\right)& =\left\{\begin{array}{cc}0,\hfill & \mathrm{i}\mathrm{f}p\le 0\hfill \\ 1,\hfill & \mathrm{i}\mathrm{f}p>0\hfill \end{array}\right.=\mathrm{s}\mathrm{g}\left(p\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \neg \neg ⟨a,b⟩& =\neg ⟨\overline{\mathrm{s}\mathrm{g}}\left(a\right),\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(a\right)\right),\mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}\left(a\right)\right)\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}⟩\hfill \\ \hfill & =⟨\mathrm{s}\mathrm{g}\left(a\right),(1-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}⟩\hfill \\ \hfill & =\left\{\begin{array}{cc}0,\hfill & \mathrm{i}\mathrm{f}a=0\hfill \\ 1,\hfill & \mathrm{i}\mathrm{f}a>0\hfill \end{array}.\right.\hfill \end{array}$$

For (a) we see that

$$\begin{array}{cc}\hfill x\to x& =⟨a,b⟩\to ⟨a,b⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(a-a)+\mathrm{s}\mathrm{g}(a-a)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-a)\frac{a-a}{1-b}⟩\hfill \\ \hfill & =⟨1,0⟩.\hfill \end{array}$$

Therefore, $x\to x$ is a tautology.

For (b) we obtain:

$$\begin{array}{cc}\hfill x\to \neg \neg x& =⟨a,b⟩\to \neg \neg ⟨a,b⟩\hfill \\ \hfill & =⟨a,b⟩\to ⟨\mathrm{s}\mathrm{g}\left(a\right),(1-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(a-\mathrm{s}\mathrm{g}\left(a\right))+\mathrm{s}\mathrm{g}(a-\mathrm{s}\mathrm{g}\left(a\right))\frac{\mathrm{s}\mathrm{g}\left(a\right)}{1-b},\mathrm{s}\mathrm{g}(a-\mathrm{s}\mathrm{g}\left(a\right))\frac{a-\mathrm{s}\mathrm{g}\left(a\right)}{1-b}⟩.\hfill \end{array}$$

If $a=0$, then $x\to \neg \neg x=⟨1+0,0⟩=⟨1,0⟩.$

If $a>0$, then $x\to \neg \neg x=⟨\overline{\mathrm{s}\mathrm{g}}(a-1)+\mathrm{s}\mathrm{g}(a-1)\frac{1}{1-b},\mathrm{s}\mathrm{g}(a-1)\frac{a-1}{1-b}⟩=⟨1,0⟩.$

Therefore, $x\to \neg \neg x$ is a tautology.

For (c) we see directly that

$$\begin{array}{cc}\hfill \neg \neg x\to x& =\neg \neg ⟨a,b⟩\to ⟨a,b⟩\hfill \\ \hfill & =⟨\mathrm{s}\mathrm{g}\left(a\right),(1-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}⟩\to ⟨a,b⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(\mathrm{s}\mathrm{g}\left(a\right)-a)+\mathrm{s}\mathrm{g}(\mathrm{s}\mathrm{g}\left(a\right)-a)\frac{a}{1-(1-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}},\hfill \\ \hfill & \mathrm{s}\mathrm{g}(\mathrm{s}\mathrm{g}\left(a\right)-a)\frac{\mathrm{s}\mathrm{g}\left(a\right)-a}{1-(1-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}}⟩.\hfill \end{array}$$

If $a=0$, then $\neg \neg x\to x=⟨1,0⟩.$ If $a>0$, then

$$\begin{array}{cc}\hfill \neg \neg x\to x& =⟨\overline{\mathrm{s}\mathrm{g}}(1-a)+\mathrm{s}\mathrm{g}(1-a)\frac{a}{1-\frac{0}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}},\mathrm{s}\mathrm{g}(1-a)\frac{1-a}{1-\frac{0}{1-\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}}}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(1-a)+\mathrm{s}\mathrm{g}(1-a)a,\mathrm{s}\mathrm{g}(1-a)(1-a)⟩.\hfill \end{array}$$

If $a<1$, then $\neg \neg x\to x=⟨a,1-a⟩.$

Obviously, if $a<0.5$, then $\neg \neg x\to x$ is not an IFT.

Finally, if $a=1$, then $\neg \neg x\to x=⟨1,0⟩.$

Therefore, $\neg \neg x\to x$, it is not an IFT and hence, it is not a tautology either. □

Theorem 2.

The new implication

(a)

satisfies Modus Ponens in the sense of a (classical) tautology,

(b)

does not satisfy Modus Ponens in the sense of an intuitionistic fuzzy tautology.

Proof. 

(a) Let $⟨a,b⟩$ be a tautology, i.e., $a=1$ and $b=0$ and let $⟨a,b⟩\to ⟨c,d⟩$ be a tautology, i.e., $\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c){\displaystyle \frac{c}{1-b}}=1$ and $\mathrm{s}\mathrm{g}(a-c){\displaystyle \frac{a-c}{1-b}}=0$. Then

$$1=\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c){\displaystyle \frac{c}{1-b}}=\overline{\mathrm{s}\mathrm{g}}(1-c)+\mathrm{s}\mathrm{g}(1-c)c.$$

If $c=1$ and hence $d=0$, the equality is valid, while if $c<1$, then the right-hand side of the equality is equal to $c<1$, that is a contradiction. Therefore, $⟨c,d⟩$ is a tautology.

(b) Let $⟨a,b⟩=⟨0,0⟩$, i.e., an IFT. Then,

$$⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}⟩=⟨1,0⟩$$

will be an IFT, e.g., for $⟨c,d⟩=⟨0.1,0.2⟩$, but the latest pair is not an IFT, i.e., the Modus Ponens is not valid. □

Some variants of fuzzy implications are described in the book of Klir and Yuan [1] and the following nine axioms are discussed, where $I(x,y)$ denotes $x\to y$ for any of the possible forms of the operation implication, N is the operation negation related with operation →:

• Axiom $A1$$(\forall x,y)(x\le y\to (\forall z\left)\right(I(x,z)\ge I(y,z)\left)\right)$,
• Axiom $A2$$(\forall x,y)(x\le y\to (\forall z\left)\right(I(z,x)\le I(z,y)\left)\right)$,
• Axiom $A3$$(\forall y)\left(I\right(0,y)=1)$,
• Axiom $A4$$(\forall y)\left(I\right(1,y)=y)$,
• Axiom $A5$$(\forall x)\left(I\right(x,x)=1)$,
• Axiom $A6$$(\forall x,y,z)\left(I\right(x,I(y,z))=I(y,I(x,z)\left)\right)$,
• Axiom $A7$$(\forall x,y)\left(I\right(x,y)=1$ iff $x\le y)$,
• Axiom $A8$$(\forall x,y)\left(I\right(x,y)=I(N\left(y\right),N\left(x\right)\left)\right)$,
• Axiom $A9$I is a continuous function.

For the purposes of our research, having in mind the specific forms of the intuitionistic fuzzy implication → and following [2], we modify three of these axioms, as follows.

• Axiom $A{4}^{*}$$(\forall y)\left(I\right(1,y)\ge y)$,
• Axiom $A{7}^{*}$$(\forall x,y)($ if $x\le y$, then, $I(x,y)$ is an IFT),
• Axiom $A{8}^{*}$$(\forall x,y)\left(I\right(I(x,y),I\left(N\right(y),N(x\left)\right)\left)\right)$ is a tautology.

In this way, the so modified axioms hold, but in weaker conditions, i.e., if the axioms $A4,A7,A8$ hold, then the weaker axioms $A{4}^{*},A{7}^{*},A{8}^{*}$ also hold, but this is not always true in the other direction.

Theorem 3.

The new intuitionistic fuzzy implication satisfies axioms $A2$, $A3$, $A{4}^{*}$, $A5$, $A{7}^{*}$ and $A{8}^{*}$ and it does not satisfy axioms $A1$, $A4$, $A6$, $A7$, $A8$ and $A9$.

Proof. 

For the validity of $A1$ we obtain the following.

Let $a\le c$ and $b\ge d$. Then

$$I(x,z)=⟨\overline{\mathrm{s}\mathrm{g}}(a-e)+\mathrm{s}\mathrm{g}(a-e)\frac{e}{1-b},\mathrm{s}\mathrm{g}(a-e)\frac{a-e}{1-b}⟩$$

$$I(y,z)=⟨\overline{\mathrm{s}\mathrm{g}}(c-e)+\mathrm{s}\mathrm{g}(c-e)\frac{e}{1-b},\mathrm{s}\mathrm{g}(c-e)\frac{c-e}{1-d}⟩$$

Now, we study the expressions

$$X\equiv \overline{\mathrm{s}\mathrm{g}}(a-e)+\mathrm{s}\mathrm{g}(a-e)\frac{e}{1-b}-\overline{\mathrm{s}\mathrm{g}}(c-e)-\mathrm{s}\mathrm{g}(c-e)\frac{e}{1-d}$$

and

$$Y\equiv \mathrm{s}\mathrm{g}(a-e)\frac{a-e}{1-b}-\mathrm{s}\mathrm{g}(c-e)\frac{c-e}{1-d}.$$

For X we obtain the following.

Let $a\le e$. Then

$$X\equiv 1-\overline{\mathrm{s}\mathrm{g}}(c-e)-\mathrm{s}\mathrm{g}(c-e)\frac{e}{1-d}.$$

If $c<e$, then $X=1-1-0=0.$

If $c\ge e$, then, due to $1-d\ge c\ge e$, $X\equiv 1-\frac{e}{1-d}\ge 0.$

Let $a>e$. Then $c\ge a>e$ and

$$X=\frac{e}{1-b}-\overline{\mathrm{s}\mathrm{g}}(c-e)-\mathrm{s}\mathrm{g}(c-e)\frac{e}{1-d}.$$

$$=\frac{e}{1-b}-\mathrm{s}\mathrm{g}(c-e)\frac{e}{1-d}.$$

If $c=a=e$, then

$$X=\frac{e}{1-b}\ge 0.$$

If $c>e$, then from $b\ge d$ it follows that

$$X=\frac{e}{1-b}-\frac{e}{1-d}=e\left(\frac{1}{1-b}-\frac{1}{1-d}\right)\ge 0.$$

Therefore, in all cases $X\ge 0$.

For Y we obtain the following.

Let $a\le e$. Then obviously $Y=-\mathrm{s}\mathrm{g}(c-e){\displaystyle \frac{c-e}{1-d}}.$

When $c>e$, then $Y<0$ and therefore the axiom is not true.

For the validity of $A2$ we obtain the following.

Let $a\le c$ and $b\ge d$. Then

$$I(z,x)=⟨\overline{\mathrm{s}\mathrm{g}}(e-a)+\mathrm{s}\mathrm{g}(e-a)\frac{a}{1-f},\mathrm{s}\mathrm{g}(e-a)\frac{e-a}{1-f}⟩,$$

$$I(z,y)=⟨\overline{\mathrm{s}\mathrm{g}}(e-c)+\mathrm{s}\mathrm{g}(e-c)\frac{c}{1-f},\mathrm{s}\mathrm{g}(e-c)\frac{e-c}{1-f}⟩.$$

Now, we study the expressions

$$X\equiv \overline{\mathrm{s}\mathrm{g}}(e-c)+\mathrm{s}\mathrm{g}(e-c)\frac{c}{1-f}-\overline{\mathrm{s}\mathrm{g}}(e-a)-\mathrm{s}\mathrm{g}(e-a)\frac{a}{1-f}$$

and

$$Y\equiv \mathrm{s}\mathrm{g}(e-a)\frac{e-a}{1-f}-\mathrm{s}\mathrm{g}(e-c)\frac{e-c}{1-f}.$$

For X we obtain the following.

Let $e\le c$. Then $X=1-\overline{\mathrm{s}\mathrm{g}}(e-a)-\mathrm{s}\mathrm{g}(e-a){\displaystyle \frac{a}{1-f}}.$

If $e\le a$, then $X=1-1=0.$

If $e>a$, then $X=1-{\displaystyle \frac{a}{1-f}}\ge 1-{\displaystyle \frac{a}{e}}>0.$

Let $e>c$. Then $e>c\ge a$ and $X=1-{\displaystyle \frac{a}{1-f}}\ge 1-{\displaystyle \frac{a}{e}}>0.$

Therefore, in all cases $X\ge 0$.

For Y we obtain the following.

Let $a<e$. Then $Y=\frac{e-a}{1-f}-\mathrm{s}\mathrm{g}(e-c){\displaystyle \frac{e-c}{1-f}}.$

If $c<e$, then $Y={\displaystyle \frac{e-a}{1-f}}-{\displaystyle \frac{e-c}{1-f}}={\displaystyle \frac{c-a}{1-f}}\ge 0.$

If $c\ge e$, then $Y={\displaystyle \frac{e-a}{1-f}}\ge 0.$

Therefore, in all cases $Y\ge 0$ and hence $A2$ is valid.

The check of $A3$ is trivial:

$$⟨0,1⟩\to ⟨a,b⟩=⟨\overline{\mathrm{s}\mathrm{g}}(-a)+\mathrm{s}\mathrm{g}(-a)\frac{0}{0},\mathrm{s}\mathrm{g}(-a)\frac{-a}{0}⟩=⟨1,0⟩.$$

For axioms $A4$ and $A{4}^{*}$ we obtain the following.

$$\begin{array}{cc}\hfill X\equiv ⟨1,0⟩\to ⟨a,b⟩& =⟨\overline{\mathrm{s}\mathrm{g}}(1-a)+\mathrm{s}\mathrm{g}(1-a)\frac{a}{1},\mathrm{s}\mathrm{g}(1-a)\frac{1-a}{1}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(1-a)+\mathrm{s}\mathrm{g}(1-a)a,\mathrm{s}\mathrm{g}(1-a)(1-a)⟩.\hfill \end{array}$$

If $a=1$, then $X=⟨1,0⟩,$ while if $a<1$, then $X=⟨a,1-a⟩\ge ⟨a,b⟩.$

Therefore, axiom $A4$ is not valid, but axiom $A{4}^{*}$ is true.

The check of axiom $A5$ is trivial:

$$⟨a,b⟩\to ⟨a,b⟩=⟨\overline{\mathrm{s}\mathrm{g}}(a-a)+\mathrm{s}\mathrm{g}(a-a)\frac{a}{1-b},\mathrm{s}\mathrm{g}(a-a)\frac{a-a}{1-b}⟩=⟨1,0⟩,$$

while the checks that axioms $A6$, $A7$ and $A8$ are similar to the check of the non-validity of axiom $A1$. For example, for $x=⟨0.2,0.0⟩$ and $y=⟨0.3,0.7⟩$, $x\to y=⟨1,0⟩$, but $x\nleqq y$.

Finally, we will check the validity of $A{8}^{*}$.

$$\begin{array}{cc}\hfill I(I& (x,y),I\left(N\right(y),N(x\left)\right))\hfill \\ \hfill & =(⟨a,b⟩\to ⟨c,d⟩)\to (\neg ⟨c,d⟩\to \neg ⟨a,b⟩)\hfill \\ \hfill & =(⟨a,b⟩\to ⟨c,d⟩)\to \left(⟨\overline{\mathrm{s}\mathrm{g}}\left(c\right),\mathrm{s}\mathrm{g}\left(c\right)\frac{c}{1-d}⟩\to ⟨\overline{\mathrm{s}\mathrm{g}}\left(a\right),\mathrm{s}\mathrm{g}\left(a\right)\frac{a}{1-b}⟩\right)\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}⟩\hfill \\ \hfill & \to ⟨\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))+\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(c\right)\frac{c}{1-d}},\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right)}{1-\mathrm{s}\mathrm{g}\left(c\right)\frac{c}{1-d}}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}⟩\hfill \\ \hfill & \to ⟨\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))+\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-d-\mathrm{s}\mathrm{g}\left(c\right)c},\hfill \\ \hfill & \mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))(1-d)}{1-d-\mathrm{s}\mathrm{g}\left(c\right)c}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b},\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}⟩\hfill \\ \hfill & \to ⟨\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))+\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d},\hfill \\ \hfill & \mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))(1-d)}{1-c-d}⟩\hfill \\ \hfill & =⟨\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d})\hfill \\ \hfill & +\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d})\hfill \\ \hfill & \frac{\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))+\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}}{1-\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}},\hfill \\ \hfill & \mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d})\hfill \\ \hfill & \frac{\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}}{1-\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}}⟩.\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill X& \equiv \overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d})\hfill \\ \hfill & +\mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}(a-c)+\mathrm{s}\mathrm{g}(a-c)\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))-\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}\right)\hfill \\ \hfill & .\frac{\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))+\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}}{1-\mathrm{s}\mathrm{g}(a-c)\frac{a-c}{1-b}}.\hfill \end{array}$$

If $a\le c$, then $\overline{\mathrm{s}\mathrm{g}}\left(c\right)\le \overline{\mathrm{s}\mathrm{g}}\left(a\right)$, i.e., $\overline{\mathrm{s}\mathrm{g}}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))=1,\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\le \overline{\mathrm{s}\mathrm{g}}\left(a\right)=0$ and

$$\begin{array}{cc}\hfill X& =\overline{\mathrm{s}\mathrm{g}}(1-1-0.\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d})+0.\mathrm{s}\mathrm{g}\left(1+0.\frac{c}{1-b}-1-0.\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}\right).\frac{1+0\frac{\overline{\mathrm{s}\mathrm{g}}\left(a\right)(1-d)}{1-c-d}}{1-0.\frac{a-c}{1-b}}\hfill \\ \hfill & =\overline{\mathrm{s}\mathrm{g}}\left(0\right)=1.\hfill \end{array}$$

If $a>c$, then $\mathrm{s}\mathrm{g}\left(a\right)=1,\overline{\mathrm{s}\mathrm{g}}\left(a\right)=0,\overline{\mathrm{s}\mathrm{g}}(a-c)=0,\mathrm{s}\mathrm{g}(a-c)=1,\overline{\mathrm{s}\mathrm{g}}\left(c\right)\ge \overline{\mathrm{s}\mathrm{g}}\left(a\right),$ i.e., $\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)-\overline{\mathrm{s}\mathrm{g}}\left(a\right))=1,\mathrm{s}\mathrm{g}(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\le \overline{\mathrm{s}\mathrm{g}}\left(a\right)=0$ and

$$\begin{array}{cc}\hfill X& =\overline{\mathrm{s}\mathrm{g}}(0+\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right)-\mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right).0)+\mathrm{s}\mathrm{g}\left(0+\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right)-\mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right).0\right)\hfill \\ \hfill & .\frac{\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right)+\mathrm{s}\mathrm{g}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right).0}{1-\frac{a-c}{1-b}}\hfill \\ \hfill & =\overline{\mathrm{s}\mathrm{g}}(\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right))+\mathrm{s}\mathrm{g}\left(\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right)\right)\frac{\overline{\mathrm{s}\mathrm{g}}\left(\overline{\mathrm{s}\mathrm{g}}\left(c\right)\right)}{1-\frac{a-c}{1-b}}.\hfill \end{array}$$

If $c=0$, then

$$\begin{array}{cc}\hfill X& =\overline{\mathrm{s}\mathrm{g}}(0-\overline{\mathrm{s}\mathrm{g}}\left(1\right))+\mathrm{s}\mathrm{g}(0-\overline{\mathrm{s}\mathrm{g}}\left(1\right))\frac{\overline{\mathrm{s}\mathrm{g}}\left(0\right)}{1-\frac{a}{1-b}}\hfill \\ \hfill & =\overline{\mathrm{s}\mathrm{g}}\left(0\right)+\mathrm{s}\mathrm{g}\left(0\right)\frac{1}{1-\frac{a}{1-b}}=1+0=1.\hfill \end{array}$$

If $c>0$, then

$$\begin{array}{cc}\hfill X& =\overline{\mathrm{s}\mathrm{g}}(\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(0\right))+\mathrm{s}\mathrm{g}\left(\frac{c}{1-b}-\overline{\mathrm{s}\mathrm{g}}\left(0\right)\right)\frac{\overline{\mathrm{s}\mathrm{g}}\left(0\right)}{1-\frac{a-c}{1-b}}\hfill \\ \hfill & =\overline{\mathrm{s}\mathrm{g}}(\frac{c}{1-b}-1)+\mathrm{s}\mathrm{g}\left(\frac{c}{1-b}-1\right)\frac{1}{1-\frac{a-c}{1-b}}\hfill \end{array}$$

and since from $\frac{c}{1-b}\le 1$ it follows that $\mathrm{s}\mathrm{g}(\frac{c}{1-b}-1)=0$ and $\overline{\mathrm{s}\mathrm{g}}(\frac{c}{1-b}-1)=1$, then

$$X=1.$$

Therefore, $A{8}^{*}$ is valid as a tautology. □

3. Conclusions

In this paper, we have introduced a new intuitionistic fuzzy implication that has intuitionistic but not classical behaviour.

In a future leg of the present research, new properties of the new implication will be studied. We will check which axioms of Brower’s intuitionistic logic and which Kolmogorov’s axioms are valid. We will study the relations between the newly proposed implication and the existing ones.

The intuitionistic fuzzy Goguen’s implication will be modified similarly to the the modification of the other implications, discussed in [2].

In future, three new intuitionistic fuzzy conjunctions and disjunctions will be defined in the sense of [13,14,15].