On the Omega Distribution: Some Properties and Estimation

Abstract

We obtain explicit expressions for single and product moments of the order statistics of an omega distribution. We also discuss seven methods to estimate the omega parameters. Various simulation results are performed to compare the performance of the proposed estimators. Furthermore, the maximum likelihood method is adopted to estimate the omega parameters under the type II censoring scheme. The usefulness of the omega distribution is proven using a real data set.

1. Introduction

Dombi et al. [1] pioneered the three-parameter omega distribution and obtained some of its mathematical properties. It allows for modeling bathtub-shaped hazard function ($hf$). This model has two characteristics: simplicity and flexibility. The simplicity is because its cumulative distribution function ($cdf$) and $hf$ include only power functions and lack exponential terms. The flexibility follows from the fact that it has bounded support, while the exponential function tends to infinity over an unbounded support. Furthermore, Dombi et al. [1] proposed two statistical estimation methods for the omega parameters: the first one depends on the log-likelihood function, the so-called global optimization method to maximize it, and the second depends on fitting its $cdf$ to an empirical $cdf$.

The probability density function ($pdf$) and $cdf$ of the omega distribution, say Omg($\alpha ,\beta ,d$), are

$$f\left(x\right)=\left\{\begin{array}{c}0,\mathrm{if}x\le 0,\hfill \\ \frac{\alpha \beta d^{2\beta }{x}^{\beta -1}}{d^{2\beta }-x^{2\beta }}{\left(\frac{d^{\beta }+x^{\beta }}{d^{\beta }-x^{\beta }}\right)}^{-\frac{\alpha d^{\beta }}{2}},\mathrm{if}0<x<d,\hfill \\ 0,\mathrm{if}x\ge d\hfill \end{array}\right.$$

(1)

and

$$F\left(x\right)=\left\{\begin{array}{c}0,\mathrm{if}x\le 0,\hfill \\ 1-{\left(\frac{d^{\beta }+x^{\beta }}{d^{\beta }-x^{\beta }}\right)}^{-\frac{\alpha d^{\beta }}{2}},\mathrm{if}0<x<d,\hfill \\ 1,\mathrm{if}x\ge d,\hfill \end{array}\right.$$

(2)

respectively, where $\alpha >0$, $\beta >0$ and $d>0$. The parameter $\alpha$ is the scale, and the maximum density function increases with it. The parameter $\beta$ is the shape, and the density function is strictly monotonously decreasing when $\beta \in (0,1)$ and unimodal when $\beta >1$. Clearly, the parameter d specifies the support.

Henceforth, we denote by X a random variable with density (1). Notice that

$$(d^{2\beta }-x^{2\beta })f\left(x\right)=\alpha \beta d^{2\beta }{x}^{\beta -1}[1-F\left(x\right)].$$

(3)

Okorie and Nadarajah [2] derived closed-form expressions for the raw moments and quantile function of the omega distribution. The applications of moments of order statistics are well-known in the statistical literature; see [3,4,5]. Explicit expressions for order statistics moments were determined by [6]. For more results in this context, one may also refer to [7,8,9,10] and the references therein.

In recent years, the importance of order statistics has increased because of the more frequent use of nonparametric inferences and robust procedures. The aim in this paper is to complete the works of Dombi et al. [1] and of Okorie and Nadarajah [2] by deriving explicit expressions for single and product moments of the order statistics of the omega distribution. The L-moments are also obtained. These results can be adopted to derive the best linear unbiased (BLU) and best linear invariant (BLI) estimators of the scale and location-scale parameters of the omega distribution as well as the BLU predictors and BLI predictors of future unobserved order statistic; see, for example [11].

The characterizations of distributions based on the moments of order statistics have also been of great interest to researchers for the past several decades. Therefore, it is important to mention that the findings of this paper can also be useful in the characterization of the omega distribution; see, for example [12,13].

We also consider different methods for estimating the omega parameters and provide numerical simulations to examine the mean square errors (MSEs) of the proposed estimators. Furthermore, the method of maximum likelihood is adopted to estimate the distribution parameters under type II censored samples. It is proven empirically that the omega distribution provides a better fit than ten extensions of the Weibull distribution (with three and four parameters), namely the modified Weibull [14], transmuted complementary Weibull-geometric [15], Lindley Weibull [16], power generalized Weibull [17], alpha power Weibull [18], alpha power exponentiated-Weibull [19], exponentiated-Weibull [20], extended odd Weibull exponential [21], logarithmic transformed Weibull [22], and Weibull distributions.

This paper is organized as follows. In Section 2, we derive explicit expressions for single and product moments of the order statistics from the omega distribution. Some of its statistical properties are obtained in Section 3. Seven estimation methods are presented in Section 4. A simulation study is done in Section 5, and some conclusions are offered in Section 6.

2. Single and Product Moments of Order Statistics

Let $X_1,\cdots ,X_n$ be a random sample of size n from the omega distribution with $pdf$$f\left(x\right)$ and $cdf$$F\left(x\right)$, given in (1) and (2), respectively, and let $X_{1:n}\le \cdots \le X_{n:n}$ be the associated order statistics. The $pdf$ of the rth-order statistic $X_{r:n}$ is given (for $1\le r\le n$) by [23,24]

$$f_{r:n}\left(x\right)={\phi }_{r:n}f\left(x\right)F{\left(x\right)}^{r-1}{[1-F\left(x\right)]}^{n-r},0<x<d,$$

(4)

and the joint $pdf$ of the rth ($X_{r:n}$) and sth ($X_{s:n}$) order statistics is (for $1\le r<s\le n$)

$$\begin{array}{c}{f}_{r,s:n}(x,y)={\phi }_{r,s:n}f\left(x\right)F{\left(x\right)}^{r-1}{[F\left(y\right)-F\left(x\right)]}^{s-r-1}f\left(y\right){[1-F\left(y\right)]}^{n-s},0<x<y<d,\end{array}$$

(5)

where

$${\phi }_{r:n}=\frac{n!}{(n-r)!(r-1)!}\mathrm{and}{\phi }_{r,s:n}=\frac{n!}{(r-1)!(n-s)!(s-r-1)!}.$$

Next, the kth single moment of $X_{r:n}$ takes the form

$${\mu }_{r:n}^{\left(k\right)}=E\left(X_{r:n}^k\right)={\int }_0^d{x}^k{f}_{r:n}\left(x\right)dx;1\le r\le n;k\in \mathbb{N},$$

(6)

and the $(k,l)$th product moment of $X_{r:n}$ and $X_{s:n}$ reduces to

$${\mu }_{r,s:n}^{(k,l)}=E\left(X_{r:n}^k{X}_{s:n}^{{}^l}\right)={\int }_0^d{\int }_x^d{x}^k{y}^l{f}_{r,s:n}(x,y)dydx,1\le r<s\le n,k,l\in \mathbb{N}.$$

(7)

Furthermore, we use the integral [25]

$${\int }_0^1{x}^{\lambda -1}{(1-x)}^{\mu -1}{(1-\eta x)}^{-\nu }dx=B(\lambda ,\nu ){}_2{F}_1\left(\nu ,\lambda ;\lambda +\mu ;\eta \right),\lambda >0,\mu >0,$$

(8)

to prove some results of this paper, where

$$B(a,b)={\int }_0^1{t}^{a-1}{(1-t)}^{b-1}dt\mathrm{and}{}_2{F}_1(a,b;c;x)=\sum _{p=0}^{\infty }\frac{{\left(a\right)}_p{\left(b\right)}_p}{{\left(c\right)}_p}\frac{x^p}{p!}$$

are the beta and Gauss hypergeometric functions, respectively, and ${\left(e\right)}_p=e(e+1)\cdots$$(e+p+1)$.

2.1. Single Moments

The results are now presented in the form of theorems.

Theorem 1.

For the omega distribution (1) ($1\le r\le n-1$, $k\in \mathbb{N}$), we have

$${\mu }_{r:n}^{\left(k\right)}=\alpha d^{k+\beta }\sum _{i=r}^n\sum _{p=0}^{i-1}{(-1)}^{p+i-r}\left(\genfrac{}{}{0pt}{}{i-1}{r-1}\right)\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i-1}{p}\right)iB\left(\frac{k}{\beta }+1,\frac{\alpha (p+1)d^{\beta }}{2}+1\right)$$

$${\times }_2{F}_1\left(\frac{\alpha (p+1)d^{\beta }}{2}+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{\alpha (p+1)d^{\beta }}{2}+1;-1\right).$$

(9)

Proof. 

In view of (6) and the result given by [23] (Page 45), we can write

$${\mu }_{r:n}^{\left(k\right)}=\sum _{i=r}^n{(-1)}^{i-r}\left(\genfrac{}{}{0pt}{}{i-1}{r-1}\right)\left(\genfrac{}{}{0pt}{}{n}{i}\right){\mu }_{i:i}^{\left(k\right)},1\le r\le n-1,k\in \mathbb{N},$$

(10)

where

$${\mu }_{i:i}^{\left(k\right)}=i{\int }_0^d{x}^{k}f\left(x\right){\left[F\right(x\left)\right]}^{i-1}dx$$

(11)

or, equivalently, from Equation (3),

$${\mu }_{i:i}^{\left(k\right)}=i\alpha \beta d^{2\beta }\sum _{p=0}^{i-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{i-1}{p}\right){\int }_0^d\frac{x^{k+\beta -1}}{(d^{2\beta }-x^{2\beta })}{[1-F(x\left)\right]}^{p+1}dx$$

$$=i\alpha \beta d^{2\beta }\sum _{p=0}^{i-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{i-1}{p}\right){\int }_0^d\frac{x^{k+\beta -1}}{(d^{\beta }+x^{\beta })(d^{\beta }-x^{\beta })}{\left(\frac{d^{\beta }+x^{\beta }}{d^{\beta }-x^{\beta }}\right)}^{-\frac{\alpha (p+1)d^{\beta }}{2}}dx.$$

(12)

Setting $z=x^{\beta }/d^{\beta }$, Equation (12) can be rewritten as

$${\mu }_{i:i}^{\left(k\right)}=i\alpha d^{k+\beta }\sum _{p=0}^{i-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{i-1}{p}\right){\int }_0^1{z}^{\frac{k}{\beta }}{\left(1-z\right)}^{\frac{\alpha (p+1)d^{\beta }}{2}-1}{\left(1+z\right)}^{-\frac{\alpha (p+1)d^{\beta }}{2}-1}dz.$$

Using the integral Formula (8), we obtain

$${\mu }_{i:i}^{\left(k\right)}=i\alpha d^{k+\beta }\sum _{p=0}^{i-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{i-1}{p}\right)B\left(\frac{k}{\beta }+1,\frac{\alpha (p+1)d^{\beta }}{2}+1\right)$$

$$\times {}_2{F}_1\left(\frac{\alpha (p+1)d^{\beta }}{2}+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{\alpha (p+1)d^{\beta }}{2}+1;-1\right).$$

Inserting ${\mu }_{i:i}^{\left(k\right)}$ in Equation (10), it follows (9).

An alternative equation for ${\mu }_{r:n}^{\left(k\right)}$ follows.    □

Theorem 2.

For $1\le r\le n$ and $k\in \mathbb{N}$, we obtain

$${\mu }_{r:n}^{\left(k\right)}={\phi }_{r:n}\alpha d^{\beta +k}\sum _{p=0}^{r-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{r-1}{p}\right)B\left(\frac{k}{\beta }+1,\frac{\alpha }{2}(p+n-r+1)d^{\beta }+1\right)$$

$${\times }_2{F}_1\left(\frac{\alpha }{2}(p+n-r+1)d^{\beta }+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{\alpha }{2}(p+n-r+1)d^{\beta }+1;-1\right),$$

(13)

where ${\phi }_{r:n}$ is defined in Section 2.

Proof. 

From Equation (6), we have

$${\mu }_{r:n}^{\left(k\right)}={\phi }_{r:n}{\int }_0^d{x}^{k}f\left(x\right){\left[F\left(x\right)\right]}^{r-1}{[1-F\left(x\right)]}^{n-r}dx.$$

$$={\phi }_{r:n}\sum _{p=0}^{r-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{r-1}{p}\right){\int }_0^d{x}^{k}f\left(x\right){[1-F\left(x\right)]}^{n-r+p}dx.$$

(14)

Applying similar steps from Theorem 1 leads to (13).    □

Remark 1.

(a) Setting $n=r=1$ in (9) or (13), we obtain

$${\mu }_{1:1}^{\left(k\right)}=E\left(X^k\right)=\alpha d^{\beta +k}B\left(\frac{k}{\beta }+1,\frac{\alpha d^{\beta }}{2}+1\right){}_2{F}_1\left(\frac{\alpha d^{\beta }}{2}+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{\alpha d^{\beta }}{2}+1;-1\right),$$

(15)

which is the kth moment of X reported by [2].

Setting $k=1,2,3$ and $k=4$ in Equation (15), one can obtain simple expressions for the first four moments of X [2].

(b) Setting $r=1$ in (13),

$${\mu }_{1:n}^{\left(k\right)}=n\alpha d^{\beta +k}B\left(\frac{k}{\beta }+1,\frac{n\alpha d^{\beta }}{2}+1\right){}_2{F}_1\left(\frac{n\alpha d^{\beta }}{2}+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{n\alpha d^{\beta }}{2}+1;-1\right),$$

(16)

and setting $r=n$ in (13),

$${\mu }_{n:n}^{\left(k\right)}=n\alpha d^{\beta +k}\sum _{p=0}^{n-1}{(-1)}^p\left(\genfrac{}{}{0pt}{}{n-1}{p}\right)B\left(\frac{k}{\beta }+1,\frac{\alpha }{2}(p+1)d^{\beta }+1\right)$$

$${\times }_2{F}_1\left(\frac{\alpha }{2}(p+1)d^{\beta }+1,\frac{k}{\beta }+1;\frac{k}{\beta }+\frac{\alpha }{2}(p+1)d^{\beta }+1;-1\right),$$

(17)

which are moments of the extremum order statistics.

Recurrence relations for single moments of order statistics from the $cdf$ (2) are given below.

Theorem 3.

For $1\le r\le n$ and $k\in \mathbb{N}$,

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}=\frac{k}{n\alpha \beta }\left[{\mu }_{r:n}^{(k-\beta )}-\frac{{\mu }_{r:n}^{(k+\beta )}}{d^{2\beta }}\right]$$

(18)

and, consequently,

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n}^{\left(k\right)}=\frac{k}{(n-r+1)\alpha \beta }\left[{\mu }_{r:n}^{(k-\beta )}-\frac{{\mu }_{r:n}^{(k+\beta )}}{d^{2\beta }}\right].$$

(19)

Proof. 

Khan et al. [26] proved that (for $1\le r\le n$)

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}=\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)k{\int }_0^{\infty }{x}^{k-1}{\left[F\left(x\right)\right]}^{r-1}{[1-F\left(x\right)]}^{n-r+1}dx.$$

(20)

or, equivalently, from (3),

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}=\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)\frac{k}{\alpha \beta }{\int }_0^d{x}^{k-\beta }f\left(x\right){\left[F\left(x\right)\right]}^{r-1}{[1-F\left(x\right)]}^{n-r}dx$$

$$-\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)\frac{k}{\alpha \beta d^{2\beta }}{\int }_0^d{x}^{k+\beta }f\left(x\right){\left[F\left(x\right)\right]}^{r-1}{[1-F\left(x\right)]}^{n-r}dx,$$

which leads to (18). Using the relation for moments ([23], p. 44)

$$n{\mu }_{r-1:n-1}^{\left(k\right)}=(n-r+1){\mu }_{r-1:n}^{\left(k\right)}+(r-1){\mu }_{r:n}^{\left(k\right)},$$

in Equation (18), we obtain (19). This completes the proof.    □

Remark 2.

We obtain the negative moments in Theorem 3 when $k<\beta$. For applications, see [27,28].

Corollary 1.

For $n\ge 1$ and $k\in \mathbb{N}$,

$${\mu }_{1:n}^{\left(k\right)}=\frac{k}{n\alpha \beta }\left[{\mu }_{1:n}^{(k-\beta )}-\frac{{\mu }_{1:n}^{(k+\beta )}}{d^{2\beta }}\right]$$

(21)

and

$${\mu }_{n:n}^{\left(k\right)}-{\mu }_{n-1:n}^{\left(k\right)}=\frac{k}{\alpha \beta }\left[{\mu }_{n:n}^{(k-\beta )}-\frac{{\mu }_{n:n}^{(k+\beta )}}{d^{2\beta }}\right].$$

(22)

Proof. 

Equations (21) and (22) follow by setting $r=1$ and $r=n$, respectively, in (19) with ${\mu }_{0:m}^{\left(k\right)}=0$ for $m\ge 1$ and $k\in \mathbb{N}$.    □

2.2. Product Moments

The product moment of order statistics from the omega distribution are reported below.

Theorem 4.

For $1\le r<s\le n$ and $k,l\in \mathbb{N}$, we can write

$${\mu }_{r,s:n}^{(k,l)}-{\mu }_{r,s-1:n}^{(k,l)}=\frac{l}{(n-s+1)\alpha \beta }\left[{\mu }_{r,s:n}^{(k,l-\beta )}-\frac{{\mu }_{r,s:n}^{(k,l+\beta )}}{d^{2\beta }}\right].$$

(23)

Proof. 

Khan et al. [29] showed that (for $1\le r<s\le n$)

$$\begin{array}{c}\hfill {\mu }_{r,s:n}^{(k,l)}-{\mu }_{r,s-1:n}^{(k,l)}={\phi }_{r,s:n}\frac{l}{(n-s+1)}{\int }_0^d{x}^{k}f\left(x\right){\left[F\left(x\right)\right]}^{r-1}\mathrm{I}\left(x\right)dx,\end{array}$$

(24)

where

$$\mathrm{I}\left(x\right)={\int }_x^d{y}^{l-1}{[1-F(y\left)\right]}^{n-s+1}{[F\left(y\right)-F\left(x\right)]}^{s-r-1}dy.$$

(25)

Using (3) in Equation (25), we obtain

$$\mathrm{I}\left(x\right)=\frac{1}{\alpha \beta }{\int }_x^d{y}^{l-\beta }{[1-F(y\left)\right]}^{n-s}{\left[F\right(y)-F(x\left)\right]}^{s-r-1}f\left(y\right)dy$$

$$-\frac{1}{\alpha \beta d^{2\beta }}{\int }_x^d{y}^{l+\beta }{[1-F(y\left)\right]}^{n-s}{\left[F\right(y)-F(x\left)\right]}^{s-r-1}f\left(y\right)dy.$$

(26)

Substituting (26) in Equation (24) and simplifying lead to (23).    □

Remark 3.

The negative moments follow in Theorem 4 when $l<\beta$.

Corollary 2.

For the omega distribution, we obtain ($k,l\in \mathbb{N}$)

$${\mu }_{r,r+1:n}^{(k,l)}-{\mu }_{r:n}^{(k+l)}=\frac{l}{(n-r)\alpha \beta }\left[{\mu }_{r,r+1:n}^{(k,l-\beta )}-\frac{{\mu }_{r,r+1:n}^{(k,l+\beta )}}{d^{2\beta }}\right],1\le r\le n-1,n\ge 3,$$

(27)

and

$${\mu }_{n-1,n:n}^{(k,l)}-{\mu }_{n-1:n}^{(k+l)}=\frac{l}{\alpha \beta }\left[{\mu }_{n-1,n:n}^{(k,l-\beta )}-\frac{{\mu }_{n-1,n:n}^{(k,l+\beta )}}{d^{2\beta }}\right],n\ge 2.$$

(28)

Proof. 

The recurrence relation (27) follows when $s=r+1$ in Equation (23) and noting that [29]

$${\mu }_{r,r:n}^{(k,l)}=E\left[X_{r:n}^k{X}_{r:n}^l\right]=E\left[X_{r:n}^{k+l}\right]={\mu }_{r:n}^{(k+l)}.$$

Furthermore, setting $s=n$ and $r=n-1$ in Equation (23), the recurrence relation (28) follows as

$${\mu }_{n-1,n-1:n}^{(k,l)}=E\left[X_{n-1:n}^k{X}_{n-1:n}^l\right]=E\left[X_{n-1:n}^{k+l}\right]={\mu }_{n-1:n}^{(k+l)}.$$

   □

Corollary 3.

For $k=0$ in Theorem 4, Theorem 3 follows.

Remark 4.

Setting $k=1$ in (13), we calculate the means and second moments of the order statistics for the omega distribution (for $n=1\left(1\right)5$) for various parameters, reported in Table 1. It can be noted that the condition ${\sum }_{r=1}^n{\mu }_{r:n}=nE\left(X\right)$ holds [23].

Table 1. Moments of order statistics from the omega distribution for several parametric values.

		$d=0.50$
		$\alpha =0.25,\beta =0.75$			$\alpha =0.75,\beta =0.25$
n	r	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$
1	1	$0.013726$	$0.004213$	$0.004024$	$0.013719$	$0.003157$	$0.002968$
2	1	$0.023849$	$0.007062$	$0.006493$	$0.013363$	$0.002548$	$0.002369$
	2	$0.003602$	$0.001363$	$0.001351$	$0.014075$	$0.003766$	$0.003568$
3	1	$0.031307$	$0.008945$	$0.007965$	$0.010607$	$0.001677$	$0.001565$
	2	$0.008935$	$0.003296$	$0.003216$	$0.018876$	$0.004288$	$0.003932$
	3	$0.000935$	$0.000397$	$0.000397$	$0.011675$	$0.003504$	$0.003368$
4	1	$0.036770$	$0.010140$	$0.008788$	$0.007984$	$0.001049$	$0.000985$
	2	$0.014916$	$0.005360$	$0.005137$	$0.018476$	$0.003562$	$0.003221$
	3	$0.002953$	$0.001231$	$0.001223$	$0.019277$	$0.005015$	$0.004643$
	4	$0.000263$	$0.000119$	$0.000119$	$0.009140$	$0.003001$	$0.002917$
5	1	$0.040730$	$0.010844$	$0.009185$	$0.005938$	$0.000649$	$0.000614$
	2	$0.020931$	$0.007325$	$0.006887$	$0.016170$	$0.002646$	$0.002385$
	3	$0.005894$	$0.002411$	$0.002377$	$0.021934$	$0.004936$	$0.004455$
	4	$0.000992$	$0.000445$	$0.000444$	$0.017505$	$0.005067$	$0.004761$
	5	$0.000081$	$0.000038$	$0.000038$	$0.007049$	$0.002484$	$0.002434$
		$d=0.90$
		$\alpha =0.25,\beta =0.75$			$\alpha =0.75,\beta =0.25$
n	r	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$
1	1	$0.035482$	$0.019216$	$0.017957$	$0.025358$	$0.010194$	$0.009551$
2	1	$0.057569$	$0.029494$	$0.026180$	$0.022597$	$0.007307$	$0.006797$
	2	$0.013394$	$0.008938$	$0.008758$	$0.028120$	$0.013081$	$0.012290$
3	1	$0.071164$	$0.034511$	$0.029446$	$0.016735$	$0.004361$	$0.004081$
	2	$0.030381$	$0.019462$	$0.018539$	$0.03432$	$0.013200$	$0.012023$
	3	$0.004901$	$0.003675$	$0.003651$	$0.02502$	$0.013021$	$0.012395$
4	1	$0.079262$	$0.036410$	$0.030127$	$0.011916$	$0.002509$	$0.002367$
	2	$0.046870$	$0.028814$	$0.026617$	$0.031192$	$0.009918$	$0.008945$
	3	$0.013891$	$0.010109$	$0.009916$	$0.037447$	$0.016483$	$0.015081$
	4	$0.001904$	$0.001531$	$0.001527$	$0.020878$	$0.011867$	$0.011431$
5	1	$0.083749$	$0.036471$	$0.029457$	$0.008468$	$0.001445$	$0.001373$
	2	$0.061312$	$0.036166$	$0.032406$	$0.025708$	$0.006763$	$0.006102$
	3	$0.025207$	$0.017787$	$0.017152$	$0.039418$	$0.014650$	$0.013096$
	4	$0.006347$	$0.004991$	$0.004951$	$0.036134$	$0.017706$	$0.016400$
	5	$0.000794$	$0.000666$	$0.000665$	$0.017064$	$0.010407$	$0.010116$

The variance in $X_{r:n}$ ($1\le r\le n$) is $V\left(X_{r:n}\right)={\mu }_{r:n}^{\left(2\right)}-{\left[{\mu }_{r:n}^{\left(1\right)}\right]}^2$, where ${\mu }_{r:n}^{\left(1\right)}$ and ${\mu }_{r:n}^{\left(2\right)}$ follow from Equation (13) when $k=1$ and $k=2$, respectively. We compute the moments using theRsoftware [30].

3. Some Statistical Properties

3.1. L-Moments

The L-moments are expectations of certain linear combinations of order statistics [31]. The mth L-moment of a distribution can be defined as

$${\lambda }_m=\frac{1}{m}\sum _{j=0}^{m-1}{(-1)}^j\left(\genfrac{}{}{0pt}{}{m-1}{j}\right){\mu }_{m-j:m},m\ge 1,$$

(29)

where

$${\mu }_{i:m}=\frac{m!}{(i-1)!(m-i)!}{\int }_0^{d}xF{\left(x\right)}^{i-1}{[1-F\left(x\right)]}^{m-i}f\left(x\right)dx.$$

The properties and applications of L-moments were explored by [31]. L-moments can also be used in model specification to characterize distributions, parameter estimation, and hypothesis testing.

Setting $n=1,2,3$ and 4 in Equation (29), the first four L-moments easily follow. The L-moments for the omega distribution can be written as ${\lambda }_1={\mu }_{1:1}{\lambda }_2={\mu }_{2:2}-{\mu }_{1:1}{\lambda }_3=2{\mu }_{3:3}-3{\mu }_{2:2}+{\mu }_{1:1}$ and ${\lambda }_4=5{\mu }_{4:4}-10{\mu }_{3:3}+6{\mu }_{2:2}-{\mu }_{1:1}$, where

$${\mu }_{i:i}=i\alpha d^{\beta +1}B\left(\frac{1}{\beta }+1,\frac{i\alpha d^{\beta }}{2}+1\right){}_2{F}_1\left(\frac{i\alpha d^{\beta }}{2}+1,\frac{1}{\beta }+1;\frac{1}{\beta }+\frac{i\alpha d^{\beta }}{2}+1;-1\right).$$

The L-moments of the omega distribution computed to six decimal places for selected parameters are reported in Table 2.

Table 2. L-moments of the omega distribution for several parametric values.

	$d=0.20$
	$\alpha =0.25,\beta =0.75$	$\alpha =0.50,\beta =0.50$	$\alpha =0.75,\beta =0.25$
${\lambda }_1$	$0.001859$	$0.004310$	$0.004390$
${\lambda }_2$	$-0.001602$	$-0.002471$	$-0.000367$
${\lambda }_3$	$0.001162$	$0.000246$	$-0.001655$
${\lambda }_4$	$-0.000661$	$0.000943$	$0.000363$
L-CV	$-0.861414$	$-0.573207$	$-0.083695$
L-skewness	$-0.725598$	$-0.099589$	$4.504543$
L-kurtosis	$0.412664$	$-0.381677$	$-0.987604$
	$d=0.50$
	$\alpha =0.25,\beta =0.75$	$\alpha =0.50,\beta =0.50$	$\alpha =0.75,\beta =0.25$
${\lambda }_1$	$0.008609$	$0.014787$	$0.011707$
${\lambda }_2$	$-0.006418$	$-0.005931$	$0.000522$
${\lambda }_3$	$0.00319$	$-0.002199$	$-0.004351$
${\lambda }_4$	$-0.000395$	$0.003567$	$-0.000487$
L-CV	$-0.745481$	$-0.401099$	$0.044580$
L-skewness	$-0.497129$	$0.370738$	$-8.33625$
L-kurtosis	$0.061485$	$-0.601398$	$-0.932747$
	$d=0.90$
	$\alpha =0.25,\beta =0.75$	$\alpha =0.50,\beta =0.50$	$\alpha =0.75,\beta =0.25$
${\lambda }_1$	$0.022307$	$0.031476$	$0.021566$
${\lambda }_2$	$-0.01418$	$-0.008611$	$0.002748$
${\lambda }_3$	$0.003914$	$-0.007655$	$-0.007433$
${\lambda }_4$	$0.002497$	$0.005752$	$-0.002429$
L-CV	$-0.635665$	$-0.273568$	$0.127432$
L-skewness	$-0.276027$	$0.888975$	$-2.704682$
L-kurtosis	$-0.176061$	$-0.668018$	$-0.883949$

3.2. Incomplete Moments

Okorie and Nadarajah [2] derived closed-form non-central moments of X, say ${\mu }_r^{\prime }=E\left(X^r\right)$, which can be obtained from (16) with $k=1$. The rth incomplete moment of X is

$$\begin{array}{c}\hfill {\mu }_r^{\prime }\left(t\right)={\int }_0^t{x}^{r}f\left(x\right)dx,\end{array}$$

(30)

and substituting from (1) gives

$$\begin{array}{c}\hfill {\mu }_r^{\prime }\left(t\right)=\alpha \beta d^{\beta }{\int }_0^t\frac{x^{r+\beta }}{d^{2\beta }-x^{2\beta }}{\left(\frac{d^{\beta }+x^{\beta }}{d^{\beta }-x^{\beta }}\right)}^{-\frac{\alpha d^{\beta }}{2}}dx.\end{array}$$

(31)

It can be easily shown that

$$\begin{array}{c}\hfill {\int }_t^{\infty }{x}^{r}f\left(x\right)dx={\mu }_r^{\prime }-{\mu }_r^{\prime }\left(t\right).\end{array}$$

(32)

The first incomplete moment of X comes from Equation (30) when $r=1$, which also gives the mean deviations and the Bonferroni and Lorenz curves.

4. Methods of Estimation

Dombi et al. [1] proposed two approaches for practical statistical estimation of the omega parameters: the first one is the global optimization method to maximize the log-likelihood function, and the second depends on fitting its cdf to an empirical cdf. Here, we discuss seven methods to estimate these parameters.

4.1. Maximum Likelihood Estimation

Let $X_1,\cdots ,X_n$ be a random sample from the omega distribution with corresponding observations $x_1,\cdots ,x_n$, and let $X_{1:n}<\cdots <X_{r:n}$ ($r\le n$) be their first r-order statistics under type II right censored mechanism. The statistical literature contains many papers for estimation under different censoring types, and all the derivations in these papers are based on the maximum likelihood method.

The complete data follow when $r=n$. The maximum likelihood estimate (MLE) of d follows by noting that $d>\max {\left\{x_i\right\}}_{i=1,\dots ,r}$. Therefore, the MLE of d is $\widehat{d}=\max {\left\{x_i\right\}}_{i=1,\dots ,r}$.

The likelihood function $L\left(\theta \right)\equiv L(\alpha ,\beta ,d)$ for the parameters under type II right censored mechanism follows from (1) and (2):

$$\begin{array}{c}\hfill L\left(\theta \right)=C{\left(\frac{d^{\beta }+x_r^{\beta }}{d^{\beta }-x_r^{\beta }}\right)}^{-\frac{1}{2}\alpha d^{\beta }(n-r)}\prod _{i=1}^r\frac{\alpha \beta d^{2\beta }{x}_i^{\beta -1}}{d^{2\beta }-x_i^{2\beta }}{\left(\frac{d^{\beta }+x_i^{\beta }}{d^{\beta }-x_i^{\beta }}\right)}^{-\frac{1}{2}\alpha d^{\beta }}.\end{array}$$

Then, the log-likelihood function is

$$\begin{array}{ccc}\hfill \ell \left(\theta \right)& =& lnC+rln\alpha +rln\beta +(2rlnd+\sum _{i=1}^{r}ln{x}_i)\beta -\sum _{i=1}^{r}ln{x}_i-\sum _{i=1}^{r}ln(d^{2\beta }-x_i^{2\beta })\hfill \\ & -& \frac{\alpha }{2}\left[d^{\beta }\left(\sum _{i=1}^{r}ln\left(\frac{d^{\beta }+x_i^{\beta }}{d^{\beta }-x_i^{\beta }}\right)-(n-r)ln\left(\frac{d^{\beta }+x_r^{\beta }}{d^{\beta }-x_r^{\beta }}\right)\right)\right].\hfill \end{array}$$

The first partial derivatives of ℓ with respect to $\alpha$ and $\beta$ are

$$\begin{array}{ccc}\hfill \frac{\partial \ell \left(\theta \right)}{\partial \alpha }& =& \frac{r}{\alpha }-\frac{1}{2}\left[d^{\beta }\left(\sum _{i=1}^{r}ln\left(\frac{d^{\beta }+x_i^{\beta }}{d^{\beta }-x_i^{\beta }}\right)-(n-r)ln\left(\frac{d^{\beta }+x_r^{\beta }}{d^{\beta }-x_r^{\beta }}\right)\right)\right],\hfill \\ \hfill \frac{\partial \ell \left(\theta \right)}{\partial \beta }& =& \frac{r}{\beta }+\frac{\alpha d^{\beta }(n-r)}{2}\left(\frac{2x_r^{\beta }\left(ln{x}_r-lnd\right)}{d^{2\beta }-x_r^{2\beta }}+ln\left(\frac{d^{\beta }+x_r^{\beta }}{d^{\beta }-x_r^{\beta }}lnd\right)\right)\hfill \\ & -& \alpha d^{\beta }\sum _{i=1}^r\frac{x_i^{\beta }\left(ln{x}_i-lnd\right)}{d^{2\beta }-x_i^{2\beta }}+(2rlnd+\sum _{i=1}^{r}ln{x}_i)-2\sum _{i=1}^r\frac{d^{2\beta }lnd-x_i^{2\beta }ln{x}_i}{d^{2\beta }-x_i^{2\beta }}\hfill \\ & -& \frac{\alpha d^{\beta }}{2}lnd\sum _{i=1}^{r}ln\left(\frac{d^{\beta }+x_i^{\beta }}{d^{\beta }-x_i^{\beta }}\right).\hfill \end{array}$$

The MLEs $\widehat{\alpha }$ and $\widehat{\beta }$ can be found from these nonlinear equations using the MLE of d therein.

4.2. Ordinary and Weighted Least-Squares

It is well-known that $E\left[F\left(X_{i:n}\right)\right]=\frac{i}{n+1}$ and $V\left[F\left(X_{i:n}\right)\right]=\frac{i(n-i+1)}{{(n+1)}^2(n+2)}$.

The least squares estimates (LSEs) $\widehat{\alpha }$, $\widehat{\beta }$ and $\widehat{d}$ can be determined by minimizing

$$\begin{array}{c}\hfill \sum _{j=1}^n{\left[1-\frac{\alpha \beta d^{2\beta }{x}_{\left(j\right)}^{\beta -1}}{d^{2\beta }-x_{\left(j\right)}^{2\beta }}{\left(\frac{d^{\beta }+x_{\left(j\right)}^{\beta }}{d^{\beta }-x_{\left(j\right)}^{\beta }}\right)}^{-\frac{1}{2}\alpha d^{\beta }}-\frac{j}{n+1}\right]}^2,\end{array}$$

in relation to $\alpha$, $\beta$, and d.

The weighted least squares estimates (WLSEs) follow by minimizing

$$\begin{array}{c}\hfill \sum _{j=1}^n{w}_j{\left[1-\frac{\alpha \beta d^{2\beta }{x}_{\left(j\right)}^{\beta -1}}{d^{2\beta }-x_{\left(j\right)}^{2\beta }}{\left(\frac{d^{\beta }+x_{\left(j\right)}^{\beta }}{d^{\beta }-x_{\left(j\right)}^{\beta }}\right)}^{-\frac{1}{2}\alpha d^{\beta }}-\frac{j}{n+1}\right]}^2,\end{array}$$

inn relation to these parameters, where the weight function $w_j$ at the jth point is $w_j=\frac{1}{V\left[F\left(X_{j:n}\right)\right]}=\frac{{(n+1)}^2(n+2)}{j(n-j+1)}$.

4.3. Maximum Product of Spacing

An alternative method to estimate the parameters of a continuous distribution is the maximum product of spacing (MPS) discussed by [32,33].

Let $x_{\left(1\right)}<\cdots <x_{\left(n\right)}$ be the observed order statistics. Then, for the omega cdf (2), the uniform spacing $D_i(\alpha ,\beta )$ (for $i=1,2,\dots ,n$) is

$$\begin{array}{c}\hfill D_i(\alpha ,\beta )=F(x_{\left(i\right)};\alpha ,\beta )-F(x_{(i-1)};\alpha ,\beta ),\end{array}$$

where $F(x_{\left(0\right)};\alpha ,\beta )=0$ and $F(x_{(n+1)};\alpha ,\beta )=1$. Note that ${\sum }_{i=1}^{n+1}{D}_i(\alpha ,\beta )=1$. The MPS estimates (MPSEs) of the parameters (for a fixed value of d) are found by maximizing

$$\begin{array}{c}\hfill G(\alpha ,\beta )={\left[\prod _{i=1}^n{D}_i(\alpha ,\beta )\right]}^{\frac{1}{n+1}}\end{array}$$

in relation to $\alpha$ and $\beta$. This can be done equivalently by maximizing

$$\begin{array}{c}\hfill M(\alpha ,\beta )=\frac{1}{n+1}\sum _{i=1}^{n}log\left[D_i(\alpha ,\beta )\right].\end{array}$$

The MPSEs of the unknown parameters can be determined by solving the nonlinear equations

$$\begin{array}{ccc}\hfill \frac{\partial M\left(\theta \right)}{\partial \alpha }& =& \frac{1}{n+1}\sum _{i=1}^n\frac{1}{D_i\left(\theta \right)}\left[g_1(x_{\left(i\right)};\theta )-g_1(x_{(i-1)};\theta )\right]=0,\hfill \\ \hfill \frac{\partial M\left(\theta \right)}{\partial \beta }& =& \frac{1}{n+1}\sum _{i=1}^n\frac{1}{D_i\left(\theta \right)}\left[g_2(x_{\left(i\right)};\theta )-g_2(x_{(i-1)};\theta )\right]=0,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill g_1(x_{(·)};\theta )=\frac{\partial F(x_{(·)};\theta )}{\partial \alpha }\mathrm{and}{g}_2(x_{(·)};\theta )=\frac{\partial F(x_{(·)};\theta )}{\partial \beta }.\end{array}$$

4.4. Percentiles

The percentile method is defined by equating the sample percentile points to the population percentiles. If $p_i$ denotes an estimate of $F(x_i:n_j;\alpha ,\beta ,d)$, then the percentile estimates (PCEs) ${\widehat{\alpha }}_{PCE}$, ${\widehat{\beta }}_{PCE}$ and ${\widehat{d}}_{PCE}$ can be obtained by minimizing

$$\begin{array}{c}\hfill P(\alpha ,\beta ,d)=\sum _{j=1}^n{\left[x_i-Q\left(p_i\right)\right]}^2,\end{array}$$

where

$$\begin{array}{c}\hfill Q\left(p_i\right)=d{\left[\frac{{\left(1-p_i\right)}^{-2/\alpha d^{\beta }}-1}{{\left(1-p_i\right)}^{-2/\alpha d^{\beta }}+1}\right]}^{\frac{1}{\beta }},\end{array}$$

and $p_i=\frac{i}{n+1}$ is the unbiased estimator of $F(X_{i:n};\alpha ,\beta ,d)$.

4.5. Anderson–Darling and Right-Tail Anderson–Darling

The Anderson–Darling estimates (ADEs) can be found by minimizing

$$A(\alpha ,\beta ,d)=-n-\frac{1}{n}\sum _{i=1}^n\left(2i-1\right)\left[logF\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)+logS\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)\right],$$

in relation to $\alpha$, $\beta$, and d. The ADEs follow by solving the equations

$$\sum _{i=1}^n\left(2i-1\right)\left[\frac{{\Delta }_s\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)}{F\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)}-\frac{{\Delta }_s\left(x_{(n+1-i)}|\alpha ,\beta ,d\right)}{S\left(x_{(n+1-i)}|\alpha ,\beta ,d\right)}\right]=0,s=1,2,3,$$

where

$$\begin{array}{ccc}\hfill {\Delta }_1\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)& =& \frac{\partial }{\partial \alpha }F\left(x_{\left(i\right)}|\alpha ,\beta ,d\right),{\Delta }_2\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)=\frac{\partial }{\partial \beta }F\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)\hfill \end{array}$$

and

$$\begin{array}{c}\hfill {\Delta }_3\left(x_{\left(i\right)}|\alpha ,\beta ,d\right)=\frac{\partial }{\partial d}F\left(x_{\left(i\right)}|\alpha ,\beta ,d\right).\end{array}$$

The right-tail Anderson–Darling estimates (RADEs) are obtained by minimizing

$$R(\alpha ,\beta ,d)=\frac{n}{2}-2\sum _{i=1}^{n}F\left(x_{i:n}|\alpha ,\beta ,d\right)-\frac{1}{n}\sum _{i=1}^n\left(2i-1\right)logS\left(x_{n+1-i:n}|\alpha ,\beta ,d\right),$$

in relation to these parameters. The RADEs can also be found by solving the equations

$$-2\sum _{i=1}^n{\Delta }_s\left(x_{i:n}|\alpha ,\beta ,d\right)+\frac{1}{n}\sum _{i=1}^n\left(2i-1\right)\frac{{\Delta }_s\left(x_{{}_{n+1-i:n}}|\alpha ,\beta ,d\right)}{S\left(x_{n+1-i:n}|\alpha ,\beta ,d\right)}=0,s=1,2,3.$$

5. Simulations

Samples of sizes $n=25,50,100$ are simulated from the Omg($\alpha ,\beta$) model, where d has two values $d=2.5,5$, whereas samples of sizes $n=100,200$ are simulated from the Omg($\alpha ,\beta ,d$) model for different values of $\alpha$, $\beta$, and d. The previous estimation methods are compared under two scenarios:

(i)

Two unknown parameters: we use the true values $\alpha =0.87,1.2$, and $\beta =0.93,1.13$. The estimates of the parameters $\alpha$ and $\beta$ from the seven previous methods and their MSEs are listed in Table 3, Table 4 and Table 5.

Table 3. The maximum likelihood estimates (MLEs), least square estimates (LSEs), weighted least squares estimates (WLSEs), maximum product of spacing estimates (MPSEs), percentile estimates (PCEs), Anderson–Darling estimates (ADEs), right-tail Anderson–Darling estimates (RADEs), and their mean square errors (MSEs).

$n=25$, $d=2.5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=19$		$r=22$		$r=25$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.90361	0.97775	1.17247	0.98500	0.70901	0.93445	1.08478	1.04719	1.07467	1.03326	0.83278	0.84073	0.84178	0.90401	0.85494	0.92186	0.84801	0.94972
		1.06834	0.00228	0.09149	0.00303	0.02592	0.00002	0.04613	0.01373	0.04189	0.01066	0.01256	0.02182	0.01404	0.02933	0.01461	0.02129	0.01488	0.02885
	1.13	1.76199	1.19622	1.12939	1.20065	0.70856	1.13624	1.16218	1.08787	1.14776	1.06316	0.84693	1.02608	0.83936	1.08234	0.85357	1.11997	0.87280	1.15809
		0.79564	0.00439	0.06728	0.00499	0.02606	0.00004	0.08537	0.00177	0.07715	0.00447	0.01372	0.03125	0.01253	0.03498	0.01788	0.02374	0.01631	0.03774
1.2	0.93	2.69826	1.02435	1.64527	1.01351	0.97872	0.93556	0.98912	0.99923	1.03952	1.001991	1.12266	0.84731	1.14453	0.87031	1.18940	0.93200	1.17475	0.94700
		2.24480	0.00890	0.19827	0.00697	0.04897	0.00003	0.04426	0.00479	0.02575	0.00808	0.02816	0.02060	0.03028	0.02721	0.02773	0.01854	0.02763	0.02239
	1.13	2.49098	1.23895	1.58396	1.22766	0.97824	1.13743	1.07621	1.02107	1.11504	1.04399	1.12919	1.02693	1.15512	1.07141	1.18158	1.12426	1.19308	1.14571
		1.66662	0.01187	0.14743	0.00954	0.04918	0.00006	0.01532	0.01187	0.00722	0.00740	0.02911	0.02749	0.02515	0.03222	0.02687	0.02214	0.02713	0.02518
$n=25$, $d=5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=19$		$r=22$		$r=25$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.54211	1.03280	1.05172	1.00841	0.70734	0.93657	1.08327	1.05595	1.05401	1.02839	0.83803	0.85779	0.84783	0.88259	0.85959	0.93044	0.85968	0.93157
		0.45173	0.01057	0.03302	0.00615	0.02646	0.00004	0.04548	0.01586	0.03386	0.00968	0.01207	0.01719	0.01629	0.02632	0.01506	0.01487	0.01665	0.01880
	1.13	1.45280	1.30177	1.01514	1.24375	0.70639	1.13942	1.16405	1.10418	1.13861	1.06261	0.85525	1.03388	0.86585	1.06827	0.88848	1.13508	0.85762	1.14933
		0.33965	0.02950	0.02107	0.01294	0.02677	0.00009	0.08647	0.00067	0.07215	0.00454	0.01174	0.02582	0.01738	0.02158	0.01738	0.02158	0.01746	0.02570
1.2	0.93	2.20326	1.04720	1.48388	1.01874	0.97695	0.93775	0.96939	0.99884	0.97100	1.00069	1.14440	0.85349	1.19189	0.92439	1.19189	0.92439	1.18214	0.95906
		1.00654	0.01373	0.08059	0.00788	0.04975	0.00006	0.05318	0.00474	0.05244	0.00500	0.02648	0.01456	0.02443	0.02621	0.02620	0.01366	0.02943	0.01693
	1.13	2.10115	1.30970	1.44094	1.25042	0.97603	1.14093	1.06191	1.02706	1.06082	1.02775	1.15861	1.03901	1.15246	1.04726	1.19892	1.13898	1.19322	1.13811
		0.81207	0.03229	0.05805	0.01450	0.05016	0.00012	0.01907	0.01060	0.01937	0.01045	0.02281	0.02187	0.02003	0.03058	0.02772	0.01767	0.02920	0.02455

Table 4. The MLEs, LSEs, WLSEs, MPSEs, PCEs, ADEs, RADEs and their MSEs.

$n=50$, $d=2.5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=43$		$r=47$		$r=50$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.34853	1.00804	1.01406	1.02278	0.78926	0.97620	1.12365	1.05208	1.11842	1.03861	0.83136	0.87720	0.86727	0.91031	0.86670	0.93192	0.86835	0.92905
		0.22899	0.00609	0.02075	0.00861	0.00652	0.00213	0.06434	0.01490	0.06171	0.01180	0.00717	0.01052	0.00786	0.01416	0.00847	0.00912	0.00689	0.01213
	1.13	1.29182	1.23316	0.99197	1.25150	0.78534	1.19121	1.20831	1.09239	1.19600	1.06877	0.84425	1.05951	0.86358	1.09930	0.85660	1.13831	0.86605	1.13738
		0.17793	0.01064	0.01488	0.01476	0.00717	0.00375	0.11445	0.00141	0.10627	0.00375	0.00732	0.01473	0.00779	0.01810	0.00802	0.01366	0.00883	0.01779
1.2	0.93	1.91432	1.04520	1.43378	1.04552	1.09919	0.98271	1.00075	0.99885	1.08239	1.02611	1.15683	0.88122	1.16811	0.90605	1.19586	0.93076	1.18405	0.93916
		0.51025	0.01327	0.05465	0.01335	0.01016	0.00278	0.03970	0.00474	0.01383	0.00924	0.01169	0.00889	0.01300	0.01205	0.01282	0.00771	0.01480	0.00941
	1.13	1.83291	1.26779	1.40502	1.27320	1.09529	1.19679	1.09726	1.02205	1.16675	1.05265	1.15442	1.07899	1.16688	1.09085	1.19491	1.11544	1.19832	1.13403
		0.40057	0.01899	0.04203	0.02051	0.01097	0.00446	0.01056	0.01165	0.00111	0.00598	0.01425	0.01164	0.01252	0.01511	0.01377	0.01384	0.01243	0.01422
$n=50$, $d=5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=43$		$r=47$		$r=50$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.19276	1.04442	0.94912	1.04919	0.77686	0.98620	1.10071	1.05384	1.06551	1.02568	0.85951	0.87735	0.86037	0.89362	0.86465	0.93171	0.86160	0.93042
		0.10418	0.01309	0.00626	0.01421	0.00868	0.00316	0.05323	0.01534	0.03822	0.00915	0.00773	0.00756	0.00906	0.01399	0.00770	0.00757	0.00718	0.00901
	1.13	1.14805	1.29397	0.92835	1.28804	0.77266	1.20042	1.19059	1.10049	1.15709	1.05861	0.85970	1.06870	0.87311	1.06892	0.87015	1.12682	0.86461	1.13474
		0.07731	0.02689	0.00341	0.02498	0.00496	0.00496	0.10278	0.00087	0.08242	0.00510	0.00674	0.01131	0.00821	0.01762	0.00704	0.01042	0.00886	0.01165
1.2	0.93	1.70553	1.05709	1.35483	1.05781	1.08732	0.98796	0.98537	1.00050	0.99420	1.00447	1.17078	0.88325	1.17816	0.89004	1.20293	0.92650	1.20355	0.93267
		0.25556	0.01615	0.02397	0.01634	0.01270	0.00336	0.04607	0.00497	0.04235	0.00555	0.01226	0.00662	0.01368	0.01235	0.01354	0.00688	0.01527	0.00945
	1.13	1.65395	1.30184	1.33259	1.29386	1.08356	1.20149	1.08266	1.02744	1.09014	1.03172	1.17186	1.06329	1.18024	1.07519	1.19245	1.12796	1.18118	1.14030
		0.20607	0.02953	0.01758	0.02685	0.01356	0.00511	0.01377	0.01052	0.01207	0.00966	0.01268	0.01144	0.01249	0.01649	0.01343	0.00903	0.01486	0.00992

Table 5. The MLEs, LSEs, WLSEs, MPSEs, PCEs, ADEs, RADEs and their MSEs.

$n=100$, $d=2.5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=85$		$r=95$		$r=100$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.45050	0.95173	0.97891	0.93983	0.74543	0.87881	1.04628	1.02686	1.05436	1.01859	0.85500	0.89777	0.86302	0.91781	0.86457	0.93082	0.86860	0.93064
		0.33698	0.00047	0.01186	0.00010	0.01552	0.00262	0.03107	0.00938	0.03399	0.00785	0.00330	0.00455	0.00315	0.00734	0.00346	0.00492	0.00373	0.00652
	1.13	1.38531	1.15687	0.96318	1.14421	0.74886	1.06856	1.12466	1.05904	1.12377	1.04149	0.86294	1.09025	0.86783	1.11965	0.86321	1.13137	0.86643	1.13577
		0.26554	0.00072	0.00868	0.00020	0.01468	0.00377	0.06485	0.00504	0.06440	0.00783	0.00311	0.00655	0.00367	0.00805	0.00315	0.00569	0.00337	0.00821
1.2	0.93	2.02646	0.98252	1.35536	0.95649	1.01827	0.87988	0.93840	0.97469	1.02700	1.01074	1.17643	0.89712	1.19057	0.91267	1.19480	0.93004	1.18940	0.93878
		0.68304	0.00276	0.02414	0.00070	0.03303	0.00251	0.06843	0.00200	0.02993	0.00652	0.00703	0.00412	0.00691	0.00725	0.00705	0.00386	0.00748	0.00581
	1.13	1.93060	1.18660	1.33287	1.16146	1.02209	1.06972	1.01866	0.98638	1.09410	1.02921	1.16278	1.09422	1.19074	1.11981	1.19849	1.12524	1.19452	1.13326
		0.53378	0.00320	0.01765	0.00099	0.03165	0.00363	0.03289	0.02063	0.01122	0.01016	0.00645	0.00585	0.00771	0.00673	0.00680	0.00490	0.00681	0.00637
$n=100$, $d=5$
Actual Value		MLE						LSE		WLSE		MPSE		PCE		ADE		RADE
		MSE						MSE		MSE		MSE		MSE		MSE		MSE
		$r=85$		$r=95$		$r=100$
$\alpha$	$\beta$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$	$\widehat{\alpha }$	$\widehat{\beta }$
0.87	0.93	1.27440	0.97197	0.93217	0.95269	0.75563	0.88071	1.02716	1.02834	1.00295	1.00369	0.86789	0.89946	0.86565	0.90885	0.86897	0.93038	0.86926	0.93136
		0.16354	0.00176	0.00387	0.00051	0.01308	0.00243	0.02470	0.00967	0.01768	0.00543	0.00314	0.00386	0.00431	0.00614	0.00350	0.00352	0.00368	0.00514
	1.13	1.22416	1.20242	0.91604	1.16740	0.75906	1.07067	1.11346	1.07054	1.08868	1.03031	0.87108	1.08931	0.87014	1.10645	0.86386	1.13887	0.87051	1.12814
		0.12543	0.00525	0.00212	0.00140	0.01231	0.00352	0.05927	0.00354	0.04782	0.00994	0.00364	0.00541	0.00413	0.00803	0.00448	0.00433	0.00452	0.00566
1.2	0.93	1.78210	0.98400	1.29300	0.96102	1.02945	0.88117	0.91602	0.97229	0.93676	0.98497	1.17599	0.89597	1.19327	0.90448	1.19926	0.93377	1.19185	0.92922
		0.33884	0.00292	0.00865	0.00096	0.02909	0.00238	0.08064	0.00179	0.06929	0.00302	0.00572	0.00408	0.00668	0.00698	0.00648	0.00359	0.00688	0.00385
	1.13	1.72137	1.21054	1.27431	1.17384	1.03305	1.07085	1.00501	0.99249	1.02174	1.00571	1.17254	1.09691	1.18779	1.09645	1.19416	1.13131	1.19843	1.13062
		0.27183	0.00649	0.00552	0.00192	0.02787	0.00350	0.03802	0.01891	0.03178	0.01545	0.00581	0.00423	0.00599	0.00672	0.00641	0.00485	0.00680	0.00630

(ii)

Three unknown parameters: we use true values $\alpha =0.87,1.2$; $\beta =0.93,1.13$; and $d=3.5,5$. The estimates of the three parameters from the seven estimation methods and their MSEs are reported in Table 6 and Table 7.

Table 6. The MLEs, LSEs, WLSEs, MPSEs, PCEs, ADEs, RADEs and their MSEs.

Actual Value			MLE			LSE			WLSE			MPSE			PCE			ADE			RADE
			MSE			MSE			MSE			MSE			MSE			MSE			MSE
			$\mathit{n}=\mathbf{25}$
$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathit{d}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$
0.87	0.93	2.5	1.16973	0.97058	2.42667	0.85797	0.89910	3.61047	0.86182	0.91653	2.57385	0.82138	0.85666	2.49664	0.84120	0.87920	2.56599	0.86459	0.94039	2.50937	0.85276	0.94735	2.50230
			0.08984	0.00165	0.00538	0.01904	0.02049	0.72080	0.01924	0.02529	0.05422	0.01618	0.02311	0.02626	0.01783	0.03123	0.05753	0.01818	0.02216	0.04243	0.0190	0.03011	0.03212
		3.5	1.10448	0.96495	3.18576	0.84108	0.90352	3.71845	0.86217	0.91164	3.85118	0.84486	0.85089	3.50032	0.83404	0.87348	3.56767	0.86606	0.92755	3.53227	0.84532	0.95100	3.55824
			0.05498	0.00122	0.09875	0.01790	0.02386	0.69853	0.01836	0.02006	0.67096	0.01564	0.02038	0.36521	0.01730	0.02721	0.50768	0.01761	0.01801	0.52519	0.01867	0.02500	0.44699
	1.13	2.5	1.12800	1.17398	2.37765	0.85638	1.10046	2.62488	0.85913	1.11324	2.62249	0.82903	1.05127	2.50626	0.83602	1.10019	2.54137	0.85524	1.14335	2.50127	0.85331	1.14198	2.49006
			0.06656	0.00193	0.01497	0.01898	0.03815	0.15516	0.01913	0.03248	0.12087	0.01773	0.03359	0.05968	0.01710	0.03425	0.09475	0.01630	0.02971	0.08296	0.01722	0.04375	0.07120
		3.5	1.07008	1.17165	2.99676	0.85381	1.07378	3.70903	0.84669	1.09664	3.92017	0.83840	1.02877	3.50698	0.84160	1.05252	3.63691	0.85842	1.12629	3.50504	0.85856	1.14217	3.58477
			0.04003	0.00174	0.25325	0.01652	0.03082	1.10097	0.01760	0.02850	1.22602	0.01700	0.03263	0.76098	0.01944	0.03263	0.92533	0.01968	0.02351	1.02916	0.01917	0.03000	0.81197
1.2	0.93	2.5	1.64792	0.99520	2.26968	1.17214	0.89429	2.67821	1.18009	0.91221	2.70901	1.10971	0.83781	2.49436	1.12330	0.87145	2.53378	1.19145	0.92422	2.49067	1.18732	0.94025	2.53305
			0.20063	0.00425	0.05305	0.03792	0.02375	0.43638	0.03870	0.02129	0.34603	0.04219	0.02233	0.22219	0.03861	0.03252	0.27448	0.03922	0.01984	0.22524	0.04339	0.02599	0.22528
		3.5	1.56192	0.97964	2.80003	1.17319	0.89346	3.78217	1.16352	0.90406	4.15396	1.12557	0.85339	3.51248	1.13180	0.84244	3.93617	1.18766	0.93411	3.54796	1.17033	0.9263	3.57184
			0.13099	0.00246	0.48996	0.03507	0.02001	2.45763	0.03566	0.01755	2.35785	0.03856	0.01838	1.48395	0.03495	0.02396	1.67699	0.04030	0.01893	1.69027	0.03634	0.01800	1.54125
	1.13	2.5	1.59148	1.19621	2.18668	1.16595	1.08608	2.54017	1.16945	1.09705	2.75583	1.14230	1.03035	2.51986	1.15041	1.06205	2.66932	1.16812	1.11271	2.45261	1.18475	1.14355	2.48243
			0.15326	0.00438	0.09817	0.04165	0.03334	0.50741	0.03596	0.02842	0.53997	0.03661	0.03082	0.31262	0.02908	0.03019	0.42781	0.03455	0.02656	0.39271	0.03716	0.03067	0.34325
		3.5	1.52164	1.18331	2.57844	1.16117	1.06498	3.50364	1.19403	1.12632	3.73279	1.11321	1.01263	3.50056	1.12579	1.01083	3.85679	1.15473	1.11011	3.63090	1.16324	1.10965	3.73028
			0.10345	0.00284	0.84928	0.03721	0.02858	2.66621	0.00876	0.00569	0.76719	0.03436	0.02751	1.84959	0.03110	0.02952	2.60923	0.02909	0.02539	2.42241	0.03863	0.02604	2.41540

Table 7. The MLEs, LSEs, WLSEs, MPSEs, PCEs, ADEs, RADEs and their MSEs.

Actual Value			MLE			LSE			WLSE			MPSE			PCE			ADE			RADE
			MSE			MSE			MSE			MSE			MSE			MSE			MSE
			$\mathit{n}=\mathbf{100}$
$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathit{d}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$	$\widehat{\mathit{d}}$
0.87	0.93	2.5	0.97880	0.93964	2.49926	0.87104	0.92841	3.54490	0.86923	0.93406	2.51990	0.85230	0.90074	2.50732	0.86208	0.90887	2.50505	0.86507	0.93647	2.50449	0.87170	0.94490	2.51283
			0.01184	0.00009	0.00000	0.00457	0.00576	0.10668	0.00466	0.00542	0.00330	0.00446	0.00519	0.00135	0.00382	0.00929	0.00719	0.00377	0.00486	0.00237	0.0045	0.00578	0.00214
		3.5	0.95295	0.94328	3.48873	0.86833	0.93153	3.52863	0.87338	0.92823	3.56461	0.86499	0.90094	3.53805	0.86773	0.92735	3.56388	0.86270	0.93799	3.52931	0.87093	0.95082	3.54010
			0.00688	0.00018	0.00013	0.00484	0.00624	0.08283	0.00456	0.00521	0.05955	0.00382	0.00470	0.03365	0.00411	0.00584	0.06303	0.00435	0.00491	0.04358	0.00379	0.00656	0.03929
	1.13	2.5	0.96291	1.14355	2.49730	0.87024	1.14195	2.53072	0.87266	1.13342	2.52735	0.86193	1.09156	2.52224	0.86641	1.10883	2.51962	0.87231	1.13790	2.50952	0.86975	1.14612	2.51740
			0.00863	0.00018	0.00001	0.00522	0.00827	0.01681	0.00442	0.00758	0.00896	0.00384	0.00708	0.00462	0.00437	0.01013	0.01299	0.00451	0.00725	0.00723	0.00483	0.00964	0.00548
		3.5	0.93611	1.15178	3.46097	0.86646	1.13147	3.61355	0.87020	1.13168	3.61366	0.86378	1.10062	3.59934	0.86611	1.11925	3.64973	0.86698	1.13708	3.53451	0.86855	1.14506	3.53665
			0.00437	0.00047	0.00152	0.00500	0.00872	0.31372	0.00442	0.00710	0.18080	0.00407	0.00677	0.10902	0.00393	0.00876	0.16244	0.00464	0.00743	0.13304	0.00495	0.00773	0.11993
1.2	0.93	2.5	1.35447	0.95561	2.49149	1.20989	0.92921	2.54467	1.20209	0.93366	2.55229	1.17249	0.89724	2.53444	1.19713	0.92500	2.55575	1.19314	0.93896	2.52120	1.20592	0.94595	2.51118
			0.02386	0.00066	0.00007	0.01142	0.00582	0.06289	0.00962	0.00499	0.03502	0.00898	0.00498	0.01908	0.00918	0.00679	0.03923	0.00948	0.00448	0.02371	0.00862	0.00643	0.02200
		3.5	1.31762	0.95387	3.43316	1.19365	0.92637	3.56898	1.19924	0.93133	3.65960	1.18870	0.90496	3.60242	1.19213	0.91665	3.66724	1.21087	0.93322	3.55809	1.19687	0.9449	3.58595
			0.01384	0.00057	0.00447	0.01008	0.00435	0.54059	0.00909	0.00472	0.35629	0.00831	0.00465	0.22486	0.00943	0.00741	0.27246	0.00902	0.00412	0.31724	0.00911	0.00557	0.23988
	1.13	2.5	1.33131	1.15920	2.47943	1.19828	1.12827	2.53089	1.20480	1.13201	2.57526	1.18642	1.09261	2.54373	1.18622	1.11948	2.54547	1.20212	1.13189	2.52018	1.21200	1.14271	2.53404
			0.01724	0.00085	0.00042	0.01001	0.00719	0.10014	0.00958	0.00705	0.06865	0.00840	0.00711	0.04119	0.00950	0.00872	0.05489	0.01020	0.00803	0.04895	0.00884	0.00893	0.05142
		3.5	1.29618	1.15965	3.34558	1.19697	1.11334	3.63626	1.19403	1.12632	3.73279	1.19482	1.10559	3.51937	1.19388	1.11944	3.77965	1.20138	1.12515	3.53402	1.19888	1.13129	3.65714
			0.00925	0.00088	0.02384	0.00941	0.00749	1.00722	0.00876	0.00569	0.76719	0.00760	0.00528	0.57646	0.00958	0.00709	0.57924	0.00843	0.00650	0.58128	0.00903	0.00723	0.68413

Based on the figures in Table 6 and Table 7, we note that decreasing the $\alpha$ actual value improves the $\beta$ estimates while increasing the $\beta$ actual value improves the $\alpha$ estimates. Furthermore, we note that increasing d gives good estimates of $\alpha$ and $\beta$. The MLEs, MPSEs, ADEs, RADEs, WLSEs, LSEs, and PCEs are evaluated based on the following quantities including the average estimates and the MSEs for each sample size. The figures in Table 3, Table 4, Table 5, Table 6 and Table 7 reveal that the estimates of the omega parameters are precise and small MSEs for all cases, i.e., these estimates are quite reliable and close to the true parameters. Moreover, the MSEs decay when n increases, thus showing that these estimators are consistent. On the other hand, the performance ordering of the estimators, from best to worst, in terms of their MSEs is MLE, MPSE, ADE, RADE, WLSE, LSE, and PCE in most of these cases.

6. Real Data Illustration

This section compares the omega distribution with the other ten competing distributions in terms of fitting a real data set, which was analyzed by [34]. The data set consists of 72 exceedances of flood peaks (in m${}^3$/s) of the Wheaton river (Canada) for the years 1958–1984: 0.4, 0.7, 1.7, 1.1, 1.9, 1.1, 2.2, 2.2, 14.4, 20.6, 5.3, 12.0, 13.0, 9.3, 1.4, 18.7, 8.5, 22.9, 1.7, 0.1, 25.5, 2.5, 14.4, 1.7, 37.6, 0.6, 11.6, 14.1, 22.1, 39.0, 0.3, 15.0, 36.4, 2.7, 64.0, 1.5, 11.0, 7.3, 1.1, 0.6, 9.0, 1.7, 7.0, 14.1, 3.6, 5.6, 30.8, 13.3, 9.9, 10.4, 10.7, 20.1, 0.4, 2.8, 30.0, 4.2, 25.5, 3.4, 11.9, 21.5, 27.6, 2.5, 27.4, 1.0, 27.1, 5.3, 9.7, 20.2, 16.8, 27.5, 2.5, and 27.0. Each observation is divided by 65 for computational stability, and hence, the estimate of the parameter d is $\widehat{d}=0.985$. The comparison is based on the Kolmogorov–Smirnov (K-S) statistic with its associated p-value.

The selected models are the modified Weibull (MW), transmuted complementary Weibull-geometric (TCWG), Lindley Weibull (LiW), power generalized Weibull (PGW), alpha power Weibull (APW), alpha power exponentiated-Weibull (APEW), exponentiated-Weibull (EW), extended odd Weibull exponential (EOWE), logarithmic transformed Weibull (LTW), and Weibull (W) distributions.

Table 8 reports the MLEs and their corresponding standard errors (SEs), and the K-S statistic (K-S (stat)) with its associated p-value (K-S (p-value)) for all models fitted to the Wheaton river data. The figures in this table indicate that the omega model gives the closest fit to these data compared to the competing distributions.

Table 8. Results from the fitted distributions.

Distribution	MLEs	SEs	K-S (Stat)	K-S (p-Value)
OMEGA	$\widehat{\alpha }=3.0305765$	0.4824807	0.0889468	0.6191953
	$\widehat{\beta }=0.7377699$	0.0810828
MW	$\widehat{\alpha }=2.0878218$	6.2615708	0.1046855	0.4091079
	$\widehat{\beta }=0.8120513$	0.4037047
	$\widehat{\lambda }=2.6780859$	6.6030829
TCWG	$\widehat{\alpha }=0.8679701$	0.8151071	0.1071177	0.3805323
	$\widehat{\beta }=0.8762272$	0.1689987
	$\widehat{\lambda }=0.0000006$	0.4452576
	$\widehat{\sigma }=6.1091600$	3.3411493
LiW	$\widehat{\alpha }=2.5936284$	5.7555398	0.1066129	0.3863592
	$\widehat{\beta }=0.8705367$	0.1103413
	$\widehat{\theta }=2.5365106$	4.2907423
PGW	$\widehat{\lambda }=0.8141584$	1.7813975	0.1062762	0.3902766
	$\widehat{\theta }=0.7440689$	0.1473203
	$\widehat{\alpha }=3.2245731$	5.5840937
APW	$\widehat{\alpha }=1.1397937$	1.269151	0.1061151	0.3921589
	$\widehat{\beta }=0.8894862$	0.132235
	$\widehat{\lambda }=4.7910660$	0.983672
APEW	$\widehat{\alpha }=0.0426735$	0.0339949	0.09805297	0.4930507
	$\widehat{\beta }=4.2287394$	0.3614408
	$\widehat{\lambda }=2.5130669$	0.3860032
	$\widehat{\theta }=0.1978522$	0.0289383
EW	$\widehat{\beta }=1.3867142$	0.5896521	0.1073935	0.377372
	$\widehat{\lambda }=5.1557944$	1.2449955
	$\widehat{\theta }=0.5185501$	0.3116688
EOWE	$\widehat{\alpha }=0.7618609$	0.1200032	0.09914981	0.4786092
	$\widehat{\beta }=0.4522144$	0.5052505
	$\widehat{\lambda }=4.4213827$	1.4535656
LTW	$\widehat{\alpha }=1.1506548$	0.9457565	0.1070967	0.380773
	$\widehat{\beta }=0.8764569$	0.1681637
	$\widehat{\lambda }=4.8816417$	1.2212993
W	$\widehat{\beta }=0.9011665$	0.08555716	0.1052065	0.402882
	$\widehat{\lambda }=4.7140919$	0.75473964

The fitted $pdf$, $cdf$, survival function, and probability–probability (PP) plots of the omega distribution are displayed in Figure 1. The PP plots for all fitted models are displayed in Figure 2. The parameters of the omega distribution are estimated using several estimation methods, as listed in Table 9. The PP plots of the omega model using different estimation methods are given in Figure 3.

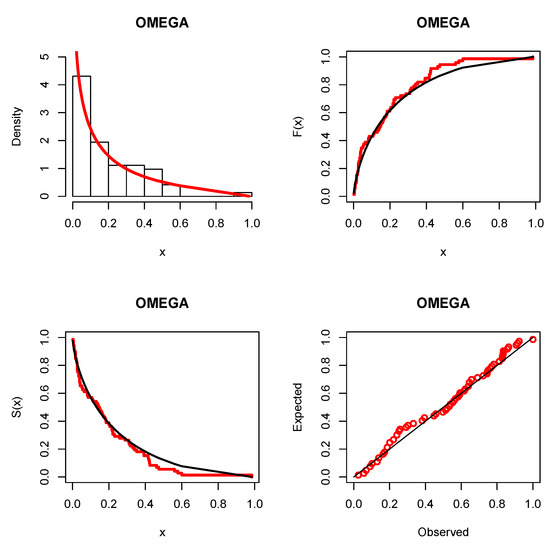
Figure 1. The fitted $pdf$, $cdf$, survival function, and probability–probability (PP) plots of the omega distribution.

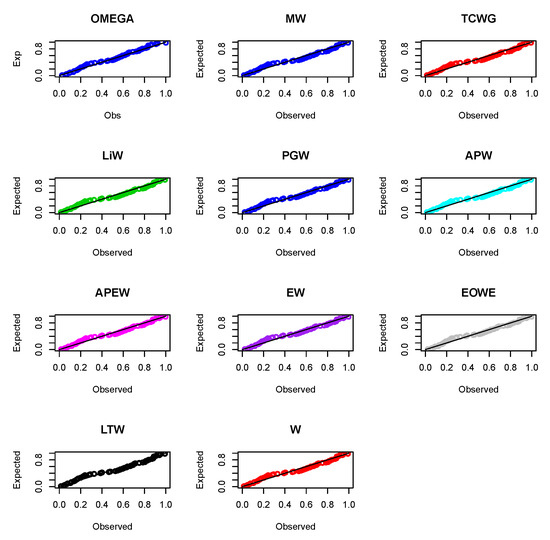
Figure 2. The PP plots of the fitted distributions.

Table 9. Estimates of the omega parameters and Kolmogorov–Smirnov (K-S) (stat) with its associated p-value from seven methods of estimation.

Method	Estimates	K-S (Stat)	K-S (p-Value)
MLE	$\widehat{\alpha }=3.0305765$	0.0889468	0.6191953
	$\widehat{\beta }=0.7377699$
LSE	$\widehat{\alpha }=3.319753$	0.07090078	0.9125179
	$\widehat{\beta }=0.8492076$
WLSE	$\widehat{\alpha }=3.565044$	0.14252334	0.1719133
	$\widehat{\beta }=0.7814565$
MPSE	$\widehat{\alpha }=2.554748$	0.11491242	0.3978472
	$\widehat{\beta }=0.7323336$
PCE	$\widehat{\alpha }=3.880584$	0.07701275	0.8553612
	$\widehat{\beta }=0.9426041$
ADE	$\widehat{\alpha }=3.473845$	0.07626228	0.8630764
	$\widehat{\beta }=0.8618174$
RADE	$\widehat{\alpha }=3.817778$	0.07102754	0.9114741
	$\widehat{\beta }=0.9260090$

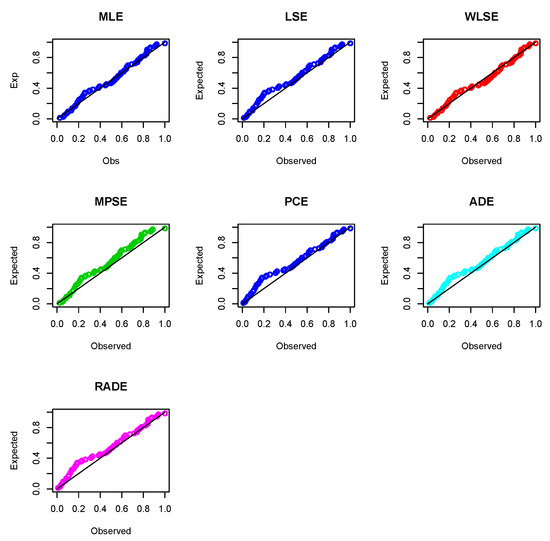
Figure 3. The PP plots of the omega distribution based on seven methods of estimation.

7. Conclusions

The omega distribution was pioneered by [1] to model reliability data, and its basic properties were studied by [2]. We obtained explicit expressions for single and product moments of order statistics of this distribution along with L-moments, which may be useful for practitioners. This will encourage researchers to conduct further works about the omega distribution and order statistics. We present seven methods to determine estimates of the parameters of the omega distribution and provide a simulation study to illustrate the performance of the different estimators. We show empirically that the maximum likelihood method gives consistent estimates of the omega parameters. An application to real data illustrates the importance of the omega distribution, which gives a superior fit compared to ten other distributions.

It is worth mentioning that this article can be extended in many ways. For example, an exponentiated version of the omega distribution can be established, among other extensions; some properties of the order statistics from this distribution can be investigated and their relations to well-known stochastic orders; and a bivariate or multivariate omega distribution can also be proposed. Furthermore, the parameters of the omega distribution can be estimated in the Bayesian approach under different losses functions.