Hypercycle Systems of 5-Cycles in Complete 3-Uniform Hypergraphs

Abstract

In this paper, we consider the problem of constructing hypercycle systems of 5-cycles in complete 3-uniform hypergraphs. A hypercycle system $\mathcal{C}(r,k,v)$ of order v is a collection of r-uniform k-cycles on a v-element vertex set, such that each r-element subset is an edge in precisely one of those k-cycles. We present cyclic hypercycle systems $\mathcal{C}(3,5,v)$ of orders $v=25,26,31,35,37,41,46,47,55,56$, a highly symmetric construction for $v=40$, and cyclic 2-split constructions of orders $32,40,50,52$. As a consequence, all orders $v\le 60$ permitted by the divisibility conditions admit a $\mathcal{C}(3,5,v)$ system. New recursive constructions are also introduced.

1. Introduction

A hypergraph H of order v is a pair $(X,E)$, where X is the vertex set with $X=v$ and E is a family of subsets of X called edges. If all edges in E have size r, then H is said to be r-uniform. The complete r-uniform hypergraph of order v, denoted by $K_v^{\left(r\right)}$, is the hypergraph in which E consists of all the r-element subsets of X.

There are various ways to define cycles in hypergraphs. In this paper, we deal with an object called the tight r-uniform hypercycle of length k ($k>r\ge 3$)—also called cycloid in another context—which consists of k vertices and k edges; namely, it is a cyclic sequence of k vertices of X in which any r consecutive vertices, and only those, form an edge. If r is understood, we simply call it a k-cycle. An r-uniform hypercycle of length k is denoted by $C(r,k)$, and the integers $0,1,\dots ,v-1$ are used for the vertices. For example, the cyclic sequence $(0,1,2,3,4)$ represents a $C(3,5)$ cycle for which the edges are the 3-sets $\{0,1,2\}$, $\{1,2,3\}$, $\{2,3,4\}$, $\{3,4,0\}$, and $\{4,0,1\}$. (Inside a 3-set, the order of vertices does not matter, but the order in a 5-tuple is of essence, except that any cyclic shift and the reversal of the sequence practically mean the same cycle.)

As a relative of Steiner systems, a hypercycle system $\mathcal{C}(r,k,v)$ of order v is a family $\mathcal{C}$ of k-cycles such that each edge of $K_v^{\left(r\right)}$ is contained in precisely one k-cycle of $\mathcal{C}$. A very natural but rather hard problem is to determine those $r,k,v$ for which a $\mathcal{C}(r,k,v)$ exists.

In the case of $k=r+1$, the cycle is a complete hypergraph at the same time; hence, there is a bijection between $\mathcal{C}(r,r+1,v)$ systems and Steiner systems $\mathcal{S}(k-1,k,v)$ of which the study is an important classical issue in design theory. Apart from this, the first paper written on hypercycle systems is [1], where Bailey and Stevens initiated the study of Hamiltonian cycle decompositions, i.e., the case of $k=v$. They showed for r = 3 that it is possible to connect any edge of $K_v^{\left(3\right)}$ to a triplet of differences, and they developed a numerical algorithm. In this way, they settled the feasible cases for $r=3$ up to $v\le 16$ in the affirmative, with two exceptions, and solved the case $v=k=9$, $r=4$. Their results on $r=3$ were extended to the larger range of $v\le 32$ by Meszka and Rosa [2], who proposed the study of a general problem with $r<k<v$, too, and introduced further variants. Before turning to 3-uniform 5-cycles, which is the main subject of the present paper, we also mention another track of a remarkably efficient computer search by Jirimutu et al. with the parameters $r=3$ and $k=7$, resulting in constructions for $v=7,8,14,16,22,23,29,37,43,44,45,58$; see the series of papers [3,4,5,6,7].

From now on, we deal with $\mathcal{C}(3,5,v)$ systems and use the shorter term “cycle system” for them. Although such systems gained some attention in the past couple of years, there are still not many previous results regarding this topic. The first constructions were published by Meszka and Rosa in [2]. Certainly, the system of order 5 is trivial as $C(3,5)$ is self-complementary. Meszka and Rosa established via a computer search that there are exactly two non-isomorphic cycle systems of order 7 (neither of them is cyclic), and there exist cycle systems of orders 10, 11, and 16. They also described a recursive rule for cases where 3-wise balanced Steiner systems of block size 5 exist and observed further that the spherical geometries $\mathcal{S}(3,5,4^n+1)$ imply the existence of a cycle system for every order v of the form $4^n+1$. The four base blocks of a cyclic $\mathcal{S}(3,5,17)$ system are listed, e.g., on page 319 of [8].

Gionfriddo, Milazzo, and the second author [9] developed further recursions for building larger cycle systems from smaller ones and applied a difference method to design new initial configurations, up to $v=22$. This work, finally published in [10], was one in an area in which the configurations were constructed by hand rather than by computer search; the paper included several hints concerning the concepts that helped establish results in this way. In the meantime, an idependent research was carried out by Li, Lei, and Jirimutu, finding constructions for $v=20$[11] and $v=32$ [12] and for $v=22$ by Huo, Zhao, Feng, and Yang, as cited in [11]. Beyond explicit constructions, that paper [13] contained the recursion $v⟶5v$ (which also follows from a more general construction in [10]) and claims a system for $v=26$. However, the generators for $v=26$ contain $(0,4,21,9,16)$ as cycle #12 and $(0,4,18,12,16)$ as cycle #18, both of them covering the vertex triple $\{0,4,16\}$, hence not satisfying the requirements. Later in this paper, we present our solution to $\mathcal{C}(3,5,26)$.

1.1. Our Results

In constructions, two types of systems occur frequently. Assuming that the vertices are represented with the integers $0,1,\dots ,v-1$, a system is cyclic if the mapping $i\mapsto i+1\left(\mathrm{mod}v\right)$ is an automorphism. In addition, if a system is of even order $2v$ and contains two vertex-disjoint subsystems of order v, we say with the terminology of [9] that it is a 2-split system.

Every $C(3,5)$ contains exactly five edges of $K_v^{\left(3\right)}$ and exactly three edges incident with any of its vertices. Hence, $(\genfrac{}{}{0pt}{}{v}{3})$ has to be a multiple of 5 and $(\genfrac{}{}{0pt}{}{v-1}{2})$ a multiple of 3. Analogous observations are valid for 2-split systems of order $2v$ and for their subsystems of order v. From these facts, one can conclude that the following conditions are necessary. Natural numbers v belonging to the listed residue classes are referred to as feasible orders.

Lemma 1. (Feasible residue classes for the spectrum) 

(i)

If there exist a system $\mathcal{C}(3,5,v)$ of order v, then $v\equiv 1,2,5,7,10,11\left(\mathrm{mod}15\right)$ [2].

(ii)

If there exists a 2-split system $\mathcal{C}(3,5,2v)$ of order $2v$, then $2v\equiv 2,10,20,22\left(\mathrm{mod}30\right)$ [10].

Divisibility conditions similar to those mentioned before the lemma can be formulated for every Steiner system $\mathcal{S}(t,k,v)$, i.e., for partitioning the edge set of $K_v^{\left(t\right)}$ into copies of $K_k^{\left(t\right)}$, and more generally for the existence of edge decompositions of $K_v^{\left(r\right)}$ into subhypergraphs isomorphic to H for any given r-uniform hypergraph H. Keevash [14] introduced deep methods and proved that all but finitely many orders v satisfying the divisibility conditions admit an $\mathcal{S}(t,k,v)$ system for any parameters t and k. Glock, Kühn, Lo, and Osthus [15] extended this result from $K_v^{\left(t\right)}$-decompositions to H-decompositions for all uniform hypergraphs H. For technical details, we refer to Theorem 1.1 of [15] and Theorem 1.5 of [16]. As a consequence, it follows for every v large enough that the conditions in $\left(i\right)$ are not only necessary but also sufficient for the existence of $\mathcal{C}(3,5,v)$ systems. Based on our results, we have the impression that they are sufficient in a much stronger sense, namely without any exceptions. This is expressed in the following two-part conjecture.

Conjecture 1. Let v be a feasible order.

$\left(i\right)$

If $v\equiv 1,2,5,7,10,11\left(\mathrm{mod}15\right)$ and $v\ne 7$, then there exists a cyclic $\mathcal{C}(3,5,v)$ system of order v.

$\left(ii\right)$

If $2v\equiv 2,10,20,22\left(\mathrm{mod}30\right)$, then there exists a cyclic 2-split $\mathcal{C}(3,5,2v)$ system of order $2v$.

Our constructions in Section 5 verify this conjecture for a certain range of orders. We summarize this in the following assertion, indicating the smallest open cases as upper bounds on the orders of cycle systems.

Theorem 1. Let v be a feasible order.

$\left(i\right)$

If $v\equiv 1,2,5,7,10,11\left(\mathrm{mod}15\right)$, and $v\ne 7$, then there exists a cyclic $\mathcal{C}(3,5,v)$ system of order v for all $v<61$.

$\left(ii\right)$

If $2v\equiv 2,10,20,22\left(\mathrm{mod}30\right)$, then there exists a cyclic 2-split $\mathcal{C}(3,5,2v)$ system of order $2v$ for all $2v<62$.

One step in the constructions of Section 5 for odd v is to find a packing of $\left(\genfrac{}{}{0pt}{}{v}{2}\right)$ symmetric cycles, a subsystem with a quadratic number of cycles that can be generated by just one cycle and two automorphisms of the subsystem. The feasibility of this step is analyzed in Section 4.

In Section 3, we describe some recursive steps applicable to building larger cycle systems from smaller ones. The prerequisites for them are given in Section 2, where we find decompositions of some auxiliary constructions. We believe that these building blocks will be useful in many further constructions in the future, too.

A remarkable particular consequence of the method is a $\mathcal{C}(3,5,40)$ system of order 40, which is generated by as few as seven cycles via two types of mappings (see Corollary 1).

In order to help the reader check the correctness of the constructions, details of the calculation are listed in numerous tables in the Appendix A.

1.2. Difference Triplets

We conclude this introduction with some technical definitions needed in the design and description of cyclic systems.

The vertex set of a cyclic system of order v is assumed to be ${\mathbb{Z}}_v$. The distance of two vertices $i,j$ is their shortest distance “along the cycle”, that is $i-j=min\{i-j,v-i-j\}$. A 5-cycle, say $C=(a,b,c,d,e)$, covers the five 3-element sets (vertex triples) $\{a,b,c\}$, $\{b,c,d\}$, $\{c,d,e\}$, $\{d,e,a\}$, and $\{e,a,b\}$.

Having fixed the value of v, a base cycle is a cycle $C=(a,b,c,d,e)$ for which the orbit under rotation $i\mapsto i+1$ (mod v) should also be included in the system. Assume that $T=\{p,q,r\}$ is a vertex triple in a base cycle C. As defined in [10], the difference triplet associated with T is a cyclic triplet of integers; it is obtained in the following way. First, find the increasing order of elements in T, i.e., let $0\le i<j<k<v$ be such that $\{i,j,k\}=\{p,q,r\}$. Then, either of

$$(i-j,j-k,k-i),(j-k,k-i,i-j),(k-i,i-j,j-k)$$

represents the difference triplet of T. Usually (but not always), we take the lexicographically smallest of these three. A difference triplet of type $(i,i,j)$ is also called a “symmetric difference”, and we use the term “reflected difference” for a pair $\left\{\right(i,j,k),(i,k,j\left)\right\}$ of difference triplets in which the three distances $i,j,k$ are all distinct.

2. Partial Cycle Systems of Orders 10 and 20

In this section, we present two auxiliary configurations that are useful in building larger cycle systems.

2.1. Decomposing a Doubled 5-Cycle

For the moment, let $X=\{a,b,c,d,e\}$ be a 5-element set on which the 3-uniform 5-cycle $C=(a,b,c,d,e)$ is taken. That is, C has five edges $abc,bcd,cde,dea,eab$ (where the order of vertices in an edge is irrelevant). We double each vertex:

$$X_1=\{a_1,b_1,c_1,d_1,e_1\},X_2=\{a_2,b_2,c_2,d_2,e_2\}.$$

In this way, each edge of C gives rise to eight vertex triples in $X_1\cup X_2$. For example, $bcd$ yields $b_1{c}_1{d}_1$, $b_1{c}_1{d}_2$, $b_1{c}_2{d}_1$, $b_1{c}_2{d}_2$, $b_2{c}_1{d}_1$, $b_2{c}_1{d}_2$, $b_2{c}_2{d}_1$, and $b_2{c}_2{d}_2$.

Definition 1.

A doubled 5-cycle consists of 10 vertices and 40 edges, as augmented from X to $X_1\cup X_2$ above.

Lemma 2.

The 40 edges of a doubled 5-cycle can be decomposed into eight 5-cycles.

Proof. 

A decomposition is obtained by taking the following eight cycles:

$$(a_1,b_1,c_1,d_1,e_1),(a_1,b_1,c_2,d_2,e_2),(a_1,b_2,c_1,d_2,e_1),(a_1,b_2,c_2,d_1,e_2),$$

$$(a_2,b_1,c_1,d_2,e_2),(a_2,b_1,c_2,d_1,e_1),(a_2,b_2,c_1,d_1,e_2),(a_2,b_2,c_2,d_2,e_1).$$

It can be checked that every edge of the doubled cycle occurs in precisely one of the eight cycles above. □

2.2. Decomposing the Complement of a Blown-Up 4-Cycle

Here, we present a partial cycle system of order 20. The complement of the structure introduced below is the 3-uniform hypergraph, which is constructed by taking four 5-element vertex classes (sets of vertices) in cyclic order and by taking all vertex triples that are either inside one class or in the union of two consecutive classes in the fixed cyclic order.

Definition 2. 

Let ${\mathcal{H}}_{⟨4\times 5⟩}$ denote the 3-uniform hypergraph of order 20 for which the vertex set is $X=A\cup B\cup C\cup D$, with $A=B=C=D=5$, and for which the edge set consists of the vertex triples that

• meet exactly three of the vertex classes $A,B,C,D$ or
• meet both A and C, or both B and D.

Lemma 3.

There exists a $\mathcal{C}(3,5,20)$ system that contains an embedded decomposition of ${\mathcal{H}}_{⟨4\times 5⟩}$ as a partial subsystem.

Proof. 

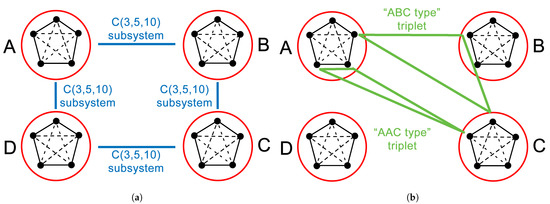
The structure of the construction is shown in Figure 1 and Figure 2. Inside each of $A,B,C,D$, we take a $\mathcal{C}(3,5,5)$. We also know that there exists a 2-split system of order 10 (see [10]); hence, the families of crossing triples of $A\cup B$, $B\cup C$, $C\cup D$, and $D\cup A$ are decomposable into 5-cycles. What remains to be covered are the triples connecting A and C, or B and D or meeting exactly three of $A,B,C,$ and D. Let us call the latter an ABC type (which can mean any of $ABC$, $BCD$, $CDA$, and $DAB$) and the former two together an $AAC$ type (which can mean $AAC$, $BBD$, $CCA$, and $DDB$).

Figure 1. $\mathcal{C}(3,5,20)$ construction step 1. (a) Inside each of $A,B,C,$ and D, we take $\mathcal{C}(3,5,5)$. The families of crossing triples of $A\cup B$, $B\cup C$, $C\cup D$, and $D\cup A$ are decomposable into 5-cycles since we know there exists a 2-split system of order 10 (see [10]). (b) The remaining triples either connect A and C, or B and D or meet exactly three of $A,B,C,$ and D. The latter is called an ABC type (which can mean any of $ABC$, $BCD$, $CDA$, and $DAB$) and the former two together are an $AAC$ type (which can mean $AAC$, $BBD$, $CCA$, and $DDB$).

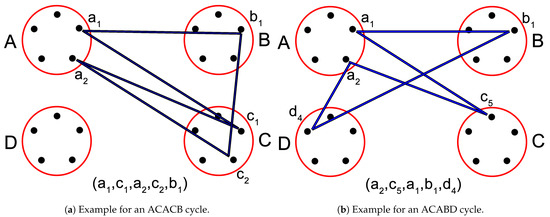
Figure 2. $\mathcal{C}(3,5,20)$ construction step 2. Two of the seven base cycles of Table 1a are illustrated.

We have to cover $4·10·5=20·10$ AAC-type triples and $4·5^3=20·25$ ABC-type triples, altogether $20·35$ triples, which therefore need $20·7$ cycles. This is generated by the seven cycles listed in Table 1a. Figure 2 illustrates ACACB and ACABD cycles of these 7 cycles, highlighted in the table.

Table 1. Subsystem ${\mathcal{H}}_{⟨4\times 5⟩}$ inside $\mathcal{C}(3,5,20)$.

(a) Seven base cycles: three ACACB cycles and four ACABD cycles.

Base Cycles (5 Vertices)

v1

v2

v3

v4

v5

a1

c1

a2

c2

b1

a1

c1

a3

c5

b3

a1

c2

a3

c1

b4

a2

c5

a1

b1

d4

a3

c5

a1

b5

d4

a4

c1

a1

b2

d4

a4

c2

a1

b2

d3

(b) Generating 20 cycles from the green base cycle of type ACACB.

ACACB cycles

BDBDC cycles

CACAD cycles

DBDBA cycles

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

a1

c1

a2

c2

b1

b1

d1

b2

d2

c1

c1

a1

c2

a2

d1

d1

b1

d2

b2

a1

a2

c2

a3

c3

b2

b2

d2

b3

d3

c2

c2

a2

c3

a3

d2

d2

b2

d3

b3

a2

a3

c3

a4

c4

b3

b3

d3

b4

d4

c3

c3

a3

c4

a4

d3

d3

b3

d4

b4

a3

a4

c4

a5

c5

b4

b4

d4

b5

d5

c4

c4

a4

c5

a5

d4

d4

b4

d5

b5

a4

a5

c5

a1

c1

b5

b5

d5

b1

d1

c5

c5

a5

c1

a1

d5

d5

b5

d1

b1

a5

(c) Generating 20 cycles from the purple base cycle of type ACABD.

ACABD cycles

BDBCA cycles

CACDB cycles

DBDAC cycles

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

v1

v2

v3

v4

v5

a2

c5

a1

b1

d4

b2

d5

b1

c1

a4

c2

a5

c1

d1

b4

d2

b5

d1

a1

c4

a3

c1

a2

b2

d5

b3

d1

b2

c2

a5

c3

a1

c2

d2

b5

d3

b1

d2

a2

c5

a4

c2

a3

b3

d1

b4

d2

b3

c3

a1

c4

a2

c3

d3

b1

d4

b2

d3

a3

c1

a5

c3

a4

b4

d2

b5

d3

b4

c4

a2

c5

a3

c4

d4

b2

d5

b3

d4

a4

c2

a1

c4

a5

b5

d3

b1

d4

b5

c5

a3

c1

a4

c5

d5

b3

d1

b4

d5

a5

c3

One can see that

• each ACACB cycle covers two AAC-type triples and three ABC-type triples,
• each ACABD cycle covers one AAC-type triple and four ABC-type triples.

Hence, the seven cycles cover $3·2+4=10$ AAC-type triples and $3·3+4·4=25$ ABC-type triples.

Now, from each of these seven cycles, we generate 20 cycles for $\mathcal{C}(3,5,20)$ by defining the following two types of automorphisms:

• rotation of order four among the vertex classes, $A\to B\to C\to D\to A$;
• simultaneous rotation among the indices $a_i\to a_{i+i}$, $b_i\to b_{i+i}$, $c_i\to c_{i+i}$, $d_i\to d_{i+i}$, for $i=1,2,3,4,5$ modulo 5 (where the image of 5 is 1).

The effect of these transformations on the cycles $\left(a_1{c}_1{a}_2{c}_2{b}_1\right)$ and $\left(a_2{c}_5{a}_1{b}_1{d}_4\right)$ is detailed in Table 1b,c, respectively.

In this way, $20·7$ cycles are defined as needed, and one can check that each vertex triple is covered exactly once. □

Remark 1.

In the system $\mathcal{C}(3,5,20)$ constructed above, each of $A\cup B$, $B\cup C$, $C\cup D$, and $D\cup A$ induces a 2-split $\mathcal{C}(3,5,10)$ system.

3. Recursive Constructions

In this section, we build some constructions that may be applied recursively. The method of the first subsection works for every order v for which there is a known 5-cycle system. The construct of the second subsection is applicable when an auxiliary partial system is available too. This requirement is fulfilled by ${\mathcal{H}}_{⟨4\times 5⟩}$, with the help of which a highly symmetric $\mathcal{C}(3,5,40)$ system can be designed.

3.1. General Step $v⟶10v$

The next construction builds 2-split systems; hence, it generates systems that are suitable for further recursions.

Theorem 2.

If there exists a $\mathcal{C}(3,5,v)$, then a 2-split $\mathcal{C}(3,5,10v)$ also exists.

Proof. 

Applying the $(\mathcal{C}(3,5,v)\wedge \mathcal{C}(3,5,w))⟶\mathcal{C}(3,5,vw)$ recursion of [10], [Theorem 4.3], for the particular case of $w=5$ starting from a $\mathcal{C}(3,5,v)$ system, we obtain a $\mathcal{C}(3,5,5v)$ that has the following structure. The vertex set is partitioned into 5-element classes, say $X=X_1\cup \dots \cup X_v$; each class $X_i$ induces a $\mathcal{C}(3,5,5)$; the union of any two classes induces a 2-split $\mathcal{C}(3,5,10)$; and every vertex triple meeting three of the classes is covered by a cycle, all of the vertices of which are in mutually distinct classes.

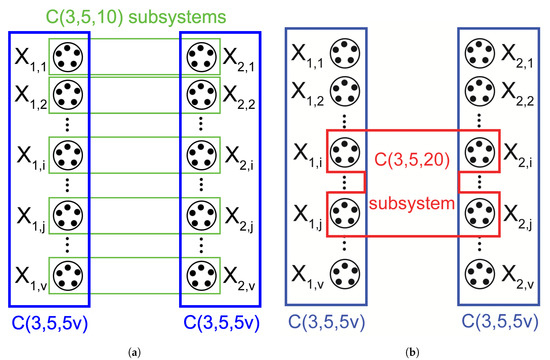
The construction for $\mathcal{C}(3,5,10v)$ is illustrated with Figure 3. We create two vertex-disjoint copies of a $\mathcal{C}(3,5,5v)$ with the structure described above, say on the vertex sets $X_1=X_{1,1}\cup \dots \cup X_{1,v}$ and $X_2=X_{2,1}\cup \dots \cup X_{2,v}$. For $i=1,\dots ,v$, we keep the $\mathcal{C}(3,5,5)$ subsystems inside both $X_{1,i}$ and $X_{2,i}$ and insert the crossing cycles of a 2-split $\mathcal{C}(3,5,10)$ between $X_{1,i}$ and $X_{2,i}$.

Figure 3. The $v⟶10v$ construction. (a) Two vertex-disjoint copies of a $\mathcal{C}(3,5,5v)$ are created. The details are explained in the proof of Theorem 2. Within the green rectangles, the two $\mathcal{C}(3,5,5)$ subsystems are kept with crossing cycles of a 2-split $\mathcal{C}(3,5,10)$ between them. (b) For all $1\le i<j\le v$, we also keep the crossing cycles of a 2-split $\mathcal{C}(3,5,10)$ inside $X_{1,i}\cup X_{1,j}$ as well as inside $X_{2,i}\cup X_{2,j}$. The remaining triples inside $X_{1,i}\cup X_{1,j}\cup X_{2,i}\cup X_{2,j}$ together form a hypergraph isomorphic to ${\mathcal{H}}_{⟨4\times 5⟩}$.

For all $1\le i<j\le v$, we also keep the crossing cycles of a 2-split $\mathcal{C}(3,5,10)$ inside $X_{1,i}\cup X_{1,j}$ as well as inside $X_{2,i}\cup X_{2,j}$. The remaining triples inside $X_{1,i}\cup X_{1,j}\cup X_{2,i}\cup X_{2,j}$ together form a hypergraph isomorphic to ${\mathcal{H}}_{⟨4\times 5⟩}$, which we decompose into 5-cycles by Lemma 3.

Finally, in order to cover the remaining vertex triples, we perform the following. Any cycle C that meets more than two classes of $\mathcal{C}(3,5,5v)$ specifies a 5-cycle $C_1$ in $X_1$ and a 5-cycle $C_2$ in $X_2$. We replace $C_1\cup C_2$ with the eight 5-cycles constructed in Lemma 2. This completes the construction of $\mathcal{C}(3,5,10v)$.

As it can be seen, in the system constructed in this way, every vertex triple is contained in one and only one 5-cycle. Hence, a $\mathcal{C}(3,5,10v)$ system is obtained. □

Remark 2.

Applying this result for known values and for the newly constructed systems, the existence problem is now solved for some further $v=$ $70,$$160,$$200,$$260,$$310,$$320,$$350,$$370,$$460,$$470,$$520,$ $550,$$560,$$700,$$800,$$820,$$1000,\dots$ Moreover, there are further values for which the existence of systems was already known, but systems with the 2-split property are new: $100,$$110,$$400,$$410,$ and 500.

3.2. Conditional Step $v⟶8v$

First, we define a parametrized hypergraph that generalizes the structure of ${\mathcal{H}}_{⟨4\times 5⟩}$. For the sake of applicability, the parameter k is assumed to be feasible for the existence of a $\mathcal{C}(3,5,k)$ system.

Definition 3.

Let ${\mathcal{H}}_{⟨4\times k⟩}$ denote the 3-uniform hypergraph of order $4k$ for which the vertex set is $X=A\cup B\cup C\cup D$, with $\left|A\right|=\left|B\right|=\left|C\right|=\left|D\right|=k$ and for which the edge set consists of those vertex triples that

• meet exactly three of the vertex classes $A,B,C,$ or D or
• meet both A and C, or both B and D.

Theorem 3.

If ${\mathcal{H}}_{⟨4\times v⟩}$ admits a decomposition into 5-cycles and there exists a 2-split $\mathcal{C}(3,5,2v)$ system, then a system $\mathcal{C}(3,5,8v)$ exists.

Proof. 

The basic scheme of the construction is as follows.

1.

Start with a Steiner Quadruple System of order 8.

2.

Take a $2K_2$-decomposition of the complete graph $K_8$ embedded into $\mathcal{SQS}\left(8\right)$.

3.

Substitute a v-element set into each point of $\mathcal{SQS}\left(8\right)$ and a $\mathcal{C}(3,5,v)$ system into each of those v-sets.

4.

Insert 14 copies of the 5-cycle decomposition of ${\mathcal{H}}_{⟨4\times v⟩}$ in each blown-up block of $\mathcal{SQS}\left(8\right)$.

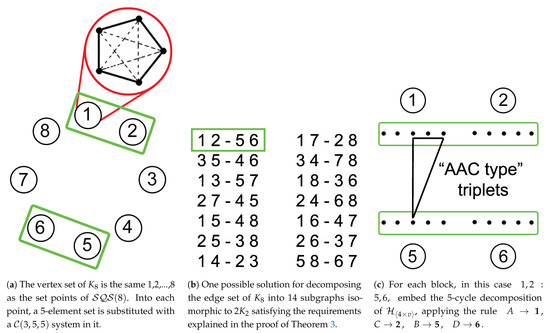
These steps are performed in the following way, illustrated in Figure 4.

Figure 4. $\mathcal{C}(3,5,40)$ construction as described in the proof of Theorem 3.

$1^{\circ }$ For a simple notation, let us assume that the eight points of $\mathcal{SQS}\left(8\right)$ are $1,2,\dots ,8$. We consider the following 14 blocks:

$$\begin{array}{cccc}A=\{1,2,5,6\},& B=\{1,2,7,8\},& C=\{3,4,5,6\},& D=\{3,4,7,8\},\\ E=\{1,3,5,7\},& F=\{1,3,6,8\},& G=\{2,4,5,7\},& H=\{2,4,6,8\},\\ J=\{1,4,5,8\},& K=\{1,4,6,7\},& L=\{2,3,5,8\},& M=\{2,3,6,7\},\\ & P=\{1,2,3,4\},& Q=\{5,6,7,8\}.& \end{array}$$

$2^{\circ }$ The complete graph $K_8$ has 28 edges. Assume that its vertex set is the same $\{1,2,\dots ,8\}$ as the set of points of $\mathcal{SQS}\left(8\right)$. We decompose the edge set into 14 subgraphs isomorphic to $2K_2$ in such a way that the union of the two edges in each copy of $2K_2$ is a distinct block of $\mathcal{SQS}\left(8\right)$. One solution is as follows:

$$\begin{array}{cccc}A-1,2:5,6;& B-1,7:2,8;& C-3,5:4,6;& D-3,4:7,8;\\ E-1,3:5,7;& F-1,8:3,6;& G-2,7:4,5;& H-2,4:6,8;\\ J-1,5:4,8;& K-1,6:4,7;& L-2,5:3,8;& M-2,6:3,7;\\ & P-1,4:2,3;& Q-5,8:6,7.& \end{array}$$

$3^{\circ }$ For each point i ($i=1,2,\dots ,8$) of $\mathcal{SQS}\left(8\right)$, we take a v-element set $X_i$, which will be the vertex set of a $\mathcal{C}(3,5,v)$, hence forming eight vertex-disjoint subsystems of the $\mathcal{C}(3,5,4v)$ under construction.

$4^{\circ }$ For each block—say, $i_1,i_2:i_3,i_4$ as partitioned in $2^{\circ }$—embed the 5-cycle decomposition of ${\mathcal{H}}_{⟨4\times v⟩}$, applying the rule

$$A\to X_{i_1},C\to X_{i_2},B\to X_{i_3},D\to X_{i_4}.$$

Hence, the two edges of $2K_2$ inside each block specify the positions of AAC triples in the blow-up of the block in question.

It can be checked that each vertex triple appears in exactly one 5-cycle:

• If a triple is a subset of one $X_i$, then it is in a cycle in the $\mathcal{C}(3,5,v)$ system embedded in $X_i$.
• If a triple meets exactly two parts, say $X_{i_1}$ and $X_{i_2}$, then the edge $i_1{i}_2$ determines a $2K_2$ in the decomposition of $K_8$; this $2K_2$ specifies a block in $\mathcal{SQS}\left(8\right)$, and then in the copy of ${\mathcal{H}}_{⟨4\times v⟩}$ embedded in the blow-up of that block, the vertex triple in question is a triple of AAC type; hence, it is contained in a 5-cycle of the system.
• If a triple meets exactly three parts, say $X_{i_1}$, $X_{i_2}$, and $X_{i_3}$, then by the definition of Steiner quadruple systems, the three points $i_1,i_2,i_3$ determine a block, and then in the copy of ${\mathcal{H}}_{⟨4\times v⟩}$ embedded in the blow-up of that block, the vertex triple in question is a triple of ABC type; hence, it is contained in a unique cycle.

This verifies the claimed properties and completes the proof. □

As a first application of this method, we derive that a highly symmetric $\mathcal{C}(3,5,40)$ system exists.

Corollary 1.

There exists a $\mathcal{C}(3,5,40)$ system generated by seven 5-cycles.

Proof. 

This follows from Theorem 3, applying Lemma 3, which ensures that ${\mathcal{H}}_{⟨4\times 5⟩}$ admits a 5-cycle decomposition generated by seven cycles and two automorphisms. □

4. General Method for Cyclic Packing of Symmetric Cycles with $\mathbf{gcd}(\mathit{v},\mathbf{10010})=\mathbf{1}$

Cyclic systems are generated by a certain number of base cycles. In this way, instead of $O\left(v^3\right)$ cycles, the task is to find $O\left(v^2\right)$ base cycles for which the orbits cover all vertex triples. In this section, we present a method that reduces the number of base cycles to be found. Although the gain is only linear in v, it is significant when v is not too large. It is applicable whenever v satisfies a simple arithmetic condition.

More explicitly, the construction works for all odd v not divisible by 5, 7, 11, and 13. We first explain these exceptions and then prove that the method is applicable for all the other values of v. This analysis also tells us which ones are the few symmetric differences to be handled separately when v is a multiple of 5, 7, 11, or 13.

Throughout this section, we assume that v is odd and consider the base cycles

$$(0,i,v-3i,3i,v-i),i=1,2,\dots ,(v-1)/2.$$

If v is a multiple of 5 or 7 or 11 or 13, then the difference triplets (see the definition in Section 1.2) listed in Table 2 are covered more than once. Marking with S means that a symmetric difference belonging to a value other than i also occurs in the 5-cycle $(0,i,v-3i,3i,v-i)$. Marking with M means that a reflected difference occurs for more than one value of i.

Table 2. Disqualified triplet types: S = symmetric triplet, and M = multiply covered triplet.

Divisor of v	Difference Triplet	Reason of Conflict	i of Cycle That Covers Triplet
5	$(v/5,v/5,2v/5)$	S	$v/5$
5	$(v/5,2v/5,2v/5)$	S	$2v/5$
7	$(v/7,v/7,2v/7)$	S	$2v/7$
7	$(2v/7,2v/7,3v/7)$	S	$3v/7$
7	$(3v/7,3v/7,v/7)$	S	$v/7$
7	$(v/7,2v/7,3v/7)$	M	$v/7$, $2v/7$, $3v/7$
11	$(v/11,2v/11,3v/11)$	M	$3v/11$, $5v/11$
11	$(v/11,3v/11,4v/11)$	M	$v/11$, $2v/11$
11	$(v/11,4v/11,5v/11)$	M	$3v/11$, $4v/11$
11	$(2v/11,3v/11,5v/11)$	M	$2v/11$, $4v/11$
11	$(2v/11,4v/11,5v/11)$	M	$v/11$, $5v/11$
13	$(v/13,3v/13,4v/13)$	M	$v/13$, $3v/13$, $4v/13$
13	$(2v/13,5v/13,6v/13)$	M	$2v/13$, $5v/13$, $6v/13$

The case of $v=7k$ is special, as it has both types of anomalies: All symmetric triplets and the (unique) reflected triplet are covered three times. To make the reason transparent, we exhibit the situation in Table 3 for $v=7$.

Table 3. Covered vertex triples and their difference triplets of $(0,i,v-3i,3i,v-i)$ for $v=7$.

cycle for $i=1$			$(0,1,4,3,6)$
covered vertex triples	$\{0,1,4\}$	$\{1,3,4\}$	$\{3,4,6\}$	$\{0,3,6\}$	$\{0,1,6\}$
difference triplets	$(1,3,3)$	$(2,1,3)$	$(1,2,3)$	$(3,3,1)$	$(1,1,2)$
cycle for $i=2$			$(0,2,1,6,5)$
covered vertex triples	$\{0,1,2\}$	$\{1,2,6\}$	$\{1,5,6\}$	$\{0,5,6\}$	$\{0,2,5\}$
difference triplets	$(1,1,2)$	$(2,1,3)$	$(1,2,3)$	$(1,1,2)$	$(2,2,3)$
cycle for $i=3$			$(0,3,5,2,4)$
covered vertex triples	$\{0,3,5\}$	$\{2,3,5\}$	$\{2,4,5\}$	$\{0,2,4\}$	$\{0,3,4\}$
difference triplets	$(2,2,3)$	$(1,2,3)$	$(2,1,3)$	$(2,2,3)$	$(3,3,1)$

Theorem 4. (Symmetric Packing Lemma)

If v is an odd feasible order, then for the symmetric base cycles

$$(0,i,v-3i,3i,v-i),i=1,2,\dots ,(v-1)/2,$$

the necessary and sufficient condition of covering each difference triplet at most once and covering each symmetric difference exactly once is that v is not divisible by any of $5,$$7,$$11,$ and 13. Moreover, if such a forbidden divisibility holds, then the multiple covers of difference triplets can be eliminated by the removal of symmetric cycles belonging to those i that are listed in the last column of Table 2.

Proof. 

The discussion preceding the theorem showed that divisibility by $5,$$7,$$11,$ and 13 must be excluded if we want to avoid multiple covers of vertex triples. Below, we see that, if v is a multiple of one or more of these numbers, then exactly the multiple covers listed in Table 2 occur. Moreover, in any other case, each cycle $(0,i,v-3i,3i,v-i)$ contains precisely one symmetric difference—namely, only the one occurring for its 3-element subset $\{0,i,v-i\}$—and that no reflected difference is generated by more than one value of i.

To do this, we consider the vertex triples $\{0,i,v-3i\}$ and $\{i,v-3i,3i\}$, compute the three differences determined by the vertex pairs in each triple, and put them in increasing order. Although we consider only two vertex triples here, they also represent the other two triples $\{v-3i,3i,v-i\}$ and $\{3i,v-i,0\}$ because the latter two yield the same increasing sequences when the three distances are put in order.

The formula for a difference, as a function of i and v, depends on the ratio $i/v$. For example, the difference between 0 and $3i$ is equal to $3i$ if $0\le i/v\le 1/6$, $v-3i$ if $1/6\le i/v\le 1/3$, and $3i-v$ if $1/3\le i/v\le 1/2$. (We may write strict inequalities here because a feasible v cannot be divisible by 2 and 3.) The same ratio $i/v$ determines which of the three differences is smallest and which of them is largest.

A further characteristic that we take into account is what we call “position”. We say that a triplet has a normal position if its largest difference equals the sum of its other two (smallest and middle) differences, and it has extra position if its three differences sum up to v. Table 4 exhibits all these pieces of information for all i, where $[a,b]$ means the range in the closed interval determined by the condition $a\le i/v\le b$. Completely identical (small, middle, and large) triplets are not repeated; for instance, $(i,3i,4i)$ is valid in the entire interval $[0,1/8]$.

Table 4. Characteristics of difference triplets depending on $i/v$.

Interval		$(0,\mathit{i},\mathit{v}-3\mathit{i})$		Cycle		$(\mathit{i},\mathit{v}-3\mathit{i},3\mathit{i})$		Cycle
$[\mathit{a},\mathit{b}]$	Small	Middle	Large	Position	Small	Middle	Large	Position
$[0,1/12]$	i	$3i$	$4i$	N	$2i$	$4i$	$6i$	N
$[1/12,1/10]$				N	$2i$	$4i$	$v-6i$	E
$[1/10,1/8]$				N	$2i$	$v-6i$	$4i$	E
$[1/8,1/7]$	i	$3i$	$v-4i$	E	$v-6i$	$2i$	$v-4i$	N
$[1/7,1/6]$	i	$v-4i$	$3i$	E				N
$[1/6,1/5]$	i	$v-4i$	$v-3i$	N	$6i-v$	$v-4i$	$2i$	N
$[1/5,1/4]$	$v-4i$	i	$v-3i$	N	$v-4i$	$6i-v$	$2i$	N
$[1/4,2/7]$	$4i-v$	$v-3i$	i	N	$4i-v$	$2v-6i$	$v-2i$	N
$[2/7,3/10]$	$v-3i$	$4i-v$	i	N				N
$[3/10,1/3]$				N	$2v-6i$	$4i-v$	$v-2i$	N
$[1/3,3/8]$	$3i-v$	i	$4i-v$	N	$6i-2v$	$v-2i$	$4i-v$	N
$[3/8,2/5]$	$3i-v$	i	$2v-4i$	E	$v-2i$	$6i-2v$	$2v-4i$	E
$[2/5,5/12]$	$3i-v$	$2v-4i$	i	E	$v-2i$	$2v-4i$	$6i-2v$	E
$[5/12,3/7]$				E	$v-2i$	$2v-4i$	$3v-6i$	N
$[3/7,1/2]$	$2v-4i$	$3i-v$	i	E				N

Hence, there are 23 possible cases altogether, 14 of which are normal and 9 of which are extra. More explicitly, the 14 normal triplets are

$$\begin{array}{ccc}A=(i,3i,4i);\hfill & B=(i,v-4i,v-3i);\hfill & C=(2i,4i,6i);\hfill \\ D=(3i-v,i,4i-v);\hfill & E=(4i-v,v-3i,i);\hfill & F=(4i-v,2v-6i,v-2i);\hfill \\ G=(6i-2v,v-2i,4i-v);\hfill & H=(6i-v,v-4i,2i);\hfill & J=(v-6i,2i,v-4i);\hfill \\ K=(v-4i,i,v-3i);\hfill & L=(v-4i,6i-v,2i);\hfill & M=(v-3i,4i-v,i);\hfill \\ N=(v-2i,2v-4i,3v-6i);\hfill & P=(2v-6i,4i-v,v-2i),\hfill & \end{array}$$

and the 9 extra triplets are

$$\begin{array}{ccc}Q=(i,3i,v-4i);\hfill & R=(i,v-4i,3i);\hfill & S=(2i,4i,v-6i);\hfill \\ T=(2i,v-6i,4i);\hfill & U=(3i-v,i,2v-4i);\hfill & V=(3i-v,2v-4i,i);\hfill \\ X=(v-2i,6i-2v,2v-4i);\hfill & Y=(v-2i,2v-4i,6i-2v);\hfill & Z=(2v-4i,3i-v,i).\hfill \end{array}$$

One has to show that no coincidences other than the ones listed in Table 2 can occur. This can be done through a case-by-case analysis, as demonstrated in Table 5 and Table 6. Note that normal triplets—as well as extra triplets—may coincide among each other, but a normal triplet can never be equal to an extra triplet. Hence, the inspections branch into two directions, one for normal triplets and one for extra triplets. In the simplified scheme, as exhibited in the tables, we use the following abbreviations:

Table 5. Infeasibility of pairs of normal triplets.

	P	N	M	L	K	J	H	G	F	E	D	C	B
A	$2\mid v$	$2\mid v$	$⟨13⟩$	$3\mid v$	$⟨13⟩$	$2\mid v$	$⟨11⟩$	$2\mid v$	$3\mid v$	$3\mid v$	$2\mid v$	contr	interv
B	$2\mid v$	$2\mid v$	$2\mid v$	$⟨5⟩$	$⟨5⟩$	$2\mid v$	$⟨5⟩$	$⟨11⟩$	$2\mid v$	interv	interv	$2\mid v$
C	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$
D	$3\mid v$	interv	$3\mid v$	$2\mid v$	interv	$2\mid v$	$2\mid v$	$3\mid v$	$⟨11⟩$	interv
E	$2\mid v$	$⟨11⟩$	$⟨7⟩$	$2\mid v$	$2\mid v$	interv	contr	$2\mid v$	$3\mid v$
F	$2\mid v$	$⟨7⟩$	$2\mid v$	$2\mid v$	$2\mid v$	$⟨7⟩$	$2\mid v$	$2\mid v$
G	$3\mid v$	$2\mid v$	$3\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$
H	$2\mid v$	$2\mid v$	$2\mid v$	$⟨5⟩$	$⟨5⟩$	$2\mid v$
J	$2\mid v$	$⟨7⟩$	$2\mid v$	$2\mid v$	contr
K	$2\mid v$	$3\mid v$	$⟨13⟩$	$⟨5⟩$
L	$2\mid v$	$2\mid v$	contr
M	$3\mid v$	$2\mid v$
N	$2\mid v$

Table 6. Infeasibility of pairs of extra triplets.

	Z	Y	X	V	U	T	S	R
Q	$3\mid v$	$2\mid v$	$2\mid v$	interv	$2\mid v$	$2\mid v$	contr	$⟨7⟩$
R	$⟨13⟩$	$2\mid v$	$2\mid v$	$2\mid v$	$⟨13⟩$	contr	$2\mid v$
S	$⟨11⟩$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$
T	$3\mid v$	$2\mid v$	$2\mid v$	$2\mid v$	$2\mid v$
U	$⟨13⟩$	$⟨5⟩$	$⟨5⟩$	$⟨5⟩$
V	$⟨7⟩$	$⟨5⟩$	$⟨5⟩$
X	$2\mid v$	$⟨5⟩$
Y	$2\mid v$

contr  :

no two values $i_1,i_2$ can make the two triplets identical;

interv  :

the possible values $i_1,i_2$ for identical triplets are not in the intervals where the formulas apply;

$2\mid v$  :

the possible values $i_1,i_2$ for identical triplets would imply that v is even;

$3\mid v$  :

the possible values $i_1,i_2$ for identical triplets would imply that v is a multiple of 3;

$⟨5⟩$  :

a disqualified triplet of Table 2 occurs if v is a multiple of 5;

$⟨7⟩$  :

a disqualified triplet of Table 2 occurs if v is a multiple of 7;

$⟨11⟩$  :

a disqualified triplet of Table 2 occurs if v is a multiple of 11;

$⟨13⟩$  :

a disqualified triplet of Table 2 occurs if v is a multiple of 13.

The cases are many but not hard. Here are some examples:

A vs. B :

the first terms of $(i_1,3i_1,4i_1)=(i_2,v-4i_2,v-3i_2)$ would require $i_1=i_2=i$ for some i and then $i=v/7$ by either of the second and third terms, but the formula $(i_1,3i_1,4i_1)$ is valid only for $i_1/v\in [0,1/8]$ (and $(i_2,v-4i_2,v-3i_2)$ is valid only for $i_2\in [1/6,1/5]$).

E vs. H :

a comparison of the corresponding terms in $(4i_1-v,v-3i_1,i_1)=(6i_2-v,v-4i_2,2i_2)$ would imply $4i_1=6i_2$, $3i_1=4i_2$, and $i_1=2i_2$, but any two of these lead to the contradiction $i_1=i_2=0$.

V vs. X :

in $(3i_1-v,2v-4i_1,i_1)=(v-2i_2,6i_2-2v,2v-4i_2)$, the equalities between the first terms and between the third terms together imply $3i_1+2i_2=2v=i_1+4i_2$; hence, $i_1=i_2=i$ for some i and then $v=5i/2$. That is, $i_1=i_2=2v/5$. For the validity of the formulas, we need $i_1\in [2/5,3/7]$ and $i_2\in [3/8,2/5]$. Both conditions are satisfied, yielding the disqualified triplet $(v/5,2v/5,2v/5)$. This means that the 5-cycle defined for $i=2v/5$ covers this symmetric triplet three times.

The same conclusion is obtained for the combinations (U, V), (U, X), (U, Y), (V, Y), and (X, Y), too, i.e., all six pairs from (U, V, X, Y) have the same implication.

U vs. Z :

starting from $(3i_1-v,i_1,2v-4i_1)=(2v-4i_2,3i_2-v,i_2)$, we multiply the second terms by 2 and compare the third terms. Then, $6i_2-2i_1=2v=4i_1+i_2$; hence, $6i_1=5i_2$. Writing $i_1=5k$ and $i_2=6k$, we obtain $v=3i_2-i_1=13k$; then, $i_1=5v/13$ and $i_2=6v/13$. These solutions are feasible because, for validity of the formulas, we need $i_1/v\in [3/8,2/5]$ and $i_2/v\in [3/7,1/2]$. These conditions are satisfied by 5/13 and 6/13, yielding the disqualified triplet $(2v/13,5v/13,6v/13)$.

The validity of all entries in Table 5 and Table 6 can be checked in a similar way. This proves the assertion since v is assumed to be odd, and there does not exist any 5-cycle system for which the order is divisible by 3. □

5. Complete Spectrum of $\mathcal{C}(\mathbf{3},\mathbf{5},\mathit{v})$ Systems for $\mathit{v}\le \mathbf{60}$

Recall that the feasible residue classes are $v\equiv 1,2,5,7,10,11$ (mod 15). The results presented in this section, together with earlier publications, imply that every feasible order $v\le 60$ admits a 3-uniform 5-cycle system. The previously known system $\mathcal{C}(3,5,55)$ (which is not cyclic) was derived from $\mathcal{C}(3,5,11)$ by the recursions of [10,12], and before the time of writing this paper, no construction was known for $v=56$.

All our constructions are cyclic here, and the systems for $v=32$, $v=40$, $v=50$, and $v=52$ are not only cyclic but also 2-split. These three are presented in the second subsection, separately from the systems of the first subsection that are cyclic but not 2-split. (The even orders 26 and 46 do not admit 2-split constructions.)

5.1. Cyclic Systems of Orders 25, 26, 31, 35, 37, 41, 46, 47, 55, and 56

Proposition 1.

There exists a cyclic $\mathcal{C}(3,5,25)$ system.

Proof. 

We have $\frac{25·24·23}{6}=25·92$ vertex triples and 12 symmetric differences.

• At the beginning, we take five subsystems isomorphic to the cyclic $\mathcal{C}(3,5,5)$ system, hence with the cycles

  $$(0,5,10,15,20),(0,10,20,5,15)$$

  in their five possible positions:

  $$(i,5+i,10+i,15+i,20+i),(i,10+i,20+i,5+i,15+i)i=0,1,2,3,4.$$
  These cover $5·10=25·2$ vertex triples and two symmetric differences. There remain $25·90$ triples to cover for which we need $90/5=18$ base cycles.
• The 10 symmetric base cycles can be defined by the rule

  $$(0,i,25-3i,3i,25-i),i=1,2,3,4,6,7,8,9,11,12$$

  according to Theorem 4.
• We just need 8 reflected base cycles that can be arranged in four pairs:
  $$\begin{array}{cccc}(0,1,5,11,10),& (0,2,5,12,10),& (0,3,13,20,8),& (0,4,14,20,9),\\ (0,24,5,9,10),& (0,23,5,8,10),& (0,13,20,5,8),& (0,14,20,5,9).\end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A2 and Table A3. □

Proposition 2.

There exists a cyclic $\mathcal{C}(3,5,26)$ system.

Proof. 

We have $\frac{26·25·24}{6}$ vertex triples; therefore, we need $26·20$ cycles that should be generated by 20 base cycles.

• The 12 symmetric base cycles are

  $$\begin{array}{cccc}(0,1,24,2,25),\hfill & (0,3,20,6,23),\hfill & (0,5,16,10,21),\hfill & (0,7,12,14,19),\hfill \\ (0,9,8,18,17),\hfill & (0,11,4,22,15),\hfill & (0,2,22,4,24),\hfill & (0,4,18,8,22),\hfill \\ (0,6,22,4,20),\hfill & (0,8,21,5,18),\hfill & (0,10,25,1,16),\hfill & (0,12,23,3,14).\hfill \end{array}$$

  Here, for odd i, the cycles are taken according to the pattern $(0,i,26-2i,2i,26-i)$, but for even i, we need to make several modifications.
• The 8 reflected base cycles are in four pairs:

  $$\begin{array}{cccc}(0,1,8,17,13),\hfill & (0,1,12,25,6),\hfill & (0,12,20,23,2),\hfill & (0,3,7,2,19),\hfill \\ (0,22,5,12,13),\hfill & (0,7,20,5,6),\hfill & (0,5,8,16,2),\hfill & (0,17,12,16,19).\hfill \end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once as it can be verified from the data in Table A4 and Table A5. □

Proposition 3.

There exists a cyclic $\mathcal{C}(3,5,31)$ system.

Proof. 

We have $\frac{31·30·29}{6}$ vertex triples; therefore, we need $31·29$ cycles, which should be generated by 29 base cycles.

• The 15 symmetric base cycles can be taken as

  $$(0,i,31-3i,3i,31-i),i=1,\dots ,15$$

  as guaranteed by Theorem 4.
• The 14 reflected base cycles are in seven pairs:

  $$\begin{array}{c}(0,1,5,8,20)-(0,12,15,19,20); (0,1,7,17,9)-(0,23,2,8,9);\hfill \\ (0,1,13,15,18)-(0,3,5,17,18); (0,2,9,22,7)-(0,16,29,5,7);\hfill \\ (0,13,27,23,3)-(0,11,7,21,3); (0,15,6,25,4)-(0,10,29,20,4);\hfill \\ (0,5,11,6,14)-(0,8,3,9,14).\end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A6 and Table A7. □

Proposition 4.

There exists a cyclic $\mathcal{C}(3,5,35)$ system.

Proof. 

We have $\frac{35·34·33}{6}=35·187$ vertex triples and 17 symmetric differences. From Theorem 4, we know that multiples of 5 and 7 have to be handled separately from the other symmetric differences.

• At the beginning, we take seven subsystems isomorphic to the cyclic $\mathcal{C}(3,5,5)$ system, hence with the cycles

  $$(i,7+i,14+i,21+i,28+i),(i,14+i,28+i,7+i,21+i)i=0,1,\dots ,6.$$
  These cover $7·10=35·2$ vertex triples and two symmetric differences. There remain $35·185$ triples to cover, for which we need $185/5=37$ base cycles.
• Now, 12 of the remaining 15 symmetric base cycles can be defined by the rule

  $$(0,i,35-3i,3i,35-i),i=1,2,3,4,6,8,9,11,12,13,16,17$$

  according to Theorem 4. For the other three, i.e., the multiples of 5, the almost general rule would not work. Therefore, we make a little modification, taking the base cycles

  $$(0,5,33,2,30),(0,10,31,4,25),(0,15,29,6,20).$$
• Furthermore, we need 22 reflected base cycles that can be arranged in 11 pairs. As the first half, we take

  $$\begin{array}{c}(0,1,5,10,7), (0,1,6,9,20), (0,1,8,10,22), (0,1,10,16,21),\hfill \\ (0,2,10,22,17), (0,3,15,31,17), (0,4,11,24,19), (0,4,24,34,10),\hfill \\ (0,5,14,33,23), (0,6,16,33,13), (0,7,15,28,18);\end{array}$$

  the reflected pairs of them are

  $$\begin{array}{c}(0,32,2,6,7), (0,11,14,19,20), (0,12,14,21,22), (0,5,11,20,21),\hfill \\ (0,30,7,15,17), (0,21,2,14,17), (0,30,8,15,19), (0,11,21,6,10),\hfill \\ (0,25,9,18,23), (0,15,32,7,13), (0,25,3,11,18).\end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A10 and Table A11. □

Proposition 5.

There exists a cyclic $\mathcal{C}(3,5,37)$ system.

Proof. 

We have $\frac{37·36·35}{6}$ vertex triples; therefore, we need $37·42$ cycles, which should be generated by 42 base cycles.

• The 18 symmetric base cycles can be taken as

  $$(0,i,37-3i,3i,37-i),i=1,\dots ,18$$

  as guaranteed by Theorem 4.
• For the first 12 reflected base cycles, we take
  $$\begin{array}{cccc}(0,1,5,8,27),\hfill & (0,1,6,3,14),\hfill & (0,1,7,11,29),\hfill & (0,1,8,3,15),\hfill \\ (0,17,25,22,1),\hfill & (0,2,9,15,25),\hfill & (0,2,17,30,12),\hfill & (0,18,14,28,2),\hfill \\ (0,4,13,29,9),\hfill & (0,5,11,26,17),\hfill & (0,6,14,4,17),\hfill & (0,7,20,34,18).\hfill \end{array}$$
• Their reflected pairs are

  $$\begin{array}{cccc}(0,19,22,26,27),\hfill & (0,11,8,13,14),\hfill & (0,18,22,28,29),\hfill & (0,12,7,14,15),\hfill \\ (0,16,13,21,1),\hfill & (0,10,16,23,25),\hfill & (0,19,32,10,12),\hfill & (0,11,25,21,2),\hfill \\ (0,17,33,5,9),\hfill & (0,28,6,12,17),\hfill & (0,13,3,11,17),\hfill & (0,21,35,11,18).\hfill \end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A12 and Table A13. □

Proposition 6.

There exists a cyclic $\mathcal{C}(3,5,41)$ system.

Proof. 

We have $\frac{41·40·39}{6}$ vertex triples; therefore, we need $41·4·13$ cycles, which should be generated by 52 base cycles.

• The 20 symmetric base cycles can be taken as

  $$(0,i,41-3i,3i,41-i),i=1,\dots ,20$$

  as guaranteed by Theorem 4.
• For the first 16 reflected base cycles, we take

  $$\begin{array}{cccc}(0,1,5,8,10),\hfill & (0,1,6,8,18),\hfill & (0,1,7,11,16),\hfill & (0,1,8,10,19),\hfill \\ (0,1,9,4,17),\hfill & (0,1,12,7,29),\hfill & (0,2,14,23,27),\hfill & (0,2,17,5,25),\hfill \\ (0,3,16,33,27),\hfill & (0,3,30,14,10),\hfill & (0,6,13,2,20),\hfill & (0,6,19,38,21),\hfill \\ (0,7,15,35,26),\hfill & (0,8,22,3,26),\hfill & (0,10,22,35,25),\hfill & (0,26,9,30,12).\hfill \end{array}$$
• Their reflected pairs are

  $$\begin{array}{cccc}(0,2,5,9,10),\hfill & (0,10,12,17,18),\hfill & (0,5,9,15,16),\hfill & (0,9,11,18,19),\hfill \\ (0,13,8,16,17),\hfill & (0,22,17,28,29),\hfill & (0,4,13,25,27),\hfill & (0,20,8,23,25),\hfill \\ (0,35,11,24,27),\hfill & (0,37,21,7,10),\hfill & (0,18,7,14,20),\hfill & (0,24,2,15,21),\hfill \\ (0,32,11,19,26),\hfill & (0,23,4,18,26),\hfill & (0,31,3,15,25),\hfill & (0,23,3,27,12).\hfill \end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A16 and Table A17. □

Proposition 7.

There exists a cyclic $\mathcal{C}(3,5,46)$ system.

Proof. 

We have $\frac{46·45·44}{6}$ vertex triples; therefore, we need $46·3·22$ cycles, which should be generated by 66 base cycles.

• The 22 symmetric base cycles can be taken as

  $$(0,i,46-2i,2i,46-i),i=1,\dots ,22.$$
  This is out of scope in Theorem 4, but one can check that these cycles do not cover any difference triplet more than once, cf. Table A18.
• For the first 22 reflected base cycles, we take
  $$\begin{array}{cccc}(0,1,5,8,10),\hfill & (0,1,6,8,17),\hfill & (0,1,7,11,18),\hfill & (0,1,8,10,23),\hfill \\ (0,1,9,4,13),\hfill & (0,1,11,4,19),\hfill & (0,1,12,4,27),\hfill & (0,1,14,9,21),\hfill \\ (0,2,14,17,27),\hfill & (0,2,17,6,23),\hfill & (0,2,19,5,28),\hfill & (0,3,14,9,25),\hfill \\ (0,3,16,25,30),\hfill & (0,3,18,40,21),\hfill & (0,3,20,35,26),\hfill & (0,4,22,35,17),\hfill \\ (0,5,19,40,27),\hfill & (0,7,19,42,26),\hfill & (0,7,24,33,17),\hfill & (0,8,20,36,14)\hfill \\ & (0,26,5,36,11),\hfill & (0,27,12,34,13).\hfill & \end{array}$$
• Their reflected pairs are

  $$\begin{array}{cccc}(0,2,5,9,10),\hfill & (0,9,11,16,17),\hfill & (0,7,11,17,18),\hfill & (0,13,15,22,23),\hfill \\ (0,9,4,12,13),\hfill & (0,15,8,18,19),\hfill & (0,23,15,26,27),\hfill & (0,12,7,20,21),\hfill \\ (0,10,13,25,27),\hfill & (0,17,6,21,23),\hfill & (0,23,9,26,28),\hfill & (0,16,11,22,25),\hfill \\ (0,5,14,27,30),\hfill & (0,27,3,18,21),\hfill & (0,37,6,23,26),\hfill & (0,28,41,13,17),\hfill \\ (0,33,8,22,27),\hfill & (0,30,7,19,26),\hfill & (0,30,39,10,17),\hfill & (0,24,40,6,14),\hfill \\ & (0,21,6,31,11),\hfill & (0,25,1,32,13).\hfill & \end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A18 and Table A23. □

Proposition 8.

There exists a cyclic $\mathcal{C}(3,5,47)$ system.

Proof. 

We have $\frac{47·46·45}{6}$ vertex triples; therefore, we need $47·23·3$ cycles, which should be generated by 69 base cycles.

• The 23 symmetric base cycles can be taken as

  $$(0,i,47-3i,3i,47-i),i=1,\dots ,23$$

  as guaranteed by Theorem 4.
• For the first 23 reflected base cycles, we take
  $$\begin{array}{c}(0,1,5,8,10), (0,1,6,8,18), (0,1,7,11,34), (0,1,8,10,21),\hfill \\ (0,1,9,4,15), (0,1,11,8,35), (0,1,19,3,26), (0,2,11,6,22),\hfill \\ (0,2,14,9,26), (0,2,16,6,19), (0,2,20,17,28), (0,3,15,22,30),\hfill \\ (0,3,16,9,31), (0,3,17,35,21), (0,23,32,40,4), (0,6,17,32,26),\hfill \\ (0,6,20,36,16), (0,23,30,39,6), (0,8,26,13,22), (0,25,5,33,10),\hfill \\ (0,23,5,35,10) (0,12,25,43,21), (0,28,13,32,12).\end{array}$$
• Their reflected pairs are

  $$\begin{array}{c}(0,2,5,9,10), (0,10,12,17,18), (0,23,27,33,34), (0,11,13,20,21),\hfill \\ (0,11,6,14,15), (0,27,24,34,35), (0,23,7,25,26), (0,16,11,20,22),\hfill \\ (0,17,12,24,26), (0,13,3,17,19), (0,11,8,26,28), (0,8,15,27,30),\hfill \\ (0,22,15,28,31), (0,33,4,18,21), (0,11,19,28,4), (0,41,9,20,26),\hfill \\ (0,27,43,10,16), (0,14,23,30,6), (0,9,43,14,22), (0,24,5,32,10),\hfill \\ (0,22,5,34,10) (0,25,43,9,21), (0,27,46,31,12).\end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A20 and Table A21. □

Proposition 9.

There exists a cyclic $\mathcal{C}(3,5,55)$ system.

Proof. 

We have $\frac{55·54·53}{6}=55·477$ vertex triples, for which we need to define $11·9·53$ cycles. The number of symmetric differences is $\frac{55-1}{2}=27$.

• We multiply the two base cycles of $\mathcal{C}(3,5,5)$ by 11 and take their 11 distinct positions:

  $$(i,11+i,22+i,33+i,44+i),(i,22+i,44+i,11+i,33+i),i=0,1,\dots ,10.$$
  These cycles cover $110=55·2$ vertex triples, including all triples belonging to two symmetric differences. There remain $55·475$ triples to be covered and 25 symmetric differences.
• The general principles cannot be applied to cover symmetric differences divisible by 5, which here means $5,10,15,20,25$. We cover those with five specially designed base cycles, most of them of the form $(0,5i,55-2i,2i,55-5i)$, as follows:

  $$(0,5,53,2,50),(0,10,51,4,45),(0,15,49,6,40),(0,20,47,8,35),(0,25,43,12,30).$$
  These cycles cover $5·25$ vertex triples, five of them are symmetric. There remain $55·450$ triples to be covered, for which we define 90 base cycles.
  (An alternative approach is to multiply the $\mathcal{C}(3,5,11)$ system by 5, hence to take the three base cycles $(0,5,30,45,10)$, $(0,5,20,10,35)$, and $(0,20,45,35,50)$; but then, the continuation would of course be different.)
• The remaining 20 symmetric base cycles can be taken as

  $$(0,i,55-3i,3i,55-i),i\in \{1,\dots ,27\}\setminus \left(\right\{11,22\}\cup \{5,10,15,20,25\left\}\right)$$

  as guaranteed by Theorem 4. There remain 70 base cycles to be defined.
• The first half of 70 reflected base cycles is

  $$\begin{array}{c}(0,1,5,10,7), (0,1,6,9,17), (0,1,8,10,21), (0,1,9,11,20),\hfill \\ (0,1,10,14,25), (0,1,11,5,16), (0,1,12,5,22), (0,1,13,3,30),\hfill \\ (0,1,15,3,23), (0,2,15,5,20), (0,2,16,5,23), (0,2,17,5,27),\hfill \\ (0,2,18,8,26), (0,2,22,6,25), (0,3,17,8,27), (0,3,18,9,33),\hfill \\ (0,3,20,14,34), (0,3,21,7,36), (0,4,19,11,24), (0,4,22,9,29),\hfill \\ (0,4,23,10,32), (0,4,25,48,33), (0,5,12,18,34), (0,5,21,49,25),\hfill \\ (0,9,34,45,26), (0,10,24,53,31), (0,10,35,48,25), (0,11,37,6,26),\hfill \\ (0,12,27,43,17), (0,12,34,6,23), (0,12,35,7,25), (0,13,28,50,36),\hfill \\ (0,16,41,8,25), (0,17,37,1,32), (0,19,40,13,33).\end{array}$$
• Their reflected pairs are

  $$\begin{array}{c}(0,52,2,6,7), (0,8,11,16,17), (0,11,13,20,21), (0,9,11,19,20),\hfill \\ (0,11,15,24,25), (0,11,5,15,16), (0,17,10,21,22), (0,27,17,29,30),\hfill \\ (0,20,8,22,23), (0,15,5,18,20), (0,18,7,21,23), (0,22,10,25,27),\hfill \\ (0,18,8,24,26), (0,19,3,23,25), (0,19,10,24,27), (0,24,15,30,33),\hfill \\ (0,20,14,31,34), (0,29,15,33,36), (0,13,5,20,24), (0,20,7,25,29),\hfill \\ (0,22,9,28,32), (0,40,8,29,33), (0,16,22,29,34), (0,31,4,20,25),\hfill \\ (0,36,47,17,26), (0,33,7,21,31), (0,32,45,15,25), (0,20,44,15,26),\hfill \\ (0,29,45,5,17), (0,17,44,11,23), (0,18,45,13,25), (0,41,8,23,36),\hfill \\ (0,17,39,9,25), (0,31,50,15,32), (0,20,48,14,33).\end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A26 and Table A27. □

Proposition 10.

There exists a cyclic $\mathcal{C}(3,5,56)$ system.

Proof. 

We have $\frac{56·55·54}{6}=56·55·9$ vertex triples, for which we need to define $11·9=99$ base cycles. The number of symmetric differences is 27. For those 27, we can start with a general formula $(0,i,56-2i,2i,56-i)$ as an approach similar to the one in the case of $v=46$. However, in the current situation, several adjustments are needed to resolve collisions.

• For odd symmetric differences, we only need to make one little change, for the difference $i=7$. Therefore, the 14 odd symmetric base cycles are
  $$\begin{array}{cccc}(0,1,54,2,55),\hfill & (0,3,50,6,53),\hfill & (0,5,46,10,51),\hfill & (0,7,44,12,49),\hfill \\ (0,9,38,18,47),\hfill & (0,11,34,22,45),\hfill & (0,13,30,26,43),\hfill & (0,15,26,30,41),\hfill \\ (0,17,22,34,39),\hfill & (0,19,18,38,37),\hfill & (0,21,14,42,35),\hfill & (0,23,10,46,33),\hfill \\ & (0,25,6,50,31),\hfill & (0,27,2,54,29).\hfill & \end{array}$$
• The even case is less favorable. Beyond the expected values 8, 16, and 24—which are multiples of $v/7$—we also need to modify the base cycle for $i=14$. Hence, we take the following 13 base cycles for the even differences:

  $$\begin{array}{c}(0,2,52,4,54), (0,4,48,8,52), (0,6,44,12,50), (0,8,42,14,48),\hfill \\ (0,10,36,20,46), (0,12,32,24,44), (0,14,32,24,42), (0,16,30,26,40),\hfill \\ (0,18,20,36,38), (0,20,16,40,36), (0,22,12,44,34), (0,24,10,46,32),\hfill \\ (0,26,4,52,30).\end{array}$$
• There remain $99-27=72$ base cycles to be defined. We arrange them in 36 reflected pairs. The first half is

  $$\begin{array}{cccc}(0,1,5,8,10),\hfill & (0,1,6,8,15),\hfill & (0,1,7,11,16),\hfill & (0,1,8,11,21),\hfill \\ (0,1,9,4,18),\hfill & (0,1,11,13,22),\hfill & (0,1,12,4,23),\hfill & (0,1,13,6,17),\hfill \\ (0,1,14,3,27),\hfill & (0,1,24,3,28),\hfill & (0,1,25,8,31),\hfill & (0,2,14,17,28),\hfill \\ (0,2,15,6,21),\hfill & (0,2,16,8,25),\hfill & (0,2,17,20,39),\hfill & (0,2,22,5,26),\hfill \\ (0,3,16,8,29),\hfill & (0,3,17,22,35),\hfill & (0,3,19,9,26),\hfill & (0,3,21,43,25),\hfill \\ (0,4,19,26,32),\hfill & (0,5,11,24,31),\hfill & (0,5,21,12,33),\hfill & (0,6,22,49,27),\hfill \\ (0,7,36,48,18),\hfill & (0,9,33,50,23),\hfill & (0,10,31,48,19),\hfill & (0,11,35,48,20),\hfill \\ (0,11,36,51,27),\hfill & (0,12,28,5,25),\hfill & (0,14,29,50,20),\hfill & (0,14,37,7,26),\hfill \\ (0,14,43,10,25),\hfill & (0,15,34,5,23),\hfill & (0,16,33,2,24),\hfill & (0,16,35,7,25).\hfill \end{array}$$
• Their reflected pairs are

  $$\begin{array}{cccc}(0,2,5,9,10),\hfill & (0,7,9,14,15),\hfill & (0,5,9,15,16),\hfill & (0,10,13,20,21),\hfill \\ (0,14,9,17,18),\hfill & (0,9,11,21,22),\hfill & (0,19,11,22,23),\hfill & (0,11,4,16,17),\hfill \\ (0,24,13,26,27),\hfill & (0,25,4,27,28),\hfill & (0,23,6,30,31),\hfill & (0,11,14,26,28),\hfill \\ (0,15,6,19,21),\hfill & (0,17,9,23,25),\hfill & (0,19,22,37,39),\hfill & (0,21,4,24,26),\hfill \\ (0,21,13,26,29),\hfill & (0,13,18,32,35),\hfill & (0,17,7,23,26),\hfill & (0,38,4,22,25),\hfill \\ (0,6,13,28,32),\hfill & (0,7,20,26,31),\hfill & (0,21,12,28,33),\hfill & (0,34,5,21,27),\hfill \\ (0,26,38,11,18),\hfill & (0,29,46,14,23),\hfill & (0,27,44,9,19),\hfill & (0,28,41,9,20),\hfill \\ (0,32,47,16,27),\hfill & (0,20,53,13,25),\hfill & (0,26,47,6,20),\hfill & (0,19,45,12,26),\hfill \\ (0,15,38,11,25),\hfill & (0,18,45,8,23),\hfill & (0,22,47,8,24),\hfill & (0,18,46,9,25).\hfill \end{array}$$

These base cycles generate a system with the required number of 5-cycles and cover each vertex triple exactly once, as it can be verified from the data in Table A28 and Table A29. □

5.2. Cyclic 2-Split Systems of Orders 32, 40, 50, and 52

In this subsection, we present constructions that are not only cyclic but also 2-split. The cases of $v=32$, $v=40$, $v=50$, and $v=52$ are considered. For $v=40$ and $v=52$, no constructions have been known so far. Although the existence of a cyclic $\mathcal{C}(3,5,32)$ and a 2-split $\mathcal{C}(3,5,50)$ was known, the former was not 2-split and the latter was not cyclic.

For a 2-split system, it is convenient to write $2v$ for its order and to assume that it is built on the vertex-disjoint union of two subsystems of order v each. Throughout this subsection, we assume that the vertex sets of those subsystems are

$$X_1=\{0,2,\dots ,2v-2\},X_2=\{1,3,\dots ,2v-1\}.$$

Then, one can start with the base blocks of a cyclic $\mathcal{C}(3,5,v)$ and multiply all its elements by 2, hence obtaining a cyclic subsystem induced by $X_1$. Moreover, rotation by 1 yields an induced cyclic subsystem on $X_2$.

Proposition 11.

There exists a cyclic 2-split $\mathcal{C}(3,5,32)$ system.

Proof. 

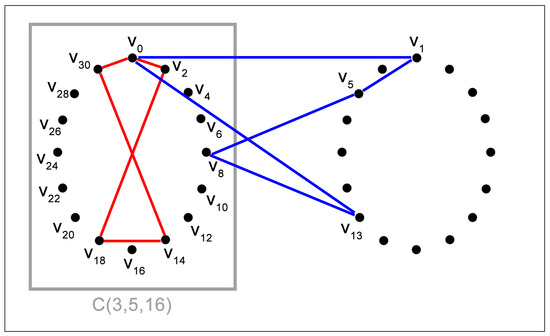
We have $\frac{32·31·30}{6}$ vertex triples; therefore, we need $32·31$ cycles that should be generated by 31 base cycles.

• The seven base cycles obtained from a cyclic $\mathcal{C}(3,5,16)$ are

  $$\begin{array}{c}(0,2,18,14,30), (0,28,26,6,4), (0,6,20,12,26), (0,24,30,2,8),\\ (0,22,30,2,10), (0,20,2,30,12), (0,18,8,24,14).\end{array}$$

  All these cycles are symmetric. They are obtained from the system given in [10] by rotating the base cycles in a way that 0 is the center of each symmetric triangle.
• The other eight symmetric base cycles are

  $$\begin{array}{cccc}(0,1,30,2,31),\hfill & (0,3,26,6,29),\hfill & (0,5,22,10,27),\hfill & (0,7,18,14,25),\hfill \\ (0,9,14,18,23),\hfill & (0,11,10,22,21),\hfill & (0,13,6,26,19),\hfill & (0,15,2,30,17).\hfill \end{array}$$
• We take the following eight base cycles as the first half of reflected crossing cycles:

  $$\begin{array}{cccc}(0,1,5,8,13),\hfill & (0,1,6,3,14),\hfill & (0,1,8,7,16),\hfill & (0,1,10,29,15),\hfill \\ (0,3,10,30,19),\hfill & (0,3,13,22,15),\hfill & (0,5,16,24,7),\hfill & (0,6,17,2,11).\hfill \end{array}$$
• Their reflected base cycles are

  $$\begin{array}{cccc}(0,5,8,12,13),\hfill & (0,11,8,13,14),\hfill & (0,9,8,15,16),\hfill & (0,18,5,14,15),\hfill \\ (0,21,9,16,19),\hfill & (0,25,2,12,15),\hfill & (0,15,23,2,7),\hfill & (0,9,26,5,11).\hfill \end{array}$$

Figure 5 exhibits one base cycle derived from $\mathcal{C}(3,5,16)$ in red and one crossing base cycle in blue.

Figure 5. $\mathcal{C}(3,5,32)$: base cycles (0,2,18,14,30) and (0,1,5,8,13).

The set of base cycles defined above generates a system with the required number of 5-cycles and covers each vertex triple exactly once, as it can be verified from the data in Table A8 and Table A9. □

Proposition 12.

There exists a cyclic 2-split $\mathcal{C}(3,5,40)$ system.

Proof. 

We have $\frac{40·39·38}{6}$ vertex triples, from which the two $\mathcal{C}(3,5,20)$ subsystems together cover $\frac{40·19·18}{6}$ triples. Hence, we need to cover the remaining $\frac{40·30·38}{6}$ triples, which therefore need $40·38$ cycles, requiring 38 additional base cycles. For the sake of completeness, we also list the base cycles that generate the $\mathcal{C}(3,5,20)$ subsystem and present them in a way that reflects the iterated doubling $5\to 10\to 20\to 40$.

• We take $\frac{1}{5}(\genfrac{}{}{0pt}{}{5}{3})=2$ base cycles, with the cyclic $\mathcal{C}(3,5,5)$ multiplied by 8:

  $$(0,8,16,24,32),(0,16,32,8,24);$$
• Furthermore, we take $\frac{1}{5}((\genfrac{}{}{0pt}{}{10}{3})-2·(\genfrac{}{}{0pt}{}{5}{3}))·\frac{1}{10}=2$ base cycles of a cyclic $\mathcal{C}(3,5,10)$ from [2], multiplied by 4:

  $$(0,4,8,20,24),(0,8,20,16,28);$$
• We also take $\frac{1}{5}((\genfrac{}{}{0pt}{}{20}{3})-2·(\genfrac{}{}{0pt}{}{10}{3}))·\frac{1}{20}=9$ base cycles of a cyclic $\mathcal{C}(3,5,20)$—five symmetric cycles and two reflected pairs—from [10], multiplied by 2:

  $$\begin{array}{c}(0,2,36,4,38), (0,6,24,16,34), (0,6,14,20,10), (0,2,16,12,26),\hfill \\ (0,34,10,4,22), (0,2,12,28,10), (0,30,14,32,2), (0,18,32,12,14),\hfill \\ (0,20,18,32,14).\end{array}$$
• The other ten symmetric base cycles are

  $$\begin{array}{c}(0,1,6,34,39), (0,3,18,22,37), (0,5,2,38,35), (0,7,2,38,33),\hfill \\ (0,9,14,26,31), (0,11,26,14,29), (0,13,38,2,27), (0,15,10,30,25),\hfill \\ (0,17,22,18,23), (0,19,34,6,21).\end{array}$$
  Note that a little adjustment was necessary for the cycle containg the symmetric difference $(5,5,10)$—the cycle $(0,5,2,38,35)$—which does not follow the general arithmetic pattern of the others.
• We take the following 14 base cycles as the first half of reflected crossing cycles:

  $$\begin{array}{cccc}(0,1,3,10,9),\hfill & (0,1,4,9,15),\hfill & (0,1,8,11,17),\hfill & (0,1,11,14,23),\hfill \\ (0,1,12,3,16),\hfill & (0,1,13,24,21),\hfill & (0,1,14,3,22),\hfill & (0,3,14,7,26),\hfill \\ (0,5,16,36,19),\hfill & (0,5,21,36,13),\hfill & (0,7,16,35,22),\hfill & (0,7,20,31,13),\hfill \\ & (0,7,24,9,17),\hfill & (0,10,29,2,19).\hfill & \end{array}$$
• Their reflected base cycles are

  $$\begin{array}{cccc}(0,39,6,8,9),\hfill & (0,6,11,14,15),\hfill & (0,6,9,16,17),\hfill & (0,9,12,22,23),\hfill \\ (0,13,4,15,16),\hfill & (0,37,8,20,21),\hfill & (0,19,8,21,22),\hfill & (0,19,12,23,26),\hfill \\ (0,23,3,14,19),\hfill & (0,17,32,8,13),\hfill & (0,27,6,15,22),\hfill & (0,22,33,6,13),\hfill \\ & (0,8,33,10,17),\hfill & (0,17,30,9,19).\hfill & \end{array}$$

Hence, the number of base cycles supplementing the two copies of $\mathcal{C}(3,5,20)$ is $10+14+14=38$ as needed. This set of base cycles generates a system with the required number of 5-cycles and covers each vertex triple exactly once, as it can be verified from the data in Table A14 and Table A15. □

Proposition 13.

There exists a cyclic 2-split $\mathcal{C}(3,5,50)$ system.

Proof. 

We have $\frac{50·49·48}{6}=50·392$ vertex triples, including 24 symmetric differences.

• We take the 20 base cycles of $\mathcal{C}(3,5,25)$, miltiplied by 2; for the sake of completeness, we also list them here:

  $$\begin{array}{cccc}(0,2,44,6,48),\hfill & (0,4,38,12,46),\hfill & (0,6,32,18,44),\hfill & (0,8,26,24,42),\hfill \\ (0,10,20,30,40),\hfill & (0,12,14,36,38),\hfill & (0,14,8,42,36),\hfill & (0,16,2,48,34),\hfill \\ (0,18,46,4,32),\hfill & (0,20,40,10,30),\hfill & (0,22,34,16,28),\hfill & (0,24,28,22,26),\hfill \\ (0,2,10,22,20),\hfill & (0,4,10,24,20),\hfill & (0,6,26,40,16),\hfill & (0,8,28,40,18),\hfill \\ (0,48,10,18,20),\hfill & (0,46,10,16,20),\hfill & (0,26,40,10,16),\hfill & (0,28,40,10,18).\hfill \end{array}$$

  These cover $2·(\genfrac{}{}{0pt}{}{25}{3})=50·92$ vertex triples. Hence, there remain $50·300$ vertex triples to be covered, which need $50·60$ cycles, that means 60 base cycles. The number of symmetric differences not covered so far is $24-12=12$.
• To define the 12 base cycles for odd symmetric differences, the “$2i$-rule” is almost perfect, with just one little adjustment for $i=5$. Namely, we take

  $$(0,i,50-2i,2i,50-i),i\in \{1,3\}\cup \{7,9,\dots ,23\}$$

  and $(0,5,38,12,45)$ for $i=5$.
• For the remaining $60-12=48$ base cycles, we define 24 reflected pairs. For the first half, we take

  $$\begin{array}{cccc}(0,1,5,8,13),\hfill & (0,1,6,3,14),\hfill & (0,1,7,12,21),\hfill & (0,1,8,3,15),\hfill \\ (0,1,9,16,19),\hfill & (0,1,10,3,16),\hfill & (0,1,11,14,29),\hfill & (0,1,12,3,20),\hfill \\ (0,1,23,4,25),\hfill & (0,2,15,6,25),\hfill & (0,2,17,6,29),\hfill & (0,3,17,34,27),\hfill \\ (0,3,21,8,25),\hfill & (0,3,23,10,29),\hfill & (0,4,33,16,11),\hfill & (0,5,21,40,29),\hfill \\ (0,5,23,34,9),\hfill & (0,5,31,4,19),\hfill & (0,6,35,26,15),\hfill & (0,9,22,39,16),\hfill \\ (0,9,24,2,33),\hfill & (0,11,30,43,18),\hfill & (0,13,36,8,23),\hfill & (0,15,32,5,25).\hfill \end{array}$$
• The reflected pairs of these cycles are

  $$\begin{array}{cccc}(0,5,8,12,13),\hfill & (0,11,8,13,14),\hfill & (0,9,14,20,21),\hfill & (0,12,7,14,15),\hfill \\ (0,3,10,18,19),\hfill & (0,13,6,15,16),\hfill & (0,15,18,28,29),\hfill & (0,17,8,19,20),\hfill \\ (0,21,2,24,25),\hfill & (0,19,10,23,25),\hfill & (0,23,12,27,29),\hfill & (0,43,10,24,27),\hfill \\ (0,17,4,22,25),\hfill & (0,19,6,26,29),\hfill & (0,45,28,7,11),\hfill & (0,39,8,24,29),\hfill \\ (0,25,36,4,9),\hfill & (0,15,38,14,19),\hfill & (0,39,30,9,15),\hfill & (0,27,44,7,16),\hfill \\ (0,31,9,24,33),\hfill & (0,25,38,7,18),\hfill & (0,15,37,10,23),\hfill & (0,20,43,10,25).\hfill \end{array}$$

This set of base cycles generates a system with the required number of 5-cycles and covers each vertex triple exactly once, as it can be verified from the data in Table A22 and Table A23. □

Proposition 14.

There exists a cyclic 2-split $\mathcal{C}(3,5,52)$ system.

Proof. 

We have $\frac{52·51·50}{6}$ vertex triples; therefore, we need $52·17·5$ cycles, which should be generated by 85 base cycles.

• The 20 base cycles of a cyclic $\mathcal{C}(3,5,26)$ system are multiplied by 2:

  $$\begin{array}{cccc}(0,2,48,4,50),\hfill & (0,6,40,12,46),\hfill & (0,10,32,20,42),\hfill & (0,14,24,28,38),\hfill \\ (0,18,16,36,34),\hfill & (0,22,8,44,30),\hfill & (0,4,44,8,48),\hfill & (0,8,36,16,44),\hfill \\ (0,12,44,8,40),\hfill & (0,16,42,10,36),\hfill & (0,20,50,2,32),\hfill & (0,24,46,6,28),\hfill \\ (0,2,16,34,26),\hfill & (0,2,24,50,12),\hfill & (0,24,40,46,4),\hfill & (0,6,14,4,38),\hfill \\ (0,44,10,24,26),\hfill & (0,14,40,10,12),\hfill & (0,10,16,32,4),\hfill & (0,34,24,32,38).\hfill \end{array}$$
  These include 12 symmetric cycles; the other eight cycles are in four reflected pairs.
• The further 13 symmetric base cycles are

  $$\begin{array}{c}(0,1,50,2,51), (0,3,46,6,49), (0,5,42,10,47), (0,7,38,14,45),\hfill \\ (0,9,34,18,43), (0,11,30,22,41), (0,13,28,24,39), (0,15,22,30,37),\hfill \\ (0,17,18,34,35), (0,19,14,38,33), (0,21,10,42,31), (0,23,6,46,29),\hfill \\ (0,25,2,50,27).\end{array}$$

  As we noted above, the even symmetric cycles of $\mathcal{C}(3,5,26)$ were irregular at several points although the odd cycles had a regular behavior. A little adjustment also occurs here, in the cycle containing the symmetric difference $(13,13,26)$—the cycle $(0,13,28,24,39)$—which does not follow the general arithmetic pattern of the others.
• We take the following 26 base cycles as the first half of reflected crossing cycles:

  $$\begin{array}{cccc}(0,1,5,8,13),\hfill & (0,1,6,3,14),\hfill & (0,1,7,12,19),\hfill & (0,1,8,3,20),\hfill \\ (0,1,9,18,11),\hfill & (0,1,10,5,21),\hfill & (0,1,12,3,16),\hfill & (0,1,15,6,25),\hfill \\ (0,1,22,3,26),\hfill & (0,1,23,10,29),\hfill & (0,2,13,6,31),\hfill & (0,2,15,8,35),\hfill \\ (0,3,10,19,31),\hfill & (0,3,13,20,33),\hfill & (0,3,15,30,21),\hfill & (0,3,18,38,27),\hfill \\ (0,25,12,36,3),\hfill & (0,23,12,38,3),\hfill & (0,4,21,46,31),\hfill & (0,5,18,41,25),\hfill \\ (0,5,27,10,23),\hfill & (0,7,30,41,24),\hfill & (0,9,32,47,24),\hfill & (0,13,30,44,21),\hfill \\ & (0,13,34,8,27),\hfill & (0,15,31,48,33).\hfill & \end{array}$$
• Their reflected base cycle pairs are

  $$\begin{array}{cccc}(0,5,8,12,13),\hfill & (0,11,8,13,14),\hfill & (0,7,12,18,19),\hfill & (0,17,12,19,20),\hfill \\ (0,45,2,10,11),\hfill & (0,16,11,20,21),\hfill & (0,13,4,15,16),\hfill & (0,19,10,24,25),\hfill \\ (0,23,4,25,26),\hfill & (0,19,6,28,29),\hfill & (0,25,18,29,31),\hfill & (0,27,20,33,35),\hfill \\ (0,12,21,28,31),\hfill & (0,13,20,30,33),\hfill & (0,43,6,18,21),\hfill & (0,41,9,24,27),\hfill \\ (0,19,43,30,3),\hfill & (0,17,43,32,3),\hfill & (0,37,10,27,31),\hfill & (0,36,7,20,25),\hfill \\ (0,13,48,18,23),\hfill & (0,35,46,17,24),\hfill & (0,29,44,15,24),\hfill & (0,29,43,8,21),\hfill \\ & (0,19,45,14,27),\hfill & (0,37,2,18,33).\hfill & \end{array}$$

This set of base cycles generates a system with the required number of 5-cycles and covers each vertex triple exactly once, as it can be verified from the data in Table A24 and Table A25. □

6. Conclusions

In this paper, we further developed the theory of decompositions of complete3-uniform hypergraphs into 5-cycles. We introduced new recursive rules to generate larger systems from known smaller ones and designed many initial constructions from which new systems can be built.

As formulated in Conjecture 1, we expect that, for all feasible orders except $v=7$, there exists a cyclic 3-uniform 5-cycle system. Analogously, we expect that, for all feasible orders, there exists a more structured 3-uniform 5-cycle system, namely a cyclic 2-split system, with no exceptions at all.

With regards to our conditional recursion $v⟶8v$ of Section 3, it is an interesting new problem to analyze for which values of v does the nypergraph ${\mathcal{H}}_{⟨4\times v⟩}$ admit an edge decomposition into 5-cycles. Perhaps the corresponding divisibility conditions will be sufficient for this type of systems too.

We presented cyclic hypercycle systems $\mathcal{C}(3,5,v)$ of orders v = 25, 26, 31, 35, 37, 41, 46, 47, 55, and 56; a highly symmetric construction for $v=40$; and cyclic 2-split constructions of orders $32,40,50,$ and 52. These systems were determined using computer-aided methods. As a consequence, we obtain that all orders $v\le 60$ permitted by the divisibility conditions admit a $\mathcal{C}(3,5,v)$ system.

The recursive constructions of Section 3 establish the existence of 2-split $\mathcal{C}(3,5,v)$ systems for many previously unsolved cases. The consequences of the $v⟶10v$ step result in an infinite set of new solutions, including $v=70$, 160, 200, 260, 310, 320, 350, 370, 460, 470, 520, 550, 560, 700, 800, 820, $1000,\dots$ Moreover, some previously solved cases, e.g., $v=100$, 110, 400, 410, and 500, are now proven to admit 2-split systems, which are suitable for serving as initial structures for further recursive operations of [10].

A useful tool in these constructions is the auxiliary system over ${\mathcal{H}}_{⟨4\times 5⟩}$, found in Section 2, for which we expect further applications in the future, too. One nice structure derived from it is the $\mathcal{C}(3,5,40)$ system of order 40 that benefits from lots of symmetries and that is built over a Steiner quadruple system using as few as seven generating cycles.

Combinatorial designs have a huge number of applications in various fields, e.g., in statistical experimental design, coding theory, optical networks, and even in music composition. Quoting from the historical introduction in the Handbook of Combinatorics ([17], p. 11), every passing year sees thousands of new published papers employing the results and techniques of combinatorial design theory. Concerning the subject of the current paper, it would be very interesting to see that hypercycle systems can also be applied to improve the efficiency of methods in the abovementioned fields. In this direction, one of our referees proposed that the constructed systems could for example be implemented in turbo coding. The connection between block design and block codes is well known, with several notable results, for example, Steiner sytems and Golay codes [18], the application of finite geometries to LDPC codes (low-density parity-check codes) [19], or a more recently published link between Steiner systems and rank metric codes [20]. It is worth mentioning that a combination of turbo coding and balanced incomplete block design was also proposed in [21] for a digital fingerprinting system. As we have shown in this paper, hypercycle and Steiner systems are closely related designs; hence, this may turn out to be an exciting track of research in the future for us. We aim to extend our work and to investigate the cases of different hypercycle lengths to make the constructions more suitable for application.