The Geometrical Characterizations of the Bertrand Curves of the Null Curves in Semi-Euclidean 4-Space

Abstract

According to the Frenet equations of the null curves in semi-Euclidean 4-space, the existence conditions and the geometrical characterizations of the Bertrand curves of the null curves are given in this paper. The examples and the graphs of the Bertrand pairs with two different conditions are also given in order to supplement the conclusion of this paper more intuitively.

1. Introduction

The study on the local and global geometric properties of curves has attracted the attention of many researchers. In case of semi-Euclidean space, there are three categories of curves: spacelike curves, timelike curves, and null (lightlike) curves. The spacelike curves and timelike curves are called non-degenerated curves, which have many similar properties with the curves in Euclidean space [1,2]. However, for the null curves (degenerate curves), with the reason of no length, compared with non-degenerate curves, there are many different geometrical properties. Seeing that, from the differential geometry point of view, the null curves have their own research value. Many researchers had focused their attention on the null curves [3,4,5,6,7,8,9,10]. The first author and Pei, D.H., obtained the singularities and other characterizations of null curves on the 3-null cone in [4,6]. The authors focused their attention on the characterizations of the pseudo-spherical null curves and Bertrand null curves in [8].

On the other hand, Bertrand stated the fact that the principal normal vector of a curve can also be the principal normal vector of another curve in Euclidean 3-space [11], and he gave a necessary and sufficient condition for the existence of the Bertrand mate. From then on, many researchers began to study the Bertrand curves and got many interesting properties [12,13,14]. The authors gave the relationship between the curvatures and the torsions of the Bertrand curve pairs in [12]. However, due to the increase of dimension, the authors gave the new definitions of the Bertrand curves in 4-space [15,16,17]. The definitions of the new Bertrand curves ((1,3)-type) and some characterizations were obtained in [15]. The characterizations of the general surfaces and generalized Bertrand curves in Galilean space were studied in [17,18].

Synthesizing the above views, in this paper, we study the existence conditions of the Bertrand curves of the null curves in semi-Euclidean 4-space. Firstly, we provide some fundamental concepts on the null curves and the semi-Euclidean 4-space. Then, we present some geometrical properties of the Bertrand curves of the null curves in Section 3, and we provide the existence conditions of the Bertrand curves for two different cases. In the last section, two examples are given to demonstrate the correctness of the conclusions in view of the geometric intuition.

2. Preliminaries

Let ${\mathbb{R}}^4=\left\{(x_1,x_2,x_3,x_4)\right|x_i\in \mathbb{R}(i=1,2,3,4)\}$ be a 4-dimensional vector space. For any vectors $\mathit{x}=(x_1,x_2,x_3,x_4)$ and $\mathit{y}=(y_1,y_2,y_3,y_4)$ in ${\mathbb{R}}^4,$ the pseudo scalar product of $\mathit{x}$ and $\mathit{y}$ is defined by $⟨\mathit{x},\mathit{y}⟩=-x_1{y}_1-x_2{y}_2+x_3{y}_3+x_4{y}_4$. $({\mathbb{R}}^4,⟨,⟩)$ is called semi-Euclidean 4-space and denoted by ${\mathbb{R}}_2^4.$

A vector $\mathit{x}$ in ${\mathbb{R}}_2^4\backslash \left\{\mathbf{0}\right\}$ is called a spacelike vector, a lightlike vector or a timelike vector if $⟨\mathit{x},\mathit{x}⟩$ is positive, zero or negative, respectively. The norm of a vector $\mathit{x}\in {\mathbb{R}}_2^4$ is defined by $\parallel \mathit{x}\parallel =\sqrt{|⟨\mathit{x},\mathit{x}⟩|}.$ For any two vectors $\mathit{x}$ and $\mathit{y}$ in ${\mathbb{R}}_2^4,$ we say that $\mathit{x}$ is pseudo-perpendicular to $\mathit{y}$ if $⟨\mathit{x},\mathit{y}⟩=0.$ The pseudo vector product of vectors $\mathit{x}$, $\mathit{y}$, and $\mathit{z}$ is defined by

$$\mathit{x}\wedge \mathit{y}\wedge \mathit{z}=\left|\begin{array}{cccc}-{\mathbf{e}}_1& -{\mathbf{e}}_2& {\mathbf{e}}_3& {\mathbf{e}}_4\\ x_1& x_2& x_3& x_4\\ y_1& y_2& y_3& y_4\\ z_1& z_2& z_3& z_4\end{array}\right|,$$

where $\{{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3,{\mathbf{e}}_4\}$ is the canonical basis of ${\mathbb{R}}_2^4$. One can easily show that $⟨\mathit{a},\mathit{x}\wedge \mathit{y}\wedge \mathit{z}⟩=\det (\mathit{a},\mathit{x},\mathit{y},\mathit{z})$. For a real number $c,$ we define the hyperplane with pseudo normal vector $\mathit{n}$ by $HP(\mathit{n},c)=\{\mathit{x}\in {\mathbb{R}}_2^4\mid ⟨\mathit{x},\mathit{n}⟩=c\}.$ We call $HP(\mathit{n},c)$ a spacelike hyperplane, a timelike hyperplane or a lightlike hyperplane if $\mathit{n}$ is a spacelike, timelike or null (lightlike) vector, respectively.

Definition 1. 

Let $\mathit{\gamma }:I\to {\mathbb{R}}_2^4$ be a curve in ${\mathbb{R}}_2^4$. Then $\mathit{\gamma }\left(s\right)$ is called a null (lightlike) curve, a spacelike curve or a timelike curve if its tangent vector ${\mathit{\gamma }}^{\prime }\left(s\right)=\mathit{\xi }\left(s\right)$ is null vector, spacelike vector or timelike vector for $s\in I$, respectively.

In this paper, we consider the null curve $\mathit{\gamma }\left(s\right)$ with pseudo parameter s satisfying $⟨\mathit{\xi }\left(s\right),\mathit{\xi }\left(s\right)⟩=0$ and $\frac{⟨{\mathit{\xi }}^{\prime }\left(s\right),{\mathit{\xi }}^{\prime }\left(s\right)⟩}{\parallel {\mathit{\xi }}^{\prime }{\left(s\right)\parallel }^2}={\epsilon }_1,$ ${\epsilon }_1^2=1.$

For a non-null curve $\mathit{C}\left(t\right)$ in ${\mathbb{R}}_2^4$, we have a non-null bundle subspace of $T{\mathbb{R}}_2^4$ satisfying

$$T{\mathbb{R}}_2^4=T\mathit{C}\perp T{\mathit{C}}^{\perp },T\mathit{C}\bigcap T{\mathit{C}}^{\perp }=Ø.$$

However, for a null curve $\mathit{\gamma }\in {\mathbb{R}}_2^4$, the tangent bundle $T{\mathbb{R}}_2^4$ can be split into three non-intersecting complementary vector bundles. For this purpose, we consider a complementary vector bundle (screen vector bundle) $S\left(T{\mathit{\gamma }}^{\perp }\right)$ to $T\mathit{\gamma }$ in $T{\mathit{\gamma }}^{\perp }$, which means

$$T{\mathit{\gamma }}^{\perp }=T\mathit{\gamma }⨁S\left(T{\mathit{\gamma }}^{\perp }\right).$$

We know $S\left(T{\mathit{\gamma }}^{\perp }\right)$ is non-degenerate. Since ${\mathbb{R}}_2^4$ is para compact, there exists a screen bundle, such that

$$T{\mathbb{R}}_2^4{\mid }_{\mathit{\gamma }}=S\left(T{\mathit{\gamma }}^{\perp }\right)⨁S{\left(T{\mathit{\gamma }}^{\perp }\right)}^{\perp }.$$

(1)

Notice that since $S{\left(T{\mathit{\gamma }}^{\perp }\right)}^{\perp }$ is of rank 2 and contains $T\mathit{\gamma }$, there exists a unique null vector bundle of rank 1, which plays a similar roll like the unique normal vector bundle of the non-null curve. Hence, the unique transversal vector $\mathit{N}$ is obtained by the following lemma [3]:

Lemma 1. 

Let $\mathit{\gamma }:I\to {\mathbb{R}}_2^4$ be a null curve in ${\mathbb{R}}_2^4$, $\pi :ntr\left(\mathit{\gamma }\right)\to {\mathbb{R}}_2^4$ be a sub bundle of a screen vector bundle $S{\left(T{\mathit{\gamma }}^{\perp }\right)}^{\perp }$, such that $S{\left(T{\mathit{\gamma }}^{\perp }\right)}^{\perp }=T\mathit{\gamma }⨁ntr\left(\mathit{\gamma }\right)$, where $ntr\left(\mathit{\gamma }\right)$ stands for the null transverse of vector $T\mathit{\gamma }$. Let $\mathit{V}\in {\Gamma }^{\infty }({\mathbb{R}}_2^4,ntr\left(\mathit{\gamma }\right))$ be a locally defined nowhere zero section.

1. 

Then $⟨\mathit{\xi },\mathit{V}⟩\ne 0$ everywhere in ${\mathbb{R}}_2^4.$

2. 

If we consider $\mathit{N}\in {\Gamma }^{\infty }({\mathbb{R}}_2^4,S{\left(T{\mathit{\gamma }}^{\perp }\right)}^{\perp })$ given by

$$\mathit{N}=\frac{1}{⟨\mathit{\xi },\mathit{V}⟩}\{\mathit{V}-\frac{⟨\mathit{V},\mathit{V}⟩}{2⟨\mathit{\xi },\mathit{V}⟩}\mathit{\xi }\},$$

(2)

then $ntr\left(\mathit{\gamma }\right)$ is a unique vector bundle over $\mathit{\gamma }$ of rank 1, and, there is a unique vector field $\mathit{N}\in \Gamma \left(ntr\left(T\mathit{\gamma }\right){\mid }_{{\mathbb{R}}_2^4}\right)$ satisfying

$$⟨\mathit{N},\mathit{N}⟩=0,⟨\mathit{\xi },\mathit{N}⟩=1.$$

3.

The tangent bundle $T{\mathbb{R}}_2^4$ splits into the following three bundle spaces:

$$T{\mathbb{R}}_2^4{|}_{\mathit{\gamma }}=T\mathit{\gamma }⨁ntr\left(\mathit{\gamma }\right)⨁S\left(T{\mathit{\gamma }}^{\perp }\right).$$

For a null curve $\mathit{\gamma }$ in ${\mathbb{R}}_2^4$, and $\mathit{N}\left(s\right)$ the unique null transversal vector field to $\mathit{\xi }\left(s\right)$, the screen vector bundle $S\left(T{\mathit{\gamma }}^{\perp }\right)$ is Lorentz. Hence, the two null vectors $\mathit{\xi }\left(s\right)$ and $\mathit{N}\left(s\right)$ are two Frenet frames of $\mathit{\gamma }$. Then, ${\kappa }_1\left(s\right)=\parallel {\mathit{\xi }}^{\prime }\left(s\right)\parallel ,$ and we construct a non null frame $\mathit{B}\left(s\right)=\frac{1}{{\kappa }_1\left(s\right)}{\mathit{\xi }}^{\prime }\left(s\right)\in span{\{\mathit{\xi }\left(s\right),\mathit{N}\left(s\right)\}}^{\perp }$, and $\mathit{W}\left(s\right)=\frac{\mathit{\xi }\left(s\right)\wedge \mathit{N}\left(s\right)\wedge \mathit{B}\left(s\right)}{\parallel \mathit{\xi }\left(s\right)\wedge \mathit{N}\left(s\right)\wedge \mathit{B}\left(s\right)\parallel }.$

A null curve $\mathit{\gamma }:I\to {\mathbb{R}}_2^4$ with the Frenet frame $\left\{\mathit{\xi }\right(s),\mathit{N}(s),\mathit{B}(s),\mathit{W}(s\left)\right\}$, satisfies

$$⟨\mathit{\xi }\left(s\right),\mathit{\xi }\left(s\right)⟩=⟨\mathit{N}\left(s\right),\mathit{N}\left(s\right)⟩=0,$$

$$⟨\mathit{\xi }\left(s\right),\mathit{N}\left(s\right)⟩=1,$$

$$⟨\mathit{B}\left(s\right),\mathit{B}\left(s\right)⟩={\epsilon }_1,⟨\mathit{W}\left(s\right),\mathit{W}\left(s\right)⟩={\epsilon }_2,{\epsilon }_1^2={\epsilon }_2^2=1,{\epsilon }_1{\epsilon }_2=-1,$$

$$⟨\mathit{N}\left(s\right),\mathit{B}\left(s\right)⟩=⟨\mathit{N}\left(s\right),\mathit{W}\left(s\right)⟩=⟨\mathit{\xi }\left(s\right),\mathit{B}\left(s\right)⟩=⟨\mathit{\xi }\left(s\right),\mathit{W}\left(s\right)⟩=⟨\mathit{B}\left(s\right),\mathit{W}\left(s\right)⟩=0,$$

where $\mathit{\xi }\left(s\right)={\mathit{\gamma }}^{\prime }\left(s\right)$ is the tangent vector, $\mathit{N}\left(s\right)$ is the normal vector, $\mathit{B}\left(s\right)$ is the first binormal vector, and $\mathit{W}\left(s\right)$ is the second binormal vector. The Frenet Equations of $\mathit{\gamma }\left(s\right)$ are given as follows [3],

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\xi }}^{\prime }\left(s\right)={\kappa }_1\left(s\right)\mathit{B}\left(s\right)\hfill \\ {\mathit{N}}^{\prime }\left(s\right)={\kappa }_2\left(s\right)\mathit{B}\left(s\right)+{\kappa }_3\left(s\right)\mathit{W}\left(s\right)\hfill \\ {\mathit{B}}^{\prime }\left(s\right)=-{\kappa }_2\left(s\right){\epsilon }_1\mathit{\xi }\left(s\right)-{\kappa }_1\left(s\right){\epsilon }_1\mathit{N}\left(s\right)\hfill \\ {\mathit{W}}^{\prime }\left(s\right)=-{\kappa }_3\left(s\right){\epsilon }_2\mathit{\xi }\left(s\right)\hfill \end{array}\right.,\end{array}$$

(3)

where ${\kappa }_1\left(s\right)={\epsilon }_1⟨{\mathit{\xi }}^{\prime }\left(s\right),\mathit{B}\left(s\right)⟩$, ${\kappa }_2\left(s\right)={\epsilon }_1⟨\mathit{B}\left(s\right),{\mathit{N}}^{\prime }\left(s\right)⟩$ and ${\kappa }_3\left(s\right)={\epsilon }_2⟨\mathit{W}\left(s\right),{\mathit{N}}^{\prime }\left(s\right)⟩$ are called the first curvature function, the second curvature function and the third curvature function of $\mathit{\gamma }\left(s\right)$, respectively.

As in [15,17], we give the definition of the Bertrand curve as following,

Definition 2. 

Let $\mathit{\gamma }$ and $\tilde{\mathit{\gamma }}$ be two curves in semi-Euclidean 4-space and $\phi :I\to \tilde{I}$ a regular $C^{\infty }$-map, such that each point $\mathit{\gamma }\left(s\right)$ of $\mathit{\gamma }$ corresponds to the point $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)=\tilde{\mathit{\gamma }}\left(\phi \left(s\right)\right)$ of $\tilde{\mathit{\gamma }}$ for all $s\in I.$ If the Frenet–Serret normal plane spanned by $\left\{\mathit{N}\right(s),\mathit{W}(s\left)\right\}$ at each point of $\mathit{\gamma }$ coincides with the Frenet–Serret normal plane spanned by $\{\tilde{\mathit{N}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right)\}$ at each corresponding point of $\tilde{\mathit{\gamma }}$, then $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ is called the Bertrand curve (mate) of $\mathit{\gamma }\left(s\right)$.

3. The Bertrand Curves of Null Curves

In this section, we present some geometrical characterizations and provide the existence conditions of the Bertrand curves of the null curves in semi-Euclidean 4-space. We also give the existence of the Bertrand curves for two cases (${\kappa }_2\ne 0,{\kappa }_2=0$) respectively.

For $\mathit{\gamma }\left(s\right)$ be a null curve in semi-Euclidean 4-space, the Bertrand curve $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ of $\mathit{\gamma }\left(s\right)$ can be written as following,

$$\tilde{\mathit{\gamma }}\left(\tilde{s}\right)=\tilde{\mathit{\gamma }}\left(\phi \left(s\right)\right)=\mathit{\gamma }\left(s\right)+\lambda \left(s\right)\mathit{N}\left(s\right)+\mu \left(s\right)\mathit{W}\left(s\right),s\in I,$$

(4)

where $\lambda \left(s\right)$ and $\mu \left(s\right)$ are $C^{\infty }-$ functions on I, ${\lambda }^2\left(s\right)+{\mu }^2\left(s\right)\ne 0$, and $\tilde{s}=\phi \left(s\right)$ is the pseudo parameter of $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$.

Differentiating the Equation (4) with respect to $s,$ we can obtain

$$\begin{array}{cc}{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right)\hfill & ={\mathit{\gamma }}^{\prime }\left(s\right)+{\lambda }^{\prime }\left(s\right)\mathit{N}\left(s\right)+\lambda \left(s\right){\mathit{N}}^{\prime }\left(s\right)+{\mu }^{\prime }\left(s\right)\mathit{W}\left(s\right)+\mu \left(s\right){\mathit{W}}^{\prime }\left(s\right)\hfill \\ \hfill & =(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))\mathit{\xi }\left(s\right)+{\lambda }^{\prime }\left(s\right)\mathit{N}\left(s\right)+\lambda \left(s\right){\kappa }_2\mathit{B}\left(s\right)+(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\mathit{W}\left(s\right).\hfill \end{array}$$

(5)

Since the plane spanned by $\mathit{N}\left(s\right)$ and $\mathit{W}\left(s\right)$ is parallel with the plane spanned by $\tilde{\mathit{N}}\left(\tilde{s}\right)$ and $\tilde{\mathit{W}}\left(\tilde{s}\right)$, we have

$$\tilde{\mathit{N}}\left(\tilde{s}\right)=f\left(s\right)\mathit{N}\left(s\right),f\left(s\right)\ne 0,$$

(6)

$$\tilde{\mathit{W}}\left(\tilde{s}\right)=g\left(s\right)\mathit{N}\left(s\right)+\mathit{W}\left(s\right),$$

(7)

where $f\left(s\right),g\left(s\right)$ are two $C^{\infty }-$ functions. By the fact

$$⟨\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩=0,⟨\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right)⟩=1,$$

(8)

we get

$$\begin{array}{cc}{\phi }^{\prime }\left(s\right)\hfill & =⟨{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right)⟩\hfill \\ \hfill & =⟨(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))\mathit{\xi }\left(s\right)+{\lambda }^{\prime }\left(s\right)\mathit{N}\left(s\right)+\lambda \left(s\right){\kappa }_2\mathit{B}\left(s\right)+(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\mathit{W}\left(s\right),f\left(s\right)\mathit{N}\left(s\right)⟩\hfill \\ \hfill & =(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))f\left(s\right).\hfill \end{array}$$

(9)

Since

$$⟨\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right)⟩=0,$$

we obtain

$$\begin{array}{cc}\hfill & ⟨{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right)⟩\hfill \\ \hfill & =⟨(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))\mathit{\xi }\left(s\right)+{\lambda }^{\prime }\left(s\right)\mathit{N}\left(s\right)+\lambda \left(s\right){\kappa }_2\mathit{B}\left(s\right)+(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\mathit{W}\left(s\right),g\left(s\right)\mathit{N}\left(s\right)+\mathit{W}\left(s\right)⟩\hfill \\ \hfill & =(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))g\left(s\right)+{\epsilon }_2(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\hfill \\ \hfill & =0.\hfill \end{array}$$

(10)

Together with the Equations (9) and (10), when $1-{\epsilon }_2{\kappa }_3\mu \left(s\right)\ne 0$, we obtain

$$\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right)=-\frac{{\epsilon }_2{\phi }^{\prime }\left(s\right)g\left(s\right)}{f\left(s\right)}.$$

(11)

From

$$\begin{array}{cc}\hfill & ⟨{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right),{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩\hfill \\ \hfill & =2{\lambda }^{\prime }\left(s\right)(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))+{\epsilon }_1{\kappa }_2^2{\lambda }^2\left(s\right)+{\epsilon }_2\left(\lambda \left(s\right){\kappa }_{3+{\mu }^{\prime }\left(s\right)}\right),\hfill \end{array}$$

(12)

together with the Equations (3) and (7), we can obtain

$${\phi }^{\prime }\left(s\right)\tilde{\mathit{W}}\left(\tilde{s}\right)=-{\epsilon }_2\widetilde{{\kappa }_3}{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right)=g^{\prime }\left(s\right)\mathit{N}\left(s\right)+g\left(s\right){\mathit{N}}^{\prime }\left(s\right)+{\mathit{W}}^{\prime }\left(s\right),$$

(13)

and

$$\begin{array}{cc}\hfill & -{\epsilon }_2\widetilde{{\kappa }_3}[(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))+{\lambda }^{\prime }\left(s\right)\mathit{N}\left(s\right)+\lambda \left(s\right){\kappa }_2\mathit{B}\left(s\right)+(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\mathit{W}\left(s\right)]\hfill \\ \hfill & =-{\epsilon }_2\widetilde{{\kappa }_3}\mathit{\xi }\left(s\right)+g^{\prime }\left(s\right)\mathit{N}\left(s\right)+{\kappa }_{2}g\left(s\right)\mathit{B}\left(s\right)+{\kappa }_{3}g\left(s\right)\mathit{W}\left(s\right).\hfill \end{array}$$

(14)

Hence,

$$\left\{\begin{array}{ccc}-{\epsilon }_2\widetilde{{\kappa }_3}(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))\hfill & =\hfill & -{\epsilon }_2{\kappa }_3,\hfill \\ -{\epsilon }_2\widetilde{{\kappa }_3}{\lambda }^{\prime }\left(s\right)\hfill & =\hfill & g^{\prime }\left(s\right),\hfill \\ -{\epsilon }_2\widetilde{{\kappa }_3}\lambda \left(s\right){\kappa }_2\hfill & =\hfill & {\kappa }_{2}g\left(s\right),\hfill \\ -{\epsilon }_2\widetilde{{\kappa }_3}(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))\hfill & =\hfill & {\kappa }_{3}g\left(s\right).\hfill \end{array}\right.$$

(15)

Theorem 1. 

Let $\mathit{\gamma }\left(s\right)$ be a null curve in semi-Euclidean 4-space with the frames $\left\{\mathit{\xi }\right(s),\mathit{N}(s),\mathit{B}(s),\mathit{W}(s),{\kappa }_1,{\kappa }_2,{\kappa }_3\}$, and the Bertrand curve $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ of $\mathit{\gamma }\left(s\right)$ with the frames $\{\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right),{\tilde{\kappa }}_1,{\tilde{\kappa }}_2,{\tilde{\kappa }}_3\}$, where $\tilde{s}=\phi \left(s\right)$. When ${\kappa }_2\ne 0$, there exist three functions $f\left(s\right),g\left(s\right),\lambda \left(s\right)$ as in the formulas (4), (6) and (7) such that:

Case 1: when ${\widetilde{{\kappa }_3}}^{\prime }=0$, the following conclusions are established:

1.

$g\left(s\right)=C_1{\epsilon }_1\lambda \left(s\right),$ and $f\left(s\right)=\frac{C_1}{C_3}$, where $C_1,C_3$ are constants;

2.

$C_1^2{({\kappa }_2^2-2C_3^2)}^2=C_1^2{\kappa }_2^2+C_3^2{\tilde{\kappa }}_2^2-{\kappa }_2^2{\tilde{\kappa }}_2^2;$

3.

$\lambda \left(s\right)=\frac{\zeta \left(s\right)({\kappa }_2^2-C_3^2)-2[C_1{C}_3+\zeta \left(s\right)]{\kappa }_2{\kappa }_2^{\prime }}{({\kappa }_2^2-C_3^2)[M_0({\kappa }_2^2-C_3^2)+({\epsilon }_1{\kappa }_2^2+{\epsilon }_2{C}_3^2)(C_1{C}_3+\zeta \left(s\right))]}$, where $\zeta \left(s\right)=\sqrt{C_1^2{\kappa }_2^2+C_3^2{\tilde{\kappa }}_2^2-{\tilde{\kappa }}_2^2{\kappa }_2^2},M_0=(1-{\epsilon }_2{C}_2{C}_3){\epsilon }_1{C}_1^2+{\epsilon }_2{C}_3{C}_1.$

Case 2: when ${\widetilde{{\kappa }_3}}^{\prime }\ne 0$, the following conclusions are established:

1.

$\lambda \left(s\right)=0,\mu \left(s\right)=K$, where K is a constant;

2.

${\tilde{\kappa }}_3=K_1(1-{\epsilon }_2{\kappa }_{3}K){\kappa }_3;$

3.

${\tilde{\kappa }}_2^2=(K_1^2{\kappa }_2^2-{\kappa }_3^2){(1-{\epsilon }_{2}K{\kappa }_3)}^2{\kappa }_2^2+2{\kappa }_3^2{K}_1(1-{\epsilon }_{2}K{\kappa }_3)-{\kappa }_3^4.$

Proof. 

When ${\kappa }_2\ne 0$, by the Equations (10) and (15), we can obtain

$${\widetilde{{\kappa }_3}}^{\prime }\lambda \left(s\right)=0.$$

Case 1: when ${\widetilde{{\kappa }_3}}^{\prime }=0,\lambda \left(s\right)\ne 0$, $\widetilde{{\kappa }_3}=C_1,$ where $C_1$ is a constant, from the third equation of (15), we have

$$g\left(s\right)=C_1{\epsilon }_1\lambda \left(s\right).$$

(16)

By differentiating the Equation (16), we obtain

$$C_1{\epsilon }_1(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))=C_1{\epsilon }_1{\kappa }_3\lambda \left(s\right),$$

and we get ${\mu }^{\prime }\left(s\right)=0$ and $\mu \left(s\right)=C_2$. Substituting $\mu \left(s\right)$ to the first equation of (15) gives us

$${\kappa }_3=\frac{C_1}{1+{\epsilon }_2{C}_1{C}_2}:=C_3,$$

where $C_1,C_2$ are two constants.

By the Equations (5)–(7), (11) and (16), we can obtain

$$\frac{{\phi }^{\prime }\left(s\right)}{f\left(s\right)}=1-{\epsilon }_2{C}_3{C}_2.$$

By differentiating the vector $\tilde{\mathit{N}}\left(\tilde{s}\right)$, we get

$$\begin{array}{cc}\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{ds}\hfill & ={\phi }^{\prime }\left(s\right)\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{d\tilde{s}}\hfill \\ \hfill & =\widetilde{{\kappa }_2}\left(\tilde{s}\right)\tilde{\mathit{B}}\left(\tilde{s}\right)+\widetilde{{\kappa }_3}\left(\tilde{s}\right)\tilde{\mathit{W}}\left(\tilde{s}\right)=\widetilde{{\kappa }_2}\left(\tilde{s}\right)\tilde{\mathit{B}}\left(\tilde{s}\right)+C_1\tilde{\mathit{W}}\left(\tilde{s}\right)\hfill \\ \hfill & =\widetilde{{\kappa }_2}\left(\tilde{s}\right)\tilde{\mathit{B}}\left(\tilde{s}\right)+C_{1}g\left(s\right)\mathit{N}\left(s\right)+C_1\mathit{W}\left(s\right).\hfill \end{array}$$

(17)

Meanwhile,

$$\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{ds}=f^{\prime }\left(s\right)\mathit{N}\left(s\right)+f\left(s\right){\mathit{N}}^{\prime }\left(s\right)=f^{\prime }\left(s\right)\mathit{N}\left(s\right)+f\left(s\right){\kappa }_2\mathit{B}\left(s\right)+f\left(s\right){\kappa }_3\mathit{W}\left(s\right),$$

hence,

$$\tilde{\mathit{B}}\left(\tilde{s}\right)=\frac{1}{\widetilde{{\kappa }_2}}[(f^{\prime }\left(s\right)-C_{1}g\left(s\right))\mathit{N}\left(s\right)+f\left(s\right){\kappa }_2\mathit{B}\left(s\right)+(f\left(s\right){\kappa }_3-C_1)\mathit{W}\left(s\right)].$$

(18)

By $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩=0$, we find

$$\begin{array}{cc}\hfill & ⟨\tilde{\mathit{B}}\left(\tilde{s}\right),{\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩\hfill \\ \hfill & =\frac{1}{\widetilde{{\kappa }_2}}[(f^{\prime }\left(s\right)-C_{1}g\left(s\right))(1-{\epsilon }_2{C}_2{C}_3)+{\epsilon }_{1}f\left(s\right){\kappa }_2\lambda \left(s\right)+{\epsilon }_2\lambda \left(s\right)C_3(f\left(s\right){\kappa }_3-C_1)\mathit{W}\left(s\right)]\hfill \\ \hfill & =0.\hfill \end{array}$$

(19)

Similarily,

$$⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right)⟩=0={\epsilon }_2(f\left(s\right)C_3-C_1),$$

and we get

$$f\left(s\right)=\frac{C_1}{C_3}.$$

(20)

From, $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right)⟩={\epsilon }_1$, we have

$$⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right)⟩=\frac{1}{\widetilde{{\kappa }_2}}[{\epsilon }_1{f}^2\left(s\right){\kappa }_2^2+{\epsilon }_2{(f\left(s\right){\kappa }_3-C_1)}^2]={\epsilon }_1,$$

and we obtain

$$f\left(s\right)=\frac{C_3{C}_1+\sqrt{C_1^2{\kappa }_2^2+C_3^2{\tilde{\kappa }}_2^2-{\tilde{\kappa }}_2^2{\kappa }_2^2}}{{\kappa }_2^2-C_3^2}.$$

(21)

By substituting (21) in (19) and (20), we have

$$C_1^2{({\kappa }_2^2-2C_3^2)}^2=C_1^2{\kappa }_2^2+C_3^2{\tilde{\kappa }}_2^2-{\kappa }_2^2{\tilde{\kappa }}_2^2,$$

(22)

${\phi }^{\prime }\left(s\right)=f\left(s\right)\frac{C_3}{C_1}=1$, $\phi \left(s\right)=s+C.$ Hence,

$$\lambda \left(s\right)=\frac{\zeta \left(s\right)({\kappa }_2^2-C_3^2)-2[C_1{C}_3+\zeta \left(s\right)]{\kappa }_2{\kappa }_2^{\prime }}{({\kappa }_2^2-C_3^2)[M_0({\kappa }_2^2-C_3^2)+({\epsilon }_1{\kappa }_2^2+{\epsilon }_2{C}_3^2)(C_1{C}_3+\zeta \left(s\right))]},$$

$${\kappa }_2^2=\frac{M_0{C}_3-{\epsilon }_2{C}_3^2}{{\epsilon }_1{C}_1},$$

$${\tilde{\kappa }}_2^2=\frac{M_0{C}_1-{\epsilon }_2{C}_3^2{C}_1}{{\epsilon }_1{C}_3},$$

where $\zeta \left(s\right)=\sqrt{C_1^2{\kappa }_2^2+C_3^2{\tilde{\kappa }}_2^2-{\tilde{\kappa }}_2^2{\kappa }_2^2},M_0=(1-{\epsilon }_2{C}_2{C}_3){\epsilon }_1{C}_1^2+{\epsilon }_2{C}_3{C}_1.$

Case 2: When ${\widetilde{{\kappa }_3}}^{\prime }\ne 0,\lambda \left(s\right)=0$, and ${\lambda }^{\prime }\left(s\right)=0$, we can obtain $g\left(s\right)=0,{\mu }^{\prime }\left(s\right)=0,$ and $\mu \left(s\right)=K,$ where K is a constant.

By substituting the above to Equation (9),

$${\tilde{\kappa }}_3-{\epsilon }_1{\tilde{\kappa }}_3{\kappa }_{3}K-{\kappa }_3=0,$$

we find

$${\phi }^{\prime }\left(s\right)\tilde{\mathit{\xi }}\left(\tilde{s}\right)=(1-{\epsilon }_2{\kappa }_{3}K)\mathit{\xi }\left(s\right),$$

$$\tilde{\mathit{N}}\left(\tilde{s}\right)=f\left(s\right)\mathit{N}\left(s\right),f\left(s\right)\ne 0,$$

$$\tilde{\mathit{W}}\left(\tilde{s}\right)=\mathit{W}\left(s\right),$$

$$f\left(s\right){\phi }^{\prime }\left(s\right)=1-{\epsilon }_2{\kappa }_{3}K.$$

(23)

By differentiating $\tilde{\mathit{N}}\left(\tilde{s}\right)$, we get

$$\begin{array}{cc}\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{ds}\hfill & ={\phi }^{\prime }\left(s\right)\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{d\tilde{s}}\hfill \\ \hfill & ={\phi }^{\prime }\left(s\right)(\widetilde{{\kappa }_2}\left(\tilde{s}\right)\tilde{\mathit{B}}\left(\tilde{s}\right)+\widetilde{{\kappa }_3}\left(\tilde{s}\right)\tilde{\mathit{W}}\left(\tilde{s}\right))\hfill \\ \hfill & ={\phi }^{\prime }\left(s\right)(\widetilde{{\kappa }_2}\left(\tilde{s}\right)\tilde{\mathit{B}}\left(\tilde{s}\right)+\widetilde{{\kappa }_3}\left(\tilde{s}\right)\tilde{\mathit{W}}\left(\tilde{s}\right))\hfill \\ \hfill & =f^{\prime }\left(s\right)\mathit{N}\left(s\right)+f\left(s\right)({\kappa }_2\mathit{B}\left(s\right)+{\kappa }_3\mathit{W}\left(s\right)),\hfill \end{array}$$

(24)

hence, we obtain

$$\tilde{\mathit{B}}\left(\tilde{s}\right)=\frac{1}{{\phi }^{\prime }\left(s\right)\widetilde{{\kappa }_2}}[f^{\prime }\left(s\right)\mathit{N}\left(s\right)+f\left(s\right){\kappa }_2\mathit{B}\left(s\right)+({\kappa }_3-{\phi }^{\prime }\left(s\right)\widetilde{{\kappa }_3})\mathit{W}\left(s\right)].$$

By the fact $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩=0$, $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right)⟩=0$, and $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right)⟩=0$, we can obtain

$$f\left(s\right)(1-{\epsilon }_2{\kappa }_{3}K){\kappa }_3={\tilde{\kappa }}_3.$$

(25)

(1).

When $1-{\epsilon }_2{\kappa }_{3}K=0,$ from (23), we know ${\phi }^{\prime }\left(s\right)=0$, which contradicts with $\phi \left(s\right)=s+C$. Hence, we omit this case.

(2).

When $1-{\epsilon }_2{\kappa }_{3}K\ne 0,$ we know $f^{\prime }\left(s\right)=0$ and $f\left(s\right)=K_1$, where $K_1$ is a constant. By substituting this in the Equation (23), we have

$${\tilde{\kappa }}_3=K_1(1-{\epsilon }_2{\kappa }_{3}K){\kappa }_3.$$

By the fact that $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right)⟩={\epsilon }_1,$ we can obtain

$${\tilde{\kappa }}_2^2=(K_1^2{\kappa }_2^2-{\kappa }_3^2){(1-{\epsilon }_{2}K{\kappa }_3)}^2{\kappa }_2^2+2{\kappa }_3^2{K}_1(1-{\epsilon }_{2}K{\kappa }_3)-{\kappa }_3^4.$$

(26)

 □

Theorem 2. 

Let $\mathit{\gamma }\left(s\right)$ be a null curve in semi-Euclidean 4-space with the frames $\left\{\mathit{\xi }\right(s),\mathit{N}(s),\mathit{B}(s),$ $\mathit{W}\left(s\right),$ ${\kappa }_1,{\kappa }_2,{\kappa }_3\}$, and the Bertrand curve $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ of $\mathit{\gamma }\left(s\right)$ with the frames $\{\tilde{\mathit{\xi }}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right),{\tilde{\kappa }}_1,{\tilde{\kappa }}_2,{\tilde{\kappa }}_3\}$, where $\tilde{s}=\phi \left(s\right)$. When ${\kappa }_2=0$, there exist three functions $f\left(s\right),\lambda \left(s\right),\mu \left(s\right)$ as in the formulas (4), (6) and (7) such that:

1.

$f\left(s\right)=K_1,K_1$ is a constant, and $\phi \left(s\right)=\int \frac{1}{(1-K{\epsilon }_2{\kappa }_3)K_1}$;

2.

${\mu }^{\prime }\left(s\right)+{\kappa }_3\lambda \left(s\right)=\frac{{\kappa }_1(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))}{\widetilde{{\kappa }_1}{e}^{\int \frac{{\kappa }_3}{{\epsilon }_1{\kappa }_1(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))}ds}};$

3.

${\mu }^{″}\left(s\right)(1+\mu \left(s\right))+{\mu }^{\prime 2}\left(s\right)-{\left(\mu \left(s\right)\lambda \left(s\right)\right)}^{\prime }-{\lambda }^{\prime }\left(s\right)-\mu \left(s\right)=1.$

Proof. 

By the Equation (15), we can obtain

$$({\kappa }_3^{\prime }\lambda \left(s\right)+{\kappa }_3{\lambda }^{\prime }\left(s\right)+{\mu }^{″}\left(s\right))(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))+{\epsilon }_2(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))({\kappa }_3^{\prime }\mu \left(s\right)+{\kappa }_3{\mu }^{\prime }\left(s\right))={\tilde{\kappa }}_3{\lambda }^{\prime }\left(s\right){(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))}^2{)}^2$$

By differentiating $\tilde{\mathit{N}}\left(\tilde{s}\right)$, we get

$$\begin{array}{cc}\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{ds}\hfill & ={\phi }^{\prime }\left(s\right)\frac{d\tilde{\mathit{N}}\left(\tilde{s}\right)}{d\tilde{s}}\hfill \\ \hfill & ={\phi }^{\prime }\left(s\right)\widetilde{{\kappa }_3}\left(\tilde{s}\right)\tilde{\mathit{W}}\left(\tilde{s}\right)\hfill \\ \hfill & ={\phi }^{\prime }\left(s\right)\widetilde{{\kappa }_3}\left(\tilde{s}\right)(g\left(s\right)\mathit{N}\left(s\right)+\mathit{W}\left(s\right))\hfill \\ \hfill & =f^{\prime }\left(s\right)\mathit{N}\left(s\right)+f\left(s\right){\kappa }_3\mathit{W}\left(s\right).\hfill \end{array}$$

(27)

Hence,

$$\widetilde{{\kappa }_3}\left(\tilde{s}\right){\phi }^{\prime }\left(s\right)g\left(s\right)=f^{\prime }\left(s\right),$$

$$\widetilde{{\kappa }_3}\left(\tilde{s}\right){\phi }^{\prime }\left(s\right)g\left(s\right)=f\left(s\right){\kappa }_3,$$

and,

$$\frac{f^{\prime }\left(s\right)}{f\left(s\right)}=\frac{{\kappa }_3}{g\left(s\right)},$$

(28)

$$f\left(s\right)=e^{\int \frac{{\kappa }_3}{g\left(s\right)}ds}.$$

(29)

Since

$${\phi }^{\prime }\left(s\right)=\frac{{\kappa }_3}{\widetilde{{\kappa }_3}}{e}^{\int \frac{{\kappa }_3}{g\left(s\right)}ds}={\epsilon }_1\frac{f\left(s\right)}{g\left(s\right)}(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right)),$$

(30)

we obtain

$$g\left(s\right)=\frac{\widetilde{{\kappa }_3}}{{\kappa }_3}(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right)).$$

(31)

Meanwhile,

$$\begin{array}{cc}\widetilde{{\mathit{\xi }}^{\prime }}\left(\tilde{s}\right)\hfill & =\widetilde{{\kappa }_1}\tilde{\mathit{B}}\left(\tilde{s}\right)\hfill \\ \hfill & =a\left(s\right)\mathit{\xi }\left(s\right)+b\left(s\right)\mathit{N}\left(s\right)+c\left(s\right)\mathit{B}\left(s\right)+d\left(s\right)\mathit{W}\left(s\right),\hfill \end{array}$$

(32)

$$\tilde{\mathit{B}}\left(\tilde{s}\right)=\frac{1}{\widetilde{{\kappa }_1}}(a\left(s\right)\mathit{\xi }\left(s\right)+b\left(s\right)\mathit{N}\left(s\right)+c\left(s\right)\mathit{B}\left(s\right)+d\left(s\right)\mathit{W}\left(s\right)),$$

where

$$a\left(s\right)=-\frac{{\phi }^{″}\left(s\right)}{{\phi }^{\prime 2}\left(s\right)}(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))+\frac{1}{{\phi }^{\prime }\left(s\right)}{(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))}^{\prime }-{\epsilon }_2{\kappa }_3(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right)),$$

$$b\left(s\right)=-\frac{{\phi }^{″}\left(s\right)}{{\phi }^{\prime 2}\left(s\right)}{\lambda }^{\prime }\left(s\right)+\frac{1}{{\phi }^{\prime }\left(s\right)}{\lambda }^{″}\left(s\right),$$

$$c\left(s\right)=\frac{1}{{\phi }^{\prime }\left(s\right)}(1-{\epsilon }_2{\kappa }_3\mu \left(s\right)){\kappa }_1,$$

$$d\left(s\right)=-\frac{{\phi }^{″}\left(s\right)}{{\phi }^{\prime 2}\left(s\right)}(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))+\frac{1}{{\phi }^{\prime }\left(s\right)}({\lambda }^{\prime }\left(s\right){\kappa }_3+\lambda \left(s\right){\kappa }_3^{\prime }+{\mu }^{″}\left(s\right).$$

By the fact $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{\xi }}\left(\tilde{s}\right)⟩=0$, $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{N}}\left(\tilde{s}\right)⟩=0$, and $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{W}}\left(\tilde{s}\right)⟩=0$, we can obtain

$$a\left(s\right)=0,d\left(s\right)=0.$$

Since $⟨\tilde{\mathit{B}}\left(\tilde{s}\right),\tilde{\mathit{B}}\left(\tilde{s}\right)⟩={\epsilon }_1,$ we have

$${\widetilde{{\kappa }_1}}^2={\left(\frac{(1-{\epsilon }_2{\kappa }_3\mu \left(s\right)){\kappa }_1}{{\phi }^{\prime }\left(s\right)}\right)}^2.$$

(33)

By substituting Equations (30), (31) and (33) into Equation (11), we obtain that there exist two functions $\lambda \left(s\right)$ and $\mu \left(s\right)$ satisfying

$${\mu }^{\prime }\left(s\right)+{\kappa }_3\lambda \left(s\right)=\frac{{\kappa }_1(1-{\epsilon }_2{\kappa }_3\mu \left(s\right))(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))}{\widetilde{{\kappa }_1}{e}^{\int \frac{{\kappa }_3}{{\epsilon }_1{\kappa }_1(\lambda \left(s\right){\kappa }_3+{\mu }^{\prime }\left(s\right))}ds}}.$$

(34)

By substituting the Equations (29), (31) and (33) into Equation (34), we can obtain

$${\mu }^{″}\left(s\right)(1+\mu \left(s\right))+{\mu }^{\prime 2}\left(s\right)-{\left(\mu \left(s\right)\lambda \left(s\right)\right)}^{\prime }-{\lambda }^{\prime }\left(s\right)-\mu \left(s\right)=1.$$

When we choose $\mu \left(s\right)=s$, then $\lambda \left(s\right)=\frac{e^{-s}}{2}(s{e}^s-e^s+C)$. □

4. Some Examples

In this section, we give two examples of the Bertrand curves of the null curves in semi-Euclidean 4-space to certificate our main conclusions. The graphics of the null curves and the Bertrand curves are described in the followings. Moreover, for the reason that it cannot draw the high dimension graph, and here, we give the projection graph of the null curve and the Bertrand curves for two cases (${\kappa }_2\ne 0,{\kappa }_2=0$), respectively.

Example 1. 

Let $\mathit{\gamma }\left(s\right)$ be a null curve in semi-Euclidean 4-space with ${\kappa }_2\ne 0$, and $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ be the Bertrand curve of $\mathit{\gamma }\left(s\right)$. The equation is as following [3],

$$\mathit{\gamma }\left(s\right)=\left\{\frac{1}{3}{(2s-1)}^{\frac{3}{2}},\frac{1}{2}{s}^2-s,ssins+coss,sins-scoss\right\},$$

and we can choose the frame of the null curve $\mathit{\gamma }\left(s\right)$:

$$\mathit{\xi }\left(s\right)=\left\{{(2s-1)}^{\frac{1}{2}},s-1,scoss,ssins\right\};$$

$$\mathit{N}\left(s\right)=-\frac{1}{2s^2}\left\{{(2s-1)}^{\frac{1}{2}},s-1,-scoss,-ssins\right\};$$

$$\mathit{B}\left(s\right)=\frac{\sqrt{2s-1}}{\sqrt{2s^3-s^2-1}}\left\{\frac{1}{\sqrt{2s-1}},1,coss-ssins,sins+scoss\right\};$$

$$\mathit{W}\left(s\right)=\frac{1}{\sqrt{2s^3-s^2-1}}\left\{(1-s)\sqrt{2s-1},2s-1,-sins,coss\right\}.$$

The curvatures are the following

$${\kappa }_1=\frac{\sqrt{2s^3-s^2-1}}{\sqrt{2s-1}},$$

$${\kappa }_2=\frac{2s^3-s^2+1}{2s^2\sqrt{2s^3-s^2-1}\sqrt{2s-1}},$$

$${\kappa }_3=\frac{6s^4-5s^3+s^2-3s+1}{{(2s^3-s^2-1)}^2\sqrt{2s-1}}.$$

By the analysis in Section 3, we can obtain $\mu \left(s\right)=constant$. We might as well choose $\mu \left(s\right)=1$. We can get

$$\lambda \left(s\right)=\frac{(\frac{{(2s^3-s^2+1)}^2}{4s^4(2s^3-s^2-1)(2s-1)}-1)-2(1+\sqrt{\frac{8s^4(2s^3-s^2-1)(2s-1)-{(2s^3-s^2+1)}^2}{4s^4(2s^3-s^2-1)(2s-1)}}\frac{2s^3-s^2+1}{2s^2\sqrt{2s^3-s^2-1}\sqrt{2s-1}})}{\frac{{(2s^3-s^2+1)}^2}{4s^4(2s^3-s^2-1)(2s-1)}[(\frac{{(2s^3-s^2+1)}^2}{4s^4(2s^3-s^2-1)(2s-1)}-1)+\sqrt{\frac{8s^4(2s^3-s^2-1)(2s-1)-{(2s^3-s^2+1)}^2}{4s^4(2s^3-s^2-1)(2s-1)}}]}.$$

Hence, we have

$$\begin{array}{cc}\tilde{\mathit{\gamma }}\left(\tilde{s}\right)\hfill & =\mathit{\gamma }\left(s\right)+\lambda \left(s\right)\mathit{N}\left(s\right)+\mu \left(s\right)\mathit{W}\left(s\right)\hfill \\ \hfill & =\{\frac{1}{3}{(2s-1)}^{\frac{3}{2}}-\lambda \left(s\right)\frac{\sqrt{2s-1}}{2s^2}+\frac{(s-1)\sqrt{2s-1}}{\sqrt{2s^3-s^2-1}},\hfill \\ \hfill & -\frac{1}{2S^2}-\lambda \left(s\right)\frac{s-1}{2s^2}-\frac{2s-1}{\sqrt{2s^3-s^2-1}},\hfill \\ \hfill & ssins+coss+\lambda \left(s\right)\frac{scoss}{2s^2}+\frac{sins}{\sqrt{2s^3-s^2-1}},\hfill \\ \hfill & sins-scoss+\lambda \left(s\right)\frac{ssins}{2s^2}+\frac{coss}{\sqrt{2s^3-s^2-1}}\}.\hfill \end{array}$$

(35)

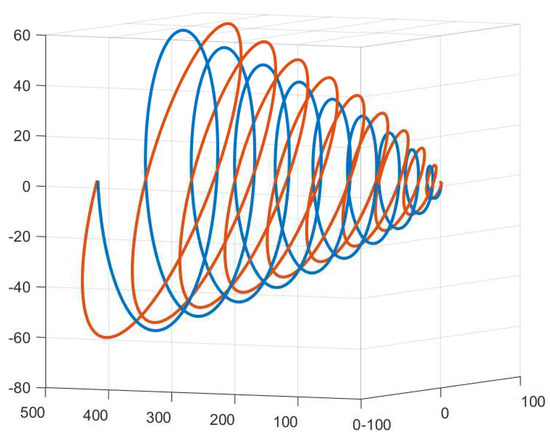
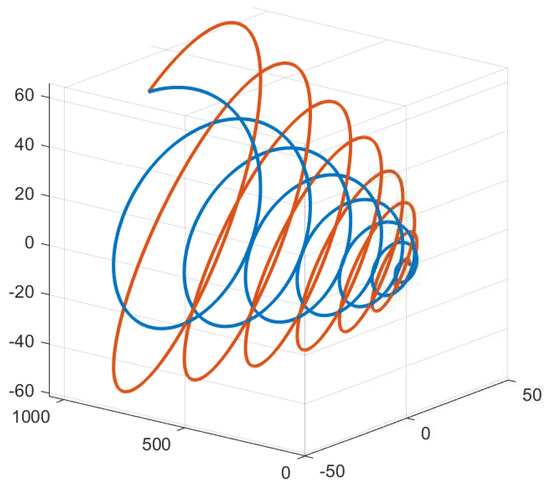
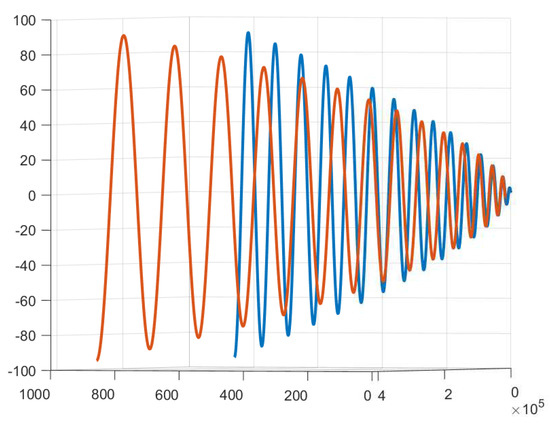
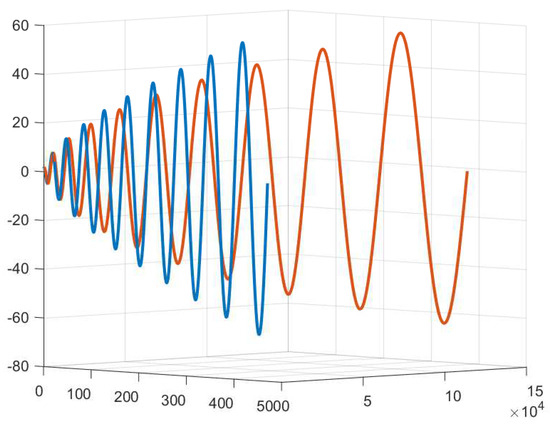
We draw four graphics from four different projection angles in the following (Figure 1, Figure 2, Figure 3 and Figure 4).

Figure 1. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{N},\mathit{B},\mathit{W}\}$.

Figure 2. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{\xi },\mathit{B},\mathit{W}\}$.

Figure 3. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{\xi },\mathit{N},\mathit{W}\}$.

Figure 4. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{\xi },\mathit{N},\mathit{B}\}$.

Example 2. 

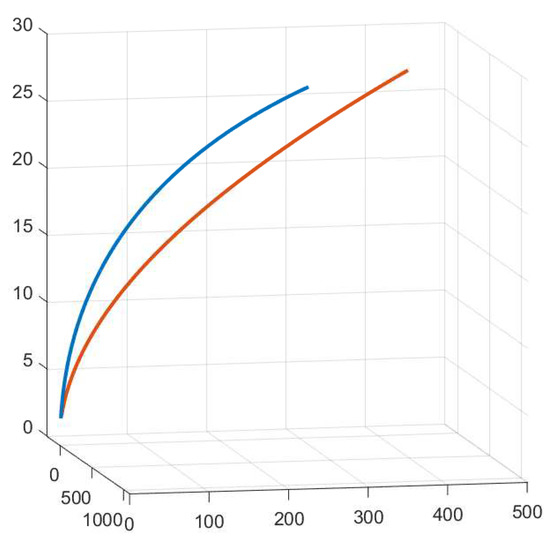
Let $\mathit{\gamma }\left(s\right)$ be a null curve in the semi-Euclidean 4-space with ${\kappa }_2=0$, and $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ be the Bertrand curve of $\mathit{\gamma }\left(s\right)$. The equation is as follows

$$\mathit{\gamma }\left(s\right)=\left\{\frac{1}{3}{s}^3-2s,s^2,\frac{1}{3}{s}^3,2s\right\},$$

and we can choose the frame of the null curve $\mathit{\gamma }\left(s\right)$:

$$\mathit{\xi }\left(s\right)=\left\{s^2-2,2s,s^2,2\right\};$$

$$\mathit{N}\left(s\right)=\frac{-1}{8}\left\{s^2-2,2s,s^2,-2\right\};$$

$$\mathit{B}\left(s\right)=\left\{s,1,s,0\right\};$$

$$\mathit{W}\left(s\right)=\frac{1}{2}\left\{s^2,2s,s^2+2,0\right\}.$$

The curvatures are ${\kappa }_1=2,{\kappa }_2=0,{\kappa }_3=-1.$ By the analysis in Section 3, when choosing $g\left(s\right)=s$, we draw two graphics from two different projection angles in the following (Figure 5 and Figure 6).

Figure 5. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{\xi },\mathit{N},\mathit{W}\}$ when we choose $\mu \left(s\right)=s$.

Figure 6. The blue curve is $\mathit{\gamma }\left(s\right)$ and the red curve is the $\tilde{\mathit{\gamma }}\left(\tilde{s}\right)$ in the projection space spanned by $\{\mathit{\xi },\mathit{N},\mathit{B}\}$ when we choose $\mu \left(s\right)=s$.