{0,1}-Brauer Configuration Algebras and Their Applications in Graph Energy Theory

Abstract

The energy $\mathcal{E}\left(G\right)$ of a graph G is the sum of the absolute values of its adjacency matrix. In contrast, the trace norm of a digraph Q, which is the sum of the singular values of the corresponding adjacency matrix, is the oriented version of the energy of a graph. It is worth pointing out that one of the main problems in this theory consists of determining appropriated bounds of these types of energies for significant classes of graphs, digraphs and matrices, provided that, in general, finding out their exact values is a problem of great difficulty. In this paper, the trace norm of a $\{0,1\}$-Brauer configuration is introduced. It is estimated and computed by associating suitable families of graphs and posets to Brauer configuration algebras.

1. Introduction

Brauer configuration algebras (BCAs) were introduced recently by Green and Schroll [1]. These algebras are multiserial symmetric algebras whose theory of representation is based on combinatorial data.

Since its introduction, BCAs have been a tool in the research of different fields of mathematics. Its role in algebra, combinatorics, and cryptography is remarkable. For instance, Malić and Schroll [2] associated a Brauer configuration algebra to some dessins d’enfants used to study Riemann surfaces, Cañadas et al. investigated the structure of the keys related to the Advanced Encryption Standard (AES) by using some so-called polygon-mutations in BCAs. On the other hand, BCAs were a helpful tool for Espinosa et al. to describe the number of perfect matchings in some snake graphs. We point out that Schiffler et al. used perfect matchings of snake graphs to provide a formula for the cluster variables associated with appropriated cluster algebras of surface type. In their doctoral dissertation, Espinosa used the notion of the message of a Brauer configuration to obtain the results [3,4]. According to him, each polygon in a Brauer configuration has associated a word. The concatenation of such words constitutes a message after applying a suitable specialization.

Perhaps, the message associated with a Brauer configuration is one of the most helpful tools to obtain applications of BCAs. In this work, we use Brauer configuration messages, some results of the theory of posets (partially ordered sets) and integer partitions to obtain the trace norm of some $\{0,1\}$-Brauer configurations, which are Brauer configurations whose sets of vertices consist only of 0’s and 1’s.

It is worth pointing out that the research on trace norm has its roots in chemistry within the Hückel molecular orbital theory (HMO) [5]. Afterwards, Gutman [6] founded an independent line of investigation in spectral graph theory based on graph energy, which is the sum $\mathcal{E}\left(G\right)={\displaystyle \sum _{\lambda \in spect\left(M_G\right)}}\left|\lambda \right|$, where $spect\left(M_G\right)$ is the set of eigenvalues of the adjacency matrix $M_G$ of a graph G. The trace norm associated with the adjacency matrix of a digraph or quiver Q denoted ${\left|\right|Q\left|\right|}_{*}$ is a generalization of the graph energy. It is also called the Schatten 1-norm, Ky Fan n-norm or nuclear norm. If ${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n$ are the singular values of the $m\times n$- adjacency matrix $M_Q$, with ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_n$ then ${\left|\right|Q\left|\right|}_{*}={\displaystyle \sum _{i=1}^{\min \{m,n\}}}{\sigma }_i$. Relationships between energy graph and trace norm were investigated first by Nikiforov [7].

One of the main problems in graph energy theory is giving the extremal values of the energy of significant classes of graphs. For instance, Gutman [6] proved that if $T_n$ is a tree with n vertices then the following identity holds:

$$\mathcal{E}\left(S_n\right)\le \mathcal{E}\left(T_n\right)\le \mathcal{E}\left({\mathbb{A}}_n\right)$$

(1)

where, $S_n$ (${\mathbb{A}}_n$) denotes the star (the Dynkin diagram of type $\mathbb{A}$) with n vertices.

Graph energy associated with digraphs was investigated first by Kharaghani–Tayfeh–Rezaie [8], afterwards by Agudelo–Nikiforov [9], who found bounds of extremal values of the trace norm for $(0,1)$-matrices. It is worth noticing that if the adjacency matrix of a graph G is normal, then the graph energy equals the trace norm. In particular, if the adjacency matrix $M_G$ of a graph G is symmetric, then $\mathcal{E}\left(G\right)=\left|\right|M_G{\left|\right|}_{*}$.

Contributions

In this paper, we introduce the notion of trace norm of a $\{0,1\}$-Brauer configuration. Bounds and explicit values of these trace norms are given for significant classes of graphs induced by this kind of configuration. In particular, the dimension of the associated algebras and their centers are obtained. These results give a relationship between Brauer configuration algebras and graph energy theories with an open problem in the field of integer partitions proposed by Andrews in 1986. Such a problem asks for sets of integer numbers $S,T$ for which $P(S,n)=P(T,n+a)$, where $P(X,n)$ denote the number of integer partitions of n into parts within the set X with a being a fixed positive integer [10].

As a consequence of their investigations regarding Andrews’s problem, Cañadas et al. [11,12] introduced and enumerated a particular class of integer compositions (i.e., partitions for which the order of the parts matter) of type ${\mathcal{D}}_n$, for which the Andrews’s problem holds if $a=1$. For each n, compositions of type ${\mathcal{D}}_n$ constitute a partially ordered set whose number of two-point antichains is given by the integer sequence encoded in the OEIS (On-Line Encyclopedia of Integer Sequences) A344791 [13]. The following identity (2) gives the nth term ${\left(\mathrm{A}344791\right)}_n$ of this sequence:

$${\left(\mathrm{A}344791\right)}_n=\underset{i=1}{\sum ^n}\underset{j=0}{\sum ^{\lfloor \frac{i}{2}\rfloor }}{h}_{ij}(t_i-2t_j).$$

(2)

where $t_k$ denotes the kth triangular number, and

$$h_{ij}=\left\{\begin{array}{cc}n+1-i,\hfill & \mathrm{if}i=2j\mathrm{and}1\le j\le \lfloor \frac{n}{2}\rfloor ,\hfill \\ 0,\hfill & \mathrm{if}i=n\mathrm{and}j=0,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

This paper uses this sequence to estimate eigenvalues sums of matrices associated with polygons of some $\{0,1\}$-Brauer configurations.

It is worth noting that the relationships introduced in this paper between the theory of Brauer configuration algebras and the graph energy theory do not appear in the current literature devoted to these topics.

This paper is distributed as follows; in Section 2, we recall definitions and notation used throughout the document. In particular, we introduce the notion of trace norm of a $\{0,1\}$-Brauer configuration. In Section 3, we give our main results, we compute and estimate the trace norm and graph energy of some families of graphs defined by Brauer configuration algebras. Concluding remarks are given in Section 4. Examples of trace norm values associated with some Brauer configurations are given in Appendix A.

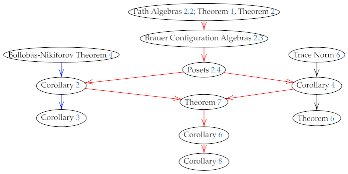
The following diagram (3) shows how the notions of Brauer configuration and trace norm are related to some of the main results presented in this paper.

(3)

2. Background and Related Work

In this section, we introduce some definitions and notations to be used throughout the paper. In particular, it is given a brief overview regarding the development of the research of graph energy theory, path algebras, and Brauer configuration algebras.

Henceforth, the symbol $A^{*}$ will denote the adjoint of a matrix A, and ${\parallel A\parallel }_F$ the Frobenius norm of a matrix A. Furthermore, $\mathbb{F}$ is a field, ${\mathbb{N}}^{+}$ is the set of positive integers, and $t_n$ denotes the nth triangular number.

2.1. Graph Energy

The notion of graph energy as the sum of the absolute values of an adjacency matrix was introduced in 1978 by Gutman based on a series of lectures held by them in Stift Rein, Austria [6]. As we explained in the introduction, he was motivated by earlier results regarding the Hückel orbital total $\pi$-electron energy. According to Gutman and Furtula [14], the results were proposed at that time in good hope that the mathematical community would recognize its significance. However, there was no interest in the subject despite Gutman’s efforts, perhaps due to the restrictions imposed on the studied graphs.

The interest in graph energy was renewed at the earliest 2000 when a plethora of results started appearing. Since then, more than one hundred variations of the initial notion have been introduced with applications in different sciences fields. In the same work, Gutman and Furtula claim that an average of two papers per week (more than one hundred in 2017) are written regarding the subject.

Some of the graph energy variations are:

• The Nikiforov energy of a matrix M, which is the sum of the singular values of a matrix.
• The Laplacian energy of a graph G of order n and size m defined as the sum of the absolute values of the eigenvalues of the matrix $L\left(G\right)-\frac{2m}{n}{I}_n$, where $I_n$ is the identity matrix of order n, and $L\left(G\right)$ is the Laplacian matrix associated with G whose entries $L{\left(G\right)}_{ij}$ are given by the following identities:

  $${\left(L\left(G\right)\right)}_{ij}=\left\{\begin{array}{cc}\mathrm{deg}\left(v_i\right)\hfill & \mathrm{if}i=j,\hfill \\ -1\hfill & \mathrm{if}i\ne j\mathrm{and}{v}_i\mathrm{is}\mathrm{adjacent}\mathrm{to}{v}_j,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  where $\mathrm{deg}\left(v\right)$ denotes the degree of a vertex v in G.
• The Randić energy, which is the sum of the absolute values of the Randić matrix $R\left(G\right)=\left(R{(G)}_{ij}\right)$ of a graph G, with

  $${\left(R\left(G\right)\right)}_{ij}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}i=j,\hfill \\ \frac{1}{\sqrt{\mathrm{deg}\left(v_i\right)\mathrm{deg}\left(v_j\right)}}\hfill & \mathrm{if}{v}_i\mathrm{is}\mathrm{adjacent}\mathrm{to}{v}_j,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Although the notion of graph energy was introduced only for theoretical purposes, currently, its applications embrace a broad class of sciences. The following Table 1 shows some examples of different works devoted to the applications of graph energy and its variations. The authors refer the reader to [14] for more examples of these types of applications.

Table 1. Works devoted to the applications of the graph energy theory. In the case of pattern recognition, the applications deal with military purposes.

Subject	Work
Chemistry	[15]
Biology	[16]
Crystallography	[17]
Epidemics	[18]
Pattern Recognition	[19]
Computer Vision	[20]
Satellite Communication	[21]
Spacecrafts Construction	[22]
Neural Networks	[23]

2.2. Path Algebras

This section recalls some facts regarding quivers, their associated path algebras, and corresponding module categories. It is worth noting that the quiver or pass graph technique is used in representation theory, and it is an important tool to solve many ring problems, as Belov-Kanel et al. report in [24].

A quiver $Q=(Q_0,Q_1,s,t)$ is a quadruple consisting of two sets $Q_0$ whose elements are called vertices and $Q_1$ whose elements are called arrows, s and t are maps $s,t:Q_1\to Q_0$ such that if $\alpha$ is an arrow, then $s\left(\alpha \right)$ is called the source of $\alpha$, whereas $t\left(\alpha \right)$ is called the target of $\alpha$ [25]. The adjacency matrix $M_Q$ and the spectral radius $\rho \left(Q\right)=\rho \left(M_Q\right)=\max \left|\lambda \right|$ (where $\lambda$ runs over all the eigenvalues of $M_{\overline{Q}}$) of a quiver Q are given by those defined by its underlying graph $\overline{Q}$.

Recall that the adjacency matrix $M_G$ associated with a graph G is defined by the following identities:

$${\left(M_G\right)}_{ij}=\left\{\begin{array}{cc}\mathrm{number}\mathrm{of}\mathrm{edges}\mathrm{between}i\mathrm{and}j,\hfill & \mathrm{if}i\ne j,\hfill \\ \mathrm{two}\mathrm{times}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{loops}\mathrm{at}i,\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

A path of length $l\ge 1$ with source a and target b is a sequence $(a\mid {\alpha }_1,{\alpha }_2,\dots ,{\alpha }_l\mid b)$ where $t\left({\alpha }_i\right)=s\left({\alpha }_{i+1}\right)$ for any $1\le i<l$. Vertices are paths of length 0 [25,26,27].

If Q is a quiver and $\mathbb{F}$ is an algebraically closed field, then the path algebra $\mathbb{F}Q$ of Q is the $\mathbb{F}$-algebra whose underlying $\mathbb{F}$-vector space has as basis the set of all paths of length $l\ge 0$ in Q, the natural graph concatenation is the product of two paths [25,26].

An $\mathbb{F}$-algebra $\Lambda$ is said to be basic if it has a complete set $\{e_1,e_2,\dots ,e_l\}$ of primitive orthogonal idempotents such that $e_{i}A\ncong e_{j}A$ for all $i\ne j$.

A relation for a quiver Q is a linear combination of paths of length $\ge 2$ with the same starting points and same endpoints, not all coefficients being zero [25,26].

Let Q be a finite and connected quiver. The two-sided ideal of the path algebra $\mathbb{F}Q$ generated by the arrows of Q is called the arrow ideal of $\mathbb{F}Q$ and is denoted by $R_Q$, $R_Q^l$ is the ideal of $\mathbb{F}Q$ generated as an $\mathbb{F}$-vector space, by the set of all paths of length $\ge l$. A two- sided ideal I of the path algebra $\mathbb{F}Q$ is said to be admissible if there exists $m\ge 2$ such that $R_Q^m\subseteq I\subseteq R_Q^2$.

If I is an admissible ideal of $\mathbb{F}Q$, the pair $(Q,I)$ is said to be a bound quiver. The quotient algebra $\mathbb{F}Q/I$ is said to be a bound quiver algebra.

Gabriel [28] proved that any basic algebra is isomorphic to a bound quiver algebra. He also showed the finiteness criterion for these algebras. Taking into account that one of the main problems in the theory of representation of algebras consists of giving a complete description of the indecomposable modules and irreducible morphisms of the category of finitely generated modules $\mathrm{mod}\Lambda$ of a given algebra $\Lambda$.

According to the number of indecomposable modules an algebra $\Lambda$ can be of finite, tame or wild representation type. We recall that if $\mathcal{C}$ is a category of finitely generated modules over an $\mathbb{F}$-algebra $\Lambda$ (in this case, $\mathbb{F}$ is an algebraically closed field). Then a one-parameter family in $\mathcal{C}$ is a set of modules of the form:

$$\overline{\mathcal{M}}=\{\mathcal{M}/(x-a)\mathcal{M}\mid a\in \mathbb{F}\}$$

(4)

where $\mathcal{M}$ is a $\Lambda -\mathbb{F}\left[x\right]$-bimodule, which is finitely generated and free over $\mathbb{F}\left[x\right]$ [29].

Category $\mathcal{C}$ is said to be of tame representation type or tame type, if $\mathcal{C}=\bigcup _n{\mathcal{C}}_n$, and for every n, the indecomposable modules form a one-parameter family with maybe finitely many exceptions equivalently in each dimension d, all but a finite number of indecomposable $\Lambda$-modules of dimension d belong to a finite number of one-parameter families. On the other hand, $\mathcal{C}$ is of wild representation type or wild type if it contains n-parameter families of indecomposable modules for arbitrarily large n [29].

It is worth noting that Drozd in 1977 and Crawley-Boevey in 1988 proved the following result known as the trichotomy theorem.

Theorem 1

([30,31], Corollary C). Let Λ be a finite-dimensional algebra over an algebraically closed field. Then Λ-mod has either tame type or wild type, and not both.

The following result proved by Smith establishes a relationship between the theory of representation of algebras and the spectra graph theory.

Theorem 2

([32]). Let G be a finite simple graph with the spectral radius (index) $\rho \left(G\right)$. Then $\rho \left(G\right)=2$ if and only if each connected component of G is one of the extended Dynkin diagram $\widetilde{{\mathbb{A}}_n}$, $\widetilde{{\mathbb{D}}_n}$, $\widetilde{{\mathbb{E}}_6}$, $\widetilde{{\mathbb{E}}_7}$, $\widetilde{{\mathbb{E}}_8}$. Moreover, $\rho \left(G\right)<2$ if and only if each connected component of G is one of Dynkin diagrams ${\mathbb{A}}_n$, ${\mathbb{D}}_n$, ${\mathbb{E}}_6$, ${\mathbb{E}}_7$, ${\mathbb{E}}_8$.

Remark 1.

Note that if Q is a connected quiver without oriented cycles, then Theorem 2 allows concluding that Q is of finite type (tame type) if and only if $\rho \left(Q\right)<2$ ($\rho \left(Q\right)=2$). Otherwise, Q is of wild type. A quiver Q has one of these three properties means that the corresponding path algebra $\mathbb{F}Q$ also does.

2.3. {0,1}-Brauer Configuration Algebras

In this section, we discuss some results regarding $\{0,1\}$-Brauer configuration algebras, we refer the reader to [1] for a more detailed study of general Brauer configuration algebras.

$\{0,1\}$-Brauer configuration algebras are bound quiver algebras induced by a Brauer configuration $\Gamma =\left({\Gamma }_0,{\Gamma }_1,\mu ,\mathcal{O}\right)$ with the following characteristics:

• ${\Gamma }_0=\{0,1\}$ is said to be the set of vertices.
• ${\Gamma }_1=\{U_1,U_2,\dots ,U_{n-1},U_n;n⩾1\}$ is a collection of multisets $U_i$ consisting of vertices called polygons.
• The word $w_i$ defined by the polygon $U_i$ has the form;

  $$w_i=w_{i,1}{w}_{i,2}\dots w_{i,{\delta }_i}.$$

  where $w_{i,j}\in \{0,1\}$, ${\alpha }_i=occ(0,U_i)$ is the number of times that the vertex 0 occurs in the polygon $U_i$, ${\delta }_i-{\alpha }_i=occ(1,U_i)$ is the number of times that the vertex 1 appears in the same polygon with ${\delta }_i=\left|U_i\right|⩾2$.
• $\mu$ is a map $\mu :{\Gamma }_0\to {\mathbb{N}}^{+}$, such that $\mu \left(0\right)=\mu \left(1\right)=1$. $\mu$ is said to be the multiplicity function associated with $\Gamma$.
• Successor sequences $S_0$ and $S_1$ associated with the vertices are defined by an orientation $\mathcal{O}$, which is an ordering on the polygons of the form:

  $$\begin{array}{cc}\hfill S_0:& \underset{{\alpha }_1-times}{\underbrace{U_1<\cdots <U_1}}<\underset{{\alpha }_2-times}{\underbrace{U_2<\cdots <U_2}}<\cdots <\underset{{\alpha }_{n-1}-times}{\underbrace{U_{n-1}<\cdots <U_{n-1}}}<\underset{{\alpha }_n-times}{\underbrace{U_n<\cdots <U_n}}\\ \hfill S_1:& \underset{({\delta }_1-{\alpha }_1)-times}{\underbrace{U_1<\cdots <U_1}}<\underset{({\delta }_2-{\alpha }_2)-times}{\underbrace{U_2<\cdots <U_2}}<\cdots <\underset{({\delta }_{n-1}-{\alpha }_{n-1})-times}{\underbrace{U_{n-1}<\cdots <U_{n-1}}}<\underset{({\delta }_n-{\alpha }_n)-times}{\underbrace{U_n<\cdots <U_n}}\end{array}$$
  Successor sequences is a way of recording how vertices appear in the polygons.

The construction of the quiver $Q_{\Gamma }$ (or simply Q, if no confusion arises) goes as follows:

• Add a circular relation $U_n<U_1$, to each successor sequence $S_0$ and $S_1$. $C^i=S_i\cup \{U_n<U_1\}$, $i\in \{0,1\}$ is said to be a special cycle associated with i.
• Define ${\Gamma }_1$ as the set of vertices $Q_0$ of Q.
• Each cover $U_i<U_j$ in a special cycle $C^i$ defines an arrow $U_i\to U_j\in Q_1$.

Note that there are different special cycles associated with a vertex $i\in \{0,1\}$ in a polygon $U_i$.

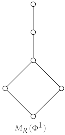
Figure 1 shows the Brauer quiver $Q_{\Gamma }$ induced by a $\{0,1\}$-Brauer configuration $\Gamma$.

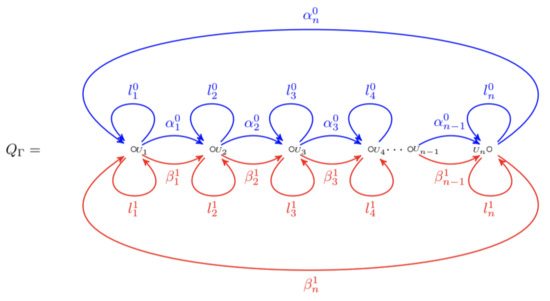
Figure 1. Brauer quiver induced by a $\{0,1\}$-Brauer configuration. Symbols $l_j^i$, $i\in \{0,1\}$, $j\in \{1,2,\dots ,n\}$ mean that the corresponding vertex $U_j$ has associated $l_j^i=occ(i,U_j)-1$ different loops.

The valency $val\left(i\right)$ of a vertex $i\in \{0,1\}$ is given by the identity:

$$val\left(i\right)=\underset{j=1}{\sum ^n}occ(i,U_j).$$

(5)

$val\left(i\right)$ is the number of arrows in the i-cycles. A vertex $i\in \{0,1\}$ is said to be truncated if $val\left(i\right)=1$, otherwise i is non-truncated. Vertices 0 and 1 are non-truncated in a $\{0,1\}$-Brauer configuration algebra.

The Brauer configuration algebra ${\Lambda }_{\Gamma }$ (or $\Lambda$) defined by the quiver Q is the path algebra $\mathbb{F}Q$ bounded by the admissible ideal $I_{\Gamma }$ (or I) generated by the following set of relations:

• If a polygon $U_k\in {\Gamma }_1$ contains vertices $i,j$ and $C^i,C^j$ are special cycles then $C^i-C^j\in I$.
• If a is the first arrow of a special cycle $C^i$ then $C^{i}a\in I$.
• ${\alpha }_i^0{\beta }_j^1$, ${\beta }_h^1{\alpha }_s^0$, for all possible values of $i,j,h,$ and s.
• ${\alpha }_i^0{\alpha }_{i+1}^0$${\beta }_i^1{\beta }_{i+1}^1$, for all possible values of i.
• ${\alpha }_i^0{l}_j^1$, ${\beta }_i^1{l}_j^0$, for all possible values of i and j.
• $l_i^0{l}_i^1$$l_j^0{\beta }_i^1$, $l_j^1{\alpha }_i^0$ for all possible values of i and j.
• ${(l_i^0)}^2$, ${(l_j^1)}^2$, for all possible values of i and j.

If there exists a word-transformation T such that $w_i=T\left(w_{i-1}\right)\left(R_i\right)$, for instance, if $w_i=w_{i-1}{R}_i$ with $R_i$ a suitable {0,1}-word, then the cumulative message$M(\Gamma$) of $\Gamma$ is defined in such a way that $M(\Gamma )=w_1{w}_2\dots w_n$ and the reduced message $M_R(\Gamma )$ is defined by the concatenation word:

$$M_R(\Gamma )=w_1{R}_2{R}_3\dots R_n$$

If $M_R(\Gamma )$ can be written as a $m\times n$ matrix, then $\rho \left(M_R(\Gamma )\right)$ denotes the spectral radius of the Brauer configuration $\Gamma$ and the trace norm of the Brauer configuration$\Gamma$ is defined as:

$$\left|\right|M_R(\Gamma ){\left|\right|}_{*}=\underset{k=1}{\sum ^{\min \{m,n\}}}{\sigma }_k\left(M_R(\Gamma )\right).$$

(6)

where ${\sigma }_1\left(M_R(\Gamma )\right)⩾{\sigma }_2\left(M_R(\Gamma )\right)⩾\cdots ⩾{\sigma }_n\left(M_R(\Gamma )\right)⩾0$ are the singular values of $M_R(\Gamma )$, i.e., the square roots of the eigenvalues of $M_R(\Gamma )M_R{(\Gamma )}^{*}$.

The following Proposition 1 and Theorem 3 prove that the dimension and the center of a Brauer configuration algebra can easily be computed from its Brauer configuration [1,33].

Proposition 1

([1], Proposition 3.13). Let Λ be a Brauer configuration algebra associated with the Brauer configuration Γ and let $\mathcal{C}=\{C_1,\dots ,C_t\}$ be a full set of equivalence class representatives of special cycles. Assume that for $i=1,\dots ,t$, $C_i$ is a special ${\alpha }_i$-cycle where ${\alpha }_i$ is a non-truncated vertex in Γ. Then

$${\dim }_{\mathbb{F}}\Lambda =2|Q_0|+\sum _{C_i\in \mathcal{C}}|C_i\left|\right(n_i|C_i|-1),$$

where $|Q_0|$ denotes the number of vertices of Q, $|C_i|$ denotes the number of arrows in the ${\alpha }_i$-cycle $C_i$ and $n_i=\mu \left({\alpha }_i\right)$.

Theorem 3

([33], Theorem 4.9). Let Γ be a reduced and connected Brauer configuration and let Q be its induced quiver and let Λ be the induced Brauer configuration algebra such that ${\mathrm{rad}}^2\Lambda \ne 0$ then the dimension of the center of Λ denoted ${\dim }_{\mathbb{F}}Z(\Lambda )$ is given by the formula:

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}Z(\Lambda )& =1+\sum _{\alpha \in {\Gamma }_0}\mu \left(\alpha \right)+|{\Gamma }_1|-|{\Gamma }_0|+\#\left(LoopsQ\right)-|{\mathcal{C}}_{\Gamma }|.\hfill \end{array}$$

where $|{\mathcal{C}}_{\Gamma }|=\{\alpha \in {\Gamma }_0\mid val\left(\alpha \right)=1,and\mu \left(\alpha \right)>1\}$.

In this case, $\mathrm{rad}M$ denotes the radical of a module M, $\mathrm{rad}M$ is the intersection of all the maximal submodules of M.

The following are properties of $\{0,1\}$-Brauer configuration algebras based on Proposition 1 and Theorem 3.

Corollary 1.

Let Λ be a Brauer configuration algebra induced by a {0,1}-Brauer configuration $\Gamma =\left({\Gamma }_0,{\Gamma }_1,\mu ,\mathcal{O}\right)$ with $ra{d}^2\Lambda \ne 0$. Then the following statements hold:

1.

Λ is reduced and connected.

2.

${dim}_{\mathbb{F}}\Lambda =2n+2t_{val\left(0\right)-1}+2t_{val\left(1\right)-1}$, where $t_j$ denotes the jth triangular number.

3.

${dim}_{\mathbb{F}}Z(\Lambda )=1+n+{\sum }_{i=0}^1{\sum }_{j=1}^n{l}_j^i$.

2.4. Posets

A partially ordered set (or poset) is an ordered pair $(\mathcal{P},\le )$ where $\mathcal{P}$ is a not empty set, and ≤ is a partial order over the elements of $\mathcal{P}$, i.e., ≤ is reflexive, antisymmetric, and transitive. Henceforth, if no confusion arises we will write $\mathcal{P}$ instead of $(\mathcal{P},\le )$ to denote a partially ordered set.

For each $x,y\in \mathcal{P}$, if $x\le y$ or $y\le x$, we say that x and y are comparable points, whereas if $x\nleqq y$ and $y\nleqq x$, we say that x and y are incomparable points (the subset $\{x,y\}$ is a two-point antichain), this situation is denoted by $x\Vert y$. An ordered set $\mathcal{C}$ is called a chain (or a totally ordered set or a linearly ordered set) if and only if for all $x,y\in \mathcal{C}$ we have $x\le y$ or $y\le x$ (i.e., x and y are comparable points).

A relation $x\le y$ in a poset $\mathcal{P}$ is said to be a covering, if for any $z\in \mathcal{P}$ such that $x\le z\le y$ it holds that $x=z$ or $y=z$ [34].

3. Applications

In this section, we give applications of $\{0,1\}$-Brauer configuration algebras in graph energy. We start by defining some suitable $\{0,1\}$- Brauer configuration algebras, dimensions of these algebras and corresponding centers are given as well. We also compute and estimate eigenvalues and trace norm of their reduced messages $M_R(\Gamma )$.

• For $n⩾2$ fixed, let us consider the {0,1}-Brauer configuration ${\Delta }^n=({\Delta }_0^n,{\Delta }_1^n,\mu ,\mathcal{O})$, such that:

  $$\begin{array}{cc}\hfill {\Delta }_0^n& =\{0,1\}.\hfill \\ \hfill {\Delta }_1^n& =\{D_1,D_2,\dots ,D_n\},\mathrm{for}1\le i\le n,\left|D_i\right|={(t_{i+2}-1)}^2.\hfill \\ \hfill \mu \left(0\right)& =\mu \left(1\right)=1.\hfill \end{array}$$

  (7)
  The orientation $\mathcal{O}$ is defined in such a way that in successor sequences associated with vertices 0 and 1, it holds that $D_i<D_{i+1}$, for $1⩽i⩽n$.
  Polygons $D_i$ can be seen as $(t_{i+2}-1)\times (t_{i+2}-1)$-matrices over ${\mathbb{Z}}_2$ or as $(t_{i+2}-1)\times 1$-matrices over the vector space $P_{t_{i+2}-2}$ of polynomials of degree $\le t_{i+2}-2$. Its construction goes as follows:

  (a)

  For any i, $1\le i\le n$, $D_i$ is a symmetric matrix,

  (b)

  $D_1=\left[\begin{array}{ccccc}1& 1& 0& 1& 1\\ 1& 1& 1& 0& 1\\ 0& 1& 1& 1& 1\\ 1& 0& 1& 1& 1\\ 1& 1& 1& 1& 1\end{array}\right]=\left[\begin{array}{c}{t}^4+t^3+t+1\\ t^4+t^3+t^2+1\\ t^3+t^2+t+1\\ t^4+t^2+t+1\\ t^4+t^3+t^2+t+1\end{array}\right]$,

  (c)

  

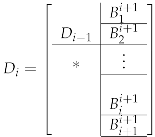
  (d)

  Blocks $B_j^{i+k}$, with $k>1$ are defined as follows:

  • Over ${\mathbb{Z}}_2$, $B_j^j\in M_{(j+1)\times (j+1)}$, $B_j^{j+s}\in M_{(j+1)\times (j+s+1)}$, $0\le s\le j+1$,
  • Over $P_{j+s+2}$, $B_j^{i+k}=\left[\begin{array}{c}{p}_1^{i+k}\left(t\right)\\ p_2^{i+k}\left(t\right)\\ ⋮\\ p_{j+1}^{i+k}\left(t\right)\end{array}\right]$,

    $$p_h^{i+k}\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{l=0}^{j-h+1}}{x}^l,\hfill & \mathrm{if}1\le h\le k,\hfill \\ {\displaystyle \sum _{l=0}^{j-h+1}}{x}^l+{\displaystyle \sum _{j=0}^{h-k-1}}{x}^{j+k-h+1},\hfill & \mathrm{if}h>k\mathrm{and}2\le k\le i+2,\hfill \\ p_h^m\left(t\right),\mathrm{if}m>i+2.\hfill \end{array}\right.$$

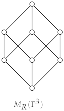
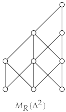
  Corollary 2.

  If ${\mathfrak{D}}^n=\mathbb{F}{Q}_{{\Delta }^n}^n/I_{{\Delta }^n}^n$ is the Brauer configuration algebra induced by the {0,1}-Brauer configuration ${\Delta }^n$ then the following statements hold:

  $$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}{\mathfrak{D}}^n& ={(e_n-d_n)}^2+{(e_n-1)}^2+(d_n-1),\hfill \\ \hfill {\dim }_{\mathbb{F}}Z\left({\mathfrak{D}}^n\right)& ={\left(t_{n+2}\right)}^2+n+3.\hfill \end{array}$$

  (8)

  where

  $$\begin{array}{cc}\hfill a_n& =\frac{1-{(-1)}^n-8n-4n^2+8n^3+2n^4}{32}={\left(\mathrm{A}344791\right)}_n,\hfill \\ \hfill b_{n+2}& =\underset{i=1}{\sum ^{n+2}}{t}_i^2-10,\hfill \\ \hfill c_{n+2}& =-\frac{(n+2)(n+3)(n+4)}{3}+8,\hfill \\ \hfill d_n& =b_{n+2}+c_{n+2}+n,n\ge 1,\hfill \\ \hfill e_n& =2\underset{i=1}{\sum ^n}{a}_{i+1}.\hfill \end{array}$$

  (9)

  Proof. 

  For $n>1$ fixed, consider the following set:

  $${\mathcal{P}}_n=\{x_{1,1},x_{1,2},x_{2,1},x_{2,2},x_{2,3},\dots ,x_{i,1},\dots ,x_{i,i+1},\dots ,x_{n,1},\dots ,x_{n,n+1}\}$$

  (10)

  ${\mathcal{P}}_n$ is endowed with a partial order ⊴, which defines the following coverings:

  $$\begin{array}{cc}\hfill x_{j,k}& ⊴x_{j,k+1},1\le j\le n,1\le k\le j,\hfill \\ \hfill x_{j,k}& ⊴x_{j+1,k+1},1\le j<n,1\le k\le j+1,\hfill \\ \hfill x_{r,k}& ⊴x_{r-1,k+1},1<r\le n,1\le k\le r.\hfill \end{array}$$

  (11)

  $({\mathcal{P}}_n,⊴)$ defines a matrix $M_n$ whose entries $m_{i,j}$ are given by the following identities:

  $$m_{i,j}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{x}_{i,r}⊴x_{j,s}\mathrm{or}{x}_{j,s}⊴x_{i,r}\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  Clearly $M_n$ is a $(t_{n+1}-1)\times (t_{n+1}-1)$ symmetric matrix with $M_n=D_{n-1}\in {\Delta }_1^n$, that is, $M_n$ is the matrix associated with the polygon $D_{n-1}\in {\Delta }_1^n$. Thus, $\frac{1}{2}\mathrm{occ}(0,D_n)$ equals the number of two-point antichains in $({\mathcal{P}}_n,⊴)$. Therefore, $\mathrm{occ}(0,D_n)$ is twice the nth term of the sequence A344791 (see (2), (9)), and $\mathrm{occ}(1,D_n)={(t_{n+1}-1)}^2-\mathrm{occ}(0,D_n)$. Since ${\dim }_{\mathbb{F}}{\mathfrak{D}}^n=2n+val\left(0\right)(val\left(0\right)-1)+val\left(1\right)(val\left(1\right)-1)$. The result holds. Since ${\mathrm{rad}}^2{\mathfrak{D}}^n\ne 0$, then ${\dim }_{\mathbb{F}}Z\left({\mathfrak{D}}^n\right)=1+n+\#\left(Loops{Q}_{{\Delta }^n}\right)$ with $\#\left(Loops{Q}_{{\Delta }^n}\right)={\left(t_{n+2}\right)}^2+2$. We are done. □
  Now we are interested in estimating the eigenvalues of $M_n$. Since the polygons $D_n\in {\Delta }_1^n$ can be seen as $(t_{n+1}-1)$ square symmetric matrices described in the previous proof as $D_{n-1}=M_n$. We will assume that for each n, the real eigenvalues of a matrix $M_n$ are indexed in the following decreasing order:

  $${\mu }_{max}\left(M_n\right)={\mu }_1\left(M_n\right)⩾{\mu }_2\left(M_n\right)⩾\cdots ⩾{\mu }_{t_{n+1}-1}\left(M_n\right)={\mu }_{min}\left(M_n\right).$$
  The next result, which derives two inequalities for the eigenvalues of Hermitian matrices, was proved by Bollobás and Nikiforov [35].
  Theorem 4

  ([35], Theorem 2). Suppose that $2⩽k⩽n$ and let $A=\left(a_{ij}\right)$ be a Hermitian matrix of size n. For every partition $\{1,2,\dots ,n\}=N_1\cup \cdots \cup N_k$ we have

  $${\mu }_1\left(A\right)+\cdots +{\mu }_k\left(A\right)⩾\sum _{r=1}^k\frac{1}{|N_r|}\sum _{i,j\in N_r}{a}_{ij}$$

  and

  $${\mu }_{k+1}\left(A\right)+\cdots +{\mu }_n\left(A\right)⩽\sum _{r=1}^k\frac{1}{|N_r|}\sum _{i,j\in N_r}{a}_{ij}-\frac{1}{n}\sum _{i,j\in 1,2,\dots ,n}{a}_{ij}.$$
  The following result on the eigenvalues of $M_n$ can be obtained by applying Theorem 4 to the matrix $M_n$ associated with the polygon $D_{n-1}\in {\Delta }_1^n$.
  Corollary 3.

  For $n>1$ and $k=n$. Let $M_n=\left(m_{ij}\right)$ be the matrix associated with the polygon $D_{n-1}\in {\Delta }_1^n$. For partition $\{1,2,\dots ,t_{n+1}-1\}=N_1\cup \cdots \cup N_n$ where $N_i=\left\{\frac{i(i+1)}{2},\dots ,\frac{i(i+3)}{2}\right\}$. We have

  $$\sum _{i=1}^n{\mu }_i\left(M_n\right)⩾t_{n+1}-1$$

  (12)

  and

  $$\sum _{i=n+1}^{t_{n+1}-1}{\mu }_i\left(M_n\right)\le \frac{2{\left(\mathrm{A}344791\right)}_n}{t_{n+1}-1}.\left(\mathrm{see}\left(2\right)\right).$$

  (13)
  Proof. 

  Since $N_i=\left\{\frac{i(i+1)}{2},\dots ,\frac{i(i+3)}{2}\right\}$, for each $i=\{1,2,\dots ,n\}$ then $|N_i|=i+1$, besides each set $N_i$ can be seen as a subset of the set ${\mathcal{P}}_n$ defined in (10) as follows:

  $$N_i=\{x_{i,1},\dots ,x_{i,i+1}\}.$$

  On the other hand, to compute ${\sum }_{i,j\in N_i}{a}_{ij}$, we will use the coverings defined in (11) and the fact that ${\mathcal{P}}_n$ is a partial order, so we obtain:

  $$\begin{array}{cc}\hfill \sum _{i,j\in N_i}{m}_{ij}& =2\sum _{j=1}^i(x_{i,j}⊴x_{i,j+1})+\sum _{j=1}^{i+1}(x_{i,j}⊴x_{i,j})+2\sum _{j=1}^{i-1}(x_{i,j}⊴x_{i,j+2})\hfill \\ \hfill & =2i+(i+1)+2t_{i-1}\hfill \\ \hfill & ={(i+1)}^2\hfill \end{array}$$

  Therefore:

  $$\begin{array}{cc}\hfill {\displaystyle \sum _{i=1}^n}\frac{1}{|N_i|}{\displaystyle \sum _{i,j\in N_i}}{m}_{ij}& =i+1and\hfill \\ \hfill \frac{1}{t_{n+1}-1}{\displaystyle \sum _{i,j\in \{1,2,\dots ,t_{n+1}-1\}}}{m}_{i,j}& =\frac{1}{t_{n+1}-1}{\parallel M_n\parallel }_F^2=\frac{1}{t_{n+1}-1}\left({(t_{n+1}-1)}^2-2{\left(A344791\right)}_n\right)\hfill \end{array}$$

  Hence, applying Theorem 4 we obtain (12) and (13). □
• For $n⩾1$ fixed, let ${\Gamma }^n=\{{\Gamma }_0^n,{\Gamma }_1^n,\mu ,\mathcal{O}\}$ be a {0,1}-Brauer configuration such that:

  $$\begin{array}{cc}\hfill {\Gamma }_0^n& =\{0,1\}.\hfill \\ \hfill {\Gamma }_1^n& =\{U_1,U_2,\dots ,U_n\},\mathrm{for}1\le i\le n,\left|U_i\right|=2^{2n}.\hfill \\ \hfill \mu \left(0\right)& =\mu \left(1\right)=1.\hfill \end{array}$$

  (14)
  The orientation $\mathcal{O}$ is defined in such a way that in successor sequences associated with vertices 0 and 1, it holds that $U_i<U_{i+1}$.
  Polygons $U_i$ can be seen as $2^n\times 2^n$-matrices over ${\mathbb{Z}}_2$ using the Kronecker product, denoted by ⊗, as follows:

  $$\begin{array}{cc}\hfill U_1& =\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]\hfill \\ \hfill U_2& =U_1\otimes U_1\hfill \\ \hfill & ⋮\hfill \\ \hfill U_i& =U_1\otimes U_{i-1}.\hfill \end{array}$$

  (15)
  Corollary 4.

  For $n⩾1$, if ${\mathfrak{G}}^n=\mathbb{F}{Q}_{{\Gamma }^n}^n/I_{{\Gamma }^n}^n$ is the Brauer configuration algebra induced by the {0,1}-Brauer configuration ${\Gamma }^n$ then the following statements hold:

  $$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}{\mathfrak{G}}^n& =2n+2r_n(r_n-1)+2s_n(s_n-1)\hfill \\ \hfill {\dim }_{\mathbb{F}}Z\left({\mathfrak{G}}^n\right)& =\left\{\begin{array}{ccc}6,\hfill & if& n=1\\ 1-n+r_n+s_n,\hfill & if& n⩾2.\end{array}\right.\hfill \end{array}$$

  (16)

  where $r_n$ and $s_n$ are the nth term of the OEIS sequences $\mathrm{A}016208$ and $\mathrm{A}029858$, respectively.
  Proof. 

  Given $n\in \mathbb{N}$, let ${\mathcal{P}}_n=\{A:A\subseteq \{1,2,\dots ,n\}\}$. For $x,y\in {\mathcal{P}}_n$, define $x<y$ if $x\subseteq y$. In this case the poset $({\mathcal{P}}_n,\subseteq )$ consists of all subsets of $\{1,2,\dots ,n\}$ ordered by inclusion.

  We associate to each finite poset ${\mathcal{P}}_n$ of size n the following $2^n\times 2^n$-matrix:

  $${\left[M_{{\mathcal{P}}_n}\right]}_{ij}=\left\{\begin{array}{ccc}1,\hfill & if& i,j \mathrm{are} \mathrm{comparable}\\ 0,\hfill & if& i,j \mathrm{are} \mathrm{incomparable}\end{array}\right.$$

  Under appropriate labeling of poset points ${\mathcal{P}}_n$, the matrix $M_{{\mathcal{P}}_n}$ can be viewed using the Kronecker product as follows:

  $$\begin{array}{cc}\hfill M_{{\mathcal{P}}_1}& =\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]\hfill \\ \hfill M_{{\mathcal{P}}_2}& =\left[\begin{array}{cc}{M}_{{\mathcal{P}}_1}& 0\\ M_{{\mathcal{P}}_1}& M_{{\mathcal{P}}_1}\end{array}\right]=M_{{\mathcal{P}}_1}\otimes M_{{\mathcal{P}}_1}\hfill \\ \hfill M_{{\mathcal{P}}_3}& =\left[\begin{array}{cc}{M}_{{\mathcal{P}}_2}& 0\\ M_{{\mathcal{P}}_2}& M_{{\mathcal{P}}_2}\end{array}\right]=M_{{\mathcal{P}}_1}\otimes M_{{\mathcal{P}}_2}\hfill \\ \hfill & ⋮\hfill \\ \hfill M_{{\mathcal{P}}_n}& =\left[\begin{array}{cc}{M}_{{\mathcal{P}}_{n-1}}& 0\\ M_{{\mathcal{P}}_{n-1}}& M_{{\mathcal{P}}_{n-1}}\end{array}\right]=M_{{\mathcal{P}}_1}\otimes M_{{\mathcal{P}}_{n-1}}\hfill \end{array}$$

  matrices $M_{{\mathcal{P}}_n}$ can be seen as pavements, cells with 1’s are colored black and those with 0’s are colored white. Figure 2 shows examples of these types of matrices.

  

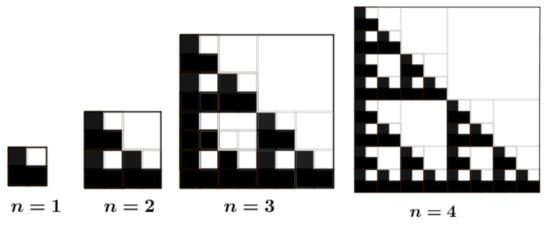  Figure 2. Matrices $M_{{\mathcal{P}}_n}$ for $n=1,2,3$ and 4.

  $M_{{\mathcal{P}}_n}$ is the matrix associated with the polygon $U_n\in {\Gamma }_1^n$, thus $\mathrm{occ}(0,U_n)$ can be computed in the following fashion:

  $$\begin{array}{cc}\hfill \mathrm{occ}(0,U_1)& =1\hfill \\ \hfill \mathrm{occ}(0,U_n)& =3\left(\mathrm{occ}(0,U_{n-1})\right)+2^{2n-2}\hfill \end{array}$$

  (17)

  Therefore $\mathrm{occ}(0,U_n)={\sum }_{k=1}^n{3}^{n-k}{2}^{2(k-1)}$ and $\mathrm{occ}(1,U_n)=3^n$ thus the result holds. □
  Now we are interested in computing the trace norm of the {0,1}-Brauer configuration ${\Gamma }^n$. For this, we recall the following theorem about the singular values of the Kronecker product:
  Theorem 5

  ([36], Theorem 4.2.15). Let $A\in M_{m,n}$ and $B\in M_{p,q}$ have singular value decompositions $A=V_1{\Sigma }_1{W}_1^{*}$ and $B=V_2{\Sigma }_2{W}_2^{*}$ and let $rankA=r_1$ and $rankB=r_2$. Then $A\otimes B=(V_1\otimes V_2)({\Sigma }_1\otimes {\Sigma }_2){(W_1\otimes W_2)}^{*}$. The nonzero singular values of $A\otimes B$ are the $r_1{r}_2$ positive numbers $\{{\sigma }_i\left(A\right){\sigma }_j\left(B\right):1⩽i⩽r_1,1⩽j⩽r_2\}$ (including multiplicities).
  The following Lemma 1 is helpful to prove Theorem 6.
  Lemma 1.

  Let $A\in M_n\left(\mathbb{C}\right)$ be a given matrix. If $B=\left[\begin{array}{cc}A& 0\\ A& A\end{array}\right]\in M_{2n}\left(\mathbb{C}\right)$ then the singular values of B are $\varphi {\sigma }_i\left(A\right)$ and ${\varphi }^{-1}{\sigma }_i\left(A\right)$ for $i=1,\dots ,n$, where $\varphi ={\displaystyle \frac{1+\sqrt{5}}{2}}$ is the golden ratio.
  Proof. 

  Note that $B=\left[\begin{array}{cc}A& 0\\ A& A\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]\otimes A$. The singular values for $\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$ are $\varphi$ and ${\varphi }^{-1}$, then by Theorem 5 the result holds. □
  Theorem 6.

  For each $n⩾1$, if $M_R\left({\Gamma }^n\right)=M_{{\mathcal{P}}_n}$ is the matrix associated with the polygon $U_n\in {\Gamma }_1^n$ then

  $$\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}=5^{n/2}$$

  (18)
  Proof. 

  By induction on n. For $n=1$, $\parallel M_{{\mathcal{P}}_1}{\parallel }_{*}=\varphi +{\varphi }^{-1}=\sqrt{5}$. Let us suppose that $\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}={(2\varphi -1)}^n=5^{n/2}$ and let us see that the result is fulfilled for $n+1$, i.e.,

  $$\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}={(2\varphi -1)}^{n+1}=5^{\frac{n+1}{2}}$$

  Since $M_{{\mathcal{P}}_{n+1}}=M_{{\mathcal{P}}_1}\otimes M_{{\mathcal{P}}_n}$, then for the Lemma 1 the singular values of $M_{{\mathcal{P}}_{n+1}}$ are

  $$\varphi {\sigma }_i\left(M_{{\mathcal{P}}_n}\right) and{\varphi }^{-1}{\sigma }_i\left(M_{{\mathcal{P}}_n}\right)$$

  for $i=1,\dots ,2^n$. Thus,

  $$\begin{array}{cc}\hfill \parallel M_{{\mathcal{P}}_{n+1}}{\parallel }_{*}& =\sum _{i=1}^{2^{n+1}}{\sigma }_i\left(M_{{\mathcal{P}}_{n+1}}\right)\hfill \\ \hfill & =\sum _{i=1}^{2^n}\varphi {\sigma }_i\left(M_{{\mathcal{P}}_n}\right)+\sum _{i=1}^{2^n}{\varphi }^{-1}{\sigma }_i\left(M_{{\mathcal{P}}_n}\right)\hfill \\ \hfill & =\varphi \parallel M_{{\mathcal{P}}_n}{\parallel }_{*}+{\varphi }^{-1}{\parallel M_{{\mathcal{P}}_n}\parallel }_{*}\hfill \\ \hfill & =\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}\left(\varphi +{\varphi }^{-1}\right)={\parallel M_{{\mathcal{P}}_n}\parallel }_{*}(2\varphi -1)\hfill \\ \hfill & ={\left(2\varphi -1\right)}^{n+1}=5^{\frac{n+1}{2}}\hfill \end{array}$$

  □
  Corollary 5.

  $$\sum _{n=2}^{\infty }{\displaystyle \frac{1}{\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}}}=\frac{1}{2(3-\varphi )}$$
  Proof. 

  By Theorem 6, we have:

  $$\sum _{n=2}^{\infty }{\displaystyle \frac{1}{\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}}}=\sum _{n=2}^{\infty }{\displaystyle \frac{1}{{(2\varphi -1)}^n}}$$

  which is a convergent geometric series with $r=\frac{1}{(2\varphi -1)}<1$ and $a=\frac{1}{{(2\varphi -1)}^2}$, therefore:

  $$\begin{array}{cc}\hfill \sum _{n=2}^{\infty }{\displaystyle \frac{1}{\parallel M_{{\mathcal{P}}_n}{\parallel }_{*}}}& ={\displaystyle \frac{{\displaystyle \frac{1}{{(2\varphi -1)}^2}}}{1-{\displaystyle \frac{1}{2\varphi -1}}}}=\frac{1}{2(3-\varphi )}\hfill \end{array}$$

  □
• For $n⩾1$ fixed, let ${\mathsf{\Phi }}^n=\{{\mathsf{\Phi }}_0^n,{\mathsf{\Phi }}_1^n,\mu ,\mathcal{O}\}$ be a {0,1}-Brauer configuration such that:

  $$\begin{array}{cc}\hfill {\Phi }_0^n& =\{0,1\}.\hfill \\ \hfill {\Phi }_1^n& =\{U_1,U_2,\dots ,U_n\},\mathrm{for}1\le i\le n,\left|U_i\right|={(i+5)}^2.\hfill \\ \hfill \mu \left(0\right)& =\mu \left(1\right)=1.\hfill \end{array}$$

  (19)
  For $i\ge 1$, the word $w_i$ associated with the polygon $U_i$ has the form $w_i=w_{i,1}{w}_{i,2}\dots w_{i,{\delta }_i}$, $w_{i,j}\in \{0,1\}$, $occ(0,U_i)=(i+5)(i+3)$, $occ(1,U_i)=2(i+5)$.
  The orientation $\mathcal{O}$ is defined in such a way that for successor sequences associated with vertices 0 and 1, it holds that $U_i<U_{i+1}$.
  Polygons $U_i$ can be seen as $(i+5)\times (i+5)$-matrices over ${\mathbb{Z}}_2$. Each row $R_j$ is defined by coefficients of a polynomial $P_j^i\left(t\right)$ with the form $P_j^i\left(t\right)=u_{j,1}^i+u_{j,2}^{i}t+\cdots +u_{j,i+4}^i{t}^{i+4}$, $u_{j,k}^i\in \{0,1\}$.

  $$\begin{array}{cc}\hfill U_1& =\left[\begin{array}{cccccc}0& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 0& 1& 1& 0& 1& 0\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 0& 1& 0\end{array}\right]\hfill \\ \hfill u_{j,k}^i& =u_{j,k}^{i-1},1\le j,k\le i+4,\hfill \\ \hfill u_{j,i+5}^i& =0,1\le j\le i+3,\hfill \\ \hfill u_{i+4,i+5}^i& =1,\hfill \\ \hfill u_{i+5,i+4}^i& =1,\hfill \\ \hfill u_{i+5,i+5}^i& =0.\hfill \end{array}$$

  (20)

Theorem 7.

For $n⩾1$, if ${\mathfrak{F}}^n=\mathbb{F}{Q}_{{\Phi }^n}^n/I_{{\Phi }^n}^n$ is the Brauer configuration algebra induced by the {0,1}-Brauer configuration ${\Phi }^n$, ${\alpha }_n=2(t_{n+5}-6)$, and ${\beta }_n={\epsilon }_{n+5}-{\epsilon }_5$, with ${\epsilon }_i=\frac{i(i+1)(2i+6)}{6}$ for $i\ge 1$ then the following statements hold:

1.

${\dim }_{\mathbb{F}}{\mathfrak{F}}^n=2n+2t_{{\alpha }_n-1}+2t_{{\beta }_n-1}$,

2.

${\dim }_{\mathbb{F}}Z\left({\mathfrak{F}}^n\right)=1+n+{\epsilon }_{n+4}-2n$,

3.

$\underset{n\to \infty }{\mathrm{Lim}}\rho \left(M_R\left({\Phi }^n\right)\right)=\sqrt{2+2\sqrt{2}}$.

Proof. 

The Formulas (1) and (2). for the dimension of the algebra ${\mathfrak{F}}^n$ and its center $Z\left({\mathfrak{F}}^n\right)$ are consequences of the definition of a Brauer configuration ${\Phi }^n$ and Corollary 1.

Let us prove identity 3. Firstly, we note that the characteristic polynomials $P_n\left(\lambda \right)$ associated with matrices $U_n$ can be obtained recursively. They obey the following general rules according to the size of the corresponding matrices.

$$\begin{array}{cc}\hfill P_3\left(\lambda \right)& ={\lambda }^3-2\lambda ,\hfill \\ \hfill P_4\left(\lambda \right)& ={\lambda }^4-4{\lambda }^2,\hfill \\ \hfill P_n\left(\lambda \right)& =\underset{j=1}{\sum ^n}{a}_j^n{\lambda }^j,\mathrm{if}n\ge 5,\hfill \\ \hfill a_n^n& =1,a_{n-1}^n=0,a_1^n={(-1)}^{n+1}2,\hfill \\ \hfill a_s^n& =a_{s-1}^{n-1}-a_s^{n-2},\mathrm{for}\mathrm{the}\mathrm{remaining}\mathrm{vertices}.\hfill \end{array}$$

$P_3\left(\lambda \right),P_4\left(\lambda \right)$ and $P_5\left(\lambda \right)$ are characteristic polynomials of the following matrices $T_3,T_4$, and $T_5$, respectively:

$T_3=\left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 0\\ 1& 0& 0\end{array}\right],T_4=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 0& 1\\ 1& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right],T_5=\left[\begin{array}{ccccc}0& 1& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0\\ 0& 1& 1& 0& 1\\ 0& 0& 0& 1& 0\end{array}\right].$

For any $k\ge 6$, $P_k\left(\lambda \right)$ is the characteristic polynomial of $U_{k-5}\in {\Phi }^n$.

We note that for $k\ge 5$, $|\sqrt{2+2\sqrt{2}}-\rho \left(M_R\left({\mathsf{\Phi }}^{(2^k-1)}\right)\right)|\le \frac{1}{{10}^{{\delta }_k}}$, where

$${\delta }_k=\left\{\begin{array}{cc}\lceil s_k\sqrt{2}Ln(2^k-1)\rceil ,\hfill & \mathrm{if}k\mathrm{is}\mathrm{odd},\hfill \\ \lfloor s_k\sqrt{2}Ln(2^k-1)\rfloor ,\hfill & \mathrm{if}k\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

$$s_k=\left\{\begin{array}{cc}k-4,\hfill & \mathrm{if}5\le k\le 7,\hfill \\ {62}^{k-8},\hfill & \mathrm{if}k\ge 8.\hfill \end{array}\right.$$

Then $\underset{k\to \infty }{\mathrm{Lim}}|\sqrt{2+2\sqrt{2}}-\rho (M_R({\Phi }^{(2^k-1)}))|=0$. Thus, $\rho (M_R({\Phi }^{(2^k-1)}))$ is a Cauchy subsequence of the sequence $\rho (M_R\left({\Phi }^n\right)$, $n\ge 5$ converging to $\sqrt{2+2\sqrt{2}}$. □

Corollary 6.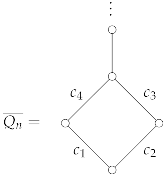

For any $n\ge 5$, an n-vertex quiver $Q_n$ with underlying graph $\overline{Q_n}$ of the form:

is of wild type.

Proof. 

Since $\rho \left(\overline{Q_5}\right)=\frac{\sqrt{\sqrt{17}+5}}{2}$, then the result holds as a consequence of Theorem 2, Remark 1, and Theorem 7. □

The following results [37] regarding some relationship between graph operations and energy graph allow finding upper and lower bounds for $\parallel M_R\left({\Phi }^n\right){\parallel }_{*}$.

Theorem 8

(Theorema 4.18 [37]). Let G, H, and $G\circ H$ be graphs as specified above. Then

$${\parallel G\circ H\parallel }_{*}⩽{\parallel G\parallel }_{*}+{\parallel H\parallel }_{*}$$

Equality is attained if and only if either u is an isolated vertex of G or v is an isolated vertex of H or both.

Corollary 7

(Corollary 4.6 [37]). If $\left\{e\right\}$ is a cut edge of a simple graph G, then ${\parallel G-\left\{e\right\}\parallel }_{*}<{\parallel G\parallel }_{*}$.

As a consequence of these results, we obtain the following Corollary 8.

Corollary 8.

For $n⩾6$.

$$2\sqrt{n-1}<{\parallel M_R\left({\Phi }^{n-5}\right)\parallel }_{*}<2+\left\{\begin{array}{ccc}2csc\left(\frac{\pi }{2(n-2)}\right),\hfill & if& n-3\equiv 0\left(mod2\right),\\ \\ 2cot\left(\frac{\pi }{2(n-2)}\right),\hfill & if& n-3\equiv 1\left(mod2\right).\end{array}\right.$$

(21)

Proof. 

The inequality at right hand holds as a consequence of Theorem 8 taking into account that $\overline{Q_n}$ is the coalescence [37] between the cycle ${\mathbb{C}}_4$ and ${\mathbb{A}}_{n-3}$, and that:

$\parallel {\mathbb{C}}_4{\parallel }_{*}=4$ and $||{\mathbb{A}}_{n-3}{||}_{*}=\left\{\begin{array}{ccc}2csc\left(\frac{\pi }{2(n-2)}\right)-2,\hfill & if& n-3\equiv 0\left(mod2\right),\\ \\ 2cot\left(\frac{\pi }{2(n-2)}\right)-2,\hfill & if& n-3\equiv 1\left(mod2\right).\end{array}\right.$

To prove the left hand inequality, we remove edges $c_1$ and $c_2$ in $\overline{Q_n}$, obtaining in this fashion a connected tree. Since among all trees of order n, $S_n$ attains the minimal energy. The result holds as a consequence of Corollary 7. □

4. Concluding Remarks

$\{0,1\}$-Brauer configuration algebras give rise to the so-called trace norm of a Brauer configuration. Such Brauer configurations are a source of a great variety of graphs and posets via its reduced message. The structure of the adjacency matrices associated with these graphs allows estimating the corresponding trace norm or graph energy values. In line with the main problem in the graph energy theory, we give explicit formulas for the trace norm of some $(0,1)$-matrices associated with these families of graphs and posets. On the other hand, bounds for the energy of some families of graphs can be obtained via graph coalescence. It is worth pointing out that some of these graphs underlying quivers of wild type.

An interesting task for the future will be to find the trace norms of a wide variety of Brauer configuration algebras.