Abstract
Social robots keep proliferating. A critical challenge remains their sensible interaction with humans, especially in real world applications. Hence, computing with real world semantics is instrumental. Recently, the Lattice Computing (LC) paradigm has been proposed with a capacity to compute with semantics represented by partial order in a mathematical lattice data domain. In the aforementioned context, this work proposes a parametric LC classifier, namely a Granule-based-Classifier (GbC), applicable in a mathematical lattice (T,⊑) of tree data structures, each of which represents a human face. A tree data structure here emerges from 68 facial landmarks (points) computed in a data preprocessing step by the OpenFace software. The proposed (tree) representation retains human anonymity during data processing. Extensive computational experiments regarding three different pattern recognition problems, namely (1) head orientation, (2) facial expressions, and (3) human face recognition, demonstrate GbC capacities, including good classification results, and a common human face representation in different pattern recognition problems, as well as data induced granular rules in (T,⊑) that allow for (a) explainable decision-making, (b) tunable generalization enabled also by formal logic/reasoning techniques, and (c) an inherent capacity for modular data fusion extensions. The potential of the proposed techniques is discussed.
1. Introduction
Advances in enabling technologies, both software and hardware, have encouraged a widespread proliferation of social robots in several application domains, including education, therapy, services, entertainment, and arts [1,2,3,4,5]. In all applications, the capacity of social robots to sensibly interact with humans is critical [6,7,8].
In general, the interaction of a social robot with a human is driven by a mathematical model implemented in software. The interest here is in “intelligence models” in the following sense. First, a “model” here is defined as “a mathematical description of a world aspect”; second, “intelligence” here is defined as “a capacity for both learning and generalization, including non-numerical data as well as explanations as described next.
Conventional models typically regard the (physical) world; therefore, they are developed in the Euclidean space RN, based on real numbers stemming from sensor measurements [9]. However, when humans are involved, in addition to sensory data during their interaction with one another, humans also employ non-numerical data, such as spoken words/language, symbols, concepts, rules, moral principles, and others. Therefore, for a seamless interaction with humans, social robots are required to also cope with non-numerical data. Another requirement, in the European Union, is the observance of the General Data Protection Regulation (GDPR); hence, anonymous data are preferable during data processing [10]. Due to the personalized character of social robot-human interaction, it is preferable to induce a model from personal data by machine-learning techniques, rather than develop a model based on “first principles”.
Learning and generalization here are considered as necessary, but not sufficient, conditions for intelligence. For instance, conventional steepest-descent methods pursue learning by optimizing an energy-type “objective function”; moreover, they pursue generalization by interpolation and/or extrapolation. However, conventional models typically operate as black-boxes that carry out number-crunching and fall short of providing with common sense explanations. In addition, the latter models cannot manipulate non-numerical data (e.g., symbols or data structures). In the aforementioned context, the long-term interest here is in a simple abductive classifier model toward inducing world representations that are not merely descriptive, but also explanatory [11].
A mathematical approach for modeling has been proposed recently, based on the fact that popular data domains are partially (lattice) ordered; for instance, the Cartesian product RN, hyperboxes in RN, Boolean algebras, measure spaces, decision trees, and distribution functions are partially (lattice) ordered. In conclusion, the Lattice Computing (LC) information processing paradigm has been proposed as “an evolving collection of tools and methodologies that process lattice ordered data per se including logic values, numbers, sets, symbols, graphs, etc.” [9,12,13,14,15,16,17]. Different authors have recently correlated the emergence of lattice theory with the proliferation of computers [18]. In the context of LC, decision-making instruments have been introduced such as metric distances, as well as fuzzy order functions; moreover, effective LC models have been proposed [12,19,20,21].
Since information granules are partially ordered [20], Granular Computing [22] can be subsumed in Lattice Computing. Note that mathematical Lattice Theory or, equivalently, Order Theory, is the common instrument for analysis regarding LC, fuzzy systems [23], formal concept analysis and rough sets approximations [24], and other.
Previous LC classifiers have engaged non-numerical data including, lattice-ordered gender symbols, and events in a probability space, as well as structured data, namely graphs. However, the latter (graphs) have been used as instruments for ad hoc feature extraction of vectors [25]. In other words, a graph in previous LC works has been used only once, for data preprocessing. Similarly, different authors have recently employed an interesting hierarchic and/or a linguistic descriptor approach for extracting vectors of features regarding face recognition problems [26,27].
This work considers three social robot-human interaction related problems regarding visual pattern recognition of (1) head orientation, in order to quantify the engagement/attention of a human, (2) facial expressions, in order to adjust behavior according to a human’s emotional state, and (3) human faces, in order to address a human personally. In fact, this work focuses on the GbC classifier itself, rather than on human-robot interaction applications. The latter application is a topic for future work.
The motivation of this work is the solution of specific research problems, as explained subsequently. A social robot-human interaction calls for decision-making based on multimodal data semantics. However, most of the state-of-the-art models are developed strictly in the Euclidean space RN, thus ignoring other types of data per se, such as structured data. On the other hand, LC based models have the capacity to rigorously fuse multimodal data per se, based on the fact that, first, popular data types are lattice-ordered and, second, the Cartesian product of mathematical lattices is also a lattice; in particular, this preliminary work considers trees data structures for classification. Furthermore, state-of-the-art models, such as deep learning neural networks, typically require huge training data sets, whereas, the proposed techniques here can be used with orders of magnitude fewer training data. In addition, state-of-the-art methods such as deep learning often cannot explain their answers, whereas the proposed method can explain its answers by granular rules induced from tree data structure. In a similar vein, note that image recognition systems have been reported lately in the context of fuzzy logic that can explain their decisions using type-2 fuzzy sets, fuzzy relations, and fuzzy IF-THEN rules [28]. Nevertheless, state-of-the-art methods typically call for a different feature extraction per classification problem, whereas the proposed method here engages the same features in three different classification problems. Finally, state-of-the-art methods often do not typically retain the anonymity of the human subjects, especially when they process images, whereas the proposed method extracts facial landmark features in a data preprocessing step and thereafter, i.e., during data processing such as training, it retains the anonymity of the human subjects.
The proposed classification techniques apply fairly “expensive” real world data. Therefore, they differ from alternative machine (deep) learning techniques, such as generative adversarial networks (GANs) [29], which massively generate new data with the same statistics as the training set. The proposed techniques also differ from probabilistic graphical models, such as the variational autoencoders (VAEs) [30], in that the latter use graphs to optimally estimate probability distributions of vector data, whereas GbC here processes graph (tree) data per se.
The novelties of this work include, first, a unifying, anonymous representation of a human face for face recognition; second, the introduction of the Granule-based-Classifier (GbC) parametric model that processes trees data structures; third, the induction of granular rules, involving tree data structures, toward an explainable artificial intelligence (AI); and fourth, the far-reaching potential of pursuing creativeness by machines based on a lattice order isomorphism.
This work is organized as follows: Section 2 outlines the mathematical background. Section 3 presents computational considerations. Section 4 describes the Granule-based-Classifier (GbC). Section 5 demonstrates computational experiments and results. Finally, Section 6 discusses comparatively the reported results; furthermore, it describes potential future work extensions.
2. Mathematical Background
Useful mathematical lattice theory definitions and instruments have been presented elsewhere [23,31,32]. This section customizes the aforementioned instruments to a specific lattice, as explained in the following.
Consider a basic tree data structure, including a specific number L + 1 of levels, as well as a specific number Ni of nodes per level, where i∈{0, …, L}; moreover, let each parent-node have a specific number of children-nodes. For instance, for the tree in Figure 1a, it is L = 3, N0 = 1, N1 = 2, N2 = 4, and N3 = 8; the root node n0 in Figure 1a has 2 children-nodes; node n1,1 has 1 child-node; node n1,2 has 3 children-nodes, etc. Each node ni,j is identified by two indices, namely a level number i and an index number j∈{1, …, Ni}; alternatively, a (tree) node can be identified by a single cardinal integer number k∈{1, …, N}, where N = N0 + N1 + … + NL. A basic tree data structure gives rise to a set T of trees as described next.
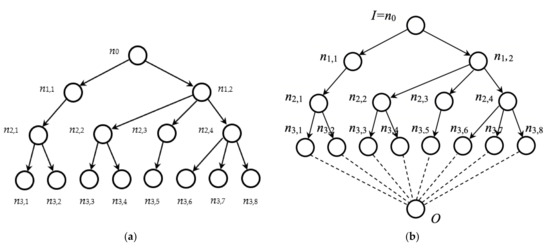
Figure 1.
(a) A tree data structure example. (b) A lattice results in from the tree above by inserting an additional level including the least lattice element O. The tree root corresponds to the greatest lattice element I.
Let each tree node nj be associated with a constituent lattice (Lj,⊑), j∈{0, …, N}. A specific tree instance emerges by attaching a specific lattice (Lj,⊑) element xj to node nj, j∈{0, …, N}. The interest here is in the set T of all tree instances—Note that all the trees in T have identical structure, and differ only in the lattice elements attached to their nodes.
Consider the Cartesian product lattice (P,⊑) = (L1 × … × LN,⊑), where, given that Px,Py∈P with Px = (x1, …, xN) and Py = (y1, …, yN), the corresponding lattice meet and join are defined as Px⊓Py = (x1, …, xN) ⊓ (y1, …, yN) = (x1⊓y1, …, xN⊓yN), and Px⊔Py = (x1, …, xN) ⊔ (y1, …, yN) = (x1⊔y1, …, xN⊔yN), respectively; moreover, (x1, …, xN) ⊑ (y1, …, yN) ⟺ x1⊑y1, …, xN⊑yN. Furthermore, consider the lattice (T,⊑) of trees defined as (order-)isomorphic with lattice (P,⊑). We remark that, on the one hand, the set T is convenient for interpretations, whereas, on the other hand, the set P lends itself to calculations. Next, a positive valuation function is defined constructively in lattice (T,⊑).
Consider a basic tree structure, e.g., the one in Figure 1a, enhanced to a complete lattice by inserting a single node O, namely the least element, at an additional level at the bottom of the lattice’s Hasse diagram, as shown in Figure 1b. The corresponding greatest element I is the tree root, i.e., I = n0.
Let vj: Lj→R, j∈{1, …, M} be a positive valuation function defined on every constituent lattice (Lj,⊑), j∈{1, …, M}. Recall that (1) a positive valuation function in lattice (L1 × … × LM,⊑) which may be defined by v = v1 + … + vM, and (2) a positive valuation function in lattice (Lj,⊑), j∈{1, …, M} which may also be defined by λjvj (.), where λj > 0 is a real number multiplier.
Given a basic tree structure, a positive valuation function V: T→R can be defined constructively (bottom up), as explained subsequently. Let np be a parent-node with children-nodes nc, c∈{1, …, C}. Let vp and vc, c∈{1, …, C} be positive valuation functions defined locally on the tree nodes, respectively. If np is a tree leaf node, at level L, then V (.) is defined as V = vp—For the least element O, it is defined as V (O) = 0; otherwise, V (.) is defined as vp + kp (v1 + … + vC) in the Cartesian product lattice (L = Lp × L1 × … × LC,⊑), where kp > 0. In conclusion, the positive valuation function on the greatest element I is defined as the positive valuation function of the whole tree. A concrete example is shown in Section 3.
We remark that, instead of attaching a single lattice element to a basic tree node, a lattice interval may be attached. In the latter case, a forest or, equivalently, grove of individual trees instances is defined in T.
The above mathematical instruments are customized further, as detailed in the following section.
3. Practical Computational Considerations
This section introduces, first, a structured representation of a human face and, second, a positive valuation function in the corresponding mathematical lattice.
All constituent lattices, considered below in a basic tree data structure, emerge from the chain of real numbers (R,≤), where “≤” is the conventional inequality relation between real numbers. A positive valuation function v: R→R in (R,≤) is a strictly increasing real function; moreover, a dual isomorphic function θ: (R,≤)→(R,≥) in (R,≤) is a strictly decreasing real function. In particular, the constituent lattice of interest here is the sublattice of conventional intervals of the Cartesian product lattice (R×R,≥×≤).
3.1. Structured Human Face Representation
The human face conveys a lot of potentially useful information. For feature extraction, in a data preprocessing step, established software was used, namely OpenFace library [33], which receives a 2-dimensional image, i.e., a camera frame as an input and outputs the 2-dimensional coordinates of 68 facial landmarks (points) on the contours of the brows, eyes, nose, mouth, and jaw, as shown in Figure 2a.
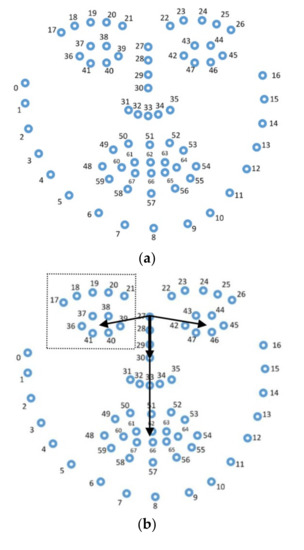
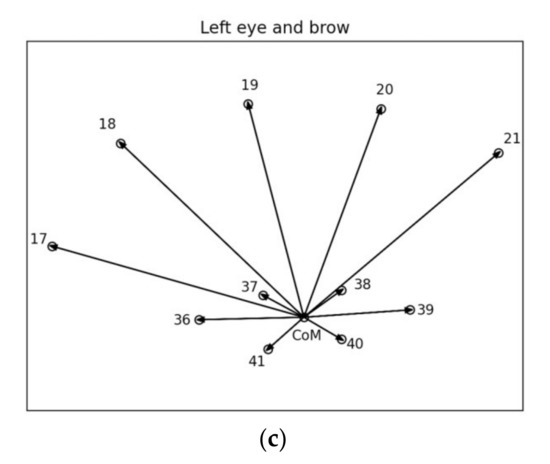
Figure 2.
(a) 68 facial landmarks points. (b) The unit vector defined along the nose from landmark point 27 to landmark point 30. The first three primary vectors are also shown from landmark point 27 to the centers of the eyes and mouth, respectively. (c) Secondary vectors from the center of the left eye (primary point) to (secondary) landmark points on the left brow and left eye contour.
A structured representation of facial landmarks points was pursued toward retaining structural semantics regarding face topology. More specifically, facial landmark points were ad hoc structured in a three-level tree hierarchy of vectors in polar coordinates (r,φ), as follows [34,35].
The first tree level includes the root of the tree which corresponds to the nose. The latter defined the unit vector u from landmark point 27 to landmark point 30 on the nose (Figure 2b). On the one hand, all vector lengths, for example, the ones shown in Figure 2b,c, were measured against the unit vector u. On the other hand, all vector angles were measured clockwise from a line with unit vector x vertical to u, such that the cross-product u × x points outward Figure 2. The second tree level includes nodes dubbed primary that identify primary features or, equivalently, primary points corresponding to primary vectors. The latter include vectors from landmark point 27 to the center of each eye, whose positions are calculated as the centers of mass of the respective eye contour; a third primary vector is again from landmark point 27 to the center of the mouth, which is computed as the center of mass of the mouth’s outer contour; the next five primary vectors are again from landmark point 27 to the five landmark points 31, …, 35 on the nose end (i.e., the nostrils). The third tree level includes nodes dubbed secondary that identify secondary features or, equivalently, secondary points corresponding to secondary vectors. The latter include vectors from the end of a primary vector to landmark points on the left/right eyes/brows, outer mouth, and jaw contours. For example, Figure 2c shows (magnified) a number of secondary vectors corresponding to the left eye/brow in the window, shown inside Figure 2b. A secondary vector is always in tandem with a primary vector. In all, there are 8 primary points and 51 secondary points.
Figure 3a summarizes the basic tree structure considered. A numerical label on a tree edge in Figure 3a indicates the index of the corresponding facial landmark point in Figure 2 that defines the end of a primary/secondary vector, where, in the interest of simplicity, adjacent tree nodes are grouped together.
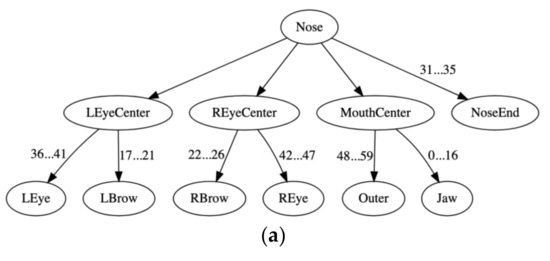
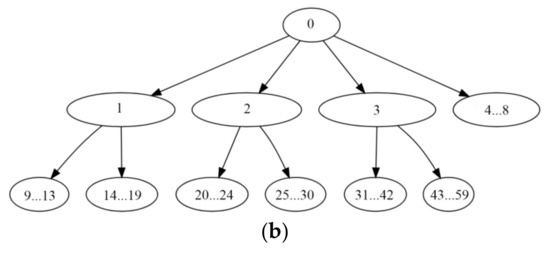
Figure 3.
The considered tree structure representation of a human face. (a) The primary points ‘LEyeCenter’, ‘REyeCenter’ and ‘MouthCenter’ are computed from facial landmark points, as detailed in the text. All facial landmark points are labeled numerically using the labels (i.e., numbers) of Figure 2. (b) The above facial points are re-numbered sequentially. In all, there are 8 primary points (on the first tree level) and 51 secondary points (on the second tree level).
By defining the back of a nose as the unit vector, the proposed tree data structure becomes a rotation/scale/translation invariant. Moreover, the proposed transformation, from a geometrical topology of facial landmark points to a basic tree data structure, is invertible. In conclusion, the tree data structure in Figure 3b emerges, which represents a human face with its nodes numbered sequentially from 0 to 59. In other words, data preprocessing considers a human face image as an input, and it outputs a human face structural representation, which is orders of magnitude smaller than an image as well as it is anonymous.
Based on the mathematics presented in Section 2, a (structured) positive valuation function is defined next.
3.2. A Structured Positive Valuation Function
Given the basic tree structure of Figure 3, according to the analysis in Section 2, consider the Cartesian product lattice (L0 × … × L59,⊑) that corresponds to all the trees of interest. A structured positive valuation function is computed as follows.
For a leaf node nj, j∈{4, …, 59} the positive valuation function is vj (uj), whereas for the nodes nj, j∈{1,2,3} it is:
n1: vb1(u1,u9, …, u19) = v1(u1) + k1[v9(u9) + … + v19(u19)]
n2: vb2(u2,u20, …, u30) = v2(u2) + k2[v20(u20) + … + v30(u30)]
n3: vb3(u3,u31, …, u59) = v3(u3) + k3[v31(u31) + … + v59(u59)].
For the root node locally, it is assumed v0 (u) = 0. Therefore, for a specific tree instance T its positive valuation is defined from the leaves upward as:
V(T) = v1(u1) + … + v8(u8) + k1[v9(u9) + … + v19(u19)] + k2[v20(u20) + … + v30(u30)] + k3[v31(u31) + … + v59(u59)]
Using basic mathematical lattice theory results, it follows that a metric distance D (.,.) between two trees Tu = (u1, …, u59) and Tw = (w1, …, w59) is computed as:
D(Tu,Tw) = V(Tu⊔Tw) − V(Tu⊓Tw)
The distance D (Tu,Tw) can be computed from local distances at each tree node as:
D(Tu,Tw) = d1(u1,w1) + … + d8(u8,w8) + k1[d9(u9,w9) + … + d19(u19,w19)] + k2[d20(u20,w20) + … + d30(u30,w30)] + k3[d31(u31,w31) + … + d59(u59,w59)]
Two fuzzy order functions are computed as:
where V (Tu⊔Tw) and V (Tu⊓Tw) are calculated, respectively, as:
and:
σ⊔(Tu,Tw) = V(Tw)/V(Tu⊔Tw)
σ⊓(Tu,Tw) = V(Tu⊓Tw)/V(Tu)
V(Tu⊔Tw) = V(u1⊔w1, …, u59⊔w59) = v1(u1⊔w1) + … + v8(u8⊔w8) + k1[v9(u9⊔w9) + … + v19(u19⊔w19)] + k2[v20(u20⊔w20) + … + v30(u30⊔w30)] + k3[v31(u31⊔w31) + … + v59(u59⊔w59)]
V(Tu⊓Tw) = V(u1⊓w1, …, u59⊓w59) = v1(u1⊓w1) + … + v8(u8⊓w8) + k1[v9(u9⊓w9) + … + v19(u19⊓w19)] + k2[v20(u20⊓w20) + … + v30(u30⊓w30)] + k3[v31(u31⊓w31) + … + v59(u59⊓w59)]
An alternative fuzzy order function σc: T × T→[0,1] can be computed by a convex combination of local fuzzy order functions at each tree node [36] as
where c1 + … + c59 = 1, and σ could be either exclusively σ⊔ or exclusively σ⊓. Recall that any engagement of a fuzzy order function is named Fuzzy Lattice Reasoning (FLR); more specifically, a fuzzy order function (σ) supports two modes of reasoning, namely Generalized Modus Ponens and Reasoning by Analogy [9].
σc(Tu,Tw) = c1σ(u1,w1) + … + c59σ(u59,w69)
4. The Granule-Based-Classifier (GbC)
The previous sections have detailed a structured human face representation by a tree data structure in lattice (T,⊑). In the following, Algorithm 1 describes a machine-learning scheme with a capacity to induce knowledge from tree data structures in the form of granular rules for classification.
| Algorithm 1. GbC: Granule-based-Classifier (training phase) |
| 0: Set a threshold size ΔT = Δ0; |
| 1: Set a (small) size step δ; |
| 2: Randomly partition the training data in each class in clusters, such that the lattice-join of all the data in a cluster has size less than ΔT; |
| 3: If two granules in different classes overlap then Abolish both (overlapping) granules into the training data they were induced from; Set ΔT ← ΔT − δ; Goto 2; else End the training phase. |
The basic idea behind GbC for training (i.e., Algorithm 1) is that, in the beginning, Algorithm 1 computes uniform granules, in the sense that all the data within a uniform granule belong to the same class of a user-defined maximum threshold size, ΔT = Δ0. If granules in different classes overlap, then, to avoid potential contradictions, overlapping granules are abolished; next, GbC resumes training on the data that induced overlapping granules, using a smaller threshold size ΔT ← ΔT − δ. The latter procedure repeats until (smaller) uniform granules are computed. Consequently, the computational complexity of Algorithm 1 (i.e., GbC training) is computed as follows. Given that the number of the training data is N, it takes time O (N × N) to compute all different sets of information granules. Then, for each set of information granules, it takes time O (N × N) to test possible overlaps between granules. The latter computations repeat O (Δ0/δ) times. Therefore, the computational complexity of Algorithm 1 (i.e., GbC training) is O (N4Δ0/δ).
As soon as the training data have been replaced by (uniform) granules, the corresponding class label is attached to each granule. In the aforementioned manner, pairs (g,l) emerge, where g is a granule, and l is its label. A pair (g,l) is interpreted as the rule “if g then l”, symbolically g→l. Decision-making, i.e., classification, is carried out by assigning a testing datum to a granule based on either a lattice metric distance (27D) or a lattice fuzzy order function (σ). In conclusion, the corresponding “winner” granule label is assigned to the testing datum as Algorithm 2 shows.
| Algorithm 2. GbC: Granule-based-Classifier (testing phase) |
| 0: Let (gi, ci), i∈{1, ..., Μ} be all the pairs of labeled granules, where gi is a granule and ci is its corresponding label Let g0 be an input granule to be classified |
| 1. Calculate |
| 2. Define the class of g0 as c0 = cj |
Apparently, the computational complexity of Algorithm 2 (i.e., GbC testing) is O (NrNs), where Nr and is Ns is the number of the training and testing data, respectively.
Recall that the representation of a granule by a lattice interval induced from all the training data in a granule involves two types of FLR generalization, namely Type I Generalization and Type II Generalization [23]; more specifically, Type I Generalization refers to inclusion of points in a granule without explicit evidence, whereas Type II Generalization means decision-making beyond a granule.
The GbC scheme is potentially applicable on any lattice data domain including, in particular, the lattice (T,⊑) of tree data structures described in Section 2. Two basic versions of GbC have been considered here, namely GbCvector and GbCtree, as subsequently explained. More specifically, for k1 = k2 = k3 = 1 in Equation (1), no tree structure is considered in the calculations; therefore, the corresponding classifier is called GbCvector. Otherwise, if at least one of k1 or k2 or k3 is different than 1, then a tree structure is considered in the calculations; therefore, the corresponding classifier is called GbCtree.
As a result of inducing trees in step-1 of Algorithm 1, a tree data structure in Figure 3b may represent a forest or, equivalently, a grove, that is a set of trees, instead of representing a single (individual) tree. We remark that a grove of trees is also called interval-tree, whereas an individual tree is a trivial interval-tree. Differences of the GbC with other decision-tree classifiers are summarized next.
The tree data structure in Algorithm 1 is constant as shown in Figure 3, whereas the data induced tree data structures of alternative decision-tree classifiers are not constant [37]. Note that GbC induces the contents of its tree nodes instead. Furthermore, the forests of trees that GbC considers are granules/neighborhoods of individual trees, whereas forests of trees in the literature typically consist of individual trees without considering any neighborhood of trees whatsoever [38].
The following section demonstrates applications of GbC.
5. Computational Experiments and Results
Recall that the motivation of this work is social robot–human interaction applications; in particular, the focus here is on machine vision applications. In particular, it turns out that during social robot–human interaction, the robot needs to keep (1) quantifying the engagement/attention of the human it interacts with, (2) modifying its behavior according to a human’s emotions—the latter is directly associated with facial expressions, and (3) personally addressing the human it interacts with. Hence, this section deals with three discrete pattern recognition problems, in a unifying manner, in the sense that the same representation of a human face is used in all three problems. Instead of developing an intelligence model based on “first principles”, a machine-learning model is assumed here that may induce explanatory knowledge (i.e., rules) from real world data; more specifically, a GbC scheme is used. The latter has the advantage of processing structured data per se as detailed next.
A tree data structure was induced from a single camera frame, as explained in Section 3.1, including 59 primary and secondary nodes each of whom stores a pair (r,φ) of polar vector coordinates. In particular, a tree data structure stored a pair ([r,r], [φ,φ]) of trivial intervals, where both values r and φ were normalized over the interval [0, 1], such that 0 corresponds to the minimum, whereas 1 corresponds to the maximum over all the corresponding feature values. Regarding the data processing time, it took clearly less than 1 s overall to compute the image’s tree data structure representation in Figure 3.
Two types of positive valuation functions were employed exclusively per node including, first, linear functions:
where j∈{1, …, N = 59}, for both variables r and φ and, second, sigmoid functions:
where j∈{1, …, N = 59}, for both variables r and φ. In addition, the following function θ (x) was used:
for both variables r and φ, always.
vj(x) = λjx
vj(x) = Aj/(1 + exp{−λj(x − μj)})
θ(x) = 1 − x
Equation (5) was used with c1 = … = c8 = 1/C, c9 = … = c19 = k1/C, c20 = …= c30 = k2/C, and c31 = … = c59 = k3/C, where C = 8 + 11k1 + 11k2 + 29k3 and k1, k2, k3 are the coefficients in Equation (1).
To optimize classification performance, a typical genetic algorithm was employed with a population of 500 individuals for 50 generations. First, for the linear Equation (6), it was λj∈[0.01,10], j∈{1, …, N = 59} for both variables r and φ. Second, for the sigmoid Equation (7), it was Aj∈[0.1,20], λj∈[0.01,10] and μj∈[−50,50], j∈{1, …, N = 59} for both variables, r and φ. Furthermore, for both linear and sigmoid positive valuation functions, it was kj∈[0.1,50], j∈{1,2,3} in Equation (1) for both variables r and φ. Figure 4 displays the genetic algorithm chromosome for linear positive valuation functions. Unless otherwise stated, the experiments below used a standard ten-fold cross-validation.

Figure 4.
Chromosome of a genetic algorithm for linear positive valuation functions.
5.1. Head Orientation Recognition Experiments
A human’s head orientation is important toward quantifying the human’s engagement/attention during interaction with a robot [39]. The estimation of head orientation was dealt with here as a classification problem, as follows.
Data were recorded in the HUMAIN-Lab, including snapshots of a human head in various head poses. Nine basic orientations (i.e., classes) of interest were considered, namely Upper Left, Up, Upper Right, Left, Front, Right, Lower Left, Down, and Lower Right. The resolution of the class “Front” was increased by considering three sub-classes, namely “Front Left”, “Front”, and “Front Right”, as shown in Figure 5.
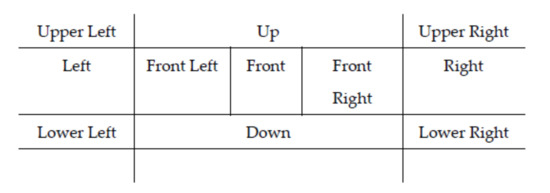
Figure 5.
A total of 11 head orientations were assigned in 9 classes. Each head orientation was assigned to a different class but the three head orientations “Front Left”, “Front”, and “Front Right” were assigned to a single class, namely “Front”.
On the one hand, the training data included 100 image frames for each one of the 11 head orientations of Figure 5. All the training data were acquired at distance 40 cm, under normal light. On the other hand, the testing data included 100 image frames for each one of the 9 basic head orientations for four different environmental conditions; in particular, all four combinations were considered of a subject distance from the camera at either 40 cm or 100 cm, under lighting conditions considered either normal or dim, corresponding to minimum light output (lumens) of 1600 and 90, respectively. In conclusion, one testing experiment was carried out for each one of the aforementioned four environmental conditions.
Training/testing data frames, where a face was fully detected by the OpenFace library, were considered exclusively. Each training/testing image was converted to its corresponding (trivial) tree representation, as described in Section 3.1, including 59 features, i.e., N = 59. Then, a GbC scheme was applied.
In this experiment interval-trees were computed of the maximum possible size, Δ. Hence, 11 interval-trees prototypes were computed; that is, one prototype per data cluster, respectively. For instance, Figure 6a displays a trivial-tree, whereas Figure 6b displays an interval-tree. Recall from Section 4 that an interval-tree T, together with the label l attached to it, is interpreted as a granular rule “if T then l”, symbolically T→l, where the label l is an element of the set {Upper Left, Up, Upper Right, Left, Front, Right, Lower Left, Down, Lower Right}.
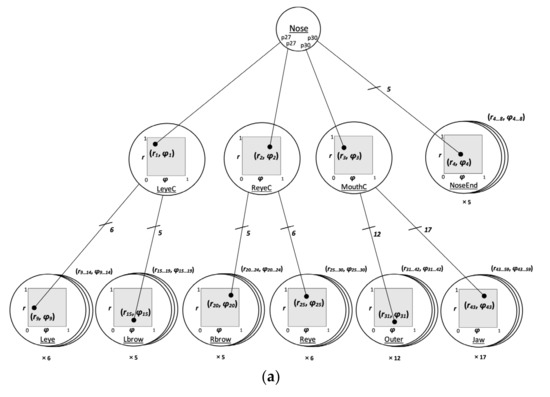
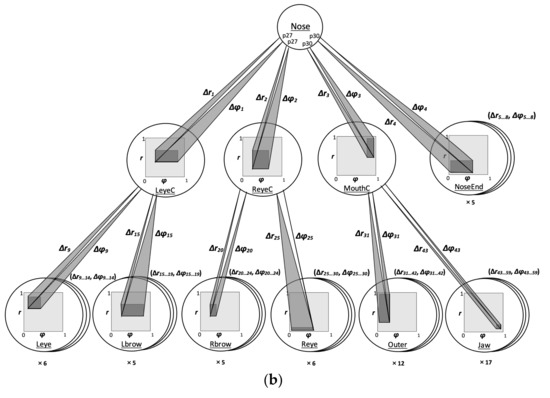
Figure 6.
(a) A trivial-tree represents a single head orientation image frame. (b) An interval-tree represents a neighborhood of trivial-trees; in other words, an interval-tree represents an information granule or, equivalently, a grove of trivial trees.
Figure 7a demonstrates how the values of the metric distance function Equation (2) change; similarly, Figure 7b demonstrates how the values of fuzzy order function Equation (3), as well as Equation (4), both change for an arbitrary frame, namely fL, of the class “Upper Left” versus all class prototypes. Figure 7a confirms, as expected, that the frame fL is nearest to the class prototype “Upper Left”; similarly, Figure 7b confirms, also as expected, that the frame fL is mostly similar to the class prototype “Upper Left”. Note that Equation (3) results in larger values than Equation (4), since partly overlapping trees result in smaller values for Equation (4) than they do for Equation (3).
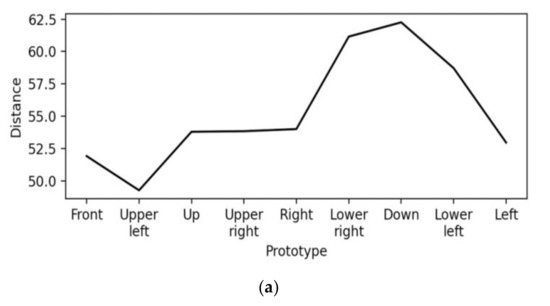
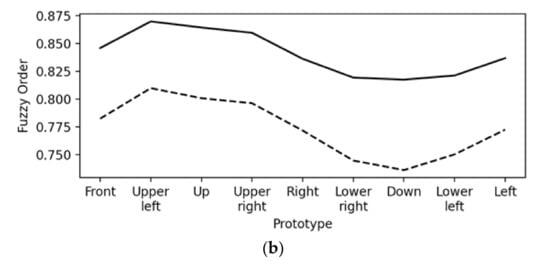
Figure 7.
Two “measures of similarity” between an arbitrary testing frame of the class ‘Upper Left’ head orientation for 40 cm/normal environmental conditions versus nine head orientations (classes) prototypes regarding (a) the metric distance function Equation (2), and (b) the fuzzy order functions Equations (3) and (4), where the solid line corresponds to Equation (3) (i.e., σ⊔), whereas the dashed line corresponds to Equation (4) (i.e., σ⊓).
A preliminary work [34] has considered (1) 11 prototypes, (2) normalized r and φ values over the interval [0,1], (3) the r and φ separately, and (4) the functions v (x) = x and θ (x) = −x. For comparison reasons, the corresponding results are repeated, in a different format, in Table 1. In particular, a generic geometrical classification scheme has employed as inputs the 68 facial landmarks (points) of Figure 2a. The results in Table 1 show that the GbCvector can be clearly superior to a generic geometrical classification scheme.

Table 1.
Results by the GbCvector classifier with separate vectors r and φ for four different environmental conditions.
Next, the r and φ were considered concatenated; all other considerations were kept the same. The corresponding classification results are shown in Table 2.

Table 2.
Results by the GbCvector classifier with concatenated vectors r and φ for four different environmental conditions.
Next, in addition to the latter consideration, the function θ (x) = 1 − x was employed by implementing the complement coding technique motivated from models of brain neurons. The corresponding classification results are shown in Table 3.

Table 3.
Results by the GbCvector classifier with complement coding for four different environmental conditions.
Next, in addition to the latter consideration, the functions vk (x) = λkx, k∈{1, …, 59} were used optimized. The corresponding classification results are shown in Table 4.

Table 4.
Results by the optimized GbCvector classifier for four different environmental conditions.
Finally, in addition to the latter consideration, the GbCtree scheme was used; furthermore, the coefficients k1, k2, k3 (for r) and k4, k5, k6 (for φ) were optimized. The corresponding head pose classification results are shown in Table 5.

Table 5.
Results by the optimized GbCtree classifier for four different environmental conditions.
The results of this experiment are discussed comparatively in Section 6.
5.2. Facial Expression Recognition Experiments
Human facial expressions are important as they are closely associated with emotions. This is essential information for a sensible social robot-human interaction. Therefore, this application regarded facial expression recognition. More specifically, the Extended Cohn-Kanade (CK+) benchmark dataset was employed, including 327 image sequences partitioned in seven discrete emotion labeled classes, namely, anger, contempt, disgust, fear, happiness, sadness, and surprise [40,41].
An individual image sequence consists of 10 to 60 (image) frames, where a frame is typically a 640 × 490 or 640 × 480 array of pixels; each of the latter stored either an 8-bit gray scale or a 24-bit color value. One of the frames per image sequence, typically the last one, was characterized in the database as “peak (of emotional intensity)”. The latter is the only image used here from its corresponding image sequence in the experiments below. Similar to before, an image was represented by a trivial-tree.
In this application, only facial landmarks points involved in facial expressions were considered (Figure 2a). The selection of the aforementioned facial landmarks was based on the Facial Action Coding System (FACS), as well as the Action Units (AU) of the facial expressions for emotions [42,43], as shown in Table 6. In particular, the first two columns of Table 6 associate an emotion with AUs whose name is shown in the third column; furthermore, the fourth column displays the corresponding landmark points selected by an expert. In conclusion, in addition to left/right eye and mouth centers from Figure 2a, the following 22 landmarks points have been selected: 31, 33, 35 (from NoseEnd), 17, 19, 21, 36, 39 (from the left eye/brow), 22, 24, 26, 42, 45 (from the right eye/brow), 48, 51, 54, 57, 60, 62, 64, 66 (from the inner/outer mouth), and 8 (from the Jaw). Hence, a reduced tree resulted compared to that of Figure 3; moreover, Equations (1) and (5) were simplified accordingly. Note that a couple of empty sets appear in the fourth column of Table 6 since, for two AUs, there were no landmark points among the 68 facial landmark points; more specifically, there were no landmarks for either AU 6 nor AU 14 in Table 6. In conclusion, the resulted tree representation consisted of 25 nodes, i.e., N = 25. Hence, the data employed for classification here were reduced from 640 × 490 = 313,600 real numbers per image down to 25 × 2 = 50 real numbers per tree, that is, orders of magnitude fewer real numbers.

Table 6.
Association of specific emotions with facial actions units and ultimately with facial landmarks points.
Table 7 displays the experimental results using both classifiers GbCtree and GbCvector with a linear Equation (6) positive valuation function, whereas Table 8 displays experimental results using both classifiers GbCtree and GbCvector with a sigmoid Equation (7) positive valuation function. Table 7 and Table 8 display the classification results both before (within parentheses) and after parameter optimization. It must be noted that Table 7 and Table 8 display results by two different sigma-join functions σ⊔ (.,.), computed by Equations (3) and (5), respectively, as well as by two different sigma-meet functions σ⊓ (.,.), computed by Equations (4) and (5), respectively.

Table 7.
Results by GbC classifiers both optimized and non-optimized (within parentheses) for linear positive valuation function regarding facial expression recognition.

Table 8.
Results by GbC classifiers both optimized and non-optimized (within parentheses) for sigmoid positive valuation function regarding facial expression recognition.
In both Table 7 and Table 8, on the one hand, when the distance D (..) was used, the best classification resulted in a zero tree size, i.e., when each training datum was represented by a trivial-tree; on the other hand, when a fuzzy order function was used, then the best classification results were obtained for 5 interval-trees prototypes per class.
Figure 8, for example, displays one rule induced from data of the class “happiness”. Note that the rule consists of 25 pairs of intervals; each interval corresponds to normalized polar, i.e., radial and angular, coordinates. It is clear that a pair of intervals defines an annulus (ring) sector. For clarity, Figure 9a displays only a pair of annulus sectors, namely the annulus sectors 21 and 23 underlined in Figure 8, on a human face in the class “happiness”. Likewise, Figure 9b displays the corresponding pair of annulus sectors of another rule, induced from data in the class “anger”.

Figure 8.
A rule R, induced from data of the class “happiness”, defines a granule of primary /secondary feature vectors by a conjunction of 25 annulus (ring) sectors in its antecedent. Underlined annulus (ring) sectors 21 and 23 are displayed in Figure 9.

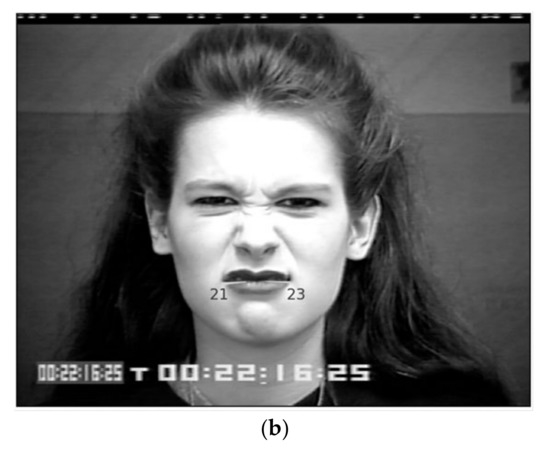
Figure 9.
Annulus sectors 21 and 23 corresponding, respectively, to two induced rule granules are displayed along the mouth on a human face regarding the classes (a) “happiness”, thus confirming the participation of AU6 (Cheek Raiser) and AU12 (Lip Corner Puller), and (b) “anger”, thus confirming the participation of AU23 (Lip Tightener) (©Jeffrey Cohn).
An annulus (ring) sector identifies a granule of primary/secondary feature vectors. For instance, Figure 9a, as well as Figure 9b, displays a pair of annulus sectors, that is, part of a rule that recognizes a facial expression either “happiness” or “anger”, respectively. Note that the aforementioned annulus sectors were computed by the lattice-join of the “outer mouth left” and “outer mouth right” secondary feature vectors in the corresponding granule. In particular, Figure 9a shows that both “happiness” prototypes are longer, wider, and have an upward inclination, whereas Figure 9b shows that both “anger” prototypes are shorter, narrower, and nearly horizontal. Figure 9 confirms that, as expected, from Table 6, AUs participate per facial expression “happiness” and “anger” regarding lip movement. Regarding “happiness”, there is a widening of the lip corners (AU6—Cheek Raiser), as well as a raising of the cheeks (AU12—Lip Corner Puller), whereas for “anger”, there is a lip tightening action (AU23—Lip Tightener). The latter is interpreted as explainable artificial intelligence (AI), enabled by the fact that AU information is retained in the proposed tree data representation all along during data processing.
The effectiveness of the 22 aforementioned selected features, corresponding to AUs associated with specific emotions, was tested by running additional experiments using all the 59 features considered in Section 3.1. In all cases, the GbCtree was employed due to its superior performance compared to GbCvector. In far more experiments, the employment of the 59 features produced results 3 to 5 percentage points less than the results shown in Table 7 and Table 8, whereas in the remaining experiments, the employment of the 59 features produced results comparable to the ones shown in Table 7 and Table 8.
The results of this experiment are discussed comparatively in Section 6.
5.3. Face Recognition Experiments
Human face recognition is important in addressing a human personally during social robot–human interaction. In this application, the ORL benchmark dataset [44] was considered, which includes 10 images of 40 different subjects. The images were acquired under slight lighting variations, and with different facial expressions, as well as varying facial details (e.g., glasses/no-glasses). All the images are taken against a dark uniform background, with the subjects in an upright/front position. The size of each image is 92 × 112 pixels with 8-bit grey levels per pixel. The tree data structure of Figure 3b was used and included 59 features, i.e., N = 59.
Table 9 displays experimental results using both classifiers GbCtree and GbCvector with a linear Equation (6) positive valuation function, whereas Table 10 displays experimental results, using both classifiers GbCtree and GbCvector with a sigmoid Equation (7) positive valuation function. Both Table 9 and Table 10 display the classification results after as well as before (within parentheses) parameter optimization. It is noted that Table 9 and Table 10 display results by two different sigma-join functions computed by Equations (3) and (5), respectively, as well as by two different sigma-meet functions, computed by Equations (4) and (5), respectively.

Table 9.
Results by GbC classifiers both optimized and non-optimized (within parentheses) for linear positive valuation function regarding face recognition.

Table 10.
Results by GbC classifiers both optimized and non-optimized (within parentheses) for sigmoid positive valuation function regarding face recognition.
In both Table 9 and Table 10, when either the distance D (..) or a fuzzy order, either σ⊔ (.,.) or σ⊓ (.,.), was used, the best classification resulted in a zero tree size, i.e., when each training datum was represented by a trivial-tree.
The results of this experiment are discussed comparatively in Section 6.
6. Discussion and Future Work
This work has introduced the Granule-based-Classifier (GbC) parametric model. Discussion of the results as well as potential future work is presented next.
6.1. Discussion
The GbC was applied here on a mathematical lattice of tree data structures, each one of whom represented a human face, thus retaining geometrical topology semantics. In conclusion, the GbC here was applied to three different classification problems regarding recognition of (1) Head Orientation, (2) Facial Expressions, and (3) Human Faces. The same (tree data structure) representation was used in all aforementioned problems with the following results.
First, in the Head Orientation recognition problem, the GbCvector performed, in general, clearly better than a conventional classification scheme, as shown in Table 1. Furthermore, Table 2, Table 3 and Table 4 have demonstrated that considering incrementally (a) concatenated vectors r and φ, (b) the complement coding technique, and (c) optimized linear positive valuation functions, the classification accuracy progressively increased. GbCtree performance versus GbCvector performance is discussed below. Note that the proposed, structural human head representation has advantages compared to alternative methods [45], in that the proposed representation can also be used for additional recognition tasks, as subsequently explained.
Second, in the Facial Expression recognition problem, the GbC performed up to nearly 85%. Note that alternative, state-of-the-art classifiers in image pattern recognition have reported performance up to 82% using an LBP scheme [46]; furthermore, deep learning methods have reported higher classification accuracies, ranging from a mean of 91.80% up to 96.92% [47], as well as from 91.64% up to 98.27% [48]. Note that alternative image recognition methods had used orders of magnitude more data than GbC. In particular, they had used multiple consecutive image frames until an emotion reaches a peak, where a single image was represented by as many as 640 × 440 = 313,600 real numbers, whereas a GbC, from an image sequence used only a single image frame, represented only by 25 × 2 = 50 real numbers; the latter are the x and y coordinates of 25 facial landmark points.
Third, in the Human Face recognition problem the GbC performed up to 88.25%. Note that alternative, state-of-the-art classifiers in image pattern recognition have reported classification accuracies ranging from 93% up to 96% by ANFIS [49], as well as from 92% up to 100% by a CNN deep learning scheme [50]. Again, alternative image recognition methods typically used orders of magnitude more data than GbC did. In particular, they have used whole image frames, where a single image was represented by as many as 640 × 440 = 313,600 real numbers, whereas a GbC represented a single image frame by 59 × 2 = 118 real numbers; the latter are the x and y coordinates of 59 facial landmark points.
The clearly better classification performance of GbC in the Head Orientation recognition, compared to its performance in either Facial Expression- or Human Faces- recognition, was attributed to the fact that the proposed tree data structure represents geometrical topology semantics of a human face.
In the Facial Expression recognition, as well as in the Human Faces recognition problem, a deep learning scheme (i.e., CNN) had better classification accuracy. It is noteworthy that deep learning is employed in the OpenFace library to calculate the 68 facial landmarks (points) in a data preprocessing step. An advantage of the proposed GbC classification schemes is that they all use the same data preprocessing to result in the same human face representation, based on 68 facial landmarks (points), in three different pattern recognition tasks. Hence, both GbC training and testing in three different pattern recognition tasks is orders of magnitude faster than training and testing by task-specific deep learning schemes for the same tasks. Such a wide applicability of the proposed GbC with good classification resulting in three different tasks suggests that the proposed human face representation method is promising. Another advantage is that the proposed tree representation of a human face retains anonymity during data processing. Furthermore, a GbC classifier induces granular rules that can be used to explain its answers, whereas a deep learning classifier operates in a way that is similar to a black box that cannot explain its answers. Note that an information granule may represent a word; in the latter sense, the GbC computes with words. Moreover, the proposed representation is modular in the sense that other parts of a human body, e.g., the hands, the shoulders-torso etc., can be straightforward incorporated, as well as additional modalities. The latter are unique capacities of a GbC scheme that no deep learning scheme possesses. In addition, compared to alternative fuzzy systems for face recognition [26,27], the GbC can operate on structured (tree) data representations of a human face instead of operating solely on vectors of features. Furthermore, by its parameters, the GbC can carry out tunable generalization. Finally, the employment of a fuzzy order function explicitly engages logic/reasoning in decision-making.
In general, the computational experiments here have involved two GbCs schemes, namely GbCtree and GbCvector. In addition, they have involved one metric distance function D (.,.) as well as fuzzy order functions σ (.,.). The typically, better performance of σ (.,.) compared to D (.,.) was attributed to the rational definition of σ (.,.), by either Equation (3) or Equation (4). It turned out that σ⊔ (.,.) in Equation (3) performed clearly better than the convex fuzzy order with all σ⊔ (.,.) in Equation (5), as a positive valuation function defined on a whole interval-tree results in a holistic comparison of two interval-trees, whereas a positive valuation function, defined as the sum of positive valuation functions on individual tree nodes, results in a fragmented comparison of two interval-trees. Similarly, and for the same reason, σ⊓ (.,.) in Equation (4) performed better than the convex fuzzy order with all σ⊓ (.,.) in Equation (5). Finally, the better performance of a sigmoid positive valuation function compared to a linear one was attributed to the larger number of parameters a sigmoid has, as detailed below. Moreover, the (marginally) better classification accuracy of an optimized GbCtree, compared to an optimized GbCvector, was attributed to the employment of a tree data structure that retains geometrical topology semantics of a human face.
A GbC classifier has clearly performed better than random guess; therefore, GbC classifiers can result in a strong classifier, in the sense of Probably Approximately Correct (PAC), by boosting techniques [51]. In addition to boosting, an alternative instrument for improving classification performance is the number of parameters as explained next.
Good classification performance is often reported by computational intelligence models with a large number of parameters, e.g., deep learning [52], or Type-2 fuzzy systems [53]. Note that LC models, including the proposed GbC schemes, can introduce an arbitrary large number of parameters via parametric functions v (.) and θ (.) per constituent lattice. It is noteworthy that a sigmoid positive valuation function with 3 parameters, resulting in a total of either (3 × 59) × 2 = 354 parameters or (3 × 25) × 2 = 150 parameters, has performed clearly better than a linear positive valuation function with 1 parameter, resulting in a total of either (1 × 59) × 2 = 118 parameters or (1 × 25) × 2 = 50 parameters, in the facial expression recognition and the face recognition problems, respectively. Note that a typical deep learning model engages millions of parameters.
The above remarks encourage the engagement of boosting techniques, as well as the increase of the number of GbC parameters toward further increasing GbC classification accuracy, in a future work.
6.2. Future Work
Future work includes shorter-term plans, as well as longer-term plans. On the one hand, shorter-term plans regard mainly technical improvements of GbC such as, firstly, real-world applications of social robot-human interaction, including additional modalities beyond machine vision for face recognition; and secondly, a quest for improved sub-optimal solutions regarding parameter estimation, also considering more parameters per positive valuation function. On the other hand, longer-term plans include a far-reaching pursuit of “understanding”, “creativity” as well as “intention sharing” by machines. Note that future AI is expected to be creative [54]; furthermore, proposed conditions for creativity include metaphors [55]. Different authors have explained how analogy is the basis of metaphors [56]. This work has demonstrated that a lattice-isomorphism can establish an analogy between two different lattice structures, possibly also toward “understanding” by machines, and “creativity” by machines as well as “intention sharing” of a machine with either another one or a human, as it will be pursued in a future work.
Author Contributions
Conceptualization, V.G.K., A.L., O.B. and T.H.; methodology, V.G.K., G.A.P., M.Y. and C.L.; software, C.L. and C.B.; validation, C.L., E.V., C.B. and V.G.K.; investigation, C.L., G.A.P. and V.G.K.; writing—original draft preparation, V.G.K. and C.L.; writing—review and editing, V.G.K., C.L., E.V., G.A.P. and M.Y.; visualization, V.G.K., A.L., O.B. and T.H.; supervision, V.G.K. and C.L.; project administration, V.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 777720.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Extended Cohn-Kanade (CK+) dataset was used after obtaining the appropriate license at http://www.jeffcohn.net/Resources/ (accessed on 10 August 2021). The ORL dataset was retrieved from https://cam-orl.co.uk/facedatabase.html (accessed on 10 August 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Belpaeme, T.; Kennedy, J.; Ramachandran, A.; Scassellati, B.; Tanaka, F. Social robots for education: A review. Sci. Robot. 2018, 3, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baxter, P.; Ashurst, E.; Kennedy, J.; Senft, E.; Lemaignan, S.; Belpaeme, T. The wider supportive role of social robots in the classroom for teachers. In Proceedings of the 1st International Workshop on Educational Robotics at the International Conference Social Robotics, Paris, France, 26 October 2015. [Google Scholar]
- Breazeal, C.; Dautenhahn, K.; Kanda, T. Social Robotics. In Springer Handbook of Robotics; Springer International Publishing: Cham, Switzerland, 2016; pp. 1935–1972. ISBN 978-3-642-34102-1. [Google Scholar]
- Mubin, O.; Ahmad, M.I.; Kaur, S.; Shi, W.; Khan, A. Social Robots in Public Spaces: A Meta-Review. In Proceedings of the Social Robotics; ICSR 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 11357, pp. 213–220. [Google Scholar]
- Lytridis, C.; Bazinas, C.; Kaburlasos, V.G.; Vassileva-Aleksandrova, V.; Youssfi, M.; Mestari, M.; Ferelis, V.; Jaki, A. Social Robots as Cyber-Physical Actors in Entertainment and Education. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 19–21 September 2019; IEEE: Split, Croatia, 2019; pp. 1–6. [Google Scholar]
- Matarić, M.J.; Scassellati, B. Socially Assistive Robotics. In Springer Handbook of Robotics; Springer International Publishing: Cham, Switzerland, 2016; Volume 6, pp. 1973–1994. [Google Scholar]
- Clabaugh, C.; Matarić, M. Escaping Oz: Autonomy in Socially Assistive Robotics. Annu. Rev. Control. Robot. Auton. Syst. 2019, 2, 33–61. [Google Scholar] [CrossRef]
- Sheridan, T.B. Human–Robot Interaction. Hum. Factors J. Hum. Factors Ergon. Soc. 2016, 58, 525–532. [Google Scholar] [CrossRef] [PubMed]
- Kaburlasos, V.G. The lattice computing (LC) paradigm. In Proceedings of the 15th International Conference on Concept Lattices and Their Applications, CLA 2020, Tallinn, Estonia, 29 June–1 July 2020; pp. 1–7. [Google Scholar]
- European Commission Data Protection in the EU. Available online: https://ec.europa.eu/info/law/law-topic/data-protection/data-protection-eu_en (accessed on 4 October 2021).
- Hashimoto, T. The emergent constructive Approach to evolinguistics: Considering hierarchy and intention sharing in linguistic communication. J. Syst. Sci. Syst. Eng. 2020, 29, 675–696. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Papakostas, G.A. Learning distributions of image features by interactive fuzzy lattice reasoning in pattern recognition applications. IEEE Comput. Intell. Mag. 2015, 10, 42–51. [Google Scholar] [CrossRef]
- Kaburlasos, V.G. Special Issue on: Information Engineering Applications Based on Lattices. Inf. Sci. 2011, 181, 1771–2060. [Google Scholar] [CrossRef]
- Sussner, P. Lattice fuzzy transforms from the perspective of mathematical morphology. Fuzzy Sets Syst. 2016, 288, 115–128. [Google Scholar] [CrossRef]
- Sussner, P.; Schuster, T. Interval-valued fuzzy morphological associative memories: Some theoretical aspects and applications. Inf. Sci. 2018, 438, 127–144. [Google Scholar] [CrossRef]
- Sussner, P.; Campiotti, I. Extreme learning machine for a new hybrid morphological/linear perceptron. Neural Netw. 2020, 123, 288–298. [Google Scholar] [CrossRef]
- Sussner, P.; Caro Contreras, D.E. Generalized morphological components based on interval descriptors and n-ary aggregation functions. Inf. Sci. 2022, 583, 14–32. [Google Scholar] [CrossRef]
- Ritter, G.X.; Urcid, G. Introduction to Lattice Algebra with Applications in AI, Pattern Recognition, Image Analysis, and Biomimetic Neural Networks; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021; ISBN 9780367720292. [Google Scholar]
- Papadakis, S.E.; Kaburlasos, V.G. Piecewise-linear approximation of non-linear models based on probabilistically/possibilistically interpreted intervals’ numbers (INs). Inf. Sci. 2010, 180, 5060–5076. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Papadakis, S.E.; Papakostas, G.A. Lattice computing extension of the FAM Neural classifier for human facial expression recognition. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1526–1538. [Google Scholar] [CrossRef]
- Bazinas, C.; Vrochidou, E.; Lytridis, C.; Kaburlasos, V.G. Time-Series of distributions forecasting in agricultural applications: An intervals’ numbers approach. Eng. Proc. 2021, 5, 12. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Kaburlasos, V.G.; Kehagias, A. Fuzzy inference system (FIS) extensions based on the lattice theory. IEEE Trans. Fuzzy Syst. 2014, 22, 531–546. [Google Scholar] [CrossRef]
- Iordache, O. Formal Concept Analysis. In Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2011; Volume 70, pp. 143–163. ISBN 9783642179457. [Google Scholar]
- Kaburlasos, V.G.; Moussiades, L.; Vakali, A. Fuzzy lattice reasoning (FLR) type neural computation for weighted graph partitioning. Neurocomputing 2009, 72, 2121–2133. [Google Scholar] [CrossRef]
- Karczmarek, P.; Pedrycz, W.; Kiersztyn, A.; Rutka, P. A study in facial features saliency in face recognition: An analytic hierarchy process approach. Soft Comput. 2017, 21, 7503–7517. [Google Scholar] [CrossRef] [Green Version]
- Karczmarek, P.; Kiersztyn, A.; Pedrycz, W.; Dolecki, M. Linguistic Descriptors in Face Recognition. Int. J. Fuzzy Syst. 2018, 20, 2668–2676. [Google Scholar] [CrossRef] [Green Version]
- Rutkowska, D.; Kurach, D.; Rakus-Andersson, E. Fuzzy Granulation Approach to Face Recognition. In Artificial Intelligence and Soft Computing; ICAISC 2021; Springer: Cham, Switzerland, 2021; pp. 495–510. ISBN 9783030878962. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2014, 63, 139–144. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, Canada, 14–16 April 2014. [Google Scholar]
- Birkhoff, G. Lattice Theory; American Mathematical Society, Colloquium Publications: Providence, RI, USA, 1967. [Google Scholar]
- Kaburlasos, V.G.; Papakostas, G.A. Introduction to Computational Intelligence—A Holistic Approach (In Greek); Kallipos: Athens, Greece, 2016. [Google Scholar]
- Amos, B.; Ludwiczuk, B.; Satyanarayanan, M. OpenFace: A General-Purpose Face Recognition Library with Mobile Applications. CMU-CS-16-118. 2016. Available online: http://reports-archive.adm.cs.cmu.edu/anon/anon/usr0/ftp/2016/CMU-CS-16-118.pdf (accessed on 10 August 2021).
- Kaburlasos, V.G.; Lytridis, C.; Bazinas, C.; Chatzistamatis, S.; Sotiropoulou, K.; Najoua, A.; Youssfi, M.; Bouattane, O. Head Pose Estimation Using Lattice Computing Techniques. In Proceedings of the 2020 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2020; IEEE: Hvar, Croatia, 2020; pp. 1–5. [Google Scholar]
- Lytridis, C.; Kaburlasos, V.G.; Bazinas, C.; Papakostas, G.A.; Papadopoulou, C.I.; Nikopoulou, V.A. A Software Toolbox for Behavioral Analysis in Robot-Assisted Special Education. In Proceedings of the 2021 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 23–25 September 2021; IEEE: Hvar, Croatia, 2021; pp. 1–5. [Google Scholar]
- Kaburlasos, V.G.; Papadakis, S.E. A granular extension of the fuzzy-ARTMAP (FAM) neural classifier based on fuzzy lattice reasoning (FLR). Neurocomputing 2009, 72, 2067–2078. [Google Scholar] [CrossRef]
- Choi, J.; Song, E.; Lee, S. L-Tree: A local-area-learning-based tree induction algorithm for image classification. Sensors 2018, 18, 306. [Google Scholar] [CrossRef] [Green Version]
- Rokach, L. Decision forest: Twenty years of research. Inf. Fusion 2016, 27, 111–125. [Google Scholar] [CrossRef]
- Langton, S.R.H. The mutual influence of gaze and head orientation in the analysis of social attention direction. Q. J. Exp. Psychol. Sect. A 2000, 53, 825–845. [Google Scholar] [CrossRef] [Green Version]
- Kanade, T.; Cohn, J.F. Yingli Tian Comprehensive Database for Facial Expression Analysis. In Proceedings of the Fourth IEEE International Conference on Automatic Face and Gesture Recognition (Cat. No. PR00580), Grenoble, France, 28–30 March 2000; pp. 46–53. [Google Scholar]
- Lucey, P.; Cohn, J.F.; Kanade, T.; Saragih, J.; Ambadar, Z.; Matthews, I. The Extended Cohn-Kanade Dataset (CK+): A Complete Dataset for Action Unit and Emotion-Specified Expression. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops, San Francisco, CA, USA, 13–18 June 2010; pp. 94–101. [Google Scholar]
- Ekman, P.; Rosenberg, E.L. What the Face Reveals: Basic and Applied Studies of Spontaneous Expression Using the Facial Action Coding System (FACS); Oxford University Press: Oxford, UK, 2005; ISBN 9780195179644. [Google Scholar]
- Friesen, W.V.; Ekman, P. EMFACS-7: Emotional Facial Action Coding System. Unpublished Manuscript. University of California: San Francisco, CA, USA, 1984. [Google Scholar]
- Samaria, F.S.; Harter, A.C. Parameterisation of a Stochastic Model for Human Face Identification. In Proceedings of the 1994 IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; IEEE Press: Los Alamitos, CA, USA, 1994; pp. 138–142. [Google Scholar]
- Kocon, M. Head Movements of 3D Virtual Head in HMI Systems Using Rigid Elements. In Proceedings of the 2021 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 23–25 September 2021; IEEE: Hvar, Croatia, 2021. [Google Scholar]
- He, Y.; Chen, S. Person-Independent Facial Expression Recognition Based on Improved Local Binary Pattern and Higher-Order Singular Value Decomposition. IEEE Access 2020, 8, 190184–190193. [Google Scholar] [CrossRef]
- Miao, Y.; Dong, H.; Al Jaam, J.M.; EI Saddik, A. A Deep Learning System for Recognizing Facial Expression in Real-Time. ACM Trans. Multimed. Comput. Commun. Appl. 2019, 15, 1–20. [Google Scholar] [CrossRef]
- Bougourzi, F.; Dornaika, F.; Mokrani, K.; Taleb-Ahmed, A.; Ruichek, Y. Fusing Transformed Deep and Shallow features (FTDS) for image-based facial expression recognition. Expert Syst. Appl. 2020, 156, 113459. [Google Scholar] [CrossRef]
- Rejeesh, M.R. Interest point based face recognition using adaptive neuro fuzzy inference system. Multimed. Tools Appl. 2019, 78, 22691–22710. [Google Scholar] [CrossRef]
- Tang, J.; Su, Q.; Su, B.; Fong, S.; Cao, W.; Gong, X. Parallel ensemble learning of convolutional neural networks and local binary patterns for face recognition. Comput. Methods Programs Biomed. 2020, 197, 105622. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Mendel, J.M.; Rajati, M.R.; Sussner, P. On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Inf. Sci. 2016, 340–341, 337–345. [Google Scholar] [CrossRef]
- Miller, A.I. The Artist in the Machine; The MIT Press: Cambridge, MA, USA, 2019; ISBN 9780262354592. [Google Scholar]
- Miller, A.I. On Creativity and Metaphor in Art and Science. Interalia Magazine. 2016. Available online: https://www.interaliamag.org/interviews/on-creativity-and-metaphor/ (accessed on 10 August 2021).
- Holyoak, K.J.; Thagard, P. Mental Leaps: Analogy in Creative Thought; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).