Pedal Curves of the Mixed-Type Curves in the Lorentz-Minkowski Plane

Abstract

In this paper, we consider the pedal curves of the mixed-type curves in the Lorentz–Minkowski plane ${\mathbb{R}}_1^2$. The pedal curve is always given by the pseudo-orthogonal projection of a fixed point on the tangent lines of the base curve. For a mixed-type curve, the pedal curve at lightlike points cannot always be defined. Herein, we investigate when the pedal curves of a mixed-type curve can be defined and define the pedal curves of the mixed-type curve using the lightcone frame. Then, we consider when the pedal curves of the mixed-type curve have singular points. We also investigate the relationship of the type of the points on the pedal curves and the type of the points on the base curve.

1. Introduction

As an important kind of submanifolds, curves in different spaces have attracted wide attention from mathematicians. Studies have focused on investigating not only regular curves, but also singular curves, and have made great achievements (see [1,2,3,4,5,6,7,8,9,10,11]). Because Lorentz space is strongly connected to the theory of general relativity, the investigation of submanifolds in Lorentz space and its subspaces has great significance. Scholars have shown interest in curves in Lorentz space and its subspace and have studied evolutes, involutes, parallels and some other associated curves in these spaces. There have been several relevant investigations in this area (see [3,4,5,6,7,12,13,14,15]). Having the appearance of a negative index, there are three types of vectors in Lorentz space. For a curve, the type of tangent vector at each point determines the type of point. As for non-lightlike curves in Lorentz space, we always select their arc-length parameters and adopt the Frenet–Serret frame to investigate them (see [8,16]).

In fact, curves in Lorentz space do not always consist of a single type of points, but rather can involve all three types of points. This is what we mean by mixed-type curves. As a more familiar condition, the investigation of mixed-type curves has important significance. Because the curvature at lightlike points cannot be defined, the classical Frenet–Serret frame does not work. Due to the lack of necessary tools for its research, almost no research has been conducted on this subject. In 2018, S. Izumiya, M. C. Romero Fuster, and M. Takahashi presented the lightcone frame and established the fundamental theory of mixed-type curves in ${\mathbb{R}}_1^2$ in [17]. As an application of the theory, they studied the evolutes of regular mixed-type curves. In [18], T. Liu and the second author of this paper gave the lightcone frame in Lorentz 3-space and considered mixed-type curves in this space. Currently, the investigation of mixed-type curves in ${\mathbb{R}}_1^2$ has not been completed. As the depth of their work, the $(n,m)$-cusp mixed-type curves in ${\mathbb{R}}_1^2$ were investigated, as well as the evolutes of the $(n,m)$-cusp mixed-type curves, as presented by us in [19]. Later, we also considered the evolutoids of mixed-type curves in ${\mathbb{R}}_1^2$.

The pedal curves is a kind of significant curves due to their geometric properties. In the Euclidean space ${\mathbb{R}}^2$, the pedal curve is always defined by the locus of the foot of the perpendicular from the given point to the tangent to the base curve. M. Bo$\check{\mathrm{z}}$ek and G. Folt$\acute{\mathrm{a}}$n considered the relationship of singular points of regular curves’ pedal curves and the inflections of the base curves in ${\mathbb{R}}^2$ in [20]. Later, in [21], Y. Li and the second author of this paper studied the pedal curve of the given curves with singular points in ${\mathbb{R}}^2$. O. O$\breve{\mathrm{g}}$ulcan Tuncer et al. described the relationship of the pedal curves and contrapedal curves in ${\mathbb{R}}^2$ in [22]. However, on the topic of pedal curves of mixed-type curves in ${\mathbb{R}}_1^2$, which is an interesting and worthy subject, there have not been relevant investigations.

Our purpose in this paper was to solve the problems related to the pedal curves of mixed-type curves in ${\mathbb{R}}_1^2$. In Section 2, we review some essential knowledge about ${\mathbb{R}}_1^2$ and introduce the lightcone frame. Then, we define the pedal curves of mixed-type curves and investigate their properties in Section 3. We consider when the pedal curves of mixed-type curves have singular points and investigate the relationship of the types of points of the pedal curves and the base curves. Finally, in Section 4, for the purpose of showing the characteristics of the pedal curves of mixed-type curves, we present two examples.

If not specifically mentioned, all maps and manifolds in this paper are infinitely differentiable.

2. Preliminaries

Here, we introduce some essential knowledge about the Lorentz–Minkowski plane for the sake of convenience.

Let ${\mathbb{R}}^2=\left\{(x_1,x_2)\right|x_i\in \mathbb{R},i=1,2\}$ be a vector space of dimension 2. If ${\mathbb{R}}^2$ is endowed with the metric which is induced by the pseudo-scalar product

$$⟨\mathit{x},\mathit{y}⟩=-x_1{y}_1+x_2{y}_2,$$

where $\mathit{x}=(x_1,x_2)$, $\mathit{y}=(y_1,y_2)$, and $\mathit{x},\mathit{y}\in {\mathbb{R}}^2$, then we call $({\mathbb{R}}^2,⟨,⟩)$ the Lorentz–Minkowski plane and denote it by ${\mathbb{R}}_1^2$.

For a non-zero vector $\mathit{x}\in {\mathbb{R}}_1^2$, there are three types of vectors in ${\mathbb{R}}_1^2$. When $⟨\mathit{x},\mathit{x}⟩$ is positive, negative and vanishing, it is called spacelike, timelike or lightlike, respectively. A non-lightlike vector refers to a vector that is spacelike or timelike.

For a vector $\mathit{x}\in {\mathbb{R}}_1^2$, if there exists a vector $\mathit{y}\in {\mathbb{R}}_1^2$, which satisfies $⟨\mathit{x},\mathit{y}⟩=0$, we say $\mathit{y}$ is pseudo-perpendicular to $\mathit{x}$.

We define the norm of $\mathit{x}=(x_1,x_2)\in {\mathbb{R}}_1^2$ by

$$\parallel \mathit{x}\parallel =\sqrt{|⟨\mathit{x},\mathit{x}⟩|},$$

and the pseudo-orthogonal complement of $\mathit{x}$ is given by ${\mathit{x}}^{\perp }=(x_2,x_1)$. By definition, $\mathit{x}$ and ${\mathit{x}}^{\perp }$ are pseudo-orthogonal to each other, and

$$\parallel \mathit{x}\parallel =\parallel {\mathit{x}}^{\perp }\parallel .$$

It is obvious that ${\mathit{x}}^{\perp }=\pm \mathit{x}$ if and only if $\mathit{x}$ is lightlike, and ${\mathit{x}}^{\perp }$ is timelike (resp. spacelike) if and only if $\mathit{x}$ is spacelike (resp. timelike).

Let $\mathbf{\rho }:I(\subseteq \mathbb{R})\to {\mathbb{R}}_1^2$ be a regular curve. Denote $\dot{\mathbf{\rho }}\left(t\right)=(d\mathbf{\rho }/dt)\left(t\right)$. Then we say $\mathbf{\rho }$ is a spacelike (resp. timelike, lightlike) curve if $⟨\dot{\mathbf{\rho }}\left(t\right),\dot{\mathbf{\rho }}\left(t\right)⟩$ is positive (resp. negative, vanishing) for any $t\in I$. Furthermore, the type of a point $\mathbf{\rho }\left(t\right)$ (or, t) is determined by the type of $\dot{\mathbf{\rho }}\left(t\right)$. For more details, see [17].

Moreover, we say a curve is non-lightlike if it is a spacelike or timelike curve and a point is non-lightlike if it is a spacelike or timelike point. If $\mathbf{\rho }\left(t\right)$ contains three types of points simultaneously, then it is exactly a mixed-type curve, which is the main research object in this paper.

Set ${\mathbb{L}}^{+}=(1,1)$ and ${\mathbb{L}}^{-}=(1,-1)$. These are linearly independent lightlike vectors. The pair {${\mathbb{L}}^{+}$, ${\mathbb{L}}^{-}$} is called a lightcone frame along $\mathbf{\rho }\left(t\right)$ in ${\mathbb{R}}_1^2$, which was introduced by S. Izumiya, M. C. Romero Fuster, and M. Takahashi in [17].

Let $\mathbf{\rho }:I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve. There exists a corresponding smooth map $(\alpha ,\beta ):I\to {\mathbb{R}}^2\setminus \left\{0\right\}$, which satisfies

$$\begin{array}{c}\hfill \dot{\mathbf{\rho }}\left(t\right)=\alpha \left(t\right){\mathbb{L}}^{+}+\beta \left(t\right){\mathbb{L}}^{-},\forall t\in I.\end{array}$$

(1)

If Equation (1) is established, $(\alpha ,\beta )$ is called the lightlike tangential data of $\mathbf{\rho }\left(t\right)$. The pseudo-orthogonal complement of $\dot{\mathbf{\rho }}\left(t\right)$ can be expressed by

$$\dot{\mathbf{\rho }}{\left(t\right)}^{\perp }=\alpha \left(t\right){\mathbb{L}}^{+}-\beta \left(t\right){\mathbb{L}}^{-}.$$

Since

$$⟨\dot{\mathbf{\rho }}\left(t\right),\dot{\mathbf{\rho }}\left(t\right)⟩=-4\alpha \left(t\right)\beta \left(t\right),$$

the type of $\mathbf{\rho }\left(t_0\right)$ can be determined by $\alpha \left(t_0\right)\beta \left(t_0\right)$. For more details about the lightcone frame and the lightlike tangential data, see [17].

Definition 1.

Let $\mathbf{\rho }:I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve. We call a point $\mathbf{\rho }\left(t_0\right)$ an inflection if $⟨\ddot{\mathbf{\rho }}\left(t_0\right),\dot{\mathbf{\rho }}{\left(t_0\right)}^{\perp }⟩=0$.

Remark 1.

When $\rho \left(t\right)$ is a non-lightlike curve, the curvature at $\rho \left(t_0\right)$ is $\kappa \left(t_0\right)=⟨\ddot{\rho }\left(t_0\right),\dot{\rho }{\left(t_0\right)}^{\perp }⟩/$$\parallel \dot{\rho }\left(t_0\right){\parallel }^3$. If $\kappa \left(t_0\right)=0$, then $\rho \left(t_0\right)$ is called an inflection of $\rho \left(t\right)$. This satisfies Definition 1.

Let $\mathbf{\rho }:I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve with the lightlike tangential date $(\alpha ,\beta )$. Then, $\mathbf{\rho }\left(t_0\right)$ is an inflection of $\mathbf{\rho }$ if and only if

$$\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0.$$

Remark 2.

Let $\mathbf{\rho }:I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve with the lightlike tangential date $(\alpha ,\beta )$. When $⟨\ddot{\mathbf{\rho }}\left(t_0\right),\dot{\mathbf{\rho }}{\left(t_0\right)}^{\perp }⟩=0$, but ${⟨\ddot{\mathbf{\rho }}\left(t_0\right),\dot{\mathbf{\rho }}{\left(t_0\right)}^{\perp }⟩}^{\prime }\ne 0$, i.e., $\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0$, but $\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right)\ne 0$, $\mathbf{\rho }\left(t_0\right)$ is called an ordinary inflection. In this paper, we only consider ordinary inflections of the mixed-type curves, and we call them inflections for short.

3. Pedal Curves of the Mixed-Type Curves in ${\mathbb{R}}_{\mathit{1}}^{\mathit{2}}$

The pedal curves of the regular curves in ${\mathbb{R}}^2$ are widely studied. As for the regular curves in ${\mathbb{R}}_1^2$, the pedal curves of them are defined similarly. They are always given by the pseudo-orthogonal projection of a fixed point on the tangent lines of the base curves. Therefore, the definitions of pedal curves of the regular non-lightlike curves are given as follows.

Definition 2.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular non-lightlike curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. Then, the pedal curve $Pe\left(\rho \right)\left(t\right)$ of the base curve $\rho \left(t\right)$ is given by

$$\begin{array}{c}\hfill Pe\left(\rho \right)\left(t\right)=\rho \left(t\right)+\frac{⟨\mathit{Q}-\rho \left(t\right),\dot{\rho }\left(t\right)⟩}{⟨\dot{\rho }\left(t\right),\dot{\rho }\left(t\right)⟩}\dot{\rho }\left(t\right).\end{array}$$

(2)

It is obvious that the pedal curve of a non-lightlike curve with the lightcone frame $\{{\mathbb{L}}^{+},{\mathbb{L}}^{-}\}$ and the lightlike tangential data $(\alpha ,\beta )$ is

$$\begin{array}{c}\hfill Pe\left(\rho \right)\left(t\right)=\rho \left(t\right)-\frac{⟨\mathit{Q}-\rho \left(t\right),\alpha \left(t\right){\mathbb{L}}^{+}+\beta \left(t\right){\mathbb{L}}^{-}⟩}{4\alpha \left(t\right)\beta \left(t\right)}(\alpha \left(t\right){\mathbb{L}}^{+}+\beta \left(t\right){\mathbb{L}}^{-}).\end{array}$$

(3)

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve. Since $⟨\dot{\rho }\left(t_0\right),\dot{\rho }\left(t_0\right)⟩=0$ when $\rho \left(t_0\right)$ is a lightlike point, it is probably not always possible to define a pedal curve of a mixed type curve. In fact, if $\mathit{Q}$ coincides with the lightlike point or $\mathit{Q}$ is on the tangent line of the lightlike point, we can define the pedal curve $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ of $\rho$ with the lightcone frame $\{{\mathbb{L}}^{+},{\mathbb{L}}^{-}\}$ and the lightlike tangential data $(\alpha ,\beta )$ by Formula (3).

When $\rho \left(t_0\right)$ is a non-lightlike point, $Pe\left(\rho \right)\left(t_0\right)$ satisfies Formula (3), obviously.

When $\rho \left(t_0\right)$ is a lightlike point, $\alpha \left(t_0\right)\beta \left(t_0\right)=0$, and we suppose that $\mathit{Q}$ coincides with the lightlike point or $\mathit{Q}$ is on the tangent line of the lightlike point. In these cases, Formula (3) also holds, and in the following, we discuss the specific forms of $Pe\left(\rho \right)\left(t_0\right)$.

If $\rho \left(t\right)$ is non-lightlike, by direct calculation,

$$\begin{array}{c}\hfill Pe\left(\rho \right)\left(t\right)=\rho \left(t\right)-(\frac{\alpha \left(t\right)}{4\beta \left(t\right)}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩+\frac{1}{4}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩){\mathbb{L}}^{+}\\ \hfill -(\frac{1}{4}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩+\frac{\beta \left(t\right)}{4\alpha \left(t\right)}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩){\mathbb{L}}^{-}.\end{array}$$

If $\rho \left(t_0\right)$ is a lightlike point. Firstly, suppose that $\alpha \left(t_0\right)\ne 0$ and $\beta \left(t_0\right)=0$, then $\mathit{Q}$ coincides with the lightlike point or $\mathit{Q}$ is on the tangent line of the lightlike point is exactly $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$. In this case, we define ${\displaystyle \frac{\alpha \left(t_0\right)⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩}{\beta \left(t_0\right)}}$ as ${\displaystyle \underset{t\to t_0}{lim}{\displaystyle \frac{\alpha \left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{\beta \left(t\right)}}}$. Then, we can find that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\alpha \left(t_0\right)⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩}{\beta \left(t_0\right)}}& {\displaystyle =\underset{t\to t_0}{lim}{\displaystyle \frac{\alpha \left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{\beta \left(t\right)}}}\hfill \\ \hfill & {\displaystyle =\underset{t\to t_0}{lim}{\displaystyle \frac{\dot{\alpha }\left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩+\alpha \left(t\right)⟨-\alpha \left(t\right){\mathbb{L}}^{+}-\beta \left(t\right){\mathbb{L}}^{-},{\mathbb{L}}^{+}⟩}{\dot{\beta }\left(t\right)}}}\hfill \\ \hfill & {\displaystyle =\underset{t\to t_0}{lim}{\displaystyle \frac{\dot{\alpha }\left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩+2\alpha \left(t\right)\beta \left(t\right)}{\dot{\beta }\left(t\right)}}.}\hfill \end{array}$$

If $\rho \left(t_0\right)$ is not an inflection, $\dot{\beta }\left(t_0\right)\ne 0$, then

$${\displaystyle \frac{\alpha \left(t_0\right)⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩}{\beta \left(t_0\right)}}=0.$$

If $\rho \left(t_0\right)$ is an inflection, we have

$$\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0$$

and

$$\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right)\ne 0.$$

Since $\dot{\beta }\left(t_0\right)=0$, we can find that $\ddot{\beta }\left(t_0\right)\ne 0$. Continue to calculate and we can get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\alpha \left(t_0\right)⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩}{\beta \left(t_0\right)}}\hfill \\ \hfill & {\displaystyle =\underset{t\to t_0}{lim}{\displaystyle \frac{\alpha \left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{\beta \left(t\right)}}}\hfill \\ \hfill & {\displaystyle =\underset{t\to t_0}{lim}{\displaystyle \frac{\ddot{\alpha }\left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩+2\dot{\alpha }\left(t\right)⟨-\alpha \left(t\right){\mathbb{L}}^{+}-\beta \left(t\right){\mathbb{L}}^{-},{\mathbb{L}}^{+}⟩+\alpha \left(t\right)⟨-\dot{\alpha }\left(t\right){\mathbb{L}}^{+}-\dot{\beta }\left(t\right){\mathbb{L}}^{-},{\mathbb{L}}^{+}⟩}{\ddot{\beta }\left(t\right)}}}\hfill \\ \hfill & =0.\hfill \end{array}$$

Therefore, when $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$, ${\displaystyle \frac{\alpha \left(t_0\right)⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩}{\beta \left(t_0\right)}}$ is always equal to 0.

By the above calculation, we can define $Pe\left(\rho \right)\left(t_0\right)$ as ${\displaystyle \underset{t\to t_0}{lim}Pe\left(\rho \right)\left(t\right)}$. To sum up, if $\mathit{Q}$ coincides with $\rho \left(t_0\right)$, then $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩=0$, $Pe\left(\rho \right)\left(t_0\right)$ is given by

$${\displaystyle Pe\left(\rho \right)\left(t_0\right)=\underset{t\to t_0}{lim}Pe\left(\rho \right)\left(t\right)=\rho \left(t_0\right).}$$

If $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, then $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩\ne 0$, $Pe\left(\rho \right)\left(t_0\right)$ is given by

$${\displaystyle Pe\left(\rho \right)\left(t_0\right)=\underset{t\to t_0}{lim}Pe\left(\rho \right)\left(t\right)=\rho \left(t_0\right)-\frac{1}{4}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩{\mathbb{L}}^{+}.}$$

As for the condition of $\alpha \left(t_0\right)=0$ and $\beta \left(t_0\right)\ne 0$, in this case $\mathit{Q}$ coincides with the lightlike point or $\mathit{Q}$ is on the tangent line of the lightlike point refers to $⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩=0$, similarly we can find that:

If $\mathit{Q}$ coincides with $\rho \left(t_0\right)$, then $Pe\left(\rho \right)\left(t_0\right)$ is given by

$${\displaystyle Pe\left(\rho \right)\left(t_0\right)=\underset{t\to t_0}{lim}Pe\left(\rho \right)\left(t\right)=\rho \left(t_0\right).}$$

If $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, then $Pe\left(\rho \right)\left(t_0\right)$ is given by

$${\displaystyle Pe\left(\rho \right)\left(t_0\right)=\underset{t\to t_0}{lim}Pe\left(\rho \right)\left(t\right)=\rho \left(t_0\right)-\frac{1}{4}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩{\mathbb{L}}^{-}.}$$

Remark 3.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of $\rho$. Suppose that $\rho \left(t_0\right)$ is a lightlike point, if $\mathit{Q}$ is neither coincident with $\rho \left(t_0\right)$ nor on the tangent line of $\rho \left(t_0\right)$, then when t approaches to $t_0$, ${\displaystyle \frac{⟨\mathit{Q}-\rho \left(t\right),\alpha \left(t\right){\mathbb{L}}^{+}+\beta \left(t\right){\mathbb{L}}^{-}⟩}{4\alpha \left(t\right)\beta \left(t\right)}}$ goes to infinity. Since one of $\alpha \left(t_0\right)$ and $\beta \left(t_0\right)$ is equal to 0, $Pe\left(\rho \right)\left(t_0\right)$ asymptotic with lightlike line of ${\mathbb{L}}^{+}$ or ${\mathbb{L}}^{-}$. Specifically, when $⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩\ne 0$, since ${\displaystyle \underset{t\to t_0}{lim}{\displaystyle \frac{\alpha \left(t\right)⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{\beta \left(t\right)}}=\infty ,}$ $Pe\left(\rho \right)\left(t_0\right)$ asymptotic with lightlike line along the positive or negative direction of ${\mathbb{L}}^{+}.$ Similarly, when $⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩\ne 0$, $Pe\left(\rho \right)\left(t_0\right)$ asymptotic with lightlike line along the positive or negative direction of ${\mathbb{L}}^{-}.$ We can see the relevant examples in Section 4.

Considering when the pedal curves of the regular mixed-type curves have singular points, we have following conclusions.

Theorem 1.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of ρ. Then

(1)

if $\rho \left(t_0\right)$ is a non-lightlike point, then $Pe\left(\rho \left(t_0\right)\right)$ is a singular point if and only if one of the following conditions occur:

(i)

$\rho \left(t_0\right)$ is an inflection but $\mathit{Q}$ is not coincides with $\rho \left(t_0\right)$;

(ii)

$\rho \left(t_0\right)$ is not an inflection, but $\mathit{Q}$ coincides with $\rho \left(t_0\right)$;

(iii)

$\rho \left(t_0\right)$ is an inflection and $\mathit{Q}$ coincides with $\rho \left(t_0\right)$.

(2)

if $\rho \left(t_0\right)$ is a lightlike point, and $\mathit{Q}$ coincides with $\rho \left(t_0\right)$ or $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, then $Pe\left(\rho \right)\left(t_0\right)$ is regular.

Proof. 

As the pedal curve of the mixed-type curve $\rho \left(t\right)$ is given by the Formula (3), by direct calculation, we can get -4.6cm0cm

$$\begin{array}{c}\hfill \dot{P}e\left(\rho \right)\left(t\right)=-\frac{\dot{\alpha }\left(t\right)\beta \left(t\right)-\alpha \left(t\right)\dot{\beta }\left(t\right)}{4{\beta }^2\left(t\right)}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩{\mathbb{L}}^{+}+\frac{\dot{\alpha }\left(t\right)\beta \left(t\right)-\alpha \left(t\right)\dot{\beta }\left(t\right)}{4{\alpha }^2\left(t\right)}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩{\mathbb{L}}^{-}.\end{array}$$

(4)

When $\rho \left(t_0\right)$ is a non-lightlike point, $\dot{P}e\left(\rho \right)\left(t_0\right)=0$ if and only if

$$-{\displaystyle \frac{\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)}{4{\beta }^2\left(t_0\right)}}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$$

and

$${\displaystyle \frac{\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)}{4{\alpha }^2\left(t_0\right)}}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩=0.$$

Specifically,

$\left(\mathrm{i}\right)$$\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0$ but $\mathit{Q}-\rho \left(t_0\right)\ne 0$ if and only if $\rho \left(t_0\right)$ is an inflection, but $\mathit{Q}$ is not coincides with $\rho \left(t_0\right)$;

$\left(\mathrm{i}\mathrm{i}\right)$$\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)\ne 0$ but $\mathit{Q}-\rho \left(t_0\right)=0$ if and only if $\rho \left(t_0\right)$ is not an inflection, but $\mathit{Q}$ coincides with $\rho \left(t_0\right)$;

$\left(\mathrm{i}\mathrm{i}\mathrm{i}\right)$$\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0$ and $\mathit{Q}-\rho \left(t_0\right)=0$ if and only if $\rho \left(t_0\right)$ is an inflection and $\mathit{Q}$ coincides with $\rho \left(t_0\right)$.

Following that, we consider the condition when $\rho \left(t_0\right)$ is a lightlike point. First, we suppose that $\alpha \left(t_0\right)\ne 0$, $\beta \left(t_0\right)=0$. Since $\beta \left(t_0\right)=0$, we cannot calculate $-{\displaystyle \frac{\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)}{4{\beta }^2\left(t_0\right)}}$$⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩{\mathbb{L}}^{+}$. When $⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩\ne 0$, we have known that $Pe\left(\rho \right)\left(t_0\right)$ is asymptotic with lightlike line along the positive or negative direction of ${\mathbb{L}}^{+}.$ So we consider the condition that $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$.

First we suppose that $\rho \left(t_0\right)$ is not an inflection of $\rho \left(t\right)$, then $\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)\ne 0$.

Since $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$, we can find that

$${\displaystyle \underset{t\to t_0}{lim}{\displaystyle \frac{⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{{\beta }^2\left(t\right)}}={\displaystyle \frac{1}{\dot{\beta }\left(t_0\right)}}.}$$

As $\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)\ne 0$, $\beta \left(t_0\right)=0$ and $\alpha \left(t_0\right)\ne 0$, we can obtain $\dot{\beta }\left(t_0\right)\ne 0$. Therefore, $Pe\left(\rho \right)\left(t_0\right)$ is a regular point.

Afterwards, we suppose that $\rho \left(t_0\right)$ is an inflection of $\rho \left(t\right)$, then $\dot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\dot{\beta }\left(t_0\right)=0$, but $\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right)\ne 0$.

Since $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$, we can obtain

$${\displaystyle \underset{t\to t_0}{lim}\frac{(\dot{\alpha }\left(t\right)\beta \left(t\right)-\alpha \left(t\right)\dot{\beta }\left(t\right))⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩}{{\beta }^2\left(t\right)}=\frac{4(\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right))}{3\ddot{\beta }\left(t_0\right)}.}$$

As $\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right)\ne 0$, $\beta \left(t_0\right)=0$ and $\alpha \left(t_0\right)\ne 0$, we can get $\ddot{\beta }\left(t_0\right)\ne 0$. Therefore,

$${\displaystyle \frac{4(\ddot{\alpha }\left(t_0\right)\beta \left(t_0\right)-\alpha \left(t_0\right)\ddot{\beta }\left(t_0\right))}{3\ddot{\beta }\left(t_0\right)}}\ne 0,$$

$Pe\left(\rho \right)\left(t_0\right)$ is a regular point.

When $\alpha \left(t_0\right)=0$, $\beta \left(t_0\right)\ne 0$ and $⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩=0$, we can get $Pe\left(\rho \right)\left(t_0\right)$ is a regular point similarly. □

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of $\rho$. If we denote $\dot{P}e\left(\rho \right)\left(t\right)={\alpha }_{Pe}\left(t\right){\mathbb{L}}^{+}+{\beta }_{Pe}\left(t\right){\mathbb{L}}^{-}$, $\ddot{P}e\left(\rho \right)\left(t\right)={\alpha }_{P{e}_1}\left(t\right){\mathbb{L}}^{+}+{\beta }_{P{e}_1}\left(t\right){\mathbb{L}}^{-}$, ⋯, $P{e}^{\left(n\right)}\left(\rho \right)\left(t\right)={\alpha }_{P{e}_{n-1}}\left(t\right){\mathbb{L}}^{+}+{\beta }_{P{e}_{n-1}}\left(t\right){\mathbb{L}}^{-}$. Then, we have the following proposition about types of the singular points of $Pe\left(\rho \right)\left(t\right)$.

Proposition 1.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of ρ. Suppose that $P{e}^{\left(n\right)}\left(\rho \right)\left(t\right)$ exists. Then, $Pe\left(\rho \right)\left(t_0\right)$ is an $(n,m)$-cusp if and only if

(1)

${\alpha }_{P{e}_{j-1}}\left(t_0\right){\beta }_{P{e}_{n-1}}\left(t_0\right)-{\alpha }_{P{e}_{n-1}}\left(t_0\right){\beta }_{P{e}_{j-1}}\left(t_0\right)=0$$(j=1,2,\cdots ,m-1)$,

(2)

${\alpha }_{P{e}_{m-1}}\left(t_0\right){\beta }_{P{e}_{n-1}}\left(t_0\right)-{\alpha }_{P{e}_{n-1}}\left(t_0\right){\beta }_{P{e}_{m-1}}\left(t_0\right)\ne 0$.

We have given the definition of $(n,m)$-cusp in [19]. According to the conclusion in [19], we can obtain Proposition 1 directly.

Proposition 2.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of ρ. Suppose that $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$.

(1)

If $\rho \left(t_0\right)$ is a non-lightlike point, then $Pe\left(\rho \right)\left(t_0\right)$ coincides with $\mathit{Q}$;

(2)

If $\rho \left(t_0\right)$ is a lightlike point, then $Pe\left(\rho \right)\left(t_0\right)$ is not coincident with $\mathit{Q}$.

Proof. 

Since the pedal curve of the mixed-type curve $\rho \left(t\right)$ is given by Formula (3).

Suppose that $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, then we have $\mathit{Q}-\rho \left(t_0\right)$ and $\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-}$ are linearly dependent.

If $\rho \left(t_0\right)$ is a non-lightlike point, then there exists $\lambda \in \mathbb{R}$, such that

$$\mathit{Q}-\rho \left(t_0\right)=\lambda (\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-}).$$

We can obtain

$$\begin{array}{cc}\hfill Pe\left(\rho \right)\left(t_0\right)& =\rho \left(t_0\right)-\lambda \frac{⟨\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-},\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-}⟩}{4\alpha \left(t_0\right)\beta \left(t_0\right)}(\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-})\hfill \\ \hfill & =\rho \left(t_0\right)-\lambda \frac{-4\alpha \left(t_0\right)\beta \left(t_0\right)}{4\alpha \left(t_0\right)\beta \left(t_0\right)}(\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-})\hfill \\ \hfill & =\rho \left(t_0\right)+\lambda (\alpha \left(t_0\right){\mathbb{L}}^{+}+\beta \left(t_0\right){\mathbb{L}}^{-})\hfill \\ \hfill & =\mathit{Q}.\hfill \end{array}$$

Therefore, $Pe\left(\rho \right)\left(t_0\right)$ coincides with $\mathit{Q}$.

If $\rho \left(t_0\right)$ is a lightlike point, we have know that when $\alpha \left(t_0\right)\ne 0$ and $\beta \left(t_0\right)=0$,

$$Pe\left(\rho \right)\left(t_0\right)=\rho \left(t_0\right)-\frac{1}{4}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩{\mathbb{L}}^{+};$$

when $\alpha \left(t_0\right)=0$ and $\beta \left(t_0\right)\ne 0$,

$$Pe\left(\rho \right)\left(t_0\right)=\rho \left(t_0\right)-\frac{1}{4}⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩{\mathbb{L}}^{-}.$$

Thus, $Pe\left(\rho \right)\left(t_0\right)$ is not coincident with $\mathit{Q}$. □

Then, we investigate the type of points of the pedal curve of the mixed-type curve in ${\mathbb{R}}_1^2$ and the following proposition can be obtained.

Proposition 3.

Let $\rho :I\to {\mathbb{R}}_1^2$ be a regular mixed-type curve and $\mathit{Q}$ be a point in ${\mathbb{R}}_1^2$. $Pe\left(\rho \right):I\to {\mathbb{R}}_1^2$ is the pedal curve of ρ. If $Pe\left(\rho \right)\left(t_0\right)$ is regular, then

(1)

When $\rho \left(t_0\right)$ is non-lightlike, $Pe\left(\rho \right)\left(t_0\right)$ is a spacelike point if and only if $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩>0$.

(2)

When $\rho \left(t_0\right)$ is non-lightlike, $Pe\left(\rho \right)\left(t_0\right)$ is a timelike point if and only if $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩<0$.

(3)

When $\rho \left(t_0\right)$ is non-lightlike, $Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point if and only if $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩=0$.

(4)

When $\rho \left(t_0\right)$ is lightlike, $\alpha \left(t_0\right)\ne 0$, $\beta \left(t_0\right)=0$ and $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩=0$,

(i)

suppose that $\rho \left(t_0\right)$ is not the inflection of ρ,

(a)

$Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point if and only if $\mathit{Q}$ coincides with $\rho \left(t_0\right)$;

(b)

$Pe\left(\rho \right)\left(t_0\right)$ is a non-lightlike point if and only if $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$. Moreover, $Pe\left(\rho \right)\left(t_0\right)$ is spacelike (or, timelike) if and only if $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩\dot{\beta }\left(t_0\right)>0$ (or, $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩\dot{\beta }\left(t_0\right)<0$).

(ii)

suppose that $\rho \left(t_0\right)$ is an inflection of ρ, $Pe\left(\rho \right)\left(t_0\right)$ is always lightlike.

(5)

When $\rho \left(t_0\right)$ is lightlike, $\alpha \left(t_0\right)=0$, $\beta \left(t_0\right)\ne 0$ and $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{-}⟩=0$,

(i)

suppose that $\rho \left(t_0\right)$ is not the inflection of ρ,

(a)

$Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point if and only if $\mathit{Q}$ coincides with $\rho \left(t_0\right)$;

(b)

$Pe\left(\rho \right)\left(t_0\right)$ is a non-lightlike point if and only if $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$. Moreover, $Pe\left(\rho \right)\left(t_0\right)$ is spacelike (or, timelike) if and only if $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩\dot{\alpha }\left(t_0\right)>0$ (or, $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩\dot{\alpha }\left(t_0\right)<0$).

(ii)

suppose that $\rho \left(t_0\right)$ is an inflection of ρ, $Pe\left(\rho \right)\left(t_0\right)$ is always lightlike.

Proof. 

Since $\dot{P}e\left(\rho \right)\left(t\right)$ is given by Formula (4), we can calculate that

$$⟨\dot{P}e\left(\rho \right)\left(t\right),\dot{P}e\left(\rho \right)\left(t\right)⟩=\frac{{(\dot{\alpha }\left(t\right)\beta \left(t\right)-\alpha \left(t\right)\dot{\beta }\left(t\right))}^2}{4{\alpha }^2\left(t\right){\beta }^2\left(t\right)}⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{+}⟩⟨\mathit{Q}-\rho \left(t\right),{\mathbb{L}}^{-}⟩.$$

When $\rho \left(t_0\right)$ is a non-lighlike point, the type of $Pe\left(\rho \right)\left(t_0\right)$ can be easily obtained.

When $\rho \left(t_0\right)$ is a lighlike point, by the proof of Theorem 1, we can get the conclusion. □

4. Examples

We would like to present the characteristics of the pedal curve of the regular mixed-type curve, especially at the lightlike point of the base curve, by the following three examples.

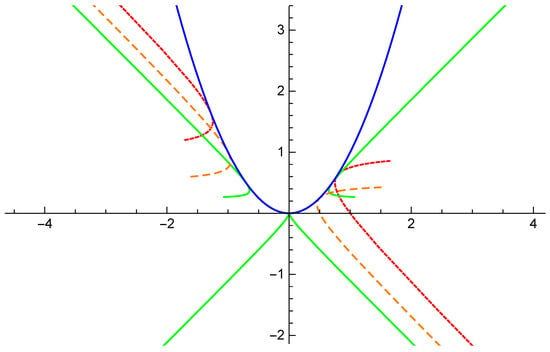
Example 1.

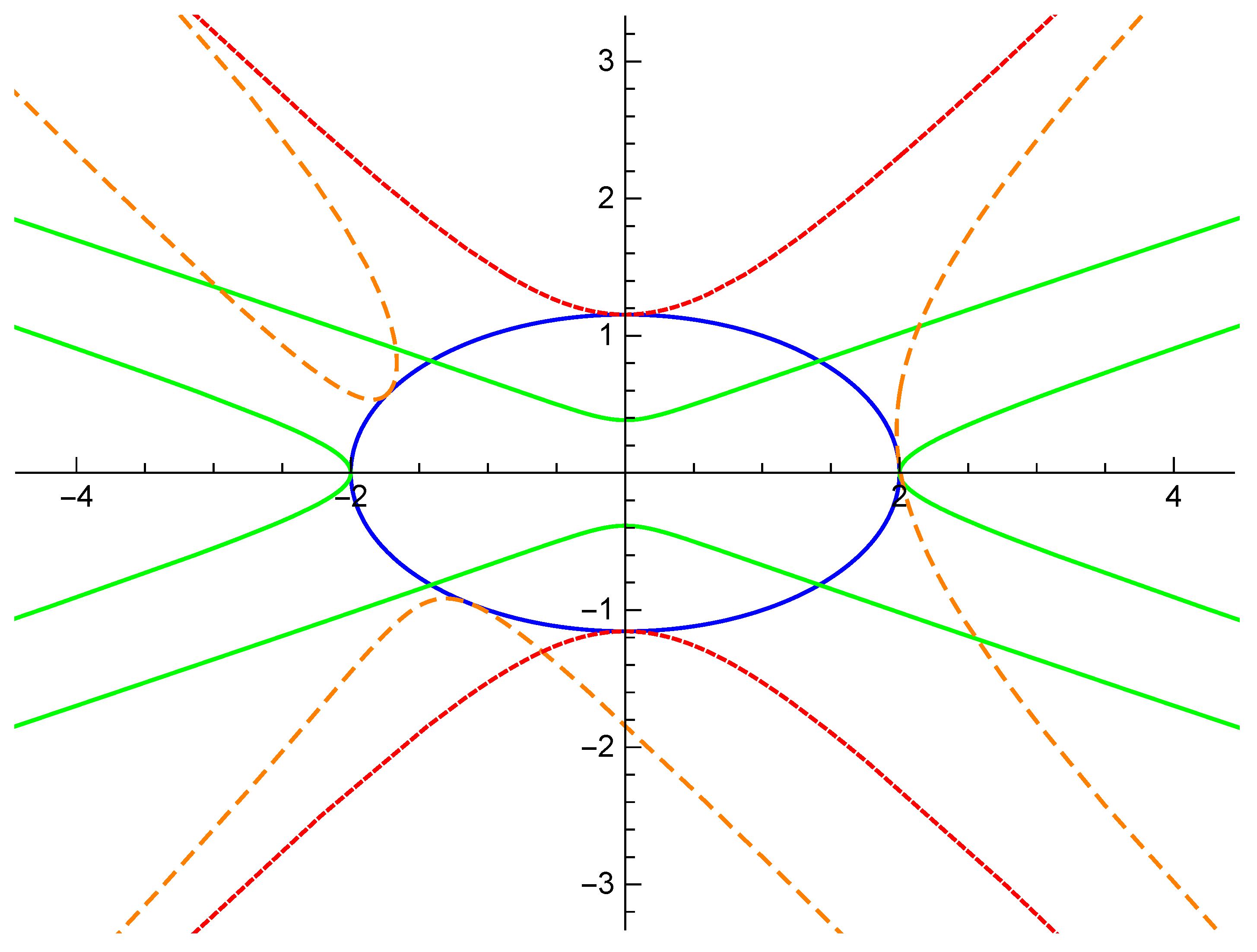
Let

$$\rho \left(t\right)=(2cost,\frac{2\sqrt{3}}{3}sint).$$

When $t_0={\displaystyle \frac{5}{6}}\pi$, $\rho \left(t_0\right)$ is a lightlike point. See the blue curve in Figure 1.

Figure 1. The mixed-type curve (blue) and the pedal curves of it.

If $\mathit{Q}=(0,0)$, then $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩\ne 0$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=({\displaystyle \frac{2cost}{{cos}^{2}t-3{sin}^{2}t}},\frac{-2\sqrt{3}sint}{{cos}^{2}t-3{sin}^{2}t}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is asymptotic with lightlike line along the positive and negative direction of ${\mathbb{L}}^{+}$. See the green curve in Figure 1.

If $\mathit{Q}=(-\sqrt{3},{\displaystyle \frac{\sqrt{3}}{3}})$, then $\mathit{Q}$ coincides with $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{2cost+3\sqrt{3}{sin}^{2}t-sintcost}{{cos}^{2}t-3{sin}^{2}t},\frac{-6\sqrt{3}sint-9sintcost+\sqrt{3}{cos}^{2}t}{3{cos}^{2}t-9{sin}^{2}t}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point. See the orange dashed curve in Figure 1.

If $\mathit{Q}=(0,{\displaystyle \frac{4\sqrt{3}}{3}})$, then $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{2cost-4sintcost}{{cos}^{2}t-3{sin}^{2}t},\frac{-6\sqrt{3}sint+4\sqrt{3}{cos}^{2}t}{3{cos}^{2}t-9{sin}^{2}t}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is a timelike point. See the red dashed curve in Figure 1.

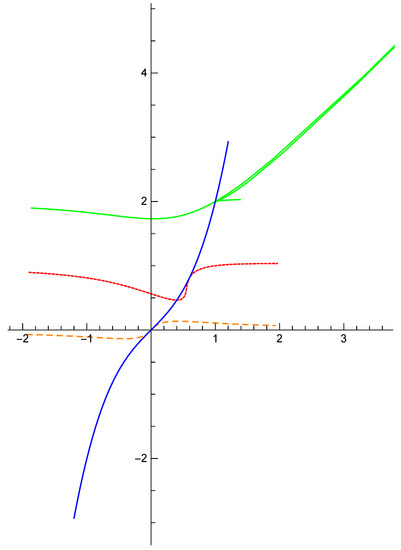
Example 2.

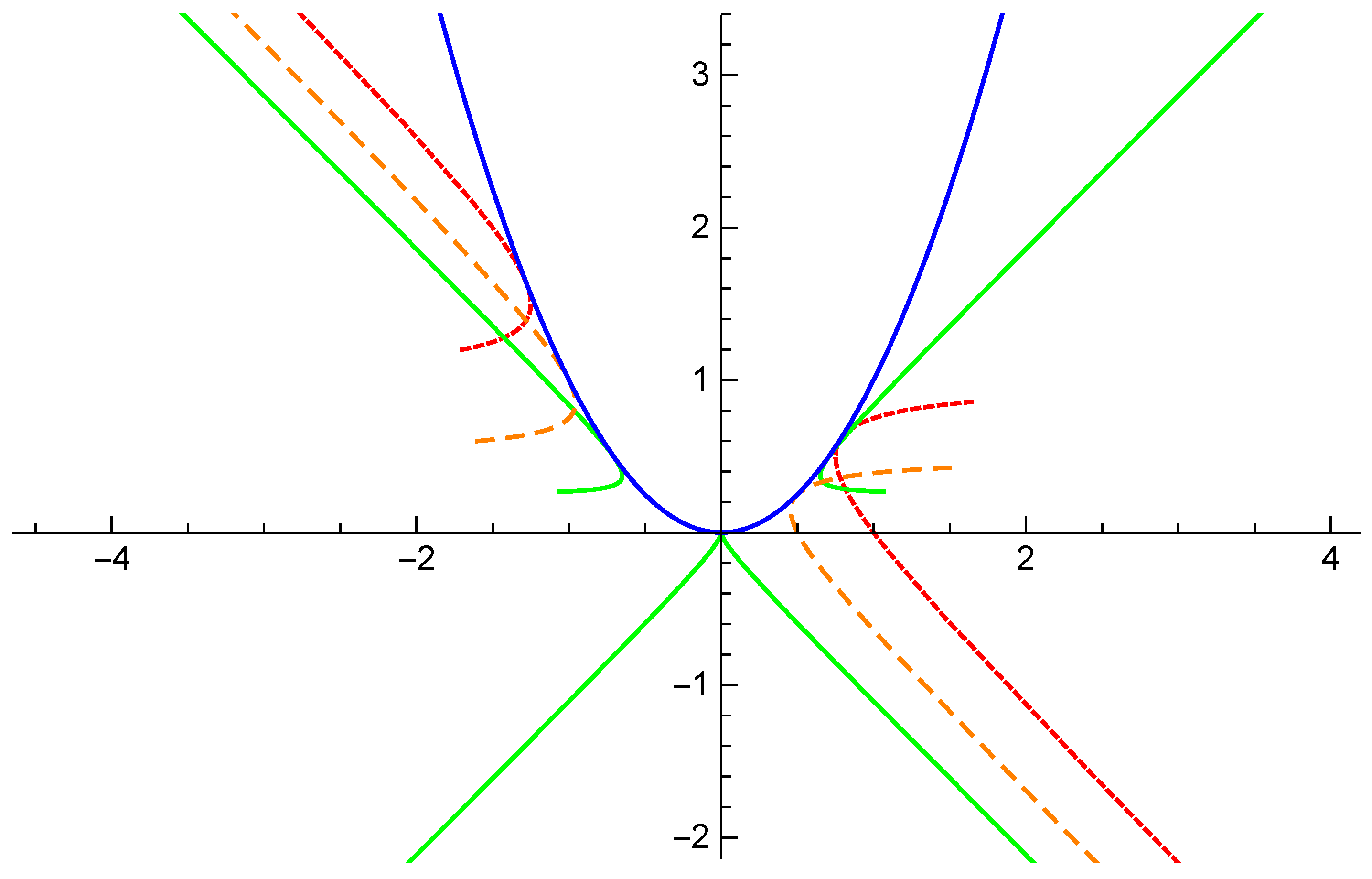
Let

$$\rho \left(t\right)=(t,t^2).$$

When $t_0={\displaystyle \frac{1}{2}}$, $\rho \left(t_0\right)$ is a lightlike point. See the blue curve in Figure 2.

Figure 2. The mixed-type curve (blue) and the pedal curves of it.

If $\mathit{Q}=(0,0)$, then $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩\ne 0$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{2t^3}{4t^2-1},\frac{t^2}{4t^2-1}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is asymptotic with lightlike line along the positive and negative direction of ${\mathbb{L}}^{+}$. See the green curve in Figure 2.

If $\mathit{Q}=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}})$, then $\mathit{Q}$ coincides with $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{2t^2+t+1}{4t+2},\frac{t}{2t+1}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point. See the orange dashed curve in Figure 2.

If $\mathit{Q}=(1,{\displaystyle \frac{3}{4}})$, then $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{2t^2+t+2}{4t+2},\frac{2t}{2t+1}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is a spacelike point. See the red dashed curve in Figure 2.

Example 3.

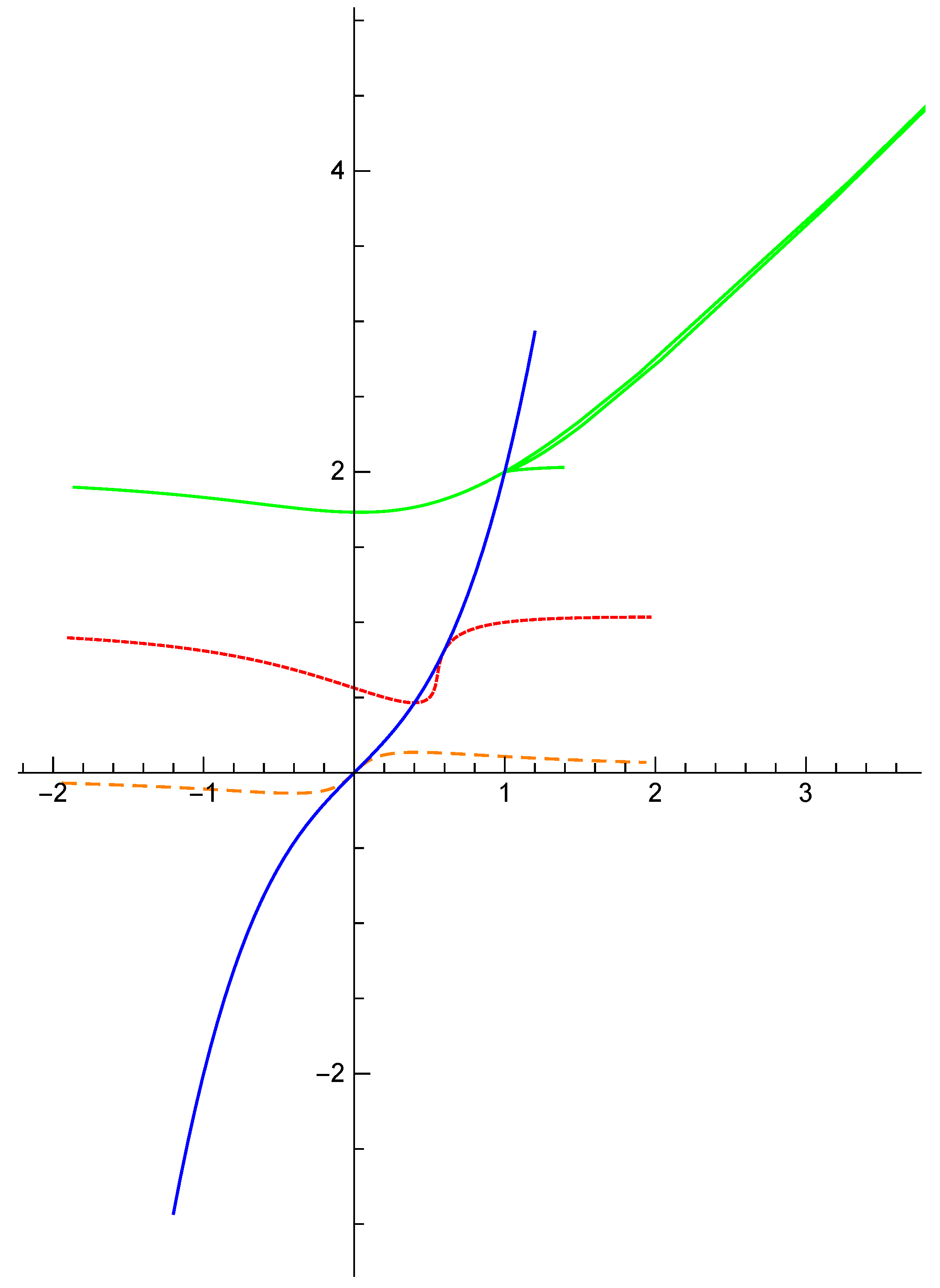
Let

$$\rho \left(t\right)=(t,t^3+t).$$

When $t_0=0$, $\rho \left(t_0\right)$ is a lightlike point and it is also an inflection. See the blue curve in Figure 3.

Figure 3. The mixed-type curve (blue) and the pedal curves of it.

If $\mathit{Q}=(1,2)$, then $⟨\mathit{Q}-\rho \left(t_0\right),{\mathbb{L}}^{+}⟩\ne 0$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{6t^5+2t^3+6t^2+1}{9t^4+6t^2},\frac{18t^4+2t^3+9t^2+1}{9t^4+6t^2}).$$

In this case $Pe\left(\rho \right)\left(t_0\right)$ is asymptotic with lightlike line along the positive and negative direction of ${\mathbb{L}}^{+}$. See the green curve in Figure 3.

If $\mathit{Q}=(0,0)$, then $\mathit{Q}$ coincides with $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{6t^3+2t}{9t^2+6},\frac{2t}{9t^2+6}).$$

In this case, $Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point. See the orange dashed curve in Figure 3.

If $\mathit{Q}=(1,1)$, then $\mathit{Q}$ is on the tangent line of $\rho \left(t_0\right)$, the pedal curve of $\rho \left(t\right)$ is

$$Pe\left(\rho \right)\left(t\right)=(\frac{6t^3+2t+3}{9t^2+6},\frac{9t^2+2t+3}{9t^2+6}).$$

In this case $Pe\left(\rho \right)\left(t_0\right)$ is a lightlike point. See the red dashed curve in Figure 3.