Abstract
In recent years, many researchers have utilized metaheuristic optimization algorithms along with fuzzy logic theory in their studies for various purposes. The harmony search (HS) algorithm is one of the metaheuristic optimization algorithms that is widely employed in different studies along with fuzzy logic (FL) theory. FL theory is a mathematical approach to expressing uncertainty by applying the conceptualization of fuzziness in a system. This review paper presents an extensive review of published papers based on the combination of HS and FL systems. In this regard, the functional characteristics of models obtained from integration of FL and HS have been reported in various articles, and the performance of each study is investigated. The basic concept of the FL approach and its derived models are introduced to familiarize readers with the principal mechanisms of FL models. Moreover, appropriate descriptions of the primary classifications acquired from the coexistence of FL and HS methods for specific purposes are reviewed. The results show that the high efficiency of HS to improve the exploration of FL in achieving the optimal solution on the one hand, and the capability of fuzzy inference systems to provide more flexible and dynamic adaptation of the HS parameters based on human perception on the other hand, can be a powerful combination for solving optimization problems. This review paper is believed to be a useful resource for students, engineers, and professionals.
1. Introduction
The complex nature of many engineering problems on the one hand and the problem of dealing with the concept of uncertainty in such problems on the other hand has led researchers to utilize metaheuristic optimization algorithms and fuzzy logic (FL) theory in solving real life optimization problems. In addition, the unique and useful features of metaheuristic optimization algorithms and FLSs have made each of these methods reinforce itself by relying on the other method advantages. Metaheuristic optimization algorithms are a sort of random algorithm that arbitrarily but intentionally and quickly scans search space to find the optimal solution [1]. FL is a mathematical approach to expressing uncertainty that helps in fuzziness conceptualization in a system to a measurable parameter. In this regard, the HS algorithm along with FL have been investigated in numerous research papers with different goals.
The HS algorithm is a metaheuristic optimization algorithm inspired by music that mimics the musical improvisational method to solve complex optimization problems. The HS algorithm aims to simulate attempts by the players to improve harmonies. Based on their observations and their attempts to identify new harmonies, musicians seek to create perfect harmonies [2]. Among the benefits of the HS algorithm are that it is relatively quick to apply and straightforward to conceptualize. Thus, in a large number of test trials, these primary benefits resulted in the substantial use of the HS algorithm compared with other methodologies for optimization [3].
The use of HS in different studies has been widely reported in the literature [3]. In a research paper by Geem [2], the theory and applications of HS have been presented. Askarzadeh [4] presented a brief review about the applications of HS in solving power systems optimization problems. Dubey et al. [5] also proposed applications of HS in a variety of fields such as civil, electrical, computer and mechanical engineering. In a study performed by Nazari-Heris et al. [6], a review of HS applications to energy systems has been presented. Ala’a et al. [7] reviewed HS applications in optimization, engineering, computer science, biology, etc. Manjarres et al. [8] addressed HS applications in optimization problems. In addition, in work conducted by Kumar et al. [9], fuzzy modeling and service control based on an optimal N-policy for fault tolerance system have been investigated using the HS algorithm.
For many difficult applications, FL is a practical option because it offers a straightforward method for designing structures using heuristic knowledge [10]. The heuristic knowledge can come from a system operator that has communicated directly with the mechanism. This operator is asked to write down a series of rules in the FL architecture framework regarding the control of the operation. A fuzzy model usually consists of a rule framework, where the available information is clear and easily readable. In some areas such as pattern recognition [11,12], PID controllers [13,14], and image processing [15,16] fuzzy design techniques have been widely utilized. In this regard, Harirchian and Lahmer [17] developed a hierarchical T2-FLS to improve the evaluation of earthquake hazard safety of existing buildings. In the study done by Zhai and Williams [18], consumer acceptance PV using fuzzy logic model has been analyzed. Korol [19] also addressed forecasting exchange rates using a FL model. Fuzzy systems have also demonstrated their ability for classification [20], fuzzy modeling [21], or FC [22], in a large number of applications. Simplicity in execution, high adaptability, low sensitivity to system fluctuations and the absence of the need for mathematical models are among the key reasons for employing FL in a wide variety of applications [23,24,25,26]. In most cases, the secret to its success has been the ability of fuzzy systems to integrate the human experience.
Despite the past good experience, the lack of learning capabilities that define much of the work in the field has led to curiosity in the study of fuzzy structures with added learning capabilities in recent decades. Recent interest in the field of computational intelligence has focused on the integration of FLSs with metaheuristic algorithms. As a result, a new class of systems has arisen, called EFSs [27,28]. Centered on a metaheuristic algorithm, these methods generally allow the automated generation and tuning of fuzzy structures through a learning process. The approaches to EFSs reported in the literature can be divided into two classes: tuning and learning [27,28].
A metaheuristic algorithm is implemented in a tuning approach to change the parameters of an embedded fuzzy system without modifying its base of rules. Some examples of tuning through the EFSs are the calibration of fuzzy controllers [29,30], the adaptation of T2-FLSs [31], and the improvement of accuracy in fuzzy models [32,33]. In the learning class, a metaheuristic optimization algorithm produces the rule base of a fuzzy system so that the final fuzzy system can correctly replicate the model framework.
There are many learning examples in EFSs that consider various types of problems, such as the selection of fuzzy rules with membership functions [34], rule generation [35], and the determination of the entire fuzzy structure [36].
There are many benefits associated with the use of FL for designing optimization methods given as follows:
- (1)
- Generation. Complex natural or social processes replicate traditional metaheuristic methods. The computational modeling of partially known behaviors and non-characterized operations, while often still undefined, requires such a replication. It is also especially difficult to accurately model even basic metaphors. However, FL offers a simple and well-known framework for designing structures by using human intelligence [37].
- (2)
- Transparency. Metaphors used by metaheuristic methods contribute to algorithms that are difficult to understand from an optimization viewpoint. However, the metaphor should not be translated specifically as a clear search technique. On the other hand, fuzzy reasoning produces entirely interpretable models whose content reflects the quest technique as human beings would execute it [38].
- (3)
- Improvement. Metaheuristic methods were configured to preserve the same protocol for the generation of candidate solutions.
As a result, every approach has its own unique features, outputs, and abilities. Nonetheless, none of the algorithms can solve all problems related to optimization alone and absolutely. Thus, new high-capacity ideas are being implemented to address specific optimization challenges and to improve the methods. One of the creative ideas proposed in recent years is the use of scientific and practical methodologies that are based on combining the metaheuristics with FL, in particular, the HS with some concepts of FL and also using the benefits of each to reinforce the other. Thus, given the unique features of fuzzy systems for the accurate and realistic modeling of different problems in various applications on the one hand, and the exceptional advantages of HS in solving problems and finding optimal values on the other hand, researchers have given much attention to employing and integrating these methods in their studies.
The aforementioned studies and reviews show that no research has reviewed and analyzed articles based on application of HS and FL in the literature so far. This paper reviews a variety of applications of HS combined with FL in different articles. However, the combination of the FL and the HS in different articles has a unique and different function. Published articles describe a combination of these two methods to achieve different goals. Thus, the main contribution of this paper is to explore the goals behind the combination of FL and HS in the literature. The main questions that arise here are: What are the major goals and applications of employing the FL theory and the HS algorithm in the studies performed? What is the efficiency of the FL concept in the HS algorithm? What is the role of the HS algorithm in fuzzy control systems?
This paper attempts to response to the aforementioned questions to provide a comprehensive overview of the concepts, applications, and various combinations of FL theory and HS. In the present study, peer-reviewed articles were divided into five main sections: hybrid HS and FL algorithm, fuzzy HS algorithm, HS algorithm and fuzzy controllers, HS algorithm and fuzzy clustering, and HS for optimizing fuzzy systems. In each section, when reviewing published articles, the full specification of the applied methods and the purpose of their combination are expressed. The paper also discusses the benefits of integrating HS and FL in various contributions.
The paper is organized as follows: Section 2 briefly represents the HS algorithm. Section 3 first outlines the theory of FL, its concept, and its models. The overall performance of the HS algorithm and FL as well as their different combinations in the literature is discussed in Section 4 with a concise explanation of its applications and contributions. Discussions on the performance and advantages of the HS algorithm and FL combinations in the literature, along with statistical results, are provided in Section 5. Finally, Section 6 concludes the findings of this review paper and indicates some directions for future study.
2. Harmony Search Algorithm
This section discusses the HS algorithm along with its inspiring definition and running searches. Driven by the excellent properties of harmony, Geem et al. [39] invented the HS algorithm. Musicians aim for a delicate equilibrium that is aesthetically determined. Similarly, optimization approaches aim to identify an ideal (global optimum) condition that is determined by the objective function value.
The aesthetic measurement of HS is based on sounds created by a musical group. The objective function was measured by a set of quantitative variables. Continuous repetition can generate more aesthetic stimuli, and frequent simulations usually improve the efficacy of the task. The main steps of the SHS are as follows:
Step 1: Generate random vectors (x1, x2, x3, …, xHMS), as many as HMS, and save them in the HM matrix.
As seen in Equation (1), the last column in HM is the fitness (cost) value.
Step 2: Create a new harmony . Here, for each component of :
- Select a value from the HM: with probability HMCR (Harmony Memory Considering Rate), 0 ≤ HMCR ≤ 1;
- Perform the uniform random search between lower and upper bounds with probability (1-HMCR).
Step 3: If a value from the HM is selected in Step 2, then:
- Slightly modify : with a probability of PAR, 0 ≤ PAR ≤ 1, where rand denotes an evenly generated random value in interval span zero and one and BW is the maximum variation in the pitch adjusting phase;
- Do not change anything with probability (1-PAR).
Step 4: Repeat Steps 2 and 3 for the number of design variables and then update the HM matrix.
Step 5: Repeat Steps 2 to 4 before the stop condition is met (e.g., the full number of evaluations of functions or iterations).
Algorithm 1 shows the pseudo-code of the regular HS.
| Algorithm 1 Pseudo-code of the HS. |
| Choose the HS user parameters: HMS, HMCR, PAR, BW, and Max_Improvisation. |
| Create randomly the (HM considering the upper and lower bounds. |
| Calculate the objective function of the HM individual. |
| while (t ≤ Max_Improvisation) or (Any Stopping Condition) |
| for each i ϵ [1, n] do |
| if rand (0,1) ≤ HMCR |
| where j ~ U (1, …, HMS). |
| if rand (0,1) ≤ PAR |
| end if |
| else |
| end if |
| Calculate the objective function (fitness/cost function) of a new harmony. |
| If cost (new harmony) < cost (worst harmony in HM) |
| Replace the worst harmony in HM with the new harmony |
| end if |
| end while |
| Post process and visualization |
3. Fuzzy Logic Theory
Fuzzy sets and FL were introduced by Zadeh [10,40] to model imprecision and deal more effectively with inaccuracies in human reasoning. FL delivers a mathematical conceptual framework for systematically expressing ambiguity and uncertainty when faced with real problems. FL, as opposed to the classical two-valued logic, seems to be more in line with the needs of today’s world in the face of reality ambiguity and uncertainty, and can provide a more realistic picture of things given uncertainty.
FL is capable of imitating human reasoning and provides the basis for inference and decision-making under imprecision in various fields and situations including engineering, economy, social sciences, etc. Many successful applications of FL fostered the development of the theory, from which subsequent generalizations emerged, including interval fuzzy sets, type-2 fuzzy sets, etc.
3.1. Fuzzy Sets
In the real world, we often encounter ambiguous or vague data such as ‘about 3’, ‘rather greater than 5’, ‘more or less between 7 and 10’, etc. Moreover, linguistically expressed outcomes such as ‘light’, ‘moderate’ or ‘severe’ occur frequently in everyday life. To model imprecise concepts and process uncertainty in information, the idea of a fuzzy set was first introduced by Zadeh in 1965. Hence, a fuzzy set A in the universe U that is defined by a function of membership that takes values in the interval [0, 1], i.e.,:
A fuzzy set in real line which is normal (i.e., there exists an element x such that ), fuzzy-convex (i.e., ) with upper-semi continuous membership function is called a fuzzy number. Various types of fuzzy numbers are shown in Figure 1. For example, (a) is a triangular fuzzy number, (b) is a trapezoidal fuzzy number, and (j) is a Gaussian fuzzy number.
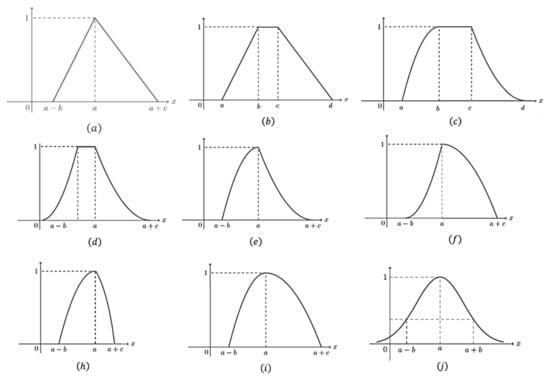
Figure 1.
Various types of fuzzy numbers.
Since Zadeh introduced a fuzzy set some criticism was made about the fact that the membership function of a fuzzy set has no uncertainty associated with it. Thus, Zadeh [41] suggested the type-2 fuzzy sets. A type-2 fuzzy set is defined as given follows:
where the membership degree of the fuzzy set is represented by U which is the primary domain and is the secondary domain. There are numerous types of type-2 fuzzy sets. Uncertainty in the primary memberships of a type-2 fuzzy set, , consists of a bounded region that we call the footprint of uncertainty (FOU). It is the union of all primary memberships, i.e.,
The shaded regions of Figure 2 show FOU of the symmetric interval types of type-2 fuzzy sets [42].
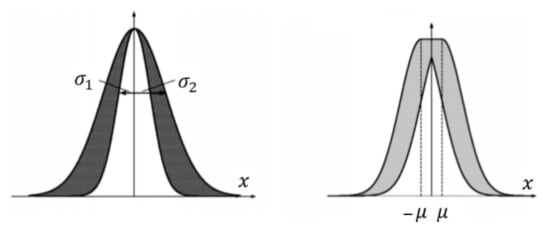
Figure 2.
FOU of symmetrical interval types of type-2 fuzzy numbers.
3.2. Type-1 Fuzzy Logic System
The main elements for a T1-FLS are depicted in Figure 3, i.e., the fuzzifier that takes crisp inputs and maps them into fuzzy sets, the rules-based inference engine which maps, fuzzy sets from the antecedents to the corresponding fuzzy sets; finally, from the fuzzy sets, the defuzzifier gets a crisp rating.

Figure 3.
Construction of a T1-FLS.
Equation (4) is an example of the rules, and the input space is mapped onto the output space and is given as follows:
where indicates a specific rule, is input , is a membership function on rule and input , and is the output on membership function . Both and have the form of and , respectively.
3.3. Type-2 Fuzzy Logic System
Zadeh initially introduced the T2-FLS in 1975 [41] as an extension of the usual fuzzy system. The T2-FLS provides additional free architecture parameters for FL systems, which can be helpful as there are several inconsistencies in the systems [42]. Most researchers are interested in the IT2-FLS due to the computational complexity of a general T2-FLS, because of its simplicity and reduced computational cost which makes the IT2-FLS very realistic [42]. The T2-FLSs were effective in many applications, such as modeling and regulation, classification, prediction, and so on [43,44].
Type-1 TSK FL system architecture can generally be divided into three parts: the determination of the number of rules, the determination of the structure of the rules, and tuning of the preceding rules and their consequent parameters. When determining the best number of rules and the best parameters of membership functions in each rule, the difficulty associated with designing an FL structure is observed.
The T2-FLS uses an ambiguity footprint, and it is the feature value at each point in the 2D space. We have uncertainty in the T1-FLS only in the precedent of the law, while in the T2-FLS, we have uncertainty in both the precedent and the result of the statement.
4. Harmony Search Algorithm and Fuzzy Logic Theory
The unique features of the fuzzy systems for accurate and realistic modeling of different problems in various applications on the one hand, and the exceptional advantages of meta-heuristic optimization algorithms in solving problems and finding optimal solutions on the other hand have led researchers to focus on employing and integrating these methods in their investigations. Therefore, recently, when solving optimization problems, one of the creative and intelligent actions of researchers and scientists has been to combine metaheuristics such as the HS algorithm and the concepts connected with FL to take advantage of both approaches. However, one can distinguish various types of combinations of the HS algorithm with FL that appear in the peer-reviewed articles. Actually, these approaches and hence the related papers can be divided into five main clusters, which are depicted in Figure 4 and discussed more thoroughly in the following sections. According to Figure 4, different categories of papers based on the HS and FL theory include Hybrid HS and FL, Fuzzy HS, HS and fuzzy controllers, HS and fuzzy clustering and HS to optimize FL systems.
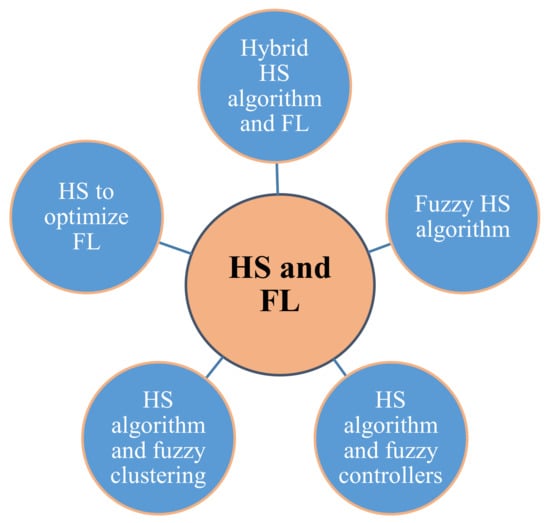
Figure 4.
Different categories of papers based on the HS and FL.
4.1. Hybrid HS Algorithm and Fuzzy Logic Theory
In many papers, researchers apply the HS and FL simultaneously to solve optimization problems. Due to the significant advantages and capabilities of the HS and FL algorithm in solving optimization problems, the hybrid methodology is expected to perform better than either method alone. In this section, articles based on the hybrid HS and FL algorithm are analyzed.
Jalili and Ghadimi [45] proposed a hybrid strategy to tackle congestion control in the energy sector based on HS and the fuzzy mechanism. The article proposes to combine the concept of HS and Fuzzy for rescheduling the system with congestion management to minimize costs and congested lines under congestion conditions, taking into account production constraints and satisfactory loads.
In [46], the problem of FJSP was presented using the DHS algorithm taking into account the fuzzy processing time. One of the seven aspects of remanufacturing is the fuzziness or volatility of the processing time. The goal was to reduce the full fuzzy completion time. To initiate the harmony population, a simple and powerful heuristic rule was proposed. Extensive quantitative tests were conducted using five benchmarks with eight remanufactured cases. The proposed DHS algorithm was contrasted with six metaheuristics. The findings and comparisons demonstrated the efficiency and usefulness of DHS in solving FJSP with fuzzy processing time.
In [47], improved optimal fuzzy C-means clustering and IHS algorithms to achieve dynamic reconfiguration of distribution networks are described. The results indicated that the proposed method can strictly limit the operation times of the switches and improve the efficiency of the HS algorithm.
In [48], the integration of the FL system with the HS algorithm was used to find the optimal solution to the problem of optimal power flow in control systems. This approach was aimed at reducing the total fuel cost of thermal units with a square cost characteristic and gravity index. The proposed algorithm parameters, such as pitch adjustment speed and bandwidth, were modified by the FL method. The optimization results indicated that the proposed algorithm was able to increase the protection of the transmission at an acceptable fuel cost.
In a study performed by Peraza et al. [49], a FHS algorithm was proposed to solve optimization problems. The FHS was based on a recent FL approach for the dynamic adaptation of harmony memory consideration and pitch change parameters, which increased the rate of convergence of the SHS algorithm. The aim of the process was to dynamically change the parameters. Since then, the FHS algorithm has been successfully extended to numerous benchmarks for optimization. The results of the simulation and comparative experiments showed the feasibility and effectiveness of the proposed method in comparison with the current optimizers.
Alia et al. [50] applied the HFISA for image segmentation. To achieve better performance while avoiding the challenges of local optimization, an HS model was implemented that used fuzzy image pixel memberships to a predefined number of clusters as decision variables, rather than cluster centroids. This hybridization strategy significantly improved HFISA convergence efficiency and speed, which outperformed the C-means fuzzy algorithm.
In research conducted by Babu and Mohan [51], to determine the location of DG units in electrical distribution systems, the FL and HS algorithm techniques were used to minimize power losses and increase the voltage profile. In particular, the FL technique was used to indicate the optimal positions of DG units, while HS was used to find their optimal sizes.
In a study by Esmaeili et al. [52], the FL method was used to solve multi-objective problems, and the FHS algorithm was proposed to obtain an optimal solution for network reconfiguration and condenser positioning in the context of a multi-objective question. The aim of the optimization was to reduce the cost of actual power losses and the construction of shunt capacitors as well as to increase the harmonic state of the network. The findings showed that simultaneous analysis of the shunt capacitor position and network reconfiguration gave better results compared to separate studies.
Geem [53] proposed combining the FL and HS theory for multi-purpose optimization of WDN. Based on the results, a Pareto set of WDNs design solutions was successfully obtained.
Varghese and Amudha [54] developed a structure based on the HHS-FL algorithm to solve the problem of unit involvement in the power industry. Wind speed was tested in the Coimbatore area and the excellent results of the proposed HHS-FL were verified.
In the paper by Peraza et al. [55] on the complex harmony memory adaptation, the FHS was used to consider parameters along the iterations and thus gain control of the intensification and diversification of the search space.
The previously proposed FHS has already been extended to classical mathematical pattern functions [49]. The comparison of the optimization results showed that the FHS approach allows finding complex functions at global minima. Previously, the proposed FHS had already been extended to classic mathematical benchmark functions [49]. A comparison of the optimization results showed that the FHS approach has the ability to find complex functions at global minima.
In a study by Dahej et al. [56], FO strategy and HS were presented for the optimal arrangement of flexible AC transmission systems devices in a multi-objective structure to increase voltage stability and reduce losses. The task of the applied HS was to simultaneously locate both the series and parallel devices and to determine the sizes, while a fuzzy method was used to find the best solution. The proper utilization of the presented algorithm can be appreciated by comparing the results obtained by the proposed algorithm with those of PSO and GAs.
In [57], a fuzzy-IHS algorithm was used to carry out the optimum multi-objective positioning and dimensioning of passive and active control filters. In their report, the pitch changing rate gradually varied with the number of generations. The results of the simulation demonstrated the adequacy and profitability of their approach.
To accomplish the optimization of the benchmark mathematical functions and to find the global optimum, Peraza et al. [58] merged the HS algorithm with type-1 and interval type-2 FL. The results obtained show that the combination of HS with type-2 FL yielded better results in most considered functions than was the case of HS with type-1 FL, and achieved greater stability for the comparison feature set.
In the study by Nie et al. [59], the image thresholding approach was tested using the fuzzy correlation parameters and HS. The maximal fuzzy correlation criterion was established in their analysis using the Z- and S-fuzzy member functions on the histogram of the picture gray level. Then HS-based image segmentation with fuzzy parameters was introduced. In other words, HS was used to obtain the optimal balance of fuzzy parameters. The results of the experiment showed that the proposed system had high efficiency compared to other methods.
In a study by Mistarihi et al. [60], a recent smooth, sophisticated HS algorithm was used to solve the single-objective BAP. The key stages of the proposed algorithm were parameter initialization, harmony memory initialization and validation, improvisation, harmony memory update, AHS parameter update, and termination criterion verification. The proposed strategy was aimed at achieving a better rate of convergence and preventing stack in the local optima. The obtained results indicate that the proposed algorithm is an effective and promising method in solving BAP.
In a study by Lu and Wang [61], the perishable food transportation problem was solved by the HS-based algorithm and a mathematical model was developed that could determine the optimal flow by taking into account certain characteristics of the problem. The aim of the model was to reduce the total cost and the weighted depreciation ratio for the transport of perishable food.
Based on a study by Aungkulanon et al. [62], various HS hybridizations for solving APP problems with a fuzzy programming approach are presented. The VHSA and NGHSA has been employed to generate new solution vectors that enhance the accuracy and convergence rate of SHS. VHSA and NGHSA have been successfully applied to this benchmarking engineering optimization problem.
Abhishek et al. [63] proposed a fuzzy-embedded HS in an experimental study in which the optimization of multiple output characteristics such as thrust, torque, and delamination factor for drilling CFRP (polyester) composite plates was carried out to achieve the most desirable parametric configuration. To transform multiple responses into a single response (objective value), called the multi-performance characteristic index, the fuzzy inference method was introduced. The success of the proposed HS in combination with the FL contrasted with GA and Taguchi’s optimization approach.
In a study by Meena et al. [64], fuzzy modeling and HS were proposed for machining systems with general repair, standby assistance, and vacation. The primary goal of the research is to build a fuzzy model and promote the cost analysis carried out with the use of HS. This paper uses fuzzy rules to develop a fuzzy model, and HS was used to reduce costs.
Diao and Shen [65] proposed a hybrid approach to the induction of the fuzzy-rough law. The proposed hybrid approach used HS to create and improvise evolving sets of rules, thus allowing the system to converge to a specific set of rules. The usefulness of the proposed algorithm, including fuzzy and rough rules, has been experimentally tested against leading classifiers. The obtained results showed that the proposed method was able to achieve better results compared to others.
In a study by Sadaei et al. [66], an updated hybrid algorithm was discussed. The proposed REWFTS-IHS algorithm was based on a complex exponentially weighted fuzzy algorithm that was compatible with an IHS. The proposed approach may have an appropriate impact on short-term load forecasting. In their study, the first step was to recognize the fuzzy logical order of relations in order to analyze the autocorrelation. The second step was to determine the optimal periods and acceptance rates using the training data. However, REWFTS was proposed at the third level. A flowchart of the proposed algorithm is shown in Figure 5. The findings of the error analysis demonstrated the advantages of the evolved algorithm with respect to its prediction accuracy.
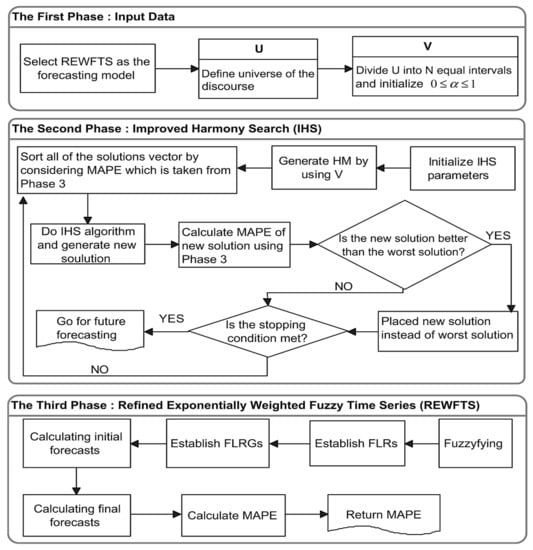
Figure 5.
REWFTS–IHS algorithm [66].
By hybridizing the FTS and GHSA with LSSVMs, the so-called GHSA-FTS-LSSVM scheme, Chen et al. [67] proposed a modern electric load forecasting model. Firstly, the clustering center of each cluster was determined using the FCC algorithm. Secondly, the LSSVM was introduced to model the resulting array, which was optimized by the GHSA. Finally, to evaluate the performance of the proposed model, a real-world example was introduced and the results obtained were correlated with the ARIMA model and other algorithms hybridized with LSSVM, including GAs, PSO, and regular HS. The results of the forecasts showed that the proposed GHSA-FTS-LSSVM model generally provides more predictable performance.
Several FTS models have already been used to solve nonlinear and complex problems in recent years. However, fuzzy time-series structures of the first order have proved insufficient to solve these problems. For this reason, several researchers have recommended a high-order FTS model to increase the accuracy of forecasting.
Van Tinh and Thi [68] proposed a high-order prediction model based on FTS and HS algorithms to improve the predictive performance of fuzzy time-series models of the first order. Firstly, a forecasting model was built based on a high-order FL relationship. The HS algorithm was then combined with the FTS model to vary the length of each interval to find the optimal interval in the discourse universe to increase prediction accuracy. To demonstrate the forecasting mechanism and the usefulness of the proposed model, two sets of figures were used: Vietnam Annual Rice Production and Alabama University enrollment. The results of the application guaranteed the advantage of the planned model over other methods of forecasting recruitment at the University of Alabama.
Dash and Dash [69] proposed a new SERNFIS that was designed to efficiently forecast highly fluctuating and erratic financial time-series results, such as stock market indices, via a modified differential HS technique. The network is modeled with fuzzy if-then rules of the first-order TSK with two types of feedback loops. The modified HS algorithm used the best mutation technique in the pitch shift procedure, and the algorithm’s control parameters were adapted using the JADE method. The effectiveness of the proposed model in relation to the current stock price forecasting models was demonstrated by the experimental results obtained as a result of testing the model on two separate stock indices.
In the interconnected power grid, Zadeh and Bathaee [70] discussed load frequency management by recognizing complexity using HS and fuzzy neural networks. In their study, the proportional-integral (PI) control coefficients were defined using HS, and then, taking into account the ambiguity, the optimal coefficients for the PI controller were obtained. Then, tests and validation of the fuzzy neural network were carried out. In a variety of complex systems with uncertainties, the proposed approach has shown the potential to regulate the regulator coefficients.
Focusing on the LNF, Miranian and Abdollahzade [71] developed a method for short-term wind energy forecasting. Local LSSVMs, which are able to deal with complex and non-linear time series (e.g., Wing-Generation Series), have been enhanced by the LNF model and equipped with an HSPS. HS was used in HSPS during the partitioning process to identify the ideal partitioning path. With the HS algorithm for wind energy forecasting applications, the calculation results showed the promising success of the LNF model. Table 1 provides a summary of the hybrid HS algorithm and FL-based articles.

Table 1.
A summary of the hybrid HS algorithm and FL based papers.
4.2. Fuzzy Harmony Search Algorithm
Metaheuristic optimization algorithms include parameters that are typically defined during successive iterations. There are different strategies for dynamically modifying these parameters such as probabilistic and fuzzy ones. However, the analysis of the available approaches shows that the adaptation of complex parameters by means of FL may provide a significant improvement in many metaheuristic optimization methods. Actually, FISs based on human understanding provide more flexible and dynamic adaptation of the metaheuristic parameters. With the advent of T2-FLS, the ability to manage complex systems has increased significantly, and recent studies have shown that the use of IT2-FIS provides better results compared to T1-FIS.
FL is sometimes used to adjust parameters of the evolutionary methods such as BA [72,73,74], GWO algorithm [75,76,77,78], ACO algorithm [31,79,80,81], ICA [82,83,84], and WCA [85,86,87]. The parameters of the PAR and BW are very important in adjusting the optimized solution vectors in the HS algorithm, and theoretically could be helpful in modifying the algorithm’s convergence rate to obtain the optimal solution.
The SHS uses the set values of PAR and BW which are only changed during initialization and cannot be modified during new iterations. The biggest drawback of this approach is that it takes several iterations to get the optimal solution. To find the optimal solution, low PAR and high BW values will result in poor algorithm performance and a large increase in the number of iterations. In the final iterations, higher PAR values at low BW values usually lead to improvement of the solutions, and the algorithm converges to the optimal solution vector. Various types of FL models are considered to tune the HS algorithm parameters and consequently, to improve the efficiency of the algorithm.
In work done by Mahmoudi and Aghaie [88], the gravitational constant in the GSA as well as the BW and PAR parameters in the HS algorithm were adjusted to increase the degree of convergence and obtain better results using a FLC. To demonstrate the FLC performance, the fuzzy gravitational search algorithm and FHS were compared with standard GSA and HS in the drop-wave function problem. The optimization findings revealed that the FHS has a better performance on average iteration number values.
Peraza et al. [89] introduced FHS with dynamic parameter modification to solve complex optimization problems. This study improved the convergence of the HS algorithm using FL and the efficiency of the IHS algorithm. On the other hand, in [74], a novel approach to adapting the HMCR which increases the HS algorithm’s accuracy and convergence rate was used. The impact of constant parameters on HS was examined and a new technique for tuning these parameters was proposed. The FHS was successfully applied to a number of benchmark optimization problems, and the numerical results showed that the proposed algorithm could find better solutions than HS and other metaheuristics.
To improve the placement of capacitors in distribution networks, Ameli et al. [90] described a variant of the discrete HS algorithm, i.e., a FDHS. The proposed FDHS uses a fuzzy scheme to dynamically modify two parameter values, that is, with respect to the normalized median of the harmony memory, HMCR, and PAR. The main feature of the FDHS is that it requires much less iteration to achieve convergence compared to the classical discrete HS. The obtained optimization results showed the effectiveness of the FDHS in comparison to previous similar tests.
In the study carried out by Peraza et al. [91], for the dynamic adaptation of parameters in the HS algorithm, a skeleton based on the interval schedule T2-FLS was introduced. A key achievement of this study was to strengthen HS in its ability to scan globally and locally by dynamically adjusting of some its parameters. The FHS algorithm has been extended to various benchmark optimization problems. The numerical results showed that compared to T1-FHS and other metaheuristics, the proposed algorithm can find better solutions.
In Castillo et al. [13], the ST2-FIS was introduced to increase the dynamic adaptation of parameters in the HS and DE optimization methods. The ST2-FIS is a GT2-FIS approximation, based on the so-called shadowed fuzzy sets. This study represents a comparison of standard static parameter and dynamic parameter adaption methods using ST2-FIS, and the approaches were evaluated in terms of solving mathematical functions and controller optimization.
Peraza et al. [92] carried out a comparative study on the use of fuzzy intervals of T1 and T2-FLS to solve optimization problems using the HS algorithm. As the number of iterations increases, the FHS dynamically updates the internal parameters of the HS algorithm to obtain a thorough analysis of the original process using a T1-FLS. The aim of the research was to evaluate the FHS refinement, in particular with regard to new input parameters and techniques, which allowed for obtaining improved methods. Indeed, the difference between the success of the analysis by Peraza et al. [93] and Peraza et al. [92] integrates the second input with a fuzzy system Type-1 and interval Type-2 and integrate the two parameters in the outputs to create a more complex approach, where problems are solved more effectively.
Peraza et al. [94] used a T2-FHS for complex parameter adaptation based on the interval T2-FLS. In their study, the HMCR and PAR parameters were modified during the iterations in the improvisation phase of this algorithm by a fuzzy method. The results of numerical optimization showed that in comparison with T1-FHS and other optimizer reported in the literature, the proposed algorithm could find better solutions. A summary of the FHS based papers is shown in Table 2.

Table 2.
A summary of the fuzzy HS algorithm-based papers.
4.3. Harmony Search Algorithm and Fuzzy Controllers
In recent years, the FLCs have been commonly used as a popular functional method for designing and applying control systems because of their unique flexibility and various abilities, such as their effective response to complicated and high-order systems. For a number of difficult control applications, FC is a practical alternative as it offers a straightforward method for creating nonlinear controllers thanks to the use of heuristic knowledge. Each FLC essentially consists of five parts, namely fuzzification, defuzzification, rule base, inference system, and database.
Furthermore, it is obvious that the selection of the fuzzy controller parameters and MF plays a key role in improving the performance of the controller. Due to the existence of many dimensions for the evaluation of fuzzy parameters, one of the better alternatives is to use intelligent algorithms that have been widely used in recent years. By using evolutionary optimization algorithms, fine-tuning of the fuzzy architecture variables reduces the need for the experience required to set these variables and achieves more detailed FLC with little effort. Due to the effectiveness and efficiency of HS, the optimal fuzzy parameters were obtained in several studies.
To enforce overshoot control in power plants, Wang et al. [95] implemented an innovative adaptive fuzzy controller using the Lyapunov-based adaptive rule to guarantee the reliability of the controller. The modified ABHS algorithm has been used to fine-tune the optimal control parameters to improve dynamic performance. The Lapunov-based adaptive FC technique modifies single output parameters of fuzzy controllers to guarantee system reliability, while the approach deals with complex performance indicators that are critical to the performance and safety of power plant systems. Finally, the proposed ABHSAFC approach, based on ABHS, has been extended to include fluidized bed rotary boiler bed temperature control. The results showed that ABHSAFC was able to successfully apply predicted control without overshoot and outperformed classical adaptive FC based on Lyapunov or ABHS, and PID control based on ABHS.
In a paper by Sharma et al. [96], a hybridization of the LSBA and the globally adaptive HSBA was proposed, combining the strong features of both approaches to improve both FLC structure and free parameters. In the case of the non-linear vine, the proposed methods have been successfully applied and tested against the real problem of DC motor speed regulation. The proposed approaches have shown that they can guarantee asymptotic consistency while achieving adequate monitoring effectiveness.
By integrating the egg laying and immigration functions of the HSCS, Gheisarnejad [97] developed a hybrid algorithm to create a second controller for two functional load frequency management problem models. Initially, the proposed approach to tuning considered a two-surface thermal energy system without reheating and modified the share of PID and fuzzy PI/PID controllers. It was observed that compared to other recorded strategies, HSCS optimizing fuzzy PID controller showed better quality of operation.
In a study by Tarkeshwar and Mukherjee [98,99] an updated variant of the HS, known as a QOHS algorithm, was used to evaluate the appropriate frequency and power deviation solution by modifying the adjustable parameters of the tested isolated DG model. In this paper, the QOBL has been combined with the traditional HS algorithm to accelerate the degree of convergence of the basic HS algorithm. Two FLCs were used to determine the order of frequency and power for output equalization. The obtained optimization results showed that the proposed model achieved minimal frequency and power deviations.
To improve the FLC I/O scaling parameters, Sambariya and Prasad [100] used HS to design a FPSS. In their study, the FPSS input/output scaling parameters were fine-tuned using the HS algorithm.
In a study by Castillo et al. [101], a comparative analysis was performed using the BCO, DE, and the HS algorithms to construct fuzzy controllers. In addition, a T1-FLS system was proposed to dynamically adjust key parameters for each algorithm. The optimization results showed that the fuzzy DE algorithm outperformed the findings of the fuzzy BCO and FHS algorithms in fuzzy controller optimization.
In Chao et al. [102], the SGHS algorithm was used to search for optimal combinations of parameters of the FCMAC. HS optimized not only the variable weights of the FCMAC network, but also the location of the center and the parameters of the standard deviation of the network receiving area. Experimental results revealed that SGHS-optimized networks showed faster convergence and higher precision.
In a study by Sharma et al. [103] to build safe, adaptive fuzzy controllers, the HS algorithm was hybridized with the Lyapunov principle. Fuzzy controllers based on a modified HS algorithm have been introduced for two nonlinear benchmark systems. The findings revealed that the proposed variance in parameters (i.e., HMCR, PAR, and BW) conveniently resulted in a better transient performance of the controlled systems compared to equivalent fuzzy regulators configured to use Lapunov’s theory and SHS algorithm hybridization.
Wang et al. [104] introduced a fuzzy PID control technique to electronic throttle control. The input variables were the error signal and its inverse in the fuzzy PID scheme, and the output variable was the PID gains expressed as fuzzy regulations. The gains from the controller were computed using fuzzy rules while the HS was applied to modify questionable rules. Simulations and laboratory tests have shown the effectiveness of the proposed controller.
Mahto and Mukherjee [105] investigated a new FLC scheme to achieve frequency and power control of an IHPS and HPS-based two-area power system. Various autonomous generation systems such as wind turbines, diesel engine generators, and energy storage units were considered in the IHPS report. The QOHS adjusted numerous tunable parameters of the model. The optimization results showed that by combining the principle of quasi-opposition in a simple HS system, and then by improving the presented control model, the QOHS increased the level of convergence.
To fine-tune the parameters of the fuzzy power system stabilizer, Sambariya and Prasad [106] used the HS algorithm. The simulation results showed the reliability of the HS and higher performance compared to the current optimizers.
Valdez and Peraza [107] represented the HS algorithm for the optimal design of the T2-FLC interval. In addition, the T2-FLC interval theory was used to dynamically modify the HS parameters to increase the efficiency of HS. Experimental simulations showed that the IT2-FLC to T1-FLC based on updated HS had better performance.
The study by Valdez et al. [108] ensured the use of the HS algorithm for benchmark problems and FLC. Additionally, the FL principle was applied to the dynamic modification of HS parameters to increase the HS performance. Updated HS has been generated increasingly focusing on linguistic variables and fuzzy rules to diversify solutions in the search process. The simulations confirmed that the updated HS, the so-called FHS, performed better than the regular HS.
Sharma et al. [109], using the structured framework of stable FLC, proposed a new version of the HS algorithm. The HS algorithm approach and the proposed group improvisation method were used to design the FLC for two benchmark case studies. The obtained results indicate the superiority of the proposed variant of the HS algorithm over other methods of designing safe fuzzy controllers.
In the paper by Sharma et al. [110], focusing on the Lapunov principle and the HS algorithm, the proposed hybrid stable adaptive fuzzy controllers were implemented for the real-life temperature regulation of the air heater process in various sections of the air flow duct. The obtained optimization results confirm the success of the proposed model.
In a study by Sharma et al. [111], the HS and Lyapunov methods were hybridized to build a stable adaptive fuzzy tracking control technique for vision-based navigation of an autonomous mobile robot. The proposed version of the HS algorithm with absolute dynamic harmony memory (hereinafter called the DyHS algorithm) was used to develop two self-adapting fuzzy controllers for movements in the X and Y directions of a mobile robot. The findings confirmed the utility of the proposed design method and, unlike GA and PSO, provided similar overall results.
In Zhou et al. [112], an IHS algorithm was implemented to train the neural networks FCMAC. FCMAC neural networks use more parameter settings than standard CMAC neural networks. An appropriate representation of FCMAC data was built for the HS algorithm. The IHS algorithm has been implemented not only to optimize the weight values of the CMAC network, but also to optimize the center positions and width parameters of the network receiver sector. The experimental results showed that the proposed system shows a high rate of convergence.
Peraza et al. [113] introduced a complex parameter adaptation framework based on FL in the HS. T1-FHS, IT2-FHS, and GT2FHS were used for adaptation. A key contribution of their work was the complex adaptation of parameters using various types of fuzzy structures in HS used to optimize the membership function for the ball and beam controller. Optimizing this topic performed better than other published approaches.
In a study by Peraza et al. [114], the optimization of the fuzzy system membership function value was assessed for three benchmark control problems (i.e., water tank, shower, and mobile robot) and the reliability achieved during trajectory monitoring in each case. The proposed approach used HS with T1 and T2-FLS with complex parameter adaptation. The registered optimization efficiency proves the advantage of this approach over the methods used so far.
In Peraza et al. [115], the FHS algorithm was developed to solve optimization problems. The FHS used a novel approach using FL to adjust a user parameter called PAR to increase the precision and convergence of the HS algorithm. The effect of continuous parameters on the HS and a technique for tuning these parameters were considered. The FHS algorithm has been successfully extended to numerous problems related to benchmark optimization. The results of the numerical optimization showed that in comparison with the regular HS and other optimizers, the proposed algorithm can find better solutions.
Amjady et al. [116] proposed a MOHSA to optimize the tuning of the fuzzy PID controller in order to solve the multi-area restructuring problem. Depending on the time domain, the problem of robust tuning of fuzzy PID-based AGC architecture was conceived as an optimization problem. The simulation results showed that the proposed model maintained a stable performance in contrast to other current models.
The study of Abedinia et al. [117] proposed a MOHSA-based multistage fuzzy controller to solve the problem of LFC of power systems under deregulation conditions. The signal was tuned online using the knowledge base and fuzzy inference inside the proposed controller. Membership functions were developed automatically using the proposed MOHSA approach to minimize the design effort and simplify the FC structure. The obtained optimization results were compared with the findings of many LFC regulators in the literature, which illustrate the effectiveness and robustness of the proposed strategy.
To solve the problem of load frequency control, Mahmudizad and Ahangar [118] applied the HS to regulate the interval parameters of Type-2 fuzzy PID controllers. The obtained optimization results showed the feasibility of the proposed approach. Table 3 summarizes the HS algorithm and fuzzy controller-based papers.

Table 3.
A summary of the HS algorithm and fuzzy controller-based papers.
4.4. Harmony Search Algorithm and Fuzzy Clustering
Clustering is an unsupervised learning approach that can partition equivalent data objects (patterns) based on some degree of similarity, increasing the similarity of objects within a category and reducing the similarity between objects in different classes [119]. As a common technique for unsupervised learning, fuzzy clustering, which is also referred to as soft clustering, is a technique that requires soft separation of underlying data points. As clustering algorithms have some disadvantages, such as selecting the starting cluster centers and the corresponding cluster number, metaheuristics have recently been used to solve fuzzy clustering problems. Reports of several papers that focus on fuzzy clustering are presented below.
Forsati et al. [120] and Mahdavi et al. [121] developed the HS for clustering web documents using the k-means methodology as a local search. This procedure was performed several times, so the clustering was obtained using k-means and the returned vector was applied to HM if it had a higher objective value than those in HM.
In a study by Wang et al. [122], a hybrid optimization approach based on the convergence of the CSA and the HS techniques was used to refine the Sugeno fuzzy classification systems for Fisher Iris data and wine data classification. The CSA was used to increase the efficiency of the HS system among HS participants and applicants. The results of computer simulations showed the feasibility of the proposed solution.
Alia et al. [50] proposed a new method to solve the well-known dilemma of initialization of FCM. This method uses the HS algorithm to obtain near-optimal starting cluster centers for the FCM algorithm. The experiments showed promising results in obtaining consistent grouping for a given problem, in contrast to FCM with randomly initiated cluster centers.
Alia et al. [123] later implemented a new hierarchical clustering algorithm based on the hybridization of HS and FCM to intelligently and automatically segment brain MRI images. SHS functionality has been updated in this approach to fit automatically the required number of clusters as well as cluster center positions.
Using the HS, Ayvaz [124] proposed a new fuzzy method to find the optimal parameter values for a zone structure problem. Based on three guidelines namely residual failure, parameter change, and structural differentiation, the issue was solved. For many solutions, a sensitivity assessment was performed to investigate the HS performance. The results show that the proposed HS is a good method of simultaneous clustering.
Malaki et al. [125] implemented a new integrated technique called FHSC, using a fuzzy approach to improve the HS performance. The FHSC results were fed into the FCM algorithm which then practiced the convergence speed to improve the solution. This technique combined the FHS gains with the acceleration of the convergence of the FCM technique. The results showed that an almost perfect solution was obtained with FHSC. Moreover, it easily converged to the optimally recognized optimum.
To address concerns about K means, Van Tinh [126] proposed a hybrid modeling approach that focused on hybridizing K-means and HS. The proposed hybrid approach allowed for better optimization results and the appropriate interval length.
Agrawal and Pandey [127] implemented a hybrid optimization approach that focused on using appropriate fuzzy decision making and the HS to defeat WSN clustering protocols. The proposed approach is called FLIHSBC, which uses the Fuzzy and IHS technique. The FLIHSBC algorithm showed lower power consumption and helped to maximize the network lifetime. The results indicated that the FLIHSBC performed well in extending the lifetime of WSN.
To handle the classification process, Feng et al. [128] proposed a fuzzy kernel clustering technique with a new differential HS. Firstly, a self-adaptive DE update approach and procedures were introduced to strengthen the simple HSA. Secondly, the differential HSA was used to assist the clustering methodology in obtaining further leading results in the fuzzy kernel clustering technique. Then the fuzzy nucleus was used for water entertainment arrangements combined with the differential HS. The proposed solution was compared with other related approaches and the results showed that, along with the differential HSA, the proposed fuzzy kernel clustering revealed a better overall performance with respect to the water diversion arrangements.
Regarding fuzzy clustering, several HS variants have been used to solve various problems using fuzzy techniques, which means that fuzzy clustering applications still have room for further research and analysis. Recently, Abualigah et al. [129] published a comprehensive analysis of HS-based clustering techniques such as fuzzy clustering and data clustering.
A new algorithm, the so-called DCHS, was proposed in Alia et al. [130]. The performance of the SHS has been modified in this algorithm by integrating the concept of variable length with each harmony memory vector to develop the required number of clusters as well as cluster core positions. In each iteration, DCHS was able to code a variable number of candidate clustering centers. Unlike other state-of-the-art algorithms in the field of dynamic clustering, experimental results have shown that the proposed DCHS provides better quality solutions.
Later, Alia et al. [131] provided the WSN with a new energy-efficient grouping protocol that can reduce overall grid energy dissipation while optimizing service life. In the HS protocol, it first automatically determined the optimal number of clusters and allocated sensors in these clusters to build infrastructure for a given WSN. The second part focused on the process of forwarding the detected data from the nodes to their cluster head and then to the base station. A clustering fuzzy clustering algorithm is suggested where, over the lifetime of the network, the set of cluster heads in each round is rendered locally on each cluster.
For localized steady-state groundwater flow models, Ayvaz [132] proposed a similar simulation and optimization model for estimating the groundwater load rate, associated zone structures, and hydraulic conductivity values. The FCM technique was used to solve the problem of zone structure assessment. Then, the zone systems were correlated with the spatial distribution of the HS load of groundwater. The Tahtali catchment case study (Izmir, Turkey) tested the suitability of the expanded model and the estimation results were compared with previous modeling results for the same model domain obtained using a different optimization methodology. The comparison of the results showed that the proposed model was an effective way to calibrate the groundwater flow models in the steady state.
In a study by Wan et al. [133], the fuzzy clustering technique based on SAMOHSFC was introduced for image segmentation. In one harmony vector, the SAMOHSFC technique encoded multiple cluster centers and optimized several goals. For the synthetic and two single images from the quantitative and visual perspective, the advantage of the proposed algorithm over three classical segmentation algorithms was confirmed. The test results on different noise images showed that SAMOHSFC has good auto-adaptation and high robustness to noise compared to the recorded results.
In studies by Satwika et al. [134], the FCM approach was proposed to obtain the focal point of the eNodeB cluster for the clustering phase followed by the HS optimization process. In this LTE service, the service upgrade phase to the next model uses the current base stations as a BTS with new hardware called eNodeB. During the optimization phase, this analysis used many variables, including traffic in the city of Denpasar, the number of eNodeB stations required in 2020, and the coverage of each current BTS.
Agrawal and Sudhakar [135] developed an optimized unequal algorithm for selecting cluster heads based on the HS and FL. The algorithm proposed in their paper extended the network lifespan as it took into account parameters that are necessary to collect temporary cluster heads as well as the end cluster heads. The number of cluster heads has been optimized by the HS. Therefore, to get a more optimized result, it was mixed with FL. The proposed algorithm was simulated and ultimately improved performance compared to other algorithms.
Using the ANFI paradigm, Ko and Sim [136] applied a tool for classifying human brain functions such as EEG signals correlated with motor imaging activities. In their method, the HS algorithm was used to distinguish EEG signals from motor images and to optimize the parameters of the ANFI model. The configured ANFI model offers better results than other approaches.
To overcome some shortcomings of conventional clustering approaches, such as slow convergence and their sensitivity to initialization values, and to improve classification accuracy, Bekkouche and Fizazi [137] hybridized the HS with the FT to obtain an FHS-FT for unsupervised classification. Experimental discoveries regarding pattern images (i.e., photographic and satellite) revealed that the FHS-FT algorithm was a recent idea that introduced major changes to the complex grouping of images and was more effective in unknown scenes for identifying real-world objects.
To increase the efficiency of the classification, the execution time and the convergence ratio, Mahmoodi and Mahmoodi [138] proposed an HS-based system for pattern classification. The proposed algorithm was used in the framework of an evolutionary fuzzy system based in Michigan. The tests also show that the proposed algorithm classifies the data with reasonable classification accuracy. Table 4 summarizes the HS algorithm and articles based on fuzzy clustering.

Table 4.
A summary of the HS algorithm and fuzzy clustering-based papers.
4.5. Harmony Search to Optimize Fuzzy Logic Systems
In recent decades, many frameworks have been used to develop FL models. However, a key disadvantage of classical approaches is that the ideal subset is not expected to be identified by either a theoretical or a functional approach. Therefore, metaheuristics have become a widely used tool for finding the optimal or near-optimal subset. In particular, due to the possibility of optimizing various fuzzy models, the HS is used to improve these models.
In Coelho et al. [139], using an exponential probability distribution, the IHS method was used to refine the FLC design parameters with fuzzy PI plus a derivative action design. In their study, the exponential probability distribution was used to generate random numbers. The numerical findings indicate that the validated IHS-tuning FLC architecture successfully regulates the non-linear pH neutralization mechanism.
Kong et al. [140] represented an approximate standard reduction of fuzzy parameters based on the harmony search algorithm. The simulation results showed that the proposed strategy was effective and feasible compared to the current methods.
Al Daoud [141] developed an algorithm that uses IHS to find the FRS reducts. The HS matching functions use classic ranking methods, a matrix for discernibility, and the degree of dependence of each individual attribute. Moreover, by transforming them into binary functions, the proposed operations could be easily accelerated. With respect to the reduct length, the proposed algorithm was equivalent to the other algorithms.
In a study by Mashinchi et al. [142], to facilitate the design of the FLR models, an unconstrained global continuous optimization approach based on the TS and the HS was introduced. Both the TS and HS were used to diversify and intensify the FLR, respectively. Three types of data sets are used to test the efficiency of the proposed method: numerical inputs—symmetrical fuzzy outputs, symmetrical fuzzy inputs—symmetrical fuzzy outputs, and numerical inputs—asymmetric fuzzy outputs. Experiments have shown that the proposed approach is superior to current approaches documented in the literature.
Dash et al. [143] proposed the use of the DHS algorithm to approximate the stock volatility estimation parameters of the proposed hybrid IT2-FLS-EGARCH method. The results of the calculations revealed that the IT2F-CE-EGARCH model using a Gaussian function with unknown variance and fixed mean provided a significant improvement in forecasting results compared to all other models of volatility.
In Aungkulanon et al. [144], the HS algorithm with several evolutionary elements was used for fuzzy APP. Various HS hybridizations to solve APP problems using a fuzzy programming approach were examined. As a result of the conducted experiments, it can be concluded that each algorithm was sufficient for various types of factory conditions. Table 5 shows a summary of HS-based papers devoted to the optimization of FL systems.

Table 5.
A summary of the HS-based studies that focus on optimizing FL systems.
5. Discussion
In this survey, more than 100 research papers were reviewed to provide a comprehensive conclusion for researchers interested in using the combination of the HS and the FL. Using Google Scholar with three keywords (i.e., harmony search, HS and fuzzy), the papers were selected. In this review, we reviewed and analyzed comprehensively papers published from 2007 to 2020 in which HS and FL were applied to diverse applications and for different goals. Figure 6 and Figure 7 display the distribution for each year of published papers related to the HS and FL from 2007 to the present. Based on the outcomes shown in Figure 6 and Figure 7, from 2007 to the present, the number of articles published has grown considerably each year. However, it is clear that the number of publications published in 2015 and 2018 is considerably greater than in other years. The results published indicate that the usage and hybridization of HS and FL in different studies are growing considerably year after year.
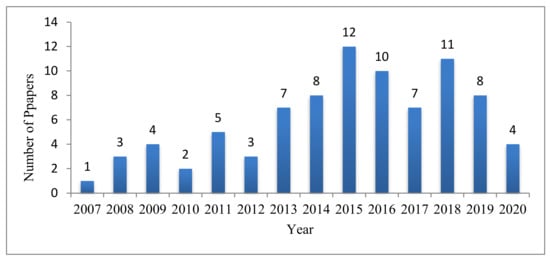
Figure 6.
Distribution per year of submitted publications applicable to the HS and FL (2007~22 August 2020).
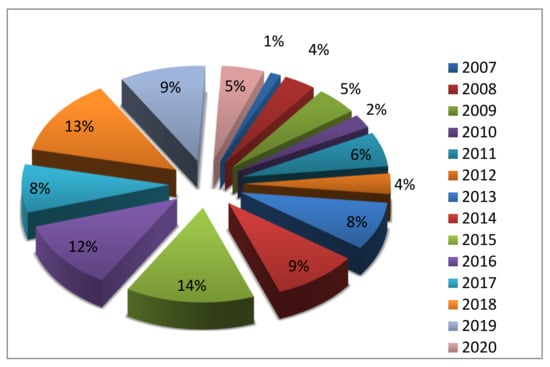
Figure 7.
Distribution per annum of presented papers applicable to the HS and FL (2007~22 August 2020).
The study of the reviewed references shows that the researchers have used the HS and FL in articles for different purposes. As mentioned in Section 4, the articles studied are divided into five categories: hybrid HS and FL, fuzzy HS, HS and fuzzy controllers, HS and fuzzy clustering and HS to optimize FLSs, according to the type of composition and function of HS and FL.
In the hybrid HS and FL, researchers applied the HS and FL simultaneously to solve optimization problems. Due to the significant advantages and capabilities of the HS and FL algorithm in solving optimization problems, the hybrid methodology proved better results than the individual methods.
In the category of the fuzzy HS, some researchers believe that by tuning the parameters of the HS such as PAR and BW by means of FL models, the algorithm performance can be improved in finding optimal solution in less number of iterations. In fact, the reason for this is that the FL models such as FISs can provide more flexible and dynamic adaptation of the metaheuristic parameters based on human perception. Recent studies have shown that using the IT2-FIS provides better results compared with the T1-FIS.
In the HS and fuzzy controllers category, the HS has been utilized for fine tuning of the fuzzy controller parameters that reduces the need for the experience required to set these variables and achieves more detailed FLC with little effort. Also, some authors believe that metaheuristics are the better solution to solve fuzzy clustering problems, as clustering algorithms have some disadvantages, such as selecting the starting cluster centers and the corresponding cluster number. In addition, the HS has been used to optimize the FLSs in some studies. In these papers, the HS has been applied to improve the exploration of the FL for finding the optimal or near-optimal subset, as a key disadvantage of classical approaches is that the ideal subset is not expected to be identified by either a theoretical or a functional approach.
5.1. Variants of HS Algorithm
In the reviewed papers, different variants of the HS algorithm are used to strengthen its performance, including hybridization of HS with other algorithms, improved versions of the HS algorithm, and variants of HS for handling multi-objective optimization, the so-called MOHSA algorithm. Table 6 shows variants of the HS algorithm combined with FL in the reviewed papers. Variants of the HS in the Table 6 include SHS, HIS, and HHS. It can be seen from Table 6 that the standard type of the HS has been used more than its improved and hybrid versions.

Table 6.
Variants of HS algorithm combined with FL in the reviewed papers.
In addition, Figure 8 demonstrates the percentage contribution of HS variants combined with the FL. According to the Figure 8, the SHS has 52% of publications in the current research regarding the HS variants combined with the FL. Moreover, the IHS and hybridizations of HS contribute 39% and 9% of published papers, respectively.
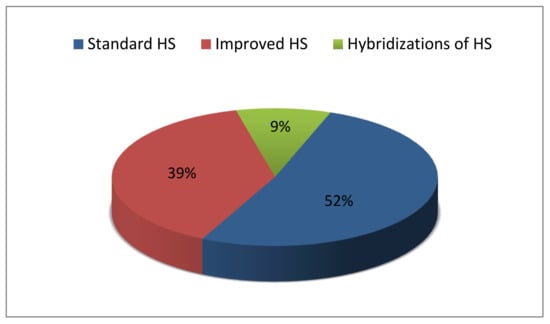
Figure 8.
Variants distribution of HS algorithm equipped with FL in the reviewed papers (2007~22 August 2020).
The strength of HS is related to its versatility and ability to adjust and be hybridized with other optimizers, while its disadvantages include a propensity to be caught in local optima owing to its emphasis on extraction rather than discovery. Because the performance of the HS algorithm is largely dependent on parameter tuning, the parameters of the HS are improved using the methods shown in Table 6. In addition, hybridization of the HS method with other optimizers compensates for its weaknesses and intensifies its advantages in accordance with FL.
5.2. Fuzzy Logic Models
FL deals with truth, and is a form of logic that is appreciated in several respects. The FL deals with logic that often has textual principles rather than crisp principles that are estimated. FL manages the definition of the value of a fact, which varies from 0 to 1 to absolutely real. FL has been introduced in several disciplines. The different ways of communicating uncertainty are FL and probability. The idea of fuzzy set inclusion was used by fuzzy set theory, while probability theory uses the idea of empirical probability. The different types of membership functions usually used in the FL are “Λ” triangular, “∏” trapezoidal, “L” feature, “Γ” feature, “S” feature, and Gaussian fuzzy collection. Both these features can be used for the design of various engineering structures.
The FL helps conceptualize the system’s fuzziness into a crisply quantifiable parameter. This allows for the introduction of FL based models to obtain efficient and optimal solutions. In reviewed papers, FL based models range in diverse kinds of problems, including FO, FTS, fuzzy neural systems, FLCs, T2-FLS, fuzzy clustering, fuzzy soft sets, fuzzy regression, and fuzzy programming models. Table 7 illustrates the FL models in combination with the HS algorithm in the assessed articles. It is seen from Table 7 that the FO, FLC and fuzzy clustering models have the most applications in the articles compared to other models.

Table 7.
FL models in combination with the HS algorithm.
In addition, the FLCs are used to monitor the transient energy supply from the energy sources. In energy systems, neural-FLCs are used. Over the past decade, neural-fuzzy models have been used extensively, especially in control systems. Moreover, other FL based hybrid models such as T2-FLHS and FDE algorithms are discussed in the simulation of energy-based applications.
Fuzzy-based advanced simulation of time series, regression, and neural networks has helped increase the predictive performance of the variables used in forecasting. The incorporation of fuzziness into the models enables us to catch in human minds the heuristic thinking that occurs. Furthermore, researchers have used fuzzy-dependent clustering models for classification purposes. The range given to the variables in fuzzy clustering helps to easily demarcate the clusters and to draw boundaries. Each of these methods is used depending on the problem domain.
In fuzzy regression, the data are captured in a fuzzy manner for the dependent and independent variables, and the influence of the independent variables on the dependent variable is calculated using the derived regression equation. Figure 9 shows the distribution of FL models in combination with the HS algorithm. According to Figure 9, the FO has 31% of publications in the current research related to fuzzy models in combination with the HS. After that, the FLC and the fuzzy clustering possess 26% and 22% of publications, respectively.
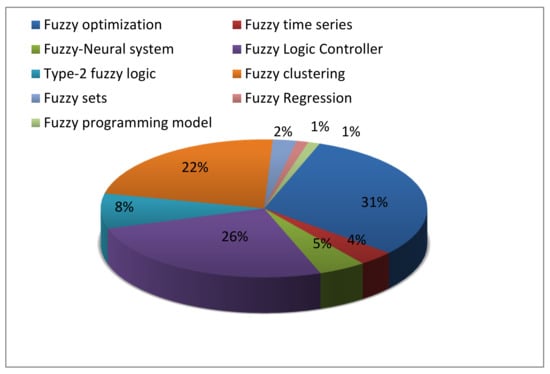
Figure 9.
Distribution of FL models in combination with the HS algorithm (2007~22 August 2020).
5.3. Combinations of HS and Fuzzy Logic Theory
As mentioned in Section 1, combinations of HS and FL are categorized into the five main sectors in this study: hybrid HS algorithm and FL, FHS algorithm, HS algorithm and fuzzy controllers, HS algorithm and fuzzy clustering, and HS to optimize FL systems. Each of these categories is classified based on a specific specification and function. In this section, the optimization problems are addressed using HS and FL simultaneously. The HS algorithm has been used to achieve the optimal solution, while the FL concept has been used to simulate fuzziness in studied systems. As expected, a hybrid approach performs better than any of the methods separately.
In the FHS algorithm, the types of FL models are used to tune the HS algorithm parameters and consequently improve the efficiency of the algorithm. In the HS algorithm and FLCs, the tuning of fuzzy design variables using the HS permits the removal of the skill prerequisite required to set these variables with little effort to achieve more precise FLCs.
Owing to the effectiveness and efficiency of the HS, the HS algorithm was used to determine the fuzzy parameters in many studies. In this regard, the HS algorithm along with fuzzy clustering, owing to the clustering algorithms drawbacks such as selecting the initial cluster centers and the appropriate cluster number, has been used to tackle fuzzy clustering problems. In addition, in the Section “HS to optimize FL systems,” the HS is used for the improvement of fuzzy models in the published papers. Table 8 shows the combination type of HS with FL. Looking at Table 8, Hybrid HS algorithm and FL has the most publications in the current research related to fuzzy models in combination with the HS. After that, the HS and fuzzy controllers and HS and fuzzy clustering have the most applications in the literature, respectively.

Table 8.
Combination type of HS with the FL.
Figure 10 depicts the distribution of the reported articles according to the combination type of HS and FL. As it can be seen from Figure 10, the hybrid HS and fuzzy logic has the largest contribution of all published articles (i.e., 32%). Then, the HS and fuzzy controllers, HS and fuzzy clustering, fuzzy HS and HS to optimize fuzzy logic systems have 28%, 22%, 11%, and 7% of publications based on the combination type of HS and FL, respectively.
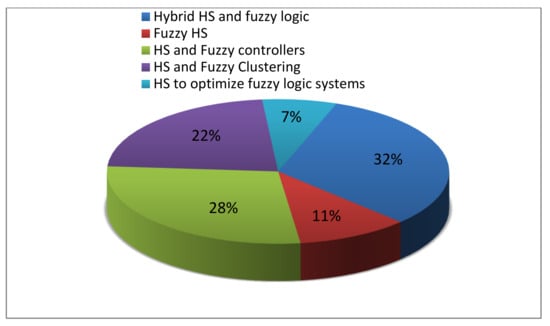
Figure 10.
Distribution of reported articles according to the combination type of HS and FL (2007~22 August 2020).
5.4. Applications of HS and Fuzzy Logic in Different Fields
Studies based on HS and FL in the literature have been published in many different fields of study. The combination has been used in many areas because of the capabilities and strengths of mixing HS and FL, including electrical and electronic engineering, mechanical engineering, civil engineering, chemical engineering, industrial engineering, water resources and hydropower engineering, computer engineering, optimization and mathematics, and control engineering. In Section 4, a general overview is given of the published research work pertaining to the combined approach. In this section, all papers published using HS and FL in their applications, including hybrid HS algorithm and FL, fuzzy HS, HS and fuzzy controllers, HS and fuzzy clustering, and HS to optimize FL systems are classified based on the variety of fields, and their applications are presented briefly in the Table 9. In accordance with the statistical results shown in Table 9 and Figure 11, majors in “computer engineering”, “electrical engineering” and “optimization & mathematics” have greater percentages of the presented applications.

Table 9.
The application of HS and FL in various fields of studies.
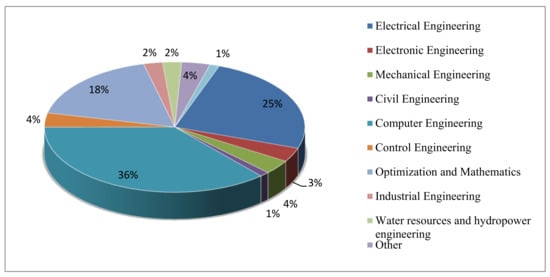
Figure 11.
Percentage of the reported articles that used HS and FL in various research fields (2012~22 August 2020).
Figure 11 indicates the proportion of published articles in various fields of studies using HS and fuzzy. Likewise, Figure 12 indicates the number of articles written depending on the mixture of the various fields of analysis. In accordance with the statistical results shown in Figure 11 and Figure 12, majors in “computer engineering”, “electrical engineering”, and “optimization & mathematics” represent a higher percentage of the presented applications.
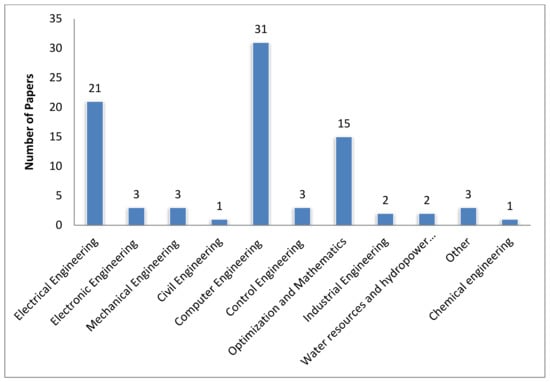
Figure 12.
Number of HS-based and fuzzy-related articles published by various research repositories (2012~22 August 2020).
6. Conclusions and Future Research
In this review paper, a comprehensive survey was conducted to recognize the advantages of combining the HS and FL and their applications in a broad and diverse research domain as well as the recent progress in the literature. In this regard, significant efforts have been made to prepare this article to establish a good understanding of the subject for readers and interested academics by reviewing and summarizing the results of HS and FL, resulting in recent scientific papers by researching and evaluating several separate research articles relevant to the subject from 2012 to the present (22 August 2020).
Owing to the performance, ability, and effective qualities of the HS among optimization algorithms and an interesting definition of FL, the distinguishing combinations of the HS and FL in terms of the type of connection were introduced in the literature. In addition, it is seen that different variants of the HS in terms of implementations, improvements, multi-objective variants, hybridizations, and various FL models were included in a full reference list. The findings collected from experiments and analyses of these references indicate that researchers have found the simultaneous use of HS and FL to solve optimization problems, the use of HS to solve FC systems, and the use of FL to enhance HC helpful and useful. Furthermore, the large number of studies conducted based on the hybrid HS algorithm and FL prove that employing such combinations can lead to the practical approach to solve engineering optimization problems. Hence, it can be viewed as a creative and detailed guide for subsequent HS and FL-related research papers and books. Besides, as future research, a detailed numerical comparison among different approaches and models related to the HS and FL theory can be considered over studied articles.
Author Contributions
Conceptualization, Z.W.G., M.N. and A.S.; validation, Z.W.G., P.G., J.H.Y., M.N. and A.S.; resources, M.N. and A.S.; data curation, M.N. and A.S.; writing—original draft preparation, J.H.Y., M.N. and A.S.; writing—review and editing, Z.W.G., P.G., J.H.Y., M.N. and A.S.; visualization, M.N.; supervision, Z.W.G., P.G. and J.H.Y.; funding acquisition, Z.W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Energy Cloud R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT [2020R1A2C1A01011131].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors claim that there is no conflict of interest concerning this review paper.
Nomenclature
| Symbol | Description |
| ABHS | Adaptive binary harmony search |
| ABHSAFC | Adaptive binary harmony search algorithm fuzzy control |
| ACO | Ant colony optimization |
| AHS | Advanced harmony search |
| ANFI | Adaptive neuro-fuzzy inference |
| APP | Aggregate production planning |
| ARIMA | Autoregressive integrated moving average |
| BA | Bat algorithm |
| BAP | Buffer allocation problem |
| BCO | Bee colony optimization |
| BTS | Base transceiver station |
| CS | Cuckoo search |
| CSA | Clone selection algorithm |
| DCHS | Dynamic clustering technique based on the harmony search |
| DE | Differential evolution |
| DG | Distributed generation |
| DHS | Discrete harmony search |
| DHS | Differential harmony search |
| EEG | Electroencephalogram |
| EFSs | Evolutionary fuzzy systems |
| FC | Fuzzy control |
| FCC | Fuzzy c-means clustering |
| FCM | Fuzzy c-means |
| FCMAC | Fuzzy cerebellar articulation controller |
| FCMAC | Fuzzy cerebellar model articulation controller |
| FCMACNN | Fuzzy cerebellar model articulation controller neural networks |
| FDE | Fuzzy differential evolution |
| FDHS | Fuzzy discrete harmony search |
| FHS | Fuzzy harmony search |
| FHSC | Fuzzy harmony search clustering |
| FHS-FT | Fuzzy harmony search-fourier transform |
| FJSP | Flexible workshop scheduling |
| FL | Fuzzy logic |
| FLC | Fuzzy logic controller |
| FLIHSBC | Fuzzy logic and improved harmony search-based clustering |
| FLR | Fuzzy linear regression |
| FLS | Fuzzy logic system |
| FNS | Fuzzy neural system |
| FO | Fuzzy optimization |
| FPSS | Fuzzy logic power system stabilizer |
| FRS | Fuzzy rough set |
| FT | Fourier transform |
| FTS | Fuzzy time series |
| GAs | Genetic algorithms |
| GHSA | Global harmony search algorithm |
| GT2FHS | Generalized type-2 fuzzy harmony search |
| GT2-FIS | General type-2 fuzzy inference system |
| GWO | Gray wolf optimization |
| HFISA | Harmony fuzzy image segmentation algorithm |
| HHS | Hybridizations of harmony search |
| HHS-FL | Hybrid harmony search and fuzzy logic |
| HM | Harmony memory |
| HMS | Harmony memory size |
| HS | Harmony search |
| HSBA | Harmony search -based approach |
| HSCS | Harmony search with cuckoo search |
| HSPS | HS optimized partitioning strategy |
| ICA | Imperial competitive algorithm |
| IHPS | Isolated hybrid power system |
| IHS | Improved harmony search |
| IT2-FIS | Interval type-2 fuzzy inference systems |
| IT2-FLS | Interval type2- fuzzy logic system |
| IT2-FLS-EGARCH | Interval type2- fuzzy logic system exponential generalized autoregressive conditional heteroscedastic |
| IT2-CE-EGARCH | Interval type2-computationally efficient- exponential generalized autoregressive conditional heteroscedastic |
| JADE | Adaptive differential evolution |
| LFC | Load frequency control |
| LNF | Local neuro-fuzzy |
| LSBA | Logic strategy-based approach |
| LSSVMs | Least square support vector machines |
| LTE | Long-term 4G |
| MF | Membership function |
| MOHSA | Multi-objective harmony search algorithm |
| NGHSA | Novel global best harmony search algorithm |
| OPF | Optimal power flow |
| PAR | Pitch adjusting rate |
| PV | Photovoltaic |
| PID | Proportional-integral-derivative |
| PSO | Particle swarm optimization |
| QOBL | Quasi-opposition-based learning principle |
| QOHS | Quasi-oppositional harmony search |
| REWFTS-IHS | Refined exponentially weighted fuzzy time series improved harmony search |
| SAMOHSFC | Self-adapting multi-objective harmony search fuzzy clustering |
| SERNFIS | Self-evolving, recursive neuro-fuzzy inference system |
| SGHS | Self-adjusting global best harmony search |
| SHS | Standard harmony search |
| ST2-FIS | Shadowed type-2 fuzzy inference scheme |
| T1-FIS | Type-1 fuzzy inference systems |
| T1-FLS | Type-1 fuzzy logic system |
| T2-FLHS | Type-2 fuzzy logic harmony search |
| T2-FLS | Type-2 fuzzy logic scheme |
| TS | Tabu search |
| TSK | Takagi sugeno kang |
| VHSA | Variable neighborhood search combined with harmony search algorithm |
| WCA | Water cycle algorithm |
| WDN | Water distribution network |
| WSN | Wireless sensor network |
References
- Nasir, M.; Sadollah, A.; Choi, Y.H.; Kim, J.H. A comprehensive review on water cycle algorithm and its applications. Neural Comput. Appl. 2020, 32, 17433–17488. [Google Scholar] [CrossRef]
- Geem, Z.W. Music-Inspired Harmony Search Algorithm: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nasir, M.; Sadollah, A.; Yoon, J.H.; Geem, Z.W. Comparative study of Harmony Search algorithm and its applications in China, Japan and Korea. Appl. Sci. 2020, 10, 3970. [Google Scholar] [CrossRef]
- Askarzadeh, A. Solving electrical power system problems by harmony search: A review. Artif. Intell. Rev. 2016, 47, 217–251. [Google Scholar] [CrossRef]
- Dubey, M.; Kumar, V.; Kaur, M.; Dao, T.-P. A systematic review on harmony search algorithm: Theory, literature, and applications. Math. Probl. Eng. 2021, 2021, 5594267. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Kim, J.-H.; Geem, Z.W. Harmony search algorithm for energy system applications: An updated review and analysis. J. Exp. Theor. Artif. Intell. 2019, 31, 723–749. [Google Scholar] [CrossRef]
- Ala’a, A.; Alsewari, A.A.; Alamri, H.S.; Zamli, K.Z. Comprehensive review of the development of the harmony search algo-rithm and its applications. IEEE Access 2019, 7, 14233–14245. [Google Scholar]
- Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, M.; Meena, R.K. Optimal control of fault tolerant machining system with reboot and recovery in fuzzy envi-ronment using harmony search algorithm. ISA Trans. 2021, in press. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy collection. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Novák, V.; Hurtík, P.; Habiballa, H.; Štepnička, M. Recognition of damaged letters based on mathematical fuzzy logic analysis. J. Appl. Log. 2015, 13, 94–104. [Google Scholar] [CrossRef]
- Papakostas, G.; Hatzimichailidis, A.; Kaburlasos, V. Distance and similarity measures between intuitionistic fuzzy sets: A comparative analysis from a pattern recognition point of view. Pattern Recognit. Lett. 2013, 34, 1609–1622. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P.; Valdez, F.; Soria, J.; Ontiveros-Robles, E.; Peraza, C.; Ochoa, P. Shadowed Type-2 Fuzzy Systems for Dy-namic Parameter Adaptation in Harmony Search and Differential Evolution Algorithms. Algorithms 2019, 12, 17. [Google Scholar] [CrossRef]
- Wang, X.; Fu, M.; Ma, H.; Yang, Y. Lateral control of autonomous vehicles based on fuzzy logic. Control Eng. Pract. 2015, 34, 1–17. [Google Scholar] [CrossRef]
- Raju, G.; Nair, M.S. A fast and efficient color image enhancement method based on fuzzy-logic and histogram. AEU Int. J. Electron. Commun. 2014, 68, 237–243. [Google Scholar] [CrossRef]
- Zareiforoush, H.; Minaei, S.; Alizadeh, M.R.; Banakar, A. A hybrid intelligent approach based on computer vision and fuzzy logic for quality measurement of milled rice. Measurement 2015, 66, 26–34. [Google Scholar] [CrossRef]
- Harirchian, E.; Lahmer, T. Developing a hierarchical type-2 fuzzy logic model to improve rapid evaluation of earthquake hazard safety of existing buildings. Structures 2020, 28, 1384–1399. [Google Scholar] [CrossRef]
- Zhai, P.; Williams, E. Analyzing consumer acceptance of photovoltaics (PV) using fuzzy logic model. Renew. Energy 2012, 41, 350–357. [Google Scholar] [CrossRef]
- Korol, T. A fuzzy logic model for forecasting exchange rates. Knowl.-Based Syst. 2014, 67, 49–60. [Google Scholar] [CrossRef]
- Chi, Z.; Yan, H.; Pham, T. Fuzzy Algorithms: With Applications to Image Processing and Pattern Recognition; World Scientific: Singapore, 1996. [Google Scholar] [CrossRef]
- Bonarini, A. Fuzzy Modelling: Paradigms and Practice; Kluwer Academic Press: Norwell, MA, USA, 1996. [Google Scholar]
- Driankov, D. An Introduction to Fuzzy Control; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Filip, I.; Szeidert, I. Adaptive fuzzy PI controller with shifted control singletons. Expert Syst. Appl. 2016, 54, 1–12. [Google Scholar] [CrossRef]
- Castro, J.R.; Sanchez, M.A.; Gonzalez, C.I.; Melin, P.; Castillo, O. A New Method for Parameterization of General Type-2 Fuzzy Sets. Fuzzy Inf. Eng. 2018, 10, 31–57. [Google Scholar] [CrossRef]
- Zangeneh, M.; Aghajari, E.; Forouzanfar, M. A survey: Fuzzify parameters and membership function in electrical applications. Int. J. Dyn. Control 2020, 8, 1040–1051. [Google Scholar] [CrossRef]
- Zangeneh, M.; Aghajari, E.; Forouzanfar, M. Fuzzy membership function selection in electrical systems: A review. J. Nov. Res. Electr. Power 2019, 8, 13–25. [Google Scholar]
- Herrera, F. Genetic fuzzy systems: Taxonomy, current research trends and prospects. Evol. Intell. 2008, 1, 27–46. [Google Scholar] [CrossRef]
- Fernández, A.; López, V.; Del Jesus, M.J.; Herrera, F. Revisiting Evolutionary Fuzzy Systems: Taxonomy, applications, new trends and challenges. Knowl.-Based Syst. 2015, 80, 109–121. [Google Scholar] [CrossRef]
- Castillo, O.; Neyoy, H.; Soria, J.; Melin, P.; Valdez, F. A new approach for dynamic fuzzy logic parameter tuning in Ant Colony Optimization and its application in fuzzy control of a mobile robot. Appl. Soft Comput. 2014, 28, 150–159. [Google Scholar] [CrossRef]
- Caraveo, C.; Valdez, F.; Castillo, O. Optimization of fuzzy controller design using a new bee colony algorithm with fuzzy dynamic parameter adaptation. Appl. Soft Comput. 2016, 43, 131–142. [Google Scholar] [CrossRef]
- Olivas, F.; Valdez, F.; Castillo, O.; Melin, P. Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic. Soft Comput. 2014, 20, 1057–1070. [Google Scholar] [CrossRef]
- Guerrero, M.; Castillo, O.; García, M. Fuzzy dynamic parameters adaptation in the Cuckoo Search Algorithm using fuzzy logic. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 441–448. [Google Scholar]
- Castillo, O.; Ochoa, P.; Soria, J. Differential evolution with fuzzy logic for dynamic adaptation of parameters in mathematical function optimization. In Imprecision and Uncertainty in Information Representation and Processing; Springer: Cham, Switzerland, 2015; pp. 361–374. [Google Scholar]
- Alcala-Fdez, J.; Alcalá, R.; Gacto, M.J.; Herrera, F. Learning the membership function contexts for mining fuzzy association rules by using genetic algorithms. Fuzzy Sets Syst. 2009, 160, 905–921. [Google Scholar] [CrossRef]
- Alcala-Fdez, J.; Alcala, R.; Herrera, F. A Fuzzy Association Rule-Based Classification Model for High-Dimensional Problems with Genetic Rule Selection and Lateral Tuning. IEEE Trans. Fuzzy Syst. 2011, 19, 857–872. [Google Scholar] [CrossRef]
- Cruz-Ramírez, M.; Hervás-Martínez, C.; Sánchez-Monedero, J.; Gutiérrez, P.A. Metrics to guide a multi-objective evolutionary algorithm for ordinal classification. Neurocomputing 2014, 135, 21–31. [Google Scholar] [CrossRef]
- Omid, M.; Lashgari, M.; Mobli, H.; Alimardani, R.; Mohtasebi, S.; Hesamifard, R. Design of fuzzy logic control system incorpo-rating human expert knowledge for combine harvester. Expert Syst. Appl. 2010, 37, 7080–7085. [Google Scholar] [CrossRef]
- Fullér, R.; Canós-Darós, L.; Canos Daros, M. Transparent fuzzy logic based methods for some human resources problems. Rect@ 2012, 13, 27–41. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy Algorithms. Inf. Control 1968, 12, 94–102. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M.; Wu, H. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: Part 1, forward problems. IEEE Trans. Fuzzy Syst. 2006, 14, 781–792. [Google Scholar] [CrossRef]
- Maldonado, Y.; Castillo, O.; Melin, P. Particle swarm optimization of interval type-2 fuzzy systems for FPGA applications. Appl. Soft Comput. 2012, 13, 496–508. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Srinivasan, D. Interval type-2 fuzzy logic systems for load forecasting: A compar-ative study. IEEE Trans. Power Syst. 2012, 27, 1274–1282. [Google Scholar] [CrossRef]
- Jalili, A.; Ghadimi, N. Hybrid harmony search algorithm and fuzzy mechanism for solving congestion management problem in an electricity market. Complexity 2016, 21, 90–98. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.; Pan, Q.-K.; Tasgetiren, M.F. An effective discrete harmony search algorithm for flexible job shop scheduling problem with fuzzy processing time. Int. J. Prod. Res. 2015, 53, 5896–5911. [Google Scholar] [CrossRef]
- Jie-jie, Z.; Ling-yan, Q.; Liang-yi, W.; Min, L.; Chuang-xin, G. Dynamic reconfiguration of distribution network based on im-proved optimal fuzzy C-means clustering and improved harmony search algorithm. J. Mech. Electr. Eng. 2015, 32, 531–536. [Google Scholar]
- Pandiarajan, K.; Babulal, C.K. Fuzzy harmony search algorithm based optimal power flow for power system security enhancement. Int. J. Electr. Power Energy Syst. 2016, 78, 72–79. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Garcia, M.; Melin, P.; Castillo, O. A New Fuzzy Harmony Search Algorithm Using Fuzzy Logic for Dy-namic Parameter Adaptation. Algorithms 2016, 9, 69. [Google Scholar] [CrossRef]
- Moh’d Alia, O.; Mandava, R.; Ramachandram, D.; Aziz, M.E. Harmony search-based cluster initialization for fuzzy c-means segmentation of mr images. In Proceedings of the TENCON 2009—2009 IEEE Region 10 Conference, Singapore, 23–26 January 2009; pp. 1–6. [Google Scholar]
- Babu, P.S.; Mohan, R.M. Notice of Removal: Optimal performance enhancement of DG for loss reduction using Fuzzy and Harmony Search Algorithm. In Proceedings of the 2015 International Conference on Electrical, Electronics, Signals, Communication and Optimization (EESCO), Visakhapatnam, India, 24–25 January 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Esmaeili, S.; Dehnavi, H.D.; Karimzadeh, F. Simultaneous Reconfiguration and Capacitor Placement with Harmonic Consid-eration Using Fuzzy Harmony Search Algorithm. Arab. J. Sci. Eng. 2014, 39, 3859–3871. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective Optimization of Water Distribution Networks Using Fuzzy Theory and Harmony Search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Varghese, M.P.; Amudha, A. Hybrid harmony search algorithm & fuzzy logic for solving unit commitment problem with wind power uncertainty. Int. J. Eng. Technol. 2018, 7, 75–83. [Google Scholar] [CrossRef][Green Version]
- Peraza, C.; Valdez, F.; Castillo, O.; Melin, P. A Fuzzy Harmony Search Algorithm for the Optimization of a Benchmark Set of Functions. In Advances in Soft Computing, Proceedings of the MICAI 2018, Guadalajara, Mexico, 22–27 October 2018; Springer: Cham, Switzerland, 2018; Volume 11288, pp. 401–412. [Google Scholar]
- Dahej, A.E.; Esmaeili, S.; Goroohi, A. Multi-objective optimal location of SSSC and STATCOM achieved by fuzzy optimization strategy and harmony search algorithm. Sci. Iran. 2013, 20, 2024–2035. [Google Scholar]
- Shivaie, M.; Salemnia, A.; Ameli, M.T. Optimal multi-objective placement and sizing of passive and active power filters by a fuzzy-improved harmony search algorithm. Int. Trans. Electr. Energy Syst. 2015, 25, 520–546. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Castillo, O. Improved Method Based on Type-2 Fuzzy Logic for the Adaptive Harmony Search Algorithm. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Springer: Cham, Switzerland, 2018; Volume 749, pp. 29–37. [Google Scholar]
- Nie, F.; Li, J.; Tu, T.; Pan, M. Image Thresholding Using Fuzzy Correlation Criterion and Harmony Search Algorithm. Int. J. Comput. Intell. Appl. 2014, 13, 1450003. [Google Scholar] [CrossRef]
- Mistarihi, M.Z.; Okour, R.A.; Magableh, G.M.; Salameh, H.B. Integrating Advanced Harmony Search with Fuzzy Logic for Solving Buffer Allocation Problems. Arab. J. Sci. Eng. 2020, 45, 3233–3244. [Google Scholar] [CrossRef]
- Lu, S.; Wang, X. A fuzzy Bi-objective multi-commodity minimum cost flow-based perishable food transportation problem and its harmony search algorithm. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 725–728. [Google Scholar]
- Aungkulanon, P.; Phruksaphanrat, B.; Luangpaiboon, P. Various hybridisations of harmony search algorithm for fuzzy pro-gramming approach to aggregate production planning. In Proceedings of the World Congress on Engineering 2012, London, UK, 4–6 July 2012; Citeseer: Princeton, NJ, USA, 2010; pp. 73–79. [Google Scholar]
- Abhishek, K.; Datta, S.; Mahapatra, S.S. Multi-objective optimization in drilling of CFRP (polyester) composites: Application of a fuzzy embedded harmony search (HS) algorithm. Measurement 2016, 77, 222–239. [Google Scholar] [CrossRef]
- Meena, R.K.; Jain, M.; Sanga, S.S.; Assad, A. Fuzzy modeling and harmony search optimization for machining system with general repair, standby support and vacation. Appl. Math. Comput. 2019, 361, 858–873. [Google Scholar] [CrossRef]
- Diao, R.; Shen, Q. A harmony search based approach to hybrid fuzzy-rough rule induction. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems, Brisbane, QLD, Australia, 10–15 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–8. [Google Scholar]
- Sadaei, H.J.; Enayatifar, R.; Abdullah, A.H.; Gani, A. Short-term load forecasting using a hybrid model with a refined expo-nentially weighted fuzzy time series and an improved harmony search. Int. J. Electr. Power Energy Syst. 2014, 62, 118–129. [Google Scholar] [CrossRef]
- Chen, Y.H.; Hong, W.-C.; Shen, W.; Huang, N.N. Electric Load Forecasting Based on a Least Squares Support Vector Machine with Fuzzy Time Series and Global Harmony Search Algorithm. Energies 2016, 9, 70. [Google Scholar] [CrossRef]
- Van Tinh, N.; Thi, B.T. Enhanced Accuracy of High–Order Fuzzy Time Series Forecasting Model Based on Harmony Search Algorithm. Int. J. Sci. Eng. Sci. 2019, 3, 6–12. [Google Scholar]
- Dash, R.; Dash, P. Efficient stock price prediction using a Self Evolving Recurrent Neuro-Fuzzy Inference System optimized through a Modified Differential Harmony Search Technique. Expert Syst. Appl. 2016, 52, 75–90. [Google Scholar] [CrossRef]
- Zadeh, M.M.; Bathaee, S. Load frequency control in interconnected power system by nonlinear term and uncertainty consid-erations by using of harmony search optimization algorithm and fuzzy-neural network. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1094–1100. [Google Scholar]
- Miranian, A.; Abdollahzade, M. A neuro-fuzzy approach with harmony search optimization for short-term wind power forecasting. Int. J. Energy Stat. 2014, 2, 71–87. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Melin, P. Optimization of Intelligent Controllers Using a Type-1 and Interval Type-2 Fuzzy Harmony Search Algorithm. Algorithms 2017, 10, 82. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Castillo, O. An Adaptive Fuzzy Control Based on Harmony Search and Its Application to Optimization. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2017; Volume 667, pp. 269–283. [Google Scholar]
- Peraza, C.; Valdez, F.; Castillo, O. Fuzzy control of parameters to dynamically adapt the HS algorithm for optimization. In Proceedings of the 2015 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS) Held Jointly with 2015 5th World Conference on Soft Computing (WConSC), Redmond, WA, USA, 17–19 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Rodríguez, L.; Castillo, O.; García, M.; Soria, J. A comparative study of dynamic adaptation of parameters in the GWO algo-rithm using type-1 and interval type-2 fuzzy logic. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Springer: Cham, Switzerland, 2018; pp. 3–16. [Google Scholar]
- Rodríguez, L.; Castillo, O.; Soria, J. A Study of Parameter Dynamic Adaptation with Fuzzy Logic for the Grey Wolf Optimizer Algorithm. In Advances in Computational Intelligence, Proceedings of the Mexican International Conference on Artificial Intelligence, MICAI 2016, Cancún, Mexico, 23–29 October 2016; Springer: Cham, Switzerland, 2017; Volume 10061, pp. 228–238. [Google Scholar]
- Rodríguez, L.; Castillo, O.; Soria, J. A study of parameters of the grey wolf optimizer algorithm for dynamic adaptation with fuzzy logic. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2017; pp. 371–390. [Google Scholar]
- Rodríguez, L.; Castillo, O.; Soria, J.; Melin, P.; Valdez, F.; Gonzalez, C.I.; Martinez, G.E.; Soto, J. A fuzzy hierarchical operator in the grey wolf optimizer algorithm. Appl. Soft Comput. 2017, 57, 315–328. [Google Scholar] [CrossRef]
- Olivas, F.; Valdez, F.; Castillo, O. A fuzzy system for parameter adaptation in ant colony optimization. In Proceedings of the 2014 IEEE Symposium on Swarm Intelligence, Orlando, FL, USA, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Olivas, F.; Valdez, F.; Castillo, O. Ant colony optimization with parameter adaptation using fuzzy logic for TSP problems. In Design of Intelligent Systems Based on Fuzzy Logic, Neural Networks and Nature-Inspired Optimization; Springer: Cham, Switzerland, 2015; pp. 593–603. [Google Scholar]
- Olivas, F.; Valdez, F.; Castillo, O.; Gonzalez, C.I.; Martinez, G.E.; Melin, P. Ant colony optimization with dynamic parameter adaptation based on interval type-2 fuzzy logic systems. Appl. Soft Comput. 2017, 53, 74–87. [Google Scholar] [CrossRef]
- Bernal, E.; Castillo, O.; Soria, J. Fuzzy logic for dynamic adaptation in the imperialist competitive algorithm. In Proceedings of the 2016 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS), El Paso, TX, USA, 31 October–4 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Bernal, E.; Castillo, O.; Soria, J.; Valdez, F. Interval Type-2 fuzzy logic for dynamic parameter adjustment in the imperialist competitive algorithm. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Bernal, E.; Castillo, O.; Soria, J.; Valdez, F. Type-2 fuzzy logic for dynamic parameter adaptation in the imperialist competitive algorithm. In Hybrid Intelligent Systems in Control, Pattern Recognition and Medicine; Springer: Amsterdam, The Netherlands, 2020; pp. 109–118. [Google Scholar]
- Méndez, E.; Castillo, O.; Soria, J.; Melin, P.; Sadollah, A. Water Cycle Algorithm with Fuzzy Logic for Dynamic Adaptation of Parameters. In Advances in Computational Intelligence, Proceedings of the Mexican International Conference on Artificial Intelligence, MICAI 2016, Cancún, Mexico, 23–29 October 2016; Springer: Cham, Switzerland, 2016; pp. 250–260. [Google Scholar]
- Méndez, E.; Castillo, O.; Soria, J.; Sadollah, A. Fuzzy Dynamic Adaptation of Parameters in the Water Cycle Algorithm. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2017; pp. 297–311. [Google Scholar]
- Castillo, O.; Ramirez, E.; Roeva, O. Water cycle algorithm augmentation with fuzzy and intuitionistic fuzzy dynamic adapta-tion of parameters. Notes Intuit. Fuzzy Sets 2017, 23, 79–94. [Google Scholar]
- Mahmoudi, S.; Aghaie, M. Evaluation of fuzzy based HS and GSA on reloading cycle length optimization of PWR nuclear power plant. Ann. Nucl. Energy 2019, 134, 1–10. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Castillo, O. An Improved Harmony Search Algorithm Using Fuzzy Logic for the Optimization of Mathematical Functions. In Design of Intelligent Systems Based on Fuzzy Logic, Neural Networks and Nature-Inspired Optimization; Springer: Cham, Switzerland, 2015; Volume 601, pp. 605–615. [Google Scholar]
- Ameli, K.; Alfi, A.; Aghaebrahimi, M. A fuzzy discrete harmony search algorithm applied to annual cost reduction in radial distribution systems. Eng. Optim. 2015, 48, 1529–1549. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Castillo, O. Interval type-2 fuzzy logic for dynamic parameter adaptation in the harmony search algo-rithm. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 1–4 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 106–112. [Google Scholar]
- Peraza, C.; Valdez, F.; Castillo, O. Comparative Study of Type-1 and Interval Type-2 Fuzzy Systems in the Fuzzy Harmony Search Algorithm Applied to Benchmark Functions. In Advances in Fuzzy Logic and Technology; Springer: Cham, Switzerland, 2017; Volume 643, pp. 162–170. [Google Scholar]
- Peraza, C.; Valdez, F.; Castillo, O. Study on the Use of Type-1 and Interval Type-2 Fuzzy Systems Applied to Benchmark Functions Using the Fuzzy Harmony Search Algorithm. In Fuzzy Logic in Intelligent System Design, Proceedings of the North American Fuzzy Information Processing Society Annual Conference, Cancun, Mexico, 16–18 October 2017; Springer: Cham, Switzerland, 2017; Volume 648, pp. 94–103. [Google Scholar]
- Peraza, C.; Valdez, F.; Castillo, O. Fuzzy Harmony Search Algorithm Using an Interval Type-2 Fuzzy Logic Applied to Benchmark Mathematical Functions. In Intuitionistic Fuzziness and Other Intelligent Theories and Their Applications; Springer: Cham, Switzerland, 2019; Volume 757, pp. 13–28. [Google Scholar]
- Wang, L.; Yang, R.; Pardalos, P.M.; Qian, L.; Fei, M. An adaptive fuzzy controller based on harmony search and its application to power plant control. Int. J. Electr. Power Energy Syst. 2013, 53, 272–278. [Google Scholar] [CrossRef]
- Das Sharma, K.; Chatterjee, A.; Rakshit, A. Design of a Hybrid Stable Adaptive Fuzzy Controller Employing Lyapunov Theory and Harmony Search Algorithm. IEEE Trans. Control Syst. Technol. 2010, 18. [Google Scholar] [CrossRef]
- Gheisarnejad, M. An effective hybrid harmony search and cuckoo optimization algorithm based fuzzy PID controller for load frequency control. Appl. Soft Comput. 2018, 65, 121–138. [Google Scholar] [CrossRef]
- Tarkeshwar; Mukherjee, V. A novel quasi-oppositional harmony search algorithm and fuzzy logic controller for frequency stabilization of an isolated hybrid power system. Int. J. Electr. Power Energy Syst. 2015, 66, 247–261. [Google Scholar] [CrossRef]
- Tarkeshwar, M.; Mukherjee, V. Quasi-oppositional harmony search algorithm and fuzzy logic controller for load frequency stabilisation of an isolated hybrid power system. IET Gener. Transm. Distrib. 2015, 9, 427–444. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Prasad, R. Optimal Tuning of Fuzzy Logic Power System Stabilizer Using Harmony Search Algorithm. Int. J. Fuzzy Syst. 2015, 17, 457–470. [Google Scholar] [CrossRef]
- Castillo, O.; Valdez, F.; Soria, J.; Amador-Angulo, L.; Ochoa, P.; Peraza, C. Comparative Study in Fuzzy Controller Optimiza-tion Using Bee Colony, Differential Evolution, and Harmony Search Algorithms. Algorithms 2018, 12, 9. [Google Scholar] [CrossRef]
- Chao, F.; Zhou, D.; Lin, C.-M.; Zhou, C.; Shi, M.; Lin, D. Fuzzy cerebellar model articulation controller network optimization via self-adaptive global best harmony search algorithm. Soft Comput. 2017, 22, 3141–3153. [Google Scholar] [CrossRef]
- Sharma, K.D.; Siarry, P.; Chatterjee, A.; Rakshit, A. Nonlinear Parameter Variation of HS Algorithm for Designing Stable Adaptive Fuzzy Controllers. Artif. Evol. (Evol. Artif.) 2013, 148, 1–13. [Google Scholar]
- Wang, H.; Yuan, X.; Wang, Y.; Yang, Y. Harmony search algorithm-based fuzzy-PID controller for electronic throttle valve. Neural Comput. Appl. 2011, 22, 329–336. [Google Scholar] [CrossRef]
- Mahto, T.; Mukherjee, V. Fractional order fuzzy PID controller for wind energy-based hybrid power system using quasi-oppositional harmony search algorithm. IET Gener. Transm. Distrib. 2017, 11, 3299–3309. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Prasad, R. Design of harmony search algorithm based tuned fuzzy logic power system stabilizer. Int. Rev. Electr. Eng. IREE 2013, 8, 1594. [Google Scholar] [CrossRef]
- Valdez, F.; Peraza, C. Dynamic parameter adaptation in the harmony search algorithm for the optimization of interval type-2 fuzzy logic controllers. Soft Comput. 2019, 24, 179–192. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Peraza, C. Fuzzy Logic in Dynamic Parameter Adaptation of Harmony Search Optimization for Benchmark Functions and Fuzzy Controllers. Int. J. Fuzzy Syst. 2020, 22, 1198–1211. [Google Scholar] [CrossRef]
- Sharma, K.D. Stable fuzzy controller design employing group improvisation based harmony search algorithm. Int. J. Control Autom. Syst. 2013, 11, 1046–1052. [Google Scholar] [CrossRef]
- Sharma, K.D.; Chatterjee, A.; Rakshit, A. Harmony search algorithm and Lyapunov theory based hybrid adaptive fuzzy con-troller for temperature control of air heater system with transport-delay. Appl. Soft Comput. 2014, 25, 40–50. [Google Scholar] [CrossRef]
- Das Sharma, K.; Chatterjee, A.; Rakshit, A. Harmony search-based hybrid stable adaptive fuzzy tracking controllers for vision-based mobile robot navigation. Mach. Vis. Appl. 2013, 25, 405–419. [Google Scholar] [CrossRef]
- Zhou, D.; Chao, F.; Lin, C.-M.; Shi, M.; Zhou, C. Harmony Search Algorithm for Fuzzy Cerebellar Model Articulation Control-ler Networks Optimization. In Advances in Computational Intelligence Systems; Springer: Cham, Switzerland, 2017; Volume 513, pp. 45–58. [Google Scholar]
- Peraza, C.; Valdez, F.; Castro, J.R.; Castillo, O. Fuzzy Dynamic Parameter Adaptation in the Harmony Search Algorithm for the Optimization of the Ball and Beam Controller. Adv. Oper. Res. 2018, 2018, 3092872. [Google Scholar] [CrossRef]
- Perez, J.; Valdez, F.; Castillo, O.; Melin, P.; Gonzalez, C.; Martinez, G. Interval type-2 fuzzy logic for dynamic parameter adap-tation in the bat algorithm. Soft Comput. 2017, 21, 667–685. [Google Scholar] [CrossRef]
- Pérez, J.; Valdez, F.; Castillo, O. Modification of the bat algorithm using type-2 fuzzy logic for dynamical parameter adaptation. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2017; pp. 343–355. [Google Scholar]
- Amjady, N.; Abedinia, O.; Shayanfar, H.; Ghasemi, A. Market Optimization Using Fuzzy Based Multiobjective Harmony Search Algorithm. Int. J. Tech. Phys. Probl. Eng. IJTPE 2012, 12, 9–15. [Google Scholar]
- Abedinia, O.; Amjady, N.; Ghasemi, A.; Shayeghi, H. Multi-Stage Fuzzy Load Frequency Control Based on Multi objective Harmony Search Algorithm in Deregulated Environment. J. Oper. Autom. Power Eng. 2013, 1, 63–73. [Google Scholar]
- Mahmudizad, M.; Ahangar, R.A. Improving load frequency control of multi-area power system by considering uncertainty by using optimized type 2 fuzzy pid controller with the harmony search algorithm. Int. J. Electr. Inf. Eng. 2016, 10, 1099–1109. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. CSUR 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Forsati, R.; Mahdavi, M.; Kangavari, M.; Safarkhani, B. Web page clustering using harmony search optimization. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 001601–001604. [Google Scholar]
- Mahdavi, M.; Chehreghani, M.H.; Abolhassani, H.; Forsati, R. Novel meta-heuristic algorithms for clustering web documents. Appl. Math. Comput. 2008, 201, 441–451. [Google Scholar] [CrossRef]
- Wang, X.; Gao, X.Z.; Ovaska, S.J. Fusion of clonal selection algorithm and harmony search method in optimisation of fuzzy classification systems. Int. J. Bio-Inspired Comput. 2009, 1, 80–88. [Google Scholar] [CrossRef]
- Alia, O.M.; Mandava, R.; Aziz, M.E. A hybrid harmony search algorithm for MRI brain segmentation. Evol. Intell. 2011, 4, 31–49. [Google Scholar] [CrossRef]
- Ayvaz, M.T. Simultaneous determination of aquifer parameters and zone structures with fuzzy c-means clustering and meta-heuristic harmony search algorithm. Adv. Water Resour. 2007, 30, 2326–2338. [Google Scholar] [CrossRef]
- Malaki, M.; Abolhassani, H. A Combinatiory Approach to Fuzzy Clustering with Harmony Search and its Applications to Space Shuttle data. In SCIS & ISIS SCIS & ISIS 2008; Japan Society for Fuzzy Theory and Intelligent Informatics: Fukuoka, Japan, 2008; pp. 1154–1159. [Google Scholar]
- Van Tinh, N. An Improved Fuzzy Time Series Forecasting Model Based on Combining K–means Clustering with Harmony Search. Am. J. Inf. Sci. Comput. Eng. 2019, 5, 94–102. [Google Scholar]
- Agrawal, D.; Pandey, S. FLIHSBC: Fuzzy Logic and Improved Harmony Search Based Clustering Algorithm for Wireless Sensor Networks to Prolong the Network Lifetime. In Ubiquitous Computing and Ambient Intelligence, Proceedings of the International Conference on Ubiquitous Computing and Ambient Intelligence 2017, Philadelphia, PA, USA, 7–10 November 2017; Springer: Cham, Switzerland, 2017; Volume 10586, pp. 570–578. [Google Scholar]
- Feng, Y.; Zhou, J.; Tayyab, M. Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification. Algorithms 2017, 10, 14. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Geem, Z.W. A Comprehensive Survey of the Harmony Search Algorithm in Clustering Applications. Appl. Sci. 2020, 10, 3827. [Google Scholar] [CrossRef]
- Moh’d Alia, O.; Mandava, R.; Ramachandram, D.; Aziz, M.E. Dynamic fuzzy clustering using harmony search with application to image segmentation. In Proceedings of the 2009 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 14–17 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 538–543. [Google Scholar]
- Alia, O.M.d. A dynamic harmony search-based fuzzy clustering protocol for energy-efficient wireless sensor networks. Ann. Telecommun. 2017, 73, 353–365. [Google Scholar] [CrossRef]
- Ayvaz, M.T.; Elçi, A. Simultaneous estimation of groundwater recharge rates, associated zone structures, and hydraulic conductivity values using fuzzy c-means clustering and harmony search optimisation algorithm: A case study of the Tahtali watershed. In Proceedings of the ModelCARE2011, Leipzig, Germany, 10 September 2011; pp. 18–22. [Google Scholar]
- Wan, C.; Yuan, X.; Dai, X.; Zhang, T.; He, Q. A self-adaptive multi-objective harmony search based fuzzy clustering technique for image segmentation. J. Ambient Intell. Humaniz. Comput. 2018, 1–16. [Google Scholar] [CrossRef]
- Satwika, I.K.S.; Swari, M.H.P. eNodeB Position Forecasting of LTE Based On BTS Existing Using Fuzzy C-Means and Harmo-ny Search Methods. IJCONSIST J. 2019, 1, 13–19. [Google Scholar]
- Agrawal, D.; Pandey, S. Optimization of the selection of cluster-head using fuzzy logic and harmony search in wireless sensor networks. Int. J. Commun. Syst. 2020, 34, e4391. [Google Scholar] [CrossRef]
- Ko, K.-E.; Sim, K.-B. An EEG signals classification system using optimized adaptive neuro-fuzzy inference model based on harmony search algorithm. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 26–29 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1457–1461. [Google Scholar]
- Bekkouche, I.; Fizazi, H. A new image clustering method based on the fuzzy harmony search algorithm and Fourier transform. J. Inf. Process. Syst. 2016, 12, 555–576. [Google Scholar]
- Mahmoodi, M.S.; Mahmoodi, S.A. Hybrid Harmony Search and Genetic for Fuzzy Classification Systems. J. Math. Comput. Sci. 2014, 10, 203–211. [Google Scholar] [CrossRef]
- Dos Santos Coelho, L.; Diego, L.d.A. A harmony search approach using exponential probability distribution applied to fuzzy logic control optimization. In Recent Advances in Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2010; pp. 77–88. [Google Scholar]
- Kong, Z.; Wang, L.; Jia, W. Approximate Normal Parameter Reduction of Fuzzy Soft Set Based on Harmony Search Algorithm. In Proceedings of the 2015 IEEE Fifth International Conference on Big Data and Cloud Computing, Dalian, China, 26–28 August 2015; pp. 321–324. [Google Scholar]
- Al Daoud, E. An Efficient Algorithm for Finding a Fuzzy Rough Set Reduct Using an Improved Harmony Search. Int. J. Mod. Educ. Comput. Sci. 2015, 7, 16–23. [Google Scholar] [CrossRef]
- Mashinchi, M.H.; Orgun, M.A.; Mashinchi, M.; Pedrycz, W. A Tabu–Harmony Search-Based Approach to Fuzzy Linear Regres-sion. IEEE Trans. Fuzzy Syst. 2011, 19, 432–448. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.; Bisoi, R. A differential harmony search based hybrid interval type2 fuzzy EGARCH model for stock market volatility prediction. Int. J. Approx. Reason. 2015, 59, 81–104. [Google Scholar] [CrossRef]
- Aungkulanon, P.; Phruksaphanrat, B.; Luangpaiboon, P. Harmony Search Algorithm with Various Evolutionary Elements for Fuzzy Aggregate Production Planning. In Intelligent Control and Innovative Computing; Springer: New York, NY, USA, 2012; Volume 110, pp. 189–201. [Google Scholar]
- Alia, O.M.; Mandava, R.; Ramachandram, D.; Aziz, M.E. A Novel Image Segmentation Algorithm Based on Harmony Fuzzy Search Algorithm. In Proceedings of the 2009 International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 335–340. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).