A Combinatorial Approach to the Computation of the Fractional Edge Dimension of Graphs

Abstract

E. Yi recently introduced the fractional edge dimension of graphs. It has many applications in different areas of computer science such as in sensor networking, intelligent systems, optimization, and robot navigation. In this paper, the fractional edge dimension of vertex and edge transitive graphs is calculated. The class of hypercube graph $Q_n$ with an odd number of vertices n is discussed. We propose the combinatorial criterion for the calculation of the fractional edge dimension of a graph, and hence applied it to calculate the fractional edge dimension of the friendship graph $F_k$ and the class of circulant graph $C_n(1,2)$.

1. Introduction and Preliminary Results

Let $G=\left(V\right(G),E(G\left)\right)$ be a finite simple connected graph and $u,v\in V\left(G\right)$. The $d(u,v)$ denotes the length of shortest path between u and v. If $X\subseteq V\left(G\right)$, then $X^c=V\left(G\right)\backslash X$. For $u,v\in V\left(G\right)$, the resolving neighborhood of u and v, denoted by $R\{u,v\}$, is given by the collection of all $w\in V\left(G\right)$, which are not equidistant from u and v. The set $W\subseteq V\left(G\right)$ is a resolving set of G if $W\cap R\{u,v\}\ne \varnothing$ for all distinct pairs of vertices $u,v$ in $V\left(G\right)$. The minimum cardinality of a resolving set is called a metric dimension, $\dim \left(G\right)$, of G. The metric dimension of a graph, mostly referred to as the conventional metric dimension of a graph, was introduced by Slater [1,2] and Harary [3] independently. This concept has been comprehensively studied by many scholars since its appearance due to its wide range of applications in science, social science, and technology. For more details on metric dimension and its applications, we refer readers to [4,5,6].

For $u,v,w\in V\left(G\right)$ and $e=vw\in E\left(G\right)$, $d(e,u)=min\left\{d\right(v,u),d(v,w\left)\right\}$ is the distance between the edge e and vertex u. Let $E_p$ denote the collection of all $\left(\genfrac{}{}{0pt}{}{\left|E\right(G\left)\right|}{2}\right)$ pairs of distinct edges in G. A vertex $u\in V\left(G\right)$ is said to resolve a pair of distinct edges $\{e,e^{{}^{\prime }}\}$ in G if $d(e,u)\ne d(e^{{}^{\prime }},u)$. An edge resolving neighborhood of a pair of edges $\{e,e^{{}^{\prime }}\}\in E_p$ is defined as $R\{e,e^{{}^{\prime }}\}=\{u\in V\left(G\right):d(e,u)\ne d(e^{{}^{\prime }},u)\}$. A non-empty set S of vertices in a connected non-trivial simple graph G is an edge generator/edge resolving set for G, if for any pair of edges $e,e^{{}^{\prime }}\in E\left(G\right),S\cap R\{e,e^{{}^{\prime }}\}\ne \varnothing$. The edge metric dimension $edim\left(G\right)$ of G is the least cardinality of the edge metric generator for G. This concept was introduced by Kelenc et al. [7] two years ago. The conventional resolving set is the set of vertices that uniquely identifies all the vertices, whereas the edge resolving set is the set of vertices that uniquely identifies all the edges of a graph. This topic is an active field of research for graph theorists, and many research articles have been published on this subject. For details, see [8,9].

In recent years, the fractionalization of various parameters of graphs has been developing rapidly. It is studied under the name of fractional graph theory. For details on fractional graph theory, see [10]. The problem of finding the metric dimension $dim\left(G\right)$ of a graph has been suggested as an integer programming problem by Chartrand and Lesniak [11]. The integer programming construction for the metric dimension of a graph is described as: Minimize $x_1+x_2+\cdots +x_n$ subject to $A\overline{X}\ge \overline{1}$, where $\overline{X}={(x_1,x_2,\dots ,x_n)}^T,x_i\in \{0,1\}$ and $\overline{1}$ is the $\left(\genfrac{}{}{0pt}{}{n}{2}\right)\times 1$ column vector, all of whose entries are 1. Afterward, Currie and Oellermann [5] fractionalized this concept. The fractional metric dimension of G is the optimal solution for the integer programming relaxation of the integer programming problem after replacing $x_i\in \{0,1\}$ with $0\le x_i\le 1$. Fehr et al. [12] asserted the equivalent formulation of the fractional metric dimension of a graph G, supposing $V\left(G\right)=X=\{v_1,v_2,\dots ,v_n\}$ and $X_p=\{s_1,s_2,\dots ,s_{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\}$, where $s_i$ denotes distinct pairs of vertices in G. Let $A={\left(a_{ij}\right)}_{\left(\genfrac{}{}{0pt}{}{n}{2}\right)\times n}$ be a matrix with

$$a_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{s}_i{v}_i\in E\left(R\left(G\right)\right);\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

where $1\le i\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)$, $1\le j\le n$. The resolving graph $R\left(G\right)$ of G is a bipartite graph with a bipartition $\left(X,X_p\right)$, where $v_i\in X$ is connected to $s_j\in X_p$ if $v_i$ resolves it. Arumugam and Matthew [13,14] formulated the fractional metric dimension of a graph in terms of resolving functions. A function $f:V\left(G\right)\to [0,1]$ is called the minimal resolving function of G if $f\left(R\{u,v\}\right)={\sum }_{x\in R\{u,v\}}f\left(x\right)\ge 1$ for any distinct pair of vertices in $V\left(G\right)$. $min\left\{\right|f|:f\mathrm{as}\mathrm{a}\mathrm{minimal}\mathrm{resolving}\mathrm{function}\mathrm{of}G\}$, where $\left|f\right|={\sum }_{u\in V\left(G\right)}f\left(u\right)$, is called a fractional metric dimension of G, denoted by $di{m}_f\left(G\right)$. The following proposition follows from the definition of the fractional metric dimension of a graph.

Proposition 1.

For any connected non-trivial graph, $1\le di{m}_f\left(G\right)\le dim\left(G\right)$.

In his recent article [15], E. Yi introduced the notion of “Fractional edge dimension of graphs” as being analogous to the fractional metric dimension of graphs. A function $g:V\left(G\right)\to [0,1]$ is called an edge resolving function (ERF) of G if $g\left(R\{e,e^{{}^{\prime }}\}\right)\ge 1$ for any two distinct edges $e,e^{{}^{\prime }}\in E\left(G\right)$, where $g\left(R\{e,e^{{}^{\prime }}\}\right)={\sum }_{u\in R\{e,e^{{}^{\prime }}\}}g\left(u\right)$. An edge resolving function g of G is the minimal edge resolving function (MERF) if any function $h:V\left(G\right)\to [0,1]$, such that $h\le g$ and $h\left(u\right)\ne g\left(u\right)$ for at least one $u\in V\left(G\right)$ is not an edge resolving function of G. The fractional edge dimension $edi{m}_f\left(G\right)$ of G is defined as $edi{m}_f\left(G\right)=min\left\{\right|g|:gistheminimaledgeresolvingfunctionofG\}$. In the same article [15], E. Yi characterized all graphs G for which $edi{m}_f\left(G\right)=1$. He also calculated the fractional edge dimensions of trees, cycle, Petersen, wheel, complete k-partite, and grid graphs. Some of these results are given below.

Theorem 1

([15]). For any connected graph G of order n, $edi{m}_f\left(G\right)=1$ if and only if $G=P_n$, a path graph of order n.

Theorem 2

([15]).

• If $C_n$ is a cycle graph of order n, then $edi{m}_f\left(C_n\right)=\left\{\begin{array}{cc}\frac{n}{n-2},\hfill & \mathrm{if}niseven;\hfill \\ \frac{n}{n-1},\hfill & \mathrm{if}nisodd;\hfill \end{array}\right.$
• For petersen graph $P,edi{m}_f\left(P\right)=\frac{5}{2}$;
• For $s,t\ge 2,edi{m}_f(P_s\times P_t)=2$. The $P_s\times P_t$ denotes the cartesian product of two Path graphs of order s and t, respectively.

Yi also gave bounds for the fractional edge dimension of a graph.

Observation 1

([15]). $1\le edi{m}_f\left(G\right)\le edim\left(G\right)\le n$.

Proposition 2

([15]). If G is a connected graph of order $n\ge 3$, then $1\le edi{m}_f\left(G\right)\le \frac{n}{2}$.

This paper aims to further explore the fractional edge dimension of graphs. The framework of this article is as follows: Section 1 is reserved for introduction and preliminaries. In Section 2, the upper bound of the fractional edge dimension is given, which is better than the upper bound stated in Proposition 2. The fractional edge dimension of vertex and edge transitive graphs is calculated. It is proved that the fractional edge dimension of vertex and edge transitive graphs is $\frac{V\left(G\right)}{\alpha \left(G\right)}$, where $\alpha \left(G\right)$ is the minimum cardinality of some edge resolving neighborhood in G. The method used here is the conventional method (using definition). In Section 3, a combinatorial criterion for the calculation of the fractional edge dimension of a graph is proposed. This criterion can be applied to any simple connected graph. Using this criterion, it is proved that the fractional edge dimension of the friendship graph $F_k$ is k. The fractional edge dimension of $C_n(1,2)$ is calculated and is equal to $\frac{n}{\lceil \frac{n}{4}\rceil }$ if $n\equiv 1,2\left(\mathrm{mod}4\right)$, and $\frac{n}{\lceil \frac{n}{4}\rceil +1}$ if otherwise. In Section 4, a summary of the work performed is given. We also cite some future research perspectives in this section.

2. Fractional Edge Dimension of Vertex and Edge Transitive Graphs

In this section, we give an improved upper bound of the fractional edge dimension of a graph. The fractional edge dimensions of class of vertex and edge transitive graphs have been computed. As an application of this result, the fractional edge dimension of a complete graph is calculated. Lastly, we calculate the fractional edge dimension of hypercubes $Q_n$ with an odd number of vertices n.

Lemma 1.

If G is a connected graph, then $\left|R\right\{e,e^{{}^{\prime }}\left\}\right|\ge 2$ for all pairs of distinct edges $e,e^{{}^{\prime }}\in E\left(G\right)$.

Proof. 

Let $e,e^{{}^{\prime }}\in E\left(G\right)$ be a distinct pair of edges such that $e=uv\mathrm{and}{e}^{{}^{\prime }}=xy$. Clearly, $e,e^{{}^{\prime }}$ either shares a vertex or not.

Case 1

: If $e,e^{{}^{\prime }}$ shares a vertex (say) $v=x$, then $u,y\in R\{e,e^{{}^{\prime }}\}$.

Case 2

: If $e,e^{{}^{\prime }}$ does not share a vertex, then $d(u,e)=d(v,e)=0$ and $d(u,e^{{}^{\prime }})\ge 1$, $d(v,e^{{}^{\prime }})\ge 1$. This shows that $u,v$ resolves the pair of edges $e,e^{{}^{\prime }}$ as $d(u,e)\ne d(u,e^{{}^{\prime }})$. Moreover, $d(v,e)\ne d(v,e^{{}^{\prime }})$. Similarly, $x,y$ resolves the pair of edges $e,e^{{}^{\prime }}$ as well. Thus, $u,v,x,y\in R\{e,e^{{}^{\prime }}\}$, which completes the proof.

□

Lemma 2.

If G is a graph with $\alpha \left(G\right)=min\left\{\right|R\{e,e^{{}^{\prime }}\}|:e,e^{{}^{\prime }}\in E\left(G\right),e\ne e^{{}^{\prime }}\}$, then $edi{m}_f\left(G\right)\le \frac{\left|V\right(G\left)\right|}{\alpha \left(G\right)}$.

Proof. 

Define $g:V\left(G\right)\to [0,1]$ by $g\left(v\right)=\frac{1}{\alpha \left(G\right)}$. Then for any pair of distinct edges $e,e^{{}^{\prime }}$,

$g\left(R\{e,e^{{}^{\prime }}\}\right)=\frac{\left|R\right\{e,e^{{}^{\prime }}\left\}\right|}{\alpha \left(G\right)}\ge 1$. It shows that g is an edge resolving function of G. Thus, $edi{m}_f\left(G\right)\le \frac{\left|V\right(G\left)\right|}{\alpha \left(G\right)}$. □

Remark 1.

Clearly the upper bound of the fractional edge dimension of a graph given in Lemma 2 is better than the upper bound given by E.Yi in Proposition 2.

Let G be a graph with vertex set $V\left(G\right)$. The automorphism group $Aut\left(G\right)$ is the set of all permutations of $V\left(G\right)$ that preserve the adjacency and non-adjacency of vertices in a graph. A graph G is called vertex transitive if for any two distinct vertices $u,v\in V\left(G\right)$ there exists an automorphism $\varphi \in Aut\left(G\right)$ such that $\varphi \left(u\right)=v$. Similarly, G is edge transitive if for every pair of edges $e,e^{{}^{\prime }}$, there exists an automorphism $\phi \in Aut\left(G\right)$ such that $\phi \left(e\right)=e^{{}^{\prime }}$.The following theorem is the main result of this section, followed by the fractional edge dimension of the complete graph.

Theorem 3.

Let G be a simple connected graph. If G is a vertex and edge transitive graph, then the fractional edge metric dimension of G is $\frac{\left|V\right(G\left)\right|}{\alpha \left(G\right)}$.

Proof. 

Since $\alpha \left(G\right)=\alpha$ (say) is the minimum cardinality of some edge resolving neighborhood, there must therefore exist a distinct pair of edges $e,e^{{}^{\prime }}$ in $E\left(G\right)$ such that $\left|R\right\{e,e^{{}^{\prime }}\left\}\right|=\alpha$. Supposing $R\{e,e^{{}^{\prime }}\}=\{u_1,u_2,\dots ,u_{\alpha }\}$, for any automorphism $\rho$ of G, $R\{\rho \left(e\right),\rho \left(e^{{}^{\prime }}\right)\}=\{\rho \left(u_1\right),\rho \left(u_2\right),\dots ,\rho \left(u_{\alpha }\right)\}$. Let $\varphi$ be an edge resolving function with $edi{m}_f\left(G\right)=\left|\varphi \right|$. Then $1\le \varphi (R\{\rho \left(e\right),\rho \left(e^{{}^{\prime }}\right\})=\varphi \left(\rho \left(u_1\right)\right)+\varphi \left(\rho \left(u_2\right)\right)+\dots +\varphi \left(\rho \left(u_{\alpha }\right)\right)$, which shows that $\left|Aut\left(G\right)\right|\le {\mathsf{\Sigma }}_{\rho \in Aut\left(G\right)}(\varphi \left(\rho \left(u_1\right)\right)+\varphi \left(\rho \left(u_2\right)\right)+\dots +\varphi \left(\rho \left(u_r\right)\right))$. Since G is vertex and edge transitive, then ${|Aut\left(G\right)}_{u_1}{|·|\varphi |+|Aut\left(G\right)}_{u_2}{|·|\varphi |+\dots +|Aut\left(G\right)}_{u_{\alpha }}|·|\varphi |\ge \left|Aut\left(G\right)\right|$, which implies $edi{m}_f\left(G\right)=\left|\varphi \right|\ge \frac{\left|V\right(G\left)\right|}{\alpha }$. Hence, $edi{m}_f\left(G\right)=\frac{\left|V\right(G\left)\right|}{\alpha \left(G\right)}$ by using Lemma 2. □

E. Yi in [15] calculated the fractional edge dimension of a complete graph. Since a complete graph is vertex and edge transitive, the fractional edge dimension of a complete graph can be calculated using Theorem 3 as well. Therefore, we give its alternative proof in the next corollary.

Corollary 1

([15]). If G is a complete graph with n vertices, then $edi{m}_f\left(G\right)$ is $\frac{n}{2}$.

Proof. 

Using Lemma 1, $\left\{\right|R\{e,e^{{}^{\prime }}\}|:e,e^{{}^{\prime }}\in E\left(G\right)\}\le 2$ if $e,e^{{}^{\prime }}$ is adjacent. Let $w\in V\left(G\right)$ such that w is not the end vertex of e or $e^{{}^{\prime }}$. Since every vertex w is at distance 1 from every other vertex of G, $w\notin R\{e,e^{{}^{\prime }}\}$. That implies $min\left\{\right|R\{e,e^{{}^{\prime }}\}|:e,e^{{}^{\prime }}\in E\left(G\right)\}=2$. Since G is a vertex and edge transitive graph, using Theorem 3, we obtain $edi{m}_f\left(G\right)=\frac{n}{2}$. □

In [8], the metric dimension and edge dimension of the hypercube graph with an odd number of vertices n has been calculated and given in the following proposition.

Proposition 3

([8]). If n is odd, then $dim\left(Q_n\right)=edim\left(Q_n\right)=2$.

The following theorem gives the fractional edge dimension of hypercube graph $Q_n$ with an odd number of vertices n.

Theorem 4.

If G is a hypercube graph $Q_n$ with an odd number of vertices n, then the fractional edge dimension, $edi{m}_f\left(G\right)$, of G is 2.

Proof. 

Let $u_1=(0,0,\dots ,0),u_2=(1,0,0,\dots ,0),u_3=(1,1,0,0,\dots ,0),u_4=(0,1,0,0,\dots ,0)\mathrm{and}{e}_1=u_1{u}_2,e_2=u_1{u}_4,e_3=u_2{u}_3$. The $R\{e_1,e_2\}=\{(0,1,{\alpha }_3,{\alpha }_4,\dots ,{\alpha }_n):{\alpha }_i\in \{0,1\}\}\cup \{(1,0,{\beta }_3,{\beta }_4,\dots ,{\beta }_n):{\beta }_i\in \{0,1\}\}$ and $R\{e_1,e_3\}=\{(0,0,{\alpha }_3^{{}^{\prime }},{\alpha }_4^{{}^{\prime }},\dots ,{\alpha }_n^{{}^{\prime }}):{\alpha }_i^{{}^{\prime }}\in \{0,1\}\}\cup \{(1,1,{\beta }_3^{{}^{\prime }},{\beta }_4^{{}^{\prime }},\dots ,{\beta }_n^{{}^{\prime }}):{\beta }_i^{{}^{\prime }}\in \{0,1\}\}$. Moreover, $R\{e_1,e_2\}\mathrm{and}R\{e_1,e_3\}$ define a partition of $V\left(G\right)$. Let f be any edge resolving function of G, then $f\left(R\{e_1,e_2\}\right)\ge 1$ and $f\left(R\{e_1,e_3\}\right)\ge 1$. Adding these, we have $\left|f\right|\ge 2$. Thus, $edi{m}_f\left(G\right)\ge 2$. Using Propositions 3 and 1, the result follows for odd n. □

3. Combinatorial Criterion for Fractional Edge Dimension of Graphs

In this section, a combinatorial criterion for the calculation of the fractional edge dimension of any graph is proposed. As an application, the fractional edge dimension of the friendship graph $F_k$ and the circulant graph $C_n(1,2)$ is computed.

The following main result of this section gives the combinatorial criterion for calculating the fractional edge dimension of any graph.

Theorem 5.

Let $S=\{S_i,S_j|i\in I\mathrm{and}j\in J\}$ be the collection of all pairwise edge resolving neighborhoods of G such that $S_i$ represent the edge resolving neighborhoods of cardinality α and $S_j$ are the remaining edge resolving neighborhoods. If $|S_i|=\alpha <|S_j|$ and $|S_j\cap (\cup S_i)|\ge \alpha$ with α from Lemma 2, then $edi{m}_f\left(G\right)=\frac{1}{\beta }·\alpha$ with $\beta =|{\cup }_{i\in I}{S}_i|$.

Proof. 

Define a minimum edge resolving function $h:V\left(G\right)\to [0,1]$ by

$$h\left(v\right)=\left\{\begin{array}{cc}\frac{1}{\alpha },\hfill & \mathrm{if}v\in \cup S_i;\hfill \\ 0,\hfill & \mathrm{if}\mathrm{otherwise}\hfill \end{array}\right.$$

for G. Since $|S_i|=\alpha <|S_j|$ and $|S_j\cap (\cup S_i)|\ge \alpha$, therefore assigning zero to all $v\in S_j-\cup S_i$ is essential to attain the least possible weight of $\left|h\right|$. Consequently, zero is assigned to all $V\left(G\right)-\cup S_i$. Computing the summation of $\frac{1}{\alpha }$ over all $v\in \cup S_i$ gives $edi{m}_f\left(G\right)={\sum }_{t=1}^{\beta }\frac{1}{\alpha }=\frac{1}{\alpha }·\beta$. □

3.1. Fractional Edge Dimension of Friendship Graph

The fractional edge dimension of the friendship graph has been calculated in the following proposition as an application of Theorem 5.

Proposition 4.

If $G=F_k$ is the friendship graph of order $2k+1$, then $edi{m}_f\left(G\right)=k$ for all k.

Proof. 

Let $V\left(G\right)=\{u,v_i,w_i:1\le i\le k\}$ and $E\left(G\right)=\{e_i=u{v}_i,l_i=u{w}_i,m_i=v_i{w}_i:1\le i\le k\}$ (see Figure 1). Then, $R\{e_i,e_j\}=\{v_i,v_j\},$

• $R\{l_i,l_j\}=\{w_i,w_j\},$
• $R\{m_i,m_j\}=\{v_i,v_j,w_i,w_j\},$
• $R\{e_i,m_j\}=R\{l_i,m_j\}=V\left(G\right)$ for $i\ne j$,
• $R\{e_i,m_i\}=R\{l_i,m_i\}={\{x:x\mathrm{is}\mathrm{their}\mathrm{common}\mathrm{vertex}\}}^c,$
• $R\{e_i,l_j\}=\{v_i,w_j\}$, where $1\le i,j\le k$ is the complete list of all possible edge resolving neighborhoods in G. If $R\{e_i,e_j\},R\{l_i,l_j\}\mathrm{for}i\ne j,\mathrm{and}R\{e_i,l_j\}\mathrm{for}\mathrm{all}i,j$ are denoted by $S_i$, then $\cup S_i={\left\{u\right\}}^c$. Clearly, $S_j\cap (\cup S_i)\ge 2$, where $S_j$ are the edge resolving neighborhoods other than $S_i$. Using the criterion given in Theorem 5, assign zero to u and $\frac{1}{2}$ to all other vertices in G. This implies $edi{m}_f\left(G\right)={\mathsf{\Sigma }}_{\beta }\frac{1}{2}=k,\mathrm{where}\beta =|\cup S_i|=2k$. □

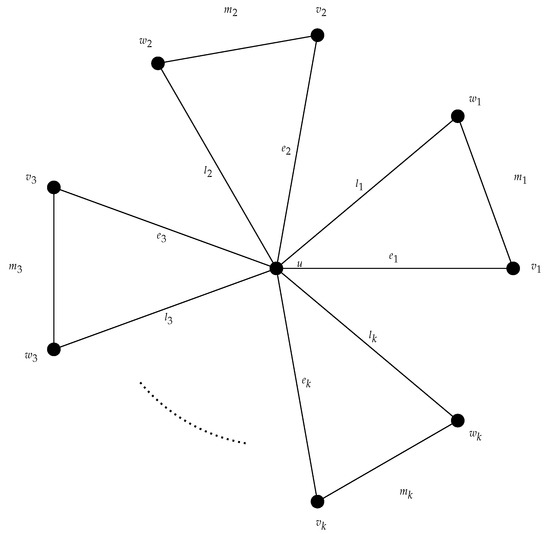
Figure 1. Friendship Graph F_k.

3.2. Fractional Edge Dimension of Circulant Graph $C_n(1,2)$

From now on, let $G=C_n(1,2)$ be a circulant graph with $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ and $E\left(G\right)=\{e_1,e_2,\dots ,e_{2n}\}$, where $n\ge 7$. Since the class of circulant graphs is vertex transitive, then label the arbitrary vertex as $v_1$ and other vertices accordingly. The set of edges of G can be partitioned as $E\left(G\right)=E_1\cup E_2\cup E_3\cup E_4$ based on labels. If n is even, $E_1=\{e_i=v_i{v}_{i+1}|1\le i\le n\}$, $E_2=\{e_{\frac{2n+i+1}{2}}=v_i{v}_{i+2}|i\mathrm{is}\mathrm{odd},1\le i<n\}$, $E_3=\{e_{\frac{3n+i+2}{2}}=v_i{v}_{i+2}|i\mathrm{is}\mathrm{even},2\le i\le n-2\}$, and $E_4=\{e_{\frac{3n}{2}+1}=v_2{v}_n\}$ (see Figure 2). If n is odd, $E_1=\{e_i=v_i{v}_{i+1}|1\le i\le n\}$, $E_2=\{e_{\frac{2n+i+1}{2}}=v_i{v}_{i+2}|i\mathrm{is}\mathrm{odd},1\le i\le n-2\}$, $E_3=\{e_{\frac{3n+i+1}{2}}=v_i{v}_{i+2}|i\mathrm{is}\mathrm{even},2\le i\le n-1\}$, and $E_4=\{e_{\frac{3n+1}{2}}=v_2{v}_n\}$ (see Figure 3). Note that the subscript of vertices is taken only over modulo n. Let $\overline{x}$ denote $x\left(\mathrm{mod}4\right)$. In the following lemmas, the cardinalities of the edge resolving neighborhoods of different pairs of distinct edges in G are computed, followed by the computation of the fractional edge dimension, $edi{m}_f\left(G\right)$, of G.

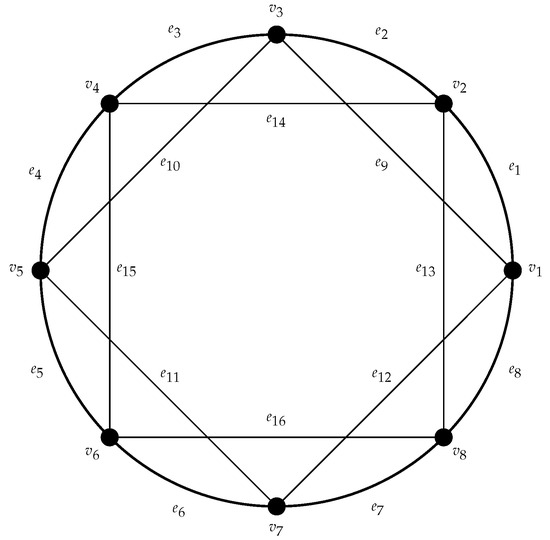
Figure 2. Circulant Graph C₈(1,2).

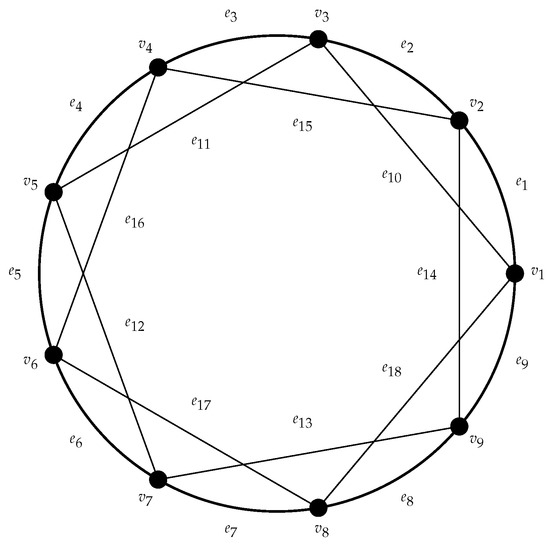
Figure 3. Circulant Graph C₉(1,2).

The following lemma gives the fractional edge dimension of $C_7(1,2)$.

Lemma 3.

If $G=C_7(1,2)$, then $edi{m}_f\left(G\right)=\frac{7}{2}$.

Proof. 

Let $V\left(G\right)=\{v_i:1\le i\le 7\}$ and $E\left(G\right)=\{e_j:1\le j\le 14\}$ be the vertex and edge set of G, respectively (see Figure 3). Due to symmetry, the edge resolving neighborhoods of some specific pairs of edges are described as:

$R\{e_1,e_2\}=\{v_1,v_3,v_5,v_6\},R\{e_1,e_3\}={\left\{v_6\right\}}^c,R\{e_1,e_4\}=\{v_1,v_2,v_4,v_5\},R\{e_1,e_8\}=\{v_2,v_3,v_5\},R\{e_1,e_9\}=\{v_1,v_2,v_3,v_5\},R\{e_1,e_{12}\}=\{v_1,v_4,v_5\},R\{e_1,e_{13}\}=\{v_1,v_2,v_4,v_5,v_6\},R\{e_8,e_9\}=\{v_1,v_5\},R\{e_8,e_{10}\}=\{v_1,v_3,v_5,v_7\},R\{e_8,e_{11}\}=\{v_1,v_2,v_3,v_7\}$. Clearly, the set of cardinalities of these edge resolving neighborhoods is $\{2,3,4,5,6\}$. Furthermore, $R\{e_{\frac{i+1}{2}+7},e_{\frac{i+1}{2}+8}\}=\{v_i,v_{i+4}\}$, where i is odd and $1\le i\le 11$. The index of vertices are taken over modulo 7. Thus, ${\bigcup }_{\frac{i+1}{2}=1}^6(R\{e_{\frac{i+1}{2}+7},e_{\frac{i+1}{2}+8}\})=V\left(G\right)$. Additionally, ${\bigcup }_{\frac{i+1}{2}=1}^6(R\{e_{\frac{i+1}{2}+7},e_{\frac{i+1}{2}+8}\})\cap R\{e_l,e_m\}=R\{e_l,e_m\}$, where $1\le l,m\le 14$. Using the criterion given in Theorem 5, define $f:V\left(G\right)\to [0,1]$ by $f\left(v_i\right)=\frac{1}{2}$, with $1\le i\le 7$ as the minimum edge resolving function of G. Hence, $edi{m}_f\left(G\right)=\left|f\right|=\sum f\left(v_i\right)=\frac{7}{2}$. □

The edge resolving neighborhoods of minimum cardinalities in G are given in the following result.

Lemma 4.

If G is a circulant graph of order $n>7$, then

$$|R\{e_1,e_{1+n}\}|=\left\{\begin{array}{cc}\lceil \frac{n}{4}\rceil ,\hfill & \mathrm{if}n\equiv \overline{1},\overline{2};\hfill \\ \lceil \frac{n}{4}\rceil +1,\hfill & \mathrm{if}\mathrm{otherwise}.\hfill \end{array}\right.$$

Furthermore $|{\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}|= n =|{\bigcup }_{i}R\{e_{2+i},e_{\frac{3n}{2}+2+\frac{i}{2}}\}|$, where i is even and $e_1,e_{1+n},e_{1+i},e_{n+1+\frac{i}{2}},e_{2+i},e_{\frac{3n}{2}+2+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

Since $R\{e_1,e_{1+n}\}=\left\{\begin{array}{cc}\{v_2,v_3,v_5,\dots ,v_{\frac{n}{2}+1}\},\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ \{v_2,v_3,v_5,\dots ,v_{\lceil \frac{n}{2}\rceil }\},\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ \{v_2,v_3,v_5,\dots ,v_{\frac{n}{2}}\},\hfill & \mathrm{if}n\equiv \overline{2};\hfill \\ \{v_2,v_3,v_5,\dots ,v_{\lceil \frac{n}{2}\rceil +1}\},\hfill & \mathrm{if}n\equiv \overline{3};\hfill \end{array}\right.$ therefore,

$$|R\{e_1,e_{1+n}\}|=\left\{\begin{array}{cc}\lceil \frac{n}{4}\rceil ,\hfill & \mathrm{if}n=\overline{1},\overline{2};\hfill \\ \lceil \frac{n}{4}\rceil +1,\hfill & \mathrm{if}\mathrm{otherwise}.\hfill \end{array}\right.$$

If i is even such that $i<n$, then

$R\{e_{1+i},e_{1+n+\frac{i}{2}}\}=\left\{\begin{array}{cc}\{v_{i+2},v_{i+3},v_{i+5},\dots ,v_{\frac{n}{2}+i+1}\},\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ \{v_{i+2},v_{i+3},v_{i+5},\dots ,v_{\lceil \frac{n}{2}\rceil +i}\},\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ \{v_{i+2},v_{i+3},v_{i+5},\dots ,v_{\frac{n}{2}+i}\},\hfill & \mathrm{if}n\equiv \overline{2};\hfill \\ \{v_{i+2},v_{i+3},v_{i+5},\dots ,v_{\lceil \frac{n}{2}\rceil +i+1}\},\hfill & \mathrm{if}n\equiv \overline{3}.\hfill \end{array}\right.$

The subscripts of vertices are taken over modulo n.

Similarly, if i is even such that $i<n$, then

$R\{e_{2+i},e_{2+\frac{3n}{2}+\frac{i}{2}}\}=\left\{\begin{array}{cc}\{v_{i+3},v_{i+4},v_{i+6},\dots ,v_{\frac{n}{2}+i+2}\},\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ \{v_{i+3},v_{i+4},v_{i+6},\dots ,v_{\lceil \frac{n}{2}\rceil +i+1}\},\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ \{v_{i+3},v_{i+4},v_{i+6},\dots ,v_{\frac{n}{2}+i+1}\},\hfill & \mathrm{if}n\equiv \overline{2};\hfill \\ \{v_{i+3},v_{i+4},v_{i+6},\dots ,v_{\lceil \frac{n}{2}\rceil +i+1}\},\hfill & \mathrm{if}n\equiv \overline{3}.\hfill \end{array}\right.$

The subscripts of vertices are taken over modulo n. This shows ${\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=V\left(G\right)={\bigcup }_{i}R\{e_{2+i},e_{\frac{3n}{2}+2+\frac{i}{2}}\}$. □

In the following lemma, the cardinality of the edge resolving neighborhood of a pair of edges $e_1\mathrm{and}{e}_2$ is calculated.

Lemma 5.

If G is a circulant graph of order $n>7$, then $|R\{e_1,e_2\}|\in \{\frac{n-2}{2},\frac{n-1}{2},\frac{n}{2},\frac{n+1}{2}\}$ and

$R\{e_1,e_2\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_2\}$, where $e_1,e_2,e_{1+i},e_{n+1+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

Since $R\{e_1,e_2\}=\left\{\begin{array}{cc}\{v_i:i\mathrm{is}\mathrm{an}\mathrm{odd}\mathrm{number}\mathrm{less}\mathrm{than}n\},\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ \{v_1,v_3,v_5,\dots ,v_{\lceil \frac{n}{2}\rceil },v_{\lceil \frac{n}{2}\rceil +3},v_{\lceil \frac{n}{2}\rceil +5},\dots ,v_{n-1}\},\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ \{v_i:i\mathrm{is}\mathrm{an}\mathrm{odd}\mathrm{number}\mathrm{less}\mathrm{than}n\}-\{v_{\frac{n}{2}},v_{\frac{n}{2}+1}\},\hfill & \mathrm{if}n\equiv \overline{2};\hfill \\ \{v_1,v_3,v_5,\dots ,v_{\lceil \frac{n}{2}\rceil +1},v_{\lceil \frac{n}{2}\rceil +2},v_{\lceil \frac{n}{2}\rceil +4},\dots ,v_{n-1}\},\hfill & \mathrm{if}n\equiv \overline{3};\hfill \end{array}\right.$ that shows $|R\{e_1,e_2\}|\in \{\frac{n-2}{2},\frac{n-1}{2},\frac{n}{2},\frac{n+1}{2}\}$ and $R\{e_1,e_2\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_2\}$ using Lemma 4. □

Next, edges $e_1\mathrm{and}{e}_t$, where $3\le t\le \frac{n}{2}+1$ if $n\equiv \overline{2}$, or $3\le t\le \lceil \frac{n}{2}\rceil$ if otherwise, are considered. The cardinalities of their edge resolving neighborhoods are computed.

Lemma 6.

Let G be a circulant graph of order $n>7$.

1.

If $n\equiv \overline{2}$ and $3\le t\le \frac{n}{2}+1$, then $\left|R\right\{e_1,e_t\}|=n-2$;

2.

If $n\equiv \overline{0},\overline{1},\overline{3}$ and $3\le t\le \lceil \frac{n}{2}\rceil$, then $|R\{e_1,e_t\}|\in \{n,n-1,n-2,n-3,n-4\}$.

Furthermore, $R\{e_1,e_t\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_t\}$, where $e_1,e_t,e_{1+i},e_{n+1+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

1.

If $n\equiv \overline{2}$ and $3\le t\le \frac{n}{2}+1$, then $R\{e_1,e_t\}=\left\{\begin{array}{cc}{\{v_{\frac{t}{2}+1},v_{\frac{n+t}{2}+1}\}}^c,\hfill & \mathrm{if}t\equiv \overline{0},\overline{2};\hfill \\ {\{v_{\frac{t+1}{2}},v_{\frac{t+3}{2}}\}}^c,\hfill & \mathrm{if}t\equiv \overline{1};\hfill \\ {\{v_{\frac{n+t+1}{2}},v_{\frac{n+t+3}{2}}\}}^c,\hfill & \mathrm{if}t\equiv \overline{3};\hfill \end{array}\right.$ which implies $|R\{e_1,e_t\}|=n-2$.

2.

If $n\equiv \overline{0},\overline{1},\overline{3}$ and $3\le t\le \lceil \frac{n}{2}\rceil$, then

$R\{e_1,e_t\}=\left\{\begin{array}{cc}V\left(G\right),\hfill & \mathrm{if}n\equiv \overline{0},t\equiv \overline{3};\hfill \\ {\{v_{\frac{t}{2}+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{1},t\equiv \overline{0}\mathrm{or}n\equiv \overline{3},t\equiv \overline{2};\hfill \\ {\{v_{\frac{t+1}{2}+\lceil \frac{n}{2}\rceil }\}}^c,\hfill & \mathrm{if}n\equiv \overline{1},\overline{3},t\equiv \overline{3};\hfill \\ {\{v_{\frac{t}{2}+1},v_{\frac{n+t}{2}+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0},t\equiv \overline{0},\overline{2};\hfill \\ {\{v_{\frac{t}{2}+1},v_{\frac{t}{2}+\lceil \frac{n}{2}\rceil },v_{\frac{t}{2}+\lceil \frac{n}{2}\rceil +1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{1},t\equiv \overline{2}\mathrm{or}n\equiv \overline{3},t\equiv \overline{0};\hfill \\ {\{v_{\frac{t+1}{2}},v_{\frac{t+3}{2}},v_{\frac{t+1}{2}+\lceil \frac{n}{2}\rceil }\}}^c,\hfill & \mathrm{if}n\equiv \overline{1},\overline{3},t\equiv \overline{1};\hfill \\ {\{v_{\frac{t+1}{2}},v_{\frac{t+3}{2}},v_{\frac{n+t+1}{2}},v_{\frac{n+t+3}{2}}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0},t\equiv \overline{1}.\hfill \end{array}\right.$

This shows $|R\{e_1,e_t\}|\in \{n,n-1,n-2,n-3,n-4\}$.

$R\{e_1,e_t\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_t\}$ follows from Lemma 4. □

In the following lemma, the edges $e_1\mathrm{and}{e}_{2+n}$ are considered.

Lemma 7.

If G is a circulant graph of order $n>7$, then $|R\{e_1,e_{2+n}\}|\in \{n-1,n-2,n-3\}$.

Furthermore, $R\{e_1,e_{2+n}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{2+n}\}$, where $e_1,e_{2+n},e_{1+i},e_{n+1+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

Since $R\{e_1,e_{2+n}\}=\left\{\begin{array}{cc}{\{v_4\}}^c,\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ {\{v_4,v_{\frac{n}{2}+3}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0},\overline{2};\hfill \\ {\{v_4,v_{\lceil \frac{n}{2}\rceil +2},v_{\lceil \frac{n}{2}\rceil +3}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3}.\hfill \end{array}\right.$

This implies $|R\{e_1,e_{2+n}\}|\in \{n-1,n-2,n-3\}$. Clearly, $R\{e_1,e_{2+n}\}$$\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}$$=R\{e_1,e_{2+n}\}$ using Lemma 4. □

In the following lemma, the cardinalities of edge resolving neighborhoods of pairs of edges $e_1\mathrm{and}{e}_{t+n}$ are computed.

Lemma 8.

Let G be a circulant graph of order $n>7$. If n is odd and $3\le t\le \lceil \frac{n}{4}\rceil$, or if n is even and $3\le t\le \frac{n}{2}$, then $|R\{e_1,e_{t+n}\}|\in \{n,n-1,n-2,n-3,n-4\}$. Furthermore, $R\{e_1,e_{t+n}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+n}\}$, where $e_1,e_{t+n},e_{1+i},e_{n+1+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

If $n>7$ is odd and $3\le t\le \lceil \frac{n}{4}\rceil$, then

$R\{e_1,e_{t+n}\}=\left\{\begin{array}{cc}V\left(G\right),\hfill & \mathrm{if}n\equiv \overline{1},t\equiv \overline{0},\overline{2};\hfill \\ {\{v_t,v_{t+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3},t\equiv \overline{1},\overline{3};\hfill \\ {\{v_t,v_{t+1},v_{\lceil \frac{n}{2}\rceil +t},v_{\lceil \frac{n}{2}\rceil +t+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{1},t\equiv \overline{1},\overline{3};\hfill \\ {\{v_{\lceil \frac{n}{2}\rceil +t},v_{\lceil \frac{n}{2}\rceil +t+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3},t\equiv \overline{0},\overline{2}.\hfill \end{array}\right.$

If $n>7$ is even and $3\le t<\frac{n}{2}$, then $R\{e_1,e_{t+n}\}=\left\{\begin{array}{cc}{\{v_t,v_{t+1},v_{\frac{n}{2}+t+1}\}}^c,\hfill & \mathrm{if}t\equiv \overline{1},\overline{3};\hfill \\ {\{v_{\frac{n}{2}+t+1}\}}^c,\hfill & \mathrm{if}t\equiv \overline{0},\overline{2}.\hfill \end{array}\right.$

Combining the cardinalities of the expressions above, $|R\{e_1,e_{t+n}\}|\in \{n,n-1,n-2,n-3,n-4\}$. Moreover, $R\{e_1,e_{t+n}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+n}\}$ is straight forward using Lemma 4. □

Now, The pairs of edges $e_1\mathrm{and}{e}_{t+\frac{3n+1}{2}}$, where $1\le t\le \frac{n-1}{4}\mathrm{or}\frac{n+1}{4}$ accordingly if $n\equiv \overline{1}\mathrm{or}\overline{3}$ are considered. The cardinalities of their edge resolving neighborhoods are computed.

Lemma 9.

Let G be a circulant graph of order $n>7$. If n is odd, then $|R\{e_1,e_{t+\frac{3n+1}{2}}\}|\in \{\frac{3n-7}{2},\frac{3n-9}{2},n-2\}$ with $n\equiv \overline{1},1\le t\le \frac{n-1}{4}$ or $n\equiv \overline{3},1\le t\le \frac{n+1}{4}$. Additionally, $R\{e_1,e_{t+\frac{3n+1}{2}}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+\frac{3n+1}{2}}\}$, where $e_1,e_{t+\frac{3n+1}{2}},e_{1+i},e_{n+1+\frac{i}{2}}\in E\left(G\right)$.

Proof. 

For $t=1$, $R\{e_1,e_{\frac{3n+1}{2}+1}\}=\left\{\begin{array}{cc}{\{v_2,v_3,v_{\lceil \frac{n}{2}\rceil +2},v_{\lceil \frac{n}{2}\rceil +4},v_{\lceil \frac{n}{2}\rceil +6},\dots ,v_n\}}^c,\hfill & \mathrm{if}n\equiv \overline{1};\hfill \\ {\{v_2,v_3,v_{\lceil \frac{n}{2}\rceil +2},v_{\lceil \frac{n}{2}\rceil +3},v_{\lceil \frac{n}{2}\rceil +5},\dots ,v_n\}}^c,\hfill & \mathrm{if}n\equiv \overline{3}.\hfill \end{array}\right.$

If $n\equiv \overline{1},2\le t\le \frac{n-1}{4}$ or $n\equiv \overline{3},2\le t\le \frac{n+1}{4}$, then $R\{e_1,e_{\frac{3n+1}{2}+t}\}={\{v_t,v_{\lceil \frac{n}{2}\rceil +t+1}\}}^c$. This implies $|R\{e_1,e_{t+\frac{3n+1}{2}}\}|\in \{\frac{3n-7}{2},\frac{3n-9}{2},n-2\}$. Using Lemma 4, $R\{e_1,e_{t+\frac{3n+1}{2}}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+\frac{3n+1}{2}}\}$ follows directly. □

Now, consider edges $e_1\mathrm{and}{e}_{n+\frac{n}{2}}$, with an even n.

Lemma 10.

Let G be a circulant graph of order $n>7$. If n is even, then $|R\{e_1,e_{n+\frac{n}{2}}\}|>|R\{e_1,e_{n+1}\}|$, where $e_1,e_{n+\frac{n}{2}},e_{n+1}\in E\left(G\right)$.

Proof. 

If $n>7$ is even, then $R\{e_1,e_{\frac{n}{2}+n}\}=\left\{\begin{array}{cc}{\{v_1,v_3,v_5,\dots ,v_{\frac{n}{2}-1},v_n\}}^c,\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ {\{v_1,v_3,v_5,\dots ,v_{\frac{n}{2}},v_{\frac{n}{2}+1},v_n\}}^c,\hfill & \mathrm{if}n\equiv \overline{2}.\hfill \end{array}\right.$

Clearly, $|R\{e_1,e_{n+\frac{n}{2}}\}|=\left\{\begin{array}{cc}\frac{3n-4}{4},\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ \frac{3n-10}{4},\hfill & \mathrm{if}n\equiv \overline{2}.\hfill \end{array}\right.$

Furthermore, $|R\{e_1,e_{n+\frac{n}{2}}\}|>|R\{e_1,e_{n+1}\}|$ using Lemma 4. □

In the following lemma, the cardinalities of the edge resolving neighborhoods of pairs of edges $e_{1+n}\mathrm{and}{e}_{n+t}$ with $2\le t\le \frac{n}{2}$ are computed.

Lemma 11.

Let G be a circulant graph of order $n>7$. If n is even and $2\le t\le \frac{n}{2}$, then $|R\{e_{1+n},e_{n+t}\}|>|R\{e_1,e_{n+1}\}|$, where $e_1,e_{n+t},e_{n+1}\in E\left(G\right)$.

Proof. 

If $n>7$ is even and $2\le t\le \frac{n}{2}$, then

$R\{e_{1+n},e_{t+n}\}=\left\{\begin{array}{cc}{\{v_2,v_3,v_4,v_{\frac{n}{2}+3}\}}^c,\hfill & \mathrm{if}t=2;\hfill \\ {\{v_{t+1},v_{\frac{n}{2}+t+1}\}}^c,\hfill & \mathrm{if}3\le t<\frac{n}{2};\hfill \\ {\{v_1,v_2,v_{\frac{n}{2}+1,v_n}\}}^c,\hfill & \mathrm{if}t=\frac{n}{2}.\hfill \end{array}\right.$

This implies $|R\{e_{1+n},e_{t+n}\}|\in \{n-2,n-4\}>\left|R\{e_1,e_{1+n}\}\right|$ using Lemma 4. □

In the following lemma, the edge resolving neighborhoods of pairs of edges $e_{1+n}\mathrm{and}{e}_{\frac{3n}{2}+t}$ with $1\le t\le \frac{n}{2}$ are considered.

Lemma 12.

Let G be a circulant graph of order $n>7$. If n is even and $1\le t\le \frac{n}{2}$, then $|R\{e_{1+n},e_{\frac{3n}{2}+t}\}|>|R\{e_1,e_{n+1}\}|$, where $e_1,e_{t+\frac{3n}{2}},e_{n+1}\in E\left(G\right)$.

Proof. 

If $n>7$ is even and $t=1$, then

$R\{e_{1+n},e_{\frac{3n}{2}+1}\}=\left\{\begin{array}{cc}{\{v_4,v_6,v_8,\dots ,v_{\frac{n}{2}},v_{\frac{n}{2}+3},v_{\frac{n}{2}+5},\dots ,v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ {\{v_4,v_6,v_8,\dots ,v_{\frac{n}{2}+1},v_{\frac{n}{2}+2},v_{\frac{n}{2}+4},\dots ,v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{2}.\hfill \end{array}\right.$

This implies $|R\{e_{1+n},e_{\frac{3n}{2}+1}\}|\in \{\frac{n+4}{2},\frac{n}{2}\}$.

Similarly, for $t=2$, $|R\{e_{1+n},e_{\frac{3n}{2}+1}\}|\in \{\frac{n+4}{2},\frac{n}{2}\}$.

For $t=3$, $R\{e_{1+n},e_{\frac{3n}{2}+3}\}=\left\{\begin{array}{cc}{\{v_2,v_5,v_{\frac{n}{2}+3},v_{\frac{n}{2}+4}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ {\{v_2,v_5\}}^c,\hfill & \mathrm{if}n\equiv \overline{2}.\hfill \end{array}\right.$

This implies $|R\{e_{1+n},e_{\frac{3n}{2}+3}\}|\in \{n-2,n-4\}$.

For $4\le t<\frac{n}{2}$, $R\{e_{1+n},e_{\frac{3n}{2}+t}\}=\left\{\begin{array}{cc}V\left(G\right),\hfill & \mathrm{if}n\equiv \overline{2},t\equiv \overline{1},\overline{3};\hfill \\ {\{v_t,v_{t+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{}0,t\equiv \overline{0},\overline{2};\hfill \\ {\{v_t,v_{t+1},v_{\frac{n}{2}+t},v_{\frac{n}{2}+t+1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{2},t\equiv \overline{0},\overline{2};\hfill \\ {\{v_{\frac{n}{2}+t},v_{\frac{n}{2}+t+1}\}}^c,-\hfill & \mathrm{if}n\equiv \overline{0},t\equiv \overline{1},\overline{3};\hfill \end{array}\right.$ which shows $|R\{e_{1+n},e_{\frac{3n}{2}+1}\}|\in \{n,n-2,n-4\}$.

For $t=\frac{n}{2}$, $R\{e_{1+n},e_{2n}\}=\left\{\begin{array}{cc}{\{v_2,v_{\frac{n}{2}},v_{\frac{n}{2}+1},v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{0};\hfill \\ {\{v_2,v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{2}.\hfill \end{array}\right.$

This implies $|R\{e_{1+n},e_{\frac{3n}{2}+t}\}|\in \{n,n-2,n-4\}$,with $3\le t\le \frac{n}{2}$. Combining the cardinalities of all these edge resolving neighborhoods, $|R\{e_{1+n},e_{\frac{3n}{2}+t}\}|\in \{n,n-2,n-4,\frac{n}{2},\frac{n+4}{2}\}$ with $1\le t\le \frac{n}{2}$. Thus, $|R\{e_{1+n},e_{\frac{3n}{2}+t}\}|>|R\{e_1,e_{n+1}\}|$, where $1\le t\le \frac{n}{2}$ using Lemma 4. □

In the following lemma, the edge resolving neighborhoods of pairs of edges $e_{1+n}\mathrm{and}{e}_{n+t}$ with $2\le t\le \frac{n+1}{2}$ are considered for odd n.

Lemma 13.

Let G be a circulant graph of order $n>7$. If n is odd and $2\le t\le \frac{n+1}{2}$, then $|R\{e_{1+n},e_{n+t}\}|>|R\{e_1,e_{n+1}\}|$, where $e_1,e_{n+t},e_{n+1}\in E\left(G\right)$.

Proof. 

For $t=2$, $R\{e_{1+n},e_{2+n}\}=\left\{\begin{array}{cc}{\{v_2,v_3,v_4,v_{\frac{n+5}{2}},v_{\frac{n+7}{2}}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3};\hfill \\ {\{v_2,v_3,v_4\}}^c,\hfill & \mathrm{if}n\equiv \overline{1}.\hfill \end{array}\right.$

For $3\le t<\frac{n-1}{2}$,

$R\{e_{1+n},e_{t+n}\}=\left\{\begin{array}{cc}{\{v_{1+t},v_{\frac{n+2t+1}{2}},v_{\frac{n+2t+3}{2}}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3},t\equiv \overline{0},\overline{2}\mathrm{or}n\equiv \overline{1},t\equiv \overline{1},\overline{3};\hfill \\ {\{v_{1+t}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3},t\equiv \overline{1},\overline{3}\mathrm{or}n\equiv \overline{1},t\equiv \overline{0},\overline{2}.\hfill \end{array}\right.$

For $t=\frac{n-1}{2}$, $R\{e_{1+n},e_{\frac{3n-1}{2}}\}={\{v_2,v_{\frac{n+1}{2}},v_{n-1}\}}^c$ ; for $t=\frac{n+1}{2}$, $R\{e_{1+n},e_{\frac{3n+1}{2}}\}=\left\{\begin{array}{cc}{\{v_4,v_6,\dots ,v_{\frac{n+1}{2}},v_{\frac{n+3}{2}},v_{\frac{n+5}{2}},\dots ,v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{3};\hfill \\ {\{v_4,v_6,\dots ,v_{n-1}\}}^c,\hfill & \mathrm{if}n\equiv \overline{1}.\hfill \end{array}\right.$

Combining the cardinalities of all these edge resolving neighborhoods implies

$|R\{e_{1+n},e_{n+t}\}|\in \{n-1,n-3,n-5,\frac{n+1}{2},\frac{n+2}{2}\}$ with $2\le t\le \frac{n+1}{2}$. Using Lemma 4, $|R\{e_{1+n},e_{n+t}\}|>|R\{e_1,e_{n+1}\}|$, where $2\le t\le \frac{n+1}{2}$. □

In the following theorem, the fractional edge dimension of $C_n(1,2)$ is calculated.

Theorem 6.

If $G=C_n(1,2)$ and $n>7$, then

$$edi{m}_f\left(G\right)=\left\{\begin{array}{cc}\frac{n}{\lceil \frac{n}{4}\rceil },\hfill & \mathrm{if}n\equiv \overline{1},\overline{2};\hfill \\ \frac{n}{\lceil \frac{n}{4}\rceil +1},\hfill & \mathrm{if}\mathrm{otherwise}.\hfill \end{array}\right.$$

Proof. 

From Lemmas 4 to 13, $|R\{e_1,e_{n+1}\}|\le |R\{e_1,e_{t+1}\}|$ with $1\le t\le 2n-1$, $|R\{e_1,e_{n+1}\}| \le | R\{e_{1+n},e_{t+n}\}|$ with $2\le t\le n$ for an even n and $2\le t\le \frac{3n+1}{2}$ for an odd n. Additionally, $R\{e_1,e_{t+1}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+1}\}$, $R\{e_{1+n},e_{t+n}\}\cap {\bigcup }_{i}R\{e_{1+i},e_{n+1+\frac{i}{2}}\}=R\{e_1,e_{t+1}\}$. Thus, using Theorem 5, a minimum edge resolving function $h:V\left(G\right)\to [0,1]$ is defined by

$$h\left(v\right)=\left\{\begin{array}{cc}\frac{1}{\lceil \frac{n}{4}\rceil },\hfill & \mathrm{if}n\equiv \overline{1},\overline{2};\hfill \\ \frac{1}{\lceil \frac{n}{4}\rceil +1},\hfill & \mathrm{if}\mathrm{otherwise}\hfill \end{array}\right.$$

for all $v\in V\left(G\right)$ of G. Hence,

$$edi{m}_f\left(G\right)=\left|h\right|={\mathsf{\Sigma }}_{i=1}^{n}h\left(v\right)=\left\{\begin{array}{cc}\frac{n}{\lceil \frac{n}{4}\rceil },\hfill & \mathrm{if}n\equiv \overline{1},\overline{2};\hfill \\ \frac{n}{\lceil \frac{n}{4}\rceil +1},\hfill & \mathrm{if}\mathrm{otherwise}.\hfill \end{array}\right.$$

□

4. Summary and Further Directions

In this article, we explored the concept of the fractional edge dimension of a graph. We improvised the upper bound proposed by E. Yi. It was also found that the class of hypercube graphs with an odd number of vertices has the fractional edge dimension equal to 2. The fractional edge dimension of the class of vertex and edge transitive graphs is $\frac{\left|V\right(G\left)\right|}{\alpha \left(G\right)}$, where $\alpha \left(G\right)$ is the minimum cardinality of the edge resolving neighborhoods of 1a graph G. We put forward the idea of combinatorics to calculate the fractional edge dimension of a graph. Using this criterion, $edi{m}_f\left(F_k\right)$ and $edi{m}_f\left(C_n(1,2)\right)$ were calculated. The fractional edge dimension of a graph is a novel idea that has many lines yet to be expedited. Some of them are listed below.

1.

Prove or disprove the converse of Theorem 3;

2.

Calculate the fractional edge dimension of different classes of graphs such as the generalized Petersen graph, Tree graph, etc.;

3.

Study the fractional edge dimension of different graph operations such as the cartesian product, etc.