Magic Square and Arrangement of Consecutive Integers That Avoids k-Term Arithmetic Progressions

Abstract

In 1977, Davis et al. proposed a method to generate an arrangement of $\left[n\right]=\{1,2,\dots ,n\}$ that avoids three-term monotone arithmetic progressions. Consequently, this arrangement avoids k-term monotone arithmetic progressions in $\left[n\right]$ for $k\ge 3$. Hence, we are interested in finding an arrangement of $\left[n\right]$ that avoids k-term monotone arithmetic progression, but allows $k-1$-term monotone arithmetic progression. In this paper, we propose a method to rearrange the rows of a magic square of order $2k-3$ and show that this arrangement does not contain a k-term monotone arithmetic progression. Consequently, we show that there exists an arrangement of n consecutive integers such that it does not contain a k-term monotone arithmetic progression, but it contains a $k-1$-term monotone arithmetic progression.

1. Introduction

A sequence $a_1,a_2,\dots ,a_n$ is said to have a k-term monotone arithmetic progression if there is a set of indices $\{i_1<i_2<\dots <i_k\}$ such that the k-term subsequence $a_{i_1},a_{i_2},\dots ,a_{i_k}$ is either an increasing or a decreasing arithmetic progression.

Davis et al. [1] proposed a way to generate an arrangement of $\left[n\right]=\{1,2,\dots ,n\}$ that avoids three-term monotone arithmetic progressions. An arrangement of $\left[n\right]$ is a sequence $a_1,a_2,\dots ,a_n$ such that $\{a_1,a_2,\dots ,a_n\}=\left[n\right]$. An arrangement of $\left[n\right]$ is also called a permutation of $\left[n\right]$.

Theorem 1

([1]). Let $n\ge 1$. There is a permutation of $\left[n\right]$ that does not contain a three-term monotone arithmetic progression.

Let ${\mathbb{Z}}^{+}$ be the set of positive integers. Davis et al. [1] and Sidorenko [2] showed that there is no permutation of ${\mathbb{Z}}^{+}$ that avoids three-term monotone arithmetic progressions. However, they [1] showed that there exists permutations of ${\mathbb{Z}}^{+}$ that avoid five-term monotone arithmetic progression, implying the existence of permutations of the integers avoiding arithmetic progressions of length seven. Recently, Geneson [3] constructed a permutation of the integers avoiding arithmetic progressions of length six. Up to now, an intriguing question, whose answer is still unknown, is whether there exists a permutation of ${\mathbb{Z}}^{+}$ that avoids four-term monotone arithmetic progressions [4].

Let $\theta \left(n\right)$ denote the number of permutations of $\left[n\right]$ that contain no three-term monotone arithmetic progressions. Davis et al. [1] established that $2^{n-1}\le \theta \left(n\right)\le \lfloor \frac{n+1}{2}\rfloor !\lceil \frac{n+1}{2}\rceil !$. These bounds were then improved by [5,6,7]. LeSaulnier and Vijay [5] also showed that any permutation of the positive integers must contain a three-term arithmetic progression with an odd common difference as a subsequence and constructed a permutation of the positive integers that does not contain any four-term arithmetic progression with an odd common difference. Geneson [3] also proved a lower bound of $\frac{1}{2}$ on the lower density of subsets of positive integers that can be permuted to avoid arithmetic progressions of length four, sharpening the lower bound of $\frac{1}{3}$ from [5].

As a consequence of Theorem 1, there exists an arrangement of $\left[n\right]$ that avoids k-term monotone arithmetic progression, where $k\ge 3$. However, up to now, there is no proposed arrangement of $\left[n\right]$ that avoids a k-term monotone arithmetic progression, but contains a $(k-1)$-term monotone arithmetic progression. In this paper, for $k\ge 3$, we show that the rows of a magic square of order $2k-3$ can be arranged in a way that the resulting arrangement does not contain a k-term monotone arithmetic progression, but it contains a $(k-1)$-term monotone arithmetic progression. Then, we apply the result to show that there exists an arrangement of n consecutive integers such that it does not contain a k-term monotone arithmetic progression, but it contains a $(k-1)$-term monotone arithmetic progression.

2. $\mathit{K}$-Term Monotone Arithmetic Progression

In this section, we prove that given any n consecutive integers with $n\ge k$, there is an arrangement that avoids k-term monotone arithmetic progressions, but contains a $(k-1)$-term monotone arithmetic progression.

2.1. Magic Square

In 1624 France, Claude Gaspard Bachet described the following “diamond method” for constructing odd ordered magic squares in his book Problèmes Plaisants [8].

Step 1:

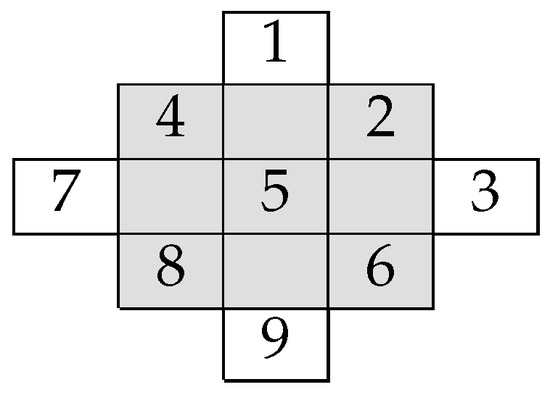
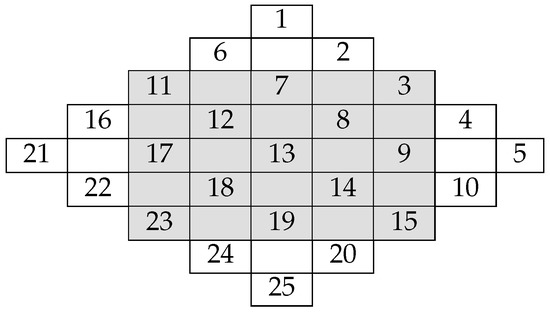
First, for $k\ge 3$, we arrange $[1,{(2k-3)}^2]$ in an $(2k-3)\times (2k-3)$ square. We extend a $(2k-3)\times (2k-3)$ square to form a diamond structure as in Figure 1. Then, we put the integers in order along descending diagonals into the square. For $k=3$ and $k=4$, Figure 1 and Figure 2 illustrate the $3\times 3$ and $5\times 5$ extended squares, respectively.

Figure 1. A $3\times 3$ square.

Figure 2. A $5\times 5$ square.

Step 2:

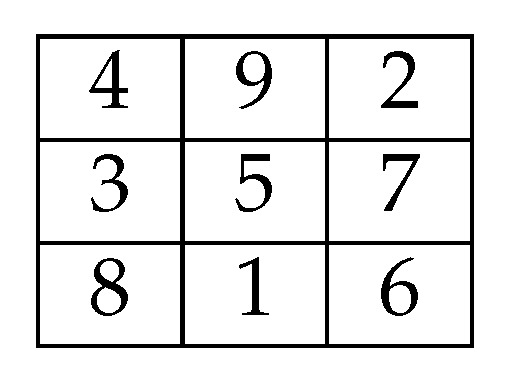
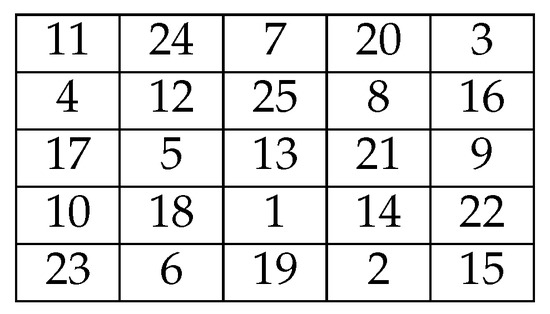
Then, move the numbers on the right leftwards in the same row. Similarly, move the numbers on the left rightwards in the same row. Furthermore, move the numbers on the top downwards in the same column, and move the numbers at the bottom upwards in the same column. See Figure 3 and Figure 4 for $k=3$ and 4. This gives a $(2k-3)\times (2k-3)$ magic square with magic sum $\frac{(2k-3)\left[{(2k-3)}^2+1\right]}{2}$.

Figure 3. A $3\times 3$ magic square.

Figure 4. A $5\times 5$ magic square.

Let $R_i$ be the i-th row of the magic square constructed this way, i.e.,

$$\begin{array}{c}\hfill R_i=a_{i,1},b_{i,1},a_{i,2},b_{i,2},\dots ,a_{i,(k-2)},b_{i,(k-2)},a_{i,(k-1)}.\end{array}$$

Note that for the first row $R_1$, we have:

$$\begin{array}{cc}\hfill a_{1,j}& =1+(k-2)(2k-3)-(j-1)(2k-4),1\le j\le k-1;\hfill \\ \hfill b_{1,j}& =k+(2k-4)(2k-3)-(j-1)(2k-4),1\le j\le k-2.\hfill \end{array}$$

(1)

For the last row $R_{2k-3}$, we have:

$$\begin{array}{cc}\hfill a_{(2k-3),j}& =k-1+(2k-4)(2k-3)-(j-1)(2k-4),1\le j\le k-1;\hfill \\ \hfill b_{(2k-3),j}& =1+(k-3)(2k-3)-(j-1)(2k-4),1\le j\le k-2.\hfill \end{array}$$

(2)

For row $R_{k-1}$, if k is odd, then:

$$\begin{array}{cc}\hfill a_{(k-1),j}& =1+(2k-4)(2k-3)-\left(\frac{3k-1}{2}+j-3\right)(2k-4),1\le j\le \frac{k-1}{2};\hfill \\ \hfill a_{(k-1),j}& =1+(2k-4)(2k-3)-\left(j-\frac{k-1}{2}-1\right)(2k-4),\frac{k-1}{2}+1\le j\le k-1;\hfill \\ \hfill b_{(k-1),j}& =1+(2k-4)(2k-3)-\left(\frac{k-1}{2}+j-1\right)(2k-4),1\le j\le k-2.\hfill \end{array}$$

(3)

whereas if k is even, then:

$$\begin{array}{cc}\hfill a_{(k-1),j}& =1+(2k-4)(2k-3)-\left(\frac{k}{2}+j-2\right)(2k-4),1\le j\le k-1;\hfill \\ \hfill b_{(k-1),j}& =1+(2k-4)(2k-3)-\left(\frac{3k}{2}+j-3\right)(2k-4),1\le j\le \frac{k}{2}-1;\hfill \\ \hfill b_{(k-1),j}& =1+(2k-4)(2k-3)-\left(j-\frac{k}{2}\right)(2k-4),\frac{k}{2}\le j\le k-2,\hfill \end{array}$$

(4)

For row $R_i$ with $2\le i\le k-2$, if i is odd, then:

$$\begin{array}{cc}\hfill a_{i,j}& =1+(k-3+i)(2k-3)-\left(\frac{i-1}{2}+j-1\right)(2k-4),1\le j\le k-1;\hfill \\ \hfill b_{i,j}& =1+(k-3+i)(2k-3)-\left(\frac{i-1}{2}+k+j-2\right)(2k-4),1\le j\le \frac{i-1}{2};\hfill \\ \hfill b_{i,j}& =k-1+i+(2k-4)(2k-3)-\left(j-\frac{i-1}{2}-1\right)(2k-4),\frac{i-1}{2}+1\le j\le k-2-\frac{i-1}{2};\hfill \\ \hfill b_{i,j}& =1+(k-3+i)(2k-3)-\left(j-k+1+\frac{i-1}{2}\right)(2k-4),k-1-\frac{i-1}{2}\le j\le k-2,\hfill \end{array}$$

(5)

whereas if i is even, then:

$$\begin{array}{cc}\hfill a_{i,j}& =1+(k-3+i)(2k-3)-\left(\frac{i}{2}+k+j-3\right)(2k-4),1\le j\le \frac{i}{2};\hfill \\ \hfill a_{i,j}& =k-1+i+(2k-4)(2k-3)-\left(j-\frac{i}{2}-1\right)(2k-4),\frac{i}{2}+1\le j\le k-1-\frac{i}{2};\hfill \\ \hfill a_{i,j}& =1+(k-3+i)(2k-3)-\left(j-k+\frac{i}{2}\right)(2k-4),k-\frac{i}{2}\le j\le k-1;\hfill \\ \hfill b_{i,j}& =1+(k-3+i)(2k-3)-\left(\frac{i}{2}+j-1\right)(2k-4),1\le j\le k-2.\hfill \end{array}$$

(6)

For row $R_i$ with $k\le i\le 2k-4$, if i is odd, then:

$$\begin{array}{cc}\hfill a_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(k-2-\frac{1+i}{2}+j\right)(2k-4),1\le j\le k-1;\hfill \\ \hfill b_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(2k-3-\frac{1+i}{2}+j\right)(2k-4),1\le j\le k-1-\frac{1+i}{2};\hfill \\ \hfill b_{i,j}& =1+(i-k)(2k-3)-\left(j-k+\frac{1+i}{2}\right)(2k-4),k-\frac{1+i}{2}\le j\le \frac{1+i}{2}-1;\hfill \\ \hfill b_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(j-\frac{1+i}{2}\right)(2k-4),\frac{1+i}{2}\le j\le k-2,\hfill \end{array}$$

(7)

whereas if i is even, then:

$$\begin{array}{cc}\hfill a_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(2k-4-\frac{i}{2}+j\right)(2k-4),1\le j\le k-1-\frac{i}{2};\hfill \\ \hfill a_{i,j}& =1+(i-k)(2k-3)-\left(j-k+\frac{i}{2}\right)(2k-4),k-\frac{i}{2}\le j\le \frac{i}{2};\hfill \\ \hfill a_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(j-\frac{i}{2}-1\right)(2k-4),\frac{i}{2}+1\le j\le k-1;\hfill \\ \hfill b_{i,j}& =2+i-k+(2k-4)(2k-3)-\left(k-2-\frac{i}{2}+j\right)(2k-4),1\le j\le k-2.\hfill \end{array}$$

(8)

2.2. Arrangement That Avoids K-Term Arithmetic Progressions

In this section, we form a sequence P, which is an arrangement of the rows of the $(2k-3)\times (2k-3)$ magic square from Section 2.1 that avoids k-term arithmetic progressions.

Theorem 2.

Suppose $k\ge 4$. Let $R_i$ be the sequence of integers in the i-th row from left to right in the magic square formed by using the method in Section 2.1 where $1\le i\le 2k-3$. Then, the sequence $P=R_1,R_2,\dots ,R_{k-2},R_k,R_{k+1},\dots ,R_{2k-4},R_{2k-3},R_{k-1}$ avoids k-term arithmetic progressions, but it has a $(k-1)$-term arithmetic progression, $k-1,k,\dots ,2k-3$.

Remark 1.

Note that Theorem 2 is not true for $k=3$. In fact, the row $R_3=3,5,7$ has a three-term arithmetic progression.

Proof. 

Note that for $k=4$,

$$\begin{array}{c}\hfill P=11,24,7,20,3,4,12,25,8,16,10,18,1,14,22,23,6,19,2,15,17,5,13,21,9,\end{array}$$

does not contain a 4-term arithmetic progression, but has a 3-term arithmetic progression $3,4,5$. Therefore, we may assume that $k\ge 5$.

By Equations (1), (5) and (6), for $1\le i\le k-2$, every integer in the row $R_i$ is either congruent with $k-2+i$ or $k-1+imod(2k-4)$. By Equations (2), (7) and (8), for $k\le i\le 2k-3$, every integer in the row $R_i$ is either congruent with $i-k+1$ or $i-k+2mod(2k-4)$. Lastly, by Equations (3) and (4), every integer in the row $R_{k-1}$ is congruent with $1mod(2k-4)$. Note that the only integer congruent with $1mod(2k-4)$ in row $R_{k-2}$ is ${(2k-3)}^2$, whereas the only integer congruent with $1mod(2k-4)$ in row $R_k$ is one. Thus, all the integers congruent with $1mod(2k-4)$ in $\mathrm{[}{(2k-3)}^2\mathrm{]}$ appear in rows $R_{k-2},R_k$, and $R_{k-1}$. For $r=2,3,\dots ,2k-4$, all the integers congruent with $rmod(2k-4)$ in $\mathrm{[}{(2k-3)}^2\mathrm{]}$ appear in exactly two different rows.

Since $k+j-2$ is in $R_j$ for $1\le j\le k-1$ and $P=R_1,R_2,\dots ,R_{k-2},R_k,R_{k+1},\dots ,R_{2k-4},R_{2k-3},R_{k-1}$, the progression $k-1,k,\dots ,2k-3$ is a $(k-1)$-term arithmetic progression in P. Now, we proceed to show that P does not have any k-term arithmetic progressions. We prove it by contradiction. Assume that there exists a k-term monotone arithmetic progression $T=\{T_1,T_2,\dots ,T_k\}$ in P. Then, there exists a nonzero integer d such that:

$$\begin{array}{c}\hfill T_j=T_1+(j-1)d,\end{array}$$

for all $1\le j\le k$. Note that $\left|d\right|\le \frac{{(2k-3)}^2-1}{k-1}=4k-8$.

Since:

$$P=R_1,R_2,\dots ,R_{k-2},R_k,R_{k+1},\dots ,R_{2k-4},R_{2k-3},R_{k-1},$$

$T_j$ should appear before $T_{j+1}$ if we read the elements from left to right in P. Thus, if $T_j$ is in $R_i$ for some $i\in \{1,2,\dots ,k-2,k,k+1,\dots ,2k-3\}$, then $T_{j+1}$ will be in $R_{i^{\prime }}$ where $i^{\prime }\ge i$ or $i^{\prime }=k-1$, and if $T_j$ is in $R_{k-1}$, then $T_{j+1}$ will be in $R_{k-1}$. Furthermore, if $T_j$ and $T_{j+1}$ are both in $R_i$ for some $1\le i\le 2k-3$, then $T_{j+1}$ will appear after $T_j$ in the sequence P when we read from left to right.

Suppose $T_j=1$ or ${(2k-3)}^2$ for some $2\le j\le k-1$. If the former holds, then $d=T_{j+1}-T_j>0$ and $d=T_j-T_{j-1}<0$, a contradiction. If the latter holds, then $d=T_{j+1}-T_j<0$ and $d=T_j-T_{j-1}>0$, a contradiction. Hence, we may assume that $T_j\ne 1$ or ${(2k-3)}^2$ for all $2\le j\le k-1$.

If two consecutive terms of T are in $R_i$ for some $1\le i\le 2k-3$, then $d\equiv \pm 1$ or $0mod(2k-4)$. Suppose no two consecutive terms of T are in $R_i$. This means that if $T_j$ is in $R_{i_j}$, then $T_{j+1}$ will be in $R_{i_{j+1}}$ where $i_{j+1}>i_j$ or $i_{j+1}=k-1$ and $i_j\in \{1,2,\dots ,k-2,k,k+1,\dots ,2k-3\}$. Since $\frac{2k-3}{2}=k-\frac{3}{2}<k$, either there exists $1\le j_0\le k-1$ such that $T_{j_0}$ and $T_{j_0+1}$ are in $R_{i_0}$ and $R_{i_0+1}$, respectively, for some $i_0\in \{1,2,\dots ,k-3,k,k+1,\dots ,2k-4\}$ or $T_{j_0}$ and $T_{j_0+1}$ are in $R_{k-2}$ and $R_k$, respectively, or $T_{k-1}$ and $T_k$ are in $R_{2k-3}$ and $R_{k-1}$, respectively. If such a $j_0$ exists, then $d\equiv 0,1$ or $2mod(2k-4)$, otherwise, $d\equiv k-2$ or $k-1mod(2k-4)$.

Case 1:

Suppose $d\equiv k-2mod(2k-4)$. This means no two consecutive terms of T are in $R_i$ and $T_{k-1}$ and $T_k$ are in $R_{2k-3}$ and $R_{k-1}$, respectively. Furthermore, $T_k\equiv 1mod(2k-4)$ and $T_{k-1}\equiv k-1mod(2k-4)$. Note that $T_{k-2}\equiv 1mod(2k-4)$. Therefore, $T_{k-2}$ is in $R_{k-2},R_k$ or $R_{k-1}$. If $T_{k-2}$ is in $R_{k-1}$, then $T_{k-1}$ will be in $R_{k-1}$, a contradiction. If $T_{k-2}$ is in $R_{k-2}$, then $T_{k-2}={(2k-3)}^2$, a contradiction. If $T_{k-2}$ is in $R_k$, then $T_{k-2}=1$, a contradiction.

Case 2:

Suppose $d\equiv k-1mod(2k-4)$. This means no two consecutive terms of T are in $R_i$ and $T_{k-1}$ and $T_k$ are in $R_{2k-3}$ and $R_{k-1}$, respectively. Furthermore, $T_k\equiv 1mod(2k-4)$ and $T_{k-1}\equiv k-2mod(2k-4)$. Note that $T_{k-2}\equiv 2k-5mod(2k-4)$ and $T_{k-3}\equiv k-4mod(2k-4)$. If $k=5$, then $T_{k-2}=T_3$ is in $R_1$ or $R_2$, whereas $T_{k-3}=T_2$ is in $R_3$ or $R_5$. This is not possible as $T_2$ should appear before $T_3$ in the sequence P. Suppose $k\ge 6$. Now, $T_{k-2}$ is in $R_{k-3}$ or $R_{k-4}$, whereas $T_{k-3}$ is in $R_{2k-6}$ or $R_{2k-5}$, again not possible.

Case 3:

Suppose $d\equiv 2mod(2k-4)$. This means no two consecutive terms of T are in $R_i$ and there exists $1\le j_0\le k-1$ such that $T_{j_0}$ and $T_{j_0+1}$ are in $R_{i_0}$ and $R_{i_0+1}$, respectively, for some $i_0\in \{1,2,\dots ,k-3,k,k+1,\dots ,2k-4\}$ or $T_{j_0}$ and $T_{j_0+1}$ are in $R_{k-2}$ and $R_k$, respectively. Now, $T_1$ cannot be in $R_{k-1}$; otherwise, $T_2$ will be in $R_{k-1}$. Note that $T_{k-1}=T_1+(k-2)d\equiv T_{1}mod(2k-4)$. Suppose $T_1$ is in $R_t$ for some $1\le t\le k-2$. Then, $T_1\equiv k-2+t$ or $k-1+tmod(2k-4)$. If $T_1\equiv 1mod(2k-4)$, then $T_1={(2k-3)}^2$. Since $T_{k-1}\ne 1$, it must be in $R_{k-1}$. Therefore, $T_k$ is in $R_{k-1}$, a contradiction. Suppose $T_1\neg \equiv 1mod(2k-4)$. Since $T_{k-1}$ must appear after $T_1$ in P, we have $T_1\equiv k-1+tmod(2k-4)$ and $T_1$ is in $R_t$ for some $1\le t\le k-3$ and $T_{k-1}$ is in $R_{t+1}$. This implies that either $T_{k-2}$ is in the same row as $T_{k-1}$ or $T_2$ is in the same row as $T_1$, a contradiction. Similarly, we also cannot have $T_1$ in $R_t$ for some $k\le t\le 2k-3$.

Case 4:

Suppose $d\equiv 1mod(2k-4)$. Now, $T_1$ cannot be in $R_{k-1}$; otherwise, $T_2$ will be in $R_{k-1}$ and $d\equiv T_2-T_1\equiv 0mod(2k-4)$. Suppose $T_1$ is in $R_i$ for some $1\le i\le k-2$. Then, $T_1$ is either congruent with $k-2+i$ or $k-1+imod(2k-4)$. Suppose $T_1\equiv k-2+imod(2k-4)$. Then, $T_{k-i}\equiv k-2+i+(k-i-1)\equiv 1mod(2k-4)$. Since $T_{k-i}\ne 1$ and ${(2k-3)}^2$, it must be in $R_{k-1}$. Thus, $T_{k-i+1}$ is also in $R_{k-1}$ and $d\equiv T_{k-i+1}-T_{k-i}\equiv 0mod(2k-4)$, a contradiction. Suppose $T_1\equiv k-1+imod(2k-4)$. Then, $T_{k-i-1}\equiv k-1+i+(k-i-2)\equiv 1mod(2k-4)$. If $i\le k-3$, then $T_{k-i-1}$ must be in $R_{k-1}$. Therefore, $T_{k-i}$ is also in $R_{k-1}$ and $d\equiv 0mod(2k-4)$, a contradiction. Suppose $i=k-2$. Then, $T_1\equiv 1mod(2k-4)$ and it is in $R_{k-2}$. Therefore, $T_1={(2k-3)}^2$. Now, $T_k\equiv 1+(k-1)\equiv kmod(2k-4)$. Since $k\ge 5$, $T_k$ is in $R_1$ or $R_2$, which is not possible as $T_1$ is in $R_{k-2}$.

Suppose $T_1$ is in $R_i$ for some $k\le i\le 2k-3$. Then, $T_1$ is either congruent with $i-k+1$ or $i-k+2mod(2k-4)$. Suppose $T_1\equiv i-k+2mod(2k-4)$. Then, $T_{k-2}\equiv i-k+2+(k-3)\equiv i-1mod2k-3$. If $i\ge k+1$, then $T_{k-2}$ is in $R_{i-k+1}$ or $R_{i-k}$, which is not possible. If $i=k$, then $T_{k-2}\equiv k-1mod(2k-4)$ and $T_{k-1}\equiv kmod(2k-4)$. Therefore, $T_{k-1}$ is in $R_1$ or $R_2$, again not possible. Suppose $T_1\equiv i-k+1mod(2k-4)$. Then, $T_{k-1}\equiv i-k+1+(k-2)\equiv i-1mod(2k-4)$. If $i\ge k+1$, then $T_{k-1}$ is in $R_{i-k+1}$ or $R_{i-k}$, which is not possible. If $i=k$, then $T_{k-1}\equiv k-1mod(2k-4)$ and $T_k\equiv kmod(2k-4)$. Therefore, $T_k$ is in $R_1$ or $R_2$, again not possible.

Case 5:

Suppose $d\equiv -1mod(2k-4)$.

If two consecutive terms of T, say $T_j$ and $T_{j+1}$ are in $R_{k-1}$, then $d=T_{j+1}-T_j\equiv 0mod(2k-4)$, a contradiction. Suppose $T_j$ and $T_{j+1}$ are in $R_1$. Then, $T_j\equiv kmod(2k-4)$ and $T_{j+1}\equiv k-1mod(2k-4)$. By Equation (1), $T_j=b_{1,j_1}$ for some $1\le j_1\le k-2$ and $T_{j+1}=a_{1,j_2}$ for some $1\le j_2\le k-1$. Now,

$$\begin{array}{cc}\hfill d& =T_{j+1}-T_j=a_{1,j_2}-b_{1,j_1}\le a_{1,1}-b_{1,(k-2)}\hfill \\ \hfill & =1+(k-2)(2k-3)-\left(k+(2k-4)(2k-3)-(k-3)(2k-4)\right)\hfill \\ \hfill & =1-2(2k-3)=-4k+7.\hfill \end{array}$$

Therefore, $\left|d\right|\ge 4k-7>4k-8$, a contradiction.

Suppose $T_j$ and $T_{j+1}$ are in $R_{2k-3}$. Then, $T_j\equiv k-1mod(2k-4)$ and $T_{j+1}\equiv k-2mod(2k-4)$. By Equation (2), $T_j=a_{(2k-3),j_1}$ for some $1\le j_1\le k-1$ and $T_{j+1}=b_{(2k-3),j_2}$ for some $1\le j_2\le k-2$. Furthermore, $j_2\ge j_1$. Now,

$$\begin{array}{cc}\hfill d& =T_{j+1}-T_j=b_{(2k-3),j_2}-b_{(2k-3),j_1}+b_{(2k-3),j_1}-a_{(2k-3),j_1}\hfill \\ \hfill & \le b_{(2k-3),j_1}-a_{(2k-3),j_1}\hfill \\ \hfill & =1+(k-3)(2k-3)-\left(k-1+(2k-4)(2k-3)\right)\hfill \\ \hfill & =2-k-(k-1)(2k-3)=1-(k-1)(2k-2).\hfill \end{array}$$

Therefore, $\left|d\right|\ge (k-1)(2k-2)-1>4k-8$, a contradiction. Hence, we may assume that no consecutive terms of T are in $R_1,R_{2k-3}$ or $R_{k-1}$.

Suppose $T_1$ is in $R_1$. Then, $T_1$ is either congruent with $k-1$ or $kmod(2k-4)$. Suppose $T_1\equiv kmod(2k-4)$. Then, $T_2\equiv k-1mod(2k-4)$. Note that $T_2$ is not in $R_1$, for no two consecutive terms of T are in $R_1$. Therefore, $T_2$ is in $R_{2k-3}$. This means $T_3$ is in $R_{k-1}$, for no two consecutive terms of T are in $R_{2k-3}$. Therefore, $T_4$ must be in $R_{k-1}$, a contradiction as no two consecutive terms of T are in $R_{k-1}$.

Suppose $T_1\equiv k-1mod(2k-4)$. Then, $T_{k-1}\equiv k-1+(k-2)(-1)\equiv 1mod(2k-4)$. Therefore, $T_{k-1}$ is in $R_{k-2},R_k$, or $R_{k-1}$. Note that $T_{k-1}$ cannot be in $R_{k-1}$, otherwise $T_k$ will be in $R_{k-1}$. If $T_{k-1}$ is in $R_{k-2}$, then $T_{k-1}={(2k-3)}^2$, a contradiction. If $T_{k-1}$ is in $R_k$, then $T_{k-1}=1$, a contradiction.

Suppose $T_1$ is in $R_i$ for some $2\le i\le k-2$. Then, $T_1$ is either congruent with $k-2+i$ or $k-1+imod(2k-4)$. Suppose $T_1\equiv k-1+imod(2k-4)$. Then, $T_2\equiv k-2+imod(2k-4)$ and $T_3\equiv k-3+imod(2k-4)$. Since $T_2$ is not in $R_{i-1}$, it must be in $R_i$. If $i=2$, then $T_3$ must be in $R_{2k-3}$, for it cannot be in $R_1$. Since $T_4\equiv k-2mod(2k-4)$, we must have $T_4$ in $R_{2k-3}$ or $R_{2k-4}$. Both cases also cannot happen. If $i\ge 3$, then $T_3$ is in $R_{i-1}$ or $R_{i-2}$, which is not possible. Suppose $T_1\equiv k-2+imod(2k-4)$. Then, $T_2\equiv k-3+imod(2k-4)$. If $i=2$, then $T_2$ must be in $R_{2k-3}$. Since $T_3$ is not in $R_{2k-3}$, it must be in $R_{k-1}$. However, then $T_4$ is also in $R_{k-1}$, a contradiction. If $i\ge 3$, then $T_2$ is in $R_{i-1}$ or $R_{i-2}$, which is not possible.

Suppose $T_1$ is in $R_i$ for some $k\le i\le 2k-3$. Then, $T_1$ is either congruent with $i-k+1$ or $i-k+2mod(2k-4)$. Suppose $T_1\equiv i-k+2mod(2k-4)$. Then, $T_{i-k+2}\equiv i-k+2+(i-k+1)(-1)\equiv 1mod(2k-4)$. Therefore, $T_{i-k+2}$ is in $R_{k-2},R_k$, or $R_{k-1}$. Note that $T_{i-k+2}$ cannot be in $R_{k-1}$; otherwise, $T_{i-k+3}$ will be in $R_{k-1}$. If $T_{i-k+2}$ is in $R_{k-2}$, then $T_{i-k+2}={(2k-3)}^2$, a contradiction. If $T_{i-k+2}$ is in $R_k$, then $T_{i-k+2}=1$, a contradiction.

Case 6:

Suppose $d\equiv 0mod(2k-4)$.

Then, $T_j\equiv T_{1}mod(2k-4)$ for all j and $d=\pm (2k-4)$ or $d=\pm (4k-8)$. If $d=4k-8$, then $T_k=T_1+(k-1)d\ge 1+(k-1)(4k-8)={(2k-3)}^2$. Therefore, we must have $T_1=1$ and $T_k={(2k-3)}^2$. Therefore, $T_1$ is in row $R_k$, whereas $T_k$ is in $R_{k-2}$, which is not possible. If $d=-(4k-8)$, then $T_k=T_1+(k-1)d\le {(2k-3)}^2-(k-1)(4k-8)=1$. Therefore, we must have $T_1={(2k-3)}^2$ and $T_k=1$. Now, $T_j\equiv T_1\equiv 1mod(2k-4)$ for $2\le j\le k-1$ imply that $T_j\in R_{k-1}$ for all $2\le j\le k-1$. This is also not possible as $T_2$ should appear after $T_1$, but before $T_k$ in P. Hence, we may assume that $d=\pm (2k-4)$.

Case 6.1:

Suppose $T_1\equiv 1mod(2k-4)$. Then, $T_j$ is either in $R_{k-2},R_k$ or $R_{k-1}$ for all j. Note that $T_j\ne 1$ and ${(2k-3)}^2$ for all $2\le j\le k$. Therefore, we may assume that $T_j$ is in $R_{k-1}$ for all $2\le j\le k$.

Case 6.1.1:

Suppose k is odd. Let

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=a_{(k-1),j}\mathrm{for} \mathrm{some} 1\le j\le \frac{k-1}{2}\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=a_{(k-1),j}\mathrm{for} \mathrm{some} \frac{k-1}{2}+1\le j\le k-1\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=b_{(k-1),j}\mathrm{for} \mathrm{some} 1\le j\le k-2\}.\hfill \end{array}$$

Note that $A_1,A_2$, and $A_3$ are disjoint. By Equation (3), $|A_1|+|A_2|+|A_3|\ge k-1\ge 4$. Therefore, one of the $A_t$ where $t\in \{1,2,3\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_1\ne ⌀$. If $k\notin A_1$, then $T_{s_1}=a_{(k-1),\frac{k-1}{2}}$ for some $1\le s_1\le k-1$. Now,

$$\begin{array}{cc}\hfill T_{s_1}& =1+(2k-4)(2k-3)-\left(\frac{3k-1}{2}+\frac{k-1}{2}-3\right)(2k-4)\hfill \\ \hfill & =1+(2k-4)\hfill \end{array}$$

and $T_{s_1+1}=1+(2k-4)-(2k-4)=1$. Therefore, $T_{s_1+1}$ is in $R_k$. This is not possible. Thus, if $A_1\ne ⌀$, then $k\in A_1$.

Suppose $A_2\ne ⌀$. If $k\notin A_2$, then $T_{s_2}=a_{(k-1),k-1}$ for some $1\le s_2\le k-1$. Since $a_{(k-1),k-1}$ is the last term in $R_{k-1}$, $T_{s_2+1}$ is not in $R_{k-1}$, a contradiction. Thus, if $A_2\ne ⌀$, then $k\in A_2$.

Suppose $A_3\ne ⌀$. If $k\notin A_3$, then $T_{s_3}=b_{(k-1),k-2}$ for some $1\le s_3\le k-1$. Now, $a_{(k-1),k-1}$ is the last term in $R_{k-1}$. Therefore, $T_{s_3+1}=a_{(k-1),k-1}$ and:

$$\begin{array}{cc}\hfill d& =T_{s_3+1}-T_{s_3}=\left(\frac{k-1}{2}+k-2-1\right)(2k-4)-\left(k-1-\frac{k-1}{2}-1\right)(2k-4)\hfill \\ \hfill & =(k-2)(2k-4),\hfill \end{array}$$

a contradiction. Thus, if $A_3\ne ⌀$, then $k\in A_3$.

Hence, $A_{t_0}\ne ⌀$ for exactly one $t_0\in \left[3\right]$. Now, $|A_1|\le \frac{k-1}{2}<k-1$, $|A_2|\le \frac{k-1}{2}<k-1$, and $|A_3|\le k-2<k-1$. Thus, $k-1\le |A_1|+|A_2|+|A_3|=|A_{t_0}|<k-1$, a contradiction.

Case 6.1.2:

Suppose k is even. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=a_{(k-1),j}\mathrm{for} \mathrm{some} 1\le j\le k-1\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=b_{(k-1),j}\mathrm{for} \mathrm{some} 1\le j\le \frac{k}{2}-1\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=b_{(k-1),j}\mathrm{for} \mathrm{some} \frac{k}{2}\le j\le k-2\}.\hfill \end{array}$$

Note that $A_1,A_2$, and $A_3$ are disjoint. By Equation (4), $|A_1|+|A_2|+|A_3|\ge k-1\ge 4$. Therefore, one of the $A_t$ where $t\in \{1,2,3\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_1\ne ⌀$. If $k\notin A_1$, then $T_{s_1}=a_{(k-1),k-1}$ for some $1\le s_1\le k-1$. Since $a_{(k-1),k-1}$ is the last term in $R_{k-1}$, $T_{s_1+1}$ is not in $R_{k-1}$, a contradiction. Thus, if $A_1\ne ⌀$, then $k\in A_1$.

Suppose $A_2\ne ⌀$. If $k\notin A_2$, then $T_{s_2}=b_{(k-1),\frac{k}{2}-1}$ for some $1\le s_2\le k-1$. Now,

$$\begin{array}{cc}\hfill T_{s_2}& =1+(2k-4)(2k-3)-\left(\frac{3k}{2}+\frac{k}{2}-1-3\right)(2k-4)\hfill \\ \hfill & =1+(2k-4)\hfill \end{array}$$

and $T_{s_2+1}=1+(2k-4)-(2k-4)=1$. Therefore, $T_{s_2+1}$ is in $R_k$. This is not possible. Thus, if $A_2\ne ⌀$, then $k\in A_2$.

Suppose $A_3\ne ⌀$. If $k\notin A_3$, $T_{s_3}=b_{(k-1),k-2}$ for some $1\le s_3\le k-1$. Now, $a_{(k-1),k-1}$ is the last term in $R_{k-1}$. Therefore, $T_{s_3+1}=a_{(k-1),k-1}$ and:

$$\begin{array}{cc}\hfill d& =T_{s_3+1}-T_{s_3}=\left(k-2-\frac{k}{2}\right)(2k-4)-\left(\frac{k}{2}+k-1-2\right)(2k-4)\hfill \\ \hfill & =-(k-1)(2k-4),\hfill \end{array}$$

a contradiction. Thus, if $A_3\ne ⌀$, then $k\in A_3$.

Hence, $A_{t_0}\ne ⌀$ for exactly one $t_0\in \left[3\right]$. Now, $|A_1|\le k-1$, $|A_2|\le \frac{k}{2}-1<k-1$, and $|A_3|\le \frac{k}{2}-1<k-1$. Thus, $t_0=1$ and $T_2=a_{(k-1),1}$. This means $T_1$ can only be in $R_{k-2}$ or $R_k$. Since $d<0$, $T_1$ must be in $R_k$, that is $T_1={(2k-3)}^2$. Now,

$$\begin{array}{cc}\hfill d& =T_2-T_1=1+(2k-4)(2k-3)-\left(\frac{k}{2}+1-2\right)(2k-4)-{(2k-3)}^2\hfill \\ \hfill & =-\left(\frac{k}{2}\right)(2k-4),\hfill \end{array}$$

a contradiction.

Case 6.2:

Suppose $T_1\equiv k-1mod(2k-4)$. Then $T_j$ is either in $R_1$ or $R_{2k-3}$ for all j. Since there are at most $k-1$ integers in $R_{2k-3}$ that are congruent with $k-1mod(2k-4)$, we must have $T_1$ in $R_1$. Suppose both $T_1$ and $T_2$ are in $R_1$. By Equation (1), we must have $d=-(2k-4)$ and $T_1=a_{1,l}$ and $T_2=a_{1,l+1}$ for some $1\le l\le k-2$. Since there are at most $k-1$ integers in $R_1$ that are congruent with $k-1mod(2k-4)$, we must have $T_k$ in $R_{2k-3}$. The largest integer congruent with $k-1mod(2k-4)$ in $R_1$ is $a_{1,1}=1+(k-2)(2k-3)$, and the smallest integer congruent with $k-1mod(2k-4)$ in $R_{2k-3}$ is $a_{(2k-3),k-1}=k-1+(2k-4)(2k-3)-(k-2)(2k-4)=(k-1)(2k-3)$. Note that $a_{1,1}-a_{(2k-3),k-1}=-(2k-4)$. Let s be the smallest integer such that $T_s$ is in $R_1$ and $T_{s+1}$ is in $R_{2k-3}$. Since both $T_1$ and $T_2$ are in $R_1$, $T_s\ne a_{1,1}$. Therefore,

$$\begin{array}{cc}\hfill 2k-4=T_s-T_{s+1}& =(T_s-a_{1,1})+a_{1,1}-a_{(2k-3),k-1}+(a_{(2k-3),k-1}-T_{s+1})\hfill \\ \hfill & \le 0-(2k-4)+0<0,\hfill \end{array}$$

a contradiction. Suppose $T_1$ is in $R_1$, but $T_2$ is in $R_{2k-3}$. Then, we must have $T_j=a_{(2k-3),j-1}$ for all $2\le j\le k$. By Equation (2), $d=T_3-T_2=a_{(2k-3),2}-a_{(2k-3),1}=-(2k-4)$. On the other hand,

$$\begin{array}{cc}\hfill 2k-4=T_1-T_2& \le a_{1,1}-a_{(2k-3),1}\hfill \\ \hfill & =1+(k-2)(2k-3)-(k-1+(2k-4\left)\right(2k-3\left)\right)\hfill \\ \hfill & =-(k-2)(2k-2)<0,\hfill \end{array}$$

a contradiction.

Case 6.3:

Suppose $T_1\equiv rmod(2k-4)$ where $k\le r\le 2k-4$. Then, for all j, $T_j$ is either in $R_{r-k+1}$ or $R_{r-k+2}$.

Case 6.3.1:

Suppose $r-k+1$ is odd. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=b_{r-k+1,j}\mathrm{for} \mathrm{some} \frac{r-k}{2}+1\le j\le k-2-\frac{r-k}{2}\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=a_{r-k+2,j}\mathrm{for} \mathrm{some} 1\le j\le \frac{r-k+2}{2}\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=a_{r-k+2,j}\mathrm{for} \mathrm{some} k-\frac{r-k+2}{2}\le j\le k-1\};\hfill \\ \hfill A_4& =\{s\in \left[k\right]:T_s=b_{r-k+2,j}\mathrm{for} \mathrm{some} 1\le j\le k-2\}.\hfill \end{array}$$

Note that $A_1,A_2,A_3$, and $A_4$ are disjoint. By Equations (5) and (6) (or Equations (1) and (6) when $r=k$), $|A_1|+|A_2|+|A_3|+|A_4|=k\ge 5$. Therefore, one of the $A_t$ where $t\in \{1,2,3,4\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_4\ne ⌀$. If $k\notin A_4$, then $T_{s_4}=b_{r-k+2,k-2}$ for some $1\le s_4\le k-1$. Now, $a_{r-k+2,k-1}$ is the last term in $R_{r-k+2}$. Therefore, $T_{s_4+1}=a_{r-k+2,k-1}$ and:

$$\begin{array}{cc}\hfill d& =T_{s_4+1}-T_{s_4}=-\left(k-1-k+\frac{r-k+2}{2}\right)(2k-4)+\left(\frac{r-k+2}{2}+k-2-1\right)(2k-4)\hfill \\ \hfill & =(k-2)(2k-4)>0,\hfill \end{array}$$

a contradiction. Thus, if $A_4\ne ⌀$, then $k\in A_4$. Now, if $1\notin A_4$, then $T_{s_5}=b_{r-k+2,1}$ for some $2\le s_5\le k$. By Equation (6), $T_{s_5-1}=a_{r-k+2,k-1}$. This is not possible as $T_{s_5-1}$ should appear before $T_{s_5}$ in P. Thus, if $A_4\ne ⌀$, then one and k must be in $A_4$. This implies that $j\in A_4$ for all $1\le j\le k$. This is not possible as $|A_4|\le k-2$. Hence, $A_4=⌀$ and $|A_1|+|A_2|+|A_3|=k$.

Suppose $A_2\ne ⌀$. If $k\notin A_2$, then $T_{s_2}=a_{r-k+2,\frac{r-k+2}{2}}$ for some $1\le s_2\le k-1$. Now,

$$\begin{array}{cc}\hfill T_{s_2}& =1+(k-3+r-k+2)(2k-3)-\left(\frac{r-k+2}{2}+k+\frac{r-k+2}{2}-3\right)(2k-4)\hfill \\ \hfill & =r,\hfill \end{array}$$

and $T_{s_2+1}=r-(2k-4)\le 0$, a contradiction. Thus, if $A_2\ne ⌀$, then $k\in A_2$.

Suppose $A_3\ne ⌀$. If $k\notin A_3$, then $T_{s_3}=a_{r-k+2,k-1}$ for some $1\le s_3\le k-1$. Since $a_{r-k+2,k-1}$ is the last term in $R_{r-k+2}$, $T_{s_3+1}$ is not in $R_{r-k+2}$, a contradiction. Thus, if $A_3\ne ⌀$, then $k\in A_3$.

Hence, $A_{t_0}\ne ⌀$ for at most one $t_0\in \{2,3\}$. If $A_3=⌀$, then:

$$\begin{array}{c}\hfill k=|A_1|+|A_2|\le k-(r-k+2)+\frac{r-k+2}{2}=k-\frac{r-k+2}{2}<k,\end{array}$$

a contradiction. Similarly, if $A_2=⌀$, then $k=|A_1|+|A_3|<k$, again a contradiction.

Case 6.3.2:

Suppose $r-k+1$ is even. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=a_{r-k+1,j}\mathrm{for} \mathrm{some} \frac{r-k+1}{2}+1\le j\le k-1-\frac{r-k+1}{2}\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=a_{r-k+2,j}\mathrm{for} \mathrm{some} 1\le j\le k-1\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=b_{r-k+2,j}\mathrm{for} \mathrm{some} 1\le j\le \frac{r-k+1}{2}\};\hfill \\ \hfill A_4& =\{s\in \left[k\right]:T_s=b_{r-k+2,j}\mathrm{for} \mathrm{some} k-1-\frac{r-k+1}{2}\le j\le k-2\}.\hfill \end{array}$$

Note that $A_1,A_2,A_3$, and $A_4$ are disjoint. By Equations (5) and (6), $|A_1|+|A_2|+|A_3|+|A_4|=k\ge 5$. Therefore, one of the $A_t$ where $t\in \{1,2,3,4\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_2\ne ⌀$. If $k\notin A_2$, then $T_{s_2}=a_{r-k+2,k-1}$ for some $1\le s_2\le k-1$. Since $a_{r-k+2,k-1}$ is the last term in $R_{r-k+2}$, $T_{s_2+1}$ is not in $R_{r-k+2}$, a contradiction. Thus, if $A_2\ne ⌀$, then $k\in A_2$. Now, if $T_1$ is not in $A_2$, then $T_{s_5}=a_{r-k+2,1}$ for some $2\le s_5\le k$. By Equation (5) $T_{s_5-1}=b_{r-k+2,k-2}$. This is not possible as $T_{s_5-1}$ should appear before $T_{s_5}$ in P. Thus, if $A_2\ne ⌀$, then one and k must be in $A_2$. This implies that $j\in A_2$ for all $1\le j\le k$. This is not possible as $|A_2|\le k-1$. Hence, $A_2=⌀$ and $|A_1|+|A_3|+|A_4|=k$.

Suppose $A_3\ne ⌀$. If $k\notin A_3$, then $T_{s_3}=b_{r-k+2,\frac{r-k+1}{2}}$ for some $1\le s_3\le k-1$. Now,

$$\begin{array}{cc}\hfill T_{s_3}& =1+(k-3+r-k+2)(2k-3)-\left(\frac{r-k+1}{2}+k+\frac{r-k+1}{2}-2\right)(2k-4)\hfill \\ \hfill & =r,\hfill \end{array}$$

and $T_{s_3+1}=r-(2k-4)\le 0$, a contradiction. Thus, if $A_3\ne ⌀$, then $k\in A_3$.

Suppose $A_4\ne ⌀$. If $k\notin A_4$, then $T_{s_4}=b_{r-k+2,k-2}$ for some $1\le s_4\le k-1$. By Equation (5), $T_{s_4+1}=a_{r-k+2,1}$, which is not possible. Thus, if $A_4\ne ⌀$, then $k\in A_4$.

Hence, $A_{t_0}\ne ⌀$ for at most one $t_0\in \{3,4\}$. If $A_3=⌀$, then:

$$\begin{array}{c}\hfill k=|A_1|+|A_4|\le k-1-(r-k+1)+\frac{r-k+1}{2}=k-1-\frac{r-k+1}{2}<k,\end{array}$$

a contradiction. Similarly, if $A_4=⌀$, then $k=|A_1|+|A_3|<k$, again a contradiction.

Case 6.4:

Suppose $T_1\equiv rmod(2k-4)$ where $2\le r\le k-2$. Then, $T_j$ is either in $R_{k-2+r}$ or $R_{k-1+r}$ for all j.

Case 6.4.1:

Suppose $k-2+r$ is odd. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=a_{k-2+r,j}\mathrm{for} \mathrm{some} 1\le j\le k-1\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=b_{k-2+r,j}\mathrm{for} \mathrm{some} 1\le j\le k-1-\frac{k-1+r}{2}\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=b_{k-2+r,j}\mathrm{for} \mathrm{some} \frac{k-1+r}{2}\le j\le k-2\};\hfill \\ \hfill A_4& =\{s\in \left[k\right]:T_s=a_{k-1+r,j}\mathrm{for} \mathrm{some} k-\frac{k-1+r}{2}\le j\le \frac{k-1+r}{2}\}.\hfill \end{array}$$

Note that $A_1,A_2,A_3$, and $A_4$ are disjoint. By Equations (7) and (8), $|A_1|+|A_2|+|A_3|+|A_4|=k\ge 5$. Therefore, one of the $A_t$ where $t\in \{1,2,3,4\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_1\ne ⌀$. If $k\notin A_1$, then $T_{s_1}=a_{k-2+r,k-1}$ for some $1\le s_1\le k-1$. Therefore, $T_{s_1+1}=b_{k-2+r,1}$, and this is not possible. Thus, if $A_1\ne ⌀$, then $k\in A_1$. Now, if $1\notin A_1$, then $T_{s_5}=a_{k-2+r,1}$ for some $2\le s_5\le k$. Therefore, $T_{s_5-1}=b_{k-2+r,k-2}$, again not possible. Thus, if $A_1\ne ⌀$, then one and k must be in $A_1$. This implies that $j\in A_1$ for all $1\le j\le k$. Therefore, $k=|A_1|\le k-1$, a contradiction. Hence, $A_1=⌀$ and $|A_2|+|A_3|+|A_4|=k$.

Suppose $A_2\ne ⌀$. If $1\notin A_2$, then $T_{s_2}=b_{k-2+r,1}$ for some $2\le s_2\le k$. Therefore, $T_{s_2-1}=a_{k-2+r,k-1}$, and this is not possible. Thus, if $A_2\ne ⌀$, then $1\in A_2$.

Suppose $A_3\ne ⌀$. If $1\notin A_3$, then $T_{s_3}=b_{k-2+r,\frac{k-1+r}{2}}$ for some $2\le s_3\le k$. Therefore,

$$\begin{array}{cc}\hfill T_{s_3}& =2+k-2+r-k+(2k-4)(2k-3)\hfill \\ \hfill & =r+(2k-4)(2k-3),\hfill \end{array}$$

and $T_{s_3-1}=r+(2k-4)(2k-2)>{(2k-3)}^2$, a contradiction. Thus, if $A_3\ne ⌀$, then $1\in A_3$. Hence, $A_{t_0}\ne ⌀$ for at most one $t_0\in \{2,3\}$. If $A_3=⌀$, then:

$$\begin{array}{c}\hfill k=|A_2|+|A_4|\le k-1-\frac{k-1+r}{2}+r=\frac{k-1+r}{2}<k,\end{array}$$

a contradiction. Similarly, if $A_2=⌀$, then $k=|A_3|+|A_4|<k$, again a contradiction.

Case 6.4.2:

Suppose $k-2+r$ is even. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=a_{k-2+r,j}\mathrm{for} \mathrm{some} 1\le j\le k-1-\frac{k-2+r}{2}\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=a_{k-2+r,j}\mathrm{for} \mathrm{some} \frac{k-2+r}{2}+1\le j\le k-1\};\hfill \\ \hfill A_3& =\{s\in \left[k\right]:T_s=b_{k-2+r,j}\mathrm{for} \mathrm{some} 1\le j\le k-2\};\hfill \\ \hfill A_4& =\{s\in \left[k\right]:T_s=b_{k-1+r,j}\mathrm{for} \mathrm{some} k-\frac{k+r}{2}\le j\le \frac{k+r}{2}-1\}.\hfill \end{array}$$

Note that $A_1,A_2,A_3$, and $A_4$ are disjoint. By Equations (7) and (8) (or Equations (2) and (6) when $r=k-2$), $|A_1|+|A_2|+|A_3|+|A_4|=k\ge 5$. Therefore, one of the $A_t$ where $t\in \{1,2,3,4\}$ must contain at least two elements. Thus, $d=-(2k-4)$.

Suppose $A_3\ne ⌀$. If $k\notin A_3$, then $T_{s_3}=b_{k-2+r,k-2}$ for some $1\le s_3\le k-1$. Therefore, $T_{s_3+1}=a_{k-2+r,1}$, and this is not possible. Thus, if $A_3\ne ⌀$, then $k\in A_3$. Now, if $1\notin A_3$, then $T_{s_5}=b_{k-2+r,1}$ for some $2\le s_5\le k$. Therefore, $T_{s_5-1}=a_{k-2+r,k-1}$, again not possible. Thus, if $A_3\ne ⌀$, then one and k must be in $A_3$. This implies that $j\in A_3$ for all $1\le j\le k$. Therefore, $k=|A_3|\le k-2$, a contradiction. Hence, $A_3=⌀$ and $|A_1|+|A_2|+|A_4|=k$.

Suppose $A_1\ne ⌀$. If $1\notin A_1$, then $T_{s_1}=a_{k-2+r,1}$ for some $2\le s_1\le k$. Therefore, $T_{s_1-1}=b_{k-2+r,k-2}$, and this is not possible. Thus, if $A_1\ne ⌀$, then $1\in A_1$.

Suppose $A_2\ne ⌀$. If $1\notin A_2$, then $T_{s_2}=a_{k-2+r,\frac{k-2+r}{2}+1}$ for some $2\le s_2\le k$. Therefore,

$$\begin{array}{cc}\hfill T_{s_2}& =2+k-2+r-k+(2k-4)(2k-3)\hfill \\ \hfill & =r+(2k-4)(2k-3),\hfill \end{array}$$

and $T_{s_2-1}=r+(2k-4)(2k-2)>{(2k-3)}^2$, a contradiction. Thus, if $A_2\ne ⌀$, then $1\in A_2$. Hence, $A_{t_0}\ne ⌀$ for at most one $t_0\in \{1,2\}$. On the other hand, if $A_1=⌀$, then:

$$\begin{array}{c}\hfill k=|A_2|+|A_4|\le k-1-\frac{k-2+r}{2}+r=\frac{k-2+r}{2}+1<k,\end{array}$$

a contradiction. Similarly, if $A_2=⌀$, then $k=|A_1|+|A_4|<k$, again a contradiction.

Hence, P does not contain any k-term monotone arithmetic progressions. This completes the proof of the theorem. □

Corollary 1.

Let $k\ge 3$. For each integer n with $k\le n\le {(2k-3)}^2$, there is an arrangement of $\left[n\right]$ that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression.

Proof. 

For $k=3$, the sequence $P=1,9,5,3,7,2,8,4,6$ avoids three-term arithmetic progressions. Now, for $3\le n\le 9$, remove $n+1,n+2,\dots ,9$ from P, and denote the resulting sequence as $P^{\prime }$. For instance, if $n=8$, then $P^{\prime }=1,5,3,7,2,8,4,6$, and if $n=5$, then $P^{\prime }=1,5,3,2,4$. Note that $P^{\prime }$ avoids three-term arithmetic progressions. Therefore, we may assume that $k\ge 4$.

Suppose $2k-3\le n\le {(2k-3)}^2$. First, we show that if $n={(2k-3)}^2$, then there is an arrangement of $\left[n\right]$ that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression. By Theorem 2, such an arrangement exists. Let us denote the arrangement by P. Now, remove $n+1,n+2,\dots ,{(2k-3)}^2$ from P, and denote the resulting sequence as $P^{\prime }$. Note that $P^{\prime }$ avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression, that is $k-1,k,\dots ,2k-3$.

Suppose $k\le n\le 2k-3$. Let $Q=2k-3,2k-4,\dots ,k,1,2,\dots ,k-1$. Then, it avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression, that is $1,2,\dots ,k-1$. Now, remove $n+1,n+2,\dots ,(2k-3)$ from Q, and denote the resulting sequence as $Q^{\prime }$. Thus, $Q^{\prime }$ avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression, that is $1,2,\dots ,k-1$. □

Lemma 1.

Let $b_n=s{a}_n+r$ for some real numbers $r,s$. Then, the sequence $a_1,a_2,\dots ,a_n$ contains a k-term monotone arithmetic progression if and only if $b_1,b_2,\dots ,b_n$ contains a k-term monotone arithmetic progression.

Proof. 

It is sufficient to show that if $a_1,a_2,\dots ,a_n$ contains a k-term monotone arithmetic progression, then $b_1,b_2,\dots ,b_n$ contains a k-term monotone arithmetic progression. Let $i_1<i_2<\dots <i_k$ be such that $a_{i_1},a_{i_2},\dots ,a_{i_k}$ is a k-term monotone arithmetic progression. Therefore,

$$\begin{array}{c}\hfill a_{i_j}=a_{i_1}+(j-1)d\end{array}$$

for some real number d. This implies that:

$$\begin{array}{cc}\hfill b_{i_j}& =s{a}_{i_j}+r=s(a_{i_1}+(j-1)d)+r\hfill \\ \hfill & =(s{a}_{i_1}+r)+(j-1)sd=b_{i_1}+(j-1)sd.\hfill \end{array}$$

Hence, $b_{i_1},b_{i_2},\dots ,b_{i_k}$ is a k-term monotone arithmetic progression. □

Let $\lceil x\rceil$ be the smallest integer such that $\lceil x\rceil -1<x\le \lceil x\rceil$ and $\lfloor x\rfloor$ be the largest integer such that $\lfloor x\rfloor \le x<\lfloor x\rfloor +1$.

Theorem 3.

Let $k\ge 3$. For each integer n with $n\ge k$, there is an arrangement of $\left[n\right]$ that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression.

Proof. 

By Corollary 1, this theorem is true for $n\le {(2k-3)}^2$. Now, we may assume $n>{(2k-3)}^2$. We also assume that the theorem is true for all $n^{\prime }$ such that $n^{\prime }<n$. Let $\left[n\right]=A_1\cup A_2$ where $A_1$ and $A_2$ are odd and even integers, respectively. Note that $|A_1|=⌈\frac{n}{2}⌉$ and $|A_2|=⌊\frac{n}{2}⌋$. Note that:

$$\begin{array}{cc}\hfill A_1& =\left\{2j-1:1\le j\le ⌈\frac{n}{2}⌉\right\};\hfill \\ \hfill A_2& =\left\{2j:1\le j\le ⌊\frac{n}{2}⌋\right\}.\hfill \end{array}$$

Since $\lceil \frac{n}{2}\rceil <n$, by assumption, the theorem is true for $\lceil \frac{n}{2}\rceil$. Let $P_1=a_1,a_2,\dots ,a_{⌈\frac{n}{2}⌉}$ be an arrangement of $\left[⌈\frac{n}{2}⌉\right]$ that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression. Furthermore, let $P_2=b_1,b_2,\dots ,b_{⌊\frac{n}{2}⌋}$ be an arrangement of $\left[⌊\frac{n}{2}⌋\right]$ that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression. We claim that:

$$\begin{array}{c}\hfill P=2a_1-1,2a_2-1,\dots ,2a_{⌈\frac{n}{2}⌉}-1,2b_1,2b_2,\dots ,2b_{⌊\frac{n}{2}⌋}\end{array}$$

is an arrangement that avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression. In fact, if $T_1,T_2,\dots ,T_k$ is a k-term monotone arithmetic progression in P, then $T_j=T_1+(j-1)d$. Let:

$$\begin{array}{cc}\hfill A_1& =\{s\in \left[k\right]:T_s=2a_j-1\mathrm{for} \mathrm{some} 1\le j\le ⌈\frac{n}{2}⌉\};\hfill \\ \hfill A_2& =\{s\in \left[k\right]:T_s=2b_j\mathrm{for} \mathrm{some} 1\le j\le ⌊\frac{n}{2}⌋\}.\hfill \end{array}$$

Since $k\ge 4$, one of the $A_t$ where $t\in \{1,2\}$ must contain at least two elements. Thus, d is even. If both $A_1$ and $A_2$ are nonempty, then there is a $1\le s\le k-1$ such that $s\in A_1$ and $s+1\in A_2$. Now, $d=T_{s+1}-T_s=2b_{j_2}-(2a_{j_1}-1)=2(b_{j_2}-a_{j_1})+1$ is odd, a contradiction. Hence, $A_{t_0}\ne ⌀$ for at most one $t_0\in \{1,2\}$. If $A_1\ne ⌀$, then by Lemma 1, $P_1$ contains a k-term arithmetic progression, a contradiction. Similarly, if $A_2\ne ⌀$, then $P_2$ contains a k-term arithmetic progression. Hence, P avoids k-term arithmetic progressions, but contains a $(k-1)$-term arithmetic progression. □