Mathematical Modelling and Study of Stochastic Parameters of Computer Data Processing

Abstract

The main goal of dispatching strategies is to minimize the total time for processing tasks at maximum performance of the computer system, which requires strict regulation of the workload of the processing units. To achieve this, it is necessary to conduct a preliminary study of the applied model for planning. The purpose of this article is to present an approach for automating the investigation and optimization of processes in a computer environment for task planning and processing. A stochastic input flow of incoming tasks for processing is considered and mathematical formalization of some probabilistic characteristics related to the complexity of its servicing has been made. On this basis, a software module by using program language APL2 has been developed to conduct experiments for analytical study and obtaining estimates of stochastic parameters of computer processing and dispatching. The proposed model is part of a generalized environment for program investigation of the computer processing organization and expands its field of application with additional research possibilities.

1. Introduction

In the general case, computer processing is a set of procedures performed on data streams. The procedures are implemented on the basis of separate algorithms, the unification of which is considered a complete algorithm of computer processing, realized at the macro level [1]. This processing forms the workload of the system, which is assessed by determining the probabilistic characteristics for the employment of the individual components.

Significant performance requirements are placed on real-time systems as well as distributed systems. When planning parallel and pseudo-parallel processes in them, the times for realization of the separate tasks must be taken into account and to be coordinated with the cyclic mode of the incoming information flow. An important criterion is the energy efficiency of the calculations in ensuring the timely delivery of services. This is the approach proposed in [2] for efficient loading in a distributed computing environment, combining the advantages of horizontal scaling and energy planning, while modelling with Matlab is applied to prove the efficiency.

When designing various computer systems, it is essential to pre-plan the calculations and the allocation of resources and to forecast the workload, which will lead to improved overall performance. For example, ref. [3] emphasizes that the development of computer and information technology, as well as Internet communications, places higher demands on the tools for process management and increasing the level of intelligence in their planning. To solve this problem, the article proposes a controller that maintains a knowledge base in the cloud and allows autonomous planning of the process. Another aspect of process-based workload planning and forecasting in distributed computing systems is presented in [4], highlighting the importance of improving service quality (QoS) and reducing energy consumption. The article provides an extensive overview of workload forecasting approaches, looking mainly at cloud services, and presents a taxonomy of workload forecasting schemes, summarizing their advantages and limitations. To achieve the required level of efficiency, a preliminary analytical study of the possibilities for defining a correct plan when performing multiple tasks is useful. Similar problems related to the energy efficiency of the actual load of the system relative to the capacity of the computing resources are discussed in [5], and a QoS-oriented mechanism for providing capacity using the queueing theory is proposed. The set goal of the developed mechanism is to predict the real demand for resource capacity without disturbing the level of service, as the experiments have shown a significant reduction in energy consumption. No less important is the determination of the optimal route in a communication environment, which reflects on the overall load of the system. This issue is discussed in [6], noting that the mechanisms for maintaining balanced, multi-band traffic and optimizing information flow are not sufficiently developed in the applied routing protocols.

Model investigation as a stage in the design of systems and processes is constantly proving its importance and usefulness. This is especially important both in the development of technologies for physical processes and in the design of complex computer processing systems. Confirmation of this is the discussion presented in [7] of the contribution of computer simulations to the design of a specific system (reactor) as a critical analysis of the possibility of integrating several tools into a common computational package. A procedure for model investigation in the development of computer systems and processes is presented in [1], emphasizing the need to choose an appropriate modelling method consistent with the goal.

The purpose of this article is to present an approach for automating the investigation of the processes of processing information units, arriving as a stochastic flow of service requests to processor devices. For this reason, a program module developed using the TryAPL2 system on the basis of preliminary formalization and mathematical modelling is presented. The choice of programming language (APL2) is made due to the supported parallelism and its good adequacy at describing processes. It is a high-level language, convenient for working with vectors and matrices and is suitable for analytical descriptions. Characteristic features are the specific alphabet, the maintenance of various data structures, the ability to work in dialog and program mode, a wide range of operations, incl. mathematical and possibility for laconic expression of complex transformations through composite operators. The order of operations in the expressions is from right to left. It is suitable for expressing the subordination between the different parts of the algorithm and allowing parallel execution of several operations. The TryAPL2 operating environment allows the creation of additional user workspaces from models designed as a separate function or as sequentially called functions. The organization of the work is done by system commands for management of the work session, storage and editing of copies of work spaces and transfer of data from one work space to another (manage APL file sharing). The environment also supports several system workspaces that can be used to create and run applications.

The present work should be considered a continuation of the research done in [1], and aims to present an addition to the developed set of modules for mathematical modelling of computer processing. For this reason, the organization of the model investigation is made on the basis of the procedure presented in [1], performing consistently the phases provided in it: goal defining; preliminary formalization of the object of study; mathematical modelling; program realization; conducting experiments; results analysis. The main contributions of the article can be summarized as follows. In the first part, a definition of the initial assumptions is made, which is used for the realization of the proposed mathematical formalization of the stochastic characteristics of the computational processes, and probabilistic characteristics are formulated that are related to the complexity of the tasks. The second part is a proposed program module for the organization of estimations, as well as the conducted experiments with summarization and analysis of their results.

The article is structured as follows. Section 2 discusses related work in the field. Section 3 presents the initial assumptions and formulates the mathematical formalization used for the realization of the program module for the estimation presented in Section 4, which discusses the obtained experimental results and assessments.

2. Brief Review of Related Works

2.1. Tasks Scheduling and Workload Evaluation

The planning of tasks in a computer system, performed by a system dispatcher, is a strictly formalized process related to the arrangement of the received program units and their allocation for execution to a free system resource. As the complexity of applications increases, so does the workload, which makes the process of planning more complex and leads to a greater loss of time, which requires a balancing of the workload and implementation of an effective task planning strategy [8]. The development of contemporary architectural solutions and technologies (multi-core and parallel architectures, cloud computing, intelligent computing environments, etc.) requires improvements in task planning strategies, especially when working in real time, as in [9] it is stated that traditional planning strategies do not lead to optimistic planning decisions and tests. The main problem is that in heterogeneous multicore platforms, a given task contains different types of peaks and loads, which requires coordination with the specific type of core.

As noted in [10], the control and coordination of all system resources and their provision of active tasks (applications) is a key function of the operating system and in particular its manager (system dispatcher). It is stated that in an autonomous computer system the processor is an important resource, which requires the application of effective techniques for planning its load based on an adequate assessment of performance. It should be added that the estimation of the level of the processor workload (as the main active node) depends on the incoming input flow of requests (service units), which has a stochastic character and can be represented analytically by an appropriate probability law with the corresponding functions of the density f(t) and of the distribution F(t). Usually, both continuous distributions are used, such as the uniform (rectangular) distribution, triangular distribution, normal (Gaussian) distribution, Student’s distribution, etc., and the discrete distributions (binomial (Bernoulli’s), geometric, etc.) As an initial statement, it is assumed that the incoming flow of service units is presented as a sequence of randomly generated events (Figure 1), and the workload is most often modelled by an analytical approximation of the probability distribution.

Figure 1. Fulfilment of a random event in time-interval T < t.

In general, in computer processing, random flows are formed by discrete service units, the simplest structure being a regular flow with constant intervals of incoming requests (τ = const) represented by a simple flow (stationary ordinary Poisson flow without consequences) defined by a Poisson distribution:

$$P_m\left(\tau \right)=\frac{a^m}{m!}{e}^{-a} \left(m=0,1,2,\dots \right)$$

It has been proven that for such a flow, the intervals τ_j between successive events (requests) are distributed exponentially with a distribution function F(t) = P(T<t) =1 − e^−λτ, expressing the probability of the random variable T to assume a value less than t (Figure 1). The stochastic parameters are λ = 1/τ (for t ≥ 0), mathematical expectation E[t] = μ = 1/λ = τ and variance V[t] = σ² = (1/λ)² = τ².

2.2. Approaches for Workload Planning and Study

Different approaches are used to study the behaviour of information flows, their proper planning and directing to processing units while ensuring optimal workload, but they are mainly based on the application of a mathematical apparatus with subsequent computer experiments. This is the approach adopted in [6] in the development of mathematical and software support for multi-parameter routing in a network environment with route optimization and efficient distribution of information flows. For the preliminary investigation, an analytical mathematical model based on the theory of Markov processes has been developed and algorithms for solving various problems in modelling routing processes have been proposed. Another approach based on simulation modelling is applied in [11] by developing a simulation model to estimate the probability parameters describing the time duration of a project and the probability of realization within a given time interval. It is stated that experiments confirm the increased accuracy of the proposed approach compared to the traditional method.

It is obvious that the applied approaches to process planning are essential for increasing the productivity and in this regard in [10] are discussed options for eliminating identified weaknesses in the strategies for the implementation of processor planning techniques and in the criteria used, which evaluate how strategies are analysed and used to evaluate effectiveness. The problem of planning and balancing the load of system resources is quite well discussed, and recently considerable attention has been paid to cloud computing. With this in mind, ref. [8] proposed an effective planning strategy that uses a hypergraph to formalize the workflow between geographically distributed data centres. A task scheduling algorithm has been designed to reduce completion time and reduce power consumption, with optimization done according to Dijkstra’s algorithm for the shortest path in the graph. The conducted experiments confirmed the balance of the load of the computing nodes while minimizing the average time for performing the tasks and the total energy consumption of the system. Another investigation is related to the problem of maximizing the expected number of tasks performed on a cloud platform with limited implementation time [12]. It was stated above that the input streams of tasks, as well as the times for their execution, are subject to different probability distribution laws. The main issue discussed is how many processor nodes to activate and what the strategy is for interrupting the task at the end. To solve the problem, an asymptotically optimal strategy with discrete probability distributions and no time limit is proposed. An additional extension of the developed strategy was made with the introduction of continuous probability distributions, and simulation experiments were performed to confirm its effectiveness.

Another area of scheduling is maintaining a high level of parallelism, and as noted above, the problem is discussed in [9], where a directed acyclic graph (DAG) is used to present and study real-time planning. A new algorithm is proposed, which assigns to each node of the graph (which describes a parallel environment) a variable criticality depending on the node load, which determines the specific level of urgency in planning for implementation. The authors have also proposed a new interpretation (presentation) of the worst-case response time (WCRT), and experiments have confirmed higher accuracy and efficiency by about 20%. Another proposal to solve the problem of minimizing the time for processing information in a system was made in [13], which is related to the general management and monitoring of information. The idea is based on the formation of groups of servers and searching for information in some of them on the basis of general control and management of servers. A statistical modelling method was applied during the development, which showed that the applied grouping can significantly reduce the time parameters of the search.

2.3. Application of the Queuing Theory in Workload Study

For a more complete consideration of the discussed problem, it should be pointed out that a suitable approach in a model investigation of workload is the queueing theory. An extensive study on the topic was made in [14], where three important tasks are determined: ✓ formulating a realistic assessment of the allocation of resources in a given service environment; ✓ efficient distribution of tasks to the service nodes to minimize the average time for realization of the process; ✓ automatic allocation of the computing resources themselves depending on the actual incoming workflows while reducing the total costs. To address these issues, novel scheduling policies for workloads of workflows and investigations into the applicability of relevant state-of-the-art policies to the online scenario have been proposed, and various simulation and real experiments have been conducted for the experimental assessment of their correctness. The application of queue theory in the mathematical modelling of computing systems is also the subject of [15], the aim of which is the study of computer systems with virtualization. The investigation used a closed queuing network and simple models for the analysis of various defined computer structures. The obtained experimental results confirmed the reliability and flexibility of the tools used in optimizing the computer structures of the IT infrastructure.

Another study, presented in [16], focuses on contemporary problems with cloud services, looking at queue theory as a tool to study the problem of waiting lines. The aim is to assess the speed of service and the time for timely response. To solve the task, an M/M/k queue with FIFO queue discipline for load balancing is proposed with exponential distribution for calculation queueing rates and Poisson distribution for calculation distribution lines. An analysis of the effects of load change in high-performance computing in web services in a cloud environment by applying queue modelling was performed in [17]. For organization of the simulation and modelling of the algorithms for automatic scaling, a specialized software environment for performance evaluation is used. With this in mind, ref. [18] employed the queueing theory to model each individual node as an independent and autonomous system of queues. The object of the study are heterogeneous data centres, with the aim of balancing workload and estimating costs and productivity (average task waiting time, average response time and productivity). Validation of the proposed model for task planning is done through simulation, and the experimental results have proven its high efficiency and reliability.

Queueing theory has also been used in research to solve the problems of reducing energy consumption, for example in QoS calculations, as indicated [5], and also in [19], applying this theory in the study of energy efficiency and minimizing energy consumption. In the second case, stochastic traffic models are used in workload analysis and power control, and an energy-efficient vehicle edge computing framework is proposed for in-vehicle user equipment with limited battery capacity.

3. Initial Assumptions and Mathematical Formalization

3.1. Initial Assumptions

The subject of discussion is a set of procedures (algorithms, tasks) that must be planned for execution in a computer environment. It was pointed out that the discrete graph theory could be applied as an initial description by drawing up a generalized graph scheme of algorithm (GSA), designed to load the processor as the main service node. This problem is discussed in [1], where the possibility of partial ordering over the set of tasks (which are characterized by absolute and relative priority) is considered. This allows us to define the so-called “complete algorithm”, which can be described logically by the individual algorithms A_i and the conditions for their activation at a specific input information flow. Such a functional description allows us to construct the graph scheme based on the matrix of connections {c_ij: A_i → A_j} between all pairs of individual algorithms. The formalization allows us to conduct a preliminary study through a chosen approach—stochastic (in probably differentiated connections) or determined (the matrix of connections is Boolean). Typically, in centralized systems, the queuing of tasks (numbering) and its maintenance is performed by the supervisor for global management of the usability of the system resource. The directing of the tasks to the free processor devices is performed by the dispatcher on the basis of the set rules (planning strategy) in the computer system and the defined priorities when arranging the tasks. In decentralized systems, the functions of a dispatcher are taken over by a supervisor, who may be part of the queue itself as an object with the highest priority.

In the case of discrete analytical formalization, the basic set of individual tasks (algorithms) for processing in a computer environment could be described by the system of equations:

$$A_j=\left\{{{\displaystyle \sum }}_{i=1}^n{a}_{ij}·A_i\right\}; j=1,2,\dots ,n.$$

In such a graph structure of discrete nodes (components), the transition from node A_i to the next node A_j in the graph depends on the coefficients a_ij: A_i → A_j, which in the general case have a probabilistic character. In this sense, each planned implementation is a realization of a predefined path {A_i → A_j} in GSA. The task of the system dispatcher is to optimize the possible paths in the set of tasks from the first task started to the last scheduled for execution so as to ensure minimum load of the processor unit at maximum performance. Two basic initial assumptions have been made for the realization of the task.

• If a fixed sequence S(A) = <A₁, …, A_i, …, A_m> is formed, consisting of m tasks with random execution time T(A_i) for each of them, it can be allowed that the total time T(S) for the realization of this sequence of tasks has a normal distribution with average time E[T(S)] = ΣE[T(A_i)] and variance D[T(S)] = ΣD[T(A_i)].
• The distribution of the earliest time to start a task A_j, which is next after the realization of the sequence S(A), is equated to the moment t_m = t(A_m) of the completion of the task A_m, which is last in S(A).

An example situation describing the statement above is shown in Figure 2. The execution of task A_j starts at time t_m. The total execution time T(A_j) is a random variable and depends on the specific conditions for the implementation of the current calculation (data, processes, management, etc.). In this sense, the mathematical expectation for the moment time t(A_j) = t_j for the completion of the task A_j (formation of the final result) is also a random variable for which the limit values can be calculated—the earliest admissible moment $(t_j^{\prime })$ and the latest allowable moment $(t_j^{″})$. Since the start of task A_j is related to the random moment to complete the previous task, the above reasoning also applies to the initial moment of execution of A_j (assessment limits can also be set).

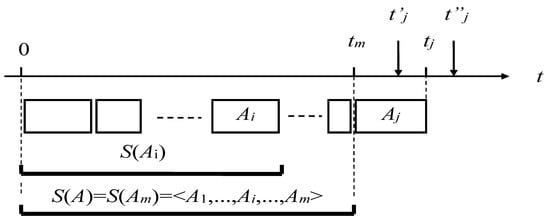
Figure 2. Example sequence of execution tasks.

3.2. Mathematical Formalization

When defining the mathematical model, a formal presentation of the following stochastic characteristics of the computational processes was performed:

• The mathematical expectation of the time-moment t_j for completing task A_j is defined as the sum of the mathematical expectations E[T(A_i)] of the times for solving (performing) the tasks in the previous sequence S(A) = < A₁, …, A_m > estimated by the longest path A₁ → A_m → A_j in the sequence if there are several equivalent ones.
• The variance D[T(A_j)] is determined analogously to the sum D[T(A₁)] + … + D[T(A_m)].
• Planning the deadlines for completion of task A_j:
  (a) the earliest allowable completion time $(t_j^{\prime })$ is estimated by the variance and the standard deviation:

  $$\begin{array}{c}D\left[t_j^{\prime }\right]=D\left[t_m\right]+D\left[t_j\right];\\ \sigma \left[t_j^{\prime }\right]=\sqrt{\left\{D\left[t_j^{\prime }\right]\right\}};\end{array}$$
  (b) the latest allowable completion time $(t_j^{″})$ is estimated by the mathematical expectation:

  $$E\left[t_j^{″}\right]=E\left[t^{″}\left(A_F\right)\right]-E\left[t\left(S_{j\to F}\right)\right],$$

  where: A_F—final task for the specific calculation; S_j→F—the longest path in the sequence <A_j, …, A_F>. The variance of $(t_j^{″})$ is estimated analogously by:

  $$D\left[t_j^{″}\right]=D\left[t^{″}\left(A_F\right)\right]-D\left[t\left(S_{j\to F}\right)\right].$$
• The probability of completing task A_j in a given time. The probability P(t_j) for completion of the calculation of task A_j is considered no later than the moment $(t_j^{*})$:

  $$P\left(t_j\right)\le t_j^{*}={{\displaystyle \int }}_{-\infty }^{t^{*}}{\phi }_j\left(x\right)·dx,$$

  where φ_j(x) is the density of the probability distribution of the random variable t_j. If φ_j(x) is a normal distribution law with parameter μ = E[t_j] and variance σ² = D[t_j], then:

  $${\phi }_j\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}·e^{-\left[\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right]}.$$

For the analytical study of the stochastic processes in the structure, it is necessary to know some estimates of the probabilistic characteristics of the individual tasks. For example, if the labor intensity τ(A_j) of the task A_j ∈ S(A) is known, then the time t(A_j) will depend on the speed B of the computer system, i.e., E[t(A_j)] = E[τ(A_j)/B], where E[x] is the mathematical expectation of the random variable x. A similar relationship exists for the variance D[x].

Therefore, if the complexity of the tasks is known, it is possible to determine the probabilistic estimates of both the random time-moments t(A_j) and the paths formed in the graph structure representing the computer processing. The definition of these estimates is as follows:

(a) an estimate of the total labor intensity of the implementation of a given S_i path in the information structure S(A):

$$\begin{array}{c}E\left[t\left(S_i\right)\right]={{\displaystyle \sum }}_{A_j\in S_i}E\left[\tau \left(A_j\right)\right];\\ D\left[t\left(S_i\right)\right]={{\displaystyle \sum }}_{A_j\in S_i}D\left[\tau \left(A_j\right)\right]={\sigma }^2\left[\tau \left(S_i\right)\right];\end{array}$$

(b) an assessment of the realization of a certain task included in a given path S_i ∈ S(A) of the structure:

$$\begin{array}{c}E\left[t\left(S_i\right)\right]=\frac{E\left[\tau \left(S_i\right)\right]}{B};\\ D\left[t\left(S_i\right)\right]=\frac{D\left[\tau \left(S_i\right)\right]}{B}=\frac{{\sigma }^2\left[\tau \left(S_i\right)\right]}{B};\end{array}$$

(c) an estimation of the correlation relationship for the pairs <S_i, S_j>:

$$r_{ij}=\frac{\left\{{{\displaystyle \sum }}_{k=1}^{n}D\left[t\left(A_k^{ij}\right)\right]\right\}}{\left\{\sigma \left[t\left(S_i\right)·\sigma \left[t\left(S_j\right)\right]\right]\right\}},$$

where $D\left[t\left(A_k^{ij}\right)\right]$ is the time variance for solving the problem A_k belonging to both paths S_i and S_j simultaneously.

4. Program Realization and Experimental Results

4.1. Program Realization

To conduct experiments in the analytical study of the stochastic time parameters of computer processing, a program module (function ESTIMATES) was created in the language environment APL2. As an input argument, it uses the matrix of determined paths SA, which is obtained after the execution of another APL2-funcion named PATHS, presented in [1] (see Figure 3 for program code and a sample experiment). As stated in [1], this function is “for reachability evaluation and determining all paths in the investigated algorithmic structure with argument matrix L”.

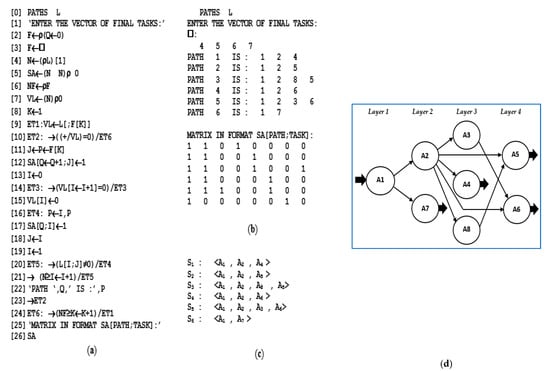
Figure 3. Program function PATHS—(a) program code; (b) execution; (c) defined paths; (d) investigated ordered graph scheme of algorithm [1].

The program code of the module ESTIMATE is shown in Figure 4. To implement an experiment with a program module, a preliminary definition (formation) of the matrix SA is required, which is a basic argument. Interactive determination of the additional operating parameters is provided—numerical estimates for the parameters E[τ(A_j)], D[τ(A_j)] and B.

Figure 4. Program function ‘ESTIMATES’.

The following assumptions and relative estimates were accepted in the organization of the experiments for processing parameters investigation with the module ‘ESTIMATES’:

(a) Numerical estimations for the stochastic characteristics of the task’s complexity (×10^k):

Task→	A1	A2	A3	A4	A5	A6	A7	A8
E[τ(Aj)]	0.5	1.0	0.4	0.2	0.4	0.3	2.0	0.4
D[τ(Aj)]	0.05	0.1	0.04	0.02	0.04	0.03	0.2	0.04

(b) Value for the speed of computer system (processing) B = 4.10^k [operations per second].

4.2. Experimental Result and Assessments

A summary of some experimental results obtained by execution of the program module ‘ESTIMATES’ for investigation of the graph structure from Figure 3d are presented below. For example, a graphical representation of the experimental estimates for mathematical expectation (E), variance (D) and standard deviation (sigma) is shown in Figure 5 and other estimates for correlation between determined paths in the structure are presented in Table 1.

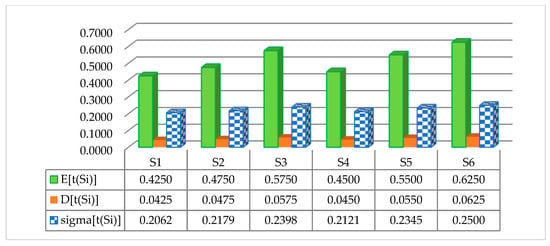
Figure 5. Results for the stochastic parameters’ mathematical expectation (E), variance (D) and standard deviation (sigma).

Table 1. Experimental estimates of the correlation between defined pathways.

	S1	S2	S3	S4	S5	S6
S1	r11 = 1	0.834622	0.758582	0.857492	0.775631	0.242535
S2		r22 = 1	0.908893	0.811107	0.733673	0.229415
S3			r33 = 1	0.737209	0.666831	0.208514
S4				r44 = 1	0.904534	0.235702
S5					r55 = 1	0.213200
S6						r66 = 1

The obtained program results confirm the estimates obtained by analytical calculation (accuracy depends on rounding). For example, the correlation coefficient for the pair S₁:<A₁ A₂ A₄> and S₂:<A₁ A₂ A₅> is calculated analytically as follows:

$$r_{12}=\frac{D[t(A_1)]+D[t(A_2)]}{\sigma [t(S_1)]\times \sigma [t(S_2)]}=\frac{(0.05/4)+(0.1/4)}{0.206\times 0.218}=\frac{0.0375}{0.0449}\approx 0.835.$$

On the other hand, calculated experimental execution results (Table 1) show that the maximum correlation exists for the equivalent pathways (for example r₂₃ and r₄₅).

4.3. Application in Parallel Processes Dispatching

Ensuring optimal performance in parallel processing of processes is associated with solving two mutually opposite tasks: (a) for the processing of a specific set of program units to determine the minimum composition of a parallel computing environment; (b) for a fixed composition of the computing environment to define an optimal plan for processing a given set of tasks in minimum time. The first task is oriented towards homogeneous architectural structures, while the second allows variable composition and the possibility of both static and dynamic parallelization. The application of the program module ‘ESTIMATES’ is aimed mainly at solving the second task, allowing us to conduct a preliminary study of the processes and to determine their characteristics, affecting the dispatch plan.

The dispatch plan is a segment function D(t) = {d₁(t), …, d_m(t)}, defined in the interval (0, τ) and accepting values from the set A = {A₁, …, A_n}, which is a basic GSA component, defined as a directed graph G = G(A, L) of the information–logical connections l_ij ∈ L for pairs of nodes (planning processes) <A_i, A_j> (i, j = 1 ÷ n)—it is possible to represent the set A as a set of indices {1, 2, …, n}. Thus, the notation d_i(t) = j (1 ≤ i ≤ m; 1 ≤ j ≤ n) reflects the occupancy of the resource S_i at the moment t with the execution of the process A_j (S = {S₁, …, S_m} e set of the system resource). Strictly connected sections in G, forming a road of type A_i → A_j, are not allowed. The relation of information dependence is transitive, i.e., if A_j depends on A_i and A_q depends on A_j, then process A_q will depend on A_i. The latter obliges the process A_i to be executed before A_q. The transitive dependence in G will be represented by the presence of the pass(A_i → A_j). The possibility of interrupting the execution of a process requires further clarification. If we assume that an interruption is not allowed, then the occupancy of the resource S_i on the execution of A_j is t_ij ∈ T*. If T = {t₁, …, t_n} is a vector of the execution times of the processes A_i (i = 1 ÷ n), then in the case of heterogeneous system resources a given process A_i can occupy several devices in succession for different times {t_i1, t_i2, …, t_ik}. Then, t_i = Σt_ik, and the vector T can be modified in the matrix T* = {t_ij} with n = |A| rows and m = |S| columns.

Based on the formalization made in the previous section, the process planning procedure can be presented as P = <S, A, G, T, F>, where in addition to the elements presented above, criterion F is included to define the type of planning strategy (for example, minimization of the total time for implementation of the global algorithm—FT, minimization of the average time for execution of a single process, minimization of resource usage, maximum workload of processors, minimization of CPU downtime, etc.). In this formulation, a plan for the realization of the processes from Figure 3d can be defined in the following way P = <{1,2,3}, {1,2,3,4,5,6,7}, G, {4,2,2,5,4,8,5}, FT>, where |S| = 3, |A| = 7, and FT is the chosen planning strategy. It is formed on the basis of determining all directed paths presented in Figure 3c in the ordered GSA after the applied module of Figure 3a. Four layers are defined, forming information-independent subsets of nodes with corresponding weights t_i (i = 1 ÷ 7): {1⁽⁴⁾; 2⁽²⁾}, {3⁽²⁾}, {4⁽⁵⁾; 5⁽⁴⁾, 6⁽⁸⁾}, {7⁽⁵⁾}, as the realization of the plan in environment S = {S₁, S₂, S₃} is shown in Figure 6 [1]. Estimates of the processes obtained after the implementation of the module ‘ESTIMATE’ were used in the formation of the dispatching plan. The maximum environment for the implementation of the plan is determined by the maximum power (number of tasks) of a layer in the ordered GSA. In this case, three processors are used, but with criterion F = “maximum workload of processors” it would be more appropriate to implement the plan at |S| = 2.

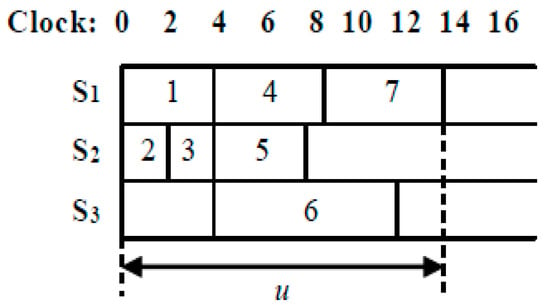
Figure 6. Plan for implementation of the processes from Figure 3d in a system with three processors.

5. Discussion and Conclusions

The organization of the planning of parallel processes is directly related to the abstract description of the processes themselves and formalization of the hierarchical structure of the algorithms generating them, as well as to the correct description and definition of the optimal parallel form for realization. From the existing possibilities for deterministic research (logical and matrix schemes of algorithms, Post’s algorithmic system, normal Markov’s algorithms, d-maps, Petri nets, generalized networks, etc.) for solving the task set in the article, the formalization of the processes by ordered graph structure is selected.

The article discusses a partial problem related to investigation of time parameters and stochastic characteristics of processing in a generalized graph-structure of algorithm (GSA), which has been used as an input element (input data) for the implementation of the module ‘PATH’ and the obtained result SA is used as an input data for the module ‘ESTIMATES’. It is accepted that the currently active program (information) units can be represented as components (elements) of this directed common graph structure GSA. In this sense, the study presented here should be seen as a continuation of the investigation published in [1]. The general task is to form a unified program space of modules, which will allow the study of various problems in the processing of computer environments at the macro and micro level. Reference [20] can be considered an extension of the discussed problem, which discusses issues with the model investigation of basic structural components of the computer environment. In particular, this article discusses some problems with the evaluation of parameters of process realization aimed at forming an adequate and optimal plan for their implementation.

The proposed approach allows automation of the evaluation of certain characteristics of computer processing (mathematical expectation E[T(A_i)] and variance D[T(A_j)] of time for task realization, deadlines for task completion, probability characteristics, etc.), presented as a sequence of relatively independent processes, but performed jointly in a common environment, which requires competition between them in borrowing resources and proper advance planning of the task implementation. The main feature is that regardless of the discrete structure of the computer environment, the processes in it, as well as the incoming flow of service tasks, are probabilistic. This requires investigation and analysis of the stochastic parameters of these processes, and such an attempt is made in this article.

The object of this analysis are the parameters of the complexity of the tasks (which affects overall performance) and the probabilities for the realization of individual activations of sequences of program units—estimates E (mathematical expectation) and D (variance) of the total intensity of the implementation of a given S_i path in the information structure S(A); the assessment E and D of the realization of a certain task included in a given path S_i ∈ S(A); and the standard deviation σ and estimation of the correlation relationship r_ij for the pairs <S_i, S_j>. Obtained experimental results are summarized in Figure 5 and Table 1. Assessments in this research are obtained by using proposed module ‘ESTIMATES’, which is developed in program spice TryAPL2 and language APL2. The choice of this environment is determined by the high possibilities for parallel calculations and work with matrices.

An application of a developed environment of program modules, including ‘ESTIMATES’, in the formation of a plan for the implementation of homogeneous processes {A_i} in the realization of the strategy “minimization of the total time for the implementation of the global algorithm G(A, L)” in a homogeneous system of computational resources {S_j}. The study was conducted on the basis of some assumptions that allow for the unification of the process. It is stated that the implementation of another planning strategy may lead to another outcome of a specific implementation.

The object of future work is the study of planning in inhomogeneous processes with different execution times t(A_i), which will allow us to expand the scope of applicability of the developed software space. For this purpose, it is necessary to set the scalar weights of the nodes when describing the initial GSA, which will not change the work of the developed modules from the program space—‘GSA’ (for determining the ordered scheme), ‘PATH’ (for forming the complete set of paths) and ‘ESTIMATES’ (for calculating assessments). The only difference will be obtained by defining the length of the roads (the sum of the weights) and calculating the critical time. On the other hand, when generating an optimal plan, it is necessary to estimate the weights of the processes in each individual layer.