Functional Partial Fuzzy Relations

Abstract

We study fuzzy relations that satisfy the functionality property and that their membership functions can be partial functions. Such fuzzy relations are called partial fuzzy relations, and the variable-domain fuzzy set theory is a framework that provides powerful tools for handling these objects. There, the special operations based on connectives and quantifiers of a partial fuzzy logic are in use. The undefined degrees of membership are carried via those special operations. Furthermore, we show that a suitable combination of these operations leads to a meaningful definition of the functionality property, and we investigate its basic characteristics.

1. Introduction

An implicative model of fuzzy IF–THEN rules is closely related to the functionality property (e.g., [1]). In practice, we can face the problem of merging two rule bases with different universes. A practical solution would consist in unifying the universes into a common one and extending the membership functions of particular fuzzy sets by filling in an appropriately chosen membership degree.

However, this solution does not necessarily lead to satisfactory behavior. Consider the following example: an automatic drug dispenser is joined with a temperature sensor, which operates over the temperature range from 0 to 100 °C, while its rule-base:

If the patient’s temperature is high, then the amount of drugs is medium.

If the patient’s temperature is very high, then the amount of drugs is high.

is designed for temperature values from 35 to 42 °C, see Figure 1a, and the amount of drugs is from 0 to 10 mL, see Figure 1b. Let us interpret the rules from the above rule-base in Mamdani’s style using the $(max,min)$ operators together with the center of gravity as a defuzzification method. If the input to this rule-base is 39.5 °C, then the drugs’ output amount is something around 8 mL and when the input is 40.5 °C, the output is approximately 9 mL.

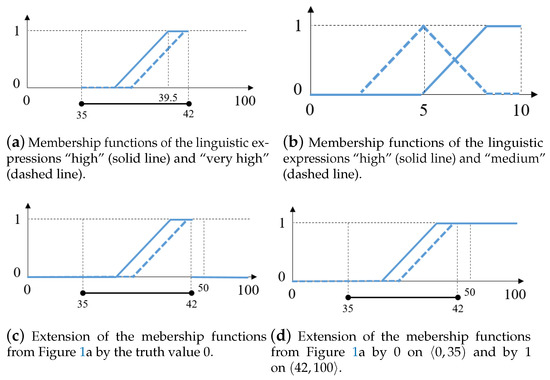
Figure 1. An illustration of membership function extensions to a wider domain using specially chosen degrees of membership.

Suppose that the interpretation of the rules is extended so as to operate on the whole scale of temperatures by setting the degree of membership to 0 for the inputs from $⟨0,100⟩\backslash ⟨35,42⟩$ as is visualized in Figure 1c. What happens if the input is 50 °C? Intuitively, this input value means there is something wrong with the measuring device or the patient; for example, they can both be exposed to an additional source of heat. In this case, the patient receives a dose of 5 mL (since defuzzification is performed on a fuzzy set with zero membership function everywhere) even though they may not have any fever at all. It gets even worse if we insert a value of 1 on $(42,100⟩$ (as shown in Figure 1d). Then the patient receives the maximum dose of drugs. Instead, the system should output an error code due to the value being out of the range.

The aforementioned situation cannot be remedied by changing the defuzzification settings, choosing a different model, etc. So far, standard fuzzy modeling tools do not allow to solve a problem such as having an input outside the domain of a fuzzy inference system internally. Such counterexamples can be found for any value from the truth scale, so none should be assigned. We can imagine many analogous real-world situations where it is necessary to encode such an error and process it further, e.g., in a complicated hierarchical rule-based system.

In particular, approximate reasoning with fuzzy IF–THEN rules often involves BK products and other generalized compositions of fuzzy relations [2,3]. As shown by Běhounek and Daňková [4] in Example 2.4, BK products produce unwanted artifacts caused by filling in membership values. In these cases, variable-domain fuzzy set theory ($\mathrm{VFST}$), developed by Běhounek and Daňková [4,5], is applicable. It formalizes the notion of partial fuzzy sets and provides basic operations for handling them. In this framework, various ways of merging fuzzy IF–THEN rules from two different domains are definable, which avoid artifacts and behave as expected.

$\mathrm{VFST}$ is based on the partial fuzzy logic introduced in [6], i.e., an “undefined-friendly” expansion of a broad class of known propositional fuzzy logics. Therein, undefined membership values are mapped to a dummy value ∗ that extends the original truth scale L (where $\ast \notin L$) and the connectives of the background fuzzy logic is extended to operate on $L\cup \{\ast \}$. Different understandings of undefined truth values lead to different behaviors of ∗, which give rise to several families of propositional connectives [6]. Note that partial fuzzy logic can only capture undefinedness that behaves functionally. Unknownness or uncertainties do not behave functionally, and therefore partial fuzzy logic does not handle these phenomena. Also note that partial fuzzy logic and $\mathrm{VFST}$ are only designed to accommodate undefined truth or membership degrees, and not undefined elements of the universe of discourse. The latter are treated in the more complex frameworks of partial fuzzy type theory [7] and free fuzzy logic [8]. Analogously to the connectives, we can extend quantifiers [5]. There are several applications of this approach, for example [9,10,11].

In this paper, we use two main families of connectives and quantifiers (for other families of connectives, consult the paper by [6]):

• The Bochvar-style family, which treats ∗ as the absorbing element;
• The Sobociński-style family, which treats ∗ as the neutral element.

It turns out that these families are rich enough to describe intuitive behaviors of basic partial fuzzy relational and set operations and their properties [12] and consequently also functional partial fuzzy relations. Our notion of functionality (Definition 12 below) stems from the functionality property of fuzzy relations studied by many authors [1,13,14,15,16]. A generalization thereof is proposed in agreement with our intuitive expectations, namely, that only defined membership values are important for checking the functionality property and undefined parts are ignored. We also recall the notion of functionality for partial fuzzy relations given in [12] and compare them. The next issue addressed in the area of functional partial fuzzy relations is the study of functionality transmission under set operations and relational compositions. It should be stressed that this paper doesnot attempt to provide a satisfactory model for a fuzzified notion of partial function. Rather, it studies the conditions under which partial fuzzy relations satisfy the property of fuzzy functionality. As mentioned above, the property is relevant, e.g., in implicative fuzzy IF–THEN rules, and these may at times be subject to partiality (esp. when the fuzzy rules have different domains of definition). Moreover, we would like to promote $\mathrm{VFST}$ by showing the easy graspability of this theoretical tool, especially via the presented proofs.

This paper extends the conference paper [12], which contains a few preliminary results without proofs. It is organized as follows: Section 2 and Section 3 briefly summarize basic notions of $\mathrm{VFST}$, most of which have been introduced in [4,17]. The definition of partial functionality together with its basic properties is presented in Section 4. Each notion is discussed in detail and equipped with examples that should help the reader with understanding. Concluding remarks are presented in Section 5.

2. Partial Fuzzy Sets

We recall the notion of partial fuzzy sets—i.e., fuzzy sets that can have undefined membership degrees, introduced in [4].

Definition 1.

Let U be a universe of discourse, $X_A\subseteq U$, and ${\mu }_A:X_A\to L$ be a membership function from $X_A$ to a suitable structure L of membership degrees.

A partial fuzzy set is a pair $A=(X_A,{\mu }_A)$. This fact is denoted by $A⫇X_A$ and $X_A$ called the crisp domain of A.

2.1. The Representation

The following representation of partial fuzzy sets taken from [6] provides a transfer of a fuzzy sets’ membership function that is a partial function to L to a total function that evaluates to the extended scale $L^{\ast }=L\cup \{\ast \}$. This technical trick allows the unification of fuzzy sets with various domains to a common universe U without loss of information on their domains.

Definition 2.

Let $L\ne \varnothing$, $\ast \notin L$, and $L^{*}=L\cup \{\ast \}$. We shall say that a partial fuzzy set $A=(X_A,{\mu }_A)$ in a universe $U\supseteq X_A$ is represented by an $L^{*}$-valued membership function $A^{*}$ on X, defined for each $x\in U$ as:

$$A^{*}\left(x\right)=\left\{\begin{array}{cc}{\mu }_A\left(x\right)\hfill & ifx\in X_A;\hfill \\ \ast \hfill & ifx\in U \backslash X_A.\hfill \end{array}\right.$$

(1)

The original $A⫇X_A$ (Figure 2a) can be recovered from $A^{*}$ (Figure 2b) by setting $X_A=\{x\in U\mid A^{*}\left(x\right)\ne \ast \}$ and restricting $A^{*}$ to $X_A$ This gives us a bijection between the set of all partial fuzzy sets on the universe $U$ and the set of all $L^{*}$-valued functions on $U$.

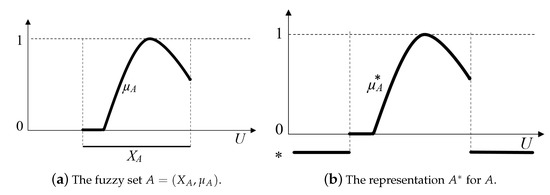
Figure 2. Representation of the fuzzy set $A=(X_A,{\mu }_A)$ on a universe $U\supseteq X_A$.

2.2. Operations with Undefined Degrees

In what follows, $\mathcal{L}$ denotes a complete residuated lattice of the form

$$\mathcal{L}=⟨L,\vee ,\wedge ,\odot ,\Rightarrow ,0,1⟩,$$

(2)

which is an algebra where:

• $⟨L,\vee ,\wedge ,0,1⟩$ is a complete lattice with the lattice order ≤.
• $⟨L,\odot ,1⟩$ is an ordered commutative monoid w.r.t. ≤.
• ⊙ and ⇒ fulfill an adjointness property, i.e., for each $x,y,z\in L$:

  $$x\odot y\le z\mathrm{iff}x\le y\Rightarrow z.$$

We call the operations ⊙ product and ⇒ residuum.

Notation 1.

To reduce the number of parentheses used in mathematical expressions we set that ⊙ has the highest priority and ⇒ the lowest priority out of all operations that are at disposal.

Recall the definitions of extended operations on $L^{*}$ from [6].

Definition 3.

The Bochvar operation $c_{\mathrm{B}}\in \{{\wedge }_{\mathrm{B}},{\vee }_{\mathrm{B}},{\odot }_{\mathrm{B}},{\Rightarrow }_{\mathrm{B}}\}$, $c_{\mathrm{B}}:L^{*}\times L^{*}\to L^{*}$ is interpreted by the following truth table for all binary operations c of $\mathcal{L}$ (and similarly for higher and lower arities):

$$\begin{array}{ccc}{c}_{\mathrm{B}}& \beta & \ast \\ \alpha & \alpha c\beta & \ast \\ \ast & \ast & \ast \end{array}$$

Definition 4.

The Sobociński operation $c_{\mathrm{S}}\in \{{\wedge }_{\mathrm{S}},{\vee }_{\mathrm{S}},{\odot }_{\mathrm{S}}\}$, $c_{\mathrm{S}}:L^{*}\times L^{*}\to L^{*}$, and the Sobociński implication ${\Rightarrow }_{\mathrm{S}}:L^{*}\times L^{*}\to L^{*}$, which treats ∗ as the neutral element, are defined by:

$$\begin{array}{ccc}{c}_{\mathrm{S}}& \beta & \ast \\ \alpha & \alpha c\beta & \alpha \\ \ast & \beta & \ast \end{array}\begin{array}{ccc}{\Rightarrow }_{\mathrm{S}}& \beta & \ast \\ \alpha & \alpha \Rightarrow \beta & \alpha \Rightarrow 0\\ \ast & \beta & \ast \end{array}$$

The Bochvar-style connectives treat * as a fatal error, whereas the Sobociński-style connectives ignore undefined inputs as long as possible. Note that the names Bochvar and Sobociński in the above definitions are due to their sameness with the three-valued case, see [18]. We recall the following definition from [17].

Definition 5.

Let ${\alpha }_i\in L^{*}$ for each $i\in I$ (where I is an arbitrary index set). Then we define:

• The Bochvar infimum ${\displaystyle \underset{i\in I}{{\bigwedge }_{\mathrm{B}}}{\alpha }_i=\left\{\begin{array}{cc}{\displaystyle \underset{i\in I}{inf}{\alpha }_i}\hfill & if{\alpha }_i\ne \ast foreachi\in I;\hfill \\ \ast \hfill & otherwise.\hfill \end{array}\right.}$
• The Bochvar supremum ${\displaystyle \underset{i\in I}{{\bigvee }_{\mathrm{B}}}{\alpha }_i=\left\{\begin{array}{cc}{\displaystyle \underset{i\in I}{sup}{\alpha }_i}\hfill & if{\alpha }_i\ne \ast foreachi\in I;\hfill \\ \ast \hfill & otherwise.\hfill \end{array}\right.}$
• The Sobociński infimum ${\displaystyle \underset{i\in I}{{\bigwedge }_{\mathrm{S}}}{\alpha }_i=\left\{\begin{array}{cc}{\displaystyle \underset{\begin{array}{c}i\in I\\ {\alpha }_i\ne \ast \end{array}}{inf}{\alpha }_i}\hfill & if{\alpha }_i\ne \ast forsomei\in I;\hfill \\ \ast \hfill & otherwise.\hfill \end{array}\right.}$
• The Sobociński supremum ${\displaystyle \underset{i\in I}{{\bigvee }_{\mathrm{S}}}{\alpha }_i=\left\{\begin{array}{cc}{\displaystyle \underset{\begin{array}{c}i\in I\\ {\alpha }_i\ne \ast \end{array}}{sup}{\alpha }_i}\hfill & if{\alpha }_i\ne \ast forsomei\in I;\hfill \\ \ast \hfill & otherwise.\hfill \end{array}\right.}$

If all inputs are defined, then the above operators yield the usual supremum and infimum. Otherwise, ${\bigwedge }_{\mathrm{B}},{\bigvee }_{\mathrm{B}}$ return ∗ provided that at least one input is undefined, while ${\bigwedge }_{\mathrm{S}},{\bigvee }_{\mathrm{S}}$ ignore ∗ and only return ∗ if all of their inputs are undefined.

Let us identify the lattice order ≤ and the identity = on L with their $\{0,1\}$-valued characteristic functions. Then, we define the following crisp binary relations on $L^{*}$ [12]:

$$\begin{array}{ccc}{\le }_{*}& \beta & \ast \\ \alpha & \alpha \le \beta & 0\\ \ast & 1& 1\end{array}\begin{array}{ccc}{\le }^{*}& \beta & \ast \\ \alpha & \alpha \le \beta & 1\\ \ast & 0& 1\end{array}\begin{array}{ccc}=& \beta & \ast \\ \alpha & \alpha =\beta & 0\\ \ast & 0& 1\end{array}\begin{array}{ccc}{=}_{\mathrm{sub}}& \beta & \ast \\ \alpha & \alpha =\beta & 0\\ \ast & 1& 1\end{array}$$

for $\alpha ,\beta \ne \ast$. We call

$$\begin{array}{cc}{\le }_{*}& \ast -\mathrm{bottom}\mathrm{ordering};\hfill \\ {\le }^{*}& \ast -\mathrm{top}\mathrm{ordering};\hfill \\ =& \mathrm{identity}\mathrm{on}{L}^{*};\hfill \\ {=}_{\mathrm{sub}}& \mathrm{subidentity}.\hfill \end{array}$$

The ∗-bottom ordering treats ∗ as the minimal element of L while the ∗-top ordering is its dual, i.e., ∗ is the maximal element w.r.t. ${\le }^{*}$. Moreover, ${\bigwedge }_{\mathrm{S}},{\bigvee }_{\mathrm{B}}$ are supremum and infimum, respectively, w.r.t. the ∗-top ordering and dually, ${\bigwedge }_{\mathrm{B}},{\bigvee }_{\mathrm{S}}$ play the same role w.r.t. the ∗-bottom ordering. Moreover, = is the identity on $L^{*}$ while therein ${=}_{\mathrm{sub}}$ is only the partial ordering.

The Bochvar-style extension as well as the Sobociński-style extension of ⇒ and ⊙ fulfill the residuation identity:

$$\begin{array}{cc}\hfill \left(a{\odot }_{\mathrm{B}}b{\Rightarrow }_{\mathrm{B}}c\right)& =\left(a{\Rightarrow }_{\mathrm{B}}\left(b{\Rightarrow }_{\mathrm{B}}c\right)\right),\hfill \\ \hfill \left(a{\odot }_{\mathrm{S}}b{\Rightarrow }_{\mathrm{S}}c\right)& =\left(a{\Rightarrow }_{\mathrm{S}}\left(b{\Rightarrow }_{\mathrm{S}}c\right)\right).\hfill \end{array}$$

Moreover, the Sobociński-style ${\odot }_{\mathrm{S}}$ and ${\Rightarrow }_{\mathrm{S}}$ fulfill the adjointness property. It is not so for ${\odot }_{\mathrm{B}}$ and ${\Rightarrow }_{\mathrm{B}}$. The Bochvar-style product and residuum fulfill the adjointness property w.r.t. the following relations

$$\begin{array}{ccc}{\le }_0& \beta & \ast \\ \alpha & \alpha \le \beta & 0\\ \ast & 0& 0\end{array}\begin{array}{ccc}{\le }_1& \beta & \ast \\ \alpha & \alpha \le \beta & 1\\ \ast & 1& 1\end{array}$$

(3)

In these cases, the adjointness property trivially follows

$$x{\odot }_{\mathrm{B}}y{\le }_{n}z\mathrm{iff}x{\le }_{n}y{\Rightarrow }_{\mathrm{B}}z,$$

for each $x,y,z\in L^{*}$, where $n\in \{0,1\}$. However, ${\le }_0,{\le }_1$ are not orderings on $L^{*}$, but they will be extensively used hereafter.

It can be shown that ${\odot }_{\mathrm{B}}$ is residuated (fulfills the adjointness property) with the following extension of the original ⇒:

$$\begin{array}{ccc}{\Rightarrow }_{*}& \beta & \ast \\ \alpha & \alpha \Rightarrow \beta & \ast \\ \ast & 1& 1\end{array}$$

Proposition 1.

Let $\mathcal{L}$ be a residuated lattice of the form (2). Then

$${\mathcal{L}}^{*}=⟨L\cup \{\ast \},{\vee }_{\mathrm{S}},{\wedge }_{\mathrm{B}},{\odot }_{\mathrm{B}},{\Rightarrow }_{*},\ast ,1⟩,$$

(4)

is a residuated lattice.

Proof. 

It follows from the observation that adding $\{\ast \}$ as a bottom element to $\mathcal{L}$ by means of the ordinal sum results in the residuated lattice (4).  □

The above proposition is particularly important for providing completeness of formal system of partial fuzzy logic; see [19].

Since ${\odot }_{\mathrm{S}}$ and ${\Rightarrow }_{\mathrm{S}}$ fulfill the adjunction property then we would expect that also $⟨L^{*},{\vee }_{\mathrm{S}},{\wedge }_{\mathrm{B}},{\odot }_{\mathrm{S}},{\Rightarrow }_{\mathrm{S}},\ast ,1⟩$ will form a residuated lattice. However, this is not true because $⟨L^{*},{\odot }_{\mathrm{S}},1⟩$ is not the ordered monoid. A counterexample is the following:

$$1{\odot }_{\mathrm{S}}\ast =1\mathrm{and}1{\odot }_{\mathrm{S}}0=0,\mathrm{while}\ast {<}_{*}0\mathrm{and}1{}_{*}>0,$$

where $x{<}_{*}y{=}_{\mathrm{df}}\left(x{\le }_{*}y\right)\wedge (x\ne y)$.

Proposition 2.

Let $\mathcal{L}$ be a residuated lattice of the form (2) and ${\mathcal{L}}^{*}$ be of the form (4).

(i)

If $\mathcal{L}$ is complete then ${\mathcal{L}}^{*}$ is complete.

(ii)

If $\mathcal{L}$ is linearly ordered then ${\mathcal{L}}^{*}$ is linearly ordered.

(iii)

If $\mathcal{L}$ satisfies the prelinearity condition then ${\mathcal{L}}^{*}$ satisfies the prelinearity condition.

(iv)

If $\mathcal{L}$ is divisible then ${\mathcal{L}}^{*}$ is divisible.

Proof. 

All claims are obvious. As an example, let us prove the last claim: the divisibility of $\mathcal{L}$ means that $x\le y$ $(x,y\in L)$ implies the existence of $z\in L$ such that $x=y\odot z$. In ${\mathcal{L}}^{*}$ we must verify only the following cases:

• Let $x=\ast$ and $y\in L^{*}$. The inequality $\ast {\le }_{*}y$ obviously holds and the choice of z is apparent, i.e., $\ast =\ast {\odot }_{\mathrm{B}}y$.
• If $y=\ast$ then from $x{\le }_{*}\ast$ it follows that $x=*$, which has been solved in the previous case.

□

Observe that in the complete residuated lattice ${\mathcal{L}}^{*}$ supremum and infimum of $A\subseteq L^{*}$ are computed as ${\bigwedge }_{\mathrm{B}}A$ and ${\bigvee }_{\mathrm{S}}A$. For example, the supremum of the empty set $\varnothing \subset L^{*}$ w.r.t. ${\le }_{*}$ is ∗ (i.e., the smallest $s\in L^{*}$ such that $x{\le }_{*}s$ for all $x\in \varnothing$) and infimum is 1. Additionally, if $A=\{\ast \}$ then ${\bigwedge }_{\mathrm{B}}A=\ast$ and ${\bigvee }_{\mathrm{S}}A=\ast$.

2.3. Unions and Intersections of Fuzzy Partial Sets

Let us consider two partial fuzzy sets $A=(X_A,{\mu }_A)$ and $B=(X_B,{\mu }_B)$. We recall the following definitions of unions and intersections of partial fuzzy sets due to [4].

Definition 6.

We define

$$\begin{array}{cc}\hfill A{\cup }_{\mathrm{B}}B=(X_A\cap X_B,{\mu }_{A{\cup }_{\mathrm{B}}B})& theBochvarunionofAandB,\hfill \\ \hfill A{\cap }_{\mathrm{B}}B=(X_A\cap X_B,{\mu }_{A{\cap }_{\mathrm{B}}B})& theBochvarintersectionofAandB,\hfill \\ \hfill A{⋒}_{\mathrm{B}}B=(X_A\cap X_B,{\mu }_{A{⋒}_{\mathrm{B}}B})& theBochvarstrongintersectionofAandB,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mu }_{A{\cup }_{\mathrm{B}}B}\left(x\right)& ={\mu }_A\left(x\right)\vee {\mu }_B\left(x\right),forallx\in X_A\cap X_B,\hfill \\ \hfill {\mu }_{A{\cap }_{\mathrm{B}}B}\left(x\right)& ={\mu }_A\left(x\right)\wedge {\mu }_B\left(x\right),forallx\in X_A\cap X_B,\hfill \\ \hfill {\mu }_{A{⋒}_{\mathrm{B}}B}\left(x\right)& ={\mu }_A\left(x\right)\odot {\mu }_B\left(x\right),forallx\in X_A\cap X_B.\hfill \end{array}$$

The Bochvar union is denoted by ${\cup }_{\mathrm{B}}$, the Bochvar intersection is denoted by ${\cap }_{\mathrm{B}}$ and the Bochvar strong intersection is denoted by ${⋒}_{\mathrm{B}}$.

The membership degree $\left(A{\cup }_{\mathrm{B}}B\right)\left(x\right)$ is defined only if $x\in X_A$ and $x\in X_B$, i.e., if $x\in X_A\cap X_B$. And analogously for other Bochvar set operations.

Definition 7.

We define

$$\begin{array}{cc}\hfill A{\cup }_{\mathrm{S}}B=(X_A\cup X_B,{\mu }_{A{\cup }_{\mathrm{S}}B})& theSobocińskiunionofAandB,\hfill \\ \hfill A{\cap }_{\mathrm{S}}B=(X_A\cup X_B,{\mu }_{A{\cap }_{\mathrm{S}}B})& theSobocińskiintersectionofAandB,\hfill \\ \hfill A{⋒}_{\mathrm{S}}B=(X_A\cup X_B,{\mu }_{A{⋒}_{\mathrm{S}}B})& theSobocińskistrongintersectionofAandB,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mu }_{A{\cup }_{\mathrm{S}}B}\left(x\right)={\mu }_A\left(x\right)\vee {\mu }_B\left(x\right),& forx\in X_A\cap X_B,\hfill \\ \hfill {\mu }_{A{\cap }_{\mathrm{S}}B}\left(x\right)={\mu }_A\left(x\right)\wedge {\mu }_B\left(x\right),& forx\in X_A\cap X_B,\hfill \\ \hfill {\mu }_{A{⋒}_{\mathrm{S}}B}\left(x\right)={\mu }_A\left(x\right)\odot {\mu }_B\left(x\right),& forx\in X_A\cap X_B,\hfill \\ \hfill {\mu }_{A{\cup }_{\mathrm{S}}B}\left(x\right)={\mu }_{A{\cap }_{\mathrm{S}}B}\left(x\right)={\mu }_{A{⋒}_{\mathrm{S}}B}\left(x\right)={\mu }_A\left(x\right),& forx\in X_A\backslash X_B,\hfill \\ \hfill {\mu }_{A{\cup }_{\mathrm{S}}B}\left(x\right)={\mu }_{A{\cap }_{\mathrm{S}}B}\left(x\right)={\mu }_{A{⋒}_{\mathrm{S}}B}\left(x\right)={\mu }_B\left(x\right),& forx\in X_B\backslash X_A.\hfill \end{array}$$

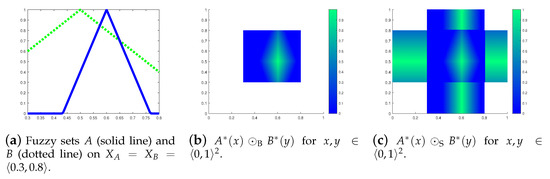
The membership degree $\left(A{\cup }_{\mathrm{S}}B\right)\left(x\right)$ (and other Sobociński set operations) is defined only if $x\in X_A\cup X_B$. Examples of Bochvar and Sobociński partial fuzzy set operations are visualized in Figure 3. The results of operations are depicted by the solid line.

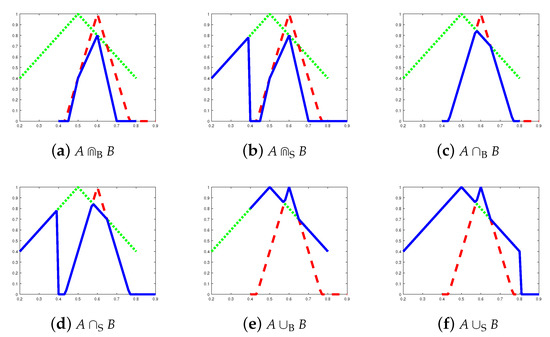
Figure 3. Bochvar and Sobociński operations depicted by the solid line with partial fuzzy sets $A=(⟨0.2,0.8⟩,\mathrm{dotted}\mathrm{line})$ and $B=(⟨0.4,0.9⟩,\mathrm{dashed}\mathrm{line})$ on the universe $U=⟨0,1⟩$.

An uniform way of the representation of unions and intersections of partial fuzzy sets from the above definitions can be obtain by means of operations given in Definitions 3 and 4:

$$\begin{array}{cc}\hfill {\left(A{\cap }_{\mathrm{B}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\wedge }_{\mathrm{B}}{B}^{*}\left(x\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\left(A{⋒}_{\mathrm{B}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\odot }_{\mathrm{B}}{B}^{*}\left(x\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\left(A{\cup }_{\mathrm{B}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\vee }_{\mathrm{B}}{B}^{*}\left(x\right),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\left(A{\cap }_{\mathrm{S}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\wedge }_{\mathrm{S}}{B}^{*}\left(x\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\left(A{⋒}_{\mathrm{S}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\odot }_{\mathrm{S}}{B}^{*}\left(x\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\left(A{\cup }_{\mathrm{S}}B\right)}^{*}\left(x\right)& =A^{*}\left(x\right){\vee }_{\mathrm{S}}{B}^{*}\left(x\right),\hfill \end{array}$$

(10)

for $x\in U$.

This representation allows us to handle partial fuzzy set operations directly by means of the extended operations of the underlying algebra.

2.4. Basic Features of Partial Fuzzy Sets

Known fuzzy sets’ features pass to partial fuzzy sets straightforwardly. In $\mathrm{VFST}$ we have several operations that differ only on undefined operands, so there are more ways to generalize concepts from fuzzy set theory; see [4].

Definition 8.

Let $A=(X_A,{\mu }_A)$ be a fuzzy set, $X_A\subseteq U$, and $A^{*}$ the representation of A due to Definition 2.

• We say that A is total on U if $X_A=U$, i.e., if $A^{*}\left(x\right)\ne \ast$ for all $x\in U$.
• We say that A is crisp if ${\mu }_A\left(x\right)\in \{0,1\}$ for all $x\in X_A$, i.e., if $A^{*}\left(x\right)\in \{0,1,\ast \}$ for all $x\in U$.

At the same time, we will use binary relations between partial fuzzy sets, such as equality and inclusion.

Definition 9.

Let $A=(X_A,{\mu }_A)$ and $B=(X_B,{\mu }_B)$ be fuzzy sets, where ${\mu }_A:X_A\to L$ and ${\mu }_B:X_B\to L$, and let $U\supseteq X_A\cup X_B$. Then we say that:

• A and B are strongly equal, written $A=B$, if $X_A=X_B$ and ${\mu }_A\left(x\right)={\mu }_B\left(x\right)$ for all $x\in X_A$.
• A and B are weakly equal, written $A{=}_{w}B$, if ${\mu }_A\left(x\right)={\mu }_B\left(x\right)$ for all $x\in X_A\cap X_B\ne \varnothing$.
• A and B are subequal, written $A{=}_{sub}B$, if $X_A\subseteq X_B$ and ${\mu }_A\left(x\right)={\mu }_B\left(x\right)$ for all $x\in X_A$.
• A is strongly included in B, written $A\subseteq B$, if $X_A=X_B$ and ${\mu }_A\left(x\right)\le {\mu }_B\left(x\right)$ for all $x\in X_A$.
• A is weakly included in B, written $A{\subseteq }_{w}B$, if ${\mu }_A\left(x\right)\le {\mu }_B\left(x\right)$ for all $x\in X_A\cap X_B\ne \varnothing$.
• A is subincluded in B, written $A{\subseteq }_{sub}B$, if $X_A\subseteq X_B$ and ${\mu }_A\left(x\right)\le {\mu }_B\left(x\right)$ for all $x\in X_A$.

Remark 1.

In this paper, we shall focus only on bivalent (yes/no) relations. However, the so-called graded notions, e.g., of inclusion or equality (cf. [20,21]), can be defined too. A meaningful definition of a graded inclusion might be of the Sobociński–Bochvar style:

$$\left(A{\subseteq }_{\mathrm{SB}}B\right)=\underset{x\in U}{{\bigwedge }_{\mathrm{S}}}\left(A^{*}\left(x\right){\Rightarrow }_{\mathrm{B}}{B}^{*}\left(x\right)\right),$$

which computes a degree of inclusion from the values of membership on $X_A\cap X_B$.

Proposition 3.

Let

$$\begin{array}{cc}\hfill \left(x{=}_{1}y\right)& {=}_{\mathrm{df}}\left(x{\le }_{1}y\right)\wedge \left(y{\le }_{1}x\right),\hfill \\ \hfill (x\le y)& {=}_{\mathrm{df}}\left(x{\le }^{*}y\right)\wedge \left(y{\le }_{*}x\right),\hfill \end{array}$$

for all $x,y\in L^{*}$. Then:

$$\begin{array}{ccc}\hfill A=B& iff& A^{*}\left(x\right)=B^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill A{=}_{w}B& iff& A^{*}\left(x\right){=}_1{B}^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill A{=}_{sub}B& iff& A^{*}\left(x\right){=}_{sub}{B}^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill A\subseteq B& iff& A^{*}\left(x\right)\le B^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill A{\subseteq }_{w}B& iff& A^{*}\left(x\right){\le }_1{B}^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill A{\subseteq }_{sub}B& iff& A^{*}\left(x\right){\le }_{*}{B}^{*}\left(x\right)forallx\in U.\hfill \end{array}$$

(16)

Proof. 

The proof is straightforward.   □

3. Partial Fuzzy Relations and Their Relational Compositions

In fuzzy set theory, fuzzy relations between two crisp sets A and B are fuzzy sets on $A\times B$. In $\mathrm{VFST}$, the domain of a partial fuzzy relation is a subset of $A\times B$, which means that the membership function of a partial fuzzy relation between A and B does not need to be fully defined on $A\times B$. Therefore, we define the notion of a partial fuzzy relation as follows:

Definition 10.

Let $A,B\ne \varnothing$ and $U\supseteq A,B$ be a common universe. Let $R=(X_R,{\mu }_R)$, where $X_R\subseteq U\times U$ and ${\mu }_R:X_R\to L$.

• If $X_R\subseteq A\times B$ then R is a partial fuzzy relation between A and B.
• If R is a partial fuzzy relation between A and B and $A=B$, then we say that R is a partial fuzzy relation on A.

Remark 2.

The above definition of partial fuzzy relations between sets that are crisp is a special case of the notion of partial fuzzy relations between two partial fuzzy sets given in [12,17]. This general definition is based on the notion of the Bochvar Cartesian product ${\times }_{\mathrm{B}}$ (see Example 1 below) of partial fuzzy sets A and B. Consequently, a partial fuzzy relation between two partial fuzzy sets is defined as a subset (in the sense of subinclusion ${\subseteq }_{\mathrm{sub}}$) of $A{\times }_{\mathrm{B}}B$. Ref. [17] provides details about partial fuzzy relations between partial fuzzy sets. For simplicity of the following exposition, we decided to consider partial fuzzy relations between crisp sets. The obtained results can be straightforwardly extended to partial fuzzy relations between partial fuzzy sets.

Remark 3.

Let the assumptions in Definition 10 hold. Moreover, let $P(A\times B)=(A\times B,{\mu }_{A\times B})$.

• R is a partial fuzzy relation between A and B if and only if $R{\subseteq }_{sub}P(A\times B)$.
• $R\subseteq P(A\times B)$ (i.e., R is strongly included in $P(A\times B)$) if and only if $X_R=A\times B$ (i.e., ${\mu }_R$ is total on $A\times B$).
• If $R{\subseteq }_{sub}P(A\times B)$ then $R{\subseteq }_{w}P(A\times B)$.

Example 1.

Let $U=⟨0,1⟩$, $X_A=X_B\subseteq U$, $A=(X_A,{\mu }_A)$, $B=(X_B,{\mu }_B)$. Then:

• $A{\times }_{\mathrm{B}}B=({\left(X_A\right)}^2,{\mu }_{A\times B})$, where ${\mu }_{A\times B}(x,y)={\mu }_A\left(x\right)\odot {\mu }_B\left(y\right)$, for all $x,y\in X_A$, is a partial fuzzy relation on $X_A$ in the universe U with the representation

  $${\left(A{\times }_{\mathrm{B}}B\right)}^{*}(x,y)=A^{*}\left(x\right){\odot }_{\mathrm{B}}{B}^{*}\left(y\right),x,y\in U,$$

  depicted in Figure 4b for the particular choice of A and B due to Figure 4a.
  

  Figure 4. Examples of partial fuzzy relations from Example 1.
• $A{\times }_{\mathrm{S}}B=((X_A\times U)\cup (U\times X_B),{\mu }_{A{\times }_{\mathrm{S}}B})$, where

  $${\mu }_{A{\times }_{\mathrm{S}}B}(x,y)=\left\{\begin{array}{cc}{\mu }_A\left(x\right)\odot {\mu }_B\left(y\right),\hfill & if(x,y)\in X_A\times X_B;\hfill \\ {\mu }_A\left(x\right),\hfill & if(x,y)\in X_A\times (U\backslash X_B);\hfill \\ {\mu }_B\left(y\right),\hfill & if(x,y)\in (U\backslash X_A)\times X_B.\hfill \end{array}\right.$$

  is a partial fuzzy relation on U with the representation

  $${\left(A{\times }_{\mathrm{S}}B\right)}^{*}(x,y)=A^{*}\left(x\right){\odot }_{\mathrm{S}}{B}^{*}\left(y\right),x,y\in U,$$

  depicted in Figure 4c, where A and B are due to Figure 4a.

Partial fuzzy relations $A{\times }_{\mathrm{B}}B$ and $A{\times }_{\mathrm{S}}B$ can be viewed as two variants of the Cartesian product of partial fuzzy sets A and B.

Example 2.

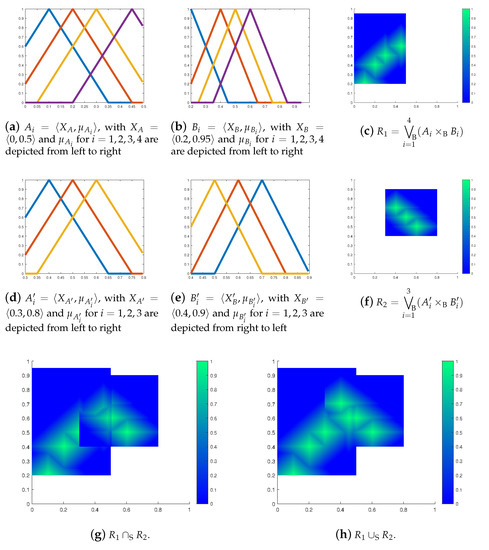
Consider two Mamdani–Assilian models of a fuzzy rule basis formalizing knowledge on different domains, as depicted in Figure 5c,f. The first one is a fuzzy relation on the domain $⟨0,0.5⟩\times ⟨0.2,0.95⟩$ specified by fuzzy sets depicted in Figure 5a,b. For the second model, see Figure 5d–e.

Figure 5. Examples of partial fuzzy relations from Example 2.

Both models are partial fuzzy relations on the common universe $U=⟨0,1⟩$ that can be written using partial fuzzy set operations as

$$R_1=\bigcup _{i=1}^4{}_{\mathrm{B}}\left(A_i{\times }_{\mathrm{B}}{B}_i\right)\mathrm{and}{R}_2=\bigcup _{i=1}^3{}_{\mathrm{B}}\left(A_i^{\prime }{\times }_{\mathrm{B}}{B}_i^{\prime }\right),$$

where ${\times }_{\mathrm{B}}$ is as introduced in Example 1, $X_{R_1}=⟨0,0.5⟩\times ⟨0.2,0.95⟩$ and $X_{R_2}=⟨0.3,0.8⟩\times ⟨0.4,0.9⟩$.

Let us join these two models into a single one as follows: the knowledge on the disjoint parts of the domains remains untouched and that on the intersection of the domains is conjoined. This leads to the Sobociński operations for combining models. Figure 5h shows the result of the Sobociński union of $R_1$ and $R_2$ and analogously, Figure 5g shows the Sobociński intersection of $R_1$ and $R_2$. $R_1{\cup }_{\mathrm{S}}{R}_2$ and $R_1{\cap }_{\mathrm{S}}{R}_2$ are partial fuzzy relations on $X_{R_1}\cup X_{R_2}\subset U\times U$.

Let $R=(X_R,{\mu }_R)$ and $S=(X_S,{\mu }_S)$, where $X_R\subseteq A\times B$ and $X_S\subseteq B\times C$. Observe that $X_R\circ X_S\subseteq A\times C$. Let sup-T and inf-R compositions of fuzzy sets be denoted by ∘ and ◃, respectively. Moreover, let us denote by ${\circ }_{*}$ and ${◃}_{*}$ extensions of ∘ and ◃ to partial fuzzy relations, respectively. We expect from ${\circ }_{*}$ and ${◃}_{*}$ the following behavior:

$$\begin{array}{cc}\hfill {\left(R{\circ }_{*}S\right)}^{*}(x,y)& =\left\{\begin{array}{cc}{\mu }_{R\circ S}(x,y)\hfill & \mathrm{for}(x,y)\in X_R\circ X_S;\hfill \\ \ast \hfill & \mathrm{for}(x,y)\in (U\times U)\backslash (X_R\circ X_S).\hfill \end{array}\right.\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\left(R{◃}_{*}S\right)}^{*}(x,y)& =\left\{\begin{array}{cc}{\mu }_{R◃S}(x,y)\hfill & \mathrm{for}(x,y)\in X_R\circ X_S;\hfill \\ \ast \hfill & \mathrm{for}(x,y)\in (U\times U)\backslash (X_R\circ X_S).\hfill \end{array}\right.\hfill \end{array}$$

(18)

These expectations are met if we combine the Bochvar operations to aggregate input partial fuzzy relations in connection with the Sobociński supremum or infimum. In this case, we obtain the following definition (by Běhounek and Daňková [17], Definition 6.6) of extended sub-T and inf-R compositions.

Definition 11.

Let $A,B,C,U$ be non-empty sets such that $A\cup B\cup C\subseteq U$, $R=(X_R,{\mu }_R)$ is a partial fuzzy relation between A and B, and $S=(X_S,{\mu }_S)$ be a partial fuzzy relation between B and C.

Let $R^{*},S^{*}:U\times U\to L^{*}$ be the respective representations of $R,S$ due to Definition 2.

Then:

• We define the Sobociński–Bochvar sup-T composition $R{\circ }_{\mathrm{SB}}S=(X_R\circ X_S,{\mu }_{R\circ S})$ as the partial fuzzy relation between A and C such that for all $x,y\in U$:

  $${\left(R{\circ }_{\mathrm{SB}}S\right)}^{*}(x,y)=\underset{z\in U}{{\bigvee }_{\mathrm{S}}}\left(R^{*}(x,z){\odot }_{\mathrm{B}}{S}^{*}(z,y)\right).$$
• We define the Sobociński–Bochvar inf-R composition $R{◃}_{\mathrm{SB}}S=(X_R\circ X_S,{\mu }_{R◃S})$ as the partial fuzzy relation between A and C such that for all $x,y\in U$:

  $${\left(R{◃}_{\mathrm{SB}}S\right)}^{*}(x,y)=\underset{z\in U}{{\bigwedge }_{\mathrm{S}}}\left(R^{*}(x,z){\Rightarrow }_{\mathrm{B}}{S}^{*}(z,y)\right).$$

Note that there is also another approach to partial compositions presented in [10], further used to deal with excluding features [9].

Example 3.

Let $R,S_1,S_2$ be partial fuzzy relations with $X_R=⟨0,0.8⟩\times ⟨0,0.6⟩$, $X_{S_1}=⟨0.2,1⟩\times ⟨0.2,0.9⟩$, $X_{S_2}=⟨0.5,1⟩\times ⟨0.2,0.9⟩$ and

$$\begin{array}{cc}\hfill {\mu }_R(x,y)& {=}_{\mathrm{df}}{\mu }_A\left(x\right)\Rightarrow {\mu }_B\left(y\right),(x,y)\in X_R,\hfill \\ \hfill {\mu }_{S_1}(x,y)& {=}_{\mathrm{df}}{\mu }_C\left(x\right)\Rightarrow {\mu }_D\left(y\right),(x,y)\in X_{S_1},\hfill \\ \hfill {\mu }_{S_2}(x,y)& {=}_{\mathrm{df}}{\mu }_E\left(x\right)\Rightarrow {\mu }_D\left(y\right),(x,y)\in X_{S_2},\hfill \end{array}$$

where ${\mu }_A,{\mu }_B,{\mu }_C,{\mu }_D,{\mu }_E$ are depicted in Figure 6.

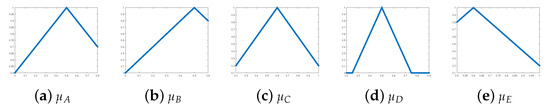
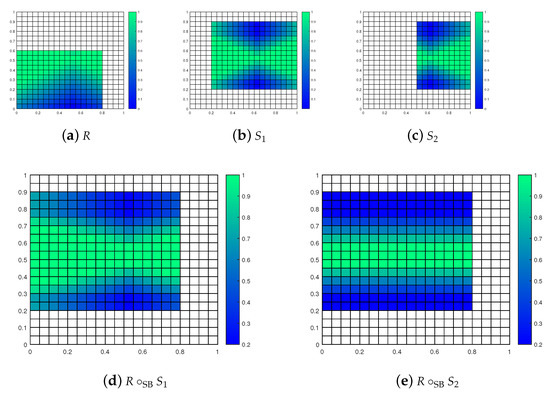
Figure 6. Membership functions of partial fuzzy sets from Example 3.

Then:

$$\begin{array}{cc}\hfill R{\circ }_{\mathrm{SB}}{S}_1& =(⟨0,0.8⟩\times ⟨0.2,0.9⟩,{\mu }_{R\circ S_1}),\hfill \\ \hfill R{\circ }_{\mathrm{SB}}{S}_2& =(⟨0,0.8⟩\times ⟨0.2,0.9⟩,{\mu }_{R\circ S_2}),\hfill \end{array}$$

are partial fuzzy relations depicted in Figure 7d,e, respectively. On these figures, we visualize an influence of a size of domains on results of compositions. In our case $S_2$ and $S_1$ are subequal, i.e., $S_2{=}_{sub}{S}_1$, and we can observe that $R{\circ }_{\mathrm{SB}}{S}_2$ is strongly included in $R{\circ }_{\mathrm{SB}}{S}_1$, i.e., $R{\circ }_{\mathrm{SB}}{S}_2\subseteq R{\circ }_{\mathrm{SB}}{S}_1$.

Figure 7. Examples of partial fuzzy compositions from Example 3.

Proposition 4.

Let $A,B,C,R,S$ be as in Definition 11. Moreover, let $R_i=(X_{R_i},{\mu }_{R_i})$ and $S_i=(X_{S_i},{\mu }_{S_i})$ be partial fuzzy relations with $X_{R_i}\subseteq A\times B,X_{S_i}\subseteq B\times C$, $i=1,2$. Then:

(i)

If $S_1{=}_{sub}{S}_2$ then $R{\circ }_{\mathrm{SB}}{S}_1{\subseteq }_{sub}R{\circ }_{\mathrm{SB}}{S}_2$.

(ii)

If $S_1{=}_{sub}{S}_2$ then $R{◃}_{\mathrm{SB}}{S}_2{\subseteq }_{w}R{◃}_{\mathrm{SB}}{S}_1$.

(iii)

If $R_1{=}_{sub}{R}_2$ then $R_2{◃}_{\mathrm{SB}}S{\subseteq }_w{R}_1{◃}_{\mathrm{SB}}S$.

(iv)

If $S_1{\subseteq }_{sub}{S}_2$ then $R{\circ }_{\mathrm{SB}}{S}_1{\subseteq }_{sub}R{\circ }_{\mathrm{SB}}{S}_2$.

(v)

If $S_1{\subseteq }_{sub}{S}_2$ then $R{◃}_{\mathrm{SB}}{S}_1{\subseteq }_{w}R{◃}_{\mathrm{SB}}{S}_2$.

(vi)

If $R_1{\subseteq }_{sub}{R}_2$ then $R_2{◃}_{\mathrm{SB}}S{\subseteq }_w{R}_1{◃}_{\mathrm{SB}}S$.

Proof. 

Claims (i)–(iii) follow from the properties of infima and suprema over the respective domains. Claim (iv) is obvious. The remaining claims follow from the monotony of ⇒ in the second argument and the antitony in the first one.  □

4. Functional Partial Fuzzy Relations

In classical set theory, partial functions are special cases of binary relations $R\subseteq A\times B$ determined by the functionality property: for all $x\in A$ and $y,z\in B$ such that $(x,y)\in R$ and $(x,y^{\prime })\in R$ then $y=y^{\prime }$. Let ${\mu }_R,{\mu }_{=}$ denote the bivalent characteristic functions of $R,=$, respectively. Moreover, let & interpret “and”; then we can express the functionality equivalently in the form of inequality:

$${\mu }_R(x,y)\& {\mu }_R(x,y^{\prime })\le {\mu }_{=}(y,y^{\prime }).$$

The functionality in fuzzy set theory as given in [22] has the same form as in the classical setting, only the membership functions of $R,\approx$ and the interpretation of conjunction is many-valued:

$${\mu }_R(x,y)\& {\mu }_R(x,y^{\prime })\le {\mu }_{\approx }(y,y^{\prime }).$$

This is a property of a binary fuzzy relation $R⫇A\times B$ w.r.t. a binary fuzzy relation $\approx ⫇B\times B$. This form of functionality, though, does not take into consideration a fuzzy indistiguishability relation on A. Let us consider ${\approx }_1⫇A\times A$ and ${\approx }_2⫇B\times B$. Following property F2 from Demirci [23], we reflect the indistinguishability also in the expression for functionality:

$${\mu }_{{\approx }_1}(x,x^{\prime })\& {\mu }_R(x,y)\& {\mu }_R(x^{\prime },y^{\prime })\le {\mu }_{{\approx }_2}(y,y^{\prime }).$$

Note that ${\approx }_1,{\approx }_2$ are usually similarity relations; we refer to [24] for representation of uncertainty in measurement by similarity relations. Generally, it is not necessary to restrict ourselves to only this kind of relations. We can also deal with proximity relations or assume even weaker requirements and make the restrictions explicit when needed, e.g., when proving particular properties.

In the sequel, let A and B be crisp sets, $A,B\subseteq U\ne \varnothing$, $R=(X_R,{\mu }_R)$ be a partial fuzzy relation between A and B, and ${\approx }_i=(X_{{\approx }_i},{\mu }_{{\approx }_i})$, for $i=1,2$, be binary fuzzy relations on $A,B$, respectively.

In $\mathrm{VFST}$, the fuzzy functionality is expected to perform as follows:

$${\mu }_{{\approx }_1}(x,x^{\prime })\odot {\mu }_R(x,y)\odot {\mu }_R(x^{\prime },y^{\prime })\le {\mu }_{{\approx }_2}(y,y^{\prime }),$$

(19)

for all $(x,x^{\prime })\in X_{{\approx }_1}$, $(y,y^{\prime })\in X_{{\approx }_2}$ and $(x,y),(x^{\prime },y^{\prime })\in X_R$.

It leads us to the following definition with Bochvar operations and ${\le }_1$.

Definition 12.

Let $U,A,B,{\approx }_1,{\approx }_2,R$ be as above. Moreover, let $R^{*},{\approx }_1^{*},{\approx }_2^{*}:U\times U\to L^{*}$ be the representation of $R,{\approx }_1,{\approx }_2$ due to (1), respectively. Then:

• We say that R is functional w.r.t. ${\approx }_1,{\approx }_2$ if

  $${\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\le }_1{\approx }_2^{*}(y,y^{\prime }),$$

  (20)

  for all $x,x^{\prime },y,y^{\prime }\in U$.
• We say that R is a partial crisp function between A and B if R is a crisp partial fuzzy relation between A and B and is functional w.r.t. ${\approx }_1,{\approx }_2$.

We call (20) the functionality inequality.

The functionality inequality is trivially valid whenever any subpart becomes undefined. It follows that it ignores membership values of R out of domains of ${\approx }_1$ and ${\approx }_2$. For example consider $U_1=\mathbb{N}$, $U_2=\{2,3\}$, $U_3=\{2,3,4\}$, $R=\{(x,y)\in U_1\times U_1\mid (y=2)\vee (y=4)\}$, moreover, ${=}_i$ is the identity on ${\left(U_i\right)}^2$ and undefined on ${(U_1\backslash U_i)}^2,i=1,2,3$. Then R is functional w.r.t. ${\approx }_1,{\approx }_2$, because $1={\mu }_R(x,2){\odot }_{\mathrm{B}}{\mu }_R(x,4){\le }_1{\mu }_{{=}_3}(2,4)=\ast$ for an arbitrary $x\in U_1$. But R is not functional w.r.t. ${\approx }_1,{\approx }_3$ since $1={\mu }_R(x,2){\odot }_{\mathrm{B}}{\mu }_R(x,4){\nleqq }_1{\mu }_{{=}_3}(2,4)=0$ for an arbitrary $x\in U_1$.

Proposition 5.

(i)

If

$${\displaystyle \underset{x,x^{\prime },y,y^{\prime }\in U}{{\bigwedge }_{\mathrm{S}}}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\Rightarrow }_{\mathrm{B}}{\approx }_2^{*}(y,y^{\prime })\right)=1,}$$

(21)

then R is functional w.r.t. ${\approx }_1,{\approx }_2$.

(ii)

R is functional w.r.t. ${\approx }_1,{\approx }_2$ iff

$$\left({\approx }_1{\circ }_{\mathrm{SB}}R\right){\subseteq }_w\left(R{◃}_{\mathrm{SB}}{\approx }_2\right).$$

(22)

Proof. 

(i) Let us use the following denotation

$$\begin{array}{cc}\hfill L(x,x^{\prime },y,y^{\prime })& {\equiv }_{\mathrm{df}}{\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }),\hfill \\ \hfill P(y,y^{\prime })& {\equiv }_{\mathrm{df}}{\approx }_2^{*}(y,y^{\prime }).\hfill \end{array}$$

From (21), it follows that $L(x,x^{\prime },y,y^{\prime }){\Rightarrow }_{\mathrm{B}}P(y,y^{\prime })\in \{\ast ,1\}$ for all $x,x^{\prime },y,y^{\prime }\in U$ and there exist $c,c^{\prime },d,d^{\prime }\in U$ such that $L(c,c^{\prime },d,d^{\prime }){\Rightarrow }_{\mathrm{B}}P(d,d^{\prime })=1$. Which implies $L(x,x^{\prime },y,y^{\prime }){\le }_{1}P(y,y^{\prime })$ for all $x,x^{\prime },y,y^{\prime }\in U$, i.e., R is functional.

(ii) By the adjunction property of ${\odot }_{\mathrm{B}}$ and ${\Rightarrow }_{\mathrm{B}}$ w.r.t. ${\le }_1$, we obtain that (20) is equivalent to

$${\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\le }_1{R}^{*}(x,y){\Rightarrow }_{\mathrm{B}}{\approx }_2^{*}(y,y^{\prime }).$$

Observe that $a{\le }_1{b}_i$ for each $i\in I$ is equivalent to ${\displaystyle a{\le }_1\underset{i\in I}{{\bigwedge }_{\mathrm{S}}}{b}_i}$, and analogously, $a_i{\le }_{1}b$ for each $i\in I$ is equivalent to ${\displaystyle \underset{i\in I}{{\bigvee }_{\mathrm{S}}}{a}_i{\le }_{1}b}$. Hence, we obtain

$${\displaystyle \underset{x^{\prime }\in U}{{\bigvee }_{\mathrm{S}}}{\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\le }_1\underset{y\in U}{{\bigwedge }_{\mathrm{S}}}{R}^{*}(x,y){\Rightarrow }_{\mathrm{B}}{\approx }_2^{*}(y,y^{\prime }),}$$

for all $x,y^{\prime }\in U$. Finally, the above inequality is equivalent to

$${\left({\approx }_1{\circ }_{\mathrm{SB}}R\right)}^{*}(x,y^{\prime }){\le }_1{\left(R{◃}_{\mathrm{SB}}{\approx }_2\right)}^{*}(x,y^{\prime }),$$

for all $x,y^{\prime }\in U$, i.e., the definition of the weak inclusion.  □

Equation (21) provides a natural way of generalization from the bivalent notion of the functionality property to a graded one that takes values from the whole scale of degrees including ∗, i.e.,

$${\displaystyle \underset{x,x^{\prime },y,y^{\prime }\in U}{{\bigwedge }_{\mathrm{S}}}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\Rightarrow }_{\mathrm{B}}{\approx }_2^{*}(y,y^{\prime })\right).}$$

This notion has been introduced in [12] and it can be viewed as a generalization of the unique mapping introduced in [13].

Provided that R would have an empty domain, i.e., $X_R=\varnothing$ and $R^{*}(x,y)=\ast$ for all $x,y\in U$, then R is functional in the sense of Definition 12, but

$${\displaystyle \underset{x,x^{\prime },y,y^{\prime }\in U}{{\bigwedge }_{\mathrm{S}}}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\Rightarrow }_{\mathrm{B}}{\approx }_2^{*}(y,y^{\prime })\right)=\ast ,}$$

which means that the degree of functionality of R is undefined.

Remark 4.

In [12], the functionality property is defined by (21), and as seen above, it is not equivalent to the notion of functionality given in Definition 12. Therefore, results from [12] do not transfer directly. The notion of functionality given here by (20) uses an inequality ${\le }_1$ that is very easy to work with as will be seen in the following proofs of the properties presented.

4.1. Set Operations and Relational Compositions of Functional Partial Fuzzy Relations

Let us summarize properties of functional partial fuzzy relations w.r.t. partial fuzzy operations. The following theorem is an analogy to the preliminary result by Daňková [12], Theorem 1.

Theorem 1.

Let $R=(X_R,{\mu }_R)$ be a partial fuzzy relation between A and B and $S=(X_S,{\mu }_S)$ be a partial fuzzy relation between C and D.

If R is functional w.r.t. ${\approx }_1,{\approx }_2$ and S is functional w.r.t. ${\approx }_3,{\approx }_4$ then:

(i)

$R{\cap }_{\mathrm{B}}S=(X_R\cap X_S,{\mu }_{R{\cap }_{\mathrm{B}}S})$ is a partial fuzzy relation between $A\cap C$ and $B\cap D$ functional w.r.t. $\left({\approx }_1{\cap }_{\mathrm{B}}{\approx }_3\right),\left({\approx }_2{\cap }_{\mathrm{B}}{\approx }_4\right)$;

(ii)

$R{⋒}_{\mathrm{B}}S=(X_R\cap X_S,{\mu }_{R{⋒}_{\mathrm{B}}S})$ is a partial fuzzy relation between $A\cap C$ and $B\cap D$ functional w.r.t. $\left({\approx }_1{⋒}_{\mathrm{B}}{\approx }_3\right),\left({\approx }_2{⋒}_{\mathrm{B}}{\approx }_4\right)$.

Proof. 

(i) We will check whether (20) is valid for all $x,x^{\prime },y,y^{\prime }\in U$. From

$$\begin{array}{cc}\hfill {\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y)& {\le }_1{\approx }_2^{*}(y,y^{\prime }),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\approx }_3^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x,y)& {\le }_1{\approx }_4^{*}(y,y^{\prime }),\hfill \end{array}$$

(24)

we obtain

$$\begin{array}{c}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime })\right){\wedge }_{\mathrm{B}}\left({\approx }_3^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x,y){\odot }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })\right)\hfill \\ \hfill {\le }_1{\approx }_2^{*}(y,y^{\prime }){\wedge }_{\mathrm{B}}{\approx }_4^{*}(y,y^{\prime }),\end{array}$$

and by ${\displaystyle \underset{i\in I}{{\bigwedge }_{\mathrm{B}}}{a}_i{\odot }_{\mathrm{B}}\underset{i\in I}{{\bigwedge }_{\mathrm{B}}}{b}_i{\le }_1\underset{i\in I}{{\bigwedge }_{\mathrm{B}}}\left(a_i{\odot }_{\mathrm{B}}{b}_i\right)}$, we obtain

$$\begin{array}{c}\left({\approx }_1^{*}(x,x^{\prime }){\wedge }_{\mathrm{B}}{\approx }_3^{*}(x,x^{\prime })\right){\odot }_{\mathrm{B}}\left(R^{*}(x,y){\wedge }_{\mathrm{B}}{S}^{*}(x,y)\right){\odot }_{\mathrm{B}}\left(R^{*}(x^{\prime },y^{\prime }){\wedge }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })\right)\hfill \\ \hfill {\le }_1{\approx }_2^{*}(y,y^{\prime }){\wedge }_{\mathrm{B}}{\approx }_4^{*}(y,y^{\prime }),\end{array}$$

which is the functionality inequality (20) for $R{\cap }_{\mathrm{B}}S$ w.r.t. $\left({\approx }_1{\cap }_{\mathrm{B}}{\approx }_3\right),\left({\approx }_2{\cap }_{\mathrm{B}}{\approx }_4\right)$.

(ii) It follows from the associativity of ${\odot }_{\mathrm{B}}$.

□

In the case of Sobociński intersections ${\cap }_{\mathrm{S}}$ and ${⋒}_{\mathrm{S}}$, it can easily happen that the functional inequality is violated (see Figure 8). Therefore, it is necessary to make more restrictive requirements on partial fuzzy relation domains to prove their strong and weak intersections’ functionality.

Figure 8. Example of a Sobociński intersection of functional partial fuzzy relations, which is not functional.

Theorem 2.

Let $R=(A\times B,{\mu }_R)$ be a partial fuzzy relation between A and B and $S=(C\times B,{\mu }_S)$ be a partial fuzzy relation between C and B.

If R is functional w.r.t. ${\approx }_1,{\approx }_2$ and S is functional w.r.t. ${\approx }_3,{\approx }_2$ then:

(i)

$R{\cap }_{\mathrm{S}}S=((A\cup C)\times B,{\mu }_{R{\cap }_{\mathrm{S}}S})$ is functional w.r.t. $\left({\approx }_1{\cap }_{\mathrm{S}}{\approx }_3\right),{\approx }_2$;

(ii)

$R{⋒}_{\mathrm{S}}S=((A\cup C)\times B,{\mu }_{R{⋒}_{\mathrm{S}}S})$ is functional w.r.t. $\left({\approx }_1{⋒}_{\mathrm{S}}{\approx }_3\right),{\approx }_2$.

Proof. 

(i) From the fact that if $x{\le }_{1}y$ and $x^{\prime }{\le }_{1}y$ then $x{\wedge }_{\mathrm{S}}{x}^{\prime }{\le }_{1}y$, it follows that

$$\begin{array}{l}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime })\right){\wedge }_{\mathrm{S}}\hfill \\ & \hfill \left({\approx }_3^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x,y){\odot }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })\right){\le }_1{\approx }_2^{*}(y,y^{\prime }),\end{array}$$

for all $x,x^{\prime },y,y^{\prime }\in U$. Next, we use that ${\displaystyle \underset{i\in I}{{\bigwedge }_{\mathrm{S}}}{a}_i{\odot }_{\mathrm{B}}\underset{i\in I}{{\bigwedge }_{\mathrm{S}}}{b}_i{\le }_1\underset{i\in I}{{\bigwedge }_{\mathrm{S}}}\left(a_i{\odot }_{\mathrm{B}}{b}_i\right)}$ and we obtain the functionality property w.r.t. $\left({\approx }_1{\cap }_{\mathrm{S}}{\approx }_3\right),{\approx }_2$.

(ii) If $x{\le }_{1}y$ and $x^{\prime }{\le }_{1}y$ then $x{\odot }_{\mathrm{S}}{x}^{\prime }{\le }_{1}y$, from which it follows that

$$\begin{array}{l}\left({\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime })\right){\odot }_{\mathrm{S}}\hfill \\ & \hfill \left({\approx }_3^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x,y){\odot }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })\right){\le }_1{\approx }_2^{*}(y,y^{\prime }),\end{array}$$

for all $x,x^{\prime },y,y^{\prime }\in U$. Finally, by ${\displaystyle \underset{i\in I}{{⨀}_{\mathrm{B}}}{a}_i{\odot }_{\mathrm{S}}\underset{i\in I}{{⨀}_{\mathrm{B}}}{b}_i{\le }_1\underset{i\in I}{{⨀}_{\mathrm{B}}}\left(a_i{\odot }_{\mathrm{S}}{b}_i\right)}$, we obtain the functionality inequality for $R{⋒}_{\mathrm{S}}S$ w.r.t. $\left({\approx }_1{⋒}_{\mathrm{S}}{\approx }_3\right),{\approx }_2$.  □

Example 4.

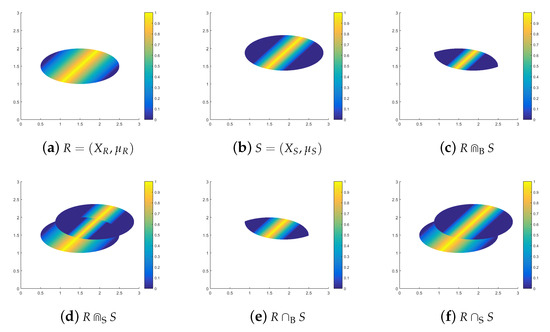
Let $\mathcal{L}$ be the standard ukasiewicz algebra. We define total fuzzy relations ${\approx }_1,{\approx }_2,{\approx }_3$ on the universe $U=⟨0,3⟩$ by the following membership functions:

$$\begin{array}{cc}\hfill {\mu }_{{\approx }_1}(x,y)& {=}_{\mathrm{df}}0\vee (1-|x-y\left|\right);\hfill \\ \hfill {\mu }_{{\approx }_2}(x,y)& {=}_{\mathrm{df}}0\vee (1-2|x-y\left|\right);\hfill \\ \hfill {\mu }_{{\approx }_3}(x,y)& {=}_{\mathrm{df}}0\vee (1-3|x-y\left|\right).\hfill \end{array}$$

The partial fuzzy relation R from Figure 9a is functional w.r.t. ${\approx }_1,{\approx }_1$, and analogously, S from Figure 9b is functional w.r.t. ${\approx }_2,{\approx }_2$.

Figure 9. Intersections of functional partial fuzzy relations.

Figure 9c–f demonstrate the Bochvar and Sobociński intersections of functional partial fuzzy relations R and S. The Bochvar strong intersection $R{⋒}_{\mathrm{B}}S$ is a functional w.r.t. ${\approx }_3,{\approx }_3$, because ${\approx }_3={\approx }_1⋒{\approx }_2$. Notice that the Bochvar strong intersections are not functional w.r.t. ${\approx }_1\cap {\approx }_2,{\approx }_1\cap {\approx }_2$, because (20) is not necessarily valid for all elements of $X_R\cap X_S$. The Bochvar intersections $R{\cap }_{\mathrm{B}}S$ is a functional w.r.t. ${\approx }_2,{\approx }_2$, because ${\approx }_2={\approx }_1\cap {\approx }_2$.

Observe that the domains of R and S do not fulfill the requirements of Theorem 2. Obviously, $R{⋒}_{\mathrm{S}}S$ is not a functional w.r.t. ${\approx }_3,{\approx }_3$. Yet in this special case, where ${\approx }_3\subseteq {\approx }_2\subseteq {\approx }_1$, we have that R is a functional w.r.t. ${\approx }_2,{\approx }_1$ and S is the functional w.r.t. ${\approx }_2,{\approx }_1$. Consequently, the functionality inequality is valid for $R⋒S$ as well as $R\cap S$ w.r.t. ${\approx }_2,{\approx }_1$.

In fuzzy set theory, the sup-T composition of functional fuzzy relations is again a functional fuzzy relation. In the case of partial fuzzy relations, the functionality of the sup-T composition also passes without much difficulty. The following theorem generalizes the preliminary result by Daňková [12], Theorem 2.

Theorem 3.

Let the assumptions of Theorem 1 hold. Moreover, let R be a functional w.r.t. ${\approx }_1,{\approx }_2$, S be functional w.r.t. ${\approx }_3,{\approx }_4$, and $T=(X_T,{\mu }_T)$ be a partial fuzzy relation between B and C functional w.r.t. ${\approx }_3,{\approx }_4$.

If ${\approx }_2{\subseteq }_{\mathrm{w}}{\approx }_3$ then $R{\circ }_{\mathrm{SB}}T$ is a partial fuzzy relation between A and C functional w.r.t. ${\approx }_1,{\approx }_4$.

Proof. 

By the adjointness property, we obtain from the functionality inequality for T that

$${\approx }_3^{*}(y,y^{\prime }){\le }_1\left(T^{*}(y,z){\odot }_{\mathrm{B}}{T}^{*}(y^{\prime },z^{\prime })\right){\Rightarrow }_{\mathrm{B}}{\approx }_4^{*}(z,z^{\prime }).$$

Combining the requirement ${\approx }_2{\subseteq }_{\mathrm{w}}{\approx }_3$, i.e., ${\approx }_2^{*}(y,y^{\prime }){\le }_1{\approx }_3^{*}(y,y^{\prime })$, with (23) yields

$${\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime }){\le }_1\left(T^{*}(y,z){\odot }_{\mathrm{B}}{T}^{*}(y^{\prime },z^{\prime })\right){\Rightarrow }_{\mathrm{B}}{\approx }_4^{*}(z,z^{\prime }),$$

which is equivalent to

$${\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}\left(R^{*}(x,y){\odot }_{\mathrm{B}}{T}^{*}(y,z)\right){\odot }_{\mathrm{B}}\left(R^{*}(x^{\prime },y^{\prime }){\odot }_{\mathrm{B}}{T}^{*}(y^{\prime },z^{\prime })\right){\le }_1{\approx }_4^{*}(z,z^{\prime }),$$

and hence

$${\displaystyle {\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}\underset{y\in U}{{\bigvee }_{\mathrm{S}}}\left(R^{*}(x,y){\odot }_{\mathrm{B}}{T}^{*}(y,z)\right){\odot }_{\mathrm{B}}\underset{y^{\prime }\in U}{{\bigvee }_{\mathrm{S}}}\left(R^{*}(x^{\prime },y^{\prime }){\odot }_{\mathrm{B}}{T}^{*}(y^{\prime },z^{\prime })\right){\le }_1{\approx }_4^{*}(z,z^{\prime }),}$$

which completes the proof.   □

What was valid above for intersections of partial fuzzy relations does not apply to their unions. However, as the following theorem shows, if the Sobociński union of partial fuzzy relations satisfies the functionality condition, then the input partial fuzzy relations must have been functional as well. In the case of the Bochvar union, only parts of the input partial fuzzy relations are surely functional, namely those lying in the intersection of the domains. The following theorem extends the preliminary result by Daňková [12], Theorem 3.

Theorem 4.

Let $R=(X_R,{\mu }_R)$, $S=(X_S,{\mu }_S)$, $R^{\prime }=(X_R\cap X_S,{\mu }_{R^{\prime }})$ and $S^{\prime }=(X_R\cap X_S,{\mu }_{S^{\prime }})$ be partial fuzzy relations between A and B such that $R^{\prime }{=}_{sub}R$ and $S^{\prime }{=}_{sub}S$.

(i)

If $R{\cup }_{\mathrm{S}}S$ is a partial fuzzy relation between A and B functional w.r.t. ${\approx }_1,{\approx }_2$ then R and S are partial fuzzy relations between A and B functional w.r.t. ${\approx }_1,{\approx }_2$.

(ii)

If $R{\cup }_{\mathrm{B}}S$ is a partial fuzzy relation between A and B functional w.r.t. ${\approx }_1,{\approx }_2$ then $R^{\prime }$ and $S^{\prime }$ are partial fuzzy relations between A and B functional w.r.t. ${\approx }_1,{\approx }_2$.

Proof. 

(i) The functionality inequality for $R{\cup }_{\mathrm{S}}S$ is the following:

$${\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}\left(R^{*}(x,y){\vee }_{\mathrm{S}}{S}^{*}(x,y)\right){\odot }_{\mathrm{B}}\left(R^{*}(x^{\prime },y^{\prime }){\vee }_{\mathrm{S}}{S}^{*}(x^{\prime },y^{\prime })\right){\le }_1{\approx }_2^{*}(y,y^{\prime }),$$

where $\left(R^{*}(x,y){\vee }_{\mathrm{S}}{S}^{*}(x,y)\right){\odot }_{\mathrm{B}}\left(R^{*}(x^{\prime },y^{\prime }){\vee }_{\mathrm{S}}{S}^{*}(x^{\prime },y^{\prime })\right)\ne *$ for all $x,x^{\prime },y,y^{\prime }\in X_R\cup X_S$. Hence,

$$\begin{array}{cc}\hfill {\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{R}^{*}(x,y){\odot }_{\mathrm{B}}{R}^{*}(x^{\prime },y^{\prime })& {\le }_1{\approx }_2^{*}(y,y^{\prime }),\hfill \\ \hfill {\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{S}^{*}(x,y){\odot }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })& {\le }_1{\approx }_2^{*}(y,y^{\prime }),\hfill \end{array}$$

for all $x,x^{\prime },y,y^{\prime }\in U$.

(ii) $\left(R^{*}(x,y){\vee }_{\mathrm{B}}{S}^{*}(x,y)\right){\odot }_{\mathrm{B}}\left(R^{*}(x^{\prime },y^{\prime }){\vee }_{\mathrm{B}}{S}^{*}(x^{\prime },y^{\prime })\right)\ne \ast$ for all $x,x^{\prime },y,y^{\prime }\in X_R\cap X_S$. It follows that the functionality inequalities will work only for the restricted membership functions of R and S to $X_R\cap X_S$, i.e., for the partial fuzzy sets $R^{\prime }$ and $S^{\prime }$.   □

If $R{\cup }_{\mathrm{B}}S$ is functional w.r.t. ${\approx }_1,{\approx }_2$ then R and S from the above theorem need not be functional w.r.t. ${\approx }_1,{\approx }_2$ (it is easy to find a crisp counterexample) because the functionality of $R{\cup }_{\mathrm{B}}S$ is checked only at the intersection of the domains $X_R\cap X_S$.

4.2. Representation of Partial Fuzzy Relations by Partial Crisp Functions

Now, let us turn our attention to the representation problem of functional partial fuzzy relations. Observe that a partial crisp function F due to Definition 12 can attain only values $\{0,1,\ast \}$. Let ${\approx }_1,{\approx }_2$ be the identity relation =. If we would like to express F using a mapping on U we need to introduce the following restriction of the identity relation on U to $X_F$:

$$\left(x{=}_{X_F}y\right){=}_{\mathrm{df}}\left\{\begin{array}{cc}x=y,\hfill & (x,y)\in X_F;\hfill \\ \ast ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Moreover, consider a function $f:U\mapsto U$ such that $F^{*}(x,f\left(x\right)){=}_{\mathrm{sub}}1$ for all $x\in U$. Then $\left(y{=}_{X_F}f\left(x\right)\right)=F^{*}(x,y)$ for all $x,y\in U$. Observe that $F_f=(U,{\mu }_{F_f})$ with ${\mu }_{F_f}(x,y){=}_{\mathrm{df}}(y=f\left(x\right))$ for all $x,y\in U$ is the total (in the sense of Definition 8) crisp function w.r.t. $=,=$.

The following theorem shows the relationship between functional partial fuzzy relations and partial crisp functions w.r.t. ${\approx }_1,{\approx }_2$.

Theorem  5.

Let $U,A,B,{\approx }_1,{\approx }_2$ be as in Definition 12. Moreover, let ${\approx }_2$ be a symmetric and transitive binary partial fuzzy relation on B, i.e., ${\mu }_{{\approx }_2}(x,y)={\mu }_{{\approx }_2}(y,x)$ and ${\mu }_{{\approx }_2}(x,y){\odot }_{\mathrm{B}}{\mu }_{{\approx }_2}(y,z){\le }_1{\mu }_{{\approx }_2}(x,z)$ for all $x,y,z\in U$, respectively.

(i)

If $F=(X_F,{\mu }_F)$ is a partial fuzzy relation between A and B functional w.r.t. ${\approx }_1,{\approx }_2$ such that F is serial from A to B, i.e., for all $x\in A$ there exists $y\in B$: ${\mu }_F(x,y)=1$, then there exists a function $f:U\mapsto U$ such that $f_F=(X_F,{\mu }_{f_F})$, where $f_F^{*}(x,y){=}_{\mathrm{df}}\left(y{=}_{X_F}f\left(x\right)\right)$ is a partial crisp function w.r.t. ${\approx }_1,{\approx }_2$.

(ii)

Let $\varnothing \ne X_F\subseteq U^2$ and $f:U\mapsto U$. If $F_f=(X_F,{\mu }_{F_f})$, where $f_F^{*}(x,y)=\left(y{=}_{X_F}f\left(x\right)\right)$ for all $x,y\in U$, is a partial crisp function w.r.t. ${\approx }_1,{\approx }_2$ then $F=(X_F,{\mu }_F)$ defined as

$${\mu }_F(x,y){=}_{\mathrm{df}}\left\{\begin{array}{cc}{\mu }_{{\approx }_2}(y,f\left(x\right)),\hfill & (x,y)\in X_F;\hfill \\ *,\hfill & otherwise.\hfill \end{array}\right.$$

is a partial fuzzy relation between A and B functional w.r.t. ${\approx }_1,{\approx }_2$.

Proof. 

(i) Define a function $f:U\mapsto U$ such that ${\mu }_F(x,f\left(x\right))=1$ for all $x\in A$ and it can be arbitrary on $U\backslash A$. Then the functionality inequality for F gives

$$\begin{array}{ll}{\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}\left(y{=}_{X_F}f\left(x\right)\right){\odot }_{\mathrm{B}}& \left(y^{\prime }{=}_{X_F}f\left(x^{\prime }\right)\right)\le \\ & {\approx }_1^{*}(x,x^{\prime }){\odot }_{\mathrm{B}}{F}^{*}(x,y){\odot }_{\mathrm{B}}{F}^{*}(x^{\prime },y^{\prime }){\le }_1{\approx }_2^{*}(y,y^{\prime }),\end{array}$$

for all $x,x^{\prime },y{,}^{\prime }\in U$, because $\left(y{=}_{X_F}f\left(x\right)\right)=1$ then ${\mu }_F(x,f\left(x\right))=1$. Hence, $f_F$ is the partial crisp function between $A$ and $B$ w.r.t. ${\approx }_1,{\approx }_2$.

(ii) $F_f=(X_F,{\mu }_{F_f})$ is the partial crisp function w.r.t. ${\approx }_1,{\approx }_2$, which gives

$${\mu }_{{\approx }_1}(x,x^{\prime }){\le }_1{\mu }_{{\approx }_2}(f\left(x\right),f\left(x^{\prime }\right)),\mathrm{for}\mathrm{all}x,x^{\prime }\in U,$$

(25)

and by the symmetry and transitivity of ${\approx }_2$, we receive the functionality inequality for F w.r.t. ${\approx }_1,{\approx }_2$:

$$\begin{array}{ll}{\mu }_{{\approx }_1}(x,x^{\prime }){\odot }_{\mathrm{B}}{\mu }_{{\approx }_2}& (y,f\left(x\right)){\odot }_{\mathrm{B}}{\mu }_{{\approx }_2}(y^{\prime },f\left(x^{\prime }\right))\\ & \hfill {\le }_1{\mu }_{{\approx }_2}(f\left(x\right),f\left(x^{\prime }\right)){\odot }_{\mathrm{B}}{\mu }_{{\approx }_2}(y,f\left(x\right)){\odot }_{\mathrm{B}}{\mu }_{{\approx }_2}(y^{\prime },f\left(x^{\prime }\right)){\le }_1{\mu }_{{\approx }_2}(y,y^{\prime }).\end{array}$$

□

Observe that (25) is the extended version of the compatibility property of a crisp function f [15]. Provided that ${\approx }_1,{\approx }_2$ would be total similarity relations then (25) is dual to the Lipschitz inequality w.r.t. pseudo-metrics dual to ${\approx }_1,{\approx }_2$.

5. Conclusions

In this paper, we recalled the essential concepts of the partial fuzzy set and relational calculus. In the center of interest was the functionality property of partial fuzzy relations, for which we proved several interesting properties w.r.t. partial fuzzy set operations and relational compositions and provided a number of motivating and illustrative examples. The important point to note here is that traditional fuzzy set theory results are not directly transferable to partial fuzzy set theory due mainly to the different nature of Bochvar and Sobociński partial fuzzy set operations. Consequently, the machinery for dealing with various domains of partial fuzzy sets must be implemented carefully. Often, the properties of functional fuzzy relations known in traditional fuzzy set theory are split into several nonequivalent variants in $\mathrm{VFST}$; see, e.g., Proposition 4 and Theorem 4.