A Cooperative Network Packing Game with Simple Paths

Abstract

We consider a cooperative packing game in which the characteristic function is defined as the maximum number of independent simple paths of a fixed length included in a given coalition. The conditions under which the core exists in this game are established, and its form is obtained. For several particular graphs, the explicit form of the core is presented.

1. Introduction

In this paper, we study cooperative games on a graph in which the vertices represent the players, and the characteristic function is defined using the maximum packing of the graph by connected coalitions. Simple paths in the graph are considered coalitions.

In particular, coalitions can be pairs of vertices connected by edges. In real life, there are many examples of paired relationships: supplier–customer, man–woman, predator–prey, source–sink, and so forth. Moreover, agents can interact with each other via vehicles, mobile devices, or social networks, forming paired communications. For example, in a mobile network, the vertices of the corresponding graph represent mobile devices, and the connections between them occur within the network coverage. In practice, it is important to find the maximum load on a mobile network under which any two devices can simultaneously communicate with one another. In sociology and various TV shows, it is important to divide the participants into the maximum number of pairs (see, for example, the popular show “Speed Dating”, https://en.wikipedia.org/wiki/Speed_dating (accessed on 10 July 2021); https://www.imdb.com/find?q=speed+dating&ref_=nv_sr_sm (accessed on 10 July 2021). The same problems arise in electrical and radio networks or the physics of magnetic structures of solid crystals.

The maximum packing is not necessarily realized through pairs of connected vertices. For example, simple paths of a fixed length can be chosen as packing coalitions. Such problems arise when laying fiber-optic lines to connect urban areas to the Internet. Another application is the development of transportation networks in a city or between cities. The network packing determines a partition of the set of players into coalitions. After defining the characteristic function, an imputation can be found to rank the graph vertices by their value for organizing links in the network or transmitting data, depending on the problem under consideration.

In the papers [1,2], a general class of such cooperative games was formulated and called combinatorial optimization games. This class includes packing games as well. In such games, the characteristic function is defined as follows. Let a matrix $A(m\times n)$ of zeros and ones, and integer vector c be given. The value of a coalition $K\subseteq N$ is a solution of the integer linear programming problem

$$max\{(y,c):y^T{A}_K\le 1_K,y\in {\{0,1\}}^m\},$$

where the matrix $A_K$ is a submatrix of A with the columns from the set K. This problem is known as the set packing problem [3]. In a similar form, such games were investigated in [4] as linear production games. In the cooperative game of this type, the core (if itexists) is a solution of the dual problem. The balancedness (non-emptiness of the core) of the cooperative game is closely related to solving both problems. As some applications, games with maximum flows on a graph, and graph packing games with pairs of connected vertices, were considered.

In packing games, other allocation principles can be adopted as imputations. Since the cooperative game is defined on a graph, the most natural approach to determine the significance of a particular graph vertex is the Myerson value [5,6]. In the papers [7,8], the Owen value [9,10,11] was used as an allocation principle in the cover game. In the paper [12], the nucleolus was proposed, including an algorithm for its construction. The paper [13] was dedicated to the Shapley value: its properties were investigated and an algorithm for calculating this value was proposed.

There are other games related to packing undirected graphs. For example, in graph coloring problems, the chromatic number of a graph can be taken as the characteristic function [1,14,15,16]. Graph clustering problems can be treated as cooperative games with a Nash stable coalition partition when none of the players benefit from changing the coalition structure. In this case, the Myerson value is used as an allocation principle; see [17,18].

In packing by pairs of connected vertices, two approaches to graph packing problems are well known: vertex cover and edge cover [1,19]. A vertex cover of a graph is any subset U of its vertex set N, such that any edge of this graph is incident to at least one vertex of the set U. Here, the characteristic function is defined using the vertex cover with the minimum number of vertices (the so-called minimum vertex cover of the graph). Given an edge cover, the characteristic function is defined as the maximum number of edges in a graph without shared vertices.

This paper deals with cooperative games on graphs in which the characteristic function is defined as the maximum number of independent simple paths of a fixed length. Note that we are interested in the paths without shared vertices. This feature distinguishes the current statement from the cooperative game in which the characteristic function is defined as the number of all simple paths of a fixed length. The latter definition of a game is often used for determining the centrality of graph vertices.

Here, it will be convenient to use “graph packing” for referring to the coalitions (paths) included in a corresponding coalition partition. The remainder of this paper is organized as follows: In Section 2, we define a cooperative packing game. Section 3 considers the graph packing problem with pairs of connected vertices. In Section 4, these results are extended to the general case. Section 5 presents the explicit-form solution of the cooperative graph packing game for several particular graphs.

2. Basic Definitions

Let $N=\{1,2,\dots ,n\}$ be the set of players. A subset $K\subseteq N$ is called a coalition. Consider a cooperative game ${\Gamma }_0=⟨N,v⟩,v:2^N\to R,v(\varnothing )=0$.

Definition 1.

A coalition K is said to be winning if $v\left(K\right)>0$.

Definition 2.

A coalition K is said to be minimal winning if $v\left(K\right)>0$ and $\forall L\subset K$ $v\left(L\right)=0$.

Definition 3.

A coalition partition of the players set N is a set $\pi =\{K_1,\dots ,K_l\}$ satisfying the following conditions:

$${\cup }_{i=1}^l{K}_i=N,K_i\cap K_j=\varnothing ,\forall i,j,i\ne j.$$

We denote by $K\left(i\right)$ an element of a coalition partition $\pi$ containing player i. Further analysis will be confined to effective coalition partitions.

Definition 4.

An effective coalition partition of the set N is a partition ${\pi }_N$ in which the number of minimal winning coalitions is the maximum.

According to this definition, an effective coalition partition has minimal winning coalitions and players not belonging to the minimal winning coalitions. For the sake of convenience, assume that these players act independently, that is, form coalitions of one player. Therefore, an effective coalition partition can be written as ${\pi }_N=\{K_1,K_2,\dots ,K_l,i_1,\dots ,i_r\}$, where $\{K_1,K_2,\dots ,K_l\}$ are the minimal winning coalitions, and $\{i_1,\dots ,i_r\}$ are individual players acting independently.

Consider an undirected graph $G=⟨N,E⟩$, in which N and E are the sets of players and edges, respectively. Consider a new cooperative game $\Gamma =⟨N,G,v^G⟩$, defining the characteristic function $v^G\left(K\right)$ as the maximum number of minimal winning coalitions:

$$v^G\left(K\right)=max\{l:{\pi }_K=\{K_1,K_2,\dots ,K_l,\left\{i_1\right\},\dots ,\left\{i_r\right\}\}\},K\subseteq N,$$

where $K_1\cup \dots \cup K_l\cup \left\{i_1\right\}\cup \dots \cup \left\{i_r\right\}=K$. A solution of the cooperative game is an imputation.

Definition 5.

An imputation in the cooperative game Γ is a vector $x=(x_1,x_2,\dots ,x_n)$, such that

$$\sum _{i\in N}{x}_i=v^G\left(N\right),x_i\ge 0,i\in N.$$

For the given characteristic function, we will adopt the core as an allocation principle.

Definition 6.

In the cooperative game with the characteristic function $v^G\left(K\right),$ the core is the set of imputations

$$C=\{x:\sum _{i\in N}{x}_i=v^G\left(N\right),\sum _{i\in S}{x}_i\ge v^G\left(S\right),\forall S\subset N\}.$$

(1)

This paper deals with cooperative games on graphs in which minimal winning coalitions are defined as simple paths of a fixed length $d\ge 2$. For a graph G, a sequence of distinct vertices $i_1,i_2,\dots ,i_k,k\ge 2,$ is a simple path connecting vertices $i_1$ and $i_k$, if for all $h=1,\dots ,k-1$, $(i_h,i_{h+1})\in G$. The length d of a path is the number of edges in it: $d=k-1$. The length of the shortest path connecting vertices i and j is called the distance between i and j. A graph G is said to be connected if there is a path in G connecting any two vertices i and $j.$

Thus, in an effective coalition partition

$${\pi }_N=\{K_1,K_2,\dots ,K_l,i_1,\dots ,i_r\},$$

the minimal winning coalitions $\{K_1,K_2,\dots ,K_l\}$ represent simple paths of a length d in the graph G, and $\{i_1,\dots ,i_r\}$ are separate vertices not included in these paths. A set $\{K_1,K_2,\dots ,K_l\}$ will henceforth be called graph packing, and the corresponding game on the graph the packing game.

First, we study packing games in which the minimal winning coalitions are of the form $\{i,j\},$ where $\{i,j\}\in E$ is an edge in the graph G.

3. Graph Packing Game with Pairs of Connected Vertices (Maximum Matching Game)

Consider a cooperative game $\Gamma =<N,G>,$ where $N=\{1,2,\dots ,n\}$ denotes the set of players, and $G=(N,E)$ is a graph with N as the vertex set and E as the edge set. The notation $G_S$ will also be used for a subgraph of the graph G defined on a vertex subset $S\subset N$.

We define the characteristic function $v^G\left(K\right)$ for a coalition $K\subset N$ as the maximum number of edges included in K without shared vertices (also called a maximum cardinality matching) [20]. This characteristic function is monotonic and superadditive. Let us demonstrate that $v^G\left(K\right)$ is not necessarily a convex function. Recall that convexity means that the inequality $v(K_1\cup K_2)+v(k_1\cap K_2)\ge v\left(K_1\right)+v\left(K_2\right)$ holds for all $K_1$ and $K_2$.

Example 1.

Consider $N=\{1,2,3\}$ and $E=\left\{\right\{1,2\},\{2,3\left\}\right\}$. For $K_1=\{1,2\}$ and $K_2=\{2,3\},$ we have

$$v^G(K_1\cup K_2)+v^G(K_1\cap K_2)=v^G(1,2,3)+v^G\left(2\right)=1.$$

At the same time,

$$v^G\left(K_1\right)+v^G\left(K_2\right)=2.$$

Thus, the function v is not convex.

The vertices of degree 1 in the graph G will be called terminal and the vertices adjacent to them preterminal. We denote these sets by $T\left(G\right)$ and $T^{\prime }\left(G\right)$, respectively. In addition, an edge connecting terminal and preterminal vertices will be called terminal. By a packing of the graph G we mean a set of edges $U\left(G\right)\subseteq E$ on which $v^G\left(N\right)$ is achieved. The set of all packings will be denoted by $\Lambda \left(G\right)$. The set $\Lambda \left(G\right)$ may be non-unique and composed of several sets.

Example 2.

Consider $N=\{1,2,3,4\}$ and $E=\left\{\right\{1,2\},\{2,3\},\{3,4\left\}\right\}$. Then $U\left(G\right)=\left\{\right\{1,2\},\{2,3\left\}\right\}$ is unique. If $E=\left\{\right\{1,2\},\{2,3\left\}\right\}$, there are two such sets:

$\Lambda \left(G\right)=\left\{\right\{\{1,2\}\},\{\{2,3\}\left\}\right\}$.

The set of vertices forming the edges from a packing $U\left(G\right)$ will be denoted by $\left\{U\right(G\left)\right\}$. We emphasize that the packing game definition implies

$$v^G\left(N\right)=\left|U\left(G\right)\right|=\frac{\left|\right\{U\left(G\right)\left\}\right|}{2},\forall U\left(G\right)\in \Lambda .$$

Let us explore the core’s properties in the graph packing game. First of all, the core does not necessarily exist.

Lemma 1.

Let G be an arbitrary connected graph such that the set of terminal vertices $T\left(G\right)$ is non-empty. Then among all packings, there exists a packing $U\left(G\right)$ with the following property:

$$\forall s\in T^{\prime }\left(G\right)\exists t\in T\left(G\right):(s,t)\in U\left(G\right).$$

(2)

Proof. 

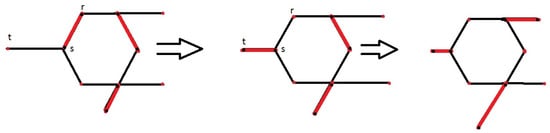
Consider an arbitrary packing $U\left(G\right)\in \Lambda \left(G\right)$. Assume that, in the graph $G,$ there is a preterminal vertex s without a pair among the terminal vertices in $U\left(G\right).$ That is, $(s,t)\notin U\left(G\right)$, where $(s,t)\in E,\forall t\in T$ (Figure 1). We take an arbitrary edge $(s,t)\notin U\left(G\right);$ if s is connected to another non-terminal edge r in $U\left(G\right),$ we replace the link $(s,r)\in U\left(G\right)$ with a new link $(s,t)$. The new packing will be denoted by $U^{\prime }\left(G\right)$. It is important that $\left|U\left(G\right)\right|=|U^{\prime }\left(G\right)$|. We perform the same procedure for all such vertices $s\in T^{\prime }\left(G\right),$ finally obtaining a packing $U^{\prime }\left(G\right)$ with the property (2).  □

Figure 1. Covers of graph G.

Lemma 2.

Let G be an arbitrary connected graph such that the set of terminal vertices $T\left(G\right)$ is non-empty. In addition, let $T_s=\{t\in T\left(G\right):(s,t)\in E\}$ be the set of all neighbors of a vertex $s\in T^{\prime }\left(G\right)$ in the terminal set, and $G^{\prime }$ be a subgraph of G defined on the vertex set $N^{\prime }=N\backslash (s\cup T_s)$. Then

$$v^{G^{\prime }}\left(N^{\prime }\right)=v^G\left(N\right)-1.$$

Proof. 

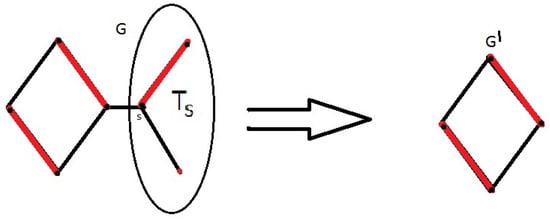
According to Lemma 1, for any $s\in T^{\prime }$, such that $T_s\ne \varnothing$, there exists a packing $U\left(G\right)$ such that $(s,t)\in U\left(G\right)$, where $t\in T_s$ (Figure 2). Then $V^G\left(N\right)=\left|U\left(G\right)\right|$. Let $N^{\prime }=N\backslash \{s,t\}$ and $U^{\prime }\left(G^{\prime }\right)$ be a subset $U\left(G\right)$ on $N^{\prime }$. Then, $|U^{\prime }\left(G^{\prime }\right)|=|U\left(G\right)|-1=V^G\left(N\right)-1$, but $U^{\prime }\left(G^{\prime }\right)$ is a set of independent edges in $G^{\prime }$, then $v^{G^{\prime }}\left(N^{\prime }\right)\ge \left|U^{\prime }\left(G^{\prime }\right)\right|=v^G\left(N\right)-1$.

Figure 2. Terminal vertices in graph.

Let $U^{\prime }\left(G^{\prime }\right)\in \Lambda \left(G^{\prime }\right)$ be a packing of $G^{\prime }$. Then, $v^{G^{\prime }}\left(N^{\prime }\right)=\left|U^{\prime }\left(G^{\prime }\right)\right|.$ Let $U^{*}\left(G\right)=U^{\prime }\left(G^{\prime }\right)\cup (s,t)$, then $|U^{*}\left(G\right)|=|U^{\prime }\left(G^{\prime }\right)|+1=v^{G^{\prime }}\left(N^{\prime }\right)+1$, but $U^{*}\left(G\right)$ is a set of independent edges in G, then $V^G\left(N\right)\ge \left|U^{*}\left(G\right)\right|=v^{G^{\prime }}\left(N^{\prime }\right)+1$. Consequently, $V^G\left(N\right)=v^{G^{\prime }}\left(N^{\prime }\right)+1$.  □

Lemma 3.

Condition (1) for the core is equivalent to

$$C=\{x:\sum _{i\in N}{x}_i=v^G\left(N\right),x_i+x_j\ge 1,(i,j)\in E,\forall i,j\in N\}.$$

(3)

Proof. 

Assume that condition (1) holds for some x. Then the inequality ${\displaystyle \sum _{i\in S}}{x}_i\ge v^G\left(S\right)$ is satisfied for all coalitions S and, particularly, for a coalition $S=\{i,j\}:(i,j)\in E$, where $v^G(i,j)=1$.

Now, assume that an imputation x satisfies (3). Consider an arbitrary coalition $S\subset N$. Let a packing $U\left(G_S\right)$ of the graph $G_S$ be composed of k edges, that is,

$$U\left(G_S\right)=\{(i_1,i_2),\dots ,(i_{2k-1},i_{2k})\}.$$

Then, $v^{G_S}\left(S\right)=k$. However, $\left\{U\left(G_S\right)\right\}=\{i_1,i_2,\dots ,i_{2k-1},i_{2k}\}\in S$ and

$${\displaystyle \sum _{i\in S}}{x}_i\ge \sum _{j=1}^{2k}{x}_{i_j}=\sum _{j=1}^k(x_{i_{2j-1}}+x_{i_{2j}})\ge k=v^G\left(S\right)$$

due to (3). Thus, conditions (1) and (3) are equivalent.  □

Remark 1.

Notice that the number of constraints in (1) drops from exponential $\left(2^n\right)$ to at most quadratic $\left(n^2\right)$ in (3).

Note that condition (1), like (3), may not hold, meaning that the core is empty. The balancedness of this cooperative game can be established by solving the linear programming problem,

$$\begin{array}{cc}\hfill min\sum _{i\in N}& x_i\hfill \\ \hfill \mathrm{s}.\mathrm{t}.x_i+x_j\ge 1,& \forall (i,j)\in E;\hfill \\ \hfill x_i\ge 0,& \forall i\in N.\hfill \end{array}$$

(4)

If the solution of this problem satisfies ${\displaystyle \sum _{i\in N}}{x}_i=v^G\left(N\right)$, then the game is balanced; otherwise, unbalanced.

Lemma 4.

If x belongs to the core, then $x_i\le 1,\forall i\in N$.

Proof. 

By definition, we have $v^G\left(N\right)=\left|U\left(G\right)\right|=k$, where the cover $U\left(G\right)$ is composed of k edges $\{(i_1,i_2),\dots ,(i_{2k-1},i_{2k})\}$. According to Lemma 3, $x_{i_l}+x_{i_{l+1}}\ge 1$. If at least one element is $x_{i_j}>1$, then the entire sum becomes

$$v^G\left(N\right)=\sum _{j=1}^k(x_{i_{2j-1}}+x_{i_{2j}})>k,$$

(5)

which contradicts the condition $v^G\left(N\right)=k$.  □

Note that the same contradicting inequality (5) will be derived by assuming $x_{i_{2j-1}}+x_{i_{2j}}>1$ for some edge $(i_{2j-1},i_{2j})$ from the cover $U\left(G\right)$. The proof is complete.

Lemma 5.

Let the core be non-empty and x belong to the core. In addition, let $U\left(G\right)\in \Lambda \left(G\right)$ be some cover. Then for any edge $(i,j)\in U\left(G\right),$ $x_i+x_j=1$; for all vertices l outside the cover, $x_l=0$.

Lemma 5 leads to the following unbalancedness condition for the cover game.

Corollary 1.

Let $N_0={\cup }_{U\left(G\right)\in \Lambda \left(G\right)}(N\backslash \left\{U\left(G\right)\right\})$ be the set of all vertices that do not simultaneously belong to all covers of the graph G. If the subgraph $G_{N_0}$ has at least one edge, then the core in the cover game is empty.

Proof. 

Assume that the core is non-empty. Let $(i,j)\in E$ be an edge in the subgraph $G_{N_0}$. Due to Lemma 5, we obtain $x_i=x_j=0$. However, according to Lemma 3, $x_i+x_j\ge 1$. This contradiction completes the proof.  □

Corollary 2.

Let the core be non-empty, and let $N_0$ be the set of all vertices that do not simultaneously belong to all covers of the graph G (Corollary 1). In addition, let $N_1=\{i\in N\backslash N_0:\exists j(i,j)\in E\}$ be the set of all vertices adjacent to those from $N_0$. Then $x_i=1$ for all $i\in N_1.$

Proof. 

Let $i\in N_1$. According to Lemma 3, we have $x_i+x_j\ge 1$ for an edge $(i,j),i\in N_1,j\in N_0$. On the other hand, due to Lemma 5, $x_j=0$. Therefore, $x_i\ge 1$, and by Lemma 4, $x_i\le 1$. This finally yields $x_i=1,i\in N_1$.  □

Corollary 3.

Let G be a connected graph and n be an odd number. In addition, let the core be non-empty and x belong to the core. Then $\exists i\in N{x}_i=0,$ and $\exists j\in N{x}_j=1$.

Proof. 

Since the cover of G is composed of an even number of vertices, the set $N_0$ is non-empty. For any $i\in N_0,$ $x_i=0$. We take a vertex j adjacent to vertex i. According to Corollary 2, $x_j=1$.  □

Lemma 6.

Let a graph G have an even number of vertices, $n=2k$ and $v^G\left(N\right)=k$. Then the core is non-empty. Moreover, $x=(\frac{1}{2},\dots ,\frac{1}{2})$ belongs to the core.

Proof. 

Consider a cover $U\left(G\right).$ It has the form $U\left(G\right)=\{(i_1,i_2),\dots ,(i_{2k-1},i_{2k})\},$ being composed of k edges. Letting $x_i=\frac{1}{2},\forall i\in N$, we obtain $x_{i_j}+x_{i_{j+1}}=\frac{1}{2}+\frac{1}{2}=1$ for any edge of the cover $U\left(G\right).$ Due to Lemma 3, x belongs to the core.  □

Lemma 7.

Let G be a connected graph and t be a pendant vertex. In addition, let $s:(s,t)\in E$ be a vertex adjacent to t. If the core in the cover game on the subgraph $G_{N\backslash (s\cup t)}$ is non-empty (empty), then the core in the cover game on the graph $G_N$ is non-empty (empty, respectively) as well.

Proof. 

For a terminal vertex t there exists a cover $U\left(G\right)$ such that $(s,t)\in U\left(G\right)$ (Lemma 1). Consequently,

$$v^G\left(N\right)=\left|U\left(G\right)\right|=|U\left(G_{N\backslash (s\cup t)}\right)|+1=v^G(N\backslash (s\cup t))+1.$$

(6)

Assume that in the game on the subgraph $G_{N\backslash (s\cup t)},$ the core is non-empty, and $x=(x_1,\dots ,x_{n-2})$ belongs to the core. According to Lemma 3, $x_i+x_j\ge 1$ for all edges $(i,j)\in E$. Since vertex t is connected to vertex s only, the imputation $x^{\prime }=(x_1,\dots ,x_{n-2},1,0)$ satisfies inequalities (3). Hence, $x^{\prime }$ belongs to the core in the game on the graph G.

Now let the game on the subgraph $G_{N\backslash (s\cup t)}$ have an empty core. In this game, the system of inequalities $x_i+x_j\ge 1,i,j\in N\backslash (s\cup t),$ for all edges $(i,j)\in E$ will therefore contradict the condition ${\sum }_{i\in N\backslash (s\cup t)}{x}_i=v^G(N\backslash (s\cup t))$. In the game on the graph $G,$ the core needs to satisfy the additional condition $x_s+x_t\ge 1,$ meaning that the system of inequalities (3) will also contradict

$$\sum _{i\in N\backslash (s\cup t)}{x}_i+x_s+x_t=v^G\left(N\right)$$

due to (6).

Returning to the linear programming problem (4), we write it as:

$$min\sum _{i\in N}{x}_i$$

subject to

$$a_{ij}(x_i+x_j-1)\ge 0,\forall (i,j)\in N;$$

$$x_i\ge 0,\forall i\in N.$$

Here, $a_{ij}$ is a corresponding element of the adjacency matrix of the graph G.

Its dual problem has the form

$$\begin{array}{cc}\hfill max\sum _{(i,j)\in E}& e_{ij}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\sum _{j:(i,j)\in N}{e}_{ij}\le 1,& i=1,\dots ,n;\hfill \\ \hfill e_{ij}\ge 0,\forall (i,j)\in N;& e_{ij}=0,\forall (i,j)\notin E.\hfill \end{array}$$

(7)

In (7), a variable $e_{ij}\ge 0$ is associated with each edge of the graph $(i,j)\in E.$ For any pairs $(i,j)$ not representing edges, $e_{ij}=0$. Thus, problem (7) contains $\left|E\right|$ non-zero variables.

Interestingly, problems (4) and (7) always have an admissible solution. Therefore, their solutions always exist, and their values coincide. (This value is not necessarily an integer.) At the same time, the maximal packing size represents an integer.

Note that if the constraints of problem (7) involve only integer variables $e_{ij}\in \{0,1\}$, then the solution of (7) yields the maximal packing of the graph G. In this case, only one edge is associated with each vertex $i:$ $e_{ij}=1$.  □

Theorem 1

([1]). The graph packing game with vertex pairs is balanced if and only if the dual linear programming problem (7) has an integer solution. The core of the balanced graph cover game is the solution of problem (4).

Example 3.

Consider a packing game on a graph $G=(N,E)$, where $N=\{1,2,3,4,5\}$ and $E\left\{\right(1,2),(2,3),(2,4),(2,5),(3,4),(4,5\left)\right\}$. The solution of the linear programming problem (7) is $e_{23}=e_{45}=1$ (the other variables are $e_{ij}=0$). Solving problem (4) yields the core $x^{*}=(0,1,0,1,0)$.

Example 4.

Consider a packing game on a graph $G=(N,E)$, where $N=\{1,2,3,4,5\}$ and $E\left\{\right(1,2),(1,5),(2,3),(2,5),(3,4),(3,5),(4,5\left)\right\}$. The solution of the linear programming problem (7) is $e_{12}=e_{23}=e_{15}=1/2,e_{34}=1$ (the other variables are $e_{23}=e_{35}=e_{45}=0$). The optimal value is 2.5, meaning that the core is empty. Solving problem (4) yields $x^{*}=(1/2,1/2,1/2,1/2,1/2)$.

4. Graph Packing Game with Simple Paths of Length d > 2

Now consider a cooperative game $\Gamma =<N,G>$, in which the characteristic function $v^G\left(K\right)$ for a coalition $K\subset N$ is defined as the maximum number of simple paths of a fixed length d included in K without shared vertices. This characteristic function is monotonic and superadditive as well.

A set of disjoint simple paths $U\left(G\right)$ of a length d, on which $v^G\left(N\right)$ is achieved, will be called a packing of a graph $G.$ The set of all packings will be denoted by $\Lambda \left(G\right)$. The set $\Lambda \left(G\right)$ may be non-unique and composed of several sets.

The set of vertices forming paths from a packing $U\left(G\right)$ will be denoted by $\left\{U\right(G\left)\right\}$. We emphasize that the packing game definition implies

$$v^G\left(N\right)=\left|U\left(G\right)\right|=\frac{\left|\right\{U\left(G\right)\left\}\right|}{d},\forall U\left(G\right)\in \Lambda .$$

Example 5.

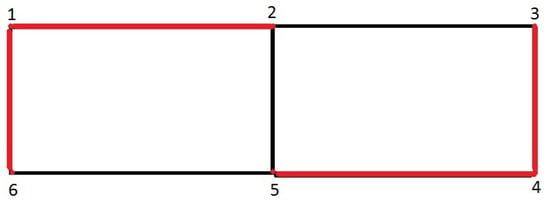
Consider a packing game on a graph $G=(N,E)$, where $N=\{1,2,3,4,5,6\}$ and $E=\left\{\right(1,2),(1,6),(2,3),(2,5),(3,4),(4,5),(5,6\left)\right\}$ (Figure 3), and let $d=3$. Then the packings are the coalition partitions $\left\{\right\{1,2,3\},\{4,5,6\left\}\right\}$, $\left\{\right\{1,6,5\},\{2,3,4\left\}\right\},$ and $\left\{\right\{2,1,6\},\{3,4,5\left\}\right\}$.

Figure 3. Graph packing by vertex triplets.

Lemma 8.

Let the core be non-empty and x belong to the core. In addition, let $U\left(G\right)\in \Lambda \left(G\right)$ be some packing. Then for any path $K\in U\left(G\right),$ ${\displaystyle \sum _{i\in K}}{x}_i=1$; for all vertices j outside the packing, $x_j=0$.

Proof. 

Let $U\left(G\right)=\{K_1,\dots ,K_l\}$. Then $v^G\left(N\right)=\left|U\left(G\right)\right|=l,$ and since $v^G\left(K\right)=1$, the existence condition of the core (1) implies ${\displaystyle \sum _{i\in K}}{x}_i\ge 1$. The effectiveness condition has the form ${\displaystyle \sum _{i\in N}}{x}_i=l$. On the other hand, ${\displaystyle \sum _{i\in N}}{x}_i={\displaystyle \sum _{j=1}^l\sum _{i\in K_j}}{x}_i+{\displaystyle \sum _{i\in N\backslash \cup K_j}}{x}_i\ge {\displaystyle \sum _{j=1}^l}1+0\ge l$. This non-strict inequality turns into equality if and only if $(\forall j\in \{1,\dots ,l\})({\displaystyle \sum _{i\in K_j}}{x}_i=1)$ and $(\forall i\in N\backslash \cup K_j)(x_i=0)$.  □

Lemma 9.

Let the number of vertices in a graph G be a multiple of the packing path length $d,$ $n=k·d,$ and $v^G\left(N\right)=k$. Then the core of G is non-empty, and the point $x=(\frac{1}{d},\dots ,\frac{1}{d})$ belongs to the core.

Proof. 

Assume that $U\left(G\right)=\{L_1,\dots ,L_k\}$ is the optimal packing of G composed of k disjoint paths of the length d. Letting $(\forall i\in N)(x_i=\frac{1}{d})$, we obtain ${\displaystyle \sum _{i=1}^n}{x}_i=\frac{1}{d}·kd=k=v^G\left(N\right)$ (the effectiveness condition holds) and ${\displaystyle \sum _{i\in L}}{x}_i=\frac{1}{d}·d=1\ge 1$ (the inequality constraints over all possible paths $L\in G$ are satisfied as equalities). Thus, the point $x=(\frac{1}{d},\dots ,\frac{1}{d})$ belongs to the core of G because it satisfies the appropriate requirements.  □

Lemma 10.

Let L be the set of paths of a fixed length d in the graph G. Then condition (1) for the core is equivalent to

$$C=\left\{x\right|{\displaystyle \sum _{i\in N}}{x}_i=v^G\left(N\right),{\displaystyle \sum _{i\in L_j}}{x}_i\ge 1,\forall L_j\in L\}.$$

(8)

Proof. 

Assume that condition (1) holds. By the definition of $v^G$, we have $v^G\left(L_j\right)=1,\forall L_j\in L$, and consequently, ${\displaystyle \sum _{i\in L_j}}{x}_i\ge v^G\left(L_j\right)=1,\forall L_j\in L$.

Now assume that condition (8) holds. Consider an arbitrary coalition S. If $v^G\left(S\right)=k$, then the coalition S contains k disjoint simple paths $\{L_1,\dots ,L_k\}$ of the length $d,$ each satisfying the inequality $({\displaystyle \sum _{i\in L_j}}{x}_i\ge 1).$ As a result, ${\displaystyle \sum _{i\in S}}{x}_i\ge {\displaystyle \sum _{i\in \{L_1,\dots ,L_k\}}}{x}_i={\displaystyle \sum _{j=1}^k\sum _{i\in L_j}}{x}_i\ge {\displaystyle \sum _{j=1}^k}1=k=v^G\left(S\right)$.  □

Remark 2.

Notice that the number of constraints for the core drops from exponential ($2^n$) to at most $\left(\genfrac{}{}{0pt}{}{n}{d}\right)$, which is polynomial in n for a fixed d.

We denote by L the set of all simple paths of a fixed length d in the graph G. With each simple path $L_k=\{i_1^{\left(k\right)},i_2^{\left(k\right)},\dots ,i_{d+1}^{\left(k\right)}\},$ $k=1,\dots ,\left|L\right|,$ of the length d in the graph G we associate a row vector $c^{\left(k\right)}=(c_{k1},\dots ,c_{kn})$, where $c_{kj}=1$ for $j=i_1,\dots ,i_{d+1}$ and $c_{kj}=0$ for other $j.$ We compile the matrix $C={(c^{\left(1\right)},\dots ,c^{\left|L\right|})}^T$ from the rows $c^{\left(1\right)},\dots ,c^{\left|L\right|}.$

Consider the linear programming problem:

$$\begin{array}{cc}\hfill min\sum _{i=1}^n& x_i\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\sum _{j=1}^{d+1}{x}_{i_j}\ge 1,& \forall L_k\in L;\hfill \\ \hfill x_i\ge 0,& \forall i\in N.\hfill \end{array}$$

(9)

The constraints can be written in the matrix form:

$$\sum _{j=1}^n{c}_{ij}{x}_j\ge 1,\forall i=1,\dots ,\left|L\right|;x_i\ge 0\forall i\in N.$$

With each path $L_k,$ $k=1,\dots ,\left|L\right|,$ we associate the variable $l_k.$

For problem (9), the dual problem is given by:

$$\begin{array}{cc}\hfill max\sum _{k=1}^{\left|L\right|}& l_k\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\sum _{i=1}^n{c}_{ij}{l}_i\le 1,& j=1,\dots ,n;\hfill \\ \hfill l_i\ge 0,& \forall i=1,\dots ,\left|L\right|.\hfill \end{array}$$

(10)

Both problems—the primal (9) and dual (10) problems—have admissible solutions. Therefore, there exist optimal solutions whose values coincide. Problem (10) contains n constraints, that is, there are no more than n non-zero variables in the solution.

Theorem 2.

The graph packing game with simple paths is balanced if and only if the dual linear programming problem (10) has an integer optimal solution. The core of the balanced graph packing game is the solution of the primal problem (9).

Proof. 

Notice that the problem of maximum packing of the graph G can be presented as the integer linear program

$$\begin{array}{cc}\hfill max\sum _{k=1}^{\left|L\right|}& l_k\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\sum _{i=1}^n{c}_{ij}{l}_i\le 1,& j=1,\dots ,n;\hfill \\ \hfill l_i\in \{0,1\},& \forall i=1,\dots ,\left|L\right|.\hfill \end{array}$$

(11)

So, if the optimal solution of the problem (10) is an integer then it gives some optimal packing of the graph. with optimal value $v^G\left(N\right)$. Then, a solution of primal linear problem (9) x will satisfy the conditions:

$$\sum _{j=1}^{d+1}{x}_{i_j}\ge 1,\forall L_k\in L;$$

and the optimal value be equal to

$${\displaystyle \sum _{i=1}^n}{x}_i=v^G\left(N\right).$$

From Lemma 10, it yields that x is in the core. Hence, the sufficiency of the statement follows.

Now assume that the core is not empty. According to Lemma 10, for x from the core: ${\displaystyle \sum _{i=1}^n}{x}_i=v^G\left(N\right)$ and ${\displaystyle \sum _{j=1}^{d+1}}{x}_{i_j}\ge 1$, for all simple paths $L_k$ of length d. According to the conditions of the problem, $v^G\left(N\right)$ is the maximum packing in the graph G. So, $v^G\left(N\right)$ is integer and a packing $\{L_k,k=1,\dots ,|L\left|\right\}$ exists, such that $v^G\left(N\right)=\left|L\right|$. This packing gives a corresponding solution of the integer linear program (11). By the duality property of linear programming, this solution is an integer optimal solution of the linear program (10). It proves the necessity of the statement.  □

Example 6

(continued).Let $N=\{1,2,3,4,5,6\}$ and the links be described by the graph in Figure 3. A solution of problems (9) and (10) is $x=(\frac{1}{2},\frac{1}{2},0,\frac{1}{2},\frac{1}{2},0)$. The values of both linear programming problems coincide, being equal to 2. The solution of the dual problem is indicated by red edges: the optimal packing is $\{6,1,2\}\cup \{3,4,5\}$. Other solutions of (9) are: $(\frac{1}{3},\frac{1}{3},\frac{1}{3},\frac{1}{3},\frac{1}{3},\frac{1}{3})$, $(0,\frac{1}{2},\frac{1}{2},0,\frac{1}{2},\frac{1}{2})$, $(0,1,0,0,1,0)$.

5. Examples of Graph Packing

5.1. Chain Graphs

5.1.1. Packing by Vertex Pairs. Chain Graph with Odd Number of Vertices

Let $N=\{1,\dots ,2k+1\}$ and $G=L_{2k+1}$ be a chain graph, that is, $E=\left\{\right(1,2),(2,3),\dots ,$ $(2k,2k+1)\}$. Then $v^G\left(N\right)=k,$ and there are $(k+1)$ packings of the following configuration. First, all vertices with even numbers are included in all these packings. Second, each vertex with odd numbers is not included in some packing. According to Lemma 5, $x_i=0$ for all odd numbers $i.$ Hence, by Corollary 2 of Lemma 5, $x_i=1$ for all even numbers $i.$ The resulting solution satisfies the effectiveness condition:

$${\displaystyle \sum _{i\in N}}{x}_i=k=v^G\left(N\right).$$

Therefore, the core exists and is composed of the unique point $(0,1,0,\dots ,1,0)$ (singleton). See Figure 4.

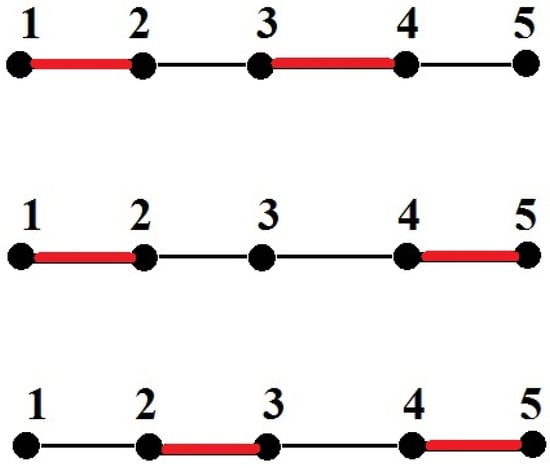
Figure 4. There are three possible packings of $L_5$ by pairs. According to Lemma 8, $x_1=x_3=x_5=0$. Moreover, $x_1+x_2=1,x_3+x_4=1$, so $x_2=x_4=1$. There is only unique point in the core: $(0;1;0;1;0)$.

5.1.2. Packing by Vertex Pairs. Chain Graph with Even Number of Vertices

Let $n=2k$ and $G=L_{2k}$ be a chain graph. Then $v^G\left(N\right)=k,$ and the unique packing has the form $\left\{\right(1,2),(3,4),\dots ,(2k-1,2k\left)\right\}$. The core of this game is non-empty and contains an infinite set of points, for example, the straight-line segment connecting the points (0, 1, …, 0, 1) and (1, 0, …, 1, 0) (Figure 5).

Figure 5. There is only unique packing of $L_4$ by pairs.

5.1.3. Packing by Vertex Triples

Let $n=3k$ and $G=L_{3k}$ be a chain graph. Then $v^G\left(N\right)=k,$ and the packing is composed of the set $\left\{\right(1,2,3),\dots ,(3k-2,3k-1,3k\left)\right\}$. The core is non-empty. For example, it contains the convex hull of the points $(1,0,0,\dots ,1,0,0)$, $(0,1,0,\dots ,0,1,0),$ and $(0,0,1,0,\dots ,0,0,1)$.

For the chain graph $G=L_{3k+1},$ $v^G\left(N\right)=k$. The packing is composed of the set $\left\{\right(1,2,3),\dots ,(3k-2,3k-1,3k\left)\right\}$. The core is non-empty and contains, for example, the straight-line segment connecting the points $(0,1,0,0,\dots ,1,0,0)$ and $(0,0,1,0,\dots ,0,1,0)$.

For the chain graph $G=L_{3k+2},$ $v^G\left(N\right)=k$. The packing is composed of the set $\left\{\right(1,2,3),\dots ,(3k-2,3k-1,3k\left)\right\}$. The core is composed of the unique point $(0,0,1,0,\dots ,1,0,0)$ (singleton). See Figure 6.

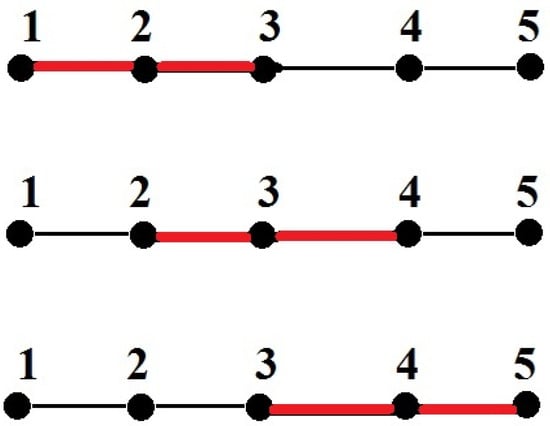
Figure 6. There are three possible packings of $L_5$ by triples. According to Lemma 8, $x_1=x_2=x_4=x_5=0$. Moreover, $x_1+x_2+x_3=1$, so $x_3=1$. There is only unique point in the core: $(0;0;1;0;0)$.

5.2. Cycle Graphs

5.2.1. Parking by Vertex Pairs. Cycle Graph with Odd Number of Vertices

Let $n=2k+1$ and $G=C_{2k+1}$ be a cycle graph, that is, $E=\left\{\right(1,2),(2,3),\dots (2k,2k+1),(2k+1,1\left)\right\}$. Then $v^G\left(N\right)=k$, and there are $(2k+1)$ packings of this graph. First, one of the vertices is not included in any packing. Second, each vertex from N is not included in some packing. According to Lemma 5, $x_1=\dots =x_{2k+1}=0,$ which contradicts the effectiveness condition $x_1+\dots +x_{2k+1}=k$. Hence, the core of the graph $C_{2k+1}$ is empty (see Figure 7).

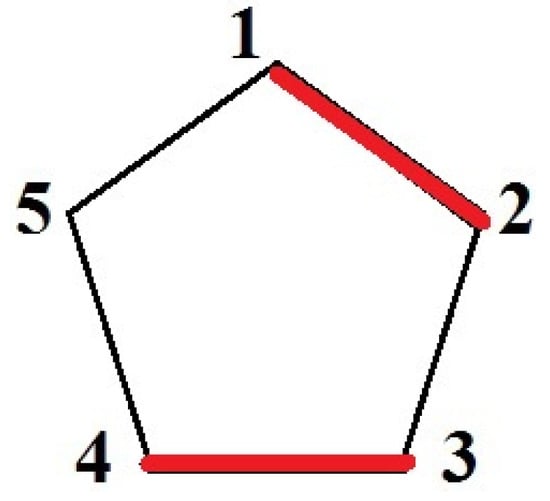
Figure 7. $C_5$: by “rotating” the packing set, one can see that each vertex is not included in some packing. So, $x_1=\dots =x_5=0$, which contradicts condition $x_1+\dots +x_5=2$.

5.2.2. Packing by Vertex Pairs. Cycle Graph with Even Number of Vertices

Let $n=2k$ and $G=C_{2k}$ be a cycle graph. Then $v^G\left(N\right)=k,$ and there are two packings only. According to Lemma 6, the core of the graph G is non-empty: it contains at least the point $B(1/2,\dots ,1/2),$ but this point is not the only one.

In this case, the system of constraints (3) for the core reduces to $x_1+\dots +x_{2k}=k,x_1+x_2\ge 1,x_2+x_3\ge 1,\dots ,x_{2k}+x_1\ge 1$. Summing all inequalities and dividing the resulting expression by 2 gives $x_1+\dots +x_{2k}\ge k$. This inequality will not contradict the equality if and only if it turns into equality. To this effect, all inequalities must hold as equalities: $x_1+x_2=1,x_2+x_3=1,\dots ,x_{2k}+x_1=1$. Letting $x_1=t,t\in [0,1],$ we obtain $x_2=1-t,x_3=t,\dots ,x_{2k}=1-t$. Hence, the core of the graph $C_{2k}$ has the form $\left\{\right(t,1-t,\dots ,t,1-t),t\in [0,1\left]\right\}$. See Figure 8.

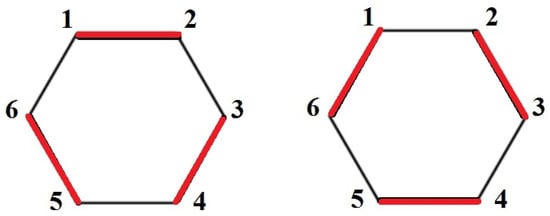
Figure 8. Two packings of $C_6$. All vertices are in the packing.

5.2.3. Packing by Vertex Triples. Cycle Graph

Let $n=3k$ and $G=C_{3k}$ be a cycle graph of length 3. Then $v^G\left(N\right)=k,$ and there are three packings, $U_1=\{(1,2,3),(4,5,6),\dots ,(3k-2,3k-1,3k)\}$, $U_2=\{(2,3,4),(5,6,7),\dots ,(3k-1,3k,1)\}$, and $U_3=\{(3,4,5),(6,7,8),\dots ,(3k,1,2)\}$. According to Lemma 8, this case generates the system of equations $x_1+x_2+x_3=1,x_2+x_3+x_4=1,\dots ,x_{3k}+x_1+x_2=1$. Its solution is defined by two degrees of freedom: $x_1,x_2,1-x_1-x_2,\dots ,x_1,x_2,1-x_1-x_2$, for example: $(\frac{1}{3},\dots ,\frac{1}{3})$ and $(1,0,0,\dots ,1,0,0)$. The core is non-empty.

Now let $C_{3k+1}$ and $C_{3k+2}$ be cycle graphs of some length not representing a multiple of 3. Then in both cases, $v^G\left(N\right)=k.$ Some vertex is not included in any packing, and each vertex is not included in some packing. According to Lemma 8, $x_1=\dots =x_n=0$, which contradicts the effectiveness condition $x_1+\dots +x_n=k$. Hence, the core is empty (see Figure 9).

Figure 9. $C_4$: by “rotating” the packing set, one can see that each vertex is not included in some packing, so $x_1=\dots =x_4=0$, which contradicts condition $x_1+\dots +x_4=1$.

5.2.4. Packing by Vertex Pairs. Hamiltonian Cycle

Let $n=2k+1$ and the graph G contain the Hamiltonian cycle $C_{2k+1}$. Then $v^G\left(N\right)=k$. We compare the systems of constraints (3) describing the cores for G and $C_{2k+1}$. In both cases, the same equality constraint $x_1+\dots +x_{2k+1}=k$ appears, corresponding to the effectiveness condition. The system of inequality constraints for G includes all inequality constraints for $C_{2k+1}$ plus some additional ones. As mentioned above, the core of $C_{2k+1}$ is empty. Therefore, the core of G is empty as well.

5.3. Packing by Vertex Pairs. Trees

Using mathematical induction, we will demonstrate that the core of the tree $T_n$ is non-empty. Obviously, the core of the trivial graph i is non-empty (equal to 0). The core of the graph $T_2$ is also non-empty: it coincides with the straight-line segment connecting the points $(1,0)$ and $(0,1)$. Assume that for all trees with at most k vertices, the core is non-empty. Let $G=T_{2k+1}$ be a tree with $(k+1)$ vertices. There are pendant vertices in G. Removing any of the pendant vertices t and the adjacent one s, we pass to the graph $G_{N\backslash (s\cup t)}$, which is a tree or a forest. According to Lemma 7, the conclusions about the existence of the core in G and $G_{N\backslash (s\cup t)}$ are the same. By the induction hypothesis, the core of $G_{N\backslash (s\cup t)}$ is non-empty. Hence, the core of G is non-empty as well. We can easily describe the procedure for finding a point from the core. If $t\in G$ is a pendant vertex, and $s\in G$ is the adjacent vertex for t, then we pass to the graph $G_{N\backslash (s\cup t)}$, letting $x_t=0$, $x_s=1$, and so forth. If the graph splits into connected components, we apply this procedure for each component separately. See Figure 10.

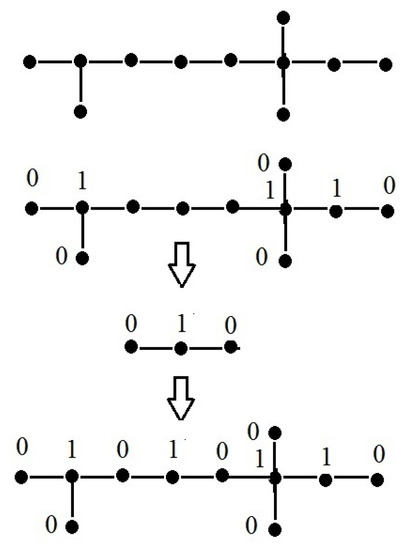
Figure 10. Finding a point in the core.

5.4. Packing by Vertex Triplets. Star Graph

Let $n\ge 4$ and G be a star graph, that is, $E=\left\{\right(1,2),(1,3),\dots ,(1,n\left)\right\}$. Then $v^G\left(N\right)=1,$ and there are $C_{n-1}^2$ packings, each composed of vertex 1 and two elements from the set $N\backslash 1$. Moreover, some vertices from $N\backslash 1$ are not included in any packing; each vertex from $N\backslash 1$ is not included in some packing. According to Lemma 8, $x_2=\dots =x_n=0$ and consequently, $x_1=1$. The point $(1,0,\dots ,0)$ is the unique one belonging to the core (see Figure 11).

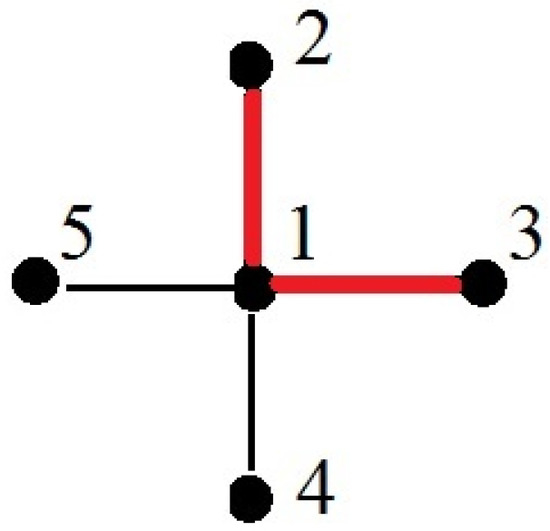
Figure 11. Star graph, $n=4$. When the graph is rotated, each vertex of the graph except vertex 1 is not included in some packing, so $x_2=\dots =x_5=0$. $x_1+x_2+x_3=1$ yields $x_1=1$.

5.5. Complete Graphs

5.5.1. Packing by Vertex Pairs. Complete Graph with Odd Number of Vertices

Let $n=2k+1$ and G be a complete graph. Then $v^G\left(N\right)=k$. The complete graph contains a Hamiltonian cycle, so that is a subcase of Section 5.2.4. Hence, the core of the graph $K_{2k+1}$ is empty.

5.5.2. Packing by Vertex Pairs. Complete Graph with Even Number of Vertices

Let $n=2k$, where $k\ge 2$ and G are complete graphs. Then $v^G\left(N\right)=k,$ and by Lemma 6, the core contains the point $(1/2,\dots ,1/2)$. Consider the system of constraints (3) describing the core. This system includes the equality $x_1+\dots +x_{2k}=k$ and $\frac{2k(2k-1)}{2}$ inequalities of the form $x_i+x_j\ge 1$. Summing all these constraints and dividing the resulting expression by $(2k-1)$ gives $x_1+\dots +x_{2k}\ge k$. This condition holds only if all inequality constraints from (3) are equalities, that is, $x_i+x_j=1,\forall i\ne j$. It yields $x_1=\dots =x_{2k}=1/2$. Assuming that $x_i<\frac{1}{2}$, we obtain $x_j>\frac{1}{2},j\in N\backslash i$ and, consequently, $x_{j_1}+x_{j_2}>1,j_1,j_2\in N\backslash i$. Analogously, the case $x_i>\frac{1}{2}$. Therefore, the core is composed of the unique point $(\frac{1}{2},\dots ,\frac{1}{2})$.

5.5.3. Packing by Vertex Triplets. Complete Graph with Number of Vertices Multiple of 3

Let $n=3k$ and G be a complete graph. Then $v^G\left(N\right)=k,$ and the set of packings has the following configuration. First, all vertices are included in each packing; second, any vertex triplet $i,j,k\in N$ is included in some packing. Consequently, all admissible vertex triplets $i,j,k$ satisfy the equality $x_i+x_j+x_k=1$. This system has the unique solution $(\frac{1}{3},\dots ,\frac{1}{3})$. For example, from $x_1+x_3+x_4=1$, $x_2+x_3+x_4=1$ it follows that $x_1=x_2$ and, in a similar way, $x_1=\dots =x_{3k}=\frac{1}{3}$. So, the core is non-empty and is composed of the unique point (singleton) $(\frac{1}{3},\dots ,\frac{1}{3})$.

Now let $n=3k+1$ or $n=3k+2,$ and let G be a complete graph. Then in both cases, $v^G\left(N\right)=k,$ and the set of optimal packings has the following configuration. First, some vertices are not included in all packings. Second, each vertex is not included in some packings. According to Lemma 8, $x_1=\dots =x_n=0$, which contradicts the effectiveness condition $x_1+\dots +x_n=k$. Hence, the core is empty.

5.6. Complete Bipartite Graphs

5.6.1. Packing by Vertex Pairs. Same Number of Vertices in Graph Parts

Consider the bipartite graph $K_{m,m}$. Then $v^G\left(N\right)=m,$ and there are $m!$ packings, each composed of all $2m$ vertices. We renumber the vertices of G so that the graph parts are composed of the sets $\{1,2,\dots ,m\}$ and $\{m+1,m+2,\dots ,2m\}$.

Then, condition (3), under which a point $(x_1,x_2,\dots ,x_{2m})$ belongs to the core, reduces to $x_1+\dots +x_{2m}=m$, $min(x_1,\dots ,x_m)+min(x_{m+1},\dots ,x_{2m})\ge 1$. However, $x_1+\dots +x_{2m}=(x_1+\dots +x_m)+(x_{m+1}+\dots +x_{2m})\ge m·min(x_1,\dots ,x_m)+m·min(x_{m+1},\dots ,x_{2m})\ge m,$ and this non-strict inequality must hold as equality. (Otherwise, it will contradict the effectiveness condition.) The equality is the case if and only if $x_1=\dots =x_m,$ $x_{m+1}=\dots =x_{2m},$ and $x_1+x_{m+1}=1$. Hence, the core has the form $(t,\dots ,t,1-t,\dots ,1-t),t\in [0,1]$ (see Figure 12).

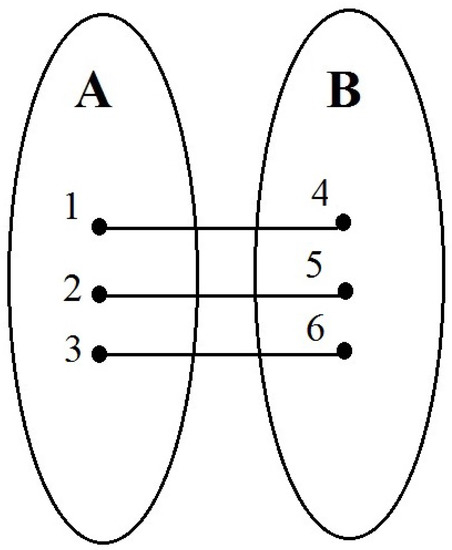
Figure 12. Each vertex is at any packing.

5.6.2. Packing by Vertex Pairs. Different Number of Vertices in Graph Parts

Consider a graph $G=K_{m,p}$, where $m<p$. Then $v^G\left(N\right)=m,$ and there are $A_p^m$ packings of the following configuration. First, all m vertices from the smaller part and some m vertices from the greater part are included in each packing. Second, each vertex from the greater part is not included in some packings. According to Lemma 5, the components $x_i$ are 0 for all vertices from the greater part. Due to Corollary 2 of Lemma 5, the components $x_i,i=1,\dots ,m,$ are 1 for all vertices from the smaller part. Consequently, $x_j=0,j=m+1,\dots ,m+p$ (see Figure 13).

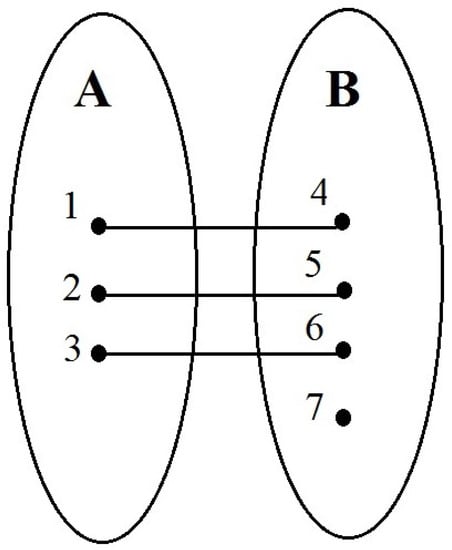
Figure 13. Each vertex from B is not included in some packings, so $x_4=\dots =x_7=0$, and $x_1=x_2=x_3=1$.

5.7. Zachary’s Karate Club Network

Consider the packing game for the well-known Zachary’s karate club network [21]. The graph of this network (Figure 14) describes the relations among 34 karate club members. There are 77 edges in total. The principal persons of the network are vertices 1 and 34.

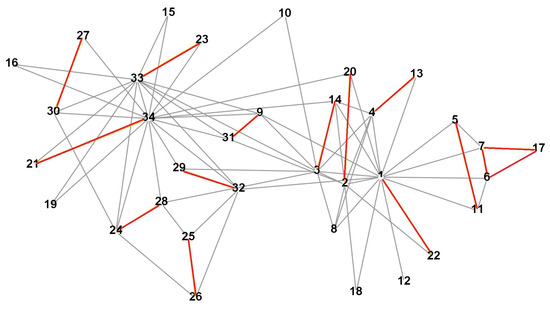
Figure 14. Packing by pairs for Zachary’s karate club network.

First, we analyze the packing by pairs case. The primal problem (4) has the solution

$$x^{*}=(1,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{2},0,0,0,\frac{1}{2},0,0,0,0,0,\frac{1}{2},0,0,0,0,0,0,1,1,0,0,0,0,1,1,1,1,1)$$

and the optimal value is 13.5.

The solution of the dual problem (7) is given by

$$e_{1,22}=1,e_{2,20}=1,e_{3,14}=1,e_{4,13}=1,e_{5,11}=1,e_{6,7}=\frac{1}{2},e_{6,17}=\frac{1}{2},e_{7,17}=\frac{1}{2},$$

$$e_{9,31}=1,e_{21,34}=1,e_{23,33}=1,e_{24,28}=1,e_{25,26}=1,e_{27,30}=1,e_{29,32}=1,$$

the other variables being equal to 0. In Figure 14, the packing corresponding to the nonzero variables is indicated by the red color. The optimal values of both problems are the same and are equal to 13.5. This game is unbalanced, and the core is empty. This result can be established directly using the lemmas provided above. There is a pendant vertex 12 in the graph. According to Lemma 7, we remove vertex 12 and its adjacent vertex 1. (The conclusions regarding the existence of the core in the original and resulting graphs will coincide.) The graph obtained by removing vertices 1 and 12 splits into two connected components, one of which contains five vertices. They are connected by the Hamiltonian cycle 5-7-17-6-11-5. Hence (see Section 5.2.4), the core of this graph is empty. This means that the core of the original graph is empty as well.

Now, consider the packing game with paths of length 3 (triplets) for this graph. The primal problem (9) have the solution:

$$x^{*}=(\frac{1}{3},1,\frac{1}{3},\frac{2}{3},\frac{1}{3},\frac{1}{3},\frac{1}{3},\frac{1}{3},\frac{2}{3},\frac{1}{3},\frac{1}{3},0,0,\frac{1}{3},0,0,\frac{1}{3},0,0,0,0,0,0,\frac{1}{3},\frac{1}{3},\frac{1}{3},0,\frac{1}{3},\frac{1}{3},\frac{2}{3},0,\frac{1}{3},1,\frac{1}{3}),$$

and the optimal value is $9\frac{2}{3}$.

The solution of the dual problems (10) is given by

$$l_{1,9,31}=1,l_{2,18,20}=1,l_{5,7,17}=l_{5,6,11}=l_{6,7,17}=l_{5,7,11}=l_{6,11,17}=\frac{1}{3},$$

$$l_{4,8,13}=1,l_{3,10,14}=1,l_{15,16,33}=1,l_{24,25,28}=1,l_{26,29,32}=1,l_{27,30,34}=1,$$

the other variables being equal to 0. In Figure 15, the cover corresponding to the nonzero variables is indicated by the red color. The optimal values of both problems coincide and are equal to $9\frac{2}{3}$. This game is also unbalanced, and the core is empty.

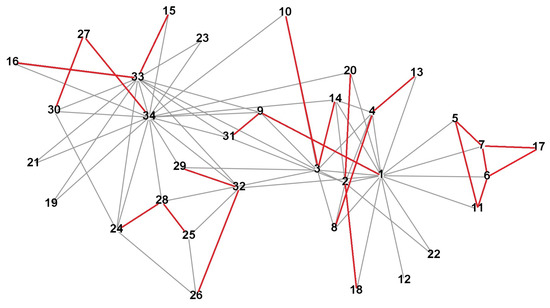
Figure 15. Packing by triplets for Zachary’s karate club network.

6. Conclusions

Important aspects in the structural analysis of networks include determining the centrality of graph vertices and the clustering of graphs, that is, identifying their most connected components. The centrality of a vertex estimates its significance for the entire network, in some sense reflected by the characteristic function. For example, if we are interested in the number of descendants, the characteristic function is the number of all edges of the graph belonging to a given coalition. If we are interested in the dissemination of information or the propagation of epidemics through a network, the characteristic function is the number of simple paths of various lengths in a given coalition.

In this paper, the characteristic function has been defined as the maximum number of disjoint simple paths of a fixed length. In a sense, this is also a centrality measure for graph vertices, which describes their significance when covering the network by independent paths of a fixed length. Possible applications include the design of telecommunications or transportation networks.

The corresponding cooperative game has been considered using the core as an optimality principle. As has been demonstrated, in this case, the graph packing problem is solved (and the centrality of graph vertices is determined) by solving primal and dual linear programming problems of a special form. Even if the game is unbalanced (the core is empty), the solution of the two linear programming problems always exists, makes sense, and can be used in practice.

The authors wish to thank the anonymous referees for their valuable suggestions which have improved the presentation of this paper.