Free Cells in Hyperspaces of Graphs

Abstract

Often for understanding a structure, other closely related structures with the former are associated. An example of this is the study of hyperspaces. In this paper, we give necessary and sufficient conditions for the existence of finitely-dimensional maximal free cells in the hyperspace $C\left(G\right)$ of a dendrite G; then, we give necessary and sufficient conditions so that the aforementioned result can be applied when G is a dendroid. Furthermore, we prove that the arc is the unique arcwise connected, compact, and metric space X for which the anchored hyperspace $C_p\left(X\right)$ is an arc for some $p\in X$.

1. Introduction

In the study of a mathematical structure, sometimes other structures that allow for visualizing problems in different ways are built.

One of the theories developed using this type of study is the Theory of Hyperspaces; this theory began with the investigations of F. Hausdorff and L. Vietoris. Given a topological space X, the $2^X$ hyperspace of all nonempty and closed subsets of X was introduced by L. Vietoris in 1922, and he proved basic facts about $2^X$—for example, compactness of X implies compactness of $2^X$ and vice versa; $2^X$ is connected if and only if X is connected. When X is a metric space, $2^X$ can be endowed with the Hausdorff metric (defined by F. Hausdorff in 1914).

The hyperspace of all nonempty, closed and connected subsets of X is denoted by $C\left(X\right)$ and considered as a subspace of $2^X$. In turn, the hyperspace of all nonempty, closed, and connected sets of X containing a point p, which is denoted by $C_p\left(X\right)$, is a subspace of $C\left(X\right)$.

The hyperspaces $C\left(X\right)$ and $C_p\left(X\right)$ are subjects of study for many researchers. Among several topics about hyperspace, one of the most interesting is to recognize a hyperspace as homeomorphic to some known space: Ref. [1] presents a special class of spaces X for which $C\left(X\right)$ is homeomorphic to the infinite cylinder $X\times {\mathbb{R}}_{\ge 0}$. Another interesting topic is to analyze topological properties: for compact, connected, and metric X, the hyperspaces $C_p\left(X\right)$ are locally connected for all $p\in X$ [2].

Graphs have been widely and deeply studied (see [3,4,5,6,7]) and have proved to be an excellent tool for representing and modeling different structures in several areas of discrete mathematics and computation (see [8,9]). As far as hyperspace is concerned, there exist some works relating both subjects. For example, Duda [10] proved that a space X is a finite graph if and only if $C\left(X\right)$ is a polyhedral. In a dendroid X smooth in a point p, $C_p\left(X\right)$ is homeomorphic to the Hilbert cube if and only if p is not in the interior of a finite tree in X, a result due to Carl Eberhart [11]. Recently, Reyna et al. proved that, in a local space X, $C_p\left(X\right)$ is a polyhedral for all p if and only if X is a finite graph [12].

In this paper, we are concerned with fully determining the existence of maximal finite dimensional free cells in the hyperspace $C\left(X\right)$, first of a dendrite and then a dendroid X, as well as examining necessary and sufficient conditions for the hyperspace $C_p\left(X\right)$ if an arc provided X is an arc-wise connected space.

2. Definitions

Throughout this paper, the term space is meant to be a connected, compact, and metric space, and a subspace is understood to be a subset of a space which is a space itself. Given a space X, the symbol $2^X$ denotes the hyperspace of non-empty closed subsets of X, and $C\left(X\right)$ is the hyperspace of non empty subspaces of X both endowed with the Hausdorff’s metric, two models of hyperspaces are shown in Figure 1. Notice that X is naturally embedded in $2^X$ via the map $x\mapsto \left\{x\right\}$ (compare with ([13] [0.48]).

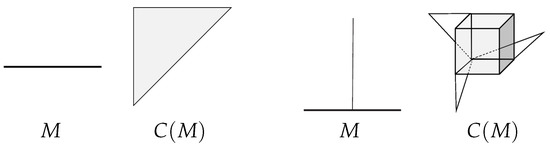
Figure 1. The hyperspaces $C\left(M\right)$ for the path $P_2$ and the star $S_3$.

Given a point $p\in X$, the anchored hyperspace of X at p, denoted by $C_p\left(X\right)$, is the subspace of $C\left(X\right)$ consisting of those elements containing p. Note that $C_p\left(X\right)$ is a subspace of $C\left(X\right)$, which in turn is a subspace of $2^X$.

A space X is unicoherent if, for any $A,B\subset X$ subspaces such that $X=A\cup B$, we have that $A\cap B$ is connected. The space X is called hereditary unicoherent if each subspace is unicoherent.

A graph G, consisting of a set $V\left(G\right)$, called the vertices of G and a set $E\left(G\right)$ of unordered pairs of elements of $V\left(G\right)$, called the edges of G. Letting G be a graph, if two vertices x and y of G form an edge, we say that they are adjacent, and this is denoted by $x\sim y$. This fact is also expressed by saying that x and y are neighbors. A vertex of G is called a ramification vertex if it has three or more neighbors and a terminal vertex if it has exactly one neighbor. G is called simple if it contains no loops (a vertex adjacent to itself) and possesses at most one edge between any two vertices. A path between two vertices u and v of G is a finite sequence of consecutive adjacent vertices such that the first one is u and the last one is v. G is connected if there is a path between any two vertices. A cycle in G is a finite sequence of at least three consecutively adjacent vertices such that the first one and the last one are adjacent. In this paper, we consider simple and connected graphs without cycles whose vertices are ramification or terminal vertices, that is, there are no vertices with exactly two neighbors.

In order to consider a graph G as a metric space, if we use the notation $[u,v]$ for the edge joining the vertices u and v, we must identify any edge $[u,v]\in E\left(G\right)$ with the closed interval $[0,l]$ (if $l:=L\left(\right[u,v]$); therefore, any point in the interior of any edge is a point of G and, if we consider the edge $[u,v]$ as a graph with just one edge, then it is identified with the closed interval $[0,l]$. A connected graph G is naturally equipped with a distance defined on its points, induced by taking shortest paths in G. Then, we see G as a metric graph (see [10,14]); according to this, a dendroid is a simple and connected graph without cycles which is a hereditary unicoherent space; the comb and the harmonic fan are examples of dendroids (see Figure 2). By dendrite, we mean a locally connected dendroid. Any tree, the $F_{\omega }$, and the Gehmann dendrite are examples of these types of graphs (see Figure 3). Throughout this paper, G denotes a dendroid or a dendrite.

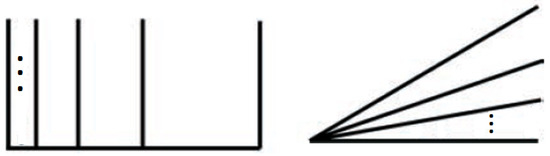
Figure 2. The comb and harmonic fan dendroids.

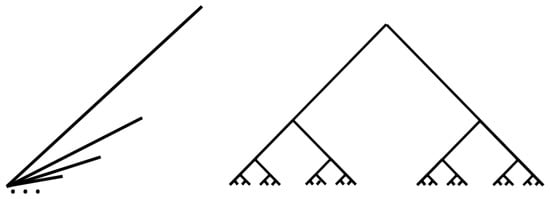
Figure 3. The $F_{\omega }$ and Gehmann dendrites.

A point $p\in G$ is called essential of type I if it is a vertex with infinitely many neighbors or essential of type II if there exists an infinite sequence of ramification vertices $\left(p_n\right)$ such that $p_n\to p$. We use the word essential to mean essential of type I or II. A point which is not a vertex, nor an essential point, is called an ordinary point; we denote $T\left(G\right)$, $O\left(G\right)$, $R\left(G\right)$, and $ES\left(G\right)$ the sets of terminal vertices, ordinary points, ramification vertices, and essential points, respectively.

The order of a point x in a dendroid G is defined as follows:

$$o_G\left(x\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} x \mathrm{is} \mathrm{a} \mathrm{terminal} \mathrm{vertex};\hfill \\ 2,\hfill & \mathrm{if} x \mathrm{is} \mathrm{an} \mathrm{ordinary} \mathrm{point};\hfill \\ n,\hfill & \mathrm{if} x \mathrm{has} \mathrm{exactly} n \mathrm{neighbors};\hfill \\ \infty ,\hfill & \mathrm{if} x \mathrm{is} \mathrm{an} \mathrm{essential} \mathrm{point}.\hfill \end{array}\right.$$

An m-dimensional cell (or m-cell for short) in a space X is a subspace M homeomorphic to ${[0,1]}^m$, the part of M homeomorphic to ${(0,1)}^m$ is called the interior manifold of M, and it is denoted by $M^{\circ }$, while $M-M^{\circ }$ is denoted with $\partial M$, and it is called the boundary manifold of M. If it occurs that the interior manifold $M^{\circ }$ is actually an open set of X, then M is called a free cell of X; Figure 4 shows a space with some free cells. In Theorem 2, we establish sufficient and necessary conditions for the existence of a maximal free m-cell in the hyperspace $C\left(G\right)$ for a dendrite G. Furthermore, in Theorem 3, we establish sufficient and necessary conditions so that Theorem 2 can be applied when G is an arbitrary dendroid.

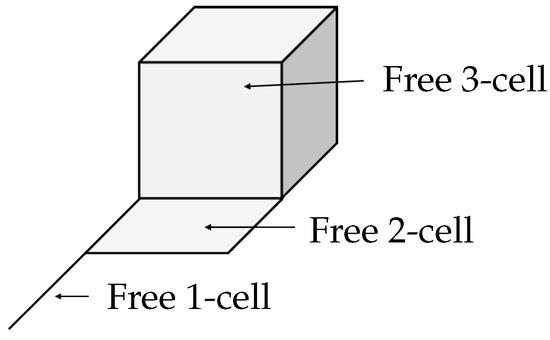
Figure 4. Free cells.

3. Preliminaries

Given $m\le n$, let A and B be $m,n$-cells, respectively, with $A\subseteq B$. If $m=n$, $A^{\circ }$ is an open subset of $B^{\circ }$. On the other hand, if $m<n$, then $A^{\circ }$ is not an open subset of $B^{\circ }$ because non-empty neighborhoods of $B^{\circ }$ contain m-dimensional open balls, and none of these can be contained in $A^{\circ }$. Therefore, the next lemma follows at once.

Lemma 1.

(a) If a cell is contained in a higher dimensional cell, then the first one is not a free cell. (b) Each m-cell contained in a free m-cell is a free m-cell.

In order to show that the cells that we are going to locate in hyperspace $C\left(G\right)$ of the dendrite G are maximal, we need Corollary 1 and Lemmas 2–5; in all of these, except Lemma 3, it is assumed that $A\subseteq B$ are m-cells.

Recall that Int A and Bd A designate, respectively, the topological interior and topological boundary of the set A.

Lemma 2.

If $\partial A=\partial B$, then $A=B$.

Proof. 

Since $A^{\circ }\subseteq B^{\circ }$, it remains to show that $B^{\circ }\subseteq A^{\circ }$. Let $x\in B^{\circ }$ and suppose $x\notin A^{\circ }$. Now, if we take $y\in A^{\circ }$, then $x,y\in B^{\circ }$. Let $\alpha$ be an arc from x to y contained in $B^{\circ }$. Then, the arc $\alpha$ contains an end point in $B-A$ and the other end point in $A^{\circ }$. It necessarily occurs that $\alpha \cap \partial A\ne \varnothing$, and this is absurd. □

Recall that the Borsuk–Ulam Theorem establishes that, for any continuous map $f:S^n\to {\mathbb{R}}^n$, there must exist some point $x\in S^n$ such that $f\left(x\right)=f(-x)$. This theorem, in particular, implies that no such maps can be one to one, and this is the key piece in the proof of next lemma.

Lemma 3.

The unique homemorphic copy of $S^n$ contained in $S^n$ is $S^n$ itself.

Proof. 

Let A be a proper homeomorphic subspace of $S^n$; notice that we can suppose that the North Pole is not contained in A (otherwise, apply a suitable rotation to $S^n$). If $\psi :S^n\to A$ is a homeomorphism and $\sigma$ is the usual stereographic projection of $S^n$ to ${\mathbb{R}}^n$ restricted to A, then $\sigma \circ \psi :S^n\to {\mathbb{R}}^n$ is a continuous one to one map, a contradiction. □

Corollary 1.

If $\partial A\subseteq \partial B$, then $A=B$.

Lemma 4.

If $B^{\circ }\subseteq A$, then $A=B$.

Proof. 

Let $x\in \partial B$ and let U be a neighborhood of x in B. Since $U\cap B^{\circ }\ne \varnothing$, $U\cap A\ne \varnothing$, and hence $x\in \overline{A}=A$. □

Lemma 5.

Let $x\in \partial A$, if $x\notin \partial B$, then $x\in$ Bd A.

Proof. 

Suppose $x\notin$ Bd A; then, $x\in$ Int A and hence Int $A\cap B^{\circ }$ is an open set in B containing x. Thus, there must exist a neighborhood V of x homeomorphic to ${(0,1)}^m$ contained in Int $A\cap B^{\circ }$, and the latter shows that x cannot belong to any face of A. In other words, $x\notin \partial A$. □

If $J=[p_1,p_2]$ is an arc, it is a well known fact that $C\left(J\right)$ is a 2-cell whose interior manifold are all subsets in the form $A=[a,b]$, where $a\ne b$ and none of these points equal to $p_1$ or $p_2$ (see [10]).

4. Free Cells in Hyperspaces of Dendrites

4.1. The Case $n=2$

We are close to announcing Theorem 2 where necessary and sufficient conditions are given for the existence of a maximal finite dimensional free n-cells in the hyperspace $C\left(G\right)$ of a dendrite G. The free cell built in its proof has the property that all of their elements contain a certain subspace A. In this particular case, the maximal free cells are the hyperspaces $C\left(J\right)$ with J an edge, and none of these cells have such a property. Therefore, the case $n=2$ needs to be treated separately. However, first, it is necessary to state the following known property about locally connected topological spaces.

Lemma 6.

In any locally connected topological space, the components of open sets are open sets.

Theorem 1.

The hyperspace $C\left(G\right)$ of a dendrite G contains a maximal free 2-cell $\mathcal{B}$ if and only if $\mathcal{B}=C\left(J\right)$ for some edge J of G.

Proof. 

Let J be an edge of G and $p_1$, $p_2$ their extremes, consider an element $A=[a,b]\in {\left(C\left(J\right)\right)}^{\circ }$ and let $\epsilon >0$ such that $N_{\epsilon }\left(A\right)\subseteq J^{\circ }$ (where $N_{\epsilon }\left(A\right)$ is the union of all open balls $B(x,\epsilon )$ as x ranges over all points of A). Hence, if $B(A,\epsilon )$ is the open ball (in the Hausdorff metric of $C\left(G\right)$) centered at A, then $B(A,\epsilon )\subseteq {\left(C\left(J\right)\right)}^{\circ }$ and $C\left(J\right)\subset C\left(G\right)$ is a free 2-cell.

Now, we see that the free cell $C\left(J\right)$ is maximal. Let $\mathcal{A}$ be a free 2-cell in $C\left(G\right)$ containing $C\left(J\right)$. If $A\in \partial C\left(J\right)$, we have (i) $A=[p_j,x]$, $(j=1orj=2)$ or else (ii) $A=\left\{x\right\}$ with $x\in [p_1,p_2]$. We claim that $A\in \partial \mathcal{A}$. If A is as (i), we have three sub-cases:

(1)

The point $p_j$ is a ramification vertex. Suppose with no loss of generality that $j=1$. If $A\notin \partial \mathcal{A}$, then $A\in {\mathcal{A}}^{\circ }$ and hence there must exist $\epsilon >0$ with $B(A,\epsilon )\subseteq {\mathcal{A}}^{\circ }$. Take $x_1,x_2\in N_{\epsilon }\left(A\right)-A$ such that $[x_1,p_1]\cap [x_2,p_1]=\left\{p_1\right\}$, $[x_i,p_1]\subseteq B(p_1,\epsilon )$ ($i\in \{1,2\}$) and a point $u\in (x,p_2)$ such that $[u,x]\subseteq B(x,\epsilon )$. The set

$$\mathcal{B}=\{A\cup [w_1,p_1]\cup [w_2,p_1]\cup [x,w_3]\mid w_1\in [x_1,p_1],w_2\in [x_2,p_1],w_3\in [u,x]\}$$

is a 3-cell (see [13] [Theorem 1.100]) contained in $B(A,\epsilon )\subseteq {\mathcal{A}}^{\circ }$, and this is absurd.

(2)

The point $p_j$ is essential.

A similar analysis as the previous case shows that a 3-cell contained in $B(A,\epsilon )$ could be built.

(3)

The point $p_j$ is a terminal vertex, and x is an ordinary point or a terminal vertex. In this case, we have $A\in$ Int $C\left(J\right)$, and this contradicts Lemma 5.

The above shows that $A\in \partial \mathcal{A}$ as desired. For the case ii), if we assume that $A=\left\{x\right\}$ and $A\notin \partial \mathcal{A}$, take $H\in {\mathcal{A}}^{\circ }-C\left(J\right)$ (see Lemma 4) and notice that H does not contain ramification points or essential points; otherwise, in a neighborhood of H contained in ${\mathcal{A}}^{\circ }$, 3-cells or even Hilbert cubes can be located (in the proof of Theorem 2, it is shown in detail how is this possible). Hence, H is an arc and let $q_1$ and $q_2$ denote their end points; according to this, it must be $p_1\in [x,q_1]$ or else $p_2\in [x,q_1]$. Suppose $p_1\in [x,q_1]$, and, using the fact that $H\ne \left\{x\right\}$ and ${\mathcal{A}}^{\circ }$ is arcwise connected, take $\alpha \subseteq {\mathcal{A}}^{\circ }$ an arc from $\left\{x\right\}$ to H. We claim that there exists $L\in \alpha$ such that $p_1\in L$. Otherwise, we have $\alpha \subseteq C\left(G\right)-C_{p_1}\left(G\right)$. Let U be the component of $G-\left\{p_1\right\}$ containing x, let V be the union of the remaining components and notice that $H\subseteq V$. By Lemma 6, U and V are open sets, hence $\mathcal{U}=\{B\in C(G)\mid B\subseteq U\}$ and $\mathcal{V}=\{B\in C(G)\mid B\subseteq V\}$ are non-empty, disjoint open sets in $C\left(G\right)-C_{p_1}\left(G\right)$ (compare with [15] [Theorem 4.5]) and therefore the sets $\alpha \cap \mathcal{U}$ and $\alpha \cap \mathcal{V}$ form a separation of $\alpha$, which is impossible, being $\alpha$ connected. This proves the existence of the desired L.

The point $p_1$ is a ramification vertex or an essential point; since $L\in {\mathcal{A}}^{\circ }$, as in the sub-cases (1) and (2) for some suitable ${\epsilon }^{\prime }>0$, it is possible to find a 3-cell contained in $B(L,{\epsilon }^{\prime })\subseteq {\mathcal{A}}^{\circ }$, and this is a contradiction once again. Therefore, in this case, it must be $A\in \partial \mathcal{A}$ and the result now follows from Corollary 1.

For the converse, let $\mathcal{B}\subseteq C\left(G\right)$ be a maximal free 2-cell and let $A\in {\mathcal{B}}^{\circ }$. Notice that A does not contain ramification vertices or essential points. The above remarks result in A needing to be an arc; if $J=[p_1,p_2]$ (where $p_1$, $p_2$ are vertices of G) is the edge containing A, we claim that $\mathcal{B}\subseteq C\left(J\right)$. Otherwise, let $B\in \mathcal{B}-C\left(J\right)$. Hence, for each $x\in B$ and for each $y\in A$, it occurs that a) $p_1\in [x,y]$ or b) $p_2\in [x,y]$. Suppose without loss of generality that a) occurs and let $\alpha$ be an arc in $\mathcal{B}$ from B to A such that $\alpha -\left\{B\right\}\subseteq {\mathcal{B}}^{\circ }$. Since $B\in C\left(J\right)$ and $A\in C\left(J\right)$, there must exist $C\in \alpha \cap \partial C\left(J\right)$. Hence, C has the form $[p_1,a]$. If $\epsilon >0$ is such that $B(C,\epsilon )\subseteq {\mathcal{B}}^{\circ }$, then $B(C,\epsilon )$ contains a 3-cell (if $p_1$ is a ramification point) or even a Hilbert cube (if $p_1$ is an essential point). This is a contradiction in any case. This shows that $B\in C\left(J\right)$ and therefore $\mathcal{B}=C\left(J\right)$. □

4.2. The Case $n>2$

We need to introduce some terminology about the hyperspace $C\left(K\right)$ for a tree K (for more details, see [10,12]).

An internal tree T of a tree K is a subgraph which is a tree not containing terminal vertices of K. Let $IT\left(K\right)$ denote the set of internal trees of K. For $T\in IT\left(K\right)$, let $I_1,\dots ,I_n$ be those edges of K such that $I_i\cap T\ne \varnothing$ and $I_i$ is not contained in T. We define

$$D(1,T)=T\cup \left({\displaystyle \bigcup _{i=1}^n{I}_i}\right),$$

and we say that this is the canonical representation of $D(1,T)$. Given an internal tree $T\subset K$, let $\mathfrak{M}\left(T\right)$ be the family of all subspaces of K in the form

$${\left({\left(c_i\right)}_{i=1}^n\right)}_T=T\cup \left({\displaystyle \bigcup _{i=1}^n[0_{I_i},c_i]}\right),$$

where $0_{I_i}$ is the vertex of $I_i$ contained in T, and $[0_{I_i},c_i]$ is the subarc of $I_i$ joining $0_{I_i}$ with $c_i$.

Lemma 7.

Let K be a tree, then

(i) 

For each internal tree $T\subset K$, the family $\mathfrak{M}\left(T\right)$ is a n-cell.

(ii) 

The hyperspace of $C\left(K\right)$ is

$$C\left(K\right)=\left[{\displaystyle \bigcup _{T\in IT\left(K\right)}\mathfrak{M}\left(T\right)}\right]\cup \left[{\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)}\right].$$

Theorem 2.

The hyperspace $C\left(G\right)$ of a dendrite G contains a maximal free n-cell ($n>2$) if and only if there exists a tree $K\subseteq G$ satisfying the following conditions:

(i) 

$T\left(K\right)=\{p_1,\dots ,p_n\}\subseteq R\left(G\right)\cup T\left(G\right)\cup ES\left(G\right)$,

(ii) 

for all $x\in K-T\left(K\right)$, $o_K\left(x\right)=o_G\left(x\right)$.

Proof. 

For each $p_i\in T\left(K\right)$, let $r_i\in R\left(K\right)$ such that $[r_i,p_i]\cap R\left(K\right)=\left\{r_i\right\}$.

Put $A=K-\left({\displaystyle \bigcup _{i=1}^n(r_i,p_i]}\right)$ and for each ${\displaystyle \mathbf{x}={\left(x_i\right)}_{i=1}^n\in \prod _{i=1}^n[r_i,p_i]}$ let $C_{\mathbf{x}}$ denote the set $A\cup \left({\displaystyle \bigcup _{i=1}^n[r_i,x_i]}\right)$. We claim that the family ${\displaystyle \mathfrak{M}\left(A\right)=\{C_{\mathbf{x}}\mid \mathbf{x}\in \prod _{i=1}^n[r_i,p_i]\}}$ is a maximal free n-cell in $C\left(G\right)$.

That $\mathfrak{M}\left(A\right)$ is actually a n-cell is due to [13], [Theorem 1.100]; therefore, we only need to verify the maximal and free properties.

Let $C_{\mathbf{x}}\in {\left(\mathfrak{M}\left(A\right)\right)}^{\circ }$ and define $L=(G-K)\cup \{p_1,p_2,\dots ,p_n\}$. Put $\alpha =d(C_{\mathbf{x}},L)=inf\{d(c,l)\mid c\in C_{\mathbf{x}},$$l\in L\}$, ${\alpha }_i=d(x_i,A),{\beta }_{ij}=d(x_i,[r_j,p_j])$, where $i\ne j$ and $i,j\in \{1,2,\dots ,n\}$. Since all these quantities are positive, take $\epsilon >0$ less than all those and $Y\in B(C_{\mathbf{x}},\epsilon )$. For each $i\in \{1,2,\dots ,n\}$, choose $z_i\in B(x_i,\epsilon )\cap Y$ and notice that $z_i\notin A\cup L\cup [r_j,p_j]$ if $i\ne j$, and hence $z_i\in (r_i,p_i)$. Now, if $x\in A$, there exists $z_i,z_j$ which are in different components of $K-\left\{x\right\}$. Then, $x\in [z_i,z_j]$, which shows that ${\displaystyle A\subseteq \bigcup _{i,j}[z_i,z_j]}$; since Y is arcwise connected, ${\displaystyle \bigcup _{i,j}[z_i,z_j]\subseteq Y}$ and therefore $A\subseteq Y$; in particular, no point belonging to A is a terminal vertex of Y.

We want to see that Y contains exactly n terminal vertices and these are contained in the arcs $(r_i,p_i)$. Let $y\in Y$ be a terminal vertex of Y. Since $y\notin L$, we have $y\ne p_i$ for all $1\le i\le n$ and $y\notin A$ gives $y\in (r_i,p_i)$ for some i. For the above argument, it follows that Y contains at most n terminal vertices; otherwise, two of them must belong to a same arc $(r_i,p_i)$ which is not possible.

Now, given $1\le i\le n,G_i=Y\cup [r_i,p_i]$ is a subspace of G. Since G is hereditary unicoherent, $Y\cap [r_i,p_i]$ is connected and non-degenerate (i.e., contains more than one point) because the arc $[r_i,z_i]$ is contained in the intersection and therefore such intersection is an arc whose extremes are $r_i$ and say $y_i$. The point $y_i$ is a terminal vertex of Y. This shows that Y contains at least n terminal vertices. We conclude $Y=C_{\mathbf{y}}\in {\left(\mathfrak{M}\left(A\right)\right)}^{\circ }$, where $y={\left(y_i\right)}_{i=1}^n$.

Let us verify that n-cell $\mathfrak{M}\left(A\right)$ is actually maximal; for this purpose, suppose there exists a free n-cell $\mathcal{A}\subseteq C\left(G\right)$ such that $\mathfrak{M}\left(A\right)\subseteq \mathcal{A}$ with $\mathfrak{M}\left(A\right)\ne \mathcal{A}$. By Corollary 1, it must occur that there exists some point $C_{\mathbf{x}}\in \partial \mathfrak{M}\left(A\right)$ such that $C_{\mathbf{x}}\in {\mathcal{A}}^{\circ }$. Take $\epsilon >0$ such that $B(C_{\mathbf{x}},\epsilon )\subseteq {\mathcal{A}}^{\circ }$.

Now, there are several cases to consider about the point $C_{\mathbf{x}}$. The first one arises when we suppose $C_{\mathbf{x}}=A\cup \left({\displaystyle \bigcup _{i=1}^n[r_i,x_i]}\right)$, where, for some index, say $i=1$, we have $x_1=p_1$ is a terminal vertex of K and, at the same time, a ramification vertex of the dendrite G.

Let $u_i\in [r_i,x_i]$ (for $2\le i\le n$) be points such that $[u_i,x_i]\subseteq B(x_i,\epsilon )$ and let $L_1,L_{n+1}$ be two different edges of G such that $L_1\cap L_{n+1}\cap K=\left\{p_1\right\}$. Consider also points $u_1\in L_1$ and $u_{n+1}\in L_{n+1}$ such that $[u_1,p_1]\subseteq B(p_1,\epsilon )$ and $[u_{n+1},p_1]\subseteq B(p_1,\epsilon )$.

For $y_1\in [p_1,u_1]$, $y_i\in [u_i,x_i](2\le i\le n)$ and $y_{n+1}\in [p_1,u_{n+1}]$, let $A_1=[p_1,y_1]$, $A_i=[u_i,y_i]$ and $A_{n+1}=[p_i,y_{n+1}]$. The family of all subspaces of the form ${\displaystyle A\cup \left(\bigcup _{i=1}^{n+1}{A}_i\right)}$ is an $(n+1)$-cell contained in $B(C_{\mathbf{x}},\epsilon )\subseteq {\mathcal{A}}^{\circ }$, and this is a contradiction. Similar considerations show that, if $x_i$ is an essential point for some i, then it is possible find an $(n+1)$-cell contained in ${\mathcal{A}}^{\circ }$.

A second case is obtained when, for some index i, say $i=1$, it occurs that $x_1=r_1$. In this case, $C_{\mathbf{x}}$ can not belong to Int $\left(\mathfrak{M}\right(A\left)\right)$ since this contradicts Lemma 5. However, if $C_{\mathbf{x}}\in$ Fr$\left(\mathfrak{M}\right(A\left)\right)$, consider the decomposition $C\left(K\right)=\left({\displaystyle \bigcup _{T\in IT\left(K\right)}\mathfrak{M}\left(T\right)}\right)\cup \left({\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)}\right)$ of Lemma 7 (ii). We claim that we may suppose $C_{\mathbf{x}}\in \left({\displaystyle \bigcup _{T\ne A}\mathfrak{M}\left(T\right)}\right)\cup \left({\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)}\right)$, where T runs over all internal trees of K different from A. Otherwise, there exists an open set $\mathcal{U}$ of $C\left(G\right)$ such that $C_{\mathbf{x}}\in \mathcal{U}\subseteq C\left(G\right)-\left({\displaystyle \bigcup _{T\ne A}\mathfrak{M}\left(T\right)}\right)\cup \left({\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)}\right)$.

Let N be the first positive integer such that $B(C_{\mathbf{x}},\frac{1}{N})\subseteq {\mathcal{A}}^{\circ }\cap \mathcal{U}$. Thus, for each $m\ge N$, there exists $Y_m\in C\left(G\right)-C\left(K\right)$, such that $H(Y_m,C_{\mathbf{x}})<\frac{1}{m}$. For each $m\ge N$, take a point $y_m\in Y_m-K$ and a point $x_m\in C_{\mathbf{x}}$ such that $d(y_m,x_m)<\frac{1}{m}$. Since G is compact, the sequence $\left(y_m\right)$ contains a convergent subsequence. We can suppose without loss of generality that $\left(y_m\right)$ is actually convergent, say, to y. We claim that $y\in C_{\mathbf{x}}$. Indeed, given $\epsilon >0$, choose $M\in \mathbb{N}$ such that $y_m\in B(y,\frac{\epsilon }{2})$ for all $m\ge M$. If $m\ge M$ satisfies $\frac{1}{m}<\frac{\epsilon }{2}$, then $d(x_m,y)\le d(x_m,y_m)+d(y_m,y)<\frac{1}{m}+\frac{\epsilon }{2}<\epsilon$, that is, $x_m\in C_{\mathbf{x}}\cap B(y,\epsilon )$. With $\epsilon >0$ being arbitrary, we conclude that $y\in C_{\mathbf{x}}$.

The above argument shows that y is a cluster point of $G-K$; this implies that $y=p_i$ for some index i, where $p_i\in R\left(G\right)\cup ES\left(G\right)$, and this case has already been analyzed. Thus, we may suppose $C_{\mathbf{x}}\in \left({\displaystyle \bigcup _{T\ne A}\mathfrak{M}\left(T\right)}\right)\cup \left({\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)}\right)$. In fact, by [10], [6.2, 6.3] or [12], [Lemma 2.6], we must suppose $C_{\mathbf{x}}\in \left({\displaystyle \bigcup _{T\ne A}\partial \mathfrak{M}\left(T\right)}\right)\cup \left({\displaystyle \bigcup _{I\in E\left(K\right)}\partial C\left(I\right)}\right)$. Supposing first that $C_{\mathbf{x}}\in \partial C\left(I\right)$ since the points belonging to the boundary manifold of a cell are cluster points of their interior manifold, we must have ${\mathcal{A}}^{\circ }\cap {\left(C\left(I\right)\right)}^{\circ }\ne \varnothing$. Now, this set is open in $\mathcal{A}$, and, on the other hand, is contained in $C\left(I\right)$; this is impossible since $Dim\left(\mathcal{A}\right)=n>2=Dim\left(C\right(I\left)\right)$.

Suppose now $C_{\mathbf{x}}\in \partial \mathfrak{M}\left(T\right)$. Recall that A is the internal tree obtained from K by removing their terminal edges. It follows by [10], [5.3, 7.1] that $Dim\left(\mathfrak{M}\right(T\left)\right)<Dim\left(\mathfrak{M}\right(A\left)\right)$. On the other hand, since $C_{\mathbf{x}}$ is a cluster point of ${\left(\mathfrak{M}\left(T\right)\right)}^{\circ }$, it must occur that ${\left(\mathcal{A}\right)}^{\circ }\cap {\left(\mathfrak{M}\left(T\right)\right)}^{\circ }\ne \varnothing$ and notice that this set is open in $C\left(G\right)$ and therefore open in ${\mathcal{A}}^{\circ }$. Hence, there exists a homeomorphic copy of ${[0,1]}^n$ contained in ${\left(\mathfrak{M}\left(T\right)\right)}^{\circ }$, which is impossible regarding the dimension of $\mathfrak{M}\left(T\right)$.

The final case to consider is obtained when, for some index i, $x_i=p_i$ with $p_i\in T\left(G\right)$ or else $x_i\in (r_i,p_i)$. In this case, it is not difficult see that $C_{\mathbf{x}}\in$ Int $\left(\mathfrak{M}\right(T\left)\right)$ contradicting Lemma 5. This shows that $\mathfrak{M}\left(A\right)$ is a maximal free n-cell as desired.

Conversely, let $\mathcal{A}$ be a free n-cell, $B\in {\mathcal{A}}^{\circ }$ and let us analyze how B looks. Let $T\left(B\right)=\{p_1,\dots ,p_k\}$ and let $r_1,\dots ,r_s\in B-T\left(B\right)$ be the points such that $o_B\left(r_i\right)<o_G\left(r_i\right)$. Put ${\alpha }_i=o_G\left(r_i\right)-o_B\left(r_i\right)$ and assume that ${\displaystyle k+\sum _{i=1}^s{\alpha }_i=m>n}$. Consider $\epsilon >0$ such that $B(B,\epsilon )\subseteq {\mathcal{A}}^{\circ }$ and for each $1\le i\le s$ consider also arcs $[u_{i_1},r_i],\dots ,[u_{i_{{\alpha }_i}},r_i]$ such that $[u_{i_j},r_i]\subseteq B(r_i,\epsilon )$ and $[u_{i_j},r_i]\cap B=\left\{r_i\right\}$. In addition, take points $v_t$ on the terminal edges of B such that $[v_t,p_t]\subseteq B(p_t,\epsilon )$ for $1\le t\le k$.

Letting $B_1=B-\left({\displaystyle \bigcup _{i=1}^n[p_t,v_t]}\right)$, we obtain that the family $\mathcal{H}$ of all subspaces of G has the form:

$$B_1\cup \left({\displaystyle \bigcup _{t=1}^k[v_t,x_t]}\right)\cap \left({\displaystyle \bigcup _{i=1}^s\left({\displaystyle \bigcup _{j=1}^{{\alpha }_i}[r_i,y_{i_j}]}\right)}\right),$$

where $x_t\in [v_t,p_t]$ and $y_{i_j}\in [r_i,u_{i_j}]$ is a m-cell contained in $\mathcal{A}$, which is absurd. Notice that the above argument in particular shows that $B-T\left(B\right)$ does not contain I-essential points. A similar reasoning shows that $B-T\left(B\right)$ also does not contain $II$-essential points. Now, assume that $m<n$. If $p_1,p_2,\dots ,p_q$ are the terminal vertices of B which are ordinal points of G, for each $1\le t\le q$, let $J_t$ be the edge of G such that $p_t\in J_t$ and for each $i\in \{1,\dots ,s\}$, let $I_{i_1},I_{i_2},\dots ,I_{i_{{\alpha }_i}}$ be the edges of G such that $J_{i_j}\cap B=\left\{r_i\right\}$. Hence, the tree $K=B\cup \left({\displaystyle \bigcup _{t=1}^q{J}_t}\right)\cup \left({\displaystyle \bigcup _{i=1}^s\left({\displaystyle \bigcup _{j=1}^{{\alpha }_i}{I}_{ij}}\right)}\right)$ has m terminal points and satisfies conditions (i) and (ii) and, by the only if part, we have already seen how to get a maximal free m-cell containing the above m-cell $\mathcal{H}$. Now, on the one hand, by Lemma 1, the cell $\mathcal{H}$ is free; on the other hand, since $\mathcal{H}\subseteq {\mathcal{A}}^{\circ }$, Lemma 1 (a) gives that $\mathcal{H}$ is not a free cell and, again, this is absurd. Thus, we conclude that $m=n$ and K is the desired tree. □

5. Free Cells in Hyperspace of Dendroids

In this section, necessary and sufficient conditions are given so that Theorem 2 can be applied for dendroids. For this purpose, the notion of convergence space is required.

A non degenerated subspace A of a space X is called convergence space if there exists a sequence $A_n$ of subspaces of X such that:

(1)

$lim{A}_n=A$,

(2)

$A_n\cap A=\varnothing$.

The subspaces $A_n$ can be chosen to be mutually disjoint (see [13] [5.11]).

Theorem 3.

Let G be a dendroid, a tree $K\subseteq G$, which satisfies the following conditions:

(i) 

$T\left(K\right)=\{p_1,\dots ,p_n\}\subseteq R\left(G\right)\cup T\left(G\right)\cup ES\left(G\right)$,

(ii) 

for all $x\in K-T\left(K\right)$, $o_K\left(x\right)=o_G\left(x\right)$.

If A is the tree obtained from K by removing their terminal edges, then A induces a maximal free n-cell $\mathfrak{M}\left(A\right)$ if and only if this cell does not contain convergence subspaces.

Proof. 

The cell $\mathfrak{M}\left(A\right)$ is constructed as in the proof of Theorem 2. It is not hard to see that, if $C_{\mathbf{x}}\in {\left(\mathfrak{M}\left(A\right)\right)}^{\circ }$ is a convergence subspace, then $\mathfrak{M}\left(A\right)$ can not be a free n-cell. On the other hand, if $\mathfrak{M}\left(A\right)$ is not a free n-cell, then there exists $Y=C_{\mathbf{x}}\in {\left(\mathfrak{M}\left(A\right)\right)}^{\circ }$ such that, for each $\epsilon >0$, there exists $Z\in C\left(G\right)-{\left(\mathfrak{M}\left(A\right)\right)}^{\circ }$ with $H(Y,Z)<\epsilon$.

Consider ${\alpha }_i=d(Y,p_i),\beta =H(Y,\partial \left(\mathfrak{M}\left(A\right)\right))$, ${\gamma }_{T^{\prime }}=H(Y,\left(\mathfrak{M}\left(A\right)\right))$ and ${\delta }_I=H(Y,C\left(I\right))$ (where T runs over the set of internal trees of K with $T\ne A$ and I runs over the set of edges of K). Since all these quantities are positive, take $\epsilon >0$ less than all of them and take $Z_1\in C\left(X\right)-\left(\mathfrak{M}\left(A\right)\right)$ such that $H(Z_1,Y)<\epsilon$. If $Z_1\cap Y\ne \varnothing$, we have the following cases:

(i)

$Z_1-K\ne \varnothing$,

in this case $p_i\in Z_1$ for some i. Hence, the ball $B(p_i,{\epsilon }_1)$ intersects Y, and this contradicts the choice of ${\epsilon }_1$.

(ii)

$Z_1\subseteq K$,

in this case, $Z_1\in C\left(K\right)=\left[{\displaystyle \bigcup _{T\in IT\left(K\right)}\mathfrak{M}\left(T\right)}\right]\cup \left[{\displaystyle \bigcup _{I\in E\left(K\right)}C\left(I\right)]}\right]$.

If $Z_1\in \partial \mathfrak{M}\left(A\right),Z_1\in \mathfrak{M}\left(T\right)$ with $T\ne A$ or $Z_1\in C\left(I\right)$, again this contradicts the choice of ${\epsilon }_1$. Therefore, $Z_1$ and Y are disjoint. Taking $0<{\epsilon }_2<H(Z_1,Y)$, in a similar way, we can obtain a subspace $Z_2$ with no points in common with Y and such that $H(Z_2,Y)<{\epsilon }_2$. Continuing with this process, we obtain a sequence $\left(Z_n\right)$ of mutually disjoint subspaces convergent to Y. □

6. Characterization of the Arc in Terms of Anchored Hyperspaces

The aim of this section is to prove that the arc is the unique arcwise connected space X, for which $C_p\left(X\right)$ is an arc for some $p\in X$ (Theorem 4). An important tool in the proof of this theorem is the use of order arcs. An order arc in $2^X$ is an arc $\alpha$ contained in $2^X$ such that, for any $A,B\in \alpha$, $A\subseteq B$ or $B\subseteq A$. The concepts and results we use for order arcs can be found in [13]. We use freely the notation found in there.

Proposition 1.

The anchored hyperspace $C_p\left(X\right)$ is an arc if and only if it is an order arc.

Proof. 

Let $\alpha$ an order arc in $C\left(X\right)$ from $\left\{p\right\}$ to X. Since $p\in A$ for all $A\in \alpha$, we have $\alpha \subseteq C_p\left(CX\right)$. Now, it is sufficient to show that $\left\{p\right\}$ and X are also the end points of $C_p\left(X\right)$, and this will be done by proving that neither $\left\{p\right\}$ nor X are cut points of $C_p\left(X\right)$ (see [16], [Theorem 1, Pag. 179]). Take different points $A,B\in C_p\left(X\right)-\left\{p\right\}$ if $\beta$ and $\gamma$ are order arcs from A to $A\cup B$ and from B to $A\cup B$ respectively, then $\beta \cup \gamma \subseteq C_p\left(X\right)-\left\{p\right\}$ is an arc containing the points A and B; this shows that $\left\{p\right\}$ is not a cut point of $C_p\left(X\right)$. Similarly, if $A,B\in C_p\left(X\right)-\left\{X\right\}$, taking $\beta$ and $\gamma$ order arcs from $\left\{p\right\}$ to A and from $\left\{p\right\}$ to B, one obtains that X is not a cut point either and therefore $\alpha =C_p\left(X\right)$. The converse is obvious. □

A point p of a space X is an irreducibility point of X if there exists another point q such that no proper subspace contains both points. The following result is due to Kuratoski and is a handy tool in the proof of Theorem 4.

Lemma 8

(Kuratoski’s Theorem, [15]). Let X be a space and let $p\in X$. Then, p is point of irreducibility of X if and only if X is not the union of two proper subspaces both of which contain p.

Theorem 4.

Let X be an arcwise connected space. Then, $C_p\left(X\right)$ is an arc for some $p\in X$ if and only if X is an arc.

Proof. 

By Proposition 1, $C_p\left(X\right)$ is an order arc from $\left\{p\right\}$ to X. It follows that X is not the union of two proper subspaces both containing the point p. By Lemma 8, it turns out that p is an irreducibility point of X, if $q\in X$ is another point such that no proper subspace of X contains the points p and q; the arcwise connectedness implies that $X=[p,q]$.

For the converse, suppose without loss of generality that $X=[0,1]$. Letting $p=0$, the map

$$x\mapsto [p,x],$$

is a homeomorphism from X to $C_p\left(X\right)$. □

The arcwise connectedness hypothesis is necessary in the above theorem (see [13] [Example 1.1]).

7. Comparative Studies and Conclusions

Some of the main goals on hyperspace research from a theoretical approach are: to obtain topological models corresponding to familiar or not difficult to handle spaces, to find relations between hyperspaces and their underlying spaces, uniqueness of hyperspaces, i.e., to investigate which spaces are the only ones whose hyperspaces possess a given structure. Motivated by the studies carried out in [17,18], the present work was deemed convenient by the authors. In the aforementioned works, the existence of cells in hyperspaces is characterized. Our work is carried out on infinite graphs and describes when such cells are free.

In [19], the arc is characterized in terms of anchored hyperspaces within the class of trees. In our work, we conduct a similar study but within a broader class of spaces, the arc-connected spaces.

Question: If the class of anchored hyperspaces of an arcwise connected space X matches the class of anchored hyperspaces of a connected graph G, does it follow that X and G are homeomorphic?