Abstract
This study presents a designated flipped classroom (FC) mathematics environment that utilizes a unique online platform designed for Arab minority students in Israel. It investigates how studying in an FC affects conceptual understanding and motivation to study mathematics among Arab high school students. The study also explores the factors that contribute to effective learning in the FC environment. Participants were 75 Arab high school students in 10th and 11th grades who studied advanced mathematics. Each grade group was randomly divided into two subgroups: an FC group and a traditional classroom group (comparison group). Quantitative questionnaires given before and after the learning program served to measure students’ motivation and conceptual understanding of the derivative and integral topics. Additionally, a random sample of students who studied in the FC group and the teacher who taught all the groups were interviewed. The study describes the positive effect an FC environment has on students’ conceptual understanding, particularly for 11th graders. The participants mostly appreciated how the FC resulted in less lecturing in class. The study contributes to the literature about FC among minorities and contributes to national and international efforts being made to reduce the gap in mathematics achievements between minorities and other sectors.
1. Introduction
Mathematics standards, e.g., [1,2], emphasize the importance of mathematics as a core subject for other disciplines, particularly in science, technology, engineering, and mathematics (STEM) domains. An effective STEM education relies essentially on strong mathematics teaching. The mathematics education that students receive in schools provides them with the tools that can be applied in solving diverse STEM problems in their future studies and careers [3], as in the case of derivatives and integrals and their profound application in chemistry and physics problems [4]. In this context, the authors of [5] described mathematics as “a gateway to many scientific and technological fields”. These standards recommend adopting learning methods and strategies that put students at the center of the learning process instead of the teacher. In the context of mathematics learning, students should be able to explore mathematical concepts and notions autonomously in order to reach a conceptual understanding of mathematics [6,7]. Conceptual understanding is considered critical for obtaining a thorough understanding of underlying and foundational mathematical concepts [6,8]. Although this helps students understand why mathematical ideas are important and useful in various contexts [9], extensive evidence in the literature shows that motivation is one of the most essential factors for students’ learning and performance, particularly in mathematics [10]. Although motivation, particularly intrinsic motivation, is an important prerequisite and mediator of learning and achievement, it is often lacking in many mathematics’ students [11].
Technology can contribute greatly to increasing students’ self-engagement and motivation towards STEM education, and mathematics in particular. One way in which technology is employed in education is through flipped classrooms (FCs), in which teachers use technology to deliver lectures and different materials to their students while they are outside the classroom [12]. An advantage of flipping the mathematics classroom is the use of a technological environment that can be available to everyone, which has the potential to make mathematics more accessible to all. This is especially significant for minority students who often lack access to excellent teachers or to advanced learning resources. In the Israeli context, the last results of the PISA study reported gaps between Arab and Jewish students in their achievements in STEM fields, and in mathematics in particular [13]. The Arab society in Israel constitutes about 21% of the general population. Due to the low socioeconomic level of a large percentage of the Arab population, they often lack adequate technological infrastructure and have only partial access to computers and therefore are characterized as having a low level of digital literacy. The COVID-19 pandemic has widened these gaps between Arab Israeli students and their Jewish counterparts even further [14]. Another important advantage of the FC in mathematics learning is its affordance of massive exercising during class [12]. Exercising in mathematics is considerably significant as it provides students with the ability to precisely process algorithms, procedures, and routines that further serve as a basis for solving more complex problems [15,16].
Several studies describe the advantages of the FC, while others discuss the challenges it poses. Further research is needed to investigate learning in this environment and its effects on students’ mathematical conceptual understanding and motivation, particularly in high school. Moreover, due to the lack of research on the Arab population, not enough is known about the effects of flipping the mathematics classroom in this minority group. The current study aims to explore the effects of integrating an FC mathematics learning environment (bscool.com) on Arab high school students’ conceptual understanding of mathematics and their motivation to study advanced mathematics. In order to reach conclusions about the advantages of integrating a flipped learning environment, the study explores the progress of a comparison group that studied in a traditional learning environment. The current study compares two age groups, namely 10th and 11th grade students, who study advanced mathematics (5 units), which is usually the choice made by students who excel in mathematics.
We chose students who studied mathematics on an advanced level because success at this level was found to be a strong predictive variable for future studies and employment in STEM fields [17]. The groups of students selected are in the critical stage of their studies, as Israeli students are explicitly prepared for the matriculation exam in mathematics starting from the 10th grade. The following sections provide a literature review about the flipped classroom, while presenting its benefits and challenges. We then review the literature about mathematical conceptual understanding and motivation to study mathematics and how they relate to studying in an FC environment.
1.1. Flipped Classroom
Contrary to the traditional approach in which the teaching process takes place inside the class via traditional, face-to-face lectures, in the flipped classroom approach, the materials and educational content are provided for students via technological means. The students learn the material while they are outside the classroom, and class time is mainly devoted to practicing that material [18,19]. This approach has two main components. One is out-of-class, independent learning using a variety of technological tools such as filmed lectures, presentations, computer simulations, and online tasks, which students can use to independently learn the content before attending class. The second component is interactive lessons that take place in the classroom and focus mainly on active learning through collaborative exercises and problem solving to achieve meaningful learning [20]. The flipped classroom approach is a method in which the student is at the center of the learning process, rather than the teacher [21,22]. The knowledge acquisition process is the responsibility of the student, who is required to independently learn the content before class and come to class prepared to complete the collective learning process.
1.2. Benefits of the FC Approach
Flipping the classroom gives the students the opportunity to learn and study the material at home so that the in-class lessons can be used mainly for interactive and cooperative learning activities with the teacher [23]. This approach provides the students with all the content material they need to learn before class. As a result, the teachers can devote most of their classroom time to practicing and helping their students master mathematical procedures and skills, which results in a more comprehensive and profound understanding of the material [24]. Proponents of this approach claim that it enables better use of class time [21,25,26] and helps teachers focus on the individual challenges faced by each student [18], explore different misconceptions, and provide deeper clarifications about incorrect notions. The increased interaction between teachers and their students that occurs when inverting the classroom enables teachers to identify the individual problems encountered by their students and to put more effort into helping them [23,27]. In the book Flip Your Classroom: Reach Every Student in Every Class Every Day [18], the authors state that the FC method allows teachers to dedicate a significant amount of class time to roaming around the classroom, monitoring their students’ learning and engagement, assessing their comprehension, and thereby providing appropriate assistance to their diverse needs. Students in flipped classrooms receive an education that is adapted to the different individual difficulties they encounter.
In order to master mathematical skills, students must adopt an excessive exercising routine, in which they need to solve an extensive amount of mathematical problems. Often, excising is considered time-consuming, as teachers are busy with trying to cover the content of the curriculum, and thus students are asked to work independently on exercises out of class or during class time when the teacher consults individual students [16]. However, in the FC, due to the extensive amount of time allocated for problem solving and exercising during class, students can not only have more time for exercising, but also demonstrate their understanding of a certain subject to their teacher, thus allowing the teacher to adapt the exercises to specific students’ needs or reduce the load of these students’ class and/or homework assignments. On the other hand, the teacher can identify the students who struggle with certain material and perform poorly when solving in-class assignments and thus provide these students with the individual assistance they need. This approach can also be beneficial for students as it makes the material readily available for them. They can access it repeatedly and view the filmed lectures as many times as needed to reach a full understanding of the material [23,27]. Moreover, students can benefit from two significant advantages of filmed lectures, namely “pause” and “rewind”. These features allow students to stop the video whenever they need to or rewind it so that they can take notes or get a better understanding of a specific part [18]. Contrary to the traditional learning approach in which students hear a lecture only once and must listen carefully to the teacher and take notes at the same time, in the FC approach, students can decide on the learning pace that is most appropriate for them in order to reach a comprehensive and complete understanding of the recorded lecture [28].
1.3. Challenges of the FC
Some studies showed that the flipped classroom can be challenging in several ways. One is the technological aspect, which is based on the premise that both teachers and students have access to the technological tools they need at all times [23,29]. Some students express antagonism towards innovative learning environments and prefer not to learn in an FC at all. Instead, they feel more comfortable with the traditional learning approach [23,27]. This can be attributed to several factors, such as their poor grasp of this unconventional learning method [23] or the need for more detailed instructions to understand how the FC works. Another possible inhibitor is that it requires students to be aware of their duties as learners and of the responsibility they must take for their own learning in the FC approach [29]. Furthermore, students may find it difficult to understand a new learning unit by themselves, without the teacher’s assistance, as they are accustomed to in the traditional classroom [29]. Flipping the classroom might also be challenging for teachers who have limited computer expertise or who lack the skills needed to prepare online, out-of-class materials, and particularly instructional videos [23,29]. The process of producing filmed content can be challenging, particularly since it requires teachers to properly and wisely determine the optimal length and quality of their videos for effective learning, in addition to investing time in producing the video [23,29].
1.4. Students’ Conceptual Understanding of Mathematics in the Flipped Classroom
The National Council of Teachers of Mathematics [2] (p. 7) defined mathematical conceptual understanding as “the comprehension and connection of concepts, operations, and relations”. According to this definition, instead of teaching concepts and operations as unrelated fields, teachers should use methods and techniques that build connections between them in order to develop students’ conceptual understanding [7]. Derivatives, for example, are a subject that most students usually have difficulty understanding and applying [30,31,32]. Despite being able to solve differentiation problems accurately, students do not fully understand how the derivative relates to its different definitions and representations such as the rates of change, slope of tangents, and limits [32,33]. Typically, most students perceive derivatives as a large number of differentiation rules without apparent reason or justification [33,34]. Therefore, it is of great importance to focus on improving students’ conceptual understanding of this topic. In the book Calculus from Graphical, Numerical, and Symbolic Points of View [35], the authors introduced the derivative concept by discussing three representations: First, they referred to it as the rate of change of a function at a specific point on it, which refers to the limit of the average rate of change in the surrounding of this given point. Then, they introduced derivatives as the slope of the tangent line in a specific point on the function, and they concluded by presenting the rules of computing derivatives. In [36], it was shown that students would succeed in understanding the concept of derivatives if they were able to successfully develop its different definitions and representations, i.e., the rate of change, the slope of the tangent line, the limit, the rules.
Another example is the concept of the definite integral. Several studies have reported that the indefinite integral is generally correlated with computing the area under a curve [4,37,38,39]. Different research studies show that students face no serious problems or challenges in computing the definite integral of a variety of functions based on the integration rules given in theory [4,40,41,42,43]. The study presented in [44] reinforces the previous statement, yet indicates that students perceived the symbolic and verbal definition of this concept as quite challenging. When the result of the definite integral comes out negative, students are not able to explain the meaning of negative areas [38]. Although this implies a high level of procedural understanding, it indicates an impaired conceptual one [4,37]. Conceptual understanding is described as an essential building block for mathematical fluency. Sometimes, it is referred to as conceptual knowledge, as it refers to obtaining an in-depth knowledge of the basic and fundamental mathematical concepts, which helps students comprehend the functionality behind these concepts [45]. In line with this definition, conceptual understanding can be evaluated based on the student’s ability to exemplify concepts, provide accurate examples, introduce a variety of mathematical representations, create connections with other concepts, and implement the functionality of the concept [45]. Several researchers demonstrated that learning mathematical algebraic operations without understanding their connection with the relevant mathematical concepts has a negative effect on learning and understanding mathematics [46].
The FC approach was found to be effective for a variety of students, including high- and low-achieving students, as this method allows the teacher to address students more individually in class and to offer them extra, detailed instructions, thus helping them better understand the mathematical concepts [47]. The main goal of the out-of-class resources available to students using this method is to provide them with a basic understanding of the mathematical concepts at an initial stage and then enhance that understanding through explanation and clarification of these mathematical concepts in the classroom [48]. In this case, the active and collaborative learning done in class facilitates teamwork and encourages massive exercising, as students solve problems with their classmates [26] and actively produce the knowledge they need to complete their assignments [12].
1.5. Students’ Motivation in Flipped Classrooms
Motivation is considered a crucial element that causes, initiates, and sustains successful learning over time [49,50,51]. According to [52], “to be motivated means to be moved to do something. A person who feels no impetus or inspiration to act is thus characterized as unmotivated, whereas someone who is energized or activated toward an end is considered motivated” [52] (p. 25). Particularly, a student’s motivation refers to their readiness and willingness to play a serious role in the learning process [53]. The self-determination theory presented by the authors of [54] highlights that motivation can emerge from experiences of autonomous learning. They differentiate between two types of motivation—external and internal. External motivation involves fostering students and encouraging them to act a certain way because of an external motive, such as receiving a reward or avoiding a punishment [54]. Internal motivation refers to the intrinsic interest and value attributed to a certain task. It is considered a motivating factor for students towards fulfilling a learning goal and therefore can play a substantial role in students’ performance and learning processes [10,55]. This is particularly true in the mathematical context, in which students often lack motivation [10]. The importance of motivating students toward mathematics learning is recognized as a way to improve their understanding. There has been much research into the relationship between cognitive, motivational, and affective factors, as well as the role of context in supporting students’ motivation [56,57].
Researchers suggested that encouraging active and collaborative learning in class, for example by raising topics for discussion, participating in discussions, and working in groups, can highly contribute to increasing students’ internal motivation towards mathematics learning [55]. Research shows that in the FC environment, students appear to be more satisfied, enjoy inverting their classroom, and cooperate better with both their teachers and peers [23,27,29,58], especially as this learning approach allows them to do their assignments at school along with their classmates and teacher, rather than at home as it is commonly accepted [59]. It is essential to emphasize that in order to ensure the success of the flipped classroom approach and to support students’ motivation to study in this environment, students must independently complete the required work before they come to class [28]. Otherwise, they will not gain the maximum benefit from the active cooperative learning that takes place in the classroom [60,61]. Several researchers claim that in addition to the need for higher autonomous learning and communication skills, students’ willingness to participate in online learning is essential for their motivation to learn in flipped classrooms [60,61]. As the preparations required of students in this case place an additional burden on learners compared to the traditional method [21,62], it certainly requires them to be highly motivated to complete them. Students who struggle with managing and controlling their online learning experience, and therefore come to class unprepared, are not likely to gain any benefits from this learning method [61]. In the traditional learning approach, students are mainly expected to attend their classes and listen to the lectures given by their instructors without prior preparation at home. Thus, motivation is a fundamental key for meeting the in-class and out-of-class requirements of the flipped classroom. Given the above, the present study addresses the following research question: will students’ conceptual understanding and motivation to study mathematics change over time, i.e., before and after studying an advanced mathematical learning unit? This research question is investigated by comparing Arab high school students who study in the FC environment using the bscool.com platform with students who study in a traditional learning environment and comparing students in 10th grade with those in 11th grade. Additionally, we explore how any differences found can be explained.
2. Materials and Methods
2.1. Context of the Study
The study was conducted within the framework of an extracurricular program at a private institute called Alkhawarizmi Institute of Languages and Mathematics, located in central Israel. Its target audience is Arab students, since it offers a large variety of educational courses in the three languages taught in Arab schools: Arabic, Hebrew, and English. Alkhawarizmi offers extracurricular courses and lessons in a variety of fields in addition to mathematics. The courses are available to students from grade 4 to grade 12. Each year, the institute welcomes nearly 1300 students from diverse cities and villages located in central Israel. One objective for founding Alkhawarizmi is to enrich the mathematical knowledge and language fluency of students from the Arab sector and contribute significantly to reducing the gaps between the performance of Jewish and Arab students in Israel. The monthly tuition at this institute is considered very reasonable compared to the cost of most private Jewish institutes. To enroll in a course at Alkhawarizmi, students pay a registration fee that includes two 90 min sessions per week, i.e., eight sessions per month. To further encourage Arab students to attend these courses and expand their mathematical knowledge, the institute offers scholarships for students from underprivileged socioeconomic backgrounds. Registration for any math course provides students with free access to bscool.com, an online platform designed by Alkhawarizmi for Arab high school students who study mathematics at all levels (from basic to advanced) according to the Israeli mathematics curriculum.
In the context of mathematics, this institute prepares Arab high school students for mathematics classes. The main reasons to attend this extracurricular program are to strengthen mathematical thinking and abilities and to receive more excessive practice than what is given in school. Moreover, the programs and courses provided by Alkhawarizmi aim to always be ahead of the teacher in school, so that students who participate in these programs gain confidence and motivation to learn mathematics. The Israeli math curriculum is taught at three main levels: 3 units, 4 units, and 5 units. These levels vary in difficulty as well as in the density of their contents. The participants in this study were students who study mathematics at the most advanced level taught in Israeli high schools, namely 5 units, which is usually the choice made by students who excel in mathematics. At this level, the focus is mainly on developing profound mathematical and scientific comprehension. This study focuses on two age groups: 10th and 11th grade students. This is due to the criticality of 10th grade in the context of mathematics studies in Israel. Israeli students are usually assigned to one of the three levels in 10th grade based on their performance in the 8th and 9th grades and on a comprehensive exam given at the beginning of 10th grade. In 10th grade, students have the opportunity of switching to a different class that studies mathematics at a higher or lower level based on their performance during the school year, and they often take advantage of this time to attempt to earn a seat in the 5-unit group. The 5-unit final matriculation grade is calculated based on the student’s grades in two final exams: Exam 806 and Exam 807. Students take the first matriculation exam (806) in 11th grade, which covers about 60% of all the material taught in the 5-unit curriculum. The second matriculation exam (807) is given in the 12th grade.
2.2. Research Participants
2.2.1. The Students
The participants in this study were 75 high school students (40% male) from the Arab sector who studied advanced mathematics (5 units) in high schools located in central Israel. Of these participants, 36 were 10th grade students, and 39 were 11th grade students. The participants were randomly assigned to one of two groups: (1) an FC learning environment, in which the students learn the mathematical content independently before class via bscool.com and engage in interactive learning in class, in which time is mainly spent on collaborative exercises with the teacher and peers, or (2) a traditional learning environment (comparison group), in which students study via the traditional, face-to-face method of learning, meaning that they attend class with no previous knowledge about the content that will be taught that day and count on their teacher to teach them the new material. In this case, less class time is spent on exercises and much more is spent on lectures. Students were enrolled in an annual course at Alkhawarizmi institute, in which they were required to attend classes twice a week. This study investigates a four-week period of this annual course, in which all the 10th graders studied the learning unit of derivatives and all the 11th graders studied the unit of integrals in accordance with the Israeli curriculum for mathematics. The participants did not study these subjects in math lessons in school, and therefore the presumption was that the first time these students were exposed to them was during this study. These two units were chosen for this study because derivatives are considered a basis for studying integrals. Students often perceive integrals as the opposite of derivatives and view the process of solving integrals as a matching game in which they try to restore the original function [63]. Both are essential subjects that are considered as a foundation for more advanced mathematical subjects [37], as well as for diverse STEM topics [64]. Thus, it is crucial that students master these topics [4,32,65]. However, several researchers have concluded that students struggle with understanding concepts such as integral, derivative, and function [4,66,67].
2.2.2. The Teacher
Saeed Watad, a mathematics teacher with approximately 25 years of experience, taught the students in both learning environments. He is the teacher who appears in the filmed lectures on the bscool.com platform. Watad is the founder of both bscool.com and Alkhawarizmi institute.
2.3. Research Environment
2.3.1. The Physical Setting
Two research environments were used in this study: an FC learning environment comprising two main settings, one physical and one online (bscool.com), and a traditional learning environment in the same physical setting as the FC environment. This section describes the physical settings used for both learning environments and the online platform bscool.com, a unique FC learning environment developed for Arab high school students. This study explores two math courses provided at the Alkhawarizmi Institute, one on derivatives (for 10th grade) and one on integrals (for 11th grade). Each course was taught by the same teacher, but using two different approaches for learning: FC vs. traditional. Students in the FC learning environment were asked to prepare the content before class by watching filmed lectures on bscool.com, taking notes on what they watched, and completing an assignment. To ensure that the students were committed and taking the program seriously, the teacher would roam around the classroom at the beginning of each lesson to check the students’ notes, glance at their solutions to the given assignment, and provide brief feedback if needed. The rest of the lesson was spent mainly on problem-solving exercises, asking questions, correcting misconceptions, and participating in discussions. In the traditional learning environment, the teacher also began the lesson by wandering around the classroom to check that students had completed the homework assignment they had been given (which was similar to the assignment given to their counterparts in the FC environment) and to provide the students with appropriate feedback. However, the remaining time was devoted to teaching the new material, mainly in a lecture, with few problem-solving exercises.
2.3.2. The FC Online Setting
The online component of the FC learning environment was bscool.com, an online platform designed for Arab students in 9th–12th grades who study mathematics according to the Israeli curriculum. This online platform contains comprehensive materials for students in this age group, at all high-school mathematics levels. When signing in to bscool.com, a menu with four math levels (3 units, 4 units, 5 units, and material for the 9th grade) opens. Students choose a level according to the one they study at school and receive access to different subfolders that list all the main subjects required by the Israeli curriculum for mathematics. When students click on a specific subject, another list of subsubjects appears. Each subsubject is a list of filmed lectures lasting about ten to fifteen minutes each. These videos were filmed in a professional studio and produced by a professional photography and editing team. In addition, bscool.com offers a large collection of matriculation exams at all levels, accompanied by detailed solutions (written or filmed).
The following figures show examples of screens that teach derivatives for 10th graders who study at the 5-unit level of mathematics. Once they sign in, students can choose a course to enroll in, in this case 5 units (see Figure 1). A page opens, presenting two subfolders—806, for 10th and 11th grades, and 807, for 12th grade. Choosing the 806 folder (see Figure 2) leads the students to the relevant subjects taught in this section of the test. The lessons shown in Figure 3 include an introduction to the subject of derivatives, explanations about the different sections in this subject, examples, and solutions for many exercises. Specifically, the subunit called “derivative of polynomial function” includes several videotaped lectures such as an introduction of the derivative concept, its meaning, and how to deal with it in linear functions; an introduction to the differentiation law in nonlinear functions; and an introduction to the laws of differentiation of the polynomial function in the case of multiplying or dividing by a number. In addition to solving examples in finding the slope of the polynomial function at different points, this unit presents the solving process of a variety of examples of finding the tangent line equation of the polynomial function or finding the tangent line equation including a parameter. The second subunit in the derivative section is the analysis of a polynomial function which consists of different filmed lectures such as identifying the extreme points of the function and their different types, the differences between open and the closed domains, and how to find the extreme points and ascending and descending areas of a function based on a given graph or the first derivative.
Figure 1.
Homepage, bscool.com.
Figure 2.
The 5 Units folder and its two subfolders, 806 (for 10th and 11th grades) and 807 (for 12th grade).

Figure 3.
Filmed lectures about different subsubjects of Derivatives.
As students choose what subunit they would like to learn, a filmed lecture starts playing, as shown in Figure 4 and Figure 5. In these figures, the teacher, Watad, appears in a filmed lecture in which he presents an example of a compound mathematical problem that requires him to find equations of the tangent lines of a function in different points.
Figure 4.
Watad, the teacher, in a filmed lecture that explains how to solve an exercise with a tangent line equation and how this relates to the function’s derivative.

Figure 5.
Watad, the teacher, in a filmed lecture that presents the solution of the exercise presented in Figure 4.
Figure 4 below describes a complex problem in which the function is given and the students are asked to find (a) the equations of the tangent lines of this function at points of intersection with the x-axis and (b,c) the equation of normal line at the same points found in section a.
Figure 5 represents an illustration of Figure 4; it further presents a detailed solution of the exercises given in the filmed lectures about finding the tangent line equation of a given polynomial function.
In the filmed solution of this exercise, Watad explains to his students the different stages for approaching such a problem. First, students need to find the points of intersection with the x-axis. Then, in order to find the equation of the tangent lines in these two points, students must apply its relation to the derivative in the solution. They must use the derivative to compute the slopes of the tangent line in the different points and subsequently find the full equation. Finally, when mentioning the normal line, students must notice the meaning of it, i.e., its slope must be negative reciprocals of the tangent line; thus, they can continue with procedurally solving the problem.
2.4. Research Tools
In this study, both quantitative and qualitative research tools were used. These included pre- and post-learning questionnaires that measured the students’ conceptual understanding before and after completing the derivative or integral learning units (for 10th and 11th grade, respectively). The pre-learning questionnaire aimed to evaluate students’ previous knowledge about the content they would be learning during this study. In these questionnaires, the students were asked to define four basic mathematical concepts related to the learning unit assigned to each grade. The concepts in the 10th grade questionnaire were (1) derivative, (2) extreme point, (3) interval of increase, and (4) domain, whereas those in the 11th grade questionnaire were (1) integral, (2) antiderivative, (3) integral constant, and (4) definite integral. These concepts were chosen based on recommendations made by four math teachers with significant experience in the mathematics education field, who were asked to express their opinion on the suitability of these basic concepts for assessing the students’ level of conceptual understanding. After an initial agreement was reached about the concepts to use, comprehensive definitions were collected from two resources for all the above-mentioned concepts. First, the basic definitions were provided by two books: the book titled Calculus from Graphical, Numerical, and Symbolic Points of View [35] and an Israeli book titled To Learn and Teach Analytics [68], which is a mathematical didactical book used by Israeli mathematics teachers. Then, based on these definitions, several math experts who are qualified high school math teachers with rich experience in the field, in addition to numerous researchers in mathematics education, were asked to provide suggestions for a full definition for each of the concepts. All definitions were analyzed using Cohen’s kappa for measuring agreement to ensure content validity and inter-rater reliability of the definitions. The results revealed a value of about 0.9 for Cohen’s kappa for each of the concepts, with more than 80% agreement between judges. Table 1 below presents the comprehensive definitions provided in the above-mention

Table 1.
Comprehensive definitions of the concepts that were provided in the conceptual understanding questionnaire on the topics of derivatives and integrals.
The second tool used was a pre- and post-learning attitude quantitative questionnaire for measuring students’ motivational attitudes. This questionnaire was based on the Motivated Strategies for Learning Questionnaire (MSLQ) [69]. In this study, we used the factors of interest and value to assess students’ motivation in the context of mathematics learning. The total number of items was seven, presented on a Likert scale ranging from 1 (disagree) to 5 (very much agree). Three of these items assessed students’ intrinsic interest, such as “In math classes, I prefer work that is challenging so I can learn new things”, and four items addressed value, such as “I think I will be able to use what I learn in this math class in other classes”.
The third tool was personal qualitative interviews. After the students completed the derivative or integral learning units, personal interviews were conducted with some of the students who studied in the FC environment. The participants in the FC group were contacted to be given the opportunity to be interviewed. From each one of these groups, roughly 31% of the 10th graders (N = 5) and 25% of the 11th graders (N = 5) agreed to be interviewed and to express their opinions about their learning experience. Another interview was conducted with the teacher who taught the learning units in both environments. The average length of each interview was 30 min, and the students were asked 13 open-ended questions regarding their experience with studying mathematics in the flipped classroom and about their perceptions of the bscool.com platform, the online component of the FC.
2.5. Data Analysis
2.5.1. Quantitative Data
The conceptual understanding questionnaire aimed to evaluate students’ understanding of different mathematical concepts. Based on the definitions that were detailed above in Table 1, an initial indicator was created to define what constitutes a complete, partial, or wrong answer for each concept. It should be noted that despite learning the formal and comprehensive definitions during the period of the study, students were not expected to provide perfect answers resembling what was set in this study as expressing a complete answer (according to experts from the mathematics education field). Thus, few students’ answers could have been assigned the score of 10. Generally, each answer was scored on a scale from 0 (wrong answer) to 10 (complete or nearly complete answer). The scores in between were given for various partial answers. In total, the maximum score for all four concepts was 40, which was then converted to a percentage scale (0–100) for the convenience of displaying the data. For example, the derivative concept was defined by experts as “the rate at which a function changes with respect to a variable at a certain point, which can be geometrically interpreted as the slope of the tangent line at this point”. Two possible definitions were considered complete, i.e., referring to the frequency of change of the function or to the slope of the tangent line, and were given the full score (10). Other possible answers that represent a partial or incorrect answer were also set in the rubric. See Table 2 for the rubric that served to assess the definition given for the “derivative” concept. Appendix B presents the other rubrics that served to assess the various concepts that relate to the derivative subject assigned to the 10th graders and the various concepts that related to the integral subject, assigned to the 11th graders.

Table 2.
The rubric for assessing students’ answers to the concept of “derivative”, within the derivative concept.
To check the validity and reliability of the indicator, before beginning this study, a group of 20 10th and 11th grade students (about 10 students in each grade) who did not participate in this study was asked to define the various concepts after learning the derivative or integral units for the first time at Alkhawarizmi. The answers given by this small sample of students were evaluated by consulting with experts in mathematics education and with several mathematics teachers to make sure that the indicator accurately assesses students’ conceptual understanding. This process yielded a Cohen’s kappa value of 0.85–0.90 for all concepts, with more than 80% agreement between judges.
Finally, after quantifying all the data collected using the conceptual understanding tool, several statistical analyses, particularly analysis of variance, were used to compare the differences in the conceptual understanding demonstrated by the FC and comparison groups before and after studying the different learning units. Additional ANOVA analysis with repeated measures was conducted, aiming to examine differences in students’ conceptual understanding over time, while comparing the FC and the comparison groups (see details in the Section 3).
Like the analysis of the conceptual understanding data, all the data collected from the quantitative pre- and post-learning attitude questionnaires for assessing students’ motivational attitudes were analyzed using ANOVA statistical analyses, particularly ANOVA with repeated measures.
2.5.2. Qualitative Data
The qualitative data collected during the interviews were analyzed in two phases. The first was thematic analysis (Creswell, 2014), in which we started by searching for recurring themes that appear in each of the three groups that were interviewed, i.e., 10th graders, 11th graders, and the teacher. The second phase applied directed content analysis, which involved quantification of the recurring answers in each category. Using a quantification table, we were able to present the number of students who made references to the various themes.
2.6. Procedure
The current study was held at Alkhawarizmi over a period of four weeks in November and December 2019. During the research period, students from both groups attended classes twice a week, for a total of eight 90 min lessons. Both the comparison and FC groups met in the same physical setting, while the FC group also had access to the bscool.com online platform for out-of-class lessons and practice. The first lesson for the FC group was mostly an introduction to the FC learning approach, including an explanation of the expectations of the students (independently watching filmed lectures, taking notes, and completing assignments). The students were also given a short introduction about the current study and its goals, i.e., to explore methods for learning advanced mathematics. They were introduced to the bscool.com online platform and were given detailed explanations about the new learning experience they would undergo during those four weeks. They were instructed how to access the learning materials they would be studying at home to prepare for the next class. Towards the end of the first lesson, the students were asked to complete the conceptual and motivational prequestionnaires. The next lesson and the remaining ones were dedicated mostly to practicing and exercising the learning materials. Students were required to watch the relevant filmed lectures at home on bscool.com before the lesson, so that class time could be used to answer students’ questions, clear any misunderstandings, and provide further clarifications and explanations as needed. During class time, students were also given a set of exercises to work on collaboratively in groups and with their teacher’s guidance. In addition to receiving an assignment to complete at home, they were also instructed to independently watch several new filmed lectures before the next class. Finally, in the final lesson, the students were asked to complete the conceptual and motivational postquestionnaires in class.
For the comparison group, the first meeting included a short introduction about the study (similar to that of the FC), and students were asked to complete the conceptual and motivational prequestionnaires. During that lesson, the teacher began teaching the relevant learning unit (derivative or integral). In the remaining lessons, the students came to class to listen to their teacher’s lectures, take notes during the lectures, copy what was written on board, see different examples, ask questions, and do several exercises in class if time allowed. At the end of each lesson, students from the comparison and FC groups received the same worksheet to complete at home. In the last lesson, the students were asked to complete the conceptual and motivational postquestionnaires. The following figures show timelines that illustrate the eight-lesson research procedure used for the 10th graders who participated in the FC group (Figure 6) and the 10th graders who participated in the comparison group (Figure 7). The process was identical for the 11th graders in both learning environments and differed only in the content taught. In both figures, the lessons that took place at Alkhawarizmi are marked in black. For the FC group (Figure 6), the lessons that the students learned independently via the bscool.com online platform are marked in purple.
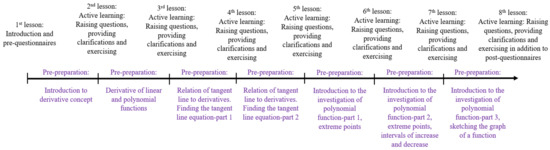
Figure 6.
Timeline of the eight-lesson research procedure for the 10th graders in the FC group.

Figure 7.
Timeline of the eight-lesson research procedure for the 10th graders in the comparison group.
3. Results
In this section, we present an analysis that addresses the three parts of the research question posed above. We start with the quantitative results that relate to the first part of the research question, which discusses the effects of the FC approach on conceptual understanding. These results are supported by qualitative data from the students’ responses to the conceptual understanding questionnaire. We then refer to the quantitative results that relate to the second part of the research question about students’ motivation in the FC environment. We end with qualitative findings regarding the last part of the research question, which seeks to explore the factors that contribute to learning in the FC environment.
3.1. Quantitative Results
3.1.1. Conceptual Understanding of Mathematics
The first part of the research question discusses the differences in conceptual understanding between students from the FC group and students from the comparison group after studying the derivative (10th grade students) or integral (11th grade students) unit. We begin by presenting findings that pertain to these differences with respect to their conceptual understanding level before studying the learning unit and then test the effect of group (FC vs. comparison) and grade (10th vs. 11th) on students’ conceptual understanding after they complete the learning unit (see Section 3.1.2). We then go on to examine the differences in students’ conceptual understanding over time, while comparing the FC and the comparison groups (see Section 3.1.3). Additionally, we calculate Cohen’s d to evaluate the size of the effect for each group over time (see Section 3.1.3).
3.1.2. Students’ Conceptual Understanding
In order to determine whether there were differences in conceptional understanding between the two research groups (FC vs. comparison) before they encountered the learning unit, we first conducted a one-way ANOVA for each grade. This analysis yielded nonsignificant differences between the research groups for both the 10th grade students (F (1, 34) = 0.737, p > 0.05, η2 = 0.021 (Figure 8A)) and for the 11th grade students (F (1, 37) = 0.249, p > 0.05, η2 = 0.007 (Figure 8B)). The lack of any significant difference in students’ conceptional understanding prior to studying the learning units indicates that both research groups in both grades had the same level of understanding at the beginning of this study.
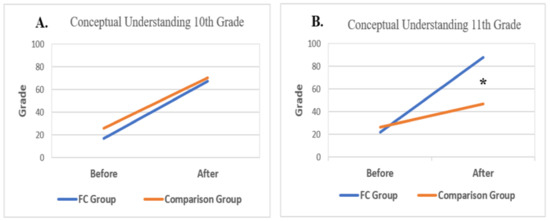
Figure 8.
(A,B) Conceptual understanding of 10th and 11th grade students by time and research group. Note. * p < 0.05.
We then ran a two-way ANOVA in order to test the effect of the two independent between-subjects variables, i.e., group and grade, on the dependent variable, i.e., conceptual understanding after studying the learning unit, without controlling for the pre-learning conceptual understanding level. Significant differences were found in post-learning conceptual understanding between the two different research groups without considering the factor of grade (F (1, 71) = 15.088, p < 0.001, η2 = 0.175). This means that in both grades collectively, students in the FC group demonstrated a higher level of conceptual understanding after studying the derivative or integral unit than their counterparts in the comparison group. See Table A1 in Appendix A for means and standard deviations.
Furthermore, the test revealed that the effect of the interaction between grade and research group on conceptual understanding after studying the learning unit was statistically significant (F (1, 71) = 20.600, p < 0.001, η2 = 0.225). To examine the source of interaction, we conducted a series of one-way ANOVAs for each grade separately, setting the conceptual understanding after studying the learning unit as the dependent variable and the group as the between-subjects independent variable. For 10th graders, the results were nonsignificant (F (1, 34) = 0.140, p > 0.05, η2 = 0.004), implying a similar level of conceptual understanding between the FC and comparison groups. For the 11th graders, we found significant differences in post-learning conceptual understanding between the FC and comparison groups (F (1, 37) = 64.393, p < 0.001, η2 = 0.635) showing that students in the FC group demonstrated a higher level of conceptual understanding than students in the comparison group. See Table A1 in Appendix A for details about means and standard deviations.
3.1.3. Differences in Conceptual Understanding over Time
We were further interested in examining the differences in conceptual understanding over time in each grade and each group. Thus, we conducted multiple one-way ANOVAs with repeated measures, with time of measurement (before or after learning the units) as the within-subjects independent variable and conceptual understanding as the dependent variable. The results revealed that over time, significant differences in conceptual understanding were found for the different research groups in both grades. The results showed that 10th graders from the FC and comparison groups exhibited an increase in conceptual understanding over time (F (1, 15) = 82.578, p < 0.001, η2 = 0.846; F (1, 19) = 37.854, p < 0.001, η2 = 0.666, respectively (Figure 8)). Similar results were found for the 11th grade students, revealing that both groups showed a significant increase in their conceptual understanding over time (F (1, 19) = 94.358, p < 0.001, η2 = 0.832; F (1, 18) = 9.437, p < 0.05, η2 = 0.344, respectively). See Table A1 in Appendix A for means and standard deviations.
Since both groups in both grades demonstrated an increase in conceptual understanding, we measured the effect size of this change by calculating Cohen’s d separately for each group in each of the grades. The results suggested that the effect of improvement was the largest among the 11th grade students who studied in the FC environment (d = 3.02), followed by the 10th grade students in the FC environment (d = 2.17), the 10th grade students who studied in the traditional classroom environment (d = 1.39), and finally, by the 11th graders who studied in the traditional environment (d = 0.87).
The following figures show a visual representation of the findings described above. Figure 8 illustrates the differences in conceptual understanding before and after studying the learning units in the FC and comparison groups for the 10th grade students who studied the derivative unit (Figure 8A) and the 11th grade students who studied the integral unit (Figure 8B).
To summarize the findings, for the 10th grade students, no differences were found between students who studied in the FC environment and those who studied in the traditional environment, in both their pre- and post-learning conceptual understanding (Figure 8A). However, although the 11th graders in the FC and comparison groups exhibited similar levels of pre-learning conceptual understanding, a higher level of post-learning conceptual understanding was revealed for the students in the FC group than for their peers in the comparison group. Figure 8 also shows that the students in all the groups improved their conceptual understanding over time. However, the effect of improvement appears to be greater among the students who studied in the FC environment, particularly for the 11th grade students.
3.1.4. Examples of Students’ Answers in the Conceptual Understanding Section
Mais and Zaid (pseudonyms) are two students who participated in this study and were selected as representatives of 10th and 11th grade students (respectively) who provided near-perfect answers after learning the units according to the FC approach. Observing these students’ answers to the pre- and post-learning questionnaires demonstrates the progress and development in their conceptual understanding.
Before learning the derivatives unit, Mais reported that she did not know what the concept “derivative” meant. She defined the extreme point as “the point in which the function has the greatest value”, and defined the interval of increase as “the area in which the function is ascending”. She defined “domain” as “a point that is on the function”. These definitions indicate a low level of conceptual understanding, as it seemed that Mais tried to guess the definition of each concept based on its name. Figure 9 below shows the definitions of the concepts provided by Mais in her pre-learning questionnaire.
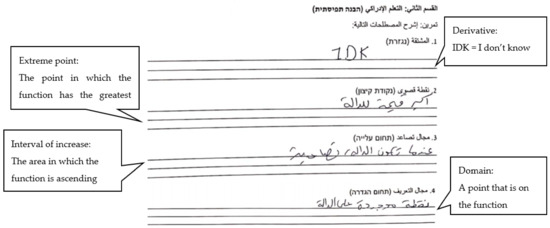
Figure 9.
The definitions of the concepts provided by Mais in the pre-learning questionnaire.
In her post-learning questionnaire, Mais defined the derivative as “the slope of the function at a specific point” and added that: “It is the frequency at which the function changes”. About the meaning of “extreme point”, she answered that: “It can be a minimum or maximum value that represents the lowest or the highest value of the function, respectively. You can find the extreme point by setting the derivative to equal zero”. She defined interval of increase as follows: “When the function is ascending from left to right, the x values are increasing at the same time that the y values are also increasing”. Finally, she said that a domain “consists of the numbers in which the function is defined, meaning the x values that we can substitute in a function and receive a valid y value. For example, if y = √x you cannot substitute x < 0. Therefore, the domain is x > 0”. Despite providing inaccurate and imperfect answers, Mais mentioned fundamental details in her definitions, which indicates that Mais had obtained a significant improvement of her conceptual understanding of the derivative subject. Figure 10 below demonstrates the answers that Mais provided in the post-learning questionnaire.

Figure 10.
The answers provided by Mais in the post-learning questionnaire.
In the 11th grade group, before starting the learning unit, Zaid defined the integral as “two functions that you wish to do an integral between them”. He defined the antiderivative as “the function that you want to apply an integral on it”. He continued by defining the integral constant as “the value of the integral that is applied between two functions”. He was unable to define the concept “definite integral”. Zaid’s superficial definitions indicated his low level of conceptual understanding before studying the integral unit. Figure 11 below shows Zaid’s definitions in the pre-learning questionnaire.
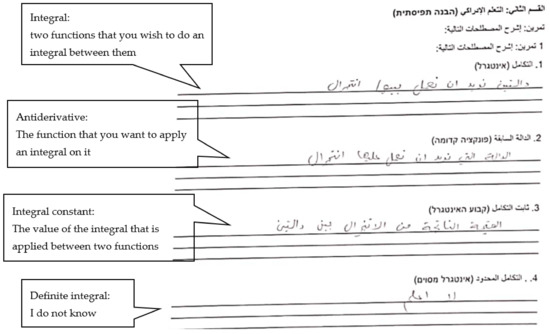
Figure 11.
The definitions of the concepts provided by Zaid in the pre-learning questionnaire.
However, in his post-learning questionnaire, he defined the integral as “the reverse process of differentiation. In addition, it is used to calculate the areas under graphs”. He defined antiderivative as “the F function we get by applying an integral on its derivative”. When asked about the integral constant he said that: “The derivative of a constant is always zero, and therefore, when integrating, we must add a constant C in order to go back to the original function”. He added that: “This is a constant C that we always add to every function”. Finally, he defined “definite integral” as “the area of a region enclosed between two limits of a curve in a certain domain”. These responses are not perfect, nor are they comprehensive, and yet they indicate that Zaid obtained a medium level of development in his conceptual understanding, as he provided detailed explanations for each of the concepts. Figure 12 below shows Zaid’s answers in the conceptual understanding postquestionnaire.
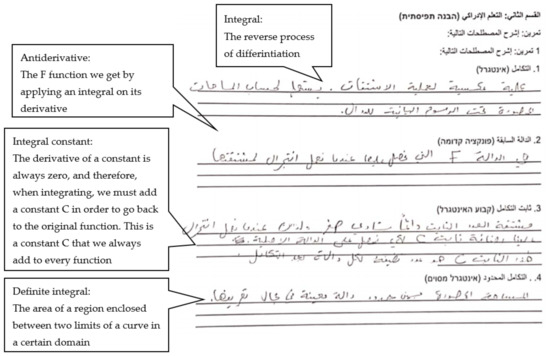
Figure 12.
The answers provided by Zaid in the post-learning questionnaire.
3.1.5. Motivation towards Studying Mathematics
This section presents our findings for the second part of the research question, which aimed to investigate the differences in motivation to learn mathematics among 10th and 11th grade Arab students studying advanced mathematics in the two different research groups. First, to confirm that all the participants started the program with similar motivation levels, we assessed differences in students’ motivation before studying the learning unit (see Section 3.1.6). Next, we examined differences in motivational attitudes among the students after studying the learning unit (see Section 3.1.6). We then explored differences in students’ motivational attitudes over time and calculated Cohen’s d to evaluate the size of the effect for each group over time (see Section 3.1.7).
3.1.6. Students’ Motivation
In order to examine if there were differences in the students’ motivation level prior to studying the learning units between the two groups (FC vs. comparison), we started by applying a series of one-way ANOVAs separately for each grade. For both the 10th and 11th graders, the results showed a nonsignificant difference in motivation between the FC and the comparison groups (F (1, 34) = 3.087, p > 0.05, η2 = 0.083 (Figure 13A); F (1, 37) = 0.578, p > 0.05, η2 = 0.15 (Figure 13B), respectively). These findings imply that before they studied the learning units, the students’ motivational attitudes were similar in the FC group and the comparison group among both 10th and 11th grade students. See Table A2 in Appendix A for means and standard deviations.
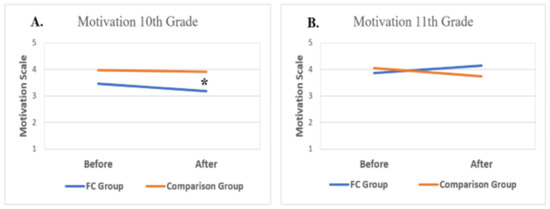
Figure 13.
(A,B) Motivation of 10th and 11th grade students toward studying mathematics, by time and research group. Note. * p < 0.05.
Since no significant differences were found in students’ motivational levels before studying the learning units, further analyses were conducted to examine the effect of the learning method on students’ motivation after studying the learning unit, without controlling for the pre-learning conceptual understanding. We conducted a two-way ANOVA in which group (FC, comparison) and grade (10th, 11th) were both set as the between-subjects independent variables and post-learning attitude motivation served as the dependent variable. This analysis revealed a significant interaction in post-learning attitude motivation by group and grade (F (1, 71) = 8.946, p < 0.05, η2 = 0.112). To examine this interaction, we conducted multiple one-way ANOVAs separately for each grade, with conceptual understanding after studying the learning unit as the dependent variable and group as the between-subjects independent variable. These analyses revealed significant differences in post-learning attitude motivation among 10th graders from the different research groups (F (1, 34) = 5.44, p < 0.05, η2 = 0.138) but no significant differences in post-learning attitude motivation among the 11th graders from the different groups (F (1, 37) = 3.30, p > 0.05, η2 = 0.082). This suggests that the 10th graders who participated in the FC environment were less motivated after studying the derivatives unit than their peers in the comparison group, while the 11th graders in both groups showed a similar level of motivation after studying the integral unit. See Table A2 in Appendix A for means and standard deviations.
3.1.7. Differences in Motivation over Time
Due to the different effects revealed in students’ post-learning attitude motivation in the different grade levels, we further conducted multiple one-way ANOVAs with repeated measures to examine differences in motivation over time. In this analysis, time of measurement (before or after studying the learning unit) served as the within-subjects independent variable, whereas motivation level served as the dependent variable. Findings revealed that for both 10th and 11th graders, no significant differences in motivation level were found over time for either of the research groups. For the 10th graders, the results showed that the FC and comparison group maintained a similar level of motivation before and after learning the derivative unit (F (1, 15) = 2.50, p > 0.05, η2 = 0.143; F (1, 19) = 0.104, p > 0.05, η2 = 0.005, respectively). Similar results were found for the 11th graders, as both groups showed no significant differences in motivational attitudes over time (F (1, 19) = 1.06, p > 0.05, η2 = 0.053; F (1, 18) = 1.84, p > 0.05, η2 = 0.093, respectively). See Table A2 in Appendix A for means and standard deviations.
Due to the similar nonsignificant effect of time for all participants, we were interested in calculating Cohen’s d to measure the effect size over time separately for each group in both grades. For the 10th graders, the results imply similar levels of motivation with a low effect size for the FC (d = −0.29) and comparison (d = −0.07) groups. However, for the 11th graders, the results yielded relatively high effect sizes for both the FC group (d = 0.41) and the comparison group (d = −0.41). This means that an effect of a similar magnitude (d = 0.4) was found, but in the opposite direction, so that motivation in the FC group increased over time but decreased in the comparison group. The following figures present a visualization of the findings described above. Figure 13 illustrates the differences in motivation before and after studying the learning unit in the two research groups for the 10th grade students who studied the derivative unit (Figure 13A) and the 11th grade students who studied the integral unit (Figure 13B).
To summarize the findings, while the 10th graders in the FC group showed a similar level of motivation to that of their peers in the comparison group before studying the derivative unit, they were less motivated than their peers in the comparison group after learning the derivative unit. However, the 11th graders in both the FC and comparison groups demonstrated similar levels of motivation before and after studying the integral unit.
3.2. Qualitative Results
This section presents findings from retrospective interviews held with a partial sample of students and with the teacher after completing the learning units. The goals of these interviews were to collect broader data about the effects of studying in an FC learning environment, to understand more about the students’ perspectives, and to explore the teacher’s opinions about the FC approach. Below are the main themes that emerged from the students’ and the teacher’s responses.
Table 3 presents the nine main themes that emerged from the interviews and their frequencies in the participants’ responses. The percentages in the table represent the frequency of the responses out of all the statements made for each theme. For example, the four responses given by the 10th grade students regarding the theme of “better use of class time” represent 50% of the total number of responses (N = 8) that mentioned this theme. This calculation allowed us to identify which theme was mentioned more by one group of interviewees (10th grade students, 11th grade students, or the teacher) than by others. The percentages that appear in the right-most column (total) were calculated out of the total number of responses retrieved for all themes (N = 64), which enabled us to sort the themes by their relative frequency.

Table 3.
Frequency of themes mentioned by the participants during retrospective interviews.
The nine themes we observed revealed that five themes present the benefits of studying in the FC, while four themes present the challenges of studying in FC. Figure 14 depicts the nine main themes, where the green themes represent the benefits and the red themes represent the challenges.
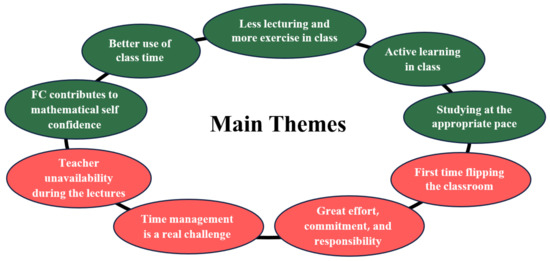
Figure 14.
The main themes mentioned by the participants during retrospective interviews.
In the following, we describe the various themes (including examples of statements) in order of their frequency—from the most frequent theme to the least frequent one.
• Less lecturing and more exercise in class
One theme that was explicitly mentioned in students’ responses was that learning based on the FC approach meant less lecturing during class time. All five of the 11th grade students stated that having the filmed lectures at their disposal before class was a huge advantage, as it resulted in less lecturing in class. They were able to learn the content before class, and therefore the class time, which is usually spent on teaching the content material, can be spent asking questions and solving a variety of exercises instead. For example, Mona reported that: “Due to this method, there was a very wise use of class time. FC helped invest in class time, because a lot of time in class was dedicated to exercises with the teacher”. Lia stressed that as well and said that: “We had the opportunity to work on all kinds of questions at different difficulty levels. There is no doubt that this helped me to better understand the material”.
Like the 11th graders, the 10th graders also explicitly stated that learning in the FC method gave them more time to exercise in class and less time for lectures. Sara, for example, stressed that: “This method allowed us to dedicate a greater part of class time for collaborative exercising rather than lecturing”. Aman also reported that: “Having previous knowledge about the content gives us an advantage with respect to class time; we now have enough time to proceed faster with the content”.
Watad, the teacher, reinforced the statements made by his 10th and 11th grade students and acknowledged this advantage of the FC learning approach. He reported that: “I noticed that this approach contributed to reducing the lecturing time in class and helped invest it mainly in exercising, listening, and answering the raised questions”. He added that: “I need to teach nearly 3000 pages to prepare 5-unit students for the first matriculation exam in math. We always need extra lessons to finish the material before the due date. Implementing FC in certain lessons can help us invest time very wisely. If students independently learn the content before class time, it will save them, the teacher, and their peers in class about 40% of the normally required time to be perfectly prepared for the matriculation exams”. Based on their responses, Watad and his students are aware of the fact that developing mathematical skills and improving mathematical comprehension requires an extensive amount of time dedicated only for exercise and problem solving, an advantage that the FC approach offers.
• Studying at the appropriate pace
Learning in a flipped classroom environment offers certain flexibility in time and location. Students can choose the time and place that are most convenient for them in order to learn the new material via bscool.com. Furthermore, students can also repeat certain parts of the filmed lectures as many times as they wish, until they reach a full understanding of its content. This is considered an advantage over the traditional method of learning, in which the lecture is held at a specified time and location and cannot be repeated easily. Some students feel embarrassed to ask questions in class, and this may ultimately prevent them from obtaining a full understanding of the lecture. The 11th grader Mona stressed this point when she mentioned that: “Sometimes in class, I feel embarrassed to ask the teacher to repeat himself or even ask a question, but here I can repeat any part of the video as many times as I need in order to find answers to my questions and ultimately understand the material”.
In their responses, most of the 11th grade students pointed out that this method motivated them to learn mathematics not only because of the flexibility in time and location that it provides but also because of the repetition feature available in the videos. This method allows students with different learning abilities to learn at the pace best suited for them. Aseel stressed this and mentioned that: “This method motivated me to learn math because it is more convenient; I choose the place and time that are the most appropriate for me to study the material. I also think this method makes the learning process easier since I study at the pace I find appropriate, unaffected by my classmates who may hold me back sometimes”. Most of the students even declared that learning the integral unit in the flipped classroom method gave them a better understanding of the subject in general and the mathematical concepts specifically. Lia, for example, mentioned that: “I learned the concepts twice, first at home by myself and then in class with my teacher”. The 10th grade students also agreed that the repetition feature in the videos can be beneficial for students with different learning abilities. Sara, for example, acknowledged this advantage and stated that: “I would frequently repeat some clips several times to reach full comprehension. I advise every student who is fortunate enough to learn based on this approach to take advantage of the repetition feature offered in the filmed lectures. They should repeat any clip that they need as much as needed until they reach a full understanding of the material”.
Watad emphasized that students vary in their learning and perception abilities. There are slow students who sometimes require the teacher to repeat a certain idea several times in class, while other students with more advanced learning abilities have faster mathematical perception. Therefore, he greatly appreciated this feature of the FC approach. He reported that: “I encounter students who feel embarrassed to repeat a question in class to better understand an explained idea, they prefer to keep this question to themselves and go home with poor understanding instead. Therefore, learning the content independently via the online platform allows students from the diverse categories to define the learning pace that best suits them. By rewatching parts of the videos to gain a better understanding, or by skipping other clips if the student already understands their content, they can control their own learning process”.
• Better use of class time
This theme refers to the fact that the FC environment is based on the students’ prior preparation for class, thus allowing class time to be spent on practicing and deepening students’ understanding of the material. Indeed, the students from both grades who mentioned this theme noted that better use of class time allows the teacher to identify the individual difficulties encountered by the students and to use class time to explore different misconceptions. For example, Mona, who is an 11th grader, emphasized how much she appreciated the individual attention that she received while learning in the FC method. She said: “The teacher had the opportunity to wander around the class, and recognize our problems, and provide us with deeper, specific advice regarding our individual misconceptions”. The students also mentioned that it not only allows the teachers to provide deeper clarifications about incorrect notions, but also enables better interaction between the teachers and students. The statements made by 11th graders Aseel and Gassan reinforced this. Aseel reported that: “This approach allows the teacher to realize what misconceptions his or her students hold and to recognize their weaknesses. Therefore, the teacher will focus only on our difficulties and will not waste time explaining everything”. Gassan said that: “Students come to class with certain knowledge about the material; they come with gaps that they want to fill, which makes them eager to meet with their teacher, participate in discussions, and ask questions. The interaction with the teacher is better than a traditional lesson”.
Like the 11th graders, the 10th graders also noted that the preparation stage allowed better use of class time. Most importantly, they emphasized that class time was mainly devoted to diverse exercising along with the teacher, and collaborative work with classmates, which are generally lacking in the traditional learning approach. Sara, for example, mentioned that: “I consider myself a student who needs extensive exercising with the teacher or classmates to better understand the material. This approach offers a good amount of time for collaborative exercising”. Most of the 10th graders also agreed that in the flipped classroom approach, teachers can identify the different misconceptions found in class and recognize individual difficulties encountered by students. In their responses, most students expressed their great appreciation for their increased interaction with the teacher in class. They particularly valued how the teacher would walk around the classroom and approach every student who needed assistance. Israa, for example, stated that: “Preparing the material before class, and more importantly, bringing questions to class, was very helpful for revealing the individual difficulties we had and the common misconceptions in the class, and therefore enabling the teacher to concentrate on these issues rather than wasting class time on less important issues”.
Like his students, Watad believes that preparing at home and attending class with a certain degree of knowledge about the content creates active learners in class and thus leaves more time to spend on exercising and asking questions. Another advantage of flipping the classroom that Watad and his students agreed upon is that it offers better interaction between the students and their teacher. He reported that: “Since more time is spent on exercise instead of lectures, the teacher can now be closer to the students during class time. Most teachers usually do not identify their students’ individual difficulties and misconceptions. This is not because they do not want to, but because they do not have enough time to open the students’ notebooks, look at their work, and provide them with appropriate feedback”.
• Active learning in class
Most of the 11th graders we talked to agreed that the FC method contributes to active and collaborative learning in the classroom. In his interview, Gassan reported that: “I liked the discussions that were carried out during class time about several misconceptions and questions that we had. I really do think that the FC helped increase active learning and promote cooperative learning as well”. Jena agreed with Gassan and said that: “The preparation process we went through before class increased active learning in class and developed more interaction with the teacher”. In her response, 10th grader Israa said: “I like the discussions that we had in class; sharing and exchanging our diverse views”. Aman, a 10th grader, said that: “Due to the preparation that we did before class, more discussions were held during our problem-solving time in class; this is very motivating and time investing”. Similarly, 10th grader Sara appreciated how FC gave her a greater opportunity to be active in class. She stated that: “I am a student who prefers to ask questions and participate in discussions during class time. I do not like being a passive learner who usually spends the entire time in class listening to lectures given by the teacher. This method allowed more time for collaborative learning and exercising in class, a great percentage of class time was spent on asking questions and participating in discussions”. Watad also expressed great appreciation of how his students got the opportunity to experience an interactive learning process, in addition to actively participating during class and collaborating on problem solving, mostly in pairs and not necessarily in groups.
• Time management is a real challenge
Most of the 11th grade students we interviewed highlighted how difficult and time-consuming it was to complete all the out-of-class assignments. Gassan, for instance, said that: “I was 80% committed to completing my assignments before class time, yet sometimes preparation at home was very time consuming, especially taking notes”. Jena agreed, reporting that: “Time management was a real challenge in this method. Time must be managed wisely to finish everything before attending class”. In their responses, most of the 10th graders reinforced statements previously made by the 11th graders. Most of them reported that the FC approach requires very wise time-management before class. Several students even stated that a schedule needs to be built beforehand for preparation time at home. Aman mentioned that: “Time management is a key factor for succeeding in this approach; students must manage their before-class time wisely, I recommend building a study schedule. It will be greatly helpful for managing the time needed to watch the filmed lectures and complete the assignments”. Like Aman, Mary also recommended that students who study in the FC approach build a studying schedule. Israa stated that: “I think time management was a serious issue in this approach. During my studies, I realized how important it was to dedicate enough time for preparation at home, especially since the learning process was independent”. Watad also agreed with his 10th and 11th grade students. He reported that: “Time management is very important when learning in the FC approach. Students need to manage their time wisely and correctly in order to gain maximum benefit from this learning experience”.
• Teacher unavailability during the lectures
One disadvantage that was frequently reported during the interviews was the unavailability of the teacher while the students learned the new content at home. Most of the students stated that when they prepared for class, particularly when they watched the filmed lectures, they had several questions about unclear issues, but the teacher was not there to provide them with an answer. The students considered this a disadvantage of the flipped classroom compared to the traditional learning method in which the teacher is available during the entire lesson to answer any questions raised during the lecture. Both Aseel and Mona from 11th grade said that: “The teacher is not there to answer your questions right away; the questions must wait until you go to class”. Similarly, Jena, who is also an 11th grader, stated that: “Sometimes I felt it was hard to watch a video and start an assignment on my own. But I used to write down all the hard questions and bring them to class to ask the teacher for clarifications”.
Similarly, all five of the 10th graders we interviewed reinforced these statements. In their responses, most of them even mentioned that they would prefer the traditional approach of learning over the flipped classroom because of this drawback. They explained that during lectures, many questions come to the student’s mind and these questions need immediate answers. It is hard to wait a few days to receive answers during class time. Sometimes the purpose of the question becomes unclear when it is not answered when it arises, especially when it is about new content that was not encountered before. Mary, for instance, mentioned that: “I would prefer to learn in the traditional approach because it is easier to ask the questions and get the answers immediately”. Israa added that: “The filmed lectures do not necessarily provide enough information. I sometimes have many questions that the videos cannot answer, whereas having the teacher available in class ensures that I will get these answers at the right time. I think the FC approach lowered my motivation to learn since I had many questions that I wanted to ask during the lecture in order to fully understand the content”.
• Great effort, commitment, and responsibility are required
The majority of the interviewed 11th grade students reported that they had put intensive effort into their studies when their math classroom was flipped, compared to the traditional method. Studying in the flipped classroom requires a lot of preparation before each class because students are expected to learn the content independently at home and come to class with certain knowledge. Besides watching the lectures at home, students were also asked to take notes about the main ideas in the lectures and to complete an assignment to ensure they understood the content they had watched. Most of the students mentioned how effortful this process was for them. Lia reported that: “When flipping the classroom, more effort is needed since we must finish watching lectures and solving the assignment before class”. The students also emphasized how essential the preparation stage was. They all agreed that it required a huge commitment and a great sense of responsibility in order to finish the assigned duties before class. In one of her responses, Jena mentioned that: “This method requires great effort, commitment, and responsibility. I once came to class unprepared and did not know what everyone was talking about. That is when I realized that preparing the learning content before class is essential for understanding”. She reported that this experience raised her awareness of how important it was to dedicate enough time and effort to finish preparing the material before class. She mentioned that: “I became committed to watching all the videos to the end and taking notes, because this was a preliminary condition for understanding the material. Moreover, I started coming to class with questions about different unclear issues”. Some students reported that they occasionally had certain urgent and personal issues that prevented them from watching the lectures, and therefore they were unable to prepare the required material and finish their assignments before class. Lia faced such an issue once. She said that: “I once attended class unprepared because of personal reasons, and this affected me negatively in class. I did not understand what the teacher was solving or explaining. I felt this held me back”.
Like the 11th graders, most of the 10th graders expressed how effortful the preparation stage was, yet highlighted its importance for benefiting from the FC approach. Moreover, they emphasized how preparation of the content independently requires great responsibility and commitment. Sara, for instance, mentioned that: “Learning in this approach requires greater effort than what is needed in the traditional approach, because I am basically teaching myself the mathematical content by myself. Great responsibility is resting upon my shoulders to complete the before-class preparation”. Israa from the same group added that: “I was committed to watching the filmed lectures and taking notes before attending class in an attempt to understand the content perfectly. I realized that this was all my responsibility, and if I failed to do so, I would negatively affect my own learning process”.
Watad reinforced all his students’ statements. and emphasized how essential it is to teach students, motivate them, and encourage them to take responsibility for learning independently. “I am sure that most students prefer the easy way of learning, that is, not having to put great effort into learning and understanding the content. But once they try to learn via the FC approach and get used to it, they learn to become independent learners who are willing to put in the required effort at home to accomplish their duties”.
• First time flipping the classroom
This theme refers to the challenge of transition from the traditional approach to the FC approach. Most of the students pointed out that they never had the opportunity before to experience a flipped classroom. They saw this as a factor that affected their learning process and made it hard at the beginning. Specifically, there was difficulty in the transition from the commonly used learning approach to this new, unfamiliar approach. This transition required a great deal of independence, which is not needed in the traditional approach in which the teacher is the center of the entire learning process. In her interview, 10th grader Aman stated that: “This was the first time that I learned in the flipped classroom approach, I have always learned in the traditional approach. I feel this transition was difficult for me, it is usually difficult to substitute something that we are used to with a new alternative”.
Supporting Aman’s statement, Watad also emphasized how challenging it was to transition to a new learning and teaching approach that has never been used in his classes before. He mentioned that: “The change was not easy; it was a real challenge at the beginning. The biggest challenge for me was to convince my students that I am not the only source of information”. Watad realized that in this approach, the students must be active learners. “They have assignments that need to be completed independently before class, and this was of great importance for successfully understanding the content. At first it was a great challenge for me to prove to my students that I am not necessarily the center of their learning process. On the contrary, they are”. He further explained that during the first week of the study, several students came to class unprepared, thinking this would drive him to teach the material as he usually does. However, these students were surprised to discover that some of their classmates knew a great deal about the content because they had watched the filmed lecture on bscool.com, and were even ready to solve mathematical problems. This is when they realized that they needed to be more serious, committed, and responsible and prepare the requested material and finish their duties independently before showing up in class.
• FC contributes to mathematical self-confidence
One benefit that was repeated in the 11th grade students’ responses was their increased self-confidence when solving mathematical problems. This confidence was acquired due to their exposure to the FC environment. Having learned the content before class, they would come to class with previous knowledge about the subject and the different kinds of exercises related to it. This gave them confidence in their own ability to approach new exercises. Both Gassan and Aseel agreed and reported that: “This opportunity has given me great confidence in my capabilities. Due to FC, I solved problems with confidence. This method contributed to my self-confidence in problem solving”.
Their teacher, Watad, also appreciated the great self-confidence his students gained due to flipping the classroom. He stressed that preparing and learning the content before class gives students significant self-confidence to participate in class and raise their hands to solve a given problem out loud. In his response, Watad reported that: “During class time, the students’ active participation reminded me of students who usually are enrolled in private mathematics courses in which they learn the content before they do in school. These students attend their math lessons with great self-confidence, and they become very eager to participate in problem solving in class to show everyone what they are capable of. This situation is exactly what I encountered frequently during the research period, when we used the FC approach”. Watad believes that before-class preparation allows students to approach different problems more wisely and creates motivation to learn math since they see themselves that they can actually solve many questions after independently teaching themselves the content.
4. Discussion
The current study follows up on 10th and 11th grade students from the Arab sector in Israel. It investigates how conceptual understanding and motivation to study math are affected by learning the derivative and integrals units (respectively) in an FC environment, compared to in the traditional learning environment. The use of a comparison group enabled us to draw conclusions about the advantages of integrating a flipped learning environment when teaching mathematics, compared to a traditional learning environment. The fact that both groups in each grade studied the same mathematical content and that all the students were exposed to similar pedagogical instruction as they were taught by the same teacher allowed us to compare the groups. A holistic view of the findings shows the effectiveness of studying in an FC environment, particularly for 11th graders, who demonstrated a similar level of motivation to study mathematics, along with a higher level of conceptual understanding compared to their peers who studied in the traditional classroom environment. For the 10th graders, the FC was found to be effective in facilitating their conceptual understanding of the derivative concept but impaired their motivation level. One reason that can explain these findings is that 11th graders are at a very critical stage in high school, only a few months before their first matriculation exam in mathematics. This might have increased their motivation to demonstrate more accountability and to complete their assignments inside and outside the class, in order to ensure optimal comprehension of the material. These students appreciated the FC learning method more than the younger students because it involved more preparation, interaction with the teacher that allowed them to ask questions about unclear issues, and completing more exercises with different kinds of problems.
The next sections discuss our findings regarding the main effects that were investigated in this study, and specifically the effects of studying in a flipped classroom on students’ conceptual understanding and motivation toward mathematics learning.
• The effect of studying in a flipped classroom on students’ conceptual understanding
This section discusses the differences in conceptual understanding between Arab high school students who studied advanced mathematics in the bscool.com FC environment (FC group) compared to students who studied the same learning units in the traditional learning environment (comparison group). Examining students’ conceptual understanding before they studied the units revealed nonsignificant differences between the FC group and the comparison group for both the 10th and 11th grade students. Further analyses revealed that while 11th graders from the FC group demonstrated a higher level of post-learning conceptual understanding than their peers who studied in the traditional environment, the 10th graders exhibited a similar level of post-learning conceptual understanding in both groups. However, considering the change over time, a great effect of improvement was found among the 10th and 11th grade students who studied in the FC environment compared to the change that their peers from the traditional environment demonstrated. As the participants in this study studied the same mathematical content, i.e., derivative unit for both 10th grade groups and integral unit for both 11th grade groups, and with the same teacher, the significant effect of improvement over time and the better achievements of the 11th graders who studied in the FC environment indicate the contribution of the FC environment to students’ development of conceptual understanding. This was evident in a huge number of answers provided in the questionnaires, where most 10th grade students developed their reasoning for the derivative concept for example and took into consideration the various representation it has. Similarly, the 11th graders exhibited such a development in their conceptual understanding of the concepts of integral and antiderivative for example and were able to correlate these concepts and provide detailed information about them. These findings support previous studies that described the effectiveness of learning in an FC environment on students’ conceptual understanding [23,29,47]. These findings coincide with previous studies that suggest that preparation for class by self-studying, mainly using the instructional videos, results in better use of class time that enables increased interaction between students and their teacher [21,25,26]. Particularly, adopting this approach in math lessons offers the students an extensive amount of time in class for exercising and practicing along with their teacher and colleagues, which is crucial to attaining a high level of math performance [15,16].
This, in turn, allows the teacher to identify the students’ individual misconceptions and difficulties [18] and thus to put more focus on individual comprehension problems and provide deeper explanations to clarify the incorrect ideas found in class [18,23,24,27]. Indeed, in a retrospective view on their experience in the FC environment, the students who were interviewed mentioned the advantages of the FC for the learning process in general, and particularly with respect to less lecturing in class. They mentioned that the FC learning method enabled wiser use of class time, as class time was spent mainly on problem solving instead of lecturing. In addition, they reported that this approach allowed greater interaction with the teacher, who was more likely to identify the students’ individual difficulties and misconceptions.
Some of the students succeeded in verbalizing the contribution of the FC to their conceptual understanding of the learning material. The teacher and several students whom we interviewed reported that this experience contributed to their comprehension and learning process and was especially beneficial for students who are often too embarrassed to ask questions in class. They said that the online component of the FC provided them with answers to their questions, as they were able to repeat specific clips and learn according to their individual pace. The 11th graders particularly appreciated how the FC approach contributed to their mathematical conceptual understanding. Some mentioned that they would learn the concept at least twice, independently before class and collaboratively in class through the questions posed and the excessive exercising. These findings coincide with prior studies which indicate that a main advantage of an FC environment is the opportunity to revisit the instructional videos and presentations as many times as the learners need, in order to explore the mathematical concepts comprehensively and ensure perfect comprehension of the content [23,27]. In addition, students can take advantage of the “pausing” and “rewinding” features found in videos to stop, rewind, or repeat any part of the lecture to better understand a certain section [18]. This allows students to set the learning pace most appropriate for them [28]. This is a significant advantage over the traditional method of learning in which the frontal lecture is held at a specific time and location and cannot be repeated easily. This is something that most of the interviewees agreed upon. They emphasized that the repetition helped them set their optimal pace of learning.
• The effect of studying in a flipped classroom on students’ motivation toward mathematics learning
This section addresses the differences in motivation towards mathematics learning between students who studied advanced mathematics in the FC environment and students who studied the same learning units in the traditional learning environment. Prior to studying the learning units, no significant differences were found in motivational levels between the FC group and the comparison group, for both the 10th and 11th grade students. Although the FC and comparison groups in both grades demonstrated similar post-learning attitude motivation levels and no change in motivation over time, further findings that relied on calculating effect sizes revealed that while the 11th graders showed a similar level of motivation in both groups after studying the learning unit, with no change in their motivation level, the 10th graders who participated in the FC environment demonstrated a lower level of motivation after learning the unit compared to students in the comparison group. This difference among the 10th graders, which was found after calculating effect sizes, can be explained by the insufficient sample size, which may have given rise to significant differences had the sample size been increased. These findings support previous studies that prove that motivation is one of the most essential factors affecting students’ learning and performance [10,55], particularly in mathematics [10].
To ensure that motivation is maintained throughout the learning process, students need responsibility, commitment, and determination to independently prepare the content before class [28]. Otherwise, they will not gain the maximum benefits of the collaborative, active learning environment [60,61]. The themes that emerged from the interviews indicate that preparation before class is a key factor for fully comprehending the material and for a successful learning process. In addition, most of the students mentioned that significant responsibility and commitment are required to complete the out-of-class preparation successfully. These claims coincide with prior research showing that students who come to class unprepared are not expected to benefit from this learning method [60,61]. Completing online learning assignments is crucial for successful results in flipped classrooms and for maintaining students’ motivation [28]. Other students mentioned how effortful and time-consuming this experience was, yet they all agreed that time management at home was essential for a successful learning experience in class.
Regarding the decrease in motivation to learn math among the 10th grade students who participated in this study, both the 10th graders and the teacher reported in the interviews that studying in the FC environment was challenging for them. They explained that this was the first time they were exposed to a learning approach that is based mainly on independent learning using an online platform. This coincides with previous studies that showed that the willingness of students to study via the online component of the FC is a crucial element that influences their motivation to study in this environment [60,61]. This finding can also be explained by the fact that the 10th grade students had just begun their advanced 5-unit level studies and thus needed substantial support from their teacher to build a solid base at this level.
4.1. Limitations and Future Research
The current study was conducted in an extracurricular program for students interested in improving their mathematics achievements in high school. The participants had already been assigned to the advanced mathematics class in school (5 units) and chose to participate in this program due to their high motivation and commitment to succeed in mathematics. Participation in this study was voluntary, and their grades in the program had no actual significance, unlike in school. According to the literature, grades are the main factor that affects students’ motivation to study mathematics, since success in mathematics, particularly in high school, is a crucial factor for the likelihood of pursuing studies in advanced mathematics [17]. Therefore, it would be valuable for further research to also investigate the effect of learning in an FC environment on a sample of students who are in the process of choosing advanced mathematics studies or on those who want to make a transition to an advanced mathematics class.
Another research limitation lies in the insufficient sample size, as the limited number of students who participated in this study do not represent the Arab population in Israel. A wider study could be conducted in an Arab high school in Israel in which the research participant are students who study math at different levels (3 to 5 units) and in different grades (10th to 12th). Furthermore, it is very important to expand the research to include other mathematical subjects in the curriculum and investigate the effects of learning different subjects in a flipped classroom. Specifically, it is widely accepted that mathematics underpins all STEM fields [70]. For example, geometry, which is an essential mathematical subject, plays a vital role in promoting spatial thinking and comprehending required in all STEM subjects [71].
4.2. Contribution of the Study
The current study provides insights on how Arab students are affected by learning in a flipped classroom vs. in a traditional classroom with respect to two significant factors that are the subject of many studies on mathematics education, namely conceptual understanding and motivation to study mathematics [47]. The results of this study support the advantages of integrating a flipped learning environment in high school mathematics and add to the limited literature about the effects of the FC approach in mathematics for minority students. As Watad summarized well in his interview: “In the traditional approach, I give the students fish and feed them for a day. Whereas in the FC approach, I teach them to fish, aiming to feed them for life”.
The practical contribution of this study is its presentation of a designated platform for FC, bscool.com, which as far as we know is unique in its suitability for the Arab sector in Israel as all the materials are in Arabic. The study thus contributes to national efforts to reduce the gaps between minorities and the Jewish sector in Israel that were reported in the latest PISA results [13]. The study highlights the importance of online technological tools in education, which in certain circumstances can be one of the only available resources that students can use to acquire knowledge, as was significantly observed during the COVID-19 pandemic. During this difficult period, the use of bscool.com was 19 times greater than before the pandemic. Another practical contribution is related to the benefits of using a hybrid learning environment with an online technological component that is available to everyone and therefore can be used to make mathematics accessible to all, especially for minority students who often lack access to excellent teachers or to advanced learning resources.
Author Contributions
Conceptualization, H.S. and Z.K.; methodology, H.S.; software, H.S.; validation, H.S.; formal analysis, H.S.; investigation, H.S.; resources, H.S.; data curation, H.S.; writing—original draft preparation, H.S.; writing—review and editing, Z.K. and H.S.; visualization, H.S.; supervision, Z.K.; project administration, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Approval for the study was received from the university’s Institutional Review Board (#IRB- 2019-022) before beginning of the study.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Due to ethical reasons data cannot be provided.
Acknowledgments
The generous financial help of the Technion is gratefully acknowledged. Moreover, the authors highly acknowledge Saeed Watad, the founder of Alkhawarizmi institute, for his great support and contribution to this research.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The tables below present the descriptive statistics obtained for the pre- and post-learning mathematical conceptual understanding and motivation questionnaires.

Table A1.
Mathematics conceptual understanding for pre- and post-learning questionnaires: means and standard deviations by time and research group within each grade.
Table A1.
Mathematics conceptual understanding for pre- and post-learning questionnaires: means and standard deviations by time and research group within each grade.
| Conceptual Understanding | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10th Grade | 11th Grade | |||||||||||
| Online (N = 16) | Comparison (N = 20) | Total (N = 36) | Online (N = 20) | Comparison (N = 19) | Total (N = 39) | |||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| Pre | 16.72 | 21.29 | 25.75 | 37.46 | 21.74 | 31.25 | 21.88 | 30.31 | 26.32 | 24.81 | 24.04 | 27.50 |
| Post | 67.19 | 25.08 | 70.38 | 25.61 | 68.96 | 25.07 | 87.88 | 6.03 | 46.84 | 22.03 | 67.88 | 26.07 |

Table A2.
Motivation towards studying mathematics for pre- and post-learning attitude questionnaires: means and standard deviations by time and grade within each research group.
Table A2.
Motivation towards studying mathematics for pre- and post-learning attitude questionnaires: means and standard deviations by time and grade within each research group.
| Motivation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10th Grade | 11th Grade | |||||||||||
| Online (N = 16) | Comparison (N = 20) | Total (N = 36) | Online (N = 20) | Comparison (N = 19) | Total (N = 39) | |||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| Pre | 3.46 | 0.97 | 3.97 | 0.80 | 3.74 | 0.90 | 3.86 | 0.72 | 4.05 | 0.76 | 3.95 | 0.74 |
| Post | 3.18 | 0.98 | 3.91 | 0.91 | 3.59 | 1.00 | 4.14 | 0.66 | 3.74 | 0.74 | 3.95 | 0.72 |
Appendix B
The tables below present the rubrics for assessing the different concepts related to the derivative subject assigned for 10th graders and the various concepts related to the integral subject assigned for the 11th graders, with examples of students’ answers, the score assigned to each answer, and the justification for this assessment.

Table A3.
The rubric for assessing students’ answers for the concept of “extreme point”, within the derivative concept.
Table A3.
The rubric for assessing students’ answers for the concept of “extreme point”, within the derivative concept.
| Extreme Point | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| It is the point at which the function changes intervals from ascending to descending or vice versa. It is where the slope of the tangent line equals zero, and it can have either a maximum value or a minimum value. | Perfect answer, consisting of all the details in the definition, as well as its relation to derivative. | 10 |
| It is a point at which the function has the highest or lowest value of y in the entire domain or solely in its surrounding. These are called maximum or minimum respectively. It represents a stage in which the function changes intervals.The derivative equals zero at this point. | Perfect answer, consisting of nearly all the details in the definition, as well as its relation to derivative. | 10 |
| It is a point at which the function has the highest or lowest value, and the derivative equals zero at it. | Nearly complete answer, missing the relation to intervals. | 9 |
| It is the point at which the function has the highest or lowest value, it can be either maximum or minimum. | Incomplete answer: missing relation to derivative. | 7 |
| It is the point at which the derivative equals zero. | Incomplete answer. Does not refer to the extreme values of the point, or to the function’s interval or “direction” change. | 5 |
| At this point, the function changes direction. | Incomplete answer missing details about “direction”, derivative, and extreme values. | 3 |
| min or max. | Incorrect answer indicating lack of understanding. | 1 |
| It is the highest point in the graph of the function. | Incorrect answer. | 0 |
| It is the highest value of the function. | Incorrect answer. | 0 |
| It is the highest point of the derivative. | Incorrect answer. | 0 |

Table A4.
The rubric for assessing students’ answers for the concept of “interval of increase”, within the derivative concept.
Table A4.
The rubric for assessing students’ answers for the concept of “interval of increase”, within the derivative concept.
| Interval of Increase | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| From left to right the function is increasing, implying the increase in y values as the x values increase. The derivative in this interval is positive. | Perfect answer consisting of all the details. | 10 |
| It is the interval in which the y values increase as the x values do, meaning that in it the values of the function increase gradually. | Nearly perfect answer, missing the relation to derivative. | 9 |
| Whenever x increases y increases. | Nearly perfect answer, missing the relation to derivative. | 9 |
| The derivative is positive in this interval. | Incomplete answer missing very important details about the function values. | 6 |
| It is when y values increase. | Imprecise and incomplete answer since it does not consider x values. The answer is also missing details about the derivative in this interval. | 3 |
| It is the interval in which the function is positive (above the x-axis). | Incorrect answer, indicating lack of understanding. This student might have mixed up the derivative and the function values. | 0 |
| The function is ascending in this interval. | Trivial answer, indicating lack of understanding. | 0 |

Table A5.
The rubric for assessing students’ answers for the concept of “domain”, within the derivative concept.
Table A5.
The rubric for assessing students’ answers for the concept of “domain”, within the derivative concept.
| Domain | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| It refers to all the numbers that are mathematically allowed to be substituted in a function. For example, these are the numbers that never give zero in the denominator of a function or negative result under the square root. | Perfect answer, consisting of full and comprehensive definition including examples. | 10 |
| It is the numbers in which the function gives out a valid y value (the x values that we substitute in the function and get a valid y value). For example, if y = √x you cannot substitute x < 0. Therefore, the domain is x > 0. | Perfect answer, consisting of full and comprehensive definition and detailed example. | 10 |
| The numbers that give us a valid result. | Nearly correct but imprecise answer, missing a few details and more precision. | 8 |
| It refers to the numbers that can be substituted instead of x in the function. | Imprecise and incomplete answer. | 5 |
| It is when the function has no answer. | Incorrect answer. | 0 |
| A point that is on the function. | Incorrect answer. | 0 |
| It is that the denominator must not equal zero. | Incorrect answer, indicating lack of understanding. | 0 |

Table A6.
The rubric for assessing students’ answers for the concept of “integral”, within the integral concept.
Table A6.
The rubric for assessing students’ answers for the concept of “integral”, within the integral concept.
| Integral | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| It is the opposite or reverse of derivative. It refers to the function before applying a derivative to it. The integral of a polynomial function can be computed using the differentiation rule: . | Perfect answer, consisting of a comprehensively detailed definition of this concept, as well as its relation to derivative. | 10 |
| It is the opposite or reverse of derivative. | Perfect answer, showing merely what the integration process is. | 10 |
| It is the function before differentiation. | Nearly complete answer, missing precision in the definition but indicating development of understanding. | 9 |
| It is the antiderivative. | Not clear since no definition of antiderivative is provided in the answer. | 5 |
| Used to find areas. | Incomplete answer and imprecise, but it implies that student relates areas to integration. | 3 |
| It is an operation that is applied on the derivative. | Unclear and imprecise answer, yet it shows that this student is relating integral to derivative. | 2 |

Table A7.
The rubric for assessing students’ answers for the concept of “antiderivative”, within the integral concept.
Table A7.
The rubric for assessing students’ answers for the concept of “antiderivative”, within the integral concept.
| Antiderivative | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| It is the original function before differentiation. | Perfect answer. | 10 |
| It is the opposite or reverse of derivative, synonym of integral. | Perfect answer, a high level of understanding and connecting mathematical concepts. | 10 |
| It is the function before differentiation. | Complete answer. | 10 |
| It is the result of the integration process. | Nearly perfect answer, missing more precision and considering derivative. | 8 |
| The function. | Unclear and imprecise answer, yet it slightly shows that this student is relating this concept to the original function. | 1 |
| The derivative. | Incorrect answer. | 0 |

Table A8.
The rubric for assessing students’ answers for the concept of “integral constant”, within the integral concept.
Table A8.
The rubric for assessing students’ answers for the concept of “integral constant”, within the integral concept.
| Integral Constant | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| When applying an integral or antiderivative to a certain function, the result is not fully determined since adding any constant to it will give out the same result (zero). So, we need to add this constant C to the result. | Perfect answer consisting of all the details about this concept, in addition to indication of understanding this concept. | 10 |
| The result of the integral is not completed unless you add this constant C. Additional information is needed to be able to get the complete form of the function. | Complete answer indicating improvement in conceptual understanding. | 10 |
| It is a parameter that we add to the result of the integral because if we apply differentiation to this result, this parameter’s derivative will equal zero. | Nearly complete yet imprecise answer. | 8 |
| This is the constant C, we cannot identify it unless we get more information about the function, its derivative equals zero. | Not enough! This answer is missing the main idea of the definition.Missing the correlation between the different information taught in class. | 5 |
| The constant C that we add to the result. | Unclear and imprecise answer. | 0 |

Table A9.
The rubric for assessing students’ answers for the concept of “definite integral”, within the integral concept.
Table A9.
The rubric for assessing students’ answers for the concept of “definite integral”, within the integral concept.
| Definite Integral | ||
|---|---|---|
| Student’s Answer | Justification for Scoring | Score (/10) |
| It is the definite integral process that is constrained between two limits on the x-axis. It is used to compute the area under different types of curves. | Perfect answer with comprehensive details. | 10 |
| It is used to compute the area under different types of curves. | Incomplete answer missing details about the limits of the integral. | 7 |
| It is the area under the curves. | Incorrect answer; it helps to compute the area, but it is not the area. | 0 |
| It is a constrained domain to compute an area. | Incorrect answer. | 0 |
References
- National Governors Association. Common Core State Standards; National Governors Association: Washington, DC, USA, 2010; Available online: http://www.corestandards.org/ (accessed on 24 December 2020).
- Leinwand, S.; Brahier, D.; Huinker, D. Principles to Actions: Ensuring Mathematical Success for All; The National Council of Teachers of Mathematics, Inc.: Reston, VA, USA, 2014. [Google Scholar]
- Honey, M.; Pearson, G.; Schweingruber, H.A. STEM Integration in K-12 Education: Status, Prospects, and an Agenda for Research; National Academies Press: Washington, DC, USA, 2014; Volume 500. [Google Scholar]
- Serhan, D. Students’ Understanding of the Definite Integral Concept. Int. J. Res. Educ. Sci. 2015, 1, 84–88. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Schoenfeld, A.H. Problematizing Teaching and Learning Mathematics as “Given” in STEM Education; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Hiebert, J.; Lefevre, P. Conceptual and procedural knowledge in mathematics: An introductory analysis. Concept. Proced. Knowl. Case Math. 1986, 2, 1–27. [Google Scholar]
- Lobato, J.; Clarke, D.; Ellis, A.B. Initiating and eliciting in teaching: A reformulation of telling. J. Res. Math. Educ. 2005, 36, 101–136. [Google Scholar]
- Zakaria, E.; Zaini, N. Conceptual and procedural knowledge of rational numbers in trainee teachers. Eur. J. Soc. Sci. 2009, 9, 202–217. [Google Scholar]
- Kilpatrick, J.; Swafford, J.; Findell, B. Adding it Up: Helping Children Learn Mathematics; National Academies Press: Washington, DC, USA, 2001. [Google Scholar]
- Leroy, N.; Bressoux, P. Does amotivation matter more than motivation in predicting mathematics learning gains? A longitudinal study of sixth-grade students in France. Contemp. Educ. Psychol. 2016, 44, 41–53. [Google Scholar] [CrossRef]
- Schukajlow, S.; Rakoczy, K.; Pekrun, R. Emotions and motivation in mathematics education: Theoretical considerations and empirical contributions. ZDM 2017, 49, 307–322. [Google Scholar] [CrossRef]
- Dori, Y.J.; Kohen, Z.; Rizowy, B. Mathematics for Computer Science: A Flipped Classroom with an Optional Project. Eurasia J. Math. Sci. Technol. Educ. 2020, 16, em1915. [Google Scholar] [CrossRef]
- OECD Library. PISA 2021 Mathematics Framework (Draft). Available online: http://www.oecd.org/pisa/publications/ (accessed on 10 December 2019).
- Friedman-Sokuler, N.; Justman, M. Gender, culture and STEM: Counter-intuitive patterns in Arab society. Econ. Educ. Rev. 2020, 74, 101947. [Google Scholar] [CrossRef]
- Kaiser, G.; Hino, K.; Knipping, C. Proposal for a framework to analyse mathematics education in Eastern and Western traditions. In Mathematics Education in Different Cultural Traditions—A Comparative Study of East Asia and the West; Springer: Berlin/Heidelberg, Germany, 2006; pp. 319–351. [Google Scholar]
- Kaiser, G.; Vollstedt, M. Teachers’ views on effective mathematics teaching: Commentaries from a European perspective. ZDM 2007, 39, 341–348. [Google Scholar] [CrossRef]
- Kohen, Z.; Nitzan, O. Excellence in Mathematics in Secondary School and Choosing and Excelling in STEM Professions over Significant Periods in Life. Int. J. Sci. Math. Educ. 2021, 1–23. [Google Scholar] [CrossRef]
- Bergmann, J.; Sams, A. Flip Your Classroom: Reach Every Student in Every Class Every Day; International Society for Technology in Education: Washington, DC, USA, 2012. [Google Scholar]
- Song, Y.; Kapur, M. How to flip the classroom—“Productive failure or traditional flipped classroom” pedagogical design? Educ. Technol. Soc. 2017, 20, 292–305. [Google Scholar]
- Barak, M.; Lipson, A.; Lerman, S. Wireless laptops as means for promoting active learning in large lecture halls. J. Res. Technol. Educ. 2006, 38, 245–263. [Google Scholar] [CrossRef] [Green Version]
- Murillo-Zamorano, L.R.; Sánchez, J.Á.L.; Godoy-Caballero, A.L. How the flipped classroom affects knowledge, skills, and engagement in higher education: Effects on students’ satisfaction. Comput. Educ. 2019, 141, 103608. [Google Scholar] [CrossRef]
- Bishop, J.L.; Verleger, M.A. The flipped classroom: A survey of the research. In Proceedings of the ASEE National Conference Proceedings, Atlanta, GA, USA, 23–26 June 2013; pp. 1–18. [Google Scholar]
- Lo, C.K.; Hew, K.F. A critical review of flipped classroom challenges in K-12 education: Possible solutions and recommendations for future research. Res. Pract. Technol. Enhanc. Learn. 2017, 12, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tabach, M.; Friedlander, A. The role of context in learning beginning algebra. Algebra Algebraic Think. Sch. Math. 2008, 70, 223. [Google Scholar]
- Aşıksoy, G.; Özdamlı, F. Flipped Classroom adapted to the ARCS Model of Motivation and applied to a Physics Course. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 1589–1603. [Google Scholar] [CrossRef]
- Fernández-Martín, F.-D.; Romero-Rodríguez, J.-M.; Gómez-García, G.; Ramos Navas-Parejo, M. Impact of the Flipped Classroom Method in the Mathematical Area: A Systematic Review. Mathematics 2020, 8, 2162. [Google Scholar] [CrossRef]
- Lundin, M.; Rensfeldt, A.B.; Hillman, T.; Lantz-Andersson, A.; Peterson, L. Higher education dominance and siloed knowledge: A systematic review of flipped classroom research. Int. J. Educ. Technol. High. Educ. 2018, 15, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-L.; Hwang, G.-J. A self-regulated flipped classroom approach to improving students’ learning performance in a mathematics course. Comput. Educ. 2016, 100, 126–140. [Google Scholar] [CrossRef]
- Akçayır, G.; Akçayır, M. The flipped classroom: A review of its advantages and challenges. Comput. Educ. 2018, 126, 334–345. [Google Scholar] [CrossRef]
- Bezuidenhout, J. First-year university students’ understanding of rate of change. Int. J. Math. Educ. Sci. Technol. 1998, 29, 389–399. [Google Scholar] [CrossRef]
- Hauger, G.S. Instantaneous rate of change: A numerical approach. Int. J. Math. Educ. Sci. Technol. 2000, 31, 891–897. [Google Scholar] [CrossRef]
- Sahin, Z.; Yenmez, A.A.; Erbas, A.K. Relational understanding of the derivative concept through mathematical modeling: A case study. Eurasia J. Math. Sci. Technol. Educ. 2015, 11, 177–188. [Google Scholar] [CrossRef]
- Akkoç, H.; Bingolbali, E.; Ozmantar, F. Investigating the technological pedagogical content knowledge: A case of derivative at a point. In Proceedings of the 32nd International Conference on the Psychology of Mathematics Education (PME32), Morelia, Mexico, 17–21 July 2008; pp. 17–21. [Google Scholar]
- Thompson, P.W. Images of rate and operational understanding of the fundamental theorem of calculus. Educ. Stud. Math. 1994, 26, 229–274. [Google Scholar] [CrossRef]
- Ostebee, A.; Zorn, P. Calculus from Graphical, Numerical, and Symbolic Points of View; Saunders College Publishing: New York, NY, USA, 1997. [Google Scholar]
- Huang, C.-H. Engineering students’ conceptual understanding of the derivative in calculus. World Trans. Eng. Technol. Educ. 2011, 9, 209–214. [Google Scholar]
- Mahir, N. Conceptual and procedural performance of undergraduate students in integration. Int. J. Math. Educ. Sci. Technol. 2009, 40, 201–211. [Google Scholar] [CrossRef]
- Rasslan, S.; Tall, D. Definitions and images for the definite integral concept. In Proceedings of the PME Conference, Norwich, UK, 21–26 July 2002; p. 4-089. [Google Scholar]
- Sealey, V. Definite integrals, Riemann sums, and area under a curve: What is necessary and sufficent. In Proceedings of the 28th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Merida, Mexico, 9–12 November 2006; pp. 46–53. [Google Scholar]
- Abdul-Rahman, S. Learning with examples and students’ understanding of integration. In Proceedings of the Mathematics Education into the 21st Century Project: Reform, Revolution and Paradigm Shifts in Mathematics Education, Bahru, Malaysia, 25 November–1 December 2005. [Google Scholar]
- Ferrini-Mundi, J.; Graham, K. Research in calculus learning: Understanding of limits, derivatives and integrals. In Research Issues in Undergraduate Mathematics Learning; Kaput, J.J., Dubinsky, E., Eds.; MAA Notes 33; MAA: Washington, DC, USA, 1994; pp. 31–45. [Google Scholar]
- Orton, A. Students’ understanding of integration. Educ. Stud. Math. 1983, 14, 1–18. [Google Scholar] [CrossRef]
- Pettersson, K.; Scheja, M. Algorithmic contexts and learning potentiality: A case study of students’ understanding of calculus. Int. J. Math. Educ. Sci. Technol. 2008, 39, 767–784. [Google Scholar] [CrossRef]
- Grundmeier, T.A.; Hansen, J.; Sousa, E. An exploration of definition and procedural fluency in integral calculus. Probl. Resour. Issues Math. Undergrad. Stud. 2006, 16, 178–191. [Google Scholar] [CrossRef]
- Setyaningrum, W. Blended Learning: Does it help students in understanding mathematical concepts? J. Ris. Pendidik. Mat. 2018, 5, 244–253. [Google Scholar] [CrossRef] [Green Version]
- Hiebert, J.; Grouws, D.A. The effects of classroom mathematics teaching on students’ learning. Second Handb. Res. Math. Teach. Learn. 2007, 1, 371–404. [Google Scholar]
- Bhagat, K.K.; Chang, C.-N.; Chang, C.-Y. The impact of the flipped classroom on mathematics concept learning in high school. J. Educ. Technol. Soc. 2016, 19, 134–142. [Google Scholar]
- Sams, A.; Bergmann, J. Flip your students’ learning. Educ. Leadersh. 2013, 70, 16–20. [Google Scholar]
- Murphy, P.K.; Alexander, P.A. A motivated exploration of motivation terminology. Contemp. Educ. Psychol. 2000, 25, 3–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pintrich, P.R. A motivational science perspective on the role of student motivation in learning and teaching contexts. J. Educ. Psychol. 2003, 95, 667. [Google Scholar] [CrossRef] [Green Version]
- Pintrich, P.R. Motivation and classroom learning. In Handbook of Psychology: Educational Psychology; Reynolds, W.M., Miller, G.E., Eds.; Wiley: New York, NY, USA, 2003; pp. 103–122. [Google Scholar]
- Ryan, R.M.; Deci, E.L. Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemp. Educ. Psychol. 2000, 25, 54–67. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.C.; Song, Y. An experience of personalized learning hub initiative embedding BYOD for reflective engagement in higher education. Comput. Educ. 2015, 88, 227–240. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M. Handbook of Self-Determination Research; University Rochester Press: Rochester, NY, USA, 2004. [Google Scholar]
- Linnenbrink, E.A.; Pintrich, P.R. Motivation as an enabler for academic success. Sch. Psychol. Rev. 2002, 31, 313–327. [Google Scholar] [CrossRef]
- Hannula, M.S. Motivation in mathematics: Goals reflected in emotions. Educ. Stud. Math. 2006, 63, 165–178. [Google Scholar] [CrossRef]
- Op’t Eynde, P.; De Corte, E.; Verschaffel, L. “Accepting emotional complexity”: A socio-constructivist perspective on the role of emotions in the mathematics classroom. Educ. Stud. Math. 2006, 63, 193–207. [Google Scholar] [CrossRef]
- Van Alten, D.C.; Phielix, C.; Janssen, J.; Kester, L. Effects of flipping the classroom on learning outcomes and satisfaction: A meta-analysis. Educ. Res. Rev. 2019, 28, 100281. [Google Scholar] [CrossRef]
- Herreid, C.F.; Schiller, N.A. Case studies and the flipped classroom. J. Coll. Sci. Teach. 2013, 42, 62–66. [Google Scholar]
- Hao, Y. Exploring undergraduates’ perspectives and flipped learning readiness in their flipped classrooms. Comput. Hum. Behav. 2016, 59, 82–92. [Google Scholar] [CrossRef]
- Yilmaz, R. Exploring the role of e-learning readiness on student satisfaction and motivation in flipped classroom. Comput. Hum. Behav. 2017, 70, 251–260. [Google Scholar] [CrossRef]
- Porcaro, P.A.; Jackson, D.E.; McLaughlin, P.M.; O’Malley, C.J. Curriculum design of a flipped classroom to enhance haematology learning. J. Sci. Educ. Technol. 2016, 25, 345–357. [Google Scholar] [CrossRef]
- Jones, S.R. Areas, anti-derivatives, and adding up pieces: Definite integrals in pure mathematics and applied science contexts. J. Math. Behav. 2015, 38, 9–28. [Google Scholar] [CrossRef]
- Jones, S.R. What education research related to calculus derivatives and integrals implies for chemistry instruction and learning. In It’s Just Math: Research on Students’ Understanding of Chemistry and Mathematics; Towns, M.H., Bain, K., Rodriguez, J.-M.G., Eds.; ACS Symposium Series1316; American Chemical Society: Washington, DC, USA, 2019; pp. 187–212. [Google Scholar]
- Habre, S.; Abboud, M. Students’ conceptual understanding of a function and its derivative in an experimental calculus course. J. Math. Behav. 2006, 25, 57–72. [Google Scholar] [CrossRef]
- Tall, D.; Vinner, S. Concept image and concept definition in mathematics with particular reference to limits and continuity. Educ. Stud. Math. 1981, 12, 151–169. [Google Scholar] [CrossRef]
- Tall, D. Whither calculus? Math. Teach. 1987, 117, 50–54. [Google Scholar]
- To Learn and Teach Analytics. 2013. Available online: https://pop.education.gov.il/tchumey_daat/matmatika/chativa-elyona/teaching-mathematics/learn-teach-analysis/ (accessed on 20 June 2021).
- Pintrich, P.R.; Smith, D.A.; Garcia, T.; McKeachie, W.J. Reliability and predictive validity of the Motivated Strategies for Learning Questionnaire (MSLQ). Educ. Psychol. Meas. 1993, 53, 801–813. [Google Scholar] [CrossRef]
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The role of mathematics in interdisciplinary STEM education. ZDM 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Mulligan, J. Looking within and beyond the geometry curriculum: Connecting spatial reasoning to mathematics learning. ZDM 2015, 47, 511–517. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).