Cauchy Problem for a Stochastic Fractional Differential Equation with Caputo-Itô Derivative

Abstract

In this note, we define an operator on a space of Itô processes, which we call Caputo-Itô derivative, then we considerer a Cauchy problem for a stochastic fractional differential equation with this derivative. We demonstrate the existence and uniqueness by a contraction mapping argument and some examples are given.

1. Introduction

Mathematical models based on ordinal or partial differential equations have been successfully used to describe the behavior of systems through the space and time. On the other hand, although the origin is very old, it was not until recent years that fractional order differential equations have gained more attention in different areas of science; for example, they are very useful to describe complex systems with memory effects (see [1,2,3,4,5] and the references therein).

However, in order to describe and forecast a real phenomenon, it is necessary to introduce a component that captures the random behavior caused by a major source of uncertainty, that usually propagates in time. When we add such a component, the model obtained is now governed by a stochastic fractional differential equation [6,7]. On the order hand, the Itô stochastic calculus has been applied in several fields of knowledge; such as, engineering, physics, biology, among others [8,9]. A stochastic process that is closely related to fractional calculus is the fractional Brownian motion (fBm); this is a centered, self-similar, and stationary-increment Gaussian stochastic process; which can be represented by a Riemann–Liouville integral [10]. However, the fBm is not a semimartingale (for Hurst index different from $1/2$), and therefore, it is not easy to define a stochastic integral with respecto to this process, under the Itô theory.

In this note, both the Caputo derivative and stochastic integral with respect to a semimartingale are used to define the Caputo-Itô derivative. The obtained processes, from applying the Caputo-Itô operator to a semimartingale, can be seen as a moving average process or a Volterra-type process, which have been studied by authors as [11] who analyses the ambit processes, which are a class of temporal-space Volterra process with semimartingale property, this processes are used to model the turbulence and tumor growth. Basse and Pedersen [12] studied the moving average processes driven by Lévy process. In the study of financial systems, an important characteristic to consider, is the memory effect, several researchers have devoted their work to that aim. Many financial variables have been found with long memory effects, such as Gross Domestic Product (GDP), interest rate, exchange rates, share price and future prices. The Caputo-Itô operator, when using the kernel of the Caputo’s fractional derivative, introduces the memory effect in the system $X_t$. In [13] a stochastic differential equation model of fractional order is used to describe the effect of memory of trends in financial prices.

In this work, we consider a Cauchy problem for a stochastic fractional differential equation with the Caputo-Itô derivative, proving existence and uniqueness of solutions. Moreover, some examples are given to illustrate the trajectories of the solutions.

2. Preliminaries

In this section we define the fractional order Caputo derivative, the Mittag-Leffler function and the stochastic Itô derivative.

Definition 1.

The fractional Caputo derivative of order α, with respect to time t is given by

$${\displaystyle D_a^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(n-\alpha )}}{\int }_a^t{\displaystyle \frac{f^{\left(n\right)}\left(s\right)}{{(t-s)}^{\alpha -n+1}}}ds,}$$

(1)

where $\alpha \ge 0$, $n=\lceil \alpha \rceil$, $a\in [-\infty ,t)$ and $f:[a,b]\to \mathbb{R}$ is such that $f^{(n-1)}\left(x\right)$ is an absoluty continuos function. Here, Γ is the Gamma function given by

$$\mathsf{\Gamma }\left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt,Re\left(z\right)>0.$$

Definition 2.

Let $\alpha ,\beta ,z\in \mathbb{R}$ and $\alpha >0$. Then, the function ${\mathrm{E}}_{\alpha ,\beta }(·)$ given by

$${\displaystyle {\mathrm{E}}_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathsf{\Gamma }(\alpha k+\beta )}}}$$

(2)

is called the two parameter Mittag-Leffler function, as long as the series (2) is convergent.

Definition 3. 

Let$Y_t$be an Itô process with$t\in J=[0,T]$ ($T<\infty$) defined by

$${\displaystyle Y_t=Y_0+{\int }_0^t\mu (Y_s,s)ds+{\int }_0^t\sigma (Y_s,s)d{B}_s}$$

(3)

where $\mu :\mathbb{R}\times J\to \mathbb{R}$ and $\sigma :\mathbb{R}\times J\to \mathbb{R}$ are ${\mathcal{F}}_t$-adapted processes. Let $V_t$ be a predictable process, such that

• ${\displaystyle {\int }_0^t\left|V_s\mu (X_s,s)\right|ds<\infty }$with probability one.
• ${\displaystyle {\int }_0^{t}E{\left(V_s\sigma (X_s,s)\right)}^{2}ds<\infty }$.

Let us define the stochastic integral for$V_t$, with respect to$Y_t$, as

$${\int }_0^t{V}_{s}d{Y}_s={\int }_0^t{V}_s\mu (Y_s,s)ds+{\int }_0^t{V}_s\sigma (Y_s,s)d{B}_s.$$

Definition 4.

A process$X_t$ ($t\in J$) is called self-similar with index $H>0$, if for all $a>0$, the processes $X_{at}$ and $a^H{X}_t$ have the same distribution, or equivalently, the processes $X_t$ y $a^{-H}{X}_{at}$ have the same distribution.

The fractional Brownian motion (fBm) is a self-similar gaussian process with index $H\in (0,1)$, [10].

3. The Caputo-Itô Derivative

Let $X_t$ be the Itô process with stochastic differential

$$d{X}_t=\mu (X_t,t)dt+\sigma (X_t,t)d{B}_t,$$

(4)

under the following conditions,

• ${\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\left|{(t-s)}^{-\alpha }\mu (X_s,s)\right|ds<\infty }$ with probability one,
• ${\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\mathbb{E}{\left({(t-s)}^{-\alpha }\sigma (X_s,s)\right)}^{2}ds<\infty ,}$

We define a Caputo-Itô derivative of $X_t$ by:

$$\begin{array}{ccc}\hfill {}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t& =& {\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }d{X}_s}\hfill \\ \hfill & =& {\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}\left[{\displaystyle {\int }_0^t{(t-s)}^{-\alpha }\mu (X_s,s)ds+{\int }_0^t{(t-s)}^{-\alpha }\sigma (X_s,s)d{B}_s}\right]\hfill \end{array}$$

(5)

where $\alpha \in (0,1)$.

Let us note that ${}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t$ is a Itô process. If we define $\tilde{\mu }(X_s,s)=\frac{{(t-s)}^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}\mu (X_s,s)$ and $\tilde{\sigma }(X_s,s)=\frac{{(t-s)}^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}\sigma (X_s,s)$, then ${}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t={\int }_0^t\tilde{\mu }(X_s,s)ds+{\int }_0^t\tilde{\sigma }(X_s,s)d{B}_s$. The process $X_t$ is a semimartingale; however, ${}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t$ is not necessarily one [14].

Let us consider Itô processes, given by the stochastic differential

$$d{X}_t=\mu \left(t\right)dt+\sigma \left(t\right)d{B}_t,$$

(6)

where $\mu \left(t\right)$ and $\sigma \left(t\right)$ are functions depending only on t variable, such that the stochastic differential exists. We denote by $Z_t$, the process obtained after applying the Caputo-Itô derivative to the process $X_t$, that is

$$Z_t={}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}\left[{\displaystyle {\int }_0^t{(t-s)}^{-\alpha }\mu \left(s\right)ds+{\int }_0^t{(t-s)}^{-\alpha }\sigma \left(s\right)d{B}_s}\right].$$

Note that $Z_t$ is a gaussian process with expected value $\mathbb{E}\left(Z_t\right)=I_0^{1-\alpha }\mu \left(t\right)$, its variance is given by $\mathrm{Var}\left(Z_t\right)=\frac{\mathsf{\Gamma }(1-\beta )}{{\mathsf{\Gamma }}^2(1-\beta /2)}{I}_0^{1-\beta }{\sigma }^2\left(t\right)$, where I is the Riemann–Liouville integral and $\beta =2\alpha$. For t, $u\ge 0$, we obtain the covariance function

$${\displaystyle \mathrm{Cov}(Z_t,Z_{t+u})=\frac{1}{{\mathsf{\Gamma }}^2(1-\alpha )}{\int }_0^t{\left[(t-s)(t+u-s)\right]}^{-\alpha }{\sigma }^2\left(s\right)ds.}$$

Example 1.

If we take $d{X}_t=t^{k}d{B}_t$, then

$$\begin{array}{ccc}\hfill Z_t={}^{CI}{\mathcal{D}}_0^{\alpha }{X}_t& =& {\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }{s}^{k}d{B}_s}\hfill \\ & =& {\displaystyle {\displaystyle \frac{t^{k+\frac{1}{2}-\alpha }}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^1{(1-u)}^{-\alpha }{u}^{k}d{B}_u}\hfill \\ & =& t^{k+\frac{1}{2}-\alpha }{Z}_1\hfill \end{array}$$

Note that ${(t-s)}^{-\alpha }{s}^k$ is not a random function and it depends on the upper limit of the integral, then $Z_t$ is not necessarily a martingale; however, it is a Gaussian process with zero mean and variance given by

$$\begin{array}{ccc}\hfill \mathrm{Var}\left(Z_t\right)& =& t^{2k+1-2\alpha }\mathrm{Var}\left(Z_1\right)\hfill \\ & =& {\displaystyle \frac{t^{2k+1-2\alpha }}{{\mathsf{\Gamma }}^2(1-\alpha )}}{\displaystyle \frac{\mathsf{\Gamma }(2k+1)\mathsf{\Gamma }(1-2\alpha )}{\mathsf{\Gamma }\left(2\right(k+1-\alpha \left)\right)}}.\hfill \end{array}$$

The variance of process $Z_t$ must be finite, then $\alpha \in (0,1/2)\cup (1/2,1)$ and $k>\alpha -1$. On the other hand, since $Z_t$ is a Gaussian process with zero mean, then it is fully determined by its covariance function, which we proceed to calculate. Let $u>0$ and $t\in [0, T]$ with $T<\infty$, then

$$\begin{array}{ccc}\hfill \mathrm{Cov}(Z_t,Z_{t+u})& =& {\displaystyle {\displaystyle \frac{1}{{\mathsf{\Gamma }}^2(1-\alpha )}}{\int }_0^t{s}^{2k}{(t-s)}^{-\alpha }{(t+u-s)}^{-\alpha }ds.}\hfill \\ & =& {\displaystyle {\displaystyle \frac{t^{2k+1-\alpha }{(t+u)}^{-\alpha }}{{\mathsf{\Gamma }}^2(1-\alpha )}}{\int }_0^1{v}^{2k}{(1-v)}^{-\alpha }{(1-zv)}^{-\alpha }dv,}\hfill \end{array}$$

where $z=\frac{t}{t+u}$, then,

$$\mathrm{Cov}(Z_t,Z_{t+u})={\displaystyle \frac{t^{2k+1-\alpha }{(t+u)}^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}}{\displaystyle \frac{\mathsf{\Gamma }(2k+1)}{\mathsf{\Gamma }\left(2\right(k+1)-\alpha )}}{}_2{F}_1(\alpha ,2k+1,2(k+1)-\alpha ,z).$$

(7)

Here, ${}_2{F}_1(a,b,c,z)$ is the Gaussian hypergeometric function,

$${\displaystyle {}_2{F}_1(a,b,c,z)={\displaystyle \frac{\mathsf{\Gamma }\left(c\right)}{\mathsf{\Gamma }\left(b\right)\mathsf{\Gamma }(c-b)}}{\int }_0^1{u}^{b-1}{(1-u)}^{c-b-1}{(1-zu)}^{-a}du,}$$

(8)

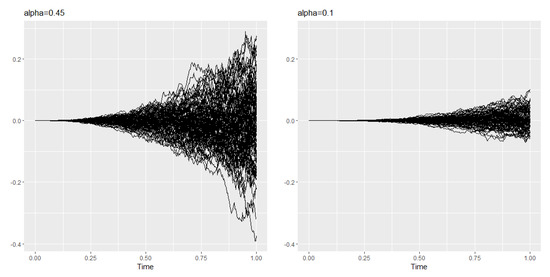
where, $a\in \mathbb{R}$, $c>b$ and $z\in \mathbb{C}$, with $\left|z\right|<1$. In Figure 1, we shown samples trajectories of $Z_t$.

Figure 1. Sample trajectories of $Z_t$, with $\alpha =0.45$, $k=3$ (left) and $\alpha =0.10$, $k=3$ (right).

In order to prove that $Z_{at}$ and $a^H{Z}_t$ have the same distribution it is sufficient to show that its covariance functions are equal, since $Z_t$ is a Gaussian process. Let $a>0$ and $s<t$, according to Definition 4, we have

$$\begin{array}{ccc}\hfill \mathrm{Cov}(Z_{as},Z_{at})& =& \mathrm{Cov}({\left(as\right)}^{k+\frac{1}{2}-\alpha }{Z}_1,{\left(at\right)}^{k+\frac{1}{2}-\alpha }{Z}_1)\hfill \\ & =& \mathrm{Cov}(a^{k+\frac{1}{2}-\alpha }{Z}_s,a^{k+\frac{1}{2}-\alpha }{Z}_t).\hfill \end{array}$$

Thus, the process $Z_t$ is self-similar, with index $H=k+\frac{1}{2}-\alpha$. The increments of the process $Z_t$ are not stationary. In fact, it is sufficient to show that $E{(Z_{t+h}-Z_h)}^2$ depends on h,

$$\begin{array}{ccc}\hfill E{(Z_{t+h}-Z_h)}^2& =& E{({(t+h)}^{k+\frac{1}{2}-\alpha }{Z}_1-h^{k+\frac{1}{2}-\alpha }{Z}_1)}^2\hfill \\ & =& {({(t+h)}^{k+\frac{1}{2}-\alpha }-h^{k+\frac{1}{2}-\alpha })}^{2}E{\left(Z_1\right)}^2.\hfill \end{array}$$

Therefore, $Z_t$ does not have stationary increments, unless $k=\alpha +1/2$. Now, to prove that the increments of the process $Z_t$ are not independents, it is sufficient to show that the covariance of the increments is not null. Indeed, let us consider $t_1<t_2<t_3<t_4$, then

$$\begin{array}{ccc}\hfill \mathrm{Cov}(Z_{t_2}-Z_{t_1},Z_{t_4}-Z_{t_3})& =& (t_2^{k+\frac{1}{2}-\alpha }-t_1^{k+\frac{1}{2}-\alpha })(t_4^{k+\frac{1}{2}-\alpha }-t_3^{k+\frac{1}{2}-\alpha })\mathrm{Var}\left(Z_1\right)>0.\hfill \end{array}$$

We conclude that process $Z_t$ is Gaussian, not necessarily a martingale and does not have stationary nor independent increments.

4. Main Problem

We denote $L^2\left(P\right)$, the space real random variables ${\mathcal{F}}_t$-measurable and square integrable, endowed with the norm $\parallel X_t{\parallel }_{L^2\left(P\right)}=\left(\mathbb{E}\right|X_t{{|}^2)}^{1/2}$ and $J=[0,T]$. Thus, $L^2\left(P\right)$ with ${\parallel ·\parallel }_{L^2\left(P\right)}$ is a Banach space. Let $C(J,L^2\left(P\right))$ be the Banach space of the continuous mapping from J to $L^2\left(P\right)$, satisfying the condition $\underset{t\in J}{sup}\mathbb{E}\left(\right|X_t{|}^2)<\infty$, and ${\mathcal{H}}_2$ be the closed subspace of the ${\mathcal{F}}_t$-measurable continuous processes $X_t$ in $C(J,L^2\left(P\right))$, where $X\left(0\right)=X_0$ is ${\mathcal{F}}_0$-measurable, with norm defined by

$$\parallel X_t{\parallel }_{{\mathcal{H}}_2}={\left(\underset{t\in J}{sup}{\parallel X_t\parallel }_{L^2\left(P\right)}^2\right)}^{1/2}.$$

Note that $({\mathcal{H}}_2,\parallel ·{\parallel }_{{\mathcal{H}}_2})$ is a Banach space.

Let’s consider the following stochastic fractional differential equation

$$\begin{array}{ccc}\hfill {}^C{\mathcal{D}}_t^{\alpha }{X}_t& =& \lambda X_t+\mu (X_t,t)+\sigma (X_t,t){\xi }_t\hfill \\ \hfill X\left(0\right)& =& X_0\hfill \end{array}$$

(9)

where $t\in J$, $0<\alpha <1$, ${\xi }_t=\frac{d{B}_t}{dt}$. Here, $\mu$ and $\sigma$ are suitable functions that will be defined below.

Definition 5. 

A stochastic process$X_t:J\to \mathbb{R}$is called a mild solution for (5), if the following conditions meet:

• $X_t$is measurable and${\mathcal{F}}_t$-adapted.
• $X\left(0\right)=X_0$
• $X_t$satisfy the following equation

  $${\displaystyle X_t={\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)X_0+{\int }_0^t{(t-s)}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda {(t-s)}^{\alpha }\right)\mu (X_s,s)ds+{\int }_0^t{(t-s)}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda {(t-s)}^{\alpha }\right)\sigma (X_s,s)d{B}_s,}$$

where ${\mathrm{E}}_{\alpha ,\beta }\left(z\right)$ is the Mittag–Leffler function.

According to [15,16], we impose the following conditions:

C1

If $\alpha \in (0,1)$, $\lambda$ is a real number and $t>0$, we have $|{\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)| \le M{e}^{wt}$ and $|t^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda t^{\alpha }\right)| \le C{e}^{\omega t}(1+t^{\alpha -1})$, for some w big enough. Thus, we obtain

$$\begin{array}{ccc}\hfill |{\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)|\le {\tilde{M}}_T& \mathsf{y}& |t^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda t^{\alpha }\right)|\le t^{\alpha -1}{\tilde{M}}_S,\hfill \end{array}$$

where ${\tilde{M}}_T={sup}_{0\le t\le T}\left|{\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)\right|$ and ${\tilde{M}}_S={sup}_{0\le t\le T}C{e}^{\omega t}(1+t^{1-\alpha })$.

C2

The functions $\mu :\mathbb{R}\times J\to \mathbb{R}$ and $\sigma :\mathbb{R}\times J\to \mathbb{R}$ are continuous and there are constants $L_{\mu }$ y $L_{\sigma }$ such that:

$$\begin{array}{ccc}\mathbb{E}\parallel \mu (X_t,t)-\mu (Y_t,t){\parallel }^2\le L_{\mu }\mathbb{E}{\parallel X_t-Y_t\parallel }^2,& & \mathbb{E}\parallel \sigma (X_t,t)-\sigma (Y_t,t){\parallel }^2\le L_{\sigma }\mathbb{E}{\parallel X_t-Y_t\parallel }^2,\end{array}$$

for all $X_t,Y_t\in {\mathcal{H}}_2$ and $t\in [0,T]$.

C3

The functions $\mu ,\sigma \in C(\mathbb{R}\times J,\mathbb{R})$. Also, for $s\in J$ and $X_t\in {\mathrm{B}}_r=\left\{X_t\in {\mathcal{H}}_2:\mathbb{E}\left|X_t^2\right|\le r\right\}$ there are two continuous functions ${\tilde{L}}_{\mu }$, ${\tilde{L}}_{\sigma }:J\to (0,\infty )$, such that

$$\begin{array}{ccc}\mathbb{E}|\mu (X_t,t){|}^2\le {\tilde{L}}_{\mu }\left(t\right)\varphi \left(\mathbb{E}\right|X_t{|}^2),& & \mathbb{E}|\sigma (X_t,t){|}^2\le {\tilde{L}}_{\sigma }\left(t\right)\psi \left(\mathbb{E}\right|X_t{|}^2),\end{array}$$

where the functions $\varphi$ and $\psi$ satisfy the following condition:

$${\displaystyle {\int }_0^T\zeta \left(s\right)ds\le {\int }_c^{\infty }{\displaystyle \frac{ds}{\varphi \left(s\right)+\psi \left(s\right)}}.}$$

Here,

$$\begin{array}{ccc}\zeta \left(t\right)=max\left\{{\displaystyle \frac{3{\tilde{M}}_s^2{T}^{\alpha }}{\alpha }}{t}^{\alpha -1}{\tilde{L}}_{\mu }\left(t\right),3{\tilde{M}}_s^2{t}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(t\right)\right\},& & c=3{\tilde{M}}_T^2\left(E\right|X_0{|}^2).\end{array}$$

Theorem 1.

On the conditions C1 y C2, the stochastic fractional Equation (9) have a unique mild solution in J, if the following inequality holds:

$$2{\tilde{M}}_S^2{T}^{2\alpha }\left({\displaystyle \frac{L_{\mu }}{{\alpha }^2}}+{\displaystyle \frac{L_{\sigma }}{T(2\alpha -1)}}\right)<1.$$

(10)

Proof. 

Let’s define the function $S_{\alpha }\left(t\right)=t^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda t^{\alpha }\right)$ and $\Pi :{\mathcal{H}}_2\to {\mathcal{H}}_2$ the operator given by

$${\displaystyle \Pi \left(X_t\right)={\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)X_0+{\int }_0^t{S}_{\alpha }(t-s)\mu (X_s,s)ds+{\int }_0^t{S}_{\alpha }(t-s)\sigma (X_s,s)d{B}_s.}$$

Note that $\Pi$ maps ${\mathcal{H}}_2$ in itself, due to $\mu$ and $\sigma$ are continuous functions and $X_t$ is a measurable and ${\mathcal{F}}_t$-adapted processes. Now, we show that $\Pi$ is a contraction mapping in ${\mathcal{H}}_2$. For $t\in J$, from C1 and C2 it follows that

$$\begin{array}{ccc}\hfill \mathbb{E}|\Pi \left(X_t\right)-\Pi \left(Y_t\right){|}^2& \le & {\displaystyle 2{\int }_0^t|S_{\alpha }(t-s)|ds\times {\int }_0^t|S_{\alpha }(t-s)\left|\mathbb{E}\right|\mu (X_s,s)-\mu (Y_s,s){|}^{2}ds}\hfill \\ & & {\displaystyle +2{\int }_0^t|S_{\alpha }{(t-s)|}^2\mathbb{E}{|\sigma (X_s,s)-\sigma (Y_s,s)|}^{2}ds}\hfill \\ & \le & {\displaystyle 2{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }}{\int }_0^t{(t-s)}^{\alpha -1}{L}_{\mu }\mathbb{E}{|X_s-Y_s|}^{2}ds}\hfill \\ & & {\displaystyle +2{\tilde{M}}_S^2{\int }_0^t{(t-s)}^{2(\alpha -1)}{L}_{\sigma }\mathbb{E}{|X_s-Y_s|}^{2}ds.}\hfill \end{array}$$

Therefore, we obtain

$$\begin{array}{ccc}\hfill \underset{t\in J}{sup}E{|\Pi \left(X_t\right)-\Pi \left(Y_t\right)|}^2& \le & {\displaystyle \left[2{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }}{L}_{\mu }\right]\underset{t\in J}{sup}{\int }_0^t{(t-s)}^{\alpha -1}E{|X_s-Y_s|}^{2}ds}\hfill \\ & & {\displaystyle +\left[2{\tilde{M}}_S^2{L}_{\sigma }\right]\underset{t\in J}{sup}{\int }_0^t{(t-s)}^{2(\alpha -1)}E{|X_s-Y_s|}^{2}ds}\hfill \\ & \le & \left[2{\tilde{M}}_S^2{L}_{\mu }{\displaystyle \frac{T^{2\alpha }}{{\alpha }^2}}+2{\tilde{M}}_S^2{L}_{\sigma }{\displaystyle \frac{T^{2\alpha -1}}{2\alpha -1}}\right]\underset{t\in J}{sup}E{|X_t-Y_t|}^2\hfill \\ & =& 2{\tilde{M}}_S^2{T}^{2\alpha }\left[{\displaystyle \frac{L_{\mu }}{{\alpha }^2}}+{\displaystyle \frac{L_{\sigma }}{T(2\alpha -1)}}\right]\underset{t\in J}{sup}E{|X_t-Y_t|}^2.\hfill \end{array}$$

Then, by condition (10), $\mathsf{\Pi }$ is a contraction mapping. Finally, by Banach contracting mapping principle, $\mathsf{\Pi }$ has a unique fixed point. □

Theorem 2.

Suppose that conditions C1, C2 and C3are true. Then, the stochastic fractional differential Equation (5) has at least one mild solution in J.

Proof. 

Let’s define $\mathsf{\Pi }:{\mathcal{H}}_2\to {\mathcal{H}}_2$ as in the proof of Theorem 1. Now, we must show that $\mathsf{\Pi }$ is a completely continuous operator. Note that $\mathsf{\Pi }$ is well defined in ${\mathcal{H}}_2$.

Step 1. First, we show that $\mathsf{\Pi }$ is a continuous operator.

Let ${\left\{X_t^n\right\}}_{n=0}^{\infty }$ be a sequence in ${\mathcal{H}}_2$, such that $X_t^n\to X_t$ in ${\mathcal{H}}_2$. Since the functions $\mu$ and $\sigma$ are continuous, we have that

$$\underset{n\to \infty }{lim}\mathbb{E}{|\mathsf{\Pi }\left(X_t^n\right)-\mathsf{\Pi }\left(X_t\right)|}^2=0,$$

in ${\mathcal{H}}_2$ for each $t\in J$. Thus, the map $\mathsf{\Pi }$ is continuous in ${\mathcal{H}}_2$.

Step 2. Now, we show that $\mathsf{\Pi }$ maps bounded sets in bounded sets on ${\mathcal{H}}_2$.

We must show that for each $r>0$, there is a $\gamma >0$, such that for $X_t\in B_r=\{X_t\in {\mathcal{H}}_2:\mathbb{E}|X_t{|}^2\le r\}$, we have $\mathbb{E}|\mathsf{\Pi }\left(X_t\right){|}^2\le \gamma$. Let’s denote $T_{\alpha }\left(t\right)=E_{\alpha ,1}\left(\lambda t^{\alpha }\right)$; for each $X_t\in B_r$, $t\in J$, we have

$$\begin{array}{ccc}\mathbb{E}|\mathsf{\Pi }\left(X_t\right){|}^2\hfill & \le & 3|T_{\alpha }{\left(t\right)|}^2\mathbb{E}{\left|X_0\right|}^2{\displaystyle +3{\int }_0^t|S_{\alpha }(t-s)|ds}\hfill \\ & & {\displaystyle \times {\int }_0^t|S_{\alpha }(t-s)\left|\mathbb{E}\right|\mu (X_s,s){|}^{2}ds}\hfill \\ & & {\displaystyle +3{\int }_0^t|S_{\alpha }{(t-s)|}^2\mathbb{E}{|\sigma (X_s,s)|}^{2}ds}\hfill \\ & \le & {\displaystyle 3{\tilde{M}}_T^{2}r+3{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }\varphi \left(r\right)}{\int }_0^t{(t-s)}^{\alpha -1}{\tilde{L}}_{\mu }\left(s\right)ds}\hfill \\ & & {\displaystyle +3{\tilde{M}}_S^2\psi (r){\int }_0^t{(t-s)}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(s\right)ds}\hfill \\ & =& {\rm Y}\hfill \end{array}$$

Step 3. We show that $\mathsf{\Pi }$ maps bounded sets sets on equicontinuous sets in $B_r$.

 Let $0<u<v\le T$, for each $X_t\in B_r$, we have

$$\begin{array}{ccc}\hfill \mathbb{E}|\mathsf{\Pi }\left(X_v\right)-\mathsf{\Pi }\left(X_u\right){|}^2& \le & 5|T_{\alpha }\left(v\right)-T_{\alpha }{\left(u\right)|}^2\mathbb{E}{\left|X_0\right|}^2\hfill \\ & & +5\mathbb{E}{\left|{\displaystyle {\int }_0^u[S_{\alpha }(v-s)-S_{\alpha }(u-s)]\mu (X_s,s)ds}\right|}^2\hfill \\ & & +5\mathbb{E}{\left|{\displaystyle {\int }_u^v{S}_{\alpha }(v-s)\mu (X_s,s)ds}\right|}^2\hfill \\ & & +5\mathbb{E}{\left|{\displaystyle {\int }_0^u[S_{\alpha }(v-s)-S_{\alpha }(u-s)]\sigma (X_s,s)d{B}_s}\right|}^2\hfill \\ & & +5\mathbb{E}{\left|{\displaystyle {\int }_u^v\left[S_{\alpha }(v-s)\right]\sigma (X_s,s)d{B}_s}\right|}^2.\hfill \end{array}$$

 Then, we obtain

$$\begin{array}{ccc}\hfill \mathbb{E}|\mathsf{\Pi }\left(X_v\right)-\mathsf{\Pi }\left(X_u\right){|}^2& \le & 5r|T_{\alpha }\left(v\right)-T_{\alpha }{\left(u\right)|}^2\hfill \\ & & {\displaystyle +5{\int }_0^u|S_{\alpha }(v-s)-S_{\alpha }(u-s)|ds}\hfill \\ & & {\displaystyle \times {\int }_0^u|S_{\alpha }(v-s)-S_{\alpha }(u-s)|\mathbb{E}|\mu (X_s,s){|}^{2}ds}\hfill \\ & & {\displaystyle +5{\int }_u^v|S_{\alpha }(v-s)|ds{\int }_u^v|S_{\alpha }(v-s)|\mathbb{E}|\mu (X_s,s){|}^{2}ds}\hfill \\ & & {\displaystyle +5{\int }_0^u|S_{\alpha }(v-s)-S_{\alpha }{(u-s)|}^2\mathbb{E}{|\sigma (X_s,s)|}^{2}ds}\hfill \\ & & {\displaystyle +5{\int }_u^v|S_{\alpha }{(v-s)|}^2\mathbb{E}{|\sigma (X_s,s)|}^{2}ds}\hfill \\ & \le & 5r|T_{\alpha }\left(v\right)-T_{\alpha }{\left(u\right)|}^2\hfill \\ & & {\displaystyle +5\varphi \left(r\right){\int }_0^u|S_{\alpha }(v-s)-S_{\alpha }(u-s)|ds}\hfill \\ & & {\displaystyle \times {\int }_0^u|S_{\alpha }(v-s)-S_{\alpha }(u-s)|{\tilde{L}}_{\mu }\left(s\right)ds}\hfill \\ & & {\displaystyle +5{\tilde{M}}_S^2{\displaystyle \frac{{(v-u)}^{\alpha }}{\alpha }}\varphi \left(r\right){\int }_u^v{(v-s)}^{\alpha -1}{\tilde{L}}_{\mu }\left(s\right)ds}\hfill \\ & & {\displaystyle +5\psi \left(r\right){\int }_0^u{|S_{\alpha }(v-s)-S_{\alpha }(u-s)|}^2{\tilde{L}}_{\sigma }\left(s\right)ds}\hfill \\ & & {\displaystyle +5{\tilde{M}}_S^2\psi \left(r\right){\int }_u^v{(v-s)}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(s\right)ds}\hfill \end{array}$$

Since $T_{\alpha }\left(t\right)$ y $S_{\alpha }\left(t\right)$ are continuous fucntions, $|T_{\alpha }\left(v\right)-T_{\alpha }\left(u\right)|\to 0$ and $|S_{\alpha }(v-s)-S_{\alpha }(u-s)|\to 0$, as $u\to v$. Then, for the above inequality, we have ${lim}_{u\to v}\mathbb{E}{|\mathsf{\Pi }\left(X_v\right)-\mathsf{\Pi }\left(X_u\right)|}^2=0$. Therefore, the set $\{\mathsf{\Pi }\left(X_t\right),X_t\in B_r\}$ is equicontinuous. Finally, from Step 1 to Step 3, and the Ascoli Theorem, we conclude that $\mathsf{\Pi }$ is a compact operator.

Step 4. Now, we show that the set

$$N=\{X_t\in {\mathcal{H}}_2, \mathsf{s}\mathsf{u}\mathsf{c}\mathsf{h} \mathsf{t}\mathsf{h}\mathsf{a}\mathsf{t} X_t=q\mathsf{\Pi }\left(X_t\right) for 0<q<1\}$$

is bounded. Let $X_t\in N$, then for each $t\in J$, we have

$$X_t=q\left({\displaystyle T_{\alpha }\left(t\right)X_0+{\int }_0^t{S}_{\alpha }(t-s)\mu (X_s,s)ds+{\int }_0^t{S}_{\alpha }(t-s)\sigma (X_s,s)d{B}_s}\right),$$

this implies

$$\begin{array}{ccc}\hfill \mathbb{E}|X_t{|}^2& \le & 3|T_{\alpha }{\left(t\right)|}^2\mathbb{E}{|X_0|}^2\hfill \\ & & {\displaystyle +3{\int }_0^t|S_{\alpha }(t-s)|ds{\int }_0^t|S_{\alpha }(t-s)|\mathbb{E}|\mu (X_s,s){|}^{2}ds}\hfill \\ & & {\displaystyle +3{\int }_0^t|S_{\alpha }{(t-s)|}^2\mathbb{E}{|\sigma (X_s,s)|}^{2}ds}\hfill \\ & \le & {\displaystyle 3{\tilde{M}}_T^2\mathbb{E}|X_0{|}^2+3{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }}{\int }_0^t{(t-s)}^{\alpha -1}{\tilde{L}}_{\mu }\left(s\right)\varphi (\mathbb{E}|X_s{|}^2)ds}\hfill \\ & & {\displaystyle +3{\tilde{M}}_S^2{\int }_0^t{(t-s)}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(s\right)\psi (\mathbb{E}|X_s{|}^2)ds.}\hfill \end{array}$$

Let’s consider the function $h\left(t\right)$ defined by

$$\begin{array}{c}h\left(t\right)=sup\{\mathbb{E}|X_s{|}^2,0\le s\le t\},0\le t\le T\hfill \\ \\ {\displaystyle h\left(t\right)\le 3{\tilde{M}}_T^2\mathbb{E}{|X_0|}^2+3{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }}{\int }_0^t{(t-s)}^{\alpha -1}{\tilde{L}}_{\mu }\left(s\right)\varphi \left(h\left(s\right)\right)ds+3{\tilde{M}}_S^2{\int }_0^t{(t-s)}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(s\right)\psi \left(h\left(s\right)\right)ds.}\hfill \end{array}$$

If we denote by $\nu \left(t\right)$ the right hand side of last inequality, we get $\nu \left(0\right)=3{\tilde{M}}_T^{2}E{|X_0|}^2$, $h\left(t\right)\le \nu \left(t\right)$, $t\in J$.

Moreover,

$$\begin{array}{ccc}\hfill {\nu }^{\prime }\left(t\right)& \le & 3{\tilde{M}}_S^2{\displaystyle \frac{T^{\alpha }}{\alpha }}{t}^{\alpha -1}{\tilde{L}}_{\mu }\left(t\right)\varphi \left(\nu \left(t\right)\right)+3{\tilde{M}}_S^2{t}^{2(\alpha -1)}{\tilde{L}}_{\sigma }\left(t\right)\psi \left(\nu \left(t\right)\right).\hfill \end{array}$$

Equivalently, by C3, we obtain

$$\begin{array}{cc}\hfill {\displaystyle {\int }_{\nu \left(0\right)}^{\nu \left(t\right)}{\displaystyle \frac{ds}{\varphi \left(s\right)+\psi \left(s\right)}}\le {\int }_0^T\zeta \left(s\right)ds\le {\int }_c^{\infty }{\displaystyle \frac{ds}{\varphi \left(s\right)+\psi \left(s\right)}},}& 0\le t\le T.\hfill \end{array}$$

The last inequality implies that there is a constant k, such that $\nu \left(t\right)\le k$, $t\in J$, therefore, $h\left(t\right)\le k$, $t\in J$. Also, we obtain that $|X_t{|}^2\le h\left(t\right)\le \nu \left(t\right)\le k$, $t\in J$. By Schaefer’s fix point Theorem, we deduce that $\mathsf{\Pi }$ has a fixed point in J, which satisfies (5). □

Example 2.

Let us consider the following simplified version of (9):

$$\begin{array}{ccc}\hfill {}^C{\mathcal{D}}_0^{\alpha }{X}_t& =& \lambda X_t+{\xi }_t{X}_t,\hfill \\ \hfill X_{t_0}& =& X_0.\hfill \end{array}$$

(11)

According to Definition 5 we have that the solution of (11) is given by:

$$\begin{array}{ccc}\hfill X_t& =& {\displaystyle X_0{\mathrm{E}}_{\alpha ,1}\left(\lambda t^{\alpha }\right)+{\int }_0^t{(t-\eta )}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda {(t-\eta )}^{\alpha }\right)X_{\eta }dB\eta .}\hfill \end{array}$$

(12)

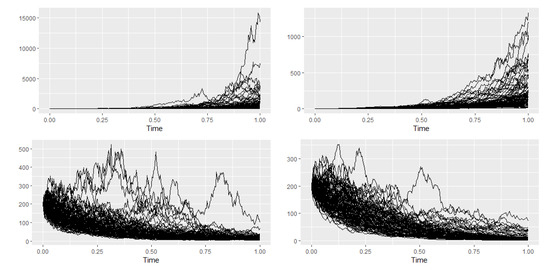
Through the numerical scheme of Euler-Maruyama [17], we simulate some trajectories of the solution process (12) on the interval $[0,1]$, see Figure 2. Let $\mathsf{\Delta }t=\frac{1}{N}$ for some positive integer N, and $t_j=j\mathsf{\Delta }t$. We denote $X_j$ as a numerical approximate to $X_{t_j}$. So, the Euler–Maruyama method is as follow

$$X_j=X_0{\mathrm{E}}_{\alpha ,1}(\lambda t_j^{\alpha })+\sum _{k=0}^{j-1}{(t_j-t_k)}^{\alpha -1}{\mathrm{E}}_{\alpha ,\alpha }\left(\lambda {(t_j-t_k)}^{\alpha }\right)X_k(B_{k+1}-B_k),j=1,\dots ,N,$$

where $B_{k+1}-B_k$ are Brownian increments.

Figure 2. Sample trajectories of $X_t$, with $\alpha =0.9$, $\lambda =3$, $X_0=2$ (up-left), sample trajectories of GBM, with $\lambda =3$, $\sigma =1$, $X_0=2$ (up-right), sample trajectories of $X_t$, with $\alpha =0.9$, $\lambda =-3$, $X_0=200$ (down-left) and sample trajectories of GBM, with $\lambda =-3$, $\sigma =1$, $X_0=200$ (down-right).