A Hybrid Whale Optimization Algorithm for Global Optimization
Abstract
:1. Introduction
2. Methods
2.1. Whale Optimization Algorithm
2.1.1. Exploitation Phases
- Shrinking encircling mechanism: This model is implemented by linearly decreasing the value of vector . Based on the vector a and the random vector , the fluctuation range of the coefficient vector is between (, ), where is reduced from 2 to 0 in the iteration process.
- Spiral updating position: The model first calculates the distance between itself and the prey, and then the humpback whale surrounds the prey in a logarithmic spiral motion, the mathematical model is shown as follows:where represents the distance between the prey and the humpback whale, is a constant for defining the shape of the logarithmic spiral, and is a random value in (−1, 1).
2.1.2. Exploration Phase
2.1.3. Overview of WOA
2.2. Thermal Exchange Optimization
2.3. Crossover Operator
3. Genetic Whale Optimization Algorithm–Thermal Exchange Optimization for Global Optimization Problem
3.1. Generate a High-Quality Initial Population
3.2. Improvement of the Exploitation Phase
3.3. The Thermal Memory of the TEO Algorithm
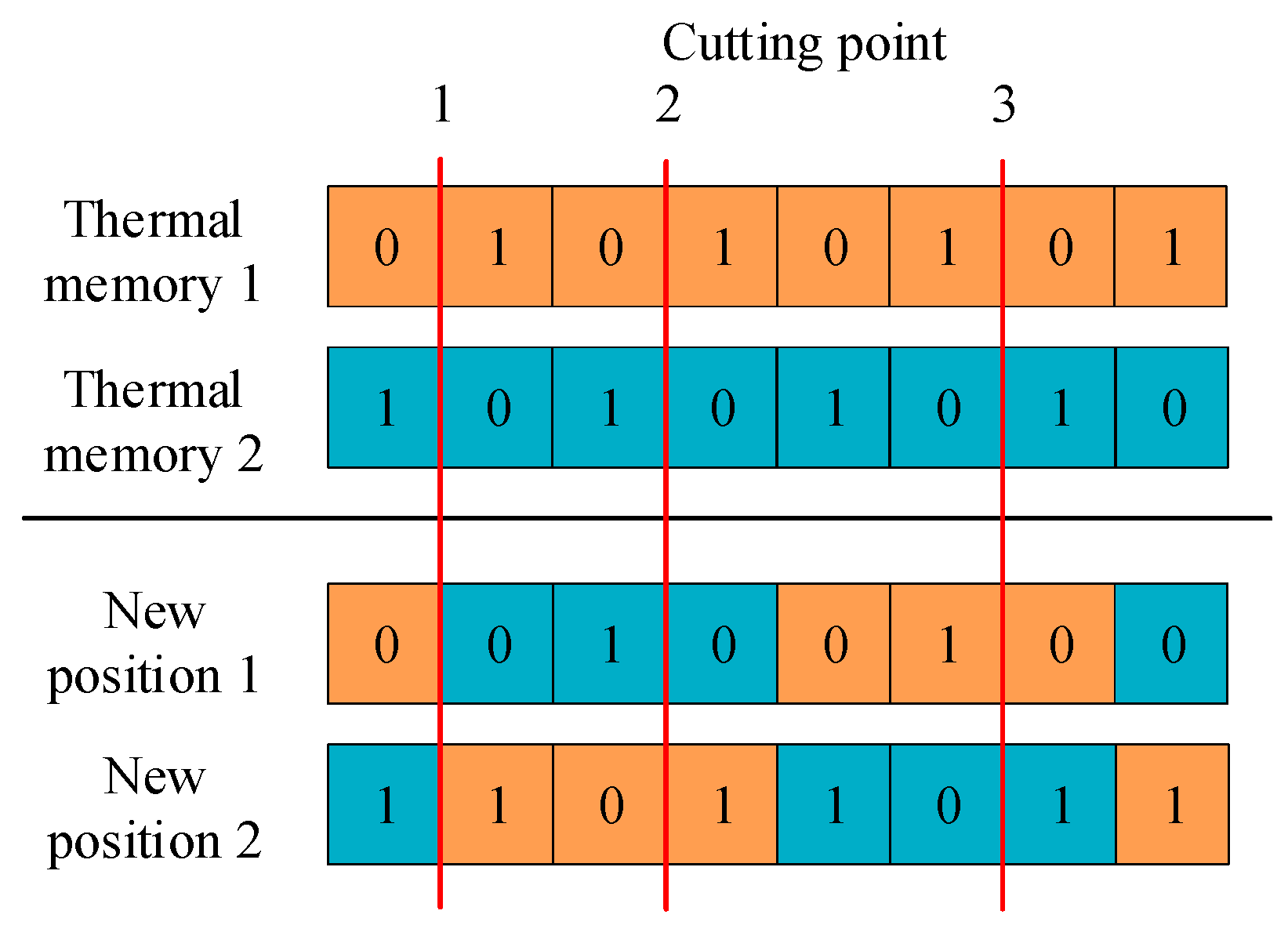
3.4. The Crossover Operator Mechanism
3.5. Update Leading Solution Based on Thermal Memory
3.6. The Proposed Algorithm GWOA-TEO
| Algorithm 1: The procedure of the proposed GWOA-TEO |
| Input: Initial population Xi (I = 1, 2, …, n)//n is population size |
| Output: Optimal solution X* |
| Initialize high-quality population Xi (I = 1, 2, …, n) |
| Evaluate the fitness value of each solution |
| Construct thermal memory TMi (I = 1, 2, …, L)//L is size of thermal memory |
| Set the best solution X* |
| while (t < T)//T is maximum number of iterations |
| Set the leading solution LX* based on TM |
| for each solution |
| Update , and //Equations (3) and (4) |
| p → probability of implement shrinking encircling or spiral updating |
| if (p < 0.5) |
| if ( < 1) |
| Use Equation (11) to update the current solution |
| else if ( ≥ 1) |
| Use Equation (8) to update the current solution |
| end if |
| else if (p ≥ 0.5) |
| Use Equation (6) to update the current solution |
| end if |
| for i < L |
| if the current solution same with TMi |
| Implement the crossover operator mechanism |
| times = times + 1 |
| end if |
| if times > IT |
| times = 0; break;//avoid infinite loop |
| end if |
| end for |
| end for |
| Evaluate the fitness value of each solution |
| Update TM if obtain the better solution |
| Update LX* based on TM |
| Update X* if X* is better solution |
| t = t + 1 |
| end while |
| return X* |
4. Experimental Results
4.1. Case Study 1: CEC 2017 Benchmark Test Functions
4.1.1. Experimental Setup
4.1.2. Parameter Setting
4.1.3. Statistical Results
4.2. Case Study 2: UCI Repository Datasets
4.2.1. Experimental Setup
4.2.2. Parameter Setting
4.2.3. Comparison with GWOA-TEO, WOA, TEO, and GA
4.2.4. Comparison with Published Algorithms
5. Discussion
- (1)
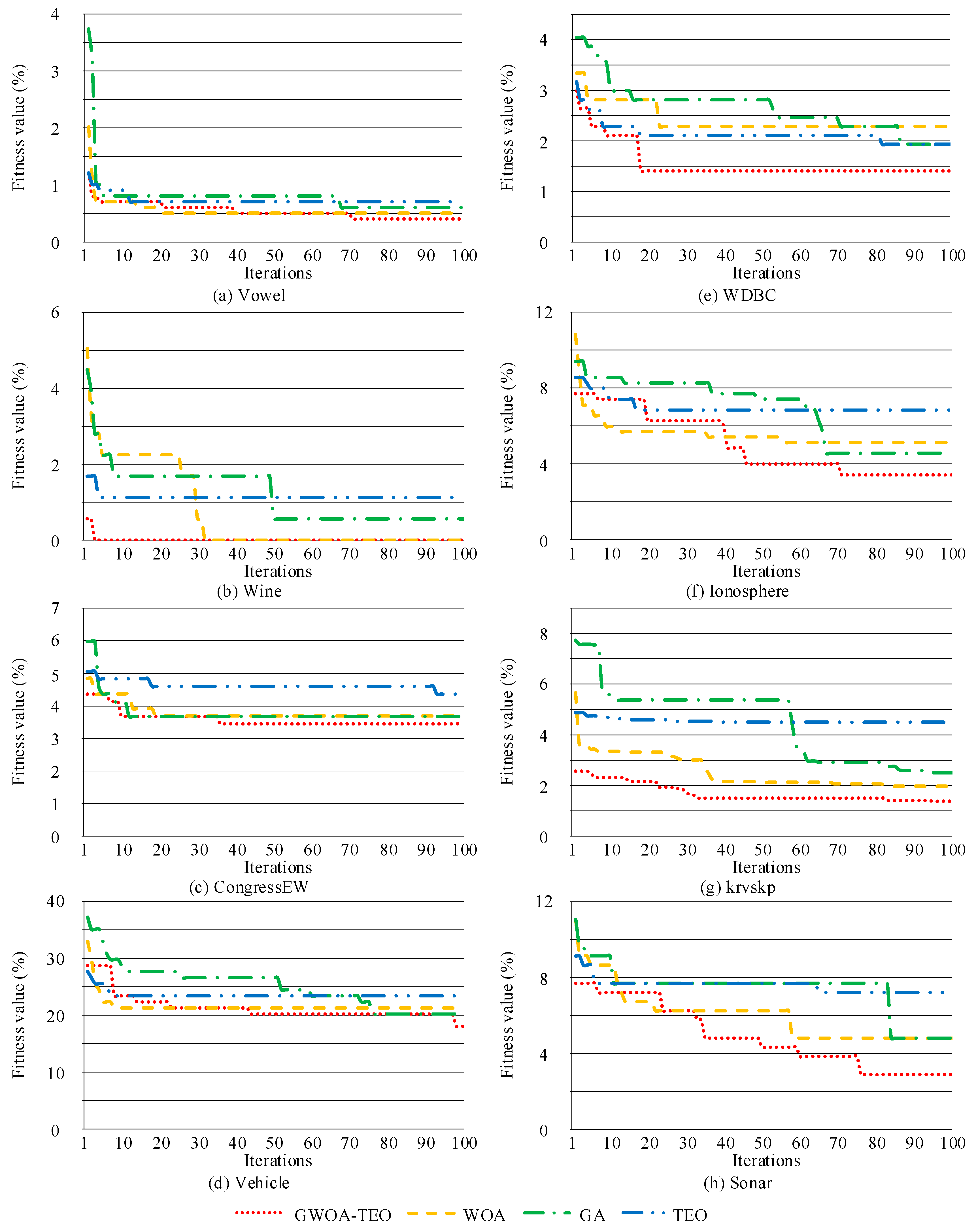
- Improvement in the initial population: in general, the traditional meta-heuristic algorithms randomly generate the initial population. However, this randomness may lead to non-uniform and low-quality population distribution and slow convergence. Therefore, an initial population generation mechanism combined with a local exploitation algorithm is proposed in this paper. This mechanism can increase the probability of the population approach being the global optimum. Figure 5 shows the convergence curve of GWOA-TEO and three comparison algorithms. The experimental results show that in seven of the eight repository data sets, including Vowel, Wine, CongressEW, WDBC, Ionosphere, krvskp and Sonar, the improved initial population has a better fitness value than the randomly generated initial population.
- (2)
- Improvement in the exploration and exploitation phase: the proposed algorithm combines GA to enhance exploration capabilities and TEO to enhance exploitation capabilities. Figure 5 shows the convergence curve of GWOA-TEO and the three comparison algorithms. In the convergence curve of the WDBC dataset, GWOA-TEO shows the advantage of fast convergence. In the convergence curves of the Ionosphere and Sonar datasets, GWOA-TEO shows strong exploration and exploitation capabilities. Compared with the original WOA, WOA converges at the 58th iteration, while GWOA-TEO converges at the 70th and 76th iterations, and has higher accuracy.
- (3)
- Improvement in escape from local optimum: in this paper, a memory that saves some historical-best-so-far solutions is proposed to further improve the avoidance of local optimum. Composition functions are challenging problems because the functions contain randomly located global optimum and several randomly located deep local optimums. Table 3 shows the statistical results of 11 composition functions in the CEC 2017 benchmark function. The proposed algorithm is better than CP-PDWOA and has competitive performance with HBO. HBO achieved the best fitness value in six composition functions, including F20, F23, F25, F26, F28 and F29, and GWOA-TEO achieved the best fitness value in seven composition functions, including F21, F22, F23, F24, F27, F29 and F30.
- (1)
- The robustness of the proposed algorithm: in this paper, the standard deviation is a parameter to evaluate the robustness of the model. The smaller the value of standard deviation, the more robust the model. In Table 3, although the algorithm achieves a higher accuracy rate, it only ranks second in standard deviation, better than WOA variants (CP-PDWOA) and WOA, but not as good as HBO. The proposed algorithm only achieved the best standard deviation in F14, F15, F21 and F28 among the 30 CEC 2017 benchmark functions.
- (2)
- Computational time and complexity: in Figure 6, the computational time of the proposed algorithm is lower than GA but higher than WOA and TEO. Although GA has powerful exploration capabilities, the implementation of the crossover operator mechanism in the proposed algorithm is the main reason for increasing the computational time. Therefore, it is necessary to study further the global exploration algorithm to reduce the complexity.
- (3)
- The generalization capacity of the proposed algorithm: the proposed algorithm is tested only on CEC 2017 benchmark functions and eight UCI repository datasets. The performance of the proposed algorithm on the actual optimization problems was not mentioned in this study. Therefore, the effectiveness of the GWOA-TEO algorithm still needs to be studied further.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic Algorithms: A Comprehensive Review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–231. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Lee, K.Y.; Yang, F.F. Optimal reactive power planning using evolutionary algorithms: A comparative study for evolutionary programming, evolutionary strategy, genetic algorithm, and linear programming. IEEE Trans. Power Syst. 1998, 13, 101–108. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategien; Springer: Berlin/Heidelberg, Germany, 1978; Volume 8, pp. 83–114. [Google Scholar]
- Zhou, X.; Yang, C.; Gui, W. State transition algorithm. J. Ind. Manag. Optim. 2012, 8, 1039–1056. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. Water evaporation optimization: A novel physically inspired optimization algorithm. Comput. Struct. 2016, 167, 69–85. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: New York, NY, USA, 2010; pp. 65–74. [Google Scholar]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Advances in Swarm Intelligence (Lecture Notes in Computer Science); Springer: Cham, Switzerland, 2014; Volume 8794, pp. 86–94. [Google Scholar]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2018, 165, 169–196. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). E Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Computat. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G.M. Evolutionary programming made faster. IEEE Trans. E Comput. 1999, 3, 82–102. [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Chakrabortty, R.K.; Ryan, M.J. An Efficient-Assembler Whale Optimization Algorithm for DNA Fragment Assembly Problem: Analysis and Validations. IEEE Access 2020, 8, 222144–222167. [Google Scholar] [CrossRef]
- Pham, Q.-V.; Mirjalili, S.; Kumar, N.; Alazab, M.; Hwang, W.-J. Whale optimization algorithm with applications to resource allocation in wireless networks. IEEE Trans. Veh. Technol. 2020, 69, 4285–4297. [Google Scholar] [CrossRef]
- Alameer, Z.; Elaziz, M.A.; Ewees, A.; Ye, H.; Jianhua, Z. Forecasting gold price fluctuations using improved multilayer perceptron neural network and whale optimization algorithm. Resour. Policy 2019, 61, 250–260. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2016, 1–15. [Google Scholar] [CrossRef]
- Medani, K.B.O.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Cherukuri, S.K.; Rayapudi, S.R. A novel global MPP tracking of photovoltaic system based on whale optimization algorithm. Int. J. Renew. Energy Dev. 2016, 5, 225–232. [Google Scholar]
- Dixit, U.; Mishra, A.; Shukla, A.; Tiwari, R. Texture classification using convolutional neural network optimized with whale optimization algorithm. SN Appl. Sci. 2019, 1, 655. [Google Scholar] [CrossRef] [Green Version]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Whale optimisation algorithm for photovoltaic model identification. J. Eng. 2017, 2017, 1906–1911. [Google Scholar] [CrossRef]
- Ghahremani-Nahr, J.; Kian, R.; Sabet, E. A robust fuzzy mathematical programming model for the closed-loop supply chain network design and a whale optimization solution algorithm. Expert Syst. Appl. 2019, 116, 454–471. [Google Scholar] [CrossRef] [Green Version]
- Hasanien, H.M. Performance improvement of photovoltaic power systems using an optimal control strategy based on whale optimization algorithm. Electr. Power Syst. Res. 2018, 157, 168–176. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Bhattacharyya, S.; Amin, M. S-shaped binary whale optimization algorithm for feature selection. In Recent Trends in Signal and Image Processing; Springer: Singapore, 2018; Volume 727, pp. 79–87. [Google Scholar]
- Garg, H. A Hybrid GA-GSA Algorithm for Optimizing the Performance of an Industrial System by Utilizing Uncertain Data. In Handbook of Research on Artificial Intelligence Techniques and Algorithms; Pandian, V., Ed.; IGI Global: Hershey, PA, USA, 2015; pp. 620–654. [Google Scholar]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Patwal, R.S.; Narang, N.; Garg, H. A novel TVAC-PSO based mutation strategies algorithm for generation scheduling of pumped storage hydrothermal system incorporating solar units. Energy 2018, 142, 822–837. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy flight trajectory-based whale optimization algorithm for global optimization. IEEE. Access 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, C.C. Analysis and forecasting of the carbon price using multi resolution singular value decomposition and extreme learning machine optimized by adaptive whale optimization algorithm. Appl. Energy 2018, 231, 1354–1371. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 171, 1843–1859. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. Tech. Rep. 2016, 201611. Available online: https://www.researchgate.net/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real-Parameter_Optimization (accessed on 14 March 2021).
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Sun, W.-Z.; Wang, J.-S.; Wei, X. An improved whale optimization algorithm based on different searching paths and perceptual disturbance. Symmetry 2018, 10, 210. [Google Scholar] [CrossRef] [Green Version]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 14 March 2021).
- Jia, H.; Xing, Z.; Song, W. A new hybrid seagull optimization algorithm for feature selection. IEEE Access 2019, 7, 49614–49631. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid whale optimization algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]



| Function | Name | ||
|---|---|---|---|
| UFs | F1 | Shifted and Rotated Bent Cigar function | 100 |
| SMFs | F3 | Shifted and Rotated Rosenbrock’s function | 300 |
| F4 | Shifted and Rotated Rastrigin’s function | 400 | |
| F5 | Shifted and Rotated Expanded Scaffer’s F6 function | 500 | |
| F6 | Shifted and Rotated Lunacek Bi_Rastrigin function | 600 | |
| F7 | Shifted and Rotated Non-Continuous Rastrigin’s function | 700 | |
| F8 | Shifted and Rotated Levy function | 800 | |
| F9 | Shifted and Rotated Schwefel’s function | 900 | |
| HFs | F10 | HF 1 (n = 3) | 1000 |
| F11 | HF 2 (n = 3) | 1100 | |
| F12 | HF 3 (n = 3) | 1200 | |
| F13 | HF 4 (n = 4) | 1300 | |
| F14 | HF 5 (n = 4) | 1400 | |
| F15 | HF 6 (n = 4) | 1500 | |
| F16 | HF 6 (n = 5) | 1600 | |
| F17 | HF 6 (n = 5) | 1700 | |
| F18 | HF 6 (n = 5) | 1800 | |
| F19 | HF (n = 6) | 1900 | |
| CFs | F20 | CF 1 (n = 3) | 2000 |
| F21 | CF 2 (n = 3) | 2100 | |
| F22 | CF 3 (n = 4) | 2200 | |
| F23 | CF 4 (n = 4) | 2300 | |
| F24 | CF 5 (n = 5) | 2400 | |
| F25 | CF 6 (n = 5) | 2500 | |
| F26 | CF 7 (n = 6) | 2600 | |
| F27 | CF 8 (n = 6) | 2700 | |
| F28 | CF 9 (n = 3) | 2800 | |
| F29 | CF 10 (n = 3) | 2900 | |
| F30 | CF 11 (n = 3) | 3000 |
| HBO [41] | CP-PDWOA [42] | WOA [17] | GWOA-TEO |
|---|---|---|---|
| Number of solutions: 40 Number of iterations: 1282 degree = 3 C = T/25 p1 = 1 − t/T p2 = p1 + [(1 − p1)/2] | Number of solutions: 40 Number of iterations: 1282 equal-pitch Archimedean spiral curve a: [0, 2] : 1 : [−1, 1] | Number of solutions: 40 Number of iterations: 1282 a: [0, 2] : 1 : [−1, 1] | Number of solutions: 40 Number of thermal objects memory: 10 Number of iterations: 1282 pro = 0.3 a: [0, 2] : 1 : [−1, 1] |
| Function | HBO [41] | CP-PDWOA [42] | WOA [17] | GWOA-TEO | ||||
|---|---|---|---|---|---|---|---|---|
| Avg | Std | Avg | Std | Avg | Std | Avg | Std | |
| F1 | 5.36 × 102 | 5.43 × 102 | 7.29 × 109 | 4.88 × 109 | 5.75 × 106 | 1.33 × 107 | 5.44 × 102 | 4.74 × 102 |
| F3 | 3.00 × 102 | 1.16 × 10−1 | 3.19 × 104 | 1.80 × 104 | 2.22 × 103 | 1.79 × 103 | 3.00 × 102 | 3.48 × 10−1 |
| F4 | 4.05 × 102 | 4.28 × 10−1 | 8.41 × 102 | 2.97 × 102 | 4.33 × 102 | 4.97 × 101 | 4.04 × 102 | 2.00 |
| F5 | 5.11 × 102 | 3.63 | 5.85 × 102 | 2.57 × 101 | 5.50 × 102 | 1.63 × 101 | 5.13 × 102 | 4.82 |
| F6 | 6.00 × 102 | 4.8 × 10−14 | 6.51 × 102 | 1.84 × 101 | 6.37 × 102 | 1.26 × 101 | 6.01 × 102 | 3.26 × 10−1 |
| F7 | 7.13 × 102 | 4.03 | 8.29 × 102 | 2.57 × 101 | 7.73 × 102 | 2.10 × 101 | 7.23 × 102 | 4.56 |
| F8 | 8.09 × 102 | 3.93 | 8.76 × 102 | 2.23 × 101 | 8.40 × 102 | 1.56 × 101 | 8.12 × 102 | 4.82 |
| F9 | 9.00 × 102 | 0.00 | 2.22 × 103 | 7.63 × 102 | 1.44 × 103 | 4.65 × 102 | 9.01 × 102 | 3.41 |
| F10 | 1.55 × 103 | 1.57 × 102 | 2.76 × 103 | 4.24 × 102 | 1.94 × 103 | 2.59 × 102 | 1.47 × 103 | 1.95 × 102 |
| F11 | 1.10 × 103 | 1.23 | 3.06 × 103 | 2.36 × 103 | 1.19 × 103 | 4.49 × 101 | 1.11 × 103 | 4.05 |
| F12 | 8.17 × 104 | 9.11 × 104 | 1.13 × 108 | 1.43 × 108 | 4.53 × 106 | 4.80 × 106 | 8.29 × 104 | 1.53 × 105 |
| F13 | 2.96 × 103 | 2.56 × 103 | 1.28 × 106 | 4.48 × 106 | 1.76 × 104 | 1.83 × 104 | 6.55 × 103 | 3.97 × 103 |
| F14 | 1.45 × 103 | 7.49 × 101 | 5.11 × 103 | 4.11 × 103 | 1.59 × 103 | 1.32 × 102 | 1.42 × 103 | 1.03 × 101 |
| F15 | 1.60 × 103 | 2.02 × 102 | 3.73 × 104 | 6.17 × 104 | 6.26 × 103 | 5.38 × 103 | 1.52 × 103 | 2.85 × 101 |
| F16 | 1.60 × 103 | 2.74 | 2.19 × 103 | 3.14 × 102 | 1.82 × 103 | 1.41 × 102 | 1.69 × 103 | 1.12 × 102 |
| F17 | 1.70 × 103 | 4.30 | 1.89 × 103 | 1.05 × 102 | 1.78 × 103 | 3.50 × 101 | 1.72 × 103 | 1.37 × 101 |
| F18 | 3.77 × 103 | 1.15 × 103 | 6.41 × 106 | 1.54 × 107 | 2.31 × 104 | 1.48 × 104 | 8.32 × 103 | 6.23 × 103 |
| F19 | 1.98 × 103 | 1.58 × 102 | 4.79 × 106 | 1.45 × 107 | 4.95 × 104 | 9.70 × 104 | 3.71 × 103 | 1.91 × 103 |
| F20 | 2.00 × 103 | 7.92 × 10−2 | 2.32 × 103 | 9.56 × 101 | 2.17 × 103 | 7.97 × 101 | 2.03 × 103 | 9.80 |
| F21 | 2.25 × 103 | 4.96 × 101 | 2.37 × 103 | 4.84 × 101 | 2.33 × 103 | 5.60 × 101 | 2.20 × 103 | 1.83 |
| F22 | 2.30 × 103 | 4.92 | 3.56 × 103 | 7.22 × 102 | 2.31 × 103 | 1.61 × 101 | 2.29 × 103 | 2.86 × 101 |
| F23 | 2.61 × 103 | 4.34 | 2.68 × 103 | 2.94 × 101 | 2.65 × 103 | 2.61 × 101 | 2.61 × 103 | 5.98 × 101 |
| F24 | 2.63 × 103 | 9.50 × 101 | 2.82 × 103 | 3.15 × 101 | 2.77 × 103 | 5.02 × 101 | 2.55 × 103 | 1.04 × 102 |
| F25 | 2.91 × 103 | 1.98 × 101 | 3.35 × 103 | 2.72 × 102 | 2.96 × 103 | 2.44 × 101 | 2.93 × 103 | 2.18 × 101 |
| F26 | 2.89 × 103 | 6.26 × 101 | 4.30 × 103 | 5.29 × 102 | 3.42 × 103 | 5.13 × 102 | 2.91 × 103 | 8.24 × 101 |
| F27 | 3.09 × 103 | 1.62 | 3.20 × 103 | 6.49 × 101 | 3.16 × 103 | 5.23 × 101 | 3.08 × 103 | 2.22 × 101 |
| F28 | 3.17 × 103 | 7.37 × 101 | 3.67 × 103 | 1.19 × 102 | 3.28 × 103 | 9.42 | 3.23 × 103 | 5.23 |
| F29 | 3.18 × 103 | 1.37 × 101 | 3.55 × 103 | 1.99 × 102 | 3.34 × 103 | 6.32 × 101 | 3.18 × 103 | 2.53 × 101 |
| F30 | 2.57 × 104 | 1.46 × 104 | 8.52 × 106 | 7.07 × 106 | 2.91 × 105 | 6.11 × 105 | 2.15 × 104 | 2.22 × 104 |
| Datasets | Features | Instances | Classes |
|---|---|---|---|
| Vowel | 10 | 990 | 11 |
| Wine | 13 | 178 | 3 |
| CongressEW | 16 | 435 | 2 |
| Vehicle | 18 | 94 | 4 |
| WDBC | 30 | 569 | 2 |
| Ionosphere | 34 | 351 | 2 |
| krvskp | 36 | 3196 | 2 |
| Sonar | 60 | 208 | 2 |
| WOA [17] | GA [4] | TEO [11] | GWOA-TEO |
|---|---|---|---|
| Number of solutions: 10 Number of iterations: 100 a: [0, 2] : 1 : [−1, 1] | Number of chromosomes: 10 Maximum number of iterations: 100Crossover rate: 0.85 Mutation rate: 0.01 Elitism rate: 0.05 | Number of thermal objects: 10 Number of thermal objects memory: 2 Number of iterations: 100 pro = 0.3 c1: {0 or 1} c2: {0 or 1} | Number of solutions: 10 Number of thermal objects memory: 10 Number of iterations: 100 pro = 0.3 a: [0, 2] : 1 : [−1, 1] |
| Datasets | WOA | GA | TEO | GWOA-TEO | ||||
|---|---|---|---|---|---|---|---|---|
| Avg Acc (%) | Avg No.F | Avg Acc (%) | Avg No.F | Avg Acc (%) | Avg No.F | Avg Acc (%) | Avg No.F | |
| Vowel | 98.35 | 9.63 | 98.17 | 7.33 | 98.04 | 7.36 | 99.47 | 9.07 |
| Wine | 97.69 | 9.37 | 97.52 | 7.63 | 97.86 | 7.8 | 99.77 | 8 |
| CongressEW | 94.73 | 2.93 | 95.24 | 6.97 | 94.94 | 8.63 | 96.12 | 3.07 |
| Vehicle | 74.33 | 9.47 | 75.74 | 8.9 | 70.95 | 8.5 | 79.15 | 6.1 |
| WDBC | 97.1 | 20.43 | 97.56 | 15.36 | 96.89 | 16.1 | 98.13 | 14.27 |
| Ionosphere | 92.64 | 11.47 | 93.47 | 14.17 | 91.53 | 16.43 | 95.37 | 8.6 |
| krvskp | 95.88 | 26.07 | 94.95 | 22.03 | 89.36 | 19 | 98.04 | 22.6 |
| Sonar | 91.35 | 40.8 | 93.27 | 31.4 | 90.3 | 30.67 | 95.63 | 29.5 |
| Datasets | Algorithms | Avg Acc (%) | Avg No.F |
|---|---|---|---|
| Vowel | HBO [41] | 99.35 | 9.27 |
| GWOA-TEO | 99.47 | 9.07 | |
| Wine | SOA-TEO3 [44] | 90.94 | 3.81 |
| HBO [41] | 99.38 | 8.77 | |
| BALO-1 [45] | 98.90 | 5.77 | |
| WOASAT-2 [46] | 99.00 | 6.4 | |
| GWOA-TEO | 99.77 | 8 | |
| CongressEW | HBO [41] | 96.05 | 4.8 |
| BALO-1 [45] | 97.00 | 5.01 | |
| WOASAT-2 [46] | 98.00 | 6.4 | |
| GWOA-TEO | 96.12 | 3.07 | |
| Vehicle | HBO [41] | 75.99 | 7.8 |
| GWOA-TEO | 79.15 | 6.1 | |
| WDBC | SOA-TEO3 [44] | 94.55 | 9.11 |
| HBO [41] | 97.76 | 15.87 | |
| BALO-1 [45] | 97.90 | 14.82 | |
| WOASAT-2 [46] | 98.00 | 11.6 | |
| GWOA-TEO | 98.13 | 14.27 | |
| Ionosphere | SOA-TEO3 [44] | 90.53 | 7.58 |
| HBO [41] | 93.96 | 12.47 | |
| BALO-1 [45] | 88.9 | 14.65 | |
| WOASAT-2 [46] | 96.00 | 12.8 | |
| GWOA-TEO | 95.37 | 8.6 | |
| krvskp | HBO [41] | 98.30 | 21.1 |
| BALO-1 [45] | 96.70 | 16.45 | |
| WOASAT-2 [46] | 98.00 | 18.4 | |
| GWOA-TEO | 98.04 | 22.6 | |
| Sonar | SOA-TEO3 [44] | 93.97 | 27.17 |
| HBO [41] | 93.85 | 31.93 | |
| BALO-1 [45] | 86.8 | 26.58 | |
| WOASAT-2 [46] | 97.00 | 26.4 | |
| GWOA-TEO | 95.63 | 29.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Zhuo, G.-L. A Hybrid Whale Optimization Algorithm for Global Optimization. Mathematics 2021, 9, 1477. https://doi.org/10.3390/math9131477
Lee C-Y, Zhuo G-L. A Hybrid Whale Optimization Algorithm for Global Optimization. Mathematics. 2021; 9(13):1477. https://doi.org/10.3390/math9131477
Chicago/Turabian StyleLee, Chun-Yao, and Guang-Lin Zhuo. 2021. "A Hybrid Whale Optimization Algorithm for Global Optimization" Mathematics 9, no. 13: 1477. https://doi.org/10.3390/math9131477
APA StyleLee, C.-Y., & Zhuo, G.-L. (2021). A Hybrid Whale Optimization Algorithm for Global Optimization. Mathematics, 9(13), 1477. https://doi.org/10.3390/math9131477







