A Convergent Three-Step Numerical Method to Solve a Double-Fractional Two-Component Bose–Einstein Condensate

Abstract

This manuscript introduces a discrete technique to estimate the solution of a double-fractional two-component Bose–Einstein condensate. The system consists of two coupled nonlinear parabolic partial differential equations whose solutions are two complex functions, and the spatial fractional derivatives are interpreted in the Riesz sense. Initial and homogeneous Dirichlet boundary data are imposed on a multidimensional spatial domain. To approximate the solutions, we employ a finite difference methodology. We rigorously establish the existence of numerical solutions along with the main numerical properties. Concretely, we show that the scheme is consistent in both space and time as well as stable and convergent. Numerical simulations in the one-dimensional scenario are presented in order to show the performance of the scheme. For the sake of convenience, A MATLAB code of the numerical model is provided in the appendix at the end of this work.

1. Introduction

In this work, $p\in \mathbb{N}$ represents the number of spatial dimensions, and $T\in {\mathbb{R}}^{+}$ defines a period of time. We agree that $I_n=\{1,2,...,n\}$ and ${\overline{I}}_n=I_n\cup \left\{0\right\}$, for each $n\in \mathbb{N}$, and assume that $a_i$ and $b_i$ are real numbers with the property that $a_i<b_i$, for all $i\in I_p$. For convenience, we use the notations $\Omega ={\Pi }_{i=1}^p(a_i,b_i)\subseteq {\mathbb{R}}^p$ and ${\Omega }_T=\Omega \times (0,T)$ and agree that $\overline{\Omega }$ and ${\overline{\Omega }}_T$ denote the closures of $\Omega$ and ${\Omega }_T$, respectively, in the Euclidean metric topology of ${\mathbb{R}}^p$. We assume that ${\psi }_1:{\overline{\Omega }}_T\to \mathbb{C}$ and ${\psi }_2:{\overline{\Omega }}_T\to \mathbb{C}$ are sufficiently smooth functions and employ the conventions $x=(x_1,x_2,\dots ,x_p)\in \Omega$ and $\mathrm{i}=\sqrt{-1}$. Throughout this manuscript, $\mathrm{\Gamma }$ will represent the usual Gamma function that extends factorials.

Definition 1

(Podlubny [1]). Suppose that f is a real function defined in all of $\mathbb{R}$ and assume that $n\in \mathbb{N}\cup \left\{0\right\}$ and $\alpha \in \mathbb{R}$ are such that $n-1<\alpha <n$. We define the fractional derivative in the Riesz sense of order α of f at the point $x\in \mathbb{R}$ as

$$\frac{d^{\alpha }f\left(x\right)}{{d\left|x\right|}^{\alpha }}=\frac{-1}{2cos\left(\frac{\pi \alpha }{2}\right)\mathrm{\Gamma }(n-\alpha )}\frac{d^n}{d{x}^n}{\int }_{-\infty }^{\infty }\frac{f\left(\xi \right)d\xi }{{|x-\xi |}^{\alpha +1-n}}.$$

(1)

Definition 2.

Let $\psi :{\overline{\Omega }}_T\to \mathbb{C}$ be a function and let $i\in I_p$. Suppose that α and n are a real and a natural number, respectively, satisfying the properties in the previous definition. Whenever it exists, the space-fractional partial derivative in the sense of Riesz of order α of ψ with respect to the variable $x_i$ at $\left(x,t\right)\in {\Omega }_T$ is defined as

$$\frac{{\partial }^{\alpha }\psi (x,t)}{\partial |x_i{|}^{\alpha }}=\frac{-1}{2cos\left(\frac{\pi \alpha }{2}\right)\mathrm{\Gamma }(n-\alpha )}\frac{{\partial }^n}{\partial x_i^n}{\int }_{-\infty }^{\infty }\frac{\psi (x_1,\dots ,x_{i-1},\xi ,x_{i+1},\dots ,x_p,t)}{|x_i{-\xi |}^{\alpha -1}}d\xi .$$

(2)

Here, we extend ψ by allowing $\psi \equiv 0$ outside of $\overline{\Omega }$. If these fractional derivatives exist for all $i\in I_p$, then we define

$${△}^{\alpha }\psi (x,t)=\sum _{i=1}^p\frac{{\partial }^{\alpha }\psi }{\partial {\left|x_i\right|}^{\alpha }}(x,t).$$

(3)

In this manuscript, we will use D, ${\beta }_{11}$, ${\beta }_{12}$,${\beta }_{22}$, and $\lambda$ to represent constant real numbers, and we employ $\mathbf{P}:\overline{\Omega }\to \mathbb{R}$ to denote a real function. Throughout, we will assume that ${\alpha }_1,{\alpha }_2\in \mathbb{R}$ satisfy the properties $1<{\alpha }_1\le 2$ and $1<{\alpha }_2\le 2$. We let ${\varphi }_1:\overline{\Omega }\to \mathbb{C}$ and ${\varphi }_2:\overline{\Omega }\to \mathbb{C}$ be sufficiently regular functions. In this work, we tackle the numerical solution of the following double-fractional initial-boundary value problem ruled by two nonlinear coupled Gross–Pitaevskii-type equations:

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}\frac{\partial {\psi }_1}{\partial t}& =\left[\mathbf{P}\left(x\right)+D+{\beta }_{11}{\left|{\psi }_1\right|}^2+{\beta }_{12}{\left|{\psi }_2\right|}^2-\frac{1}{2}{△}^{{\alpha }_1}\right]{\psi }_1+\lambda {\psi }_2,\forall (x,t)\in {\Omega }_T,\hfill \\ \hfill \mathrm{i}\frac{\partial {\psi }_2}{\partial t}& =\left[\mathbf{P}\left(x\right)+{\beta }_{12}{\left|{\psi }_1\right|}^2+{\beta }_{22}{\left|{\psi }_2\right|}^2-\frac{1}{2}{△}^{{\alpha }_2}\right]{\psi }_2+\lambda {\psi }_1,\forall (x,t)\in {\Omega }_T,\hfill \end{array}\\ \mathrm{satisfying}\left\{\begin{array}{cc}{\psi }_1(x,0)={\varphi }_1\left(x\right),\hfill & \forall x\in \overline{\Omega },\hfill \\ {\psi }_2(x,0)={\varphi }_2\left(x\right),\hfill & \forall x\in \overline{\Omega },\hfill \\ {\psi }_1(x,t)={\psi }_2(x,t)=0,\hfill & \forall (x,t)\in \partial \Omega \times (0,T).\hfill \end{array}\right.\end{array}$$

(4)

This system is a two-component Bose–Einstein condensate that considers the presence of an internal atomic Josephson junction. In this physical context, ${\psi }_1$ and ${\psi }_2$ denote the two-component condensate wave functions.

There are systems that describe single-component Bose–Einstein condensates. As examples, there are works that investigate round, symmetric, and central vortex states in rotating Bose–Einstein condensates [2], considering only a parameter that characterizes the interaction between particles and a constant that corresponds to the angular speed of the laser beam. As in the present work, a real-valued external trapping potential is employed in those models. From the numerical point of view, there are already works that tackle the numerical solution of single-component fractional Nose–Einstein condensates.

As an example, there are papers that computationally studied the ground states of space-fractinoal nonlinear Schrödinger–Gross–Pitaevskii equations with a rotation term and non-local nonlinear interactions [3]. However, we must clarify that the single-component non-fractional case has been more studied that the double-component fully fractional scenario [4,5], possibly due to the mathematical difficulties in the double-component and fractional scenario. Clearly, this case is physically more relevant as it describes the dynamics of mixtures Bose–Einstein condensates that have been experimentally observed in the laboratory [6,7,8,9,10].

The following are crucial definitions and properties to discretize the fractional derivatives in the initial-boundary value problem in Equation (4).

Definition 3

(Ortigueira [11]). Let f be any real function defined on $\mathbb{R}$. Suppose that $h\in {\mathbb{R}}^{+}$ and that α is a real number satisfying $\alpha >-1$. We define the centered difference of fractional order α of f at the number x as

$${\mathrm{\Delta }}_h^{\left(\alpha \right)}f\left(x\right)=\sum _{k=-\infty }^{\infty }f(x-kh)g_k^{\left(\alpha \right)},\forall x\in \mathbb{R},$$

(5)

with

$$g_k^{\left(\alpha \right)}=\frac{{(-1)}^k\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(\frac{\alpha }{2}+k+1)\mathrm{\Gamma }(\frac{\alpha }{2}-k+1)},\forall k\in \mathbb{Z}.$$

(6)

Lemma 1

(Wang et al. [12]). Let $0<\alpha \le 2$ and $\alpha \ne 1$.

(a) 

If $k\ne 0$, then $g_k^{\left(\alpha \right)}=g_{-k}^{\left(\alpha \right)}<0$.

(b) 

$g_0^{\left(\alpha \right)}\in {\mathbb{R}}^{+}$.

(c) 

${\displaystyle \sum _{k=-\infty }^{\infty }{g}_k^{\left(\alpha \right)}=0}$.

Lemma 2

(Wang et al. [12]). Let $f:\mathbb{R}\to \mathbb{R}$ be a function in the set ${\mathcal{C}}^5\left(\mathbb{R}\right)$, which has integrable derivatives to the fifth order on $\mathbb{R}$. If $\alpha \in (0,1)\cup (1,2]$, then

$$-\frac{{\mathrm{\Delta }}_h^{\alpha }f\left(x\right)}{h^{\alpha }}=\frac{{\partial }^{\alpha }f\left(x\right)}{{\partial \left|x\right|}^{\alpha }}+\mathcal{O}\left(h^2\right),$$

(7)

for almost all $x\in \mathbb{R}$.

The field of fractional calculus has witnessed a vertiginous development in recent years, partly due to the vast amount of potential applications in the physical sciences [13]. Today, many different fractional derivatives and integrals have been proposed. For example, some of the first fractional derivatives introduced historically in mathematics were the Riemann–Liouville fractional derivatives [14], which generalized the classical integer-order derivatives with respect to specific analytical properties [1].

The fractional derivatives in the senses of Caputo, Riesz, and Grünwald–Letnikov are also extensions of the traditional derivatives of integer order. These fractional operators are nonequivalent in general, and various applications of all of them have been proposed in science and engineering [15,16]. For instance, some reports have provided theoretical foundations for the application of fractional calculus to the theory of viscoelasticity [17], while others have proposed possible applications of fractional calculus to dynamic problems of solid mechanics [18], continuous-time financial economics [19,20], Earth system dynamics [21], mathematical modeling of biological phenomena [22], and the modeling of two-phase gas/liquid flow systems [23], to mention some potential applications.

However, it is important to recall that Riesz-type derivatives may be the only fractional derivatives that have real physical applications. This is due to a well-known result by Tarasov, which establishes that Riesz fractional derivatives result from systems with long-range interactions in a continuum-limit case [24]. In turn, systems consisting of particles with long-range interactions are useful in statistical mechanics, thermostatics [25,26], and the theory of biological oscillator networks [27].

From the mathematical point of view, many interesting avenues of investigation have been opened by the progress in fractional calculus. Indeed, the different fractional derivatives have found discrete analogues, which have been used extensively in the literature. As examples, Riesz fractional derivatives have been discretized consistently in various fashions using fractional-order centered differences [11,28] and weighted-shifted Grünwald differences [29,30].

Clearly, those discrete approaches have been studied to determine their analytical properties, and they have been used extensively to provide discrete models to solve Riesz space-fractional conservative/dissipative space-fractional wave equations [31], a Hamiltonian fractional nonlinear elastic string equation [32], an energy-preserving double fractional Klein–Gordon–Zakharov system [33], and even a Riesz space-fractional generalization with generalized time-dependent diffusion coefficient and potential of the Higgs boson equation in the de Sitter space-time [32], among other complex systems.

On the other hand, Caputo fractional derivatives have been discretized consistently using various criteria. For instance, some high-order $L2$-compact difference approaches have used to that end [34], as well as $L1$ formulas [35,36] and $L1$–2 methodologies [37]. Using those approaches, various numerical schemes have been proposed to efficiently solve Caputo time-fractional diffusive and wave differential equations [38,39,40]. Various potential applications of these systems have been reported in the sciences [25,41].

From the analytical point of view, the literature offers a wide range of reports that focus on the extension of integer-order methods and results for the fractional case. For example, there are various articles that tackle the existence, uniqueness, regularity, and asymptotic behavior of the solution for the fractional porous medium equation [42], nonlinear fractional diffusion equations [43], nonlinear fractional heat equations [44], the Fisher–Kolmogorov–Petrovskii–Piscounov equation with nonlinear fractional diffusion [45], fractional thin-film equations [46], and the fractional Schrödinger equation with general nonnegative potentials [47].

From a more particular point of view, the fractional generalization of the classical vector calculus operators (that is, the gradient, divergence, curl, and Laplacian operators) has also been an active topic of research developed from different approaches. Some of the first attempts to extend those operators to the fractional scenario were proposed in [48,49] using the Nishimoto fractional derivative.

These operators were used later on in [50] to provide a physical interpretation for the fractional advection-dispersion equation for flow in heterogeneous porous media (see [51] and the references therein for a historic account of the efforts to formulate a fractional form of vector calculus). More recently, a new generalization of the Helmholtz decomposition theorem for both fractional time and space was proposed in [52,53] using the discrete Grünwald–Letnikov fractional derivative. As in the present manuscript, the authors of [52,53] considered different derivative orders assuming non-homogeneous models and non-isotropic spaces.

This manuscript is organized as follows. Section 2 is devoted to present the discrete nomenclature and the numerical model to solve the continuous problem under investigation in this work. We introduce suitable discrete norms and recall a useful theorem by Desplanques. With that result at hand, we rigorously establish the properties of existence and uniqueness of numerical solutions. Section 3 is devoted to establishing the most important computational features of our numerical scheme. More concretely, we show that the discrete model proposed in this work has second order consistency under suitable conditions on the smoothness of the solutions.

We also rigorously prove the stability property of the scheme along with its quadratic order of convergence in both time and space. In turn, Section 4 is devoted to show some illustrative simulations that exhibit the stability and the convergence of the method proposed in this work. We will also provide numerical evidence that the finite-difference scheme proposed here has a quadratic order of convergence in both space and time. Finally, we close this manuscript with some concluding remarks. For the sake of convenience to the reader, an appendix is provided at the end of this paper, in which we present the numerical scheme used to produce the simulations.

2. Numerical Method

Throughout this manuscript, we let $M_i,N\in \mathbb{N}$, for each $i\in I_p$, and fix the spatial and temporal step-sizes $h_i=\left(b_i-a_i\right)/M_i$ and $\tau =T/N$, for each $i\in I_p$. We will consider regular partitions of the intervals $[a_i,b_i]$ and $[0,T]$ represented as

$$\begin{array}{cc}\hfill x_{i,j_i}& =a_i+j_i{h}_i,\forall i\in I_p,\forall j_i\in {\overline{I}}_{M_i},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill t_n& =n\tau ,\forall n\in {\overline{I}}_N,\hfill \end{array}$$

(9)

respectively. Let $J={\prod }_{i=1}^p{I}_{M_i-1}$ and $\overline{J}={\prod }_{i=1}^p{\overline{I}}_{M_i}$, and convey that $x_j=(x_{1,j_1},\dots ,x_{p,j_p})$, for each $j=(j_1,\dots ,j_p)\in \overline{J}$. Throughout this work, we will employ the symbol $(u_j^n,v_j^n)$ to denote a numerical approximation to $(U_j^n,V_j^n)$, where $U_j^n={\psi }_1(x_j,t_n)$ and $V_j^n={\psi }_2(x_j,t_n))$, for each $(j,n)\in \overline{J}\times {\overline{I}}_N$. Let us agree that ${\mathbf{P}}_j=\mathbf{P}\left(x_j\right)$, for each $j\in \overline{J}$. We will employ the symbol $\partial J$ to represent the boundary of $\overline{J}$, which is defined as the set of all multi-indexes $j\in J$ that satisfy $x_j\in \partial \Omega$.

Definition 4.

We introduce the following average operators, for each $\alpha \in (0,1)\cup (1,2]$, $(j,n)\in J\times I_{N-1}$ and $w=u,v$:

$$\begin{array}{cc}\hfill {\mu }_t{w}_j^n& =\frac{w_j^{n+1}+w_j^n}{2},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mu }_t^{\left(1\right)}{w}_j^n& =\frac{3w_j^n-w_j^{n-1}}{2}.\hfill \end{array}$$

(11)

Under the same conditions, we introduce the difference operators

$$\begin{array}{cc}\hfill {\delta }_t{w}_j^n& =\frac{w_j^{n+1}-w_j^n}{\tau },\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\delta }_{x_i}^{\left(\alpha \right)}{w}_j^n& =-\frac{1}{h_i^{\alpha }}\sum _{k=0}^{M_i}{g}_{j_i-k}^{\left(\alpha \right)}w(x_{1,j_1},\dots ,x_{i-1,j_{i-1}},x_{i,k},x_{i+1,j_{i+1}},\dots ,x_{p,j_p},t_n).\hfill \end{array}$$

(13)

In the present manuscript, we convey that

$${△}_h^{\left(\alpha \right)}{w}_j^n={\delta }_{x_1}^{\left(\alpha \right)}{w}_j^n+{\delta }_{x_2}^{\left(\alpha \right)}{w}_j^n+\dots +{\delta }_{x_p}^{\left(\alpha \right)}{w}_j^n.$$

(14)

Moreover, for the sake of convenience, we also introduce the discrete fractional gradient vector

$${▽}_h^{\left(\alpha \right)}=({\delta }_{x_1}^{\left(\alpha \right)}{w}_j^n,{\delta }_{x_2}^{\left(\alpha \right)}{w}_j^n,\dots ,{\delta }_{x_p}^{\left(\alpha \right)}{w}_j^n).$$

(15)

With this nomenclature at hand, the following numerical method will be employed in this work to approximate the solution of the initial-boundary value problem Equation (4) on the set $\overline{\Omega }\times [0,T]$, for each $(j,n)\in J\times {\overline{I}}_{N-1}$:   

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}{\delta }_t{u}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right]{\mu }_t{u}_j^n+\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{u}_j^n+\lambda {\mu }_t^{\left(1\right)}{v}_j^n,\hfill \\ \hfill \mathrm{i}{\delta }_t{v}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right]{\mu }_t{v}_j^n+\left[{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2+{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{v}_j^n+\lambda {\mu }_t^{\left(1\right)}{u}_j^n,\hfill \end{array}\\ \mathrm{such}\mathrm{that}\left\{\begin{array}{cc}{u}_j^0={\mu }_t{u}_j^0={\mu }_t^{\left(1\right)}{u}_j^0={\varphi }_1\left(x_j\right),\hfill & \forall j\in J,\hfill \\ v_j^0={\mu }_t{v}_j^0={\mu }_t^{\left(1\right)}{v}_j^0={\varphi }_2\left(x_j\right),\hfill & \forall j\in J,\hfill \\ u_j^n=v_j^n=0,\hfill & \forall (j,n)\in \partial J\times {\overline{I}}_N.\hfill \end{array}\right.\end{array}$$

(16)

One may readily check that the general iterative formula of this numerical model makes it a three-step implicit model. On the other hand, to determine the approximations at the time $t_1$, we need to employ the initial conditions $u_j^0={\mu }_t{u}_j^0={\mu }_t^{\left(1\right)}{u}_j^0={\varphi }_1\left(x_j\right)$ and $v_j^0={\mu }_t{v}_j^0={\mu }_t^{\left(1\right)}{v}_j^0={\varphi }_2\left(x_j\right)$, for all $j\in J$. Substituting these formulas into the general iterative equations at time $t_0$, we obtain

$$\begin{array}{cc}\hfill u_j^1& ={\varphi }_1\left(x_j\right)+\mathrm{i}\tau \left[\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}-{\mathbf{P}}_j-D\right]{\varphi }_1\left(x_j\right)-\mathrm{i}\tau \lambda {\varphi }_2\left(x_j\right)\hfill \\ \hfill & -\mathrm{i}\tau \left[{\beta }_{11}{\left|{\varphi }_1\left(x_j\right)\right|}^2+{\beta }_{12}{\left|{\varphi }_2\left(x_j\right)\right|}^2\right]{\varphi }_1\left(x_j\right),\forall j\in J,\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill v_j^1& ={\varphi }_2\left(x_j\right)+i\tau \left[\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}-{\mathbf{P}}_j\right]{\varphi }_2\left(x_j\right)-i\tau \lambda {\varphi }_1\left(x_j\right)\hfill \\ \hfill & -i\tau \left[{\beta }_{12}{\left|{\varphi }_1\left(x_j\right)\right|}^2+{\beta }_{22}{\left|{\varphi }_2\left(x_j\right)\right|}^2\right]{\varphi }_2\left(x_j\right),\forall j\in J.\hfill \end{array}$$

(18)

For the remainder of his manuscript, we define $h=(h_1,\dots ,h_p)$ and $h_{*}={\prod }_{i=1}^p{h}_i$. We will employ ${\mathcal{V}}_h$ to represent the collection of all complex functions on the spatial mesh $\{x_j:j\in \overline{J}\}\subseteq {\mathbb{R}}^p$. Finally, for each $w\in {\mathcal{V}}_h$ and all $j\in \overline{J}$, let $w_j=w\left(x_j\right)$.

Definition 5.

Let us introduce the functions $⟨·,·⟩:{\mathcal{V}}_h\times {\mathcal{V}}_h\to \mathbb{C}$ and ${\parallel ·\parallel }_1:{\mathcal{V}}_h\to \mathbb{R}$, defined respectively by

$$\begin{array}{cc}\hfill ⟨u,v⟩& =h_{*}\sum _{j\in I}{u}_j\overline{v_j},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\parallel u\parallel }_1& =h_{*}\sum _{j\in I}\left|u_j\right|,\hfill \end{array}$$

(20)

for any $u,v\in {\mathcal{V}}_h$. We define the function ${\parallel ·\parallel }_2:{\mathcal{V}}_h\to \mathbb{R}$ as the Euclidean norm obtained from $⟨·,·⟩$. If $u,v\in {\mathcal{V}}_h$, then we agree that $uv\in {\mathcal{V}}_h$ represents the pointwise multiplication of u and v. Moreover, $\left|u\right|\in {\mathcal{V}}_h$ will denote the absolute value of the complex function u.

Lemma 3

(Desplanques [54]). Let A be a square complex matrix. If A is strictly diagonally dominant, then A is invertible.

Theorem 1

(Unique solvability). If $({\varphi }_1,{\varphi }_2)$ is any set of initial conditions, then the finite-difference model Equation (16) has a unique solution.

Proof. 

The proof will be provided for the one-dimensional scenario only in view that the case for higher dimensions is similar. Note that, beforehand, the approximations $u^0$, $v^0$, $u^1$ and $v^1$ are provided explicitly by the initial conditions and the formulas Equations (17) and (18). Proceeding by induction, suppose that $u^n$, $v^n$, $u^{n-1}$, and $v^{n-1}$ were calculated, for some $n\in I_{N-1}$. It is important to observe now that the first equation of the numerical method can be equivalently rewritten as

$$\begin{array}{cc}\hfill & \left(\frac{\mathrm{i}}{\tau }-\frac{1}{4h^{{\alpha }_1}}{g}_0^{{\alpha }_1}-\frac{1}{2}\left({\mathbf{P}}_j+D\right)\right)u_j^{n+1}-\frac{1}{4h^{{\alpha }_1}}\sum _{\begin{array}{c}l=0\\ l\ne j\end{array}}^{M_1}{g}_{l-j}^{\left({\alpha }_1\right)}{u}_l^{n+1}\hfill \\ \hfill & =b\left(u_j^n\right)+a(u_j^{n-1},u_j^n,v_j^{n-1},v_j^n),\forall (j,n)\in J\times I_{N-1},\hfill \end{array}$$

(21)

where

$$\begin{array}{cc}\hfill a(u_j^{n-1},u_j^n,v_j^{n-1},v_j^n)& =({\beta }_{11}|{\mu }_t^{\left(1\right)}{u}_j^n{|}^2+{\beta }_{12}|{\mu }_t^{\left(1\right)}{v}_j^n{|}^2){\mu }_t^{\left(1\right)}{u}_j^n+\lambda {\mu }_t^{\left(1\right)}{v}_j^n,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill b\left(u_j^n\right)& =\left(\frac{\mathrm{i}}{\tau }+\frac{1}{2}\left(-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right)\right)u_j^n,\hfill \end{array}$$

(23)

for each $(j,n)\in J\times I_{N-1}$. It follows that the first identity of the numerical scheme Equation (16) can be alternatively expressed in vector form as

$$A{u}^{n+1}=-b\left(u^n\right)-a(u^{n-1},u^n,v^{n-1},v^n),\forall n\in I_{N-1}.$$

(24)

In this expression, the square complex matrix $A=\left(a_{ij}\right)$ is defined by -4.6cm0cm

$$A=\left(\begin{array}{cccc}{\displaystyle \frac{g_0^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}+{\displaystyle \frac{{\mathbf{P}}_0+D}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}& {\displaystyle \frac{g_{-1}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}& \cdots & {\displaystyle \frac{g_{2-M_1}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}\\ {\displaystyle \frac{g_1^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}& {\displaystyle \frac{g_0^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}+{\displaystyle \frac{{\mathbf{P}}_1+D}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}& \cdots & {\displaystyle \frac{g_{3-M_1}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{g_{M_1-2}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}& {\displaystyle \frac{g_{M_1-3}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}& \cdots & {\displaystyle \frac{g_0^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}}+{\displaystyle \frac{{\mathbf{P}}_{M_1}+D}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}\end{array}\right).$$

(25)

Notice now that the diagonal entries of A satisfy

$$\left|a_{ii}\right|=\sqrt{{\left(\frac{g_0^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}+\frac{1}{2}\left({\mathbf{P}}_{i-1}+D\right)\right)}^2+{\left(\frac{-1}{\tau }\right)}^2}.$$

(26)

On the other hand, the numbers in the real sequence ${\left(g_k^{\left({\alpha }_1\right)}\right)}_{k=-\infty }^{\infty }$ guarantee that

$$\sum _{j\ne i}^{M_1}\left|a_{ij}\right|=\sum _{j\ne i}^{M_1}\left|\frac{g_{l-j}^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_1}}\right|=-\sum _{j\ne i}^{M_1}\frac{g_{l-j}^{{\alpha }_1}}{4h^{{\alpha }_1}}<-\sum _{\begin{array}{c}l=-\infty \\ l\ne j\end{array}}^{\infty }\frac{g_{l-j}^{{\alpha }_1}}{4h^{{\alpha }_1}}=\frac{g_0^{{\alpha }_1}}{4h^{{\alpha }_1}}\le \left|a_{ii}\right|.$$

(27)

It follows that the matrix A is non-singular by the previous lemma, which implies then that there exists a unique solution $u^{n+1}$ of the vector equation Equation (24). In similar fashion, we can readily prove the existence of the vector $v^{n+1}$ after noticing that the second difference equation of the discrete system Equation (16) may be rewritten in vector form as

$$B{v}^{n+1}=-d\left(v^n\right)-c(u^{n-1},u^n,v^{n-1},v^n),$$

(28)

where, for each $(j,n)\in J\times I_{N-1}$,

$$\begin{array}{cc}\hfill c(u^{n-1},u^n,v^{n-1},v^n)& =({\beta }_{12}|{\mu }_t^{\left(1\right)}{u}_j^n{|}^2+{\beta }_{22}|{\mu }_t^{\left(1\right)}{v}_j^n{|}^2){\mu }_t^{\left(1\right)}{v}_j^n+\lambda {\mu }_t^{\left(1\right)}{u}_j^n,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill d\left(v_j^n\right)& =\left(\frac{\mathrm{i}}{\tau }+\frac{1}{2}\left(-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right)\right)v_j^n.\hfill \end{array}$$

(30)

In this expression, B is the square complex matrix given by

$$B=\left(\begin{array}{cccc}{\displaystyle \frac{g_0^{\left({\alpha }_1\right)}}{4h_1^{{\alpha }_2}}}+{\displaystyle \frac{{\mathbf{P}}_0}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}& {\displaystyle \frac{g_{-1}^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}& \cdots & {\displaystyle \frac{g_{2-M_1}^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}\\ {\displaystyle \frac{g_1^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}& {\displaystyle \frac{g_0^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}+{\displaystyle \frac{{\mathbf{P}}_1}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}& \cdots & {\displaystyle \frac{g_{3-M_1}^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{g_{M_1-2}^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}& {\displaystyle \frac{g_{M_1-3}^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}& \cdots & {\displaystyle \frac{g_0^{\left({\alpha }_2\right)}}{4h_1^{{\alpha }_2}}}+{\displaystyle \frac{{\mathbf{P}}_{M_1}}{2}}-{\displaystyle \frac{\mathrm{i}}{\tau }}\end{array}\right).$$

(31)

One may readily check that this matrix is strictly diagonally dominant; therefore, Equation (28) has a unique solution $v^{n+1}$. The conclusion of this theorem readily follows now by mathematical induction.    □

3. Numerical Properties

The aim of the present section is to theoretically demonstrate the most relevant features of the discrete model Equation (16). Concretely, we, herein, prove properties, including the consistency, stability, and convergence of our numerical model. In a first stage, we will require to define the following continuous operators for each $(x,t)\in {\Omega }_T$:

$$\begin{array}{cc}\hfill {\mathcal{L}}_1({\psi }_1(x,t),{\psi }_2(x,t))& =\mathrm{i}\frac{\partial {\psi }_1(x,t)}{\partial t}+\left[\frac{1}{2}{△}^{{\alpha }_1}-\mathbf{P}\left(x\right)-D-{\beta }_{11}{\left|{\psi }_1(x,t)\right|}^2\right.\hfill \\ \hfill & \left.-{\beta }_{12}{\left|{\psi }_2(x,t)\right|}^2\right]{\psi }_1(x,t)-\lambda {\psi }_2(x,t),\hfill \end{array}$$

(32)

and

$$\begin{array}{cc}\hfill {\mathcal{L}}_2({\psi }_1(x,t),{\psi }_2(x,t))& =\mathrm{i}\frac{\partial {\psi }_2(x,t)}{\partial t}+\left[\frac{1}{2}{△}^{{\alpha }_2}-\mathbf{P}\left(x\right)\right.\hfill \\ \hfill & \left.-{\beta }_{12}{\left|{\psi }_1(x,t)\right|}^2-{\beta }_{22}{\left|{\psi }_2(x,t)\right|}^2\right]{\psi }_2(x,t)-\lambda {\psi }_1(x,t).\hfill \end{array}$$

(33)

For each $(j,n)\in J\times I_{N-1}$, we also introduce the discrete operators

$$\begin{array}{cc}\hfill L_1(U_j^n,V_j^n)& =\mathrm{i}{\delta }_t{U}_j^n+\left[\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}-{\mathbf{P}}_j-D\right]{\mu }_t{U}_j^n\hfill \\ \hfill & -\left[{\beta }_{11}{\left|{\mu }^{\left(1\right)}{U}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }^{\left(1\right)}{V}_j^n\right|}^2\right]{\mu }^{\left(1\right)}{U}_j^n-\lambda {\mu }^{\left(1\right)}{V}_j^n,\hfill \end{array}$$

(34)

and

$$\begin{array}{cc}\hfill L_2(U_j^n,V_j^n)& =\mathrm{i}{\delta }_t{V}_j^n+\left[\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}-{\mathbf{P}}_j\right]{\mu }_t{V}_j^n\hfill \\ \hfill & -\left[{\beta }_{12}{\left|{\mu }^{\left(1\right)}{U}_j^n\right|}^2+{\beta }_{22}{\left|{\mu }^{\left(1\right)}{V}_j^n\right|}^2\right]{\mu }^{\left(1\right)}{V}_j^n-\lambda {\mu }^{\left(1\right)}{U}_j^n.\hfill \end{array}$$

(35)

Here, recall that we previously agreed that $U_j^n={\psi }_1(x_j,t_n)$ and $V_j^n={\psi }_2(x_j,t_n)$, for each $(j,n)\in \overline{J}\times {\overline{I}}_N$. For the sake of convenience, when $(x,t)\in {\Omega }_T$ and $(j,n)\in J\times I_{N-1}$, then we agree that

$$\begin{array}{cc}\hfill \mathcal{L}({\psi }_1(x,t),{\psi }_2(x,t))& =\left({\mathcal{L}}_1({\psi }_1(x,t),{\psi }_2(x,t)),{\mathcal{L}}_2({\psi }_1(x,t),{\psi }_2(x,t))\right),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill L({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n))& =(L_1({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n)),L_2({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n))).\hfill \end{array}$$

(37)

Theorem 2

(Consistency). Suppose that ${\psi }_1,{\psi }_2\in {\mathcal{C}}_{x,t}^{5,4}\left(\overline{{\Omega }_T}\right)$ and $\mathbf{P}\in \mathcal{C}\left(\overline{\Omega }\right)$. There are positive numbers $C_1$ and $C_2$ independent of h and τ, which satisfy the inequalities

$$\begin{array}{cc}\hfill \parallel L({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n))-\mathcal{L}({\psi }_1(x_j,t_{n+\frac{1}{2}}),{\psi }_2(x_j,t_{n+\frac{1}{2}})){\parallel }_{\infty }& \le C_1({\tau }^2+{\parallel h\parallel }_2^2),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \parallel L({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n))-\mathcal{L}({\psi }_1(x_j,t_n),{\psi }_2(x_j,t_n)){\parallel }_{\infty }& \le C_2{(\tau +\parallel h\parallel }_2^2),\hfill \end{array}$$

(39)

for each $(j,n)\in J\times I_{N-1}$.

Proof. 

To prove these results, we require Taylor’s theorem, Lemma 2, and the smoothness assumptions on the functions ${\psi }_1$ and ${\psi }_2$. There exist nonnegative constants $C_{1,k}$, $C_{2,k}$, $C_{3,k,i}$, $C_{4,k}$, and $C_{5,k.l}$, which are independent of $\tau$ and h, for each $i\in I_p$ and $k,l\in I_2$, with the property that

$$\begin{array}{cc}\hfill \left|{\mu }_t^{\left(1\right)}{\psi }_k(x_j,t_n)-{\psi }_k(x_j,t_{n+\frac{1}{2}})\right|& \le C_{1,k}{\tau }^2,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \left|{\delta }_t{\psi }_k(x_j,t_n)-\frac{\partial {\psi }_k}{\partial t}(x_j,t_{n+\frac{1}{2}})\right|& \le C_{2,k}{\tau }^2,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill \left|{\mu }_t{\delta }_{x_i}^{\left({\alpha }_1\right)}{\psi }_k(x_j,t_n)-\frac{{\partial }^{{\alpha }_1}{\psi }_k}{{\partial \left|x\right|}^{{\alpha }_1}}(x_j,t_{n+\frac{1}{2}})\right|& \le C_{3,k,i}({\tau }^2+h_i^2),\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill \left|\mathbf{P}\left(x_j\right){\mu }_t{\psi }_k(x_j,t_n)-\mathbf{P}\left(x_j\right){\psi }_k(x_j,t_{n+\frac{1}{2}})\right|& \le C_{4,k}{\tau }^2,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \left|{\left|{\mu }_t^{\left(1\right)}{\psi }_k(x_j,t_n)\right|}^2{\mu }_t^{\left(1\right)}{\psi }_l(x_j,t_n)-{\left|{\psi }_k(x_j,t_{n+\frac{1}{2}})\right|}^2{\psi }_l(x_j,t_{n+\frac{1}{2}})\right|& \le C_{5,k,l}{\tau }^2,\hfill \end{array}$$

(44)

for each $(j,n)\in J\times I_{N-1}$. The inequality in the conclusion of this proposition follows now applying the triangle inequality for an appropriate number $C_1$, which depends only on $C_{1,k}$, $C_{2,k}$, $C_{3,k,i}$, $C_{4,k}$, and $C_{5,k.l}$ for each $i\in I_p$ and $k,l\in I_2$, and the model parameters. This implies, in particular, that $C_2$ is independent of h and $\tau$, as desired. The constant $C_2$ is obtained applying the same arguments around the node $(x_j,t_n)$ instead of $(x_j,t_{n+\frac{1}{2}})$.    □

We tackle now the stability and the convergence of the numerical scheme Equation (16). We require the next technical results.

Lemma 4

(Pen-Yu [55]). Suppose that ${\left({\omega }^n\right)}_{n=0}^N$ and ${\left({\rho }^n\right)}_{n=0}^N$ are sequences of non-negative numbers. Let $C\ge 0$ satisfy the inequality

$${\omega }^n\le {\rho }^n+C\tau \sum _{k=0}^{n-1}{\omega }^k.$$

(45)

Then, ${\omega }^n\le {\rho }^n{e}^{Cn\tau }$ for each $0\le n\le N$.

Lemma 5

(Macías-Díaz [56]). Suppose that α is a real number with $\alpha \in (0,1)\cup (1,2]$. If $u,v\in {\mathcal{V}}_h$, then $⟨-{△}_h^{\left(\alpha \right)}u,v⟩=⟨{△}_h^{(\alpha /2)}u,{△}_h^{(\alpha /2)}v⟩$.

Lemma 6.

If $\alpha \in (1,2]$ and $w={\left(w^n\right)}_{n=1}^N\subseteq {\mathcal{V}}_h$, then the following holds, for each $n\in I_{N-1}$:

(a) 

$2⟨{\delta }_t{w}^n,{\mu }_t{w}^n⟩={\delta }_t{\parallel w^n\parallel }_2^2+\frac{\mathrm{i}}{\tau }2Im⟨w^{n+1},w^n⟩$,

(b) 

$2⟨-{△}_h^{\left(\alpha \right)}{\mu }_t{w}^n,{\mu }_t{w}^n⟩=2{\parallel {▽}_h^{(\alpha /2)}{\mu }_t{w}^n\parallel }_2^2$,

(c) 

$2⟨V{\mu }_t{w}^n,{\mu }_t{w}^n⟩=2⟨V,|{\mu }_t{w}^n{|}^2⟩$.

Lemma 7.

Let $ϵ={\left({ϵ}^n\right)}_{n=0}^N$ and $\zeta ={\left({\zeta }^n\right)}_{n=0}^N$ be sequences in ${\mathcal{V}}_h$. If $m\in I_{N-1}$, then

$$\begin{array}{cc}\hfill & 2\sum _{n=1}^m\left[Im⟨{\mu }_t^{\left(1\right)}{ϵ}^n,{\mu }_t{\zeta }^n⟩+Im⟨{\mu }_t^{\left(1\right)}{\zeta }^n,{\mu }_t{ϵ}^n⟩\right]\hfill \\ \hfill & \le \frac{1}{4}\left(\parallel {ϵ}^0{\parallel }_2^2+{\parallel {\zeta }^0\parallel }_2^2\right)+\frac{3}{2}\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)+\parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2.\hfill \end{array}$$

(46)

Proof. 

The proof follows after applications of Young’s inequality and some algebraic regrouping.    □

The stability of the discrete method Equation (16) will require us to consider two sets of initial conditions, namely $({\varphi }_1,{\varphi }_2)$ and $({\tilde{\varphi }}_1,{\tilde{\varphi }}_2)$, where all the initial data are complex functions, which are defined on $\overline{\Omega }$. The respective solutions will be denoted by $(u,v)$ and $(\tilde{u},\tilde{v})$. This means that $(u,v)$ satisfies Equation (16), while $(\tilde{u},\tilde{v})$ satisfies the problem

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}{\delta }_t{\tilde{u}}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right]{\mu }_t{\tilde{u}}_j^n+\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n\hfill \\ \hfill & +\lambda {\mu }_t^{\left(1\right)}{\tilde{v}}_j^n,\hfill \\ \hfill \mathrm{i}{\delta }_t{\tilde{v}}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right]{\mu }_t{\tilde{v}}_j^n+\left[{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n\right|}^2+{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n+\lambda {\mu }_t^{\left(1\right)}{\tilde{u}}_j^n,\hfill \end{array}\\ \mathrm{such}\mathrm{that}\left\{\begin{array}{cc}{\tilde{u}}_j^0={\mu }_t^{\left(1\right)}{\tilde{u}}_j^0={\tilde{\varphi }}_1\left(x_j\right),\hfill & \forall j\in J,\hfill \\ {\tilde{v}}_j^0={\mu }_t^{\left(1\right)}{\tilde{v}}_j^0={\tilde{\varphi }}_2\left(x_j\right),\hfill & \forall j\in J,\hfill \\ {\tilde{u}}_j^n={\tilde{v}}_j^n=0,\hfill & \forall (j,n)\in \partial J\times {\overline{I}}_N.\hfill \end{array}\right.\end{array}$$

(47)

for each $(j,n)\in J\times I_{N-1}$.

Lemma 8.

Let $(u,v)$ and $(\tilde{u},\tilde{v})$ be solutions of Equation (16), respectively, and let ${ϵ}^n=u^n-{\tilde{u}}^n$ and ${\zeta }^n=v^n-{\tilde{v}}^n$, for each $n\in {\overline{I}}_N$. For each $(j,n)\in J\times I_{N-1}$, let us define

$$\begin{array}{cc}\hfill P_j^n& =\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{u}_j^n-\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n,\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill Q_j^n& =\left[{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{v}_j^n-\left[{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{\tilde{u}}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{\tilde{v}}_j^n.\hfill \end{array}$$

(49)

Then, there exists a constant $C\ge 0$, which is independent of h and τ, with the property that

$$max\left\{\right|P_j^n|,|Q_j^n\left|\right\}\le C\left(\right|{ϵ}_j^{n-1}|+|{\zeta }_j^{n-1}|+|{ϵ}_j^n|+|{\zeta }_j^n\left|\right),\forall (j,n)\in J\times I_{N-1}.$$

(50)

Proof. 

The result is straightforward.    □

Theorem 3

(Nonlinear stability). Consider the solutions $(u,v)$ and $(\tilde{u},\tilde{v})$ of Equation (16) corresponding to initial conditions $({\varphi }_1,{\varphi }_2)$ and $({\tilde{\varphi }}_1,{\tilde{\varphi }}_2)$, respectively. For each $n\in {\overline{I}}_N$, define ${ϵ}^n=u^n-{\tilde{u}}^n$ and ${\zeta }^n=v^n-{\tilde{v}}^n$. If $(C^{\prime }+\lambda )\tau <\frac{1}{2}$, then there is a nonnegative constant $C^{″}$ that is not dependent on τ and h, such that

$$\parallel {ϵ}^n{\parallel }_2^2+\parallel {\zeta }^n{\parallel }_2^2\le (1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)e^{2C^{″}T},\forall n\in {\overline{I}}_N.$$

(51)

Proof. 

Beforehand, take C as in the last result. Note that the existence of $(u,v)$ and $(\tilde{u},\tilde{v})$ is guaranteed by Theorem 1. It is clear that $(ϵ,\eta )$ satisfies the following discrete problem, for each $(j,n)\in J\times I_{N-1}$:

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}{\delta }_t{ϵ}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right]{\mu }_t{ϵ}_j^n+P_j^n+\lambda {\mu }_t^{\left(1\right)}{\zeta }_j^n,\hfill \\ \hfill \mathrm{i}{\delta }_t{\zeta }_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right]{\mu }_t{\zeta }_j^n+Q_j^n+\lambda {\mu }_t^{\left(1\right)}{ϵ}_j^n,\hfill \end{array}\\ \mathrm{such}\mathrm{that}\left\{\begin{array}{cc}{ϵ}_j^0={\mu }_t^{\left(1\right)}{ϵ}_j^0={\varphi }_1\left(x_j\right)-{\tilde{\varphi }}_1\left(x_j\right),\hfill & \forall j\in \overline{J},\hfill \\ {\zeta }_j^0={\mu }_t^{\left(1\right)}{\zeta }_j^0={\varphi }_2\left(x_j\right)-{\tilde{\varphi }}_2\left(x_j\right),\hfill & \forall j\in \overline{J},\hfill \\ {ϵ}_j^n={\zeta }_j^n=0,\hfill & \forall (j,n)\in \partial J\times {\overline{I}}_N.\hfill \end{array}\right.\end{array}$$

(52)

Here, $P_j^n$ and $Q_j^n$ are as in Lemma 8. Then, there is a nonnegative real number $C^{\prime }$ such that, for each $n\in I_{N-1}$,

$$max\{\parallel P^n{\parallel }_2^2,\parallel Q^n{\parallel }_2^2\}\le C^{\prime }\left(\parallel {ϵ}^{n-1}{\parallel }_2^2+\parallel {\zeta }^{n-1}{\parallel }_2^2+\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right).$$

(53)

The number $C^{\prime }$ does not depend on h and $\tau$. Take the first identity in Equation (52) and calculate its inner product with $2{\mu }_t^{\left(1\right)}{ϵ}^n$. On both sides of the result, next calculate the imaginary part. Similarly, consider the second identity of Equation (52) and take the inner product with $2{\mu }_t^{\left(1\right)}{\zeta }^n$. Calculate the imaginary part on both sides. After applying the identities after Theorem 6, we readily obtain that

$$\begin{array}{cc}\hfill {\delta }_t{\parallel {ϵ}^n\parallel }_2^2& =2Im⟨P^n,{\mu }_t{ϵ}^n⟩+2\lambda Im⟨{\mu }_t^{\left(1\right)}{\zeta }^n,{\mu }_t{ϵ}^n⟩,\forall n\in I_{N-1},\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill {\delta }_t{\parallel {\zeta }^n\parallel }_2^2& =2Im⟨Q^n,{\mu }_t{\zeta }^n⟩+2\lambda Im⟨{\mu }_t^{\left(1\right)}{ϵ}^n,{\mu }_t{\zeta }^n⟩,\forall n\in I_{N-1}.\hfill \end{array}$$

(55)

After adding those two results side by side and bounding from above, we notice that there exists a nonnegative number $C^{″}$ that is not dependent on $\tau$ and h, with

$$\begin{array}{cc}\hfill & \parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\hfill \\ \hfill & =\parallel {ϵ}^0{\parallel }_2^2+{\parallel {\zeta }^0\parallel }_2^2+2\tau \sum _{n=1}^{m}Im(⟨P^n,{\mu }_t{ϵ}^n⟩+⟨Q^n,{\mu }_t{\zeta }^n⟩)\hfill \\ \hfill & +\frac{\lambda \tau }{4}\left[\parallel {ϵ}^0{\parallel }_2^2+{\parallel {\zeta }^0\parallel }_2^2+4\left(\parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\right)+6\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)\right]\hfill \\ \hfill & \le (1+\frac{\lambda \tau }{4})(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)+\frac{\tau }{2}\sum _{n=1}^m\left[2\parallel P^n{\parallel }_2^2+2{\parallel Q^n\parallel }_2^2\right.\hfill \\ \hfill & \left.+\parallel {ϵ}^n{\parallel }_2^2+\parallel {\zeta }^n{\parallel }_2^2+\parallel {ϵ}^{n+1}{\parallel }_2^2+{\parallel {\zeta }^{n+1}\parallel }_2^2\right]\hfill \\ \hfill & +\frac{\lambda \tau }{2}\left[2\left(\parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\right)+3\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)\right]\hfill \\ \hfill & \le (1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)+3\tau \left(C^{″}+\frac{\lambda }{2}\right)\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)\hfill \\ \hfill & +\tau (C^{″}+\lambda )(\parallel {ϵ}^{m+1}{\parallel }_2^2+\parallel {\zeta }^{m+1}{\parallel }_2^2),\forall m\in I_{M-1}.\hfill \end{array}$$

(56)

Subtract the term $\tau (C^{″}+\lambda )(\parallel {ϵ}^{m+1}{\parallel }_2^2+\parallel {\zeta }^{m+1}{\parallel }_2^2)$ from both ends of this chain of inequalities, group the common terms, and we notice that $(C^{\prime }+\lambda )\tau <\frac{1}{2}$. As a consequence,

$$\begin{array}{cc}\hfill \parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2& \le (1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)\hfill \\ \hfill & +3\tau \left(C^{″}+\frac{\lambda }{2}\right)\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right),\hfill \end{array}$$

(57)

for each $m\in I_{M-1}$. The conclusion is reached then using Lemma 4 with the constants ${\omega }^n=\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2$ and ${\rho }^n=(1+(C^{″}+\frac{\lambda }{4})\tau )\parallel {ϵ}^0{\parallel }_2^2+{\parallel {\zeta }^0\parallel }_2^2$, for each $n\in {\overline{I}}_{N-1}$.    □

Finally, we investigate now the convergence of the finite-difference method Equation (16). As mentioned previously, $(u,v)$ represents a solution of the numerical model, while $(U,V)=({\psi }_1,{\psi }_2)$ denotes a solution of the continuous problem. It is clear that $(U,V)$ satisfies the discrete initial-boundary value problem

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}{\delta }_t{U}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right]{\mu }_t{U}_j^n+\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{U}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{V}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{U}_j^n\hfill \\ \hfill & +\lambda {\mu }_t^{\left(1\right)}{V}_j^n+{\rho }_j^n,\hfill \\ \hfill \mathrm{i}{\delta }_t{V}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right]{\mu }_t{V}_j^n+\left[{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{U}_j^n\right|}^2+{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{V}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{V}_j^n\hfill \\ \hfill & +\lambda {\mu }_t^{\left(1\right)}{U}_j^n+{\sigma }_j^n,\hfill \end{array}\\ \mathrm{such}\mathrm{that}\left\{\begin{array}{cc}{U}_j^0={\mu }_t^{\left(1\right)}{U}_j^0={\varphi }_1\left(x_j\right),\hfill & \forall j\in J,\hfill \\ V_j^0={\mu }_t^{\left(1\right)}{V}_j^0={\varphi }_2\left(x_j\right),\hfill & \forall j\in J,\hfill \\ U_j^n=V_j^n=0,\hfill & \forall (j,n)\in \partial J\times {\overline{I}}_N.\hfill \end{array}\right.\end{array}$$

(58)

Here, ${\rho }_j^n$ and ${\sigma }_j^n$ denote local truncation errors. Under the regularity assumptions on the solutions U and V stated in Theorem 2, there is a nonnegative number $C_0$, such that $\parallel {\rho }^n{\parallel }_2,\parallel {\sigma }^n{\parallel }_2\le C_0({\tau }^2+{\parallel h\parallel }_2^2)$. This number is independent of $\tau$ and h. This fact will be employed in the proof of the following theorem.

Theorem 4

(Convergence). Let $(U,V)$ be a solution of Equation (4), such that $U,V\in {\mathcal{C}}_{x,t}\left(\overline{{\Omega }_T}\right)$ and $\mathbf{P}\in \mathcal{C}\left(\overline{\Omega }\right)$. If τ is sufficiently small, then the corresponding solution of the finite-difference scheme Equation (16) converges to $(U,V)$ with order $\mathcal{O}({\tau }^2+\parallel h{\parallel }_2^2)$ in the $L_2$-norm.

Proof. 

The proof is analogous to the previous result. Beforehand, let ${ϵ}^n=u^n-U^n$ and ${\zeta }^n=v^n-V^n$, for each $n\in {\overline{I}}_N$. It is clear then that the pair $(ϵ,\zeta )$ satisfies

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{i}{\delta }_t{ϵ}_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_1\right)}+{\mathbf{P}}_j+D\right]{\mu }_t{ϵ}_j^n+P_j^n+\lambda {\mu }_t^{\left(1\right)}{\zeta }_j^n+{\rho }_j^n,\hfill \\ \hfill \mathrm{i}{\delta }_t{\zeta }_j^n& =\left[-\frac{1}{2}{△}_h^{\left({\alpha }_2\right)}+{\mathbf{P}}_j\right]{\mu }_t{\zeta }_j^n+Q_j^n+\lambda {\mu }_t^{\left(1\right)}{ϵ}_j^n+{\sigma }_j^n,\hfill \end{array}\\ \mathrm{such}\mathrm{that}\left\{\begin{array}{cc}{ϵ}_j^0={\mu }_t^{\left(1\right)}{ϵ}_j^0=0,\hfill & \forall j\in \overline{J},\hfill \\ {\zeta }_j^0={\mu }_t^{\left(1\right)}{\zeta }_j^0=0,\hfill & \forall j\in \overline{J},\hfill \\ {ϵ}_j^n={\zeta }_j^n=0,\hfill & \forall (j,n)\in \partial J\times {\overline{I}}_N,\hfill \end{array}\right.\end{array}$$

(59)

where, for each $(j,n)\in J\times I_{N-1}$,

$$\begin{array}{cc}\hfill P_j^n& =\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{u}_j^n\hfill \\ \hfill & -\left[{\beta }_{11}{\left|{\mu }_t^{\left(1\right)}{U}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{V}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{U}_j^n\hfill \end{array}$$

(60)

and

$$\begin{array}{cc}\hfill Q_j^n& =\left[{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{v}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{u}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{v}_j^n\hfill \\ \hfill & -\left[{\beta }_{22}{\left|{\mu }_t^{\left(1\right)}{V}_j^n\right|}^2+{\beta }_{12}{\left|{\mu }_t^{\left(1\right)}{U}_j^n\right|}^2\right]{\mu }_t^{\left(1\right)}{V}_j^n.\hfill \end{array}$$

(61)

Proceeding now as in the proof of Theorem 3, we obtain a nonnegative number $C^{\prime }$, which does not depend on $\tau$ and h, with the property that Equation (53) is satisfied. Applying the same steps used to obtain Equations (54) and (), we may readily obtain the following identities, valid for each $n\in I_{N-1}$:

$$\begin{array}{cc}\hfill {\delta }_t{\parallel {ϵ}^n\parallel }_2^2& =2Im⟨P^n,{\mu }_t{ϵ}^n⟩+2\lambda Im⟨{\mu }_t^{\left(1\right)}{\zeta }^n,{\mu }_t{ϵ}^n⟩+2Im⟨{\rho }^n,\mu {ϵ}^n⟩,\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill {\delta }_t{\parallel {\zeta }^n\parallel }_2^2& =2Im⟨Q^n,{\mu }_t{\zeta }^n⟩+2\lambda Im⟨{\mu }_t^{\left(1\right)}{ϵ}^n,{\mu }_t{\zeta }^n⟩+2Im⟨{\sigma }^n,{\mu }_t{\zeta }^n⟩.\hfill \end{array}$$

(63)

From here, it is possible to check that there are numbers $C_3,C_4\ge 0$ independent of $\tau$ and h, such that

$$\begin{array}{cc}\hfill & \parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\hfill \\ \hfill & \le 2\tau \sum _{n=0}^m\left(Im⟨P^n,{\mu }_t{ϵ}^n⟩+Im⟨Q^n,{\mu }_t{\zeta }^n⟩+Im⟨{\rho }^n,{\mu }_t{ϵ}^n⟩+Im⟨{\sigma }^n,{\mu }_t{\zeta }^n⟩\right)\hfill \\ \hfill & \le (1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)+3\tau \left(C^{″}+\frac{\lambda }{2}\right)\sum _{n=1}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)\hfill \\ \hfill & +\tau (C^{″}+\lambda )(\parallel {ϵ}^{m+1}{\parallel }_2^2+\parallel {\zeta }^{m+1}{\parallel }_2^2)\hfill \\ \hfill & +\frac{\tau }{2}\sum _{n=1}^m\left(2\parallel P^n{\parallel }_2^2+2\parallel Q^n{\parallel }_2^2+\parallel {ϵ}^n{\parallel }_2^2+\parallel {\zeta }^n{\parallel }_2^2+\parallel {ϵ}^{n+1}{\parallel }_2^2+{\parallel {\zeta }^{n+1}\parallel }_2^2\right)\hfill \\ \hfill & \le (1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)+C_3({\tau }^2+{\parallel h\parallel }_2^2{)}^2\hfill \\ \hfill & +C_4\tau \sum _{n=0}^m\left(\parallel {ϵ}^n{\parallel }_2^2+{\parallel {\zeta }^n\parallel }_2^2\right)+\tau (C^{″}+\lambda +\frac{1}{2})\left(\parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\right).\hfill \end{array}$$

(64)

Subtract the term $\tau (C^{″}+\lambda +\frac{1}{2})\left(\parallel {ϵ}^{m+1}{\parallel }_2^2+{\parallel {\zeta }^{m+1}\parallel }_2^2\right)$ from both ends of this series of inequalities. Notice now that Equation (45) is satisfied, for each $m\in I_{N-1}$, letting $C_0=C_4$, and

$$\begin{array}{cc}\hfill {\omega }^m& =\parallel {ϵ}^m{\parallel }_2^2+{\parallel {\zeta }^m\parallel }_2^2,\forall m\in I_{N-1},\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill {\rho }^m& =(1+(C^{″}+\frac{\lambda }{4})\tau )(\parallel {ϵ}^0{\parallel }_2^2+\parallel {\zeta }^0{\parallel }_2^2)+C_3({\tau }^2+{\parallel h\parallel }_2^2{)}^2,\forall m\in {\overline{I}}_N.\hfill \end{array}$$

(66)

Lemma 4 guarantees now that

$$\parallel {ϵ}^n{\parallel }_2^2+\parallel {\zeta }^n{\parallel }_2^2\le C_5({\tau }^2+{\parallel h\parallel }_2^2{)}^2,\forall (j,n)\in J\times {\overline{I}}_N,$$

(67)

where $C_5=C_3{e}^{C_{0}T}$. From this, it follows that $\parallel {ϵ}^n{\parallel }_2,\parallel {\zeta }^n{\parallel }_2\le \sqrt{C_5}({\tau }^2+{\parallel h\parallel }_2^2)$, for each $(j,n)\in J\times {\overline{I}}_N$. The conclusion of this proposition readily follows now.    □

4. Illustrative Simulations

We provide illustrative simulations to show the main properties of Equation (16). In particular, we provide a numerical study of the convergence of the scheme, and we confirm the validity of the conclusion of Theorem 4. The experiments provided in this section make use of the Algorithm provided in Appendix A, which is a MATLAB implementation of Equation (16).

In this section, we consider only the spatially one-dimensional scenario. To that end, let $p=1$. We employ the set of parameters in Table 1. In particular, notice that $\Omega =(-7,7)$. The parameters ${\alpha }_1$ and ${\alpha }_2$ may change values from one simulation to the other, and the function V is defined by $V\left(x\right)=\frac{1}{2}{x}^2$, for each $x\in \Omega$. Finally, the initial data is defined by ${\varphi }_1\left(x\right)={\varphi }_2\left(x\right)=\frac{1}{\sqrt{\pi }}exp(-x^2)$, for each $x\in \Omega$.

Table 1. Table of the parameter values employed in the numerical simulations of this manuscript.

p	${\mathit{a}}_1$	${\mathit{b}}_1$	${\mathit{\beta }}_{11}$	${\mathit{\beta }}_{12}$	${\mathit{\beta }}_{22}$	$\mathit{\lambda }$	D
1	$-7$	7	$1.5$	$0.5$	$1.5$	$0.5$	2

Example 1.

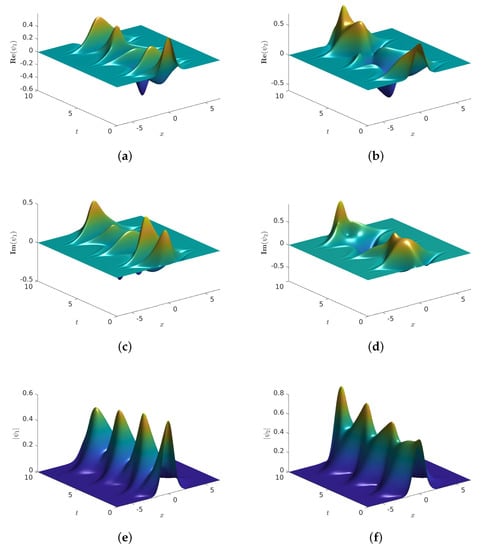
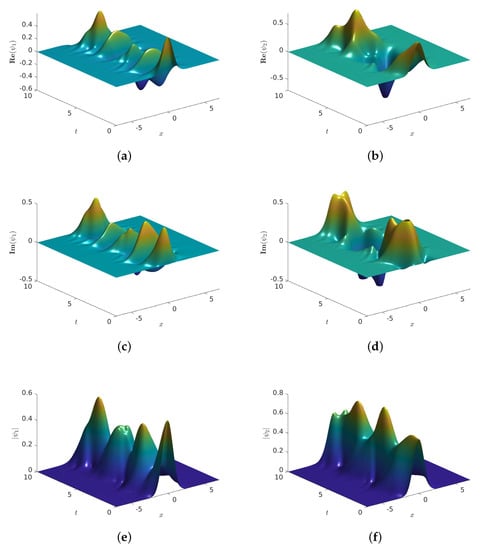
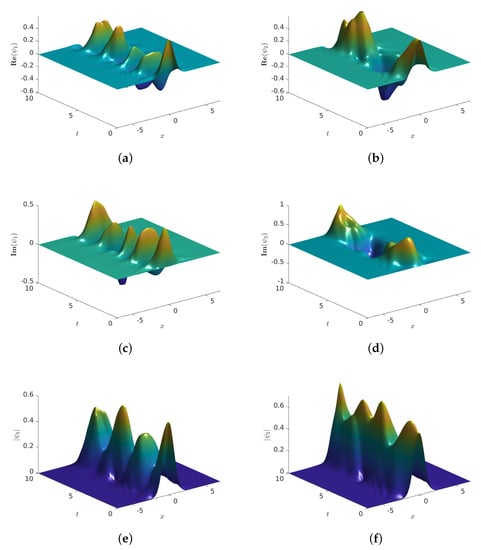
Throughout this example, we let $T=10$ and fix the computer parameters $\tau =0.01$ and $h_1=0.1$. The results of our simulations are provided in Figure 1. In that figure, we provide the graphs of the approximate solutions of the problem Equation (4) as functions of $(x,t)\in \overline{\Omega }\times [0,T]$ using the scheme Equation (16). More precisely, graphs show the numerical solution of the real parts of (a) ${\psi }_1$ and (b) ${\psi }_2$, the imaginary parts of (c) ${\psi }_1$ and ${\psi }_2$, and the absolute values of (e) ${\psi }_1$ and (f) ${\psi }_2$. The graphs show that the scheme is a stable technique. We repeated this experiment using all the parameters as before, and ${\alpha }_1={\alpha }_2=1.5$. The results are provided in Figure 2, and they suggest that the scheme Equation (16) is stable, in agreement with Theorem 3. For illustration purposes, Figure 3 shows the simulations corresponding to ${\alpha }_1={\alpha }_2=1$, and they also support the conclusions of this example.

Figure 1. Numerical approximations to the solutions of Equation (4) versus x and t, using the constants of Table 1. The graphs were obtained using the finite-difference method of Equation (16) with $T=10$, ${\alpha }_1={\alpha }_2=2$, $\tau =0.01$, and $h-1=0.1$. We also let $V\left(x\right)=\frac{1}{2}{x}^2$ and ${\varphi }_1\left(x\right)={\varphi }_2\left(x\right)=\frac{1}{\sqrt{\pi }}exp(-x^2)$, for each $x\in \Omega$. The graphs provide (a) $Re\left({\psi }_1\right)$, (b) $Re\left({\psi }_2\right)$, (c) $Im\left({\psi }_1\right)$, (d) $Im\left({\psi }_2\right)$, (e) $|{\psi }_1|$, and (f) $|{\psi }_2|$.

Figure 2. Numerical approximations to the solutions of Equation (4) versus x and t, using the constants of Table 1. The graphs were obtained using the finite-difference method of Equation (16) with $T=10$, ${\alpha }_1={\alpha }_2=1.5$, $\tau =0.01$ and $h-1=0.1$. We also let $V\left(x\right)=\frac{1}{2}{x}^2$ and ${\varphi }_1\left(x\right)={\varphi }_2\left(x\right)=\frac{1}{\sqrt{\pi }}exp(-x^2)$, for each $x\in \Omega$. The graphs provide (a) $Re\left({\mathrm{\Psi }}_1\right)$, (b) $Re\left({\mathrm{\Psi }}_2\right)$, (c) $Im\left({\mathrm{\Psi }}_1\right)$, (d) $Im\left({\mathrm{\Psi }}_2\right)$, (e) $|{\mathrm{\Psi }}_1|$, and (f) $|{\mathrm{\Psi }}_2|$.

Figure 3. Numerical approximations to the solutions of Equation (4) versus x and t, using the constants of Table 1. The graphs were obtained using the finite-difference method of Equation (16) with $T=10$, ${\alpha }_1={\alpha }_2=1$, $\tau =0.01$ and $h-1=0.1$. We also let $V\left(x\right)=\frac{1}{2}{x}^2$ and ${\varphi }_1\left(x\right)={\varphi }_2\left(x\right)=\frac{1}{\sqrt{\pi }}exp(-x^2)$ for each $x\in \Omega$. The graphs provide (a) $Re\left({\mathrm{\Psi }}_1\right)$, (b) $Re\left({\mathrm{\Psi }}_2\right)$, (c) $Im\left({\mathrm{\Psi }}_1\right)$, (d) $Im\left({\mathrm{\Psi }}_2\right)$, (e) $|{\mathrm{\Psi }}_1|$, and (f) $|{\mathrm{\Psi }}_2|$.

Example 2.

We numerically studied the convergence of the scheme Equation (16), using the parameters in Table 1 along with the functions V, ${\varphi }_1$ and ${\varphi }_2$ defined in the paragraph before Example 1. In the following experiments, we fix $T=0.5$ and ${\alpha }_1={\alpha }_2=1.5$, though similar results have been obtained for other values of these parameters (we did not include them to avoid redundancy). The exact solution of the problem is calculated using $\tau =5\times {10}^{-5}$ and $h=h_1=0.02$. Let $(u,v)$ be the solution of the scheme Equation (16) at the time $t_N$, obtained using the computer parameters τ and h. Under these circumstances, let us define the complex constants ${ϵ}_{\tau ,h}\left(x_j\right)={\psi }_1\left(x_j\right)-u_j^N$, for each $j\in J$. In turn, we define the temporal and spatial convergence rates, respectively, as

$$\begin{array}{cc}\hfill {\rho }_{\tau ,h}& ={log}_2\left(\frac{\parallel {ϵ}_{2\tau ,h}{\parallel }_2}{\parallel {ϵ}_{\tau ,h}{\parallel }_2}\right),\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill {\sigma }_{\tau ,h}& ={log}_2\left(\frac{\parallel {ϵ}_{\tau ,2h}{\parallel }_2}{\parallel {ϵ}_{\tau ,h}{\parallel }_2}\right).\hfill \end{array}$$

(69)

With these conventions, Table 2a,b provides numerical studies of convergence in time and in space, respectively, for the problem described in this example. Various values of τ and h were chosen to that end. However, in any case, the results seem to support that the scheme Equation (16) is quadratically convergent, in agreement with Theorem 4.

Table 2. Absolute errors and the rates of convergence (a) in time and (b) in space. Example 2 describes the experimental setting for these results.

(a) Temporal Study of Convergence.
$\tau$	$0.08$		$h=0.04$		$h=0.02$
	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\rho }_{\tau ,h}$	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\rho }_{\tau ,h}$	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\rho }_{\tau ,h}$
$0.04$	$7.1074\times {10}^{-2}$	−	$1.9124\times {10}^{-2}$	−	$3.9163\times {10}^{-3}$	−
$0.02$	$1.2825\times {10}^{-2}$	$2.4703$	$2.9995\times {10}^{-3}$	$2.6726$	$8.6646\times {10}^{-4}$	$2.1763$
$0.01$	$2.6863\times {10}^{-3}$	$2.2553$	$6.0564\times {10}^{-4}$	$2.3082$	$2.3468\times {10}^{-4}$	$1.8844$
(b) Spatial Study of Convergence.
h	$\tau =0.001$		$\tau =0.0005$		$\tau =0.00025$
	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\sigma }_{\tau ,h}$	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\sigma }_{\tau ,h}$	$\parallel {ϵ}_{t,h}{\parallel }_2$	${\sigma }_{\tau ,h}$
$0.08$	$1.6737\times {10}^{-5}$	−	$3.9923\times {10}^{-6}$	−	$9.3696\times {10}^{-7}$	−
$0.04$	$3.3586\times {10}^{-6}$	$2.3171$	$8.3193\times {10}^{-7}$	$2.2627$	$2.4757\times {10}^{-7}$	$1.9201$
$0.02$	$7.5983\times {10}^{-7}$	$2.1441$	$2.2384\times {10}^{-7}$	$1.8940$	$6.8871\times {10}^{-8}$	$1.8459$

5. Conclusions

We proposed a three-level discrete model to solve a double-fractional coupled Bose–Einstein system considering Riesz spatial fractional operators along with two different orders of differentiation. The system is a fractional generalization of the two-component Gross–Pitaevskii system investigated in physics. The solutions of the continuous system are complex; therefore, the computational complexity for solving the system is a shortcoming to be considered.

To alleviate this problem, a three-level scheme was designed to solve our continuous model. This scheme is linear and explicit, which implies that the computational implementation is relatively easy to propose. Indeed, a numerical algorithm to solve this system is presented in the appendix of this work. The code is provided in MATLAB for the sake of convenience, and the nomenclature used to describe it follows that of the theoretical description.

In this manuscript, we proved the existence and uniqueness of the solutions using arguments of linear algebra. We also established that the algorithm is spatially and temporally quadratically consistent. We proved that the finite-difference scheme is spatially and temporally quadratically convergent to the solution of the differential problem. Computational simulations are presented in this work to illustrate this fact.