Finite-Time Projective Synchronization of Caputo Type Fractional Complex-Valued Delayed Neural Networks

Abstract

This paper focuses on investigating the finite-time projective synchronization of Caputo type fractional-order complex-valued neural networks with time delay (FOCVNNTD). Based on the properties of fractional calculus and various inequality techniques, by constructing suitable the Lyapunov function and designing two new types controllers, i.e., feedback controller and adaptive controller, two sufficient criteria are derived to ensure the projective finite-time synchronization between drive and response systems, and the synchronization time can effectively be estimated. Finally, two numerical examples are presented to verify the effectiveness and feasibility of the proposed results.

1. Introduction

As a branch of mathematical analysis, fractional calculus mainly deals with differential or integration of arbitrary non-integer order. Fractional calculus is especially suitable for describing the physical change process with memory property and historical dependence, and most of the research objects in the actual system have such properties, which are also main advantages. Compared with the integer-order derivative model, their differences are mainly reflected in the following aspects: in time, the integer-order differential equation represents a change or a certain property of a physical or mechanical process at a certain moment, which cannot describe the memory characteristics of neurons, while the fractional derivative contains all the information from the start time to the present time, so that it can describe the memory property of neurons more truly. With the deepening of the theoretical research of fractional calculus, fractional calculus has been widely used in various fields.

Recently, researchers have found that it was excellent to introduce fractional calculus theory into the research of neural networks. Since fractional calculus has infinite memory, some scholars have turned it into neural networks and established fractional-order neural network models, it can better describe the dynamic behaviors of neurons. Since there are many types of input variables, state variables, activation functions, and connection weights, neural networks can be divided into two categories: real-valued neural networks (RVNNs) and complex-valued neural networks (CVNNs). However, the CVNNs completes the information processing in the complex number domain, which is still very different from the RVNNs. It should be pointed that CVNNs has advantage in solving some difficult real-world problems [1,2,3,4,5,6].

As a typical phenomenon, synchronization is widely concerned because of its application in signal processing [7], image encryption [8], and pattern recognition [9]. So far, several types of synchronization have been studied, such as complete synchronization [10], lag projective synchronization [11], antisynchronization [12], quasiuniform synchronization [13], projective synchronization [14], global asymptotical synchronization [15], and global Mittag-Leffler synchronization [16,17]. Compared with the above synchronization types, projective synchronization can achieve faster communication due to its proportional characteristics. Recently, in order to realize the synchronization of two chaotic systems, many synchronization strategies have been designed, including adaptive control [18,19], pulse control [20], intermittent control [21], and feedback control [22,23]. It shows that an appropriate controller can synchronize the response system with the drive system at an infinite level. Self-adaptation is a feature that the research object can change its own habits to adapt to the new environment. Adaptive control is an unpredictable change of the system, which can make the system adjust its own characteristics according to the environmental changes to achieve the desired optimal state. According to the obtained process information and a certain design method, the adaptive control system makes control decisions to modify the structure, parameters or control function of the controller, so that the control effect is optimal or approximately better.

Based on the above discussion, under the premise that the complex-valued system is regarded as a whole, this paper mainly studies the finite-time projective synchronization problem of a class of FOCVNNTD. Firstly, based on the finite-time projective synchronization theory, two different types of controllers are introduced. Then by constructing the Lyapunov function, using feedback controller and adaptive controller, some new sufficient conditions for the finite-time projective synchronization of the considered FOCVNNTD are given. Furthermore, the synchronization time is effectively estimated, which is related to the order of the fractional derivative and the control parameters. Finally, the theoretical results in this thesis are verified by numerical simulations.

The main structure of this thesis: In the Section 2, the definition of fractional derivative and several important lemmas are presented. In the Section 3, by using a feedback controller and adaptive controller, some different synchronization criteria are established. The fourth part gives numerical exercises to demonstrate the effectiveness and applicability of the obtained results. Finally, the direction of future work is pointed out.

2. Preliminaries and Model Description

In this section, we first review some basic knowledge about the fractional calculus. Then several key lemmas and requisite assumptions are introduced for the following discussion. Finally, we establish a FOCVNNTD model.

Definition 1

([24]). The Caputo fractional derivative of order $\mu$ for a function $h\left(t\right)\in C^{n+1}(\left[0,+\infty \right),R)$ is defined as:

$${}_{t_0}D{}_t^{\mu }h(t)=\frac{1}{\Gamma (n-\mu )}{{\displaystyle {\int }_{t_0}^t(t-\tau )}}^{n-\mu -1}{h}^{(n)}(\tau )d\tau ,$$

and $t>t_0$, $n-1<\mu <n\in Z^{+}$, $\Gamma (\cdot )$ is the Gamma function, where

$$\Gamma (\mu )={\displaystyle {\int }_0^{\infty }{t}^{\mu -1}}{e}^{-t}dt.$$

Particularly, when$0<\mu <1$,

$${}_{t_0}D{{}_t}^{\mu }h(t)=\frac{1}{\Gamma (1-\mu )}{\displaystyle {\int }_{t_0}^t{(t-\tau )}^{-\alpha }{h}^{\prime }(\tau )d\tau }$$

Lemma 1

([25]). Let $h(t)\in C^n[0,+\infty )$, ${}_{0}D{}_t^{-\mu }h(t)$ is the Riemann–Liouville fractional integral, where $n-1<\mu ,\nu <n\in Z^{+}$,

(1) 

${}_{0}D{}_t^{-\mu }{}_{0}D{}_t^{-\nu }h(t)={}_{0}D{}_t^{-(\mu +\nu )}h(t)$, $\mu ,\nu \ge 0$;

(2) 

${}_{0}D{}_t^{-\mu }{}_{0}D{}_t^{-\nu }h(t)$, $\mu =\nu \ge 0$;

(3) 

${}_{0}D{}_t^{-\mu }{}_{0}D{}_t^{\nu }h(t)=h(t)-{\displaystyle {\sum }_{k=0}^{n-1}\frac{t^k}{k!}}{h}^{(k)}(0)$, $\mu =\nu \ge 0$.

Lemma 2

([26]). Let $h(t)\in C^n[0,+\infty )$ is continuous and analytic function, the following inequality holds:

$${}_{t_0}{}^{C}D{}_t^{\mu }h(t)\overline{h(t)}\le h(t){}_{t_0}{}^{C}D{}_t^{\mu }\overline{h(t)}+\overline{h(t)}{}_{t_0}{}^{C}D{}_t^{\mu }h(t),$$

(1)

and $t\ge t_0$, $0<\mu <1$.

Lemma 3

([27]). If $x$ and $y$ are any two complex numbers, and for any real constant $\rho$, then the inequality is established as follows:

$$x\overline{y}+\overline{x}y\le \rho x\overline{x}+\frac{1}{\rho }y\overline{y}.$$

(2)

Lemma 4

([28]). Suppose that function $h(t)\in C^n[0,+\infty )$ is continuous and differentiable on  $t\in \left[t_0,\infty \right)$, then for any real constant $\omega$, it has

$${}_{t_0}{}^{C}D{}_t^{\mu }{(h(t)-\omega )}^2\le 2(h(t)-\omega ){}_{t_0}{}^{C}D{}_t^{\mu }h(t).$$

(3)

Lemma 5

([29]). Let $m\in {\rm N}$, $x_1,x_2,\cdots ,x_m$ are non-negative real numbers, then for  $m>1$,

$${\left({\displaystyle \sum _{k=1}^n{x}_k}\right)}^m\le n^{m-1}{\displaystyle \sum _{k=1}^n{x}_k^m}.$$

(4)

Lemma 6

([30]). Assume that function $H(t)$ is continuous, positive-definite, and satisfies the following inequality,

$${}_{t_0}{}^{C}D{}_t^{\mu }H(t)\le -d{H}^{\gamma }(t),$$

(5)

where $d>0$, $0<\gamma <\mu$ and all of them are constants. Then $H(t)$ satisfies the inequality as follows:

$$H^{\mu -\gamma }(t)\le H^{\mu -\gamma }(t_0)-\frac{d\Gamma (1+\mu -\gamma ){(t-t_0)}^{\mu }}{\Gamma (1+\mu )\Gamma (1-\gamma )},t_0\le t\le t_1,$$

(6)

and $\underset{t\to \infty }{\lim }H(t)=0$, for all $t\ge T$, here $T$ is expressed by

$$T=t_0+{(\frac{\Gamma (1+\mu )\Gamma (1-\gamma )H^{\mu -\gamma }(t_0)}{d\Gamma (1+\mu -\gamma )})}^{\frac{1}{\mu }}.$$

(7)

Consider a class of FOCVNNTD as the drive system:

$$\{\begin{array}{l}{D}^{\mu }{x}_k(t)=-c_k{x}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{f}_j}(x_j(t))+{\displaystyle \sum _{j=1}^n{b}_{kj}{g}_j}(x_j(t-\tau ))+I_k\\ x_k(s)={\phi }_k(s),s\in \left[t_0-\tau ,t_0\right]\end{array},$$

(8)

where $D^{\mu }$ is the Caputo derivative, $k,j\in N=(1,2,\cdots ,n)$, $0<\mu <1$, $n$ corresponds to the number of units; $x_k(t)\in C$ denotes the state variable of the drives system in time $t$, $f_j(\cdot ),g_j(\cdot )\in C\to C$ represent the activation function without time delay and with time delay, respectively. $a_{kj},b_{kj}\in C$ stand for the connection weight and the delay connection weight, respectively, $c_k>0$ is the self-regulating parameters; $\tau >0$ is time delay; and $I_k$ denotes the external input. ${\phi }_k(t)$ is real-valued continuous function on $[-\tau ,0]$, its norm is given by $\Vert \phi \Vert =\underset{t\in \left[-\tau ,0\right]}{\sup }{\displaystyle \sum _{k=1}^n\left|{\phi }_k(t)\right|}$.

In order to study the finite-time projective synchronization of the FOCVNNTD, the corresponding response system is defined by:

$$\{\begin{array}{l}{D}^{\mu }{y}_k(t)=-c_k{y}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{f}_j}(y_j(t))+{\displaystyle \sum _{j=1}^n{b}_{kj}{g}_j}(y_j(t-\tau ))+I_k+u_k(t)\\ y_k(s)={\varphi }_k(s),s\in \left[t_0-\tau ,t_0\right]\end{array},$$

(9)

$y_k(t)$ is the state variable of the response system and $u_k(t)$ denotes appropriate controller. For the sake of the main results can be obtained, an assumption is given below:

Assumption 1.

Assume that$f(\cdot )$and$g(\cdot )$satisfy the Lipschitz condition, for any$x,y\in R$, there exists two real number$F_j$and$G_j$$(j=1,2,\cdots ,n)$, such that$\left|f_j(x)-f_j(y)\right|\le F_j\left|x-y\right|$,$\left|g_j(x)-g_j(y)\right|\le G_j\left|x-y\right|$.

Definition 2

([31]). Under the appropriate controller, there exist numbers $\{t_0,J,\delta ,\epsilon \}$, $\delta <\epsilon$, if and only if, for $\forall t\in J=[t_0,t_0+T]$, there exists a small error bound $\epsilon >0$ such that $\Vert \mathit{e}(t)\Vert <\epsilon$, then the drive system (8) and the response system (9) can realize finite-time projective synchronization, where $t_0$ is the initial observation time.

3. Results

In this section, we will discuss the finite-time projective synchronization of FOCVNNTD by designing feedback controller and adaptive controller. Define the error system $e_k(t)=y_k(t)-\beta x_k(t)$ between drive system (8) and response system (9), where $\beta$ is the projective coefficient. Then

$$\begin{gathered} D^{\mu }{e}_k(t)=-c_k{e}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}}\left[f_j(y_j(t))-\beta f_j(x_j(t))\right] \\ +{\displaystyle \sum _{j=1}^n{b}_{kj}}\left[g_j(y_j(t-\tau ))-\beta f_j(x_j(t-\tau ))\right]+(1-\beta )I_k+u_k(t) \end{gathered}$$

(10)

3.1. Finite-Time Projective Synchronization with Feedback Controller

To achieve the finite-time projective synchronization between drive system (8) and response system (9), select the feedback controller as follows:

$$\{\begin{array}{l}{u}_k(t)={\pi }_k(t)+w_k(t)\\ {\pi }_k(t)={\displaystyle \sum _{j=1}^n{a}_{kj}}\left[\beta f_j(x_j(t))-f_j(\beta x_j(t))\right]\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}+{\displaystyle \sum _{j=1}^n{b}_{kj}}\left[\beta g_j(x_j(t-\tau ))-f_j(\beta x_j(t-\tau ))\right]+(\beta -1)I_k\\ w_k(t)=-{\eta }_k{e}_k(t)-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}\end{array}$$

(11)

where $q\in (1-\mu ,1)$, ${\eta }_k,{\gamma }_k\in C$, ${\eta }_k^R$, and ${\lambda }_k^R$ are all real numbers.

Theorem 1.

On the premise of assumption 1 and the feedback controller (11), if the following conditions hold

$$P>n\zeta ,\zeta >1,$$

(12)

then drive system (8) and response system (9) can achieve the finite-time projective synchronization, where

$$P=\underset{1\le k\le n}{\min }\left[\left(c_k+{\overline{c}}_k+{\eta }_k+{\overline{\eta }}_k\right)-{\displaystyle \sum _{j=1}^n(a_{kj}{\overline{a}}_{kj}{F}_j{\overline{F}}_j+b_{kj}{\overline{b}}_{kj}{G}_j{\overline{G}}_j)}-n\right].$$

Proof of Theorem 1.

Based on the feedback controller (11), by using Lipschtz condition, one has

$$\begin{gathered} \begin{array}{l}{D}^{\mu }{e}_k(t)=-(c_k+{\eta }_k)e_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}}\left[f_j(y_j(t))-f_j(\beta x_j(t))\right]\\ \begin{array}{cccc}& & & +{\displaystyle \sum _{j=1}^n{b}_{kj}}\left[g_j(y_j(t-\tau ))-g_j(\beta x_j(t-\tau ))\right]-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}\end{array}\end{array} \\ \le -(c_k+{\eta }_k)e_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{F}_j}{e}_j(t)+{\displaystyle \sum _{j=1}^n{b}_{kj}{G}_j}{e}_j(t-\tau )-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}, \end{gathered}$$

(13)

The Lyapunov function is chosen as follows:

$$V_1(t)={\displaystyle \sum _{k=1}^n{e}_k(t)}\overline{e_k(t)}.$$

Using Lemmas 1–5, according to Equation (10), we obtain

$$\begin{gathered} \begin{array}{l}{D}^{\mu }{V}_1(t)\le {\displaystyle \sum _{k=1}^n(e_k(t)D^{\mu }\overline{e_k(t)}+\overline{e_k(t)}{D}^{\mu }{e}_k(t))}\\ ={\displaystyle \sum _{k=1}^n[-\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)}{e}_k(t)\overline{e_k(t)}+{\displaystyle \sum _{j=1}^n(a_{kj}{F}_j\overline{e_k(t)}{e}_j(t)+\overline{a_{kj}}\overline{F_j}{e}_k(t)\overline{e_j(t)})}\\ \begin{array}{ccc}& & +{\displaystyle \sum _{j=1}^n(b_{kj}{G}_j\overline{e_k(t)}{e}_j(t-\tau )+\overline{b_{kj}}\overline{G_j}{e}_k(t)\overline{e_j(t-\tau )})}-({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}]\end{array}\end{array} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n[e_k(t)\cdot (-({\overline{c}}_k+{\overline{\eta }}_k)\overline{e_k(t)}+{\displaystyle \sum _{j=1}^n{\overline{a}}_{kj}{\overline{F}}_j}\overline{e_j(t)}+{\displaystyle \sum _{j=1}^n{\overline{b}}_{kj}\overline{G_j}}\overline{e_j(t-\tau )}-\frac{\overline{{\lambda }_k}\cdot \overline{e_k(t)}}{{(e_k(t)\overline{e_k(t)})}^q})}\\ \begin{array}{cc}& \begin{array}{cc}& +\overline{e_k(t)}(-(c_k+{\eta }_k)e_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{F}_j}{e}_j(t)+{\displaystyle \sum _{j=1}^n{b}_{kj}{G}_j}{e}_j(t-\tau )-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q})]\end{array}\end{array}\end{array} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n[-\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)}{e}_k(t)\overline{e_k(t)}+{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}{e}_k(t)\overline{e_k(t)}+e_j(t)\overline{e_j(t)})}\\ \begin{array}{ccc}& & +{\displaystyle \sum _{j=1}^n(b_{kj}\overline{b_{kj}}{G}_j\overline{G_j}{e}_k(t)\overline{e_k(t)}+e_j(t-\tau )\overline{e_j(t-\tau )})}-({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}]\end{array}\end{array} \\ \begin{array}{l}=-{\displaystyle \sum _{k=1}^n\left[\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +{\displaystyle \sum _{k,j=1}^n(e_j(t)\overline{e_j(t)}+e_j(t-\tau )\overline{e_j(t-\tau )})}-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}\end{array}\end{array} \\ \begin{array}{l}\le -{\displaystyle \sum _{k=1}^n\left[\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +n{\displaystyle \sum _{k=1}^n(e_k(t)\overline{e_k(t)}+e_k(t-\tau )\overline{e_k(t-\tau )})}-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}\end{array}\end{array} \\ \begin{array}{l}=-{\displaystyle \sum _{k=1}^n\left[\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +n{\displaystyle \sum _{k=1}^n{e}_k(t-\tau )\overline{e_k(t-\tau )}}-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}\end{array}\end{array} \\ \le -P{V}_1(t)+n{V}_1(t-\tau )-d{V}_1^{1-q}(t) \\ \le -(P-n\zeta )V_1(t)-d{V}_1^{1-q}(t) \end{gathered}$$

for $\zeta >1$, $d=\underset{1\le k\le n}{\min }({\lambda }_k+\overline{{\lambda }_k})$, if $P>n\zeta$,

$$P=\underset{1\le k\le n}{\min }\left[\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right],$$

according to Lemma 6, one can get

$$D^{\mu }{V}_1(t)\le -d{V}_1^{1-q}(t),$$

then

$$V_1^{(\mu +q-1)}(t)\le V_1^{(\mu +q-1)}(0)-\frac{d\Gamma (\mu +q)t^{\mu }}{\Gamma (1+\mu )\Gamma (q)},0\le t\le t_1$$

for $t\ge t_1$, we have $V(t)=0$, here $t_1$ can be estimated by

$$t_1={(\frac{\Gamma (1+\mu )\Gamma (q)V_1^{\mu +q-1}(0)}{d\Gamma (\mu +q)})}^{\frac{1}{\mu }}.$$

So when $t\ge t_1$, we have $\underset{t\to \infty }{\lim }\Vert e_k(t)\Vert =0$, then system (8) and system (9) will reach the finite-time projective synchronization under the feedback controller (11).  □

3.2. Finite-Time Projective Synchronization with Adaptive Controller

To achieve the finite-time projective synchronization between the drive system (8) and response system (9), we can design the following adaptive controller

$$\{\begin{array}{l}{u}_k(t)={\pi }_k(t)+{\nu }_k(t)\\ {\pi }_k(t)={\displaystyle \sum _{j=1}^n{a}_{kj}}\left[\beta f_j(x_j(t))-f_j(\beta x_j(t))\right]\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}+{\displaystyle \sum _{j=1}^n{b}_{kj}}\left[\beta g_j(x_j(t-\tau ))-f_j(\beta x_j(t-\tau ))\right]+(\beta -1)I_k\\ {\nu }_k(t)=-{\eta }_k(t)e_k(t)-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}\end{array},$$

(14)

where

$$\mu \in (\frac{1}{2},1),q\in (1-\mu ,\frac{1}{2}),D^{\mu }{\eta }_k(t)=e_k(t)\overline{e_k(t)}-{\sigma }_k\mathrm{sign}({\eta }_k(t)-{\tilde{\eta }}_k){\left|{\eta }_k(t)-{\overline{\eta }}_k\right|}^{1-2q}.$$

In the controller (14), ${\eta }_k(t)$ is determined by the input, state, output or performance parameters of the system.

Theorem 2.

On the premise of assumption 1 and the adaptive controller (14), if the following conditions are satisfied

$$Q>n{\zeta }^{\prime },{\zeta }^{\prime }>1,$$

(15)

then the finite-time projective synchronization between the system (8) and the system (9) will be completed, where

$$Q=\underset{1\le k\le n}{\min }\left[\left(c_k+{\overline{c}}_k+2{\tilde{\eta }}_k\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right].$$

Proof of Theorem 2.

Based on the adaptive controller (14) and Lipschtz condition, we have

$$\begin{gathered} \begin{array}{l}{D}^{\mu }{e}_k(t)=-c_k{e}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}}\left[f_j(y_j(t))-f_j(\beta x_j(t))\right]\\ \begin{array}{cccc}& & & +{\displaystyle \sum _{j=1}^n{b}_{kj}}\left[g_j(y_j(t-\tau ))-g_j(\beta x_j(t-\tau ))\right]-{\eta }_k(t)e_k(t)-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}\end{array}\end{array} \\ \le -c_k{e}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{F}_j}{e}_j(t)+{\displaystyle \sum _{j=1}^n{b}_{kj}{G}_j}{e}_j(t-\tau )-{\eta }_k(t)e_k(t)-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q}, \end{gathered}$$

(16)

Then, we choose the following Lyapunov function:

$$V_2(t)={\displaystyle \sum _{k=1}^n{e}_k(t)}\overline{e_k(t)}+{\displaystyle \sum _{k=1}^n{({\eta }_k(t)-{\tilde{\eta }}_k)}^2}.$$

By using Lemmas 2–5, Equation (16) can be obtained as follows:

$$\begin{gathered} D^{\mu }{V}_2(t)\le {\displaystyle \sum _{k=1}^n(e_k(t)D^{\mu }\overline{e_k(t)}+\overline{e_k(t)}{D}^{\mu }{e}_k(t))}+D^{\mu }{\displaystyle \sum _{k=1}^n{({\eta }_k(t)-{\tilde{\eta }}_k)}^2} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n[\overline{e_k(t)}(-c_k{e}_k(t)+{\displaystyle \sum _{j=1}^n{a}_{kj}{F}_j}{e}_j(t)+{\displaystyle \sum _{j=1}^n{b}_{kj}{G}_j}{e}_j(t-\tau )-{\eta }_k(t)e_k(t)-\frac{{\lambda }_k{e}_k(t)}{{(e_k(t)\overline{e_k(t)})}^q})}\\ \begin{array}{ccc}& & +e_k(t)(-\overline{c_k}\overline{e_k(t)}+{\displaystyle \sum _{j=1}^n\overline{a_{kj}}\overline{F_j}}\overline{e_j(t)}+{\displaystyle \sum _{j=1}^n\overline{b_{kj}}\overline{G_j}}\overline{e_j(t-\tau )}-\overline{{\eta }_k(t)}\overline{e_k(t)}-\frac{\overline{{\lambda }_k}\overline{e_k(t)}}{{(e_k(t)\overline{e_k(t)})}^q})]\end{array}\\ \begin{array}{ccc}& & +2{\displaystyle \sum _{k=1}^n({\eta }_k(t)-{\tilde{\eta }}_k)D^{\mu }{\eta }_k(t)}\end{array}\end{array} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n\left[-({\mathrm{c}}_k+\overline{c_k})+{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-({\eta }_k(t)+\overline{{\eta }_k(t)})\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +{\displaystyle \sum _{k,j=1}^n(e_j(t)\overline{e_j(t)}}+e_j(t-\tau )\overline{e_j(t-\tau )})-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}\end{array}\\ \begin{array}{ccc}& & +2{\displaystyle \sum _{k=1}^n({\eta }_k(t)-{\tilde{\eta }}_k)\left[e_k(t)\overline{e_k(t)}-{\sigma }_{k}sign({\eta }_k(t)-{\tilde{\eta }}_k){\left|{\eta }_k(t)-{\tilde{\eta }}_k\right|}^{1-2q}\right]}\end{array}\end{array} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n\left[-(c_k+\overline{c_k})+{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-({\eta }_k(t)+\overline{{\eta }_k(t)})\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +n{\displaystyle \sum _{k=1}^n(e_k(t)\overline{e_k(t)}}+e_k(t-\tau )\overline{e_k(t-\tau )})-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}\end{array}\\ \begin{array}{ccc}& & +2{\displaystyle \sum _{k=1}^n({\eta }_k(t)-{\tilde{\eta }}_k)\left[e_k(t)\overline{e_k(t)}-{\sigma }_{k}sign({\eta }_k(t)-{\tilde{\eta }}_k){\left|{\eta }_k(t)-{\tilde{\eta }}_k\right|}^{1-2q}\right]}\end{array}\end{array} \\ \begin{array}{l}\le {\displaystyle \sum _{k=1}^n\left[-(c_k+{\overline{c}}_k+2{\tilde{\eta }}_k)+{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}+n\right]}{e}_k(t)\overline{e_k(t)}\\ \begin{array}{ccc}& & +n{\displaystyle \sum _{k=1}^n{e}_k(t-\tau )\overline{e_k(t-\tau )}}-{\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}-2{\displaystyle \sum _{k=1}^n{\sigma }_k{({({\eta }_k(t)-{\tilde{\eta }}_k)}^2)}^{1-q}}\end{array}.\end{array} \end{gathered}$$

By utilizing Lemma 5, one can get

$$\begin{gathered} {\displaystyle \sum _{k=1}^n({\lambda }_k+\overline{{\lambda }_k}){(e_k(t)\overline{e_k(t)})}^{1-q}}+2{\displaystyle \sum _{k=1}^n{\sigma }_k{({({\eta }_k(t)-{\tilde{\eta }}_k)}^2)}^{1-q}} \\ \ge \underset{1\le k\le n}{\min }\left\{({\lambda }_i+{\overline{\lambda }}_k),2{\sigma }_k\right\}\cdot \left[{\displaystyle \sum _{k=1}^n{(e_k(t)\overline{e_k(t)})}^{1-q}}+{\displaystyle \sum _{k=1}^n{({({\eta }_k(t)-{\tilde{\eta }}_k)}^2)}^{1-q}}\right] \\ \ge \tilde{d}\left[{\displaystyle \sum _{k=1}^n{(e_k(t)\overline{e_k(t)})}^{1-q}}+{\displaystyle \sum _{k=1}^n{({({\eta }_k(t)-{\tilde{\eta }}_k)}^2)}^{1-q}}\right] \\ \ge \tilde{d}{\left[{\displaystyle \sum _{k=1}^n{e}_k(t)\overline{e_k(t)}}+{\displaystyle \sum _{k=1}^n{({\eta }_k(t)-\widetilde{{\eta }_k})}^2}\right]}^{1-q} \\ =\tilde{d}{V}_2^{1-q}(t). \end{gathered}$$

(17)

In summary, we can deduce

$$D^{\mu }{V}_2(t)\le -Q{V}_1(t)+n{V}_1(t-\tau )-\tilde{d}{V}_2^{1-q}(t)\le -(Q-n{\zeta }^{\prime })V_1(t)-\tilde{d}{V}_2^{1-q}(t),$$

(18)

for ${\zeta }^{\prime }>1$, $\tilde{d}=\underset{1\le k\le n}{\min }\left\{({\lambda }_k+{\overline{\lambda }}_k),2{\sigma }_k\right\}$, if $Q>n{\zeta }^{\prime }$, where

$$Q=\underset{1\le k\le n}{\min }\left[\left(c_k+{\overline{c}}_k+2{\tilde{\eta }}_k\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right],$$

according to Lemma 6, we have

$$D^{\mu }{V}_2(t)\le -\tilde{d}{V}_2^{1-q}(t),$$

then

$$V_2^{(\mu +q-1)}(t)\le V_2^{(\mu +q-1)}(0)-\frac{\tilde{d}\Gamma (\mu +q)t^{\mu }}{\Gamma (1+\mu )\Gamma (q)},0\le t\le t_2,$$

for $t\ge t_2$, $V_2(t)=0$, here $t_2$ can be estimated by

$$t_2={(\frac{\Gamma (1+\mu )\Gamma (q)V_2^{\mu +q-1}(0)}{\tilde{d}\Gamma (\mu +q)})}^{\frac{1}{\mu }}.$$

when $t\ge t_2$, we get $\underset{t\to \infty }{\lim }\Vert e_k(t)\Vert =0$, then system (8) and system (9) will achieve the finite-time projective synchronization under the adaptive controller (14).  □

Remark 1.

If the projective coefficient$\beta =1$, system (8) and system (9) become complete synchronization.

Remark 2.

In the existing literature, the finite-time projective synchronization problems of FOCVNNTD in the complex field have not been investigated, and only the finite-time projective synchronization of fractional-order real-valued systems was considered in [32].

Remark 3.

In [14], through the simple feedback controller and adaptive controller, the quasi-projective synchronization and complete synchronization of FOCVNNTD are considered. In [33], in the light of the graph theory method, the criteria for ensuring finite-time synchronization of fractional-order complex-valued coupled systems are obtained. Compared with [33], this paper has designed two new types of feedback controller (11) and adaptive controller (14) to realize the finite-time projective synchronization of FOCVNNs.

Remark 4.

Linear feedback controller can restrain the influence of internal characteristics and external disturbances. However, the parameters of the controller are fixed, when the internal characteristics of the system change or the external disturbances change greatly, the performance of the system is often greatly reduced or even unstable. Therefore, it is appropriate to adopt adaptive controller for a class of systems whose object characteristics or disturbance characteristics vary widely, moreover, it is required to keep high performance indexes.

4. Numerical Simulations

In this section, there are two numerical simulations are be given to verify the effectiveness and feasibility of the obtained results. The FOCVNNTD are considered as the drive system, the form is as follows:

$$D^{\mu }{x}_k(t)=-c_k{x}_k(t)+{\displaystyle \sum _{j=1}^2{a}_{kj}{f}_j}(x_j(t))+{\displaystyle \sum _{j=1}^2{b}_{kj}{g}_j}(x_j(t-\tau ))+I_k,k=1,2,$$

(19)

where $\mu =0.7$, $x_j(t)=z_j(t)+i{\widehat{z}}_j(t)$, $\tau =1$, $I(t)={(I_1(t),I_2(t))}^T=(0,0)$.

$$\begin{gathered} f_j(x_j)=\frac{1-e^{-z_j}}{1+e^{-z_j}}+i\frac{1}{1+e^{-{\widehat{z}}_j}},g_j(x_j)=\frac{1-e^{-{\widehat{z}}_j}}{1+e^{-{\widehat{z}}_j}}+i\frac{1}{1+e^{-z_j}}. \\ A={(a_{kj})}_{2\times 2}=\left(\begin{array}{cc}3+3i& -0.2-0.2i\\ -2-2i& 1+i\end{array}\right), \\ C=\mathrm{diag}(c_1,c_2)=(1+i,1+i), \\ B={(b_{kj})}_{2\times 2}=\left(\begin{array}{cc}-0.2-0.2i& -1.5-1.5i\\ -0.5-0.5i& 0.3+0.3i\end{array}\right). \end{gathered}$$

The response system is given by:

$$D^{\mu }{y}_k(t)=-c_k{y}_k(t)+{\displaystyle \sum _{j=1}^2{a}_{kj}{f}_j}(y_j(t))+{\displaystyle \sum _{j=1}^2{b}_{kj}{g}_j}(y_j(t-\tau ))+I_k+u_k(t),k=1,2.$$

(20)

For $s\in \left[-1,0\right]$, take the initial conditions

$$\begin{gathered} x(s)=(x_1(s),x_2(s))=(-0.1+0.2i,1+0.3i), \\ y(s)=(y_1(s),y_2(s))=(0.8+0.5i,0.9-0.6i). \end{gathered}$$

For convenience of calculation, choose $F_j=G_j=\sqrt{2}$.

Figure 1 shows the phase trajectories of the real and imaginary parts of the error system (10).

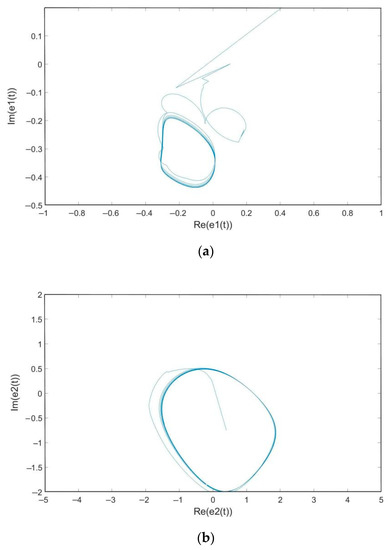
Figure 1. (a) The phase trajectories of real and imaginary part of system (10). (b) The phase trajectories of real and imaginary part of system (10).

Example 1.

In order to realize the finite-time projective synchronization of the drive system (19) and the response system (20), the system (11) is designed as a linear feedback controller, where

$$\begin{gathered} q=0.1,take{\eta }_1=30+30i,{\eta }_2=35+35i,\zeta =1.5, \\ \lambda =({\lambda }_1,{\lambda }_2)=(2.5+2.5i,3+3i). \end{gathered}$$

By simple calculation,

$$P=\underset{1\le k\le 2}{\min }\left[\left(c_k+\overline{c_k}+{\eta }_k+\overline{{\eta }_k}\right)-{\displaystyle \sum _{j=1}^2(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right]=14.68,$$

$n\zeta =3<P$. Therefore, the conditions and assumptions are satisfied in Theorem 1, and the obtained settling timeis $t_1\approx 1.1678$.

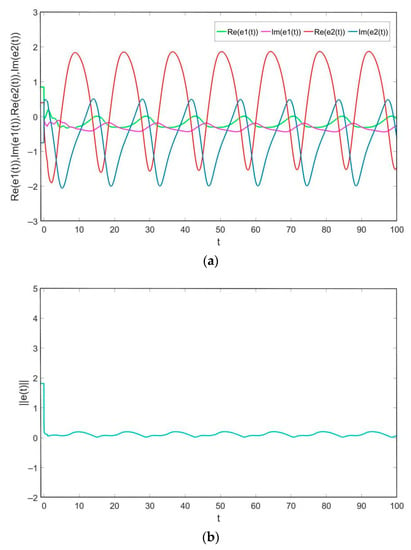
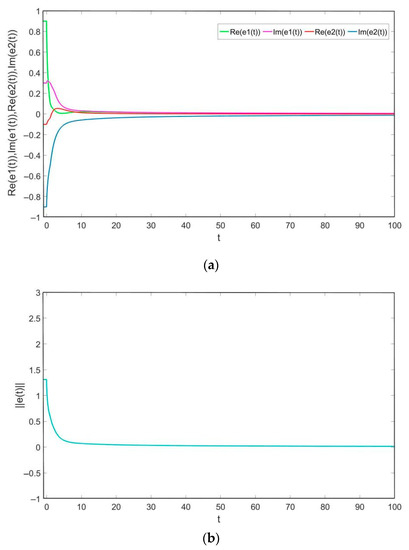
The state trajectories of the real and imaginary parts of the error system (10) and error norm trajectory curve are depicted in Figure 2 when $\beta =0.6+0.5i$, which shows that the system (19) and the system (20) can reach the finite-timeprojective synchronization under the feedback controller(11). Figure 3 displays the state trajectories of the real and imaginary parts of the error system (10) and error norm trajectory curve when $\beta =1$, which shows that the system (19) and the system (20) will accomplish the complete synchronization under the feedback controller(11).

Figure 2. (a) The state trajectory of the error system when $\beta =0.6+0.5i$. (b) The trajectory of the error norm $\beta =0.6+0.5i$.

Figure 3. (a) The state trajectory of the error system when $\beta =1$. (b). The trajectory of the error norm $\beta =1$.

Example 2.

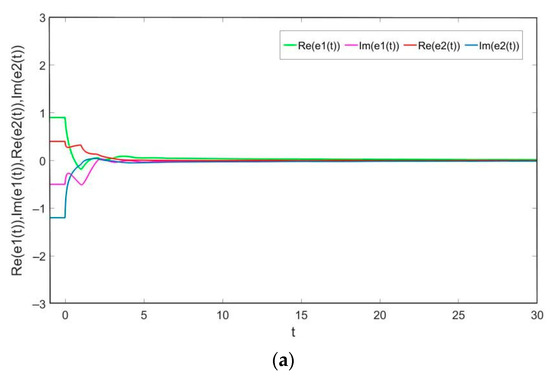
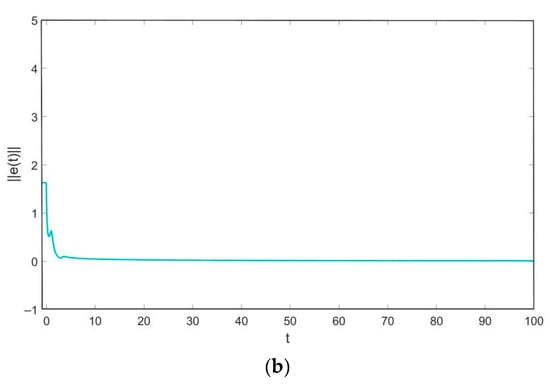
In order to realize the finite-time projective synchronization of the system (19) and the system (20), the system (14) is built as an adaptive controller, where$q=0.4$,   ${\zeta }^{\prime }=1.8$, ${\sigma }_1=0.3$, ${\sigma }_2=0.6$, ${\tilde{\eta }}_1=25$, ${\tilde{\eta }}_2=20$, ${\eta }_1(0)=0.1$, ${\eta }_2(0)=0.2$, $\lambda =({\lambda }_1,{\lambda }_2)=(2.5+2.5i,3+3i)$. By simple calculation, we have

$$Q=\underset{1\le k\le 2}{\min }\left[\left(c_k+{\overline{c}}_k+2{\tilde{\eta }}_k\right)-{\displaystyle \sum _{j=1}^n(a_{kj}\overline{a_{kj}}{F}_j\overline{F_j}+b_{kj}\overline{b_{kj}}{G}_j\overline{G_j})}-n\right]=4.68,$$

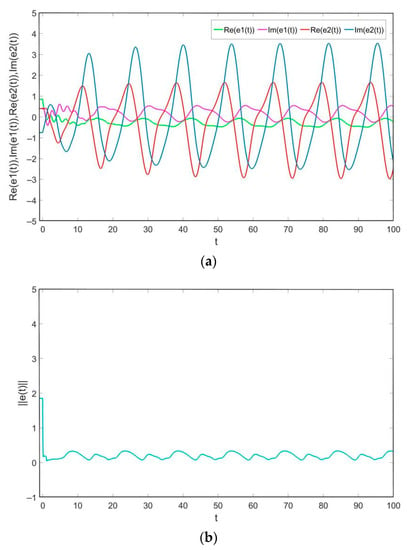
$n{\zeta }^{\prime }=3.6<Q$. Similarly, the conditions and assumptions are satisfied in Theorem 2, and the obtained settling time is $t_2\approx 1.6169$. The state trajectories of the real and imaginary parts of the error system (10) and error norm trajectory curve are showed in Figure 4 when $\beta =0.6+0.5i$, which shows that the system (19) and the system (20) will achieve the finite-time projective synchronization under the adaptive controller (14). Figure 5 depicts the state trajectories of the real and imaginary parts of the error system (10) and error norm trajectory curve when $\beta =1$, which shows that the system (19) and the system (20) will achieve the complete synchronization under the adaptive controller (14).

Figure 4. (a) The state trajectory of the error system when $\beta =0.6+0.5i$. (b) The trajectory of the error norm $\beta =0.6+0.5i$.

Figure 5. (a) The state trajectory of the error system when $\beta =1$. (b) The trajectory of the error norm $\beta =1$.

5. Conclusions

In this paper, a feedback controller and adaptive controller were designed to study the finite-time projective synchronization problem of the FOCVNNTD. Some different criteria for ensuring the finite-time projective synchronization of the FOCVNNTD were established. Furthermore, the synchronization time was estimated effectively. Finally, some numerical simulations are given to illustrate the effectiveness and applicability of the obtained results.