Extended Hamilton–Jacobi Theory, Symmetries and Integrability by Quadratures

Abstract

In this paper, we study the extended Hamilton–Jacobi Theory in the context of dynamical systems with symmetries. Given an action of a Lie group G on a manifold M and a G-invariant vector field X on M, we construct complete solutions of the Hamilton–Jacobi equation (HJE) related to X (and a given fibration on M). We do that along each open subset $U\subseteq M$, such that $\pi \left(U\right)$ has a manifold structure and ${\pi }_{\left|U\right.}:U\to \pi \left(U\right)$, the restriction to U of the canonical projection $\pi :M\to M/G$, is a surjective submersion. If $X_{\left|U\right.}$ is not vertical with respect to ${\pi }_{\left|U\right.}$, we show that such complete solutions solve the reconstruction equations related to $X_{\left|U\right.}$ and G, i.e., the equations that enable us to write the integral curves of $X_{\left|U\right.}$ in terms of those of its projection on $\pi \left(U\right)$. On the other hand, if $X_{\left|U\right.}$ is vertical, we show that such complete solutions can be used to construct (around some points of U) the integral curves of $X_{\left|U\right.}$ up to quadratures. To do that, we give, for some elements $\xi$ of the Lie algebra $\mathfrak{g}$ of G, an explicit expression up to quadratures of the exponential curve $exp\left(\xi t\right)$, different to that appearing in the literature for matrix Lie groups. In the case of compact and of semisimple Lie groups, we show that such expression of $exp\left(\xi t\right)$ is valid for all $\xi$ inside an open dense subset of $\mathfrak{g}$.

1. Introduction

In the last few years, several generalizations of the classical Hamilton–Jacobi equation (HJE) have been developed for Hamiltonian systems on different contexts: on symplectic, cosymplectic, contact, Poisson and almost-Poisson manifolds, and also on Lie algebroids. The resulting Hamilton–Jacobi theories were applied to nonholonomic systems, dissipative and time-dependent Hamiltonian systems, reduced systems by symmetries and Hamiltonian systems with external forces [1,2,3,4,5,6,7,8]. In all of them, the following ingredients are present: $\left(1\right)$ a fibration $\Pi :M\to N$ (i.e., a surjective submersion) defined on the phase space M of each system; $\left(2\right)$ the solutions of the generalized HJE, which we shall call $\Pi$-HJE, given by sections $\sigma :N\to M$ of such a fibration $\Pi$; $\left(3\right)$ the complete solutions $\Sigma :N\times \Lambda \to M$, given by local diffeomorphisms such that, for each $\lambda \in \Lambda$, ${\sigma }_{\lambda }:=\Sigma (·,\lambda )$ is a solution of the $\Pi$-HJE. This clearly generalizes the classical situation [9,10], where the involved fibration is the cotangent projection ${\pi }_Q:T^{*}Q\to Q$ of a manifold Q and the solutions $\sigma :Q\to T^{*}Q$ are exact 1-forms on Q.

In [11], an extension to general (i.e., not necessarily Hamiltonian) dynamical systems, of the previously mentioned Hamilton–Jacobi theories, was carried out, focusing on the connection between complete solutions and the integrability by quadratures of the involved systems.

The main aim of the present paper is to further study such an extended theory in the context of dynamical systems with symmetry. Concretely, given a general action $\rho :G\times M\to M$ (not necessarily free or proper) of a Lie group G on a manifold M and a G-invariant vector field X on M (with respect to $\rho$), we investigate how to use $\rho$ to construct (local) fibrations $\Pi$ of M and related solutions of the $\Pi$-HJE for X. We first show that, around almost every point of M (depending on the isotropy subgroups of G), there exists a neighborhood U, such that the canonical projection $\pi :M\to M/G$ restricted to U, namely ${\pi }_{\left|U\right.}:U\to \pi \left(U\right)$, defines a fibration (even though $\rho$ is neither free nor proper). Then, we consider two kinds of vector fields: $\left(a\right)$ those for which $X_{\left|U\right.}$ is not vertical with respect to ${\pi }_{\left|U\right.}$, which we call horizontal, and $\left(b\right)$ the vertical ones. For the horizontal vector fields, we show that, related to the action $\rho$, there exists a submersion $\Theta$ transverse to ${\pi }_{\left|U\right.}$ (which plays the role of a flat principal connection), such that

$$\Sigma :={\left({\pi }_{\left|U\right.},\Theta \right)}^{-1}:\pi \left(U\right)\times \Lambda \to U,$$

(1)

with $\Lambda$ a submanifold of G, is a complete solution of the ${\pi }_{\left|U\right.}$-HJE for $X_{\left|U\right.}$. Such a $\Sigma$ can be seen as a solution of a reconstruction problem, in the sense that, if we know the integral curves $\gamma \left(t\right)$ of the projected vector field Y of $X_{\left|U\right.}$ on $\pi \left(U\right)$, then the integral curves of $X_{\left|U\right.}$ are given by $\Gamma \left(t\right)=\Sigma \left(\gamma \left(t\right),\lambda \right)$, with $\lambda \in \Lambda$. For the vertical vector fields, we show that we can construct up to quadratures a submersion $\Theta$ transverse to ${\pi }_{\left|U\right.}$, such that

$$\Sigma :={\left(\Theta ,{\pi }_{\left|U\right.}\right)}^{-1}:N\times \pi \left(U\right)\to U,$$

(2)

with N a submanifold of G, is a complete solution of the $\Theta$-HJE for $X_{\left|U\right.}$. Moreover, we prove that the integral curves of $X_{\left|U\right.}$ also can be constructed up to quadratures around some points of M. To do that, we first show that the exponential curves $t\mapsto exp\left(\xi t\right)$ of G, for some elements $\xi$ of its Lie algebra $\mathfrak{g}$, can be constructed up to quadratures. As it is well-known, there exist several explicit expressions of $exp(\xi ,t)$ for the case of matrix Lie groups. What we are giving here is an alternative expression for such curves, valid also for non-matrix Lie groups. In the case in which G is semisimple or compact, we show that such an expression is valid for all $\xi$ in an open dense subset of $\mathfrak{g}$.

The paper is organized as follows. In Section 2, we make a brief review of the extended Hamilton–Jacobi Theory appearing in [11,12]. We also present a result that ensures, in the presence of a complete solution and in the context of symplectic manifolds, the integrability by quadratures of general vector fields. It extends a result proved in [11] for Hamiltonian vector fields only. In Section 3, given a dynamical system with symmetry, we construct the complete solutions (1) and (2) for horizontal and vertical vector fields, respectively. In Section 4, we show the intimate relationship that exists between the complete solutions of a horizontal (and invariant) vector field and the so-called reconstruction processes. Finally, in Section 5, using the abovementioned result of Section 2, we show that the exponential curves $t\mapsto exp\left(\xi t\right)$ of G, for some points $\xi \in \mathfrak{g}$, can be constructed up to quadratures. Then, based on that, we state sufficient conditions under which a vertical (and invariant) vector field can also be integrable up to quadratures.

We assume that the reader is familiar with the main concepts of differential geometry (see [13,14,15]) and with the basic ideas related to Hamiltonian systems, symplectic geometry and Poisson geometry in the context of geometric mechanics (see for instance [9,16,17,18]). We shall work in the smooth (i.e., $C^{\infty }$) category, focusing exclusively on finite-dimensional smooth manifolds. Regarding the terminology associated to the concept of “integrability by quadratures,” we shall adopt the following convention. We shall say that “a function" $F:P\to Q$ can be constructed up to quadratures ,” or simply “can be constructed,” if its domain P and its values $F\left(p\right)$ (for all $p\in P$):

• are simply known;
• they can be determined by making a finite number of arithmetic operations (as the calculation of a determinant) and/or solving a finite set of linear equations (which actually can be reduced to arithmetic operations);
• or they can be expressed in terms of the derivatives, primitives (i.e., quadratures) and/or lateral inverses (by using the implicit or inverse function theorem) of other known functions.

When the function F above is an integral curve $\Gamma$ of a vector field and such a curve can be constructed up to quadratures, we shall say that $\Gamma$ can be integrated up to quadratures, or by quadratures.

2. Preliminaries: Complete Solutions, First Integrals and Integrability

2.1. The Extended Hamilton–Jacobi Equation

Consider a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a surjective submersion $\Pi :M\to N$ (ipso facto an open map). Related to these data (see [11]), we have the $\Pi$-Hamilton–Jacobi equation ($\Pi$-HJE) for X:

$${\sigma }_{*}\circ {\Pi }_{*}\circ X\circ \sigma =X\circ \sigma ,$$

(3)

whose unknown is a section $\sigma :N\to M$ of $\Pi$ (ipso facto a closed map). If $\sigma$ solves the equation above, we shall say that $\sigma$ is a (global) solution of the $\Pi$-HJE for X. On the other hand, given an open subset $U\subseteq M$, we shall call local solution of the $\Pi$-HJE for X along U to any solution of the ${\Pi }_{\left|U\right.}$-HJE for $X_{\left|U\right.}$. (Here, we are seeing ${\Pi }_{\left|U\right.}$ as a submersion onto $\Pi \left(U\right)$ and $X_{\left|U\right.}$ as an element of $\mathfrak{X}\left(U\right)$). Note that $\sigma$ is a solution of the $\Pi$-HJE for X if, and only if,

$${\sigma }_{*}\circ X^{\sigma }=X\circ \sigma ,$$

(4)

where

$$X^{\sigma }:={\Pi }_{*}\circ X\circ \sigma ,$$

(5)

i.e., the vector fields $X\in \mathfrak{X}\left(M\right)$ and $X^{\sigma }\in \mathfrak{X}\left(N\right)$ are $\sigma$-related. (Moreover, it can be shown that $\sigma$ is a solution of Equation (3) if, and only if, its image is an X-invariant closed submanifold). This means that, in order to find the trajectories of X along the image of $\sigma$, we can look for the integral curves of $X^{\sigma }$.

Given another manifold $\Lambda$ such that $dim\Lambda +dimN=dimM$, a complete solution of the $\Pi$-HJE for X is a surjective local diffeomorphism $\Sigma :N\times \Lambda \to M$ such that, for all $\lambda \in \Lambda$,

$${\sigma }_{\lambda }:=\Sigma \left(·,\lambda \right):p\in N⟼\Sigma \left(p,\lambda \right)\in M$$

(6)

is a solution of the $\Pi$-HJE for X. The local version is obtained by replacing M, X, $\Pi$ and N by U, $X_{\left|U\right.}$, ${\Pi }_{\left|U\right.}$ and $\Pi \left(U\right)$, respectively, being U an open subset of M. Each section ${\sigma }_{\lambda }$ is called a partial solution. We showed in [11] that a (local) complete solution $\Sigma$ exists around every point $m\in M$ for which $X\left(m\right)\notin \mathsf{Ker}{\Pi }_{*,m}$.

Denoting by ${\mathfrak{p}}_N$ and ${\mathfrak{p}}_{\Lambda }$ the projections of $N\times \Lambda$ onto N and $\Lambda$, respectively, it is easy to prove that a surjective local diffeomorphism $\Sigma$ is a complete solution if, and only if,

$$\Pi \circ \Sigma ={\mathfrak{p}}_N\mathrm{and}{\Sigma }_{*}\circ X^{\Sigma }=X\circ \Sigma ,$$

(7)

being $X^{\Sigma }\in \mathfrak{X}\left(N\times \Lambda \right)$ the unique vector field on $N\times \Lambda$ satisfying

$${\left({\mathfrak{p}}_N\right)}_{*}\circ X^{\Sigma }={\Pi }_{*}\circ X\circ \Sigma \mathrm{and}{\left({\mathfrak{p}}_{\Lambda }\right)}_{*}\circ X^{\Sigma }=0.$$

(8)

Note that $X^{\Sigma }\left(p,\lambda \right)=\left(X^{{\sigma }_{\lambda }}\left(p\right),0\right)$, with $X^{{\sigma }_{\lambda }}:={\Pi }_{*}\circ X\circ {\sigma }_{\lambda }\in \mathfrak{X}\left(N\right)$, so, in particular,

$$\mathsf{Im}{X}^{\Sigma }\subseteq TN\times \left\{0\right\}.$$

(9)

Furthermore, the fields X and $X^{\Sigma }$ are $\Sigma$-related. This implies that all the trajectories of X can be obtained from those of $X^{\Sigma }$. More precisely, since each integral curve of $X^{\Sigma }$ is clearly of the form $t\mapsto \left(\gamma \left(t\right),\lambda \right)\in N\times \Lambda$, for some fixed point $\lambda \in \Lambda$ (see Equation (9)), those of X are given by

$$t\mapsto \Sigma \left(\gamma \left(t\right),\lambda \right)={\sigma }_{\lambda }\left(\gamma \left(t\right)\right).$$

(10)

So, for each $\lambda$, we only need to find the curves $\gamma$, which are the integral curves of the vector field $X^{{\sigma }_{\lambda }}\in \mathfrak{X}\left(N\right)$.

2.2. The “Complete Solutions—First Integrals” Duality

Consider again a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a surjective submersion $\Pi :M\to N$. We shall say that a submersion $F:M\to \Lambda$ is a first integrals submersion if

$$\mathsf{Im}X\subseteq \mathsf{Ker}{F}_{*}.$$

(11)

Remark 1.

Note that, if $\Lambda ={\mathbb{R}}^l$, the components $f_1,...,f_l:M\to \mathbb{R}$ of F define a set of l (functionally) independent first integrals, in the usual sense.

Moreover, we shall say that F is transverse to $\Pi$ if

$$TM=\mathsf{Ker}{\Pi }_{*}\oplus \mathsf{Ker}{F}_{*}.$$

(12)

It was shown in [11] that, given a complete solution $\Sigma :N\times \Lambda \to M$ of the $\Pi$-HJE for X, we can construct around every point of M a neighborhood U and a submersion $F:U\to \Lambda$ such that

• $\mathsf{Im}{X}_{\left|U\right.}\subseteq \mathsf{Ker}{F}_{*}$ (first integrals),
• $TU=\mathsf{Ker}{\left({\Pi }_{\left|U\right.}\right)}_{*}\oplus \mathsf{Ker}{F}_{*}$ (transversality).

In other words, from $\Sigma$ we have, around every point of M, a first integrals submersion transverse to $\Pi$. The subset U and the function F are given by the formulae

$$U:=\Sigma \left(V\right)\mathrm{and}F:={\mathfrak{p}}_{\Lambda }\circ {\left({\Sigma }_{\left|V\right.}\right)}^{-1},$$

(13)

where $V\subseteq N\times \Lambda$ is an open subset for which ${\Sigma }_{\left|V\right.}$ is a diffeomorphism onto its image.

Conversely (see also [11]), from a submersion $F:M\to \Lambda$ satisfying Equations (11) and (12), we can construct, around every point of M, a neighborhood U and a local complete solution $\Sigma$ of the $\Pi$-HJE. The involved subset U is one for which ${\left(\Pi ,F\right)}_{\left|U\right.}$ is a diffeomorphism onto its image, and $\Sigma$ is given by

$$\Sigma ={\left({\Pi }_{\left|U\right.},F_{\left|U\right.}\right)}^{-1}:\Pi \left(U\right)\times F\left(U\right)\to U.$$

(14)

In summary, a complete solution gives rise to local first integrals via Equation (13), and first integrals give rise to a local complete solution via Equation (14).

2.3. Integrability by Quadratures on Symplectic Manifolds

Let $\left(M,\omega \right)$ be a symplectic manifold. Given a distribution $\mathcal{V}\subseteq TM$ (resp. $m\in M$ and a linear subspace $\mathcal{V}\subseteq T_{m}M$), by ${\mathcal{V}}^{\perp }$, we shall denote, as usual, the symplectic orthogonal of $\mathcal{V}$ w.r.t. $\omega$. The following result is a slight extension to general dynamical systems of a result given in [11] (only valid for Hamiltonian systems).

Theorem 1.

Let $F:M\to \Lambda$ be a surjective submersion and $X\in \mathfrak{X}\left(M\right)$ a vector field, such that:

I. 

$\mathsf{Im}X\subseteq \mathsf{Ker}{F}_{*}$ (first integrals);

II. 

$\mathsf{Ker}{F}_{*}\subseteq {\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$,i.e., F isisotropic;

III. 

and $L_X\beta =0$, with $\beta ={\mathfrak{i}}_X\omega$ (if $\beta =dH$ for some function $H\in C^{\infty }\left(M\right)$, i.e., $X=X_H={\omega }^{♯}\circ dH$, this point is always satisfied);

then the trajectories of X can be integrated up to quadratures.

Proof. 

We shall proceed in four steps.

a.

Given a point $m\in M$, consider an open neighborhood U of m and a surjective submersion $\Pi :U\to \Pi \left(U\right)$ transverse to $F_{\left|U\right.}:U\to F\left(U\right)$. (As it is well-known, such $\Pi$ can be constructed just by fixing a coordinate chart and solving linear equations). Using the point (I) above and the results of the last section, it is clear (shrinking U if necessary) that $\Sigma ={\left(\Pi ,F_{\left|U\right.}\right)}^{-1}$ (see Equation (14)), which can be constructed by using the inverse function theorem, is a local complete solution of the $\Pi$-HJE for X. According to Theorem 3.12 of [11] (replacing there $dH$ by $\beta$), this implies that (recall Equation (8))

$${\mathfrak{i}}_{X^{\Sigma }}{\Sigma }^{*}\omega ={\Sigma }^{*}\beta ,$$

(15)

omitting the restrictions to U of $\omega$ and $\beta$.

b.

Using Equation (7) and the fact that $\Sigma$ is a diffeomorphism, the point (III) is equivalent to

$$L_{X^{\Sigma }}{\Sigma }^{*}\beta =0.$$

(16)

For each $n\in \Pi \left(U\right)$, let us define ${\beta }_n\in {\Omega }^1\left(F\left(U\right)\right)$ such that

$$⟨{\beta }_n\left(\lambda \right),z⟩=⟨{\Sigma }^{*}\beta \left(n,\lambda \right),\left(0,z\right)⟩,\forall \lambda \in F\left(U\right),z\in T_{\lambda }\Lambda .$$

(17)

Then, along an integral curve $\left(\gamma \left(t\right),\lambda \right)$ of $X^{\Sigma }$, it can be shown from Equation (16) that

$$\frac{d}{dt}⟨{\beta }_{\gamma \left(t\right)}\left(\lambda \right),z⟩=0$$

(18)

and, consequently,

$$⟨{\beta }_{\gamma \left(t\right)}\left(\lambda \right),z⟩=⟨{\beta }_{\gamma \left(0\right)}\left(\lambda \right),z⟩,\forall \lambda \in F\left(U\right),z\in T_{\lambda }\Lambda .$$

Let us prove it. From (I) and (II), we have that ${\mathfrak{i}}_Y\beta ={\mathfrak{i}}_Y{\mathfrak{i}}_X\omega =0$ for all Y, such that $\mathsf{Im}Y\subseteq \mathsf{Ker}{F}_{*}$. This implies that

$${\mathfrak{i}}_{\widehat{Y}}{\Sigma }^{*}\beta =0$$

for all $\widehat{Y}\in \mathfrak{X}\left(\Pi \left(U\right)\times F\left(U\right)\right)$ of the form $\left(y,0\right)$, i.e., $\mathsf{Im}\widehat{Y}\subseteq T\Pi \left(U\right)\times \left\{0\right\}$ (compare with Equation (9)). On the other hand, given a vector field $z\in \mathfrak{X}\left(F\left(U\right)\right)$, for $Z=\left(0,z\right)$, it is easy to see that $\left[X^{\Sigma },Z\right]$ is of the form $\left(y,0\right)$. Then, from that and Equation (16),

$$L_{X^{\Sigma }}\circ {\mathfrak{i}}_Z\left({\Sigma }^{*}\beta \right)=\left({\mathfrak{i}}_Z\circ L_{X^{\Sigma }}+{\mathfrak{i}}_{\left[X^{\Sigma },Z\right]}\right)\left({\Sigma }^{*}\beta \right)={\mathfrak{i}}_Z\circ L_{X^{\Sigma }}\left({\Sigma }^{*}\beta \right)=0.$$

Hence, Equation (18) follows by combining Equation (17) and the last equation.

c.

Assuming that $\omega$ is closed, we can assume (without loss of generality) that

$$\omega =-d\theta ,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \theta \in {\Omega }^1\left(U\right).$$

Now, we can proceed as in [11] (see Section 3.3.1 in [11]). In fact,

$$0={\sigma }_{\lambda }^{*}\omega =-{\sigma }_{\lambda }^{*}\left(d\theta \right)=-d\left({\sigma }_{\lambda }^{*}\theta \right)$$

and, thus, a real $C^{\infty }$-function $W_{\lambda }:\Pi \left(U\right)\to ℝ$ can be constructed up to quadratures (shrinking U if needed), such that

$${\sigma }_{\lambda }^{*}\theta =d{W}_{\lambda }.$$

In turn, the family of functions $W_{\lambda }$’s gives rise to a real $C^{\infty }$-function $W:\Pi \left(U\right)\times F\left(U\right)\to ℝ$ satisfying

$$⟨(dW-{\Sigma }^{*}\theta )(n,\lambda ),(y,0)⟩=0,\mathrm{for}(n,\lambda )\in \Pi \left(U\right)\times F\left(U\right)\mathrm{and} y\in T_n\Pi \left(U\right).$$

In particular, since $X^{\Sigma }\in \mathsf{Ker}{F}_{*}$, it follows that

$$i_{X^{\Sigma }}{\Sigma }^{*}\theta =i_{X^{\Sigma }}dW.$$

Therefore, we deduce that

$$\begin{array}{c}\hfill i_{X^{\Sigma }}{\Sigma }^{*}\omega =-i_{X^{\Sigma }}d\left({\Sigma }^{*}\theta \right)=-L_{X^{\Sigma }}{\Sigma }^{*}\theta +d{i}_{X^{\Sigma }}\left({\Sigma }^{*}\theta \right)=L_{X^{\Sigma }}(dW-{\Sigma }^{*}\theta ).\end{array}$$

(19)

Then, combining Equations (15) and (19),

$$L_{X^{\Sigma }}\left(dW-{\Sigma }^{*}\theta \right)={\Sigma }^{*}\beta .$$

(20)

As a consequence, in terms of the functions ${\phi }_{\lambda }:\Pi \left(U\right)\to T_{\lambda }^{*}F\left(U\right)$, given by

$$⟨{\phi }_{\lambda }\left(n\right),z⟩=⟨\left(dW-{\Sigma }^{*}\theta \right)\left(n,\lambda \right),\left(0,z\right)⟩,\forall z\in T_{\lambda }F\left(U\right),$$

(21)

the Equation (20) along an integral curve $\left(\gamma \left(t\right),\lambda \right)$ of $X^{\Sigma }$ translates to (using similar calculations as in the previous step)

$$\frac{d}{dt}{\phi }_{\lambda }\left(\gamma \left(t\right)\right)={\beta }_{\gamma \left(0\right)}\left(\lambda \right),$$

or equivalently,

$${\phi }_{\lambda }\left(\gamma \left(t\right)\right)={\phi }_{\lambda }\left(\gamma \left(0\right)\right)+t{\beta }_{\gamma \left(0\right)}\left(\lambda \right).$$

(22)

d.

Finally, since each ${\phi }_{\lambda }$ is an immersion (see Proposition 3.16, [11]), from the above equation, we can construct the curves $\gamma$ (by using the implicit function theorem), from which all the integral curves of $X_{\left|U\right.}$ can be obtained. In fact, the latter are given by the formula $\Gamma \left(t\right)=\Sigma \left(\gamma \left(t\right),\lambda \right)$, as explained at the end of Section 2.1 (see Equation (10)). Since all that can be done around every $m\in M$, then all the integral curves of X can be constructed in the same way.

□

Given a surjective submersion $G:M\to Y$ and a 1-form $\varphi \in {\Omega }^1\left({\rm Y}\right)$, the vector field

$$X={\omega }^{♯}\circ G^{*}\varphi$$

(23)

satisfies the point (I) above, for another submersion $F:M\to \Lambda$, if, and only if,

$$F_{*,m}\circ {\omega }^{♯}\circ G_m^{*}\left(\varphi \left(G\left(m\right)\right)\right)=0,\forall m\in M.$$

(24)

If, in addition,

$$\mathsf{Ker}{F}_{*}\subseteq \mathsf{Ker}{G}_{*},$$

(25)

then ${\mathfrak{i}}_X\circ F^{*}={\mathfrak{i}}_X\circ G^{*}=0$ and consequently

$$L_X\beta =L_X{G}^{*}\varphi =\left({\mathfrak{i}}_X\circ G^{*}d\varphi +d\left({\mathfrak{i}}_X\circ G^{*}\varphi \right)\right)=0.$$

(26)

So, given a symplectic manifold $\left(M,\omega \right)$, examples of dynamical systems satisfying the points (I)–(III) of Theorem 1 are given by submersions F and G satisfying (25), being F isotropic, 1-forms $\varphi$ satisfying (24) and vector fields given by (23). These examples can be seen as a generalization of the non-commutative integrable systems, as we show below, and they will appear in the last section of the paper.

2.4. Non-Commutative Integrability and Casimir 1-Forms

A Mishchenko-Fomenko or non-commutative integrable (NCI) system [19] (see also [20] and references therein) can be defined as a triple given by a symplectic manifold $\left(M,\omega \right)$, a Hamiltonian vector field $X_H={\omega }^{♯}\circ dH$ and a surjective submersion $F:M\to \Lambda$ such that:

1.

$\mathsf{Im}{X}_H\subseteq \mathsf{Ker}{F}_{*}$;

2.

$\mathsf{Ker}{F}_{*}\subseteq {\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$;

3.

${\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$ is integrable.

When $\mathsf{Ker}{F}_{*}={\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$, i.e. F is Lagrangian, the third point is automatic. In such a case, we have a so-called Liouville-Arnold or commutative integrable (CI) system [16,21]. It is well-known that all these systems are integrable by quadratures. The traditional way of proving that relies on the Lie theorem on integrability by quadratures [14,22] (see also [23]).

Usually, in the definition of NCI and CI systems, one more requirement is included: F has compact and connected leaves. In such a case, besides integrability by quadratures, action-angle coordinates can be found for such systems (see [24,25]). We do not consider this case here.

Remark 2.

An alternative definition can be given in terms of subsets of functions $\mathcal{F}\subseteq C^{\infty }\left(M\right)$. The conditions 3 and 2 above are replaced by asking $\mathcal{F}$ to be a Poisson sub-algebra and complete (see [20]), respectively, and 1 is replaced by asking that the elements of $\mathcal{F}$ Poisson commute with H.

To analyze the relationship between NCI systems and the systems given at the end of the last section, let us consider an arbitrary surjective submersion $F:M\to \Lambda$. On the one hand, it can be shown that a Hamiltonian vector field $X_H$ belongs to ${\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$ if, and only if, there exists a function $h:\Lambda \to \mathbb{R}$, such that $h\circ F=H$. So, if we ask that $\mathsf{Im}{X}_H\subseteq \mathsf{Ker}{F}_{*}$ and that F is isotropic, then

$$X_H={\omega }^{♯}\circ F^{*}dh.$$

(27)

On the other hand, it is well-known (see, for instance, [26] Prop. 7.18) that ${\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$ is integrable if, and only if, $\Lambda$ is a Poisson manifold with bi-vector $\Xi$, given by the formula

$${\Xi }^{♯}\left(\alpha \right)=F_{*,m}\circ {\omega }^{♯}\circ F_m^{*}\left(\alpha \right),\alpha \in T_{F\left(m\right)}^{*}\Lambda ,$$

and F is a Poisson morphism. In such a case, the condition $\mathsf{Im}{X}_H\subseteq \mathsf{Ker}{F}_{*}$, for $X_H$ given by Equation (27), is equivalent to (compare to Equation (24))

$${\Xi }^{♯}\left(dh\left(F\left(m\right)\right)\right)=F_{*,m}\circ {\omega }^{♯}\circ F_m^{*}\left(dh\left(F\left(m\right)\right)\right)=0,$$

which says precisely that $dh$ is a Casimir 1-form for $\Xi$ (and h is a Casimir function). In the case when F is Lagrangian, then $\Xi =0$, and consequently every 1-form on $\Lambda$ is a Casimir. Thus, the NCI systems are a subclass of the systems given at the end of the last section, where $\Lambda$ is a Poisson manifold, $G=F:M\to \Lambda$ is a Poisson morphism and $\varphi =dh$ is an exact Casimir 1-form with respect to the Poisson structure on $\Lambda$.

3. Complete Solutions and Symmetries

Given a general action $\rho :G\times M\to M$ (not necessarily free or proper) of a Lie group G on a manifold M and a G-invariant vector field X on M (with respect to $\rho$), we shall construct in this section, based on $\rho$ and the canonical projection $\pi :M\to M/G$, local fibrations $\Pi$ of M and related complete solutions of the $\Pi$-HJE for X. Let us begin with the local fibrations $\Pi$ based on $\pi$.

3.1. The Vertical Submersions

3.1.1. General Actions and Regular Points

Let $\rho :G\times M\to M$ be an action of a Lie group G on M. Let us introduce some basic notation and recall some well-known facts.

As usual, given $g\in G$ and $m\in M$, by ${\rho }_g$ and ${\rho }_m$ we shall denote the maps ${\rho }_g:M\to M$ and ${\rho }_m:G\to M$, such that ${\rho }_g\left(m\right)={\rho }_m\left(g\right)=\rho \left(g,m\right)$. Moreover, we shall denote by $\mathfrak{g}$ the Lie algebra of G and by $G_m$ the isotropy subgroup of m.

For latter convenience, let us note that

$$\mathsf{Ker}{\left({\rho }_m\right)}_{*,e}={\mathfrak{g}}_m,$$

(28)

where $e\in G$ is the identity element and ${\mathfrak{g}}_m$ is the Lie algebra of $G_m$. Furthermore, recall that the fundamental vector field associated with $\eta \in \mathfrak{g}$ is given by

$${\eta }_M\left(m\right)={\left({\rho }_m\right)}_{*,e}\left(\eta \right).$$

(29)

Let $\pi :M\to M/G$ be the canonical projection and consider on $M/G$ the quotient topology. Recall that, since each ${\rho }_g:M\to M$ is a homeomorphism for all $g\in G$, then $\pi$ is open (besides continuous). Recall also the identities

$$\pi \circ {\rho }_m\left(g\right)=\pi \circ {\rho }_g\left(m\right)=\pi \left(m\right),\forall m\in M,g\in G.$$

(30)

When $\rho$ is free (i.e., if $G_m=\left\{e\right\}$ for all $m\in M$) and proper, then, as it is well-known (see [9]), $M/G$ has a unique manifold structure, such that $\pi :M\to M/G$ is a surjective submersion. For more general actions, we shall show a similar result, but at a local level around a regular point.

Definition 1.

We shall say that $m_0\in M$ is ρ-regular if there exists an open neighborhood U of $m_0$, such that

$$dim{G}_m=dim{G}_{m_0},for every m\in U.$$

(31)

We shall call such neighborhood U admissible if, in addition, U is connected. The (open) subset of all the ρ-regular points will be denoted ${\mathcal{R}}_{\rho }$.

Remark 3.

Note that if $m_0$ is a ρ-regular point, then the assigning

$$m\in U⟼{\mathfrak{g}}_m\subseteq \mathfrak{g}$$

defines a vector subbundle of the trivial vector bundle $p{r}_1:U\times \mathfrak{g}\to U$ for each admissible neighborhood U.

Given $m_0\in {\mathcal{R}}_{\rho }$, there exists an admissible neighborhood U of $m_0$, such that ${\rho }_g\left(U\right)\subseteq U$ for all $g\in G$, i.e., U is a G-invariant subset. To show it, note that given $m,m^{\prime }\in M$ such that $m^{\prime }=\rho \left(g,m\right)$ for some g, we have that $g·G_m·g^{-1}=G_{m^{\prime }}$, and consequently

$$dim{G}_m=dim{G}_{{\rho }_g\left(m\right)},\forall g\in G,m\in M.$$

Then, given any admissible neighborhood V of $m_0$, it is clear that

$$V_G=\bigcup _{g\in G}{\rho }_g\left(V\right)$$

(32)

includes $m_0$, is open, G-invariant and admissible. As a consequence, the set ${\mathcal{R}}_{\rho }$ is G-invariant.

If the action $\rho$ is free, then every element of M is $\rho$-regular, and M (if connected) is an admissible neighborhood. For $G=SO\left(3\right)$ acting on $M={\mathbb{R}}^3$ with the natural action ${\rho }_{nat}$, we have that $dim{G}_m=1$ for $m\in {\mathbb{R}}^3-\left\{0\right\}$ and $dim{G}_0=dimG=3$. Thus, all the points of ${\mathbb{R}}^3$ except 0 are ${\rho }_{nat}$-regular. In general, we have the following result.

Proposition 1.

${\mathcal{R}}_{\rho }$ is a G-invariant open dense subset of $M.$

Proof. 

We already saw that ${\mathcal{R}}_{\rho }$ is G-invariant. We shall prove that

1.

if k is the minimum dimension of the isotropy subgroups and $dim{G}_{m_0}=k,$ then $m_0$ is a $\rho$-regular point;

2.

the complement of ${\mathcal{R}}_{\rho }$ has an empty interior.

For the first point, define

$$k:=min\left\{dim{G}_m:m\in M\right\}$$

and $m_0$ such that $dim{G}_{m_0}=k.$ Consider the Lie algebra ${\mathfrak{g}}_{m_0}$ of $G_{m_0}$ and a linear complement ${\mathfrak{g}}_{m_0}^c$ of it. For any element $v\in {\mathfrak{g}}_{m_0}^c-\left\{0\right\}$, we have that

$$\tilde{\rho }\left(v,m_0\right)\ne 0,$$

where $\tilde{\rho }$ is the action of $\mathfrak{g}$ on M induced by $\rho$. Then, by continuity, there exists a neighborhood U of $m_0$, such that

$$\tilde{\rho }\left(v,m\right)\ne 0,\forall m\in U.$$

This means that $dim{\mathfrak{g}}_m\le dim{\mathfrak{g}}_{m_0}=k$ for all $m\in U$. However, k is the minimum dimension, hence $dim{\mathfrak{g}}_m=k$ for all $m\in U$. This says precisely that $m_0$ is a $\rho$-regular point.

For the second point, suppose that the complement ${\mathcal{R}}_{\rho }^c$ has interior, i.e., for some $m_1\in {\mathcal{R}}_{\rho }^c$ there exists an open subset $U_1$, such that $m_1\in U_1\subseteq {\mathcal{R}}_{\rho }^c$. Consider the Lie algebra ${\mathfrak{g}}_{m_1}$ of $G_{m_1}$ and a linear complement ${\mathfrak{g}}_{m_1}^c$ of it. Proceeding as above, we can ensure that there exists a neighborhood $U_2\subseteq U_1$ of $m_1$, such that $dim{\mathfrak{g}}_m\le dim{\mathfrak{g}}_{m_1}$ for all $m\in U_2$. Since $U_2\subseteq {\mathcal{R}}_{\rho }^c$, there must exist $m_2\in U_2$, such that $dim{\mathfrak{g}}_{m_2}<dim{\mathfrak{g}}_{m_1}$. Otherwise, $m_1$ would be a $\rho$-regular point (with admissible neighborhood $U_2$). Repeating this reasoning for $m_2$, we can ensure the existence of a neighborhood $U_3\subseteq U_1$ of $m_2$, for which $dim{\mathfrak{g}}_m\le dim{\mathfrak{g}}_{m_2}$ for all $m\in U_3$, and consequently, the existence of a point $m_3\in U_3$, such that $dim{\mathfrak{g}}_{m_3}<dim{\mathfrak{g}}_{m_2}$. In this way, since the dimension of $\mathfrak{g}$ is finite, in some step of this procedure, we shall find $m_0\in U_1\subseteq {\mathcal{R}}_{\rho }^c$, such that $dim{\mathfrak{g}}_{m_0}=k$. Since such $m_0$ must belong to ${\mathcal{R}}_{\rho }$, we have arrived at a contradiction. □

3.1.2. The Submersions ${\pi }_{\left|U\right.}$

Now, let us construct smooth local versions of the canonical projection $\pi$.

Proposition 2.

Given $m_0\in {\mathcal{R}}_{\rho }$, there exists a neighborhood U for $m_0$, such that the open subset $\pi \left(U\right)$ has a manifold structure and the restriction ${\pi }_{\left|U\right.}:U\to \pi \left(U\right)$ is a submersion satisfying

$$\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m}=\mathsf{Im}{\left({\rho }_m\right)}_{*,e},\forall m\in U,$$

(33)

and, consequently,

$$dim\left(\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*}\right)=dimG-dim{G}_{m_0}.$$

(34)

Moreover, U can be taken G-invariant.

Proof. 

Let $U_1$ be an admissible neighborhood of $m_0$ and consider the distribution given by

$${\mathfrak{F}}_1\left(m\right)=\mathsf{Im}{\left({\rho }_m\right)}_{*,e}.$$

Since ${\mathfrak{F}}_1$ is clearly generated by the fundamental vector fields ${\eta }_M$ (see Equation (29)), with $\eta \in \mathfrak{g}$, then ${\mathfrak{F}}_1$ is involutive (see, for instance, [9]). Moreover, for the same reason,

$$dim\left(\mathsf{Im}{\left({\rho }_m\right)}_{*,e}\right)=dim\mathfrak{g}-dim\left(\mathsf{Ker}{\left({\rho }_m\right)}_{*,e}\right)=dim\mathfrak{g}-dim{\mathfrak{g}}_m=dimG-dim{G}_m,$$

which is constant and equal to $r_1=dimG-dim{G}_{m_0}$ for all $m\in U_1$ (because of Equation (31)). Then, defining $r=dimM$ and using the Frobenius Theorem, we can find a local chart

$$(U_2,\phi \equiv (x^1,\dots ,x^{r_1},x^{r_1+1},\dots ,x^r))$$

in $U_1$ such that $m_0\in U_2$,

$$\phi \left(U_2\right)=V_2\times V_2^{\prime }\subseteq {ℝ}^{r_1}\times {ℝ}^{r-r_1},$$

with $V_2$ and $V_2^{\prime }$ open subsets in ${ℝ}^{r_1}$ and ${ℝ}^{r-r_1}$, respectively, and

$${\mathfrak{F}}_1\left(m\right)=⟨{\left.\frac{\partial }{\partial x^1}\right|}_m,\dots ,{\left.\frac{\partial }{\partial x^{r_1}}\right|}_m⟩\mathrm{for}\mathrm{all}m\in U_2.$$

Now, we can consider the G-invariant open subset U of M given by

$$U=\bigcup _{g\in G}{\rho }_g\left(U_2\right).$$

It is clear that $m_0\in U_2\subseteq U$ and, moreover, $U/G\cong V_2^{\prime }$ and the canonical projection ${\pi }_{|U}:U\to U/G\cong V_2^{\prime }$ is a surjective submersion. □

From now on, by admissible, we shall mean any admissible neighborhood U of $m_0$ for which the last proposition holds.

The following result will be useful later.

Proposition 3.

Given $m_0\in {\mathcal{R}}_{\rho }$ and an admissible neighborhood U of $m_0$, the subset

$$R_U=\left\{\left(m,{\rho }_g\left(m\right)\right):g\in G,m\in U\right\}\subseteq U\times M$$

(35)

is a closed submanifold of $U\times M$, of dimension $dimM+dimG-dim{G}_{m_0}$, and the surjective map

$${\Phi }_U:\left(g,m\right)\in G\times U⟼\left(m,{\rho }_g\left(m\right)\right)\in R_U$$

(36)

is smooth and also a submersion.

Proof. 

Consider the admissible G-invariant open subset $\tilde{U}={\bigcup }_{g\in G}{\rho }_g\left(U\right)$ (see Equation (32)), the related subset $R_{\tilde{U}}$ and the related surjective map ${\Phi }_{\tilde{U}}:G\times \tilde{U}\to R_{\tilde{U}}$ (given as in Equations (35) and (36)). If we prove the proposition for $\tilde{U}$, since $R_U=R_{\tilde{U}}\cap \left(U\times M\right)$ and ${\Phi }_U={\left.{\Phi }_{\tilde{U}}\right|}_{G\times U}$, then we would proved it for U.

Using that the space of orbits $\pi \left(\tilde{U}\right)=\tilde{U}/G$ is a quotient smooth manifold and a classical result (see, for instance, [27]), we deduce that $R_{\tilde{U}}\subseteq \tilde{U}\times \tilde{U}$ is a closed submanifold of $\tilde{U}\times \tilde{U}$ (and of $\tilde{U}\times M$). As a consequence, since

$$\left(g,m\right)\in G\times \tilde{U}⟼\left(m,{\rho }_g\left(m\right)\right)\in \tilde{U}\times \tilde{U}$$

is smooth, the same is true for the surjection ${\Phi }_{\tilde{U}}:G\times \tilde{U}\to R_{\tilde{U}}$. To find the dimension of $R_{\tilde{U}}$ and show that ${\Phi }_{\tilde{U}}$ is a submersion, it is enough to calculate the rank of ${\Phi }_{\tilde{U}}$ and show that it is constant (since ${\Phi }_{\tilde{U}}$ is surjective). Let us do that.

From Equation (36) and the identity ${\rho }_m\circ L_g={\rho }_g\circ {\rho }_m$, it follows that

$${\left({\Phi }_{\tilde{U}}\right)}_{*,(g,m)}(u,v)=(v,{\left({\rho }_g\right)}_{*,m}(v+{\left({\rho }_m\right)}_{*,e}\left({\left(L_{g^{-1}}\right)}_{*,g}\left(u\right)\right))),\forall u\in T_{g}G,v\in T_m\tilde{U},$$

(37)

and in particular, for $g=e$,

$${\left({\Phi }_{\tilde{U}}\right)}_{*,(e,m)}(\eta ,v)=(v,v+{\left({\rho }_m\right)}_{*,e}\left(\eta \right)),\forall \eta \in \mathfrak{g},v\in T_m\tilde{U}.$$

(38)

Then, from Equations (37) and (38), we have that

$${\left({\Phi }_{\tilde{U}}\right)}_{*,(g,m)}=(i{d}_{T_{m}M}\times {\left({\rho }_g\right)}_{*,m})\circ {\left({\Phi }_{\tilde{U}}\right)}_{*,(e.m)}\circ ({\left(L_{g^{-1}}\right)}_{*,g}\times i{d}_{T_{m}M}).$$

Consequently, for all $\left(g,m\right)\in G\times \tilde{U}$,

$$\left(\mathrm{rank}{\Phi }_{\tilde{U}}\right)(g,m)=\left(\mathrm{rank}{\Phi }_{\tilde{U}}\right)(e,m)=dimM+(dimG-dim{G}_{m_0}),$$

which ends our proof. □

3.1.3. Symplectic Actions and Momentum Maps

Suppose that M is a symplectic manifold, with symplectic form $\omega$, and $\rho$ is a symplectic action , i.e.,

$${\left({\rho }_g\right)}^{*}\circ \omega =\omega ,\forall g\in G,$$

or equivalently

$${\left({\rho }_g\right)}_{*,m}\circ {\omega }_m^{♯}={\omega }_{{\rho }_g\left(m\right)}^{♯}\circ {\left({\rho }_{g^{-1}}\right)}_{{\rho }_g\left(m\right)}^{*},\forall m\in M,g\in G.$$

(39)

Proposition 4.

Under the above conditions, for each admissible neighborhood U, we have that:

1. 

The manifold $\pi \left(U\right)$ has a Poisson structure ${\Xi }_U$, characterized by the condition

$${\Xi }_U\left(\alpha ,\beta \right)\circ \pi =\omega \left({\omega }^{♯}\left({\pi }^{*}\alpha \right),{\omega }^{♯}\left({\pi }^{*}\beta \right)\right),\forall \alpha ,\beta \in {\Omega }^1\left(\pi \left(U\right)\right),$$

(40)

with respect to which ${\pi }_{\left|U\right.}$ is a Poisson morphism.

2. 

Let X be a G-invariant vector field, i.e.,

$${\left({\rho }_g\right)}_{*}\circ X=X\circ {\rho }_g,\forall g\in G.$$

(41)

Then there exists a unique vector field $Y\in \mathfrak{X}\left(\pi \left(U\right)\right)$ such that

$${\left({\pi }_{\left|U\right.}\right)}_{*}\circ X_{\left|U\right.}=Y\circ {\pi }_{\left|U\right.}.$$

Proof. 

$\left(1\right)$ This result is proven in [18] under the hypothesis that U is G-invariant and that the G-action on U is free and proper. However, in that proof, the key point is that the space of orbits $\pi \left(U\right)$ is a quotient manifold, as in our case.

$\left(2\right)$ It is also a well-known result (see, for instance [28]) that if U is a principal G-bundle over $U/G$, then every G-invariant vector field over U is projectable over $U/G$. However, as in $\left(1\right)$, the key point in order to prove this fact is that $U/G$ is a quotient manifold. So, proceeding in a similar way as in [28], we deduce $\left(2\right)$. □

Suppose that $\rho$ has a (global) momentum map, i.e., a function $K:M\to {\mathfrak{g}}^{*}$, such that

$$⟨{\omega }^{♭}\left({\left({\rho }_m\right)}_{*,e}\left(\eta \right)\right),v⟩=⟨K_{*,m}\left(v\right),\eta ⟩,\forall m\in M,v\in T_{m}M,\eta \in \mathfrak{g}.$$

(42)

Proposition 5.

For each admissible neighborhood U,

$$\mathsf{Ker}{\left(K_{\left|U\right.}\right)}_{*}={\left(\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*}\right)}^{\perp }.$$

(43)

For proof of this result see, for instance, [9].

Suppose in addition that K can be chosen $A{d}^{*}$-equivariant, i.e.,

$$K\left(\rho \left(g,m\right)\right)=A{d}_g^{*}\left(K\left(m\right)\right).$$

(44)

where, as usual, $Ad:G\times \mathfrak{g}\to \mathfrak{g}:\left(g,\eta \right)\mapsto A{d}_g\eta$ denotes the adjoint action and

$$A{d}^{*}:G\times {\mathfrak{g}}^{*}\to {\mathfrak{g}}^{*}:\left(g,\alpha \right)⟼{\left(A{d}_{g^{-1}}\right)}^{*}\left(\alpha \right)$$

the co-adjoint one.

Proposition 6.

If $K\left({\mathcal{R}}_{\rho }\right)\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing$, then there exists a G-invariant open subset $U\subseteq {\mathcal{R}}_{\rho }$, such that

$$K\left(U\right)\subseteq {\mathcal{R}}_{A{d}^{*}}.$$

Proof. 

Let $m_1\in {\mathcal{R}}_{\rho }$ be such that $K\left(m_1\right)\in {\mathcal{R}}_{A{d}^{*}}\subseteq {\mathfrak{g}}^{*}$, and let $U_1$ be an admissible neighborhood of $m_1$. Given a G-invariant admissible neighborhood $V\subseteq {\mathcal{R}}_{A{d}^{*}}$ of $K\left(m_1\right)$ (with respect to the co-adjoint action), define

$$U=\bigcup _{g\in G}{\rho }_g\left(U_1\cap K^{-1}\left(V\right)\right).$$

It is clear that U is a G-invariant open subset and $U\subseteq {\mathcal{R}}_{\rho }.$ Moreover, $K\left(m\right)\in V$ for all $m\in U_1\cap K^{-1}\left(V\right)$. Then $A{d}_g^{*}K\left(m\right)\in V$ for all $g\in G$, because of the G-invariance of V, and consequently (see Equation (44))

$$K\left({\rho }_g\left(m\right)\right)=A{d}_g^{*}K\left(m\right)\in V.$$

This completes our proof. □

The previous result will be useful at the end of the paper.

3.2. The Horizontal Submersions

In this subsection, for each admissible neighborhood U, we shall construct submersions $\Theta$ transverse to the restricted canonical projection ${\pi }_{\left|U\right.}$. In terms of such submersions $\Theta$, we shall present at the end of the section the complete solutions that we are looking for.

3.2.1. Trivializations and (Local) Flat Connections for Principal Bundles

Suppose that $\rho :G\times M\to M$ is free and proper and consider the associated principal G-bundle $\pi :M\to M/G$. Given a local section $s:V\to U$ of $\pi$, with $U={\pi }^{-1}\left(V\right)\subseteq M$ and $V\subseteq M/G$ an open subset, we have a trivialization

$$\Psi =\left(\pi ,\psi \right):U\to \pi \left(U\right)\times G$$

(45)

given by $\Psi \left(\rho \left(g,s\left(\lambda \right)\right)\right)=\left(\lambda ,g\right)$, or equivalently

$${\Psi }^{-1}\left(\lambda ,g\right)=\rho \left(g,s\left(\lambda \right)\right),\forall \lambda \in \pi \left(U\right),g\in G.$$

($\Psi$ is well-defined and invertible because $\rho$ is free). Note that the map $\psi :U\to G$ satisfies

$$\rho \left(\psi \left(m\right),s\left(\pi \left(m\right)\right)\right)={\Psi }^{-1}\left(\pi \left(m\right),\psi \left(m\right)\right)=m,\forall m\in U.$$

(46)

Furthermore,

$$\psi \left(\rho \left(g,m\right)\right)=\psi \left(\rho \left(g,\rho \left(\psi \left(m\right),s\left(\pi \left(m\right)\right)\right)\right)\right)=\psi \left(\rho \left(g\psi \left(m\right),s\left(\pi \left(m\right)\right)\right)\right)=g\psi \left(m\right),$$

and consequently

$$\psi \circ {\rho }_g=L_g\circ \psi \mathrm{and}\psi \circ {\rho }_m=R_{\psi \left(m\right)}.$$

(47)

On the other hand, it is easy to show that the map $A:TU\to \mathfrak{g}$ given by

$$A\left(v\right)={\left(R_{\psi \left(m\right)}\right)}_{*,e}^{-1}{\psi }_{*,m}\left(v\right),\mathrm{for}\mathrm{all}v\in T_{m}M,$$

(48)

is a local principal connection for $\pi$. In fact, for all $m\in U$, it follows from Equations (47) and (48) that

$$A\left({\left({\rho }_m\right)}_{*,e}\left(\eta \right)\right)=\eta ,\forall \eta \in \mathfrak{g},$$

(49)

and

$$A\left({\left({\rho }_g\right)}_{*,m}\left(v\right)\right)=A{d}_g\left(A\left(v\right)\right),\forall v\in T_{m}U,\forall g\in G.$$

(50)

In addition, since $\mathsf{Ker}A=\mathsf{Ker}{\psi }_{*}$, the horizontal distribution is integrable, i.e., A is a flat connection. In the next section, we shall construct an object similar to A, but related to an arbitrary action and its regular points.

3.2.2. A Flat-Connection-Like Object for ${\pi }_{\left|U\right.}$

Now, suppose that $\rho$ is a general Lie group action. For each $\rho$-regular point $m_0$, we shall construct a family of submersions transverse to ${\pi }_{\left|U\right.}$ (being U an admissible neighborhood of $m_0$). To do that, we need the next results.

Lemma 1.

Let $G:P\to Q$ be a submersion, $p_0\in P$ and $\mathcal{W}\subseteq T_{p_0}P$ a linear complement of $\mathsf{Ker}{G}_{*,p_0}$. Then, there exists a neighborhood V of $G\left(p\right)\in Q$ and a local section $S:V\to P$ of G, such that

$$S\left(G\left(p_0\right)\right)=p_{0}and\mathsf{Im}{S}_{*,G\left(p_0\right)}=\mathcal{W}.$$

Proof. 

Let $\phi =\left(x_1,...,x_n\right):U\to \phi \left(U\right)$ be a coordinate system of P around $p_0$. Consider the annihilator ${\mathcal{W}}^0\subseteq T_{p_0}^{*}P$ of $\mathcal{W}$ and suppose that the co-vectors

$${\xi }_i=\sum _{j=1}^n{w}_i^{j}d{x}_j\left(p_0\right),i=1,...,k,$$

give a basis for ${\mathcal{W}}^0$. Define $F:U\to {\mathbb{R}}^k$ as

$$F\left({\phi }^{-1}\left(x_1,...,x_n\right)\right)=\left(\sum _{j=1}^n{w}_1^j{x}_j,...,\sum _{j=1}^n{w}_k^j{x}_j\right).$$

It is clear that $\mathsf{Ker}{F}_{*,p_0}=\mathcal{W}$. Then, since $\mathsf{Ker}{G}_{*,p_0}$ and $\mathcal{W}$ are complementary, $\left(G,F\right)$ is a diffeomorphism onto its image $G\left(U\right)\times F\left(U\right)$, shrinking U if needed. As a consequence, the function $S:G\left(U\right)\to P$ such that

$$S\left(q\right)={\left(G,F\right)}^{-1}\left(q,F\left(p_0\right)\right)$$

is a smooth local section of G and satisfies $S\left(G\left(p_0\right)\right)=p_0$. Furthermore, given $w\in \mathcal{W}$, $S_{*,G\left(p_0\right)}\left(G_{*,p_0}\left(w\right)\right)=w$. In particular, since $G_{*,p_0}$ is surjective, even restricted to $\mathcal{W}$, then $\mathsf{Im}{S}_{*,G\left(p_0\right)}=\mathcal{W}$. So, the wanted result follows for $V=G\left(U\right)$. □

Note that the construction of the section S has been made just by using algebraic manipulations and the inverse function theorem.

For the rest of the section, fix a $\rho$-regular point $m_0$, an admissible neighborhood U and a section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ such that

$$s\left(\pi \left(m_0\right)\right)=m_0.$$

(51)

Lemma 2.

The function

$$\mathcal{F}:G\times \pi \left(U\right)\to M:\left(g,\lambda \right)\mapsto \rho \left(g,s\left(\lambda \right)\right)$$

is an open map around $\left(e,\pi \left(m_0\right)\right)$.

Proof. 

Note first that (according to Equation (34))

$$dim\left(\pi \left(U\right)\right)=dimM-\left(dimG-dim{G}_{m_0}\right),$$

and consequently

$$dim\left(G\times \pi \left(U\right)\right)=dimM+dim{G}_{m_0}.$$

So, it is enough to show that $dim\left(\mathsf{Ker}{\mathcal{F}}_{*,\left(e,\pi \left(m_0\right)\right)}\right)=dim{G}_{m_0}$. Given $X\in \mathfrak{g}$ and $Y\in T_{\pi \left(m_0\right)}\pi \left(U\right)$, if

$$0={\mathcal{F}}_{*,\left(e,\pi \left(m_0\right)\right)}\left(X,Y\right)={\rho }_{*,\left(e,m_0\right)}\left(X,s_{*,\pi \left(m_0\right)}\left(Y\right)\right)={\left({\rho }_{m_0}\right)}_{*,e}\left(X\right)+{\left({\rho }_e\right)}_{*,m_0}\left(s_{*,\pi \left(m_0\right)}\left(Y\right)\right)$$

(where we have used Equation (51)), then, applying ${\left({\pi }_{\left|U\right.}\right)}_{*,m_0}$ above,

$$0={\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\circ {\left({\rho }_{m_0}\right)}_{*,e}\left(X\right)+{\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\circ {\left({\rho }_e\right)}_{*,m_0}\circ \left(s_{*,\pi \left(m_0\right)}\left(Y\right)\right).$$

On the other hand, from Equation (30), we have that

$${\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\circ {\left({\rho }_{m_0}\right)}_{*,e}=0\mathrm{and}{\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\circ {\left({\rho }_e\right)}_{*,m_0}={\left({\pi }_{\left|U\right.}\right)}_{*,m_0}.$$

(52)

Since in addition ${\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\circ s_{*,\pi \left(m_0\right)}$ is the identity, then $Y=0$. Hence, $\mathsf{Ker}{\mathcal{F}}_{*,\left(e,m_0\right)}$ is given by the vectors $\left(X,0\right)$, such that ${\left({\rho }_{m_0}\right)}_{*,e}\left(X\right)=0$, i.e., $X\in {\mathfrak{g}}_{m_0}$ (recall Equation (28)). This ends our proof. □

Now, the main result of the section.

Theorem 2.

Given an admissible neighborhood U of $m_0\in {\mathcal{R}}_{\rho }$ and a section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ satisfying Equation (51), we can construct, shrinking U if necessary, a surjective submersion $\Theta :U\to \Theta \left(U\right)\subseteq G$ transverse to ${\pi }_{\left|U\right.}$ (see Equation (12)) such that $\Theta \left(m_0\right)=e$ and

$$\rho \left(\Theta \left(m\right),s\left(\pi \left(m\right)\right)\right)=m,\forall m\in U.$$

(53)

We shall call s-horizontal, or simply horizontal, to such submersions Θ.

Proof. 

First, let us make some observations about the submersion ${\Phi }_U$ of Proposition 3.

• We have that ${\Phi }_U\left(e,m\right)=\left(m,m\right)$ and from Equation (38), it follows that

  $$\mathsf{Ker}\left({\Phi }_U\right){}_{*,\left(e,m\right)}={\mathfrak{g}}_m\times \left\{0\right\}.$$

  (54)
• Then, using Lemma 1, we can construct a local section S of the submersion ${\Phi }_U$, such that $S\left(m_0,m_0\right)=\left(e,m_0\right)$ and

  $$\mathsf{Im}\left(S_{*,\left(m_0,m_0\right)}\right)={\mathfrak{g}}_{m_0}^c\times T_{m_0}M,$$

  (55)

  being ${\mathfrak{g}}_{m_0}^c\subseteq \mathfrak{g}$ some complement of ${\mathfrak{g}}_{m_0}$ (because Equations (54) and (55) are complementary).

For simplicity, let us restrict ${\Phi }_U$ to a subset $W\times U^{\prime }\subseteq G\times U$, with $W\subseteq G$ an open neighborhood of e and $U^{\prime }\subseteq U\subseteq M$ an open neighborhood of $m_0$, such that the above mentioned section S becomes a global section $S:{\Phi }_U\left(W\times U^{\prime }\right)\to W\times U^{\prime }$. Moreover, take $U^{\prime }$ such that

$$s\left(\pi \left(U^{\prime }\right)\right)\subseteq U^{\prime },$$

(56)

which can be done because of Equation (51). Let us write

$$S\left(m_1,m_2\right)=\left(g_S\left(m_1,m_2\right),m_1\right).$$

Notice that, since

$$\left(m_1,m_2\right)={\Phi }_U\left(S\left(m_1,m_2\right)\right)={\Phi }_U\left(g_S\left(m_1,m_2\right),m_1\right)=\left(m_1,\rho \left(g_S\left(m_1,m_2\right),m_1\right)\right),$$

then

$$\rho \left(g_S\left(m_1,m_2\right),m_1\right)=m_2.$$

(57)

On the other hand, since $S\left(m_0,m_0\right)=\left(e,m_0\right)$, then

$$g_S\left(m_0,m_0\right)=e.$$

(58)

Moreover, from Equation (55), it follows that $\mathsf{Im}{\left(g_S\right)}_{*,\left(m_0,m_0\right)}\subseteq {\mathfrak{g}}_{m_0}^c$, and consequently (recall Equation (28))

$${\left({\rho }_{m_0}\right)}_{*,e}\circ {\left(g_S\right)}_{*,\left(m_0,m_0\right)}\left(x,y\right)=0⟺{\left(g_S\right)}_{*,\left(m_0,m_0\right)}\left(x,y\right)=0.$$

(59)

Now, consider the subset

$$U^{″}=U^{\prime }\cap \left(\rho \left(W,s\left(\pi \left(U^{\prime }\right)\right)\right)\right).$$

According to Lemma 2, $U^{″}$ is open (shrinking W and $U^{\prime }$ if needed) and, since $m_0$ is there (see Equation (51)), it is nonempty. Finally, define $\Theta :U^{″}\to G$ as

$$\Theta \left(m\right)=g_S\left(s\left(\pi \left(m\right)\right),m\right).$$

Let us see that $\Theta$ is well defined. If $m\in U^{″}$, then $m\in U^{\prime }$ and

$$m=\rho \left(g,s\left(\pi \left(m^{\prime }\right)\right)\right),\mathrm{with}g\in W\mathrm{and}{m}^{\prime }\in U^{\prime }.$$

Then, applying $\pi$ on both members of above equality, it follows that $\pi \left(m\right)=\pi \left(m^{\prime }\right)$, and consequently

$$m=\rho \left(g,s\left(\pi \left(m\right)\right)\right),\mathrm{with}g\in W.$$

In addition, since $m\in U^{\prime }$, then $s\left(\pi \left(m\right)\right)\in U^{\prime }$ (see Equation (56)). Thus, given $m\in U^{″}$ we have that

$$\left(s\left(\pi \left(m\right)\right),m\right)=\left(s\left(\pi \left(m\right)\right),\rho \left(g,s\left(\pi \left(m\right)\right)\right)\right)\in {\Phi }_U\left(W\times U^{\prime }\right),$$

i.e., $\left(s\left(\pi \left(m\right)\right),m\right)$ belongs to the domain of S. From Equation (58), it is clear that $\Theta \left(m_0\right)=e$ and, using Equation (57), the identity Equation (53) follows. A direct consequence of the latter is that, for all $m\in U^{″}$,

$$\left(i{d}_M\right){}_{*,m}={\left({\rho }_{\Theta \left(m\right)}\right)}_{*,s\left(\pi \left(m\right)\right)}\circ s_{*,\pi \left(m\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m}+{\left({\rho }_{s\left(\pi \left(m\right)\right)}\right)}_{*,\Theta \left(m\right)}\circ {\Theta }_{*,m},$$

(60)

which, in turn, implies that

$$\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m}\cap \mathsf{Ker}{\Theta }_{*,m}=\left\{0\right\},\forall m\in U^{″}.$$

(61)

Also, it implies that

$$v\in \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m}⟺v={\left({\rho }_{s\left(\pi \left(m\right)\right)}\right)}_{*,\Theta \left(m\right)}\circ {\Theta }_{*,m}\left(w\right),$$

(62)

for some w. Let us show it. The first implication is immediate by applying both sides of Equation (60) to v, and it is fulfilled for $w=v$. For the converse, it is enough to note that, from Equation (30),

$${\left({\pi }_{\left|U\right.}\right)}_{*,m}\circ {\left({\rho }_{s\left(\pi \left(m\right)\right)}\right)}_{*,\Theta \left(m\right)}=0.$$

Something similar to Equation (62) can be said about $\mathsf{Ker}{\Theta }_{*,m}$ for $m=m_0$. Let us see that. Equation (60) for $m=m_0$ decreases to

$$\left(i{d}_M\right){}_{*,m_0}=s_{*,\pi \left(m_0\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m_0}+{\left({\rho }_{m_0}\right)}_{*,e}\circ {\Theta }_{*,m_0},$$

(63)

since $s\left(\pi \left(m_0\right)\right)=m_0$ and $\Theta \left(m_0\right)=e.$

Then

$$v\in \mathsf{Ker}{\Theta }_{*,m_0}⟺v=s_{*,\pi \left(m_0\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(w\right),$$

(64)

for some w. The first implication follows by applying both sides of Equation (63) to v, and it is fulfilled for $w=v$. For the converse, note first that, using Equation (63),

$$s_{*,\pi \left(m_0\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(w\right)=v=s_{*,\pi \left(m_0\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(v\right)+{\left({\rho }_{m_0}\right)}_{*,e}\circ {\Theta }_{*,m_0}\left(v\right).$$

Then, applying ${\left({\pi }_{\left|U\right.}\right)}_{*,m_0}$ to the first and the last members and using the first part of Equation (52) and the fact that s is a section of ${\pi }_{\left|U\right.}$, we have that

$${\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(w\right)={\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(v\right),$$

and consequently $v=s_{*,\pi \left(m_0\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m_0}\left(v\right)$. Finally, combining Equations (59) and (63), the converse of Equation (64) follows. So, from Equation (62) at $m_0$ and Equation (64),

$$\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m_0}+\mathsf{Ker}{\Theta }_{*,m_0}=T_{m_0}M.$$

(65)

As a consequence (from Equations (61) and (65)), there exists an admissible neighborhood $\widehat{U}\subseteq U^{″}$ of $m_0$, such that

$$\mathsf{Ker}{\left({\pi }_{\left|\widehat{U}\right.}\right)}_{*,m}\oplus \mathsf{Ker}{\Theta }_{*,m}=T_{m}M,\forall m\in \widehat{U},$$

(66)

which tells us that the rank of $\Theta$ is constant and given by $\mathsf{k}=dimG-dim{G}_{m_0}$ (see Equation (34)). In resume, using the constant rank theorem, we can say that, shrinking the original admissible neighborhood U (if necessary), $\Theta \left(U\right)\subseteq G$ is a closed $\mathsf{k}$-dimensional submanifold and $\Theta :U\to \Theta \left(U\right)$ is a surjective submersion transverse to ${\pi }_{\left|U\right.}$, as we wanted to show. □

Remark 4.

It is worth mentioning that, combining Equations (60), (62) and (66), it follows for all $m\in U$ that

$$v\in \mathsf{Ker}{\Theta }_{*,m}⟺v={\left({\rho }_{\Theta \left(m\right)}\right)}_{*,s\left(\pi \left(m\right)\right)}\circ s_{*,\pi \left(m\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m}\left(v\right).$$

(67)

Let us study some properties of $\Theta$.

Proposition 7.

For any s-horizontal submersion $\Theta :U\to \Theta \left(U\right)$, we have that

$$\Theta \left(s\left(\lambda \right)\right)=e,\forall \lambda \in \pi \left(U\right).$$

(68)

Proof. 

First, recall that U is connected (ipso facto path connected) and consequently, the same is true for $\pi \left(U\right)$. On the one hand, given $\lambda \in \Pi \left(U\right)$, it follows from Equation (53) for $m=s\left(\lambda \right)$ that

$$\rho \left(\Theta \left(s\left(\lambda \right)\right),s\left(\lambda \right)\right)=s\left(\lambda \right),$$

which implies that $\Theta \left(s\left(\lambda \right)\right)\in G_{s\left(\lambda \right)}$. On the other hand, it is easy to see that, for all $g\in G$ and $m\in M$,

$$T_g{G}_m=\mathsf{Ker}{\left({\rho }_m\right)}_{*,g}.$$

Then, for every vector $w\in T_{\lambda }\pi \left(U\right)$,

$${\Theta }_{*,s\left(\lambda \right)}\left(s_{*,\lambda }\left(w\right)\right)\in \mathsf{Ker}{\left({\rho }_{s\left(\lambda \right)}\right)}_{*,\Theta \left(s\left(\lambda \right)\right)}.$$

As a consequence, applying Equation (60) to $v=s_{*,\lambda }\left(w\right)$ and using Equation (67), we have that

$$s_{*,\lambda }\left(w\right)\in \mathsf{Ker}{\Theta }_{*,s\left(\lambda \right)}.$$

So, given a curve $t\in \left(-ϵ,ϵ\right)\mapsto \lambda \left(t\right)\in \pi \left(U\right)$ such that $\lambda \left(0\right)=\pi \left(m_0\right)$, we have that

$$\Theta \left(s\left(\lambda \left(0\right)\right)\right)=\Theta \left(s\left(\pi \left(m_0\right)\right)\right)=\Theta \left(m_0\right)=e$$

and

$$\frac{d}{dt}\Theta \left(s\left(\lambda \left(t\right)\right)\right)=0,\forall t\in \left(-ϵ,ϵ\right),$$

from which, and the fact that $\pi \left(U\right)$ is connected, the proposition follows. □

Furthermore, given $m\in U$ and $g\in G$, such that $\rho \left(g,m\right)\in U$, it can be shown from Equation (53) that

$$\Theta \left(\rho \left(g,m\right)\right)=g·\Theta \left(m\right)·h$$

(69)

for a unique $h\in G_{s\left(\pi \left(m\right)\right)}$. Moreover, in infinitesimal terms around $g=e$,

$${\Theta }_{*,m}\circ {\left({\rho }_m\right)}_{*,e}\left(\eta \right)={\left(R_{\Theta \left(m\right)}\right)}_{*,e}\left(\eta \right)+{\left(L_{\Theta \left(m\right)}\right)}_{*,e}\left(\xi \right),$$

for some $\xi \in {\mathfrak{g}}_{s\left(\pi \left(m\right)\right)}$. In particular, if $m=s\left(\lambda \right)$ (see Equation (68)),

$${\Theta }_{*,s\left(\lambda \right)}\circ {\left({\rho }_{s\left(\lambda \right)}\right)}_{*,e}\left(\eta \right)=\eta +\xi .$$

(70)

As we anticipate at the end of the last subsection, the submersions $\Theta$ above defined play a role similar to that of $\psi$ in a trivialization of a principal bundle (see Equation (45)). This follows, for instance, by comparing Equations (46) and (53). In particular, we can see the map

$$A:v\in T_{m}U⟼{\left(R_{\Theta \left(m\right)}\right)}_{*,e}^{-1}{\Theta }_{*,m}\left(v\right)\in \mathfrak{g}$$

as some kind of flat connection for the submersion ${\pi }_{\left|U\right.}$. Nevertheless, Equations (49) and (50) are not satisfied in general. In fact, we have from Equation (69) that (for $g\in G$ and $m\in U$ such that $\rho \left(g,m\right)\in U$)

$$A\left({\left({\rho }_m\right)}_{*,e}\left(\eta \right)\right)=\eta +A{d}_{\Theta \left(m\right)}\xi ,\mathrm{for}\mathrm{some}\xi \in {\mathfrak{g}}_m,$$

and

$$A\left({\left({\rho }_g\right)}_{*,m}\left(v\right)\right)=A{d}_g\left(A\left(v\right)+A{d}_{\Theta \left(m\right)}\xi \right),\mathrm{for}\mathrm{some}\xi \in {\mathfrak{g}}_m.$$

3.3. Vertical and Horizontal Vector Fields

Fix again a point $m_0\in {\mathcal{R}}_{\rho }$.

Definition 2.

We shall say that $X\in \mathfrak{X}\left(M\right)$ is vertical around $m_0$ if

$$X\left(m\right)\in \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m},\forall m\in U,$$

and that X is horizontal at $m_0$ if

$$X\left(m_0\right)\notin \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m_0},$$

for some admissible neighborhood U of $m_0$. Finally, we shall say that X is Θ-horizontal if $\mathsf{Im}{X}_{\left|U\right.}\subseteq \mathsf{Ker}{\Theta }_{*}$ for some horizontal submersion $\Theta :U\to \Theta \left(U\right)$ and some admissible neighborhood U of $m_0$.

From Equation (33), it is clear that if there exists a function $\eta :U\to \mathfrak{g}$ such that $X\left(m\right)={\left({\rho }_m\right)}_{*,e}\left(\eta \left(m\right)\right),$ for all $m\in U,$, then X is vertical along $U.$ We are interested in vertical fields which are in addition G-invariant (see Equation (41)). For them, we have the next result.

Proposition 8.

Consider $X\in \mathfrak{X}\left(M\right)$ such that, for some function $\eta :M\to \mathfrak{g}$,

$$X\left(m\right)={\left({\rho }_m\right)}_{*,e}\left(\eta \left(m\right)\right),\forall m\in M.$$

(71)

Then X is G-invariant if, and only if,

$$\eta \left({\rho }_g\left(m\right)\right)=A{d}_g\left(\eta \left(m\right)\right)+{\xi }_{g,m},$$

(72)

for some ${\xi }_{g,m}\in {\mathfrak{g}}_{{\rho }_g\left(m\right)}$. We shall say that η is $Ad$-equivariant if ${\xi }_{g,m}=0$ for all $g,m$.

Proof. 

Since ${\rho }_{{\rho }_g\left(m\right)}={\rho }_m\circ R_g$ and ${\rho }_g\circ {\rho }_m={\rho }_m\circ L_g$, then

$$\begin{array}{ccc}{\left({\rho }_g\right)}_{*,m}^{-1}\circ X\left({\rho }_g\left(m\right)\right)\hfill & =\hfill & {\left({\rho }_m\right)}_{*,e}\circ {\left(L_{g^{-1}}\right)}_{*,g}\circ {\left(R_g\right)}_{*,e}\left(\eta \left({\rho }_g\left(m\right)\right)\right)\hfill \\ & =\hfill & {\left({\rho }_m\right)}_{*,e}\circ A{d}_{g^{-1}}\left(\eta \left({\rho }_g\left(m\right)\right)\right).\hfill \end{array}$$

Hence, Equation (41) is fulfilled if, and only if,

$$A{d}_{g^{-1}}\left(\eta \left({\rho }_g\left(m\right)\right)\right)-\eta \left(m\right)\in \mathsf{Ker}\left({\left({\rho }_m\right)}_{*,e}\right)={\mathfrak{g}}_m,$$

and the proposition follows from the fact that $A{d}_g\left({\mathfrak{g}}_m\right)={\mathfrak{g}}_{{\rho }_g\left(m\right)}$. □

Regarding horizontal fields, note that if X is $\Theta$-horizontal and $X\left(m_0\right)\ne 0$, then X is horizontal at $m_0$. Reciprocally, we have the next result.

Proposition 9.

If X is horizontal at $m_0$ and G-invariant, then there exist an admissible neighborhood U of $m_0$, a section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ satisfying Equation (51) and a horizontal submersion $\Theta :U\to \Theta \left(U\right)$ such that X is Θ-horizontal.

Proof. 

According to Proposition 4.13 of [11], if $X\left(m_0\right)\notin \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m_0}$ for some admissible neighborhood U of $m_0$, then, shrinking U if necessary, there exists a submersion $F:U\to F\left(U\right)$ transverse to ${\pi }_{\left|U\right.}$ such that

$$X\left(m\right)\in \mathsf{Ker}{F}_{*,m},\forall m\in U.$$

(73)

On the one hand, shrinking U again, this gives rise to a diffeomorphism

$$\mathfrak{D}=\left({\pi }_{\left|U\right.},F\right):U\to \pi \left(U\right)\times F\left(U\right).$$

In terms of the latter, we have the section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ given by

$$s\left(\pi \left(m\right)\right)={\mathfrak{D}}^{-1}\left(\pi \left(m\right),F\left(m_0\right)\right),$$

which satisfies $s\left(\pi \left(m_0\right)\right)=m_0$. So, we have a section of ${\pi }_{\left|U\right.}$ satisfying Equation (51) and, according to Theorem 2, this enables us to construct a horizontal submersion $\Theta :U\to \Theta \left(U\right)$. On the other hand, writing $s\left(\pi \left(m\right)\right)=\tilde{m}$, Equation (73) says that

$${\mathfrak{D}}_{*,\tilde{m}}\left(X\left(\tilde{m}\right)\right)=\left({\left({\pi }_{\left|U\right.}\right)}_{*,\tilde{m}}\left(X\left(\tilde{m}\right)\right),0\right),$$

or equivalently

$$X\left(\tilde{m}\right)={\left({\mathfrak{D}}^{-1}\right)}_{*,\left(\pi \left(m\right),F\left(m_0\right)\right)}\left({\left({\pi }_{\left|U\right.}\right)}_{*,\tilde{m}}\left(X\left(\tilde{m}\right)\right),0\right)=s_{*,\pi \left(m\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,\tilde{m}}\left(X\left(\tilde{m}\right)\right).$$

(74)

In addition, the fact that X is G-invariant ensures that (combine Equations (41) and (53))

$${\left({\rho }_{\Theta \left(m\right)}\right)}_{*,\tilde{m}}X\left(\tilde{m}\right)=X\left(m\right),$$

and consequently (see Equation (30))

$${\left({\pi }_{\left|U\right.}\right)}_{*,m}\left(X\left(m\right)\right)={\left({\pi }_{\left|U\right.}\right)}_{*,m}\circ {\left({\rho }_{\Theta \left(m\right)}\right)}_{*,\tilde{m}}X\left(\tilde{m}\right)={\left({\pi }_{\left|U\right.}\right)}_{*,\tilde{m}}\left(X\left(\tilde{m}\right)\right)$$

and (applying ${\left({\rho }_{\Theta \left(m\right)}\right)}_{*,\tilde{m}}$ to Equation (74))

$$X\left(m\right)={\left({\rho }_{\Theta \left(m\right)}\right)}_{*,\tilde{m}}\circ s_{*,\pi \left(m\right)}\circ {\left({\pi }_{\left|U\right.}\right)}_{*,m}\left(X\left(m\right)\right).$$

Finally, using Equation (67), it follows that $\mathsf{Im}{X}_{\left|U\right.}\subseteq \mathsf{Ker}{\Theta }_{*}$, as wanted. □

3.4. Local Complete Solutions from General Group Actions

From the above results and the duality between complete solutions and first integrals, the theorem below easily follows.

Theorem 3.

Fix $m_0\in {\mathcal{R}}_{\rho }$.

1. 

If X is vertical around $m_0$, then there exists an admissible neighborhood U of $m_0$ such that, for every section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ satisfying Equation (51) and every s-horizontal submersion $\Theta :U\to \Theta \left(U\right)$, the map

$$\Sigma ={\left(\Theta ,{\pi }_{\left|U\right.}\right)}^{-1}=\rho \circ \left(i{d}_{\Theta \left(U\right)}\times s\right):\Theta \left(U\right)\times \pi \left(U\right)\to U$$

is a complete solution of the Θ-HJE for $X_{\left|U\right.}$.

2. 

If X is horizontal at $m_0$ and G-invariant, then there exist an admissible neighborhood U of $m_0$, a section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ satisfying Equation (51) and a s-horizontal submersion $\Theta :U\to \Theta \left(U\right)$ such that (by τ we are denoting the flipping map $\tau \left(x,y\right)=\left(y,x\right)$)

$$\Sigma ={\left({\pi }_{\left|U\right.},\Theta \right)}^{-1}=\rho \circ \tau \circ \left(s\times i{d}_{\Theta \left(U\right)}\right):\pi \left(U\right)\times \Theta \left(U\right)\to U$$

is a complete solution of the ${\pi }_{\left|U\right.}$-HJE for $X_{\left|U\right.}$.

Proof. 

In the first case, we have that $\mathsf{Im}{X}_{\left|U\right.}\subseteq \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*}$ and that ${\pi }_{\left|U\right.}$ and $\Theta$ are transverse. Using the results of Section 2.2, it follows that, shrinking U if needed, $\Sigma ={\left(\Theta ,{\pi }_{\left|U\right.}\right)}^{-1}$ is a complete solution of the $\Theta$-HJE for $X_{\left|U\right.}$. We only need to show that ${\left(\Theta ,{\pi }_{\left|U\right.}\right)}^{-1}=\rho \circ \left(i{d}_{\Theta \left(U\right)}\times s\right)$ . However, from Equation (53), we have for all $m\in U$ that

$$\rho \circ \left(i{d}_{\Theta \left(U\right)}\times s\right)\circ \left(\Theta ,{\pi }_{\left|U\right.}\right)\left(m\right)=\rho \left(\Theta \left(m\right),s\left(\pi \left(m\right)\right)\right)=m.$$

The second case can be proven in the same way, but used in addition to Proposition 9 in order to ensure the existence of the section s and the submersion $\Theta$, such that $\mathsf{Im}{X}_{\left|U\right.}\in \mathsf{Ker}{\Theta }_{*}$. □

Remark 5.

Regarding the objects described in Section 3.2.1, it is clear that the complete solutions Σ given in the last theorem, or more precisely, their inverses ${\Sigma }^{-1}$, define the analogue of a trivialization $\Psi :U\to \pi \left(U\right)\times G$ of a principal bundle.

In summary, given a vertical vector field X around $m_0\in {\mathcal{R}}_{\rho }$, an admissible neighborhood U of $m_0$ and a smooth section $s:\pi \left(U\right)\to U$ of ${\pi }_{|U},$, we have shown that a submersion $\Theta :U\to \Theta \left(U\right)$ and a complete solution of the $\Theta$-HJE for $X_{\left|U\right.}$ can be constructed up to quadratures. Moreover, given a horizontal vector field X at $m_0$, if X is G-invariant, then there exists a complete solution of the ${\pi }_{\left|U\right.}$-HJE for $X_{\left|U\right.}$. However, the latter has not been constructed up to quadratures (the proof of Proposition 4.13 of [11], which is used in Proposition 9, is based on the rectification of the field X).

4. Horizontal Dynamical Systems and Reconstruction

Consider again a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a group action $\rho :G\times M\to M$. Assume by now that $\rho$ is free and proper, which implies that $\pi :M\to M/G$ defines a principal fiber bundle. Assume also that X is G-invariant, and consequently $\pi$-related with a unique vector field $Y\in \mathfrak{X}\left(M/G\right)$, i.e., ${\pi }_{*}\circ X=Y\circ \pi$. In many cases, the integral curves of Y are known, and one is interested in constructing the integral curves of X from those of Y. Any procedure that enables us to do that is usually called reconstruction. The purpose of this section is to show that there exists a deep connection between reconstruction procedures and the complete solutions of a horizontal vector field presented in Theorem 3, even though the action $\rho$ is neither free nor proper.

4.1. The Usual Reconstruction Process

Assume that we are in the setting of the beginning of this section and we want to find the integral curve $\Gamma$ of X such that $\Gamma \left(0\right)=p_0$. Then, we can (see, for instance, [29]):

1.

consider the integral curve $\gamma \left(t\right)$ of Y such that $\gamma \left(0\right)=\pi \left(p_0\right)$;

2.

fix a principal connection $A:TM\to \mathfrak{g}$;

3.

find a curve $d\left(t\right)$ such that

$$A\left(d^{\prime }\left(t\right)\right)=0\mathrm{and}\pi \left(d\left(t\right)\right)=\gamma \left(t\right),$$

(75)

i.e., $d\left(t\right)$ is the horizontal lift of $\gamma \left(t\right)$;

4.

find $g\left(t\right)$, such that

$$g^{\prime }\left(t\right)={\left(L_{g\left(t\right)}\right)}_{*,e}\left(\xi \left(t\right)\right)\mathrm{and}g\left(0\right)=g_0,$$

(76)

with $\xi \left(t\right)=A\left(X\left(d\left(t\right)\right)\right)$ and $g_0$ such that $p_0=\rho \left(g_0,d\left(0\right)\right)$.

It is easy to show that $\Gamma \left(t\right)=\rho \left(g\left(t\right),d\left(t\right)\right)$ is the integral curve that we are looking for. The four steps above constitute the usual reconstruction process , and Equations (75) and (76) the related reconstruction problem.

If X is vertical along all of M (in the usual sense), i.e., $\mathsf{Im}X\subseteq \mathsf{Ker}{\pi }_{*}$, then, $Y=0$ and consequently the curves $d\left(t\right)$ and $\xi \left(t\right)$ are constant. In this case, we only have to solve Equation (76), whose solutions are given by the exponential curves. We shall consider this situation in the next section. So, suppose that $X\left(m\right)\notin \mathsf{Ker}{\pi }_{*,m}$, for all $m\in M$. In that case, we can consider a connection A such that $X\in \mathsf{Ker}A$, i.e., X is horizontal with respect to A (in the usual sense). Then, $\xi \left(t\right)=0$ and $g\left(t\right)=g_0$ for all t. Consequently, the reconstruction problem decreases to solve Equation (75). In other words, we have the following alternative (three steps) reconstruction process:

1.

consider the integral curve $\gamma \left(t\right)$ of Y such that $\gamma \left(0\right)=\pi \left(p_0\right)$;

2.

find a principal connection $A:TM\to \mathfrak{g}$ such that X is horizontal;

3.

find a curve $d\left(t\right)$ satisfying Equation (75).

Then, the curve $\Gamma \left(t\right)=\rho \left(g_0,d\left(t\right)\right)$, with $g_0$ such that $p_0=\rho \left(g_0,d\left(0\right)\right)$, is the integral curve of X through $p_0$. In the next subsection, we shall extend this procedure to Lie group actions which are not necessarily free and proper.

4.2. Reconstruction from Complete Solutions

Let us go back to the general setting: a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a general Lie group action $\rho :G\times M\to M$. Assume that X is G-invariant and horizontal at every $m_0\in {\mathcal{R}}_{\rho }$ (see Definition 2). According to the second part of Theorem 3, there exist an admissible neighborhood U of $m_0$, a section $s:\pi \left(U\right)\to U$ of ${\pi }_{\left|U\right.}$ satisfying Equation (51) and a s-horizontal submersion $\Theta :U\to \Theta \left(U\right)$ such that

$$\Sigma =\rho \circ \tau \circ \left(s\times i{d}_{\Theta \left(U\right)}\right):\pi \left(U\right)\times \Theta \left(U\right)\to U$$

is a complete solution of the ${\pi }_{\left|U\right.}$-HJE for $X_{\left|U\right.}$. The related partial solutions are functions

$${\sigma }_g:\pi \left(U\right)\to U,g\in \Theta \left(U\right),$$

such that ${\sigma }_g\left(\lambda \right)=\rho \left(g,s\left(\lambda \right)\right)$ for all $\lambda \in \pi \left(U\right)$ (see (6)). In other words,

$${\sigma }_g={\rho }_g\circ s,g\in \Theta \left(U\right).$$

(77)

Theorem 4.

Each vector field $X^{{\sigma }_g}\in \mathfrak{X}\left(\pi \left(U\right)\right)$ (see (5)) is equal, for all $g\in \Theta \left(U\right)$, to the unique vector field $Y\in \mathfrak{X}\left(\pi \left(U\right)\right)$ such that

$${\left({\pi }_{\left|U\right.}\right)}_{*}\circ X_{\left|U\right.}=Y\circ {\pi }_{\left|U\right.}.$$

(78)

Proof. 

The Proposition 4 ensures the existence of a unique vector field $Y\in \mathfrak{X}\left(\pi \left(U\right)\right)$ satisfying Equation (78). So, we only must prove that $Y=X^{{\sigma }_g}$ for all $g\in \Theta \left(U\right)$. However, from Equations (5), (77) and (78),

$$\begin{array}{ccc}{X}^{{\sigma }_g}\hfill & =\hfill & {\left({\pi }_{\left|U\right.}\right)}_{*}\circ X_{\left|U\right.}\circ {\sigma }_g={\left({\pi }_{\left|U\right.}\right)}_{*}\circ X_{\left|U\right.}\circ {\rho }_g\circ s\hfill \\ & =\hfill & Y\circ {\pi }_{\left|U\right.}\circ {\rho }_g\circ s=Y\circ {\pi }_{\left|U\right.}\circ s=Y,\hfill \end{array}$$

as we wanted to show. □

According to Equation (10), the integral curves $\Gamma$ of X are given by

$$\Gamma \left(t\right)={\sigma }_g\left(\gamma \left(t\right)\right)=\rho \left(g,s\left(\gamma \left(t\right)\right)\right),$$

where $\gamma$ is an integral curve of $Y=X^{{\sigma }_g}$. In other words, the above formula enables us to construct the integral curves of X from those of a vector field in the quotient. Note that $\pi \left(\Gamma \left(t\right)\right)=\gamma \left(t\right)$ and $\Theta \left(\Gamma \left(t\right)\right)=g$ for all t. Then, given $p_0\in U$, in order to find the integral curve $\Gamma$ of $X_{\left|U\right.}$ such that $\Gamma \left(0\right)=p{}_0$, we have the following (two steps) reconstruction process:

1.

consider the integral curve $\gamma \left(t\right)$ of Y such that $\gamma \left(0\right)=\pi \left(p_0\right)$;

2.

find a submersion $\Theta :U\to \Theta \left(U\right)$ such that X is $\Theta$-horizontal.

The curve

$$\Gamma \left(t\right)=\Sigma \left(\gamma \left(t\right),g_0\right)=\rho \left(g_0,s\left(\gamma \left(t\right)\right)\right),\mathrm{with} g_0=\Theta \left(p_0\right),$$

is the one we are looking for. So, the complete solution $\Sigma$ solves the reconstruction problem (around $m_0$).

5. Vertical Dynamical Systems and Integrability by Quadratures

In this section, using the integrability result of Section 2 (see Theorem 1), we show that the exponential curves $t\mapsto exp\left(\xi t\right)$ of a Lie group G, for some points $\xi$ of its Lie algebra $\mathfrak{g}$, can be explicitly constructed up to quadratures. Moreover, we show that, for compact and for semisimple Lie groups, such a construction works for all $\xi$ inside a dense open subset of $\mathfrak{g}$. Then, we state sufficient conditions under which a vertical (and invariant) vector field is integrable up to quadratures.

5.1. Invariant and Vertical Vector Fields

Consider again a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a Lie group action $\rho :G\times M\to M$. Assume that X is vertical around every $\rho$-regular point $m_0$ (see Definition 2) and consider a complete solution

$$\Sigma =\rho \circ \left(i{d}_{\Theta \left(U\right)}\times s\right):\Theta \left(U\right)\times \pi \left(U\right)\to U$$

(79)

as those given in the first part of Theorem 3. The related partial solutions are

$${\sigma }_{\lambda }:\Theta \left(U\right)\subseteq G\to U,\lambda \in \pi \left(U\right),$$

with ${\sigma }_{\lambda }\left(g\right)=\rho \left(g,s\left(\lambda \right)\right)$ for all $g\in \Theta \left(U\right)$ (see Equation (6)). In other words,

$${\sigma }_{\lambda }={\rho }_{s\left(\lambda \right)},\lambda \in \pi \left(U\right).$$

Theorem 5.

If X is G-invariant, then the vector field $X^{{\sigma }_{\lambda }}\in \mathfrak{X}\left(\Theta \left(U\right)\right)$ (see Equation (5)) is given by

$$X^{{\sigma }_{\lambda }}\left(g\right)={\left(L_g\right)}_{*,e}\left({\eta }_{\lambda }\right)$$

(80)

for a unique vector (recall Equation (68))

$${\eta }_{\lambda }={\Theta }_{*,s\left(\lambda \right)}\circ X\left(s\left(\lambda \right)\right)\in T_e\Theta \left(U\right)\subseteq \mathfrak{g}.$$

(81)

In particular, if X is given by Equations (71) and (72), then

$${\eta }_{\lambda }=\eta \left(s\left(\lambda \right)\right)+{\xi }_{\lambda }$$

(82)

for some ${\xi }_{\lambda }\in {\mathfrak{g}}_{s\left(\lambda \right)}$. In any case, the integral curve of X passing through $p_0\in U$ at $t=0$ can be written

$$\Gamma \left(t\right)=\rho \left(g_{0}exp\left(\left({\eta }_{\lambda }+{\chi }_{\lambda }\right)t\right),s\left(\lambda \right)\right),$$

(83)

with $\left(g_0,\lambda \right)=\left(\Theta \left(p_0\right),\pi \left(p_0\right)\right)$ and ${\chi }_{\lambda }\in {\mathfrak{g}}_{s\left(\lambda \right)}$ arbitrary.

Proof. 

We know that (see Equation (4))

$$X\circ {\sigma }_{\lambda }={\left({\sigma }_{\lambda }\right)}_{*}\circ X^{{\sigma }_{\lambda }},$$

(84)

and consequently $\mathsf{Im}\left(X\circ {\sigma }_{\lambda }\right)\subseteq \mathsf{Im}{\left({\sigma }_{\lambda }\right)}_{*}$. Since ${\sigma }_{\lambda }$ is a diffeomorphism onto its image, then

$${\left({\sigma }_{\lambda }\right)}_{*,e}:T_e\Theta \left(U\right)\to T_{s\left(\lambda \right)}\mathsf{Im}{\sigma }_{\lambda }=\mathsf{Im}{\left({\sigma }_{\lambda }\right)}_{*,e}$$

is a linear isomorphism. So, for $X\circ {\sigma }_{\lambda }\left(e\right)=X\left(s\left(\lambda \right)\right)\in \mathsf{Im}{\left({\sigma }_{\lambda }\right)}_{*,e}$, there exists a unique vector ${\eta }_{\lambda }\in \mathfrak{g}$, such that

$${\left({\sigma }_{\lambda }\right)}_{*,e}\left({\eta }_{\lambda }\right)=X\left(s\left(\lambda \right)\right).$$

Let us apply ${\left({\rho }_g\right)}_{*,s\left(\lambda \right)}$ on both members of above equation. For the first member, we have that

$${\left({\rho }_g\right)}_{*,s\left(\lambda \right)}\circ {\left({\sigma }_{\lambda }\right)}_{*,e}\left({\eta }_{\lambda }\right)={\left({\sigma }_{\lambda }\right)}_{*,g}\circ {\left(L_g\right)}_{*,e}\left({\eta }_{\lambda }\right),$$

where we have used that ${\sigma }_{\lambda }={\rho }_{s\left(\lambda \right)}$ and the identity

$${\rho }_g\circ {\rho }_{s\left(\lambda \right)}={\rho }_{s\left(\lambda \right)}\circ L_g.$$

For the second member, using the G-invariance of X (recall Equation (41)), we have that

$${\left({\rho }_g\right)}_{*,s\left(\lambda \right)}\left(X\left(s\left(\lambda \right)\right)\right)=X\left({\rho }_g\left(s\left(\lambda \right)\right)\right)=X\left({\sigma }_{\lambda }\left(g\right)\right).$$

Then

$${\left({\sigma }_{\lambda }\right)}_{*,g}\circ {\left(L_g\right)}_{*,e}\left({\eta }_{\lambda }\right)=X\left({\sigma }_{\lambda }\left(g\right)\right)$$

and, consequently, Equation (80) follows from Equation (84) and the injectivity of ${\sigma }_{\lambda }$. Finally, using Equation (80) and the fact that $X^{{\sigma }_{\lambda }}={\Theta }_{*}\circ X\circ {\sigma }_{\lambda }$ (see Equation (5)),

$${\eta }_{\lambda }=X^{{\sigma }_{\lambda }}\left(e\right)={\Theta }_{*}\circ X\circ {\sigma }_{\lambda }\left(e\right)={\Theta }_{*,s\left(\lambda \right)}\circ X\left(s\left(\lambda \right)\right),$$

which gives precisely Equation (81). In particular, if X is given by Equations (71) and (72), using Equation (70), we easily obtain Equation (82).

Now, let us prove Equation (83). Given a curve

$$\Gamma \left(t\right)=\rho \left(\gamma \left(t\right),s\left(\lambda \right)\right)={\rho }_{s\left(\lambda \right)}\left(\gamma \left(t\right)\right)={\sigma }_{\lambda }\left(\gamma \left(t\right)\right),$$

with $\gamma \left(t\right)=g_{0}exp\left(\left({\eta }_{\lambda }+{\chi }_{\lambda }\right)t\right)$, since ${\gamma }^{\prime }\left(t\right)={\left(L_{\gamma \left(t\right)}\right)}_{*,e}\left({\eta }_{\lambda }+{\chi }_{\lambda }\right)$, then

$${\Gamma }^{\prime }\left(t\right)={\left({\sigma }_{\lambda }\right)}_{*,\gamma \left(t\right)}\circ {\left(L_{\gamma \left(t\right)}\right)}_{*,e}\left({\eta }_{\lambda }\right)+{\left({\sigma }_{\lambda }\right)}_{*,\gamma \left(t\right)}\circ {\left(L_{\gamma \left(t\right)}\right)}_{*,e}\left({\chi }_{\lambda }\right).$$

On the other hand, given a curve $h\left(x\right)$ on $G_{s\left(\lambda \right)}$ such that $h\left(0\right)=e$ and $h^{\prime }\left(0\right)={\chi }_{\lambda }$, since

$${\sigma }_{\lambda }\left(L_g\left(h\left(x\right)\right)\right)=\rho \left(gh\left(x\right),s\left(\lambda \right)\right)=\rho \left(g,s\left(\lambda \right)\right),\forall g\in G,$$

then ${\left({\sigma }_{\lambda }\right)}_{*,\gamma \left(t\right)}\circ {\left(L_{\gamma \left(t\right)}\right)}_{*,e}\left({\chi }_{\lambda }\right)=0$ for all t. Accordingly, using Equations (80) and (84),

$${\Gamma }^{\prime }\left(t\right)={\left({\sigma }_{\lambda }\right)}_{*,\gamma \left(t\right)}\circ {\left(L_{\gamma \left(t\right)}\right)}_{*,e}\left({\eta }_{\lambda }\right)={\left({\sigma }_{\lambda }\right)}_{*,\gamma \left(t\right)}\circ X^{{\sigma }_{\lambda }}\left(\gamma \left(t\right)\right)=X\left({\sigma }_{\lambda }\left(\gamma \left(t\right)\right)\right)=X\left(\Gamma \left(t\right)\right),$$

i.e., $\Gamma$ is an integral curve of X. If $\Gamma \left(0\right)=p_0$, then (see Equation (79))

$$p_0={\sigma }_{\lambda }\left(g_0\right)=\Sigma \left(g_0,\lambda \right)={\left(\Theta ,{\pi }_{\left|U\right.}\right)}^{-1}\left(g_0,\lambda \right),$$

which ends our proof. □

In order to consider concrete examples of vertical and G-invariant fields, suppose that M is a symplectic manifold, with symplectic form $\omega$, and $\rho$ is a symplectic action with an $A{d}^{*}$-equivariant momentum map K.

Proposition 10.

If $\varphi :{\mathfrak{g}}^{*}\to \mathfrak{g}$ is equivariant, i.e.,

$$A{d}_g\varphi \left(\alpha \right)=\varphi \left(A{d}_g^{*}\alpha \right),\forall \alpha \in {\mathfrak{g}}^{*},g\in G,$$

(85)

then

$$X={\omega }^{♯}\circ K^{*}\varphi$$

is vertical and G-invariant. Furthermore, given an admissible neighborhood U and a complete solution Equation (79), the related vector ${\eta }_{\lambda }\in \mathfrak{g}$ (see Equation (81)), for each $\lambda \in \pi \left(U\right)$, is given by

$${\eta }_{\lambda }=\varphi \left(K\left(s\left(\lambda \right)\right)\right)+{\xi }_{\lambda },$$

(86)

for some ${\xi }_{\lambda }\in {\mathfrak{g}}_{s\left(\lambda \right)}$. In particular, the integral curve of X passing through $p_0\in U$ at $t=0$ can be written

$$\Gamma \left(t\right)=\rho \left(g_{0}exp\left(\varphi \left(K\left(s\left(\lambda \right)\right)\right)t\right),s\left(\lambda \right)\right),$$

(87)

with $\left(g_0,\lambda \right)=\left(\Theta \left(p_0\right),\pi \left(p_0\right)\right)$.

Proof. 

The form of X ensures that $X\left(m\right)\in {\left(\mathsf{Ker}{K}_{*,m}\right)}^{\perp }$, for all $m\in M$. Then, for every admissible neighborhood U, we have from Equation (43) that

$$X\left(m\right)\in \left(\mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*,m}\right),\forall m\in U,$$

i.e., X is vertical. To show G-invariance, note first that Equation (44) implies the equality

$$K_{*,{\rho }_g\left(m\right)}\circ {\left({\rho }_g\right)}_{*,m}=A{d}_g^{*}\circ K_{*,m},$$

and in dual form (changing g by $g^{-1}$ and m by ${\rho }_g\left(m\right)$)

$${\left({\rho }_{g^{-1}}\right)}_{{\rho }_g\left(m\right)}^{*}\circ K_m^{*}=K_{{\rho }_g\left(m\right)}^{*}\circ A{d}_g.$$

Combining the equation above, Equations (39), (44) and (85), we obtain

$${\left({\rho }_g\right)}_{*,m}\left(X\left(m\right)\right)={\left({\rho }_g\right)}_{*,m}\left({\omega }_m^{♯}\circ K_m^{*}\left(\varphi \left(K\left(m\right)\right)\right)\right)=X\left({\rho }_g\left(m\right)\right),$$

as desired. Now, we will show Equation (86). From the very definition of K (see Equation (42)), we have that ${\omega }_m^{♭}\circ {\left({\rho }_m\right)}_{*,e}=K_m^{*}$, so

$${\eta }_{\lambda }={\Theta }_{*,s\left(\lambda \right)}\circ X\left(s\left(\lambda \right)\right)={\Theta }_{*,s\left(\lambda \right)}\circ {\left({\rho }_{s\left(\lambda \right)}\right)}_{*,e}\left(\varphi \left(K\left(s\left(\lambda \right)\right)\right)\right).$$

Thus, Equation (86) follows from Equation (70). Finally, Equation (87) is a direct consequence of the previous theorem. □

5.2. The Cotangent Bundle and the Left Multiplication

5.2.1. A Class of Invariant Vertical Vectors

Given a Lie group G, consider its cotangent bundle $T^{*}G$ with its canonical symplectic structure ${\omega }_G=-d{\theta }_G$. Consider also the action

$$\rho :G\times T^{*}G\to T^{*}G$$

such that, for all $g\in G$ and ${\alpha }_h\in T_h^{*}G$,

$$\rho \left(g,{\alpha }_h\right)={\left[{\left(L_g\right)}_h^{*}\right]}^{-1}\left({\alpha }_h\right)\in T_{gh}^{*}G.$$

Note that $\rho$ is symplectic (see Equation (39)) and has an $A{d}^{*}$-equivariant momentum map $J:T^{*}G\to {\mathfrak{g}}^{*}$ given by

$$J\left({\alpha }_g\right)={\left(R_g\right)}_e^{*}\left({\alpha }_g\right).$$

Furthermore, $\rho$ is a free and proper action, the quotient $T^{*}G/G$ is a manifold diffeomorphic to ${\mathfrak{g}}^{*}$ and the canonical projection $\pi$ can be seen as the submersion

$$\pi :T^{*}G\to {\mathfrak{g}}^{*}:{\alpha }_g⟼{\left(L_g\right)}_e^{*}\left({\alpha }_g\right).$$

In other words, every point of $T^{*}G$ is $\rho$-regular and the whole of $T^{*}G$ is an admissible neighborhood. Then, according to Proposition 4 (see Equation (40)),

$${\Xi }^{♯}\left(\eta \right)={\pi }_{*,\alpha }\circ {\omega }_G^{♯}\circ {\pi }_{\alpha }^{*}\left(\eta \right),\eta \in T_{\alpha }^{*}{\mathfrak{g}}^{*},$$

(88)

defines a Poisson bracket on ${\mathfrak{g}}^{*}$ and $\pi$ is a Poisson morphism between $\left(T^{*}G,{\omega }_G\right)$ (with its related Poisson structure) and $\left({\mathfrak{g}}^{*},\Xi \right)$. Moreover, it can be shown that $\Xi$ is the Kirillov–Kostant bracket on ${\mathfrak{g}}^{*}$ (see [18]), i.e.,

$${\Xi }^{♯}\left(\eta \right)=a{d}_{\eta }^{*}\alpha ,\eta \in T_{\alpha }^{*}{\mathfrak{g}}^{*}\cong \mathfrak{g}.$$

(89)

On the other hand, the map $s:{\mathfrak{g}}^{*}\to T^{*}G$, such that $s\left(\alpha \right)=\alpha \in T_e^{*}G={\mathfrak{g}}^{*}$ is a global section of $\pi$ and satisfies $s\left(\pi \left(\alpha \right)\right)=\alpha$ for all $\alpha \in {\mathfrak{g}}^{*}$. A related horizontal submersion is the map $\Theta :T^{*}G\to G$ such that $\Theta \left({\alpha }_g\right)=g$, i.e., the canonical cotangent projection ${\pi }_G:T^{*}G\to G$. In fact,

$$\rho \left({\pi }_G\left({\alpha }_g\right),s\left(\pi \left({\alpha }_g\right)\right)\right)=\rho \left(g,{\left(L_g\right)}_e^{*}\left({\alpha }_g\right)\right)={\left[{\left(L_g\right)}_e^{*}\right]}^{-1}\left({\left(L_g\right)}_e^{*}\left({\alpha }_g\right)\right)={\alpha }_g,$$

for all ${\alpha }_g\in T_g^{*}G$.

Remark 6.

Note that $\left({\pi }_G,\pi \right):T^{*}G\to G\times {\mathfrak{g}}^{*}$ is the left trivialization of $T^{*}G.$ Thus, $T^{*}G$ may be identified with $G\times \mathfrak{g}$ and, under this identification, the projections ${\pi }_G:T^{*}G\to G$ and $\pi :T^{*}G\to {\mathfrak{g}}^{*}$ are just the canonical projections

$$p{r}_1:G\times {\mathfrak{g}}^{*}\to Gandp{r}_2:G\times {\mathfrak{g}}^{*}\to {\mathfrak{g}}^{*}$$

on the first and second factor, respectively. Moreover, the canonical symplectic structure ${\omega }_G$ on $T^{*}G$ is the 2-form on $G\times {\mathfrak{g}}^{*}$ given by

$${\omega }_G(g,\alpha )((v_g,\beta ),(v_g^{\prime },{\beta }^{\prime }))={\beta }^{\prime }\left({\left(L_{g^{-1}}\right)}_{*g}\left(v_g\right)\right)-\beta \left({\left(L_{g^{-1}}\right)}_{*g}\left(v_g^{\prime }\right)\right)+\left(a{d}_{{\left(L_{g^{-1}}\right)}_{*g}\left(v_g\right)}^{*}\alpha \right)\left({\left(L_{g^{-1}}\right)}_{*g}\left(v_g^{\prime }\right)\right),$$

(90)

for $(g,\alpha )\in G\times {\mathfrak{g}}^{*}$ and $(v_g,\beta ),(v_g^{\prime },{\beta }^{\prime })\in T_{g}G\times {\mathfrak{g}}^{*}\cong T_{g}G\times T_{\alpha }{\mathfrak{g}}^{*}$ (see [9]). In addition, the action $\rho :G\times (G\times {\mathfrak{g}}^{*})\to G\times {\mathfrak{g}}^{*}$ is just the left translation on the first factor, that is,

$$\rho \left(g,\left(g^{\prime },\alpha \right)\right)=\left(g{g}^{\prime },\alpha \right)forg,g^{\prime }\in Gand\alpha \in {\mathfrak{g}}^{*},$$

and the momentum map $J:G\times \mathfrak{g}\to {\mathfrak{g}}^{*}$ is just the co-adjoint action of G on ${\mathfrak{g}}^{*}$

$$J\left(g,\alpha \right)=A{d}_{g^{-1}}^{*}\alpha$$

(for more details, see [9]).

According to Theorem 3 (part 1), for every vertical vector field $X\in \mathfrak{X}\left(T^{*}G\right)$ along all of $T^{*}G$,

$$\Sigma ={\left({\pi }_G,\pi \right)}^{-1}=\rho \circ \left(i{d}_G\times s\right):G\times {\mathfrak{g}}^{*}\to T^{*}G$$

(91)

is a (global) complete solution of the ${\pi }_G$-HJE for X. If, in addition, X is G-invariant, then its integral curve with initial condition $\Gamma \left(0\right)={\left({\pi }_G,\pi \right)}^{-1}\left(g_0,\alpha \right)$ is (recall Equations (81) and (83))

$$\Gamma \left(t\right)=\rho \left(g_{0}exp\left({\eta }_{\alpha }t\right),s\left(\alpha \right)\right)={\left[{\left(L_{g_{0}exp\left({\eta }_{\alpha }t\right)}\right)}_e^{*}\right]}^{-1}\left(\alpha \right),$$

with

$${\eta }_{\alpha }={\left({\pi }_G\right)}_{*,\alpha }\left(X\left(\alpha \right)\right).$$

(92)

We have used above that $s\left(\alpha \right)=\alpha$. This is the case, for instance, of a vector field X of the form

$$X^{\varphi }={\omega }_G^{♯}\circ {\pi }^{*}\varphi ,$$

(93)

with $\varphi \in {\Omega }^1\left({\mathfrak{g}}^{*}\right)$ such that

$${\Xi }^{♯}\left(\varphi \left(\alpha \right)\right)=a{d}_{\varphi \left(\alpha \right)}^{*}\alpha =0,$$

(94)

i.e., $\varphi$ is a Casimir 1-form with respect to the Poisson bracket Equation (89). The G-invariance of $X^{\varphi }$ is immediate from Equations (39) and (41), and the verticality is ensured by Equations (88) and (94). On the other hand, it can be shown that ${\eta }_{\alpha }=\varphi \left(\alpha \right)$. In fact, using the left trivialization of $T^{*}G,$, we can identify $T^{*}G$ with $G\times {\mathfrak{g}}^{*}$ (see Remark 6). Under this identification, $X^{\varphi }$ may be considered as a vector field on $G\times {\mathfrak{g}}^{*}$ and, from Equations (90) and (93), it follows that

$$X^{\varphi }\left(g,\alpha \right)=\left(\left(L_g\right){}_{*,e}\left(\varphi \left(\alpha \right)\right),a{d}_{\varphi \left(\alpha \right)}^{*}\alpha \right)=\left(\left(L_g\right){}_{*,e}\left(\varphi \left(\alpha \right)\right),0\right),$$

for all $(g,\alpha )\in G\times {\mathfrak{g}}^{*}$. Thus, using Equation (92) and Remark 6, we deduce that

$${\eta }_{\alpha }=\left({\pi }_G\right){}_{*,\alpha }\left(X_{\left(e,\alpha \right)}^{\varphi }\right)=\varphi \left(\alpha \right),\mathrm{for} \mathrm{all} \alpha \in {\mathfrak{g}}^{*}.$$

So, in terms of $\Sigma$, the trajectories of $X^{\varphi }$ can be written

$$\Gamma \left(t\right)=\Sigma \left(g_{0}exp\left(\varphi \left(\alpha \right)t\right),\alpha \right)=\rho \left(g_{0}exp\left(\varphi \left(\alpha \right)t),\alpha \right)\right).$$

5.2.2. Construction of the Exponential Curves up to Quadratures

In this subsection, we are going to show that $X^{\varphi }$ (see Equation (93)) is integrable up to quadratures (on a dense subset of $T^{*}G$) and, consequently, the exponential curves $exp\left(\varphi \left(\alpha \right)t\right)$ can be explicitly obtained, also up to quadratures. The proof will be based on Theorem 1.

Proposition 11.

Consider the co-adjoint action $A{d}^{*}:G\times {\mathfrak{g}}^{*}\to {\mathfrak{g}}^{*}$ and the related isotropy subgroups $G_{\alpha }$, with $\alpha \in {\mathfrak{g}}^{*}$. Then, for every $A{d}^{*}$-regular point ${\alpha }_0$ and any admissible neighborhood $V\subseteq {\mathfrak{g}}^{*}$ of ${\alpha }_0$, the function

$$F={\left(J,\pi \right)}_{\left|U\right.}:U=J^{-1}\left(V\right)\subseteq T^{*}G\to {\mathfrak{g}}^{*}\times {\mathfrak{g}}^{*}$$

(95)

is a submersion onto the closed submanifold

$$F\left(U\right)=\left\{\left(\alpha ,A{d}_g^{*}\alpha \right):\alpha \in V,g\in G\right\}\subseteq {\mathfrak{g}}^{*}\times {\mathfrak{g}}^{*}.$$

Moreover,

$$\mathsf{Ker}{F}_{*}=\mathsf{Ker}{\left(J_{\left|U\right.}\right)}_{*}\cap \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*}$$

(96)

and

$$\mathsf{Ker}{F}_{*}\subseteq {\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }.$$

(97)

Proof. 

It is easy to see that the composition of $\left(J,\pi \right):T^{*}G\to {\mathfrak{g}}^{*}\times {\mathfrak{g}}^{*}$ and

$${\mathfrak{R}}^{-1}:G\times {\mathfrak{g}}^{*}\to T^{*}G:\left(g,\alpha \right)\to {\left({\left(R_g\right)}_e^{*}\right)}^{-1}\left(\alpha \right)$$

(the inverse of the right trivialization) gives

$$\left(J,\pi \right)\circ {\mathfrak{R}}^{-1}\left(g,\alpha \right)=\left(\alpha ,A{d}_g^{*}\alpha \right).$$

Then, given an $A{d}^{*}$-regular point ${\alpha }_0$ and an admissible neighborhood $V\subseteq {\mathfrak{g}}^{*}$ of ${\alpha }_0$, we have from Proposition 3 (applied to the action $A{d}^{*}$) that $\left(J,\pi \right)\circ {\mathfrak{R}}^{-1}$ restricted to $G\times V$ is a submersion onto the closed submanifold $F\left(U\right)\subseteq V\times {\mathfrak{g}}^{*}$. As a consequence, since ${\mathfrak{R}}^{-1}$ is a diffeomorphism, the first affirmation of the proposition follows. On the other hand, Equation (96) follows straightforwardly and Equation (97) is a direct consequence of the identity $\mathsf{Ker}{J}_{*}={\left(\mathsf{Ker}{\pi }_{*}\right)}^{\perp }$ and the inclusion

$$\begin{array}{ccc}{\left(\mathsf{Ker}{J}_{*}\cap \mathsf{Ker}{\pi }_{*}\right)}^{\perp }\hfill & =\hfill & {\left(\mathsf{Ker}{J}_{*}\right)}^{\perp }+{\left(\mathsf{Ker}{\pi }_{*}\right)}^{\perp }\hfill \\ & =\hfill & \mathsf{Ker}{\pi }_{*}+\mathsf{Ker}{J}_{*}\supseteq \mathsf{Ker}{J}_{*}\cap \mathsf{Ker}{\pi }_{*}.\hfill \end{array}$$

□

Remark 7.

A similar result was proved in [20] (see Theorem 4.1 there), but in terms of Poisson sub-algebras (see Remark 2).

Because of the form of $X^{\varphi }$, it is clear that $\mathsf{Im}{X}^{\varphi }\subseteq {\left(\mathsf{Ker}{\pi }_{*}\right)}^{\perp }$. As a consequence, (recall Equation (43))

$$\mathsf{Im}{X}^{\varphi }\subseteq \mathsf{Ker}{J}_{*}\cap \mathsf{Ker}{\pi }_{*}.$$

(98)

So, using the last proposition and combining Equations (96)–(98), it follows that, for each $A{d}^{*}$-regular point ${\alpha }_0$, we can construct a neighborhood U of ${\alpha }_0$ and a submersion $F:U\to F\left(U\right)$ (given by Equation (95)), such that

$$\mathsf{Im}{X}_{\left|U\right.}^{\varphi }\subseteq \mathsf{Ker}{F}_{*}\mathrm{and}\mathsf{Ker}{F}_{*}\subseteq {\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }.$$

Remark 8.

It can be shown that ${\left(\mathsf{Ker}{F}_{*}\right)}^{\perp }$ is an integrable distribution. Then, if ϕ is an exact 1-form, $X_{\left|U\right.}^{\varphi }$ and F define a NCI system on U (see Section 2.4).

In addition, since $\mathsf{Ker}{F}_{*}\subseteq \mathsf{Ker}{\left({\pi }_{\left|U\right.}\right)}_{*}$, we have that

$$L_{X^{\varphi }}{\beta }^{\varphi }=0,\mathrm{with}{\beta }^{\varphi }={\pi }^{*}\varphi ,$$

as we saw at the end of Section 2.3 (recall Equations (25) and (26)). This enables us to apply Theorem 1 to $X_{\left|U\right.}^{\varphi }$.

Remark 9.

For each $n\in \Pi \left(U\right)$, the map ${\beta }_n^{\varphi }\in {\Omega }^1\left(F\left(U\right)\right)$ related to ${\beta }^{\varphi }$ and defined by Equation (17), is given by

$${\beta }_n^{\varphi }=p{r}_1^{*}\varphi ,$$

(99)

with $p{r}_1:{\mathfrak{g}}^{*}\times {\mathfrak{g}}^{*}\to {\mathfrak{g}}^{*}$ the projection onto the first factor.

According to the proof of Theorem 1, we can construct up to quadratures, a submersion $\Pi :U\to \Pi \left(U\right)$ transverse to F, a complete solution $\widehat{\Sigma }={\left(\Pi ,F\right)}^{-1}$ and a family of immersions (see Equation (21))

$${\phi }_{\lambda }:\Pi \left(U\right)\to T_{\lambda }^{*}F\left(U\right),\lambda \in F\left(U\right),$$

such that the integral curves of $X_{\left|U\right.}^{\varphi }$ are given by $\Gamma \left(t\right)=\widehat{\Sigma }\left(\gamma \left(t\right),\lambda \right)$, with $\gamma$ satisfying (see Equations (22) and (99))

$${\phi }_{\lambda }\left(\gamma \left(t\right)\right)={\phi }_{\lambda }\left(\gamma \left(0\right)\right)+t\varphi \left(p{r}_1\left(\lambda \right)\right).$$

(100)

On the other hand, we know that $\Gamma \left(t\right)=\Sigma \left(g_{0}exp\left(\varphi \left(\alpha \right)t\right),\alpha \right)$ for some $g_0$ and $\alpha$, with $\Sigma$ given by Equation (91). So, for an integral curve passing through

$$\Gamma \left(0\right)=\Sigma \left(e,\alpha \right)=\alpha =\widehat{\Sigma }\left(\gamma \left(0\right),\lambda \right),$$

(101)

since

$$\lambda =F\circ \widehat{\Sigma }\left(\gamma \left(0\right),\lambda \right)=F\left(\alpha \right)=\left(J,\pi \right)\left(\alpha \right)=\left(\alpha ,\alpha \right),$$

we have that $\Sigma \left(exp\left(\varphi \left(\alpha \right)t\right),\alpha \right)=\widehat{\Sigma }\left(\gamma \left(t\right),\left(\alpha ,\alpha \right)\right)$. Consequently

$$exp\left(\varphi \left(\alpha \right)t\right)={\pi }_G\circ \widehat{\Sigma }\left(\gamma \left(t\right),\left(\alpha ,\alpha \right)\right),$$

with $\gamma$ satisfying (see Equation (100))

$${\phi }_{\left(\alpha ,\alpha \right)}\left(\gamma \left(t\right)\right)={\phi }_{\left(\alpha ,\alpha \right)}\left(\Pi \left(\alpha \right)\right)+t\varphi \left(\alpha \right),$$

and where we have used that (see Equation (101))

$$\gamma \left(0\right)=\Pi \circ \widehat{\Sigma }\left(\gamma \left(0\right),\lambda \right)=\Pi \circ \Sigma \left(e,\alpha \right)=\Pi \left(\alpha \right).$$

Hence, we have shown the next result.

Proposition 12.

Given a Casimir 1-form $\varphi :{\mathfrak{g}}^{*}\to \mathfrak{g}$ and a point $\alpha \in {\mathcal{R}}_{A{d}^{*}}$, the exponential curve $exp\left(\varphi \left(\alpha \right)t\right)$ can be constructed up to quadratures. More explicitly, it is given by the formula

$$exp\left(\varphi \left(\alpha \right)t\right)={\pi }_G\left({\left(\Pi ,F\right)}^{-1}\left({\phi }_{\left(\alpha ,\alpha \right)}^{-1}\left[{\phi }_{\left(\alpha ,\alpha \right)}\left(\Pi \left(\alpha \right)\right)+t\varphi \left(\alpha \right)\right],\left(\alpha ,\alpha \right)\right)\right),$$

(102)

being ${\phi }_{\left(\alpha ,\alpha \right)}^{-1}$ a local lateral inverse of the immersion ${\phi }_{\left(\alpha ,\alpha \right)}$.

It is natural to ask, given $\xi \in \mathfrak{g}$, if we can construct $exp\left(\xi t\right)$ up to quadratures. In the following subsection, we shall give a partial answer to that question.

5.2.3. The Case of Semisimple and Compact Lie Groups

Let G be a Lie group with Lie algebra $\mathfrak{g}.$

Theorem 6.

Consider $\xi \in \mathfrak{g}$ such that

$$a{d}_{\xi }\left(\mathfrak{g}\right){}^0\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing ,$$

where $a{d}_{\xi }\left(\mathfrak{g}\right){}^0$ is the annihilator in ${\mathfrak{g}}^{*}$ of the subspace $a{d}_{\xi }\left(\mathfrak{g}\right)\subseteq \mathfrak{g}$.

1. 

If ${\alpha }_0\in a{d}_{\xi }\left(\mathfrak{g}\right){}^0\cap {\mathcal{R}}_{A{d}^{*}}$, then, we can construct a Casimir 1-form $\varphi :{\mathfrak{g}}^{*}\to \mathfrak{g}$ such that $\varphi \left({\alpha }_0\right)=\xi .$

2. 

The curve $t\mapsto exp\left(\xi t\right)$ can be obtained by quadratures.

Proof. 

Take ${\alpha }_0\in a{d}_{\xi }\left(\mathfrak{g}\right){}^0\cap {\mathcal{R}}_{A{d}^{*}}$. Then, ${\alpha }_0\left([\xi ,\eta ]\right)=0,$ for all $\eta \in \mathfrak{g}$ or, in other words, $\xi \in {\mathfrak{g}}_{{\alpha }_0}$ with ${\mathfrak{g}}_{{\alpha }_0}$ the isotropy algebra of ${\alpha }_0$ with respect to the co-adjoint representation of G on ${\mathfrak{g}}^{*}$. Let $V\subseteq {\mathfrak{g}}^{*}$ be an admissible neighborhood of ${\alpha }_0$. Then (see Remark 3) the assigning

$$\alpha \in V⟼{\mathfrak{g}}_{\alpha }\subseteq \mathfrak{g}$$

defines a vector subbundle $W={\coprod }_{\alpha \in V}{\mathfrak{g}}_{\alpha }\to V$ of the trivial vector bundle $p{r}_1:V\times \mathfrak{g}\to V$. By using the Inverse Function Theorem, we can construct an open subset $\tilde{V}\subseteq V$ containing ${\alpha }_0$ and a section $\tilde{\varphi }:\tilde{V}\subseteq {\mathfrak{g}}^{*}\to W$ (of such a bundle) satisfying $\tilde{\varphi }\left({\alpha }_0\right)=\xi .$ Note that, since $\tilde{\varphi }\left(\alpha \right)\in {\mathfrak{g}}_{\alpha }$, then $a{d}_{\tilde{\varphi }\left(\alpha \right)}\alpha =0$, for all $\alpha \in \tilde{V}$. Moreover, consider another open subsets $V_{1,2}$ such that ${\alpha }_0\in V_1\subseteq {\overline{V}}_1\subseteq V_2\subseteq {\overline{V}}_2\subseteq \tilde{V}$ and the bump function $\chi :{\mathfrak{g}}^{*}\to \mathbb{R}$ related to $V_{1,2}$, i.e., $\chi$ is equal to 1 inside ${\overline{V}}_1$ and equal to 0 outside $V_2$. It is clear that $\varphi :{\mathfrak{g}}^{*}\to \mathfrak{g}$ given by

$$\varphi \left(\alpha \right)=\left\{\begin{array}{cc}\tilde{\varphi }\left(\alpha \right)\chi \left(\alpha \right),\hfill & \alpha \in \tilde{V},\hfill \\ 0,\hfill & \alpha \notin \tilde{V},\hfill \end{array}\right.$$

satisfies the point $1.$ The point 2 follows from 1 and Proposition 12 for $\alpha ={\alpha }_0$. □

For an important subclass of Lie groups, we have the following result.

Theorem 7.

Let G be a connected Lie group with Lie algebra $\mathfrak{g}$ and ${\mathcal{R}}_{Ad}$ the open dense subset of $\mathfrak{g}$, which consists of the regular points in $\mathfrak{g}$ with respect to the adjoint action of G on $\mathfrak{g}.$ Suppose that there exists a non-degenerate ad-invariant symmetric bilinear form $B:\mathfrak{g}\times \mathfrak{g}\to \mathbb{R}$. Then,

1. 

The linear map $B^{♭}:\mathfrak{g}\to {\mathfrak{g}}^{*}$ given by $⟨B^{♭}\left(\xi \right),\eta ⟩=B\left(\xi ,\eta \right)$, for all $\xi ,\eta \in \mathfrak{g}$, is a isomorphism satisfying $B^{♭}\left({\mathcal{R}}_{Ad}\right)={\mathcal{R}}_{A{d}^{*}}$, and its inverse $B^{♯}:{\mathfrak{g}}^{*}\to \mathfrak{g}$ is a Casimir 1-form.

2. 

For every $\xi \in {\mathcal{R}}_{Ad}$, the curve $t\mapsto exp\left(\xi t\right)$ can be obtained by quadratures.

Proof. 

We have that (non-degeneracy)

$$B\left(\xi ,\eta \right)=0,\mathrm{for}\mathrm{all}\eta \in \mathfrak{g}⟹\xi =0,$$

(103)

and (ad-invariance)

$$B\left(\left[\xi ,\eta \right],\nu \right)+B\left(\eta ,\left[\xi ,\nu \right]\right)=0,\mathrm{for}\mathrm{all}\xi ,\eta ,\nu \in \mathfrak{g}.$$

(104)

From Equation (103), we deduce that $B^{♭}$ is an isomorphism of vector spaces. Moreover, using Equation (104), it follows that the following diagram

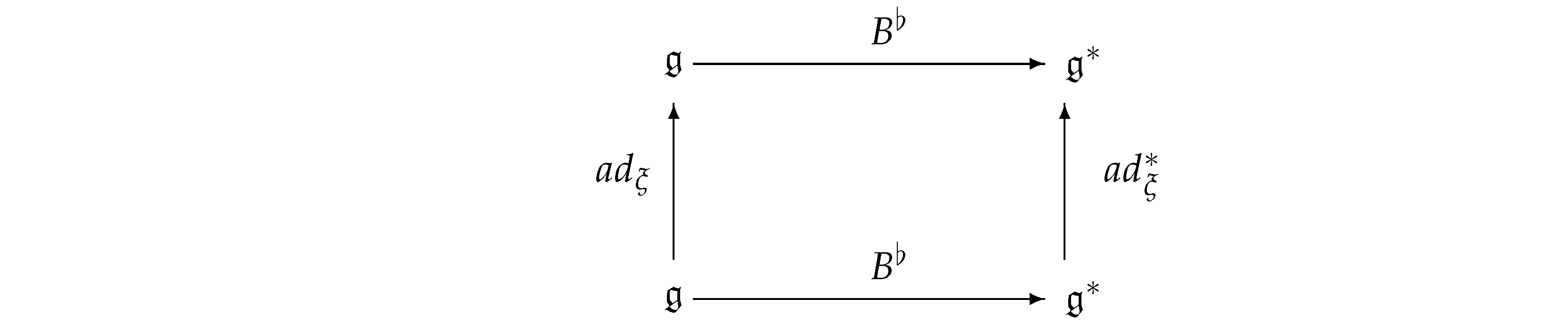is commutative, for every $\xi \in \mathfrak{g}.$ So, since G is a connected Lie group, we also have that the diagram

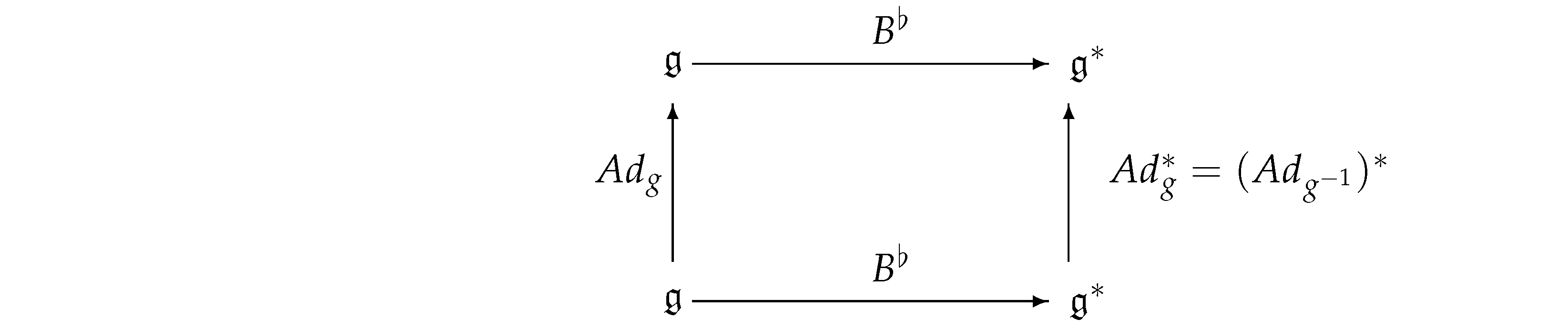is commutative for every $g\in G.$ Thus, if $G_{\xi }$ (resp. $G_{B^{♭}\left(\xi \right)}$) is the isotropy group of $\xi \in \mathfrak{g}$ (resp. $B^{♭}\left(\xi \right)\in {\mathfrak{g}}^{*})$ with respect to the adjoint (resp. co-adjoint) action of G on $\mathfrak{g}$ (resp. ${\mathfrak{g}}^{*}$), we deduce that

$$G_{\xi }=G_{B^{♭}\left(\xi \right)}.$$

This implies that

$$B^{♭}\left({\mathcal{R}}_{Ad}\right)={\mathcal{R}}_{A{d}^{*}}.$$

(105)

On the other hand, from Equation (104), we have that

$$B\left(\left[\xi ,\eta \right],\xi \right)=0,\mathrm{for} \mathrm{all} \xi ,\eta \in \mathfrak{g}.$$

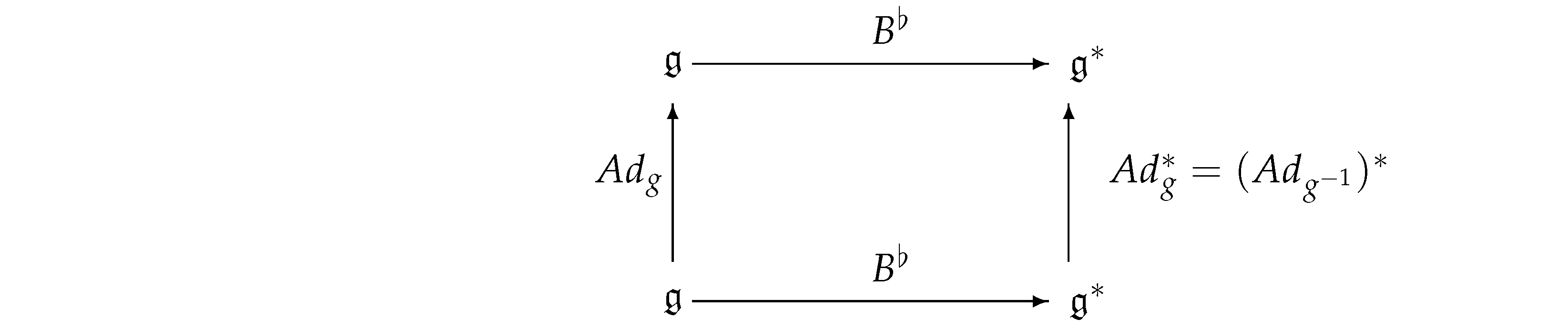
Therefore, given $\alpha \in {\mathfrak{g}}^{*}$, if we write $\alpha =B^{♭}\left(\xi \right)$ for some $\xi \in \mathfrak{g}$, we have for $B^{♯}={\left(B^{♭}\right)}^{-1}:{\mathfrak{g}}^{*}\to \mathfrak{g}$ that

$$⟨a{d}_{B^{♯}\left(\alpha \right)}^{*}\alpha ,\eta ⟩=⟨\alpha ,\left[B^{♯}\left(\alpha \right),\eta \right]⟩=⟨B^{♭}\left(\xi \right),\left[\xi ,\eta \right]⟩=B\left(\left[\xi ,\eta \right],\xi \right)=0,$$

for all $\eta \in \mathfrak{g}$. Then, $B^{♯}$ is a Casimir 1-form. This proves the first point. To prove the second point, note that, according to Equation (105), for every $\xi \in {\mathcal{R}}_{Ad}$, there exists $\alpha \in {\mathcal{R}}_{A{d}^{*}}$ such that $\xi =B^{♯}\left(\alpha \right)$. Then, it is enough to use Proposition 12 for $\varphi =B^{♯}$. □

Remark 10.

It can be show that, under the conditions of the theorem above,

$$a{d}_{\xi }{\left(\mathfrak{g}\right)}^0\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing ,\forall \xi \in {\mathcal{R}}_{Ad}.$$

So, the point 2 of Theorem 7 can also be proven by combining the equation above and Theorem 6.

Under the conditions of the last theorem, we can use Equation (102) for $\varphi =B^{♯}$ and for all $\xi \in {\mathcal{R}}_{Ad}$, which gives

$$exp\left(\xi t\right)={\pi }_G\left({\left(\Pi ,F\right)}^{-1}\left(a_{\xi }\left(t\right),b_{\xi }\right)\right),$$

with

$$\begin{array}{c}{a}_{\xi }\left(t\right)={\phi }_{b_{\xi }}^{-1}\left[{\phi }_{b_{\xi }}\left(\Pi \left(B^{♭}\left(\xi \right)\right)\right)+t\xi \right]\mathrm{and}{b}_{\xi }=F\left(B^{♭}\left(\xi \right)\right)=\left(B^{♭}\left(\xi \right),B^{♭}\left(\xi \right)\right).\hfill \end{array}$$

Remark 11.

In particular, for $\xi \in {\mathcal{R}}_{Ad}$ and close to 0 (in order for $a_{\xi }\left(t\right)$ to be defined when $t=1$), we have the following expression of the exponential map:

$$exp\left(\xi \right)={\pi }_G\left({\left(\Pi ,F\right)}^{-1}\left({\phi }_{b_{\xi }}^{-1}\left[{\phi }_{b_{\xi }}\left(\Pi \left(B^{♭}\left(\xi \right)\right)\right)+\xi \right],b_{\xi }\right)\right).$$

Remark 12.

It is worth mentioning that $B^{♯}$ is an exact 1-form, i.e., $B^{♯}=dh$ with $h:{\mathfrak{g}}^{*}\to \mathbb{R}$ given by

$$h\left(\alpha \right)=\frac{1}{2}⟨\alpha ,B^{♯}\left(\alpha \right)⟩.$$

Then, according to Remark 8, the related vector field $X_{\left|U\right.}^{B^{♯}}$ and the submersion F define a NCI Hamiltonian system on U.

For a semisimple Lie group G with Lie algebra $\mathfrak{g}$, the killing form on $\mathfrak{g}$ satisfies the conditions in Theorem 7 (see for example [30]). On the other hand, a Lie algebra $\mathfrak{g}$ is the Lie algebra of a compact Lie group if and only if $\mathfrak{g}$ admits an ad-invariant scalar product (see, for instance, [31]). So, using Theorem 7, we have the next corollary.

Corollary 1.

Let G be a connected Lie group with Lie algebra $\mathfrak{g}$ and $\xi \in {\mathcal{R}}_{Ad}\subseteq \mathfrak{g}$. If G is semisimple or compact, then $t\mapsto exp\left(\xi t\right)$ can be obtained by quadratures.

The last two results tell us that the exponential curve $exp\left(\xi t\right)$ can be constructed by quadratures for $\xi$ living in an open dense subset of $\mathfrak{g}$. Unfortunately, we cannot ensure the same for every Lie group.

Remark 13.

If $\mathfrak{g}$ is an arbitrary Lie algebra, then the subset

$$\left\{\xi \in \mathfrak{g}:a{d}_{\xi }{\left(\mathfrak{g}\right)}^0\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing \right\}$$

is not, in general, dense in $\mathfrak{g}$. In fact, let $\mathfrak{h}(1,1)$ be the nilpotent Lie algebra of the Heisenberg group $H(1,1)$ of dimension 3. Then, we can consider a basis $\{{\xi }_1,{\xi }_2,{\xi }_3\}$ of $\mathfrak{h}(1,1)$, such that

$$[{\xi }_1,{\xi }_2]=-[{\xi }_2,{\xi }_1]={\xi }_3$$

and the rest of the basic Lie brackets are zero. So, if $({\alpha }_1,{\alpha }_2,{\alpha }_3)\in R^3\cong \mathfrak{h}{(1,1)}^{*},$ we have that

$${\mathfrak{g}}_{({\alpha }_1,{\alpha }_2,{\alpha }_3)}=\mathfrak{h}(1,1),if {\alpha }_3=0,$$

and

$${\mathfrak{g}}_{({\alpha }_1,{\alpha }_2,{\alpha }_3)}=⟨{\xi }_3⟩,if {\alpha }_3\ne 0.$$

Thus, we deduce that

$${\mathcal{R}}_{A{d}^{*}}=\left\{({\alpha }_1,{\alpha }_2,{\alpha }_3)\in {\mathbb{R}}^3:{\alpha }_3\ne 0\right\},$$

which implies for $\xi =a^1{\xi }_1+a^2{\xi }_2+a^3{\xi }_3\in \mathfrak{g}$ that

$$a{d}_{\xi }\mathfrak{h}{(1,1)}^0\cap {\mathcal{R}}_{A{d}^{*}}={\mathcal{R}}_{A{d}^{*}}if a^1=a^2,$$

and

$$a{d}_{\xi }\mathfrak{h}{(1,1)}^0\cap {\mathcal{R}}_{A{d}^{*}}=\varnothing if a^1\ne a^2.$$

5.3. Integrability Conditions for Invariant Vertical Fields

Let us go back to Section 5.1. Consider a manifold M, a vector field $X\in \mathfrak{X}\left(M\right)$ and a Lie group action $\rho :G\times M\to M$. Assume that X is vertical around every point $m_0\in {\mathcal{R}}_{\rho }$ and G-invariant. Consider a covering of ${\mathcal{R}}_{\rho }$ given by admissible neighborhoods U, each one of them with an associated complete solution ${\Sigma }_U=\rho \circ \left(i{d}_{\Theta \left(U\right)}\times s\right)$, as those given in Theorem 3, and the map

$${\eta }_U:\pi \left(U\right)\to \mathfrak{g}:\lambda \mapsto {\Theta }_{*,s\left(\lambda \right)}\circ X\left(s\left(\lambda \right)\right)$$

given by Equation (81) in Theorem 5. From now on, we shall denote ${\mathfrak{g}}_{\rho ,m}$ the isotropy sub-algebra related to the point m and the action $\rho$.

Theorem 8.

If for each U and $\lambda \in \pi \left(U\right)$, we have that

$$a{d}_{{\eta }_U\left(\lambda \right)+{\varsigma }_{\lambda }}{\left(\mathfrak{g}\right)}^0\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing ,$$

for some ${\varsigma }_{\lambda }\in {\mathfrak{g}}_{\rho ,s\left(\lambda \right)}$, then X is integrable up to quadratures along ${\mathcal{R}}_{\rho }$.

Proof. 

For a given U and $\lambda \in \pi \left(U\right)$, we know that the integral curves of X, with initial conditions inside U, are given by the formula (see Equation (83))

$$\Gamma \left(t\right)=\rho \left(g_{0}exp\left(\left({\eta }_U\left(\lambda \right)+{\chi }_{\lambda }\right)t\right),s\left(\lambda \right)\right),$$

with $\lambda \in \pi \left(U\right)$ and ${\chi }_{\lambda }\in {\mathfrak{g}}_{\rho ,s\left(\lambda \right)}$ arbitrary. On the other hand, using Theorem 6, given

$$\alpha \in a{d}_{{\eta }_U\left(\lambda \right)+{\varsigma }_{\lambda }}{\left(\mathfrak{g}\right)}^0\cap {\mathcal{R}}_{A{d}^{*}},$$

we can construct a Casimir 1-form ${\varphi }_{\lambda }:{\mathfrak{g}}^{*}\to \mathfrak{g}$ such that ${\varphi }_{\lambda }\left(\alpha \right)={\eta }_U\left(\lambda \right)+{\varsigma }_{\lambda }$. Thus, taking ${\chi }_{\lambda }={\varsigma }_{\lambda }$, we have that

$$\Gamma \left(t\right)=\rho (g_{0}exp\left({\varphi }_{\lambda }\left(\alpha \right)t\right),s\left(\lambda \right))$$

and, using Proposition 12 for $\varphi ={\varphi }_{\lambda }$, it follows that $\Gamma$ can be constructed up to quadratures. □

Now, let us suppose that M is a symplectic manifold, with symplectic structure $\omega$, and $\rho :G\times M\to M$ is a symplectic action with $A{d}^{*}$-equivariant momentum map $K:M\to {\mathfrak{g}}^{*}$.

Theorem 9.

Consider an equivariant function $\varphi :{\mathfrak{g}}^{*}\to \mathfrak{g}$ and the vector field $X={\omega }^{♯}\circ K^{*}\varphi$. If

$$K\left({\mathcal{R}}_{\rho }\right)\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing$$

and ϕ is also a Casimir 1-form, then there exists a G-invariant open subset of $V\subseteq {\mathcal{R}}_{\rho }$ where X is integrable up to quadratures.

Proof. 

Under above condition, according to Proposition 10, $X={\omega }^{♯}\circ K^{*}\varphi$ is vertical and G-invariant. On the other hand, if $K\left({\mathcal{R}}_{\rho }\right)\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing$, according to Proposition 6, there exists a G-invariant open subset $V\subseteq {\mathcal{R}}_{\rho }$ such that $K\left(V\right)\subseteq {\mathcal{R}}_{A{d}^{*}}$. Consider a covering of V as above and the related maps ${\eta }_U$. Using Proposition 10 again,

$${\eta }_U\left(\lambda \right)=\varphi \left(K\left(s\left(\lambda \right)\right)\right)+{\xi }_{\lambda },$$

for some ${\xi }_{\lambda }\in {\mathfrak{g}}_{\rho ,s\left(\lambda \right)}$, and the integral curves of X by points of U are of the form

$$\Gamma \left(t\right)=\rho \left(gexp\left(\varphi \left(K\left(s\left(\lambda \right)\right)\right)t\right),s\left(\lambda \right)\right),\mathrm{with} \lambda \in \Pi \left(U\right) \mathrm{and} g\in \Theta \left(U\right).$$

(106)

Then, since $s\left(\lambda \right)\in U\subseteq V$, it follows that $K\left(s\left(\lambda \right)\right)\in {\mathcal{R}}_{A{d}^{*}}$, and consequently, using Equation (106) and Proposition 12 for $\alpha =K\left(s\left(\lambda \right)\right)$, we deduce the result. □

More interesting examples can be constructed by using the next lemma.

Lemma 3.

If $h:{\mathfrak{g}}^{*}\to \mathbb{R}$ is a G-invariant function with respect to $A{d}^{*}$, then $dh:{\mathfrak{g}}^{*}\to \mathfrak{g}$ is equivariant and a Casimir 1-form.

For a proof, see [32], Lemma 2.9.

Theorem 10.

Consider G-invariant functions $h_i:{\mathfrak{g}}^{*}\to \mathbb{R}$ (resp. $f_i:M\to \mathbb{R}$), $i=1,...,k$, with respect to $A{d}^{*}$ (resp. ρ). Suppose that $K\left({\mathcal{R}}_{\rho }\right)\cap {\mathcal{R}}_{A{d}^{*}}\ne \varnothing$ and define

$$X\left(m\right)=\sum _{i=1}^k{f}_i\left(m\right)\left({\omega }^{♯}\circ K^{*}d{h}_i\right)\left(m\right),\forall m\in M.$$

(107)

Then, there exists a G-invariant open subset $V\subseteq {\mathcal{R}}_{\rho }$ where the vector field X is integrable up to quadratures.

Proof. 

Since each field ${\omega }^{♯}\circ K^{*}d{h}_i$ is G-invariant and vertical, the same is true for X. On the other hand, given (as in the proof of Theorem Equation (9)) a G-invariant open subset of $V\subseteq {\mathcal{R}}_{\rho }$ such that $K\left(V\right)\subseteq {\mathcal{R}}_{A{d}^{*}}$, a covering of V by admissible neighborhoods U and the related maps ${\eta }_U$, for each $\lambda \in \pi \left(U\right)$, we have that

$${\eta }_U\left(\lambda \right)=\sum _{i=1}^k{f}_i\left(s\left(\lambda \right)\right)d{h}_i\left(K\left(s\left(\lambda \right)\right)\right)+{\xi }_{\lambda },$$

for some ${\xi }_{\lambda }\in {\mathfrak{g}}_{\rho ,s\left(\lambda \right)}$. Then, defining ${\varphi }_{\lambda }:{\mathfrak{g}}^{*}\to \mathfrak{g}$ by

$${\varphi }_{\lambda }\left(\alpha \right)=\sum _{i=1}^k{f}_i\left(s\left(\lambda \right)\right)d{h}_i\left(\alpha \right),$$

which is a Casimir 1-form, we have that

$${\eta }_U\left(\lambda \right)={\varphi }_{\lambda }\left(K\left(s\left(\lambda \right)\right)\right)+{\xi }_{\lambda }.$$

Finally, since $K\left(s\left(\lambda \right)\right)\in {\mathcal{R}}_{A{d}^{*}}$ (as we saw in the previous theorem), the theorem follows from Proposition 12 for $\varphi ={\varphi }_{\lambda }$ and $\alpha =K\left(s\left(\lambda \right)\right)$. □

It is worth mentioning that the vector field X given by Equation (107) is not, in general, a Hamiltonian vector field.