Revision of Pseudo-Ultrametric Spaces Based on m-Polar T-Equivalences and Its Application in Decision Making

Abstract

In mathematics, distance and similarity are known as dual concepts. However, the concept of similarity is interpreted as fuzzy similarity or T-equivalence relation, where T is a triangular norm (t-norm in brief), when we discuss a fuzzy environment. Dealing with multi-polarity in practical examples with fuzzy data leadsus to introduce a new concept called m-polar $\mathbf{T}$-equivalence relations based on a finitely multivalued t-norm $\mathbf{T}$, and to study the metric behavior of such relations. First, we study the new operators including the m-polar triangular norm $\mathbf{T}$ and conorm $\mathbf{S}$ as well as m-polar implication $\mathbf{I}$ and m-polar negation $\mathbf{N}$, acting on the Cartesian product of $[0,1]$m-times.Then, using the m-polar negations $\mathbf{N}$, we provide a method to construct a new type of metric spaces, called m-polar $\mathbf{S}$-pseudo-ultrametric, from the m-polar $\mathbf{T}$-equivalences, and reciprocally for constructing m-polar $\mathbf{T}$-equivalences based on the m-polar $\mathbf{S}$-pseudo-ultrametrics. Finally, the link between fuzzy graphs and m-polar $\mathbf{S}$-pseudo-ultrametrics is considered. An algorithm is designed to plot a fuzzy graph based on the m-polar ${\mathbf{S}}_L$-pseudo-ultrametric, where ${\mathbf{S}}_L$ is the m-polar Lukasiewicz t-conorm, and is illustrated by a numerical example which verifies our method.

1. Introduction

The pairwise comparison and classification of objects is one of the main steps in any field dealing with data analysis. This task is generally handled by equivalence relations for crisp data and T-equivalences in fuzzy environments, where T is a triangular norm called briefly a t-norm [1,2]. Traditionally, the equivalence relations (known also as indistinguishability relations) and (pseudo-)metrics (or distinguishability relations) have a close link, where one can be defined as the dual of the other. However, in fuzzy environments, the T-equivalences usually produce pseudo-ultrametrics, rather than standard metric spaces, in which the triangular inequality of a metric has been generalized by the maximum operator [3,4,5,6].

Recently, the notion of multi-polarity, arising from multi-source data, has been introduced in the fuzzy context to achieve higher accuracy in data analysis. However, this concept has two sides. From the first perspective, it describes fuzzy rule-based classification systems, designed based on different categories, where the final rule (which consists of a set of fuzzy rules) contains the consequent class of the final rule from the m predefined classes/categories/patterns [7,8,9,10]. From another direction, multi-polarity provides a flexible framework for input and output data in information systems, applied in computer science, multi-criteria decision making, and graph theory, where instead of one absolute value $u\in [0,1]$ the m-tuple $\mathbf{u}=(u_1,\cdots ,u_m)\in [0,1]\times \cdots \times [0,1]$ is employed to describe data based on different parameters/criteria [11,12,13]. Note that this paper follows the second case, which is known as m-polar fuzzy set theory.

The widespread use of m-polar fuzzy sets in decision making (see [14,15,16,17]) led us to consider fuzzy similarity relations for information systems dealing with m-polar fuzzy data. Since finitely multivalued logic is the background idea to construct m-polar fuzzy sets, in which the truth values are modeled by the Cartesian product of the unit interval $[0,1]$ m-times, an extension of the classical fuzzy logic into m-polar fuzzy logic is required. In such a new multivalued logic, we need to study the concepts of conjunction (usually interpreted by t-norms), disjunction (defined by t-conorms), implication, and negation for the m-polar case. Our interest in solving the problem of classification and ranking in decision making situations motivated us to consider the application of m-polar t-norm operators for defining the m-polar fuzzy similarity relations. As t-norms are used to develop T-equivalences (see [18]), by extending the concept of the t-norm T into the m-polar t-norm $\mathbf{T}$, we suggest the new concept of m-polar $\mathbf{T}$-equivalences to interpret fuzzy indistinguishability relations between m-polar fuzzy data. Note that, in this study, the bold letters refer to the m-polar case.

On the other hand, in fuzzy logic, the use of the concept of duality leads to a one-to-one correspondence between T-equivalences and pseudo-(ultra)metrics (see [3,4,19]), where a pseudo-(ultra)metric on a set X is a mapping $d:X\times X\to [0,1]$ equipped with the inequality $d(x,z)\le max\left\{d\right(x,y),d(y,z\left)\right\}$ for all $x,y,z\in X$ rather than the well-known triangular inequality $d(x,z)\le d(x,y)+d(y,z)$ in the standard definition of metric spaces. Because the maximum operator is a t-conorm, it seems natural to consider a stronger version of pseudo-ultrametric for the m-polar case as a $\mathbf{S}$-pseudo-ultrametric where $\mathbf{S}$ is any m-polar t-conorm. Moreover, it can be determined whether or not the result is always an m-polar pseudo-(ultra)metric if the traditional concept of fuzzy duality, which is used to define the induced metrics by T-equivalences, is replaced by an m-polar negation $\mathbf{N}$.

Therefore, in this contribution we give an introduction of m-polar t-norms, m-polar t-conorms, m-polar implications, and m-polar negations in Section 2 and Section 3. We also aim to explore in greater depth the one-to-one correspondence between m-polar $\mathbf{T}$-equivalences and m-polar $\mathbf{S}$-pseudo-(ultra)metrics in Section 4 by using m-polar negations. Finally, in Section 5, we present a link between fuzzy graphs and m-polar $\mathbf{S}$-pseudo-ultrametrics, built by m-polar $\mathbf{T}$-equivalences. An algorithm is then designed to compute a fuzzy graph based on the m-polar ${\mathbf{S}}_L$-pseudo-ultrametric, where ${\mathbf{S}}_L$ is the m-polar Lukasiewicz t-conorm, and we illustrate it with an example.

2. Fuzzy T-Orderings

In this section, we first recall some theoretical background needed to develop the main results of this paper. Then, we introduce some new concepts including m-polar t-norms $\mathbf{T}$, m-polar t-conorms $\mathbf{S}$, and m-polar $\mathbf{T}$-orderings as natural extensions of the corresponding definitions in traditional fuzzy set theory.

The binary operation $T:{[0,1]}^2\to [0,1]$ and its dual (i.e., $S:{[0,1]}^2\to [0,1]$) are respectively called triangular norm and conorm, or t-norm and t-conorm in brief, if they are associative and commutative with the neutral elements $e_T=1$ and $e_S=0$ (c.f. [5]). The t-norms T and the t-conorms S are in fact different membership functions to model conjunction (i.e., the logical AND) and disjunction (i.e., the logical OR) in fuzzy logic. To interpret the concept of logical implication in fuzzy logic, a binary operation $I:{[0,1]}^2\to [0,1]$ is used to define the fuzzy implication which admits the following conditions:

• If $u\le v$, then $I(u,w)\ge I(v,w)$;
• If $u\le v$, then $I(w,u)\le I(w,v)$;
• $I(0,0)=1$ and $I(1,1)=1$;
• $I(1,0)=0$,

where $u,v,w\in [0,1]$. Moreover, the concept of negation is developed in fuzzy logic by using a decreasing operator $N:[0,1]\to [0,1]$ with boundary conditions $N\left(0\right)=1$ and $N\left(1\right)=0$. For more details, we recommend [20].

By using the t-norms and t-conorms, particular classes of implication and negation operators are formulated as follows.

Definition 1

([20]). Let T be a left-continuous t-norm. The implication operation $\overrightarrow{T}:{[0,1]}^2\to [0,1]$ (which is also called residuum) with respect to the t-norm T is defined as

$$\overrightarrow{T}(u,v)=sup\{\alpha \in \mathbb{I}:T(\alpha ,u)\le v\},$$

(1)

for any $u,v\in [0,1]$.

Definition 2

([20]). Let T be a left-continuous t-norm and S be a right-continuous t-conorm.

• The induced negation operation $N_T:[0,1]\to [0,1]$ by T is defined as

  $$N_T\left(u\right)=sup\{\alpha \in \mathbb{I}:T(\alpha ,u)=0\},$$

  (2)
• The induced negation operation $N_S:[0,1]\to [0,1]$ by S is defined as

  $$N_S\left(u\right)=inf\{\alpha \in \mathbb{I}:S(\alpha ,u)=1\},$$

  (3)

for any $u\in [0,1]$.

Note that in the above Equations (1)–(3) the operators “sup” and “inf” can be respectively replaced by “max” and “min” since T is a left-continuous t-norm and S is a right-continuous t-conorm [20].

2.1. m-Polar Fuzzy $\mathbf{T}$-Orderings

By expanding the range of membership functions from the unit interval $[0,1]$ into the mth power of $[0,1]$, that is, ${[0,1]}^m=[0,1]\times \cdots \times [0,1]$ where $\mathbf{0}=(0,0,\cdots ,0)$ and $\mathbf{1}=(1,1,\cdots ,1)$ are respectively the least and greatest elements, we can extend the traditional fuzzy set (dealing with uni-polar data) into the new concept called m-polar fuzzy set, which deals with multi-polar information.

The set ${[0,1]}^m$ is considered as a poset (preordered set) with order “≤” such that for any $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ where $\mathbf{u}=(u_1,\cdots ,u_m)$ and $\mathbf{v}=(v_1,\cdots ,v_m)$, we have the point-wise ordering over them, that is, $\mathbf{u}\le \mathbf{v}$ iff ${\pi }_i\left(\mathbf{u}\right)\le {\pi }_i\left(\mathbf{v}\right)$ for each $i=1,2\cdots ,m$ where ${\pi }_i:{[0,1]}^m\to [0,1]$ is the ith projection mapping and ${\pi }_i\left(\mathbf{u}\right)=u_i,{\pi }_i\left(\mathbf{v}\right)=v_i$.

Definition 3

([11]). An m-polar fuzzy set μ on the universe X is a mapping $\mathit{\mu }:X\to {[0,1]}^m$ such that $\mathit{\mu }\left(x\right)=({\pi }_1\circ \mathit{\mu }\left(x\right),\cdots ,{\pi }_m\circ \mu \left(x\right))$ for any $x\in X$ where ${\pi }_i:{[0,1]}^m\to [0,1]$ is the ith projection mapping. In fact, the map ${\pi }_i\circ \mathit{\mu }:X\to [0,1]$ is a fuzzy set on X, called the ith degree of membership function μ.

The concept of m-polar fuzzy relation $\mathbf{R}$ is also discussed in [10,13] as a mapping $\mathbf{R}:X\times X\to {[0,1]}^m$ such that $\mathbf{R}(x,y)=({\pi }_1\circ \mathbf{R}(x,y),\cdots ,{\pi }_m\circ \mathbf{R}(x,y))$ for any $x,y\in X$ where for each $i=1:m$, the value ${\pi }_s\circ \mathbf{R}(x,y)$ shows the relationship between x and y in direction i.

To define the concept of m-polar $\mathbf{T}$-ordering, we first need to introduce the concept of t-norm $\mathbf{T}$ for the m-polar case.

Definition 4.

Let $\mathbf{T}:{[0,1]}^m\times {[0,1]}^m\to {[0,1]}^m$. The operator $\mathbf{T}$ is called an m-polar t-norm if for any $\mathbf{u},\mathbf{v},\mathbf{w}\in {[0,1]}^m$ it admits the following conditions:

1. 

$\mathbf{T}\left(\mathbf{T}\right(\mathbf{u},\mathbf{v}),\mathbf{w})=\mathbf{T}(\mathbf{u},\mathbf{T}(\mathbf{v},\mathbf{w}\left)\right)$;

2. 

$\mathbf{T}(\mathbf{u},\mathbf{v})=\mathbf{T}(\mathbf{v},\mathbf{u})$;

3. 

$\mathbf{T}(\mathbf{u},\mathbf{1})=\mathbf{u}$,

where we define $\mathbf{T}(\mathbf{u},\mathbf{v})=({\pi }_1\circ \mathbf{T}(\mathbf{u},\mathbf{v}),\cdots ,{\pi }_m\circ \mathbf{T}(\mathbf{u},\mathbf{v}))$ such that for any $i=1:m$; ${\pi }_i\circ \mathbf{T}:{[0,1]}^m\times {[0,1]}^m\to [0,1]$ shows the ith degree of $\mathbf{T}$.

Note that the concept of the m-polar t-conorm $\mathbf{S}$ is defined as the dual of $\mathbf{T}$, that is, $\mathbf{S}(\mathbf{u},\mathbf{v})=\mathbf{1}-\mathbf{T}(\mathbf{1}-\mathbf{u},\mathbf{1}-\mathbf{v})$, by the following definition.

Definition 5.

The operator $\mathbf{S}:{[0,1]}^m\times {[0,1]}^m\to {[0,1]}^m$ is called an m-polar t-conorm if for any $\mathbf{u},\mathbf{v},\mathbf{w}\in {[0,1]}^m$ it admits the following conditions:

1. 

$\mathbf{S}\left(\mathbf{S}\right(\mathbf{u},\mathbf{v}),\mathbf{w})=\mathbf{S}(\mathbf{u},\mathbf{S}(\mathbf{v},\mathbf{w}\left)\right)$;

2. 

$\mathbf{S}(\mathbf{u},\mathbf{v})=\mathbf{S}(\mathbf{v},\mathbf{u})$;

3. 

$\mathbf{S}(\mathbf{u},\mathbf{0})=\mathbf{u}$.

The introduced m-polar t-norm $\mathbf{T}$ and m-polar t-conorm $\mathbf{S}$ in Definitions 4 and 5 come from the original definitions of t-norms and t-conorms discussed earlier in Section 2, where each component ${\pi }_i\circ \mathbf{T}$ of $\mathbf{T}$ (${\pi }_i\circ \mathbf{S}$ of $\mathbf{S}$) for $i=1:m$ may be defined by a t-norm $T_i$ (t-conorm $S_i$). This issue is discussed in the following proposition.

Proposition 1.

Consider the operators $T_i:{[0,1]}^2\to [0,1]$ for $i=1,\cdots ,m$. If $\mathbf{T}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ is defined by $\mathbf{T}:=(T_1,\cdots ,T_m)$ such that for any $i=1:m$; ${\pi }_i\circ \mathbf{T}(\mathbf{u},\mathbf{v})=T_i({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{v}\right))$. Then $\mathbf{T}$ is an m-polar t-norm iff for each i the operator $T_i$ is a t-norm.

Proof. 

See Appendix A.1. □

We use the concept of m-polar t-norms to develop $\mathbf{T}$-properties of the m-polar fuzzy relation $\mathbf{R}$ in Definition 6. However, first we recall from [1,21] that a fuzzy relation $R:X\times X\to [0,1]$ is called

• Reflexive if $\forall x\in X:R(x,x)=1$;
• Symmetric if $\forall x,y\in X:R(x,y)=R(y,x)$;
• T-antisymmetric if $\forall x,y\in X$ such that $x\ne y$: $T\left(R\right(x,y),R(y,x\left)\right)=0$;
• T-asymmetric if $\forall x,y\in X$: $T\left(R\right(x,y),R(y,x\left)\right)=0$;
• T-transitive if $\forall x,y,z\in X:T\left(R\right(x,y),R(y,z)\le R(x,z)$;
• T-preorder if reflexive and T-transitive;
• T-equivalence if reflexive, T-transitive and symmetric,

where $T:{[0,1]}^2\to [0,1]$ is a t-norm.

Definition 6.

Let $\mathbf{T}:{[0,1]}^m\times {[0,1]}^m\to {[0,1]}^m$ be an m-polar t-norm. The m-polar fuzzy relation $\mathbf{R}:X\times X\to {[0,1]}^m$ is called

• Reflexive if $\forall x\in X:\mathbf{R}(x,x)=(1,\cdots ,1)$, i.e, ${\pi }_i\circ \mathbf{R}(x,x)=1$ for each $i=1:m$;
• Symmetric if $\forall x,y\in X:\mathbf{R}(x,y)=\mathbf{R}(y,x)$, i.e, ${\pi }_i\circ \mathbf{R}(x,y)={\pi }_i\circ \mathbf{R}(y,x)$ for each $i=1:m$;
• $\mathbf{T}$-antisymmetric if $\forall x,y\in X$ such that $x\ne y$: $\mathbf{T}\left(\mathbf{R}\right(x,y),\mathbf{R}(y,x\left)\right)=(0,\cdots ,0)$, i.e, ${\pi }_i\circ \mathbf{T}(\mathbf{R}(x,y),\mathbf{R}(y,x))=0$ for each $i=1:m$;
• $\mathbf{T}$-asymmetric if $\forall x,y\in X$: $\mathbf{T}\left(\mathbf{R}\right(x,y),\mathbf{R}(y,x\left)\right)=(0,\cdots ,0)$;
• $\mathbf{T}$-transitive if $\forall x,y,z\in X:\mathbf{T}\left(\mathbf{R}\right(x,y),\mathbf{R}(y,z)\le \mathbf{R}(x,z)$, i.e, ${\pi }_i\circ \mathbf{T}(\mathbf{R}(x,y),\mathbf{R}(y,z))\le {\pi }_i\circ \mathbf{R}(x,z)$ for each $i=1:m$.

Accordingly, m-polar fuzzy $\mathbf{T}$-orderings can be defined as below.

Definition 7.

Let $\mathbf{R}$ be an m-polar fuzzy relation on X. If $\mathbf{R}$ is reflexive and $\mathbf{T}$-transitive, then it is called m-polar $\mathbf{T}$-preordering. If it is an m-polar $\mathbf{T}$-preorder relation which is also symmetric, then it is called an m-polar $\mathbf{T}$-equivalence relation.

Proposition 2.

Let $\mathbf{T}:=(T_1,\cdots ,T_m)$ be an m-polar t-norm characterized by t-norms $T_i:{[0,1]}^2\to [0,1]$ for $i=1:m$. Then, the m-polar $\mathbf{T}$-property of $\mathbf{R}$ is equivalent to the $T_i$-property of each component ${\pi }_i\circ \mathbf{R}$ of $\mathbf{R}$.

Proof. 

See Appendix A.2. □

3. m-Polar Implications and Negations Induced by m-Polar t-Norms $\mathbf{T}$

In this section, we first introduce the m-polar implications and the m-polar negations as generalizations of the corresponding concepts in traditional fuzzy logic. We also discuss how to generate the m-polar implications and negations by using m-polar t-norms.

Definition 8.

Let $\mathbf{u},\mathbf{v},\mathbf{w}\in {[0,1]}^m$ such that $\mathbf{u}=(u_1,\cdots ,u_m)$, $\mathbf{v}=(v_1,\cdots ,v_m)$ and $\mathbf{w}=(w_1,\cdots ,w_m)$. A function $\mathbf{I}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ is called an m-polar fuzzy implication if it satisfies the following conditions:

1. 

If $\mathbf{u}\le \mathbf{v}$, then $\mathbf{I}(\mathbf{u},\mathbf{w})\ge \mathbf{I}(\mathbf{v},\mathbf{w})$;

2. 

If $\mathbf{u}\le \mathbf{v}$, then $\mathbf{I}(\mathbf{w},\mathbf{u})\le \mathbf{I}(\mathbf{w},\mathbf{v})$;

3. 

$\mathbf{I}(\mathbf{0},\mathbf{0})=\mathbf{1}$ and $\mathbf{I}(\mathbf{1},\mathbf{1})=\mathbf{1}$;

4. 

$\mathbf{I}(\mathbf{1},\mathbf{0})=\mathbf{0}$,

such that $\mathbf{I}(\mathbf{u},\mathbf{v})=({\pi }_1\circ \mathbf{I}(\mathbf{u},\mathbf{v}),\cdots ,{\pi }_m\circ \mathbf{I}(\mathbf{u},\mathbf{v}))$ for any $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ where ${\pi }_i\circ \mathbf{I}:{[0,1]}^m\times {[0,1]}^m\to [0,1]$ shows the ith degree of $\mathbf{I}$.

If $\mathbf{u},\mathbf{v}\in {[0,1]}^m$, then the following boundary conditions are obtained directly from Definition 8:

• $\mathbf{I}(\mathbf{0},\mathbf{v})=\mathbf{1}$;
• $\mathbf{I}(\mathbf{u},\mathbf{1})=\mathbf{1}$;
• $\mathbf{I}(\mathbf{0},\mathbf{1})=\mathbf{1}$.

Theorem 1.

Suppose the operation $\mathbf{I}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$, defined by $\mathbf{I}=({\pi }_1\circ \mathbf{I},\cdots ,{\pi }_m\circ \mathbf{I})$, is characterized as $\mathbf{I}:=(I_1,\cdots ,I_m)$ where for any $i=1:m$, $I_i:{[0,1]}^2\to [0,1]$ is a binary operator. Then $\mathbf{I}$ is an m-polar fuzzy implication iff for each i the $I_i$ is a fuzzy implication.

Proof. 

See Appendix B.1. □

Theorem 2.

Let the operators $T_i:{[0,1]}^2\to [0,1]$, for $i=1:m$, be left-continuous t-norms. Suppose the m-polar t-norm $\mathbf{T}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ is given as $\mathbf{T}:=(T_1,\cdots ,T_m)$. Operator $\overrightarrow{\mathbf{T}}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ defined by

$$\overrightarrow{\mathbf{T}}(\mathbf{u},\mathbf{v})=sup\{\alpha =({\alpha }_1,\cdots ,{\alpha }_m)\in {[0,1]}^m:\mathbf{T}(\alpha ,\mathbf{u})\le \mathbf{v}\},$$

(4)

is an m-polar fuzzy implication induced by $\mathbf{T}:=(T_1,\cdots ,T_m)$.

Proof. 

See Appendix B.2. □

Analogously to Equation (1), Theorem 2 allows us to apply any m-polar left-continuous t-norm $\mathbf{T}$ to generate the m-polar fuzzy implications without any violations of the axioms.

Example 1.

Let $\mathbf{T}:=(T_1,T_2)$ where $T_1:=T_M$ (the minimum operator) and $T_2:=T_L$ (the Lukasiewicz operator). Then, $\overrightarrow{\mathbf{T}}:=(\overrightarrow{T_1},\overrightarrow{T_2})$ is a 2-polar fuzzy implication induced by t-norms $T_M$ and $T_L$ such that

$$\overrightarrow{T_1}(u,v)=\left\{\begin{array}{cc}1\hfill & u\le v\hfill \\ v\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

and $\overrightarrow{T_2}(u,v)=min(1,1-u+v)$ for any $u,v\in [0,1]$.

In order to develop an m-polar $\mathbf{S}$-pseudo-ultrametric based on the $\mathbf{T}$-equivalences (see the related Theorem 7), we first need to define the concept of m-polar negation.

Definition 9.

A function $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ is called an m-polar fuzzy negation if it satisfies the following conditions:

1. 

$\mathbf{N}(0,\cdots ,0)=\mathbf{0}$ and $\mathbf{N}(1,\cdots ,1)=\mathbf{1}$;

2. 

$\mathbf{N}\left(\mathbf{u}\right)\ge \mathbf{N}\left(\mathbf{v}\right)$ if $\mathbf{u}\le \mathbf{v}$,

for any $\mathbf{u},\mathbf{v}\in {[0,1]}^m$. Note that we define $\mathbf{N}\left(\mathbf{u}\right)=({\pi }_1\circ \mathbf{N}\left(\mathbf{u}\right),\cdots ,{\pi }_m\circ \mathbf{N}\left(\mathbf{u}\right))$, where ${\pi }_i\circ \mathbf{N}:{[0,1]}^m\to [0,1]$ shows the ith degree of $\mathbf{N}$.

Theorem 3.

Let $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ is characterized by $\mathbf{N}:=(N_1,\cdots ,N_m)$ where for any $i=1:m$, $N_i:[0,1]\to [0,1]$ is an operator such that ${\pi }_i\circ \mathbf{N}\left(\mathbf{u}\right)=N_i\left({\pi }_i\left(\mathbf{u}\right)\right)$. Then, $\mathbf{N}$ is an m-polar fuzzy negation iff functions $N_i$, for all i, are fuzzy negations.

Proof. 

See Appendix B.3. □

For instance, a natural m-polar negation $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ can be defined as ${\mathbf{N}}_c\left(\mathbf{u}\right)=\mathbf{1}-\mathbf{u}$ for any $\mathbf{u}\in {[0,1]}^m$, where c stands for complement, such that for each $i=1:m$;

$${\pi }_i\circ {\mathbf{N}}_c\left(\mathbf{u}\right)=N_c\left({\pi }_i\left(\mathbf{u}\right)\right),$$

(5)

where $N_c:[0,1]\to [0,1]$ is the natural fuzzy negation operator, that is, $N_c\left({\pi }_i\left(\mathbf{u}\right)\right)=1-u_i$ for each i. We call ${\mathbf{N}}_c$ the standard m-polar fuzzy negation.

According to Theorem 3, the given Equations (2) and (3) in Definition 2 can be adapted with the m-polar fuzzy case to explain some procedures for producing the special classes of m-polar fuzzy negation based on the m-polar t-norm $\mathbf{T}$.

Corollary 1.

Consider the m-polar fuzzy implication $\mathbf{I}:=(I_1,\cdots ,I_m)$. The operator ${\mathbf{N}}_{\mathbf{I}}:{[0,1]}^m\to {[0,1]}^m$ defined by ${\mathbf{N}}_{\mathbf{I}}:=(N_{I_1},\cdots ,N_{I_m})$ such that ${\pi }_i\circ {\mathbf{N}}_{\mathbf{I}}\left(\mathbf{u}\right)=N_{I_i}\left({\pi }_i\left(\mathbf{u}\right)\right)=I_i(u_i,0)$ where $\mathbf{u}=(u_1,\cdots ,u_m)\in {[0,1]}^m$ is an m-polar fuzzy negation which is called the m-polar negation induced by $\mathbf{I}$.

Corollary 2.

Consider the m-polar t-norm $\mathbf{T}:=(T_1,\cdots ,T_m)$ such that for any $i=1:m$ the operator $T_i$ is a left-continuous t-norm. The operator ${\mathbf{N}}_{\mathbf{T}}:{[0,1]}^m\to {[0,1]}^m$ defined by ${\mathbf{N}}_{\mathbf{T}}:=(N_{T_1},\cdots ,N_{T_m})$ such that ${\pi }_i\circ {\mathbf{N}}_{\mathbf{T}}\left(\mathbf{u}\right)=N_{T_i}\left({\pi }_i\left(\mathbf{u}\right)\right)=sup\{\beta \in [0,1]:T_i(\beta ,{\pi }_i\left(\mathbf{u}\right))=0\}$ is an m-polar fuzzy negation which is called the m-polar negation induced by $\mathbf{T}$.

In Corollary 2, if $\mathbf{I}=\overrightarrow{\mathbf{T}}$, then ${\mathbf{N}}_{\mathbf{T}}={\mathbf{N}}_{\overrightarrow{\mathbf{T}}}$ where $\mathbf{T}:=(T_1,\cdots ,T_m)$ and for all $i=1:m$ the operators $T_i$ are left-continuous t-norms.

Corollary 3.

Consider the m-polar t-conorm $\mathbf{S}:=(S_1,\cdots ,S_m)$ such that for any $i=1:m$ the operator $S_i$ is a right-continuous t-conorm. The operator ${\mathbf{N}}_{\mathbf{S}}:{[0,1]}^m\to {[0,1]}^m$ defined by ${\mathbf{N}}_{\mathbf{S}}:=(N_{S_1},\cdots ,N_{S_m})$ such that ${\pi }_i\circ {\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right)=N_{S_i}\left({\pi }_i\left(\mathbf{u}\right)\right)=inf\{\beta \in [0,1]:S_i(\beta ,{\pi }_i\left(\mathbf{u}\right))=1\}$ is an m-polar fuzzy negation which is called the m-polar negation induced by $\mathbf{S}$.

Remark 1.

From Corollaries 1, 2, and 3, it is easy to check that if $\mathbf{I}$ and ${\mathbf{I}}^{\ast }$ are two m-polar implications such that $\mathbf{I}\le {\mathbf{I}}^{\ast }$, then ${\mathbf{N}}_{\mathbf{I}}\le {\mathbf{N}}_{{\mathbf{I}}^{\ast }}$. If $\mathbf{T}$ and ${\mathbf{T}}^{\ast }$ are two m-polar t-norms such that $\mathbf{T}\le {\mathbf{T}}^{\ast }$, then ${\mathbf{N}}_{\mathbf{T}}\ge {\mathbf{N}}_{{\mathbf{T}}^{\ast }}$. Moreover, if $\mathbf{S}$ and ${\mathbf{S}}^{\ast }$ are two m-polar t-conorms such that $\mathbf{S}\le {\mathbf{S}}^{\ast }$, then ${\mathbf{N}}_{\mathbf{S}}\le {\mathbf{N}}_{{\mathbf{S}}^{\ast }}$.

Proposition 3.

Let $\mathbf{T}$ and $\mathbf{S}$ be an m-polar t-norm and an m-polar t-conorm, respectively. Then, $\mathbf{u}\le {\mathbf{N}}_{\mathbf{T}}\left({\mathbf{N}}_{\mathbf{T}}\left(\mathbf{u}\right)\right)$ and $\mathbf{u}\ge {\mathbf{N}}_{\mathbf{S}}\left({\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right)\right)$ for any $\mathbf{u}=(u_1,\cdots ,u_m)\in {[0,1]}^m$.

Proof. 

See Appendix B.4. □

Definition 10.

Let $\mathbf{N}$ be an m-polar fuzzy negation. Then, it is called

• Strict if it is strictly decreasing and continuous at any component ${\pi }_i\circ \mathbf{N}$.
• Strong if $\mathbf{u}=\mathbf{N}\left(\mathbf{N}\right(\mathbf{u}\left)\right)$ for any $\mathbf{u}\in {[0,1]}^m$.
• Weak if $\mathbf{u}\le \mathbf{N}\left(\mathbf{N}\right(\mathbf{u}\left)\right)$ for any $\mathbf{u}\in {[0,1]}^m$.

Theorem 4.

Suppose $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ is an m-polar fuzzy negation defined by $\mathbf{N}:=(N_1,\cdots ,N_m)$ where for all $i=1:m$, the operators $N_i:[0,1]\to [0,1]$ are fuzzy negations. Then, $\mathbf{N}$ is strong iff for all i, the operators $N_i$ are strong.

Proof. 

See Appendix B.5. □

Analogously, the following theorems can be proved.

Suppose $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ is an m-polar fuzzy negation defined by $\mathbf{N}:=(N_1,\cdots ,N_m)$ where for any $i=1:m$, the operator $N_i:[0,1]\to [0,1]$ is a fuzzy negation.

Theorem 5.

The m-polar fuzzy negation $\mathbf{N}$ is weak iff for all $i=1:m$, the operators $N_i$ are weak.

Proof. 

This proof is similar to Theorem 4. □

Theorem 6.

The m-polar fuzzy negation $\mathbf{N}$ is strict iff for all $i=1:m$, the operators $N_i$ are strict.

Proof. 

It is similar to Theorem 4. □

4. m-Polar $\mathbf{S}$-Pseudo-Ultrametric

A pseudo-metric on a (nonempty) set X is a function $d:X\times X\to [0,\infty ]$ such that for all $x,y,z\in X$ we have

1.

$d(x,x)=0$;

2.

$d(x,y)=d(y,x)$;

3.

$d(x,z)\le d(x,y)+d(y,z)$.

If the first axiom is replaced by the following stronger version $d(x,y)=0\iff x=y$ for all $x,y\in X$, then the pseudo-metric d is indeed a metric on X. Moreover, if the last axiom of the pseudo-metric d is replaced by the condition $d(x,z)\le max\left(d\right(x,y),d(y,z\left)\right)$, then d is called a pseudo-ultrametric on X. However, because the maximum operator is a t-conorm, it seems natural to generalize the third axiom of pseudo-ultrametrics by using any t-conorm S. By expanding this idea for m-polar fuzzy sets, a new concept, namely, the m-polar $\mathbf{S}$-pseudo-ultrametric, can be defined as below.

Definition 11.

An m-polar $\mathbf{S}$-pseudo-ultrametric on a (nonempty) set X is a function $\mathbf{d}:X\times X\to {[0,1]}^m$ such that for all $x,y,z\in X$ we have

1. 

$\mathbf{d}(x,x)=\mathbf{0}$;

2. 

$\mathbf{d}(x,y)=\mathbf{d}(y,x)$;

3. 

$\mathbf{d}(x,z)\le \mathbf{S}\left(\mathbf{d}\right(x,y),\mathbf{d}(y,z\left)\right)$,

where $\mathbf{S}$ is an m-polar t-conorm and $\mathbf{d}(x,y)=({\pi }_1\circ \mathbf{d}(x,y),\cdots ,{\pi }_m\circ \mathbf{d}(x,y))$.

The following theorem discusses how to build an m-polar $\mathbf{S}$-pseudo-ultrametric from an m-polar $\mathbf{T}$-equivalence $\mathbf{E}$.

Theorem 7.

Suppose $\mathbf{N}:=(N_1,\cdots ,N_m)$ is an m-polar negation where for all $i=1:m$ the operators $N_i$ are strong fuzzy negations (i.e., $N_i\left(N_i\left(u\right)\right)=u$). Let $\mathbf{T}:=(T_1,\cdots ,T_m)$ be an m-polar t-norm characterized by left-continuous t-norms $T_1,\cdots ,T_m$ and $\mathbf{S}:=(S_1,\cdots ,S_m)$ be an m-polar t-conorm such that for each $i=1:m$ the t-conorm $S_i$ is a $N_i$-dual of t-norm $T_i$—that is, $S_i(u,v)=N_i\left(T_i(N_i\left(u\right),N_i\left(v\right))\right)$. Then, the function $\mathbf{d}:X\times X\to {[0,1]}^m$ defined by

$${\pi }_i\circ \mathbf{d}(x,y)=N_i({\pi }_i\circ \mathbf{E}(x,y));i=1:m$$

(6)

is an m-polar $\mathbf{S}$-pseudo-ultrametric on X generated by an m-polar $\mathbf{T}$-equivalence relation $\mathbf{E}$ on X.

Proof. 

See Appendix C.1. □

Analogously, we have the following result.

Theorem 8.

Suppose $\mathbf{N}:=(N_1,\cdots ,N_m)$ is an m-polar negation where for all $i=1:m$ the operators $N_i$ are strong fuzzy negations. Let $\mathbf{T}:=(T_1,\cdots ,T_m)$ be an m-polar t-norm characterized by left-continuous t-norms $T_1,\cdots ,T_m$ and $\mathbf{S}:=(S_1,\cdots ,S_m)$ be an m-polar t-conorm such that for each $i=1:m$ the t-conorm $S_i$ is a $N_i$-dual of t-norm $T_i$. Then, function $\mathbf{E}:X\times X\to {[0,1]}^m$ defined by

$${\pi }_i\circ \mathbf{E}(x,y)=N_i({\pi }_i\circ \mathbf{d}(x,y));i=1:m$$

(7)

is an m-polar $\mathbf{T}$-equivalence relation on X generated by an m-polar $\mathbf{S}$-pseudo-ultrametric $\mathbf{d}$ on X.

Corollary 4.

Let $\mathbf{E}$ be an m-polar fuzzy relation on a set X. The following conditions are equivalent:

1. 

$\mathbf{E}$ is an m-polar ${\mathbf{T}}_M$-equivalence on X;

2. 

The function $\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-ultrametric on X,

where the m-polar t-norm ${\mathbf{T}}_M:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ is defined as ${\pi }_i\circ {\mathbf{T}}_M(\mathbf{u},\mathbf{v})=min({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{v}\right))$ for any $i=1:m$.

Proof. 

See Appendix C.2. □

Corollary 5.

Let $\mathbf{E}$ be an m-polar fuzzy relation on a set X. The following conditions are equivalent:

1. 

$\mathbf{E}$ is an m-polar ${\mathbf{T}}_L$-equivalence on X;

2. 

The function $\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-metric on X,

where the Lukasiewicz m-polar t-norm ${\mathbf{T}}_L:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ is defined by ${\pi }_i\circ {\mathbf{T}}_L(\mathbf{u},\mathbf{v})=max({\pi }_i\left(\mathbf{u}\right)+{\pi }_i\left(\mathbf{v}\right)-{\pi }_i\left(\mathbf{1}\right),{\pi }_i\left(\mathbf{0}\right))$ for any $i=1:m$.

Proof. 

See Appendix C.3. □

Proposition 4.

Let $\mathbf{S}:=(S_1,\cdots ,S_m)$ be an m-polar t-conorm characterized by right-continuous t-conorms $S_i$ for $i=1:m$. Suppose $\mathbf{T}:=(T_1,\cdots ,T_m)$ is an m-polar t-norm induced by $\mathbf{S}$ such that for any $i=1:m$: $T_i(u,v)=N_{S_i}\left(S_i(N_{S_i}\left(u\right),N_{S_i}\left(v\right))\right)$ for $u,v\in [0,1]$. Then, function $\mathbf{d}:X\times X\to {[0,1]}^m$ defined by

$${\pi }_i\circ \mathbf{d}(x,y)=N_{S_i}({\pi }_i\circ \mathbf{E}(x,y))=min\{\alpha \in [0,1]:S_i({\pi }_i\circ \mathbf{E}(x,y),\alpha )=1\}$$

(8)

is an m-polar $\mathbf{S}$-pseudo-ultrametric on X generated by an m-polar $\mathbf{T}$-equivalence relation $\mathbf{E}$ on X.

Proof. 

See Appendix C.4. □

Corollary 6.

Let $\mathbf{S}$ and ${\mathbf{S}}^{\ast }$ be two m-polar t-conorms such that $\mathbf{S}\le {\mathbf{S}}^{\ast }$ and $\mathbf{E}$ be an m-polar $\mathbf{T}$-equivalence on X. Then, $\mathbf{d}\le {\mathbf{d}}^{\ast }$ where $\mathbf{d}(x,y)={\mathbf{N}}_S\left(\mathbf{E}(x,y)\right)$ and ${\mathbf{d}}^{\ast }(x,y)={\mathbf{N}}_{S^{\ast }}\left(\mathbf{E}(x,y)\right)$.

5. Generating Fuzzy Graphs from m-Polar $\mathbf{S}$-Pseudo-Ultrametrics

Graphs, representing objects and their relationships, are widely used to model real-world problems from biology and chemistry to decision making and computer sciences, especially in social networks, traffic networks, influence networks, and so on [22,23,24,25]. In general, a graph $G^{\ast }=(V,E)$ includes a set of nodes V and a set of edges $E\subseteq V\times V$ between the nodes. The concepts of a fuzzy graph [26,27,28] and recently an m-polar fuzzy graph [11,12,29,30,31] were developed by combining graph theory and fuzzy set theory to visualize the problems in which different aspects of objects (nodes) as well as pairwise relations between the nodes are uncertain and vague.

Roughly speaking, in a fuzzy graph, nodes and edges are described by membership degrees, where the degree of each vertex presents its satisfaction level regarding the given parameter or criteria and the weight of each edge between a pair of nodes shows how much these nodes are related to each other. Mathematically, a triplet $G=(V,\varphi ,\psi )$ where $\varphi :V\to [0,1]$ and $\psi :V\times V\to [0,1]$ are fuzzy sets on V and $V^2$, respectively, such that $\psi \left(uv\right)\le min\left\{\varphi \right(u),\varphi (v\left)\right\}$ for all $u,v\in V$ is called a fuzzy graph where $\varphi$ are called fuzzy nodes and $\psi$ are called fuzzy edges. Note that if in the fuzzy graph G we put $\varphi :={\chi }_V$ then G is defined on the crisp node set V and known as a weighted graph on V.

The pair $G_0=(V_0,E_0)$ is called the underlying crisp graph of the fuzzy graph G where $V_0=\{v\in V:\varphi \left(v\right)>0\}$ and $E_0=\{uv\in V^2:\psi \left(uv\right)>0\}$. The fuzzy graph G is called strong if $\psi \left(uv\right)=min\left\{\varphi \right(u),\varphi (v\left)\right\}$ for all $uv\in E_0$ and it is called complete if $\psi \left(uv\right)=min\left\{\varphi \right(u),\varphi (v\left)\right\}$ for all $u,v\in V_0$. A path p of length n between u and v is a sequence of different nodes $u=u_0,u_1,\cdots ,u_{n-1},u_n=v$ where $\psi \left(u_{i-1}{u}_i\right)>0$ for $i=1,2,\cdots ,n$. The strength of p is defined as the minimum of the membership degrees $\psi (u_{i-1},u_i)$ which is referred to the weakest arc. The $sup\{{\psi }^n\left(uv\right):n=1,2,\cdots \}$, where ${\psi }^n\left(uv\right)=sup\{min\{\psi \left(u{u}_1\right),\psi \left(u_1{u}_2\right),\cdots ,\psi \left(u_{n-1}v\right)\}:u_1,\cdots ,u_{n-1}\in V\}$, shows the strength of connectedness between any two nodes u and v and is denoted by $CON{N}_G\left(uv\right)$. If for all $u,v\in V$ the $CON{N}_G\left(uv\right)>0$, then G is called connected. The fuzzy graph G is called regular if the neighborhood degrees of all vertices u in G, defined by $de{g}_G\left(u\right)={\sum }_{v\in N_G\left(u\right)}\varphi \left(v\right)$ where $N_G\left(u\right)=\{v\in V:0<\psi \left(uv\right)\le min\{\varphi \left(u\right),\varphi \left(v\right)\}\}$, is the same value.

By extending the mappings $\varphi$ and $\psi$ from the uni-polar case into the m-polar case as functions $\mathit{\varphi }:V\to {[0,1]}^m$ and $\mathit{\psi }:V\times V\to {[0,1]}^m$, the triplet $\mathbf{G}=(V,\mathit{\varphi },\mathit{\psi })$ can be defined as an m-polar fuzzy graph which serves as a mathematical model for situations where positive and negative sides (where $m=2$) or different aspects/directions/categories (where $m>2$) of given information affect the resultant outputs.

Since the weights of edges in an undirected graph, where edges link two vertices symmetrically, can be obtained based on a distance function over the set of alternatives [32], a special type of m-polar fuzzy undirected graph based on the m-polar $\mathbf{S}$-pseudo-ultrametric $\mathbf{d}$, discussed in the previous section, can be defined over the set of crisp nodes. However, drawing an m-polar fuzzy graph is a complicated and complex task when we deal with a large number of m. One way to overcome this difficulty is to use aggregation functions in order to combine different edges in different directions between each pair of nodes into a unique one.

In this section, we propose a procedure to draw a fuzzy or weighted graph over the set of alternatives by using a distance function between them, built from m-polar $\mathbf{T}$-equivalences. We first obtain an m-polar $\mathbf{S}$-pseudo-ultrametric $\mathbf{d}$ over the alternatives (see Theorem 7 and Proposition 4) and then derive a new S-pseudo-ultrametric on X, where S is a t-conorm, with the help of aggregation function F as below.

Theorem 9.

Let $S:{[0,1]}^2\to [0,1]$ be a t-conorm and $\mathbf{d}$ be an m-polar $\mathbf{S}$-pseudo-ultrametric on X where $\mathbf{S}:=(S,\cdots ,S)$ is characterized by S. Suppose that $F:{[0,1]}^m\to [0,1]$ is an aggregation operator. Function $\rho :X\times X\to [0,1]$ defined by

$$\rho (x,y)=F({\pi }_1\circ \mathbf{d}(x,y),\cdots ,{\pi }_m\circ \mathbf{d}(x,y))$$

(9)

is an S-pseudo-ultrametric on X if $S\gg F$.

Proof. 

See Appendix D.1. □

Corollary 7.

Let X be a nonempty set and $\mathbf{E}$ be an m-polar fuzzy relation on X.

1. 

If $\mathbf{E}$ is an m-polar ${\mathbf{T}}_M$-equivalence on X, then ρ is a pseudo-ultrametric on X for $F:=Max$, the maximum operator.

2. 

If $\mathbf{E}$ is an m-polar ${\mathbf{T}}_L$-equivalence on X, then ρ is a pseudo-metric on X for $F:=WAM$, the weighted arithmetic mean operator.

Definition 12.

Let X be a nonempty set of objects and $\rho :X\times X\to [0,1]$ be the pseudo-ultrametric given by Equation (9). The triplet $G=(X,\chi ,\rho )$ is a fuzzy (or weighted) graph on X induced by ρ, where χ is the characteristic function on X, which is called a fuzzy dissimilarity graph. The weight of each edge between a pair of nodes shows the degree of distinguishability between these two points.

Clearly, the order of G (i.e., $O\left(G\right)$) equals to the cardinality of X (i.e., $\mid X\mid$), while the size of G is $S\left(G\right)={\sum }_{x,y\in X}\rho (x,y)$. Moreover, G does not have any loop since $\rho (x,x)=0$ for all $x\in X$.

Remark 2.

Because ρ is a pseudo-(ultra)metric, that is, $\rho (x,y)=0$ does not necessarily imply that $x=y$, we cannot talk about the connectedness, regularity, and completeness of the fuzzy graph $G=(X,\chi ,\rho )$ in general. However, these properties can be considered in some special cases.

If $\mathbf{E}$ is an m-polar $\mathbf{T}$-equivalence relation on X where for some $j=1:m$; $0\le {\pi }_j\circ \mathbf{E}(x,y)<1$, then G is a fuzzy connected graph iff the aggregation function F defined in Equation (9) does not have a zero element 0. If for some j, ${\pi }_j\circ \mathbf{E}(x,y)=0$, then the fuzzy graph G is completed iff the aggregation function F has a zero element 1.

Proposition 5.

Let X be a nonempty set and $\mathbf{E}$ be an m-polar fuzzy relation on X. Suppose $G=(X,\chi ,\rho )$ is the fuzzy graph defined by Equation (9).

1. 

Let $\mathbf{E}$ be an m-polar ${\mathbf{T}}_M$-equivalence on X. Suppose $\rho (x,y)=max(1-{\pi }_1\circ \mathbf{E}(x,y),\cdots ,$$1-{\pi }_m\circ \mathbf{E}(x,y))$ for $x,y\in X$. Then, the fuzzy graph G is connected iff for some j,${\pi }_j\circ \mathbf{E}(x,y)\ne 1$. Moreover, the fuzzy graph G is completed iff there exists j such that ${\pi }_j\circ \mathbf{E}(x,y)=0$.

2. 

Let $\mathbf{E}$ be an m-polar ${\mathbf{T}}_L$-equivalence on X. Suppose $\rho (x,y)=WAM(1-{\pi }_1\circ \mathbf{E}(x,y),\cdots ,$$1-{\pi }_m\circ \mathbf{E}(x,y))$ for $x,y\in X$. Then, the fuzzy graph G is connected iff for some j,${\pi }_j\circ \mathbf{E}(x,y)\ne 1$.

Proof. 

See Appendix D.2. □

5.1. Application in Group Decision Making

In a group decision making problem with m-polar fuzzy information, let $X=\{x_1,x_2,\cdots ,x_n\}$ and $P=\{p_1,p_2,\cdots ,p_m\}$ be the finite sets of alternatives and parameters, respectively, where $\lambda =({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_m)$ is the weighting vector for the parameter set P such that $\forall j$: ${\lambda }_j\in [0,1]$ and ${\sum }_{j=1}^m{\lambda }_j=1$. Suppose that $D_K=\{1\cdots ,K\}$ is the set of decision makers and $\mathbf{w}=(w_1,\cdots ,w_K)$ is their weighting vector where for all k: $w_k\in [0,1]$ and ${\sum }_{k=1}^K{w}_k=1$. Assume that each decision maker k applies an m-polar fuzzy set to present their evaluation of alternatives such that ${\mathit{\mu }}_k\left(x_i\right)=({\pi }_1\circ {\mathit{\mu }}_k\left(x_i\right),\cdots ,{\pi }_m\circ {\mathit{\mu }}_k\left(x_i\right))\in {[0,1]}^m$ where for any j, ${\pi }_j\circ {\mathit{\mu }}_k\left(x_i\right)$ shows the satisfaction degree/level of alternative $x_i$ regarding the attribute $p_j$ in the view of decision maker k.

After each expert prepares a numerical judgment of alternatives based on the given parameters, the first stage is to get an m-polar fuzzy $\mathbf{T}$-equivalence relation on the set X, where $\mathbf{T}$ is a given m-polar t-norm. This issue has been discussed in our previous paper [33]. We recall from [33] that if $\mathbf{T}:=(T_1,\cdots ,T_m)$ is an m-polar t-norm characterized by left-continuous t-norms $T_1,\cdots ,T_m$ and $\overrightarrow{\mathbf{T}}:=(\overrightarrow{T_1},\cdots ,\overrightarrow{T_m})$ is the m-polar implication generated by $\mathbf{T}$. Then, the m-polar fuzzy relation $\mathbf{R}:X\times X\to {[0,1]}^m$ defined by $\mathbf{R}(x,y)=({\pi }_1\circ \mathbf{R}(x,y),\cdots ,{\pi }_m\circ \mathbf{R}(x,y))$ such that for any $i=1:m$:

$${\pi }_i\circ \mathbf{R}(x,y)=A_i[\overrightarrow{T_i}({\pi }_i\circ {\mathit{\mu }}_1\left(x\right),{\pi }_i\circ {\mathit{\mu }}_1\left(y\right)),\cdots ,\overrightarrow{T_i}({\pi }_i\circ {\mathit{\mu }}_K\left(x\right),{\pi }_i\circ {\mathit{\mu }}_K\left(y\right))]$$

(10)

is an m-polar $\mathbf{T}$-preorder on X if for each i, $A_i\gg T_i$ where $A_i$ is an aggregation function. Moreover, the m-polar fuzzy relation $\mathbf{E}:X\times X\to {[0,1]}^m$ defined by

$${\pi }_i\circ \mathbf{E}(x,y)=B_i[{\pi }_i\circ \mathbf{R}(x,y),{\pi }_i\circ \mathbf{R}(y,x)]:i=1,\cdots ,m$$

(11)

is an m-polar $\mathbf{T}$-equivalence on X if for any $i:1=m$, $B_i\gg T_i$ where $B_i$ is a symmetric aggregation function.

Consequently, an m-polar $\mathbf{S}$-pseudo-ultrametric can be obtained (see Theorem 7). The next stage is to reach a new S-pseudo-ultrametric over X which is handled through an aggregation operator F, where S is a t-conorm. The final stage of the proposed approach aims to find a fuzzy graph which shows the distance between alternatives with respect to the parameter set P.

Since the Lukasiewicz t-norm $T_L$ is an appropriate choice for practical situations, we apply the approach proposed above for the Lukasiewicz m-polar t-norm ${\mathbf{T}}_L$ and the aggregation function $WAM$ (the weighted arithmetic mean) to design the following algorithm.

Remark 3.

According to Proposition 5, if there exits j such that for any $x_i,x_l\in X$ the value ${\pi }_j\circ \mathbf{R}(x_i,x_l)$ of the positive ${\mathbf{T}}_L$-preordering $\mathbf{R}$ used in Algorithm 1 is not equal to 1, then the resultant fuzzy graph G is connected since $WAM$ does not have zero elements 0 and 1 and $Min$ does not have zero element 1.

Algorithm 1: Fuzzy dissimilarity graph generated by an m-polar pseudo-metric.

Numerical Example

To illustrate the proposed approach, let $X=\{x_1=a,x_2=b,x_3=c,x_4=d\}$ be a set of alternatives which are evaluated by three experts with weights $w_1=0.3,w_2=0.5,w_3=0.2$ based on two parameters $p_1$ and $p_2$ with different importance degrees ${\lambda }_1=0.65$ and ${\lambda }_2=0.35$. The experts’ judgments about these four alternatives can be modeled by three 2-polar fuzzy sets given by the following matrices:

$${\mathit{\mu }}_1=\left[\begin{array}{cc}0.5& 0.3\\ 0.34& 0.25\\ 0.7& 0.8\\ 0.6& 0.41\end{array}\right],{\mathit{\mu }}_2=\left[\begin{array}{cc}0.7& 0.5\\ 0.25& 0.3\\ 0.37& 0.6\\ 0.8& 0.9\end{array}\right],{\mathit{\mu }}_3=\left[\begin{array}{cc}0.41& 0.8\\ 0.7& 0.8\\ 0.2& 0.2\\ 0.3& 0.4\end{array}\right]$$

Based on each evaluation matrix ${\mu }_k$, for $k=1,2,3$, the 2-polar fuzzy implication matrix ${\overrightarrow{\mathbf{T}}}_L^k$, induced by 2-polar Lukasiewicz t-norm ${\mathbf{T}}_L$, is computed as below (Step 1):

$${\overrightarrow{\mathbf{T}}}_L^1=\left[\stackrel{p_1}{\left[\begin{array}{cccc}1& 0.84& 1& 1\\ 1& 1& 1& 1\\ 0.8& 0.64& 1& 0.9\\ 0.9& 0.74& 1& 1\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}1& 0.95& 1& 1\\ 1& 1& 1& 1\\ 0.5& 0.45& 1& 0.61\\ 0.89& 0.84& 1& 1\end{array}\right]}\right]$$

$${\overrightarrow{\mathbf{T}}}_L^2=\left[\stackrel{p_1}{\left[\begin{array}{cccc}1& 0.55& 0.67& 1\\ 1& 1& 1& 1\\ 1& 0.88& 1& 1\\ 0.9& 0.45& 0.57& 1\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}1& 0.8& 1& 1\\ 1& 1& 1& 1\\ 0.9& 0.7& 1& 1\\ 0.6& 0.4& 0.7& 1\end{array}\right]}\right]$$

$${\overrightarrow{\mathbf{T}}}_L^3=\left[\stackrel{p_1}{\left[\begin{array}{cccc}1& 1& 0.79& 0.89\\ 0.71& 1& 0.5& 0.6\\ 1& 1& 1& 1\\ 1& 1& 0.9& 1\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}1& 1& 0.4& 0.6\\ 1& 1& 0.4& 0.6\\ 1& 1& 1& 1\\ 1& 1& 0.8& 1\end{array}\right]}\right]$$

To draw a fuzzy graph based on these data, we need first to derive the 2-polar ${\mathbf{T}}_L$-equivalence matrix $\mathbf{E}$ with respect to 2-polar ${\mathbf{T}}_L$-preorder matrix $\mathbf{R}$ (Steps 2 and 3).

$$\mathbf{R}=\left[\stackrel{p_1}{\left[\begin{array}{cccc}1& 0.727& 0.793& 0.978\\ 0.942& 1& 0.9& 0.92\\ 0.94& 0.832& 1& 0.97\\ 0.92& 0.647& 0.765& 1\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}1& 0.885& 0.88& 0.92\\ 1& 1& 0.88& 0.92\\ 0.8& 0.685& 1& 0.883\\ 0.767& 0.652& 0.81& 1\end{array}\right]}\right]$$

$$\mathbf{E}=\left[\stackrel{p_1}{\left[\begin{array}{cccc}1& 0.727& 0.793& 0.92\\ 0.727& 1& 0.832& 0.647\\ 0.793& 0.832& 1& 0.765\\ 0.92& 0.647& 0.765& 1\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}1& 0.885& 0.8& 0.767\\ 0.885& 1& 0.685& 0.652\\ 0.8& 0.685& 1& 0.81\\ 0.767& 0.652& 0.81& 1\end{array}\right]}\right]$$

Now, the 2-polar pseudo-metric $\mathbf{d}=1-\mathbf{E}$ is obtained as below (Step 4):

$$\mathbf{d}=\left[\stackrel{p_1}{\left[\begin{array}{cccc}0& 0.273& 0.207& 0.08\\ 0.273& 0& 0.168& 0.353\\ 0.207& 0.168& 0& 0.235\\ 0.08& 0.353& 0.235& 0\end{array}\right]}\stackrel{p_2}{\left[\begin{array}{cccc}0& 0.115& 0.2& 0.233\\ 0.115& 0& 0.315& 0.348\\ 0.2& 0.315& 0& 0.19\\ 0.233& 0.348& 0.19& 0\end{array}\right]}\right]$$

Figure 1 shows the 2-polar fuzzy graph generated by the 2-polar pseudo-metric $\mathbf{d}$.

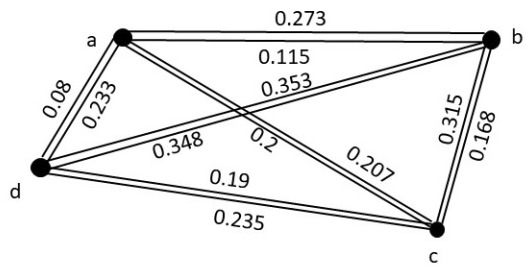
Figure 1. 2-Polar fuzzy graph of 2-polar pseudo-metric $\mathbf{d}$.

The pseudo-metric $\rho$ is then computed based on $\mathbf{d}$ (Step 5):

$$\rho =\left[\begin{array}{cccc}0& 0.2177& 0.20455& 0.13355\\ 0.2177& 0& 0.21945& 0.35125\\ 0.20455& 0.21945& 0& 0.21925\\ 0.13355& 0.35125& 0.21925& 0\end{array}\right]$$

Thus, the following fuzzy dissimilarity graph G, see Figure 2, is obtained (Step 6).

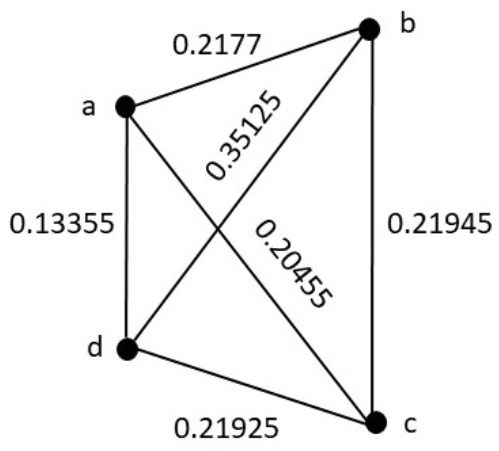
Figure 2. Fuzzy dissimilarity graph G of pseudo-metric $\rho$.

6. Conclusions

Fuzzy similarity, formulated as T-equivalence relations, is a well-known method to measure the similarity degree among fuzzy concepts. There is a close link in theory between similarity and dissimilarity (distance) measures, such that one is the dual of another. Despite different proposed formulas in the literature to define the distance functions in an m-dimensional space in order to calculate the dissimilarity degree between each component of two points with m aspects, and consequently to measure the degree of similarity among them, such methods usually have a main drawback: defining based on a predefined metric that leads to a fix formula for all cases $i=1:m$.

Introducing the new concept of similarity for m-polar fuzzy data, called m-polar $\mathbf{T}$-equivalences, allowed us to measure the similarity degree among m-polar fuzzy sets independently from any metric (Equations (10) and (11)). Moreover, using membership functions to model the m-polar $\mathbf{T}$-equivalences helped us to define the similarity degree in each direction $i=1:m$ (Theorem 2 and Example 1). Therefore, to measure the similarity between each component of two m-polar fuzzy items, different formulas can be applied for each case i.

In this paper, we extended the standard definitions of t-norm, t-conorm, fuzzy implication, and fuzzy negation to the m-polar case by operators acting on the Cartesian product $[0,1]\times \cdots \times [0,1]$, m-times, rather than the unit interval $[0,1]$. The main contribution of this study is the use of the concept of m-polar negation $\mathbf{N}$ to define a stronger version of pseudo-ultrametrics, namely, m-polar $\mathbf{S}$-pseudo-ultrametric, based on the m-polar t-conorm $\mathbf{S}$ and $\mathbf{T}$-equivalence $\mathbf{E}$ where $\mathbf{T}$ is an m-polar t-norm (Theorem 7). By replacing the third axiom $d(x,z)\le max\left(d\right(x,y),d(y,z\left)\right)$ of pseudo-ultrametrics with the new condition $d(x,z)\le S\left(d\right(x,y),d(y,z\left)\right)$, where S is a t-conorm, for each case $i=1:m$,this new metric space enables us to offer a more general version of the transitivity property in pseudo-ultrametric spaces with respect to all three sides, not just the maximum one. Algorithm 1 was then designed to derive an m-polar ${\mathbf{S}}_L$-pseudo-ultrametric, which can be visualized by an m-polar fuzzy graph. The complexity problem of the m-polar fuzzy graphs was overcome by using the aggregation functions (Theorem 9) and the output was presented in the form of fuzzy graphs, namely, fuzzy dissimilarity graphs. Finally, the computational steps of the proposed approach were demonstrated by a numerical example.

The proposed method can be also considered for m-polar fuzzy data with membership degrees in the form of interval values rather than exact values (known as interval-valued m-polar fuzzy sets). This may help experts to provide more realistic solutions during a decision making process. So, further work is needed to convert the steps of Algorithm 1 to the new format. Moreover, the theoretical results of the paper can be applied to develop fuzzy digraphs, which are widely used in behavioral sciences such as psychology and management, based on the m-polar $\mathbf{T}$-preorder relations. In our future work, we may mainly focus on using the proposed similarity measurement for data clustering based on the fuzzy multigraph models.

Appendix A.1. Proof of Proposition 1

Let $\mathbf{T}:=(T_1,\cdots ,T_m)$ be an m-polar t-norm. Take $u,v,w\in [0,1]$ and $i=1:m$. Put $\mathbf{u}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{u}},0,\cdots ,0)$, $\mathbf{v}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{v}},0,\cdots ,0)$ and $\mathbf{w}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{w}},0,\cdots ,0)$.

Then

$$\begin{array}{cc}\hfill T_i(T_i(u,v),w)& =T_i(T_i({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{v}\right)),{\pi }_i\left(\mathbf{w}\right))\hfill \\ \hfill & =T_i({\pi }_i\left(\mathbf{T}(\mathbf{u},\mathbf{v})\right),{\pi }_i\left(\mathbf{w}\right))={\pi }_i\circ \mathbf{T}(\mathbf{T}(\mathbf{u},\mathbf{v}),\mathbf{w})\hfill \\ \hfill & ={\pi }_i\circ \mathbf{T}(\mathbf{u},\mathbf{T}(\mathbf{v},\mathbf{w}))=T_i(u,{\pi }_i\left(\mathbf{T}(\mathbf{v},\mathbf{w})\right))\hfill \\ \hfill & =T_i(u,T_i(v,w))\hfill \end{array}$$

Moreover, $T_i(u,v)=T_i({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{v}\right))={\pi }_i\circ \mathbf{T}(\mathbf{u},\mathbf{v})={\pi }_i\circ \mathbf{T}(\mathbf{v},\mathbf{u})=T_i({\pi }_i\left(\mathbf{v}\right),$${\pi }_i\left(\mathbf{u}\right))=T_i(v,u)$. Finally, $T_i(u,1)=T_i({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{1}\right))={\pi }_i\circ \mathbf{T}(\mathbf{u},\mathbf{1})={\pi }_i\left(\mathbf{u}\right)=u$. The converse is clear.

Appendix A.2. Proof of Proposition 2

We only consider the transitivity property. The rest can be proved analogously.

Let $\mathbf{T}:=(T_1,\cdots ,T_m)$ be an m-polar t-norm such that for any $i=1:m$, $T_i$ is a t-norm. Consider the m-polar fuzzy relation $\mathbf{R}:X\times X\to {[0,1]}^m$ on the nonempty set X which is $\mathbf{T}$-transitive. Take $x,y,z\in X$. For any $1\le i\le m$ we have $T_i({\pi }_i\left(\mathbf{R}(x,y)\right),{\pi }_i\left(\mathbf{R}(y,z)\right))={\pi }_i\circ \mathbf{T}(\mathbf{R}(x,y),\mathbf{R}(y,z))\le {\pi }_i\circ \mathbf{R}(x,z)$, which means that ${\pi }_i\circ \mathbf{R}$ is $T_i$-transitive. Conversely, let for any $1\le i\le m$, ${\pi }_i\circ \mathbf{R}$ be $T_i$-transitive. Take $x,y,z\in X$. Then ${\pi }_i\circ \mathbf{T}(\mathbf{R}(x,y),\mathbf{R}(y,z))=T_i({\pi }_i\circ \mathbf{R}(x,y),{\pi }_i\circ \mathbf{R}(y,z))\le {\pi }_i\circ \mathbf{R}(x,z)$ for any $i=1:m$. Therefore, $\mathbf{T}\left(\mathbf{R}\right(x,y),\mathbf{R}(y,z\left)\right)\le \mathbf{R}(x,z)$, which means that $\mathbf{R}$ is m-polar $\mathbf{T}$-transitive.

Appendix B.1. Proof of Theorem 1

First let $\mathbf{I}:{\left({[0,1]}^m\right)}^2\to {[0,1]}^m$ be an m-polar fuzzy implication. Take $u,v\in [0,1]$ such that $u\le v$. For any $i=1:m$, consider $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ where $\mathbf{u}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{u}},0,\cdots ,0)$ and $\mathbf{v}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{v}},0,\cdots ,0)$. Then, clearly, $\mathbf{u}\le \mathbf{v}$. Thus, $\mathbf{I}(\mathbf{u},\mathbf{w})\ge \mathbf{I}(\mathbf{v},\mathbf{w})$ for any $\mathbf{w}\in {[0,1]}^m$, where $\mathbf{w}=(w_1,\cdots ,w_m)$. This implies ${\pi }_i\circ \mathbf{I}(\mathbf{u},\mathbf{w})\ge {\pi }_i\circ \mathbf{I}(\mathbf{u},\mathbf{w})$. On the other hand, since $\mathbf{I}:=(I_1,\cdots ,I_m)$, then $I_i({\pi }_s\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{w}\right))\ge I_i({\pi }_s\left(\mathbf{v}\right),{\pi }_i\left(\mathbf{w}\right))$ or equivalently, $I_i(u,w_i)\ge I_i(v,w_i)$ that $w_i\in [0,1]$. This shows that $I_i$ is decreasing at the first variable. Similarly, we can prove that it is increasing at the second variable. Moreover, because $\mathbf{I}(\mathbf{0},\mathbf{0})=(1,\cdots ,1)$ and $\mathbf{I}(\mathbf{1},\mathbf{1})=(1,\cdots ,1)$, then $I_i({\pi }_i\left(\mathbf{0}\right),{\pi }_i\left(\mathbf{0}\right))=I_i(0,0)=1$ and $I_i({\pi }_i\left(\mathbf{1}\right),{\pi }_i\left(\mathbf{1}\right))=I_i(1,1)=1$. In a similar manner, $I_i(1,0)=0$ is followed from $\mathbf{I}(\mathbf{1},\mathbf{0})=\mathbf{0}$.

Conversely, let $\mathbf{I}:=(I_1,\cdots ,I_m)$ where for any $1\le i\le m$, $I_i:{[0,1]}^2\to [0,1]$ are fuzzy implications. Then, axioms a–d of Definition 8 are obtained easily.

Appendix B.2. Proof of Theorem 2

It is sufficient to show that $\overrightarrow{\mathbf{T}}:=(\overrightarrow{T_1},\cdots ,\overrightarrow{T_m}($. Then, by using Theorem 1, it is proved.

Take $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ such that $\mathbf{u}=(u_1,\cdots ,u_m)$ and $\mathbf{v}=(v_1,\cdots ,v_m)$. Put $\overrightarrow{\mathbf{T}}(\mathbf{u},\mathbf{v})=\mathit{\beta }\in {[0,1]}^m$ where $\mathit{\beta }=({\beta }_1,\cdots ,{\beta }_m)$. Then

$$\begin{array}{cc}\hfill ({\beta }_1,\cdots ,{\beta }_m)& =sup\{\mathit{\alpha }\in {[0,1]}^m:\mathbf{T}(\alpha ,\mathbf{u})\le \mathbf{v}\}\hfill \\ \hfill & =sup\{\mathit{\alpha }\in {[0,1]}^m:T_i({\pi }_i\left(\mathit{\alpha }\right),{\pi }_i\left(\mathbf{u}\right))\le {\pi }_i\left(\mathbf{v}\right);1\le i\le m\}\hfill \end{array}$$

which means ${\beta }_i=sup\{{\alpha }_i\in [0,1]:T_i({\alpha }_i,u_i)\le v_i\}$ for each $1\le i\le m$, which implies that ${\pi }_i\circ \overrightarrow{\mathbf{T}}(\mathbf{u},\mathbf{v})=\overrightarrow{T_i}({\pi }_i\left(\mathbf{u}\right),{\pi }_i\left(\mathbf{v}\right))$, or equivalently, $\overrightarrow{\mathbf{T}}:=(\overrightarrow{T_1},\cdots ,\overrightarrow{T_m})$.

Appendix B.3. Proof of Theorem 3

Let $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ be defined by $\mathbf{N}:=(N_1,\cdots ,N_m)$ such that ${\pi }_i\circ \mathbf{N}\left(\mathbf{u}\right)=N_i\left({\pi }_i\left(\mathbf{u}\right)\right)$ for each $i=1:m$, where $N_i:[0,1]\to [0,1]$. If for all i the operators $N_i$ are fuzzy negations, then, clearly, $\mathbf{N}(0,\cdots ,0)=(N_1\left(0\right),\cdots ,N_m\left(0\right))=\mathbf{0}$ and $\mathbf{N}(1,\cdots ,1)=(N_1\left(1\right),\cdots ,N_m\left(1\right))=\mathbf{1}$. Moreover, if $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ such that $\mathbf{u}\le \mathbf{v}$, then $\mathbf{N}\left(\mathbf{u}\right)\ge \mathbf{N}\left(\mathbf{v}\right)$ comes from $N_i\left({\pi }_i\left(\mathbf{u}\right)\right)\ge N_i\left({\pi }_i\left(\mathbf{v}\right)\right)$. Conversely, let $u\le v$. Take $1\le i\le m$. Consider $\mathbf{u},\mathbf{v}\in {[0,1]}^m$ where $\mathbf{u}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{u}},0,\cdots ,0)$ and $\mathbf{v}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{v}},0,\cdots ,0)$. Then, clearly, $\mathbf{u}\le \mathbf{v}$. Thus, $\mathbf{N}\left(\mathbf{u}\right)\ge \mathbf{N}\left(\mathbf{v}\right)$, which means $N_i\left({\pi }_i\left(\mathbf{u}\right)\right)\ge N_i\left({\pi }_i\left(\mathbf{v}\right)\right)$, or equivalently $N_i\left(u\right)\ge N_i\left(v\right)$. The boundary conditions $N_i\left(0\right)=0$ and $N_i\left(1\right)=1$ are implied easily from $\mathbf{N}(0,\cdots ,0)=\mathbf{0}$ and $\mathbf{N}(1,\cdots ,1)=\mathbf{1}$.

Appendix B.4. Proof of Proposition 3

Let $\mathbf{S}$ be an m-polar t-conorm and $\mathbf{u}=(u_1,\cdots ,u_m)\in {[0,1]}^m$. By Corollary 3 and for any $1\le i\le m$, we have:

$$\begin{array}{cc}\hfill {\pi }_i\circ {\mathbf{N}}_{\mathbf{S}}\left({\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right)\right)& =N_{S_i}({\pi }_i\circ {\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right))=N_{S_i}\left(N_{S_i}\left({\pi }_i\left(\mathbf{u}\right)\right)\right)\hfill \\ \hfill & =inf\{\beta \in [0,1]:S_i(\beta ,N_{S_i}\left({\pi }_i\left(\mathbf{u}\right)\right))=1\}\hfill \end{array}$$

If we put $\beta =u_i\in [0,1]$, then by Definition 2 we clearly get $S_i(u_i,N_{S_i}\left(u_i\right))=1$. This means ${\pi }_i\circ {\mathbf{N}}_{\mathbf{S}}\left({\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right)\right)\le u_i$ for any $1\le i\le m$. Thus, we get $\mathbf{u}\ge {\mathbf{N}}_{\mathbf{S}}\left({\mathbf{N}}_{\mathbf{S}}\left(\mathbf{u}\right)\right)$. The inequality $\mathbf{u}\le {\mathbf{N}}_{\mathbf{T}}\left({\mathbf{N}}_{\mathbf{T}}\left(\mathbf{u}\right)\right)$ is proved similarly.

Appendix B.5. Proof of Theorem 4

Consider the m-polar fuzzy negation $\mathbf{N}:{[0,1]}^m\to {[0,1]}^m$ defined by $\mathbf{N}:=(N_1,\cdots ,N_m)$ such that ${\pi }_i\circ \mathbf{N}\left(\mathbf{u}\right)=N_i\left({\pi }_i\left(\mathbf{u}\right)\right)$ for each $i=1:m$, where $N_i:[0,1]\to [0,1]$ are fuzzy negations. Let, first, for all $1\le i\le m$, the operators $N_i$ be strong fuzzy negations. Take $\mathbf{u}\in {[0,1]}^m$. Then, for any i, ${\pi }_i\circ \mathbf{N}\left(\mathbf{N}\left(\mathbf{u}\right)\right)=N_i({\pi }_i\circ \mathbf{N}\left(\mathbf{u}\right))=N_i\left(N_i\left({\pi }_i\left(\mathbf{u}\right)\right)\right)=u_i={\pi }_i\left(\mathbf{u}\right)$.

Conversely, take any $1\le i\le m$. Consider $\mathbf{u}\in {[0,1]}^m$, where $\mathbf{u}=(0,\cdots ,0,\stackrel{i-th}{\overbrace{u}},0,\cdots ,0)$. Then, $\mathbf{u}=\mathbf{N}\left(\mathbf{N}\right(\mathbf{u}\left)\right)$, which implies ${\pi }_i\left(\mathbf{u}\right)={\pi }_i\circ N({\pi }_i\circ N\left(\mathbf{u}\right))=N_i\left(N_i\left({\pi }_i\left(\mathbf{u}\right)\right)\right)$, or equivalently $u=N_i\left(N_i\left(u\right)\right)$, which means $N_i$ is strong.

Appendix C.1. Proof of Theorem 7

Assume that $\mathbf{E}$ is an m-polar $\mathbf{T}$-equivalence relation on X. Take $x,y\in X$ such that $x=y$. Then, for any $i=1:m$, ${\pi }_i\circ \mathbf{d}(x,x)=N_i({\pi }_i\circ \mathbf{E}(x,x))=N_i\left(1\right)=0$, and consequently $\mathbf{d}(x,x)=\mathbf{0}$. Moreover, the symmetry condition for $\mathbf{d}$ is followed from the symmetry property of $\mathbf{E}$. For axiom (3), let $x,y,z\in X$. Then, for any $1\le i\le m$:

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{d}(x,z)=N_i[{\pi }_i\circ \mathbf{E}(x,z)]& \le N_i\left[T_i({\pi }_i\circ \mathbf{E}(x,y),{\pi }_i\circ \mathbf{E}(y,z))\right]\hfill \\ \hfill & =N_i\left[T_i(N_i\left(N_i({\pi }_i\circ \mathbf{E}(x,y))\right),N_i\left(N_i({\pi }_i\circ \mathbf{E}(y,z))\right))\right]\hfill \\ \hfill & =N_i\left[T_i(N_i({\pi }_i\circ \mathbf{d}(x,y)),N_i({\pi }_i\circ \mathbf{d}(y,z)))\right]\hfill \\ \hfill & =S_i[{\pi }_i\circ \mathbf{d}(x,y),{\pi }_i\circ \mathbf{d}(y,z)]\hfill \end{array}$$

because $\mathbf{E}$ is an m-polar $\mathbf{T}$-transitive and for any $i=1:m$, $N_i$ is strong. Therefore, $\mathbf{d}$ is an m-polar $\mathbf{S}$-pseudo-ultrametric on X.

Appendix C.2. Proof of Corollary 4

First, let $\mathbf{E}$ be an m-polar ${\mathbf{T}}_M$-equivalence on X. Axioms (1) and (2) can be easily checked. To prove axiom (3), let $x,y,z\in X$, then for any $i=1:m$:

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{d}(x,z)=1-{\pi }_i\circ \mathbf{E}(x,z)& \le 1-min({\pi }_i\circ \mathbf{E}(x,y),{\pi }_i\circ \mathbf{E}(y,z))\hfill \\ \hfill & =max(1-{\pi }_i\circ \mathbf{E}(x,y),1-{\pi }_i\circ \mathbf{E}(y,z))\hfill \\ \hfill & =max({\pi }_i\circ \mathbf{d}(x,y),{\pi }_i\circ \mathbf{d}(y,z))\hfill \end{array}$$

which means $\mathbf{d}=\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-ultrametric on X. Conversely, let $\mathbf{E}$ be an m-polar fuzzy relation on a set X such that $\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-ultrametric. Then, $\mathbf{E}(\mathbf{x},\mathbf{x})=\mathbf{1}$ and $\mathbf{E}(\mathbf{x},\mathbf{y})=\mathbf{E}(\mathbf{y},\mathbf{x})$ for any $x,y\in X$ and $i=1:m$. Now take $x,y,z\in X$, then

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{E}(x,z)=1-{\pi }_i\circ \mathbf{d}(x,z)& \ge 1-max({\pi }_i\circ \mathbf{d}(x,y),{\pi }_i\circ \mathbf{d}(y,z))\hfill \\ \hfill & =min(1-{\pi }_i\circ \mathbf{d}(x,y),1-{\pi }_i\circ \mathbf{d}(y,z))\hfill \\ \hfill & =min({\pi }_i\circ \mathbf{E}(x,y),{\pi }_i\circ \mathbf{E}(y,z))\hfill \end{array}$$

This shows $\mathbf{E}$ is ${\mathbf{T}}_M$-transitive. Therefore, $\mathbf{E}$ is an m-polar ${\mathbf{T}}_M$-equivalence on X.

Appendix C.3. Proof of Corollary 5

First, let $\mathbf{E}$ be an m-polar ${\mathbf{T}}_L$-equivalence on X. Axioms (1) and (2) are clearly obtained for $\mathbf{d}=\mathbf{1}-\mathbf{E}$. To prove axiom (3), let $x,y,z\in X$, then for any $1\le i\le m$:

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{d}(x,z)=1-{\pi }_i\circ \mathbf{E}(x,z)& \le 1-max({\pi }_i\circ \mathbf{E}(x,y)+{\pi }_i\circ \mathbf{E}(y,z)-1,0)\hfill \\ \hfill & =min(2-{\pi }_i\circ \mathbf{E}(x,y)-{\pi }_i\circ \mathbf{E}(y,z),1)\hfill \\ \hfill & =min(1-{\pi }_i\circ \mathbf{E}(x,y)+1-{\pi }_i\circ \mathbf{E}(y,z),1)\hfill \\ \hfill & =min({\pi }_i\circ \mathbf{d}(x,y)+{\pi }_i\circ \mathbf{d}(y,z),1)\hfill \\ \hfill & \le {\pi }_i\circ \mathbf{d}(x,y)+{\pi }_i\circ \mathbf{d}(y,z)\hfill \end{array}$$

which means that $\mathbf{d}=\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-metric on X. Clearly, $\mathbf{d}$ is also an m-polar ${\mathbf{S}}_L$-pseudo-ultrametric on X. Conversely, let $\mathbf{E}$ be an m-polar fuzzy relation on a set X such that $\mathbf{1}-\mathbf{E}$ is an m-polar pseudo-metric. Then, clearly, $\mathbf{E}(\mathbf{x},\mathbf{x})=\mathbf{1}$ and $\mathbf{E}(\mathbf{x},\mathbf{y})=\mathbf{E}(\mathbf{y},\mathbf{x})$ for any $x,y\in X$ and $i=1:m$. Now take $x,y,z\in X$, then

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{E}(x,z)=1-{\pi }_i\circ \mathbf{d}(x,z)& \ge 1-({\pi }_i\circ \mathbf{d}(x,y)+{\pi }_i\circ \mathbf{d}(y,z))\hfill \\ \hfill & =1-(1-{\pi }_i\circ \mathbf{E}(x,y)+1-{\pi }_i\circ \mathbf{E}(y,z))\hfill \\ \hfill & ={\pi }_i\circ \mathbf{E}(x,y)+{\pi }_i\circ \mathbf{E}(y,z)-1\hfill \end{array}$$

where ${\pi }_i\circ \mathbf{E}(x,z)\ge 0$. These imply that ${\pi }_i\circ \mathbf{E}(x,z)\ge max({\pi }_i\circ \mathbf{E}(x,y)+{\pi }_i\circ \mathbf{E}(y,z)-1,0)={\pi }_i\circ {\mathbf{T}}_L({\pi }_i\circ \mathbf{E}(x,y),{\pi }_i\circ \mathbf{E}(y,z))$. This means $\mathbf{E}$ is ${\mathbf{T}}_L$-transitive, and consequently $\mathbf{E}$ is an m-polar ${\mathbf{T}}_L$-equivalence on X.

Appendix C.4. Proof of Proposition 4

Axioms (1) and (2) are easily obtained. To prove axiom (3), let $x,y,z\in X$. Then for any $i=1:m$ we have

$$\begin{array}{cc}\hfill {\pi }_i\circ \mathbf{d}(x,z)=N_{S_i}[{\pi }_i\circ \mathbf{E}(x,z)]& \le N_{S_i}\left[T_i({\pi }_i\circ \mathbf{E}(x,y),{\pi }_i\circ \mathbf{E}(y,z))\right]\hfill \\ \hfill & =N_{S_i}\left[N_{S_i}\left(S_i(N_{S_i}({\pi }_i\circ \mathbf{E}(x,y)),N_{S_i}({\pi }_i\circ \mathbf{E}(y,z)))\right)\right]\hfill \\ \hfill & \le S_i(N_{S_i}({\pi }_i\circ \mathbf{E}(x,y)),N_{S_i}({\pi }_i\circ \mathbf{E}(y,z)))\hfill \\ \hfill & =S_i[{\pi }_i\circ \mathbf{d}(x,y),{\pi }_i\circ \mathbf{d}(y,z)]\hfill \end{array}$$

This completes the proof.

Appendix D.1. Proof of Theorem 9

The axioms of $\rho (x,x)=0$ and $\rho (x,y)=\rho (y,x)$ are easily obtained because $\mathbf{d}$ is an m-polar $\mathbf{S}$-pseudo-ultrametric. To prove the last axiom, take $x,y,z\in X$. Then

$$\begin{array}{cc}\hfill \rho (x,z)& =F({\pi }_1\circ \mathbf{d}(x,z),\cdots ,{\pi }_m\circ \mathbf{d}(x,z))\hfill \\ \hfill & \le F(S({\pi }_1\circ \mathbf{d}(x,y),{\pi }_1\circ \mathbf{d}(y,z)),\cdots ,S({\pi }_m\circ \mathbf{d}(x,y),{\pi }_m\circ \mathbf{d}(y,z)))\hfill \\ \hfill & \le S(F({\pi }_1\circ \mathbf{d}(x,y),\cdots ,{\pi }_m\circ \mathbf{d}(x,y)),F({\pi }_1\circ \mathbf{d}(y,z),\cdots ,{\pi }_m\circ \mathbf{d}(y,z)))\hfill \\ \hfill & =S\left(\rho \right(x,y),\rho (y,z\left)\right)\hfill \end{array}$$

This shows $\rho$ is an S-pseudo-ultrametric on X.

Appendix D.2. Proof of Proposition 5

Let $\mathbf{E}$ be an m-polar ${\mathbf{T}}_M$-equivalence on X such that for some $j=1:m$; $0\le {\pi }_j\circ \mathbf{E}(x,y)<1$. Take $x,y\in X$ where $x\ne y$. Then, $\rho (x,y)=max(1-{\pi }_1\circ \mathbf{E}(x,y),\cdots ,1-{\pi }_j\circ \mathbf{E}(x,y),\cdots ,1-{\pi }_m\circ \mathbf{E}(x,y))>0$. Now consider the path $x=u_0,u_1=y$ of G. Then, $CON{N}_G\left(xy\right)>0$ since $\rho (x,y)>0$, which means G is a fuzzy connected graph. Conversely, let G be a fuzzy connected graph. So, $CON{N}_G\left(uv\right)>0$ for any $u,v\in X$. This implies that there exists at least one path between any pair of nodes. Consider a path p of length n between u and v such that $p:u=u_0,u_1,\cdots ,u_{n-1},u_n=v$, where $\rho (u_{i-1},u_i)>0$ for all $1\le i\le n$. Therefore, $0<\rho (u_{i-1},u_i)=max(1-{\pi }_1\circ \mathbf{E}(u_{i-1},u_i),\cdots ,1-{\pi }_m\circ \mathbf{E}(u_{i-1},u_i))$, implying there exits $1\le j\le m$ such that $0<1-{\pi }_j\circ \mathbf{E}(u_{i-1},u_i)$, equivalently $0\le {\pi }_j\circ \mathbf{E}(u_{i-1},u_i)<1$.

The completeness of $G=(X,{\chi }_X,\rho )$ is equivalent to the fact that $1=\rho (x,y)=max(1-{\pi }_1\circ \mathbf{E}(x,y),\cdots ,1-{\pi }_j\circ \mathbf{E}(x,y),\cdots ,1-{\pi }_m\circ \mathbf{E}(x,y))$ for any $x,y\in X$, equivalently, there exists $1\le j\le m$ such that $1-{\pi }_j\circ \mathbf{E}(x,y)=1$ or ${\pi }_j\circ \mathbf{E}(x,y)=0$.

The second part is proved analogously.