Some Extremal Graphs with Respect to Sombor Index

Abstract

Let G be a graph with set of vertices $V\left(G\right)$$\left(\right|V\left(G\right)|=n)$ and edge set $E\left(G\right)$. Very recently, a new degree-based molecular structure descriptor, called Sombor index is denoted by $SO\left(G\right)$ and is defined as $SO=SO\left(G\right)={\displaystyle \sum _{v_i{v}_j\in E\left(G\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}$, where $d_G\left(v_i\right)$ is the degree of the vertex $v_i$ in G. In this paper we present some lower and upper bounds on the Sombor index of graph G in terms of graph parameters (clique number, chromatic number, number of pendant vertices, etc.) and characterize the extremal graphs.

1. Introduction

Let $G=(V,E)$ be a graph with vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ and edge set $E=E\left(G\right)$, where $\left|V\right(G\left)\right|=n$ and $\left|E\right(G\left)\right|=m$. If the vertices $v_i$ and $v_j$ are adjacent, we write $v_i{v}_j\in E\left(G\right)$. For $i\in \{1,2,\dots ,n\}$, let $d_G\left(v_i\right)$ be the degree of the vertex $v_i$. The maximum degree of a graph G will be denoted by $\Delta$. A vertex $v_i$ of degree 1 is called a pendant vertex (also known as leaf), the edge incident with a pendant vertex is called a pendant edge. For any two nonadjacent vertices $v_i$ and $v_j$ of a graph G, we let $G+v_i{v}_j$ be the graph obtained from G by adding the edge $v_i{v}_j$. For a subset W of $V\left(G\right)$, let $G-W$ be the subgraph of G obtained by deleting the vertices of W and the edges incident with them. Similarly, for a subset $E^{\prime }$ of $E\left(G\right)$, we denote by $G-E^{\prime }$ the subgraph of G obtained by deleting the edges of $E^{\prime }$. If $W=\left\{v_i\right\}$ and $E^{\prime }=\left\{v_i{v}_j\right\}$, the subgraphs $G-W$ and $G-E^{\prime }$ will be written as $G-v_i$ and $G-v_i{v}_j$ for short, respectively. The chromatic number of a graph G, denoted by $\chi \left(G\right)$, is the minimum number of colors such that vertices of G can be colored with these colors in order that no two adjacent vertices have the same color. A clique of graph G is a subset $V_0$ of $V\left(G\right)$ such that in $G\left[V_0\right]$, the subgraph of G induced by $V_0$, any two vertices are adjacent. The clique number of G, denoted by $\omega \left(G\right)$, is the number of vertices in a largest clique of G. For two vertex-disjoint graphs $G_1$ and $G_2$, we denote by $G_1\bigcup G_2$ the graph which consists of two components $G_1$ and $G_2$. As usual, $P_n$, $C_n$, $K_{1,n-1}$ and $K_{p,q}$$(p+q=n)$, denote, respectively, the path, the cycle, the star and the complete bipartite graph on n vertices. Other undefined notations and terminology on the graph theory can be found in [1].

A topological descriptor is a numerical descriptor of the topology of a molecule. These topological descriptors are used for predicting the physico-chemical and/or biological properties of molecules in quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) studies [2,3]. In the literature, several degree- and distance-based topological descriptors were proposed and studied by some researchers [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Very recently, a new degree-based molecular structure descriptor was introduced, the Sombor index is denoted by $SO\left(G\right)$ and is defined as follows [18]:

$$SO=SO\left(G\right)=\sum _{v_i{v}_j\in E\left(G\right)}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}.$$

(1)

Many fundamental mathematical properties such as lower and upper bounds can be found in, e.g., [3,10,18,19,20,21,22,23,24,25,26]. This topological index was motivated by the geometric interpretation of the degree radius of an edge $v_i{v}_j$, which is the distance from the origin to the ordered pair $(d_G\left(v_i\right),d_G\left(v_j\right))$.

Denote by $\mathcal{W}(n,\omega )$ the set of connected graphs of order n with clique number $\omega$. The long kite graph $K{i}_{n,\omega }$ (see, Figure 1) is a graph of order n obtained from a clique $K_{\omega }$ and a path $P_{n-\omega }$ by adding an edge between a vertex from the clique and an endpoint from the path. In particular, for $\omega =n$, $K{i}_{n,\omega }\cong K_n$. Let $G\cong K{i}_{n,\omega }$. For $\omega \le n-2$, we have

$$\begin{array}{cc}\hfill & \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V\left(K_{\omega }\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}\hfill \\ \hfill =& \left(\genfrac{}{}{0pt}{}{\omega -1}{2}\right)\sqrt{{(\omega -1)}^2+{(\omega -1)}^2}+(\omega -1)\sqrt{{\omega }^2+{(\omega -1)}^2}\hfill \\ \hfill =& \left(\genfrac{}{}{0pt}{}{\omega -1}{2}\right)\sqrt{2}(\omega -1)+(\omega -1)\sqrt{2{\omega }^2-2\omega +1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V(G-V\left(K_{\omega }\right))}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}& =(n-\omega -2)\sqrt{8}+\sqrt{5}\hfill \end{array}$$

and hence

$$\begin{array}{cc}\hfill SO\left(K{i}_{n,\omega }\right)& =\sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V\left(K_{\omega }\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}+\sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V(G-V\left(K_{\omega }\right))}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}\hfill \\ \hfill & +\sqrt{{\omega }^2+4}\hfill \\ \hfill & =\left(\genfrac{}{}{0pt}{}{\omega -1}{2}\right)\sqrt{2}(\omega -1)+(\omega -1)\sqrt{2{\omega }^2-2\omega +1}+\sqrt{{\omega }^2+4}\hfill \\ \hfill & +(n-\omega -2)\sqrt{8}+\sqrt{5}.\hfill \end{array}$$

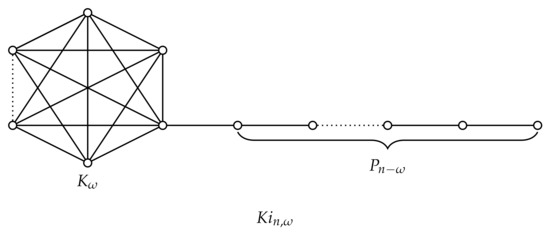
Figure 1. The long kite graph $K{i}_{n,\omega }$.

In this paper, we present a lower bound on $SO$ of graph G in terms of n and clique number $\omega$, and characterize the extremal graphs.

Theorem 1.

Let $G\in \mathcal{W}(n,\omega )$. Then $SO\left(G\right)\ge SO\left(K{i}_{n,\omega }\right)$ with equality holding if and only if $G\cong K{i}_{n,\omega }$.

Corollary 1.

[18] Let G be a connected graph of order n. Then $SO\left(G\right)\ge SO\left(P_n\right)$ with equality holding if and only if $G\cong P_n$.

Proofof Corollary 1.

Let $\omega$ be the clique number of graph G. Then $\omega \ge 2$. Therefore one can easily see that

$$SO\left(G\right)\ge SO\left(K{i}_{n,\omega }\right)\ge SO\left(K{i}_{n,\omega -1}\right)\ge \cdots \ge SO\left(K{i}_{n,3}\right)\ge SO\left(K{i}_{n,2}\right)=SO\left(P_n\right).$$

hence we obtain the required result. □

Let $\mathcal{X}(n,k)$ be the set of connected graphs of order n with chromatic number k. Recall that the Turán graph $T_n\left(k\right)$ is a complete k-partite graph of order n whose partition sets differ in size by at most 1. When $k=n$, the only graph in $\mathcal{X}(n,k)$ is $K_n$. So, we now assume that $n=kq+r$ where $0\le r<k$, i.e., ${\displaystyle q=⌊\frac{n}{k}⌋}$ in $\mathcal{X}(n,k)$. We now give an upper bound on $SO$ of graph G in terms of n and chromatic number k, and characterize the extremal graphs.

Theorem 2.

For any graph $G\in \mathcal{X}(n,k)$, we have

$$\begin{array}{cc}\hfill SO\left(G\right)& \le r(k-r)⌊\frac{n}{k}⌋⌈\frac{n}{k}⌉\sqrt{{\left(n-⌊\frac{n}{k}⌋\right)}^2+{\left(n-⌈\frac{n}{k}⌉\right)}^2}+\sqrt{2}\left(\genfrac{}{}{0pt}{}{r}{2}\right){⌈\frac{n}{k}⌉}^2\left(n-⌈\frac{n}{k}⌉\right)\hfill \\ \hfill & +\sqrt{2}\left(\genfrac{}{}{0pt}{}{k-r}{2}\right){⌊\frac{n}{k}⌋}^2\left(n-⌊\frac{n}{k}⌋\right)\hfill \end{array}$$

with equality holding if and only if $G\cong T_n\left(k\right)$.

Recall that a short kite graph $K{i}_n^{\omega }$ obtained by adding $n-\omega$ pendant vertices to the unique vertex of clique $K_{\omega }$; see Figure 2. Let $G\cong K{i}_n^{n-p}$. We have

$$\begin{array}{cc}\hfill \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V\left(K_{\omega }\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}& =\frac{(n-p-1)(n-p-2)}{2}\sqrt{{(n-p-1)}^2+{(n-p-1)}^2}\hfill \\ \hfill & +(n-p-1)\sqrt{{(n-1)}^2+{(n-p-1)}^2}\hfill \\ \hfill & =\frac{(n-p-1)(n-p-2)}{\sqrt{2}}(n-p-1)\hfill \\ \hfill & +(n-p-1)\sqrt{{(n-1)}^2+{(n-p-1)}^2}\hfill \end{array}$$

and hence

$$\begin{array}{cc}\hfill SO\left(K{i}_n^{n-p}\right)& =\sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right)}{v_i,v_j\in V\left(K_{\omega }\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}+\sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(G\right),v_i\in V\left(K_{\omega }\right)}{v_j\in V(G-V\left(K_{\omega }\right))}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}\hfill \\ \hfill & =p\sqrt{{(n-1)}^2+1}+\frac{(n-p-1)(n-p-2)}{\sqrt{2}}(n-p-1)\hfill \\ \hfill & +(n-p-1)\sqrt{{(n-1)}^2+{(n-p-1)}^2}.\hfill \end{array}$$

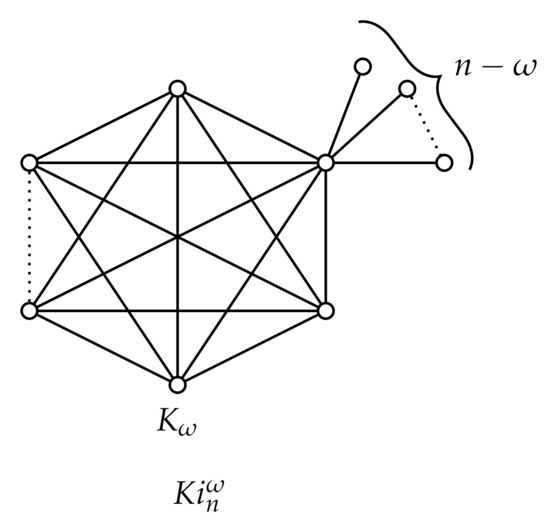
Figure 2. The short kite graph $K{i}_n^{\omega }$.

Finally we give an upper bound on Sombor index in terms of n, p pendant vertices, and characterize the extremal graphs.

Theorem 3.

Let G be a graph of order n with p pendant vertices. Then

$$SO\left(G\right)\le SO\left(K{i}_n^{n-p}\right)$$

(2)

with equality holding if and only if $G\cong K{i}_n^{n-p}$.

2. Preliminaries

From the definition of Sombor index, we have

Lemma 1.

Let G be a graph. Then $SO\left(G\right)>SO(G-e)$, where e is any edge in G.

Lemma 2.

[18] Let T be a tree of order n. Then $SO\left(T\right)\ge (n-3)\sqrt{8}+2\sqrt{5}$ with equality if and only if $T\cong P_n$.

Lemma 3.

[10] Let T be a tree of order $n(>4)$ with $T\ncong P_n$. Then $SO\left(T\right)>(n-1)\sqrt{8}$.

In [10], the following two sets are defined:

$$\begin{array}{ccc}& & A=\{v_i{v}_j\in E\left(G\right):d_G\left(v_i\right)=2>1=d_G\left(v_j\right)\},\hfill \\ & & D=\{v_i{v}_j\in E\left(G\right):d_G\left(v_i\right)\ge 3,d_G\left(v_j\right)\ge 2or{d}_G\left(v_i\right)\ge 4,d_G\left(v_j\right)=1\}.\hfill \end{array}$$

The following result has been proved in [10].

Lemma 4.

[10] Let T$(\ncong P_n)$ be a tree of order n. Then $\left|D\right|\ge \left|A\right|$.

3. Proofs

Proof of Theorem 1.

For $\omega =n$, we have $G\cong K_n$ and hence the equality holds. For $\omega =n-1$, $K{i}_{n,n-1}$ is a subgraph of G as $G\in \mathcal{W}(n,\omega )$. Hence by Lemma 1, we obtain

$$SO\left(G\right)\ge SO\left(K{i}_{n,n-1}\right)=\left(\genfrac{}{}{0pt}{}{n-2}{2}\right)\sqrt{2}(n-2)+(n-2)\sqrt{2n^2-6n+5}+\sqrt{n^2-2n+2}$$

with equality if and only if $G\cong K{i}_{n,n-1}$. For $\omega =2$, we have $G\cong T_n$ or $T_n$ is a subgraph of G, where $T_n$ is a tree of order n. By Lemmas 1 and 2, we have $SO\left(G\right)\ge SO\left(T_n\right)\ge (n-3)\sqrt{8}+2\sqrt{5}$. Moreover, $SO\left(G\right)=(n-3)\sqrt{8}+2\sqrt{5}$ if and only if $G\cong P_n$.

Otherwise, $3\le \omega \le n-2$. Since the clique number of G is $\omega$, we can assume that a clique of G is $S\left(G\right)=\{v_1,v_2,\dots ,v_{\omega }\}$. Let H be a connected graph with $H\subseteq G$ such that $V\left(H\right)=V\left(G\right)$ and $H-E\left(K_{\omega }\right)\cong T_1\cup T_2\cup \cdots \cup T_{\omega }$, where $T_1,T_2,\dots ,T_{\omega }$ are the trees with $v_i\in V\left(T_i\right)$, $|V\left(T_i\right)|=n_i$$(1\le i\le \omega )$, $n_1\ge n_2\ge \cdots \ge n_{\omega }$ and $n_1+n_2+\cdots +n_{\omega }=n$. Moreover, $S\left(G\right)=S\left(H\right)$. By Lemma 1, we have $SO\left(G\right)\ge SO\left(H\right)$ with equality if and only if $G\cong H$. For $1\le i\le \omega$, we have $v_i\in V\left(T_i\right)$ and $d_H\left(v_i\right)=d_{T_i}\left(v_i\right)+\omega -1$. Moreover, $d_H\left(v_i\right)=d_T\left(v_i\right)$ for $\omega +1\le i\le n$ and $T\in \{T_1,\dots ,T_{\omega }\}$. Thus, we have

$$\begin{array}{cc}\hfill SO\left(G\right)& ={\displaystyle \sum _{v_i{v}_j\in E\left(G\right)}}\sqrt{d_G{\left(v_i\right)}^2+d_G{\left(v_j\right)}^2}\hfill \\ & \ge {\displaystyle \sum _{v_i{v}_j\in E\left(H\right)}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}\hfill \\ & ={\displaystyle \sum _{v_i{v}_j\in E\left(K_{\omega }\right)}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(H\right),v_i\in V(G-V\left(K_{\omega }\right)),}{v_j\in V\left(K_{\omega }\right)or{v}_j\in V(G-V\left(K_{\omega }\right))}}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}\hfill \\ & ={\displaystyle \sum _{v_i{v}_j\in E\left(K_{\omega }\right)}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}+{\displaystyle \sum _{k=1}^{\omega }}{\displaystyle \sum _{v_i{v}_j\in E\left(T_k\right)}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}.\hfill \end{array}$$

(3)

Claim 1.

For $2\le i\le \omega$, ${\displaystyle \sum _{v_k{v}_{\ell }\in E\left(T_i\right)}}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}\ge (n_i-1)\sqrt{8}$ with equality if and only if $n_i=1$.

Proof of Claim 1.

Let

$$A_i=\sum _{v_k{v}_{\ell }\in E\left(T_i\right)}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2},2\le i\le \omega .$$

For $n_i=1$$(2\le i\le \omega )$, then $A_i=(n_i-1)\sqrt{8}=0,$ the equality holds in Claim 1. For $n_i=2$$(2\le i\le \omega )$, then

$$A_i=\sqrt{{\omega }^2+1}>(n_i-1)\sqrt{8}$$

as $\omega \ge 3$, the inequality strictly holds in Claim 1. Otherwise, $n_i\ge 3$. First we assume that $T_i\cong P_{n_i}$. Thus, we have $d_{T_i}\left(v_i\right)=1$ or $d_{T_i}\left(v_i\right)=2$. When $d_{T_i}\left(v_i\right)=1$, we obtain

$$A_i=\sqrt{{\omega }^2+4}+(n_i-3)\sqrt{8}+\sqrt{5}>(n_i-1)\sqrt{8}$$

as $\omega \ge 3$ and $\sqrt{13}+\sqrt{5}>2\sqrt{8}$. When $d_{T_i}\left(v_i\right)=2$, we obtain

$$\begin{array}{cc}\hfill & A_i=\sqrt{{\omega }^2+4}+\sqrt{{\omega }^2+1}+(n_i-4)\sqrt{8}+\sqrt{5}>(n_i-1)\sqrt{8}\hfill \\ \hfill or& A_i=2\sqrt{{\omega }^2+4}+(n_i-5)\sqrt{8}+2\sqrt{5}>(n_i-1)\sqrt{8}\hfill \end{array}$$

as $\omega \ge 3$ and $\sqrt{13}+\sqrt{5}>2\sqrt{8}$.

Next we assume that $T_i\ncong P_{n_i}$. Since $d_H\left(v_i\right)>d_{T_i}\left(v_i\right)$$(2\le i\le \omega )$ with Lemma 3, we obtain

$$A_i>\sum _{v_k{v}_{\ell }\in E\left(T_i\right)}\sqrt{d_{T_i}{\left(v_k\right)}^2+d_{T_i}{\left(v_{\ell }\right)}^2}>(n_i-1)\sqrt{8}.$$

Claim 1.

is proved. □

Claim 2.

$$\sum _{v_k{v}_{\ell }\in E\left(T_1\right)}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}\ge \left\{\begin{array}{cc}\sqrt{{\omega }^2+1}\hfill & \mathrm{if}{n}_1=2,\hfill \\ \sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}\hfill & \mathrm{if}{n}_1\ge 3\hfill \end{array}\right.$$

with equality if and only if $T_1\cong P_{n_1}$ with $d_{T_1}\left(v_1\right)=1$.

Proof of Claim 2.

Let

$$A_1=\sum _{v_k{v}_{\ell }\in E\left(T_1\right)}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}.$$

Since $\omega \le n-2$ and $n_1\ge n_i$$(2\le i\le \omega )$, we have $n_1\ge 2$. For $n_1=2$, we have $A_1=\sqrt{{\omega }^2+1},$ the equality holds in Claim 2. Otherwise, $n_1\ge 3$. We have $v_1\in V\left(T_1\right)$. First we assume that $T_1\cong P_{n_1}$. Thus, we have $d_{T_1}\left(v_1\right)=1$ or $d_{T_1}\left(v_1\right)=2$. If $d_{T_1}\left(v_1\right)=1$, then we obtain

$$A_1=\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}.$$

The equality holds in Claim 2. Otherwise, $d_{T_1}\left(v_1\right)=2$. We consider two cases:

Case 1.

$n_1=3$. In this case

$$A_1=2\sqrt{{(\omega +1)}^2+1}>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}$$

as $\omega \ge 3$.

Case 2.

$n_1\ge 4$. We obtain

$$\begin{array}{cc}\hfill A_1& =\sqrt{{(\omega +1)}^2+4}+\sqrt{{(\omega +1)}^2+1}+(n_1-4)\sqrt{8}+\sqrt{5}\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}\hfill \\ \hfill or& A_1=2\sqrt{{(\omega +1)}^2+4}+(n_1-5)\sqrt{8}+2\sqrt{5}>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}\hfill \end{array}$$

as $\omega \ge 3$ and $\sqrt{20}+\sqrt{5}>2\sqrt{8}$.

Next we assume that $T_1\ncong P_{n_1}$. Then $n_1\ge 4$. If $n_1=4$, then $T_1\cong K_{1,3}$ and one can easily check that $A_1>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}.$ Otherwise, $n_1\ge 5$. We consider the following two cases:

Case 3.

$d_{T_1}\left(v_1\right)=1$. Let $v_r$ be a vertex adjacent to $v_1$ in tree $T_1$. Then $d_{T_1}\left(v_r\right)\ge 2$ as $n_1\ge 5$. First suppose that $T_1-v_1\cong P_{n_1-1}$. Then $d_{T_1}\left(v_r\right)=3$. One can easily see that

$$\begin{array}{cc}\hfill A_1& =\sqrt{{(d_{T_1}\left(v_1\right)+\omega -1)}^2+9}+\sum _{v_k{v}_{\ell }\in E(T_1-v_1)}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & =\sqrt{{\omega }^2+9}+\sum _{v_k{v}_{\ell }\in E(T_1-v_1)}\sqrt{d_{T_1}{\left(v_k\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & >\sqrt{{\omega }^2+9}+\sqrt{13}+(n_1-4)\sqrt{8}+\sqrt{5}>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}\hfill \end{array}$$

as $\sqrt{13}+\sqrt{5}>2\sqrt{8}$.

Next suppose that $T_1-v_1\ncong P_{n_1-1}$. In this case $d_{T_1}\left(v_r\right)\ge 2$. Since $T_1-v_1$ is a tree of order $n_1-1$, by Lemma 3, we obtain

$$\begin{array}{cc}\hfill A_1& =\sqrt{{(d_{T_1}\left(v_1\right)+\omega -1)}^2+d_{T_1}{\left(v_r\right)}^2}+\sum _{v_k{v}_{\ell }\in E(T_1-v_1)}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & \ge \sqrt{{\omega }^2+4}+\sum _{v_k{v}_{\ell }\in E(T_1-v_1)}\sqrt{d_{T_1}{\left(v_k\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+\sum _{v_k{v}_{\ell }\in E(T_1-v_1)}\sqrt{d_{T_1-v_1}{\left(v_k\right)}^2+d_{T_1-v_1}{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+(n_1-2)\sqrt{8}>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}.\hfill \end{array}$$

Case 4.

$d_{T_1}\left(v_1\right)\ge 2$. For $d_{T_1}\left(v_1\right)=n_1-1$, one can easily check that $A_1>\sqrt{{\omega }^2+4}+(n_1-3)\sqrt{8}+\sqrt{5}$. So now we have $d_{T_1}\left(v_1\right)\le n_1-2$. Since $n_1\ge 5$ and $T_1$ is a tree, $T_1-v_1=\ell K_1\cup T_1^1\cup T_1^2\cup \cdots \cup T_1^k$$(\ell \ge 0,k\ge 1)$, (say), where $T_1^i$$(1\le i\le k)$ is a tree of order $n_1^i(=|V\left(T_1^i\right)|\ge 2)$ with $\sum _{i=1}^k{n}_1^i=n_1-\ell -1$. Thus, we have $d_H\left(v_1\right)=d_{T_1}\left(v_1\right)+\omega -1=\omega +k+\ell -1$. Let $v_r$ be a vertex in $T_1^i$ such that $v_1{v}_r\in E\left(T_1\right)$, where $1\le i\le k$. We now prove that

$$\sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}\ge (n_1^i-2)\sqrt{8}+\sqrt{5}.$$

(4)

First we assume that $T_1^i\ncong P_{n_1^i}$. Then by Lemma 3, $SO\left(T_1^{\prime }\right)>(n_1^i-1)\sqrt{8}$. We obtain

$$\begin{array}{cc}\hfill {\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}& >\sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}\sqrt{d_{T_1^i}{\left(v_j\right)}^2+d_{T_1^i}{\left(v_{\ell }\right)}^2}\hfill \\ \hfill & =SO\left(T_1^i\right)\hfill \\ \hfill & >(n_1^i-1)\sqrt{8}>(n_1^i-2)\sqrt{8}+\sqrt{5}.\hfill \end{array}$$

the result strictly holds in (4).

Next we assume that $T_1^i\cong P_{n_1^i}$. For $d_{T_1^i}\left(v_r\right)=1$, we have $d_{T_1}\left(v_r\right)=d_{T_1^i}\left(v_r\right)+1=2$, $d_{T_1}\left(v_k\right)=d_{T_1^i}\left(v_k\right)$ for $v_k\in V(T_1^i-v_r)$, and hence we obtain

$$\begin{array}{cc}\hfill {\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}& =(n_1^i-2)\sqrt{8}+\sqrt{5}.\hfill \end{array}$$

The equality holds in (4). Otherwise, $d_{T_1^i}\left(v_r\right)=2$. In this case $d_{T_1}\left(v_r\right)=d_{T_1^i}\left(v_r\right)+1=3$ and $d_{T_1}\left(v_k\right)=d_{T_1^i}\left(v_k\right)$ for $v_k\in V(T_1^i-v_r)$. If $2\le n_1^i\le 3$, then one can easily check that the result holds in (4). Otherwise, $n_1^i\ge 4$. We obtain

$$\begin{array}{cc}\hfill {\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}& =2\sqrt{13}+2\sqrt{5}+(n_1^i-5)\sqrt{8}\hfill \end{array}$$

or

$$\begin{array}{cc}\hfill {\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}& =\sqrt{13}+\sqrt{10}+2\sqrt{5}+(n_1^i-5)\sqrt{8}.\hfill \end{array}$$

One can easily check that

$$\sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}>(n_1^i-2)\sqrt{8}+\sqrt{5}as\sqrt{13}+\sqrt{5}>2\sqrt{8}.$$

Again the result holds in (3).

Using the result in (3), we obtain

$$\begin{array}{cc}\hfill A_1=& {\displaystyle \sum _{v_k{v}_{\ell }\in E\left(T_1\right)}}\sqrt{d_H{\left(v_k\right)}^2+d_H{\left(v_{\ell }\right)}^2}\hfill \\ \hfill =& {\displaystyle \sum _{v_i:v_1{v}_i\in E\left(T_1\right)}}\sqrt{d_H{\left(v_1\right)}^2+d_H{\left(v_i\right)}^2}+\sum _{i=1}^k{\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_H{\left(v_j\right)}^2+d_H{\left(v_{\ell }\right)}^2}\hfill \\ \hfill =& \ell \sqrt{d_H{\left(v_1\right)}^2+1}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_i:v_1{v}_i\in E\left(T_1\right)}{d_{T_1}\left(v_i\right)\ge 2}}}\sqrt{d_H{\left(v_1\right)}^2+d_H{\left(v_i\right)}^2}\hfill \\ \hfill & +\sum _{i=1}^k{\displaystyle \sum _{v_j{v}_{\ell }\in E\left(T_1^i\right)}}\sqrt{d_{T_1}{\left(v_j\right)}^2+d_{T_1}{\left(v_{\ell }\right)}^2}\hfill \\ \hfill \ge & \ell \sqrt{d_H{\left(v_1\right)}^2+1}+k\sqrt{d_H{\left(v_1\right)}^2+4}+\sum _{i=1}^k\left[(n_1^i-2)\sqrt{8}+\sqrt{5}\right]\hfill \\ \hfill =& \ell \sqrt{{(\omega +k+\ell -1)}^2+1}+k\sqrt{{(\omega +k+\ell -1)}^2+4}\hfill \\ \hfill & +(n_1-1-\ell -2k)\sqrt{8}+k\sqrt{5}.\hfill \end{array}$$

(5)

If $\ell \ge 1$, then from (5), we obtain

$$\begin{array}{cc}\hfill A_1& >\sqrt{{\omega }^2+4}+(\ell -1)\sqrt{{(\omega +k+\ell -1)}^2+1}+k\sqrt{{(\omega +k+\ell -1)}^2+4}\hfill \\ \hfill & +(n_1-1-\ell -2k)\sqrt{8}+k\sqrt{5}\hfill \\ \hfill & \ge \sqrt{{\omega }^2+4}+\sqrt{5}+(n_1-1-2k)\sqrt{8}+(k-1)(\sqrt{13}+\sqrt{5})\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+\sqrt{5}+(n_1-3)\sqrt{8}\hfill \end{array}$$

as $\sqrt{13}+\sqrt{5}>2\sqrt{8}$. Otherwise, $\ell =0$. In this case $k\ge 2$. From (5), we obtain

$$\begin{array}{cc}\hfill A_1& \ge k\sqrt{{(\omega +k-1)}^2+4}+(n_1-1-2k)\sqrt{8}+k\sqrt{5}\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+\sqrt{5}+(n_1-1-2k)\sqrt{8}+(k-1)(\sqrt{13}+\sqrt{5})\hfill \\ \hfill & >\sqrt{{\omega }^2+4}+\sqrt{5}+(n_1-3)\sqrt{8}\hfill \end{array}$$

as $\sqrt{13}+\sqrt{5}>2\sqrt{8}$. Claim 2 is proved. □

Using Claim 1 and Claim 2, we obtain

$$\sum _{k=1}^{\omega }\sum _{v_i{v}_j\in E\left(T_k\right)}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}\ge \sqrt{{\omega }^2+4}+(n-\omega -2)\sqrt{8}+\sqrt{5}$$

with equality if and only if $n_2=\cdots =n_{\omega }=1$ and $T_1\cong P_{n_1}$ with $d_{T_1}\left(v_1\right)=1$, i.e., $G\cong K{i}_{n,\omega }$.

Since $n\ge \omega +2$, we have $d_H\left(v_1\right)\ge \omega$ and $d_H\left(v_i\right)\ge \omega -1$$(2\le i\le \omega )$. Using the above result in (3), we obtain

$$\begin{array}{cc}\hfill SO\left(G\right)& \ge \sum _{i=2}^{\omega }\sqrt{d_H{\left(v_1\right)}^2+d_H{\left(v_i\right)}^2}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_i{v}_j\in E\left(K_{\omega }\right)}{2\le i<j\le \omega }}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}\hfill \\ \hfill & +\sum _{k=1}^{\omega }{\displaystyle \sum _{v_i{v}_j\in E\left(T_k\right)}}\sqrt{d_H{\left(v_i\right)}^2+d_H{\left(v_j\right)}^2}\hfill \\ \hfill & \ge (\omega -1)\sqrt{2{\omega }^2-2\omega +1}+\left(\genfrac{}{}{0pt}{}{\omega -1}{2}\right)\sqrt{2}(\omega -1)+\sqrt{{\omega }^2+4}\hfill \\ \hfill & +(n-\omega -2)\sqrt{8}+\sqrt{5}\hfill \\ \hfill & =SO\left(K{i}_{n,\omega }\right).\hfill \end{array}$$

This completes the proof of the theorem. □

Let $n_1,n_2,\dots ,n_k$ be positive integers with $\sum _{i=1}^k{n}_i=n$. Denote by $K_{n_1,n_2,\dots ,n_k}$ a complete k-partite graph of order n whose partition sets are of size $n_1,n_2,\dots ,n_k$, respectively. We will determine the extremal graph in $\mathcal{X}(n,k)$ with respect to Sombor index of graphs G. For this we first prove a related lemma below.

Lemma 5.

Let $K_{n_1,n_2,\dots ,n_k}$ be a graph defined as above with $n_i-n_j\ge 2$ for $i<j$. Then

$$SO\left(K_{n_1,n_2,\dots ,n_i,\dots ,n_j,\dots ,n_k}\right)<SO\left(K_{n_1,n_2,\dots ,n_i-1,\dots ,n_j+1,\dots ,n_k}\right).$$

Proof. 

Without loss of generality, we can assume that $n_1-n_2\ge 2$. This lemma will be proved if we can prove the following:

$$SO\left(K_{n_1,n_2,\dots ,n_k}\right)<SO\left(K_{n_1-1,n_2+1,\dots ,n_k}\right).$$

By the definition of Sombor index, we obtain

$$\begin{array}{cc}\hfill SO\left(K_{n_1,n_2,\dots ,n_k}\right)& ={\displaystyle \sum _{1\le i<j\le k}}{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}\hfill \\ \hfill & ={\displaystyle \sum _{3\le i<j\le k}}{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}+n_1{n}_2\sqrt{{(n-n_1)}^2+{(n-n_2)}^2}\hfill \\ \hfill & +n_1\sum _{i=3}^k{n}_i\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}+n_2\sum _{i=3}^k{n}_i\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}.\hfill \end{array}$$

Then, in view of the fact that $n_1-1\ge n_2+1$, we obtain

$$\begin{array}{c}SO\left(K_{n_1-1,n_2+1,n_3,\dots ,n_k}\right)-SO\left(K_{n_1,n_2,n_3,\dots ,n_k}\right)\hfill \\ =(n_1-1)(n_2+1)\sqrt{{(n-n_1+1)}^2+{(n-n_2-1)}^2}-n_1{n}_2\sqrt{{(n-n_1)}^2+{(n-n_2)}^2}\hfill \\ +(n_1-1){\displaystyle \sum _{i=3}^k}{n}_i\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}-n_1{\displaystyle \sum _{i=3}^k}{n}_i\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}\hfill \\ +(n_2+1){\displaystyle \sum _{i=3}^k}{n}_i\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}-n_2{\displaystyle \sum _{i=3}^k}{n}_i\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}\hfill \\ =(n_1{n}_2+n_1-n_2-1)\sqrt{{(n-n_1+1)}^2+{(n-n_2-1)}^2}-n_1{n}_2\sqrt{{(n-n_1)}^2+{(n-n_2)}^2}\hfill \\ +n_1{\displaystyle \sum _{i=3}^k}{n}_i\left[\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}-\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}\right]\hfill \\ -n_2{\displaystyle \sum _{i=3}^k}{n}_i\left[\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}-\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}\right]\hfill \\ +{\displaystyle \sum _{i=3}^k}{n}_i\left[\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}-\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}\right].\hfill \end{array}$$

(6)

Claim 3.

$$(n_1{n}_2+n_1-n_2-1)\sqrt{{(n-n_1+1)}^2+{(n-n_2-1)}^2}>n_1{n}_2\sqrt{{(n-n_1)}^2+{(n-n_2)}^2}.$$

Proof of Claim 3.

Since $n_1\ge n_2+2$, we have

$${(n-n_2-1)}^2\ge {(n_1-1)}^2\ge (n_1-1)(n_2+1)=n_1{n}_2+n_1-n_2-1>n_1{n}_2,$$

that is,

$${(n-n_1+1)}^2+{(n-n_2-1)}^2>n_1{n}_2,$$

that is,

$$\frac{2(n_1-n_2-1)}{n_1{n}_2}>\frac{2(n_1-n_2-1)}{{(n-n_1+1)}^2+{(n-n_2-1)}^2},$$

that is,

$$1+\frac{2(n_1-n_2-1)}{n_1{n}_2}>\frac{{(n-n_1)}^2+{(n-n_2)}^2}{{(n-n_1+1)}^2+{(n-n_2-1)}^2},$$

that is,

$$\begin{array}{c}\hfill {\left(1+\frac{n_1-n_2-1}{n_1{n}_2}\right)}^2>\frac{{(n-n_1)}^2+{(n-n_2)}^2}{{(n-n_1+1)}^2+{(n-n_2-1)}^2},\end{array}$$

which finishes the proof of $\mathbf{Claim}\mathbf{3}$. □

Claim 4.

For $3\le i\le k$,

$$\begin{array}{cc}\hfill & n_1\left[\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}-\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}\right]\hfill \\ \hfill & >n_2\left[\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}-\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}\right].\hfill \end{array}$$

Proof of Claim 4.

Since $n_1-n_2\ge 2$, we have

$$2(n_1-n_2)(n-n_1-n_2)+n_1+n_2>0,thatis,n_1\left[2(n-n_1)+1\right]>n_2\left[2(n-n_2)-1\right].$$

Moreover,

$$\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}\le \sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}$$

and

$$\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}<\sqrt{{(n-n_2)}^2+{(n-n_i)}^2},$$

that is,

$$\begin{array}{cc}\hfill & \sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}\hfill \\ \hfill & <\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}.\hfill \end{array}$$

From the above results, we obtain

$$\begin{array}{cc}\hfill & \frac{n_1\left[2(n-n_1)+1\right]}{\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}}\hfill \\ \hfill & >\frac{n_2\left[2(n-n_2)-1\right]}{\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}},\hfill \end{array}$$

that is,

$$\begin{array}{cc}\hfill & \frac{n_1\left[{(n-n_1+1)}^2+{(n-n_i)}^2-{(n-n_1)}^2-{(n-n_i)}^2\right]}{\sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_1)}^2+{(n-n_i)}^2}}\hfill \\ \hfill & >\frac{n_2\left[{(n-n_2)}^2+{(n-n_i)}^2-{(n-n_2-1)}^2-{(n-n_i)}^2\right]}{\sqrt{{(n-n_2)}^2+{(n-n_i)}^2}+\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}},\hfill \end{array}$$

which finishes the proof of Claim 4. □

Since $n_1\ge n_2+2$, we have $n-n_2-1\ge n-n_1+1$ and hence

$$\sqrt{{(n-n_2-1)}^2+{(n-n_i)}^2}\ge \sqrt{{(n-n_1+1)}^2+{(n-n_i)}^2}$$

for $3\le i\le k$. Using the above result with Claims 3 and 4, from (6), we obtain

$$SO\left(K_{n_1-1,n_2+1,n_3,\dots ,n_k}\right)>SO\left(K_{n_1,n_2,n_3,\dots ,n_k}\right).$$

This completes the proof of the lemma. □

We are now ready to proof of Theorem 2.

Proof of Theorem 2.

From the definition of chromatic number, any graph G from $\mathcal{X}(n,k)$ has k color classes each of which is an independent set. Suppose that these k classes have order $n_1,n_2,\dots ,n_k$, respectively. By Lemma 1, we obtain $SO\left(G\right)\le SO\left(K_{n_1,n_2,\dots ,n_k}\right)$ with equality holding if and only if $G\cong K_{n_1,n_2,\dots ,n_k}$. We now apply Lemma 5 several times (if needed) and we obtain $SO\left(K_{n_1,n_2,\dots ,n_k}\right)\le SO\left(T_n\left(k\right)\right)$ with equality holding if and only if $G\cong T_n\left(k\right)$. From the above two results with

$$\begin{array}{cc}\hfill SO\left(T_n\left(k\right)\right)& =r(k-r)⌊\frac{n}{k}⌋⌈\frac{n}{k}⌉\sqrt{{\left(n-⌊\frac{n}{k}⌋\right)}^2+{\left(n-⌈\frac{n}{k}⌉\right)}^2}+\sqrt{2}\left(\genfrac{}{}{0pt}{}{r}{2}\right){⌈\frac{n}{k}⌉}^2\left(n-⌈\frac{n}{k}⌉\right)\hfill \\ \hfill & +\sqrt{2}\left(\genfrac{}{}{0pt}{}{k-r}{2}\right){⌊\frac{n}{k}⌋}^2\left(n-⌊\frac{n}{k}⌋\right),\hfill \end{array}$$

we obtain the required result. This finishes the proof of this theorem. □

Proof of Theorem 3.

Let $S=\{v_{n-p+1},v_{n-p+2},\dots ,v_n\}$$\left(\right|S|=p)$ be the set of pendant vertices in G. Let $H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}$ be a graph obtained from G such that any two vertices $v_i$ and $v_j$$(v_i,v_j\in V\left(G\right)\setminus S,v_i{v}_j\notin E\left(G\right))$ join by an edge, where $n_i(\ge 0,1\le i\le n-p)$ is the number of pendant vertices adjacent to the vertex $v_i$ and $n_1\ge n_2\ge \cdots \ge n_{n-p}$, $n_1+n_2+\cdots +n_{n-p}=p$. Then by Lemma 1, one can easily see that $SO\left(G\right)\le SO\left(H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}\right)$. If $H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}\cong K{i}_n^{n-p}$, then the equality holds in (2). Otherwise, $H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}\ncong K{i}_n^{n-p}$. Let $H_{n,{\displaystyle \underbrace{n_1+1,n_2-1,\dots ,n_{n-p}}}}\cong H_1,H_{n,{\displaystyle \underbrace{n_1,n_2,\dots ,n_{n-p}}}}\cong H_2$. Since $n_1\ge n_2$, we obtain

$$\begin{array}{c}SO\left(H_1\right)-SO\left(H_2\right)\hfill \\ ={\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_1{v}_k\in E\left(H_1\right)}{d_{H_1}\left(v_k\right)=1}}}\sqrt{d_{H_1}{\left(v_1\right)}^2+1}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_1{v}_k\in E\left(H_1\right)}{d_{H_1}\left(v_k\right)>1}}}\sqrt{d_{H_1}{\left(v_1\right)}^2+d_{H_1}{\left(v_k\right)}^2}\hfill \\ +{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_2{v}_k\in E\left(H_1\right)}{d_{H_1}\left(v_k\right)=1}}}\sqrt{d_{H_1}{\left(v_2\right)}^2+1}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_2{v}_k\in E\left(H_1\right)}{d_{H_1}\left(v_k\right)>1}}}\sqrt{d_{H_1}{\left(v_1\right)}^2+d_{H_1}{\left(v_k\right)}^2}\hfill \\ -{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_1{v}_k\in E\left(H_2\right)}{d_{H_2}\left(v_k\right)=1}}}\sqrt{d_{H_2}{\left(v_1\right)}^2+1}-{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_1{v}_k\in E\left(H_2\right)}{d_{H_2}\left(v_k\right)>1}}}\sqrt{d_{H_2}{\left(v_1\right)}^2+d_{H_2}{\left(v_k\right)}^2}\hfill \\ -{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_2{v}_k\in E\left(H_2\right)}{d_{H_2}\left(v_k\right)=1}}}\sqrt{d_{H_2}{\left(v_2\right)}^2+1}-{\displaystyle \sum _{\genfrac{}{}{0pt}{}{v_k:v_2{v}_k\in E\left(H_2\right)}{d_{H_2}\left(v_k\right)>1}}}\sqrt{d_{H_2}{\left(v_2\right)}^2+d_{H_2}{\left(v_k\right)}^2}\hfill \\ =(n_1+1)\sqrt{{(n+n_1-p)}^2+1}+{\displaystyle \sum _{i=3}^{n-p}}\sqrt{{(n+n_1-p)}^2+{(n+n_i-p-1)}^2}\hfill \\ +(n_2-1)\sqrt{{(n+n_2-p-2)}^2+1}+{\displaystyle \sum _{i=3}^{n-p}}\sqrt{{(n+n_2-p-2)}^2+{(n+n_i-p-1)}^2}\hfill \\ -n_1\sqrt{{(n+n_1-p-1)}^2+1}-{\displaystyle \sum _{i=3}^{n-p}}\sqrt{{(n+n_1-p-1)}^2+{(n+n_i-p-1)}^2}\hfill \\ -n_2\sqrt{{(n+n_2-p-1)}^2+1}-{\displaystyle \sum _{i=3}^{n-p}}\sqrt{{(n+n_2-p-1)}^2+{(n+n_i-p-1)}^2}\hfill \\ +\sqrt{{(n+n_1-p)}^2+{(n+n_2-p-2)}^2}-\sqrt{{(n+n_1-p-1)}^2+{(n+n_2-p-1)}^2}.\hfill \end{array}$$

(7)

Claim 5.

$n_1\sqrt{a^2+1}+n_2\sqrt{{(b-1)}^2+1}>n_1\sqrt{{(a-1)}^2+1}+n_2\sqrt{b^2+1}$, where $a=n+n_1-p$ and $b=n+n_2-p-1$.

Proof of Claim 5.

First we assume that $n_1=n_2$. Thus, we have $a=b+1$. In this case we have to prove that

$$\sqrt{{(b+1)}^2+1}+\sqrt{{(b-1)}^2+1}>\sqrt{b^2+1}+\sqrt{b^2+1},$$

that is,

$$\sqrt{{(b+1)}^2+1}-\sqrt{b^2+1}>\sqrt{b^2+1}-\sqrt{{(b-1)}^2+1},$$

that is,

$$2b+\sqrt{b^2+1}\sqrt{{(b-1)}^2+1}>\sqrt{b^2+1}\sqrt{{(b+1)}^2+1},$$

that is,

$$\sqrt{b^2+1}\sqrt{{(b-1)}^2+1}>b^2-b+1,$$

after squaring both sides, one can easily check that the above result is true. Hence the Claim 5 is true for $n_1=n_2$.

Next we assume that $n_1\ge n_2+1$. In this case we have to prove that

$$n_1(\sqrt{a^2+1}-\sqrt{{(a-1)}^2+1})>n_2(\sqrt{b^2+1}-\sqrt{{(b-1)}^2+1}).$$

One can easily see that

$$\sqrt{b^2+1}-\sqrt{{(b-1)}^2+1}<1.$$

Using this, from the above, we have to prove that

$$\frac{n_1}{n_2}>\frac{1}{\sqrt{a^2+1}-\sqrt{{(a-1)}^2+1}},$$

that is,

$$\sqrt{a^2+1}>\sqrt{{(a-1)}^2+1}+\frac{n_2}{n_2+1},$$

that is,

$$2a-1>\frac{2n_2}{n_2+1}\sqrt{{(a-1)}^2+1}+{\left(\frac{n_2}{n_2+1}\right)}^2,$$

that is,

$$2a-2>\frac{2n_2}{n_2+1}\sqrt{{(a-1)}^2+1},$$

that is,

$${(a-1)}^2{(n_2+1)}^2>n_2^2\left({(a-1)}^2+1\right),$$

that is,

$${(a-1)}^2(2n_2+1)>n_2^2,$$

which is always true as $a\ge n_1+1\ge n_2+2$. This completes the proof of Claim 5. □

Claim 6.

$\sqrt{{(r+1)}^2+t^2}+\sqrt{{(s-1)}^2+t^2}>\sqrt{r^2+t^2}+\sqrt{s^2+t^2}$, where $r=n+n_1-p-1$, $s=n+n_2-p-1$ and $t=n+n_i-p-1$.

Proof of Claim 6.

We have to prove that

$$\sqrt{{(r+1)}^2+t^2}-\sqrt{s^2+t^2}>\sqrt{r^2+t^2}-\sqrt{{(s-1)}^2+t^2},$$

that is,

$$\begin{array}{cc}\hfill & {(r+1)}^2+t^2+s^2+t^2-2\sqrt{{(r+1)}^2+t^2}\sqrt{s^2+t^2}\hfill \\ \hfill & >r^2+t^2+{(s-1)}^2+t^2-2\sqrt{r^2+t^2}\sqrt{{(s-1)}^2+t^2},\hfill \end{array}$$

that is,

$${\left(r+s+\sqrt{r^2+t^2}\sqrt{{(s-1)}^2+t^2}\right)}^2>\left({(r+1)}^2+t^2\right)(s^2+t^2),$$

that is,

$$\sqrt{r^2+t^2}\sqrt{{(s-1)}^2+t^2}>r(s-1)+t^2,$$

that is,

$${(r-s+1)}^2>0,$$

which is true always. This completes the proof of Claim 6. □

Claim 7.

$\sqrt{{(n+n_1-p)}^2+{(n+n_2-p-2)}^2}>\sqrt{{(n+n_1-p-1)}^2+{(n+n_2-p-1)}^2}$.

Proof of Claim 7.

We have to prove that

$${(n+n_1-p)}^2+{(n+n_2-p-2)}^2>{(n+n_1-p-1)}^2+{(n+n_2-p-1)}^2,$$

that is,

$$2(n+n_1-p)>2(n+n_2-p)-2,$$

that is,

$$n_1-n_2+1>0,$$

which is true always. This completes the proof of Claim 7. □

By Claim 5, we obtain

$$\begin{array}{c}(n_1+1)\sqrt{a^2+1}+(n_2-1)\sqrt{{(b-1)}^2+1}-n_1\sqrt{{(a-1)}^2+1}-n_2\sqrt{b^2+1}\hfill \\ =n_1\sqrt{a^2+1}+n_2\sqrt{{(b-1)}^2+1}-n_1\sqrt{{(a-1)}^2+1}-n_2\sqrt{b^2+1}\hfill \\ +\sqrt{a^2+1}-\sqrt{{(b-1)}^2+1}\hfill \\ >\sqrt{a^2+1}-\sqrt{{(b-1)}^2+1}>0.\hfill \end{array}$$

(8)

By Claim 6, we obtain

$$\begin{array}{c}\sum _{i=3}^{n-p}[\sqrt{{(n+n_1-p)}^2+{(n+n_i-p-1)}^2}+\sqrt{{(n+n_2-p-2)}^2+{(n+n_i-p-1)}^2}\hfill \\ -\sqrt{{(n+n_1-p-1)}^2+{(n+n_i-p-1)}^2}-\sqrt{{(n+n_2-p-1)}^2+{(n+n_i-p-1)}^2}]\hfill \\ >0.\hfill \end{array}$$

(9)

Using (8), (9) with Claim 7 in (7), we obtain $SO\left(H_1\right)>SO\left(H_2\right)$. Using this result several times (if needed), we obtain

$$SO\left(H_{n,{\displaystyle \underbrace{n_1,n_2,\dots ,n_{n-p}}}}\right)<SO\left(H_{n,{\displaystyle \underbrace{n_1+1,n_2-1,\dots ,n_{n-p}}}}\right)<\cdots <SO\left(K{i}_n^{n-p}\right).$$

as $H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}\ncong K{i}_n^{n-p}$. Hence

$$SO\left(G\right)\le SO\left(H_{n,{\displaystyle \underbrace{n_1,\dots ,n_{n-p}}}}\right)<SO\left(K{i}_n^{n-p}\right).$$

This completes the proof of the theorem. □

4. Conclusions

Sombor index was used to model entropy and enthalpy of vaporization of alkanes with satisfactory prediction potential, indicating that this topological index may be used successfully on modeling thermodynamic properties of compounds. In this paper we presented some lower and upper bounds on the Sombor index of graph G in terms of graph parameters (clique number, chromatic number, number of pendant vertices, etc.) and characterize the extremal graphs. Here we pose two related problems.

Problem 1.

Characterize the maximal graph with respect to Sombor index among all connected graphs of order n with clique number $\omega$.

Problem 2.

Characterize the minimal graph with respect to Sombor index among all connected graphs of order n with p pendant vertices.