Abstract
We study an energy-dependent potential related to the Rosen–Morse potential. We give in closed-form the expression of a system of eigenfunctions of the Schrödinger operator in terms of a class of functions associated to a family of hypergeometric para-orthogonal polynomials on the unit circle. We also present modified relations of orthogonality and an asymptotic formula. Consequently, bound state solutions can be obtained for some values of the parameters that define the model. As a particular case, we obtain the symmetric trigonometric Rosen–Morse potential for which there exists an orthogonal basis of eigenstates in a Hilbert space. By comparing the existent solutions for the symmetric trigonometric Rosen–Morse potential, an identity involving Gegenbauer polynomials is obtained.
Keywords:
orthogonal polynomials; Schrödinger equation; ordinary differential equations; energy-dependent potential; hypergeometric functions; asymptotic expansions MSC:
42C05; 33C45; 33C05; 34A05; 34E05
1. Introduction
An energy-dependent Schrödinger equation appears for the first time in relativistic quantum mechanics with the Pauli–Schrödinger equation, given by Pauli [1] in the description of the spectrum of an electron in the presence of a magnetic field. Further developments in relativistic and non relativistic quantum mechanics was made by many authors [2,3,4,5,6,7,8,9,10]. The list is by no means exhaustive.
These classes of quantum potentials appear frequently in many areas of quantum mechanics. A relativistic scalar particle in presence of an electromagnetic field can be studied by means of a Klein–Gordon equation with an energy dependent potential [4,8]. In [11], the authors have applied energy dependent potentials with emphasis on confining potentials to the description of heavy quark systems. Furthermore, the description of systems of N bosons bound is considered in [12] and the Hamiltonian formulation of the relativistic many-body problem in [4,5,13] also lead to energy dependent potential models. For physical applications in hydrodynamics, see [14].
Mathematical aspects of wave equations with energy-dependent potentials have been studied by several authors. The presence of an energy-dependence in the potential in the nonrelativistic context requires a modification of the underlying quantum theory, principally affecting orthogonality relation and norm [15]. An analogous modification is required in the relativistic framework [16]. An extension of the quantum mechanical formalism of systems with energy-dependent potentials to systems defined by generalized Schrödinger equations including a position-dependent mass was studied in [7]. Energy-dependence in the framework of noncommutative quantum mechanics has been recently considered in [17].
The search of solutions for energy dependent potentials in wave equations has attracted considerable attention since the appearance of Pauli’s work. In the present manuscript we study a quantum system with energy dependent potential related to the Rosen–Morse trigonometric potential, used in describing the interatomic interaction of linear molecules and for describing polyatomic vibration states and energies of the molecule [18]. It has long been known that some mathematical features of quantum systems with an energy-dependent potential have several non-trivial implications; for instance, it is necessary to modify the scalar product to guarantee the conservation of the norm [15,19]. In the present manuscript we give closed-form of solutions, modified relations of orthogonality given by a indefinite (in general) bilinear form and an asymptotic formula of the solutions. Consequently, bound state solutions can be obtained for some values of the parameters that define the model. The solutions are given in terms of a class of functions derived from a sequence of hypergeometric para-orthogonal polynomials on the unit circle. We obtain, as a particular case, the symmetric trigonometric Rosen–Morse potential. In such case, the solutions reduce to an orthogonal basis of eigenfunctions defined in a Hilbert space and are expressed in terms of the Gegenbauer or ultraspherical polynomials. By comparing this solution with other solutions given in the literature we obtain, as a consequence, an identity involving Gegenbauer polynomials. Our procedure to obtain the energy dependent potential is based in a classical technique developed by Bose in [20] to construct solvable one-variable Schrödinger potentials.
2. Basic Notations and Statement of the Results
Let be a measure on the unit circle with support consisting of an infinite number of points. We remind that is the sequence of orthonormal polynomials on the unit circle associated to (also termed as Szegő polynomials, after their introduction by G. Szegő), if
where lower order terms and .
An exposition of the theory of orthogonal polynomials systems on the unit circle is presented in the monographs [21,22,23]. More recent surveys in [24,25].
If is a polynomial of degree n, the reciprocal polynomial is defined as , or equivalently
Let denote the Gauss hypergeometric function of the variable z with parameters ; cf. [26] (p. 56), given by
for and for other values of by analytic continuation appropriately; the Pochhammer symbol is defined by .
For , the function will be defined on the branch for which arguments are restricted between and . We also denote by the floor function, defined as the greatest integer less than or equal to x.
A fundamental role in this manuscript is played by the sequence of functions
where and x are such that and .
The functions were introduced in [27] and are defined from the sequence of para-orthogonal polynomials, cf. [28]
associated to the Szegő hypergeometric polynomials, cf. [29,30]
These polynomials satisfy the orthogonality relations in the unit disk through the parametrization
where
here the constant
is such that the moment .
In the sequel, we denote by and the monic and orthonormal polynomials of degree n respectively associated to . From (4) it follows that
is the main coefficient of .
It should be noted that the polynomials are of hypergeometric type. According to [30] (Th. 5.1), one has
This last relation can also be extended to if one takes
for .
In the present manuscript we prove the following results.
Theorem 1.
Let . Then, the stationary one-dimensional Schrödinger equation with energy dependent potential
where
has by solution the system of wave functions
in .
The usual continuity equation
where P denotes the probability density and J the probability current, governs the conservation of mass, charge, and probability of any closed system. If the potential is energy-dependent, it is necessary to modify the definition of the usual orthogonality relations in order to satisfy the continuity equation, [5,15]. More precisely, let be a system of normalizable wave functions solutions of an energy dependent potential Schrödinger equation defined through the boundary value problem
where V is of class with respect to the variable E, being I an open interval of the real line and .
The continuity equation read as
and is satisfied by the probability density P and probability current J
where is a solution to the time-dependent Schrödinger equation
The orthogonality relation between two states n and m, reads as
now, by using the smooth dependence of V in relation to E one obtains
In that regard, for the present quantum model we have the following relations of orthogonality. Notice that the presence of the function in the definition implies that the associated bilinear form is not in general of a definite sign. When , we have bound states solutions.
Theorem 2.
Let and be the wave functions of Theorem 1. Then, satisfy the relation of orthogonality
where . When and one has
For the particular case we obtain the symmetric trigonometric Rosen–Morse potential, cf. [31] (Prob. 12), [23,32,33] ((4.7.11) p. 81). Let , be the Gegenbauer polynomial of degree n cf. [23] (p. 80). As a consequence of Theorem 1 we obtain
Corollary 1.
The stationary one-dimensional Schrödinger equation
admits the energy eigenstates
and the complete orthogonal system of wave functions
in the Hilbert space with the inner product .
Notice that from this corollary it follows immediately that the ground state energy for the symmetric trigonometric Rosen–Morse potential reduces to
The asymmetric trigonometric Rosen–Morse potential or Rosen–Morse I potential, cf. [32,34,35] whose associated Schrödinger equation reads as
is among the exactly solvable potentials. Bound state solutions can be given in terms of the Jacobi polynomials with purely imaginary arguments and complex conjugate parameters, cf. [32] (pp. 296–297).
This potential has also been studied in [36,37] and solved in terms of the real Romanovski polynomials [38,39] (also known as Romanovsky–Routh or Pseudo–Jacobi polynomial as in [40]). These polynomials are defined as the polynomial solution of degree n of the differential equation
and can be expressed in terms of the Jacobi polynomials , cf. [24] [(20.1.1) p. 509], [23] [(4.21.2) p. 62] as
For convenience, we will adopt the parametrization given in [41] for the solution to (10) in terms of the real Romanovski polynomials (expressed also in terms of author’s parametrization), which reads
for , and the corresponding energies
In particular, the symmetric trigonometric Rosen–Morse is obtained by taking in (10). In such case we have that
is a solution for the Schrödinger equation associated to the symmetric Rosen–Morse potential.
By identifying the parameters we obtain
is also a solution of (9), which coincides, up to a multiplicative factor with , as shows the following identity
Theorem 3.
Let and . Then,
For those values of λ, say , for which we have a zero or pole in the expressions or the formula may be interpreted as a limit when . In such cases, the limit exists and is finite.
For the next result, let be fixed quantities sufficiently small so that the interval lies wholly in . We have that
Theorem 4.
Let . Then,
The bound for the error holds uniformly in .
2.1. Some Basic Facts about the Functions
We recall that a polynomial is conjugate reciprocal if satisfies the identity,
that is, . From (1), it follows that takes real values.
Let , define the sequences
it follows from [42] (Section 2) that the functions satisfy the recurrence relation
where and .
Let and . It follows from [42] (Th. 5.2),
where
Let be a finite positive Borel measure supported in and its Lebesgue decomposition. Recall that for , the Szegő function, cf. [25] (§2.4 p. 143, Part I), is defined as
whenever is the Szegő class. For almost every , the boundary value is defined as the radial limit:
From [30] (Th. 4.3), the Szegő function , (or for short) reads as
The function satisfy the differential equation, [27] (Th. 2.2)
When , we obtain the differential equation that defines the ultraspherical polynomials cf. [23] (p. 80). Notice that from (1) and (2), reduces to a polynomial. Therefore, coincides, up to a constant factor, with the n degree Gegenbauer polynomial.
Remark 1.
We remark that in [27] (Th. 2.2), the term m should be corrected in the last summand of the left hand side of the differential equation.
The Schrödinger Invariant of a Second Order Differential Equation
Quantum systems with energy-dependent potentials have been studied following several approaches such as supersymmetric quantum mechanics, Darboux transformations, exceptional orthogonal polynomials, among others, see [7] for a review. In this subsection we summarize the method we followed, introduced by Bose in [20] in order to construct one-variable Schrödinger solvable potentials.
Let us have a second order differential equation
being I an open subset of the real line and where p and q are functions defined on I. A straightforward calculation shows that the middle term in (19) can be eliminated by taking the substitution
Under the above substitution, the Equation (19) transforms to the canonical form
where I is given by
the term I is named by Milson in [43] as the Bose invariant.
By applying now the transformation , we obtain the normal form
being
the Schrödinger invariant, named by Bose in [20] and is the Schwartzian derivative
3. Proof of the Results
Proof of Theorem 1.
Proof of Theorem 2.
On the one hand, by applying iterated integration to the left hand side of (7) and taking into account the definition of P we obtain
On the other hand, for the right hand side of (7) we have
Now, from the definition of J and the fact that when one has
By substituting the value of V given in Theorem 1 we obtain (8).
To evaluate the numerical value of the constant , notice that if , from the recurrence relations (15) and (16) we have
hence,
This completes the proof of the theorem. □
Proof of Corollary 1.
From Theorem 1, the eigenstates are given by the system of real functions
From (18), reduces, up to a multiplicative constant factor, to the Gegenbauer polynomial of degree n, cf. [23] (§4.7 p. 80). To find the multiplicative constant , note that from (1), (2) and (3) we deduce that
therefore, from [23] [(4.7.3) p. 80] one obtains
The corresponding energy eigenstates read as
From the orthogonality relation for Gegenbauer polynomials
one has that is an orthogonal system in the Hilbert space with the scalar product
□
Proof of Theorem 3.
From Corollary 1 and the relation (14) we have that and are solutions of the differential equation
hence, the transformations (21) and (23) give that
are solutions of the differential equation
notice that reduces, up to a constant factor, to the Gegenbauer polynomial of degree n.
Notice that the relation (34) defines the left hand side as a polynomial of degree n whose coefficients are rational functions of the variable varying in .
Now, (33) is a solution to (32). Since this solution is a polynomial of degree n, it follows from [23] (Th. 4.2.2 p. 61) that
when . Using formula [44] [(6.4.12) p. 303], by comparing with and with , from (35) we obtain
Let us consider n fixed. Since the coefficients of and are rational functions of and are equal when , it follows from [45] (Th. 17.1 p. 369) that the relation is valid for , with exception of a finite number of special values of . Notice that from [44] [(6.4.12) p. 303], the zeros of the functions and are removable singularities of the left hand side and right hand side respectively of (36). Furthermore, when is a zero of or we have simple poles in the main coefficients of the left hand side or right hand side accordingly. For these values of , the formula may be interpreted as a limit as . This completes the proof of the theorem. □
To prove Theorem 4 a preliminary lemma is necessary.
Lemma 1.
Let and be fixed and define for ,
Then,
being any fixed quantities sufficiently small so that .
Proof.
Let us denote
From (17), we have that for fixed, is continuous as a function of , hence
therefore, from Lemma [21] (Lem. 4.2 p. 220)
pointwise in the interval .
Let be any fixed quantities sufficiently small so that . Since is continuous in the compact set , the Heine–Cantor Theorem cf. [46] (Th. 2 p. 201) implies that is uniformly continuous in . Hence, for every there exists such that if , then
therefore,
this shows that the family is equicontinuous.
On the other hand, we have also that there exists such that
this shows that the family is uniformly bounded.
From Arzela’s Theorem, cf. [47] (p. 54) it follows that the family of functions is compact in equipped the uniform norm. Therefore, from (37) every uniform convergent subsequence of converges to the same limit, hence for the whole sequence we have
By using a similar argument, we also conclude that
□
Proof of Theorem 4.
From [21] [(2.7) p. 200] we have that
where is the solution of the Szegő extremum problem, [21] (p. 200 & Th. 2.5 p. 204).
From the relation [21] (p. 206)
where
cf. [21] [(3.4) p. 209], one finds that
The representation [21] [(4.6) p. 220] gives
with and defined as in Lemma 1.
Taking into account the representation
from [26] [(4) p. 47] one has
Now, Lemma 1 gives us that,
uniformly in , being any fixed quantities sufficiently small so that . This completes the proof of the theorem. □
4. Discussion
The present work is devoted to the study an energy-dependent potential related to the Rosen–Morse potential. The system is obtained by the addition of a potential term which depends on the function and an energy dependence through a square root.
In order to show some numerical comparisons we will identify accordingly the parameters of the quantum model given by Theorem 1 and the parameters of the asymmetric trigonometric Rosen–Morse model, following the form given in [41]. In effect, by identifying the parameters one has . Consequently, the quantum system defined by Theorem 1, in terms of the parameters and reads as,
which has, when , the system of solutions
and the corresponding energy levels,
On the other hand, following Theorem 3, we will multiply by an adequate numerical constant the expression that defines the functions (12),
Notice that, by virtue of Corollary 1 and [23] [(4.7.1) p. 80] one has now that
we recover in particular, the symmetric trigonometric Rosen–Morse oscillator.
In Figure 1 and Figure 2 we plotted the wave functions for several toy values of the parameters. In Figure 3 and Figure 4 we plotted the densities (see Theorem 2) and for the same values of the parameters with n fixed (). As can be appreciated, by fixing and making variable, the abscissas of the local maxima of the densities tend to be localized at the same points in both models, as increases. These points correspond to the regions where it is most likely the particle to be found. It should be also noticed from the expressions of the energies (13) and (42) that
for and n fixed. It could be interesting the further study of these facts.
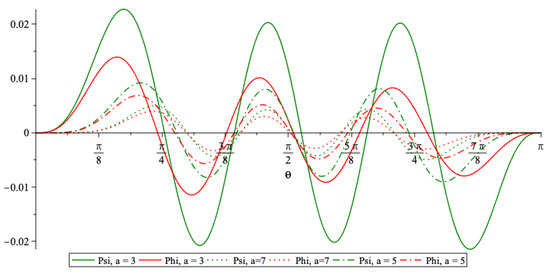
Figure 1.
in green and in red with , and .
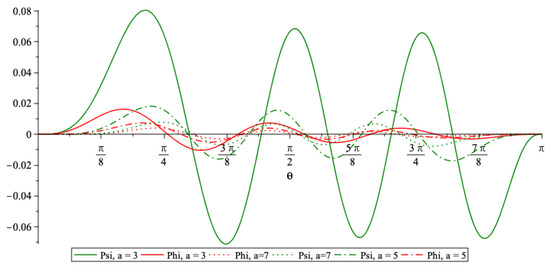
Figure 2.
in green and in red with , and .
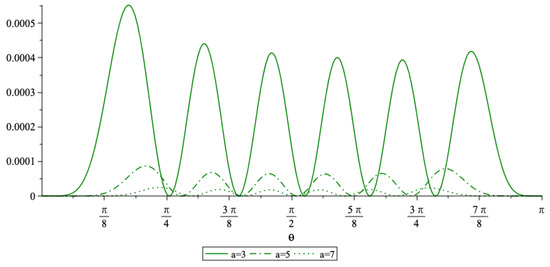
Figure 3.
Density with , and .
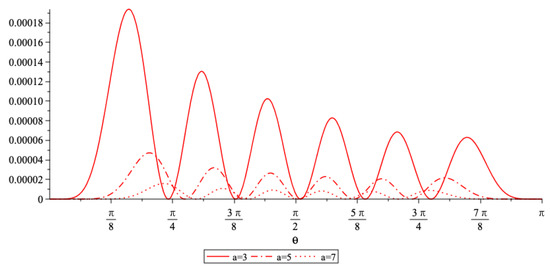
Figure 4.
Density with , and .
Author Contributions
Conceptualization, J.A.B.-M., C.F.B. and A.S.R.; methodology, J.A.B.-M., C.F.B. and A.S.R.; software, J.A.B.-M., C.F.B. and A.S.R.; validation, J.A.B.-M., C.F.B. and A.S.R.; formal analysis, J.A.B.-M., C.F.B. and A.S.R.; investigation, J.A.B.-M., C.F.B. and A.S.R.; resources, J.A.B.-M., C.F.B. and A.S.R.; data curation, J.A.B.-M., C.F.B. and A.S.R.; writing—original draft preparation, J.A.B.-M., C.F.B. and A.S.R.; writing—review and editing, J.A.B.-M., C.F.B. and A.S.R.; visualization, J.A.B.-M., C.F.B. and A.S.R.; supervision, J.A.B.-M., C.F.B. and A.S.R.; project administration, J.A.B.-M., C.F.B. and A.S.R.; funding acquisition, J.A.B.-M., C.F.B. and A.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
The author’s (C. F. Bracciali and A. Sri Ranga) research has been partially supported by grants from FAPESP (2016/09906–0) and from CNPq (402939/2016–6 and 304087/2018-1) of Brazil.
Acknowledgments
We thank the anonymous referees for carefully reviewing our manuscript. We also thank to Elso Drigo Filho from UNESP—Universidade Estadual Paulista, Campus São José do Rio Preto for helpful conversations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pauli, W. Zur Quantenmechanik des magnetischen Elektrons. Z. Phys. 1927, 43, 601–623. [Google Scholar] [CrossRef]
- Garcia-Martinez, J.; Garcia-Ravelo, J.; Peña, J.J.; Schulze-Halberg, A. Exactly solvable energy-dependent potentials. Phys. Lett. A 2009, 373, 3619–3623. [Google Scholar] [CrossRef]
- Langueur, O.; Merad, M.; Hamil, B. DKP Equation with Energy Dependent Potentials. Commun. Theor. Phys. 2019, 71, 1069–1074. [Google Scholar] [CrossRef]
- Rizov, V.A.; Sazdjian, H.; Todorov, T. On the relativistic quantum mechanics of two interacting spinless particles. Ann. Phys. 1985, 165, 59–97. [Google Scholar] [CrossRef]
- Sazdjian, H. Relativistic wave equations for the dynamics of two interacting particles. Phys. Rev. D 1986, 33, 3401. [Google Scholar] [CrossRef]
- Schiff, L.I.; Snyder, H.; Weinberg, J. On the existence of stationary states of the mesotron field. Phys. Rev. 1940, 57, 315–318. [Google Scholar] [CrossRef]
- Schulze-Halberg, A.; Yeşiltaş, Ö. Generalized Schrödinger equations with energy-dependent potentials: Formalism and applications. J. Math. Phys. 2018, 59, 113503. [Google Scholar] [CrossRef]
- Snyder, H.; Weinberg, J. Stationary states of scalar and vector fields. Phys. Rev. 1940, 57, 307–314. [Google Scholar] [CrossRef]
- Yekken, R.; Lassaut, M.; Lombard, R.J. Applying supersymmetry to energy dependent potentials. Ann. Phys. 2013, 338, 195–206. [Google Scholar] [CrossRef]
- Schulze-Halberg, A. Higher–order Darboux transformations and Wronskian representations for Schrödinger equations with quadratically energy–dependent potentials. J. Math. Phys. 2020, 61, 023503. [Google Scholar] [CrossRef]
- Lombard, R.J.; Mares, J.; Volpe, C. Wave equation with energy-dependent potentials for confined systems. J. Phys. G 2007, 34, 1–11. [Google Scholar] [CrossRef]
- Lombard, R.J.; Mares, J. The many-body problem with an energy-dependent confining potential. Phys. Lett. A 2009, 373, 426–429. [Google Scholar] [CrossRef]
- Mourad, J.; Sazdjian, H. The two-fermion relativistic wave equations of constraint theory in the Pauli–Schrödinger form. J. Math. Phys. 1998, 35, 6379–6406. [Google Scholar] [CrossRef]
- Li, Y. Some water wave equations and integrability. J. Nonlinear Math. Phys. 2005, 12, 466–481. [Google Scholar] [CrossRef]
- Formanek, J.; Lombard, R.J.; Mares, J. Wave equations with energy-dependent potentials. Czechoslov. J. Phys 2004, 54, 289–315. [Google Scholar] [CrossRef]
- Schulze-Halberg, A.; Roy, P. Bound states of the two-dimensional Dirac equation for an energy-dependent hyperbolic Scarf potential. J. Math. Phys. 2017, 58, 113507. [Google Scholar] [CrossRef]
- Harko, T.; Liang, S.-D. Energy-dependent noncommutative quantum mechanics. Eur. Phys. J. C 2019, 79, 1–22. [Google Scholar] [CrossRef]
- Rosen, N.; Morse, P.M. On the Vibrations of Polyatomic Molecules. Phys. Rev. 1932, 42, 210–217. [Google Scholar] [CrossRef]
- Sazdjian, H. The scalar product in two-particle relativistic quantum mechanics. J. Math. Phys. 1988, 29, 1620–1633. [Google Scholar] [CrossRef]
- Bose, A.K. A class of solvable potentials. Il Nuovo Cimento 1964, 32, 679–688. [Google Scholar] [CrossRef]
- Freud, G. Orthogonal Polynomials; Pergamon: Oxford, UK, 1971. [Google Scholar]
- Geronimus, L.Y. Polynomials Orthogonal on a Circle and Their Applications; American Mathematical Society Translations; American Mathematical Society: Providence, RI, USA, 1962; Volume 104, pp. 1–78. [Google Scholar]
- Szegő, G. Orthogonal Polynomials, 4th ed.; American Mathematical Society Colloquium Publications; American Mathematical Society: Providence, RI, USA, 1975; Volume 23. [Google Scholar]
- Ismail, M.E.H. Classical and Quantum Orthogonal Polynomials in One Variable; Encyclopedia of Mathematics and Its Applications; Cambridge Univ Press: Cambridge UK, 2005; Volume 98. [Google Scholar]
- Simon, B. Orthogonal Polynomials on the Unit Circle, Part 1: Classical Theory, Part 2: Spectral Theory; American Mathematical Society Colloquium Publications; American Mathematical Society: Providence, RI, USA, 2005; Volume 54. [Google Scholar]
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume I. [Google Scholar]
- Dimitrov, D.K.; Sri Ranga, A. Zeros of a family of hypergeometric paraorthogonal polynomials on the unit circle. Math. Nachr. 2013, 286, 1778–1791. [Google Scholar] [CrossRef]
- Jones, W.B.; Njåstad, O.; Thron, W.J. Moment theory, orthogonal polynomials, quadrature, and continued fractions associated with the unit circle. Bull. Lond. Math. Soc. 1989, 21, 113–152. [Google Scholar] [CrossRef]
- Askey, R. Discussion of Szegő’s paper: Beiträge zur Theorie der Toeplitzschen Formen. In Gabor Szegő. Collected Works; Askey, R., Ed.; Birkhäuser: Boston, MA, USA, 1982; Volume I, pp. 303–305. [Google Scholar]
- Sri Ranga, A. Szegő polynomials from hypergeometric functions. Proc. Amer. Math. Soc. 2010, 138, 4259–4270. [Google Scholar] [CrossRef]
- ter Haar, D. Problems in Quantum Mechanics, 3rd ed.; Pion Ltd.: London, UK, 1975. [Google Scholar]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry in Quantum Mechanics; World Scientific U P: Singapore, 2001. [Google Scholar]
- Sun, G.H.; Dong, S.H. Quantum information entropies of the eigenstates for a symmetrically trigonometric Rosen-Morse potential. Phys. Scr. 2013, 87, 7. [Google Scholar] [CrossRef]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and Quantum Mechanics. Phys. Rep. 1995, 251, 267–385. [Google Scholar] [CrossRef]
- de Lange, O.L.; Raab, R.E. Operator Methods in Quantum Mechanics; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Compean, C.B.; Kirchbach, M. The trigonometric Rosen-Morse potential in supersymmetric quantum mechanics and its exact solutions. J. Phys. A Math. Gen. 2006, 39, 547–557. [Google Scholar] [CrossRef]
- Raposo, A.; Weber, H.J.; Alvarez-Castillo, D.E.; Kirchbach, M. Romanovski polynomials in selected physics problems. Cent. Eur. J. Phys. 2007, 5, 253–284. [Google Scholar] [CrossRef]
- Romanovski, V. Sur quelques classes nouvelles de polynomes orthogonaux. CR Acad. Sci. Paris 1929, 188, 1023–1025. [Google Scholar]
- Routh, E.J. On some properties of certain solutions of a differential equation of second order. Proc. Lond. Math. Soc. 1884, 16, 245–261. [Google Scholar] [CrossRef]
- Lesky, P.A. Endliche und unendliche systeme von kontinuierlichen klassischen orthogonalpolynomen. Z. Angew. Math. Mech. 1996, 76, 181–184. [Google Scholar] [CrossRef]
- Quesne, C. Extending Romanovski polynomials in quantum mechanics. J. Math. Phys. 2013, 54, 122103. [Google Scholar] [CrossRef]
- Dimitrov, D.K.; Ismail, M.E.H.; Sri Ranga, A. A class of hypergeometric polynomials with zeros on the unit circle: Extremal and orthogonal properties and quadrature formulas. Appl. Numer. Math. 2013, 65, 41–52. [Google Scholar] [CrossRef]
- Milson, R. On the Liouville transformation and exactly-solvable Schrödinger equations. Int. J. Theor. Phys. 1998, 37, 1735–1752. [Google Scholar] [CrossRef]
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions. In Encyclopedia of Mathematics and Its Applications; Cambridge Univ. Press: Cambridge, UK, 2000; Volume 71. [Google Scholar]
- Markushevich, A.I. Theory of Functions of a Complex Variable; Prentice-Hall: Englewood Cliffs, NJ, USA, 1965; Volume I. [Google Scholar]
- Bourbaki, N. Elements of Mathematics. General Topology; Addison-Wesley: Paris/Reading, MA, USA, 1966; Volume I, (Translated from French). [Google Scholar]
- Kolmogorov, A.N.; Fomin, S.V. Elements of the Theory of Functions and Functional Analysis; Graylock Press: Rochester, NY, USA, 1957; Volume I. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).