Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula
Abstract
1. Introduction
2. Functionally Graded (FG) Orthotropic Nanoplates
3. Nonlocal Mixed Formula for FG Orthotropic Nanoplates
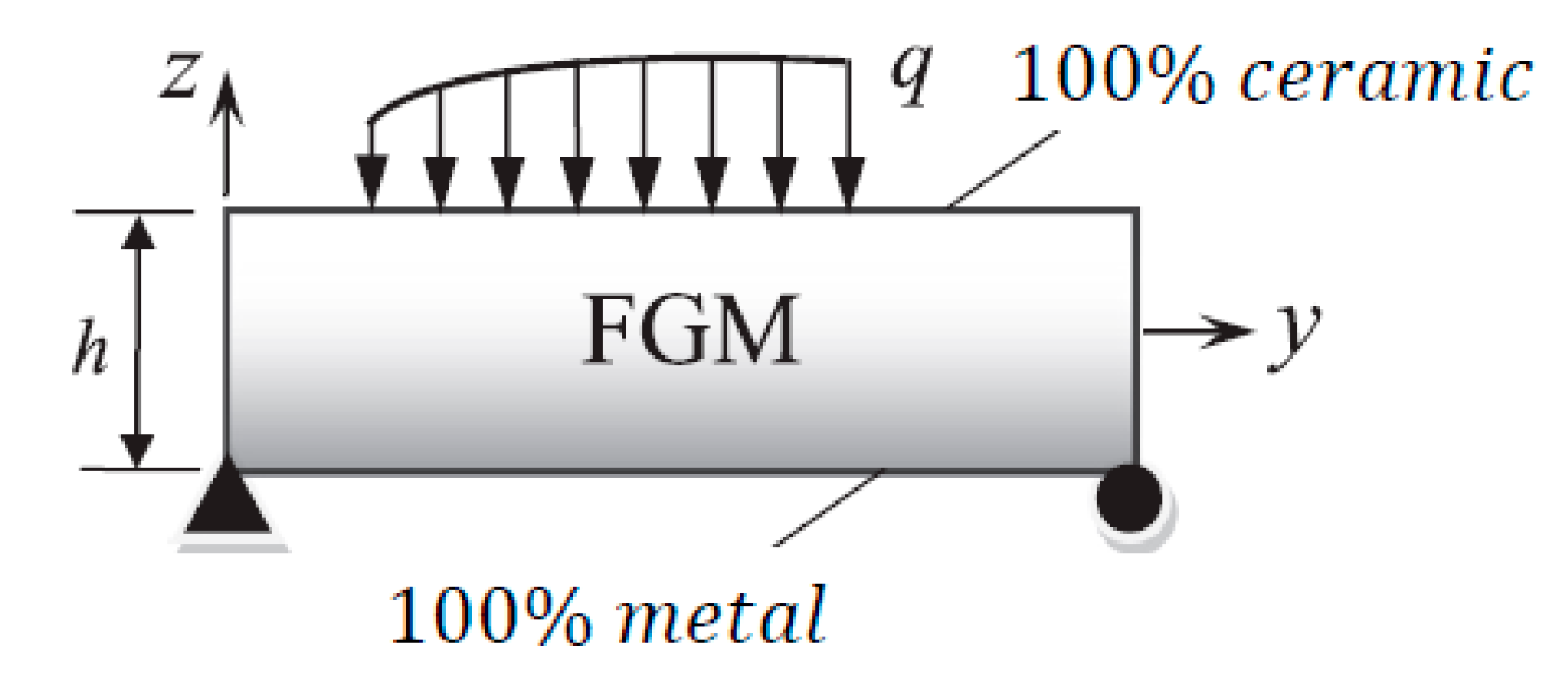
4. Formulations of the Problem
5. Exact Solution
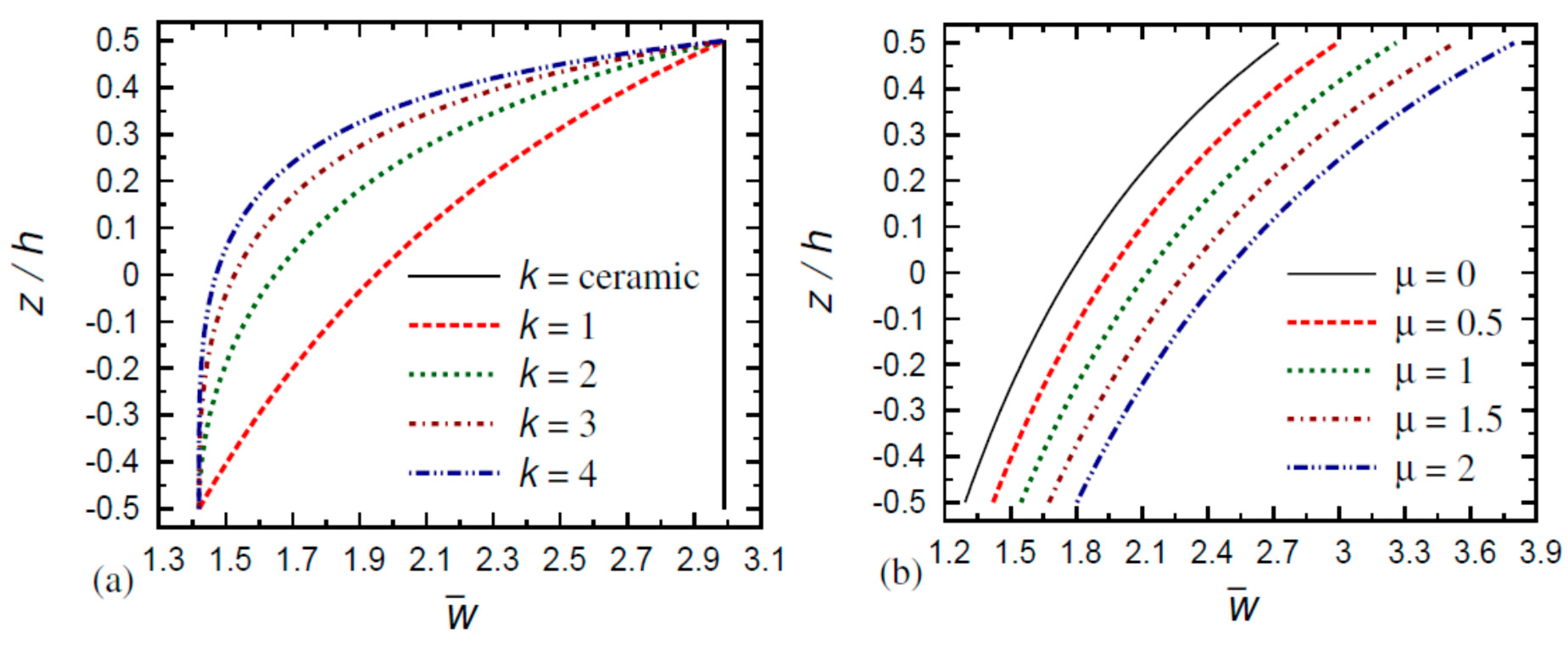
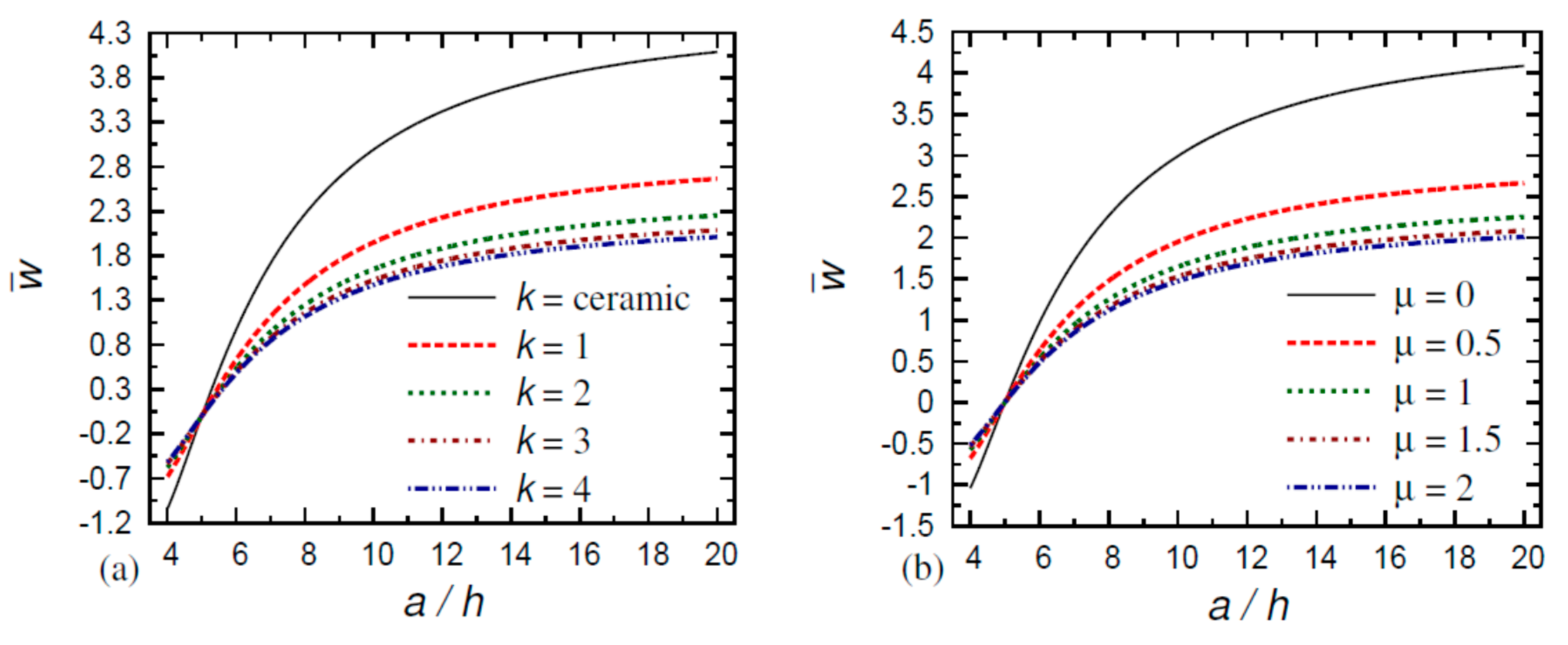
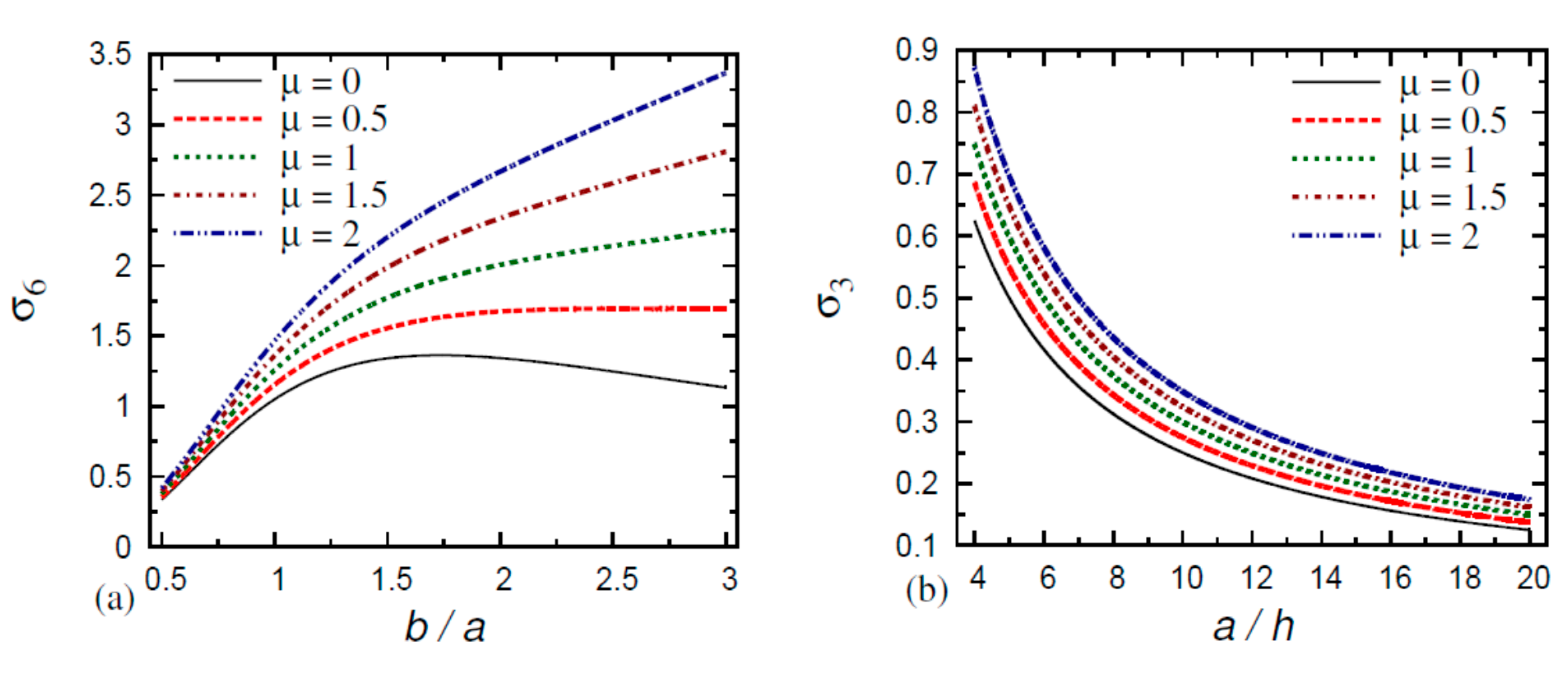
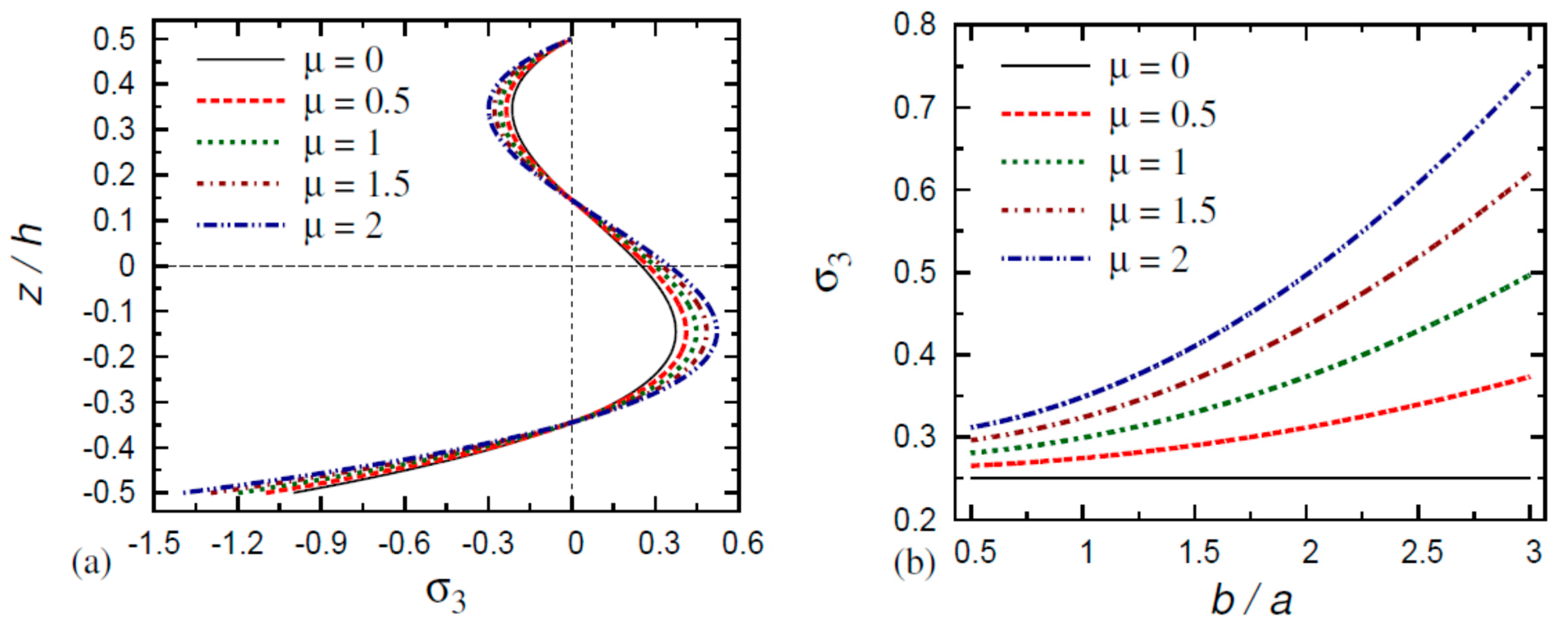
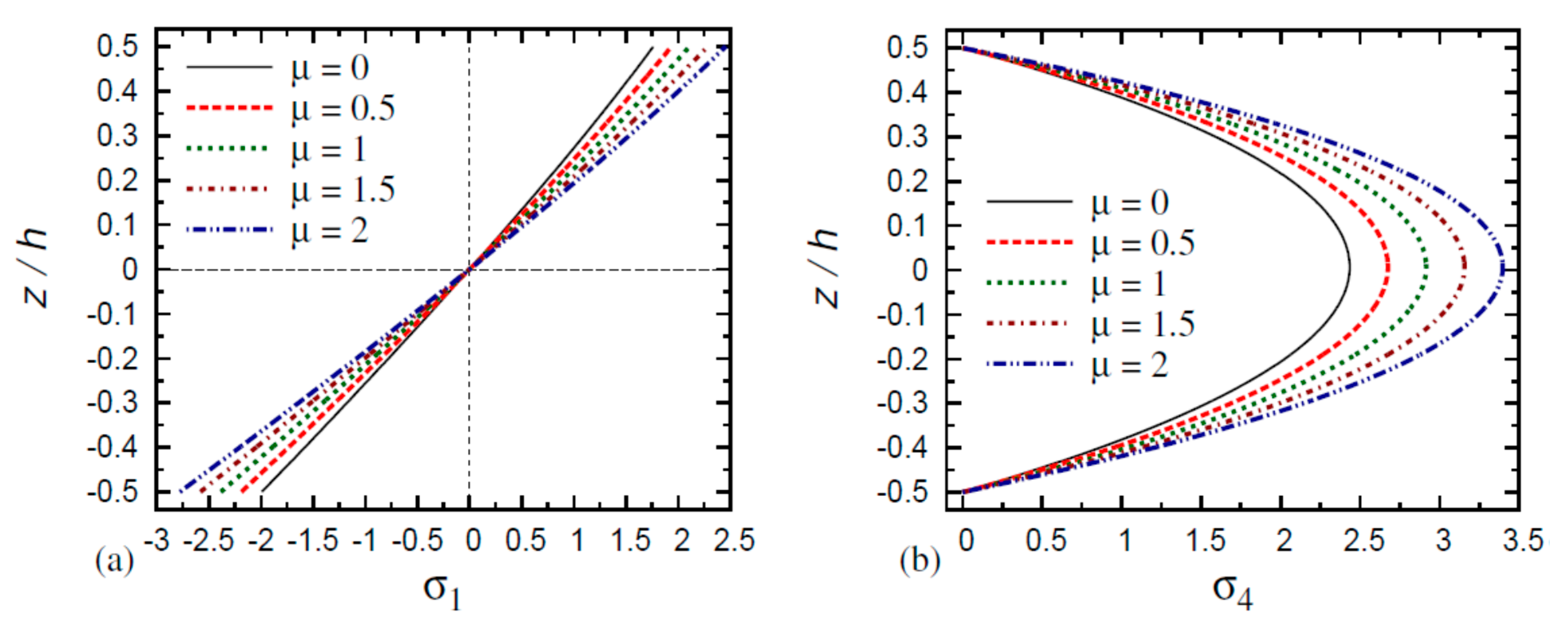
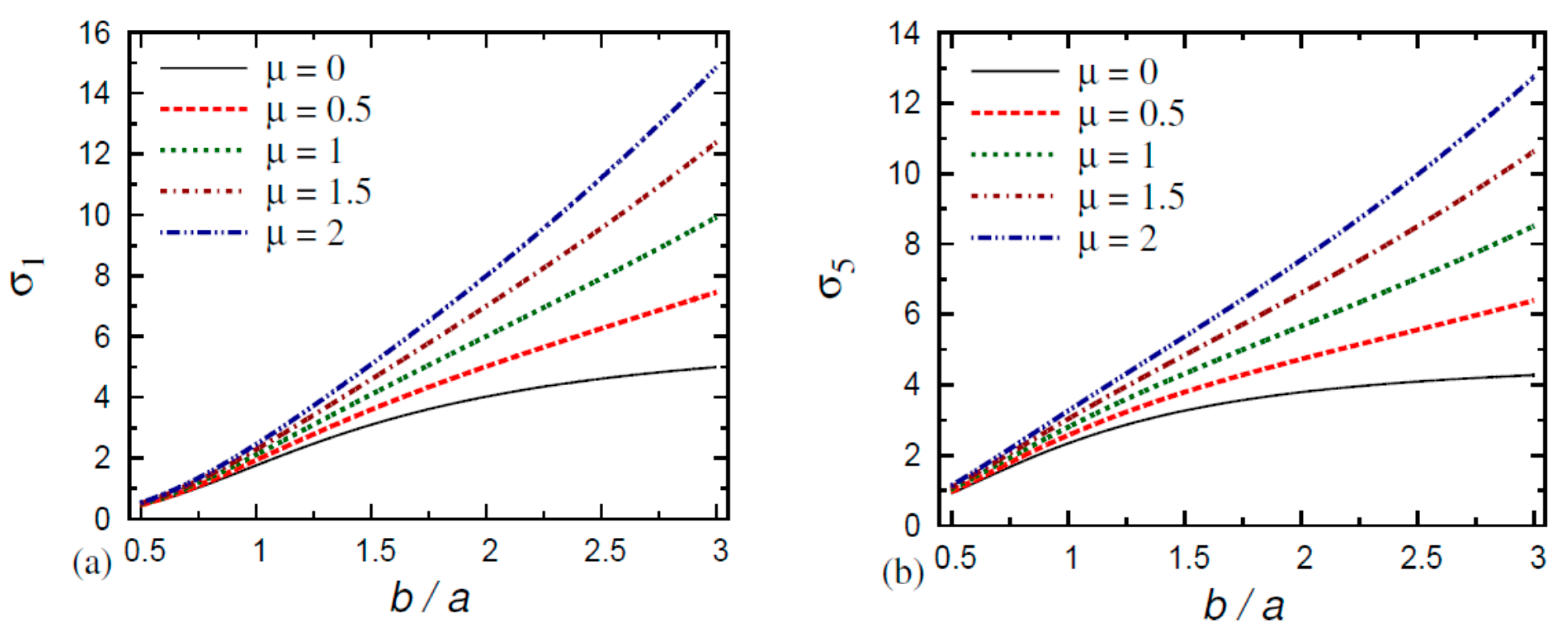
6. Numerical Results and Discussion
7. Conclusions
- The displacement difference of the FG nanoplate increases as the small-scale parameter increases and the gradient index decreases;
- The displacement difference of the purely ceramic and purely metal nanoplates decreases as the thickness ratio increases;
- The normal stress in the FG nanoplate decreases as the thickness and aspect ratios increase and as the gradient index and small-scale parameter decrease;
- The normal stress in the FG nanoplate increases as the thickness ratio, aspect ratio, gradient index, and small-scale parameter decrease;
- The transverse shear stresses and in the FG nanoplate increase as the thickness ratio, aspect ratio, gradient index, and small-scale parameter decrease.
Author Contributions
Funding
Conflicts of Interest
References
- Lebaschi, A.H.; Deng, X.H.; Camp, C.L.; Zong, J.; Cong, G.T.; Carballo, C.B.; Album, Z.; Radeo, S. Biomechanical, histologic, and molecular evaluation of tendon healing in a new murine model of rotator cuff repair. Arthrosc. J. Arthrosc. Relat. Surg. 2018, 34, 1173–1183. [Google Scholar] [CrossRef]
- Johnson, K.L.; Gidley, M.J.; Bacic, A.; Doblin, M.S. Cell wall biomechanics: A tractable challenge in manipulating plant cell walls ‘fit for purpose’. Curr. Opin. Biotechnol. 2018, 49, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Jandaghian, A.A.; Rahmani, O. Size-dependent free vibration analysis of functionally graded piezoelectric plate subjected to thermo-electromechanical loading. J. Intell. Mater. Syst. Struct. 2017, 28, 3039–3053. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. Int. J. Eng. Sci. 2016, 105, 12–27. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; de Sciarra, F.M. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Barretta, R.; Čanadija, M.; Feo, L.; Luciano, R.; de Sciarra, F.M.; Penna, R. Exact solutions of inflected functionally graded nano-beams in integral elasticity. Compos. B Eng. 2018, 142, 273–286. [Google Scholar] [CrossRef]
- Barretta, R.; Diaco, M.; Feo, L.; Luciano, R.; de Sciarra, F.M.; Penna, R. Stress-driven integral elastic theory for torsion of nano-beams. Mech. Res. Commun. 2018, 87, 35–41. [Google Scholar] [CrossRef]
- Barretta, R.; Canadija, M.; Luciano, R.; de Sciarra, F.M. Stress-driven modeling of nonlocal thermoelastic behavior of nanobeams. Int. J. Eng. Sci. 2018, 126, 53–67. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, Y.H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Woo, J.; Meguid, S.A.; Ong, L.S. Nonlinear free vibration behavior of functionally graded plates. J. Sound Vib. 2006, 289, 595–611. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.S. Dynamic response of initially stressed functionally graded rectangular thin plates. Compos. Struct. 2001, 54, 497–508. [Google Scholar] [CrossRef]
- Hebali, H.; Tounsi, A.; Houari, M.S.A.; Bessaim, A.; Bedia, E.A.A. New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J. Eng. Mech. 2014, 140, 374–383. [Google Scholar] [CrossRef]
- Mahi, A.; Adda Bedia, E.A.; Tounsi, A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl. Math. Model. 2015, 39, 2489–2508. [Google Scholar] [CrossRef]
- He, J.; Lilley, C.M. Surface effect on the elastic behavior of static bending nanowires. Nano Lett. 2008, 8, 1798–1802. [Google Scholar] [CrossRef]
- Asghari, M.; Rahaeifard, M.; Kahrobaiyan, M.; Ahmadian, M. The modified couple stress functionally graded Timoshenko beam formulation. Mater. Des. 2011, 32, 1435–1443. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Sahmani, S. Free vibration analysis of size-dependent functionally graded microbeams based on the strain gradient Timoshenko beam theory. Compos. Struct. 2011, 94, 221–228. [Google Scholar] [CrossRef]
- Rahmani, O.; Pedram, O. Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. Int. J. Eng. Sci. 2014, 77, 55–70. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Thai, H.T. A nonlocal beam theory for bending, buckling, and vibration of nanobeams. Int. J. Eng. Sci. 2012, 52, 56–64. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. A simplified shear and normal deformations nonlocal theory for bending of nanobeams in thermal environment. Phys. E 2015, 70, 121–128. [Google Scholar] [CrossRef]
- Zenkour, A.M. Torsional dynamic response of a carbon nanotube embedded in visco-Pasternak’s medium. Math. Model. Anal. 2016, 21, 852–868. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Thermo-electro-mechanical bending behavior of sandwich nanoplate integrated with piezoelectric face-sheets based on trigonometric plate theory. Compos. Struct. 2017, 162, 108–122. [Google Scholar] [CrossRef]
- Zenkour, A.M. Nonlocal thermoelasticity theory without energy dissipation for nano-machined beam resonators subjected to various boundary conditions. Microsyst. Technol. 2017, 23, 55–65. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Wave propagation analysis of a functionally graded magneto-electro-elastic nanobeam rest on visco-Pasternak foundation. Mech. Res. Commun. 2017, 79, 51–62. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Aljadani, M.H. Thermo-electrical buckling response of actuated functionally graded piezoelectric nanoscale plates. Res. Phys. 2019, 13, 102192. [Google Scholar] [CrossRef]
- Mashat, D.S.; Zenkour, A.M. Modified DPL Green–Naghdi theory for thermoelastic vibration of temperature-dependent nanobeams. Res. Phys. 2020, 16, 102845. [Google Scholar] [CrossRef]
- Ahouel, M.; Houari, M.S.A.; Bedia, E.A.; Tounsi, A. Size-dependent mechanical behavior of functionally graded trigonometric shear deformable nanobeams including neutral surface position concept. Steel Compos. Struct. 2016, 20, 963–981. [Google Scholar] [CrossRef]
- Zenkour, A.M. Buckling and free vibration of elastic plates using simple and mixed shear deformation theories. Acta Mech. 2001, 146, 183–197. [Google Scholar] [CrossRef]
- Zenkour, A.M. Natural vibration analysis of symmetrical cross-ply laminated elastic plates using mixed variational formulation. Eur. J. Mech. A/Solids 2000, 19, 469–485. [Google Scholar] [CrossRef]
- Zenkour, A.M. Stress analysis of axisymmetric shear deformable cross-ply circular laminated cylindrical shells. J. Eng. Math. 2001, 40, 315–332. [Google Scholar] [CrossRef]
- Zenkour, A.M. A simple four-unknown refined theory for bending analysis of functionally graded plates. Appl. Math. Model. 2013, 37, 9041–9051. [Google Scholar] [CrossRef]
- Zenkour, A.M. A novel mixed nonlocal elasticity theory for thermoelastic vibration of nanoplates. Compos. Struct. 2018, 185, 821–833. [Google Scholar] [CrossRef]
- Goli, E.; Bayesteh, H.; Mohammadi, S. Mixed mode fracture analysis of adiabatic cracks in homogeneous and non-homogeneous materials in the framework of partition of unity and the path-independent interaction integral. Eng. Fract. Mech. 2014, 131, 100–127. [Google Scholar] [CrossRef]
- Srinivas, S.; Rao, A.K. Bending, vibration and buckling of simply-supported thick orthotropic rectangular plates and laminates. Int. J. Solids Struct. 1970, 6, 1463–1481. [Google Scholar] [CrossRef]

| (GPa) | |
| (GPa) | |
| Theory | ||||
|---|---|---|---|---|
| 0.14 | 0.10 | 0.05 | ||
| 2 | Ref. [37] (Exact) | 387.23 | 1408.5 | 21,542 |
| Ref. [37] (CLPT) | 344.93 | 1325.1 | 21,201 | |
| Present | 388.14 | 1411.1 | 21,577 | |
| 1 | Ref. [37] (Exact) | 191.07 | 688.57 | 10,443 |
| Ref. [37] (CLPT) | 166.70 | 640.39 | 10,246 | |
| Present | 191.92 | 690.63 | 10,463 | |
| 0.5 | Ref. [37] (Exact) | 39.790 | 139.08 | 2048.7 |
| Ref. [37] (CLPT) | 32.345 | 124.26 | 1988.1 | |
| Present | 40.2749 | 140.021 | 2054.3 | |
| Ceramic | 2.7222 | 2.9909 | 3.2596 | 3.5282 | 3.7969 | 4.0656 | 4.3342 |
| 1 | 1.7761 | 1.9515 | 2.1268 | 2.3023 | 2.4774 | 2.6527 | 2.8280 |
| 2 | 1.5012 | 1.6494 | 1.7976 | 1.9458 | 2.0938 | 2.2420 | 2.3903 |
| 3 | 1.3906 | 1.5279 | 1.6651 | 1.8022 | 1.9395 | 2.0767 | 2.2142 |
| 4 | 1.3407 | 1.4731 | 1.6054 | 1.7376 | 1.8700 | 2.0021 | 2.1346 |
| 5 | 1.3172 | 1.4473 | 1.5773 | 1.7072 | 1.8373 | 1.9672 | 2.0972 |
| Metal | 1.2923 | 1.4199 | 1.5474 | 1.6749 | 1.8025 | 1.9300 | 2.0576 |
| 1 | 10 | 0 | 0.1760 | 0.1763 | 0.1833 | 0.1762 | 0.2146 | 0.2149 | 0.2148 | 0.2150 |
| 0.5 | 0.1934 | 0.1936 | 0.2003 | 0.1937 | 0.2358 | 0.2361 | 0.2358 | 0.2362 | ||
| 1 | 0.2108 | 0.2110 | 0.2176 | 0.2111 | 0.2569 | 0.2573 | 0.2572 | 0.2574 | ||
| 2 | 0.2455 | 0.2459 | 0.2517 | 0.2459 | 0.2993 | 0.2998 | 0.2992 | 0.2998 | ||
| 30 | 0 | 0.1771 | 0.1769 | 0.1769 | 0.1769 | 0.2166 | 0.2165 | 0.2165 | 0.2162 | |
| 1 | 0.1946 | 0.1944 | 0.1945 | 0.1935 | 0.2379 | 0.2378 | 0.2379 | 0.2373 | ||
| 2 | 0.2121 | 0.2119 | 0.2118 | 0.2111 | 0.2593 | 0.2592 | 0.2592 | 0.2593 | ||
| 4 | 0.2470 | 0.2468 | 0.2468 | 0.2466 | 0.3021 | 0.3019 | 0.3019 | 0.3016 | ||
| 2 | 10 | 0 | 0.4021 | 0.4026 | 0.4027 | 0.4028 | 0.2269 | 0.2269 | 0.2272 | 0.2271 |
| 1 | 0.5013 | 0.5019 | 0.5020 | 0.5023 | 0.2828 | 0.2829 | 0.2832 | 0.2832 | ||
| 2 | 0.6006 | 0.6011 | 0.6013 | 0.6017 | 0.3388 | 0.3389 | 0.3393 | 0.3392 | ||
| 4 | 0.7990 | 0.7998 | 0.7999 | 0.8003 | 0.4508 | 0.4509 | 0.4514 | 0.4512 | ||
| 30 | 0 | 0.4068 | 0.3975 | 0.3971 | 0.4143 | 0.2297 | 0.2255 | 0.2246 | 0.2191 | |
| 1 | 0.5071 | 0.4921 | 0.4954 | 0.5081 | 0.2864 | 0.2780 | 0.2799 | 0.2744 | ||
| 2 | 0.6075 | 0.5884 | 0.5934 | 0.6068 | 0.3430 | 0.3387 | 0.3353 | 0.3298 | ||
| 4 | 0.8082 | 0.7841 | 0.7903 | 0.8089 | 0.4564 | 0.4492 | 0.4462 | 0.4375 | ||
| 1 | 10 | 0 | 0.2233 | 0.2339 | 0.2384 | 0.2386 | 0.1085 | 0.1049 | 0.1049 | 0.1049 |
| 1 | 0.2674 | 0.2800 | 0.2855 | 0.2858 | 0.1299 | 0.1257 | 0.1257 | 0.1257 | ||
| 2 | 0.3115 | 0.3261 | 0.3326 | 0.3329 | 0.1514 | 0.1464 | 0.1464 | 0.1464 | ||
| 4 | 0.3997 | 0.4183 | 0.4268 | 0.4271 | 0.1942 | 0.1879 | 0.1879 | 0.1878 | ||
| 30 | 0 | 0.2234 | 0.2354 | 0.2444 | 0.2353 | 0.1094 | 0.1056 | 0.1056 | 0.0973 | |
| 1 | 0.2675 | 0.2815 | 0.2929 | 0.2812 | 0.1309 | 0.1264 | 0.1264 | 0.1202 | ||
| 2 | 0.3116 | 0.3274 | 0.3414 | 0.3270 | 0.1525 | 0.1473 | 0.1473 | 0.1429 | ||
| 4 | 0.3998 | 0.4195 | 0.4385 | 0.4186 | 0.1957 | 0.1889 | 0.1889 | 0.1886 | ||
| 2 | 10 | 0 | 0.3739 | 0.3787 | 0.3796 | 0.3821 | 0.1486 | 0.1343 | 0.1343 | 0.1343 |
| 1 | 0.5584 | 0.5663 | 0.5673 | 0.5709 | 0.2219 | 0.2006 | 0.2006 | 0.2006 | ||
| 2 | 0.7429 | 0.7539 | 0.7548 | 0.7599 | 0.2953 | 0.2668 | 0.2669 | 0.2669 | ||
| 4 | 1.1119 | 1.1292 | 1.1299 | 1.1374 | 0.4420 | 0.3994 | 0.3995 | 0.3995 | ||
| 30 | 0 | 0.3829 | 0.3880 | 0.4149 | 0.3406 | 0.1505 | 0.1331 | 0.1342 | 0.7146 | |
| 1 | 0.5720 | 0.5754 | 0.6208 | 0.5106 | 0.2248 | 0.1987 | 0.1998 | 1.1152 | ||
| 2 | 0.7609 | 0.7627 | 0.8269 | 0.6813 | 0.2990 | 0.2644 | 0.2653 | 1.5142 | ||
| 4 | 1.1390 | 1.1375 | 1.2388 | 1.0219 | 0.4476 | 0.3958 | 0.3964 | 2.3117 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zenkour, A.M.; Hafed, Z.S.; Radwan, A.F. Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula. Mathematics 2020, 8, 1162. https://doi.org/10.3390/math8071162
Zenkour AM, Hafed ZS, Radwan AF. Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula. Mathematics. 2020; 8(7):1162. https://doi.org/10.3390/math8071162
Chicago/Turabian StyleZenkour, Ashraf M., Zahra S. Hafed, and Ahmed F. Radwan. 2020. "Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula" Mathematics 8, no. 7: 1162. https://doi.org/10.3390/math8071162
APA StyleZenkour, A. M., Hafed, Z. S., & Radwan, A. F. (2020). Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula. Mathematics, 8(7), 1162. https://doi.org/10.3390/math8071162






