Abstract
This study creates indicators of adequacy and excellence based on multiple-criteria decision-making (MCDM) methods and fuzzy logic. The calculation of indicators presents two main difficulties: The nature of the data (numerical, interval, and linguistic values are mixed) and the objective of each criterion (which does not have to reach either the maximum or the minimum). A method is proposed, based on similarity measures with predetermined ideals, that is capable of overcoming these difficulties to provide easy-to-interpret information about the quality of the alternatives. To illustrate the usefulness of this proposed method, it has been applied to data collected from students across nine semesters at the Bucaramanga campus of the Industrial University of Santander in Colombia. This case study demonstrates that the proposed method can facilitate strategic decisions at an institution and open the way for the establishment of action policies regarding gender inequality and economic disparity, among other things.
1. Introduction
Complexity in decision-making often forces institutions to find a solution that considers multiple criteria with objectives that may conflict with each other [1]. A significant part of an institution′s competitive advantage lies in its ability to find a consensual solution [2,3]. Among the many areas of application of the multiple-criteria decision-making (MCDM) methods [1], in our work, the evaluation and identification of a company’s ability to compare their performance with that of their competitors [4], the process of personnel selection [5], and the analysis of students′ preferences in the choice of the university where they want to carry out their studies [6,7] are particularly useful.
It is essential for institutions to be aware of the adequacy of their staff and their ability to undertake a task. This requires strategic actions involving many people and usually depends on the coordinated actions of several employees from different departments, along with the adequate allocation of resources. Knowing the degree of compliance with this strategic plan, based on indicators capable of handling various criteria, the achievement of objectives can substantially increase. In short, this is achieved using decision support systems (DSS) based on MCDM methods [8].
The majority of DSS assume that the best outcome for each criterion (separately) is to try to reach the maximum or minimum value, depending on the specific case [9]. However, in many real cases, this is not the best outcome [10]; for example, in health-related models, intermediate values are often desirable, such as for weight and blood pressure. In addition to this, managers encounter other difficulties when calculating their estimates, as follows:
- The values come from several sections that use their own criteria and are expressed in different ways [11,12].
- The scales are diverse, and their sizes are extremely heterogeneous, which does not allow aggregated operators to be applied directly [12,13,14].
- The pre-established objectives for each criterion are future estimates, which are not usually precise [15].
Given this situation, it is necessary to determine appropriate indicators for each section so that the complete assessment is as faithful as possible to the actual performance of the activity, and the results are expressed clearly. In this work, we use a method that seeks to standardize and normalize the data by comparing them with the ideal objectives set by the institution. It is not only about transferring all the data to the interval [0, 1], but the intention is also to express the similarity of each value with the ideal.
Following this process, it is possible to both define a synthetic indicator that provides a global value for each alternative and to estimate its quality (Figure 1). To show the usefulness of the method, a real example is studied using data from students enrolled at the Industrial University of Santander in Colombia (its acronym in Spanish is UIS).
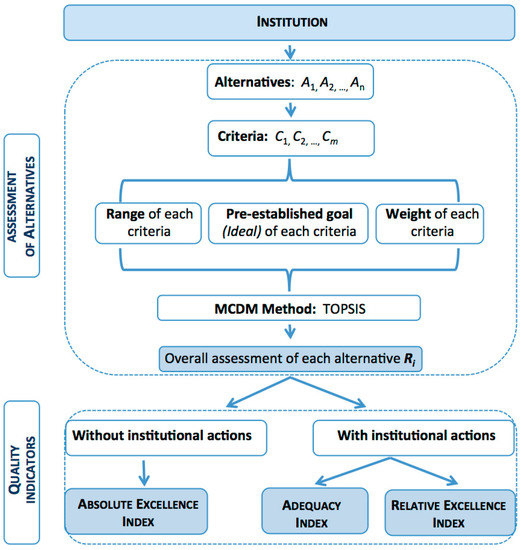
Figure 1.
Scheme of our proposal.
For almost five years, since the UIS created the Student Academic Excellence Support System (its acronym in Spanish is SEA) to coordinate and manage programs and strategies, five types of data have been collected from students enrolled at the university: economic, social, health, academic, and cognitive [16]. This is a clear example where the measurement methods, the participants in the evaluations, and even the managers of the initiative have changed; therefore, exclusively using numerical indicators does not guarantee success. The instruments used need to be sufficiently flexible to provide plausible results [17].
Once the students have been assessed in a convincing manner, they can then be subdivided into three groups, according to whether they show significant, an average amount, or no difficulty in carrying out their studies. The proposed method accounts for students in different groups and aims to determine how this can affect the management of the institution in order to achieve its objective—Establishing adequate and excellent indices that allow the entity to make strategic decisions.
This study used data from UIS students enrolled from 2014 to the first semester of 2018. It confirmed that, in the analysis period, between 65% and 73% of the students were considered to have an adequate ability to carry out their studies successfully, while the excellence index did not exceed 20%. This means that the UIS should provide additional support to approximately one-third of the enrolled students and plan activities that promote equal opportunities and high performance for one or two out of every 10 students.
2. Homogenization and Normalization of the Data Based on the Similarity Measures
Depending on the type of criteria analyzed, an evaluation using real numbers, intervals, linguistic evaluation, or finite collections of linguistic evaluations may give a more realistic result [12]. In this section, we show how to transform a set of data extracted from a finite and totally ordered discrete term (or numerical) set into real numbers or real intervals. Once transformed, we normalize the data in the interval [0, 1], taking into account the similarity of each of them with a pattern fixed a priori [12,13].
2.1. Data Homogenization
The use of intervals in decision-making processes is very common and does not usually add many operational difficulties to the use of real numbers [13,18]. However, the use of linguistic data usually requires the use of previous processes for their conversion into numbers. For that reason, it is necessary to specify the treatment that will be carried out on them. Considering the work of Yager [19], Herrera and Martínez [20,21], and Xu [12,22], it can be assumed that a linguistic evaluation scale is a set
which must satisfy the following conditions:
- (1)
- The set is ordered: if > ;
- (2)
- There is a negation operator: neg( such that ;
- (3)
- There are max. and min. operators: max() = if , and min() = if
Given a collection of elements of , where according to [12], we can express the collection as an interval . Formally, a linguistic interval evaluation scale can be expressed as [12]
In we can also establish an order. Let and be two elements of and let According to Xu [12,22], the degree of possibility of is obtained as
To put the sets in and into arithmetic form and to convert the elements of into intervals of real numbers and to provide an arithmetic form in the sets and , these sets are extended to continuous scales as follows [12,20,22]:
If the data are to be contained in a linguistic evaluation scale, as in (2), in many situations, it is more appropriate to transform linguistic variables into intervals instead of real numbers [20,23]. Taking into account the information presented in [23], given the linguistic scale with H values, we make a partition of the interval into H disjoint sub-intervals, such that If we make
we can transform each term of into an interval contained in [0, H].
Taking into account all the cases we have mentioned in this section, the data we are going to handle can be converted into real numbers (Type I) or into real intervals (Type II). Table 1 shows the types of data that we will use in a schematic way.

Table 1.
Types of data.
2.2. Normalization Based on an Ideal
In Cables et al. [10] and Acuña-Soto et al. [11], the normalization of each x data contained in a range is proposed by measuring the similarity with an ideal fixed by the interval The resulting normalization function is as follows:
The normalization can be extended to data intervals [11,24]. Given the normalization is performed by measuring the similarity with by means of the Manhattan distance,
that is,
The normalization method proposed in (10) is very useful, especially for applying multicriteria optimization methods [25], but the goal is to extend these methods in order to broaden their field of application.
To this end, two inconveniences of (8) need to be avoided:
- (a)
- Linearity cannot always be assumed for the manner of approaching or moving away from the ideal. The effect of having values below the ideal may be very different from that of having values greater than the ideal [26].
- (b)
- The normalization proposed in (10) is not very sensitive to the position of the interval with respect to the ideal
In order to reduce these drawbacks, we build functions that take into account the range mentioned (it is the support of the function), the ideal [a, b], and the way to approach this ideal. To do this, given six real numbers A, a, b, B, k1, and k2, such that , we define the function , given by
The values k1 and k2 determine the way to approach or leave from the ideal—for positive values, it is convex and for negative values, it is concave (see Figure 2). In addition, the higher the absolute values of k1 and k2, , the further we move away from the linear functions and , which appear in (7).
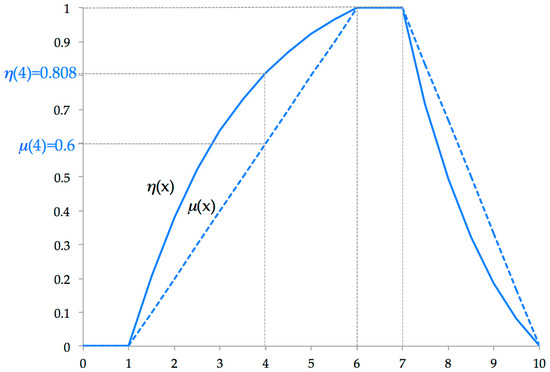
Figure 2.
Representation of and . Data from Example 1.
Remark 1.
When A = a (resp. b = B) we say that is degenerated. Using the same notation as in (9), we write k1 = 0 (resp. k2 = 0). With this, the functions,are as follows:
As in when the similarity to the ideal is piecewise linear, with the function we can normalize the data if they are real numbers [11]. However, to be able to normalize interval data, we need some previous results.
Proposition 1.
Given a continuous function and a non-empty interval, if , then
In addition, and exist such that
Proof.
and In addition, the same theorem guarantees the existence of , satisfying □
The f function is continuous and restricted to ; therefore, for any non-empty interval , f is Riemann integrable in . In addition, since exists. As the function f satisfies through the mean value theorem for integrals [27] in ,
Definition 1.
Letbe a continuous function. The valuegiven in (11) is called the normalization of the interval with respect to the function
In fact, can be extended to the case defining
Remark 2.
If, for operational reasons, it is preferable to avoid the calculation of the integral, the normalization could be approximated, for example, using the Simpson method [27]:
If is a piecewise function, defined for example in , so that , the normalization can be approximated by
Also, if the function is linear in pieces, the approximation is exact.
Taking into account Definition 1, we can normalize data with respect to the function . In the following example, we illustrate how this normalization works and compare it with the normalization N given in (8).
Example 1.
The range of a data set is considered to beand the ideal is . We assume that, according to our information, the similarity with can be estimated by means of , i.e.,
We compare the normalizations provided by N and n (given in (8) and (12), respectively) for the data v1 = 4, v2 = [4, 9], and v3 = [8, 9].
As can be observed in Figure 2, there must be differences between the two normalizations. For , we have and .
If we calculate the normalization of v2 = [4, 9] and v3 = [8, 9] using N, we have
In other words, v2 and v3 are transformed into the same value. However, the relationships of and with the ideal are very different: , whilst For this reason, if the actual situation requires it, it may be important to distinguish between both situations.
If we normalize with n given in (12), we obtain
Clearly, , i.e., n reflects the reality in a more accurate way than the normalization N.
Remark 3.
Note that, if in Example 1, linearity is assumed instead of the function , we can normalize it by making in the expression (12). In this case, the normalization of v2 = [4, 9] and v3 = [8, 9] results in
It is clear that even in the linear case, the normalization of intervals by means of Definition 1 is better adjusted to the similarity with the ideal since it distinguishes clearly between v2 = [4, 9] and v3 = [8, 9].
Taking into account Example 1 and Remark 3, in this work, we use the normalization proposed in (12).
3. Ideal Similarity and Multiple-Criteria Decision-Making Methods
An institution is interested in assigning values to n alternatives Ai, i = 1,…, n to perform an expensive activity on time and with the appropriate resources and efforts of personnel. To manage it, a value is assigned to each alternative in m criteria, Cj, j = 1,…, m. Depending on the nature of the criteria, an evaluation is carried out using numerical values, intervals, linguistic values, or sets of linguistic values [17]. According to Section 2.1, all of these values could be expressed by means of intervals In addition, each criterion, Cj, j = 1,…, m, has a range [Aj, Bj] where the values may vary:
On the other hand, the institution establishes [aj, bj] as an ideal (or pre-established goal) for each criterion, so that
Once the ranges and ideals of each Cj criterion are set [25], a similarity function with the ideal could be established, like the proposal in (7). From this function, the normalization for each criterion can be performed with the following function:
Consequently, by applying (15) to all of the criteria, a normalization of the original data is obtained, which expresses, by means of a real number rij of the interval [0, 1], similarity with the ideal set for the criterion.
In order to obtain a multi-criteria global assessment of each alternative, the Technique for Order of Preference by Similarity (TOPSIS) method is used [9]; this is one of the most popular sorting methods and fits perfectly with the needs of this work [28]. Specifically, data normalization based on the similarity with the ideal solution has already been used successfully with the TOPSIS method in other contexts [10,11].
Next, the method′s steps are expressed algorithmically.
Step 1. Determine the decision matrix where each data point is an interval , as shown in Table 1, where n is the number of alternatives, and the number of criteria is m.
Step 2. According to (15), we construct the normalized decision matrix by means of
Step 3. Determine the weighted normalized decision matrix. Given , with , we calculate
Step 4. Calculate two separation measures for each alternative:
Step 5. Calculate the relative proximity to the ideal solution using the relative index:
Once the TOPSIS method has been applied, a sorting of the alternatives is obtained.
Definition 2.
Given the alternatives and the relative proximity obtained in (17), it can be said that is preferred to only if
In addition to the sorting, a cluster in the set of alternatives could be established. If two values, and , are set, so that
a partition of the alternatives can be established:
In fact, if we consider
the set of n alternatives can be decomposed as , i.e., .
4. Construction of Quality Indices
For the managers of any entity, having an overall estimate of the percentage of people in their institution that are considered adequate for carrying out an activity could be very useful. This allows them to determine whether they should consider complementary actions and modifications in their strategies for the activity to be successful.
From now on, the alternatives are considered to be people who must perform a task, and S0 represents a value below which individuals are not suitable for the task, while S1 represents the threshold above which adaptation is excellent. Considering (20), the institution knows that n1 individuals will perform the task successfully, n2 people will be inadequate, unless they undertake additional training activities ( activities per person, ), and n3 individuals can perform the task, although some of them might have some difficulty with it ( people are adequate, ).
It is clear that the percentage of individuals that are part of provides a measure of absolute quality.
Definition 3:
With the previous notation, the index of absolute excellence is defined as
Using similar reasoning, from , and , an adequacy indicator that increases as n1 increases and decreases as n2 increases was constructed in Parada et al. [17]. With A(n), the institution can estimate who is suitable for the activity.
Definition 4:
With the previous notation, the adequacy index is defined as
By construction, and its variation is as follows [17].
Proposition 2:
The indicatorverifies:
- (a)
- It is increasing with respect to n1 with n2 and n3 being constants.
- (b)
- It is decreasing with respect to n2 with n1 and n3 being constants.
- (c)
- When n3 varies, and n1 and n2 remain constant,
is increasing if and decreasing if .
On the other hand, , which is seen as a function of α and β, can also be represented as
However, this is not enough to determine the quality of an institution; it also depends on the estimate of its percentage of excellence. In Parada et al. [15], a measure of excellence called ILSAE (Integral Level of Student′s Academic Excellence) is defined, which, in the present work, is called weak excellence.
Definition 5:
With the previous notation, the weak excellence index is defined as
By means of a direct calculation, it can be proved that
In accordance with (21), is the geometric mean between the absolute excellence, , and the ,
Therefore, it constitutes an optimistic estimate of excellence, hence the nickname ‘weak’. For this reason, a more representative excellence index of the real situation is introduced.
Definition 6:
With the previous notation, the excellence index is defined as the geometric mean between adequacy and absolute excellence ,
The three indices of excellence that have been introduced are related.
Proposition 3.
With the previous notation, if it can be proven that
Proof.
By construction, If or are nil, the result is obvious. If by a direct calculation, when , then is obtained. Therefore, if then, For (23), if , then,
and therefore, □
Remark 4.
The conditionusually does not involve any restrictions. For example, the data in Section 5 only imply that no more than 452 actions should be performed for each individual at risk,
5. Case Study
The proposed methods were applied to the Industrial University of Santander (UIS) at its main campus in Bucaramanga, Colombia. The Academic Excellence Support System (SEA) analyses data of newly enrolled students in five areas: economic, social, health, academic, and cognitive [16]. The aim of this work was to help the UIS design strategic plans that improve the results of its students based on data from nine semesters (from 2014 to 2018).
5.1. Data Used
The SEA assigns values to the areas using five synthetic indicators, which are the ones used here.
(a) Economic dimension (PE): This is obtained from three variables: income from economic dependence, (where is the greatest integer that is less than or equal to x and SMMLV is the current legal minimum monthly wage), the number of siblings (NS), and the position between siblings (PS). The economic dimension indicator is
where each variable can take the values that appear in Table 2.

Table 2.
Assigning values to all dimensions.
(b) Social Dimension (Ps): This is determined by family dysfunction (FAD), measured using the Family APGAR (Adaptability, Partnership, Growth, Affection, and Resolve) [29],
which can take four values {0.1, 0.5, 0.7, 1}, as shown in Table 2.
PS = FAD,
(c) Academic dimension (PA): This is obtained through three valuations [17]: a diagnostic test of UIS Math (DTM), the EFAI-4 numerical ability (NUA), and the 11-Math Knowledge Test (PSO), such that
where each variable takes a value between 1 and 3. Once the assessment of the academic indicator is known, PA, the level of mathematical performance of each student is determined using a linguistic scale, as expressed in Table 2.
(d) Cognitive dimension (PC). This is estimated through five tests: verbal reasoning (VR), numerical reasoning (NR), abstract reasoning (ABR), memory (MEM), and spatial awareness (SA). Therefore,
As shown in Table 3, the values of the variables involved in the cognitive dimension are discrete quantities from the set {0.1, 0.5, 1}, so that the closer a student is to 0, the greater their risk and the greater the need for action.

Table 3.
Range, ideal, and weighting of each dimension.
(e) Health dimension (PH). This is made up of five variables: anxiety (ANX), depression (DEP), emotional adjustment (EMA), alcohol dependence (ALD), and psychoactive substance abuse (PSA), which are measured using qualitative variables (Table 2):
An in-depth study should consider circumstances that may influence a student′s academic performance. For example, students with parents who are highly educated but lack financial resources may perform better than students who are very well-off but whose parents are less educated. However, we think that the Industrial University of Santander has these issues included in some way because of the way it values the economic and social dimensions. Thus, while in the economic dimension, they try to determine the economic resources from the variables described previously, in the social dimension, by analyzing the Family APGAR [29], they want to determine the affection, adaptation, family life, and help that students receive from their family members. On the other hand, adding these circumstances imply a new institutional consensus that would involve a new scenario and a complete reformulation of the institution′s inclusion policies.
5.2. Calculation of Indicators
First, the ranges, ideals, and weighting of each criterion were agreed on with the UIS specialists [16]. In Table 3, these values are shown in their original form and also transformed into intervals, while in column 6, it can be confirmed that the cognitive and academic part accounts for 50% of the value, and the remaining dimensions account for the other 50%.
The cognitive and academic dimensions represent 50% of student assessment (see column 6 of Table 3). The SEA experts proposed a non-linear normalization of the assessments of these dimensions. In the words of the experts, “reinforcement of a student with very low scores usually results in much less improvement than a student with high scores”; hence, the convex form is preferred for the function (see Figure 3). In the cognitive case, the opposite is true; a concave function is preferred. This is due to the inclusive policies of the Industrial University of Santander for students with problems and to attempt a trade-off between the two dimensions (see Figure 3).
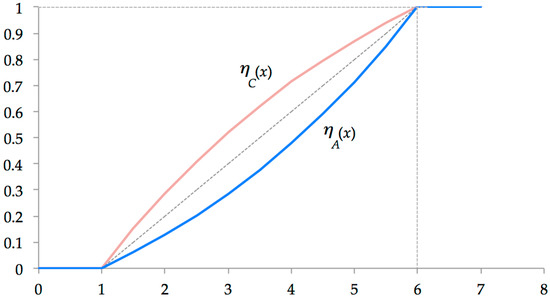
Figure 3.
Similarity functions of academic, , and cognitive dimensions.
Taking into account the ranges and ideals for these dimensions (see Table 3), according to (10), the similarity to the ideal was estimated by means of the following functions:
Using the notation of (10), the above functions were
For the other dimensions, the similarity with the ideal was estimated with piecewise linear functions (see (7)). Column 5 of Table 4 shows the similarity functions for each dimension.

Table 4.
Range, ideal, and similarity functions of each dimension.
Economic, social, cognitive, and health dimension data are expressed as real numbers (column 4 of Table 4). However, academic dimension data are presented as intervals. The following process used to value this dimension varied greatly in the period analyzed (from 2014 to 2018). The steps followed were as follows: (a) qualitative assessment, (b) numerical transformation, (c) calculation of , and (d) qualitative expression of “academic risk” using the scale {Very Low, Low, Low to Medium, Medium, Medium to High, High, Very High}. After going through this process, the SEA experts stated that it was less realistic to directly transform words into real numbers than to estimate them by means of intervals, as follows (6):
VL = [1, 2], L = [2, 2.75], LM = [2.75, 3.5], M = [3.5, 4.75], MH = [4.75, 5.5], H = [5.5, 6.25], VH = [6.25, 7].
Considering the similarity functions in Table 4 and (34), data could be normalized with (12). Table A1 shows the TOPSIS results for 10 students in the period 2018_1 (see Appendix A).
According to the criteria of the Academic Excellence Support System (SEA), the students , assessed above 85% are not at risk, and those who are under 45% are at high risk. By using this, we divided the students into risk-free , those with obvious risk , and those in an intermediate state:
The values obtained are shown in columns 2–5 of Table 5.

Table 5.
Comparison between adequacy and excellence indices.
Following the expert indications, 20% of were predicted to end up needing help, and high-risk students would usually require two or more interventions; therefore, the values were estimated to calculate the adequacy index (16). Finally, with (21), (22), (24), and (27), the excellence indicators that appear in columns 6–9 of Table 5 were obtained.
It could be observed that the adequacy indices took values between 65.83% and 72.40%, with oscillations that were not very significant (Figure 4). This means that between 27.60% and 34.17% of students could be considered to have global deficiencies when it comes to properly carrying out their studies. Although the adequacy percentage was found to be slightly lower in women than in men, between 0.5% and 4.5% (see Figure 5b), this trend was reversed for excellence. As of 2015, excellence in women was higher than in men, sometimes by up to 5% (Figure 5a).
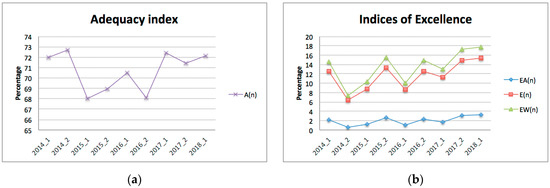
Figure 4.
Adequacy (a) and excellence (b) indices expressed in Table 5.
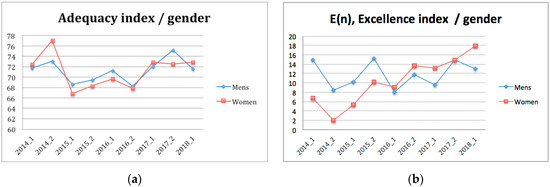
Figure 5.
Adequacy (a) and excellence (b) indices, distinguished by gender.
In Figure 4b, we represent the three quality indices that were defined: . As stated in Proposition 3, we verified that . Note that absolute excellence never exceeded 3.25%, while excellence ranged from 6.33% to 15.31%, and weak excellence sat between 7.36% and 17.86%.
When the discriminant analysis was performed for economic risk, the results were much more alarming (Figure 6). The adequacy of students without economic risk showed a 54% gap to the detriment of the students at risk (Figure 6a). Regarding excellence, the differences were evident. For example, 17.69% of the students without economic risk were excellent in 2018_1, whilst none of the at-risk students were excellent in the same period (Figure 6b).
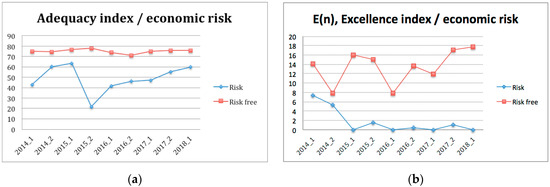
Figure 6.
Adequacy (a) and excellence (b) indices, distinguished by the level of economic risk.
6. Discussion
Our proposal contains three processes: a normalization method based on similarity with pre-established goals, an MCDM method (in which the weights of each criterion are given by the institution) to assess each alternative, and the calculation of indicators using parameters set by the managers (see Figure 1). In general, the values of the weights and the parameters are the result of a consensus that may have been difficult to achieve and, therefore, should not be modified without the approval of the institution. This is the case for the Industrial University of Santander, in which the weights shown in Table 2 for the parameters α, β of (22), and the thresholds of inadequacy and excellence were provided by SEA experts [16].
The main utility of the TOPSIS method is to order alternatives but, in this work, we not only took into account this possibility but also used the value of the relative proximity to the ideal solution, Ri, as the global assessment for each alternative. This is justified because using (16), regardless of the data set, the ideal and anti-ideal values of the classic TOPSIS method [9] correspond to (1,1, ..., 1) and (0,0, ..., 0), respectively. This fact prevents Ri values from changing when new data are incorporated, that is, the phenomenon known as the rank reversal is avoided [10].
From a mathematical point of view, for the real case study, we generated different scenarios where we were able to verify that the indicators are much more sensitive to changes in the value of α than to changes in β (22). Furthermore, the sensitivity to weights of each dimension was also not the same. From the highest to the lowest sensitivity, the order was academic, cognitive, economic, social, and health. However, as noted, the sensitivity study could not be used because the values were set by experts.
In our opinion, it is useful to compare our proposal with others that could be similar in some parts of the process, specifically, normalization and the chosen MCDM method.
6.1. Comparison with Other Methods
Before opting for our proposal of normalization (12) and the TOPSIS method, other existing alternatives were analyzed. The only conditions that could not be modified were the values established by the experts of the Industrial University of Santander by consensus. These values were the weights and thresholds of inadequacy and excellence. Furthermore, the values obtained with the indicators had to be consistent with the institution′s academic historical results. Thus, we assume that more than 50% of students are adequate to carry out their studies, and we suppose that less than 20% is excellent. With these conditions, we tested other normalizations and another MCDM method.
Firstly, we compared the results obtained with TOPSIS with the proposed normalization given in (12) and the direct calibration used in the fsqca method [30]. In the calibration, both the numerical variables and the non-verbal categories are assigned a degree of belonging, fixed around three theoretical anchors established between the value of total membership, 1, the cross-over point, 0.5, and the value of total exclusion, 0. In this work, the thresholds and the border point were set based on the ranges and transformed ideals of each dimension (see Table 3). The calibrated values were obtained using the function calibrate in the R package QCA [31].
We compared the TOPSIS results with the results of VIKOR [32], another MCDM method that also allows n alternatives valued with m criteria to be ordered. The VIKOR and TOPSIS methods are based on an aggregation function that represents the proximity to some reference points [33], which, in our case, are (1,1, ..., 1) and (0,0, ..., 0). For the VIKOR method, we used three different normalizations: linear (proposed in the classic VIKOR method [32]), the normalization given in (12), and the calibration obtained with R package QCA. The calculations were performed using the VIKOR function in the R package MCDM v 1.2. [34].
In Table 6, we show the values of n1, n2, and n3 obtained with the different methods and in different periods.

Table 6.
Values of n1, n2, and n3 in the cases analyzed.
Using the values in Table 6, the proposed indicator values are shown in Table 7 and Table 8. Values of adequacy indices below 50% and values of excellence indices above 20% are highlighted with boxes.

Table 7.
Values of indicators obtained with TOPSIS method.

Table 8.
Values of indicators obtained with VIKOR method.
According to the results shown in Table 6, Table 7 and Table 8, there are apparently no significant differences between the analyzed scenarios. However, after considering the historical results of the UIS, the experts of the institution decided to set a lower bound for the percentage of adequacy (50%) and an upper bound for the percentage of excellence (20%). Of all the possibilities, the only one that met such required bounds was the TOPSIS method with the normalization proposed in (12). Note that this option is the only one having no values out of the bounds (i.e., without any highlighting boxes in Table 7 and Table 8). This fact, together with the simplicity of the TOPSIS calculation and the opinions of the experts of the SEA [16], led to the construction of the indicators used in this work.
6.2. Strengths and Weaknesses of Our Proposal
When quality indicators are proposed to analyze an institution, the intention is that actions that allow the optimization of resources of all kinds can be planned. In general, the indicators obtained through the presented method meet this intention. In fact, the proposed indicators and the way to obtain them have been very useful for the managers of the Industrial University of Santander. However, our proposal is not without limitations; therefore, below, we summarize the strengths and weaknesses of the method.
The strengths of the method are as follows:
- (1)
- The opinions of the experts, who have been working on the question for years, are taken into account in all parts of the process: the choice of the ideal situation for each dimension, the nature of the data (numbers, intervals or linguistic expressions), the weight given to each dimension, the thresholds S0 and S1 that determine the inadequacy and excellence, and the parameters that appear in the indicators.
- (2)
- All steps of the method can be calculated with basic tools that any participant in the process can see on their own computer. Specifically, all calculations were performed with Microsoft Excel (see Appendix B).
- (3)
- The indicators are easily interpretable and allow comparison with other achievement indicators of the institution. For example, in the case of the Industrial University of Santander, the values of the proposed indicators are very consistent with the results obtained by its students.
As for the weaknesses, we have the following:
- (1)
- As can be seen in Section 6.1, the proposed method clearly depends on the normalization used and, therefore, on the choice of ideals for each dimension. This makes the consensus among experts decisive in the process.
- (2)
- The weights that have been set for each dimension to determine the solution to the TOPSIS method and; therefore, the values of the indicators. That these weights are accepted by the institution is a key element in the process.
- (3)
- To determine the evolution of the institution, the data handled in each period have not always followed the same criteria, scales, etc. In addition, some data collected over the years cannot be used, for example, because data protection laws prohibit it.
To avoid, to a large extent, the limitations of the method, we are working on making both the weights and the values of the different parameters flexible through intervals. This will greatly facilitate consensus among experts, but we must be able to avoid an excessive increase in computational complexity so that all participants can follow the process.
7. Conclusions
Measuring the quality of institutions, or some of their services, constitutes a challenge for managers, since it requires them to design strategic actions and increase their competitive advantage. To this end, the use of the indicators built using MCDM methods has become a very useful tool in the decision-making process. On the one hand, they allow the selection of the best alternatives, and on the other, they allow the synthetization of information in order to draw conclusions quickly. These were the objectives of this approach.
The first obstacle is the homogenization and normalization of data of very different natures, such as real numbers, intervals, or linguistic variables, which assign a value to very different characteristics and whose aggregation cannot be performed directly. This study proposed a method of standardization based on similarity to the ideal objectives set by the institution for each criterion.
The manner of treating quality has been gradual. It started with the construction of a synthetic indicator to measure the adequacy of each alternative and, subsequently, three indicators of excellence were defined. They report the quality in different contexts and with varying degrees of demand so that the institution can design strategic actions. Meanwhile, the methodology employed provides a classification of the alternatives into groups, depending on the adequacy for a specific task.
This proposal was applied to a real decision-making case at the Industrial University of Santander. One of the objectives of this university is to provide support to students who show deficiencies in the global value of the five dimensions assessed by the institution.
Given that the resources, both economic and human, of universities, in general, do not allow students to be offered all the necessary support, actions should be established in order to:
- Estimate the percentages of students who will not have problems carrying out their studies successfully and those who will need some support.
- Understand each student’s personal situation in order to try to guarantee support for those who need it most.
Using the UIS data, we demonstrated that gender differences (in terms of excellence) are not very significant, although, from 2016, women have slightly exceeded men. However, the differences when taking account of the economic level are very important. The intention of applying this methodology is that these actions can be planned and generalized in order to achieve optimization of resources of all kinds so that inequalities can be reduced and excellence objectives can be established in both the medium and long term.
Author Contributions
Investigation, V.L., S.E.P.-R. and O.B.-B. All authors contributed equally to this research paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Spanish Ministerio de Ciencia, Innovación y Universidades, project numbers: RTI2018-093541-B-I00, RTI2018-096065-B-I00.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we show the TOPSIS steps followed in Section 3 with the scores obtained by 10 students out of the 1,047 who participated in the study in the 2018_1 period. These students were chosen at random, with the only requirement being that we included at least one student from each group (see (19)). The assessments of the Economic (E), Social (S), Health (H), and Cognitive (C) dimensions were transformed into real numbers, and the Academic (A) dimension was transformed into intervals, taking (B) into account. Normalizations were calculated with (12) for the similarity functions expressed in Table 4.

Table A1.
Steps of the Technique for Order of Preference by Similarity (TOPSIS) method.
Table A1.
Steps of the Technique for Order of Preference by Similarity (TOPSIS) method.
| 2018_1 | Original Numerical Data (Step 1) | Normalized Data (Step 2) | Weighted Normalized Data (Step 3) | Distances (Step 4) | Score (Step 5) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Students | E | S | H | A | C | E | S | H | A | C | w1E | w1S | w1H | w1A | w1C | D+ | D- | Ri |
| #1 | 1 | 0.5 | 0.55 | [3.5, 4.75] | 6.00 | 1.000 | 0.667 | 0.846 | 0.508 | 1.000 | 0.250 | 0.083 | 0.106 | 0.152 | 0.200 | 0.379 | 0.144 | 0.725 |
| #2 | 0.77 | 1 | 0.65 | [3.5, 4.75] | 6.00 | 0.963 | 1.000 | 1.000 | 0.508 | 1.000 | 0.241 | 0.125 | 0.125 | 0.152 | 0.200 | 0.390 | 0.137 | 0.741 |
| #3 | 1 | 0.7 | 0.65 | [3.5, 4.75] | 1.00 | 1.000 | 1.000 | 1.000 | 0.508 | 0.000 | 0.250 | 0.125 | 0.125 | 0.152 | 0.000 | 0.342 | 0.242 | 0.586 |
| #4 | 1 | 1 | 0.65 | [5.5, 6.25] | 4.00 | 1.000 | 1.000 | 1.000 | 0.962 | 0.714 | 0.250 | 0.125 | 0.125 | 0.289 | 0.143 | 0.444 | 0.057 | 0.886 |
| #5 | 1 | 0.5 | 0.55 | [5.5, 6.25] | 5.00 | 1.000 | 0.667 | 0.846 | 0.962 | 0.871 | 0.250 | 0.083 | 0.106 | 0.289 | 0.174 | 0.441 | 0.053 | 0.893 |
| #6 | 0.03 | 0.5 | 0.52 | [3.5, 4.75] | 2.00 | 0.038 | 0.667 | 0.800 | 0.508 | 0.287 | 0.009 | 0.083 | 0.100 | 0.152 | 0.057 | 0.209 | 0.315 | 0.399 |
| #7 | 1 | 0.7 | 0.52 | [2.0, 2.75] | 3.00 | 1.000 | 1.000 | 0.800 | 0.185 | 0.522 | 0.250 | 0.125 | 0.100 | 0.055 | 0.104 | 0.320 | 0.253 | 0.558 |
| #8 | 0.03 | 1 | 0.65 | [3.5, 4.75] | 2.00 | 0.038 | 1.000 | 1.000 | 0.508 | 0.287 | 0.009 | 0.125 | 0.125 | 0.152 | 0.057 | 0.241 | 0.311 | 0.436 |
| #9 | 1 | 0.7 | 0.65 | [5.5, 6.25] | 3.00 | 1.000 | 1.000 | 1.000 | 0.962 | 0.522 | 0.250 | 0.125 | 0.125 | 0.289 | 0.104 | 0.434 | 0.096 | 0.819 |
| #10 | 1 | 0.7 | 0.65 | [2.0, 2.75] | 6.00 | 1.000 | 1.000 | 1.000 | 0.185 | 1.000 | 0.250 | 0.125 | 0.125 | 0.055 | 0.200 | 0.370 | 0.233 | 0.613 |
Appendix B
In this appendix, we show the source code used to obtain the results for the data implementation. Starting from either numerical or interval data as input data, this code delivers, as output data, the values of n1, n2, and n3.
- Sub Mathematics_Excel()
- ‘Part0. Create variable sheet
- Sheets.Add.Name = “Var”
- Range(“A1”).FormulaR1C1 = “=COUNTA(Data!C)-3”
- ‘Variable with the number of students
- Dim n As Integer
- n = Cells(1, 1)
- ‘Part1. Set the ideal and the columns
- Sheets(“Data”).Select
- Range(“B3”).FormulaR1C1 = “=MAX(R [3]C[11]:R[1048573]C[11])”
- Range(“B3:F3”).Select
- Selection.FillRight
- ‘Name of each variable
- Range(“H5”).FormulaR1C1 = “E”
- Range(“I5”).FormulaR1C1 = “S”
- Range(“J5”).FormulaR1C1 = “H”
- Range(“K5”).FormulaR1C1 = “A”
- Range(“L5”).FormulaR1C1 = “C”
- Range(“M5”).FormulaR1C1 = “wE”
- Range(“N5”).FormulaR1C1 = “wS”
- Range(“O5”).FormulaR1C1 = “wH”
- Range(“P5”).FormulaR1C1 = “wA”
- Range(“Q5”).FormulaR1C1 = “wC”
- Range(“R5”).FormulaR1C1 = “d-”
- Range(“S5”).FormulaR1C1 = “d+”
- Range(“T5”).FormulaR1C1 = “R”
- Range(“H1”).FormulaR1C1 = “N1”
- Range(“I1”).FormulaR1C1 = “N2”
- Range(“J1”).FormulaR1C1 = “N3”
- Range(“K1”).FormulaR1C1 = “N”
- ‘Part 2. Calculating
- Range(“H6”).FormulaR1C1 = “=+IF(RC[-6]<0.8, RC[-6]/0.8, 1)”
- Range(“I6”).FormulaR1C1 = “=+IF(RC[-6]<0.7,(RC[-6]-0.1)/0.6,1)”
- Range(“J6”).FormulaR1C1 = “=+IF(RC[-6]<0.65,RC[-6]/0.65,1)”
- Range(“K6”).FormulaR1C1 = _”=1/(RC[-5]-RC[-6])*(1/(1-EXP(1))*(RC[-5]-RC[-6]+5*EXP((RC[-6]-1)/5)-5*EXP((RC[-5]-1)/5)))+MAX(0,RC[-5]-6/(RC[-5]-RC[-6]))”
- Range(“L6”).FormulaR1C1 = “=+IF(RC[-5]<6, (1-EXP((1-RC[-5])/5))/(1-EXP(-1)), 1)”
- Range(“M6”).FormulaR1C1 = “=RC[-5]*R2C[-11]”
- Range(“N6”).FormulaR1C1 = “=RC[-5]*R2C[-11]”
- Range(“O6”).FormulaR1C1 = “=RC[-5]*R2C[-11]”
- Range(“P6”).FormulaR1C1 = “=RC[-5]*R2C[-11]”
- Range(“Q6”).FormulaR1C1 = “=RC[-5]*R2C[-11]”
- Range(“R6”).FormulaR1C1 = “=SUMPRODUCT(RC[-5]:RC[-1],RC[-5]:RC[-1])^0.5”
- Range(“S6”).FormulaR1C1 = “=((RC[-6]-R3C2)^2+(RC[-5]-R3C3)^2+(RC[-4]-R3C4)^2+(RC[-3]-R3C5)^2+(RC[-2]-R3C6)^2)^0.5”
- Range(“T6”).FormulaR1C1 = “=RC[-2]/(RC[-2]+RC[-1])”
- Range(“H2”).FormulaR1C1 = “=COUNTIF(R[4]C[12]:R[13]C[12],”“>0,85”“)”
- Range(“I2”).FormulaR1C1 = “=COUNTIF(R[4]C[11]:R[13]C[11],”“<0,45”“)”
- Range(“J2”).FormulaR1C1 = “=RC[1]-RC[-2]-RC[-1]”
- Range(“K2”).FormulaR1C1 = “=COUNTA(C[-10])-3”
- ‘Set the formula per each column
- Range(Cells(6, 8), Cells(6, 20)).Select
- Selection.AutoFill Destination:=Range(Cells(6, 8), Cells(6 + n − 1, 20))
- Selection.NumberFormat = “0.000”
End Sub
References
- Roy, B. Multicriteria Methodology for Decision Aiding; Springer: Boston, MA, USA, 1996. [Google Scholar]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision Making Methods and Applications; Springer: Berlin, Germany, 1992. [Google Scholar]
- Chou, T.-Y.; Chen, Y.-T. Applying Fuzzy AHP and TOPSIS Method to Identify Key Organizational Capabilities. Mathematics 2020, 8, 836. [Google Scholar] [CrossRef]
- Kabak, M.; Burmaoğlu, S.; Kazançoğlu, Y. A fuzzy hybrid MCDM approach for professional selection. Expert Syst. Appl. 2012, 39, 3516–3525. [Google Scholar] [CrossRef]
- Kabak, M.; Dağdeviren, M. A Hybrid MCDM Approach to Assess the Sustainability of students’ Preferences for University Selection. Technol. Econ. Dev. Econ. 2014, 20, 391–418. [Google Scholar] [CrossRef]
- Pekkaya, M. Career preference of university students: An application of MCDM methods. Procedia Econ. Financ. 2015, 23, 249–255. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R. Fuzzy Reasoning in Decision Making and Optimization; Physica-Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Cables, E.; Lamata, M.T.; Verdegay, J.L. RIM-reference ideal method in multicriteria decision making. Inf. Sci. 2016, 337, 1–10. [Google Scholar] [CrossRef]
- Acuña-Soto, C.M.; Liern, V.; Pérez-Gladish, B. Multiple Criteria performance evaluation of YouTube mathematical educational videos by IS-TOPSIS. Oper. Res. 2018, 1–23. [Google Scholar] [CrossRef]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Liern, V.; Perez-Gladish, B. Ranking corporate sustainability: A flexible multidimensional approach based on linguistic variables. Int. Trans. Oper. Res. 2018, 25, 1081–1100. [Google Scholar] [CrossRef]
- González del Pozo, R.; Dias, L.C.; García-Lapresta, J.L. Using different qualitative scales in a Multi-Criteria Decision-Making procedure. Mathematics 2020, 8, 458. [Google Scholar] [CrossRef]
- Parada, S.E.; Fiallo, J.E.; Blasco-Blasco, O. Construcción de indicadores sintéticos basados en juicio experto: Aplicación a una medida integral de la excelencia académica. Rect@ 2015, 16, 51–67. [Google Scholar]
- SEA-UIS. Sistema de Excelencia Académica. Universidad Industrial Santander. Available online: https://www.uis.edu.co/webUIS/es/estudiantes/excelenciaAcademica/index.html (accessed on 7 November 2019).
- Parada, S.E.; Blasco-Blasco, O.; Liern, V. Adequacy Indicators Based on Pre-established Goals: An Implementation in a Colombian University. Soc. Indic. Res. 2019, 143, 1–24. [Google Scholar] [CrossRef]
- Jahanshahloo, G.R.; Hosseinzadeh Lotfi, F.; Izadikhah, M. An algorithmic method to extend TOPSIS for decision-making problems with interval data. Appl. Math. Comput. 2006, 175, 1375–1384. [Google Scholar] [CrossRef]
- Yager, R.R. An approach to ordinal decision making. Int. J. Approx. Reason. 1995, 12, 237–261. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Herrera, F.; Martínez, L. The 2-tuple linguistic computational model: Advantages of its linguistic description, accuracy and consistency. Int. J. Uncertain. Fuzziness Knowledge-Based Syst. 2001, 9, 33–48. [Google Scholar] [CrossRef]
- Xu, Z.S. Linguistic Decision Making: Theory and Methods; Springer: Berlin, Germany, 2012. [Google Scholar]
- Delgado, M.; Herrera, F.; Herrera-Viedma, E.; Martínez, L. Combining numerical and linguistic information in group decision making. Inf. Sci. 1998, 107, 177–194. [Google Scholar] [CrossRef]
- Zeng, W.; Guo, P. Normalized distance, similarity measure, inclusion measure and entropy of interval-valued fuzzy sets and their relationship. Inf. Sci. 2008, 178, 1334–1342. [Google Scholar] [CrossRef]
- Acuña-Soto, C.M.; Liern, V.; Pérez-Gladish, B. Normalization in TOPSIS based approaches with non-compensatory criteria: Application to the ranking of mathematical videos. Ann. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Courant, R.; John, F. Introdution to Calculus and Analysis. Volume I; Springer: New York, NY, USA, 1989. [Google Scholar]
- Ouenniche, J.; Pérez-Gladish, B.; Bouslah, K. An out-of-sample framework for TOPSIS-based classifiers with application in bankruptcy prediction. Technol. Forecast. Soc. Chang. 2018, 131, 111–116. [Google Scholar] [CrossRef]
- Smilkstein, G. The family APGAR: A proposal for family function test and its use by physicians. J. Fam. Pract. 1978, 6, 1231–1239. [Google Scholar] [PubMed]
- Ragin, C.C. Redesigning Social Inquiry: Fuzzy Sets and Beyond; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Dusa, A. QCA with R. A Comprehensive Resource; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems; Faculty of Civil Engineering: Belgrade, Serbia, 1998; Volume 2, pp. 5–21. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Ceballos, B. Multi-Criteria Decision Making Methods for Crisp Data. 2016. Available online: https://www.rdocumentation.org/packages/MCDM (accessed on 24 April 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).