On a Relation between the Perfect Roman Domination and Perfect Domination Numbers of a Tree

Abstract

A dominating set in a graph G is a set of vertices $S\subseteq V(G)$ such that any vertex of $V-S$ is adjacent to at least one vertex of $S.$ A dominating set S of G is said to be a perfect dominating set if each vertex in $V-S$ is adjacent to exactly one vertex in S. The minimum cardinality of a perfect dominating set is the perfect domination number ${\gamma }^p(G).$ A function $f:V(G)\to \{0,1,2\}$ is a perfect Roman dominating function (PRDF) on G if every vertex $u\in V$ for which $f(u)=0$ is adjacent to exactly one vertex v for which $f(v)=2$. The weight of a PRDF is the sum of its function values over all vertices, and the minimum weight of a PRDF of G is the perfect Roman domination number ${\gamma }_R^p(G).$ In this paper, we prove that for any nontrivial tree T, ${\gamma }_R^p(T)\ge {\gamma }^p(T)+1$ and we characterize all trees attaining this bound.

1. Introduction

In this paper, only simple and undirected graph without isolated vertices will be considered. The set of vertices of the graph G is denoted by $V=V(G)$ and the edge set is $E=E(G)$. The order of a graph G is the number of vertices of the graph G and it is denoted by $n=n(G)$. The size of G is the cardinality of the edge set and it is denoted by $m=m(G).$ For a vertex $v\in V$, the open neighbourhood $N(v)$ is the set $\{u\in V(\Gamma ):uv\in E(G)\}$, the closed neighbourhood of v is the set $N\left[v\right]=N(v)\cup \left\{v\right\}$, and the degree of v is ${deg}_G(u)=\left|N(v)\right|$. Any vertex of degree one is called a leaf, a support vertex is a vertex adjacent to a leaf, a strong support vertex is a support vertex adjacent to at least two leaves and an end support vertex is a support vertex such that all its neighbors, except possibly one, are leaves. For a graph G, let $L(G)=\{v\in V(G)\mid {deg}_G(v)=1\}$ and $L_v=N(v)\cap L(G)$. The distance $d_G(u,v)$ between two vertices u and v in a connected graph G is the length of a shortest $u-v$ path in $G.$ The diameter of G, denoted by $\mathrm{diam}(G)$, is the maximum value among distances between all pair of vertices of G. For a vertex v in a rooted tree T, let $C(v)$ and $D(v)$ denote the set of children and descendants of v, respectively and let $D\left[v\right]=D(v)\cup \left\{v\right\}$. Moreover, the depth of v, $\mathrm{depth}(v)$, is the largest distance from v to a vertex in $D(v)$. The maximal subtree rooted at v, denoted by $T_v$, consists of v and all its descendants. We write $P_n$ for the path of order n. A tree T is a double star if it contains exactly two vertices that are not leaves. A double star with, respectively p and q leaves attached at each support vertex is denoted $D{S}_{p,q}.$ For a real-valued function $f:V⟶\mathbb{R},$ the weight of f is $w(f)={\sum }_{v\in V}f(v)$, and for $S\subseteq V$ we define $f(S)={\sum }_{v\in S}f(v)$. So $w(f)=f(V)$.

A dominating set (DS) in a graph G is a set of vertices $S\subseteq V(G)$ such that any vertex of $V-S$ is adjacent to at least one vertex of $S.$ A dominating set S of G is said to be a perfect dominating set (PDS) if each vertex in $V-S$ is adjacent to exactly one vertex in S. The minimum cardinality of a (perfect) dominating set of a graph G is the (perfect) domination number$\gamma (G)$ (${\gamma }^p(G)$). Perfect domination was introduced by Livingston and Stout in [1] and has been studied by several authors [2,3,4,5,6].

A function $f:V(\Gamma )\to \{0,1,2\}$ is a Roman dominating function (RDF) on G if every vertex $u\in V$ for which $f(u)=0$ is adjacent to at least one vertex v for which $f(v)=2$. A perfect Roman dominating function (PRDF) on a graph G is an RDF f such that every vertex assigned a 0 is adjacent to exactly one vertex assigned a 2 under $f.$ The minimum weight of a (perfect) RDF on a graph G is the (perfect) Roman domination number${\gamma }_R(G)$ (${\gamma }_R^p(G)$). A (perfect) RDF on G with weight ${\gamma }_R(G)$ (${\gamma }_R^p(G)$) is called a ${\gamma }_R(G)$-function (${\gamma }_R^p(G)$-function). An RDF f on a graph $G=(V,E)$ can be represented by the ordered partition $(V_0,V_1,V_2)$ of V, where $V_i=\{v\in V|f(v)=i\}$ for $i=0,1,2$. The concept of Roman domination was introduced by Cockayne et al. in [7] and was inspired by the manuscript of the authors of [8], and Stewart [9] about the defensive strategy of the Roman Empire decreed by Constantine I The Great, while perfect Roman domination was introduced by Henning, Klostermeyer and MacGillivray in [10] and has been studied in [11,12,13]. For more on Roman domination, we refer the reader to the book chapters [14,15] and surveys [16,17,18].

It was shown in [10] that for any tree G of order $n\ge 3$, ${\gamma }_R^p(G)\le \frac{4n}{5}$. Moreover, the authors have characterized all trees attaining this upper bound. Note that the previous upper bound have been improved by Henning and Klostermeyer [13] for cubic graphs of order n by showing that ${\gamma }_R^p(G)\le \frac{3n}{4}$.

It is worth mentioning that if S is a minimum (perfect) dominating set of a graph G, then clearly $(V-S,\varnothing ,S)$ is a (perfect) RDF and thus

$${\gamma }_R(G)\le 2\gamma (G)\mathrm{and}{\gamma }_R^p(G)\le 2{\gamma }^p(G).$$

(1)

On the other hand, if $f=(V_0,V_1,V_2)$ is a ${\gamma }_R(G)$-function, then $V_1\cup V_2$ is a dominating set of G yielding

$$\gamma (G)\le {\gamma }_R(G).$$

(2)

It is natural to ask whether the inequality (2) remains valid between ${\gamma }^P(G)$ and ${\gamma }_R^p(G)$ for any graph $G.$ The answer is negative as it can be seen by considering the graph H obtained from a double star $D{S}_{p,p},(p\ge 3)$ with central vertices $u,v$ by subdividing the edge $uv$ with vertex w, and adding $2k$$(k\ge 3)$ new vertices, where k vertices are attached to both u and w and the remaining k vertices are attached to both v and w (see Figure 1). Clearly, ${\gamma }^p(H)=2k+3$ while ${\gamma }_R^p(H)=5$ and so the difference ${\gamma }^p(H)-{\gamma }_R^p(H)$ can be even very large.

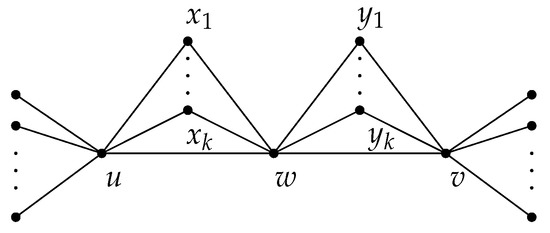
Figure 1. The graph H.

Motivated by the above example, we shall show in this paper that ${\gamma }_R^p(T)\ge {\gamma }^p(T)+1$ for every nontrivial tree T, and we characterize all trees attaining this bound.

2. Preliminaries

We start by providing some useful definitions and observations throughout the paper.

Definition 1.

For any graph G, let

$$\begin{array}{ccc}{W}_G^{R,1}\hfill & =\hfill & \{u\in V\mid thereexistsa{\gamma }_R^p(G)-functionfsuchthatf(u)=2\},\hfill \\ W_G^{R,\le 1}\hfill & =\hfill & \{u\in V\mid f(u)\le 1forsome{\gamma }_R^p(G)-functionf\},\hfill \\ W_G^{R,\ge 1}\hfill & =\hfill & \{u\in V\mid foreachv\in N_G(u),f(v)\le 1forevery{\gamma }_R^p(G)-functionf\},\hfill \\ W_G^{P,A}\hfill & =\hfill & \{u\in V\mid u\mathrm{belongs}\mathrm{to}\mathrm{every}{\gamma }^p(G)-\mathrm{set}\}.\hfill \end{array}$$

Definition 2.

Let u be a vertex of a graph G. A set S is said to be an almost perfect dominating set (almost PDS) with respect to $u,$ (i) if each vertex $x\in V\backslash (S\cup \{u\})$ has exactly one neighbor in $S,$ and (ii) if $u\in V\backslash S$, then u has at most one neighbor in S. Let

$${\gamma }^p(G;u)=min\left\{\right|S|:S\mathrm{is}\mathrm{an}\mathrm{almost}\mathrm{PDS}\mathrm{with}\mathrm{respect}\mathrm{to}u\}.$$

Trivially, every PDS of G is an almost PDS with respect to any vertex of G and thus ${\gamma }^p(G;u)$ is well defined. Hence ${\gamma }^p(G;u)\le {\gamma }^p(G)$ for each vertex $u\in V$. Let

$$\begin{array}{ccc}{W}_G^{APD}\hfill & =& \{u\in V\mid {\gamma }^p(G;u)={\gamma }^p(G)\}.\hfill \\ \hfill & \end{array}$$

The proof of the following two results are given in [12].

Observation 1.

Let G be a graph.

1. 

Any strong support vertex belongs to $W_G^{P,A}$.

2. 

Any support vertex adjacent to a strong support vertex, belongs to $W_G^{P,A}$.

3. 

For any leaf u of G, there is a ${\gamma }_R^p(G)$-function f such that $f(u)\le 1$.

Proposition 1.

Let G be a graph. G has a ${\gamma }_R^p(G)$-function that assigns 2 to every end strong support vertex. Thus every end strong support vertex of a graph G belongs to $W_G^{R,1}$.

The next result is a consequence of Observation 1 and Proposition 1.

Corollary 1.

Let u be an end strong support vertex of a graph H. If G is the graph obtained from H by adding a vertex x and an edge$ux$, then${\gamma }^p(G)={\gamma }^p(H)$and${\gamma }_R^p(G)={\gamma }_R^p(H)$.

Proposition 2.

Let H be a graph and $u\in V(H)$. If G is a graph obtained from H by adding a path $P_2:x_1{x}_2$ attached at u by an edge $u{x}_1,$ then:

1. 

${\gamma }^p(G)\le {\gamma }^p(H)+1$ and ${\gamma }_R^p(G)\ge {\gamma }_R^p(H)+1.$

2. 

If $u\in W_H^{R,1}\cup W_H^{R,\ge 1}$, then ${\gamma }_R^p(G)={\gamma }_R^p(H)+1.$

3. 

If $u\in W_H^{APD}$, then ${\gamma }^p(G)={\gamma }^p(H)+1.$

Proof. 

• For a ${\gamma }^p(H)$-set $S,$ let $S^{\prime }=S\cup \left\{x_1\right\}$ if $u\in S$, and $S^{\prime }=S\cup \left\{x_2\right\}$ if $u\notin S$. Clearly, $S^{\prime }$ is a PDS of G and thus ${\gamma }^p(G)\le {\gamma }^p(H)+1$.
  Now let f be a ${\gamma }_R^p(G)$-function. Obviously, $f(x_1)+f(x_2)\ge 1$. If $f(u)\ge 1$, then the function f restricted to H is a PRDF on H yielding ${\gamma }_R^p(G)\ge {\gamma }_R^p(H)+1$. Thus assume that $f(u)=0$. Then $f(x_1)+f(x_2)=2$ and the function $g:V(H)\to \{0,1,2\}$ defined by $g(u)=1$ and $g(x)=f(x)$ for $x\in V(H)\backslash \left\{u\right\}$ is a PRDF on H of weight ${\gamma }_R^p(G)-1.$ Hence in any case, ${\gamma }_R^p(G)\ge {\gamma }_R^p(H)+1$.
• Assume first that $u\in W_H^{R,1}$ and let f be a ${\gamma }_R^p(H)$-function with $f(u)=2$. Then f can be extended to a PRDF of G by assigning a 1 to $x_2$ and a 0 to $x_1$ and thus ${\gamma }_R^p(G)\le {\gamma }_R^p(H)+1$. The equality follows by item $1.$ Assume now that $u\in W_{G^{\prime }}^{R,\ge 1}$ and let f be a ${\gamma }_R^p(H)$-function. By the definition of $W_H^{R,\ge 1}$, we must have $f(u)\ge 1$ to Roman dominate u. Now, if $f(u)=2$, then using the same argument as above we obtain ${\gamma }_R^p(G)={\gamma }_R^p(H)+1$. Hence assume that $f(u)=1$. Then the function $g:V(G)\to \{0,1,2\}$ defined by $g(x_1)=2$, $g(u)=g(x_2)=0$ and $g(x)=f(x)$ for all $x\in V(H)\backslash \left\{u\right\}$ is a PRDF of G of weight ${\gamma }_R^p(H)+1$. Therefore ${\gamma }_R^p(G)\le {\gamma }_R^p(H)+1$, and the equality follows by item 1.
• Let S be a ${\gamma }^p(G)$-set. Clearly, $|S\cap \{x_1,x_2\left\}\right|\ge 1$ and $S-\{x_1,x_2\}$ is an almost PDS of H with respect to u. Since $u\in W_H^{APD}$, we have $|S-\{x_1,x_2\}|\ge {\gamma }^p(G^{\prime };u)={\gamma }^p(H)$. Therefore ${\gamma }^p(G)=\left|S\right|\ge {\gamma }^p(H)+1$, and the equality follows from item 1. □

For a graph G and a vertex u of G, we denote by $G_{K_{1,3}}^u$ the graph obtained from G by adding a star $K_{1,3}$ and joining one of its leaf to u.

Proposition 3.

Let G be a graph and u a vertex of G.

1. 

${\gamma }^p(G_{K_{1,3}}^u)\le {\gamma }^p(G)+2$ and ${\gamma }_R^p(G)+2\le {\gamma }_R^p(G_{K_{1,3}}^u).$

2. 

If $u\in W_G^{P,A}\cap W_G^{APD}$, then ${\gamma }^p(G_{K_{1,3}}^u)={\gamma }^p(G)+2$.

3. 

If $u\in W_G^{R,\le 1}$, then ${\gamma }_R^p(G_{K_{1,3}}^u)={\gamma }_R^p(G)+2$.

Proof. 

Let x be the center of the star $K_{1,3}$ and $x_1$ a leaf of $K_{1,3}$ attached at u by an edge $u{x}_1.$

• For a ${\gamma }^p(G)$-set $S,$ let $S^{\prime }=S\cup \{x,x_1\}$ if $u\in S,$ and $S^{\prime }=S\cup \left\{x\right\}$ for otherwise. Clearly, $S^{\prime }$ is a PDS of $G_{K_{1,3}}^u$ and thus ${\gamma }^p(G_{K_{1,3}}^u)\le {\gamma }^p(G)+2$.
  Now, let f be a ${\gamma }_R^p(G_{K_{1,3}}^u)$-function. By Proposition 1, we may assume that $f(x)=2$. If $f(x_1)\le 1$, then the function f restricted to G is a PRDF on G of weight at most ${\gamma }_R^p(G_{K_{1,3}}^u)-2$. Thus, we assume that $f(x_1)=2$. Then the function $g:V(G)\to \{0,1,2\}$ defined by $g(u)=1$ and $g(x)=f(x)$ for all $x\in V(G)\backslash \left\{u\right\}$ is a PRDF on G of weight ${\gamma }_R^p(G_{K_{1,3}}^u)-3.$ In any case, ${\gamma }_R^p(G)\le {\gamma }_R^p(G_{K_{1,3}}^u)-2$.
• Let S be a ${\gamma }^p(G_{K_{1,3}}^u)$-set. By Observation 1-(1), we have $x\in S$. Now, if $u\in S$, then $x_1\in S$ and clearly $S-\{x,x_1\}$ is a PDS of $G,$ implying that ${\gamma }^p(G_{K_{1,3}}^u)\ge {\gamma }^p(G)+2$. Thus, assume that $u\notin S$. If $x_1\notin S$, then $S-\left\{x\right\}$ is a PDS of G that does not contain u and since $u\in W_G^{P,A}$ we deduce that $|S-\left\{x\right\}|\ge {\gamma }^p(G)+1.$ Hence ${\gamma }^p(G_{K_{1,3}}^u)\ge {\gamma }^p(G)+2$. If $x_1\in S$, then $S-\{x,x_1\}$ is an almost PDS of G and since $u\in W_G^{APD}$ we conclude that $|S-\{x,x_1\}|\ge {\gamma }^p(G).$ Hence ${\gamma }^p(G_{K_{1,3}}^u)\ge {\gamma }^p(G)+2$. Whatever the case, the equality follows from item 1.
• Assume that $u\in W_G^{R,\le 1}$ and let f be a ${\gamma }_R^p(G)$-function such that $f(u)\le 1$. Then f can be extended to a PRDF on $G_{K_{1,3}}^u$ by assigning a 2 to x and a 0 to every neighbor of x and thus ${\gamma }_R^p(G_{K_{1,3}}^u)\le {\gamma }_R^p(G)+2$. The equality follows from item 1. □

Proposition 4.

Let $G^{\prime }$ be a graph and let u be an end support vertex of $G^{\prime }$ which is adjacent to a strong support vertex v. If G is a graph obtained from $G^{\prime }$ by adding a vertex x and an edge $ux$, then ${\gamma }^p(G)={\gamma }^p(G^{\prime })$ and ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })$. Moreover, if $u\in W_{G^{\prime }}^{R,1}$, then ${\gamma }_R^p(G)={\gamma }_R^p(G^{\prime })$.

Proof. 

Let S be a ${\gamma }^p(G^{\prime })$-set. By Observation 1, $v\in S.$ Thus $u\in S$ for otherwise u would have two neighbors in $S.$ Hence S is a PDS of G and so ${\gamma }^p(G)\le {\gamma }^p(G^{\prime })$. On the other hand, by Observation 1, any ${\gamma }^p(G)$-set contains both u and $v,$ and thus remains a PDS of $G^{\prime }.$ It follows that ${\gamma }^p(G)\ge {\gamma }^p(G^{\prime })$, and the desired equality is obtained.

Since u is an end strong support vertex in $G,$$u\in W_G^{R,1}.$ By Proposition 1, there is a ${\gamma }_R^p(G)$-function f such that $f(u)=2$, and clearly f restricted to $G^{\prime }$ is a PRDF on $G^{\prime }$ yielding ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })$.

Now, assume that $u\in W_{G^{\prime }}^{R,1}$ and let g be a ${\gamma }_R^p(G^{\prime })$-function with $g(u)=2.$ Then g can be extended to a PRDF on G by assigning a 0 to $x.$ Thus ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })$, and the desired equality follows. □

Proposition 5.

Let $G^{\prime }$ be a graph and u a vertex of $G^{\prime }.$ If G is a graph obtained from $G^{\prime }$ by adding a double star $D{S}_{2,2}$ attached at u by one of its leaves, then:

1. 

${\gamma }^p(G)\le {\gamma }^p(G^{\prime })+3$ and ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+3$.

2. 

If $u\in W_{G^{\prime }}^{R,1}$, then ${\gamma }_R^p(G)={\gamma }_R^p(G^{\prime })+3$.

3. 

If $u\in W_{G^{\prime }}^{P,A}\cap W_{G^{\prime }}^{APD}$, then ${\gamma }^p(G)={\gamma }^p(G^{\prime })+3$.

Proof. 

Let $x,y$ be the non-leaf vertices of the double star $D{S}_{2,2}$, and let $L_x=\{x_1,x_2\}$ and $L_y=\{y_1,y_2\}$. We assume that $x_{1}u\in E(G).$

• For a ${\gamma }^p(G^{\prime })$-set $S,$ let $S^{\prime }=S\cup \{x,y\}$ if $u\notin S,$ and $S^{\prime }=S\cup \{x_1,x,y\}$ if $u\in S$. Clearly, $S^{\prime }$ is a PDS of G and thus ${\gamma }^p(G)\le {\gamma }^p(G^{\prime })+3$.
  Consider now a ${\gamma }_R^p(G)$-function f such that $f(y)=2$ (according to Proposition 1). Clearly, $f(x)+f(x_2)\ge 1$. If $f(x_1)\le 1$, then f restricted to $G^{\prime }$ is a PRDF on $G^{\prime }$ of weight at most ${\gamma }_R^p(G)-3$ and thus ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+3$. If $f(x_1)=2$, then $f(u)=0$ and the function $g:V(G^{\prime })\to \{0,1,2\}$ defined by $g(u)=1$ and $g(w)=f(w)$ otherwise, is a PRDF on $G^{\prime }$ of weight at most ${\gamma }_R^p(G)-4$ yielding ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+4$. In any case we have ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+3$.
• Assume that $u\in W_{G^{\prime }}^{R,1}$ and let f be a ${\gamma }_R^p(G^{\prime })$-function such that $f(u)=2$. Then f can be extended to a PRDF on G by assigning a 2 to y, a 1 to $x_2$ and a 0 to $x,x_1,y_1,y_2.$ Hence ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })+3$, and the desired equality follows from item 1.
• Assume that $u\in W_{G^{\prime }}^{P,A}\cap W_{G^{\prime }}^{APD}$, and let S be a ${\gamma }^p(G)$-set. By items 1 and 2 of Observation 1, $x,y\in S$. If $u\in S$, then $x_1\in S$ and thus $S-\{x,y,x_1\}$ is a PDS of $G^{\prime },$ implying that ${\gamma }^p(G)\ge {\gamma }^p(G^{\prime })+3$. Hence, assume that $u\notin S$. If $x_1\notin S$, then $S-\{x,y\}$ is a PDS of $G^{\prime }$ that does not contain u. But since $u\in W_{G^{\prime }}^3$ we deduce that $|S-\{x,y\}|\ge {\gamma }^p(G^{\prime })+1$ which yields ${\gamma }^p(G)\ge {\gamma }^p(G^{\prime })+3$. Thus suppose that $x_1\in S$. Then $S-\{x,y,x_1\}$ is an almost PDS of $G^{\prime },$ and since $u\in W_{G^{\prime }}^{APD}$ we conclude that $|S-\{x,y,x_1\}|\ge {\gamma }^p(G^{\prime };u)={\gamma }^p(G^{\prime })$. Hence ${\gamma }^p(G)\ge {\gamma }^p(G^{\prime })+3$, and the desired equality is obtained by item 1. □

Proposition 6.

Let $G^{\prime }$ be a graph and let u be an end strong support vertex of degree 3 whose non-leaf neighbor is a support vertex, say $v,$ of degree 3, where $\left|L_v\right|=1.$ Let G be a graph obtained from $G^{\prime }$ by adding four vertices, where two are attached to a leaf of u and the other two are attached to the leaf of v. Then ${\gamma }^p(G)={\gamma }^p(G^{\prime })+2$ and ${\gamma }_R^p(G)={\gamma }_R^p(G^{\prime })+2$.

Proof. 

Let $L_u=\{x,x^{\prime }\}$ and $L_v=\left\{y\right\}.$ Let $x_1,x_2,y_1$ and $y_2$ be the four added vertices, where $x{x}_1,x{x}_2,y{y}_1,y{y}_2\in E(G).$ By items 1 and 2 of Observation 1, any ${\gamma }^p(G^{\prime })$-set contains u and $v.$ Clearly such a set can be extended to a PDS of G by adding $x,y$ which yields ${\gamma }^p(G)\le {\gamma }^p(G^{\prime })+2$. On the other hand, let D be a ${\gamma }^p(G)$-set. Then by items 1 and 2 of Observation 1, we have $x,u,y,v\in D$, and thus $D\backslash \{x,y\}$ is a PDS of $G^{\prime },$ implying that ${\gamma }^p(G)\ge {\gamma }^p(G^{\prime })+2$. Therefore ${\gamma }^p(G)={\gamma }^p(G^{\prime })+2$.

Next we shall show that ${\gamma }_R^p(G)={\gamma }_R^p(G^{\prime })+2$. First we show that ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })+2$. Since u is an end strong support vertex of $G^{\prime },$ let f be a ${\gamma }_R^p(G^{\prime })$-function with $f(u)=2$ (by Proposition 1) such that $f(v)$ is as small as possible. If $f(v)\le 1$, then $f(y)=1,$ and thus the function $g:V(G)\to \{0,1,2\}$ defined by $g(x)=g(y)=2$, $g(x^{\prime })=1$, $g(u)=g(x_1)=g(x_2)=g(y_1)=g(y_2)=0$ and $g(w)=f(w)$ otherwise, is a PRDF on $G.$ Hence ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })+2$. If $f(v)=2$, then by our choice of $f,$ we have $f(z)=0$ for any $z\in N(v)\backslash \left\{u\right\}$ and thus the function $h:V(G)\to \{0,1,2\}$ defined by $h(z)=1$ for $z\in N(v)\setminus \{u,y\}$ and $h(x^{\prime })=1$, $h(x)=h(y)=2$, $h(u)=h(v)=h(x_1)=h(x_2)=h(y_1)=h(y_2)=0$ and $h(w)=f(w)$ otherwise, is a PRDF on G yielding ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })+2$. Hence ${\gamma }_R^p(G)\le {\gamma }_R^p(G^{\prime })+2$. Now we show that ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+2$. By Proposition, let g be a ${\gamma }_R^p(G)$-function such that $g(x)=g(y)=2.$ It can be seen that $g(x^{\prime })=1$. If $f(v)=0$, then the function $h:V(G^{\prime })\to \{0,1,2\}$ defined by $h(u)=2$, $h(y)=1$, $h(x)=h(x^{\prime })=0$ and $h(w)=g(w)$ otherwise, is a PRDF on $G^{\prime }$ of weight at most ${\gamma }_R^p(G)-2$. If $f(v)\ge 1$, then the function $h:V(G^{\prime })\to \{0,1,2\}$ defined by $h(u)=h(v)=2$, $h(x)=h(x^{\prime })=h(y)=0$ and $h(w)=g(w)$ otherwise, is a PRDF on $G^{\prime }$ of weight at most ${\gamma }_R^p(G)-2.$ In any case, ${\gamma }_R^p(G)\ge {\gamma }_R^p(G^{\prime })+2$, and the equality follows. □

3. The Family $\mathcal{T}$

In this section, we define the family $\mathcal{T}$ of unlabeled trees T that can be obtained from a sequence $T_1,T_2,\dots ,$$T_k$$(k\ge 1)$ of trees such that $T_1\in \{P_2,P_3\}$ and $T=T_k$. If $k\ge 2$, then $T_{i+1}$ is obtained recursively from $T_i$ by one of the following operations.

Operation ${\mathcal{O}}_1$: If $u\in V(T_i)$ is an end strong support vertex, then ${\mathcal{O}}_1$ adds a vertex x attached at u by an edge $ux$ to obtain $T_{i+1}$.

Operation ${\mathcal{O}}_2$: If $u\in (W_{T_i}^{R,1}\cup W_{T_i}^{R,\ge 1})\cap W_{T_i}^{APD}$, then ${\mathcal{O}}_2$ adds a path $P_2=x_1{x}_2$ attached at u by an edge $u{x}_1$ to obtain $T_{i+1}$.

Operation ${\mathcal{O}}_3$: If $u\in W_{T_i}^{R,\le 1}\cap W_{T_i}^{P,A}\cap W_{T_i}^{APD}$, then ${\mathcal{O}}_3$ adds a star $K_{1,3}$ centered at x by attaching one of its leaves, say $x_1$, to u to obtain $T_{i+1}$.

Operation ${\mathcal{O}}_4$: If $u\in W_{T_i}^{R,1}$ is an end support vertex which is adjacent to a strong support vertex, then ${\mathcal{O}}_4$ adds a vertex x attached at u by an edge $ux$ to obtain $T_{i+1}$.

Operation ${\mathcal{O}}_5$: If $u\in W_{T_i}^{R,1}\cap W_{T_i}^{P,A}\cap W_{T_i}^{APD}$, then ${\mathcal{O}}_5$ adds a double star $D{S}_{2,2}$ by attaching one of its leaves, say $x_1$, to u to obtain $T_{i+1}$.

Operation ${\mathcal{O}}_6$: If $u\in V(T_i)$ is an end strong support vertex of degree 3 with $x\in L_u$ such that u is adjacent to a support vertex v of degree 3 with $L_v=\left\{y\right\},$ then ${\mathcal{O}}_6$ adds four vertices $x_1,x_2,y_1,y_2$ attached at x and y by edges $x{x}_1,x{x}_2,y{y}_1,y{y}_2$ to obtain $T_{i+1}$.

Lemma 1.

If $T_i$ is a tree with ${\gamma }_R^p(T_i)={\gamma }^p(T_i)+1$ and $T_{i+1}$ is a tree obtained from $T_i$ by one of the Operations ${\mathcal{O}}_1,\dots ,{\mathcal{O}}_6$, then ${\gamma }_R^p(T_{i+1})={\gamma }^p(T_{i+1})+1$.

Proof. 

If $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_1$, then by Corollary 1 and the assumption ${\gamma }_R^p(T_i)={\gamma }^p(T_i)+1$, we have ${\gamma }_R^p(T_{i+1})={\gamma }_R^p(T_i)={\gamma }^p(T_i)+1={\gamma }^p(T_{i+1})+1.$ If $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_2$, then as above the result follows from Proposition 2 (items 2, 3 and 4). If $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_3$, then the result follows from Proposition 3 (items 2 and 3). If $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_4$, then the result follows from Proposition 4. If $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_5$, then the result follows from Proposition 5. Finally, if $T_{i+1}$ is obtained from $T_i$ by Operation ${\mathcal{O}}_6$, then the result follows from Proposition 6. □

In the rest of the paper, we shall prove our main result:

Theorem 1.

For any tree T of order $n\ge 2$,

$${\gamma }_R^p(T)\ge {\gamma }^p(T)+1,$$

with equality if and only if $T\in \mathcal{T}$.

4. Proof of Theorem 1

Lemma 2.

If $T\in \mathcal{T}$, then ${\gamma }_R^p(T)={\gamma }^p(T)+1$.

Proof. 

Let T be a tree of $\mathcal{T}$. Then there exists a sequence of trees $T_1,T_2,\dots ,T_k$$(k\ge 1)$ such that $T_1\in \{P_2,P_3\}$, and if $k\ge 2$, then $T_{i+1}$ can be obtained from $T_i$ by one of the aforementioned operations. We proceed by induction on the number of operations used to construct T. If $k=1$, then $T\in \{P_2,P_3\}$ and clearly ${\gamma }_R^p(T)={\gamma }^p(T)+1$. This establishes our basis case. Let $k\ge 2$ and assume that the result holds for each tree $T\in \mathcal{T}$ which can be obtained from a sequence of operations of length $k-1$ and let $T^{\prime }=T_{k-1}$. By the induction hypothesis, ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. Since $T=T_k$ is obtained from $T^{\prime }$ by one of the Operations ${\mathcal{O}}_i$ ($i\in \{1,2,\dots ,6\}$), we conclude from Lemma 1 that ${\gamma }_R^p(T)={\gamma }^p(T)+1$. □

Theorem 2.

For any tree T of order $n\ge 2$,

$${\gamma }_R^p(T)\ge {\gamma }^p(T)+1,$$

with equality only if $T\in \mathcal{T}$.

Proof. 

We use an induction on n. If $n\in \{2,3\}$, then $T\in \{P_2,P_3\}$, where ${\gamma }_R^p(T)=2={\gamma }^p(T)+1$ and $T\in \mathcal{T}$. If $n=4$ and $\mathrm{diam}(T)=2$, then $T=K_{1,3},$ where ${\gamma }_R^p(T)=2={\gamma }^p(T)+1$ and $T\in \mathcal{T}$ because it can be obtained from $P_3$ by applying Operation ${\mathcal{O}}_1$. If $n=4$ and $\mathrm{diam}(T)=3$, then $T=P_4,$ where ${\gamma }_R^p(T)=3={\gamma }^p(T)+1$ and clearly $T\in \mathcal{T}$ since it can be obtained from $P_2$ by Operation ${\mathcal{O}}_2$. Let $n\ge 5$ and assume that every tree $T^{\prime }$ of order $n^{\prime }$ with $2\le n^{\prime }<n$ satisfies ${\gamma }_R^p(T^{\prime })\ge {\gamma }^p(T^{\prime })+1$ with equality only if $T^{\prime }\in \mathcal{T}$.

Let T be a tree of order $n.$ If $\mathrm{diam}(T)=2$, then T is a star, where ${\gamma }_R^p(T)=2={\gamma }^p(T)+1$ and $T\in \mathcal{T}$ because T it can be obtained from $P_3$ by frequently use of Operation ${\mathcal{O}}_1$. Hence assume that $\mathrm{diam}(T)=3$, and thus T is a double star $D{S}_{p,q},(q\ge p\ge 1)$. If $T=D{S}_{1,q}(q\ge 2)$, then ${\gamma }_R^p(T)=3={\gamma }^p(T)+1$ and $T\in \mathcal{T}$ since it is obtained from $P_3$ by applying Operation ${\mathcal{O}}_2$. If $T=D{S}_{p,q},(q\ge p\ge 2)$, then ${\gamma }^p(T)=2$, ${\gamma }_R^p(T)=4$ and so ${\gamma }_R^p(T)>{\gamma }^p(T)+1$. Henceforth, we assume that $\mathrm{diam}(T)\ge 4$. Let $v_1{v}_2\dots v_k(k\ge 5)$ be a diametrical path in T such that ${deg}_T(v_2)$ is as large as possible. Root T at $v_k$ and consider the following cases.

Case 1.${deg}_T(v_2)\ge 4$.

Let $T^{\prime }=T-v_1$. By Corollary 1 and the induction hypothesis on $T^{\prime }$, we obtain

$${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })\ge {\gamma }^p(T^{\prime })+1={\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1.$ By induction on $T^{\prime },$ we have $T^{\prime }\in \mathcal{T}$. It follows that $T\in \mathcal{T}$ since it can be obtained from $T^{\prime }$ by applying operation ${\mathcal{O}}_1.$

Case 2.${deg}_T(v_2)={deg}_T(v_3)=2$.

Let $T^{\prime }=T-T_{v_3}$. For a ${\gamma }^p(T^{\prime })$-set $S,$ let $S^{\prime }=S\cup \left\{v_1\right\}$ if $v_4\in S$ and $S^{\prime }=S\cup \left\{v_2\right\}$ for otherwise. Clearly $S^{\prime }$ is a PDS of T and thus ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+1$. Consider now a ${\gamma }_R^p(T)$-function f. If $f(v_3)\in \{0,1\}$, then $f(v_1)+f(v_2)=2$ and the function f, restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight at most ${\gamma }_R^p(T)-2$. If $f(v_3)=2$, then $f(v_4)=0$ and the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_4)=1$ and $g(z)=f(z)$ otherwise, is a PRDF on $T^{\prime }.$ In any case, ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2$. By the induction hypothesis on $T^{\prime },$ we obtain

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2\ge {\gamma }^p(T^{\prime })+1+2\ge {\gamma }^p(T)-1+3>{\gamma }^p(T)+1.$$

Case 3.${deg}_T(v_2)=2$ and ${deg}_T(v_3)\ge 3$.

Let $T^{\prime }=T-T_{v_2}$. By Proposition 2, we have ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+1$ and ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+1$. It follows from the induction hypothesis that

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+1\ge {\gamma }^p(T^{\prime })+1+1\ge {\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }^p(T)={\gamma }^p(T^{\prime })+1$, ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+1$ and ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. By induction on $T^{\prime },$ we deduce that $T^{\prime }\in \mathcal{T}$. Next, we shall show that $v_3\in (W_{T^{\prime }}^{R,1}\cup W_{T^{\prime }}^{R,\ge 1})\cap W_{T^{\prime }}^{APD}$. Let f be a ${\gamma }_R^p(T)$-function. If $f(v_3)=2$, then $f(v_1)=1$ and $f(v_2)=0$ and the function ${f|}_{V(T^{\prime })}$ is a ${\gamma }_R^p(T^{\prime })$-function with $f(v_3)=2$ and hence $v_3\in W_{T^{\prime }}^{R,1}$. Hence, assume that $f(v_3)\le 1$. Then $f(v_1)+f(v_2)=2$. If $f(v_2)\le 1$ or $f(v_2)=2$ and $f(v_3)=1$, then the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight ${\gamma }_R^p(T)-2,$ contradicting the fact ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+1$. Hence we assume $f(v_2)=2$ and $f(v_3)=0$. Then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_3)=1$ and $g(x)=f(x)$ otherwise, is a ${\gamma }_R^p(T^{\prime })$-function and so $v_3\in W_{T^{\prime }}^{R,\ge 1}$. Hence $v_3\in W_{T^{\prime }}^{R,1}\cup W_{T^{\prime }}^{R,\ge 1}.$ It remains to show that $v_3\in W_{T^{\prime }}^{APD}$. Suppose that $v_3\notin W_{T^{\prime }}^5$ and let S be an almost PDS of $T^{\prime }$ of size less that ${\gamma }^p(T^{\prime }).$ Clearly, $v_3\notin S$ and $v_3$ has no neighbor in S. Therefore, $S\cup \left\{v_2\right\}$ is a PDS of T of size at most ${\gamma }^p(T^{\prime })={\gamma }^p(T)-1$, a contradiction. Hence $v_3\in W_{T^{\prime }}^{APD}$. It follows that $T\in \mathcal{T}$ since it can be obtained from $T^{\prime }$ by Operation ${\mathcal{O}}_2.$

Case 4.${deg}_T(v_2)=3$.

Let $L_{v_2}=\{v_1,w\}$. According to Cases 1, 2 and 3, we may assume that any end support vertex on a diametrical path has degree 3. Consider the following subcases.

Subcase 4.1.${deg}_T(v_3)=2$.

Let $T^{\prime }=T-T_{v_3}$. By Proposition 3-(1) and the induction hypothesis we have:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2\ge {\gamma }^p(T^{\prime })+1+2\ge {\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+2$, ${\gamma }^p(T)={\gamma }^p(T^{\prime })+2$ and ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. It follows from the induction hypothesis that $T^{\prime }\in \mathcal{T}$. In the next, we shall show that $v_4\in W_{T^{\prime }}^{R,\le 1}\cap W_{T^{\prime }}^{P,A}\cap W_{T^{\prime }}^{APD}$.

Suppose that $v_4\notin W_{T^{\prime }}^{P,A}$ and let S be a ${\gamma }^p(T^{\prime })$-set that does not contain $v_4$. Then $S\cup \left\{v_2\right\}$ is a PDS of T, contradicting the fact ${\gamma }^p(T)={\gamma }^p(T^{\prime })+2$. Hence $v_4\in W_{T^{\prime }}^{P,A}$. Suppose now that $v_4\notin W_{T^{\prime }}^{APD}$ and let D be an almost PDS of $T^{\prime }$ with respect to $v_4$ such that $\left|D\right|<{\gamma }^p(T^{\prime })$. Then $v_4\notin D$ and $v_4$ has no neighbor in D, and thus $D\cup \{v_2,v_3\}$ is a PDS of T of cardinality less ${\gamma }^p(T^{\prime })+2,$ a contradiction. Hence $v_4\in W_{T^{\prime }}^{APD}$. It remains to show that $v_4\in W_{T^{\prime }}^{R,\le 1}$. By Proposition 1, let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2.$ If $f(v_4)=2$, then we must have $f(v_3)\ge 1.$ But f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight at most ${\gamma }_R^p(T)-3,$ contradicting ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+2$. Hence $f(v_4)\le 1$. If $f(v_4)=0$ and $f(v_3)=2$, then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_4)=1$ and $g(x)=f(x)$ otherwise, is a PRDF of $T^{\prime }$ of weight at most ${\gamma }_R^p(T)-3,$ a contradiction as above. Thus $f(v_4)=1$ or $f(v_4)=0$ and $f(v_3)\le 1$. Then f restricted to $T^{\prime }$ is a ${\gamma }_R^p(T^{\prime })$-function showing that $v_4\in W_{T^{\prime }}^{R,\le 1}$. Hence $v_4\in W_{T^{\prime }}^{R,\le 1}\cap W_{T^{\prime }}^{P,A}\cap W_{T^{\prime }}^{APD}$. Therefore, $T\in \mathcal{T}$ because it can be obtained from $T^{\prime }$ by Operation ${\mathcal{O}}_3.$

Subcase 4.2.${deg}_T(v_3)\ge 3$.

We distinguish between some situations.

(a) 

$v_3$ is a strong support vertex.

Let $T^{\prime }=T-v_1$. By Proposition 4 and the induction hypothesis we have:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })\ge {\gamma }^p(T^{\prime })+1={\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })$, ${\gamma }^p(T)={\gamma }^p(T^{\prime })$ and ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. By the induction hypothesis, $T^{\prime }\in \mathcal{T}$. To show $v_2\in W_{T^{\prime }}^{R,1}$, let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$ (by Proposition 1). Since ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime }),$f is also a ${\gamma }_R^p(T^{\prime })$-function with $f(v_2)=2,$ implying that $v_2\in W_{T^{\prime }}^{R,1}$. Therefore $T\in \mathcal{T}$ because it can be obtained from $T^{\prime }$ by Operation ${\mathcal{O}}_4.$

(b) 

$v_3$ has two children $x,y$ with depth one, different from $v_2$.

Then u and w are both strong support vertices of degree 3. Let $T^{\prime }=T-T_{v_2}$. By Observation 1, any ${\gamma }^p(T^{\prime })$-set S contains x and y and thus $v_3\in S$. Hence $S\cup \left\{v_2\right\}$ is a PDS of T yielding ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+1$. Now, let f be a ${\gamma }_R^p(T)$ function such that $f(v_2)=2$ and $f(x)=2$ (by Proposition 1). Then $f(v_3)\ge 1$. It follows that the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight ${\gamma }_R^p(T)-2$, and hence ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2$. By the induction hypothesis we have

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2\ge {\gamma }^p(T^{\prime })+3\ge {\gamma }^p(T)+2>{\gamma }^p(T)+1.$$

(c) 

$v_3$ is a support vertex and has a child u with depth one different from $v_2$.

Let $w_1$ be the unique leaf adjacent to $v_3$. Note that u is a strong support vertices of degree 3. Let $T^{\prime }=T-T_{v_2}$. If S is a ${\gamma }^p(T^{\prime })$-set, then by Observation 1-(2), $v_3\in S$ and thus $S\cup \left\{v_2\right\}$ is a PDS of T yielding ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+1$. By Proposition 1, let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$ and $f(u)=2.$ By the definition of perfect Roman dominating functions, we have $f(v_3)\ge 1$. Then, the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight ${\gamma }_R^p(T)-2$ and thus ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2$. It follows from the induction hypothesis that

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+2\ge {\gamma }^p(T^{\prime })+3\ge {\gamma }^p(T)+2>{\gamma }^p(T)+1.$$

According to (a), (b) and (c), we can assume for the next that ${deg}_T(v_3)=3$.

(d) 

${deg}_T(v_3)=3$ and $v_3$ has a child x with depth one different from $v_2$.

Note that x is a strong support vertices of degree 3. Let $L_x=\{x_1,x_2\}$ and let $T^{\prime }$ be the tree obtained from T by removing the set of vertices $\{v_1,v_2,w,x,x_1,x_2\}$. For a ${\gamma }^p(T^{\prime })$-set $S,$ let $S^{\prime }=S\cup \{v_2,x\}$ if $v_3\in S$ and $S^{\prime }=S\cup \{v_2,v_3,x\}$ when $v_3\notin S$. Clearly, $S^{\prime }$ is a PDS of T and so ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+3$. Now let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=f(x)=2$. Then $f(v_3)\ge 1$ and the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ of weight at most ${\gamma }_R^p(T)-4$. By the induction hypothesis we have:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4\ge {\gamma }^p(T^{\prime })+1+4\ge {\gamma }^p(T)-3+5>{\gamma }^p(T)+1.$$

(e) 

${deg}_T(v_3)=3$ and $v_3$ is adjacent to exactly one leaf $w^{\prime }$.

If $v_4$ has a child s with depth one and degree two, then let $T^{\prime }$ be the tree obtained from T by removing s and its unique leaf. This case can be treated in the same way as in Case 3. Moreover, if $v_4$ has a child s with depth one and degree at least four, then let $T^{\prime }$ be the tree obtained from T by removing a leaf neighbor of $s.$ This case can be treated in the same way as in Case 1. Hence, we may assume that each child of $v_4$ is a leaf or a vertex with depth one and degree 3 or a vertex with depth two whose maximal subtree is isomorphic to $T_{v_3}$. First assume that ${deg}_T(v_4)\ge 4$, and let $T=T-T_{v_3}$. Clearly, any ${\gamma }^p(T^{\prime })$-set contains $v_4$ and such a set can be extended to a PDS of T by adding $v_2,v_3$. Hence ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+2$. Now let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$. Clearly, $f(v_3)+f(w^{\prime })\ge 1$. If $f(v_3)\le 1$ or $f(v_3)=2$ and $f(v_4)\ge 1$, then the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ and thus ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+3$. Hence assume that $f(v_3)=2$ and $f(v_4)=0$. Then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_4)=1$ and $g(u)=f(u)$ otherwise, is a PRDF of $T^{\prime }$ of weight ${\gamma }_R^p(T)-3$ and thus ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+3$. By the induction hypothesis we have:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+3\ge {\gamma }^p(T^{\prime })+1+3\ge {\gamma }^p(T)-2+4>{\gamma }^p(T)+1.$$

From now on, we can assume that ${deg}_T(v_4)\le 3$. We examine different cases.

(e.1.)

$v_4$ has a child x of degree 3 and depth 1.

Let $L_x=\{z_1,z_2\}$ and let $T^{\prime }$ be the tree obtained from T by removing the set $\{v_1,w,z_1,z_2\}$. By Proposition 6, we have ${\gamma }^p(T)={\gamma }^p(T^{\prime })+2$ and ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+2$. We deduce from the induction hypothesis that

$${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+2\ge {\gamma }^p(T^{\prime })+1+2={\gamma }^p(T)-2+3={\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. By induction on $T^{\prime },$ we have $T^{\prime }\in \mathcal{T}$. Therefore $T\in \mathcal{T}$ since it can be obtained from $T^{\prime }$ by Operation ${\mathcal{O}}_6$.

(e.2.)

$v_4$ has a child $v_3^{\prime }$ with depth two.

Note that $T_{v_3^{\prime }}$ and $T_{v_3}$ are isomorphic. Let $T^{\prime }=T-(T_{v_3}\cup T_{v_3^{\prime }})$, and observe that $v_4$ is a leaf in $T^{\prime }.$ Since any ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_4$ and the support vertices of $T_{v_3}\cup T_{v_3^{\prime }}$ we obtain ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+5$. Moreover, as above we can see that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6.$ Now, by induction hypothesis we obtain:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6\ge {\gamma }^p(T^{\prime })+1+6\ge {\gamma }^p(T)-5+7>{\gamma }^p(T)+1.$$

(e.3.)

${deg}_T(v_4)=2$.

Let $T^{\prime }=T-T_{v_4}$. If $V(T^{\prime })=\left\{v_5\right\},$ then it can be seen that T is tree with ${\gamma }_R^p(T)=5$ and ${\gamma }^p(T)=3,$ implying that ${\gamma }_R^p(T)>$${\gamma }^p(T)+1.$ Hence we assume that $T^{\prime }$ is nontrivial. By Proposition 5 and by the inductive hypothesis we have:

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+3\ge {\gamma }^p(T^{\prime })+1+3\ge {\gamma }^p(T)-3+4={\gamma }^p(T)+1.$$

Further if ${\gamma }_R^p(T)={\gamma }^p(T)+1,$ then we have equality throughout this inequality chain. In particular, ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+3$, ${\gamma }^p(T)={\gamma }^p(T^{\prime })+3$ and ${\gamma }_R^p(T^{\prime })={\gamma }^p(T^{\prime })+1$. By induction on $T^{\prime },$ we have $T^{\prime }\in \mathcal{T}$. Next, we shall show that $v_5\in W_{T^{\prime }}^{R,1}\cap W_{T^{\prime }}^{P,A}\cap W_{T^{\prime }}^{APD}$. Suppose that $v_5\notin W_{T^{\prime }}^{P,A}$ and let S be a ${\gamma }^p(T^{\prime })$-set that does not contain $v_5$. Then $S\cup \{v_2,v_3\}$ is a PDS of T contradicting ${\gamma }^p(T^{\prime })={\gamma }^p(T^{\prime })+3$. Hence $v_5\in W_{T^{\prime }}^{P,A}$. Suppose that $v_5\notin W_{T^{\prime }}^{APD}$ and let S be an almost PDS of $T^{\prime }$ such that $\left|S\right|\le {\gamma }^p(T^{\prime })-1.$ Clearly, $v_5\notin S$ and $v_5$ has no neighbor in S. It follows that $S\cup \{v_4,v_3,v_2\}$ is a PDS of T of size $\left|S\right|+3\le {\gamma }^p(T)-1,$ a contradiction. Thus $v_5\in W_{T^{\prime }}^{APD}$. Next we show that $v_5\in W_{T^{\prime }}^{R,1}$. Let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$. To Roman dominate $w^{\prime }$, we must have either $f(w^{\prime })=1$ or $f(v_3)=2$. We claim that $f(v_4)\le 1$. Suppose, to the contrary, that $f(v_4)=2$. By definition of perfect Roman dominating functions, we may assume that $f(v_3)=2$. But then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_5)=1$ and $g(x)=f(x)$ otherwise, is a PRDF of $T^{\prime }$ of weight ${\gamma }_R^p(T^{\prime })-5$ contradicting ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+3$. Hence $f(v_4)\le 1$. It follows that the function f restricted to $T^{\prime }$ is a PRDF of $T^{\prime }$ of weight at most ${\gamma }_R^p(T)-3$ for which we conclude from ${\gamma }_R^p(T)={\gamma }_R^p(T^{\prime })+3$ that $f(v_3)=f(v_4)=0$ and $f(w^{\prime })=1$. Hence to Roman dominate $v_4$, we must have $f(v_5)=2$ and thus function f restricted to $T^{\prime }$ is a ${\gamma }_R^p(T^{\prime })$-function that assigns a a 2 to $v_5.$ Hence $v_5\in W_{T^{\prime }}^{R,1}$, and thus $v_5\in W_{T^{\prime }}^{R,1}\cap W_{T^{\prime }}^{P,A}\cap W_{T^{\prime }}^{APD}$. Therefore, $T\in \mathcal{T}$ since it can be obtained from $T^{\prime }$ by Operation ${\mathcal{O}}_5.$

(e.4.)

${deg}_T(v_4)=3$ and $v_4$ has a child z with depth 0.

Seeing the above Cases and Subcases as we did in the beginning of Case (e), we may assume that any child of $v_5$ is a leaf, or an end strong support vertex of degree 3, or a vertex with depth 2 whose maximal subtree is isomorphic to $T_{v_3}$, or a vertex with depth 3 whose maximal subtree is isomorphic to $T_{v_4}$. Assume first that ${deg}_T(v_5)\ge 4$, and let $T^{\prime }=T-T_{v_4}$. Clearly, $v_5$ belongs to any ${\gamma }^p(T^{\prime })$-set and such a set ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_2,v_3,v_4,$ implying that ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+3$. Next we show that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4$. Let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$. Clearly $f(v_3)+f(w^{\prime })\ge 1$ and $f(v_4)+f(z)\ge 1$. If $f(v_4)\le 1$ or $f(v_5)\ge 1$, then the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ yielding ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4$. Hence assume that $f(v_4)=2$ and $f(v_5)=0$. Then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_5)=1$ and $g(u)=f(u)$ otherwise, is a PRDF of $T^{\prime }$ yielding ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4$. By induction on $T^{\prime },$ it follows that

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4\ge {\gamma }^p(T^{\prime })+5\ge {\gamma }^p(T)+2>{\gamma }^p(T)+1.$$

For the next, we assume that ${deg}_T(v_5)\le 3$. If ${deg}_T(v_5)=1,$ then it can be seen that T is a tree with ${\gamma }_R^p(T)=6,$${\gamma }^p(T)$ and so ${\gamma }_R^p(T)>{\gamma }^p(T)+1.$ Hence we assume that ${deg}_T(v_5)\in \{2,3\}.$ Consider the following situations.

(e.4.1.)

${deg}_T(v_5)=2$.

Let $T^{\prime }=T-T_{v_5}$. If $V(T^{\prime })=\left\{v_6\right\},$ then T is a tree with ${\gamma }_R^p(T)=6$ and ${\gamma }^p(T)=4,$ yielding ${\gamma }_R^p(T)>$${\gamma }^p(T)+1.$ Hence, assume that $T^{\prime }$ is nontrivial. For a ${\gamma }^p(T^{\prime })$-set S, let $S^{\prime }=S\cup \{v_2,v_3,v_4,v_5\}$ if $v_6\in S,$ and $S^{\prime }=S\cup \{v_2,v_3,v_4\}$ if $v_6\notin S$. Then $S^{\prime }$ is a PDS of $T,$ implying that ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+4$. Moreover, it is easy to see that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+5$. By induction on $T^{\prime },$ we obtain ${\gamma }_R^p(T)>{\gamma }^p(T)+1$.

(e.4.3.)

${deg}_T(v_5)=3$ and $v_5$ has a child $v_4^{\prime }$ with depth 3.

Then $T_{v_4}$ and $T_{v_4^{\prime }}$ are isomorphic. If u is a vertex in $T_{v_4}$, then let $u^{\prime }$ be the vertex of $T_{v_4^{\prime }}$ corresponding to u in $T_{v_4}$. Let $T=T-(T_{v_4}\cup T_{v_4^{\prime }})$. Clearly, any ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_5,v_2,v_3,v_4,v_2^{\prime },v_3^{\prime },v_4^{\prime }$ and thus ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+7$. Moreover, it is not hard to see that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+8.$ By induction on $T^{\prime },$ we obtain ${\gamma }_R^p(T)>{\gamma }^p(T)+1$.

(e.4.4.)

${deg}_T(v_5)=3$ and $v_5$ has a children y with depth 1 and degree 3.

Let $T^{\prime }=T-(T_{v_4}\cup T_y)$. Clearly, any ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_5,v_2,v_3,v_4,y$ and thus ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+5$. Next, we show that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6$. Let f be a ${\gamma }_R^p(T)$-function such that $f(v_2)=2$ and $f(y)=2$ (by Proposition 1). Clearly $f(v_3)+f(w^{\prime })\ge 1$ and $f(v_4)+f(z)\ge 1$. If $f(v_5)\ge 1$, then the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ yielding ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6$. Thus, let $f(v_5)=0$. Then to Roman dominate $z,v_4,w^{\prime }$, we must have $f(z)+f(v_4)+f(v_3)+f(w^{\prime })\ge 4$. Then the function $g:V(T^{\prime })\to \{0,1,2\}$ defined by $g(v_5)=1$ and $g(u)=f(u)$ otherwise, is a PRDF on $T^{\prime }$ yielding ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6$. It follows from the induction hypothesis that

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+6\ge {\gamma }^p(T^{\prime })+7\ge {\gamma }^p(T)+2>{\gamma }^p(T)+1.$$

(e.4.5.)

${deg}_T(v_5)=3$ and $v_5$ has a child $v_3^{\prime }$ with depth 2 such that $T_{v_3^{\prime }}\cong T_{v_3}$.

If u is a vertex in $T_{v_3}$, then let $u^{\prime }$ be the vertex of $T_{v_3^{\prime }}$ corresponding to u in $T_{v_3}$. Let $T=T-(T_{v_4}\cup T_{v_3^{\prime }})$. Clearly, any ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_5,v_2,v_3,v_4,v_2^{\prime },v_3^{\prime }$ and so ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+6$. Moreover, it is not hard to see that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+7.$ By the induction hypothesis we obtain ${\gamma }_R^p(T)>{\gamma }^p(T)+1.$

(e.4.6.)

${deg}_T(v_5)=3$ and $v_5$ has a children $z^{\prime }$ with depth 0.

If $V(T^{\prime })=\left\{v_6\right\},$ then T is a tree with ${\gamma }_R^p(T)=6$ and ${\gamma }^p(T)=4,$ yielding ${\gamma }_R^p(T)>$${\gamma }^p(T)+1.$ Hence we assume that ${deg}_T(v_6)\ge 2.$ Suppose first that ${deg}_T(v_6)=2$ and let $T^{\prime }=T-T_{v_6}$. If $V(T^{\prime })=\left\{v_7\right\},$ then T is a tree with ${\gamma }_R^p(T)\ge 7$ and ${\gamma }^p(T)=5,$ yielding ${\gamma }_R^p(T)>$${\gamma }^p(T)+1.$ Hence assume that $T^{\prime }$ is nontrivial. Clearly, any ${\gamma }^p(T^{\prime })$-set can be extended to a PDS of T by adding $v_2,v_3,v_4,v_5,v_6$ and thus ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+5$. On the other hand, it is not hard to see that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+7$. By the induction hypothesis we obtain ${\gamma }_R^p(T)>{\gamma }^p(T)+1$.

Assume now that ${deg}_T(v_6)\ge 3$. By above Cases and Subcases, we may assume that any child of $v_6$ is a leaf, or a vertex with depth j whose maximal subtree is isomorphic to $T_{v_{j+1}}$ for $j=2,3,4$. Let $T^{\prime }$ be a tree obtained from T by removing $v_3,w^{\prime },v_4,z,v_5,z^{\prime }$ and joining $v_2$ to $v_6$. Clearly, any ${\gamma }^p(T^{\prime })$-set contains $v_2,v_6$ and such a set can be extended to a PDS of T by $v_3,v_4,v_5$ yielding ${\gamma }^p(T)\le {\gamma }^p(T^{\prime })+3$. Now, let f be a ${\gamma }_R^p(T)$-function, and let $r=f(v_3)+f(w^{\prime })+f(v_4)+f(z)+f(v_5)+f(z^{\prime })$. To Roman dominate the vertices $v_3,w^{\prime },v_4,z,v_5,z^{\prime }$, we must have $r\ge 5$ when $f(v_5)\le 1$ or $r=4$ when $f(v_5)=2$. If $r=4$ or $r\ge 5$ and $f(v_6)\ge 1$, then the function f restricted to $T^{\prime }$ is a PRDF on $T^{\prime }$ implying that ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4$. Hence assume that $r\ge 5$ and $f(v_6)=0$. Then the function $h:V(T^{\prime })\to \{0,1,2\}$ defined by $h(v_6)=1$ and $h(x)=f(x)$ otherwise, is a PRDF on $T^{\prime }$ yielding ${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4$. By the induction hypothesis we obtain

$${\gamma }_R^p(T)\ge {\gamma }_R^p(T^{\prime })+4\ge {\gamma }^p(T^{\prime })+1+4\ge {\gamma }^p(T)-3+5>{\gamma }^p(T)+1,$$

and the proof is complete.

□

According to Lemma 2 and Theorem 2, we have proven Theorem 1.