Averaging Methods for Second-Order Differential Equations and Their Application for Impact Systems

Abstract

In this paper, we discuss the averaging method for periodic systems of second order and the behavior of solutions that intersect a hyperplane. We prove an averaging theorem for impact systems. This allows us to investigate the approximate dynamics of mechanical systems, such as the weakly nonlinear and weakly periodically forced Duffing’s equation of a hard spring with an impact wall, or a weakly nonlinear and weakly periodically forced inverted pendulum with double impacts.

1. Introduction

In this paper, we deal with averaging methods for differential equations of second order. More precisely, we derive averaging estimates for the following equation

$$\ddot{x}={ϵ}^{2}f(x,t,ϵ),$$

(1)

where $(x,ϵ,t)\in {\mathbb{R}}^N\times [0,1]\times \mathbb{R}$, $\mathbb{R}=(-\infty ,\infty )$ and f is specified in further text, particularly in (2), (3) or (4). We also present a result concerning an application of these averaging estimates on impact systems. Physically, (1) represents, among other things, a moving particle under weak nonlinearities and weak forces. Moreover, if we apply scaling $y\left(\tau \right)=x(\tau /ϵ)$ we get

$$\ddot{y}=f(x,\tau /ϵ,ϵ),$$

which is a differential equation with a rapid forcing widely studied in [1,2].

The theory of differential equations is a powerful tool for modeling and studying real problems with interesting outputs; see, e.g., [3,4]. It has broad ranges of approaches, as is demonstrated in recent works [5,6]. An averaging method, as a part of those approaches, has many applications and it is well-developed for ordinary, partial, delay and stochastic differential equations; see, e.g., [3,4,7,8,9,10,11,12,13,14] for more motivations and applications. One can find another applications in the field of non-smooth dynamical systems; see, e.g., [15]. In most cases, the averaging estimates are derived for differential equations of first order and often cannot be used for second order equations. We study second order differential equations subjected to impacts. We derive an $O\left(ϵ\right)$ estimate between solutions of (1) and averaged system (see (5)) on a time scale $[0,O(1/ϵ\left)\right]$ that allows one to compare dynamics of these two differential equations. The advantage of this estimate is based on the fact that averaged system is autonomous and thus its dynamics should be more predictable than of (1). For instance, an averaged system can be Hamiltonian or even integrable, or if $N=2$, then its dynamics are described by Poincaré-Bendixson theorem; see [3,9]. On the other hand, (1) may have very complicated dynamics up to chaotic; see [3,9,16]. Moreover, we study impact systems. We also present an example of a weakly nonlinear and weakly periodically forced Duffing’s equation of a hard spring with an impact wall. For simplicity, we focus our study to system with one impact, but our method holds for multiple impacts. These are novelties of our paper.

The proofs in this paper are based on ideas from [13,17]; these ideas involve classical estimates of integral forms of Equation (1) and a standard application of Gronwall Lemma. Theorem 1 below can be proven by these techniques for a more general set of right-hand-side functions f in (1) if, for example, we require basic assumptions on f; e.g., boundedness, Lipschitz continuity and periodicity in time variable or continuous differentiability. This paper reveals that if f is of some special form then it is possible to prove useful averaging estimates.

2. Preliminaries

Throughout the paper, we will use the following notation:

• $u·v$—the inner product of vectors $u,v\in {\mathbb{R}}^N$;
• $\left|u\right|$—the Euclidean norm of $u\in {\mathbb{R}}^N$;
• $\mathrm{dist}(A,B):=inf\left\{\right|a-b|\mid a\in A,b\in B\}$—the distance of nonempty sets $A,B\subset {\mathbb{R}}^N$;
• $\dot{x}\left(t\right)$ ($\ddot{x}\left(t\right)$)—the first (second) derivative of function x at time t;
• $\dot{x}{\left(t\right)}^{+}$ ($\dot{x}{\left(t\right)}^{-}$)—the right (left) derivative of function x at time t.

Let $\mathrm{\Omega }\subset {\mathbb{R}}^N$ be a domain, $a\in \mathrm{\Omega }$ and $b\in {\mathbb{R}}^N$. We consider the initial value problem

$${\displaystyle \ddot{x}={ϵ}^{2}f(x,t,ϵ),x\left(0\right)=a,\dot{x}\left(0\right)=b,}$$

(2)

defined for $(x,ϵ,t)\in \mathrm{\Omega }\times [0,1]\times \mathbb{R}$. We will assume that f is equal to one of the following special forms

$$f(x,t,ϵ)=\overline{f}(x,ϵ)+g\left(t\right),$$

(3)

or

$$f(x,t,ϵ)=\overline{f}(x,ϵ)+ϵh(x,t),$$

(4)

where $\overline{f}:\mathrm{\Omega }\times [0,1]\to {\mathbb{R}}^N$ is a Lipschitz continuous, $C^2$ smooth in $\mathrm{\Omega }\times [0,1]$ with respect to x; $ϵ$, $g:\mathbb{R}\to {\mathbb{R}}^N$ is a $C^2$ smooth, bounded function that is periodic in the time variable t with the period T and $h:\mathrm{\Omega }\times \mathbb{R}\to {\mathbb{R}}^N$ is a $C^2$ smooth in $\mathrm{\Omega }\times \mathbb{R}$ with respect to x, t, bounded function that is periodic in the time variable t with the period T. In the case of (3), the average of right-hand-side function f is equal to [3,13],

$$\frac{1}{T}{\int }_0^{T}f(x,t,0)\mathrm{d}t=\overline{f}(x,0)+\overline{g}$$

where $\overline{g}=\frac{1}{T}{\int }_0^{T}g\left(t\right)\mathrm{d}t\in \mathbb{R}$ is the average of g. In the case of (4), the average of f is equal to $\overline{f}(.,0)$, since $f(x,t,0)=\overline{f}(x,0)$. For the case (3), we state the following definition:

Definition 1.

The averaged system associated with (2) is the system

$${\displaystyle \ddot{z}={ϵ}^2(\overline{f}(z,0)+\overline{g}),}$$

(5)

and the guiding system associated with (2) is the system

$${\displaystyle \ddot{w}=\overline{f}(w,0)+\overline{g}.}$$

Let $\mathrm{\Gamma }=\mathrm{\Gamma }(n,\alpha )$ be the hyperplane in ${\mathbb{R}}^N$ that is orthogonal to unit vector n and $\alpha \in \mathbb{R}$ is given parameter. This hyperplane can be defined by the means of the scalar product in ${\mathbb{R}}^N$ as

$$\mathrm{\Gamma }(n,\alpha ):=\{y\in {\mathbb{R}}^N;y·n=\alpha \}.$$

(6)

The hyperplane $\mathrm{\Gamma }$ divides ${\mathbb{R}}^N$ into two open half-spaces ${\mathrm{\Gamma }}^{-}:=\{y\in {\mathbb{R}}^N;y·n<\alpha \}$ and ${\mathrm{\Gamma }}^{+}:=\{y\in {\mathbb{R}}^N;y·n>\alpha \}$. Let b be a vector that is transversal to the hyperplane $\mathrm{\Gamma }$ and points towards $\mathrm{\Gamma }$; i.e., $b·n>0$. In this context, we call b the impact vector. The reflection vector $b^{\prime }$ of vector b is given due to the reflection law as

$$b^{\prime }=b-2(b·n)n.$$

(7)

Clearly, it holds $b^{\prime }·n<0$; i.e., the reflection vector $b^{\prime }$ points away from $\mathrm{\Gamma }$. Moreover, the angle between $b^{\prime }$ and $\mathrm{\Gamma }$ is the same as the angle between b and $\mathrm{\Gamma }$.

According to the definition of the reflection vector, we can proceed to the following definition of solution of impact system.

Let $a,\overline{b}\in {\mathbb{R}}^N$ be vectors, $L>0$ be a constant and $a·n<\alpha$. We say that a function x is the solution of impact system

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\displaystyle \ddot{x}}& =& {ϵ}^{2}f(x,t,ϵ),\hfill \\ \hfill x\left(0\right)& =& a,\hfill \\ \hfill \dot{x}\left(0\right)& =& \overline{b},\hfill \\ \hfill x·n& \le & \alpha \hfill \end{array}\end{array}$$

(8)

if whenever x reaches the hyperplane $\mathrm{\Gamma }$ at some point $x_0\in \mathrm{\Omega }$ attained at time ${\tau }_0\in (0,L)$ then it continues as a solution of the same equation equipped with new initial conditions; i.e.,

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\displaystyle \ddot{x}}& =& {ϵ}^{2}f(x,t,ϵ),\hfill \\ \hfill x\left({\tau }_0\right)& =& x_0,\hfill \\ \hfill \dot{x}\left({\tau }_0\right)& =& b^{\prime }.\hfill \end{array}\end{array}$$

Here $x_0$ is the impact point and $b^{\prime }$ is the reflection vector of the impact vector $b=\dot{x}{\left({\tau }_0\right)}^{-}$; then clearly $b^{\prime }=\dot{x}{\left({\tau }_0\right)}^{+}$. If this happens we say that x reflects back to ${\mathrm{\Gamma }}^{-}$. We assume that motion is free to move in the region ${\mathrm{\Gamma }}^{-}\cup \mathrm{\Gamma }$, until some time ${\tau }_0$ at which $x\left({\tau }_0\right)\in \mathrm{\Gamma }$ where there is an impact with a rigid obstacle represented by $\mathrm{\Gamma }$. Within this definition, it is natural to require that if the solution starts in ${\mathrm{\Gamma }}^{-}$ and impacts $\mathrm{\Gamma }$ at the time ${\tau }_0$, the left derivative $\dot{x}{\left({\tau }_0\right)}^{-}$ should be transversal to hyperplane $\mathrm{\Gamma }$ and be directed towards $\mathrm{\Gamma }$; i.e., $\dot{x}{\left({\tau }_0\right)}^{-}·n>0$. Otherwise, if $\dot{x}{\left({\tau }_0\right)}^{-}·n=0$ then the solution x need not either continue to ${\mathrm{\Gamma }}^{+}$, nor return back to ${\mathrm{\Gamma }}^{-}$. If $\dot{x}{\left({\tau }_0\right)}^{-}·n<0$ then the solution cannot even attain $\mathrm{\Gamma }$. Thus, if $\dot{x}{\left({\tau }_0\right)}^{-}·n>0$ then it holds $\dot{x}{\left({\tau }_0\right)}^{+}·n<0$ and the solution x returns back to ${\mathrm{\Gamma }}^{-}$.

3. Results and Proofs

The following Theorem gives averaging estimates and is important for the second result of this paper.

Theorem 1.

Let $L_2>L_1>0$, $ϵ\in (0,1]$ be given parameters and $z:\left[\frac{L_1}{ϵ},\frac{L_2}{ϵ}\right]\to \mathrm{\Omega }$ be a solution of the averaged system (5) satisfying initial conditions

$$z\left(\frac{L_1}{ϵ}\right)=a,\dot{z}\left(\frac{L_1}{ϵ}\right)=b,$$

(9)

where $a\in \mathrm{\Omega }$ and $b\in {\mathbb{R}}^N$. Let $A_{ϵ}\in \mathbb{R}$ be a parameter such that $|A_{ϵ}|\le Dϵ$ for some $D>0$ and consider the local solution $x_{ϵ}$ of initial value problem

$${\displaystyle \ddot{x}={ϵ}^{2}f(x,t,ϵ),x\left(\frac{L_1}{ϵ}+A_{ϵ}\right)=a_{ϵ},\dot{x}\left(\frac{L_1}{ϵ}+A_{ϵ}\right)=b_{ϵ},}$$

(10)

for $a_{ϵ}\in \mathrm{\Omega }$, $b_{ϵ}\in {\mathbb{R}}^N$ and f satisfies either the assumption (3), or (4). Assume that there exists $D>0$ such that

$$|a-a_{ϵ}{|}^2+|b-b_{ϵ}|\le D{ϵ}^2.$$

(11)

Then there exist ${ϵ}_0\in (0,1]$ and $C>0$ such that the solution $x_{ϵ}$ of (10) can be extended up to interval $\left[\frac{L_1}{ϵ}+max\{A_{ϵ},0\},\frac{L_2}{ϵ}\right]$, stays within Ω for all $ϵ\in (0,{ϵ}_0]$. Moreover, the following estimates are true

$$|x_{ϵ}\left(t\right)-z\left(t\right)|\le Cϵ,$$

and

$$|{\dot{x}}_{ϵ}\left(t\right)-\dot{z}\left(t\right)|\le C{ϵ}^2,$$

for $t\in \left[\frac{L_1}{ϵ}+max\{A_{ϵ},0\},\frac{L_2}{ϵ}\right]$ and $ϵ\in (0,{ϵ}_0]$.

Proof. 

Throughout the whole proof, we will assume that $A_{ϵ}\ge 0$ since the case $A_{ϵ}<0$ would be proven in an analogous way. In the proof, we will deal with the case (3); the other case should be dealt with in a similar way. For fixed $ϵ\in (0,1]$, let $x_{ϵ}$ be the unique solution that exists on some interval $\left[\frac{L_1}{ϵ}+A_{ϵ},s\right)$ for some $s\le \frac{L_2}{ϵ}$ and satisfies the initial value problem (10). The only difficulty that prevents $x_{ϵ}$ from existence on the whole interval $\left[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}\right]$ is that $x_{ϵ}$ may approach to the boundary of $\mathrm{\Omega }$ in some earlier time s. In the rest of the proof we will write x instead of $x_{ϵ}$.

We will prove that the solution x can be extended up to interval $\left[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}\right]$, i.e., $s=\frac{L_2}{ϵ}$ and the inequality (12) is true for $t\in \left[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}\right]$. Integrating the equation in (10) with respect to t two times and using notation of initial conditions from (10), we obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill x\left(t\right)& =& {\displaystyle a_{ϵ}+{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\dot{x}\left(\xi \right)\mathrm{d}\xi }\hfill \\ & =& {\displaystyle a_{ϵ}+{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t{b}_{ϵ}\mathrm{d}\xi +{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{\xi }f(x\left(\tau \right),\tau ,ϵ)\mathrm{d}\tau \mathrm{d}\xi }\hfill \\ & =& {\displaystyle a_{ϵ}+b_{ϵ}\left(t-\frac{L_1}{ϵ}-A_{ϵ}\right)+{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{\xi }f(x\left(\tau \right),\tau ,ϵ)\mathrm{d}\tau \mathrm{d}\xi }\hfill \\ & =& {\displaystyle a_{ϵ}+b_{ϵ}\left(t-\frac{L_1}{ϵ}-A_{ϵ}\right)+{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)f(x\left(\tau \right),\tau ,ϵ)\mathrm{d}\tau .}\hfill \end{array}\end{array}$$

In the last equality, we used the Fubini’s Theorem. A similar equation is true for the solution z but with $\frac{L_1}{ϵ}+A_{ϵ}$ replaced by $\frac{L_1}{ϵ}$ and f replaced by $\overline{f}+\overline{g}$. Hence, for $t\in \left[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}\right]$, we come to the expression

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill x\left(t\right)-z\left(t\right)& =& a_{ϵ}-a+(b_{ϵ}-b)\left(t-\frac{L_1}{ϵ}\right)-b_{ϵ}{A}_{ϵ}\hfill \\ & +& {\displaystyle {ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)(f(x,\tau ,ϵ)-\overline{f}(z,0)-\overline{g})\mathrm{d}\tau }\hfill \\ & -& {\displaystyle {ϵ}^2{\int }_{\frac{L_1}{ϵ}}^{\frac{L_1}{ϵ}+A_{ϵ}}\left(t-\tau \right)(\overline{f}(z,0)+\overline{g})\mathrm{d}\tau .}\hfill \end{array}\end{array}$$

From the last equality, we can derive the following estimation

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \left|x\right(t)-z(t\left)\right|& \le & |a_{ϵ}-a|+\left(t-\frac{L_1}{ϵ}\right)|b_{ϵ}-b|+Dϵ|b_{ϵ}|\hfill \\ & +& {\displaystyle {ϵ}^2\left|{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)\left(f(x,\tau ,ϵ)-\overline{f}(z,0)-\overline{g}\right)\mathrm{d}\tau \right|}\hfill \\ & +& {\displaystyle {ϵ}^2{\int }_{\frac{L_1}{ϵ}}^{\frac{L_1}{ϵ}+A_{ϵ}}\left(t-\tau \right)|\overline{f}(z,0)+\overline{g}|\mathrm{d}\tau .}\hfill \end{array}\end{array}$$

(12)

In the following estimates, the constant C may vary from step to step. Clearly, if $t,\tau \in \left[\frac{L_1}{ϵ},\frac{L_2}{ϵ}\right]$ then

$$t-\tau \le \frac{L_2-L_1}{ϵ}.$$

Since the function g is periodic, the function $g_1\left(\xi \right):={\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{\xi }g\left(\tau \right)-\overline{g}\mathrm{d}\tau$ is bounded and its boundedness is independent of $ϵ$ and $\xi$. Using this fact and the Lipschitz continuity of $\overline{f}$, the first integral in (12) can be estimated in the following way

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \left|{\displaystyle {\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)\left(f(x,\tau ,ϵ)-\overline{f}(z,0)-\overline{g}\right)\mathrm{d}\tau }\right|& \le & {\displaystyle {\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)\left|\overline{f}(x,ϵ)-\overline{f}(z,0)\right|\mathrm{d}\tau }\hfill \\ & +& \left|{\displaystyle {\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{\xi }g\left(\tau \right)-\overline{g}\mathrm{d}\tau \mathrm{d}\xi }\right|\hfill \\ & \le & {\displaystyle C{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)(\left|x\left(\tau \right)-z\left(\tau \right)\right|+ϵ)\mathrm{d}\tau +\frac{C}{ϵ}.}\hfill \end{array}\end{array}$$

(13)

Combining the estimates (12) and (13) and the assumption (11), we get

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \left|x\right(t)-z(t\left)\right|& \le & \sqrt{D}ϵ+ϵ\left(L_2-L_1\right)D+ϵ(D{ϵ}^2+D\left|b\right|)\hfill \\ & +& {\displaystyle C{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left(t-\tau \right)\left|x\left(\tau \right)-z\left(\tau \right)\right|\mathrm{d}\tau +Cϵ{\left(L_2-L_1\right)}^2}\hfill \\ & \le & {\displaystyle Cϵ+{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{t}Cϵ\left|x\left(\tau \right)-z\left(\tau \right)\right|\mathrm{d}\tau .}\hfill \end{array}\end{array}$$

Now, an obvious application of the General Gronwall Lemma (see, e.g., [13]) yields

$$|x\left(t\right)-z\left(t\right)|\le Cϵe^{C(L_2-L_1)}\le Cϵ.$$

Note that the constant C depends on $L_{1,2},D,A$ and b but is independent of $ϵ$ and s. Thus we proved the estimate (12) for $t\in \left[\frac{L_1}{ϵ}+A_{ϵ},s\right)$. Now, we prove that $s=\frac{L_2}{ϵ}$; i.e., the solution x can be extended up to the interval $[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}]$. It is sufficient to prove that the solution x is bounded away from the boundary $\partial \mathrm{\Omega }$. Denote $d=\mathrm{dist}(\partial \mathrm{\Omega },w\left([L_1,L_2]\right))$, where w solves the guiding system (6) and $w\left([L_1,L_2]\right)=\{w\left(t\right)\mid t\in [L_1,L_2]\}$. It is clear that $d>0$ and there is some ${ϵ}_0>0$ such that

$$|x_{ϵ}\left(t\right)-w\left(ϵt\right)|\le Cϵ\le \frac{d}{2}$$

for every $ϵ\in (0,{ϵ}_0]$ and $t\in [\frac{L_1}{ϵ}+A_{ϵ},s)$. Since C is independent of $ϵ$ and s, it is ${ϵ}_0$, and it means that $\mathrm{dist}(\partial \mathrm{\Omega },x\left([\frac{L_1}{ϵ}+A_{ϵ},s)\right)\ge \frac{d}{2}$ for all $t\in [\frac{L_1}{ϵ}+A_{ϵ},s)$, and moreover, the solution x can be extended. Therefore x exists globally on interval $[\frac{L_1}{ϵ}+A_{ϵ},\frac{L_2}{ϵ}]$. It remains to prove the estimate (12). As before, we start with following equality

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \dot{x}\left(t\right)& =& {\displaystyle b_{ϵ}+{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^{t}f(x\left(\tau \right),\tau ,ϵ)\mathrm{d}\tau }\hfill \end{array}\end{array}$$

(14)

and an estimation similar to (12) yields

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill |\dot{x}\left(t\right)-\dot{z}\left(t\right)|& \le & {\displaystyle |b_{ϵ}-b|+{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left|f(x,\tau ,ϵ)-\overline{f}(z,0)-\overline{g}\right|\mathrm{d}\tau +{ϵ}^2{\int }_{\frac{L_1}{ϵ}}^{\frac{L_1}{ϵ}+A_{ϵ}}|\overline{f}(z,0)+\overline{g}|\mathrm{d}\tau .}\hfill \end{array}\end{array}$$

(15)

Now using the assumption (11) and estimates similar to (13), we obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill |\dot{x}\left(t\right)-\dot{z}\left(t\right)|& \le & {\displaystyle D{ϵ}^2+C{ϵ}^2{\int }_{\frac{L_1}{ϵ}+A_{ϵ}}^t\left|x\left(\tau \right)-z\left(\tau \right)\right|\mathrm{d}\tau +C{ϵ}^2(1+ϵ).}\hfill \end{array}\end{array}$$

We apply the estimate (12) that has been proven before and we get the desired estimate (12). □

Remark 1.

The estimates (12) and (12) resemble to Hyers–Ulam stability—see [18]—but the purpose of these estimates is to compare solutions of averaged and original differential equations.

Here we state an important lemma that is useful in the study of averaged impact systems or some other applications. The proof of this lemma is based only on the estimates (12) and (12) and can be used for any right-hand-side function f for which these estimates are valid.

Lemma 1.

Let f be a function such that for the initial value system (2), the estimates (12) and (12) are valid, Γ is a hyperplane defined by (6) with unit normal vector n and parameter α, $L>0$ be a given constant and $w:\left[0,L\right]\to \mathrm{\Omega }$ be a solution of the guiding system (6) satisfying initial conditions

$$w\left(0\right)=a,\dot{w}\left(0\right)=b$$

(16)

where $a\in \mathrm{\Omega }\backslash \mathrm{\Gamma }$ and $b\in {\mathbb{R}}^N$. Assume that $a·n<\alpha <w\left(L\right)·n$, w intersects Γ in exactly one point $x_0$ at ${\tau }_0\in (0,L)$ and $\dot{w}\left({\tau }_0\right)·n>0$.

Then there exist positive constants ${ϵ}_0$ and B such that for all $ϵ\in (0,{ϵ}_0]$, the solution $x_{ϵ}$ of initial value problem (10) with $a_{ϵ}=a$ and $b_{ϵ}=b$ intersects Γ at exactly one point $x_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)$, there holds $x_{ϵ}\left(\frac{L}{ϵ}\right)·n>\alpha$, ${\dot{x}}_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)·n>0$ and the following inequalities are true

$$\begin{array}{c}\left|\frac{t_{ϵ}}{ϵ}-\frac{{\tau }_0}{ϵ}\right|\le ϵB,\left|x_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)-x_0\right|\le Bϵand\left|{\dot{x}}_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)-ϵ\dot{w}\left({\tau }_0\right)\right|\le B{ϵ}^2.\end{array}$$

Proof. 

Denote $z_{ϵ}$ the solution of Equation (5) satisfying the initial conditions (9). Fix $ϵ\in (0,{ϵ}_0]$. Due to the assumption, $z_{ϵ}$ intersects $\mathrm{\Gamma }$ at exactly one point $x_0=z_{ϵ}\left(\frac{{\tau }_0}{ϵ}\right)$. Denote

$$u\left(t\right):=x_{ϵ}\left(t\right)·n\mathrm{and}v\left(\frac{t}{ϵ}\right):=z_{ϵ}\left(\frac{t}{ϵ}\right)·n=w\left(t\right)·n.$$

Due to the assumption on w, we know that $v\left(0\right)<\alpha <v\left(\frac{L}{ϵ}\right)$ and v attains the value $\alpha$ only at one time ${\tau }_0$. Due to the assumption, there exist some $\delta ,\beta >0$ such that $\dot{w}\left(t\right)·n\ge 2\beta$ for $t\in ({\tau }_0-\delta ,{\tau }_0+\delta )$ or $\dot{v}\left(\frac{t}{ϵ}\right)\ge 2ϵ\beta$. The estimate (12) implies that $\dot{u}\left(\frac{t}{ϵ}\right)\ge ϵ\beta$ for ${ϵ}_0>0$ sufficiently small.

Let C be the constant from (12) and we fix some $A>\frac{C}{\beta }$ Then we have

$$v\left(\frac{{\tau }_0+ϵA}{ϵ}\right)-v\left(\frac{{\tau }_0}{ϵ}\right)={\int }_{\frac{{\tau }_0}{ϵ}}^{\frac{{\tau }_0+ϵA}{ϵ}}\dot{v}\left(\tau \right)\mathrm{d}\tau \ge A\beta ϵ;$$

(17)

then, the last estimate together with (12) yield

$$u\left(\frac{{\tau }_0+ϵA}{ϵ}\right)\ge \alpha +(A\beta -C)ϵ\ge \alpha +Dϵ\mathrm{for}ϵ\in (0,{ϵ}_0].$$

(18)

Recall that ${ϵ}_0>0$ is sufficiently small and fixed in (18), while $ϵ\in (0,{ϵ}_0]$ is a parameter.

Similarly, we obtain

$$u\left(\frac{{\tau }_0-ϵA}{ϵ}\right)\le \alpha -Dϵ\mathrm{for}ϵ\in (0,{ϵ}_0].$$

(19)

The estimates (18) and (19) show that there exists some $t_{ϵ}\in ({\tau }_0-ϵA,{\tau }_0+ϵA)$ such that $v\left(\frac{t_{ϵ}}{ϵ}\right)=\alpha$ which means that $x_{ϵ}$ intersects $\mathrm{\Gamma }$ at some time $\frac{t_{ϵ}}{ϵ}$. Moreover, the point $x_{ϵ}\left(\frac{{\tau }_0-ϵA}{ϵ}\right)$ lies in ${\mathrm{\Gamma }}^{-}$ and $x_{ϵ}\left(\frac{{\tau }_0+ϵA}{ϵ}\right)$ in ${\mathrm{\Gamma }}^{+}$. If we lower ${ϵ}_0$ then the estimate (12) implies that $\mathrm{dist}\left(\mathrm{\Gamma },x_{ϵ}\left(\left[0,\frac{{\tau }_0-ϵA}{ϵ}\right]\right)\right)>0$ and $\mathrm{dist}\left(\mathrm{\Gamma },x_{ϵ}\left(\left[\frac{{\tau }_0+ϵA}{ϵ},\frac{L}{ϵ}\right]\right)\right)>0$ which means that $x_{ϵ}\left(\left[0,\frac{{\tau }_0-ϵA}{ϵ}\right]\right)\subset {\mathrm{\Gamma }}^{-}$ and $x_{ϵ}\left(\left[\frac{{\tau }_0+ϵA}{ϵ},\frac{L}{ϵ}\right]\right)\subset {\mathrm{\Gamma }}^{+}$. Hence $x_{ϵ}$ intersects $\mathrm{\Gamma }$ at exactly one time $\frac{t_{ϵ}}{ϵ}$.

Till now we proved that $t_{ϵ}\in ({\tau }_0-ϵA,{\tau }_0+ϵA)$ and this is equivalent to $\left|\frac{t_{ϵ}}{ϵ}-\frac{{\tau }_0}{ϵ}\right|\le A$. In the following, we will find out that some better estimation is actually true. Since ${\tau }_0$ is the intersection time for w and $\frac{t_{ϵ}}{ϵ}$ is for u we can write

$$\alpha =w\left({\tau }_0\right)·n=u\left(\frac{t_{ϵ}}{ϵ}\right).$$

(20)

Note that the function u defined on $[{\tau }_0-\delta ,{\tau }_0+\delta ]$ is increasing and $Aϵ\le \delta$ for some ${ϵ}_0$ sufficiently small. Then $t_{ϵ}\in ({\tau }_0-\delta ,{\tau }_0+\delta )$, i.e., $t_{ϵ}$ is close enough to ${\tau }_0$ and it is possible to apply the inverse function $u^{-1}$ to the equality (20) and obtain

$$\phi \left(ϵ\right):=ϵu^{-1}\left(\alpha \right)=t_{ϵ}.$$

Recall that $\phi$ depends on parameter $ϵ$, more precisely, $\phi \left(ϵ\right)=ϵ{(x_{ϵ}·n)}^{-1}\left(\alpha \right)$. We know that due to the $C^2$ smoothness of the right-hand side in (2), the function $\phi$ is $C^2$ smooth and $\phi \left(ϵ\right)={\tau }_0+\kappa ϵ+\lambda {ϵ}^2+\mathcal{O}\left({ϵ}^2\right)$ as $ϵ\to 0^{+}$. On the other hand, from the estimate (12) we see that $u\left(\frac{{\tau }_0}{ϵ}\right)-\alpha =\mathcal{O}\left(1\right)$. Since $u^{-1}$ is continuous, there holds $\frac{{\tau }_0}{ϵ}-u^{-1}\left(\alpha \right)=\frac{{\tau }_0}{ϵ}-\frac{t_{ϵ}}{ϵ}=\mathcal{O}\left(1\right)$. Hence

$$\mathcal{O}\left(ϵ\right)={\tau }_0-t_{ϵ}=\kappa ϵ+\lambda {ϵ}^2+\mathcal{O}\left({ϵ}^2\right),$$

consequently $\kappa =0$ and we proved the first estimate in (1).

Now we prove the second estimate in (1). Observe that the derivative ${\dot{z}}_{ϵ}\left(\frac{t}{ϵ}\right)$ is bounded; its bound depends only on the initial value b and is independent of $ϵ$ and t. This follows easily from an equation similar to (14). Hence the estimate (12) implies the uniform Lipschitz continuity of $x_{ϵ}$. Thus, due to (12) and the first inequality in (1), the following holds:

$$\left|x_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)-x_0\right|\le \left|x_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)-x_{ϵ}\left(\frac{{\tau }_0}{ϵ}\right)\right|+\left|x_{ϵ}\left(\frac{{\tau }_0}{ϵ}\right)-z_{ϵ}\left(\frac{{\tau }_0}{ϵ}\right)\right|\le Cϵ,$$

(21)

which was required.

The third estimate in (1) can be proven similarly to the second one. First, one has to prove the uniform Lipschitz continuity of $z_{ϵ}$ by using an equation similar to (14). Then the desired estimate follows from (12) and the first inequality in (1). □

Remark 2.

The value of $L>0$ in Lemma 1 is finite. In general, L cannot be equal to ∞; otherwise, a solution, if one exists, may be unstable. However, one can find several very interesting results in Chapter 5 of [13] regarding case $L=\infty$.

Now we are ready to state and prove the following theorem concerning the relationship between solutions of an impact system and the corresponding guiding system. The theorem is actually a consequence of Lemma 1 and Theorem 1. This is the main result of this paper that extends averaging principles in [3,9,13] to second order differential equations with impacts.

Theorem 2.

Let f, Γ, n, α, $L>0$ be as in Lemma 1, and $w:\left[0,L\right]\to \mathrm{\Omega }$ be a solution of the guiding system associated with the impact problem (8) satisfying initial conditions (16). Assume that w starts in ${\mathrm{\Gamma }}^{-}$; i.e., $a·n<\alpha$, w impacts on Γ in exactly one point $x_0$ at ${\tau }_0\in (0,L)$; it holds $\dot{w}{\left({\tau }_0\right)}^{-}·n>0$ and reflects back to ${\mathrm{\Gamma }}^{-}$ in direction $\dot{w}{\left({\tau }_0\right)}^{\prime }$ in sense of the reflection law (7) at point $w\left({\tau }_0\right)\in \mathrm{\Gamma }$.

Then there exist positive constants ${ϵ}_0$, C and a time $t_{ϵ}\in (0,L)$ such that for all $ϵ\in (0,{ϵ}_0]$, the solution $x_{ϵ}$ of the impact initial value problem (8) starts in ${\mathrm{\Gamma }}^{-}$, impacts on Γ at point $x_{ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)\in \mathrm{\Gamma }$ and reflects back to ${\mathrm{\Gamma }}^{-}$. Moreover, the following inequalities are true

$$|x_{ϵ}\left(t\right)-w\left(ϵt\right)|\le Cϵfort\in \left[0,\frac{L}{ϵ}\right],$$

(22)

and

$$|{\dot{x}}_{ϵ}\left(t\right)-ϵ\dot{w}\left(ϵt\right)|\le C{ϵ}^{2}fort\in \left[0,\frac{L}{ϵ}\right]\backslash \left[\frac{min\{{\tau }_0,t_{ϵ}\}}{ϵ},\frac{max\{{\tau }_0,t_{ϵ}\}}{ϵ}\right].$$

(23)

Remark 3.

If, e.g., ${\tau }_0<t_{ϵ}$ for fixed $ϵ>0$, then obviously, the estimate (23) cannot be true for $t\in \left[\frac{{\tau }_0}{ϵ},\frac{t_{ϵ}}{ϵ}\right]$ if ϵ is sufficiently small. Due to the assumption $\dot{w}{\left({\tau }_0\right)}^{-}·n>0$, the solution w takes at ${\tau }_0$ a completely different direction equal to the reflection vector of $\dot{w}{\left({\tau }_0\right)}^{-}$.

Proof. 

Let w be the solution of system (8). Then due to the assumptions, w touches $\mathrm{\Gamma }$ at the point $w\left({\tau }_0\right)$ and reflects back to ${\mathrm{\Gamma }}^{-}$. We define v as the local solution of problem

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \ddot{v}& =& \overline{f}(v,0),\hfill \\ \hfill v\left(0\right)& =& w\left({\tau }_0\right),\hfill \\ \hfill \dot{v}\left(0\right)& =& \dot{w}{\left({\tau }_0\right)}^{-}.\hfill \end{array}\end{array}$$

Since $\dot{w}{\left({\tau }_0\right)}^{-}·n>0$ it is clear that there exists $\delta >0$ such that $v\left(t\right)\in {\mathrm{\Gamma }}^{+}$ for $t\in (0,\delta )$. Observe that the function

$$u\left(t\right)=\left\{\begin{array}{cc}w\left(t\right),\hfill & t\in [0,{\tau }_0],\hfill \\ v(t-{\tau }_0),\hfill & t\in ({\tau }_0,{\tau }_0+\delta ],\hfill \end{array}\right.$$

is the solution of the Equation (6) with initial conditions (16) and satisfies the assumptions of Lemma 1. Hence there exists ${ϵ}_0>0$ such that for all $ϵ\in (0,{ϵ}_0]$, the solution $x_{1,ϵ}:\left[0,\frac{{\tau }_0+\delta }{ϵ}\right]\to \mathrm{\Omega }$ of initial value problem (10) intersects $\mathrm{\Gamma }$ at exactly one time $\frac{t_{ϵ}}{ϵ}$ with $t_{ϵ}\in (0,{\tau }_0+\delta )$.

Fix $ϵ>0$. From Lemma 1, we know that there holds ${\dot{x}}_{1,ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)·n>0$. Thus, the vector ${\dot{x}}_{1,ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)$ is transversal to $\mathrm{\Gamma }$ and we can define a local solution $x_{2,ϵ}:\left[0,s\right]\to \mathrm{\Omega }$ of equation (2). Let the initial value $x_{2,ϵ}\left(0\right)$ be equal to $x_{1,ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)$ and ${\dot{x}}_{2,ϵ}\left(0\right)$ be the reflection vector of ${\dot{x}}_{1,ϵ}\left(\frac{t_{ϵ}}{ϵ}\right)$ due to the reflection law (7).

In the following, we will assume that ${\tau }_0\le t_{ϵ}$. We define a function

$$x_{ϵ}\left(t\right)=\left\{\begin{array}{cc}{x}_{1,ϵ}\left(t\right),\hfill & t\in \left[0,\frac{t_{ϵ}}{ϵ}\right],\hfill \\ x_{2,ϵ}\left(t-\frac{t_{ϵ}}{ϵ}\right),\hfill & t\in \left(\frac{t_{ϵ}}{ϵ},\frac{t_{ϵ}}{ϵ}+s\right].\hfill \end{array}\right.$$

It is clear that $x_{ϵ}$ is a solution of impact system (8). We are yet to prove the estimates (22) and (23). The validity of the estimates (22) and (23) for $t\in \left[0,\frac{{\tau }_0}{ϵ}\right)$ follows immediately from Theorem 1 and for $t\in \left(\frac{t_{ϵ}}{ϵ},\frac{t_{ϵ}}{ϵ}+s\right]$ from (1), due to Lemma 1 and Theorem 1. Using similar argument as in the proof of Theorem 1, we conclude that $s=\frac{L-t_{ϵ}}{ϵ}$ and so $x\left(\left[0,\frac{L}{ϵ}\right]\right)\subset \mathrm{\Omega }$. The estimate (22) for $t\in \left[\frac{{\tau }_0}{ϵ},\frac{t_{ϵ}}{ϵ}\right]$ follows from the Lipschitz continuity of w, $x_{ϵ}$ and from the first inequality in (1). □

Remark 4.

Since deriving the optimal value of positive constants ${ϵ}_0$, C, and a computation of $t_{ϵ}$ in Theorem 2 would lead to awkward and messy formulas, we do not go into details in this paper.

4. Example

We consider a second order differential equation

$$\ddot{x}={ϵ}^2(-x-x^3+cos2\pi t),$$

(24)

with impact wall

$$x=1.$$

(25)

Thus, we have $N=1$, $n=1$ and $\alpha =1$ in (6). Clearly, $T=1$ and the guiding system (6) is as follows

$$\ddot{w}=-w-w^3.$$

(26)

This equation is called Duffing’s equation of a hard spring ([19], Section 5.2). Its solution has the form

$$w_{w_0}\left(t\right)=w_0\mathrm{cn}(\sqrt{(1+w_0^2)t},k\left(w_0\right)),w_{w_0}\left(0\right)=w_0<0,\dot{w}\left(0\right)=0$$

(27)

where $\mathrm{cn}$ is a Jacobi elliptic function with modulus

$$k\left(w_0\right)=-\frac{w_0}{\sqrt{2+2w_0^2}}.$$

Note that the functions (27) are periodic with periods

$$T\left(w_0\right)=\frac{4K\left(k\left(w_0\right)\right)}{\sqrt{1+w_0^2}}$$

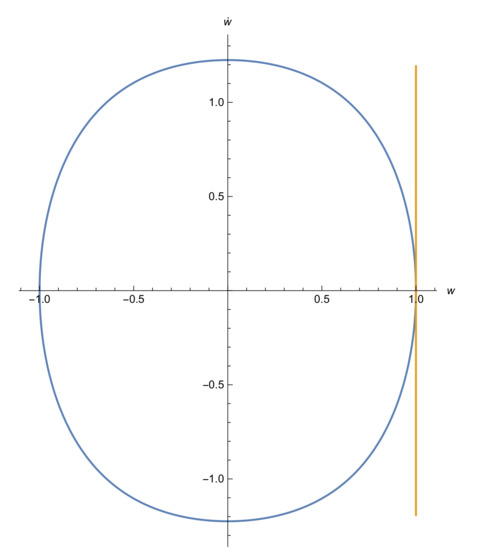
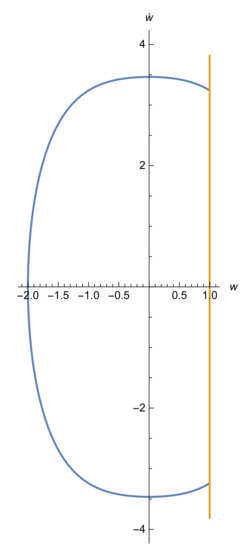
where $K\left(k\right)$ is the complete elliptic integral of the first kind. To get impact (25), we need $w_0\le -1$. When $w_0=-1$, we have a periodic grazing impact solution [20] (see Figure 1), so this solution $w_{-1}\left(t\right)$ is just touching the impact wall at $(1,0)$ for ${\tau }_0(-1)=\frac{T(-1)}{2}=\sqrt{2}K\left(\frac{1}{4}\right)\approx 2.38401$.

Figure 1. Periodic grazing impact solution of (25) and (26).

For $w_0<-1$, the impact time ${\tau }_0$ from Theorem 2 is given by $w\left({\tau }_0\right)=1$, which means to solve

$$w_0\mathrm{cn}(\sqrt{(1+w_0^2){\tau }_0},k\left(w_0\right))=-1,$$

so

$${\tau }_0\left(w_0\right)=\frac{{\mathrm{cn}}^{-1}(-w_0^{-1},k\left(w_0\right))}{\sqrt{1+w_0^2}}.$$

(28)

One can numerically check that ${\tau }_0\left(w_0\right)$ is increasing with ${lim}_{w_0\to -\infty }{\tau }_0\left(w_0\right)=0$ (see Figure 2).

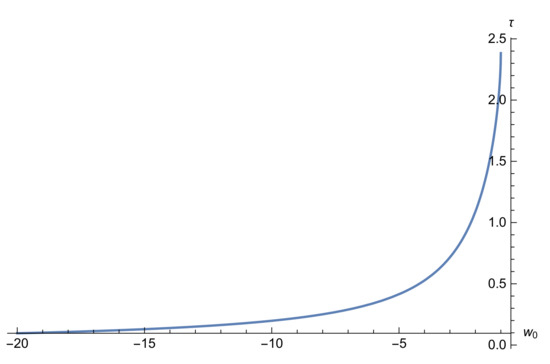
Figure 2. The graph of (28) on $[-20,-1]$.

For any $w_0<-1$, we have periodic impact solutions; see Figure 3.

Figure 3. Impact solution of (25) and (26) for $w_0=-2$.

Consequently, we can apply Theorem 2 to (24) with (25) for any fixed $L\in ({\tau }_0\left(w_0\right),T\left(w_0\right)]$, $w_0<-1$, to see that $x\left(t\right)$ is $O\left(ϵ\right)$-near to $w_{w_0}\left(ϵt\right)$ on $\left[0,\frac{L}{ϵ}\right]$ for any $ϵ>0$ sufficiently small. This means that we know $O\left(ϵ\right)$-approximately dynamics of (24) with (25) on a time scale $[0,O(1/ϵ\left)\right]$ for any $ϵ>0$ sufficiently small.

Similarly, we can investigate a weakly nonlinear and weakly periodically forced inverted pendulum with double impacts [21].

5. Conclusions

An averaging method was developed for weakly nonlinear and periodic second order differential equations subjected to impacts. Asymptotic estimation was derived between solutions of original and averaged equations. In this paper, we focused on the theoretical justification of the averaging principle for periodic second order differential equations and its applications to impact systems. The next step would be a numerical implementation of the above approach and method. This means an extension of averaging method for first order difference equations (see [22,23,24]) to second order ones, as in this paper, and a combination with discrete numerical schemes [25]. Another further direction would be dealt with more general discontinuous cases.