d-Path Laplacians and Quantum Transport on Graphs

Abstract

We generalize the Schrödinger equation on graphs to include long-range interactions (LRI) by means of the Mellin-transformed d-path Laplacian operators. We find analytical expressions for the transition and return probabilities of a quantum particle at the nodes of a ring graph. We show that the average return probability in ring graphs decays as a power law with time when LRI is present. In contrast, we prove analytically that the transition and return probabilities on a complete and start graphs oscillate around a constant value. This allowed us to infer that in a barbell graph—a graph consisting of two cliques separated by a path—the quantum particle get trapped and oscillates across the nodes of the path without visiting the nodes of the cliques. We then compare the use of the Mellin-transformed d-path Laplacian operators versus the use of fractional powers of the combinatorial Laplacian to account for LRI. Apart from some important differences observed at the limit of the strongest LRI, the d-path Laplacian operators produces the emergence of new phenomena related to the location of the wave packet in graphs with barriers, which are not observed neither for the Schrödinger equation without LRI nor for the one using fractional powers of the Laplacian.

1. Introduction

In applications of graph theory to sciences and engineering, it is very common to study the evolution of the heat equation on graphs [1,2,3,4,5]:

$${\displaystyle \frac{\partial \overrightarrow{\Psi }\left(t\right)}{\partial t}}=-L\overrightarrow{\Psi }\left(t\right),\overrightarrow{\Psi }\left(0\right)={\overrightarrow{\Psi }}_0,$$

(1)

where $\overrightarrow{\Psi }\left(t\right)\in {\mathbb{C}}^{n\times 1}$ is a complex state vector which varies with time $t>0$, and L is the combinatorial graph Laplacian. The solution of this model, known in engineering as the consensus protocol [4,5], always converges in a connected graph to the average of the values of ${\overrightarrow{\Psi }}_0$. That is, $\overrightarrow{\Psi }\left(t\right)=e^{-itL}{\overrightarrow{\Psi }}_0$, where

$$exp\left(-tL\right)={\displaystyle \sum _{j=1}^n}{\overrightarrow{\sigma }}_j{\overrightarrow{\varphi }}_j^{T}exp\left(-t{\mu }_j\right),$$

(2)

in which ${\overrightarrow{\sigma }}_j$ and ${\overrightarrow{\varphi }}_j$ are the jth column of the matrix of eigenvectors of L and its inverse, respectively, and ${\mu }_j\left(L\right)$ are the corresponding eigenvalues of L. Here, as usual, ${\overrightarrow{v}}^T$ means the transpose of the column vector v. Then, for very long times, ${lim}_{t\to \infty }exp\left(-tL\right)={\overrightarrow{\sigma }}_1{\overrightarrow{\varphi }}_1^T,$ where ${\overrightarrow{\sigma }}_1^T{\overrightarrow{\varphi }}_1=1$. Then, by taking ${\overrightarrow{\sigma }}_1=\overrightarrow{1}$, where $\overrightarrow{1}$ is the all-ones column vector of appropriate dimension, we have

$${\displaystyle \underset{t\to \infty }{lim}}\overrightarrow{\Psi }\left(t\right)=\left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\overrightarrow{\Psi }}_0\left(i\right)\right)\overrightarrow{1}.$$

(3)

This behavior, which is illustrated in Figure 1a, contrasts with that of the Schrödinger equation on graphs, which has been defined by [6,7,8,9]

$${\displaystyle \frac{\partial \overrightarrow{\Psi }\left(t\right)}{\partial t}}=-iL\overrightarrow{\Psi }\left(t\right),$$

(4)

with initial state $\overrightarrow{\Psi }\left(0\right)={\overrightarrow{\Psi }}_0$, which shows the characteristic wave behavior illustrated in Figure 1b. The wave nature of the solution comes from the fact that it is given by ${\overrightarrow{\Psi }}_{0}exp\left(-itL\right)$, where

$$exp\left(-itL\right)={\displaystyle \sum _{j=1}^n}\overrightarrow{{\sigma }_j}{\overrightarrow{\varphi }}_j^{T}cos\left(t{\mu }_j\left(L\right)\right)-i{\displaystyle \sum _{j=1}^n}{\overrightarrow{\sigma }}_j{\overrightarrow{\varphi }}_j^{T}sin\left(t{\mu }_j\left(L\right)\right).$$

(5)

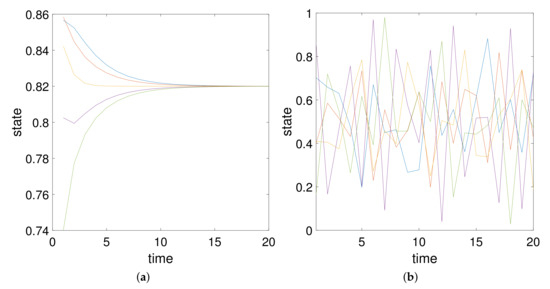
Figure 1. Illustration of the time evolution of the states of the nodes in a linear chain of five nodes using a classical (a) and quantum (b) transport dynamics with random initial condition at the nodes.

Notice that a different field is the consideration of the Schrödinger equation on metric graphs, which are known as quantum graphs [10], and which is not the topic of the current work.

The influence of the graph topology on the dynamics is captured in both models by the combinatorial Laplacian [11,12,13,14], which accounts for the hops of diffusive (classical or quantum) particles from one node to any of its nearest neighbors. An important characteristics of a few real-world systems, which is not accounted for by the combinatorial Laplacian, is the non-locality of certain processes taken place on discrete structures. For instance, it is nowadays well documented that, in the self-diffusion processes of metallic atoms weakly bounded to metallic surfaces, there are not only nearest-neighbor hops but also long-range ones [15,16,17,18], which are not captured by the combinatorial Laplacian. Similar processes are also found in light-harvesting complexes [19,20], Rydberg atoms [21,22], and other systems [23,24].

In December 2011, Estrada proposed an extension of the combinatorial Laplacian to account for the long-range hops of diffusive particles on graphs [25]. In this work, the concept of graph Laplacian is generalized by introducing the d-path Laplacians, which were then plugged into a generalized diffusion equation to study the influence of long-range jumps on diffusive processes on graphs (see Preliminaries for definitions). A year later, in November 2012, Riascos and Mateos proposed the use of fractional powers of the combinatorial Laplacian to capture nonlocalities in random walks on graphs [26]. Recently, Estrada et al. [27,28] have proved analytically that the generalized diffusion equation with d-path Laplacians produces superdiffusive behavior in 1- and 2-dimensions, in agreement with recent experiments in physics, and have shown some other applications to real-world systems [29]. On the other hand, in 2015, Riascos and Mateos extended their fractional approach to quantum systems by studying quantum transport on simple graphs [30].

The topic of the current work resonates with an important area of research in physics, which is the so-called many-body localization (MBL) under long-range hopping. MBL is a phenomenon occurring in sufficiently disordered quantum systems and represents an interesting and unusual phase of matter [31,32,33]. The existence of MBL under long-range hopping has been widely debated in the physics literature. For instance, many numerical experiments have shown that MBL cannot survive in systems with strong power–law interactions [34,35]. However, other theoretical frameworks used for disordered spin chain has shown the existence of MBL for strong LRI [36]. More recently, Nag and Garg [37] demonstrated that MBL persists in the presence strong long-range hopping. They studied a one-dimensional system of spinless fermions with a deterministic aperiodic potential in the presence of long-range interactions and long-range hopping.

Here, we will consider the use of the d-path Laplacians on a generalized Schrödinger equation on graphs that account for both short and long-range hops of a quantum diffusive particle. We will consider analytically the solution of the generalized Schrödinger equation for certain classes of graphs and will provide some evidence of the differences between this approach and the one using fractional powers of the Laplacian. In particular, we show an example where the fractional Laplacian behaves similarly to the Schrödinger equation without long-range interactions, while the generalized d-path Schrödinger equation displays a qualitatively different phenomena. We finish by mentioning some open problems for the mathematical analysis of the d-path Laplacians in general, and its use in quantum systems in particular.

2. Preliminaries

In this work, we always consider $\mathsf{\Gamma }=(V,E)$ to be an undirected finite or infinite graph with vertices V and edges E. We assume that $\mathsf{\Gamma }$ is connected and locally finite (i.e., each vertex has only finitely many edges emanating from it). Let d be the shortest path distance metric on $\mathsf{\Gamma }$, i.e., $d(v,w)$ is the length of the shortest path from v to w, and let ${\delta }_d\left(v\right)$ be the d-path degree of the vertex v [25,27], i.e.,

$${\delta }_d\left(v\right)=\#\{w\in V:d(v,w)=d\}.$$

(6)

Let ${\ell }^2\left(V\right)$ be the Hilbert space of square-summable functions on V with inner product

$$\begin{array}{c}\hfill ⟨f,g⟩={\displaystyle \sum _{v\in V}}f\left(v\right)\overline{g\left(v\right)},f,g\in {\ell }^2\left(V\right),\end{array}$$

(7)

where $\overline{g\left(v\right)}$ represents the complex conjugate of $g\left(v\right).$ In ${\ell }^2\left(V\right)$, there is a standard orthonormal basis consisting of the vectors $e_v$, $v\in V$, where

$$e_v\left(w\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}w=v,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(8)

For $d\in \mathbb{N}$, the following operator defined in ${\ell }^2\left(V\right)$ is the d-path Laplacian of the graph

$$\left(L_{d}f\right)\left(v\right):={\displaystyle \sum _{w\in V:d(v,w)=d}}\left(f\left(v\right)-f\left(w\right)\right),f\in \mathrm{dom}\left(L_d\right),$$

(9)

which act on the vectors $e_v$ it acts as follows:

$$\left(L_d{e}_v\right)\left(w\right)=\left\{\begin{array}{cc}{\delta }_d\left(v\right)\hfill & \mathrm{if}w=v,\hfill \\ -1\hfill & \mathrm{if}d(v,w)=k,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(10)

For each $d\in \mathbb{N}$, the d-path Laplacian $L_d$ is a self-adjoined operator in ${\ell }^2\left(V\right)$. Furthermore, the operator $L_d$ is bounded if and only if the function ${\delta }_d:V\to \mathbb{N}$ is bounded.

In order to account for a gradual influence of first, second, and thus nearest neighbors, we consider a transformation of the d-path Laplacian operators of the form [25,27,28]

$${\displaystyle \sum _{d=1}^{▵}}{c}_d{L}_d$$

(11)

with $c_d\in \mathbb{C}$ and ▵ being the diameter of the graph. In particular, we will consider here the Mellin-transformed d-Laplacian

$${\mathcal{L}}_s:=L_s{\displaystyle \sum _{d=1}^{▵}}{d}^{-s}{L}_d,$$

(12)

where $s\in {\mathbb{R}}^{+}.$ For infinite graphs if ${\delta }_{d,max}\le C{d}^{\alpha }$ for some $\alpha \ge 0$ and $C>0$, then ${\mathcal{L}}_s$ is a bounded operator for $s\in \mathbb{C}$ with $\mathrm{Re}\left(s\right)>\alpha +1$. If the graph is finite, then there is no restriction on the parameter s.

For a connected graph, the matrix ${\mathcal{L}}_s$ is positive semidefinite with real eigenvalues $0={\mu }_1\left({\mathcal{L}}_s\right)<{\mu }_2\left({\mathcal{L}}_s\right)\le \cdots \le {\mu }_n\left({\mathcal{L}}_s\right)$ and the corresponding orthonormalized eigenvectors ${\overrightarrow{\psi }}_j$, $j=1,\dots ,n$, such that it can be written as ${\mathcal{L}}_R=U\Lambda U^{-1}$, where $\Lambda$ is the diagonal matrix of eigenvalues and the columns of U are the corresponding eigenvectors.

3. Quantum Transport Controlled by d-Path Laplacians

In order to study the quantum transport with long-range hops on graphs, we plug the transformed d-path Laplacian operators into the Schrödinger equation as considered by Hancock et al. [6,7,8,9] on graphs to obtain

$${\displaystyle \frac{\partial \overrightarrow{\Psi }\left(t\right)}{\partial t}}=-i{\mathcal{L}}_s\overrightarrow{\Psi }\left(t\right),\overrightarrow{\Psi }\left(0\right)={\overrightarrow{\Psi }}_0,$$

(13)

where ${\mathcal{L}}_s$ is the Mellin transformed d-path Laplacians as defined in the previous section. The solution of the Schrödinger equation with the transformed d-path Laplacian operators is ${\overrightarrow{exp\left(-it{\mathcal{L}}_s\right)\Psi }}_0$, where

$$exp\left(-it{\mathcal{L}}_s\right)=Uexp\left(-it\Lambda \right)U^{-1}.$$

(14)

For the analysis of quantum transport on a graph, it is common to consider the transition probability between two nodes p and q, ${\pi }_{pq}\left(s,t\right)$, at a given time t and for a given values of the parameter s,

$${\pi }_{pq}\left(s,t\right)={\left|{\displaystyle \sum _{j=1}^n}{e}^{-it{\mu }_j\left({\mathcal{L}}_s\right)}{\psi }_{j,p}{\psi }_{j,q}\right|}^2.$$

(15)

In particular, ${\pi }_{pp}\left(s,t\right)$ is the return probability to the node p–the probability that the particle return to its origin p after a given time t–and $\overline{\pi }\left(s,t\right)=\frac{1}{n}{\sum }_{p=1}^n{\pi }_{pp}\left(s,t\right)$ is the average probability of return. We are going to analyze the evolution of the quantum transport in some simple graphs.

3.1. Quantum Transport on a Ring

We will start the analysis of quantum transport on graphs by considering a ring (cycle graph) without LRI using (4). The cycle graph consists of n nodes all of degree 2. In particular, we will consider the solution $\overrightarrow{\Psi }\left(t\right)=e^{-itL}{\overrightarrow{\Psi }}_0$, where ${\overrightarrow{\Psi }}_0={\left[1,0,\cdots ,0\right]}^T$ due to the equivalence of all nodes in the ring. The following is a result obtained by Riascos and Mateos.

Lemma 1.

(Riascos and Mateos) Let G be a ring (cycle graph) with n nodes. Then, if n is sufficiently large ${\pi }_{pq}\left(t\right)={\left|J_d\left(2t\right)\right|}^2$, where d is the shortest path separation between the two nodes and $J_{\nu }\left(z\right)$ is the corresponding Bessel function of the first kind.

For the sake of simplicity and without any loss of generality hereafter, we will consider a ring graph with an odd number of nodes.

Lemma 2.

Let G be a ring (cycle graph) with an odd number n of nodes and let ${\mathcal{L}}_s$ be the Mellin transformed d-path Laplacian of G with parameter s. Then,

$${\mu }_j\left({\mathcal{L}}_s\right)=2H_s\left(\frac{n-1}{2}\right)-2{\displaystyle \sum _{k=1}^{\frac{n-1}{2}}}{k}^{-s}cos\left(jk\theta \right),$$

(16)

where $H_l\left(k\right)={\sum }_{r=1}^k{r}^{-l}$ are the generalized harmonic numbers and $\theta =2\pi /n$.

Proof. 

For a cycle graph, ${\mathcal{L}}_s$ is a circulant matrix with structure

$${\mathcal{L}}_s=\left(\begin{array}{ccccc}\delta & -1& \cdots & -2^{-s}& -1\\ -1& \delta & -1& & -2^{-s}\\ ⋮& -1& \delta & \ddots & ⋮\\ -2^{-s}& & \ddots & \ddots & -1\\ -1& -2^{-s}& \cdots & -1& \delta \end{array}\right),$$

(17)

where $\delta =1+2^{-s}+\cdots +{\left({\displaystyle \frac{n-1}{2}}\right)}^{-s}+{\left({\displaystyle \frac{n-1}{2}}\right)}^{-s}+\cdots +2^{-s}+1=2{\sum }_{k=1}^{\frac{n-1}{2}}{k}^{-s}=H_s\left(\frac{n-1}{2}\right)$. The eigenvalues of ${\mathcal{L}}_s$ are then

$${\mu }_j=\delta -{\omega }_j-2^{-s}{\omega }_j^2-\cdots -{\left({\displaystyle \frac{n-1}{2}}\right)}^{-s}{\omega }_j^{\left(\frac{n-1}{2}\right)}-\cdots -2^{-s}{\omega }_j^{n-2}-{\omega }_j^{n-1},$$

(18)

where ${\omega }_j=exp\left(\frac{2i\pi j}{n}\right)$, which can be rearranged as

$${\mu }_j=\delta -\left({\omega }_j+{\omega }_j^{n-1}\right)-2^{-s}\left({\omega }_j^2+{\omega }_j^{n-2}\right)-\cdots =\delta -{\displaystyle \sum _{k=1}^{\frac{n-1}{2}}}{k}^{-s}\left({\omega }_j^k+{\omega }_j^{n-k}\right),$$

(19)

from which the result finally arises. □

The trigonometric series of the form

$$C_{\alpha }={\displaystyle \sum _{r=1}^{\infty }}{\displaystyle \frac{cos\left(rx\right)}{r^{\alpha }}}$$

(20)

were studied by Stanković et al. [38] who for the case in which $\alpha =2r$, $r\in \mathbb{N}$ obtained

$$C_{2k}={\displaystyle \frac{{\left(-1\right)}^k\pi x^{2k-1}}{2\left(2k-1\right)!}}+{\displaystyle \sum _{l=0}^k}{\displaystyle \frac{{\left(-1\right)}^l\zeta \left(2k-2l\right)}{\left(2l\right)!}}{x}^{2l},$$

(21)

where $\zeta \left(z\right)$ is the Riemann zeta function. As an example, we are going to study ${\mathcal{L}}_{s=2}$ in order to compare with $\mathcal{L}$.

Theorem 1.

Let G be a ring (cycle graph) with an odd number n of nodes and let${\mathcal{L}}_{s=2}$be the Mellin transformed d-path Laplacian of G with parameter $s=2$. Then, the transition probability between a node labeled as $v=1$ and a node q at a shortest path distance d from $v=1$ is, for sufficiently large n,

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim}}{\pi }_{1d}& \left(t\right)=\left|\frac{1}{n}+\frac{2}{n}{e}^{-2i{H}_2\left(\frac{n-1}{2}\right)}{e}^{-2it\zeta \left(2\right)}\right.\hfill \\ \hfill & \times \frac{1}{\theta \sqrt{t}}\left(\frac{1}{4}-\frac{i}{4}\right)\sqrt{\pi }{e}^{\frac{-i{\left(d-\pi t\right)}^2}{2t}}\left[\mathrm{erfi}\left(\frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(d+\frac{1}{2}\left(n-1\right)t\theta -\pi t\right)}{\sqrt{t}}\right)\right.\hfill \\ \hfill & -\mathrm{erfi}\left(\frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(d+t\left(\pi -\frac{1}{2}\left(n-1\right)\theta \right)\right)}{\sqrt{t}}\right)+\mathrm{erfi}\left(\frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(d+t\left(\pi -\theta \right)\right)}{\sqrt{t}}\right)\hfill \\ \hfill & {\left.\left.-\mathrm{erfi}\left(\frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(d+t\theta -\pi t\right)}{\sqrt{t}}\right)\right]\right|}^2,\hfill \end{array}$$

(22)

where $\mathrm{erfi}\left(z\right)=-i\mathrm{erf}\left(iz\right)$.

Proof. 

Because ${\mathcal{L}}_s$ is circulant, we have that $U=\left[{\overrightarrow{\psi }}_1,{\overrightarrow{\psi }}_2,\cdots ,{\overrightarrow{\psi }}_n\right]$ is given by

$$U=\frac{1}{\sqrt{n}}\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& \omega & {\omega }^2& \cdots & {\omega }^{n-1}\\ 1& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2\left(n-1\right)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{n-1}& {\omega }^{2\left(n-1\right)}& \cdots & {\omega }^{\left(n-1\right)\left(n-1\right)}\end{array}\right)$$

(23)

where $\omega =exp\left(2\pi i/n\right)$. Every nontrivial eigenvalue of ${\mathcal{L}}_s$ has multiplicity two for n odd (when n is even, there is one nontrivial eigenvalue with multiplicity one). Then, we should notice that the eigenvectors ${\overrightarrow{\psi }}_j$ and ${\overrightarrow{\psi }}_{n-j+2}$ are associated with the same eigenvalue ${\mu }_{2j-2}$. For instance, in a ring with seven nodes, the eigenvectors ${\overrightarrow{\psi }}_2$ and ${\overrightarrow{\psi }}_7$ are both associated with ${\mu }_2$; ${\overrightarrow{\psi }}_3$ and ${\overrightarrow{\psi }}_6$ with ${\mu }_4$; ${\overrightarrow{\psi }}_4$ and ${\overrightarrow{\psi }}_5$ with ${\mu }_6$. Therefore, by selecting the node $p=1$ (first row of U), we have for any node at a shortest path distance d from p:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=1}^n}{e}^{-it{\mu }_j\left({\mathcal{L}}_s\right)}{\psi }_{jp}{\psi }_{jq}& =\frac{1}{n}+\frac{1}{n}{\displaystyle \sum _{j=1}^{\frac{n-1}{2}}}\left({\omega }^{jd}+{\omega }^{d\left(n-j\right)}\right)e^{-it{\mu }_{2j}}\hfill \\ \hfill & =\frac{1}{n}+\frac{2}{n}{\displaystyle \sum _{j=1}^{\frac{n-1}{2}}}{e}^{i\pi d}cos\left(d\left(\pi -\theta j\right)\right)e^{-it{\mu }_{2j}},\hfill \end{array}$$

(24)

where $\theta =2\pi /n$. We now consider the case $s=2$ for which the trigonometric series converges to

$$C_{2j}={\displaystyle \sum _{k=1}^{\infty }}{k}^{-2}cos\left(kj\theta \right)={\displaystyle \frac{{\left(j\theta \right)}^2}{4}}-{\displaystyle \frac{\pi j\theta }{2}}+\zeta \left(2\right).$$

(25)

Then, for a sufficiently large ring graph, i.e., $n\to \infty ,$ we have

$${\displaystyle \underset{n\to \infty }{lim}}{\mu }_{2j}\left({\mathcal{L}}_{s=2}\right)=2H_s\left(\frac{n-1}{2}\right)-{\displaystyle \frac{{\left(j\theta \right)}^2}{2}}+\pi j\theta -2\zeta \left(2\right),$$

(26)

Then, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim}}{\displaystyle \sum _{j=1}^n}{e}^{-it{\mu }_j\left({\mathcal{L}}_s\right)}{\psi }_{jp}{\psi }_{jq}& =\frac{1}{n}+\frac{2}{n}{e}^{-2i{H}_2\left(\frac{n-1}{2}\right)}{e}^{-2it\zeta \left(2\right)}\hfill \\ \hfill & \times {\int }_1^{\frac{n-1}{2}}{e}^{\frac{2it{\pi }^2{j}^2}{n^2}}{e}^{-\frac{2it{\pi }^{2}j}{n}}{e}^{i\pi d}cos\left(d\left(\pi -\theta j\right)\right)dj.\hfill \end{array}$$

(27)

After integration, we finally obtain the result. □

Corollary 1.

Let G be a ring (cycle graph) with odd number n of nodes and let${\mathcal{L}}_{s=2}$be the Mellin transformed d-path Laplacian of G with parameter $s=2$. Then, the return probability is$\overline{\pi }=\frac{1}{n}{\left|tr\left(e^{-it{\mathcal{L}}_{s=2}}\right)\right|}^2$, which for a sufficiently large ring is

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim}}\overline{\pi }& \left(t\right)=\left|\frac{1}{n}+\frac{2}{n}{e}^{-2i{H}_2\left(\frac{n-1}{2}\right)}{e}^{-2it\zeta \left(2\right)}\right.\hfill \\ \hfill & {\left.\times {\displaystyle \frac{{\left(-1\right)}^{3/4}n{e}^{-1/2i{\pi }^{2}t}\left(\mathrm{erfi}\left(\frac{1}{n}\left(\frac{1+i}{2}\right)\pi \sqrt{t}\right)+\mathrm{erfi}\left(\frac{1}{n}\left(\frac{1+i}{2}\right)\pi \left(2-n\right)\sqrt{t}\right)\right)}{2\sqrt{2\pi t}}}\right|}^2.\hfill \end{array}$$

(28)

We checked here that the values obtained for $\overline{\pi }$ from Theorem (1) and those from using the function $eig$ implemented in Matlab for the eigenvalues of a matrix are exactly the same for rings of size $n\ge 5001$. Therefore, we now study the evolution of the probability of return in a ring of size $n=100,001$ for the Schrödinger equation using the combinatorial Laplacian as well as the Mellin transformed d-path Laplacian. The results illustrated in Figure 2 illustrate the main difference between the use of the SE without (red dotted line) and with (continuous blue line) long-range hops. Similar results were reported for ring graphs by Riascos and Mateos [30].

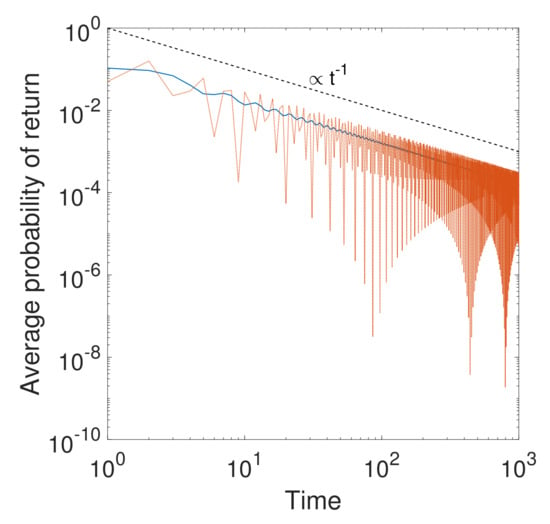
Figure 2. Probability of return for a given vertex of a ring graph with $n=100,001$ nodes using combinatorial Laplacian $\mathcal{L}$ (red dotted line) and using ${\mathcal{L}}_{s=2}$ (blue continuous line). The broken black line indicates the behavior $\overline{\pi }\propto t^{-1}.$

In Figure 3, we illustrate the evolution of ${\pi }_{50,j}\left(s,t\right)$ in a ring graph having 101 nodes for $s=2$ (a) and for $s\to \infty$ (b). The effects of LRI are very clear, in particular the fact that, at very short times, the probability of transition from $v=50$ to the most distant nodes, e.g., nodes labeled as 1 and 101, is much higher when $s=2$ than when there are no LRI effects.

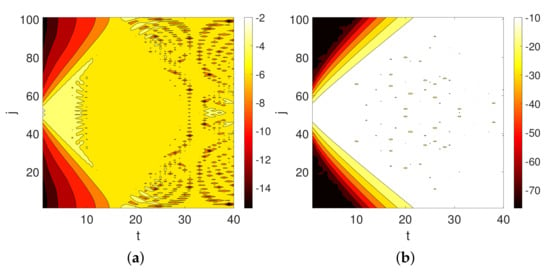
Figure 3. Plot of the transition probability ${\pi }_{50,j}$ for a quantum particle located at $t=0$ at position 51 of a ring having 101 nodes. (a) quantum transport controlled by the Schrödinger equation with d-path Laplacian ${\mathcal{L}}_{s=2}$; (b) quantum transport controlled by the Schrödinger equation without LRI ${\mathcal{L}}_{s\to \infty }$. The values of ${\pi }_{50,j}$ are given in logarithmic scale for better visualization. The colobar corresponds to the transition probability in logarithmic scale.

In Figure 4, we illustrate the evolution of the transition probability for Schrödinger equation without LRI (top panels) and with Mellin transform using $s=2$ (bottom panels).

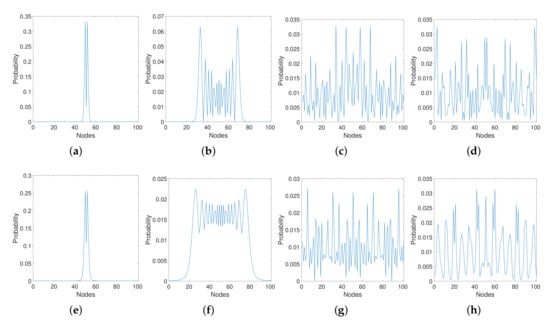
Figure 4. Probability at every node of a ring of 101 nodes using the Schrödinger equation without LRI (a–d) and with Mellin transform using $s=2$ (e–h). The probability at t = 0 is equal to one at the node 51 and zero elsewhere. The plots correspond to times $t=1$ (a,e), 10 (b,f), 100 (c,g), 1000 (g,h).

Although both Figure 3 and Figure 4 are only partial snapshots of the dynamics taking place for the quantum particle in a ring, they allow us to observe some important differences between the consideration of LRI in relation to the dynamics without LRI. In Figure 3, it can be seen that at short times the probability of locating the particle at its origin is significantly higher when there are LRI than when there are not. Even at longer times, e.g., $t=40$, the probability of finding the particle in the dynamics without LRI is almost the same at every node of the ring, while, for the case when there are LRI, this probability is higher around the origin. In Figure 4, there are more snapshots of the dynamics and we can observe part of the oscillations that the probability displays at different times. For instance, at $t=10$, the particle oscillates between nodes 30 and 70 in both dynamics, i.e., with and without LRI. However, when there are no LRI, the probability of finding the particle at certain nodes with label between 30 and 70 is almost zero, and the probabilities of finding the particle at either node 30 or 70 is significantly higher than at any of the rest of the nodes. In the case of the dynamics with LRI, this probability is never close to zero for any node in this interval and almost all the nodes in it have probabilities between 0.01 and 0.025. That is, the particle is trapped in the region between nodes 30 and 70 with almost the same probability of being found at any of these nodes. When the time is bigger, it is more difficult to extract some general observations, but in any case the behavior of both dynamics show significant differences as previously seen in Figure 3.

3.2. Quantum Transport in Complete and Star Graphs

We study here analytically two other classes of graphs, namely the complete and star graphs. The complete graph of n nodes $K_n$ is the graph in which every pair of nodes is connected by an edge. The star graph $S_n$ has one node of degree $n-1$ and $n-1$ nodes of degree one.

Lemma 3.

Let $K_n$ be a complete graph with n vertices. Then, the transition probability is

$${\pi }_{pq}\left(t,s\right)={\displaystyle \frac{{sin}^2\left(nt\right)+{\left(1-cos\left(nt\right)\right)}^2}{n^2}},$$

(29)

and the average probability of return is

$$\overline{\pi }\left(t,s\right)={\pi }_{pp}\left(t,s\right)={\displaystyle \frac{{\left(n-1\right)}^2{sin}^2\left(nt\right)+{\left(\left(n-1\right)cos\left(nt\right)+1\right)}^2}{n^2}}.$$

(30)

Proof. 

The eigenvalues of ${\mathcal{L}}_s$ for the complete graph are ${\mu }_1=0$ with multiplicity one and ${\mu }_j=n$ with multiplicity $n-1.$ Then, because in $K_n$ all vertices are equivalent, we have that $G_{pp}={\left(exp\left(-it{\mathcal{L}}_s\right)\right)}_{pp}={\displaystyle \frac{1}{n}}trexp\left(-it{\tilde{L}}_{M,s}\right)={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{e}^{-it{\mu }_j}$. That is,

$$G_{pp}={\displaystyle \frac{1}{n}}\left(1+\left(n-1\right)e^{-itn}\right).$$

(31)

The eigenvector associated with ${\mu }_1=0$ is ${\overrightarrow{\psi }}_1=n^{-1/2}\overrightarrow{1}$. Then, the term $G_{pq}={\left(exp\left(-it{\mathcal{L}}_s\right)\right)}_{pq}$ is given by

$$G_{pq}={\displaystyle \frac{1}{n}}+e^{-itn}{\displaystyle \sum _{j=2}^n}{\psi }_{jp}{\psi }_{jq}.$$

(32)

Then, because ${\sum }_{j=1}^n{\psi }_{jp}{\psi }_{jq}=0$, we have ${\sum }_{j=2}^n{\psi }_{jp}{\psi }_{jq}=-{\displaystyle \frac{1}{n}}$ and

$$G_{pq}={\displaystyle \frac{1}{n}}\left(1-e^{-itn}\right).$$

(33)

The final result comes from the fact that ${\pi }_{pq}={\left|G_{pq}\right|}^2$. □

Theorem 2.

Let $S_n$ be a star graph with n vertices labeled in such a way that the vertex with degree $n-1$ is labeled as the number 1. Let $p\ne q\ne 1.$ Then, the average probability of return is $\overline{\pi }\left(t,s\right)=\frac{1}{n}\left({\pi }_{11}\left(t,s\right)+\left(n-1\right){\pi }_{pp}\left(t,s\right)\right)$, where

$${\pi }_{11}\left(t,s\right)={\displaystyle \frac{{\left(n-1\right)}^2{sin}^2\left(nt\right)+{\left(\left(n-1\right)cos\left(nt\right)+1\right)}^2}{n^2}},$$

(34)

$$\begin{array}{cc}\hfill {\pi }_{pp}\left(t,s\right)& ={\left({\displaystyle \frac{\left(n-2\right)sin\left(t\left(\left(n-1\right)\left(-2^{-s}\right)-1\right)\right)}{n-1}}-{\displaystyle \frac{sin\left(nt\right)}{n\left(n-1\right)}}\right)}^2\hfill \\ \hfill & +{\left({\displaystyle \frac{\left(n-2\right)cos\left(t\left(\left(n-1\right)\left(-2^{-s}\right)-1\right)\right)}{n-1}}+{\displaystyle \frac{1}{n}}+{\displaystyle \frac{cos\left(nt\right)}{n\left(n-1\right)}}\right)}^2.\hfill \end{array}$$

(35)

In addition, the transition probabilities are

$${\pi }_{1q}\left(t,s\right)={\displaystyle \frac{{sin}^2\left(nt\right)+{\left(1-cos\left(nt\right)\right)}^2}{n^2}},$$

(36)

$$\begin{array}{cc}\hfill {\pi }_{pq}\left(t,s\right)& ={\left(-{\displaystyle \frac{sin\left(t\left(\left(n-1\right)\left(-2^{-s}\right)-1\right)\right)}{n-1}}-{\displaystyle \frac{sin\left(nt\right)}{n\left(n-1\right)}}\right)}^2\hfill \\ \hfill & +{\left({\displaystyle \frac{1}{n}}+{\displaystyle \frac{cos\left(nt\right)}{n\left(n-1\right)}}-{\displaystyle \frac{\left(cost\left(\left(n-1\right)\left(-2^{-s}\right)-1\right)\right)}{n-1}}\right)}^2.\hfill \end{array}$$

(37)

Proof. 

The eigenvalues of ${\tilde{L}}_{M,s}$ for $S_n$ are: ${\mu }_1=0$ with multiplicity one, ${\mu }_2=2^{-s}\left(n-1\right)+1$ with multiplicity $n-2$ and ${\mu }_n=n$ with multiplicity one. It is easy to check that ${\overrightarrow{\psi }}_1=n^{-1/2}\overrightarrow{1}$ and that ${\overrightarrow{\psi }}_n={\left[-\sqrt{{\displaystyle \frac{n-1}{n}}},{\displaystyle \frac{1}{\sqrt{n\left(n-1\right)}}},\cdots ,{\displaystyle \frac{1}{\sqrt{n\left(n-1\right)}}}\right]}^T.$ The communicability function for any pair of vertices can be written as

$$G_{pq}={\displaystyle \frac{1}{n}}+e^{-i\left(2^{-s}\left(n-1\right)+1\right)t}{\displaystyle \sum _{j=2}^{n-1}}{\psi }_{jp}{\psi }_{jq}+e^{-int}{\psi }_{np}{\psi }_{nq}.$$

(38)

Now, because ${\sum }_{j=1}^n{\psi }_{jp}^2=1$, we have that ${\sum }_{j=2}^{n-1}{\psi }_{jp}^2=1-\left({\displaystyle \frac{1}{n}}+{\psi }_{np}^2\right)$. Therefore, if $p=q=1$, we have ${\sum }_{j=2}^{n-1}{\psi }_{jp}^2=1-\left({\displaystyle \frac{1}{n}}+{\displaystyle \frac{n-1}{n}}\right)=0,$ which means that

$$G_{11}={\displaystyle \frac{1+\left(n-1\right)e^{-itn}}{n}}.$$

(39)

If $p=q\ne 1,$ ${\sum }_{j=2}^{n-1}{\psi }_{jp}^2=1-\left({\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{n\left(n-1\right)}}\right)={\displaystyle \frac{n-2}{n-1}},$ such that

$$G_{pp}={\displaystyle \frac{1}{n}}+{\displaystyle \frac{n-2}{n-1}}{e}^{-i\left(2^{-s}\left(n-1\right)+1\right)t}+{\displaystyle \frac{e^{-int}}{n\left(n-1\right)}}.$$

(40)

We also have that ${\sum }_{j=1}^n{\psi }_{jp}{\psi }_{jq}=0$, such that ${\sum }_{j=2}^{n-1}{\psi }_{jp}{\psi }_{jq}=-\left({\displaystyle \frac{1}{n}}+{\psi }_{np}{\psi }_{nq}\right)$. Thus, for the case $p=1$, $q\ne 1$, we obtain ${\sum }_{j=2}^{n-1}{\psi }_{jp}{\psi }_{jq}=-\left({\displaystyle \frac{1}{n}}-\sqrt{{\displaystyle \frac{n-1}{n}}}{\displaystyle \frac{1}{\sqrt{n\left(n-1\right)}}}\right)=-{\displaystyle \frac{1}{n}}$. Therefore,

$$G_{1q}={\displaystyle \frac{1-e^{-itn}}{n}}.$$

(41)

Finally, if $p\ne q\ne 1,$ ${\sum }_{j=2}^{n-1}{\psi }_{jp}{\psi }_{jq}=-\left({\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{n\left(n-1\right)}}\right)={\displaystyle \frac{1}{n-1}},$ such that

$$G_{pq}={\displaystyle \frac{1}{n}}-{\displaystyle \frac{1}{n-1}}{e}^{-i\left(2^{-s}\left(n-1\right)+1\right)t}+{\displaystyle \frac{e^{-int}}{n\left(n-1\right)}}.$$

(42)

The final result comes from the fact that ${\pi }_{pq}={\left|G_{pq}\right|}^2$. □

These results indicate that, for the case of the complete and the star graphs, the wave packet remains constant and does not decay with time as in the case of the ring graph. Indeed, in these graphs, the quantum particle remains located at the initial position at any time. For instance, in Figure 5a, we illustrate the evolution of the return probability of a quantum particle in a complete graph with 100 nodes, $K_{100}.$ It can be seen that the probability always oscillates between 0.96 and 1.0 not showing a decay as the one observed for the case of the ring in Figure 2 in which the probability decays as a power-law. Here, the mean probability is just a horizontal line at probability 0.98. In Figure 5b, we show for the same graph that the probability of finding the particle at the origin is always close to unity (white color in Figure 5), indicating that the particle is always localized at the origin at any time (notice the logarithmic scale in Figure 5).

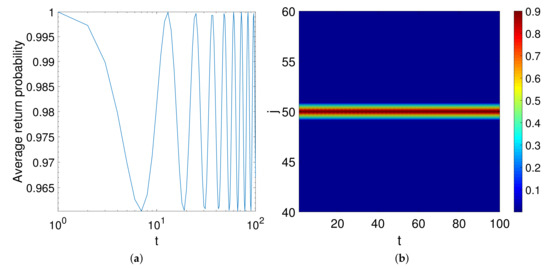
Figure 5. (a) plot of the average return probability versus time in a complete graph $K_{100};$ (b) transition probabilities between the node $v=50$ and the rest of the nodes in the complete graph $K_{100}.$ Only the zoomed region between nodes 40 and 60 is shown for the sake of visibility. The colobar in (b) corresponds to the return probability.

In agreement with these results, a quantum particle located in a region between two cliques oscillates among the nodes in that region without visiting the nodes of the cliques. For instance, in a barbell graph (see [29] for results using the classical diffusion equation), i.e., a graph consisting of two cliques separated by a path, if the particle is located at node of the path, it gets trapped in the nodes of the path without visiting the two cliques (see Figure 6).

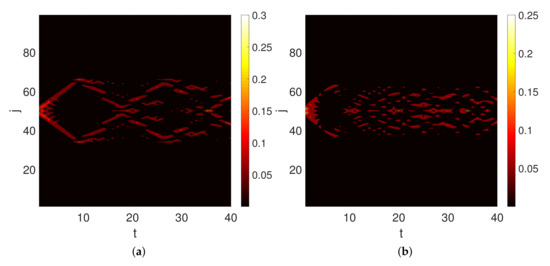
Figure 6. Plot of the transition probability ${\pi }_{50,j}$ for a quantum particle located at $t=0$ at position $v=50$ of a barbell graph consisting of two cliques of 33 nodes separated by a path of 33 nodes (a) without LRI (b) and with ${\mathcal{L}}_{s=2}$. The central region consisting of nodes 34–66 is formed by the path. The colobars correspond to the transition probability.

4. d-Path Laplacians versus Fractional Graph Laplacian

We are not interested here in a deep comparison between the use of the d-path Laplacians and that of the fractional graph Laplacian in the Schrödinger equation. However, we would like to make some remarks about some important differences which may guide the reader to select between one or the other for the studies they conduct. First, we should remark that the “fractional” graph Laplacian corresponds to the fractional powers of the combinatorial Laplacian, which can be defined by the following integral (see [39]):

$$L^{1/p}={\displaystyle \frac{psin\left(\pi /p\right)}{\pi }}{\int }_0^{\infty }{\left(t^{p}I+L\right)}^{-1}dt.$$

(43)

Then, because the combinatorial graph Laplacian is positive semidefinite, we have the following result about the existence of $L^{1/p}$ [39].

Theorem 3.

Let $G=\left(V,E\right)$ be a simple graph. Then, because L has no eigenvalues in ${\mathbb{R}}^{-}$, there is a unique pth root of $L.$ In addition, because L is real, then $L^{1/p}$ is real.

Obviously, ${\mathcal{L}}_s$ always exists for any connected graph. Another similarity between both approaches is that $L^{\gamma =1}$ and ${\displaystyle \underset{s\to \infty }{lim}}{\mathcal{L}}_s$ are both the same, i.e., they are equal to L. However, there is an important difference between these two concepts when we consider the limits of the coefficients $\gamma$ and s to zero: ${\displaystyle \underset{\gamma \to 0}{lim}}{L}^{\gamma }=I$ and ${\displaystyle \underset{s\to 0}{lim}}{\mathcal{L}}_s=nI-E$, where E is the all-ones matrix of order n and I the identity matrix of order n. That is, while ${\displaystyle \underset{\gamma \to 0}{lim}}{L}^{\gamma }$ does not represent a Laplacian matrix, ${\displaystyle \underset{s\to 0}{lim}}{\mathcal{L}}_s$ corresponds to the Laplacian matrix of the complete graph $K_n$. Conceptually, this is also important because ${\displaystyle \underset{\gamma \to 0}{lim}}{L}^{\gamma }$ is telling us that, in this limit, there are no dynamics between the nodes of the graph, while ${\displaystyle \underset{s\to 0}{lim}}{\mathcal{L}}_s$ is telling us that there is a dynamics between every pair of nodes, which is the real limit of the strongest possible LRI. This is well described by the following result.

Lemma 4.

Let $G=\left(V,E\right)$ be a simple graph and let L and ${\mathcal{L}}_s$ be the combinatorial Laplacian and the Mellin transformed d-path Laplacian with parameter s. Then,

$${\displaystyle \underset{\gamma \to 0}{lim}}exp\left(-it{L}^{\gamma }\right)=e^{-it}I,$$

(44)

and

$${\displaystyle \underset{s\to 0}{lim}}exp\left(-it{\mathcal{L}}_s\right)=\left({\displaystyle \frac{1-e^{-itn}}{n}}\right)E+e^{-itn}I,$$

(45)

where n is the number of nodes, E is the all-ones matrix of order n and I the identity matrix of order n.

These differences are not only clear at this limit but also when we use both approaches for studying quantum transport in certain simple graphs. For instance, in Figure 7a, we illustrate a simple graph consisting of a long path with a “barrier” in the middle, consisting of a star subgraph. If we locate a quantum particle at the position labeled as one, which is one of the endpoints of the long path, it gets trapped in the branch of the tree consisting of nodes 1–8 when there is no LRI in the Schrödinger equation (see Figure 7b). However, the use of the d-path Laplacian in the Schrödinger equation makes the particle hop over the barrier and visiting the nodes in the other branch of the tree (Figure 7c). It is remarkable that this effect is not observed when the fractional Laplacian $L^{\gamma }$ is used, which then behaves like the Schrödinger equation without LRI. We explored different values of $0<\gamma <1$ and in no case did we observe trans-barrier hopping (see Figure 7d for the case $\gamma =0.25$). This is a clear evidence of the qualitatively, even conceptually, new phenomena that can emerge from the consideration of LRI effects accounted for by the d-path Laplacian on graphs.

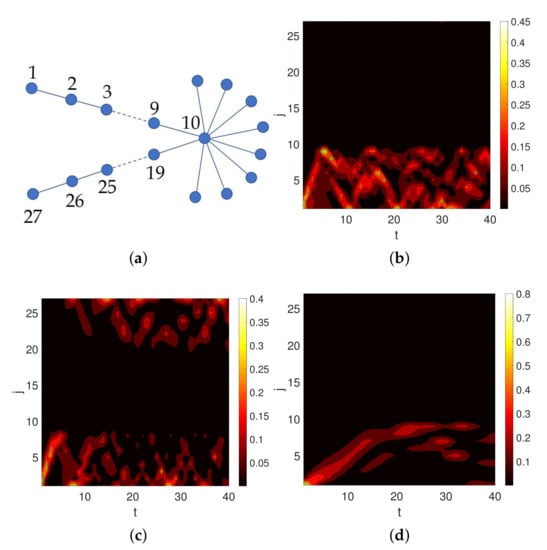
Figure 7. Plot of the transition probability ${\pi }_{1,j}$ for a quantum particle located at $t=0$ at position $v=1$ of the tree illustrated in (a) without LRI (b), with ${\mathcal{L}}_{s=2}$ (c) and with $L^{\gamma =0.25}$ (d). The colobar corresponds to the transition probability.

Finally, we should remark the fact that the use of fractional powers of a matrix/operator is limited to the case in which it has no eigenvalues in ${\mathbb{R}}^{-}.$ This situation limits its use to other important graph matrices/operators such as the adjacency and the incidence matrix/operator. The use of d-path matrices/operators are easily extended to those cases as it has been shown in the recent literature [40,41]. Then, quantum mechanical models such as the tight-binding model [42], which is based on the adjacency operators on graphs, can be extended to consider LRI through the use of transformed d-path adjacency matrices/operators. In a similar way, quantum synchronization systems, such as the quantum Kuramoto models [43,44], can also be extended in similar ways by using transformed d-path incidence matrices/operators.

5. Conclusions and Future Outlook

We have defined a Schrödinger equation with long-range interactions via the use of the transformed d-path Laplacian matrix. In a similar way as we have previously studied for the diffusion equation, the d-path Schrödinger equation can be considered for locally finite infinite graphs. We reported here analytical expressions for the transition and return probabilities of a quantum particle at the nodes of a ring graph. We show that the average return probability in ring graphs decays as a power law with time when LRI is present. In contrast, we prove analytically that the transition and return probabilities on a complete and start graphs oscillate around a constant value. Therefore, we inferred that in a barbell graph the quantum particle get trapped and oscillates across the nodes of the path without visiting the nodes of the cliques. When compared with the fractional powers of the Laplacian previously used in the literature, the d-path Laplacian operators produce the emergence of new phenomena related to the location of the wave packet in graphs with barriers, which are not observed neither for the Schrödinger equation without LRI nor for the one using fractional powers of the Laplacian.

The study of the d-path Laplacian formalism in both classical and quantum mechanics is still in its infancy. Therefore, there are still many open questions. They are important for a better understanding of the mathematical properties of the transformed d-path Laplacian matrices/operators and their applications. In no particular order and in a non-exhaustive manner we mention here: (i) the analysis of the spectral properties of the transformed d-path Laplacian matrices/operators for certain families of simple and random graphs; (ii) the detailed analysis of the similarities and differences between the (classical and quantum) diffusion equations using transformed d-path Laplacians versus those using fractional powers of the combinatorial Laplacian; (iii) the analysis of quantum transport on graphs with the d-path Schrödinger equation based on moments of the wave packet and on the temporal autocorrelation function [45,46], among others. In addition, due to the easy computational implementation of the current formalism, it would be desirable to see a wider range of applications in different real-world scenarios to gain more insights about its scope of applications.